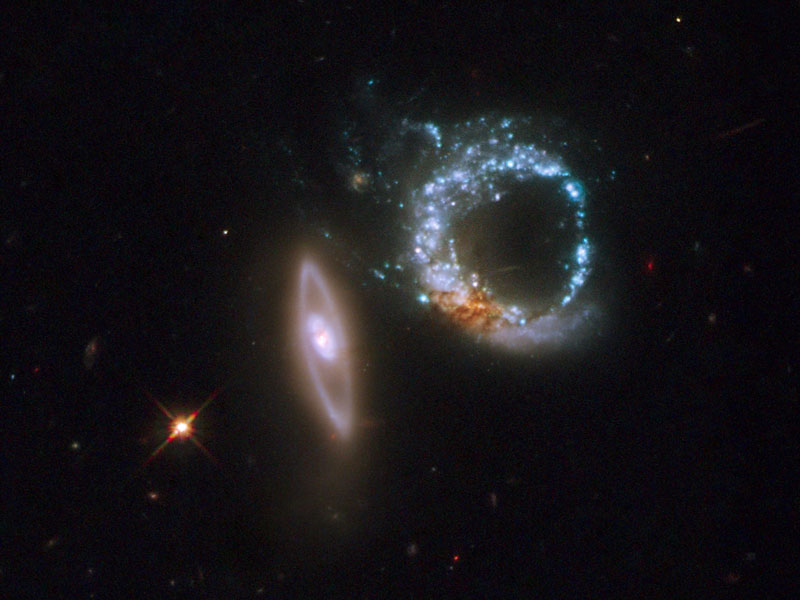Lo revolucionario de la Teoría de Copérnico (aunque lo mismo dijo Aristarco de Samos muchos años antes que él), residía en la afirmación de que la propia Tierra se movía y, si nuestro planeta se movía alrededor del Sol, entonces, era el Sol el Centro del Universo y no la Tierra.
Del mismo modo que Colón de fió de Ptolomeo y de otros textos tradicionales cuyas sugerencias, pensaban él, no habían sido llevadas a la práctica con la suficiente energía, también Cop´çernico halló referencias en las teroías antiguas. En primer lugar en el pitagorismo, la ionfluyente doctrina de los seguidores de Pitágoras de Samos, filósofo y matemático griego del siglo VI a. C.
No nos ha llegado ninguna obra del propio Pitágoras, pero las ideas que le atribuyen sus seguidores están entre las más influyentes de la histortia moderna. De hecho, no podemos pasear por las grandes calles de las importantes ciudades del mundo sin contemplar, la esencia de su teorema, plasma en los mejores y más grandiosos edificios.



Sí, del teorema de Pitágoras tendríamos mucho que decir y, desde luego, aunque se saber que antes que él otros matemáticos ya lo sacaron a la luz, lo cierto es que, en su escuela se le dio la imagen que hoy de él tenemos y, el aprovechamiento de que este teorema hizo la Humanidad, tenemos las puebas plasmadas por todas partes.
El conocimiento puro, sostenían los pitagóricos, era la purificación (catharsis) del Alma. Esto significaba elevarse por encima de los datos procedentes de los sentidos humanos. La realidad puro y esencial, decían, se hallaba solamente el el reino de los números. La simple y maravilloso proporción de los números explicaría la armonía musical que que constituía la belleza del oído. Por esta razón introdujeron la terminología musical de la octava, la quinta y la cuarta, expresadas como 2:1, 3:1, y 4:3.
Para la Astronomía la adoración pitagórica de los números llevaba consigo un mensaje arrollador. Aristóteles lo resumía sucintamente en la Matafísica:

Dicen que las propias cosas son números, y no sitían los objetos de las matemáticas entre las formas y las cosas sensibles. Pues de nuevo, percibieron que las modificaciones y las relaciones de las escalas musicales podían expresarse con números; y, siendo así, parecía que todas las demás cosas por su naturaleza tomaban los números como modelo, y parecía que los números eran las primeras cosas de toda la naturaleza, supinían que los elementos de los números eran los elementos de todas las cosas y que todo el cielo era una escala musical y un número… y recogieron la distribución del cielo y la acomodaron a su esquema; y, si en elagún lugar había una laguna, añadieron inmediatamente lo necesario para que toda su propia teoría fuera coherente.
(En realidad, hacúan la misma cosa que hoy hacen los físicos con sus teorías que, cuando no saben cuadrarla, lo hacen con bosones de Higgs o los cosmólogos con Materia Oscura). Claro que los pitágóricosm en la época de Copérnico, aún creían ciegamente que la única manera, la única forma, de llegar a la verdad era a través de las matemáticas que, en definitiva, era el mejor lenguaje para expresar la ciencia y la naturaleza del “mundo” (del universo).

En la llamada “Escuela de Alejandría”, el neoplatonismo tiene sus últimos representantes en el círculo que Olimpiodoro fundó en Alejandría en el siglo IV, y que continuó con varios autores de no mucho relieve, entre otros: la filósofa Hipatia, Hierocles, Filipón (ca. 490-530) —comentador de Aristóteles convertido luego al cristianismo— y por último, ya en el siglo VII, otro comentador de Aristóteles, Esteban de Alejandría.
También los neoplatónicos basaron toda su visión del mundo en unas matemáticas ideales. De hecho, se dice que sobre la puerta de entrada a la Academia de Platón habia un letrero que decía: “Que nadie vacío de Geometría entre por mis puertas”. Los números ofrecían la mejor visión humana de dios y del mundo-alma. Proclo (410?-485 d.C.), el último y más grande de los exponentes griegos del neoplatonismo, observó que “… todas las especies matemáticas… tienen una subsistencia primaria en el alma, de modo que antes que los números sensibles, se encuentran en los rincones más escondidos de ésta los números automotrices… proporciones ideales de armonías previas a sonidos concordantes; y de las órbitas invisibles, anteriores a los cuerpos que giran en círculo… debemos seguir la doctrina de Timeo, que fija el origen y completa la estructura del alma en las formas matemáticas y basa en su naturaleza las causas de todo lo que existe.”

La filósofa Hipatia Aprendió también sobre la historia de las diferentes religiones que se conocían en aquel entonces, sobre oratoria, sobre el pensamiento de los filósofos y sobre los principios de la enseñanza. Viajó a Atenas y a Roma siempre con el mismo afán de aprender y de enseñar. La casa de Hipatia se convirtió en un lugar de enseñanza donde acudían estudiantes de todas partes del mundo conocido, atraídos por su fama.
Uno de sus alumnos fue Sinesio de Cirene, obispo de Ptolemaida (en Fenicia), rico y con mucho poder. Este personaje dejó escrita mucha información sobre Hipatia, su maestra. Por medio de él pueden llegar a conocerse los libros que ella escribió para la enseñanza, aunque ninguno ha llegado a nuestros días. Otro alumno llamado Hesiquio el hebreo escribió unas obras que se conservan, en las que también hace una descripción sobre las actividades de Hipatia y asegura que los magistrados acudían a ella para consultarle sobre asuntos de la administración.
Dice también que fue una persona muy influyente en el aspecto político. También se interesaba por la mecánica y ponía en práctica la tecnología. Se sabe que inventó un aparato para destilar el agua, un hidrómetro graduado para medir la densidad de los líquidos y un artefacto para medir el nivel del agua.

El neoplatonismo que surgío en el Renacimiento -época en la que nació Copérnico- emprendió la batalla contra el espíritu frío y prosaico de los escolásticos. El enfoque aristotélico, caracterizado por un obstenido sentido común, se había visto reforzado por el descubrimiento de nuevos textos de Aristóteles en el siglo XII. Los neoplatónicos esgrimían contra esto las armas de la poesía y la libre imaginación.
Claro que todas aquellas nuevas perspectivas de mirar el “mundo” y lo que más tarde se veía por los telescopios y microscopios, llevaron al John Donne, poeta inglés, a decir de las ideas copernicanas, “pueden ser ciertas” y, se están “introduciendo furtivamente en la mente de los hombres” y, espresa su enorme desazón de esta manera:
John Donne escribía cosas como éstas:
Y la nueva filosofía lo pone todo en duda,
El elemento del fuego se ha apagado; el Sol se ha perdido, y la tierra, y el juicio de los hombres,
Ya no puede guiarlos en su búsqueda.
Y los hombres confiesan libremente que el mundo ya no es lo que era,
Cuando en los planetas y en el firmamento
Ellos buscan tanta novedad, y luego ven que esto
Se dewsmenuza otra vez en sus átomos.
Todo está en pedazos, toda coherencia ha desaparecido;
Todo es simple suministro, y es todo relación…
Y en estas constelaciones se alzan entonces
Nuevas estrellas, y las antiguas desaparecen ante nuestros ojos.
Durante 1619, en un viaje que Donne hizo por el continente europeo, se tomó la molestia de ir a ver a Kepler a la remota población austríaca de Linz. También John Milton se sentía desconcertado por todos aquellos cambios de la nueva cosmología que venían a desterrar pensamientos hondamente asentados en la mente de los humanos.

La más antigua de las Ciencias, alrededor de la cual, podríamos hacer una lista de nombres que sería interminable de todos aquellas y aquellas que, de aluna manera, han contribuído al saber del mundo, de la Naturaleza del Universo y de los objetos que lo pueblan.
La capacidad del ojo desnudo para observar e interpretar el cielo llegó al límite de sus posibilidades de la mano de un incansable astrónomo danés nacido sólo tres años después de la muerte de Copérnico: Tycho Brahe. Detrás de él llegó el gran Kepler que retomó los trabajos de las observaciones de Tycho y, a partir de ellos, pudo hacer formulaciones que, todqavía hoy en día causan admiración.
El salto de la observación a simple vista a la visión con la ayuda de instrumentos habría de ser uno de los grandes avances de la historia de la Humanidad. Pero el telescopio (como las gafas o el microscopio) no se inventó de forma deliberada, sino que, casualmente, un viejo cristalero que fabricaba piezas redondas para ventanas emplomadas de iglesias, probó a mirar a tavés de uno de aquellos discos y, para su delite y asombro, descubrió que podía ver mucho mejor. Haciendo pruebas distintas, según la elaboración, servía para la cercanía, en la que se descubrían minúsculos objetos y, en la lejanía, se podían ver, como si a dos metros estuvieran situados, objetos lejanos.
Desde entonces, mucho ha llovido sobre la Tierra, y, todos sabemos de los vances logrados en sofisticados intrumentos que nos han permitido llegar a captar, imágenes de ensueño que han fascinado nuestra imaginación. Lo que hemos visto, ha traspasado todo lo imaginado y mucho más. Es cierto, siempre la realidad ha ha ido más allá de la ficción.
De la historia de Galileo hemos hablado aquí muchas veces y conocemos sus peripecias y sus problemas con la Iglesia. Él se pudo salvar, lo que muchos otros, no pudieron. Algunos dieron su vida por decir públicamente que había muchos mundos que, como el nuestro, estarían llenos de criaturas llenas de vida.
Así, el telecopio y el microscopio fueron ambos producto de la misma era, pero mientras que Copérnico y Galileo se han convertido en héroes populares, en los profestas de la modernidad, Hooke y Leeuwenhoek, sus equivalentes el mundo microscópico, han quedado relegados al panteón de las ciencias especializadas.
Al igual que el Telescopio había unido la Tierra y los cuerpos celestes más distantes en un solo esquema de pensamiento, las imágenes del microscópio revelaban un mundo minúsculo que se asemejaba de modo sorprendente al que se veía diariamente a gran escala. En Historias Insectorum Generalis, Jan Swammerdam desmostraba que los insectos, como los animales “superiores” poseían una intrincada anatomía y no se reproducían por generación espontánea. En el microscopio vio que los insectos se desarrollaban igual que el hombre, por epigénesis, o desarrollo gradual de un órgano después de otro. Con todo, sobrevivió la creencia en otras formas de generación espontánea, hasta que, en el siglo XIX, Luis Pasteur realizó sus brillantes experimentos.
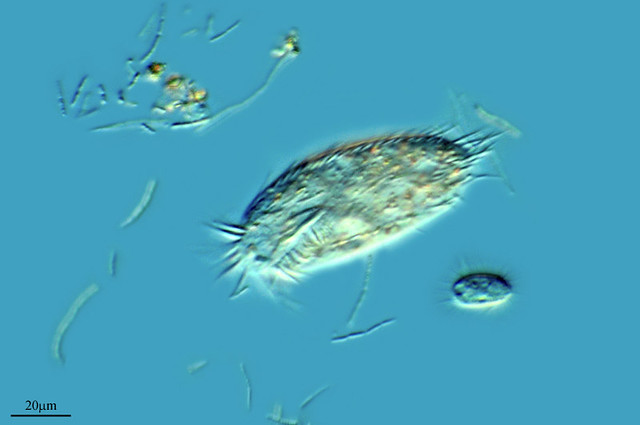
Leeuwenhoek, en relación al microscopio decía: “Con este apartato he vistos bichitos que parecían tan grandes como corderos, he descubiertos que están cubiertos de pelos y, algunos, hasta tienen uñas”. Antoni van Leeuwenhoek fue con su microscopio el primer promotor de esta nueva ciencia de la exploración de otros mundos que resultaron estar en este. Sería bonito relatar aquí la historia del personaje pero, no tenemos el espacio necesario para ello.
Os contaré que, en una ocasión, disponiendo de un microscópico, comenzó a buscar algo que hace con él. En septiembre de 1674, por pura curiosidad, llenó un frasco de cristal de un agua turbia y verdosa, que la gente de campo llamaba “rocío de miel”, procedente de un lago pantanoso situado a tres kilómetros de Delft, y bajo la mente de aumento descubrió “muchísimos animáculos diminutos”. A continuación dirigió su microscopio hacia una gota de agua de pimienta, infusión a base de pimienta negra utilizada en sus observaciones:
“Entonces vi con claridad que se trataba de pequeñas anguilas o lombrices apiñadas y culebreando, igual que si viera en un charco lleno de pequeñas anguilas y agua, todas retorciéndose por encima de otras, y parecía que toda el agua estaba vivía y llena de estos múltiples animáculos. Para mí, ésta fue, entre todas las maravillas que he descubierto en la naturaleza, la más maravillosa de todas; y he de decir, en lo que a mí concierne, que no se ha presentado ante mis ojos ninguna visión más agradable que esos miles de criaturas vivientes, todas vivas en un diminuta gota de agua, moviéndose unas junto a otras, y cada una de ellas con su propio movimiento…”

En otro ámbito del saber, podríamos hablar de Galeno, aquel médico que dejó una inmensa obra y legó conocimientos a los europeos que estuvieron en vigor durante más de mil quinientos años, él, un médico de la Grecia antigüa, les dijo a los que vinieron detrás cómo era el cuerpo humano y le habló de sus funciones, miembro por miembro explicándoles para que servían cada uno de ellos. Se trasladó a Roma y fue el médico de Marco Aurelio y de su hijo Cómodo. En su Pérgamo natal fue médico de Gladiadores.
Su prolija obra fue bien conservada y , cuando el mundo árabe asimiló la ciencia de los griegos, tradujeron la obra de Galeno y le convirtieron en su modelo de médico. Más tarde, sus libros se contaminaron y se combinaron con textos árabes. Finalmente, sus enseñanazas fueron superadas por Raziz, Avicena, Averroes y Maimónides, que se atrevieron a escribir sus propias críticas a la medicina de Galeno.

Fuente de la Imagen: Astronomy Picture Of The Day de la NASA.
Hoy sabemos algunas cosas que hemos podido ir descubriendo a lo largo de los siglos, mientras que el tiempo transcurre inexorable, lqa curiosidad humana, ha posibilidato “saber” sobre dos mundos que, aunque parecen antagónicos, en realidad, son parte de lo mismo: El Universo infinito que todo lo contiene: La materia, las fuerzas que con ella interaccionan y el espaciotiempo y, en todos esos ingredientes, están inmersos los diferentes y maravillosos (a veces extraños) objetos que, con nuestros ingenios podemos ver.
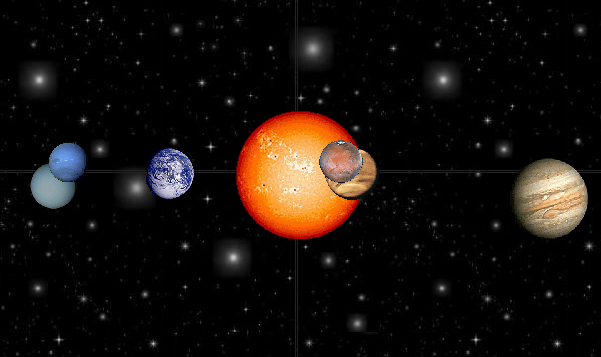
Sabemos que, a partir de una estrella que implisionó para sembrar el espacio interestelar con una inmenso y hermosqa nebulosa como la que arriba contemplamos, pudo surgir nuestro Sistema Solar. El Sol y los mundos que lo forman son sólo una mínima fracción, una pequña parte de la inmensa Galaxia que los acoge. En aquella nube, ya estaban presentes los átomos que, más tarde, formaron la Tierra con sus montañas y Océanos, sus volvanes y sus valles, sus lagos y ríos y, de todo aquello, pudimos surgir nosotros para que, ahora, podamos hablar de todo lo que aquí relatamos que es, una ínfima parte de lo que, la Humanidad, ha hecho desde que llegó a este mundo.
emilio silvera


















 Totales: 77.774.718
Totales: 77.774.718 Conectados: 16
Conectados: 16 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en
Clasificado en