Nov
20
¡Cuántas maravillas! Y, nuestra Mente, entre ellas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Las prodigiosas ideas ~
Clasificado en Las prodigiosas ideas ~
 Comments (0)
Comments (0)



El paso del tiempo lo cambia todo en todos los ámbitos y niveles


¿Onda o partícula? ¡Ambas a la vez! ¿Cómo es eso?


Radiantes estrellas nuevas que brillan con la luz de la “juventud” en ultravioleta de fotones


La importancia de la Simetría en la Naturaleza






La simetría en la Naturaleza está por todas partes
No sería descabellado decir que las simetrías que vemos a nuestro alrededor, desde un arco iris a las flores y a los cristales, pueden considerarse en última instancia como manifestaciones de fragmentos de la teoría decadimensional original. Riemann y Einstein habían confiado en llegar a una comprensión geométrica de por qué las fuerzas pueden determinar el movimiento y la naturaleza de la materia. Por ejemplo, la fuerza de Gravedad generada por la presencia de la materia, determina la geometría del espacio-tiempo.
Dado el enorme poder de sus simetrías, no es sorprendente que la teoría de supercuerdas sea radicalmente diferente de cualquier otro de física. De hecho, fue descubierta casi por casualidad. Muchos físicos han comentado que si este accidente fortuito no hubiese ocurrido, entonces la teoría no se hubiese descubierto hasta bien entrado el siglo XXI. Esto es así porque supone una neta desviación de todas las ideas ensayadas en este siglo. No es una extensión natural de tendencias y teorías populares en este siglo que ha pasado; permanece aparte.

11 de mayo de 1916 – Albert Einstein presenta su Teoría de la Relatividad General que nos trajo una nueva Cosmología.
Por el contrario, la teoría de la relatividad general de Einstein tuvo una evolución normal y lógica. En primer lugar, su autor, postula el principio de equivalencia. Luego reformuló principio físico en las matemáticas de una teoría de campos de la gravitación basada en los campos de Faraday y en el tensor métrico de Riemann. Más tarde llegaron las “soluciones clásicas”, tales el agujero negro y el Big Bang. Finalmente, la última etapa es el intento actual de formular una teoría cuántica de la gravedad. Por lo tanto, la relatividad general siguió una progresión lógica, un principio físico a una teoría cuántica.

Geometría → teoría de campos → teoría clásica → teoría cuántica
Contrariamente, la teoría de supercuerdas ha estado evolucionando hacia atrás su descubrimiento accidental en 1.968. Esta es la razón de que nos parezca extraña y poco familiar, estamos aún buscando un principio físico subyacente, la contrapartida del principio de equivalencia de Einstein.
La teoría nació casi por casualidad en 1.968 cuando dos jóvenes físicos teóricos, Gabriel Veneziano y Mahiko Suzuki, estaban hojeando independientemente libros de matemáticas. Figúrense ustedes que estaban buscando funciones matemáticas que describieran las interacciones de partículas fuertemente interactivas. Mientras estudiaban en el CERN, el Centro Europeo de Física Teórica en Ginebra, Suiza, tropezaron independientemente con la función beta de Euler, una función matemática desarrollada en el S. XIX por el matemático Leonhard Euler. Se quedaron sorprendidos al que la función beta de Euler ajustaba casi todas las propiedades requeridas para describir interacciones fuertes de partículas elementales.
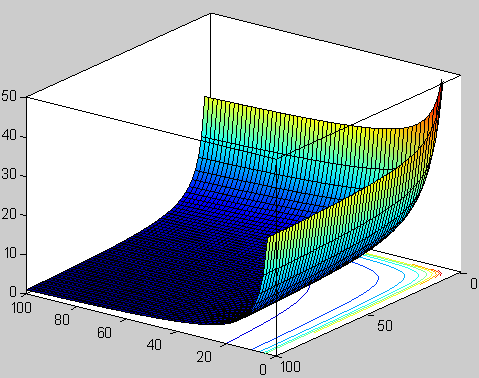
Función beta. Representación de la función valores reales positivos de x e y
Según he leído, durante un almuerzo en el Lawrence Berkeley Laboratory en California, con una espectacular vista del Sol brillando sobre el puerto de San Francisco, Suzuki le explicó a Michio Kaku mientras almorzaban la excitación de , prácticamente por casualidad, un resultado parcialmente importante. No se suponía que la física se pudiera hacer de ese modo casual.
Tras el descubrimiento, Suzuki, muy excitado, mostró el hallazgo a un físico veterano del CERN. Tras oír a Suzuki, el físico veterano no se impresionó. De hecho le dijo a Suzuki que otro físico joven (Veneziano) había descubierto la misma función unas semanas antes. Disuadió a Suzuki de publicar su resultado. Hoy, esta función beta se conoce con el de modelo Veneziano, que ha inspirado miles de artículos de investigación iniciando una importante escuela de física y actualmente pretende unificar todas las leyes de la física.

Gabriele Veneziano Mahiko Suzuki
En 1.970, el Modelo de Veneziano-Suzuki (que contenía un misterio), fue parcialmente explicado cuando Yoichiro Nambu, de la Universidad de Chicago, y Tetsuo Goto, de la Nihon University, descubrieron que una cuerda vibrante yace detrás de sus maravillosas propiedades. Así que, como la teoría de cuerdas fue descubierta atrás y por casualidad, los físicos aún no conocen el principio físico que subyace en la teoría de cuerdas vibrantes y sus maravillosas propiedades. El último paso en la evolución de la teoría de cuerdas (y el primer paso en la evolución de la relatividad general) aún está pendiente de que alguien sea capaz de darlo.
Así, Witten dice:
“Los seres humanos en el planeta tierra nunca dispusieron del marco conceptual que les llevara a concebir la teoría de supercuerdas de manera intencionada, surgió por razones del azar, por un feliz accidente. Por sus propios méritos, los físicos c del siglo XX no deberían haber tenido el privilegio de estudiar esta teoría muy avanzada a su tiempo y a su conocimiento. No tenían (ni tenemos mismo) los conocimientos y los prerrequisitos necesarios para desarrollar dicha teoría, no tenemos los conceptos correctos y necesarios.”
Actualmente, como ha quedado dicho en este mismo , Edwar Witten es el físico teórico que, al frente de un equipo de físicos de Princeton, lleva la bandera de la teoría de supercuerdas con aportaciones muy importantes en el desarrollo de la misma. De todas las maneras, aunque los resultados y avances son prometedores, el camino por andar es largo y la teoría de supercuerdas en su conjunto es un edificio con muchas puertas cerradas de las que no tenemos las llaves acceder a su interior y mirar lo que allí nos aguarda.


Ni con una gran colección de llaves podríamos abrir la puerta que nos lleve a la Teoría cuántica de la gravedad que, según dicen, subyace en la Teoría M, la más moderna versión de la cuerdas expuesta por E. Witten y que, según contaron los que estuvieron presentes en su presentación, Witten les introdujo en un “universo” fascinante de inmensa belleza que, sin embargo, no puede ser verificado por el experimento.
El problema está en que nadie es lo suficientemente inteligente para resolver la teoría de campos de cuerdas o cualquier otro enfoque no perturbativo de teoría. Se requieren técnicas que están actualmente más allá de nuestras capacidades. Para encontrar la solución deben ser empleadas técnicas no perturbativas, que son terriblemente difíciles. Puesto que el 99 por ciento de lo que conocemos sobre física de altas energías se basa en la teoría de perturbaciones, esto significa que estamos totalmente perdidos a la hora de encontrar la verdadera solución de la teoría.
¿Por qué diez. once y veintiséis dimensiones? ¿Es acaso la teoría del caos?
Uno de los secretos más profundos de la teoría de cuerdas, que aún no es bien comprendido, es por qué está definida sólo en diez, once y veintiséis dimensiones. Si calculamos cómo se rompen y se vuelven a juntar las cuerdas en el espacio N-dimensional, constantemente descubrimos que pululan términos absurdos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos indeseados aparecen multiplicados por (N-10). Por consiguiente, para hacer que desaparezcan estas anomalías, no tenemos otra elección cuántica que fijar N = 10. La teoría de cuerdas, de hecho, es la única teoría cuántica conocida que exige completamente que la dimensión del espacio-tiempo esté fijada en un único, el diez.
¿Quieren que veamos lo que no existe?
Por desgracia, los teóricos de cuerdas están, por el momento, completamente perdidos explicar por qué se discriminan las diez dimensiones. La respuesta está en las profundidades de las matemáticas, en un área denominada funciones modulares.
Al manipular los diagramas de lazos1 de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el 10 aparecen en los lugares más extraños. Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del este. Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro universo actual.

Cuando nos asomamos a la Teoría de cuerdas, entramos en un “mundo” lleno de sombras en los que podemos ver brillar, a lo lejos, un resplandor cegador. Todos los físicos coinciden en el hecho de que es una teoría muy prometedora y de la que parece se podrán obtener buenos rendimientos en el futuro pero, de , es imposible verificarla.
Es esencialmente la función gamma incompleta
El misterio de las funciones modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y Riemann antes que él, trabajó en total aislamiento en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.
Dispersas oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre las más extrañas jamás encontradas en matemáticas. Ellas reaparecen en las ramas más distantes e inconexas de las matemáticas. Una función que aparece una y otra vez en la teoría de las funciones modulares se denomina (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. extraña función contiene un término elevado a la potencia veinticuatro.

La magia esconde una realidad
El 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente donde menos se esperan por razones que nadie entiende. Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas. En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio-tiempo debe tener 24 + 2 = 26 dimensiones espacio-temporales.

Comprender este misterioso factor de dos (que añaden los físicos), consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada puede vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista Aµ cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell. Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones. Sin embargo, dos de estos modos vibracionales pueden ser eliminados rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.

“En matemática, la función theta de Ramanujan generaliza la forma de las funciones theta de Jacobi, a la vez que conserva sus propiedades generales. En particular, el producto triple de Jacobi se puede escribir elegantemente en términos de la función theta de Ramanujan. La función toma nombre de Srinivasa Ramanujan, y fue su última gran contribución a las matemáticas.”

Como un revoltijo de hilos entrecruzados que son difíciles de seguir, así son las matemáticas de la teoría de cuerdas.
Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio-tiempo sea diez.
En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “no lo sé”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una cuánticamente autoconsistente), pero no sabemos por qué se seleccionan estos números concretos.
Godfrey Harold Hardy
G. H. Hardy, el mentor de Ramanujan, trató de estimar la capacidad matemática que poseía Ramanujan. Concedió a David Hilbert, universalmente conocido y reconocido uno de los mayores matemáticos occidentales del siglo XIX, una puntuación de 80. A Ramanujan le asignó una puntuación de 100. Así mismo, Hardy se concedió un 25.

Por desgracia, ni Hardy ni Ramanujan parecían interesados en la psicología a los procesos de pensamiento mediante los cuales Ramanujan descubría estos increíbles teoremas, especialmente cuando diluvio material brotaba de sus sueños con semejante frecuencia. Hardy señaló:
“Parecía ridículo importunarle sobre como había descubierto o ese teorema conocido, cuando él me estaba mostrando media docena cada día, de nuevos teoremas”.
Ramanujan
Hardy recordaba vivamente:
-”Recuerdo una vez que fui a visitarle cuando estaba enfermo en Putney. Yo había tomado el taxi 1.729, y comenté que el numero me parecía bastante feo, y que esperaba que no fuese mal presagio.”
– No. -Replicó Ramanujan postrado en su cama-. Es un número muy interesante; es el número más pequeño expresable una suma de dos cubos en dos formas diferentes.
(Es la suma de 1 x 1 x 1 y 12 x 12 x 12, y la suma de 9 x 9 x 9 y 10 x 10 x 10).

Era capaz de recitar en el acto teoremas complejos de aritmética cuya demostración requeriría un ordenador moderno.
En 1.919 volvió a casa, en la India, donde un año más tarde murió enfermo.
El legado de Ramanujan es su obra, que consta de 4.000 fórmulas en cuatrocientas páginas que llenan tres volúmenes de notas, todas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario o, lo que es más frustrante, sin ninguna demostración. En 1.976, sin embargo, se hizo un nuevo descubrimiento. Ciento treinta páginas de borradores, que contenían los resultados del último año de su vida, fueron descubiertas por casualidad en una caja en el Trinity Collage. Esto se conoce ahora con el de “Cuaderno Perdido” de Ramanujan.

Comentando el cuaderno perdido, el matemático Richard Askey dice:
“El de este año, mientras se estaba muriendo, era el equivalente a una vida entera de un matemático muy grande”. Lo que él consiguió era increíble. Los matemáticos Jonathan Borwien y Meter Borwein, en relación a la dificultad y la ardua tarea de descifrar los cuadernos perdidos, dijeron: “Que nosotros sepamos nunca se ha intentado una redacción matemática de este alcance o dificultad”.
Por mi parte creo que, Ramanujan, fue un genio matemático muy adelantado a su tiempo y que pasaran algunos años que podamos descifrar al cien por ciento sus trabajos, especialmente, sus funciones modulares que guardan el secreto de la teoría más avanzada de la física moderna, la única capaz de unir la mecánica cuántica y la Gravedad.
Fórmula de Ramanujan determinar los decimales de pi
Las matemáticas de Ramanujan son como una sinfonía, la progresión de sus ecuaciones era algo nunca vísto, él trabajaba otro nivel, los números se combinaban y fluían de su cabeza a velocidad de vértigo y con precisión nunca antes conseguida por nadie. Tenía tal intuición de las cosas que éstas simplemente fluían de su cerebro. Quizá no los veía de una manera que sea traducible y el único lenguaje eran los números.
Como saben los físicos, los “accidentes” no aparecen sin ninguna razón. Cuando están realizando un cálculo largo y difícil, y entonces resulta de repente que miles de términos indeseados suman milagrosamente cero, los físicos saben que esto no sucede sin una razón más profunda subyacente. Hoy, los físicos conocen que estos “accidentes” son una indicación de que hay una simetría en juego. Para las cuerdas, la simetría se denomina simetría conforme, la simetría de estirar y deformar la hoja del Universo de la cuerda.

Nuestro mundo a-simétrico hermosas simetrías
Aquí es precisamente donde entra el trabajo de Ramanujan. Para proteger la simetría conforme original contra su destrucción por la teoría cuántica, deben ser milagrosamente satisfechas cierto de identidades matemáticas que, son precisamente las identidades de la función modular de Ramanujan. ¡Increíble! Pero, cierto.

Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan su punto más débil. Cualquier teoría, afirman, debe ser verificable. Puesto que ninguna teoría definida a la energía de Planck de 1019 miles de millones de eV es verificable, ¡La teoría de cuerdas no es realmente una teoría!
El principal problema, es teórico más que experimental. Si fuéramos suficientemente inteligentes, podríamos resolver exactamente la teoría y encontrar la verdadera solución no perturbativa de la teoría. Sin embargo, esto no nos excusa de encontrar algún medio por el que verificar experimentalmente la teoría, debemos esperar señales de la décima dimensión.

Volviendo a Ramanujan…
Es innegable lo sorprendente de su historia, un muchacho pobre con escasa preparación y arraigado como pocos a sus creencias y tradiciones, es considerado como una de los mayores genios de las matemáticas del siglo XX. Su legado a la teoría de números, a la teoría de las funciones theta y a las series hipergeométricas, además de ser invaluable aún sigue estudiándose por muchos prominentes matemáticos de todo el mundo. Una de sus fórmulas más famosas es la que aparece más arriba en el lugar número 21 de las imágenes expuestas y utilizada para realizar aproximaciones del Pi con más de dos millones de cifras decimales. Otra de las sorprendentes fórmulas descubiertas por Ramanujan es un igualdad en que era “casi” un número entero (la diferencia era de milmillonésimas). De hecho, durante un tiempo se llegó a sospechar que el número era efectivamente entero. No lo es, pero este hallazgo sirvió de base la teoría de los “Cuasi enteros”. A veces nos tenemos que sorprender al comprobar hasta donde puede llegar la mente humana que, prácticamente de “la nada”, es capaz de sondear los misterios de la Naturaleza para dejarlos al descubierto ante nuestros asombros ojos que, se abren como platos ante tales maravillas.
Publica: El Blog de Emilio Silvera
Para saber más: “HIPERESPACIO”, de Michio Kaku,( 1996 CRÍTICA-Grijalbo Mondadori,S.A. Barcelona) profesor de física teórica en la City University de Nueva York. Es un especialista a nivel mundial en la física de las dimensiones superiores ( hiperespacio). Despide el libro con unas palabras preciosas:”Algunas personas buscan un significado a la vida a través del beneficio, a través de las relaciones personales, o a través de experiencias propias. Sin embargo, creo que el estar bendecido con el intelecto para adivinar los últimos secretos de la naturaleza da significado suficiente a la vida”.
Abr
1
Siempre es la misma cosa…que adopta distintas formas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Las prodigiosas ideas ~
Clasificado en Las prodigiosas ideas ~
 Comments (0)
Comments (0)


La Mente, el mundo, el Universo
Nuestra estrategia para explicar la base neuronal de la conciencia consiste en centrarse en las propiedades más generales de la experiencia consciente, es decir, aquella que todos los estados conscientes comparte. De estas propiedades, una de las más importantes es la integración o unidad. La integración se refiere a que el sujeto de la experiencia no puede en ningún momento dividir un estado consciente en una serie de componentes independientes. Es una propiedad que está relacionada con nuestra incapacidad para hacer conscientemente dos cosas al mismo tiempo, como, por ejemplo relacionar en un papel todas las familias de partículas que conocemos mientras que, al mismo tiempo, se mantiene una discusión sobre los agujeros negros.

Aplicando la atención hemos llegado a saber que, el electrón tiene una masa en reposo (me) de 9,109 3897 (54) x 10-31 kg y una carga negativa de 1,602 177 33(49) x 10-19 culombios. Esa realidad, aunque vinieran los sabios físicos de un planeta habitable situado en la estrella Resplandor de una Galaxia muy lejana, cuando hicieran los cálculos matemáticos y los experimentos necesarios, las cifras seguirían siendo las mismas, toda vez que, al tratarse de constantes fundamentales, ni la masa ni la carga pueden tener otra realidad distinta sea cual fuere el observador. Esto nos quiere decir que, hay realidades que nunca varían y, eso, nos puede traer alguna esperanza de que, alguna vez, podríamos conocer el Universo, tal como es.

Esta sí es una realidad, sin ella, el mundo no sería tal como lo conocemos.
Sin embargo, no podemos negar nuestras limitaciones tanto de percepción como intelectuales para reconocer “el mundo” tal como es. Es “nuestro mundo” que, cuando sea visitado por “otros”, pudiera ser muy distinto al que nosotros percibimos y, podrían “ver” cosas que nosotros no vemos.
Vivímos en nuestra propia realidad, la que forja nuestras mentes a través de los sentidos y la experiencia. Incluso entre nosotros mismos, los seres de la misma especie, no percibimos de la misma manera las mismas cosas. Sí, muchos podemos coincidir en la percepción de algo, sin embargo, otros muchos diferirán de nuestra percepción y tendrán la suya propia. Esa prueba se ha realizado y la diversidad estuvo presente.

Estará aquí, la llave de la sabiduría
No, no será nada fácil despejar las incógnitas presentes en esta inmensa complejidad que llamamos Mente. Creo de manera firme que, finalmente, todo se traduce a Química y Luz. Energías de velocidades alucinantes que recorren el enmarañado entramado de neuronas y que hace posible todas y cada una de las maravillas que “real”mente se producen en nosotros y que no siempre sabemos traducir ni comprender.
Es tan grande el poder de nuestra mente que nada hay tan distante que no podamos, virtualmente hablando, traer ante nosotros. Somos capaces ya de escrutar el espacio y vislumbrar los confines del universo en edades muy cercanas a su nacimiento y, merced a los microscopios, nos acercamos al universo atómico para explorar los componentes de la materia. Parece que nada podrá (con el tiempo) escapar a nuestro control, con lo que todo nuevo “mundo” se revelará a nuestro entendimiento.
Nunca estamos satisfechos de los logros alcanzados (menos mal) y siempre surgirán seres especiales (Copérnico, Kepler, Galileo, Hooke, Newton…) que nos guiarán por el camino iluminado de su genio para mostrarnos la auténtica sabiduría mediante un pensamiento evolutivo que siempre dará un paso adelante, superando así el pensamiento nuevo al anterior. Pero, eso sí, esos avances han sido posible gracias a que hombres y mujeres pensaron con la lógica pero…, nunca dejaron de lado la imaginación.
La prueba de ello la podemos encontrar en Newton y Einstein. ¿Quién puede dudar de la grandeza de Newton? La pregunta está contestada de antemano. Sin embargo, los ejemplos de la historia son muy elocuentes: Newton con su física, Leibniz con su metafísica, con sus principios filosóficos como el de la razón suficiente. Y la física ganó a la metafísica; Newton a Leibniz, aunque de aquella batalla…habría mucho que hablar.
Durante mucho tiempo, espacio y tiempo se entendieron como entes absolutos, hasta que llegó Einsteincon sus dos teorías de la relatividad, la especial y la general, y aunque los caminos que siguió para conseguirlos no fueron metafísicos, no podemos negar la intervención de un genio de inspiración superior que a veces, nos puede llevar a pensar que, en algún sentido, finalmente Leibniz había sido el más acertado, ya que las teorías einstenianas pueden ser clasificadas dentro de un orden del pensamiento superior.
Así, la evolución continuó su camino imparable y el espacio y el tiempo absolutos de Newton, resultaron ser menos absolutos de lo que se pensaba; eran relativos y, además, eran una misma cosa, que a partir de ahí pasó a llamarse espacio-tiempo unidos y no separados. Así fue deducido por Minkouski al leer la teoría de Einstein.

Laplace
Quiero mencionar en este punto a dos grandes newtonianos: Lagrange y Laplace.
La obra de Newton, como todas las grandes obras, fue discutida y sometida a estudios rigurosos, analizada y removida. La ciencia del genio, claro, permaneció al margen de todas las críticas para dejar de ser discutida y pasar a ser desarrollada. Así ha resultado ser la Historia.
Recordemos en este sentido la cumbre de la física y de las matemáticas del siglo XVIII que es la Méchanique analytique (Chez la Veuve Desaint, París 1788), de Joseph-Louis Lagrange (1736 – 1813), un íntimo amigo de d’Alembert, en la que la mecánica de Newton alcanzó un nuevo nivel de pureza al reducir el sistema a un conjunto de fórmulas generales de las que se podían deducir todas las expresiones necesarias para resolver un problema. O los cinco tomos del Traité de mécanique céleste (Crapelet para J. B. M. Duprat, París 1799 – 1827) de Pierre-Simón Laplace (1749 – 1827), en los que se erradican numerosas anomalías de las explicaciones originales de Newton sobre los movimientos de los cuerpos celestes.
El texto de Laplace, al igual que el de Lagrange, era de difícil lectura para legos en las ciencias matemáticas, y tal complejidad dio lugar a versiones posteriores más sencillas para el entendimiento general, que finalmente hizo posible divulgar los enormes conocimientos alcanzados a partir de Newton, gracias a estos dos genios.
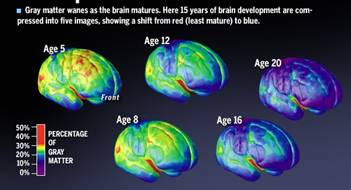
“Se puede apreciar en la anterior gráfica de resonancia como la neurocientífica nos muestra la evolución de la zona del córtex según la edad, desde la primera infancia va evolucionando y no se detiene dentro de la escala evolutiva. Explica que el neocortex nos capacita para adquirir conocimientos, desarrollar sociedades, culturas y tecnologías.”
Sí, se vislumbra, a lo lejos, una esplendorosa luz que, sin embargo, tiene en todo su centro un signo de interrogación que viene a significar lo que no sabemos. Es mucho lo que nos queda por descubrir y, hombres que, como Newton, Lagrange y Laplace y después Planck, Maxwell y Einstein nos han dejado un camino que seguir, sin embargo, no estamos situados aún en esa zona luminosa del saber sino que…
Un respiro en el camino:
- El ignorante, teme o adora lo que no comprende.
- Los ingratos acaban por disuadir a los virtuosos de poner en prácticas sus bondades.
- Amigo leal y franco, mirlo blanco.
Esto me recuerda aquella aseveración atribuida indistintamente a Séneca y Aristóteles:
“¡Oh, amigos míos, no hay ningún amigo!”
Hay otra que nos da a entender que los amigos egoístas y poco dispuestos a prestarnos su ayuda, en momentos necesarios son inútiles y no importa, pues, prescindir de ellos:
“Amigo que no presta y cuchillo que no corta,
que se pierdan poco importa.”
¡Esto de los amigos! Hay otra que dice:
“El que tiene un amigo, tiene un tesoro.
El que tiene un tesoro, tiene muchos ‘amigos’.”
“Si un amigo se comporta como la sombra que,
cuando luce el Sol nos abandona, no era un amigo.”
Pero volvamos al trabajo y continuemos repasando cosas interesantes y viajemos hasta el siglo XIX, que fue vital para la ciencia. Aunque la ciencia ya había mostrado para entonces su capacidad única para estudiar qué sucede en la naturaleza y qué principio (o leyes) la gobiernan, y contaba por entonces con una larga lista de teorías, datos y héroes científicos, no se había convertido todavía en una gran empresa, en la “profesión” que terminaría siendo.
La “profesionalización” e “institución” de la ciencia, entendiendo por tal que la práctica de la investigación científica se convirtiese en una profesión cada vez más abierta a personas sin medios económicos propios, que se ganaban la vida a través de la ciencia y que llegasen a atraer la atención de gobiernos e industrias, tuvo su explosión a lo largo de 1800, y muy especialmente gracias al desarrollo de dos disciplinas, la química orgánica y el electromagnetismo. Estas disciplinas, junto a las matemáticas, la biología y las ciencias naturales (sin las cuales sería una necedad pretender que se entiende la naturaleza, pero con menos repercusiones socio-económicas), experimentaron un gran desarrollo entonces, tanto en nuevas ideas como en el número de científicos importantes: Faraday, Maxwell, Lyell, Darwin y Pasteur, son un ejemplo. Sin olvidar a otros como Mendel, Helmholtz, Koch, Virchow, Lister o Kelvin, o la matemática de Cauchy, de Gauss, Galois, Fourier, Lobachevski, Riemann, Klein, Cantor, Russell, Hilbert o Poincaré. Pero vamos a pararnos un momento en Faraday y Maxwell.

Faraday
Para la electricidad, magnetismo y óptica, fenómenos conocidos desde la antigüedad, no hubo mejor época que el siglo XIX. El núcleo principal de los avances que se produjeron en esa rama de la física (de los que tanto se benefició la sociedad –comunicaciones telegráficas, iluminación, tranvías y metros, etc.–) se encuentra en que, frente a lo que se suponía con anterioridad, se descubrió que la electricidad y el magnetismo no eran fenómenos separados.
El punto de partida para llegar a este resultado crucial fue el descubrimiento realizado en 1.820 por el danés Hans Christian Oersted (1777 – 1851) de que la electricidad produce efectos magnéticos: observó que una corriente eléctrica desvía una aguja imanada. La noticia del hallazgo del profesor danés se difundió rápidamente, y en París André-Marie Ampère (1775 – 1836) demostró experimentalmente que dos hilos paralelos por los que circulan corrientes eléctricas de igual sentido, se atraen, repeliéndose en el caso de que los sentidos sean opuestos.
Poco después, Ampère avanzaba la expresión matemática que representaba aquellas fuerzas. Su propósito era dar una teoría de la electricidad sin más que introducir esa fuerza (para él “a distancia”).

Pero el mundo de la electricidad y el magnetismo resultó ser demasiado complejo como para que se pudiera simplificar en un gráfico sencillo, como se encargó de demostrar uno de los grandes nombres de la historia de la ciencia: Michael Faraday (1791 – 1867), un aprendiz de encuadernador que ascendió de ayudante de Humphry Davy (1778 – 1829) en la Royal Intitution londinense.
En 1821, poco después de saber de los trabajos de Oersted, Faraday, que también dejó su impronta en la química, demostró que un hilo por el que pasaba una corriente eléctrica podía girar de manera continua alrededor de un imán, con lo que vio que era posible obtener efectos mecánicos (movimiento) de una corriente que interacciona con un imán. Sin pretenderlo, había sentado el principio del motor eléctrico, cuyo primer prototipo sería construido en 1.831 por el físico estadounidense Joseph Henry (1797 – 1878).
Lo que le interesaba a Faraday no eran necesariamente las aplicaciones prácticas, sino principalmente los principios que gobiernan el comportamiento de la naturaleza, y en particular las relaciones mutuas entre fuerzas, de entrada, diferentes. En este sentido, dio otro paso importante al descubrir, en 1.831, la inducción electromagnética, un fenómeno que liga en general los movimientos mecánicos y el magnetismo con la producción de corriente eléctrica.
Este fenómeno, que llevaría a la dinamo, representaba el efecto recíproco al descubierto por Oersted; ahora el magnetismo producía electricidad , lo que reforzó la idea de que un lugar de hablar de electricidad y magnetismo como entes separados, sería más preciso referirse al electromagnetismo.
La intuición natural y la habilidad experimental de Faraday hicieron avanzar enormemente el estudio de todos los fenómenos electromagnéticos. De él es, precisamente, el concepto de campo que tanto juego ha dado a la física.
Sin embargo, para desarrollar una teoría consistente del electromagnetismo se necesitaba un científico distinto: Faraday era hábil experimentador con enorme intuición, pero no sabía expresar matemáticamente lo que descubría, y se limitaba a contarlo. No hubo que esperar mucho, ni salir de Gran Bretaña para que un científico adecuado, un escocés de nombre James Clerk Maxwell (1831 – 1879), hiciera acto de presencia.
Maxwell
Maxwell desarrolló las matemáticas para expresar una teoría del magnetismo-electricidad (o al revés) que sentó las bases físicas de aquel fenómeno y contestaba a todas las preguntas de los dos aspectos de aquella misma cosa, el electromagnetismo. En sus ecuaciones vectoriales estaban todos los experimentos de Faraday, que le escribió una carta pidiéndole que le explicara, con palabras sencillas, aquellos números y letras que no podía entender.
Pero además, Maxwell también contribuyó a la física estadística y fue el primer director del Laboratorio Cavendish, unido de manera indisoluble a la física de los siglos XIX y XX (y también al de biología molecular) con sede en Cambridge.

Su conjunto de ecuaciones de, o en, derivadas parciales rigen el comportamiento de un medio (el campo electromagnético) que él supuso “transportaba” las fuerzas eléctricas y magnéticas; ecuaciones que hoy se denominan “de Maxwell”. Con su teoría de campo electromagnético, o electrodinámica, Maxwell logró, además, unir electricidad, magnetismo y óptica. Las dos primeras, como manifestaciones de un mismo substrato físico, electromagnético, que se comporta como una onda, y la luz, que es ella misma, una onda electromagnética, lo que, en su tiempo, resultó sorprendente.
Más de ciento treinta años después, todavía se podía o se puede apreciar la excitación que sintió Maxwell cuando escribió en el artículo Sobre las líneas físicas de la fuerza, 1.861 – 62, en el que presentó esta idea: “Difícilmente podemos evitar la inferencia de que la luz consiste de ondulaciones transversales del mismo medio que es la causa de los fenómenos eléctricos y magnéticos.”
Todo aquello fue posible gracias a las bases sentadas por otros y a los trabajos de Faraday como experimentador infatigable, que publicaba sus resultados en artículos y los divulgaba en conferencias en la sede de la Royal Institution londinense. Todos estos artículos y conferencias fueron finalmente publicados en el libro que llamaron Philosophical transactions de la Royal Society, y Experimental researches in chemistry and physics (Richard Taylor y William Francis, Londres, 1.859; dos grandes científicos unidos por la historia de la ciencia que nos abrieron puertas cerradas que nos dejaron entrar al futuro).
No quiero seguir por este camino de personajes y sus obras ya que están enmarcados y recogidos en mi libreta (primera parte de personajes), así que desviaré mis pensamientos hacia otras diversas cuestiones de mi interés, y espero que también del vuestro. Antes dejaba la reseña de algún refrán o pensamiento sobre la amistad, y en realidad también podemos ver la cara amable de esta forma de sentimiento-aprecio-amor que llamamos amistad.
¡La fuerza que nos lleva a conseguir mucho más!
Nosotros, los seres humanos, nunca vemos a nuestros semejantes como objetos o cuerpos neutros, sino que los miramos como personas con una riqueza interior que refleja su estado de ánimo o forma de ser, y de cada uno de ellos nos llegan vibraciones que, sin poderlo evitar, nos transmiten atracción o rechazo (nos caen bien o nos caen mal).
Son muchos y diversos los signos sensoriales que, en silencio, nos llegan de los demás y son recogidos por nuestros sensores en una enorme gama de mensajes sensitivos que llamamos indistintamente simpatía, pasión, antipatía, odio, etc.
Está claro que cuando el sentimiento percibido es positivo, la satisfacción se produce por el mero hecho de estar junto a la persona que nos lo transmite, que con su sola presencia, nos está ofreciendo un regalo, y si apuramos mucho, a veces lo podríamos llamar incluso “alimento del alma”. Estar junto a quien nos agrada es siempre muy reconfortante, y según el grado de afinidad, amistad o amor, el sentimiento alcanzará un nivel de distinto valor.

Caigo en la cuenta de que, además de la materia, el espaciotiempo, y las fuerzas de la Naturaleza, aquí existe algo más que, está dentro de nuestras mentes y que, de momento, no podemos comprender. Sin embargo, si podemos sentir los sentimientos o la satisfacción que nos produce el el querer y poder amar, aprender y descubrir.
¡La Humanidad! ¿Quién la entiende?
emilio silvera
















 Totales: 77.909.498
Totales: 77.909.498 Conectados: 61
Conectados: 61






























