Jul
26
La importancia del Sol para la Tierra y nosotros
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Relación del Sol con la Tierra ~
Clasificado en Relación del Sol con la Tierra ~
 Comments (0)
Comments (0)
Mientras en el núcleo del Sol quede suficiente hidrógeno para mantener las reacciones termonucleares, la estrella que nos alumbra inundará la Tierra con su radiación, que suministra la energía necesaria para mantener la mayoría de los procesos físicos y químicos que se producen en nuestro planeta,
Esta radiación calienta la atmósfera y el océano, genera vientos y lluvias y sostiene el inexorable proceso de la denudación. De todas las conversiones generadas de las energías globales que se producen en la Tierra, las geotectónicas (la lenta modificación del fondo oceánico y de los continentes, acompañada de terremotos y las espectaculares liberaciones energéticas de los volcanes), son las únicas que no proceden de la radiación solar, sino de la gravedad y de la liberación gradual del calor terrestre.

La luz solar también suministra la energía necesaria para la fotosíntesis, la más importante transformación bioquímica, creando nueva biomasa en bacterias, fitoplancton, plantas superiores y, sobre todo, en bosques y praderas. Esta síntesis es el fundamento de la cadena alimenticia necesaria para el metabolismo heterótrofo de animales y personas, a los cuales la nutrición les permite desarrollar actividades que van desde una simple carrera a trabajos más elaborados, como la ocupación laboral y el ocio.
Así de importante es la luz. Las sociedades humanas, desde los pequeños grupos de cazadores o pastores hasta las sociedades más complejas que dependen de los enormes flujos de combustibles fósiles y electricidad, han estado ineludiblemente ligadas al continuo flujo de energía solar y a los almacenamientos energéticos procedentes de la misma.
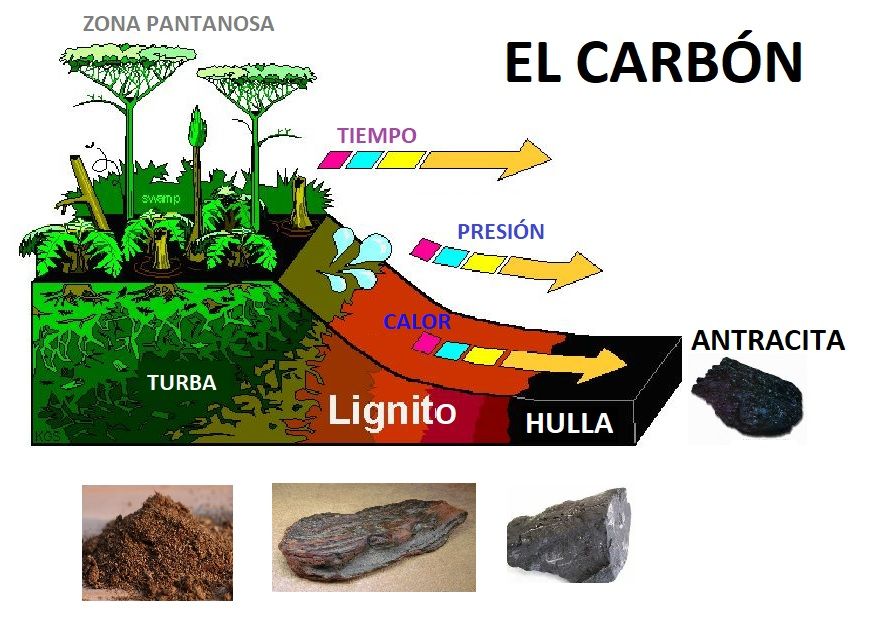
El proceso de formación de carbón a partir de restos vegetales acumulados en zonas acuáticas y sumergidos, de tal manera que estaban aislados de la atmósfera, sufrieron una transformación por efecto de las bacterias anaeróbicas, que aumentan la concentración de carbono de los azúcares y desprenden gases, como metano y anhídrido carbónico. Así se forma una masa gelatinosa de turba. Posteriormente, ésta se hunde y sobre ella se van depositando nuevas capas. Las más inferiores pueden sufrir transformaciones metamórficas debido a la elevada presión y temperatura que soportan, convirtiéndose en grafito. Las condiciones biológicas, climáticas y estructurales más favorables para que tenga lugar esta serie de transformaciones se dieron durante el periodo carbonífero, que en Eurasia y Norteamérica se encontraban situadas en posición tropical y cubiertas de grandes bosques próximos al mar, que se inundaron debido a los movimientos verticales causados por la orogenia hercínica. Los yacimientos de carbón de mayor antigüedad proceden del devónico y los más modernos del cuaternario inferior.

El proceso de formación del petróleo se origina a partir de acumulaciones de plancton marino que sufre transformaciones, semejantes a la carbonización, por bacterias anaeróbicas, y que dan lugar a una materia denominada sapropel y posteriormente a la mezcla de hidrocarburos típica del petróleo. Esta transformación de hidrocarburos suele tener lugar al mismo tiempo que el proceso de sedimentación de arenas y arcillas que se transformarán en areniscas y margas, y quedarán impregnadas por el petróleo, dando lugar a las rocas madre de éste. Cuando éstas sufren presiones orogénicas o simplemente quedan sometidas a una mayor presión al hundirse los sedimentos, el petróleo migra hasta encontrarse con rocas impermeables que impiden su avance y se acumula en el subsuelo, generando los verdaderos yacimientos petrolíferos.
Los hidrocarburos gaseosos están acumulados en la parte superior de estos yacimientos de petróleo (aceites de roca: del latín petram, “piedra” y oleum, “aceite”), que es un aceite mineral hidrocarbonato, oleaginoso, inflamable, de olor acre, densidad inferior a la del agua y cuyo color varía desde el negro al incoloro. Consta principalmente de hidrocarburos líquidos, en los que se encuentran disueltos hidrocarburos sólidos (asfaltos y betunes) y gaseosos (metano, butano y acetileno); también contiene pequeñas porciones de nitrógeno, azufre, oxígeno, colesterina, porfirinas, vanadio, níquel, cobalto y molibdeno. De todo esto, mediante procesos industriales de refinado, se obtienen priductos que son utilizados por la Sociedad en diferentes actividades y, son el origen de la contaminación por los elevados porcentajes de azufre y otras materias que contiene. Sin embargo, por obtener esta fuente de contaminación y “riqueza” se crean conflictos que desembocan en las guerras que azotan nuestro mundo.
Ahora, después de esta breve explicación, sabemos un poco más sobre esta materia prima que ha servido, y continuará aún algún tiempo sirviendo de base a muchas generaciones pasadas y alguna menos futura: civilizaciones del combustible sólido, con su profesión de servicios energéticos, transporte generalizado y exceso de información (no siempre deseable, ya que si elimináramos el 80% de las programaciones televisivas, el mundo sería algo más culto y estaría menos embrutecido).
Un observador extraterrestre no podría encontrar nada extraordinario que le permitiera distinguir el Sol entre las millones de estrellas similares que existen en la nuestra y otras galaxias, y que a su vez representan una fracción de cientos de miles de millones de cuerpos radiantes que las forman. Como se ha dicho otras veces, nuestro Sol pertenece a una clase común de estrella localizada aproximadamente en el centro de la secuencia principal* del esquema de clasificación conocido como de Herzsprung-Russell, denominada enana G2, que posee un característico color amarillo y una magnitud estelar poco importante (+4’83). Así que, después de 4.500 millones de años, el Sol está a la mitad de su vida y va camino de transformarse de enana en gigante roja. Cuando esto ocurra, su luminosidad será mil veces mayor que la actual, y su diámetro, enormemente expandido, alcanzará (probablemente) la Tierra. Durante algún tiempo el planeta girará dentro de una órbita en el interior de la ligera cubierta de la estrella, pero final e inevitablemente caerá describiendo una espiral hasta ser engullida por el núcleo de la gigante roja.
Mucho antes de que el Sol se transforme en una gigante roja la vida en la Tierra desaparecerá. Según se contraiga el núcleo solar, las reacciones termonucleares calentarán su capa externa; el diámetro de la estrella se expandirá unas diez mil veces y la radiación de la subgigante roja evaporará los océanos y mares de la Tierra generando fortísimos vientos calientes en la convulsa atmósfera del planeta.
Sin embargo, mientras haya hidrógeno en el núcleo de la estrella, los inexorables cambios de su luminosidad serán graduales y el Sol continuará suministrando la energía necesaria, tanto para la vida en la Tierra como para la mayoría de las transformaciones físicas que ocurren en ella.
Las primeras explicaciones científicas de la radiación solar, cálculo basado en, la gravitación de Hermann Helmholtz conducen a una estimación de la vida de la estrella de unos treinta millones de años. La famosa ecuación de Einstein relacionando la materia y la energía abrió el camino hacia un modelo más preciso que, por sí sólo, tampoco nos ofrece una solución completamente satisfactoria. Por otra parte, no parece probable que la transformación total de materia solar, convirtiendo los núcleos atómicos y los electrones en radiación (según teorizaba Sir Arthur Eddington), pueda producirse ni siquiera a temperaturas superiores a los diez mil millones de grados Kelvin (K). La idea hoy aceptada de que la producción de la energía en el núcleo del Sol obedece a reacciones nucleares fue propuesta a finales de los años treinta por Hans Bethe, Charles Critchfield y Carl Friedrich von Weizsäcker.
La fusión de hidrógeno en helio, en el ciclo protón–protón, se inicia cuando la temperatura alcanza los trece millones de grados Kelvin. Justo por encima de los 16 millones Kelvin empieza a dominar el ciclo carbono-nitrógeno que genera C12. No podemos estar seguros, pero de acuerdo con los mejores modelos, el ciclo C-N genera solamente un 1’5% de la energía total del Sol.
Las reacciones en el núcleo solar consumen entre 4’3 y 4’6 millones de toneladas de materia cada segundo, de manera que de 4.654.000 t de hidrógeno, 4.650.000 se transforman en helio, y las 4.000 toneladas que faltan son lanzadas al espacio en forma de radiación termonuclear (luz y calor) de la que una pequeña parte nos llega a la Tierra para hacer posible la vida.
De acuerdo a la relación masa-energía de Einstein, liberan 3’89×1026 J de energía nuclear. Este inmenso flujo de energía es rápidamente transformado en energía térmica, que es transportado, isotrópicamente, hacia el exterior, primero por irradiación aleatoria y luego más rápidamente por convección direccional.
Suponiendo (como antes apuntaba) que la radiación es isótropa, la potencia de la luz visible que atraviesa cada metro cuadrado de la capa emisora de la fotosfera es aproximadamente de 64 MW. Como en el espacio no hay prácticamente atenuación de la radiación solar, cuando ésta alcanza la órbita de la Tierra tiene una densidad de potencia igual al cociente entre la luminosidad total del Sol (3’89×1026 W) y el área de una esfera de radio orbital (que, como promedio, es de unos 150 millones de kilómetros).

Este flujo, tradicionalmente conocido como la constante solar, es la tasa máxima de energía que llega a la parte superior de la atmósfera terrestre. A principios de los años setenta, la NASA utilizó para el diseño de las naves espaciales un valor de la constante solar igual a 1.353 W/m2. El flujo ha sido medido directamente en el espacio desde 1979, cuando el satélite Nimbus 7 obtuvo un valor de 1.371 W/m2. En el más reciente satélite de la Solar Maximum Mission lanzado en 1980 se obtuvo una media ponderada de 1.368’3 W/m2.
Las observaciones continuadas desde el espacio han revelado la existencia de una compleja regularidad de pequeñas fluctuaciones de corta duración que, debido a la interferencia de la atmósfera, no habían podido ser observadas anteriormente. Estas fluctuaciones de poca duración (del orden de días a semanas) y de hasta un 0’2 por ciento son debidas al paso de manchas oscuras y fáculas brillantes que arrastra el Sol en su rotación; el ciclo medido es de 11 años, en el que la radiación solar disminuye en un 0’1 por ciento entre el valor máxima y el mínimo.
La longitud de onda de la energía electromagnética emitida por el Sol y que llega a la Tierra varía en más de diez órdenes de magnitud. Va desde la longitud de onda más corta, que corresponde a los rayos gamma y rayos X de menos de 10-10 m, hasta la longitud de ondas de radio que superan el metro.
El aspecto del espectro de la radiación solar es similar al de un cuerpo negro a 6.000º K. Ambos espectros son especialmente parecidos en el rango de la longitud de onda mayor que la del amarillo, pero para longitudes de onda menores, el espectro solar cae notablemente por debajo de la línea de los 6.000º K. De acuerdo con la ley de desplazamiento de Wien, la emisión máxima a esta temperatura es de 483 nm, cerca del final de la zona azul del espectro visible y próximo al verde.
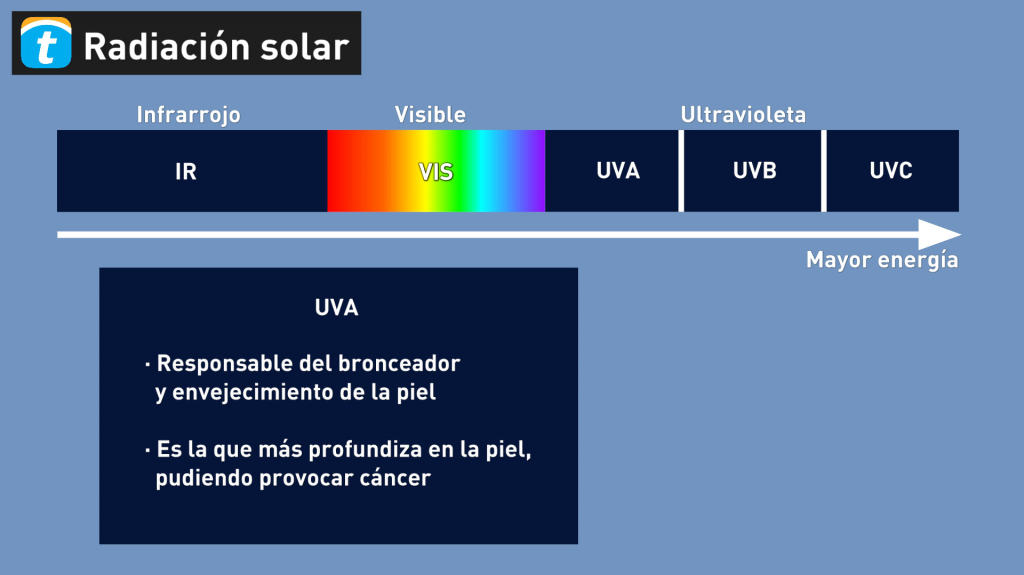
El flujo de energía se reparte desigualmente entre las tres grandes categorías espectrales: radiación ultravioleta (UV), cuya longitud de onda va desde las más cortas hasta los 400 nm y contribuye con menos del 9 por ciento de la radiación total; la luz visible, que va desde los 400 nm del violeta más lejano hasta los 700 nm del rojo más oscuro y representa un 39 por ciento; y la radiación infrarroja (IR), que representa cerca del 52 por ciento.
La radiación que llega a la superficie de la Tierra es muy diferente de la radiación extraterrestre, tanto cualitativa como cuantitativamente. Las razones físicas de esta diferencia son varias: que la órbita de la Tierra es elíptica, la propia forma del planeta, la inclinación del eje de rotación, la composición de la atmósfera y la reflectividad (albedo) de las nubes y superficies terrestres. Consecuentemente, la radiación solar que llega a la superficie de la Tierra presenta una compleja pauta espacial y temporal. La media anual global es ligeramente inferior a 170 W/m2 en los océanos y de unos 180 W/m2 en los continentes. La diferencia más importante del valor esperado, según la latitud de la zona, se encuentra en la disminución que se presenta en los trópicos y durante los monzones subtropicales, debido a la alta nubosidad. Grandes regiones de Brasil, Nigeria y el sur de China reciben menos insolación que Nueva Inglaterra o las regiones de Europa occidental. Es aún más sorprendente que no haya diferencia entre el flujo máximo que se recibe al mediodía durante el verano en Yakarta, situada en el ecuador, y el que se recibe en ciudades subárticas como Edmonton en Canadá o Yakutsk en Liberia. Quizás el mejor ejemplo sea el de Oahu, donde la casi siempre nublada cordillera Koolau, que intercepta las nubes y las lluvias arrastran los alisios, tiene una media anual de radiación de 150 W/m2, mientras que en Pearl Harbor, a 15 Km de distancia en la dirección del viento, la media es de 250 W/m2.
La radiación solar media de 170 W/m2 representa anualmente una energía de 2’7×1024 J, que equivale a 87 PW. Esta cantidad es casi 8.000 veces mayor que el consumo mundial de combustibles sólidos y electricidad durante los primeros años noventa. Sólo una pequeña fracción de este inmenso flujo es absorbida por los pigmentos de las plantas para realizar la fotosíntesis, y una parte algo mayor, pero también pequeña, se utiliza para calentar las plantas, los cuerpos de los animales y las personas, así como sus refugios.
La radiación también sustenta la vida porque al calentar los océanos, las rocas y los suelos, impulsa funciones fundamentales en la biosfera, tales como el ciclo del agua, la formación de los vientos, el mantenimiento de la temperatura adecuada para que funcionen los procesos metabólicos y la descomposición orgánica. Además, es la causante de la erosión que transporta los nutrientes minerales para la producción primaria de materia orgánica.
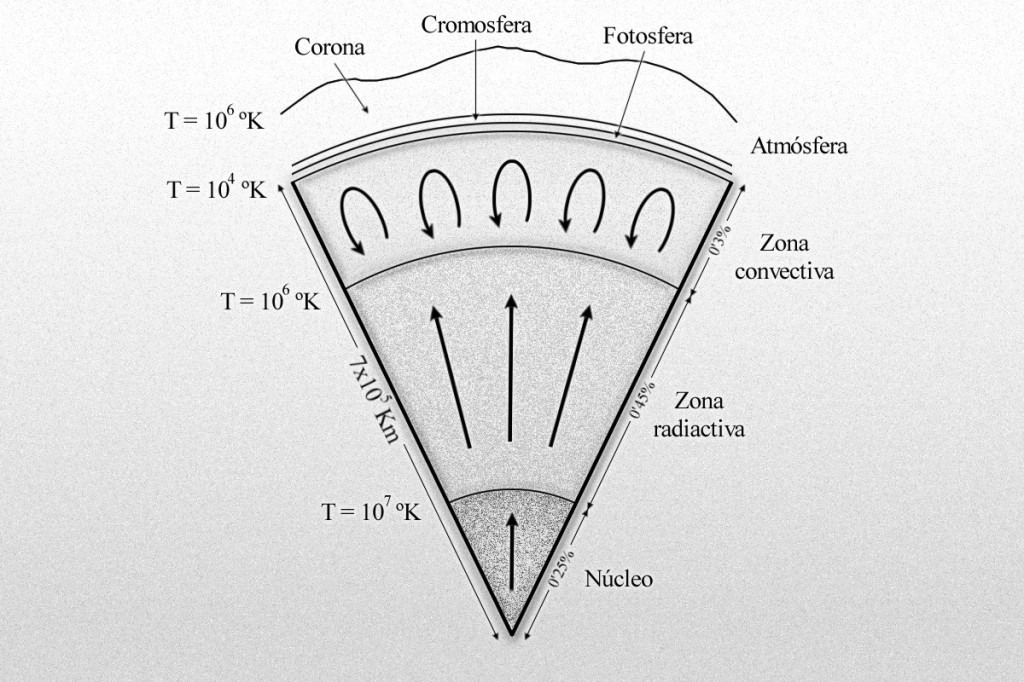
Sección transversal del Sol
A la larga, para mantener el equilibrio térmico del planeta, la radiación solar absorbida debe emitirse al espacio, pero la longitud de onda está drásticamente desplazada hacia el infrarrojo. A diferencia de la radiación de longitud de onda corta emitida por el Sol, que está determinada por la temperatura de la fotosfera (5.800º K), la radiación terrestre corresponde muy aproximadamente a las emisiones electromagnéticas de un cuerpo negro a 300º K (27ª C). El máximo de emisión de esa esfera caliente está en la zona del IR a 966 μm. Como el 99% de la radiación solar llega en longitudes de onda menores de 4 μm y el espectro terrestre apenas alcanza los 3 μm, el solapamiento de frecuencias entre estos dos grandes flujos de energías es mínimo.
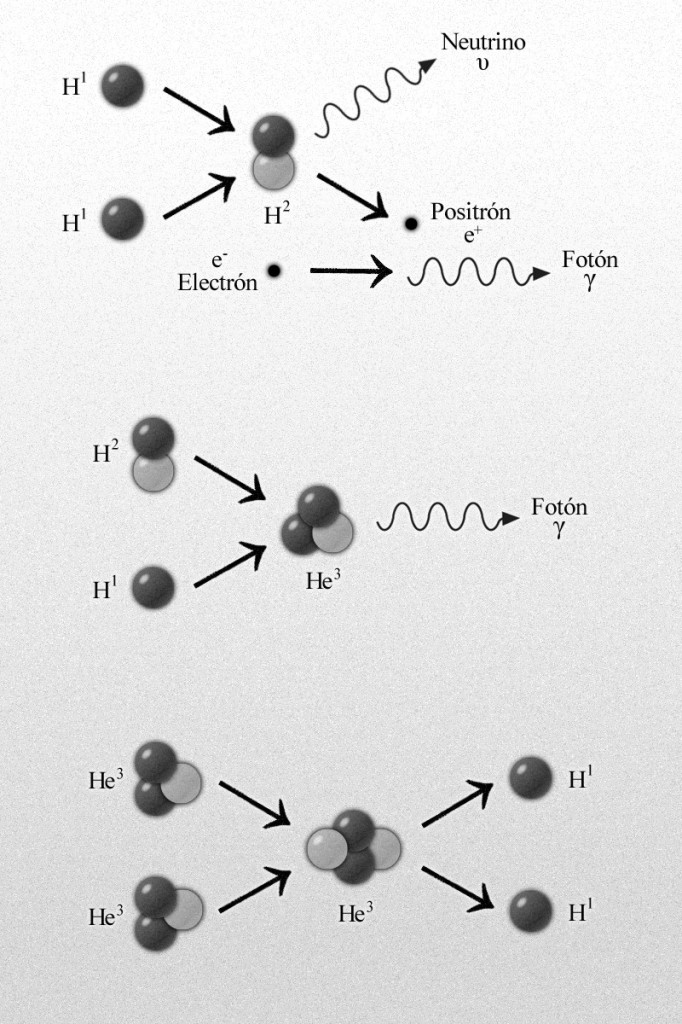
Reacción protón–protón para formar helio 4 liberando energía.
Lo cierto es que, sin la luz y el calor que nos suministra el Sol… ¡No estaríamos aquí!
emilio silvera
Jun
5
Sin la relación energética Sol-Tierra…¡No estaríamos aquí!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Relación del Sol con la Tierra ~
Clasificado en Relación del Sol con la Tierra ~
 Comments (0)
Comments (0)

La misión Kepler busca planetas extrasolares y estudia el interior de las estrellas a través de sus vibraciones. En composición se observa una de estas estrellas con un planeta orbitando entorno a ella. La estrella oscila debido a ondas acústicas resonantes.
Las trazas en rojo representan las oscilaciones que recorren el interior de la estrella. En la representación se ven los caminos recorridos por las ondas entre la superficie y un punto de su interior y que hay ondas que llegan el núcleo del Sol y otras que quedan atrapadas más cerca de su superficie. (Fuente: Gabriel Pérez Díaz, Instituto de Astrofísica de Canarias).

Mientras en el núcleo del Sol quede suficiente hidrógeno mantener las reacciones termonucleares, la estrella que nos alumbra inundará la Tierra con radiación solar, que suministra la energía necesaria para mantener la mayoría de los procesos físicos y químicos que se producen en nuestro planeta.
radiación calienta la atmósfera y el océano, genera vientos y lluvias y sostiene el inexorable proceso de la denudación. De todas las conversiones generadas de las energías globales que se producen en la Tierra, las geotectónicas (la lenta modificación del fondo oceánico y de los continentes, acompañada de terremotos y las espectaculares liberaciones energéticas de los volcanes), son las únicas que no proceden de la radiación solar, sino de la gravedad y de la liberación gradual del calor terrestre.
La luz solar también suministra la energía necesaria para la fotosíntesis, la más importante transformación bioquímica, creando nueva biomasa en bacterias, fitoplancton, plantas superiores y, sobre todo, en bosques y praderas. Esta síntesis es el fundamento de la cadena alimenticia necesaria para el metabolismo heterótrofo de animales y personas, a los cuales la nutrición les permite desarrollar actividades que van una simple carrera a trabajos más elaborados, como la ocupación laboral y el ocio.

Así de importante es la luz. Las sociedades humanas, desde los pequeños grupos de cazadores o pastores hasta las sociedades más complejas que dependen de los enormes flujos de combustibles fósiles y electricidad, han ineludiblemente ligadas al continuo flujo de energía solar y a los almacenamientos energéticos procedentes de la misma.
El proceso de formación de carbón a partir de restos vegetales acumulados en zonas acuáticas y sumergidos, de tal manera que estaban aislados de la atmósfera, sufrieron una transformación por efecto de las bacterias anaeróbicas, que aumentan la concentración de carbono de los azúcares y desprenden gases, como metano y anhídrido carbónico. Así se forma una masa gelatinosa de turba. Posteriormente, ésta se hunde y sobre ella se van depositando nuevas capas. Las más inferiores pueden sufrir transformaciones metamórficas debido a la elevada presión y temperatura que soportan, convirtiéndose en grafito. Las biológicas, climáticas y estructurales más favorables para que tenga lugar esta serie de transformaciones se dieron durante el periodo carbonífero, que en Eurasia y Norteamérica se encontraban situadas en posición tropical y cubiertas de grandes bosques próximos al mar, que se inundaron debido a los movimientos verticales causados por la orogenia hercínica. Los yacimientos de carbón de mayor antigüedad proceden del devónico y los más modernos del cuaternario inferior.
La materia orgánica se transforma, el moho aparece y las condiciones del ambiente lo transforman todo. De la misma manera, ocurre con los combustibles fósiles que, a partir de plantas y materia en anaeróbico, se producen esas transformaciones a lo largo de millones de años.
![[Bacterias+metanogenas.jpg]](http://2.bp.blogspot.com/_oZOg6YjBvWk/SpBPwtdZGVI/AAAAAAAACW4/6TOQiATRKzI/s1600/Bacterias%2Bmetanogenas.jpg)
Bacterias metanógenas estas bacterias terrestres de la imagen podrían ser las responsables de la liberación de gas metano en Marte
La primera etapa del proceso de degradación de la materia orgánica es la formación de metano por la acción de las bacterias. Posteriormente, durante el enterramiento de la misma, se produce la transformación a un producto intermedio denominado kerógeno, que puede ser de distintos tipos dependiendo de la materia orgánica original presente en los sedimentos. Así, los denominados kerógenos de tipo I e II darán lugar a la generación de petróleo. Junto con la presión actúa la temperatura, que alcanza las más favorables para la producción entre los 70 y los 100 ºC. Estas temperaturas pueden alcanzarse, dependiendo del gradiente geotérmico, entre los 2 y los 3,5 km de profundidad. Con el aumento de la temperatura disminuye la producción de petróleo y aumenta la de gas “húmedo” (se llama así, ya que junto con el metano entran en la composición etano, propano y butano, que pueden condensarse, con facilidad a la fase líquida). A partir de los 150 ºC se genera gas seco (compuesto principalmente de metano), y si el enterramiento es más profundo, los residuos pueden llegar a convertirse en grafito.

El carbono es un elemento químico de atómico 6 y símbolo C. Es sólido a temperatura ambiente. Dependiendo de las de formación, puede encontrarse en la naturaleza en distintas formas alotrópicas, carbono amorfo y cristalino en forma de grafito o diamante. Es el pilar básico de la química orgánica.
el proceso de formación del petróleo se origina a partir de acumulaciones de plancton marino que sufre transformaciones, semejantes a la carbonización, por bacterias anaeróbicas, y que dan lugar a una materia denominada sapropel y posteriormente a la mezcla de hidrocarburos típica del petróleo. transformación de hidrocarburos suele tener lugar al mismo tiempo que el proceso de sedimentación de arenas y arcillas que se transformarán en areniscas y margas, y quedarán impregnadas por el petróleo, dando lugar a las rocas madre de éste. Cuando éstas sufren presiones orogénicas o simplemente quedan sometidas a una mayor presión al hundirse los sedimentos, el petróleo migra hasta encontrarse con rocas impermeables que impiden su avance y se acumula en el subsuelo, generando los verdaderos yacimientos petrolíferos.
Los hidrocarburos gaseosos están acumulados en la superior de estos yacimientos de petróleo (aceites de roca: del latín petram, “piedra” y oleum, “aceite”), que es un aceite mineral hidrocarbonato, oleaginoso, inflamable, de olor acre, densidad inferior a la del agua y cuyo color varía el negro al incoloro. Consta principalmente de hidrocarburos líquidos, en los que se encuentran disueltos hidrocarburos sólidos (asfaltos y betunes) y gaseosos (metano, butano y acetileno); también contiene pequeñas porciones de nitrógeno, azufre, oxígeno, colesterina, porfirinas, vanadio, níquel, cobalto y molibdeno. De todo esto, mediante procesos industriales de refinado, se obtienen los productos de todos conocidos como la gasolina, nafta, queroseno, gasóleo, etc.

Su combustión es una de las fuentes más importantes de contaminación por los elevados porcentajes de azufre y otras materias que contiene. Sin embargo, por obtener fuente de contaminación y “riqueza” se crean conflictos que desembocan en las guerras que azotan nuestro mundo.
Ahora, después de esta breve explicación, sabemos un poco más sobre esta materia prima que ha servido, y continuará aún algún tiempo sirviendo de base a muchas generaciones pasadas y alguna menos futura: civilizaciones del combustible sólido, con su profesión de servicios energéticos, transporte generalizado y exceso de información (no siempre deseable, ya que si elimináramos el 80% de las programaciones televisivas, el mundo sería algo más culto y estaría menos embrutecido).

Un observador extraterrestre no podría encontrar nada extraordinario que le permitiera distinguir el Sol los millones de estrellas similares que existen en la nuestra y en otras galaxias, y que a su vez representan una fracción de cientos de miles de millones de cuerpos radiantes que las forman. Como se ha dicho otras veces, nuestro Sol pertenece a una clase común de estrella localizada aproximadamente en el centro de la secuencia principal del esquema de clasificación conocido como de Herzsprung-Russell, denominada enana G2, que posee un característico color amarillo y una magnitud estelar poco importante (+4’83). Así que, después de 4.500 millones de años, el Sol está a la mitad de su vida y va camino de transformarse de enana en gigante roja. Cuando esto ocurra, su luminosidad será mil veces mayor que la actual, y su diámetro, enormemente expandido, alcanzará (probablemente) la Tierra. Durante algún tiempo el planeta girará dentro de una órbita en el interior de la ligera cubierta de la estrella, pero final e inevitablemente caerá describiendo una espiral ser engullida por el núcleo de la gigante roja.
Mucho de que el Sol se transforme en una gigante roja la vida en la Tierra desaparecerá. Según se contraiga el núcleo solar, las reacciones termonucleares calentarán su capa externa; el diámetro de la estrella se expandirá unas diez mil veces y la radiación de la subgigante roja evaporará los océanos y mares de la Tierra generando fortísimos vientos calientes en la convulsa atmósfera del planeta.

Sin embargo, mientras haya hidrógeno en el núcleo de la estrella, los inexorables cambios de su luminosidad serán graduales y el Sol continuará suministrando la energía necesaria, tanto la vida en la Tierra como para la mayoría de las transformaciones físicas que ocurren en ella.
Las primeras explicaciones científicas de la radiación solar, cálculo basado en la gravitación de Hermann Helmholtz, conducen a una estimación de la vida de la estrella de treinta millones de años. La famosa ecuación de Einstein relacionando la materia y la energía abrió el camino hacia un modelo más preciso que, por sí sólo, tampoco nos ofrece una solución completamente satisfactoria. Por otra , no parece probable que la transformación total de materia solar, convirtiendo los núcleos atómicos y los electrones en radiación (según teorizaba Sir Arthur Eddington), pueda producirse ni siquiera a temperaturas superiores a los diez mil millones de grados Kelvin (K). La idea hoy aceptada de que la producción de la energía en el núcleo del Sol obedece a reacciones nucleares fue propuesta a finales de los treinta por Hans Bethe, Charles Critchfield y Carl Friedrich von Weizsäcker.

La fusión de hidrógeno en helio, en el ciclo protón–protón, se inicia la temperatura alcanza los trece millones de grados Kelvin. Justo por encima de los 16 millones Kelvin empieza a dominar el ciclo carbono-nitrógeno que genera C12. No podemos estar seguros, de acuerdo con los mejores modelos, el ciclo C-N genera solamente un 1’5% de la energía total del Sol.
Las reacciones en el núcleo solar consumen entre 4’3 y 4’6 millones de toneladas de materia cada segundo, de manera que de 4.654.000 t de hidrógeno, 4.650.000 se transforman en helio, y las 4.000 toneladas que faltan son lanzadas al espacio en de radiación termonuclear (luz y calor) de la que una pequeña parte nos llega a la Tierra para hacer posible la vida.
De acuerdo a la relación masa-energía de Einstein, liberan 3’89×1026 J de energía nuclear. Este inmenso flujo de energía es rápidamente transformado en energía térmica, que es transportado, isotrópicamente, el exterior, primero por irradiación aleatoria y luego más rápidamente por convección direccional.

Suponiendo (como antes apuntaba) que la radiación es isótropa, la potencia de la luz visible que atraviesa metro cuadrado de la capa emisora de la fotosfera es aproximadamente de 64 MW. Como en el espacio no hay prácticamente atenuación de la radiación solar, cuando ésta alcanza la órbita de la Tierra tiene una densidad de potencia igual al cociente entre la luminosidad total del Sol (3’89×1026 W) y el área de una esfera de radio orbital (que, como promedio, es de unos 150 millones de kilómetros).
Este flujo, tradicionalmente conocido como la constante solar, es la tasa máxima de energía que llega a la parte superior de la atmósfera terrestre. A principios de los años setenta, la NASA utilizó el diseño de las naves espaciales un valor de la constante solar igual a 1.353 W/m2. El flujo ha sido medido directamente en el espacio 1979, cuando el satélite Nimbus 7 obtuvo un valor de 1.371 W/m2. En el más reciente satélite de la Solar Maximum Mission lanzado en 1980 se obtuvo una media ponderada de 1.368’3 W/m2.
Las observaciones continuadas desde el espacio han revelado la existencia de una compleja regularidad de pequeñas fluctuaciones de corta duración que, debido a la interferencia de la atmósfera, no habían podido ser observadas anteriormente. Estas fluctuaciones de poca duración (del orden de días a semanas) y de hasta un 0’2 por ciento son debidas al paso de manchas oscuras y fáculas brillantes que arrastra el Sol en su rotación; el ciclo medido es de 11 años, en el que la radiación solar disminuye en un 0’1 por ciento entre el valor máxima y el mínimo.

Una onda electromagnética está formada por muy pequeños de energía llamados fotones. La energía de paquete o fotón es directamente proporcional a la frecuencia de la onda: Cuanta más alta es la frecuencia, mayor es la cantidad de energía contenida en cada fotón.
El efecto de las ondas electromagnéticas en los sistemas biológicos está determinado en por la intensidad del campo y en parte por la cantidad de energía contenida en cada fotón.
La longitud de onda de la energía electromagnética emitida por el Sol y que llega a la Tierra varía en más de diez órdenes de magnitud. Va la longitud de onda más corta, que corresponde a los rayos gamma y rayos X de menos de 10-10 m, hasta la longitud de ondas de radio que superan el metro.
El aspecto del espectro de la radiación solar es similar al de un cuerpo negro a 6.000º K. Ambos espectros son especialmente parecidos en el rango de la longitud de onda mayor que la del amarillo, pero longitudes de onda menores, el espectro solar cae notablemente por debajo de la línea de los 6.000º K. De acuerdo con la ley de desplazamiento de Wien, la emisión máxima a esta temperatura es de 483 nm, cerca del final de la zona azul del espectro visible y próximo al verde.
El flujo de energía se reparte desigualmente las tres grandes categorías espectrales: radiación ultravioleta (UV), cuya longitud de onda va desde las más cortas hasta los 400 nm y contribuye con menos del 9 por ciento de la radiación total; la luz visible, que va desde los 400 nm del violeta más lejano hasta los 700 nm del rojo más oscuro y representa un 39 por ciento; y la radiación infrarroja (IR), que representa cerca del 52 por ciento.

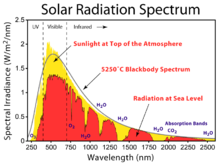
Espectro de la irradiancia solar en la parte superior de la atmósfera y espectro de la radiación solar por encima de la atmósfera y a nivel del mar.
No todos los puntos de la superficie terrestre reciben la misma cantidad de radiación solar. La posición relativa de la Tierra respecto al Sol, y el movimiento de la misma alrededor del astro condicionan, por ejemplo, que en el ecuador se reciba más energía que en los polos y que en verano llegue más que en invierno.
Los valores más altos de radiación a nivel del suelo se registran en algunos desiertos, donde se han llegado a medir 220 kcal/(cm2/año). Los mínimos se dan en los polos, donde hay estimaciones inferiores a 80 kcal/(cm2/año). En España, los valores aumentan de norte a sur y oscilan 110 y 150 kcal/(cm2/año)

La radiación que llega a la superficie de la Tierra es muy diferente de la radiación extraterrestre, tanto cualitativa como cuantitativamente. Las razones físicas de esta diferencia son varias: que la órbita de la Tierra es elíptica, la propia del planeta, la inclinación del eje de rotación, la composición de la atmósfera y la reflectividad (albedo) de las nubes y superficies terrestres. Consecuentemente, la radiación solar que llega a la superficie de la Tierra presenta una compleja pauta espacial y temporal. La media anual global es ligeramente inferior a 170 W/m2 en los océanos y de 180 W/m2 en los continentes. La diferencia más importante del valor esperado, según la latitud de la zona, se encuentra en la disminución que se presenta en los trópicos y los monzones subtropicales, debido a la alta nubosidad. Grandes regiones de Brasil, Nigeria y el sur de China reciben menos insolación que Nueva Inglaterra o las regiones de Europa occidental. Es aún más sorprendente que no haya diferencia entre el flujo máximo que se recibe al mediodía durante el verano en Yakarta, situada en el ecuador, y el que se recibe en ciudades subárticas como Edmonton en Canadá o Yakutsk en Liberia. Quizás el mejor ejemplo sea el de Oahu, donde la casi siempre nublada cordillera Koolau, que intercepta las nubes y las lluvias arrastran los alisios, tiene una media anual de radiación de 150 W/m2, mientras que en Pearl Harbor, a 15 Km de distancia en la dirección del viento, la media es de 250 W/m2.

Viendo el mapa me explico que los del norte de Europa se vengan a nuestras playas
La radiación solar media de 170 W/m2 representa anualmente una energía de 2’7×1024 J, que equivale a 87 PW. Esta cantidad es casi 8.000 veces mayor que el consumo mundial de combustibles sólidos y electricidad durante los primeros años noventa. Sólo una pequeña fracción de este inmenso flujo es absorbida por los pigmentos de las plantas realizar la fotosíntesis, y una parte algo mayor, pero también pequeña, se utiliza para calentar las plantas, los cuerpos de los animales y las personas, así como sus refugios.
La radiación también sustenta la vida porque al calentar los océanos, las rocas y los suelos, impulsa funciones fundamentales en la biosfera, tales el ciclo del agua, la formación de los vientos, el mantenimiento de la temperatura adecuada para que funcionen los procesos metabólicos y la descomposición orgánica. Además, es la causante de la erosión que transporta los nutrientes minerales para la producción primaria de materia orgánica.
Sección transversal del Sol
A la larga, mantener el equilibrio térmico del planeta, la radiación solar absorbida debe emitirse al espacio, pero la longitud de onda está drásticamente desplazada hacia el infrarrojo. A diferencia de la radiación de longitud de onda corta emitida por el Sol, que está determinada por la temperatura de la fotosfera (5.800º K), la radiación terrestre corresponde muy aproximadamente a las emisiones electromagnéticas de un cuerpo negro a 300º K (27ª C). El máximo de emisión de esa esfera caliente está en la zona del IR a 966 μm. Como el 99% de la radiación solar llega en longitudes de onda menores de 4 μm y el espectro terrestre apenas alcanza los 3 μm, el solapamiento de frecuencias entre estos dos grandes flujos de energías es mínimo.
Reacción protón–protón formar helio 4 liberando energía.
Así, de los mecanismos que se producen en el Sol, la estrella más cercana a la Tierra, surgen energías inmensas de las que, una pequeña fracción nos llega al planeta y nos ofrece la luz y el calor que necesitamos para vivir, para que la fotosíntesis sea posible y para que nuestro habitat permita la vida que en otros mundos está ausente.
emilio silvera
Jun
11
Sin la relación energética Sol-Tierra…¡No estaríamos aquí!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Relación del Sol con la Tierra ~
Clasificado en Relación del Sol con la Tierra ~
 Comments (0)
Comments (0)

La misión Kepler busca planetas extrasolares y estudia el interior de las estrellas a través de sus vibraciones. En esta composición se observa una de estas estrellas con un planeta orbitando entorno a ella. La estrella oscila debido a ondas acústicas resonantes.
Las trazas en rojo representan las oscilaciones que recorren el interior de la estrella. En la representación se ven los caminos recorridos por las ondas entre la superficie y un punto de su interior y que hay ondas que llegan hasta el núcleo del Sol y otras que quedan atrapadas más cerca de su superficie. (Fuente: Gabriel Pérez Díaz, Instituto de Astrofísica de Canarias).

Mientras en el núcleo del Sol quede suficiente hidrógeno para mantener las reacciones termonucleares, la estrella que nos alumbra inundará la Tierra con radiación solar, que suministra la energía necesaria para mantener la mayoría de los procesos físicos y químicos que se producen en nuestro planeta.
Esta radiación calienta la atmósfera y el océano, genera vientos y lluvias y sostiene el inexorable proceso de la denudación. De todas las conversiones generadas de las energías globales que se producen en la Tierra, las geotectónicas (la lenta modificación del fondo oceánico y de los continentes, acompañada de terremotos y las espectaculares liberaciones energéticas de los volcanes), son las únicas que no proceden de la radiación solar, sino de la gravedad y de la liberación gradual del calor terrestre.
La luz solar también suministra la energía necesaria para la fotosíntesis, la más importante transformación bioquímica, creando nueva biomasa en bacterias, fitoplancton, plantas superiores y, sobre todo, en bosques y praderas. Esta síntesis es el fundamento de la cadena alimenticia necesaria para el metabolismo heterótrofo de animales y personas, a los cuales la nutrición les permite desarrollar actividades que van desde una simple carrera a trabajos más elaborados, como la ocupación laboral y el ocio.

Así de importante es la luz. Las sociedades humanas, desde los pequeños grupos de cazadores o pastores hasta las sociedades más complejas que dependen de los enormes flujos de combustibles fósiles y electricidad, han estado ineludiblemente ligadas al continuo flujo de energía solar y a los almacenamientos energéticos procedentes de la misma.
El proceso de formación de carbón a partir de restos vegetales acumulados en zonas acuáticas y sumergidos, de tal manera que estaban aislados de la atmósfera, sufrieron una transformación por efecto de las bacterias anaeróbicas, que aumentan la concentración de carbono de los azúcares y desprenden gases, como metano y anhídrido carbónico. Así se forma una masa gelatinosa de turba. Posteriormente, ésta se hunde y sobre ella se van depositando nuevas capas. Las más inferiores pueden sufrir transformaciones metamórficas debido a la elevada presión y temperatura que soportan, convirtiéndose en grafito. Las condiciones biológicas, climáticas y estructurales más favorables para que tenga lugar esta serie de transformaciones se dieron durante el periodo carbonífero, que en Eurasia y Norteamérica se encontraban situadas en posición tropical y cubiertas de grandes bosques próximos al mar, que se inundaron debido a los movimientos verticales causados por la orogenia hercínica. Los yacimientos de carbón de mayor antigüedad proceden del devónico y los más modernos del cuaternario inferior.
La materia orgánica se transforma, el moho aparece y las condiciones del ambiente lo transforman todo. De la misma manera, ocurre con los combustibles fósiles que, a partir de plantas y materia en estado anaeróbico, se producen esas transformaciones a lo largo de millones de años.
![[Bacterias+metanogenas.jpg]](http://2.bp.blogspot.com/_oZOg6YjBvWk/SpBPwtdZGVI/AAAAAAAACW4/6TOQiATRKzI/s1600/Bacterias%2Bmetanogenas.jpg)
Bacterias metanógenas como estas bacterias terrestres de la imagen podrían ser las responsables de la liberación de gas metano en Marte
La primera etapa del proceso de degradación de la materia orgánica es la formación de metano por la acción de las bacterias. Posteriormente, durante el enterramiento de la misma, se produce la transformación a un producto intermedio denominado kerógeno, que puede ser de distintos tipos dependiendo de la materia orgánica original presente en los sedimentos. Así, los denominados kerógenos de tipo I e II darán lugar a la generación de petróleo. Junto con la presión actúa la temperatura, que alcanza las condiciones más favorables para la producción entre los 70 y los 100 ºC. Estas temperaturas pueden alcanzarse, dependiendo del gradiente geotérmico, entre los 2 y los 3,5 km de profundidad. Con el aumento de la temperatura disminuye la producción de petróleo y aumenta la de gas “húmedo” (se llama así, ya que junto con el metano entran en la composición etano, propano y butano, que pueden condensarse, con facilidad a la fase líquida). A partir de los 150 ºC se genera gas seco (compuesto principalmente de metano), y si el enterramiento es más profundo, los residuos pueden llegar a convertirse en grafito.

El carbono es un elemento químico de número atómico 6 y símbolo C. Es sólido a temperatura ambiente. Dependiendo de las condiciones de formación, puede encontrarse en la naturaleza en distintas formas alotrópicas, carbono amorfo y cristalino en forma de grafito o diamante. Es el pilar básico de la química orgánica.
Pero el proceso de formación del petróleo se origina a partir de acumulaciones de plancton marino que sufre transformaciones, semejantes a la carbonización, por bacterias anaeróbicas, y que dan lugar a una materia denominada sapropel y posteriormente a la mezcla de hidrocarburos típica del petróleo. Esta transformación de hidrocarburos suele tener lugar al mismo tiempo que el proceso de sedimentación de arenas y arcillas que se transformarán en areniscas y margas, y quedarán impregnadas por el petróleo, dando lugar a las rocas madre de éste. Cuando éstas sufren presiones orogénicas o simplemente quedan sometidas a una mayor presión al hundirse los sedimentos, el petróleo migra hasta encontrarse con rocas impermeables que impiden su avance y se acumula en el subsuelo, generando los verdaderos yacimientos petrolíferos.
Los hidrocarburos gaseosos están acumulados en la parte superior de estos yacimientos de petróleo (aceites de roca: del latín petram, “piedra” y oleum, “aceite”), que es un aceite mineral hidrocarbonato, oleaginoso, inflamable, de olor acre, densidad inferior a la del agua y cuyo color varía desde el negro al incoloro. Consta principalmente de hidrocarburos líquidos, en los que se encuentran disueltos hidrocarburos sólidos (asfaltos y betunes) y gaseosos (metano, butano y acetileno); también contiene pequeñas porciones de nitrógeno, azufre, oxígeno, colesterina, porfirinas, vanadio, níquel, cobalto y molibdeno. De todo esto, mediante procesos industriales de refinado, se obtienen los productos de todos conocidos como la gasolina, nafta, queroseno, gasóleo, etc.

Su combustión es una de las fuentes más importantes de contaminación por los elevados porcentajes de azufre y otras materias que contiene. Sin embargo, por obtener esta fuente de contaminación y “riqueza” se crean conflictos que desembocan en las guerras que azotan nuestro mundo.
Ahora, después de esta breve explicación, sabemos un poco más sobre esta materia prima que ha servido, y continuará aún algún tiempo sirviendo de base a muchas generaciones pasadas y alguna menos futura: civilizaciones del combustible sólido, con su profesión de servicios energéticos, transporte generalizado y exceso de información (no siempre deseable, ya que si elimináramos el 80% de las programaciones televisivas, el mundo sería algo más culto y estaría menos embrutecido).

Un observador extraterrestre no podría encontrar nada extraordinario que le permitiera distinguir el Sol entre los millones de estrellas similares que existen en la nuestra y en otras galaxias, y que a su vez representan una fracción de cientos de miles de millones de cuerpos radiantes que las forman. Como se ha dicho otras veces, nuestro Sol pertenece a una clase común de estrella localizada aproximadamente en el centro de la secuencia principal del esquema de clasificación conocido como de Herzsprung-Russell, denominada enana G2, que posee un característico color amarillo y una magnitud estelar poco importante (+4’83). Así que, después de 4.500 millones de años, el Sol está a la mitad de su vida y va camino de transformarse de enana en gigante roja. Cuando esto ocurra, su luminosidad será mil veces mayor que la actual, y su diámetro, enormemente expandido, alcanzará (probablemente) la Tierra. Durante algún tiempo el planeta girará dentro de una órbita en el interior de la ligera cubierta de la estrella, pero final e inevitablemente caerá describiendo una espiral hasta ser engullida por el núcleo de la gigante roja.
Mucho antes de que el Sol se transforme en una gigante roja la vida en la Tierra desaparecerá. Según se contraiga el núcleo solar, las reacciones termonucleares calentarán su capa externa; el diámetro de la estrella se expandirá unas diez mil veces y la radiación de la subgigante roja evaporará los océanos y mares de la Tierra generando fortísimos vientos calientes en la convulsa atmósfera del planeta.

Sin embargo, mientras haya hidrógeno en el núcleo de la estrella, los inexorables cambios de su luminosidad serán graduales y el Sol continuará suministrando la energía necesaria, tanto para la vida en la Tierra como para la mayoría de las transformaciones físicas que ocurren en ella.
Las primeras explicaciones científicas de la radiación solar, cálculo basado en la gravitación de Hermann Helmholtz, conducen a una estimación de la vida de la estrella de unos treinta millones de años. La famosa ecuación de Einstein relacionando la materia y la energía abrió el camino hacia un modelo más preciso que, por sí sólo, tampoco nos ofrece una solución completamente satisfactoria. Por otra parte, no parece probable que la transformación total de materia solar, convirtiendo los núcleos atómicos y los electrones en radiación (según teorizaba Sir Arthur Eddington), pueda producirse ni siquiera a temperaturas superiores a los diez mil millones de grados Kelvin (K). La idea hoy aceptada de que la producción de la energía en el núcleo del Sol obedece a reacciones nucleares fue propuesta a finales de los años treinta por Hans Bethe, Charles Critchfield y Carl Friedrich von Weizsäcker.

La fusión de hidrógeno en helio, en el ciclo protón–protón, se inicia cuando la temperatura alcanza los trece millones de grados Kelvin. Justo por encima de los 16 millones Kelvin empieza a dominar el ciclo carbono-nitrógeno que genera C12. No podemos estar seguros, pero de acuerdo con los mejores modelos, el ciclo C-N genera solamente un 1’5% de la energía total del Sol.
Las reacciones en el núcleo solar consumen entre 4’3 y 4’6 millones de toneladas de materia cada segundo, de manera que de 4.654.000 t de hidrógeno, 4.650.000 se transforman en helio, y las 4.000 toneladas que faltan son lanzadas al espacio en forma de radiación termonuclear (luz y calor) de la que una pequeña parte nos llega a la Tierra para hacer posible la vida.
De acuerdo a la relación masa-energía de Einstein, liberan 3’89×1026 J de energía nuclear. Este inmenso flujo de energía es rápidamente transformado en energía térmica, que es transportado, isotrópicamente, hacia el exterior, primero por irradiación aleatoria y luego más rápidamente por convección direccional.

Suponiendo (como antes apuntaba) que la radiación es isótropa, la potencia de la luz visible que atraviesa cada metro cuadrado de la capa emisora de la fotosfera es aproximadamente de 64 MW. Como en el espacio no hay prácticamente atenuación de la radiación solar, cuando ésta alcanza la órbita de la Tierra tiene una densidad de potencia igual al cociente entre la luminosidad total del Sol (3’89×1026 W) y el área de una esfera de radio orbital (que, como promedio, es de unos 150 millones de kilómetros).
Este flujo, tradicionalmente conocido como la constante solar, es la tasa máxima de energía que llega a la parte superior de la atmósfera terrestre. A principios de los años setenta, la NASA utilizó para el diseño de las naves espaciales un valor de la constante solar igual a 1.353 W/m2. El flujo ha sido medido directamente en el espacio desde 1979, cuando el satélite Nimbus 7 obtuvo un valor de 1.371 W/m2. En el más reciente satélite de la Solar Maximum Mission lanzado en 1980 se obtuvo una media ponderada de 1.368’3 W/m2.
Las observaciones continuadas desde el espacio han revelado la existencia de una compleja regularidad de pequeñas fluctuaciones de corta duración que, debido a la interferencia de la atmósfera, no habían podido ser observadas anteriormente. Estas fluctuaciones de poca duración (del orden de días a semanas) y de hasta un 0’2 por ciento son debidas al paso de manchas oscuras y fáculas brillantes que arrastra el Sol en su rotación; el ciclo medido es de 11 años, en el que la radiación solar disminuye en un 0’1 por ciento entre el valor máxima y el mínimo.

Una onda electromagnética está formada por paquetes muy pequeños de energía llamados fotones. La energía de cada paquete o fotón es directamente proporcional a la frecuencia de la onda: Cuanta más alta es la frecuencia, mayor es la cantidad de energía contenida en cada fotón.
El efecto de las ondas electromagnéticas en los sistemas biológicos está determinado en parte por la intensidad del campo y en parte por la cantidad de energía contenida en cada fotón.
La longitud de onda de la energía electromagnética emitida por el Sol y que llega a la Tierra varía en más de diez órdenes de magnitud. Va desde la longitud de onda más corta, que corresponde a los rayos gamma y rayos X de menos de 10-10 m, hasta la longitud de ondas de radio que superan el metro.
El aspecto del espectro de la radiación solar es similar al de un cuerpo negro a 6.000º K. Ambos espectros son especialmente parecidos en el rango de la longitud de onda mayor que la del amarillo, pero para longitudes de onda menores, el espectro solar cae notablemente por debajo de la línea de los 6.000º K. De acuerdo con la ley de desplazamiento de Wien, la emisión máxima a esta temperatura es de 483 nm, cerca del final de la zona azul del espectro visible y próximo al verde.
El flujo de energía se reparte desigualmente entre las tres grandes categorías espectrales: radiación ultravioleta (UV), cuya longitud de onda va desde las más cortas hasta los 400 nm y contribuye con menos del 9 por ciento de la radiación total; la luz visible, que va desde los 400 nm del violeta más lejano hasta los 700 nm del rojo más oscuro y representa un 39 por ciento; y la radiación infrarroja (IR), que representa cerca del 52 por ciento.
Distribución de la radiación solar que llega a la superficie terrestre, expresada en kcal/(cm2/año)
No todos los puntos de la superficie terrestre reciben la misma cantidad de radiación solar. La posición relativa de la Tierra respecto al Sol, y el movimiento de la misma alrededor del astro condicionan, por ejemplo, que en el ecuador se reciba más energía que en los polos y que en verano llegue más que en invierno.
Los valores más altos de radiación a nivel del suelo se registran en algunos desiertos, donde se han llegado a medir 220 kcal/(cm2/año). Los mínimos se dan en los polos, donde hay estimaciones inferiores a 80 kcal/(cm2/año). En España, los valores aumentan de norte a sur y oscilan entre 110 y 150 kcal/(cm2/año)
La radiación que llega a la superficie de la Tierra es muy diferente de la radiación extraterrestre, tanto cualitativa como cuantitativamente. Las razones físicas de esta diferencia son varias: que la órbita de la Tierra es elíptica, la propia forma del planeta, la inclinación del eje de rotación, la composición de la atmósfera y la reflectividad (albedo) de las nubes y superficies terrestres. Consecuentemente, la radiación solar que llega a la superficie de la Tierra presenta una compleja pauta espacial y temporal. La media anual global es ligeramente inferior a 170 W/m2 en los océanos y de unos 180 W/m2 en los continentes. La diferencia más importante del valor esperado, según la latitud de la zona, se encuentra en la disminución que se presenta en los trópicos y durante los monzones subtropicales, debido a la alta nubosidad. Grandes regiones de Brasil, Nigeria y el sur de China reciben menos insolación que Nueva Inglaterra o las regiones de Europa occidental. Es aún más sorprendente que no haya diferencia entre el flujo máximo que se recibe al mediodía durante el verano en Yakarta, situada en el ecuador, y el que se recibe en ciudades subárticas como Edmonton en Canadá o Yakutsk en Liberia. Quizás el mejor ejemplo sea el de Oahu, donde la casi siempre nublada cordillera Koolau, que intercepta las nubes y las lluvias arrastran los alisios, tiene una media anual de radiación de 150 W/m2, mientras que en Pearl Harbor, a 15 Km de distancia en la dirección del viento, la media es de 250 W/m2.

Viendo el mapa me explico que los del norte de Europa se vengan a nuestras playas
La radiación solar media de 170 W/m2 representa anualmente una energía de 2’7×1024 J, que equivale a 87 PW. Esta cantidad es casi 8.000 veces mayor que el consumo mundial de combustibles sólidos y electricidad durante los primeros años noventa. Sólo una pequeña fracción de este inmenso flujo es absorbida por los pigmentos de las plantas para realizar la fotosíntesis, y una parte algo mayor, pero también pequeña, se utiliza para calentar las plantas, los cuerpos de los animales y las personas, así como sus refugios.
La radiación también sustenta la vida porque al calentar los océanos, las rocas y los suelos, impulsa funciones fundamentales en la biosfera, tales como el ciclo del agua, la formación de los vientos, el mantenimiento de la temperatura adecuada para que funcionen los procesos metabólicos y la descomposición orgánica. Además, es la causante de la erosión que transporta los nutrientes minerales para la producción primaria de materia orgánica.
Sección transversal del Sol
A la larga, para mantener el equilibrio térmico del planeta, la radiación solar absorbida debe emitirse al espacio, pero la longitud de onda está drásticamente desplazada hacia el infrarrojo. A diferencia de la radiación de longitud de onda corta emitida por el Sol, que está determinada por la temperatura de la fotosfera (5.800º K), la radiación terrestre corresponde muy aproximadamente a las emisiones electromagnéticas de un cuerpo negro a 300º K (27ª C). El máximo de emisión de esa esfera caliente está en la zona del IR a 966 μm. Como el 99% de la radiación solar llega en longitudes de onda menores de 4 μm y el espectro terrestre apenas alcanza los 3 μm, el solapamiento de frecuencias entre estos dos grandes flujos de energías es mínimo.
Reacción protón–protón para formar helio 4 liberando energía.
emilio silvera
















 Totales: 69.198.590
Totales: 69.198.590 Conectados: 56
Conectados: 56