Abr
8
¡Aquellos viajeros!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Rumores del saber del mundo ~
Clasificado en Rumores del saber del mundo ~
 Comments (0)
Comments (0)

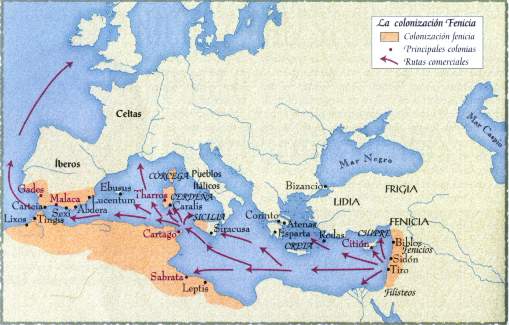
Esta misma entrada ha sido vista aquí en varias ocasiones pero, lo que representa, tiene el derecho a que sea divulgada una y otra vez. Se trata de la historia de intrépidos viajeros-aventureros que con su valor, hicieron posible el conocimiento de nuevas tierras y nuevas gentes. Algunos tenían en la mente la existencia de lugares maravillosos y no se paraban a pensar en los peligros que tratar de descubrirlos conlleva. Otros, buscaban tesoros y no pocos salían en busca de las aventuras que esperaban vivir en asombrosas situaciones, lugares y gente que ni podían imaginar.
Parecida era la concepción de la tierra representada en el primer mapamundi griego del que se tienen referencias. Hablan de él y lo describen Heródoto y Estrabón. Lo dibujó Anaximandro (ca. 611-545 a.C.) y sabemos que el mapa abarcaba todo el ámbito de la tierra habitable con todos los mares y ríos conocidos. La tierra, según la representó Anaximandro, era un cilindro oblongo, dos veces más ancho (de Este a Oeste) que alto (de norte a sur). Se distribuía alrededor del mar Mediterráneo y estaba a su vez rodeada por un río-océano. Esta tierra cilíndrica y oblonga estaba habitada únicamente en su disco superior -al que los griegos llamaban ecúmenos, diferenciando la tierra habitada y habitable de la tierra-planeta-, y permanecía libremente suspendida en el centro de una esfera completa que era el cielo. No se caía, porque al ser equidistante de todo, no podía caer hacia ningún lado.

La concepción del mundo ha sido siempre muy variada para los distintos pueblos
Pasamos a comentar hechos y sobre personajes que, en distintas épocas y partes del mundo, hicieron posible el avance de nuestros conocimientos, todos y todo contribuyó a ello, cada cosa y cada personaje en su medida, y, unificados lo hicieron posible. Hoy nosotros, podemos aprender de todo aquello, y podemos saber como llegaron a conseguir los conocimientos que tenemos en muchos aspectos de nuestras experiencias transmitidas por estudiosos de hace muchos siglos.
Aquellos hombres arriesgaban sus vidas por saber, fueron muchos de los clásicos griegos los pertenecientes a este grupo viajero, y, a pesar del riesgo que ello conllevaba, viajaban a lugares lejanos buscando saber de matemáticas o de astronomía.

Por estas aguas del Mediterráneo, en el Estrecho de Gibraltar, pasaron aquellas embarcaciones milenarias que, en busca de aventuras y para descubrir nuevas tierras, alcanzaron el conocimiento de nuevas civilizaciones y nuevas gentes.
También proliferaban los viajeros guerreros y aventureros. Los mercaderes y comerciantes, por aquellos tiempos, fueron el ejemplo de hombres viajeros audaces que, buscando fortuna eran capaces de llegar hasta el fin del mundo (como se solía decir entonces).

Los griegos había descubierto el Atlántico en el s. VII a.C., cuando dieron el nombre de columnas de Hércules a la que hoy es el estrecho de Gibraltar. Según Hecateo, el mundo era básicamente un plato plano y circular, cuyo centro estaba cerca de Troya o de la actual Estambul, y el mar Mediterráneo era una vía de acceso a un océano que circundaba toda la tierra. A finales del S. VI, en el sur de Italia, un seguidor de Pitágoras propuso la idea de que la tierra era una esfera, una de los diez unidades de ese tipo que giraban alrededor de un fuego ubicado en el centro. Sócrates y Platón aceptaron la perspectiva pitagórica y el primero llegó a decir que la tierra era plana en apariencia debido a su enorme tamaño.
Los griegos sabían que la tierra firme se extendía desde España hasta la India y había rumores de que incluso más allá.
El primer viajero del que se tiene noticias es Piteas, que vivió en Massalia (la actual Marsella). Gracias a barqueros que habían recorrido el Ródano y conocido a otros viajeros, los habitantes de Massalia sabían que existía al norte un mar lo suficientemente grande como para contener islas, en las que se producían metales preciosos y una sustancia resinosa de color amarillo oscuro, muy apreciada debido a su belleza, denominada ámbar. Sin embargo, el Ródano no llegaba hasta este mar y nadie sabía en realidad lo lejos que estaba.
Aquellos Viajeros cambiaron el Mundo y lo descubrieron
Hacia el año 330 a.C., unos marineros que regresaban tras viajar al Mediterráneo occidental informaron de que, en esta ocasión, las Columnas de Hércules no estaban siendo defendidas. Era la oportunidad que los mercaderes de Messalia habían estado esperando:
Se escogió a Piteas para realizar este viaje y se le equipó con una embarcación de unos cuarenta metros de largo (más grande de las que emplearía Colón). Bordeando el continente, Piteas finalmente alcanzó el norte de Francia y luego, en medio de la niebla y la lluvia, pasó entre Inglaterra e Irlanda en dirección norte hasta llegar a las Orcadas y a continuación fue más allá de los Shetland y las Feroe y se encontró con una tierra en la que, durante el primer día del verano, el Sol permanecía durante veinticuatro horas por encima del horizonte.
Los antiguos griegos asentaban las Columnas de Hercules en el Estrecho de Gibraltar, paso hacia el Mar mayor, hoy Océano Atlántico. Platón mencionaba al historiador Solón para hablar de la ciudad perdida, la Atlántida, uno de los mitos históricos más antiguos. La Civilización floreciente situada en una Isla más allá de las Columnas de Hércules. La historia fue contado por Platón en sus diálogos Timeo y Critias. Pero sigamos con la historia del intrépido Piteas.
Piteas denominó a este lugar Tule, y durante siglos Última Tule se consideró el fin del mundo en esta dirección (es posible que se tratara de Islandia, Noruega o incluso algunas de los Shettand o las Faroe). Piteas regresó por Dinamarca y Suecia y descubrió un gran mar interior, el Báltico, donde comenzó su búsqueda del País del Ámbar. En su recorrido, descubrió ríos que fluían de sur a norte (como el Oder y el Vistula) y entendió que a través de ellos las noticias sobre el mar del norte habían llegado al Mediterráneo.

Estas aguas en la antigüedad fueron el testigos mudo de aquellos acontecimientos
Cuando regresó a casa, muchos se negaron a creer su historia y luego los cartagineses se hicieron con el control de las Columnas de Hércules, cerrando de nuevo el paso del Atlántico.
Por otro lado, los griegos sabían que más allá de Persia había un lugar llamado India. Habían escuchado relatos fabulosos sobre un rey tan poderoso que podía usar en la guerra mil elefantes, e historias de hombres con cabezas de perro y de gusanos enormes, capaces de arrastrar un buey o un caballo hasta el río para devorarlos allí.
El año 331 a.C., Alejandro Magno comenzó la serie de conquistas que lo llevarían más allá de Persia, hasta Afganistán y el río Indo, en el que encontró a los cocodrilos, los gigantescos gusanos de los que hablaban las leyendas.

¿Qué lugares contemplarían aquellos viajeros? Son muchos los pueblos que emprendieron viajes sin saber si podrían regresar, sus deseos de aventura y conquista les llevaron no pocas veces a jugarse la vida en busca de quiméricos sueños
Siguió el curso del río hasta llegar al gran océano del que le habían llegado rumores. Era un hecho: la tierra estaba en verdad ordenada por el mar como los antiguos habían dicho.
Todos los detalles de estos viajes empezaron más tarde a ser reunidos por los estudiosos, especialmente en la famosa biblioteca de Alejandría (ya comentaré algo sobre este tema más adelante), donde Eratóstenes (276-196 a.C.), probablemente el primer geógrafo matemático de la historia y uno de los bibliotecarios más destacados de la institución, se propuso crear el mapa más preciso del mundo. Igualmente, calculó que la circunferencia de la Tierra tenía algo menos de 40.200km.

Eratóstenes de Cirene fue un célebre matemático, astrónomo y geógrafo griego, de origen probablemente caldeo. Son muchos los estudiosos que en la Antigüedad nos dejaron su huella en forma de pensamientos que aún hoy perduran
Eratóstenes, que también calculó la cantidad de tierra habitable del planeta según el clima y desarrolló el concepto de latitud, lo que le permitió localizar de forma más precisa ciudades como Alejandría misma, Massalia, Asmán y Meroe, que había sido descubierta río arriba. Más tarde, Hiparlo amplió el trabajo de Eratóstenes, quien hacia 140 a.c., ajustó la circunferencia de la tierra propuesta por su predecesor y trazó líneas de latitud separadas un grado entre y a las que demonio klimata, que es de donde procede nuestra palabra clima.

San Brandán el Navegante
El primer gran aventurero del Atlántico, después de Piteas, y el primer explorador cristiano de la historia fue el monje irlandés conocido como san Brandán (o Barandán) el Navegante. Nacido hacia el año 484 cerca de Tralee y ordenado sacerdote en 512, Brandán creció escuchando los relatos de muchos pescadores irlandeses que se habían hecho a la mar y habían regresado con historias sobre unas islas situadas al oeste del país.
Brandán, según cuentan, era hombre decidido y, en compañía de otros dieciséis monjes, allá por el año 539, partió a la búsqueda de la “Tierra prometida de los Santos” en un viaje de los viajes de proporciones épicas. Fue tal su reputación que, incluso se le atribuyen viajes de otros.
Viajaban guiados por las estrellas y habiendo prestado atención a la migración de las aves, navegaron hacia el oeste durante cincuenta y dos días, tras lo cual llegaron a una isla y desembarcaron en ella. Allí sólo había un perro para recibirles, pero en cualquier caso, levantaron un refugio y descansaron. Cuando iban a partir de nuevo, apareció un isleño y les ofreció comida. Seguidamente encontraron una isla en la que había rebaños de ovejas blanquísimas y arroyos repletos de peces. Decidieron pasar allí el invierno y fueron acogidos en un monasterio.
La Histortia está llena de historias de viajeros que abrieron nuevos caminos en regiones ignotas.
Continuaron el viaje y visitaron otras islas del Atlántico, como por ejemplo la Isla de los hombres fuertes, que estaba cubierta por una alfombra de flores blancas y púrpuras. Los monjes también navegaron alrededor de una enorme columna de cristal que flotaba en el océano y pasaron cerca de una isla de “herreros gigantes” que le arrojaron terrones de escoria al rojo vivo. (Decidieron que ésta era la frontera exterior de infierno). Otra montaña que vieron más al norte, arrojaba fuego y humo al cielo.
En ningún lugar pudieron hallar la tierra que constituía el objetivo del viaje. Se especuló mucho, pero nadie sabe a ciencia cierta, qué lugares visitaron.
La historia de los mongoles, escrita por Juan de Plano Carpini, que inició su viaje en la Pascua de 1.245, tuvo un gran éxito y, su viaje y descripción contada en este libro, fue una importante contribución al conocimiento de Oriente.


El interés por Oriente podía advertirse especialmente en Europa en un punto de Italia, Venecia, cuyos mercaderes se habían mantenido vinculados con los comerciantes árabes y musulmanes, que les proporcionaban artículos procedentes de países situados más al este.
Esta fue la razón de que los hermanos Polo, Nicolás y Mateo, decidieran abrirse camino en Asia en 1.260. Este primer viaje resultó muy fructífero ya que el líder mongol de la época, el gran kublai kan, estaba muy interesado en Europa, y los hermanos Polo regresaron convertidos en sus embajadores.
Marco Polo, uno de los grandes viajeros
En 1.271, cuando los Venecianos regresaron a Oriente, llevaron consigo a Maroc, hijo de Nicolás, que entonces tenía diecisiete años, al que se convertiría en uno de los viajes más épicos de todos los tiempos.
Los Polos siguieron la antigua Ruta de la Sed (cincuenta y dos días de viaje) hasta alcanzar kashgar y Yarkand, en los límites de China. Desde allí atravesaron el desierto y llegaron finalmente a kambalu (la actual Beijing) donde se había trasladado la capital del kan desde karakorum. La ciudad fascinó a Marco Polo, que la describe como “más grande de lo que la mente puede imaginar… no menos de mil carruajes y caballos de carga entran en ella diariamente cargados con seda cruda; Brocados y sedas de distintos tipos y colores que se fabrican allí en enormes cantidades.”

Como su padre, Marco era un astuto comerciante, con una profunda sensibilidad para los negocios, y también se convirtió en favorito del Kan. Durante quince años le sirvió como embajador de China y el Oriente. De hecho, los Polo sólo regresaron a su ciudad cuando Kublai Kan y el gobernante de Persia hubieron acordado un contrato de matrimonio en el que se establecía el envió a Occidente de una joven prometida.
Con el fin de realizar el acuerdo, se preparó una escolta de catorce naves, de la que formaban parte los Polo. Las embarcaciones partieron de Ziton (la actual Amoy). En la costa del Pacífico (el cual, pensaban los Polo, daba la vuelta al mundo hasta alcanzar Europa), pero antes de llegar allí los Polos pasaron por Kinsai, la moderna Hangchow, lo que les deparó otra fantástica experiencia:

Los Polos presentan sus respetos al Emperador Kublai
La ciudad tenía sesenta kilómetros de circunferencia, contaba con diez grandes mercados y tenía doce mil puentes. “Cada día se comercia en los mercados de kinsai cuarenta y tres cargas de pimienta, cada una de ciento diez kilos.”
Marco Polo escuchó hablar de Cipango (Japón) a los marineros del Convoy, quienes le dijeron que quedaba a unos dos mil cuatrocientos kilómetros del continente (en realidad queda a menos de mil kilómetros de Shangai y a unos trescientos veinte de Corea).
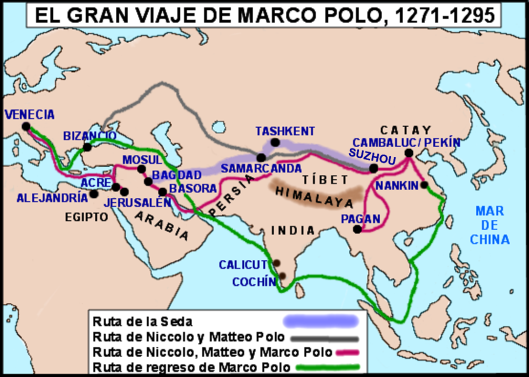
Cuando los Polo finalmente llegaron a casa, sus amigos les recibieron sorprendidos, pues hacía mucho tiempo que pensaban que estaban muertos.


Marco escribió el relato de sus viajes, La descripción del mundo, pero como al principio nadie creyó en lo que decía, se le apodó, Il Milione debido a los “increíbles cuentos” que narraba (el libro fue dictado a Rustichello de Pisa). Pese a la incredulidad de algunos de sus contemporáneos, los Polo habían llegado a los confines de Asia y habían conocido un nuevo y vasto océano.
En este pequeño resumen de las aventuras viajeras de Marco Polo, me he saltado la parte más fantástica y me he querido ajustar a los hechos históricos.
Emilio Silvera
Feb
15
Comentario sobre Lovejoy y sobre la idea del Alma
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Rumores del saber del mundo ~
Clasificado en Rumores del saber del mundo ~
 Comments (1)
Comments (1)



Si queréis saber sobre cosas extraordinarias y personajes asombrosos…. Buscad el libro que arriba aparece
Recordemos aquí algunos pasajes que pude encontrar en fuentes diversas, sobre todo, en el Libro Ideas de cuyo autor, PETER WATSON, podríamos decir que aquí, nos dejó un enorme estudio del saber del mundo y de aquellos acontecimientos del pasado que, desde luego, no deberíamos olvidar. Aquí os dejo algunos pasajes que, de vez en cuando , apostillo con alguna que otra frase mía.
, apostillo con alguna que otra frase mía.
Arthur Oncken Lovejoy, historian and philosopher of science
Lovejoy era en todos los sentidos una figura impresionante. Leía libros en inglés, alemán, francés, griego, latín, italiano y español, y sus estudiantes contaban como anécdota que, había pasado su año sabático de la Johns Hopkins dedicado a leer “los pocos libros de la biblioteca del Museo Británico que aún no había leído. Sin embargo, se le reprochó por tratar las ideas como “unidades” entidades subyacentes e inalterables, como los elementos químicos.
anécdota que, había pasado su año sabático de la Johns Hopkins dedicado a leer “los pocos libros de la biblioteca del Museo Británico que aún no había leído. Sin embargo, se le reprochó por tratar las ideas como “unidades” entidades subyacentes e inalterables, como los elementos químicos.
¡Qué cosas!

Beltrand Russell
Lovejoy fue ciertamente quien dio el impulso inicial a la historia de las ideas al convertirse en el primer director del Journal of the History of ideas, fundado en 1.940 (entre los primeros colaboradores estaban Bertrand Russell y Paul O. Kristeller). En el primer ejemplar, Lovejoy expuso el objetivo primordial del Journal: explorar la influencia de las ideas clásicas en el pensamiento moderno.
los primeros colaboradores estaban Bertrand Russell y Paul O. Kristeller). En el primer ejemplar, Lovejoy expuso el objetivo primordial del Journal: explorar la influencia de las ideas clásicas en el pensamiento moderno.
Lo curioso del caso es que, en los años transcurridos desde su fundación (hace más de 70 años), el Journal of the History of ideas ha continuado explorando la sutil forma en que una idea lleva a otra a lo largo de la historia. He aquí algunos de los temas tratados en números recientes: El efecto de Platón en Calvino; la admiración que Nietzsche profesaba por Sócrates; el budismo en el pensamiento alemán del siglo XIX; la relación de Newton y Adam Smith; el vínculo de Emerson con el hinduismo; Bayle como precursor de Kart Popper; el paralelismo entre la antigüedad tardía y la Florencia del Renacimiento; etc.
en que una idea lleva a otra a lo largo de la historia. He aquí algunos de los temas tratados en números recientes: El efecto de Platón en Calvino; la admiración que Nietzsche profesaba por Sócrates; el budismo en el pensamiento alemán del siglo XIX; la relación de Newton y Adam Smith; el vínculo de Emerson con el hinduismo; Bayle como precursor de Kart Popper; el paralelismo entre la antigüedad tardía y la Florencia del Renacimiento; etc.

Karl Popper
En su ensayo aparecido en el Journal para celebrar el cincuentenario de su publicación, el colaborador que lo escribía identificaba tres fallos dignos de ser señalados.
celebrar el cincuentenario de su publicación, el colaborador que lo escribía identificaba tres fallos dignos de ser señalados.
Uno de ellos era la incapacidad de los historiadores para comprender el verdadero significado de una de las grandes ideas modernas, la “secularización”.
Otro, la generalizada decepción respecto a la “psicohistoria”, cuando existían santísimas figuras que reclamaban una comprensión psicológica profunda: Erasmos, Lutero, Rousseau, Newton, Descartes, Vico, Goethe, Emerson, Nietzche…
existían santísimas figuras que reclamaban una comprensión psicológica profunda: Erasmos, Lutero, Rousseau, Newton, Descartes, Vico, Goethe, Emerson, Nietzche…


Descartes – Nietzche – Goethe
Y, por último, el fracaso de historiadores y científicos para dar cuenta de la “imaginación” como una dimensión de la vida en general y, especialmente, de la producción de ideas.
dar cuenta de la “imaginación” como una dimensión de la vida en general y, especialmente, de la producción de ideas.
¡Las ideas, qué peligro!
Es la única libertad que nos podemos permitir. El pensar libremente y para nosotros mismos, otra cosa es el exponer nuestros pensamientos a los demás. Unas veces por inconveniente, otras por pudor, otras por temor a las críticas, y otras por parecernos a nosotros mismos indignas de ser conocidas, así, se pierden grandes ideas.
Alguna vez he comentado sobre el Laboratorio Cavendish, y me viene a la memoria que fue allí, donde Thomson, en 1.897, realizó el descubrimiento que vino a coronar anteriores ideas y trabajos de Benjanmin Franklin, Euge Goldstein, Wilhelm Röntgen, Henri Becquernel y otros.
Durante la antigüedad tardía y la Edad Media, la tecnología del Alma…
la antigüedad tardía y la Edad Media, la tecnología del Alma…

Al percatarse de que todos veían el deterioro del cuerpo comido por los gusanos con la llegada de la muerte, el clero, se inventó la “salvación del Alma”, nuestro Yo especial que, podía ser salvado si nuestra contribución era generosa.
Pero, ¿Qué es el Alma? Acaso un invento de los hombres para tener la esperanza de que, todavía pueden salvar algo. Su relación con la “otra vida”, con la divinidad y, en especial, con el clero, permitió a las autoridades religiosas ejercer un poder extraordinario.
tener la esperanza de que, todavía pueden salvar algo. Su relación con la “otra vida”, con la divinidad y, en especial, con el clero, permitió a las autoridades religiosas ejercer un poder extraordinario.
No se puede negar que, la idea del Alma, enriqueció inmensamente la mente de los seres humanos a lo largo de los siglos, pero tampoco se puede negar que también es cierto que durante ese mismo tiempo mantuvo a raya el pensamiento y la libertad. ¿Os acordáis de Giordano Bruno y Galileo? Aquello retrasó el progreso y contribuyó a mantener el pueblo (en su mayor parte ) ignorante y sometido al clero educado y culto.
) ignorante y sometido al clero educado y culto.

El Papa que renunció a todo y se marchó
Si él mirara hacia atrás, hasta la Edad Media, vería con vergüenza como sus iguales, vendían indulgencias. Es decir, cobraban por salvar las “Almas” de los pecadores que, con riquezas, no con arrepentimientos, se creían a salvo de sus maldades. ¿habrá mirado y, al ver aquello, ha decidió marcharse?
atrás, hasta la Edad Media, vería con vergüenza como sus iguales, vendían indulgencias. Es decir, cobraban por salvar las “Almas” de los pecadores que, con riquezas, no con arrepentimientos, se creían a salvo de sus maldades. ¿habrá mirado y, al ver aquello, ha decidió marcharse?

Sólo tenemos que pensar en la desfachatez con la que el fraile Tetzel afirmaba que era posible comprar indulgencias para las “almas” del purgatorio, y que estas saldrían volando al cielo tan pronto como las monedas golpearan el plato. Los abusos como estos, aún persisten hoy en día, nada más claro como ejemplo el ver la cantidad de ancianos y viudas que solos en la vida y enfermos, dejan sus fortunas a la Iglesia que, por cierto, tienen situadas sus propiedades en las mejores enclaves de las ciudades.
las monedas golpearan el plato. Los abusos como estos, aún persisten hoy en día, nada más claro como ejemplo el ver la cantidad de ancianos y viudas que solos en la vida y enfermos, dejan sus fortunas a la Iglesia que, por cierto, tienen situadas sus propiedades en las mejores enclaves de las ciudades.
Los abusos a que se prestaba lo que algunos llaman “tecnologías del alma” fueron uno de los principales factores que condujeron a la Reforma, la cual, a pesar de lo ocurrido con Juan Calvino en Ginebra, fundamentalmente despojó al clero del control de la fe e impulsó la duda y el descreimiento.
Sí, de muchas maneras nos pintaron el Alma que, para muchos, abusando de la ignorancia del pueblo, supuso un gran negocio “su salvación”. Aun hoy, desgraciadamente, prevalece mucho de aquel mundo.
muchos, abusando de la ignorancia del pueblo, supuso un gran negocio “su salvación”. Aun hoy, desgraciadamente, prevalece mucho de aquel mundo.
Las diversa transformaciones del alma (la idea de que estaba contenida en el semen en la Grecia de Aristóteles, el alma tripartita del Timen platónico, la concepción medieval y renacentista del Homo duplex, la idea del alma como mujer, o como ave, el diálogo entre el alma y el cuerpo de Marvell, “las monadas” de Leibniz) pueden resultar hoy bastante pintorescas, pero en su época fueron cuestiones muy serias, y constituyeron importantes etapas en la ruta hacia la idea moderna del ser.
el alma y el cuerpo de Marvell, “las monadas” de Leibniz) pueden resultar hoy bastante pintorescas, pero en su época fueron cuestiones muy serias, y constituyeron importantes etapas en la ruta hacia la idea moderna del ser.

Cada cual se despachó a su gusto a la hora de explicar lo que el Alma podía significar
En mi anterior trabajo os hablé de manera bastante extensa sobre estas cuestiones del ser, el alma, la conciencia y, en definitiva, del cerebro que es habitad natural de todas estas cuestiones. La filosofía y la metafísica están presentes haciendo compañía a lo que entendemos por ser consciente.
os hablé de manera bastante extensa sobre estas cuestiones del ser, el alma, la conciencia y, en definitiva, del cerebro que es habitad natural de todas estas cuestiones. La filosofía y la metafísica están presentes haciendo compañía a lo que entendemos por ser consciente.
Las profundidades del ser (nuestro complejo de interioridad) se manisfestó en la llamada Era Axial, en términos aproximados, entre los siglos VII y IV a. de C.

Repartían oraciones como placebos para mitigar las penas a cambio de prebendas
mitigar las penas a cambio de prebendas
Por aquella época, más o menos de manera simultánea, ocurrió algo similar en Palestina, la India, China, Grecia y muy posiblemente también en Persia. En cada uno de estos casos, la religión establecida se había vuelto en extremo ritualista y exhibicionista. En particular, en todas partes habían surgido sacerdotes que se habían adjudicado una posición de altísimos privilegios, con lo cual, Vivian de manera totalmente opuesta a lo que predicaban.
uno de estos casos, la religión establecida se había vuelto en extremo ritualista y exhibicionista. En particular, en todas partes habían surgido sacerdotes que se habían adjudicado una posición de altísimos privilegios, con lo cual, Vivian de manera totalmente opuesta a lo que predicaban.
Aquella casta privilegiada, controlaba el acceso a Dios o a los Dioses (según los casos), y se beneficiaba de su elevado estatus que, sobre todo, ponían al servicio de los poderosos de turno.
Pero en todas estas culturas, surgieron profetas molestos que, al pregonar la salvación del Alma desde otro prisma distinto, dejaban al descubierto las mentiras interesadas de estos sacerdotes y falsas religiones.
otro prisma distinto, dejaban al descubierto las mentiras interesadas de estos sacerdotes y falsas religiones.

Buda
Surgieron profetas (en Israel) u hombres sabios (Buda y los autores de los Upanishads en la India, Confusio en China, etc.) que denunciaron al clero y recomendaron la introspección, a sostener que la ruta hacia la auténtica santidad implicaba algún tipo de abnegación y de estudio íntimo. Platón sentó las bases de la supremacía de la mente sobre la materia.
de abnegación y de estudio íntimo. Platón sentó las bases de la supremacía de la mente sobre la materia.

Confucio
Todos estos hombres mostraron el camino a través del ejemplo personal , y su mensaje es muy similar al que más tarde predicaron Jesús y, más tarde, San Agustín y algún otro.
, y su mensaje es muy similar al que más tarde predicaron Jesús y, más tarde, San Agustín y algún otro.
De éstos auténticos hombres buenos que incluso sacrificaron sus vidas para dedicar todo su esfuerzo al bien de los demás, se han aprovechado, desde tiempos inmemoriales, la legión de espabilados que amparados y enmascarados en las distintas religiones han utilizado toda esa bondad para el propio lucro, engañando a los fieles de buena fe de manera inmisericorde y en ausencia total de conciencia, moral y ética. ¡Que gentuza!
tiempos inmemoriales, la legión de espabilados que amparados y enmascarados en las distintas religiones han utilizado toda esa bondad para el propio lucro, engañando a los fieles de buena fe de manera inmisericorde y en ausencia total de conciencia, moral y ética. ¡Que gentuza!
Prefiero no seguir por este camino y dejo aquí el comentario, ya que, de seguir este sendero espinoso estaría recorriendo un escabroso historial lleno de barbaridades e injusticias del ser humano y, todo ello, en el nombre de Dios.
de Dios.
Emilio Silvera
Ene
13
¿Qué nos trajo la Arqueología?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Rumores del saber del mundo ~
Clasificado en Rumores del saber del mundo ~
 Comments (1)
Comments (1)

La arqueología (un término que se uso por primera vez en la década de 1860) amplió y profundizó el trabajo de la filología, al ir más allá de los textos y confirmar que, en efecto, los hombres tenían un pasado distante anterior a la escritura, una prehistoria.
En 1802, el maestro de escuela Georg Friedrich Grotefend (1775 – 1853) envió tres artículos a la Academia de Ciencias de Gotinga en los que revelaba que había descifrado la escritura cuneiforme de Persépolis, algo que había conseguido principalmente reorganizando los grupos de cuñas (similares a las huellas de los pájaros sobre la arena) y añadiendo espacios entre grupos de letras, y relacionando luego su forma con el sánscrito, una lengua (geográficamente) cercana.

Grotefend consideraba que algunas de las inscripciones eran listas de reyes y que el nombre de algunos de estos era conocido. Las demás formas de cuneiforme, incluida la babilónica, se descifraron algunos años más tarde. En la década de 1820, Champollion descifró los jeroglíficos egipcios, en 1847 sir Austen Layrd excavó Nínive y Ninrud, en lo que hoy es Irak, y descubrió las maravillosos palacios de Assurnasirpal II, rey de Asira (885 – 859 a.c.), y Sennacherib (704 – 681 a.c.). Los enormes guardianes de las puertas encontrados allí, semitoros y leones de dimensiones mucho más grandes que las reales, causaron sensación en Europa, todo aquello popularizó la Arqueología.

Estas excavaciones condujeron finalmente al descubrimiento de una tablilla en cuneiforme en la que estaba escrita la epopeya de Gilgamesh, notable por dos razones: en primer lugar, era mucho más antigua que los poemas homéricos y la Biblia; en segundo lugar, diversos episodios del relato, como el de la gran inundación, eran similares a los que recogía el Antiguo Testamento.
Cada uno de aquellos descubrimientos aumentaba la edad de la Humanidad y arrojaba nueva luz obre las Sagradas Escrituras. Sin embargo, con excepción de la epopeya de Gilgamesh, ninguno de ellos aportaba nada realmente nuevo en términos de datación, en el sentido de que no contradecían de forma significativa la cronología bíblica.

Todo aquello empezó a cambiar hacia 1856 cuando se empezó a limpiar a fondo una pequeña cueva en un costado del valle Neander (Neander Thal en alemán), a través del cual el río Düssel desemboca en el Rin. En ella se encontró un cráneo, enterrado bajo más de un metro de barro, así como algunos otros huesos.
Aquellos huesos fueron a parar a manos del profesor de anatomía de la Universidad de Bonn, Schaaffhausen que, identificó la parte superior de un cráneo, dos fémures, parte de un brazo izquierdo, parte de una pelvis, y algunos otros vestigios de menor tamaño.
En el artículo que escribió sobre aquello, Schaaffausen llamaba la atención sobre el grosor de los huesos, el gran tamaño de las marcas dejadas por los músculos que estuvieron unidos a ellos, el pronunciamiento de los arcos supraorbitales, y la frente pequeña y estrecha.
Concluyo el profesor diciendo que:
“Hay indicios racionales suficientes para sostener, que el hombre coexistió con los animales descubiertos en el diluvio; y muchas razas bárbaras quizá hayan desaparecido antes de todo el tiempo histórico, junto a los animales del mundo antiguo, mientras que las razas cuya organización mejoró continuaron el género.”
El profesor concluyó proponiendo que el espécimen “probablemente perteneciera al pueblo bárbaro original que habitaba el norte de Europa antes de los Germanos.”
Esto no es exactamente lo mismo que hoy entendemos por hombre Neandertal, pero en cualquier caso el hallazgo supuso un gran avance para el conocimiento de nosotros mismos.
Escribiendo sobre estos temas de la antigüedad y de los hechos pasados en los distintos lugares y épocas a distintas culturas, he caído en la cuenta de que el futuro estuvo antes del pasado, me explico:

Real Conservatorio de Música de Madrid
Lo que pretendo decir es que cada uno tenemos nuestro propio pasado, presente y futuro. Si retrocedo unos años en el tiempo, imaginarme a mi hija Maria estudiando en el Conservatorio Superior de Música en Madrid, era el futuro. Sin embargo ahora es presente y, dentro de poco será el pasado. Todo esto nos lleva de nuevo a lo que escribí en otro trabajo: Pasado, presente y futuro. Una ilusión llamada tiempo.
El tiempo es una abstracción de nuestra mente. Algún científico ha dicho (quiero recordar que el Nobel de Física de 2.004 Frank Wilczek) que el tiempo no pasa, es algo que está ahí. Sin embargo, como me ocurre con la luz y con otras cosas, a mí el tiempo me llama la atención y despierta mi curiosidad.
Sigamos con el tema que estaba comentando. Por aquella época, la palabra “ciencia” había empezado a adquirir su significado moderno. (El término “científico” fue acuñado por William Whewell en 1833.) Hasta finales del siglo XVIII, se había preferido el uso de las expresiones “filosofía natural” e “historia natural”. De manera natural y gradual, a medida que diversas disciplinas especializadas fueron surgiendo, primero en Alemania y después en otros lugares, la palabra “ciencia” empezó a ser el término preferido para designar a estas nuevas actividades.
Es curioso ver como, por aquella época también (finales de S.XVIII), algunos empezaron a cuestionar los fundamentos básicos del cristianismo, aunque la mayoría de los hombres de ciencia no se apresuraron a apoyar la idea. Por lo general, los biólogos, químicos y fisiólogos de la época eran todavía hombres religiosos y devotos.

El caso de Linneo es en este sentido ejemplar. Pese a ser una de las figuras de la ilustración (figuras principales) y uno de los padres de la biología moderna, cuyos aportes forman parte de los antecedentes de la teoría de la evolución, Linneo era muy diferente de, por ejemplo, Voltaire. El naturalista John Ray (1627 – 1705) ya había advertido que no todas las especies (miles de las cuales se había encontrado en el Nuevo Mundo y África) podían ordenarse en una jerarquía significativa, y que las formas de la vida variaban de muchas maneras diferentes, una concepción que suponía la ruptura temprana con la idea de una gran cadena del ser.
Me he salido del tema, de Linneo os hablaré otro día.
emilio silvera
Abr
3
Rumores del saber del mundo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Rumores del saber del mundo ~
Clasificado en Rumores del saber del mundo ~
 Comments (0)
Comments (0)

Mundos de fascinante belleza que nos hablan de lo que fue.
En la serie rumores del saber del mundo, hemos ido dejando aquí, de manera esporádica, algunos retazos de ese saber que por el mundo, a lo largo y a lo ancho del discurrir del tiempo, han ido dejando los pueblos y civilizaciones que nos precedieron. Ellos sentaron las bases de lo que hoy somos. Hemos hablado aquí de los sumerios, egipcios, hindúes, chinos y de otras civilizaciones también misteriosas. Hemos dedicado algún tiempo al surgir de la escritura y de los números, sin dejar de lado a los grandes filósofos naturales que estudiaban la Naturaleza para tratar de desvelar sus secretos.

Tiempos de Oráculos y Deidades
Sin embargo, en Alejandría, las matemáticas o, al menos, los números tuvieron otro aspecto muy importante, y también muy diferente. Se trata de los denominados “misterios órficos” y su énfasis místico.
Según Marsilio Ficino, autor del siglo XV d.C., hay seis grandes teólogos de la antigüedad que forman una linea sucesoria. Zoroastro fue “el principal referente de los Magos”; el segundo era Hermes Trismegisto, el líder de los sacerdotes egipcios; Orfeo fue el sucesor de Trismegisto y a él le siguió Agla-ofemo, que fue el encargado de iniciar a Pitágoras en los secretos, quien a su vez los confió a Platón. En Alejandría, Platón fue desarrollado por clemente y Filón, para crear lo que se conocería como neoplatonismo.
Comienza XIV
Tres ideas conforman los cimientos de los misterios órficos. Una es el poder místico de los números. La existencia de los números, su cualidad abstracta y su comportamiento, tan vinculado como el del Universo, ejercieron una permanente fascinación sobre los antiguos, que veían en ellos la explicación de lo que percibían como armonía celestial.

“El número once y su par, 11:11, engloban un código sincromístico, relacionado para muchas personas con la comunicación de una inteligencia cósmica que busca abrir un portal en la conciencia y en la genética humana. Aparte de ésto, esta cifra tiene una resonancia y una simbología profunda que hace reparar en este código, más allá de cultos y creencias, como un atisbo de la naturaleza matemática que subyace, como código de programación, el mundo en el que vivimos.“

La naturaleza abstracta de los números contribuyó a reforzar la idea de un alma abstracta, en la que estaba implícita la idea (trascendental en este contexto) de la salvación: la creencia de que habrá un futuro estado de éxtasis, al que es posible llegar a través de la trasmigración o reencarnación.
Por último, estaba el principio de emanación, esto es, que existe un bien eterno, una unidad o “monada”, de la que brotaba toda la creación. Como el número, esta era considerada una entidad básicamente abstracta. El alma ocupada una posición intermedia entre la monada y el mundo material, entre la mente, abstracta en su totalidad, y los sentidos.
Según los órficos, la monada enviaba (“emanaba”) proyecciones de sí misma al mundo material y la tarea del alma era aprender usando los sentidos. De esta forma, a través de sucesivas reencarnaciones, el alma evolucionaba hasta el punto en el que ya no eran necesarias más reencarnaciones y se alcanzaba el momento de profunda iluminación que daba lugar a una forma conocida como gnosis, allí la mente esta fundida con lo que percibe. Es posible reconocer que esta idea, original de Zoroastro, subyace en muchas de las regiones principales del mundo, con distintas variantes o matices que, en esencia, viene a ser los mismos.

Pitágoras, en particular, creía que el estudio de los números y la armonía conducían a la gnosis. Para los pitagóricos, el número uno no era un número en realidad, sino la “esencia” del número, de la cual surge todo el sistema numérico. Su división en dos creaba un triángulo, una trinidad, la forma armónica más básica, idea de la que encontramos ecos en santísimas religiones.
Platón, en su versión más mítica, estaba convencido de que existía un “alma mundial”, también fundada en la armonía y el número, y de la cual brotaba toda la creación. Pero añadió un importante refinamiento al considerar que la dialéctica, el examen crítico de las opiniones era el método para acceder a la gnosis.
La tradición sostiene que el cristianismo llegó a Alejandría a mediados del siglo I d.C., cuando Marcos el evangelista llegó a la ciudad para predicar la nueva religión.
Las similitudes espirituales entre el platonismo y el cristianismo fueron advertidas de forma muy clara por Clemente de Alejandría (150-215 d.C.), pero fue Filón el indio quien primero desarrolló esta nueva fusión. En Alejandría habían existido escuelas pitagóricas y platónicas desde hacía un largo tiempo, y los judíos cultos conocían los paralelos entre las ideas judías y las tradiciones Geténicas, hasta el punto de que para muchos de ellos el orfismo no era otra cosa que “una emanación de la Torá de la que no había quedado constancia”.
Filón era el típico alejandrino que “nunca confiaba en el sentido literal de las cosas y siempre estaba a la búsqueda de interpretaciones músticas y alegóricas”. Pensaba que podía “conectar” con Dios a través de ideas divinas, que las ideas eran “los pensamientos de Dios” porque ponían orden a la “materia informe”. Al igual que Platón, tenía una noción dualista de la Humanidad:

“De las almas puras que habitan el espacio etéreo, aquellas más cercanas a la tierra resultan atraídas por los seres sensibles y descienden a sus cuerpos”.
Las almas son el lado divino del hombre.
Es interesante reparar los hechos pasados y la evolución del pensamiento humano que, en distintos lugares del mundo y bajo distintas formas, todos iban en realidad a desembocar en el mismo mar del pensamiento.
La naturaleza humana y el orden universal, el primero unido a un alto concepto cuasi divino, el Alma, el segundo regido por la energía cósmica de las fuerzas naturales creadoras de la materia y, todo esto, desarrollado de una u otra manera por los grandes pensadores de todos los tiempos que hicieron posible la evolución del saber para tomar posesión de profundos conocimiento que, en un futuro, nos podrán permitir alcanzar metas, que aún hoy, serían negadas por muchos.
No deberíamos perder de vista la Historia de la Humanidad
Para mí, el mirar los hechos pasados y estudiar los logros alcanzados en todos los campos del saber, es una auténtica aventura que profundiza y lleva al conocimiento del ser humano que, según la historia, es capaz de lo mejor y de lo pero, sin embargo, nadie podrá negarle grandeza ni imaginación.

Los pensadores del Renacimiento creían que todo el Universo era un modelo de la idea divina y que el hombre era “un creador que venía después del creador divino”. Esta concepción era el concepto de belleza, una forma de armonía que reflejaba las intenciones de la divinidad.
Lo que era placentero para los ojos, el oído y la mente era bueno, moralmente valioso en sí mismo. Más aún: revelaba parte del plan divino para la Humanidad, pues evidenciaba la relación de las partes con el todo.
Este ideal renacentista de belleza respaldaba la noción de que esta tenía dos funciones, noción aplicable a todas las disciplinas. En un nivel, la arquitectura, las artes visuales, la música y los aspectos formales de las artes literarias y dramáticas informaban a la mente; en segundo nivel, la complacían mediante el decoro, el estilo y la simetría. De esta forma se estableció una asociación entre belleza e ilustración. También esto era lo que entonces significaba la sabiduría.

Algunos quisieron abarcarlo todo
El fin perseguido era el deseo de universalidad personal, la consecución de conocimientos universales, la conjunción de disciplinas diferentes como ramas del todo, del saber profundo que abarcaba desde el núcleo las distintas esferas del conocimiento universales, la conjunción de disciplinas diferentes como ramas del todo, del saber profundo que abarcaba desde el núcleo las distintas esferas del conocimiento como partes de ese todo.
El reconocimiento de la belleza se funda en los dones divinos del intelecto humano. Durante el Renacimiento se escribieron unos cuarenta y tres tratados sobre la belleza. La idea de hombre universal es una idea común a casi todos ellos.
emilio silvera
Jun
9
“Herbarios” y “Bestiarios”
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Rumores del saber del mundo ~
Clasificado en Rumores del saber del mundo ~
 Comments (0)
Comments (0)
Nunca dejará de asombrarme los hallazgos que podemos efectuar si buceamos en el fondo de nuestra biblioteca. Allí, en la más profundo, detrás de otra hilera de libros que los están tapando, se encuentran obras olvidadas que, de vez en cuando, nos gusta repasar y, aunque ya nos son conocidas por haberlas leído en su momento, no por ello dejan de causarnos “nueva sorpresa” sus contenidos.

Una de ellas, la encontré ayer por la tarde mientras buscaba una obra “perdida” de Gerard ´t Hofft (cualquiera sabe dónde la puse la última vez que la leí), su título: Los Descubridores de la Naturaleza. En la portada, grabado con letras doradas nos dice: “Para descubrir la Naturaleza, la Ciencia no avanzó dando cuenta de la experiencia cotidiana, sino aferrándose a la paradoja, aventurándose en lo desconocido…
Al abrir la tapa y después de una breve presentación, me doy de bruces con una cita de Thomas Henry Huxley (1871) que nos dice:
La investigación de la naturaleza es un campo de pastoreo infinito,
de donde todos pueden nutrirse,
y cuanto más comen,
más abundante crece la hierba, su sabor es más dulce,
y es más alimenticia.

En los lugares más remotos e impensables, si observamos con atención, nos podemos llevar sorpresas inesperadas que nos llevaran directamente al asombro. En esa imagen de arriba, donde todo parece estar muerto, hay mucho, muchísimo más de lo que el ojo puede ver.

La segunda cita del libro es de Victor Hugo, en Los miserables (1862), que nos dice:
Allí donde termina el telescopio,
comienza el microscopio.
¿Cuál de los dos proporciona una visión más amplia?

Sin un microscopio nunca podríamos ver el “universo” de lo muy pequeño. Arriba, alucinante lo que hace un microscopio electrónico de barrido, aquí vemos microfibras y microesferas de fibra textil

El telescopio también nos lleva lejos, al “universo” de lo muy grande
Seguimos ojeando el libro encontrado y, simplemente con leer el título de sus capítulos, hacemos un viaje fascinante, toda vez que, sin leer sus contenidos, por el simple enunciado del comienzo, nuestra imaginación, se desboca y construye un “mundo” a partir de esas primeras palabras. Veamos los que son:
- En “Las brumas de las paradojas”
- La evidencia del ojo desnudo
- Una visión angustiosa y sorprendente
- Atrapado en un fuego cruzado
- Nuevos mundos interiores
- Galileo en China
- Dentro de Nosotros mismos
- Un Profeta demente señala el Camino
- La Tiranía de Galeno
- De los animales al hombre
- Corrientes interiores invisibles…
Y, así, continúan capítulo tras capítulo que, simplemente con el título, ya te prometen que podrás sumergirte en fantásticos mundos que, en ocasiones, ni podías pensar que pudieran existir. De entre todos ellos, esta vez me quedé con este que aquí os dejo (parcialmente), y que comienza diciendo:
Aprender a mirar
Durante mil quinientos años, la Europa culta que deseaba saber cosas sobre la naturaleza recurría a los “bestiarios”, autoridades textuales cuya tiranía era equiparable a la de Galeno en medicina, y cuyas delicias poéticas tentaban a los lectores y los apartaban del mundo real de las plantas y los animales. En la actualidad, al leer esas guías, comprendemos por qué los europeos medievales tardaron tanto en aprender a mirar. Las páginas de los herbarios y bestiarios ilustrados nunca han sido superadas, tanto por su encantadora fantasía como por las recopilaciones de remedios caseros.

Estas fuentes de la botánica medieval, los herbarios, eran el legado de Dioscórides, cirujano griego que había viajado por todo el Mediterráneo con los ejércitos del emperador Nerón. Su De materia médica (c. 77) presentaba la botánica como un tipo de farmacología. Los médicos intentaron con toda seriedad y durante largo tiempo hacer coincidir la descripción de las plantas que Dioscórides había visto en las orillas del tibio Mediterráneo con las que ellos mismos encontraban en Alemania, Suiza o Escocia.

Dioscórides
Al igual que Galeno, Dioscórides había estudiado la Naturaleza, pero los discípulos de Dioscórides estudiaron a Dioscórides. Él esperó en vano que sus lectores “no sólo prestaran atención a la fuerza de las palabras sino también al trabajo y la experiencia que he aplicado al asunto”. Los escritores anteriores mediante una clasificación alfabética, habían separado “tanto los tipos como los funcionamiento de las cosas que están íntimamente relacionadas, de modo que son así más difíciles de recordar”. En cambio, el estudio dónde crecían las plantas, cuándo y cómo debían recogerse, e incluso los tipos de recipientes en que debían almacenarse. Al igual que otros autores clásicos, tuvo pocos discípulos y muchos exégetas. Éstos atesoraban sus palabras pero olvidaron su ejemplo. Dioscórides, a medida que dejaba de ser un maestro, se transformaba en un texto.
Sin embargo, para las mentes prácticas de la época medieval Dioscórides era deliciosamente atractivo, ya que no perturbaba a sus lectores con teorías ni taxonomías. El herbario de Dioscórides estaba escrito en griego e incluía más de seiscientas plantas agrupadas bajo encabezamientos prácticos. ¿Cuáles debían buscarse para obtener aceites, ungüentos, grasas o perfumes? ¿Cuáles curaban el dolor de cabeza o quitaban las manchas de la piel? ¿Qué frutas, verduras o raíces eran comestibles? ¿Cuáles eran las especias locales? ¿Qué plantas eran venenosas y cuáles eran sus antídotos? ¿Qué medicinas podían hacerse a base de plantas?

La obra originaria de Dioscórides nos ha llegado con dificultad; particularmente notable es el códice denominado Costantinopolitanus, creado en el 512 d.C., obra manuscrita con preciosas ilustraciones conservadas en la Nationalbibliothek de Viena.
Los numerosísimos manuscritos de «Dioscórides» que nos han quedado dan testimonio de su popularidad durante la Edad Media. Cuanto más leemos los textos menos nos sorprende su popularidad, la supervivencia de su nomenclatura. Por ejemplo, ésta es la primera entrada del apartado de «plantas aromáticas», en la traducción de John Goodyer (1665):
El iris se llama así por su parecido con el arco iris del cielo… Sus raíces son nudosas, fuertes, de sabor dulce, y después de cortarlas deben dejarse secar a la sombra, y así (atadas con un hilo de lino) guardarse. Pero el mejor es el de Iliria y Macedonia… El segundo de Libia… Todos tienen la facultad de calentar y aliviar, atenúan la tos y los humores mucosos difíciles de evacuar. Actúan contra los humores espesos y la bilis; si se beben en hidromiel en la cantidad de siete dragmas también causan el sueño, provocan las lágrimas y curan los tormentos del estómago. Pero bebidos con vinagre ayudan a los que han sido mordidos por bestias venenosas, a los que han sido mordidos por bestias venenosas, a los que están tiesos de frío y a los que no retienen la comida.

A este herbario, como reporta Plinio en el siglo I d.C., le siguieron otros muchos, desgraciadamente perdidos en los avatares del tiempo, de autores menos conocidos como Crateo y Diocle, que pasaron el tiempo enriqueciéndose con ensayos de ilustraciones a color.
La baya del enebro es «buena para el estómago y en infusión es buena para las enfermedades del tórax, la tos, las inflamaciones, los retortijones y los venenos de los animales. También es diurética y por consiguiente buena tanto para las convulsiones como para las hernias y para las que tienen estrangulamiento de útero». El rábano común «también provoca ventosidades y calienta, es bueno para la boca pero no para el estómago tomado después de comer, pues ayuda a la digestión, pero si se toma antes interrumpe la comida; por tanto es bueno para los que desean vomitar tomarlo antes de comer». La raíz de la mandrágora puede prepararse par servir de anestesia «para aquellos que van a ser cortados o cauterizados»… Pues no perciben el dolor porque les embarga un sueño de muerte… Pero si se usa mucho puede hacer perder el habla a los hombres».
Mil años de manuscritos de «Diocórides» nos demuestran nos demuestran lo que significaba estar a merced de los copistas. Con los copistas. Con los siglos, las ilustraciones se apartan cada vez más de la realidad. Las copias de las incluyen hojas imaginarias para hacer lo dibujos simétricos y raíces aumentadas de tamaño para llenar el espacio sobrante. Los caprichos de los copistas se convirtieron luego en convenciones.

Le Livre des simples médecines, (El Libro de los medicamentos simples), de la Biblioteca Nacional de Rusia, en San Petersburgo, es un códice singular, no solo por la gran belleza de sus ilustraciones, sino porque corresponde a la culminación de los saberes medievales europeos acerca de las sustancias de los tres reinos de la naturaleza que sirven para curar o aliviar las enfermedades.
Tiene un texto de 220 páginas dividido en cinco partes: hierbas y flores, árboles y sus gomas y resinas, metales y minerales, productos animales y otras materias.

A finales de la Edad Media, príncipes y poderosos aprendían las reglas de salud e higiene de la medicina racional en el Tacuinum Sanitatis, un tratado sobre el bienestar y la salud muy difundido durante los siglos XIV y XV.
El tratado fue escrito en árabe por Ububchasym de Baldach, también conocido como Ibn Butlân, médico cristiano nacido en Bagdad y muerto en 1068. Propone seis elementos necesarios para el mantenimiento cotidiano de la salud: la comida y la bebida, el aire y el ambiente, el movimiento y el reposo, el sueño y la vigilia, las secreciones y excreciones de los humores, los movimientos o afectos del ánimo (la alegría, la ira, la vergüenza…). Según Ibn Butlân, las enfermedades surgen de la alteración en el equilibrio de alguno de estos elementos, por lo que aconseja la vida en armonía con la naturaleza para conservar o recuperar la salud.
Los escribas fantasiosos tomaban ideas tanto de los nombres como de las propiedades de las plantas, convirtiendo de este modo la botánica en una rama de la filología. De las flores del narciso salían pequeñas figuras humanas, que recordaban al desafortunado que miraba y amaba su imagen reflejada en todas partes. El «el árbol» de la vida llevaba enroscada una serpiente de cabeza femenina, el grosello silvestre llevaba unas conchas que se abrían y expulsaban ocas berniclas típicas del norte de Escocia. Cuando apareció la imprenta en Europa, la información botánica más útil se encontraba todavía en los antiguos herbarios, ampliados y «mejorados» por generaciones de escribas. Los impresores, que habían hecho grandes inversiones en las planchas de madera o de cobre, no se mostraban muy dispuestos a desecharlas simplemente porque las ilustraciones no se correspondiesen con las palabras del texto. Incluso los eruditos que podían haber sentido la tentación de mirar las plantas con sus propios ojos encontraban más cómodo comparar los manuscritos y glosar los textos.

Los herbarios se convirtieron pronto en artículos indispensables. El Liber de propietatiibus rerum (c. 1470), obra de un monje inglés que vivió en el siglo XII, fue reeditado veinticinco veces antes del fin del siglo XV. Las lenguas vernáculas permitieron la llegada de datos nuevos de toda Europa. Pero los herbarios tenían unos límites evidentes. A cada planta se le hacía siempre la misma pregunta: ¿Cómo puedes divertirme, alimentarme, salvarme o curarme?
A fines del siglo XVI, el catedrático de botánica de la universidad de Bolonia todavía era descrito como el «lector de Dioscórides». Dado que cada generación había hacho sus pequeñas aportaciones, que no se distinguían del original casi nunca, los botánicos y farmacólogos eran meros comentaristas. El herbario era un catálogo de medicinas «simples», cada una de las cuales tenía un componente único que por lo general procedía de una sola planta.

El médico italiano Pier Andrea Mattioli (1501-1577) hizo la primera traducción de Dioscórides a una lengua vernácula europea.
Sus comentarios en italiano se convirtieron en un acontecimiento editorial al vender treinta mil ejemplares (Venecia, 1544). Luego, traduciendo a Dioscórides al latín y añadiendo sinónimos de los nombres de las plantas en varias lenguas, contribuyó a popularizar la obra por toda Europa. Más de cincuenta ediciones en alemán, francés, checo, y otras lenguas europeas hicieron del Dioscórides revisado de Mattioli el rey de la botánica en todo el continente.


Los herbarios significaron para la botánica lo mismo que los bestiarios para la para la zoología. También estos derivaban de un original antiguo único, embellecido a lo largo de los siglos. Durante la Edad Media sólo la Biblia era más popular que estos libros. En nuestra época el bestseller impreso atraviesa rápidamente el espacio pero raras veces viaja mucho en el tiempo. En la época de los manuscritos, el poder de un único autor clásico era imperecedero. El imperio de los cultos estaba gobernado por una oligarquía de unos pocos «autores camaleón». Los nombres clásicos se volvían útiles para las generaciones posteriores después de incontables revisiones, y el autor original se convertía en un espectro. La mano del escriba derrocaba al autor.

El primero de los bestiarios recibió su nombre de un griego, Fisiólogo («naturalista»), del cual sabemos muy poco. Su obra, probablemente escrita antes de mediados del siglo II, parece haber estado dividida en cuarenta y ocho capítulos, cada uno de ellos relacionado con un texto de la Biblia. Unos pocos datos, embellecidos con abundante teología, moral, folklore, mitología, rumores y fábulas, constituyeron la zoología durante varias generaciones. En el siglo v existían ya traducciones, aparte del latín, al armenio, árabe y etíope. Posteriormente, se encontró entre los primeros libros traducidos a las lenguas vernáculas europeas, incluido el antiguo alto-alemán, el anglosajón, el inglés antiguo, el inglés medio, el francés antiguo, el provenzal y el islandés.

La versión griega incluía unos cuarenta animales en un delicioso revoltillo. Como es natural, el león, rey de las bestias, era el primero, y sobre él se cuentan tres hechos destacados: usa la cola para borrar sus huellas, de modo que los cazadores no puedan seguirlo; duerme con los ojos abiertos, y el cachorro recién nacido permanece muerto durante tres días hasta que el león padre le da el aliento de la vida. De igual manera, el cuerpo de Cristo estuvo muerto y, como el león recién nacido, permaneció despierto esperando la resurrección al tercer día.
Los animales restantes- lagarto, cuervo nocturno, fénix, abubilla y treinta y pico más-llevan una gran carga moral. Ninguno es más vivaz que el «león hormiguero», nacido de la anti- natural unión de un león y una hormiga, que está condenado a morir de hambre porque la naturaleza de la hormiga no le permite comer carne, y la naturaleza del león hace que se abstenga de comer plantas. Y al igual que esta bestia, nadie que pretenda servir a Dios y al diablo podrá sobrevivir.
En aquellos tiempos, auténticos artistas, a mano y de manera artesanal, editaban libros en miniatura que eran únicos y en ellos, reproducían las recetas de Dioscórides que eran muy populares y todos acudían a ellas para sanar esta o aquella enfermedad.
El capítulo es tan largo que lo he tenido que dejar aquí por falta de tiempo para transcribirlo entero.
Que os guste recordar aquel pasado que, como tantos otros, nos trajeron aquí.
emilio silvera
















 Totales: 69.196.384
Totales: 69.196.384 Conectados: 14
Conectados: 14




























