Jun
25
¿Qué es un bosón? y ¿qué es un bosón gauge?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

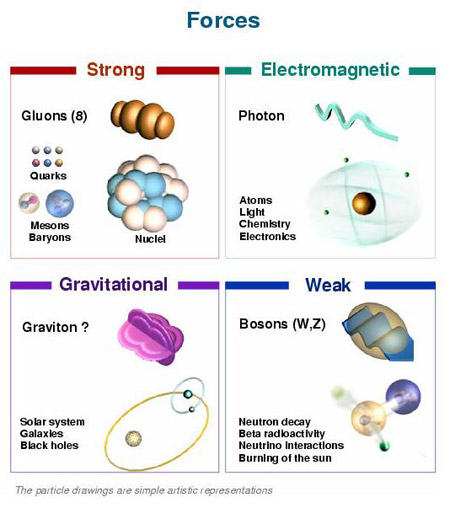
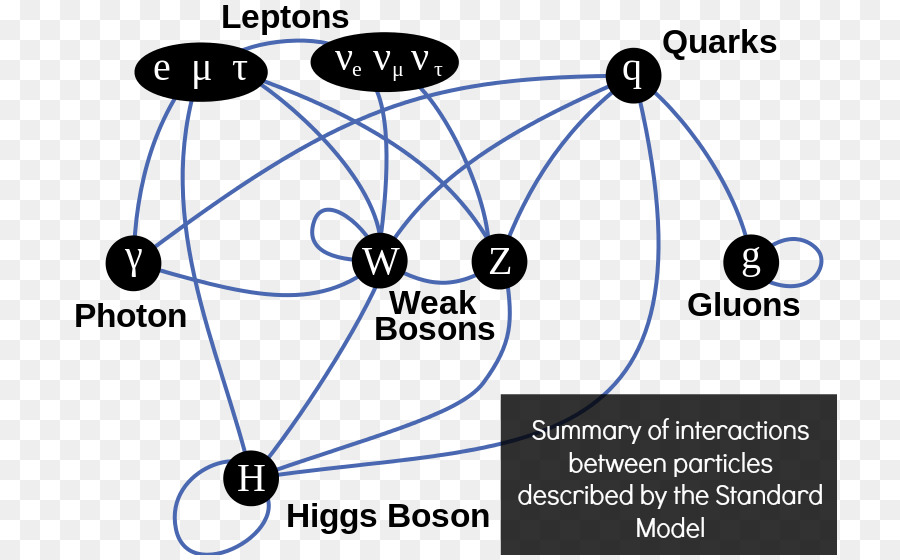
Un bosón es una partícula elemental (o estado ligado de partículas elementales, por ejemplo, un núcleo atómico o átomo) con espín entero, es decir, una partícula que obedece a la estadísitca de Bose-Einstein (estadísictica cuántica), de la cual deriva su nombre. Los bosones son importantes para el Modelo estándar de las partículas. Son bosones vectoriales de espín uno que hacen de intermediarios de las interacciones gobernadas por teorías gauge. Los Fotones, los Gluones, el hipotético Gravitón, las partículas W y Z son todos bosones mensajeros del electromagnetismo y todas las formas de radiación, de la fuerza nuclear fuerte, de la Gravedad, y, de la fuerza nuclear débil.
En física se ha sabido crear lo que se llama el Modelo estándar y, en él, los Bosones quedan asociados a las tres fuerzas que lo conforman, el fotón es el Bosón intermediario del electromagnetismo, los W+, w–y Zº son bosones gauge que transmiten la fiuerza en la teoría electrodébil, mientras que los gluones son los bosones de la fuerza fuerte, los que se encargan de tener bien confinados a los Quarks conformando protones y neutrones para que el núcleo del átomo sea estable. La Gravedad, no se ha dejado meter en el modelo y, por eso su bosón no es de gauge. El gravitón que sería la partícula mediadora de la gravitación sería el hipótetico cuanto de energía que se intercambia en la interacción gravitacional.

Ejemplos de los Bosones gauge son los fotones en electrodinámica cuántica (en física, el fotón se representa normalmente con el símbolo 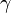 , que es la letra griega gamma), los gluones en cromodinámica cuántica y los bosones W y Z en el modelo de Winberg-Salam en la teoría electrodébil que unifica el electromagnetismo con la fuerza débil. Si la simetría gauge de la teoría no está rota, el bosón gauge es no masivo. Ejemplos de bosones gauge no masivos son el fotón y el gluón.
, que es la letra griega gamma), los gluones en cromodinámica cuántica y los bosones W y Z en el modelo de Winberg-Salam en la teoría electrodébil que unifica el electromagnetismo con la fuerza débil. Si la simetría gauge de la teoría no está rota, el bosón gauge es no masivo. Ejemplos de bosones gauge no masivos son el fotón y el gluón.

Si la simetría gauge de la teoría es una simetría rota el bosón gauge tiene masa no nula, ejemplo de ello son los bosones W y Z . Tratando la Gravedad, descrita según la teoría de la relatividad general, como una teoría gauge, el bosón gauge sería el gravitón, partícula no masiva y de espín dos.

Diagrama de Feynman mostrando el intercambio de un fotón virtual (simbolizado por una línea ondulada y  ) entre un positrón y un electrón.De esta manera podemos llegar a comprender la construcción que se ha hecho de las interacciones que están siempre intermediadas por un nosón mensajero de la fuerza.
) entre un positrón y un electrón.De esta manera podemos llegar a comprender la construcción que se ha hecho de las interacciones que están siempre intermediadas por un nosón mensajero de la fuerza.
En el modelo estándar, como queda explicado, hay tres tipos de bosones de gauge: fotones, bosones W y Z y gluones. Cada uno corresponde a tres de las cuatro interacciones: fotones son los bosones de gauge de la interacciones electromagnética, los bosones W y Z traen la interacción débil, los gluones transportan la interacción fuerte. El gravitón, que sería responsable por la interacción gravitacional, es una proposición teórica que a la fecha no ha sido detectada. Debido al confinamiento del color, los gluones aislados no aparecen a bajas energías.
Aquí, en el gráfico, quedan representadas todas las partículas del Modelo estándar, las familias de Quarks y Leptones que conforman la materia y los bones que intermedian en las interacciones o fuerzas fundamentales que están presentes en el Universo. La Gravedad no ha podido ser incluida y se ha negado a estar unida a las otras fuerzas. Así el bosón que la transnmite, tampoco está en el modelo que es incompleto al dejar fuera la fuerza que mantiene unidos los planetas en los sistemas solares, a las galaxias en los cúmulos y nuestros pies unidos a la superficie del planeta que habitamos. Se busca una teoría que permita esta unión y, los físicos, la laman gravedad cuántica pero… ¡no aparece por ninguna parte!

Llegados a este punto tendremos que retroceder, para poder comprender las cosas, hasta aquel trabajo de sólo ocho páginas que publicó Max Planck en 1.900 y lo cambió todo. El mismo Planck se dió cuenta de que, todo lo que él había tenido por cierto durante cuarenta años, se derrumbaba con ese trabajo suyo que, venía a decirnos que el mundo de la materia y la nergía estaba hecho a partir de lo que el llamaba “cuantos”.
Supuso el nacimiento de la Mecánica Cuántica (MC), el fin del determinismo clásico y el comienzo de una nueva física, la Física Moderna, de la que la Cuántica sería uno de sus tres pilares junto con la Relatividad y la Teoría del Caos. Más tarde, ha aparecido otra teoría más moderna aún por comprobar, ¿las cuerdas…?
El universo según la teoría de las cuerdas sería entonces una completa extensa polícroma SINFONIA ETERNA de vibraciones, un multiverso infinito de esferas, cada una de ellas un universo independiente causalmente, en una de esas esferas nuestra vía láctea, en ella nuestro sistema solar, en él nuestro planeta, el planeta tierra en el cual por una secuencia milagrosa de hechos se dió origen a la vida autoconsciente que nos permite preguntarnos del cómo y del por qué de todas las cosas que podemos observar y, también, de las que intiuimos que están ahí sin que se dejen ver.

Claro que, cuando nos adentramos en ese minúsculo “mundo” de lo muy pequeño, las cosas difieren y se apartan de lo que nos dicta el sentido común que, por otra parte, es posible que sea el menos común de los sentidos. Nos dejamos guiar por lo que observamos, por ese mundo macroscópico que nos rodea y, no somos consciente de ese otro “mundo” que está ahí formando parte del universo y que, de una manera muy importante incide en el mundo de lo grande, sin lo que allí existe, no podría existir lo que existe aquí.
Interacciones en la naturaleza
Albert Einstein habría dicho que “es más importante la imaginación que el conocimiento”, el filósofo Nelson Goodman ha dicho que “las formas y las leyes de nuestros mundos no se encuentran ahí, ante nosotros, listas para ser descubiertas, sino que vienen impuestas por las versiones-del-mundo que nosotros inventamos – ya sea en las ciencias, en las artes, en la percepción y en la práctica cotidiana-.”
ser descubiertas, sino que vienen impuestas por las versiones-del-mundo que nosotros inventamos – ya sea en las ciencias, en las artes, en la percepción y en la práctica cotidiana-.”
Sin embargo yo, humilde pensador, me decanto por el hecho cierto de que, nuestra especie, siempre llegó al conocimiento a través de la imaginación y la experiencia primero, a la que más tarde, acompañó largas secciones de estudio y muchas horas de mediatación y, al final de todo eso, llego la experimentación que hizo posible llegar a lugarés ignotos que antes nunca, habían podido ser visitados. De todo ello, pudieron surgir todos esos “nuevos mundos” que, como la Mecanica Cuántica y la Relatividad, nos describían el propio mundo que antes nos era desconocido.
Cuando comencé éste trabajo sólo quería dar una simple explicación de los bosones y su intervención en el mundo de lo muy pequeño pero…

Demócrito de Abdera
No estaría mal echar una mirada hacia atrás en el tiempo y recordar, en este momento, a Demócrito que, con sus postulados, de alguna manera venía a echar un poco de luz sobre el asunto, dado que él decía que para determinar si algo era un á-tomo habría que ver si era indivisible. En el modelo de los quarks, el protón, en realidad, un conglomerado pegajoso de tres quarks que se mueven rápidamente. Pero como esos quarks están siempre ineludiblemente encadenados los unos a los otros, experimentalmente el protón aparece indivisible.
Acordémonos aquí de que Boscovich decía que, una partícula elemental, o un “á-tomo”, tiene que ser puntual. Y, desde luego, esa prueba, no la pasaba el protón. El equipo del MIT y el SLAC, con la asesoría de Feynman y Bjorken, cayó en la cuenta de que en este caso el criterio operativo era el de los “puntos” y no el de la indivisibilidad. La traducción de sus datos a un modelo de constituyentes puntuales requería una sutileza mucho mayor que el experimento de Rutherford.

Precisamente por eso era tan conveniente fue tan conveniente para Richard Edward Taylor y su equipo, tener a dos de los mejores teóricos del mundo en el equipo aportando su ingenio, agudeza e intuición en todas las fases del proceso experimental. El resultado fue que los datos indicaron, efectivamente, la presencia de objetos puntuales en movimiento dentro del protón.

En 1990 Taylor, Friedman y Kendall recogieron su premio Nobel por haber establecido la realidad de los quarks. Sin embargo, a mí lo que siempre me ha llamado más la atención es el hecho cierto de que, este descubrimiento como otros muchos (el caso del positrón de Dirac, por ejemplo), han sido posible gracias al ingenio de los teóricos que han sabido vislumbrar cómo era en realidad la Naturaleza.
A todo esto, una buena pregunta sería: ¿cómo pudieron ver este tipo de partículas de tamaño infinitesimal, si los quarks no están libres y están confinados -en este caso- dentro del protón? Hoy, la respuesta tiene poco misterio sabiendo lo que sabemos y hasta donde hemos llegado con el LHC que, con sus inmensas energías “desmenuza” un protón hasta dejar desnudos sus más íntimos secretos.

Este es, el resultado ahora de la colisión de protones en el LHC
Lo cierto es que, en su momento, la teoría de los Quarks hizo muchos conversos, especialmente a medida que los teóricos que escrutaban los datos fueron imbuyendo a los quarks una realidad creciente, conociendo mejor sus propiedades y convirtiendo la incapacidad de ver quarks libres en una virtud. La palabra de moda en aquellos momentos era “confinamiento”. Los Quarks están confinados permanentemente porque la energía requerida para separarlos aumenta a medida que la distancia entre ellos crece. Esa es, la fuerza nuclear fuerte que está presente dentro del átomo y que se encarga de transmitir los ocho Gluones que mantienen confinados a los Quarks.
Así, cuando el intento de separar a los Quarks es demasiado intenso, la energía se vuelve lo bastante grande para crear un par de quark-anti-quark, y ya tenemos cuatro quarks, o dos mesones. Es como intentar conseguir un cabo de cuerda. Se corta y… ¡ya tenemos dos!
¿Cuerdas? Me parece que estoy confundiendo el principal objetivo de este trabajo y, me quiero situar en el tiempo futuro que va, desde los quarks de Gell-Mann hasta las cuerdas de Veneziano y John Schwarz y más tarde Witten. Esto de la Física, a veces te juega malas pasadas y sus complejos caminos te llevan a confundir conceptos y momentos que, en realidad, y de manera individualizada, todos han tenido su propio tiempo y lugar.
¿Cuántas veces no habré pensado, en la posibilidad de tomar el elixir de la sabiduría para poder comprenderlo todo? Sin embargo, esa pósima mágica no existe y, si queremos saber , el único camino que tenemos a nuestro alcance es la observación, el estudio, el experimento… ¡La Ciencia!, que en definitiva, es la única que nos dirá como es, y como se producen los fenómenos que podemos contemplar en la Naturaleza y, si de camino, podemos llegar a saber el por qué de su comportamiento… ¡mucho mejor!
, el único camino que tenemos a nuestro alcance es la observación, el estudio, el experimento… ¡La Ciencia!, que en definitiva, es la única que nos dirá como es, y como se producen los fenómenos que podemos contemplar en la Naturaleza y, si de camino, podemos llegar a saber el por qué de su comportamiento… ¡mucho mejor!

El camino será largo y, a veces, penoso pero… ¡llegaremos!
Nuestra insaciable curiosidad nos llevará lejos en el saber del “mundo”. llegaremos al corazón mismo de la materia para conmprobar si allí, como algunos imaginan, habitan las cuerdas vibrantes escondidas tan profundamente que no se dejan ver. Sabremos de muchos mundos habitados y podremos hacer ese primer contacto tantas veces soñado con otros seres que, lejos de nuestro región del Sistema solar, también, de manera independiente y con otros nombres, descubrieron la cuántica y la relatividad. Sabremos al fín qué es la Gravedad y por qué no se dejaba juntar con la cuántica. Podremos realizar maravillas que ahora, aunque nuestra imaginación es grande, ni podemos intuir por no tener la información necesaria que requiere la imaginación.
En fín, como decía Hilbert: ¡”Tenemos que saber, sabremos”!
Emilio Silvera
Jun
4
El “universo” de las partículas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)

Solo el 1% de las formas de vida que han vivido en la Tierra están ahora presentes, el 99%, por una u otra razón se han extinguido. Sin embargo, ese pequeño tanto por ciento de la vida actual, supone unos cinco millones de especies según algunas estimaciones. La Tierra acoge a todas esas especies u palpita de vida que prolifera por doquier. Hay seres vivos por todas partes y por todos los rincones del inmenso mosaico de ambientes que constituye nuestro planeta encontramos formas de vida, cuyos diseños parecen hechos a propósito para adaptarse a su hábitat, desde las profundidades abisales de los océanos hasta las más altas cumbres, desde las espesas selvas tropicales a las planicies de hielo de los casquetes polares. Se ha estimado la edad de 3.800 millones de años desde que aparecieron los primeros “seres vivos” sobre el planeta (dato de los primeros microfósiles). Desde entonces no han dejado de aparecer más y más especies, de las que la mayoría se han ido extinguiendo. Desde el siglo XVIII en que Carlos Linneo propuso su Systema Naturae no han cesado los intentos por conocer la Biodiversidad…, de la que por cierto nuestra especie, bautizada como Homo sapiens por el propio Linneo, es una recién llegada de apenas 200.000 años.

Ahora, hablaremos de la vida media de las partículas elementales (algunas no tanto). Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida media, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.
También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.
Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, psi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales maneras de desintegración, veríamos como difieren las unas de las otras.”
Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.

¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.

Una colisión entre un protón y un antiprotón registrada mediante una cámara de chispas del experimento UA5 del CERN.
En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su carta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas, Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.
¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, …
Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.
Se habla de ondas cuánticas y también, de ondas gravitacionales. Las primeras han sido localizadas y las segundas están siendo perseguidas.
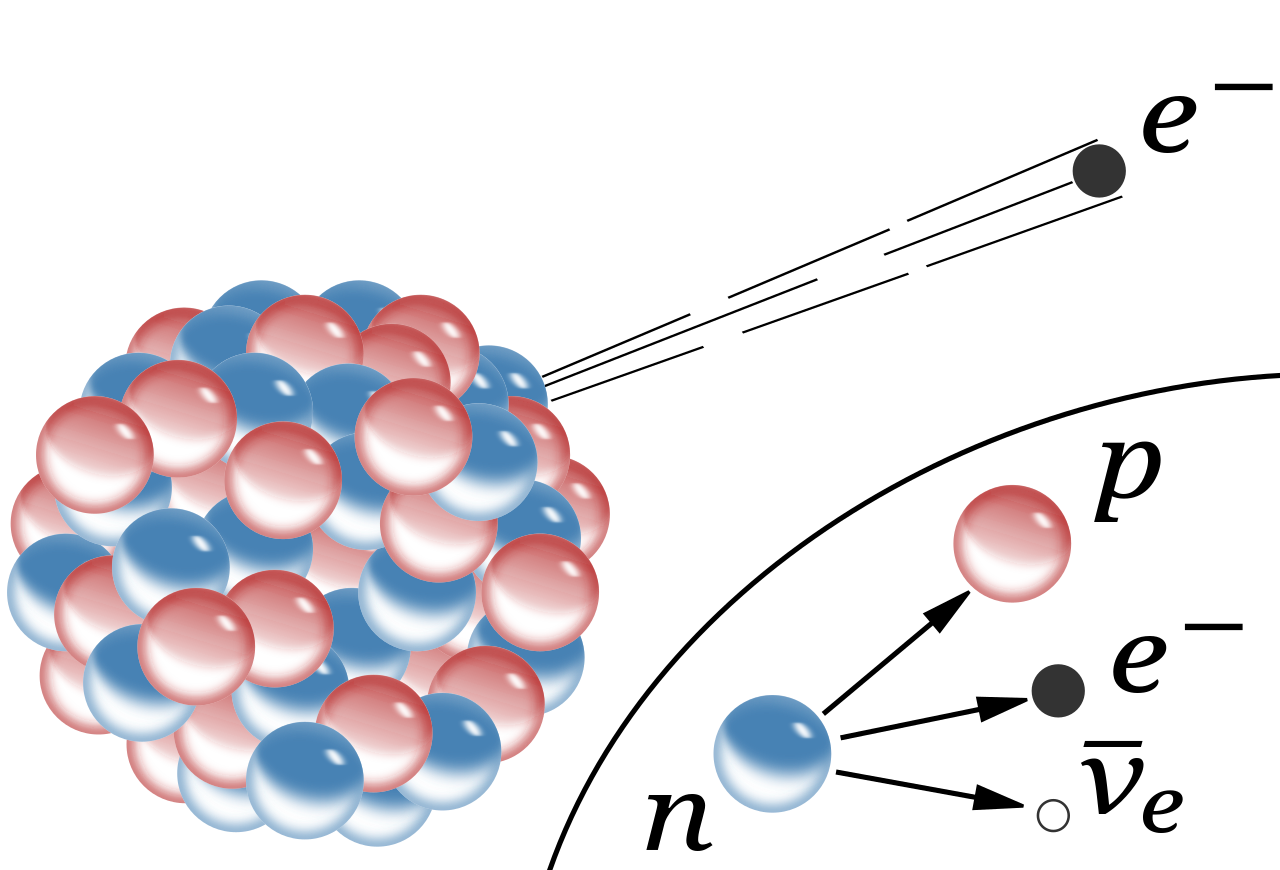
Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.
Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.
Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”

Si la vida de una partícula es tan corta como 10ˉ²³ segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.
Bariones Delta. Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.
Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).
Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.
Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:
∆⁺⁺→р + π⁺; ∆⁰→р + πˉ; o п+π⁰
En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.
El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (aunque nos parezca lo contrario), son aún bastante limitados, nos queda mucho por descubrir antes de que podamos decir que dominamos la materia y sabemos de todos sus componentes. Antes de que eso llegue, tendremos que conocer, en profundidad, el verdadero origen de la Luz que esconde muchos secretos que tendremos que desvelar.
Esperemos que con los futuros experimentos del LHC y de los grandes Aceleradores de partículas del futuro, se nos aclaren algo las cosas y podamos avanzar en el perfeccionamiento del Modelo Estándar de la Física de Partículas que, como todos sabemos es un Modelo incompleto que no contiene a todas las fuerzas de la Naturaleza y, cerca de una veintena de sus parámetros son aleatorios y no han sido explicados. Uno de ellos, el Bosón de Higgs, dicen que ha sido encontrado. Sin embargo, a mí particularmente me quedan muchas dudas al respecto.
Emilio Silvera Vázquez
May
31
Cosas de la Mecánica Cuántica
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
¡La Física! Esa maravilla que está presente en todo lo que podemos ver y en aquello donde la vista no llega. La infinitud de las partículas elementales que forman todo cuanto existe en la Naturaleza, no siempre se dejan ver ni hacen posible que podamos observar las maravillas que pueden llevar a cabo,
Las sustancias formadas por una sola clase de átomos se llaman elementos químicos, y, si está conformada por distintos átomos, son compuestos. La palabra “átomo” procede del griego ατομος, que significa “indivisible” y el uso de la palabra “elemento” sugiere que se ha llegado a los ladrillos básicos con los que está formada la materia. De hecho, esta es la imagen que se tenía a mediados del siglo XIX cuando se acuñaron estos términos. Sin embargo, hoy sabemos que todo esto es falso, que los átomos se pueden dividir y que, de esta manera, los elementos han dejado de ser verdaderamente elementales. Los físicos continúan con esta nomenclatura aunque sea formalmente incorrecta, ya que, la costumbre, como dicen los juristas, no pocas veces rigen la jerga de las leyes.
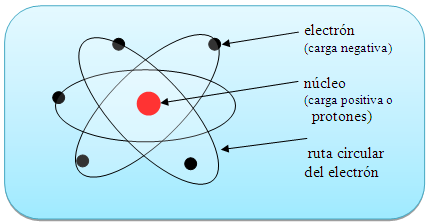
A todo esto y hablando de los átomos, por fuerza, nos tenemos que acordar del electrón que da al átomo su forma esférica. Son partículas cargadas eléctricamente que se mueven alegremente alrededor del núcleo. El electrón es muy ligero: su masa es solamente 1/1.8836 de la del núcleo más ligero (el hidrógeno). La carga eléctrica del electrón es de signo opuesto a la del núcleo, de manera que los electrones están fuertemente atraídos hacia el núcleo y se repelen mutuamente. Si la carga eléctrica total de los electrones en un átomo iguala a la del núcleo, para lo que generalmente se necesitan varios electrones, se dice que el átomo está en equilibrio o que es eléctricamente neutro.
Claro que, no debemos olvidarnos de que, ¡Todo lo grande está hecho de cosas pequeñas! Una inmensa galaxia se conforma de un conjunto inmenso de átomos infinitesimales que juntos, hace ese gran todo.

La fuerza a la que obedecen los electrones, la denominada fuerza electrostática o de Coulomb, es matemáticamente bastante sencilla y, sin embargo, los electrones son los responsables de las importantes propiedades de los “enlaces químicos”. Esto se debe a que las leyes de movimiento de los electrones están regidas completamente por la “mecánica cuántica”, teoría que se completó a principios del siglo XX. Es una teoría paradójica y difícil de entender y explicar, pero al mismo tiempo es muy interesante, fantástica y revolucionaria. Cuando uno se introduce en las maravillas de la mecánica cuántica es como si hiciera un viaje a un universo que está situado fuera de este mundo nuestro, ya que, las cosas que allí se ven, desdicen todo lo que dicta nuestro sentido común de cómo tiene que ser el mundo que nos rodea.
La perfecta sincronía Está en la Naturaleza
No solamente los electrones, sino también los núcleos atómicos y los átomos en su conjunto obedecen y se rigen por la mecánica cuántica. La Física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck, escribió un artículo de ocho páginas y allí propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menos intensidad, por los objetos más fríos.
Radiación electromagnética
Estaban bien aceptados entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si usamos las leyes de la termodinámica para calcular la intensidad de la radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano, y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para las longitudes mayores como para las longitudes menores. Esta longitud característica es inversamente proporcional a la temperatura absoluta del objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273 ºC bajo cero). Cuando a 1.000 ºC un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.

Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de la onda y, por lo tanto, proporcional a la frecuencia de la radiación emitida. La sencilla fórmula es:
E = h x v
Donde E es la energía del paquete, v la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.



Los cuantos de energía están presentes por todas partes y en todos los objetos


El Efecto Foto-eléctrico
Dualidad onda partícula

Los paquetes de energía de Planck
Poco tiempo después, en 1905, Einstein formuló esta teoría de una forma mucho más tajante: el sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos de los paquetes de energía de Planck. El príncipe francés Louis-Víctor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene una energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta región del espacio, y que la frecuencia, v, de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilatorias de campos de fuerza.

El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de De Broglie. Poco después, en 1926, Erwin Schrödinger descubrió como escribir la teoría ondulatoria de De Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños estaban exactamente determinados por la recién descubiertas “ecuaciones de onda cuánticas”.

14 de diciembre de 1900: Max Planck publica un arículo de ocho páginas y quedó sembrada la semilla de lo que, más tarde, sería la Mecánica Cuántica.
https://youtu.be/bzFWEHaOj0Q
En 1905 y más tarde en 1915, Einstein publicó la Teoría de la Relatividad Especial y General, lo que dio un giro al entendimiento de la Física, y, en la segunda parte, nos trajo una nueva forma de ver y entender el Universo.
Pocas dudas nos pueden caber a estas alturas de que la mecánica cuántica (de Planck) y, la Relatividad –tanto especial como general- (de Einstein), además de ser las dos teorías más importantes de la Física de nuestro tiempo, funcionan de tal forma que uno, cuando profundiza en sus predicciones y las compara con lo que ocurre en el Universo, no puede por menos que, asombrarse, al comprobar como unas mentes humanas han sido capaces de llegar a estos profundos pensamientos que nos acerca a la realidad de la Naturaleza.
No me parece completa la reseña anterior sin repasar un poco lo que concierne al llamado Modelo Estándar de la Física de partículas, que supone una gran herramienta de trabajo para los físicos.
Precisamente, en los dos últimos comentarios del contertulio Sr. Fandila y otro mío, nos estábamos refiriendo a las teorías y, los dos coincidimos en que, a medida que se avanza y se descubren nuevos parámentros, tienen que ser refinadas para que reflejen de manera más real lo que quieren representar de los fenómenos que vemos en la Naturaleza.
“El modelo estándar de la física de partículas es una teoría relativista de campos cuánticos desarrollada entre 1970 y 1973[cita requerida] basada en las ideas de la unificación y simetrías1 que describe la estructura fundamental de la materia y el vacío considerando las partículas elementales como entes irreducibles cuya cinemática está regida por las cuatro interacciones fundamentales conocidas (exceptuando la gravedad, cuya principal teoría, la relatividad general, no encaja con los modelos matemáticos del mundo cuántico). La palabra “modelo” en el nombre viene del período de los 70 cuando no había suficiente evidencia experimental que confirmara el modelo.1 Hasta la fecha, casi todas las pruebas experimentales de las tres fuerzas descritas por el modelo estándar están de acuerdo con sus predicciones. Sin embargo el modelo estándar no alcanza a ser una teoría completa de las interacciones fundamentales debido a varias cuestiones sin resolver.”

Han pasado 50 años desde que Steven Weinberg y Abdus Salam publicaran aquel artículo en el que formalizaron el llamado Modelo Estándar de las Interacciones Fundamentales. Han sido 5 décadas de actividad científica muy intensa en las que se han realizado toda clase de experimentos para someter a esta teoría a las más complicadas pruebas que nos dijeran si realmente era un modelo que reflejaba la realidad que la naturaleza nos quiere transmitir.
El Modelo Estándar está construido de manera imperfecta, y aunque ha sido y será una herramienta de un enorme rendimiento para los físicos, hay que reconocer que estaba construido con 20 parámetros aleatorios (metidos con calzador) y, de los cuales solo uno de ellos (el Bosón de Higgs) ha sido hallado.
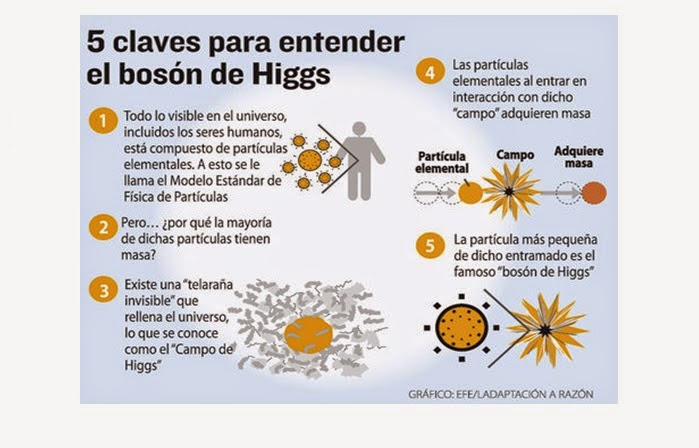
En el modelo estándar que nos habla de las familias de partículas subatómicas que conforman la materia y también de aquellas otras que son intermediarias en la transmisión de las fuerzas fundamentales. Las partículas están divididas en familias como los quarks, los leptones y los hadrones. En realidad, los hadrones que se dividen en bariones y mesones se consideran una clase de subpartículas al estar conformadas por tripletes de quarks los bariones, y, por quarks y anti-quarks los mesones.

Además de las partículas mencionadas, en el Modelo Estándar están incluidas tres de las cuatro fuerzas fundamentales de la Naturaleza: Fuerza Nuclear Fuerte, Fuerza Nuclear Débil y, Electromagnetismo. La cuarta fuerza que es la Gravedad se resiste a reunirse en el modelo con las otras tres, y, precisamente por eso, los físicos están tratando de construir el modelo de la Gravedad Cuántica que por fin, reúna a todas las fuerzas.
Parece (aunque esto será objeto de un artículo a parte) que en la teoría de cuerdas (pendiente de ser verificada) puede subyacer esa teoría cuántica de la gravedad.
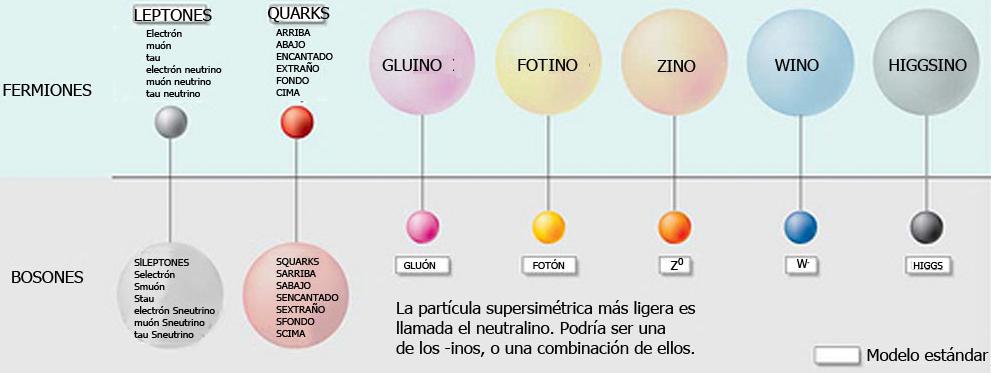
La teoría estándar constituye un logro científico de inmensa importancia. A partir de simples postulados de simetría, es posible deducir las propiedades dinámicas de las interacciones electrodébil y fuerte, es decir, el lagrangiano completo que rige las fuerzas entre los constituyentes básicos de la materia, prediciendo así el comportamiento del mundo microscópico, de forma muy precisa y en perfecto acuerdo con las observaciones experimentales.
Más aún, la consistencia matemática de la teoría hizo necesario introducir un nuevo campo de fuerza escalar, el campo de Higgs, del que no teníamos ninguna evidencia empírica hasta que los experimentos realizados en el acelerador de partículas LHC, encontraron el Bosón de Higgs y se consiguió añadir uno de los veinte parámetros aleatorios que tenía el modelo para convertirlo en un parámetro real y muy positivo, de tal manera que 50 años más tarde, lo que era una hipótesis teórica se ha convertido en una realidad tangible.

Desde la perspectiva actual, la Teoría Estándar se obtiene fácilmente a partir de un mínimo número de ingredientes: la existencia de constituyentes elementales de la materia con espín ½, quarks y leptones, y las propiedades de simetría de los campos cuánticos que los describen.
La derivación matemática de su estructura parece tan simple y elegante que se podría llegar a pensar que es el resultado de una idea brillante (¿por qué no se nos había ocurrido antes?). Nada más lejos de la realidad. El desarrollo histórico de la teoría se produjo mediante una concatenación de pequeños pasos, no siempre en la buena dirección, en los que poco a poco se fueron superando grandes dificultades técnicas y conceptuales.
El modelo que formularon Weinberg y Salam en 1967-1968 estaba basado en los desarrollos anteriores realizados por muchos otros científicos. Además, era un modelo solo de leptones y por lo tanto, tal como ahora sabemos, matemáticamente inconsistente debido a anomalías cuánticas. Harían falta todavía algunos años de profunda investigación y nuevas ideas para hacer posible la incorporación de los quarks, dando lugar al modelo definitivo. La celebración de este cincuentenario es una buena oportunidad para analizar retrospectivamente la evolución conceptual que ha permitido alcanzar este gran éxito científico.
Para terminar este trabajo, me retrotraigo a ese “puntito” infinitesimal que es el Núcleo Atómico
Rutherford con su experimento, descubrió que en el átomo existía un pequeño núcleo cargado positivamente, rodeado de electrones cargados negativamente. Los experimentos sobre la dispersión de partículas pusieron de manifiesto que el núcleo tiene dimensiones del orden de 10-14 m. Dado que el diámetro de un átomo es del orden de 10-10 m, el núcleo ocupa solo una fracción muy pequeña del volumen de un átomo. Sin embargo, el núcleo contiene casi toda la masa del átomo, como también demostraron esos experimentos.
Pero profundicemos un poco más
El núcleo atómico está constituido de los llamados Nucleones (es decir: Protones y Neutrones, partículas no elementales de la familia de los Hadrones en su rama Bariónica). Pero resulta que los nucleones están conformados, al mismo tiempo, por tripletes de partículas elementales de la familia Quarks, un protón tiene en sus entrañas a dos Quarks Up y un Quark Down, mientras que el Neutrón, tiene en su interior a dos Quarks Down y un Quarks Up.
Estos Quarks están allí confinados mediante la fuerza nuclear fuerte (la más potente de las cuatro fuerzas fundamentales), que es la única fuerza que crece con la distancia. Pues bien, la fuerza es transmitida e intermediada por otra familia de partícula que se llaman Bosones, y, aquí aparecen los Gluones que retienen a los Quarks confinados en el interior de los nucleones, y, cuando los Quarks tratan de separarse… ¡La fuerza nuclear aumenta y lo impide! Es lo que se conoce como libertad Asintótica de los Quarks.
Es difícil imaginar como en un espacio tan diminuto como lo es el núcleo atómico, puedan existir tantas cosas y ocurran tantos sucesos, realmente la Naturaleza es Asombrosa.
Emilio Silvera Vázquez
May
24
Superconductividad
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)

“Hace algunos años me hallé a mi mismo en un lugar completamente inesperado: una conferencia sobre teoría de cuerdas. Mi campo de investigación es la materia condensada, el estudio de materiales como metales y superconductores a temperaturas próximas al cero absoluto. Esta disciplina se halla todo lo lejos de la teoría de cuerdas como podría estarlo sin salirse de la física. La Teoría de cuerdas intenta describir la Naturaleza a energía muhco mayores a las que puedan alcanzarse en los laboratorios terrestres o, de hecho, en cualquier lugar del universo conocido. Quienes a ella se dedican estudian las exóticas leyes que gobiernan los agujeros negros y postulan que el universo posee otras dimensiones espaciales, además de las tres que podemos ver. Para ellos, la Gravedad constituye la interacción dominante de la Naturaleza. Para mí, no desempaña ningún papel.”

La mecánica cuántica fue desarrollada en el siglo XX para describir el movimiento de un electrón en un átomo de hidrógeno. Más tarde, Einstein y otros señalaron que la teoría cuántica de un par de electrones no tenía funciones intuitivas que encontraron difícil de aceptar: dos electrones bien pueden tener sus estados cuánticos “enredado”, indicando que hablan el uno al otro la mecánica cuántica, incluso a pesar de que están muy separados. Hoy en día, el entrelazamiento cuántico no es visto como un sutil efecto microscópico de interés sólo para unos pocos físicos, sino como un ingrediente crucial necesaria para una comprensión completa de las muchas fases de la materia. Un cristal puede tener unos billones de billones de electrones entrelazados unos con otros, y los diferentes patrones de entrelazamiento conducir a fases que son imanes, metales, o superconductores. Voy a dar una simple discusión de estas y otras características notables de la mecánica cuántica de un trillón de trillones de electrones, y de su importancia para una variedad de materiales tecnológicamente importantes. La teoría también tiene conexiones sorprendentes e inesperados a la teoría de cuerdas: notablemente, esto se conecta el movimiento de los electrones dentro de un plano de un cristal en el laboratorio, a la teoría de los agujeros negros astrofísicos similares a los estudiados por Chandrasekhar
Si hay algo que le gusta a la ciencia es estudiar los extremos de la naturaleza, incluso a veces forzarlos un poco. Cada vez construimos telescopios para ver más lejos, naves para viajar más rápido, combustibles de mayor rendimiento, etc. Y uno de los aspectos de la naturaleza que no se escapa de está búsqueda de los límites extremos es la temperatura.
Efectivamente, porque en el año 1997 el premio Nobel de física fue a parar a tres investigadores: Steven Chu (Universidad de Standford, California), Claude Cohen (Collage de France and Ecole Normale, Paris) y william D. Phillips (National Institute of Standards an Technology, Maryland), por el desarrollo de técnicas para lograr las temperaturas más bajas jamás alcanzadas.

Esta investigación abrió la puerta a todo un nuevo campo de investigación. Gracias a ella estamos conociendo mejor la estructura más íntima de la materia, y lo que es más importante comenzando a controlarla.
Vórtices cuánticos en un condensado rotante de átomos de sodio. Pero sigamos con el Profesor Sachdev que, nos sigue contando:
“Estas diferencias entre los físicos de cuerdas y los de la materia condensada, se plasman en un abismo cultural. Los investigadores de teorías de cuerdas gozan de una excelente reputación, por lo que asistí a aquella conferencia con un temor casi reverencial a su pericia matemática. Había invertido meses en la lectura de artículos y libros sobre el tema, a menudo quedándome empantanado. Estaba seguro de que sería rechazado como un advenedizo ignorante. Por su parte, los teóricos de cuerdas tenían dificultades con algunos de los conceptos más simples de mi campo. Llegué a verme dibujando esquemas que con anterioridad solo había empleado con mis estudiantes de doctorado primerizos.

Varios científicos encabezados por el físico de Oxford Ian Walmsley han conseguido relacionar y hacer vibrar a dos diamantes en el proceso conocido como entrelazamiento cuántico. El misterioso proceso, al que el propio Eisntein no supo darle comprensión completa, supone el mayor avance hasta la fecha y abre las puertas de la computación cuántica.
Así pues, ¿porque había asistido? Durante los últimos años, los expertos en materia condensada hemos observado que algunos materiales pueden comportarse de un modo que hasta ahora juzgábamos imposible. Se trata de fases marcadamente cuánticas de la materia cuya estructura se caracteriza por la aparición de uno de los fenómenos más chocantes de la naturaleza: el entrelazamiento cuántico. En un célebre artículo escrito en 1935, Albert Einstein, Boris Podolski y Nathan Rosen señalaron que la teoría cuántica implicaba la existencia de ciertas conexiones “espeluzmantes” entre partículas. Cuando aparecen, las partículas se coordinan sin que haya entre ellas una acción física directa. Einstein y sus colaboradores consideraron el caso de dos electrones, pero un metal o un superconductor contienen muchísimos más: del orden de 1023, en una muestra de laboratorio típica. La complejidad que exhiben algunos materiales resulta sobrecogedora, y a ella he dedicado gran parte de mi carrera. Pero el problema no se reduce a lo meramente académico:

Se trabajo con superconductores de baja y de alta temperatura. Bueno, al menos se está intentando saber más de ambos métodos. Los superconductores revisten una enorme importancia técnica, por lo que se han dedicado ingentes esfuerzos a entender sus propiedades y su potencial.
Hace unos años descubrimos que la Teoría de cuerdas nos brindaba una manera completamente inesperada de enfocar el problema. En su camino hacia una formulación que unifique las interacciones cuánticas entre partículas y la Teoría de la Gravedad de Einstein, los físicos de cuerdas se han topado con lo que ellos denominan “dualidades”: relaciones ocultas entre áreas de la física muy apartadas entre sí. Las dualidades que nos interesan relacionan dos tipos de teorías: por un lado, las que funcionan bien cuando los fenómenos cuánticos no resultan significativos pero la gravedad es muy intensa; por otro lado, aquellas que describen efectos cuánticos fuertes en situaciones con campos gravitatorios débiles [vease “El Espacio, ¿una ilusión”, por Juan Maldacena; Investigación y Ciencia, enero 2006]. Esta equivalencia permite traducir los hallazgos hallados en un campo al otro. Gracias a ella, descubrimos que podíamos expresar nuestras preguntas sobre el entrelazamiento en términos de un problema gravitatorio para, después, servirnos de los descubrimientos que los físicos de cuerdas habían realizado sobre las matemáticas de los agujeros negros. Un ejemplo de epnsamiento refinado al máximo.

Fases Ocultas
Para entender ese círculo de ideas debemos volver por un momento a la física del bachillerato. Según esta, las fases de la materia corresponden a los estados sólidos, líquido y gaseoso. Un sólido posee tamaño y forma fijos; un líquido toma la forma del recipiente que lo contiene;, aunque se parecen en este último aspecto a los líquidos, pueden alterar su volumen con facilidad. Aunque se trata de conceptos simples, hasta principios del siglo XX carecíamos de un entendimiento preciso de las fases de la materia. Los átomos se disponen de manera ordenada en los sólidos cristalinos, pero pueden moverse en líquidos y gases.

Sin embargo, las tres fases anteriores no bastan en absoluto para describir todos los aspectos de la materia. Un sólido no se compone solo de una red de átomos, sino también de un enjambre de electrones. Cada átomo libera unos pocos electrones que pueden pulular por todo el cristal. Cuando conectamos una batería a un pedazo de metal, la corriente eléctrica fluye por él.
Casi todos los metales obedecen la ley de Ohm: la intensidad de la corriente es igual al voltaje aplicado dividido por la resistencia del material. Los aislantes, como el teflón, presentan una resistencia muy elevada; en los metales, la resistencia es baja. Los superconductores destacan por poseer una resistencia inconmensurablemente pequeña. En 1911, Helke Kamerlingh Onnes descubrió el fenómeno al refrigerar mercurio sólido a 4 grados Kelvin (269 grados Celcius bajo cero). Hoy conocemos materiales en los que la superconductividad aparece a temperaturas mucho mayores (hasta 138 grados Celcius bajo cero).

Aunque tal vez no resulte obvio, aislantes y superconductores representan fases diferentes de la materia. El enjambre de electrones que los caracteriza adquiere en cada caso propiedades distintas. Durante las dos últimas décadas, hemos descubierto que los sólidos poseen fases electrónicas adicionales. Entre ellas, una especialmente interesante que, de tan insólita, ni siquiera tiene nombre: los físicos hemos dado en llamarla “metal extraño”. Se caracteriza por una dependencia inusual entre su resistencia eléctrica y su temperatura.”
Durante décadas, los físicos han estado tratando de conciliar las dos teorías principales que describen el comportamiento físico. La primera, la teoría de Einstein de la relatividad general, utiliza la gravedad – Las fuerzas de atracción – para explicar el comportamiento de los objetos con masas grandes, tales como la caída de los árboles o los planetas en órbita. Sin embargo, a nivel atómico y subatómico, las partículas con masas despreciables se describen mejor con otra teoría: la mecánica cuántica.
Una “teoría del todo” que unificara a la relatividad general con la mecánica cuántica abarcaría todas las interacciones físicas, sin importar el tamaño del objeto. Uno de los candidatos más populares para una teoría unificada es la teoría de cuerdas, desarrollada por primera vez a finales de 1960 y principios de 1970.
La teoría de cuerdas explica que los electrones y los quarks (los bloques de construcción de las partículas más grandes) son cadenas unidimensionales oscilantes, no objetos sin dimensiones como tradicionalmente se pensaba.
Los físicos están divididos sobre si la teoría de cuerdas es una teoría viable del todo, pero muchos están de acuerdo que ofrece una nueva manera de mirar a los fenómenos físicos que han demostrado ser de otro modo difíciles de describir. En la última década, los físicos han usado la teoría de cuerdas para construir una conexión entre la gravedad y la mecánica cuántica, conocida como “Gauge / dualidad gravedad”.

Hace unos 20 años que los científicos encontraron un inexplicable vacío en la estructura electrónica de ciertos supeconductores de alta temperatura. Ahora, una nueva investigación realizada por un equipo liderado por el físico Zhi-Xun Shen podría haber descubierto las razones de este misterio: la brecha podría evidenciar la existencia de un nuevo estado de la materia. El descubrimiento podría servir para conseguir materiales que presenten superconductividad a temperatura ambiente, algo que seguramente cambiaría nuestras vidas.
Es posible que uno de los misterios más antiguos que poseen los materiales superconductores haya sido resuelto. Desde hace unos 20 años que los científicos saben que, a determinadas temperaturas, los materiales superconductores presentan un vacío inexplicable en sus estructuras electrónicas. Este fenómeno podría ser explicado por la presencia de un nuevo estado -previamente desconocido- de la materia. O al menos, esta conclusión es a la que ha llegado un equipo de científicos liderado por el físico Zhi-Xun Shen, del Instituto de Stanford para la Ciencia de los materiales y energía (SIMES), que es una empresa conjunta del Departamento de energía (DOE) SLAC National Accelerator Laboratory y la Universidad de Stanford.
Zhi-Xun Shen está convencido que este trabajo proporciona la más fuerte evidencia encontrada hasta la fecha de la existencia de un nuevo estado de la materia. Además, la investigación podría brindar las claves necesarias para lograr materiales superconductores capaces de funcionar a temperatura ambiente.

Zhi-Xun Shen
Los supeconductores no presentan resistencia al paso de la energía eléctrica, permitiendo la construcción de electroimanes extremadamente potentes, como los utilizados en trenes de levitación magnética o aceleradores de partículas como el LHC. Sin embargo, estos materiales solo mantienen sus propiedades a temperaturas muy bajas, a menudo cercanas al cero absoluto. Los detalles del trabajo de Zhi-Xun Shen fueron publicados en el número 25 de marzo de la revista Science, y en él se destaca que uno de los obstáculos más importante que impiden el desarrollo de superconductores a altas temperaturas es el hecho de que aún los que poseen esa propiedad a temperaturas bastante mayores que cero absoluto deben ser refrigerados a mitad de camino a 0 grados Kelvin antes de que funcionen. Conseguir que un material presenten superconductividad a temperatura ambiente sin necesidad de este enfriamiento previo haría posible la distribución de electricidad sin pérdidas y muchos otros adelantos que, en conjunto, cambiarían nuestras vida

los principios físicos de la superconductividad no se comprendieron hasta 1957, cuando los físicos estadounidenses John Bardeen, León N. Cooper y John R. Schrieffer propusieron una teoría que ahora se conoce como teoría BCS por las iniciales de sus apellidos, y por la que sus autores recibieron el Premio Nobel de Física en 1972. La teoría BCS describe la superconductividad como un fenómeno cuántico, en el que los electrones de conducción se desplazan en pares, que no muestran resistencia eléctrica. Esta teoría explicaba satisfactoriamente la superconducción a altas temperaturas en los metales, pero no en los materiales cerámicos. En 1962, el físico británico Brian Josephson estudió la naturaleza cuántica de la superconductividad y predijo la existencia de oscilaciones en la corriente eléctrica que fluye a través de dos superconductores separados por una delgada capa aislante en un campo eléctrico o magnético. Este fenómeno, conocido como efecto Josephson, fue posteriormente confirmado experimentalmente.
Los científicos han usado electroimanes para generar campos magnéticos desde hace mucho tiempo. Haciendo fluir corriente eléctrica por un anillo conductor se induce campo magnético. Sustituyendo el conductor por un superconductor y enfriándolo a la temperatura necesaria, podría ser posible generar campos magnéticos mucho mas potentes debido a la falta de resistencia, y por tanto de generación de calor en el anillo. Sin embargo, esto no pudo hacerse en un principio. Cuando el campo magnético alcanzaba una determinada intensidad, el superconductor perdía sus propiedades y se comportaba como un conductor ordinario. Hasta la década de los cuarenta no se resolvieron los problemas de los campos magnéticos y solo muy recientemente se ha superado el problema de las bajas temperaturas.
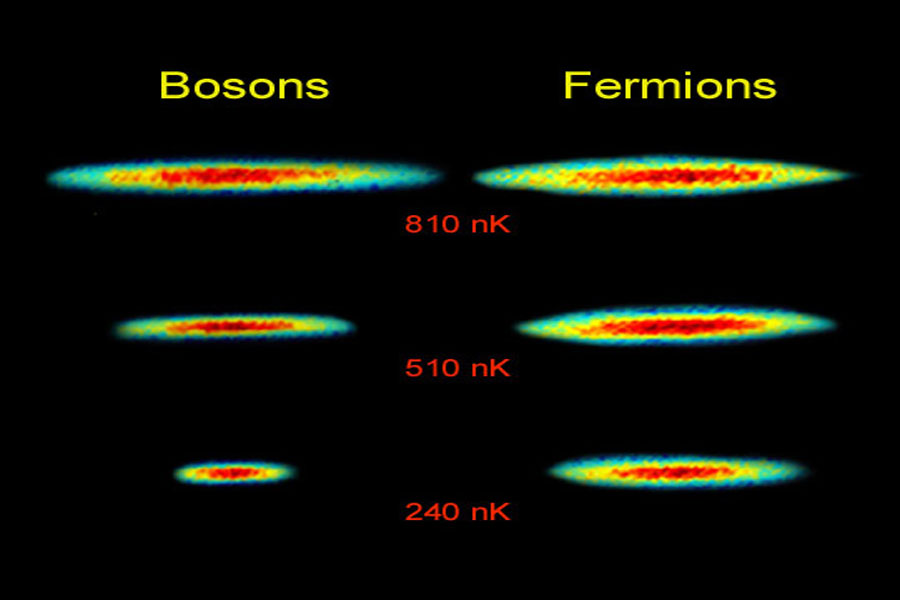
“¿Cuál es la razón por la que la materia no se colapsa sobre sí misma? El mismo principio que impide que las estrellas de neutrones y las enanas blancas implosionen y que hace que la materia normal sea en su mayor parte espacio vacio también permite la existencia de los seres humanos. El nombre técnico de este principio es el Principio de Exclusión de Pauli, y dice que dos fermiones (un tipo de partículas fundamentales) idénticos y con la misma orientación no pueden ocupar simultáneamente el mismo lugar en el espacio. Por el contrario, los bosones (otro tipo de partículas) no se comportan así, tal y como se ha demostrado recientemente por medio de la creación en el laboratorio de los condensados de Bose-Einstein.
A principios del s. XXI se hizo posible demostrar gráficamente el Principio de Exclusión de Pauli. Hoy ofrecemos esta demonstración como nuestra imagen del día. Lo que vemos arriba son nubes compuestas por dos isótopos de litio: la de la izquierda está formada a partir de bosones, mientras que la de la derecha está formada a partir de fermiones. A medida que baja la temperatura, los bosones se apilan unos sobre otros, pero los fermiones se mantienen separados.”
Otras veces hemos explicado aquí que los Bosones no obedecen al Principio de exclusión de Pauli, por lo que todos los pares de electrones de un superconductor pueden englobarse en el estado de mínima energía, lo que da lugar a un fenómeno conocido como condensación de Bose-Einstein. Vendría a ser como verter agua en un vaso y observar que, en vez de llenarse, se forma una fina capa de hielo en el fondo que absorbe tanta agua como tenemos sin aumentar su espesor.
Si a un material de tales características le aplicamos un voltaje, veremos que este promociona los pares de electrones hacia un estado que posee una diminuta cantidad de energía adicional, con lo que se genera una corriente eléctrica. Dicho estado de energía superior se encuentra por lo demás vacío, por lo que nada impide el flujo de pares y el superconductor transmite la corriente sin oponer resistencia.
Puntos Críticos



A principio de los ochenta, el éxito de la mecánica cuántica a la hora de explicar las propiedades de los metales, aislantes, superconductores y otros materiales, como los semiconductores (la base de la electrónica moderna) generó -la engañosa- sensación de que ya no quedaban grandes descubrimientos que hacer. Esa convicción se vino abajo cuando aparecieron los superconductores de altas temperaturas.
Un ejemplo nos lo proporciona el arseniuro de hierro y bario cuando una fracción del arsénico ha sido reemplazada por fósforo. A bajas temperaturas este material se comporta como un superconductor. Se cree que obedece a una teoría similar a la propuesta por BCS, pero en la que los pares de electrones no se crean por las vibraciones de la red cristalina, sino por efectos debidos a la física del espín.
Seguir ahondando en este tema de la superconductividad, nos llevaría muy lejos hasta comprobar, que no conocemos esencialmente lo que la materia es y, lo que de ella podemos esperar en circunstancias especiales. Nada es lo que parece a primera vista y, cuando conozcamos bien ese mundo extraño y misterioso que llamamos mecánica cuántica… ¿Qué podremos encontrar? Seguramente, allí estarán esos fantásticos y maravillosos “mundos” largamente buscados por los físicos y en los que, ¡Oh! ¡sorpresa! aparecerán las predicciones de la Teoría de cuerdas a la que no podemos llegar por no disponer de la energía necesaria.
El trabajo tiene varias fuentes pero, de manera muy especial, señaló aquí la Revista Investigación y ciencia en su artículo sobre el reportaje de Subir Sachdev que, entre otros datos recogidos al azar, conforman el presente trabajo que, de mi parte, contiene sólo algunos apuntes que tratan de conexionar el conjunto.
Publica: Emilio Silvera Vázquez
May
23
Partículas “bellas” de materia y antimateria II
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)
Hace ya algún tiempo que os puse aquí mismo la primera parte del artículo publicado en la Revista de Física de la RSEF, os pongo el comienzo de aquella primera parte y el final, así, recordareis.
Un magnífico artículo de Don Alberto Ruiz Jimeno, miembro del Grupo de Altas Energías del Instituto de Física Moderna Universidad de Cantabria y Jefe del Grupo de Altas Energías. En él nos dice que:
Nuevos bariones constituidos por tres Quarks, como los protones, pero conteniendo el quarks b (“belleza”) han sido observado en el experimento CDF del Acelerador del Tevatrón de protones y antiprotones. Por otra parte (nos dice), se ha observado por primera vez la oscilación de los mesones B, entre materia y antimateria. Dado que el artículo puede tener un alto interés para ustedes, he creído positivo transcribirlo aquí para gozo del personal que, con estos nuevos conocimientos (como me pasó a mí), podrán aumentar los suyos.
La física de partículas elementales tiene por objeto el estudio de los constituyentes más elementales de la materia y de las fuerzas fundamentales que rigen su comportamiento. La dinámica de estos bloques fundamentales viene formulada por la mecánica cuántica relativista.
Terminaba esta primera parte así:
El Modelo Estándar ha sido comprobado desde su desarrollo formal, a mediados de 1960, y sus parámetros han sido medidos con extraordinaria precisión, gracias al desarrollo de experimentos muy potentes, entre los que destacan los realizados en el acelerador LEP (“Large Electrón Positrón”) del CERN (Centro Europeo de Física de Partículas, en Ginebra), durante la última década del siglo XX, y del Tevatrón del Laboratorio Fermilab (Chicago, USA), aún en funcionamiento.















 Totales: 77.947.160
Totales: 77.947.160 Conectados: 26
Conectados: 26