Mar
4
¡La Curiosidad! La madre del saber
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Cosas curiosas ~
Clasificado en Cosas curiosas ~
 Comments (9)
Comments (9)

¡Qué bonito sería si las piedras pudieran hablar! ¿Qué nos contarían éstas?
Todos los asiduos a este lugar, sabéis de mi curiosidad insaciable por las cosas, por lo que pasó, por las Civilizaciones antiguas, por los misterios que la materia encierra, y, en fin, por el Universo y las historias de las criaturas que lo pueblan y que, en la antigüedad, estuvieron aquí.

Ellos inventaron el Cero que cambio po completo las matemáticas, a la izquierda no vale nada pero… ¡A la Derecha…!
En el siglo V, Aryabhata escribe el Aryabhatiya, un delgado volumen concebido para complementar las reglas de cálculo utilizadas en astronomía y en medida matemática. Escrito en verso, carece de rigor lógico o metodología deductiva. Aunque casi la mitad de las entradas son incorrectas, es en el Aryabhatiya en donde el sistema decimal posicional aparece por vez primera. Siglos más tarde, el matemático árabe Abu Rayhan Biruni describiría este tratado como «una mezcla de guijarros ordinarios y cristales onerosos». En 499, Aryabhata.

Existen lugares en los que, se han conservado más vivos y realistas los recuerdos del pasado y, en la India, donde al contrario que en la China, no cruzan el cielo los Dragones, serpientes o Aves monstruosas, nos dicen que fueron máquinas, las que, para el asombro de todos, cruzaban el cielo.

James Churchward, el desconcertante estudioso inglés cuyas investigaciones no son nada desdeñables, siempre y cuando no se aproximan a las especulaciones teo-sofistas, nos habla de un manuscrito que contiene la descripción de una nave aérea de hace 20.000 años.
“La energía” –detalla en una obra redactada varios lustros antes de que se hablara de astronaves y satélites artificiales- se obtiene de la atmósfera de manera simple y poco costosa. En la obra daba una amplia explicación del motor y sus compartimentos y cámaras y de las increíbles propiedades que la nave tenía que, incluso, podía quedar estática en el aire, o, salir disparada como un rayo hacia lo más alto del cielo hasta desaparecer de la vista.

Enormes máquinas voladoras que surcaban los cielos
¿Fantasías? Escuchemos un relato de la Academia Internacional de Investigaciones sánscritas de Mysore: “Los manuscritos cuya traducción del sánscrito presentamos, describen varios tipos de “vimana” (naves que se mueven por sí mismas), capaces de viajar por su propio impulso por tierra, agua y aire, y, asimismo, de planeta a planeta. Parece que los vehículos aéreos podían detenerse en el cielo hasta quedar inmóviles, y que estaban dotados de instrumentos capaces de señalar, incluso a distancia, la presencia de aparatos enemigos.
(El relato fue publicado en la India por el especialista Maharshi Bharadaja con el título Aeronáutica del pasado prehistórico.)
Numerosísimos testimonios nos vienen a confirman ampliamente lo anterior. Por ejemplo tenemos una amplia muestra en el Samaranganasutradhara que narra la historia de vuelos fantásticos realizados por el mundo, y hacia el Sol y las estrellas. Un documento de época precristiana nos suministra una detallada descripción del carro celeste de Rama. La narración nos dice: “…el carro se movía por sí solo y era grande y estaba bien pintado; tenía dos pisos, muchas habitaciones y ventanas…”, cuyas hazañas, canta Valmiki el Herodoto indio: “El carro celeste, que posee una fuerza admirable, alada de velocidad, dorado en su forma y en su esplendor… El carro celeste ascendió por encima de la colina y del valle boscoso…alado como el rayo, dardo de Indra, fatal como el relámpago del cielo, envuelto en humo y destellos flameantes, rápida proa circular” (del Ramayana, que narra la epopeya de Rama).
Centenares y centenares de historias semejantes nos podemos encontrar a lo largo de las tradiciones hundúes: “ahí va la divina Maya volando en un carro de oro circular, que mide 12.000 codos de circunferencia, capaz de alcanzar las estrellas”, y, hete aquí el “caballo metálico del cielo” del rey Satrugit y el “carruaje del aire” del rey Pururavas. También el siglo IV de nuestra era encontramos a un héroe aeronauta, el monje budista Gunarvarman, quien se va desde Ceylán a Java en un aparato similar a los antiguos, sacado quién sabe de dónde.
Según se deduce de estos antiquísimos manuscritos en sánscrito, aquellos hindúes prehistóricos (o lo que realmente pudieran ser), no utilizaban aquellos ingenios voladores para excursiones de placer, sino que, según nos cuentan los relatos, las acciones bélicas eran también cotidianas que describen terribles batallas.
Un bajorrelieve en Angkor Wat (Camboya) representa a Rávana Rávana peleando en la batalla de Lanka, el clímax del Ramaiana.
Rávana, el rey de los demonios de Ceylán, enemigo mortal de Rama, “voló sobre los adversarios (según nos narra un manuscrito del año 500 a, de C.) haciendo caer ingenios que causaron grandes destrucciones. Finalmente, fue capturado y muerto, y su máquina celeste cayó en manos del capitán hindú Ram Chandra, quién, sirviéndose de ella, voló a la capital, Adjhudia…”
Y esto no son más que bagatelas. “El Bhisma Parva –recuerda Drake- menciona armas como la “verga de Brahma” y el “Rayo de Indra”, cuyos efectos se parecen a los producidos por la energía nuclear. El Drona Parva nos habla del “señor Mahadeva” y de sus terribles lanzas volantes (¿misiles?) capaces de destruir ciudades enteras fortificadas…, y describe las fantásticas armas de Agni, que aniquilaron ejércitos completos y devastaron la Tierra como bombas de Hidrógeno.”
¿Es posible que no se hayan conservado trazas de estos alucinantes conflictos? Los restos existen, y numerosísimos –responden los investigadores-. Basta que nos tomemos la molestia de ir en su busca. No es una empresa fácil, desde luego, puesto que, desde hace milenios la jungla se ha espesado sobre las ruinas, pero si consiguiéramos localizar todas las “ciudades muertas” de la gran península, constelaríamos el mapa de la India de tantos puntos como los que, en un Atlas, nos indican los centros de población actuales.

De vez en cuando aparecen descripciones a este respecto que nos dejan perplejos. El explorador De Camp, por ejemplo, refirió haber visto, en la zona que se extiende entre el Ganges y los montes Rajmahal, ruinas carbonizadas por algo que no podía ser un simple incendio, por violento que éste fuera. Algunas piedras gigantescas aparecían fundidas y desenterradas en varios puntos, “como bloques de estaño afectados por la salpicadura de una colada de acero”.
Más al Sur, el oficial británico J. Campbell se topó, en los años veinte, con ruinas similares, y quedó sorprendido por un extrañísimo detalle: en el pavimento semivitrificado de lo que debió de ser un patio interior, parecían haber sido impresas, por una fuerza desconocida, formas de cuerpos humanos.

Otros viajeros refieren haber descubierto en el corazón de los bosques indios ruinas de edificios nunca vistos, con paredes “semejantes a gruesas losas de cristal” asimismo perforadas, resquebrajadas y corroídas por agentes desconocidos. Y habiendo penetrado en una de estas construcciones, parecida a una cúpula baja, el explorador y cazador H. J. Hamilton se encontró con la mayor sorpresa de su vida.ç
“En una parte –recuerda-, el suelo cedió bajo mis pies con un extraño crujido. Me puse a seguro y, luego, ensanché con la culata del fusil el boquete que se había abierto, y me introduje en él. Me encontré en una estancia larga y estrecha que recibía luz por una grieta de la bóveda. Al fondo, vi una especie de mesa y un asiento del mismo “cristal” de que estaban hechas las paredes.

En el asiento, se enroscaba una forma extraña, de contornos vagamente humanos. Observándola de cerca, me pareció, al principio, que se trataba de una estatua deteriorada por la acción del tiempo, pero, luego, descubrí algo que me llenó de horror: bajo el “vidrio” que revestía aquella estatua, ¡se podían distinguir claramente los detalles del esqueleto!”.
Muros, muebles y seres humanos vitrificados… ¿Qué tremendos secretos se esconden entre las líneas del Mahabrata y del Drona Parva?
Emilio Silvera Vázquez
Oct
25
¡La Curiosidad! La madre del saber
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Cosas curiosas ~
Clasificado en Cosas curiosas ~
 Comments (2)
Comments (2)

¡Qué bonito sería si las piedras pudieran hablar! ¿Qué nos contarían éstas? Yo, os lo puedo decir: Nos hablaría de Colón, acogido aquí, en el Monasterio de la Rábida en la Villa de Palos de la Frontera en Huelva, donde muchos de los marineros de La Niña, la Santa María y la Pinta eran de aquí.

Todos los asiduos a este lugar, sabéis de mi curiosidad insaciable por las cosas, por lo que pasó, por las Civilizaciones antiguas, por los misterios que la materia encierra, y, en fin, por el Universo y las historias de las criaturas que lo pueblan y que, en la antigüedad, estuvieron aquí.


Existen lugares en los que, se han conservado más vivos y realistas los recuerdos del pasado y, en la India, donde al contrario que en la China, no cruzan el cielo los Dragones, serpientes o Aves monstruosas, nos dicen que fueron máquinas, las que, para el asombro de todos, cruzaban el cielo.

James Churchward, el desconcertante estudioso inglés cuyas investigaciones no son nada desdeñables, siempre y cuando no se aproximan a las especulaciones teosofistas (1), nos habla de un manuscrito que contiene la descripción de una nave aérea de hace 20.000 años.
(1) El nombre teosofía es uno de los tantos que se utiliza para designar a una sabiduría sin edad, eterna, que no es otra que el conocimiento de la verdadera realidad. Del mismo modo que la ciencia no crea las leyes que rigen la naturaleza sino que las descubre, la teosofía es la realidad, y los seres humanos van aprendiendo.

Pushpaka Vimana: una máquina voladora de la antigua India
“La energía” –detalla en una obra redactada varios lustros antes de que se hablara de astronaves y satélites artificiales- se obtiene de la atmósfera de manera simple y poco costosa. En la obra daba una amplia explicación del motor y sus compartimentos y cámaras y de las increíbles propiedades que la nave tenía que, incluso, podía quedar estática en el aire, o, salir disparada como un rayo hacia lo más alto del cielo hasta desaparecer de la vista.
:format(jpg)/f.elconfidencial.com%2Foriginal%2F641%2Ff73%2Fa9e%2F641f73a9eb982aa918974867cbda706b.jpg)
Los científicos indios que defienden que sus ancestros ya inventaron las naves espaciales
¿Fantasías? Escuchemos un relato de la Academia Internacional de Investigaciones sánscritas de Mysore: “Los manuscritos cuya traducción del sánscrito presentamos, describen varios tipos de “vimana” (naves que se mueven por sí mismas), capaces de viajar por su propio impulso por tierra, agua y aire, y, asimismo, de planeta a planeta. Parece que los vehículos aéreos podían detenerse en el cielo hasta quedar inmóviles, y que estaban dotados de instrumentos capaces de señalar, incluso a distancia, la presencia de aparatos enemigos.
(El relato fue publicado en la India por el especialista Maharshi Bharadaja con el título Aeronáutica del pasado prehistórico.)
Numerosísimos testimonios nos vienen a confirman ampliamente lo anterior. Por ejemplo tenemos una amplia muestra en el Samaranganasutradharaque narra la historia de vuelos fantásticos realizados por el mundo, y hacia el Sol y las estrellas. Un documento de época precristiana nos suministra una detallada descripción del carro celeste de Rama. La narración nos dice: “…el carro se movía por sí solo y era grande y estaba bien pintado; tenía dos pisos, muchas habitaciones y ventanas…”, cuyas hazañas, canta Valmiki el Herodoto indio: “El carro celeste, que posee una fuerza admirable, alada de velocidad, dorado en su forma y en su esplendor… El carro celeste ascendió por encima de la colina y del valle boscoso…alado como el rayo, dardo de Indra, fatal como el relámpago del cielo, envuelto en humo y destellos flameantes, rápida proa circular” (del Ramayana, que narra la epopeya de Rama).

Centenares y centenares de historias semejantes nos podemos encontrar a lo largo de las tradiciones hundúes: “ahí va la divina Maya volando en un carro de oro circular, que mide 12.000 codos de circunferencia, capaz de alcanzar las estrellas”, y, hete aquí el “caballo metálico del cielo” del rey Satrugit y el “carruaje del aire” del rey Pururavas. También el siglo IV de nuestra era encontramos a un héroe aeronauta, el monje budista Gunarvarman, quien se va desde Ceylán a Java en un aparato similar a los antiguos, sacado quién sabe de dónde.
Según se deduce de estos antiquísimos manuscritos en sánscrito, aquellos hindúes prehistóricos (o lo que realmente pudieran ser), no utilizaban aquellos ingenios voladores para excursiones de placer, sino que, según nos cuentan los relatos, las acciones bélicas eran también cotidianas que describen terribles batallas.
Un bajorrelieve en Angkor Wat (Camboya) representa a Rávana peleando en la batalla de Lanka, el clímax del Ramaiana.

Rávana, rey de los demonios rakshasas
Rávana, el rey de los demonios de Ceylán, enemigo mortal de Rama, “voló sobre los adversarios (según nos narra un manuscrito del año 500 a, de C.) haciendo caer ingenios que causaron grandes destrucciones. Finalmente, fue capturado y muerto, y su máquina celeste cayó en manos del capitán hindú Ram Chandra, quién, sirviéndose de ella, voló a la capital, Adjhudia…”

Bhishma Parva
“Dhritarashtra dijo: “Cuéntame, oh Sanjaya, acerca del período de vida, la fuerza, las cosas buenas y malas, el futuro, el pasado y el presente de los residentes, oh Suta, de este Varsha de Bharata, y del Himavat-varsha, como también del Hari-varsha, en detalle”.
Read more https://spiritualworld.co.in/mahabharat-in-english-bhishma-parva/
Y esto no son más que bagatelas. “El Bhisma Parva –recuerda Drake- menciona armas como la “verga de Brahma” y el “Rayo de Indra”, cuyos efectos se parecen a los producidos por la energía nuclear. El Drona Parva nos habla del “señor Mahadeva” y de sus terribles lanzas volantes (¿misiles?) capaces de destruir ciudades enteras fortificadas…, y describe las fantásticas armas de Agni, que aniquilaron ejércitos completos y devastaron la Tierra como bombas de Hidrógeno.”

¿Es posible que no se hayan conservado trazas de estos alucinantes conflictos? Los restos existen, y numerosísimos –responden los investigadores-. Basta que nos tomemos la molestia de ir en su busca. No es una empresa fácil, desde luego, puesto que, desde hace milenios la jungla se ha espesado sobre las ruinas, pero si consiguiéramos localizar todas las “ciudades muertas” de la gran península, constelaríamos el mapa de la India de tantos puntos como los que, en un Atlas, nos indican los centros de población actuales.

De vez en cuando aparecen descripciones a este respecto que nos dejan perplejos. El explorador De Camp, por ejemplo, refirió haber visto, en la zona que se extiende entre el Ganges y los montes Rajmahal, ruinas carbonizadas por algo que no podía ser un simple incendio, por violento que éste fuera. Algunas piedras gigantescas aparecían fundidas y desenterradas en varios puntos, “como bloques de estaño afectados por la salpicadura de una colada de acero”.
Más al Sur, el oficial británico J. Campbell se topó, en los años veinte, con ruinas similares, y quedó sorprendido por un extrañísimo detalle: en el pavimento semivitrificado de lo que debió de ser un patio interior, parecían haber sido impresas, por una fuerza desconocida, formas de cuerpos humanos.

Otros viajeros refieren haber descubierto en el corazón de los bosques indios ruinas de edificios nunca vistos, con paredes “semejantes a gruesas losas de cristal” asimismo perforadas, resquebrajadas y corroídas por agentes desconocidos. Y habiendo penetrado en una de estas construcciones, parecida a una cúpula baja, el explorador y cazador H. J. Hamilton se encontró con la mayor sorpresa de su vida.

Así son las momias encontradas.
Podría seguir con este trabajo pero… Todo esto me parece tan increíble… ¿Pero como lo cuentan con tanto lujo de detalles.
Emilio Silvera Vázquez
Ago
7
¿La Mente Humana? ¡Un prodigio de la Naturaleza!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Cosas curiosas ~
Clasificado en Cosas curiosas ~
 Comments (0)
Comments (0)

Téngase en cuenta que este es un tiempo característico, por lo que su orden de magnitud es lo que debe tenerse en cuenta. A veces se define con la longitud de onda de arriba dividida por 2π, así que no se debe preocupar por el número de dígitos significativos
Antes del tiempo clasificado como tiepo de Planck, 10-43 segundos, todas las cuatro fuerzas fundamentales se presumía que estaban unificadas en una sola fuerza. Toda la materia, energía, espacio y tiempo se suponía que se dispararon hacia el exterior desde una singularidad original. No se sabe nada de este período.
Era del Tiempo de Planck
En la era de alrededor del tiempo de Planck 1, 10-43 segundos, se proyecta por el modelado actual de las fuerzas fundamentales fuerzas, que la fuerza de la gravedad comienza a diferenciarse de las otras tres fuerzas. Esta es la primera de las roturas espontáneas de la simetría, que desembocan en los cuatro tipos de interacciones observadas en el universo actual.
Las Unidades de Planck
Tampoco es que sepamos mucho acerca de períodos posteriores, es sólo que no tenemos verdaderos modelos coherentes de lo que podría suceder bajo tales condiciones. La unificación electrodébil ha sido apoyada por el descubrimiento de las patículas W y Z, y se puede utilizar como una plataforma de debate sobre el siguiente paso, la Teoría de la Gran Unificación (GUT). La unificación final ha sido llamada “teoría de la super unificación”, y cada vez más popular es la denominada “Teoría del Todo” (TOE). Sin embargo, “las teorías del todo” están separadas por dos grandes saltos, más allá de los experimentos que se pueda desear hacer en la Tierra.
El tiempo de Planck o cronón (término acuñado en 1926 por Robert Lévi) es una unidad de tiempo, considerada como el intervalo temporal más pequeño que puede ser medido. Se denota mediante el símbolo tP. En cosmología, el tiempo de Planck representa el instante de tiempo más pequeño en el que las leyes de la física pueden ser utilizadas para estudiar la naturaleza y evolución del Universo. Se determina como combinación de otras constantes físicas en la forma siguiente:
 segundos
segundos
donde:
 es la constante de Planck reducida (conocida también como la constante de Dirac).
es la constante de Planck reducida (conocida también como la constante de Dirac). - G es la constante de Gravitación Universal; c es la velocidad de la luz en el vacío.
Los números entre paréntesis muestran la desviación estándar.
En este ámbito hablamos de las cosas muy pequeñas, las que no se ven
El Tiempo de Planck es:
Es el tiempo que necesita el fotón (viajando a la velocidad de la luz, c, para moverse a través de una distancia igual a la longitud de Planck. Está dado por , donde G es la constante gravitacional (6, 672 59 (85) x 10-11 N m2 kg-2), ħ es la constante de Planck racionalizada (ħ = h/2л = 1,054589 x 10-34 Julios segundo), c, es la velocidad de la luz (299.792.458 m/s).
El valor del tiempo del Planck es del orden de 10-44 segundos. En la cosmología del Big Bang, hasta un tiempo Tp después del instante inicial, es necesaria usar una teoría cuántica de la gravedad para describir la evolución del Universo. Todo, desde Einstein, es relativo. Depende de la pregunta que se formule y de quién nos de la respuesta.
¿El Tiempo? Muchos Filósofos lo quisieron explicar pero… ¡No pudieron!
Si preguntamos ¿Qué es el tiempo?, tendríamos que ser precisos y especificar si estamos preguntando por esa dimensión temporal que no deja de fluir desde el Big Bang y que nos acompaña a lo largo de nuestras vidas, o nos referimos al tiempo atómico, ese adoptado por el SI, cuya unidad es el segundo y se basa en las frecuencias atómicas, definida a partir de una línea espectral particular de átomo de cesio 133, o nos referimos a lo que se conoce como tiempo civil, tiempo coordinado, tiempo de crecimiento, tiempo de cruce, tiempo de integración, tiempo de relajación, tiempo dinámico o dinámico de Bari-céntrico, dinámico terrestre, tiempo terrestre, tiempo de Efemérides, de huso horario, tiempo estándar, tiempo local, tiempo luz, tiempo medio, etc. etc. Cada una de estas versiones del tiempo, tiene una respuesta diferente, ya que, no es lo mismo el tiempo propio que el tiempo sidéreo o el tiempo solar, o solar aparente, o solar medio, o tiempo terrestre, o tiempo Universal. Como se puede ver, la respuesta dependerá de cómo hagamos la pregunta.

… Y que el mismo tiempo suele borrar
En realidad, para todos nosotros el único tiempo que rige es el que tenemos a lo largo de nuestras vidas, los otros tiempos, son inventos del hombre para facilitar sus tareas de medida, de convivencia o de otras cuestiones técnicas o astronómicas pero, sin embargo, el tiempo es solo uno; ese que comenzó cuando nació el Universo y que finalizará cuando este llegue a su final.
Lo cierto es que, para las estrellas supermasivas, cuando llegan al final de su ciclo y deja de brillar por agotamiento de su combustible nuclear, en ese preciso instante, el tiempo se agota para ella. Cuando una estrella pierde el equilibrio existente entre la energía termonuclear (que tiende a expandir la estrella), y, la fuerza de gravedad (que tiende a comprimirla), al quedar sin oposición esta última, la estrella supermasiva se contrae aplastada bajo su propia masa. Queda comprimida hasta tal nivel que llega un momento que desaparece, para convertirse en un Agujero Negro, una singularidad, donde dejan de existir el “tiempo” y el espacio. A su alrededor nace un horizonte de sucesos que, si se traspasa, se es engullido por la enorme gravedad del Agujero Negro.

En la singularidad no se distorsiona, se para
El tiempo, de ésta manera, deja de existir en estas regiones del Universo que conocemos como singularidad. El mismo Big Bang -dicen- surgió de una singularidad de energía y densidad infinitas que, al explotar, se expandió y creó el tiempo, el espacio y la materia.
Como contraposición a estas enormes densidades de las enanas blancas, estrellas de neutrones y Agujeros Negros, existen regiones del espacio que contienen menos galaxias que el promedio o incluso ninguna galaxia; a estas regiones las conocemos como vacío cósmico. Han sido detectados vacíos con menos de una décima de la densidad promedio del Universo en escalas de hasta 200 millones de años luz en exploraciones a gran escala. Estas regiones son a menudo esféricas. El primer gran vacío en ser detectado fue el de Boötes en 1.981; tiene un radio de unos 180 millones de años luz y su centro se encuentra aproximadamente a 500 millones de años luz de la Vía Láctea. La existencia de grandes vacíos no es sorprendente, dada la existencia de cúmulos de galaxias y supercúmulos a escalas muy grandes.
Mientras que en estas regiones la materia es muy escasa, en una sola estrella de neutrones, si pudiéramos retirar 1 cm3 de su masa, obtendríamos una cantidad de materia increíble. Su densidad es de 1017 kg/m3, los electrones y los protones están tan juntos que se combinan y forman neutrones que se degeneran haciendo estable la estrella de ese nombre que, después del agujero negro, es el objeto estelar más denso del Universo.
Es interesante ver cómo a través de las matemáticas y la geometría, han sabido los humanos encontrar la forma de medir el mundo y encontrar las formas del Universo. Pasando por Arquímedes, Pitágoras, Newton, Gauss o Riemann (entre otros), siempre hemos tratado de buscar las respuestas de las cosas por medio de las matemáticas.

“Magia es cualquier tecnología suficientemente avanzada”
Arthur C. Clarke
Pero también es magia el hecho de que, en cualquier tiempo y lugar, de manera inesperada, aparezca una persona dotada de condiciones especiales que le permiten ver, estructuras complejas matemáticas que hacen posible que la Humanidad avance considerablemente a través de esos nuevos conceptos que nos permiten entrar en espacios antes cerrados, ampliando el horizonte de nuestro saber.


Recuerdo aquí uno de esos extraños casos que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: La teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann dio su célebre conferencia en la facultad de la Universidad de Gotinga en Alemania. Aquello fue como abrir de golpe, todas las ventanas cerradas durante 2.000 años, de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.
Su ensayo de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la Literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del Universo y su evolución mediante su asombrosa teoría de la relatividad general Ciento treinta años después de su conferencia, los físicos utilizarían la geometría deca-dimensional para intentar unir todas las leyes del Universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.

Contradictoriamente, Riemann era la persona menos indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria que arruinó su vida en la miseria abyecta y la tuberculosis.
Riemann nació en 1.826 en Hannover, Alemania, segundo de los seis hijos de un pobre pastor luterano que trabajó y se esforzó como humilde predicador para alimentar a su numerosa familia que, mal alimentada, tendrían una delicada salud que les llevaría a una temprana muerte. La madre de Riemann también murió antes de que sus hijos hubieran crecido.
A edad muy temprana, Riemann mostraba ya los rasgos que le hicieron famoso: increíble capacidad de cálculo que era el contrapunto a su gran timidez y temor a expresarse en público. Terriblemente apocado era objeto de bromas de otros niños, lo que le hizo recogerse aún más en un mundo matemático intensamente privado que le salvaba del mundo hostil exterior.
Para complacer a su padre, Riemann se propuso hacerse estudiante de teología, obtener un puesto remunerado como pastor y ayudar a su familia. En la escuela secundaria estudió la Biblia con intensidad, pero sus pensamientos volvían siempre a las matemáticas. Aprendía tan rápidamente que siempre estaba por delante de los conocimientos de sus instructores, que encontraron imposible mantenerse a su altura. Finalmente, el director de la escuela dio a Riemann un pesado libro para mantenerle ocupado. El libro era la Teoría de números de Adrien-Marie Legendre, una voluminosa obra maestra de 859 páginas, el tratado más avanzado del mundo sobre el difícil tema de la teoría de números. Riemann devoró el libro en seis días.

Cuando el director le preguntó: “¿Hasta dónde has leído?”, el joven Riemann respondió: “Este es un libro maravilloso. Ya me lo sé todo”.
Sin creerse realmente la afirmación de su pupilo, el director le planteó varios meses después cuestiones complejas sobre el contenido del libro, que Riemann respondió correctamente.
Con mil sacrificios, el padre de Riemann consiguió reunir los fondos necesarios para que, a los 19 años pudiera acudir a la Universidad de Gotinga, donde encontró a Carl Friedrich Gauss, el aclamado por todos “Príncipe de las Matemáticas”, uno de los mayores matemáticos de todos los tiempos. Incluso hoy, si hacemos una selección por expertos para distinguir a los matemáticos más grandes de la Historia, aparecerá indudablemente Euclides, Arquímedes, Newton y Gauss.

Hannover, Alemania
Los estudios de Riemann no fueron un camino de rosas precisamente. Alemania sacudida por disturbios, manifestaciones y levantamientos, fue reclutado en el cuerpo de estudiantes para proteger al rey en el palacio real de Berlín y sus estudios quedaron interrumpidos.
En aquel ambiente el problema que captó el interés de Riemann, fue el colapso que, según el pensaba, suponía la geometría euclidiana, que mantiene que el espacio es tridimensional y “plano” (en el espacio plano, la distancia más corta entre dos puntos es la línea recta; lo que descarta la posibilidad de que el espacio pueda estar curvado, como en una esfera).
Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna parte vería Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita. Riemann, ante aquella realidad se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos., descubrió el, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.
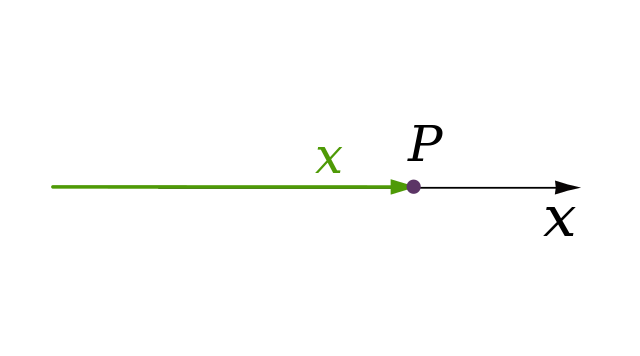
Euclides nos habló de la obviedad de que un punto no tiene dimensión. Una línea tiene una dimensión: longitud. Un plano tiene dos dimensiones: longitud y anchura. Un sólido tiene tres dimensiones: longitud, anchura y altura. Y allí se detiene. Nada tiene cuatro dimensiones, incluso Aristóteles afirmó que la cuarta dimensión era imposible. En Sobre el cielo, escribió: “La línea tiene magnitud en una dirección, el plano en dos direcciones, y el sólido en tres direcciones, y más allá de éstas no hay otra magnitud porque los tres son todas.” Además, en el año 150 d. C. el astrónomo Ptolomeo de Alejandría fue más allá de Aristóteles y ofreció, en su libro sobre la distancia, la primera “demostración” ingeniosa de que la cuarta dimensión es imposible.

Hemos querido ver la cuarta dimensión pero… No deja ver. Sin embargo, su transcurrir se siente. En ella está la Entropía.
En realidad, lo único que Ptolomeo demostraba era que, era imposible visualizar la cuarta dimensión con nuestros cerebros tridimensionales (de hecho, hoy sabemos que muchos objetos matemáticos no pueden ser visualizados, aunque puede demostrarse que en realidad, existen). Ptolomeo puede pasar a la Historia como el hombre que se opuso a dos grandes ideas en la ciencia: el sistema solar heliocéntrico y la cuarta dimensión.
La ruptura decisiva con la geometría euclidiana llegó cuando Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.
Riemann desarrolló su teoría de dimensiones más altas.
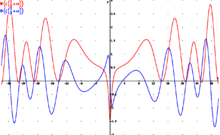
Parte real (rojo) y parte imaginaria (azul) de la línea crítica Re(s) = 1/2 de la función zeta de Riemann. Pueden verse los primeros ceros no triviales en Im(s) = ±14,135, ±21,022 y ±25,011. La hipótesis de Riemann, por su relación con la distribución de los números primos en el conjunto de los naturales, es uno de los problemas abiertos más importantes en la matemática contemporánea.
Finalmente, cuando hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, esta fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante los milenios.
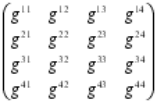
Riemann creó el tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresar a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a2 + b2 = c2. El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional.)
El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann, permitió a Einstein formular su teoría de la gravedad y, posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de super-gravedad, supersimetría y, finalmente las supercuerdas.

Para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854, que le había enviado su amigo Marcel Grossman, rápidamente se dio cuenta de que allí estaba la clave para resolver su problema. Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de a relatividad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E=mc2. La reinterpretación física de la famosa conferencia de Riemann se denomina ahora relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.
Emilio Silvera V.
Ene
10
Lo cierto es que…, nunca dejáremos de hacernos preguntas.
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Cosas curiosas ~
Clasificado en Cosas curiosas ~
 Comments (1)
Comments (1)

Aunque es cierto que “sobre gustos no hay nada escrito”, los humanos nos sentimos más a gusto con las caras más simétricas. En la cultura popular, y salvo alguna rara excepción, las caras asimétricas están relacionadas con la maldad. Los biólogos encontraron rápidamente una explicación evolutiva: los individuos más evolucionados pueden mantener sus formas simétricas inclusive cuando están expuestos al estrés y las enfermedades. Es decir, cuando las partes del cuerpo que tienden a la simetría no lo son, costará más pasar esos genes porque será rechazado por potenciales parejas. De esta manera la evolución distingue a la simetría como una característica valiosa.

David (1501-1504), de Miguel Ángel, Galería de la Academia de Florencia.
El desnudo de una figura presenta una simetría bilateral casi perfecta. Ciertamente, parte del atractivo del mismo, tanto en la realidad como en el arte, reside en la identificación de los lados derecho e izquierdo del cuerpo mediante mediante una simetría especular. La figura femenina raramente presenta asimetrías. La asimetría de un varón se rompe solamente por la curiosa circunstancia de que su testículo izquierdo cuelga más bajo que el derecho.

(1532), de Lucas Cranach el Viejo, Städelsches Kunstinstitut, Fráncfort del Meno, censurada por el Metro de Londres en 2008.
Evidentemente, cada cuerpo, considerado de forma individual, puede otras desviaciones menores de su simetría: un hombro más alto que otro, un pecho mayor que su pareja, una ligera desviación de la columna, una peca o un antojo en un costado…, pero tales anomalías, en su mayor parte, pueden encontrarse tanto a un lado como al otro.
La simetría bilateral se mantiene en el interior del cuerpo, en en los músculos y en el esqueleto, pero queda rota por la disposición fuertemente asimétrica de algunos órganos. El corazón, el estómago y el páncreas están desviados hacia la izquierda; el hígado y el apéndice, hacia la derecha. El pulmón derecho es mayor que el izquierdo. Los retorcimientos y vueltas de los intestinos son completamente asimétricos. El cordón umbilical humano, una magnifica hélice triple formada por dos arterias y una vena, puede enrollarse en cualquiera de los dos sentidos.

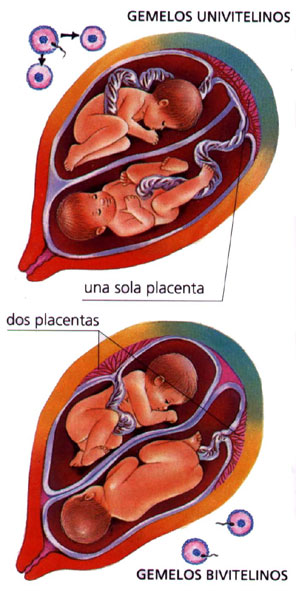
Los mellizos que se desarrollan por la fecundación simultánea de dos óvulos separados, pueden tener detalles asimétricos en un sentido en uno de ellos, y en el contrario en el otro, pero esto no ocurre con mayor frecuencia que la que cabría esperar como fruto del azar. Es una creencia generalizada que los gemelos (formados a partir de un único óvulo, que se divide inmediatamente después de la fecundación) tiene una marcada tendencia a aparentar especulares recíprocas. Por desgracia, las estadísticas al respecto son confusas y muchos expertos creen que los gemelos idénticos no se presentan como imágenes especulares uno de otro en mayor medida que cualquier otro tipo de hermanos.

En el caso de gemelos siameses (gemelos idénticos, unidos uno a otro a causa de un a partición tardía e incompleta del óvulo), el tema no ofrece duda alguna. Son exactamente enantiomorfos en casi todos los detalles: si uno es diestro, el otro es zurdo; si uno tiene el remolino del pelo que va en el sentido de las agujas del reloj, el de su hermano/hermana irá en el sentido contrario. Diferencias en los oídos, los dientes…, aparecen en ambos como especulares unas respecto de otras (hasta en eso es perfecta la Naturaleza). Las huellas dactilares o de la palma de la mano derecha de uno serán muy parecidas a las correspondientes a la mano izquierda del otro.
Todavía más: un gemelo siamés tendrá “vísceras transpuestas”; sus órganos internos estarán colocados de manera inversa, el corazón a la derecha, el hígado a la izquierda. Esta transposición de órganos, o inverse situs, como se denomina a veces, se da siempre en cualquier par de gemelos siameses, pero puede aparecer también en no incluidas en estas circunstancias.

Merece la pena hacer notar que Lewis Carroll, en A través del espejo (Alianza Editorial, 1990), pretende tomar los gemelos idénticos Tararí y Tarará como imágenes especulares uno de otro. Cuando los hermanos Tara ofrecen enlazar sus manos con Alicia, uno de ellos alarga su derecha; el otro la izquierda. Si observamos detenidamente las ilustraciones de Tenniel, especialmente la que muestra los dos gemelos uno frente a otro, para la batalla, veremos que los ha dibujado como si fueran enantiomorfos.
Claro que, algunos son completos
En el comportamiento y los hábitos de los seres humanos hay muchos ejemplos de marcada asimetría; los más evidentes son consecuencia de que la mayoría de las personas son diestras. La mano derecha está controlada por la parte izquierda del cerebro, y la parte derecha de éste controla la mano izquierda, por lo que la condición de diestro es, en realidad, un fenómeno de lateralidad izquierda del cerebro. Hubo un tiempo en el que se creía que los bebés nacían sin tendencia alguna de tipo genético que favoreciera el uso de una mano concreta, que la lateralidad de un niño era exclusivamente el resultado de las enseñanzas de sus padres. Platón era un notable defensor de esta opinión.
“En el uso de las manos estamos, y estábamos, viciados por las manías de nuestras intitutrices y madres -escribe Platón en sus Leyes-, pues aunque nuestros miembros están compensados por naturaleza, creamos una diferencia entre ellos como consecuencia de un mal hábito.”
Sabemos hoy en día que Platón estaba equivocado. Como hace notar Aristóteles con buen criterio. De todas las maneras, la tendencia innata para muchas personas de usar preferentemente la mano derecha es común desde que la puede constatarlo de manera evidente.
Los antropólogos culturales no han encontrado todavía ni una sola sociedad, o incluso una tribu , en la que la norma sea la lateralidad izquierda: los esquimos, los indios americanos, los maoríes y los africanos son todos diestros. Los antiguos egipcios, griegos y romanos eran diestros. Naturalmente, si retrocemos todavía más en la Historia, la evidencia de la lateralidad diestra es ya escasa e indirecta y hay que dilucidarla a partir del estudio de la forma de sus utensilios y armas, así como de las pinturas que muestran los hombres trabajando o en la batalla.
Las propias palabras que se usan en muchas lenguas para designar la izquierda y la derecha dan testimonio de un sesgo universal hacia el lado derecho. En , ir a derechas es hacer las cosas correctamente, mientras que no dar una a derechas, es sinónimo de hacerlo todo mal.
Ser diestro en algo es lo mismo que poseer una habilidad especial para ello, mientras que una cosa siniestra (del latín sinester, izquierda) es una cosa hecha con mala intención. En otras lenguas el significado viene a ser más o menos el mismo. Los italianos, tan suyos ellos, llaman a la mano izquierda stanca, fatigada, o manca, la que no se tiene. Lo cierto es que, por lo , los zurdos son ambidiestros.
Para tener una buena visión histórica de malos prejuicios virulentos contra los zurdos en cualquier parte del mundo, véase el séptimo capítulo de The Dragons of Eden, de Carl Sagan (Random House, 1977), y el delicioso de Jack Fincher, Sinister People (Putnam, 1977). Este último da una lista de más de cien personajes famosos que fueron zurdos.

Por lo demás, y…, hasta donde sabemos, la especie humana tiene la tendencia a utilizar la mano derecha. Claro que no sabemos. La mayoría de los mamíferos subhumanos son ambidiestros y, ¿Cómo serán las especies que viven en otros mundos? El personaje de arriba, al menos, parece que es zurdo.
Lo cierto es que, poco importa si somos zurdos o no, la igualdad en lo esencial es casi idéntica. La verdadera diferencia está en el cerebro, en la manera de ver las cosas, en cómo cada cual enfoca los problemas y qué soluciones aplica a cada situación, en que perspectiva podamos tener de nuestra Sociedad, de nuestras leyes, de nuestros derechos, de la moral y la ética… Todo lo demás, son circunstancias anecdóticas que poco influyen en el devenir del mundo.
emilio silvera
Sep
11
¡Era un Agujero Negro! No una estrella brillante
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Cosas curiosas ~
Clasificado en Cosas curiosas ~
 Comments (0)
Comments (0)
No siempre podemos explicar las cosas que suceden en el Universo. Este reportaje lo demuestra
El canibalismo cósmico causó el estallido de luz más intenso captado en la Tierra, según un estudio
Hace algún tiempo ya que, dos telescopios en Chile, captaron un estallido de luz que nadie consiguió explicar. Los fotones habían pasado 3.800 millones de años viajando por el universo. Al llegar a la Tierra, eran 20 veces más brillantes que todas las estrellas de nuestra galaxia, la Vía Láctea.
Los científicos que detectaron la deflagración sugirieron que se trataba de una supernova superluminosa, de lejos la más brillante jamás observada. A renglón seguido reconocieron que con las leyes de la física en la mano no podían explicar de dónde podía salir tanta energía.

Ahora, otro equipo científico acaba de proponer una explicación alternativa. La estrella ASASSN-15lh no sería una supernova, sino una víctima del canibalismo cósmico.
“Creemos que lo que causó este evento fue un agujero negro supermasivo que devoró a la estrella, que pasó demasiado cerca”, explica Giorgos Leloudas, del Instituto Niels Bohr, en Dinamarca. Su equipo ha estado analizado el fenómeno durante 10 meses con telescopios terrestres y el Telescopio Espacial Hubble. Sus resultados, en Nature Astronomy, apuntan a que la intensa fuerza de la gravedad “desgarró” la estrella hasta convertirla en una masa de gas y esta después fue tragada por el agujero negro. “Esta es una forma muy eficiente de producir energía”, razona Leloudas, miembro del equipo de 50 astrónomos de más de 10 países, incluida España, que ha realizado el estudio.

El evento emitió en unos meses 30 veces más energía que la que contiene el Sol
Los investigadores creen que una estrella similar al Sol cruzó el llamado horizonte de sucesos, el punto de no retorno del agujero negro. Este monstruo tendría una masa 100 millones de veces mayor que el Sol. “La energía liberada en forma de luz visible y ultravioleta que hemos observado es unas 30 veces mayor que toda la energía que el Sol emitirá durante toda su vida”, resalta el astrónomo.
Un agujero negro normal no podría producir este fenómeno, porque la estrella caería al agujero como un bola de billar, sin tiempo a ser despedazada y emitir un estallido de luz como el observado, razona Leloudas. Según la teoría de la relatividad, sí sería posible si ese agujero negro está girando sobre sí mismo. Eso es exactamente lo que el equipo propone. El agujero negro estaría en el centro de su galaxia. Según el estudio, la composición del gas y la carga eléctrica de los átomos que se observan no es compatible con una explosión estelar, pero sí con un evento de desintegración.

La batalla por entender este fenómeno no acaba aquí. José Prieto, astrónomo del Instituto Milenio de Astrofísica en Chile, es uno de los descubridores del evento y propuso que se trataba de una supernova superluminosa en Science. “No estoy convencido con esta explicación, pero también reconozco que nuestra interpretación original ya no parece tan clara”, señala. “En ambos casos sería un evento muy extremo que no entra fácilmente en ninguna de las dos clasificaciones”. En cualquier caso, admite, “es un evento fascinante”. Aunque ha perdido fuerza, el fogonazo sigue siendo visible para los telescopios terrestres y ambos equipos lo seguirán estudiando para intentar desvelar su origen.
Reportaje de prensa















 Totales: 77.947.037
Totales: 77.947.037 Conectados: 70
Conectados: 70




























