Los tiempos cambian, y, con los cambios llegan las nuevas doctrinas o creencias, o, ¿por qué no? nuevas teorías. Desde hace algún tiempo venimos dando vueltas y vueltas, en el campo de la Física, a esas avanzadas teorías que no podemos demostrar, toda vez que, al contrario del Modelo Estándar, no son (por ahora) verificables sus predicciones. Me estoy refiriendo, como habéis podido suponer a la Teoría de supercuerdas, La cuerda Heterótica, la Supergravedad y Supersimetría, y, finalmente, la última versión que viene a ser un compendio de todas las demás, la Teoría M.

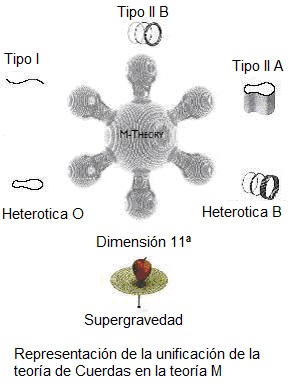
Como nos dice Brian Greene en uno de los capítulos del libro El tejido del cosmos, que él titula: “Especulaciones sobre el Espacio y el Tiempo en la teoría M”, hoy, tres décadas después de la articulación de la teoría de cuerdas,la mayoría de los que trabajan en ella, creen que aún no tenemos una respuesta general para la pregunta fundamental: ¿qué es la teoría de cuerdas? A pesar de que sabemos bastante de la teoría, sus características más elementales son familiares y, a estas alturas, casi cercanas. Tampoco debemos despreciar los éxitos que ha cosechado y, desde luego, es bien sabido todo lo que nos promete y también ¿cómo no? los desafíos que suponen lograr todas esas promesas que en ella están encerradas.

                           La velocidad de la luz y las distancias en el Universo

La relatividad especial tiene la constancia de la Velocidad de la luz, la relatividad general tiene el principio de Equivalencia, la mecánica cuántica tiene, el principio de Incertidumbre y, sin embargo, los teóricos de cuerdas aún siguen buscando algo de lo que carece la teoría de cuerdas que, precisamente es: el tipo de principio nuclear que se encontraron en aquellas otras teorías y le dan razón de ser y la sólida base que toda teo´ria necesita para ser.

Esa nueva teorías quiere explicarlo todo. Nada puede estar fuera de ella: El Universo que es, todo lo que existe, ahí estará

Un universo de Supercuerdas. El sueño de Einstein comienza a tomar realidad, a través de un nuevo paradigma de la ciencia que viene a romper con la toda la visión del mundo y del universo que teníamos hasta ahora, más allá de lo imaginable. Si la Teoría de cuerdas, finalmente resultase ser cierta, ese descubrimiento llevaría al mundo y a la conciencia humana hasta una nueva dimensión de su propia conciencia.

Una de las primeras controversias sobre la teoría de supercuerdas que salta al tapete en las discusiones entre físicos teóricos es aquella en las que se subrayan diferencias como el caso del modelo estándar (que explica la interacción de fuerzas y partículas) y sobre el cual la física ha sido capaz de extraer predicciones contrastables en laboratorios, a diferencia en el marco de las supercuerdas que ello no ha sido posible, ya que no se han logrado hacer predicciones verificables con experimentos. Es decir, que todos los esfuerzos que se han gastado en su elaboración pueden acabar siendo un excelente ejercicio de especulación matemática. Claro que, de tener éxito, no sería esta la primera vez que un descubrimiento puramente teórico en la ciencia de la física acaba dando en el clavo y profundizando espectacularmente en el conocimiento de la naturaleza.

Según la Teoría de Supercuerdas, todo el universo manifestado, todo lo que percibimos como materia, desde las partículas subatómicas, hasta las galaxias, estaría soportado por una gran Matriz Subyacente, o Supercuerdas, que actuaría como una “gran sinfonía musical” detrás de todo lo que contemplamos como materia.

Ciertamente, si en realidad existen, están tan lejos de nosotros que, el viaje para “verlas” es demasiado costoso…, al menos de momento.

Hemos tratado, sin conseguirlo, de llegar hasta ellas, hasta las cuerdas vibrantes que residen en lo más profundo, más allá de los propios Quarks, y, hemos podido constatar que, nuestros ingenios y aceleradores, no son suficientes, no disponen la energía requerida para llegar hasta las cuerdas que serían la matriz del mundo. Allí, en su región de once dimensiones, todo es comprensión y armonía, todo cabe e incluso, la díscola Gravedad se junta de manera natural con la Mecánica cuántica. Por eso algunos la llaman la Teoría del Todo, allí podemos encontrar todas las respuestas.

La supercuerda una poderosa estructura que no podemos localizar. Dicen que para poder hacerlo necesitamos de la energía de Planck, es decir, 10¹⁹ GeV, y, tal fuente de energía no existe aquí en nuestro mundo. Bueno, al menos no podemos disponer de ella, nuestras tecnologías no llegan a tener esa capacidad.

De la misma manera que no podemos sostener una galaxia en la mano, su inmensidad nos lo impide. Tampoco tenemos la capacidad de poder sujetar una “cuerda”, su infinitesimal tamaño, tampoco nos lo permite. Y, lo curioso del caso es que, de existir las cuerdas, esas enormes galaxias que podemos captar en el espacio interestelar, todas ellas, sin excepción, estarían hechas de cuerdas vibrantes que, al parecer, son los objetos que estarían más allá de los Quarks.

Uno de los problemas ligados a la teoría de supercuerdas y que más resalta es el que tiene que ver con la propia pequeñez de las cuerdas. Mientras más pequeño es algo, más difícil es de ver. Y estas supercuerdas son tan superpequeñas que no se observan esperanzas para hacer experimentos que nos puedan acercar a sus dimensiones. Sin experimentos no se pueden hacer comprobaciones de sus predicciones ni saber si son correctas o no. Exagerado, puede ser. Pero cada día se hace más insostenible su consideración sosteniéndola, tan sólo, con los fundamentos de un muy bien elaborado pensamiento experimental con el soporte de bellas ecuaciones matemáticas, o con algunas verificaciones experimentales que, para este caso, vienen a ser como indirectas, llámese Helio-3 y su superfluidez, etc…

               Branas, universos paralelos…¡cuerdas!

En esta teoría, hay problemas que se encuentran dentro de los enunciados de sus propios conceptos. Para desarrollar su formulación es necesario apelar a lo menos a diez dimensiones (en algunos casos, se han llegado hasta un número de veintiséis): espacio (3), tiempo (1) y a ellas se le agregan seis más como mínimo, que parecen estar enroscadas e invisibles para nosotros. Por qué aparecieron estas dimensiones adicionales a las cuatro que nos son familiares y por qué se atrofiaron en algún momento. Si en verdad existen, no lo sabemos. También, la teoría tiene decenas de miles de alternativas aparentemente posibles que no sabemos si son reales, si corresponden a miles de posibles universos distintos, o si sólo hay una realmente posible. En algunas de sus versiones se predice la existencia de 496 fuerzones, partículas como el fotón, que transmiten la fuerza entre 16 diferentes tipos de carga como la carga eléctrica. Afirmaciones como éstas, no comprobables por la imposibilidad de hacer experimentos, son las que plagan a la teoría de una multiplicidad de cuerdas. Ahora, las explicaciones más frecuentes que se dan para lo anterior, es de que los problemas surgen porque esta teoría se adelantó a su tiempo y no existe aún la estructura matemática consistente para formularla adecuadamente.

      Incluso el salto cuántico es más fácil de verificar

Las conclusiones a las que periódicamente llegan los adeptos a la TSC, se centran en el entusiasmo de proclamar que ésta otorga la única forma, hasta ahora, de poder contar en un futuro con una Teoría Cuántica consistente con la Gravedad. Como prácticamente todas las teorías de cuerdas, la TSC’s comienza con el concepto de dimensiones adicionales de Kaluza-Klein y comporta una enorme complejidad muy difícil de comprender para los que no están directamente involucrados en sus modelos. Con ella se aspira a resolver el más enigmático problema matemático que comporta la Física teórica en los finales del siglo veinte: la incompatibilidad matemática de los pilares fundamentales de la Mecánica Cuántica con la Teoría de la Relatividad General.

En cosmología, las partículas exóticas no sólo hay que proponerlas, es necesario también comprobar su existencia en experimentos de laboratorio y/o en observaciones.

La carencia de esa estructura matemática ha sido uno de los inconvenientes más serios que enfrentaba, y todavía lo es, la TSC y ello radica en las dificultades que presenta para hacer cálculos detallados. Sin embargo, en los últimos años, en alguna medida, especialmente después de la reunión de físicos teóricos cuerdistas realizada en la ciudad de Madrid, España, en el año 1995, ello se ha venido soslayando, ya que a través de el desarrollo de un conjunto de nuevas herramientas se ha logrado superar, en parte, las limitaciones matemáticas de la teoría.

Esas herramientas son las dualidades que vienen a ser como una especie, si se puede llamar así, de diccionario unificador que permite a los físicos «traducir» sus cálculos realizados en marcos teóricos asequibles a los modelos conocidos a marcos en que lo convencional no funciona. Es como si sabiendo calcular la electricidad y no el magnetismo; al descubrir que ambas fuerzas son dos caras de la misma moneda, se traducen las cantidades de una a otra, haciendo abordable el problema.

Sabemos de átomos y de Galaxias pero, ¿que es una cuerda?

Hasta ahora, ninguna propuesta de la teoría de supercuerdas ha podido ser contrastada con experiencias experimentales y, mucho menos, observacionales. Sus logros sólo han podido ser chequeados en los correspondientes archivos computacionales y las pizarras de las oficinas de los matemáticos. Ellos han demostrado una serie de conjeturas matemáticas que surgen de manera natural de la TSC. Ahora, ello también a implicado que se haya venido generando una coincidencia o relación entre distintas estructuras matemáticas, de las que ni se sospechaba su existencia y han servido de motor e inspiración para algunos matemáticos.

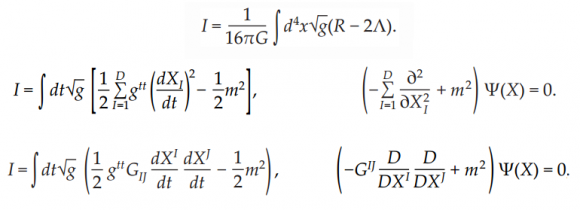
La interpretación de los cálculos que se realizan describe un objeto tan diminuto, como las supercuerdas, que querer imaginarlas es como querer encontrar un grano de arroz perdido en algún lugar del Universo; es imposible. Su calculada pequeñez las hace inimaginable para la gran mayoría de los mortales humanos. Por hacernos una idea: la Tierra es 10^-20 más pequeña que el universo y el núcleo atómico es 10^-20 veces más pequeño que la Tierra. Pues bien, una supercuerda es 10^-20 veces más pequeña que el núcleo atómico.

Es indudable que se trata de una teorización matemática que expuesta al común de la gente se hace casi «indigerible» o poco realista. A los especialistas en física teórica les pasa lo mismo. La física que hoy se maneja se hace cada vez más distante de la generalidad de los seres humanos, ya que no es tan sencilla como la de antaño; no sólo por que la descripción matemática de los fenómenos naturales se haya vuelto más complicada, sino porque resulta cada vez más difícil de imaginar. Esto se debe a que cada vez nos alejamos más y más de los objetos de nuestra experiencia cotidiana. Adentrándonos en el “universo” de la física cuántica, llegamos a ser conscientes de que, nuestro mundo, es una realidad propia de nuestras mentes, ya que, el “mundo real” la Naturaleza, es otra cosa bien distinta y, precisamente por eso, nos cuesta tanto comprender.

    Ese “universo” de lo infinitamente pequeño, vibrante y luminoso, ¿dónde estará?

Con la teoría de supercuerdas se ha llegado a un punto de abstracción que cuando nos zambullimos en su estudio y cálculos se llega a un momento en que la cabeza parece estallar, no por asombro, sino que por las incertidumbres que llega a concitar. Se parte con esperanzas y en el camino afloran –no voy a decir frustraciones– sino que una multiplicidad de inquietudes, ya que se va generando la sensación de que los resultados de los esfuerzos que se están realizando, nunca podrán ser comprobados.

Es cierto que en los procesos de hacer ciencia no se ha establecido como requisito que las teorías que se elaboran deban ser comprobadas en un pari-paso, de ello los científicos, por formación, están muy consciente. Pero la mera especulación intelectual, limitada para ser experimentada, en el tiempo tampoco es muy útil, ya que dejaría de ser considerada inserta dentro de los rangos de las exigencias consuetudinarias de lo que llamamos hacer ciencia.

Es aceptable considerar que aún la teoría de supercuerdas no ha alcanzado un desarrollo suficiente en el cual sus pronósticos puedan ser contrastados con experimentaciones en los actuales aceleradores de partículas. Pienso que aún se encuentra lejos de arrimarse a una maduración matemática que permita precisar cuales son sus predicciones. Los cálculos son bellos, pero sumamente difíciles.

Y, a todo esto, las ecuaciones de Eisntein de la Relatividad General, subyacen en lo más profundo de la Teoría de Cuerdas, ya que, cuando se están desarrollando sus ecuaciones, allí aparecen, sin que nadie las llame, las ecuaciones de campo de la relatividad general que, es un subproducto de aquella otra teoría más avanzada. Tal secuencia, nos lleva a pensar que, la Teoría de supercuerdas es cierta, ya que, en caso contrario, ¿Por qué estaría allí Einstein?

También en la TSC, se encuentran involucradas las fuerzas fuertes de una manera tal que, antes de comenzar, comúnmente ya se encuentra limitadas las actuales capacidades humanas para calcular. Hay importantes pasos a realizar para poder aprender como llegar a inferir cálculos predictibles y poder ser testeados experimentalmente. Está claro que esta teoría se adelantó a su tiempo.

Es posible que para algunos sea inadmisible que se encuentre en el tapete de las discusiones de física teórica una teoría que todavía no precisa sus predicciones con una verificación experimental. Sin embargo, por las trayectorias que ya han experimentado las teorías de cuerdas, no reúnen aún los méritos como para ser consideradas científicas, o meros ejercicios de matemática abstracta. Por ahora, se puede señalar que parece ser que los físicos cuerdistas han ido más allá de los umbrales matemáticos aconsejables, con saltos de pasos que algún día deberán dar.

En el mundo de la física existen detractores de las supercuerdas de la talla y del genio como la de Richard Feymman, quien acerca del trabajo de los teóricos de las supercuerdas, afirmaba en una entrevista poco antes de morir, en 1988, «No me gusta que no calculen nada, no me gusta que no comprueben sus ideas, no me gusta que, para cada cosa que está en desacuerdo con un experimento, cocinen una explicación, un arreglo para decir bueno, todavía podría ser verdad.»

La teoría de supercuerdas es relativamente joven aún y durante su existencia ha mostrado una alta propensión a ser enfermiza. Surgen problemas, y se la deja de lado; se solucionan los problemas y una avalancha de trabajos resucitan la esperanza. En sus cerca de treinta años de vida, este vaivén ha ocurrido más de una vez.

Todo tiene su tiempo, y, Feynman, era ya un físico de bastante edad y de que ello a lo mejor era la causa de su resistencia a las ideas nuevas como algunos de sus maestros se resistían ante los profundos cambios conceptuales registrados en la física cuando él era joven. Las supercuerdas, dicen sus defensores, integrarían la física actual como la teoría de la relatividad de Einstein integró la gravitación de Newton explicando que sólo era un caso (el de nuestra escala del universo) de leyes más profundas y generales.

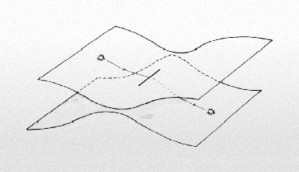
Nuevas geometrías, como en aquel tiempo en que llegó el llamado corte de Riemann, mediante el cual, se podia acceder a dos regiones distantes del espacio, nos han traído estas nuevas teorías que cambian el concepto actual que, del Universo tenemos. El tensor métrico de Riemann permitió a Einstein formular su famosa teoría de la gravedad. Siempre ha sido así, las nuevas ideas nos trajeron las nuevas realidades de la Naturaleza y, si es así (que lo es), ¿por qué la teoría de cuerdas sería diferente?

Los matemáticos encuentran interesante esta teoría porque las dimensiones extra pueden tener geometrías muy complicadas y hay toda una rama matemática dedicada a explicar sus propiedades.

Los físicos-matemáticos piensan que, por ahora, es más lógico estudiar y observar el desarrollo de estas ideas teóricas como una consecuencia estética y grata en la consecución de una simple y definitiva teoría unificadora que reúna todos los requisitos necesarios para que pueda ser contrastada con pruebas experimentales.

Hemos sido capaces de inventar aparatos para medir las ondas gravitatorias provenientes de los agujeros negros, y, como no podemos parar en el querer descubrir y saber lo que el Universo es, queremos seguir avanzando y tratamos de conseguir una teoría de la Gravedad Cuántica que, según todos los indicios va implícita en esta teoría de supercuerdas de más dimensiones.

No sé si se ha llegado a un límite en que la abstracción matemática sea un medio coadyuvante o una pesadilla para los físicos. Se quiere simplificar las cosas y, al final, se hacen más incomprensibles y complejas. Ya convertimos la gravedad, la fuerza electromagnética y las fuerzas nuclear fuerte y débil en campos. La gravedad, que no sabemos qué cosa es, pero que hace caer una piedra, ha pasado a ser algo mucho más abstracto que lo propuesto por Newton: un campo, una modificación de la estructura del espacio que nos rodea. Como nos movemos dentro de ese espacio, su estructura nos influye y nos hace actuar de cierta manera. Por eso caen la piedras, porque seguimos la forma del espacio, su geometría que viene dada por la materia que contiene.

Ya para el común de los humano ese, el más simple nivel de abstracción, les parece que se trata de algo que nunca podrán llegar a comprender. Pero ese sentimiento empeora cuando se pasa al siguiente nivel. Se trata de aquel que es considerado como los grandes almacenes de la física teórica, el objeto de estudio son los grupos de simetría mediante los cuales se relacionan esos campos y las partículas.

Grupos de simetría que relacionan campos y partículas donde las fuerzas están presentes.

El no va más del nivel de abstracción, se encuentra el mundo donde se creee que vive el constituyente fundamental de la materia: las supercuerdas. Estos objetos definen a través de su comportamiento esos estados que provocan la aparición de los grupo de simetría que a su vez relacionan la fuerza con la materia, y que al mismo tiempo explican la interacción de las partículas subatómicas y el comportamiento de los átomos.

Y, a todo esto, la Topología tiene mucho que decir en el mundo de la cuerda, toda vez que, en esta rama de las matemáticas pueden estar las respuestas a tan extraño objeto vibrante que nos dicen que podría ser lo más pequeño y al mismo tiempo lo más esencial que en el universo existe para su conformación

Al final, se trata de explicar todo y, a su vez, complicar todo. Por ello, decir que una supercuerda es un diminuto objeto vibrante que cohabita en un espacio con más dimensiones de simetría peculiar que el conocido tetradimensional es, prácticamente, no decir nada.

Hasta principios del año 2001, la premisa que se habían colocado los físicos de contar ya con una muy simple y gran teoría unificadora de las cuatro fuerzas, no se ha cumplido. Es posible que dentro del primer cuarto del siglo el intento culmine con un final feliz. Pero también es probable que no encontremos esa anhelada teoría, sino sólo una multiplicidad de teorías, cada vez más bellas y mejores.

Por ahora, lo cierto del caso es que, a pesar de algunas luces y pequeños éxitos, lo único firme y coherente es que el mundo se puede armar a partir de sesenta objetos puntuales cuyo origen desconocemos. Si se alcanzara algún día el objetivo de obtener todas las partículas y sus propiedades a partir de principios de simetría o de alguna cuerda única, por ejemplo, habríamos encontrado un nuevo nivel donde se concentra lo más elemental. Ya no serían los átomos, ni tampoco las partículas puntuales mismas, sino las simetrías o la cuerda. ¿Habríamos terminado? Es más que probable que no, pues nos preguntaríamos entonces de dónde salen esas simetrías o esa cuerda, y con alta probabilidad su estudio en detalle nos mostraría que en realidad hay más complejidad que la que aparecía a simple vista. La historia (¡la sabia historia!) muestra que este es un cuento sin final, y pareciera que cada vez que simplificamos las cosas, nuevos niveles de complejidad aparecen como fantasmas que están siempre acechándonos a la vuelta de cada esquina.

Parece que siempre estaremos entrando por una puerta misteriosa que nos lleva a un lugar oscuro en el que nunca sabemos lo que podemos encontrar. Es la Incertidumbre de la mecánica cuántica que, no se limita a estar allí, en ese mini-universo de lo pequeño. La Incertidumbre está presente en todo el Universo, y, nosotros, curiosos y deseosos de saber, no dudamos de adentrarnos en esos lugares desconocidos en busca de esas respuestas anheladas.

Así, podemos leer en cualquier diccionario que si preguntamos por la supercuerda, comienza diciéndonos: “La teoría de supercuerdas es un esquema teórico para explicar todas las partículas y fuerzas fundamentales de la naturaleza en una sola teoría, que modela las partículas y campos físicos como vibraciones de delgadas cuerdas supersimétricas, las cuales se mueven en un espacio-tiempo de más de 4 dimensiones.”

Y, a todo esto, de vez en cuando podemos encontrarnos con noticias llamativas como esta:

“Científicos norteamericanos detectan la existencia de dimensiones adicionales. Las colisiones de neutrinos de alta energía con otras partículas corroboran uno de los postulados de la Teoría de Supercuerdas.

Científicos norteamericanos han detectado por primera vez indicios de la existencia de otras dimensiones más allá de las tres conocidas. Utilizando datos del telescopio Amanda, enterrado en el Polo Sur, han podido observar una decena de colisiones de neutrinos de alta energía con otras partículas elementales, obteniendo así la evidencia de las dimensiones adicionales sugerida por la Teoría de Supercuerdas. El descubrimiento no es concluyente y encontrará nuevas oportunidades cuando se inicie en 2009 el funcionamiento de otro telescopio 30 veces más potente, el Ice Cube, en el que participan diversas universidades europeas.”

 

¡Vivir para ver! Claro que, nosotros,  que vivimos en un mundo de tres dimensiones espaciales y una temporal, lo único que podemos hacer es tener paciencia y esperar a que, esas lumbreras de la física, nos lleven de la mano hacia ese mundo mágico de las cuerdas que, según parece, nos mostrará un universo diferente, más completo y más real que el que ahora podemos observar.

emilio silvera

“La teoría de cuerdas es física del siglo XXI,  que cayó accidentalmente en el siglo XX.”

Edward  Witten

 

Lo cierto es que aún en la segunda década del siglo XXI, andamos a tientas con ésta sugestiva teoría que es tan prometedora parro que no podemos verificar al no contar con los adecuados medios para ellos. Nos ha costado mucho poder llegar al núcleo de los átomos para vislumbrar los Quarks que en tripletes, conforman protones y neutrones, y, hablamos de lo que podría existir más allá de los Quarks pero, ahí nos quedamos, como los Quarks están confinados en un océano de gluones, nosotros, amigos míos, también lo estamos en un océano de ignorancia del que sólo podremos escapar cuando podamos utilizar energías mucho más grandes que nos puedan llevar a regiones tan profundas en las que, posiblemente, habitan esas briznas vibrantes que serían las semillas de la materia.

 

 

explicó la Teoría M, algunos salieron de la conferencia asombrados

 

Edward Witten, del Instituto Estudios Avanzados de Princeton,  New Jersey, domina el mundo de la física teórica.  Podríamos decir que Witten, es el que tira del pelotón, el más brillante físico de altas energías que marca las tendencias actuales en la comunidad científica de la física teórica y el que ha sido capaz de plantear la versión más moderna de la teoría de supercuerdas, conocida teoría M.

Algunos se han atrevido a compararlo con Einstein. Ha ganado la medalla Field de 1.990, una especie de Premio Nobel de las matemáticas. Dice su mujer ( físico de profesión), que Witten permanece sentado con la mirada perdida en el horizonte a través de una ventana, manipulando y reordenando grandes conjuntos de complejas ecuaciones en su mente. Su esposa señala: “Nunca hace cálculos excepto en su mente. Yo llenaría páginas con cálculos antes de llegar a comprender lo que está haciendo, Edward sólo se sienta para calcular un signo menos o un factor dos”.

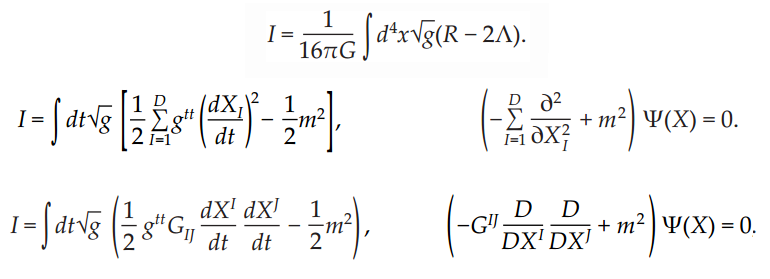
   Witten dice:

“La mayoría de las personas que no han estudiado física probablemente piensan que lo que hacen los físicos es cuestión de cálculos increíblemente complicados, pero eso no es realmente lo esencial. Lo esencial es que la física trata de conceptos, busca comprender los conceptos, los principios mediante los cuales opera el mundo, el universo”.

 

Así que Witten se ha enfrascado en la nada fácil tarea de unir la mecánica cuántica con la gravedad mediante la teoría de supercuerdas que, según él, nos puede incluso el instante mismo de la creación. El aspecto clave de esta teoría, el factor que le da su potencia tanto como su unicidad, es su geometría inusual. Las cuerdas (que según parece) pueden vibrar autoconsistentemente sólo en 10, 11 y 26 dimensiones.

La esencia de la teoría de cuerdas consiste en que puede explicar la naturaleza de la materia y del espacio-tiempo; es decir, la naturaleza del universo entero. Esta teoría responde a una serie de cuestiones enigmáticas acerca de las partículas, tales como por qué existen tantas en la naturaleza.   Cuanto más profundamente sondeamos en la naturaleza de las partículas subatómicas, más partículas aparecen. Existen varios centenares de ellas y sus propiedades llenan volúmenes y volúmenes. Incluso con el Modelo Estándar tenemos un desconcertante de “partículas elementales”. La teoría de cuerdas responde a esta pregunta porque la cuerda, alrededor de 100 trillones de veces más pequeña que un protón, esta vibrando; cada modo de vibración representa una resonancia o partícula distinta. La cuerda es tan increíblemente pequeña que, a cierta distancia, una resonancia de una cuerda y una partícula son indistinguibles. Sólo cuando ampliamos de alguna la partícula podemos ver que no es en absoluto un punto, sino un modo de una cuerda vibrante.

Según la teoría de cuerdas, la materia no es nada más que las armonías creadas por cuerdas vibrantes. Del mismo modo que se puede componer un infinito de armonías para el violín, puede construirse un número infinito de formas de materia a partir de cuerdas vibrantes. Esto explica la riqueza de las partículas en la naturaleza. Análogamente, las leyes de la física pueden ser comparadas a las leyes de la armonía permitida en la cuerda. El propio universo, compuesto de innumerables cuerdas vibrantes, sería entonces comparable a una sinfonía.

La teoría de cuerdas explica la naturaleza de las partículas y del espacio-tiempo. Cuando una cuerda se mueve en el espacio-tiempo, ejecuta un conjunto de complicados movimientos. La cuerda , a su vez, romperse en cuerdas más pequeñas o colisionar con otras cuerdas para formar cuerdas más largas. El punto clave es que todas estas correcciones cuánticas o diagramas cerrados son finitos y calculables. Esta es la primera teoría cuántica de la gravedad en la historia de la física que tiene correcciones cuánticas finitas (recordemos que todas las teorías previas conocidas – incluyendo la teoría original de Einstein, la de Kaluza-Klein y la teoría de supergravedad – fallaban en criterio clave).

                                            Lazos

En la teoría de cuerdas, la fuerza gravitatoria se representa mediante el intercambio de cuerdas cerradas, que barren tubos en el espacio-tiempo. Incluso si usamos una serie infinita de diagramas con un gran de agujeros, nunca aparecen infinitos en la teoría, dándonos una teoría de gravedad cuántica.

Cuando se calcularon por primera vez las ligaduras que impone la cuerda sobre el espacio-tiempo, los físicos quedaron sorprendidos al que las ecuaciones de Einstein emergían de la cuerda. Esto era notable; sin suponer ninguna de las ecuaciones de Einstein, los físicos asombrados descubrían que ellas emergían de la teoría de cuerdas como por encanto.   Las ecuaciones de Einstein ya no resultaban ser fundamentales; podían derivarse de la teoría de cuerdas de la que formaban . Einstein pensaba que la geometría por sí sola explicaría un día todas las propiedades de la materia; él la materia era sólo un nudo o vibración del espacio-tiempo, ni más ni menos. Los físicos cuánticos, por el contrario, pensaban de manera distinta a la de Einstein, es decir, que el tensor métrico de Riemann-Einstein podía convertirse en un gravitón, el paquete discreto de energía que transporta la fuerza gravitatoria y, en este preciso punto, aparece la cuerda, que según todos los indicios ser el “eslabón perdido” entre la mecánica cuántica y la relatividad general, el que permita la unificación ambas teorías de manera natural y complete el circulo de una teoría de “todo” que explique el universo, la materia y el espacio-tiempo con todas sus constantes universales y las fuerzas de la naturaleza que lo rigen todo.

                     ¿Qué sabemos nosotros de lo que hay más allá de los Quarks?

La teoría de cuerdas, por consiguiente, es suficientemente rica para explicar todas las leyes fundamentales de la naturaleza. Partiendo de una simple teoría de una cuerda vibrante, uno extraer la teoría de Einstein, la teoría de Kaluza-Klein, la supergravedad, el Modelo Estándar e incluso una teoría GUT (Gran Teoría Unificada). Parece un milagro que partiendo de unos argumentos puramente geométricos acerca de una cuerda, se pueda desarrollar totalmente por derivación la física de los últimos dos mil años.   Todas las teorías discutidas hasta están incluidas automáticamente en la teoría de cuerdas.

                                              John H. Schwarz

En 1.984, John Schwarz del Instituto Tecnológico de California y su colaborador Michael Green del Queen Mary’s Collage de Londres, demostraron que la teoría de cuerdas podía ser autoconsistente, lo que desencadenó una carrera de los físicos más jóvenes resolver esta teoría.

El concepto de órbitas, por ejemplo, se da repetidamente en la naturaleza en diferentes variaciones; la obra de Copérnico, las órbitas han proporcionado un tema esencial que se repite constantemente a lo largo de la naturaleza en diferentes variaciones, desde las galaxias más grandes hasta los átomos y los más diminutas partículas subatómicas, tanto las unas como las otras describen órbitas en su deambular por el espacio. De manera análoga, los campos de Faraday se han mostrado como uno de los temas favoritos de la naturaleza. Los campos pueden describir el magnetismo de la naturaleza de las galaxias y la gravitación, o pueden describir la teoría electromagnética de Maxwell, la teoría métrica de Riemann-Einstein, los campos de Yang-Mills encontrados en el Modelo Estándar, y así todas las formas conocidas de materia y energía han sido expresadas en términos de teoría de campos. Las estructuras, entonces, los temas y variaciones en una sinfonía, son repetidas constantemente.

   Buscamos un Universo de 11 dimensiones y sólo vemos 3

¿Pero las cuerdas? Las cuerdas no parecen ser una estructura preferida por la naturaleza en el diseño de los cielos. No vemos cuerdas en el espacio exterior. De hecho no las vemos por ninguna y, sin embargo, todos los indicios teóricos y las complejas matemáticas topológicas nos dicen que… ¡Están ahí!

Un momento de reflexión, sin embargo, revelará que la naturaleza ha reservado un papel especial a las cuerdas, como un ladrillo básico para otras formas. Por ejemplo, la característica esencial de la vida en el planeta Tierra es la molécula de ADN similar a una cuerda, que contiene la información compleja y el código de la propia vida. Para construir la materia de la vida, tanto como la materia subatómica, las cuerdas parecen ser la respuesta perfecta. En ambos casos, queremos encerrar una gran cantidad de información en una estructura reproducible y relativamente simple. La característica distintiva de una cuerda es que es una de la forma más compacta de almacenar grandes cantidades de de un modo en que la información pueda ser replicada.

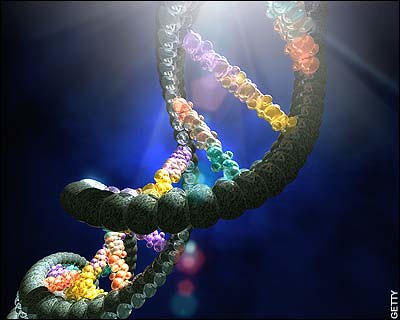
Para los seres vivos la naturaleza utiliza la doble cadena de la molécula de ADN, que se separa y forma copias duplicadas de cada una de ellas.   Nuestros cuerpos también contienen millones de millones de cadenas de proteínas, formadas de ladrillos de aminoácidos. Nuestro cuerpo, en cierto sentido, puede ser considerado como una enorme colección de cuerdas: moléculas de proteínas que revisten nuestros huesos. Sin embargo, nadie puede dar una explicación de nuestro entendimiento, de la inteligencia que se crea y que llevamos con nosotros desde el mismo momento del nacimiento, está ahí presente, a la espera de que se la despierte, es la inteligencia dormida y evolucionada por el conocimiento de las cosas. La conciencia de SER a la que llamamos alma, y que de alguna manera es inmortal, ya que lo que sabemos lo cedemos y lo dejamos aquí para los que nos siguen en la tarea emprendida por la humanidad desde que, en el preciso momento en que surgió aquella primera célula original que fue capaz de dividirse para replicarse a sí misma, se dio el primer paso para el nacimiento de la vida en nuestro planeta. Pero esa es otra cuestión que será tratada en otro próximo , ahora volvamos al tema de la teoría de cuerdas de la física.

En la década de los noventa se creó una versión de mucho éxito de la teoría de cuerdas. Sus autores, los físicos de Princeton David Gross, Emil Martinec, Jeffrey Harvey y Ryan Rohn, a quienes se dio en llamar el cuarteto de cuerdas de Princeton.

El de más edad de los cuatro, David Gross, hombre de temperamento imperativo, es temible en los seminarios al final de la charla, en el tiempo de preguntas, con su inconfundible vozarrón dispara certeros e inquisidoras preguntas al ponente. Lo que resulta sorprendente es el hecho de que sus preguntas dan normalmente en el clavo.

Gross y sus colegas propusieron lo que se denomina la cuerda heterótica. Hoy día, de todas las variedades de teorías Kaluza-Klein que se propusieron en el pasado, es precisamente la cuerda heterótica la que tiene mayor potencial unificar todas las leyes de la naturaleza en una teoría.  Gross cree que la teoría de cuerdas resuelve el problema de construir la propia materia a partir de la geometría de la que emergen las partículas de materia y también la gravedad en presencia de las otras fuerzas de la naturaleza.

Es curioso constatar que si abandonamos la teoría de la gravedad de Einstein como una vibración de la cuerda, entonces la teoría se vuelve inconsistente e inútil. Esta, de hecho, es la razón por la que Witten se sintió atraído inicialmente hacia la teoría de cuerdas. En 1.982 leyó un artículo de revisión de John Schwarz y quedó sorprendido al darse de que la gravedad emerge de la teoría de supercuerdas a partir solamente de los requisitos de auto consistencia. Recuerda que fue “la mayor excitación intelectual de mi vida”.

Las ideas de Einstein subyacen en la teoría de cuerdas y, sus ecuaciones de la Relatividad general, sin que nadie las llame, aparecen cuando los físicos elaboran y profundizan en las cuerdas cibrantes de esa nueva teoría que tantas esperanzas han puesto en la mente de muchos para a través de ellas, los más profundos secretos de la Naturaleza.

Gross se siente satisfecho pensando que Einstein, si viviera, disfrutaría con la teoría de supercuerdas que sólo es válida si incluye su propia teoría de la relatividad general, y amaría el hecho de que la belleza y la simplicidad de esa teoría proceden en última instancia de un principio geométrico, cuya naturaleza exacta es aún desconocida.

Witten llega incluso a decir que:

“todas las ideas realmente grandes en la física, son retornos de la teoría de supercuerdas”.

 

Con esto, él quiere decir que todos los grandes avances en física teórica están incluidos en la teoría de supercuerdas. Incluso afirma el hecho de que la teoría de supercuerdas fue “un accidente del desarrollo intelectual en el planeta Tierra, ocurrido de su tiempo”. Y continúa diciendo:

“En alguna en el espacio exterior, otras civilizaciones en el universo pudieron haber descubierto primero la teoría de supercuerdas y derivado de ella la teoría de la relatividad general que lleva dentro”.

 

La cuerda heterótica de Gross y sus colegas, consiste en una cuerda cerrada que tiene dos tipos de vibraciones, en el sentido de las agujas del reloj y en sentido contrario, que son tratadas de diferente. Las vibraciones en el sentido de las agujas del reloj viven en un espacio de diez dimensiones. Las vibraciones de sentido contrario viven en un espacio de veintiséis dimensiones, de las que dieciséis han sido compactificadas. Lo mismo ocurría en la teoría de la quinta dimensión de Kaluza-Klein, donde la quinta dimensión estaba compactificada curvándose en un círculo en el límite de Planck.

La cuerda heterótica debe su al hecho de que las vibraciones en el sentido de las agujas del reloj y en el sentido contrario viven en dos dimensiones diferentes pero se combinan para producir una sola teoría de supercuerdas. es la razón de que se denomine según la palabra griega heterosis, que significa “vigor hibrido”.

El espacio compactificado de dieciséis dimensiones es el más interesante. fue analizado por el “cuarteto de cuerda” de Princeton (Gross y su equipo), descubrieron que contiene una simetría de enormes dimensiones, denominada E (8) × E (8), que es mucho mayor que cualquier simetría GUT que se hubiese intentado jamás. Esta simetría es mucho mayor que el grupo de simetría que aparece en el Modelo Estándar, dado por SU(3) × SU(2) × U(1) que es un subconjunto de la anterior donde está acomodado también (dada su amplitud) el Modelo Estándar.

Nuestras Mentes están conformadas de tridimensional, nuestro mundo es de tres dimensiones espaciales. La cuarta dimensión de nuestro mundo, el Tiempo, incide en la posible alteración evolutiva que podríamos experimentar para poder vislumbrar más altas dimensiones pero…, ¿podrán alterarse las percepciones?

ver cómo dimensiones más altas simplifican las leyes de la Naturaleza, recordemos que un objeto tiene longitud, anchura y altura.  Puesto que tenemos libertad para girar un objeto 90º, podemos transformar su longitud en anchura y su anchura en altura.   Mediante una simple rotación, podemos intercambiar cualquiera de las tres dimensiones espaciales.

bien, si el tiempo es la cuarta dimensión, entonces es posible hacer “rotaciones” que convierten el espacio en tiempo y el tiempo en espacio.  Estas rotaciones tetradimensionales son precisamente las distorsiones del espacio y del tiempo exigidas por la relatividad especial. En otras palabras, espacio y tiempo se mezclan de una forma esencial, gobernada por la relatividad.  El significado del tiempo como la cuarta dimensión es que pueden hacerse relaciones entre el tiempo y el espacio de una forma matemáticamente precisa.  A partir de entonces, deben ser tratados como dos aspectos de la misma magnitud: el espacio-tiempo. Así han quedado unificadas las leyes de la Naturaleza al pasar de tres a cuatro dimensiones. Como nuestra imaginación no cesa de generar ideas y nuestra curiosidad insiste en querer saber más, de todo esto pasamos a las cuerdas añadiendo más dimensiones al planteamiento.

Las leyes de la física se simplifican en dimensiones más altas.

En caso, en el espacio 26–dimensional de las vibraciones de sentido contrario a las agujas del reloj de la cuerda heterótica que tiene espacio suficiente para explicar todas las simetrías encontradas en la teoría de Einstein y en la teoría cuántica. Así, por primera vez, la geometría pura ha dado una simple explicación de por qué el mundo subatómico debería exhibir necesariamente ciertas simetrías que emergen del enrollamiento del espacio de más dimensiones: Las simetrías del dominio subatómico no son sino remanentes de la simetría del espacio de más dimensiones.

Esto significa que la belleza y simetrías encontradas en la naturaleza pueden ser rastreadas en última instancia hasta el espacio multidimensional.  Por ejemplo, los copos de nieve crean bellas figuras hexagonales, ninguna de las cuales es exactamente igual a otra, han heredado sus estructuras de las formas en que sus moléculas han sido dispuestas geométricamente, determinada básicamente por las cortezas electrónicas de estas moléculas, que a su vez nos llevan de a las simetrías rotacionales de la teoría cuántica, dadas por O (3).

Podemos concluir diciendo que las simetrías que vemos a nuestro alrededor, desde un arco iris a las flores y a los cristales, pueden considerarse en última instancia manifestaciones de fragmentos de la teoría decadimensional original. Riemann y Einstein habían confiado en llegar a una comprensión geométrica de por qué las fuerzas pueden determinar el movimiento y la naturaleza de la materia.

      Superficie de Riemann que aparece al extender el dominio de la función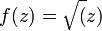

Dado el enorme poder de sus simetrías, no es sorprendente que la teoría de supercuerdas sea radicalmente diferente de cualquier otro de física.  De hecho, fue descubierta casi por casualidad. Muchos físicos han comentado que si este accidente fortuito no hubiese ocurrido, entonces la teoría no se hubiese descubierto hasta bien entrado el siglo XXI. Esto es así porque supone una neta desviación de todas las ideas ensayadas en este siglo. No es una extensión natural de tendencias y teorías populares en este siglo que ha pasado; permanece aparte.

Por el contrario, la teoría de la relatividad general de Einstein tuvo una evolución normal y lógica. En primer lugar, su autor, postula el principio de equivalencia. Luego reformuló principio físico en las matemáticas de una teoría de campos de la gravitación basada en los campos de Faraday y en el tensor métrico de Riemann. Más tarde llegaron las “soluciones clásicas”, tales como el agujero negro y el Big Bang. Finalmente, la última etapa es el intento actual de formular una teoría cuántica de la gravedad. Por lo tanto, la relatividad general siguió una progresión lógica, un principio físico a una teoría cuántica.

 Y la historia continúa: Geometría → teoría de campos → teoría clásica → teoría cuántica. Y, a todo esto, ¿habrá en ese océano profundo donde habitan las cuerdas, unas de materia y otras de antimateria. ¿Quién puedo saberlo? El día que podamos llegar a ese profundo lugar, lo que allí pudiéramos encontrar, nos es totalmente desconocido y, de él sólo sabemos lo que nos dicen las matemáticas pero, la realidad es, que nunca nadie estuvo allí.

Contrariamente, la teoría de supercuerdas ha evolucionando hacia atrás desde su descubrimiento accidental en 1.968. Esta es la razón de que nos parezca extraña y poco familiar, estamos aún buscando un principio físico subyacente, la contrapartida del principio de equivalencia de Einstein.

La teoría nació casi por casualidad en 1.968 cuando dos jóvenes físicos teóricos, Gabriel Veneziano y Mahiko Suzuki, estaban hojeando independientemente libros de matemáticas. Figúrense ustedes que estaban buscando funciones matemáticas que describieran las interacciones de partículas fuertemente interactivas. Mientras estudiaban en el CERN, el Centro Europeo de Física Teórica en Ginebra, Suiza, tropezaron independientemente con la función beta de Euler, una función matemática desarrollada en el S. XIX por el matemático Leonhard Euler. Se quedaron sorprendidos al que la función beta de Euler ajustaba casi todas las propiedades requeridas para describir interacciones fuertes de partículas elementales.

                Gabriele Veneziano es un físico italiano

Tras el descubrimiento, Suzuki, muy excitado, mostró el hallazgo a un físico veterano del CERN. Tras oír a Suzuki, el físico veterano no se impresionó. De hecho le dijo a Suzuki que otro físico joven (Veneziano) había descubierto la misma función unas semanas antes. Disuadió a Suzuki de publicar su resultado. Hoy, esta función beta se conoce con el de modelo Veneziano, que ha inspirado miles de artículos de investigación iniciando una importante escuela de física y actualmente pretende unificar todas las leyes de la física.

En 1.970, el Modelo de Veneziano-Suzuki (que contenía un misterio), fue parcialmente explicado Yoichiro Nambu, de la Universidad de Chicago, y Tetsuo Goto, de la Nihon University, descubrieron que una cuerda vibrante yace detrás de sus maravillosas propiedades. Así que, como la teoría de cuerdas fue descubierta hacia atrás y por casualidad, los físicos aún no conocen el principio físico que subyace en la teoría de cuerdas vibrantes y sus maravillosas propiedades.

El último paso en la evolución de la teoría de cuerdas (y el primer paso en la evolución de la relatividad general) aún está pendiente de que alguien sea capaz de darlo.

Así, Witten dice:

“Los seres humanos en el planeta Tierra nunca dispusieron del marco conceptual que les llevara a concebir la teoría de supercuerdas de manera intencionada, surgió por razones del azar, por un feliz accidente. Por sus propios méritos, los físicos del siglo XX no deberían haber tenido el privilegio de estudiar esta teoría muy avanzada a su tiempo y a su conocimiento. No tenían (ni tenemos ahora mismo) los conocimientos y los prerrequisitos necesarios desarrollar dicha teoría, no tenemos los conceptos correctos y necesarios.”

 

                                  Andamos a la búsqueda de todo pero, saber… ¡sabemos tan poco!

Actualmente, como ha quedado dicho en este mismo , Edwar Witten es el físico teórico que, al frente de un equipo de físicos de Princeton, lleva la bandera de la teoría de supercuerdas con aportaciones muy importantes en el desarrollo de la misma.

De todas las maneras, aunque los resultados y avances son prometedores, el camino por andar es largo y la teoría de supercuerdas en su conjunto es un edificio con muchas puertas cerradas de las que no tenemos las llaves acceder a su interior y mirar lo que allí nos aguarda.

El problema está en que nadie es lo suficientemente inteligente para resolver la teoría de campos de cuerdas o cualquier otro enfoque no perturbativo de teoría. Se requieren técnicas que están actualmente más allá de nuestras capacidades.

Para encontrar la solución deben ser empleadas técnicas no perturbativas, que son terriblemente difíciles. Puesto que el 99 por ciento de lo que conocemos sobre física de altas energías se basa en la teoría de perturbaciones, esto significa que estamos totalmente perdidos a la hora de encontrar la verdadera solución de la teoría.

Hacemos uso de gráficas psicodélicas, pero la décima dimensión podría ejemplificarse como un árbol de infinitas ramas cuyas hojas son diferentes entre sí, tienen orígenes diferentes y crean, a su vez, cada una, árboles diferentes.Lo cierto es que, al vivir en sólo tres dimensiones espaciales, lo demás son imaginaciones, de manera real no se han podido ver, esas dimensiones extra por ninguna parte.

¿Por qué diez dimensiones? Uno de los secretos más profundos de la teoría de cuerdas, que aún no es bien comprendido, es por qué está definida sólo en diez y veintiséis dimensiones. Si calculamos cómo se rompen y se vuelven a juntar las cuerdas en el espacio N-dimensional, constantemente descubrimos que pululan términos absurdos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos indeseados aparecen multiplicados por (N-10). Por consiguiente, para hacer que desaparezcan estas anomalías, no tenemos otra elección cuántica que fijar N = 10. La teoría de cuerdas, de hecho, es la única teoría cuántica conocida que exige completamente que la dimensión del espacio-tiempo esté fijada en un único, el diez.

Por desgracia, los teóricos de cuerdas están, por el momento, completamente perdidos explicar por que se discriminan las diez dimensiones.  La respuesta está en las profundidades de las matemáticas, en un área denominada funciones modulares.

Al manipular los diagramas de lazos de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el 10 aparecen en los lugares más extraños.

Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del este, Ramanujan. Quizá si entendiéramos mejor el de este genio indio, comprenderíamos por qué vivimos en nuestro universo actual.

El misterio de las funciones modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y Riemann antes que él, trabajó en total aislamiento en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.

Dispersas oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre las más extrañas jamás encontradas en matemáticas. Ellas reaparecen en las ramas más distantes e inconexas de las matemáticas. Una función que aparece una y otra vez en la teoría de las funciones modulares se denomina (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. Esta extraña función contiene un término elevado a la potencia veinticuatro.

                                           Sí, estamos en el Universo … ¿Lo comprendemos?

El 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente donde menos se esperan por razones que nadie entiende.   Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas.  En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio-tiempo debe tener 24 + 2 = 26 dimensiones espacio-temporales.

Buscando las dimensiones extras hemos acudido a la microscopía de la luz

Para comprender este misterioso factor de dos (que añaden los físicos), consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista A_µ cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell.  Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones.  Sin embargo, dos de estos modos vibracionales pueden ser eliminados rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.

Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio-tiempo sea diez.

En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “no lo sé”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una cuánticamente autoconsistente), pero no sabemos por qué se seleccionan estos números concretos.

, una vez unificadas todas las versiones existentes de esta Teoría, en la llamada Teoría M, el espacio que exige es de 11 dimensiones que, según parece, será el defintivo para que la teoría sea autoconsistente y en ella pueda caber todo lo que tiene que tener.

¡Habrá que esperar!

emilio silvera

“La teoría de cuerdas es física del siglo XXI,  que cayó accidentalmente en el siglo XX.”

Edward  Witten

Lo cierto es que aún en la segunda década del siglo XXI, andamos a tientas con ésta sugestiva teoría que es tan prometedora parro que no podemos verificar al no contar con los adecuados medios para ellos. Nos ha costado mucho poder llegar al núcleo de los átomos para vislumbrar los Quarks que en tripletes, conforman protones y neutrones, y, hablamos de lo que podría existir más allá de los Quarks pero, ahí nos quedamos, como los Quarks están confinados en un océano de gluones, nosotros, amigos míos, también lo estamos en un océano de ignorancia del que sólo podremos escapar cuando podamos utilizar energías mucho más grandes que nos puedan llevar a regiones tan profundas en las que, posiblemente, habitan esas briznas vibrantes que serían las semillas de la materia.

 

 

explicó la Teoría M, algunos salieron de la conferencia asombrados

 

Edward Witten, del Instituto Estudios Avanzados de Princeton,  New Jersey, domina el mundo de la física teórica.  Podríamos decir que Witten, es el que tira del pelotón, el más brillante físico de altas energías que marca las tendencias actuales en la comunidad científica de la física teórica y el que ha sido capaz de plantear la versión más moderna de la teoría de supercuerdas, conocida teoría M.

Algunos se han atrevido a compararlo con Einstein. Ha ganado la medalla Field de 1.990, una especie de Premio Nobel de las matemáticas. Dice su mujer ( físico de profesión), que Witten permanece sentado con la mirada perdida en el horizonte a través de una ventana, manipulando y reordenando grandes conjuntos de complejas ecuaciones en su mente. Su esposa señala: “Nunca hace cálculos excepto en su mente. Yo llenaría páginas con cálculos antes de llegar a comprender lo que está haciendo, Edward sólo se sienta para calcular un signo menos o un factor dos”.

   Witten dice:

“La mayoría de las personas que no han estudiado física probablemente piensan que lo que hacen los físicos es cuestión de cálculos increíblemente complicados, pero eso no es realmente lo esencial. Lo esencial es que la física trata de conceptos, busca comprender los conceptos, los principios mediante los cuales opera el mundo, el universo”.

 

Así que Witten se ha enfrascado en la nada fácil tarea de unir la mecánica cuántica con la gravedad mediante la teoría de supercuerdas que, según él, nos puede incluso el instante mismo de la creación. El aspecto clave de esta teoría, el factor que le da su potencia tanto como su unicidad, es su geometría inusual. Las cuerdas (que según parece) pueden vibrar autoconsistentemente sólo en 10, 11 y 26 dimensiones.

La esencia de la teoría de cuerdas consiste en que puede explicar la naturaleza de la materia y del espacio-tiempo; es decir, la naturaleza del universo entero. Esta teoría responde a una serie de cuestiones enigmáticas acerca de las partículas, tales como por qué existen tantas en la naturaleza.   Cuanto más profundamente sondeamos en la naturaleza de las partículas subatómicas, más partículas aparecen. Existen varios centenares de ellas y sus propiedades llenan volúmenes y volúmenes. Incluso con el Modelo Estándar tenemos un desconcertante de “partículas elementales”. La teoría de cuerdas responde a esta pregunta porque la cuerda, alrededor de 100 trillones de veces más pequeña que un protón, esta vibrando; cada modo de vibración representa una resonancia o partícula distinta. La cuerda es tan increíblemente pequeña que, a cierta distancia, una resonancia de una cuerda y una partícula son indistinguibles. Sólo cuando ampliamos de alguna la partícula podemos ver que no es en absoluto un punto, sino un modo de una cuerda vibrante.

Según la teoría de cuerdas, la materia no es nada más que las armonías creadas por cuerdas vibrantes. Del mismo modo que se puede componer un infinito de armonías para el violín, puede construirse un número infinito de formas de materia a partir de cuerdas vibrantes. Esto explica la riqueza de las partículas en la naturaleza. Análogamente, las leyes de la física pueden ser comparadas a las leyes de la armonía permitida en la cuerda. El propio universo, compuesto de innumerables cuerdas vibrantes, sería entonces comparable a una sinfonía.

La teoría de cuerdas explica la naturaleza de las partículas y del espacio-tiempo. Cuando una cuerda se mueve en el espacio-tiempo, ejecuta un conjunto de complicados movimientos. La cuerda , a su vez, romperse en cuerdas más pequeñas o colisionar con otras cuerdas para formar cuerdas más largas. El punto clave es que todas estas correcciones cuánticas o diagramas cerrados son finitos y calculables. Esta es la primera teoría cuántica de la gravedad en la historia de la física que tiene correcciones cuánticas finitas (recordemos que todas las teorías previas conocidas – incluyendo la teoría original de Einstein, la de Kaluza-Klein y la teoría de supergravedad – fallaban en criterio clave).

                                            Lazos

En la teoría de cuerdas, la fuerza gravitatoria se representa mediante el intercambio de cuerdas cerradas, que barren tubos en el espacio-tiempo. Incluso si usamos una serie infinita de diagramas con un gran de agujeros, nunca aparecen infinitos en la teoría, dándonos una teoría de gravedad cuántica.

Cuando se calcularon por primera vez las ligaduras que impone la cuerda sobre el espacio-tiempo, los físicos quedaron sorprendidos al que las ecuaciones de Einstein emergían de la cuerda. Esto era notable; sin suponer ninguna de las ecuaciones de Einstein, los físicos asombrados descubrían que ellas emergían de la teoría de cuerdas como por encanto.   Las ecuaciones de Einstein ya no resultaban ser fundamentales; podían derivarse de la teoría de cuerdas de la que formaban . Einstein pensaba que la geometría por sí sola explicaría un día todas las propiedades de la materia; él la materia era sólo un nudo o vibración del espacio-tiempo, ni más ni menos. Los físicos cuánticos, por el contrario, pensaban de manera distinta a la de Einstein, es decir, que el tensor métrico de Riemann-Einstein podía convertirse en un gravitón, el paquete discreto de energía que transporta la fuerza gravitatoria y, en este preciso punto, aparece la cuerda, que según todos los indicios ser el “eslabón perdido” entre la mecánica cuántica y la relatividad general, el que permita la unificación ambas teorías de manera natural y complete el circulo de una teoría de “todo” que explique el universo, la materia y el espacio-tiempo con todas sus constantes universales y las fuerzas de la naturaleza que lo rigen todo.

                     ¿Qué sabemos nosotros de lo que hay más allá de los Quarks?

La teoría de cuerdas, por consiguiente, es suficientemente rica para explicar todas las leyes fundamentales de la naturaleza. Partiendo de una simple teoría de una cuerda vibrante, uno extraer la teoría de Einstein, la teoría de Kaluza-Klein, la supergravedad, el Modelo Estándar e incluso una teoría GUT (Gran Teoría Unificada). Parece un milagro que partiendo de unos argumentos puramente geométricos acerca de una cuerda, se pueda desarrollar totalmente por derivación la física de los últimos dos mil años.   Todas las teorías discutidas hasta están incluidas automáticamente en la teoría de cuerdas.

                                              John H. Schawarz

En 1.984, John Schwarz del Instituto Tecnológico de California y su colaborador Michael Green del Queen Mary’s Collage de Londres, demostraron que la teoría de cuerdas podía ser autoconsistente, lo que desencadenó una carrera de los físicos más jóvenes resolver esta teoría.

El concepto de órbitas, por ejemplo, se da repetidamente en la naturaleza en diferentes variaciones; la obra de Copérnico, las órbitas han proporcionado un tema esencial que se repite constantemente a lo largo de la naturaleza en diferentes variaciones, desde las galaxias más grandes hasta los átomos y los más diminutas partículas subatómicas, tanto las unas como las otras describen órbitas en su deambular por el espacio. De manera análoga, los campos de Faraday se han mostrado como uno de los temas favoritos de la naturaleza. Los campos pueden describir el magnetismo de la naturaleza de las galaxias y la gravitación, o pueden describir la teoría electromagnética de Maxwell, la teoría métrica de Riemann-Einstein, los campos de Yang-Mills encontrados en el Modelo Estándar, y así todas las formas conocidas de materia y energía han sido expresadas en términos de teoría de campos. Las estructuras, entonces, los temas y variaciones en una sinfonía, son repetidas constantemente.

   Buscamos un Universo de 11 dimensiones y sólo vemos 3

¿Pero las cuerdas? Las cuerdas no parecen ser una estructura preferida por la naturaleza en el diseño de los cielos. No vemos cuerdas en el espacio exterior. De hecho no las vemos por ninguna y, sin embargo, todos los indicios teóricos y las complejas matemáticas topológicas nos dicen que… ¡Están ahí!

Un momento de reflexión, sin embargo, revelará que la naturaleza ha reservado un papel especial a las cuerdas, como un ladrillo básico para otras formas. Por ejemplo, la característica esencial de la vida en el planeta Tierra es la molécula de ADN similar a una cuerda, que contiene la información compleja y el código de la propia vida. Para construir la materia de la vida, tanto como la materia subatómica, las cuerdas parecen ser la respuesta perfecta. En ambos casos, queremos encerrar una gran cantidad de información en una estructura reproducible y relativamente simple. La característica distintiva de una cuerda es que es una de la forma más compacta de almacenar grandes cantidades de de un modo en que la información pueda ser replicada.

Para los seres vivos la naturaleza utiliza la doble cadena de la molécula de ADN, que se separa y forma copias duplicadas de cada una de ellas.   Nuestros cuerpos también contienen millones de millones de cadenas de proteínas, formadas de ladrillos de aminoácidos. Nuestro cuerpo, en cierto sentido, puede ser considerado como una enorme colección de cuerdas: moléculas de proteínas que revisten nuestros huesos. Sin embargo, nadie puede dar una explicación de nuestro entendimiento, de la inteligencia que se crea y que llevamos con nosotros desde el mismo momento del nacimiento, está ahí presente, a la espera de que se la despierte, es la inteligencia dormida y evolucionada por el conocimiento de las cosas. La conciencia de SER a la que llamamos alma, y que de alguna manera es inmortal, ya que lo que sabemos lo cedemos y lo dejamos aquí para los que nos siguen en la tarea emprendida por la humanidad desde que, en el preciso momento en que surgió aquella primera célula original que fue capaz de dividirse para replicarse a sí misma, se dio el primer paso para el nacimiento de la vida en nuestro planeta. Pero esa es otra cuestión que será tratada en otro próximo , ahora volvamos al tema de la teoría de cuerdas de la física.

En la década de los noventa se creó una versión de mucho éxito de la teoría de cuerdas. Sus autores, los físicos de Princeton David Gross, Emil Martinec, Jeffrey Harvey y Ryan Rohn, a quienes se dio en llamar el cuarteto de cuerdas de Princeton.

El de más edad de los cuatro, David Gross, hombre de temperamento imperativo, es temible en los seminarios al final de la charla, en el tiempo de preguntas, con su inconfundible vozarrón dispara certeros e inquisidoras preguntas al ponente. Lo que resulta sorprendente es el hecho de que sus preguntas dan normalmente en el clavo.

Gross y sus colegas propusieron lo que se denomina la cuerda heterótica. Hoy día, de todas las variedades de teorías Kaluza-Klein que se propusieron en el pasado, es precisamente la cuerda heterótica la que tiene mayor potencial unificar todas las leyes de la naturaleza en una teoría.  Gross cree que la teoría de cuerdas resuelve el problema de construir la propia materia a partir de la geometría de la que emergen las partículas de materia y también la gravedad en presencia de las otras fuerzas de la naturaleza.

Es curioso constatar que si abandonamos la teoría de la gravedad de Einstein como una vibración de la cuerda, entonces la teoría se vuelve inconsistente e inútil. Esta, de hecho, es la razón por la que Witten se sintió atraído inicialmente hacia la teoría de cuerdas. En 1.982 leyó un artículo de revisión de John Schwarz y quedó sorprendido al darse de que la gravedad emerge de la teoría de supercuerdas a partir solamente de los requisitos de auto consistencia. Recuerda que fue “la mayor excitación intelectual de mi vida”.

Las ideas de Einstein subyacen en la teoría de cuerdas y, sus ecuaciones de la Relatividad general, sin que nadie las llame, aparecen cuando los físicos elaboran y profundizan en las cuerdas cibrantes de esa nueva teoría que tantas esperanzas han puesto en la mente de muchos para a través de ellas, los más profundos secretos de la Naturaleza.

Gross se siente satisfecho pensando que Einstein, si viviera, disfrutaría con la teoría de supercuerdas que sólo es válida si incluye su propia teoría de la relatividad general, y amaría el hecho de que la belleza y la simplicidad de esa teoría proceden en última instancia de un principio geométrico, cuya naturaleza exacta es aún desconocida.

Witten llega incluso a decir que:

“todas las ideas realmente grandes en la física, son retornos de la teoría de supercuerdas”.

 

Con esto, él quiere decir que todos los grandes avances en física teórica están incluidos en la teoría de supercuerdas. Incluso afirma el hecho de que la teoría de supercuerdas fue “un accidente del desarrollo intelectual en el planeta Tierra, ocurrido de su tiempo”. Y continúa diciendo:

“En alguna en el espacio exterior, otras civilizaciones en el universo pudieron haber descubierto primero la teoría de supercuerdas y derivado de ella la teoría de la relatividad general que lleva dentro”.

La cuerda heterótica de Gross y sus colegas, consiste en una cuerda cerrada que tiene dos tipos de vibraciones, en el sentido de las agujas del reloj y en sentido contrario, que son tratadas de diferente. Las vibraciones en el sentido de las agujas del reloj viven en un espacio de diez dimensiones. Las vibraciones de sentido contrario viven en un espacio de veintiséis dimensiones, de las que dieciséis han sido compactificadas. Lo mismo ocurría en la teoría de la quinta dimensión de Kaluza-Klein, donde la quinta dimensión estaba compactificada curvándose en un círculo en el límite de Planck.

La cuerda heterótica debe su al hecho de que las vibraciones en el sentido de las agujas del reloj y en el sentido contrario viven en dos dimensiones diferentes pero se combinan para producir una sola teoría de supercuerdas. es la razón de que se denomine según la palabra griega heterosis, que significa “vigor hibrido”.

El espacio compactificado de dieciséis dimensiones es el más interesante. fue analizado por el “cuarteto de cuerda” de Princeton (Gross y su equipo), descubrieron que contiene una simetría de enormes dimensiones, denominada E (8) × E (8), que es mucho mayor que cualquier simetría GUT que se hubiese intentado jamás. Esta simetría es mucho mayor que el grupo de simetría que aparece en el Modelo Estándar, dado por SU(3) × SU(2) × U(1) que es un subconjunto de la anterior donde está acomodado también (dada su amplitud) el Modelo Estándar.

Nuestras Mentes están conformadas de tridimensional, nuestro mundo es de tres dimensiones espaciales. La cuarta dimensión de nuestro mundo, el Tiempo, incide en la posible alteración evolutiva que podríamos experimentar para poder vislumbrar más altas dimensiones pero…, ¿podrán alterarse las percepciones?

ver cómo dimensiones más altas simplifican las leyes de la Naturaleza, recordemos que un objeto tiene longitud, anchura y altura.  Puesto que tenemos libertad para girar un objeto 90º, podemos transformar su longitud en anchura y su anchura en altura.   Mediante una simple rotación, podemos intercambiar cualquiera de las tres dimensiones espaciales.

bien, si el tiempo es la cuarta dimensión, entonces es posible hacer “rotaciones” que convierten el espacio en tiempo y el tiempo en espacio.  Estas rotaciones tetradimensionales son precisamente las distorsiones del espacio y del tiempo exigidas por la relatividad especial. En otras palabras, espacio y tiempo se mezclan de una forma esencial, gobernada por la relatividad.  El significado del tiempo como la cuarta dimensión es que pueden hacerse relaciones entre el tiempo y el espacio de una forma matemáticamente precisa.  A partir de entonces, deben ser tratados como dos aspectos de la misma magnitud: el espacio-tiempo. Así han quedado unificadas las leyes de la Naturaleza al pasar de tres a cuatro dimensiones. Como nuestra imaginación no cesa de generar ideas y nuestra curiosidad insiste en querer saber más, de todo esto pasamos a las cuerdas añadiendo más dimensiones al planteamiento.

Las leyes de la física se simplifican en dimensiones más altas.

En caso, en el espacio 26–dimensional de las vibraciones de sentido contrario a las agujas del reloj de la cuerda heterótica que tiene espacio suficiente para explicar todas las simetrías encontradas en la teoría de Einstein y en la teoría cuántica. Así, por primera vez, la geometría pura ha dado una simple explicación de por qué el mundo subatómico debería exhibir necesariamente ciertas simetrías que emergen del enrollamiento del espacio de más dimensiones: Las simetrías del dominio subatómico no son sino remanentes de la simetría del espacio de más dimensiones.

Esto significa que la belleza y simetrías encontradas en la naturaleza pueden ser rastreadas en última instancia hasta el espacio multidimensional.  Por ejemplo, los copos de nieve crean bellas figuras hexagonales, ninguna de las cuales es exactamente igual a otra, han heredado sus estructuras de las formas en que sus moléculas han sido dispuestas geométricamente, determinada básicamente por las cortezas electrónicas de estas moléculas, que a su vez nos llevan de a las simetrías rotacionales de la teoría cuántica, dadas por O (3).

Podemos concluir diciendo que las simetrías que vemos a nuestro alrededor, desde un arco iris a las flores y a los cristales, pueden considerarse en última instancia manifestaciones de fragmentos de la teoría decadimensional original. Riemann y Einstein habían confiado en llegar a una comprensión geométrica de por qué las fuerzas pueden determinar el movimiento y la naturaleza de la materia.

Superficie de Riemann que aparece al extender el dominio de la función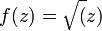

Dado el enorme poder de sus simetrías, no es sorprendente que la teoría de supercuerdas sea radicalmente diferente de cualquier otro de física.  De hecho, fue descubierta casi por casualidad. Muchos físicos han comentado que si este accidente fortuito no hubiese ocurrido, entonces la teoría no se hubiese descubierto hasta bien entrado el siglo XXI. Esto es así porque supone una neta desviación de todas las ideas ensayadas en este siglo. No es una extensión natural de tendencias y teorías populares en este siglo que ha pasado; permanece aparte.

Por el contrario, la teoría de la relatividad general de Einstein tuvo una evolución normal y lógica. En primer lugar, su autor, postula el principio de equivalencia. Luego reformuló principio físico en las matemáticas de una teoría de campos de la gravitación basada en los campos de Faraday y en el tensor métrico de Riemann. Más tarde llegaron las “soluciones clásicas”, tales como el agujero negro y el Big Bang. Finalmente, la última etapa es el intento actual de formular una teoría cuántica de la gravedad. Por lo tanto, la relatividad general siguió una progresión lógica, un principio físico a una teoría cuántica.

 Y la historia continúa: Geometría → teoría de campos → teoría clásica → teoría cuántica. Y, a todo esto, ¿habrá en ese océano profundo donde habitan las cuerdas, unas de materia y otras de antimateria. ¿Quién puedo saberlo? El día que podamos llegar a ese profundo lugar, lo que allí pudiéramos encontrar, nos es totalmente desconocido y, de él sólo sabemos lo que nos dicen las matemáticas pero, la realidad es, que nunca nadie estuvo allí.

Contrariamente, la teoría de supercuerdas ha evolucionando hacia atrás desde su descubrimiento accidental en 1.968. Esta es la razón de que nos parezca extraña y poco familiar, estamos aún buscando un principio físico subyacente, la contrapartida del principio de equivalencia de Einstein.

La teoría nació casi por casualidad en 1.968 cuando dos jóvenes físicos teóricos, Gabriel Veneziano y Mahiko Suzuki, estaban hojeando independientemente libros de matemáticas. Figúrense ustedes que estaban buscando funciones matemáticas que describieran las interacciones de partículas fuertemente interactivas. Mientras estudiaban en el CERN, el Centro Europeo de Física Teórica en Ginebra, Suiza, tropezaron independientemente con la función beta de Euler, una función matemática desarrollada en el S. XIX por el matemático Leonhard Euler. Se quedaron sorprendidos al que la función beta de Euler ajustaba casi todas las propiedades requeridas para describir interacciones fuertes de partículas elementales.

                Gabriele Veneziano es un físico italiano

Tras el descubrimiento, Suzuki, muy excitado, mostró el hallazgo a un físico veterano del CERN. Tras oír a Suzuki, el físico veterano no se impresionó. De hecho le dijo a Suzuki que otro físico joven (Veneziano) había descubierto la misma función unas semanas antes. Disuadió a Suzuki de publicar su resultado. Hoy, esta función beta se conoce con el de modelo Veneziano, que ha inspirado miles de artículos de investigación iniciando una importante escuela de física y actualmente pretende unificar todas las leyes de la física.

En 1.970, el Modelo de Veneziano-Suzuki (que contenía un misterio), fue parcialmente explicado Yoichiro Nambu, de la Universidad de Chicago, y Tetsuo Goto, de la Nihon University, descubrieron que una cuerda vibrante yace detrás de sus maravillosas propiedades. Así que, como la teoría de cuerdas fue descubierta hacia atrás y por casualidad, los físicos aún no conocen el principio físico que subyace en la teoría de cuerdas vibrantes y sus maravillosas propiedades.

El último paso en la evolución de la teoría de cuerdas (y el primer paso en la evolución de la relatividad general) aún está pendiente de que alguien sea capaz de darlo.

Así, Witten dice:

“Los seres humanos en el planeta Tierra nunca dispusieron del marco conceptual que les llevara a concebir la teoría de supercuerdas de manera intencionada, surgió por razones del azar, por un feliz accidente. Por sus propios méritos, los físicos del siglo XX no deberían haber tenido el privilegio de estudiar esta teoría muy avanzada a su tiempo y a su conocimiento. No tenían (ni tenemos ahora mismo) los conocimientos y los prerrequisitos necesarios desarrollar dicha teoría, no tenemos los conceptos correctos y necesarios.”

 

                                  Andamos a la búsqueda de todo pero, saber… ¡sabemos tan poco!

Actualmente, como ha quedado dicho en este mismo , Edwar Witten es el físico teórico que, al frente de un equipo de físicos de Princeton, lleva la bandera de la teoría de supercuerdas con aportaciones muy importantes en el desarrollo de la misma.

De todas las maneras, aunque los resultados y avances son prometedores, el camino por andar es largo y la teoría de supercuerdas en su conjunto es un edificio con muchas puertas cerradas de las que no tenemos las llaves acceder a su interior y mirar lo que allí nos aguarda.

El problema está en que nadie es lo suficientemente inteligente para resolver la teoría de campos de cuerdas o cualquier otro enfoque no perturbativo de teoría. Se requieren técnicas que están actualmente más allá de nuestras capacidades.

Para encontrar la solución deben ser empleadas técnicas no perturbativas, que son terriblemente difíciles. Puesto que el 99 por ciento de lo que conocemos sobre física de altas energías se basa en la teoría de perturbaciones, esto significa que estamos totalmente perdidos a la hora de encontrar la verdadera solución de la teoría.

¿Por qué diez dimensiones? Uno de los secretos más profundos de la teoría de cuerdas, que aún no es bien comprendido, es por qué está definida sólo en diez y veintiséis dimensiones. Si calculamos cómo se rompen y se vuelven a juntar las cuerdas en el espacio N-dimensional, constantemente descubrimos que pululan términos absurdos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos indeseados aparecen multiplicados por (N-10). Por consiguiente, para hacer que desaparezcan estas anomalías, no tenemos otra elección cuántica que fijar N = 10. La teoría de cuerdas, de hecho, es la única teoría cuántica conocida que exige completamente que la dimensión del espacio-tiempo esté fijada en un único, el diez.

Por desgracia, los teóricos de cuerdas están, por el momento, completamente perdidos explicar por que se discriminan las diez dimensiones.  La respuesta está en las profundidades de las matemáticas, en un área denominada funciones modulares.

Al manipular los diagramas de lazos de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el 10 aparecen en los lugares más extraños.

Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del este, Ramanujan. Quizá si entendiéramos mejor el de este genio indio, comprenderíamos por qué vivimos en nuestro universo actual.

El misterio de las funciones modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y Riemann antes que él, trabajó en total aislamiento en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.

Dispersas oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre las más extrañas jamás encontradas en matemáticas. Ellas reaparecen en las ramas más distantes e inconexas de las matemáticas. Una función que aparece una y otra vez en la teoría de las funciones modulares se denomina (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. Esta extraña función contiene un término elevado a la potencia veinticuatro.

                               Sí, estamos en el Universo … ¿Lo comprendemos?

El 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente donde menos se esperan por razones que nadie entiende.   Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas.  En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio-tiempo debe tener 24 + 2 = 26 dimensiones espacio-temporales.

Para comprender este misterioso factor de dos (que añaden los físicos), consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista A_µ cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell.  Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones.  Sin embargo, dos de estos modos vibracionales pueden ser eliminados rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.

Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio-tiempo sea diez.

En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “no lo sé”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una cuánticamente autoconsistente), pero no sabemos por qué se seleccionan estos números concretos.

, una vez unificadas todas las versiones existentes de esta Teoría, en la llamada Teoría M, el espacio que exige es de 11 dimensiones que, según parece, será el defintivo para que la teoría sea autoconsistente y en ella pueda caber todo lo que tiene que tener.

¡Habrá que esperar!

emilio silvera

 El “universo” de lo muy pequeño. ¡Resulta fasciante!

El 21 de diciembre de 2010 científicos estadounidenses descubrieron “un vimana atrapado en un pozo del tiempo“ (un campo gravitatorio electromagnético, que sólo puede ocurrir en una dimensión invisible del espacio) en la ciudad de Balkh, Afganistán, lugar que alguna vez Marco Polo catalogó como “una de las ciudades más nobles y grandiosas” del mundo”.

Los intentos por retirar el misterioso Vimana de la cueva donde había estado oculto durante por lo menos 5.000 años, causaron la “desaparición” de por lo menos 8 soldados norteamericanos, atrapados por el vórtex temporal ( nuestros cuerpos no pueden desplazarse como si nada del presente al futuro y del futuro al pasado sin cargarse el peso destructivo de las leyes de la fìsica, salvo si se logra bloquear el campo magnético, algo que aparentemente los científicos norteamericanos tardaron ocho cadáveres en descubrir y solucionar, probablemente con jaulas de Faraday ).

La existencia de este tipo de fenómenos no está demostrado por los científicos (caso contrario estaríamos hablando de leyes), pero los físicos teóricos coinciden en general que podrían ser posibles si se acepta la teoría del Multiuniverso (un universo de por lo menos 11 dimensiones espaciotemporales) como estructura lógica y matemática. Atravesando esa especie de plasma líquido, nos podríamos trasladar a otros mundos, a otras galaxias.

Theodor Kaluza, ya en 1921 conjeturaba que si ampliáramos nuestra visión del universo a 5 dimensiones, entonces no habría más que un solo campo de fuerza: la gravedad, y lo que llamamos electromagnetismo sería tan sólo la parte del campo gravitatorio que opera en la quinta dimensión, una realidad espacial que jamás reconoceríamos si persistiéramos en nuestros conceptos de realidad lineal, similar a un holograma.

Bueno, independientemente de que todo esto pueda ser una realidad, lo cierto es que, nosotros, ahora en nuestro tiempo, hablamos de un universo con más dimensiones y, la carrera de las más altas dimensiones la inicio (como arrtiba se menciona) en el año 1919 (no el 1921) por Theodor Kaluza, un osucro y desconocido matemático,  cuando le presentó a Einstein mediante un escrito una teoría unificada que podía unificar, las dos grandes teorías del momento, la Relatividad General con el Magnetismo y podía realizarse si elaboraba sus ecuciones  en un espaciotiempo de cinco dimensiones.

Así estaban las cosas cuando en 1.919 recibió Einstein un trabajo de Theodor Kaluza, un privatdozent en la Universidad de Königsberg, en el que extendía la Relatividad General a cinco dimensiones. Kaluza consideraba un espacio con cuatro dimensiones, más la correspondiente dimensión temporal y suponía que la métrica del espacio-tiempo se podía escribir como:

                                   Klein

Así que, como hemos dicho, ese mismo año, Oskar Klein publicaba un trabajo sobre la relación entre la teoría cuántica y la relatividad en cinco dimensiones. Uno de los principales defectos del modelo de Kaluza era la interpretación física de la quinta dimensión. La condición cilíndrica impuesta ad hoc hacía que ningún campo dependiera de la dimensión extra, pero no se justificaba de manera alguna.

Klein propuso que los campos podrían depender de ella, pero que ésta tendría la topología de un círculo con un radio muy pequeño, lo cual garantizaría la cuantización de la carga eléctrica. Su diminuto tamaño, R₅ ≈ 8×10^{-31 cm}, cercano a la longitud de Planck, explicaría el hecho de que la dimensión extra no se observe en los experimentos ordinarios, y en particular, que la ley del inverso del cuadrado se cumpla para distancias r » R₅. Pero además, la condición de periodicidad implica que existe una isometría de la métrica bajo traslaciones en la quinta dimensión, cuyo grupo U(1), coincide con el grupo de simetría gauge del electromagnetismo.

Einstein al principio se burló de aquella disparatada idea pero, más tarde, habiendo leido y pensado con más atenci`´on en lo que aquello podía significar, ayudó a Kaluza a publicar su idea de un mundo con cinco dimensiones (allí quedó abierta la puerta que más tarde, traspasarían los teóricos de las teorías de más altas dimensiones). Algunos años más tarde, , el físico sueco Oskar Klein publicó una versión cuántica del artículo de Kaluza. La Teoría Kaluza-Klein que resultó parecía interesante, pero, en realidad, nadie sabía que hacer con ella hasta que, en los años setenta; cuando pareció beneficioso trabajar en la supersimetría, la sacaron del baúl de los recuerdos, la desempolvaron y la tomaron como modelo.

Pronto, Kaluza y Klein estuvieron en los labios de todo el mundo  (con Murray Gell-Mann, en su papel de centinela lingüistico, regañando a sus colegas que no lo sabían pronunciar “Ka-wu-sah-Klein”.

        Pero, ¿Existen en nuestro Universo dimensiones ocultas?

Aunque la teoría de cuerdas en particular y la supersimetría en general apelaban a mayores dimensiones, las cuerdas tenian un modo de seleccionar su dimensionalidad requerida. Pronto se hizo evidente que la Teoría de cuerdas sólo sería eficaz, en dos, diez y veintiseis dimensiones, y sólo invocaba dos posibles grupos de simetría: SO(32) o E₈ x E_8. Cuando una teoría apunta hacia algo tan tajante, los científicos prestan atención, y a finales de los años ochenta había decenas de ellos que trabajaban en las cuerdas. Por aquel entonces, quedaba mucho trabajo duro por hacer, pero las perspectivas era brillantes. “Es posible que las décadas futuras -escribieron Schwarz y sus colaboradores en supercuerdas Green y Edward Witten- sea un excepcional período de aventura intelectual.” Desde luego, la aventura comenzó y, ¡qué aventura!

Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck).  Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.

Puesto que el radio de compactificación es tan pequeño, el valor típico de las masas será muy elevado, cercano a la masa de Planck M_p = k^-12 = 1’2 × 10¹⁹ GeV*, y por tanto, a las energías accesibles hoy día (y previsiblemente, tampoco en un futuro cercano – qué más quisieran E. Witten y los perseguidores de las supercuerdas -), únicamente el modo cero n = 0 será relevante. Esto plantea un serio problema para la teoría, pues no contendría partículas ligeras cargadas como las que conocemos.

¿Y si llevamos a Kaluza-Klein a dimensiones superiores para unificar todas las interacciones?

En este proceso llamado desintegración beta y debido a la interacción débil, un neutrón se transforma en un protón, un electrón y un (anti)neutrino electrónico cuando uno de los quarks del neutrón emite una partícula W–. Aquí queda claro que el término “interacción” es más general que “fuerza”; esta interacción que hace cambiar la identidad de las partículas no podría llamarse fuerza (todo representado en uno de los famosos diagramas de Feyman).

La descripción de las interacciones débiles y fuertes a través de teorías gauge no abelianas mostró las limitaciones de los modelos en cincodimensiones, pues éstas requerirían grupos de simetría mayores que el del electromagnetismo. En 1964 Bryce de UIT presentó el primer modelo de tipo Kaluza-Klein–Yang-Mills en el que el espacio extra contenía más de una dimensión.

El siguiente paso sería construir un modelo cuyo grupo de isometría contuviese el del Modelo Estándar SU(3)_c × SU(2)_l × U(1)_y, y que unificara por tanto la gravitación con el resto de las interacciones.

Edward Witten demostró en 1981 que el número total de dimensiones que se necesitarían sería al menos de once. Sin embargo, se pudo comprobar que la extensión de la teoría a once dimensiones no podía contener fermiones quirales, y por tanto sería incapaz de describir los campos de leptones y quarks.

Por otra parte, la supersimetría implica que por cada bosón existe un fermión con las mismas propiedades. La extensión supersimétrica de la Relatividad General es lo que se conoce como supergravedad (supersimetría local).

Joël Scherk (1946-1980) (a menudo citado como Joel Scherk) fue un francés teórico físico que estudió la teoría de cuerdas ysupergravedad ^[1] . Junto con John H. Schwarz , pensaba que la teoría de cuerdas es una teoría de la gravedad cuántica en 1974. En 1978, junto con Eugène Cremmer y Julia Bernard , Scherk construyó el lagrangiano y supersimetría transformaciones parasupergravedad en once dimensiones, que es uno de los fundamentos de la teoría-M .

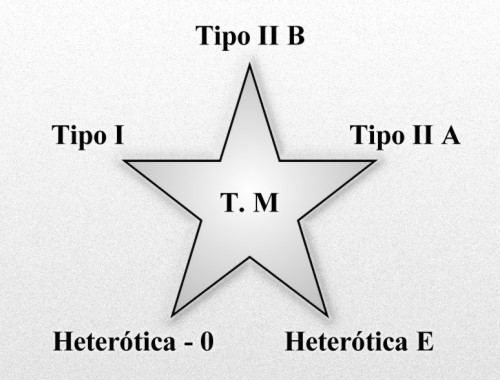
Unos años antes, en 1978, Cremmer, Julia y Scherk habían encontrado que la supergravedad, precisamente en once dimensiones, tenía propiedades de unicidad que no se encontraban en otras dimensiones. A pesar de ello, la teoría no contenía fermiones quirales, como los que conocemos, cuando se compactaba en cuatro dimensiones. Estos problemas llevaron a gran parte de los teóricos al estudio de otro programa de unificación a través de dimensiones extra aún más ambicioso, la teoría de cuerdas.

No por haberme referido a ella en otros trabajos anteriores estará de más dar un breve repaso a las supercuerdas. Siempre surge algún matiz nuevo que enriquece lo que ya sabemos.

El origen de la teoría de supercuerdas data de 1968, cuando Gabriela Veneziano introdujo los modelos duales en un intento de describir las amplitudes de interacción hadrónicas, que en aquellos tiempos no parecía provenir de ninguna teoría cuántica de campos del tipo de la electrodinámica cuántica. Posteriormente, en 1979, Yaichiro Nambu, Leonard Susskind y Holger Nielsen demostraron de forma independiente que las amplitudes duales podían obtenerse como resultado de la dinámica de objetos unidimensionales cuánticos y relativistas dando comienzo la teoría de cuerdas.

En 1971, Pierre Ramona, André Neveu y otros desarrollaron una teoría de cuerdas con fermiones y bosones que resultó ser supersimétrica, inaugurando de esta forma la era de las supercuerdas.

              David Jonathan Gross

Sin embargo, en 1973 David Gross, David Politzer y Frank Wilczek descubrieron que la Cromodinámica Cuántica, que es una teoría de campos gauge no abeliana basada en el grupo de color SU(3)_c, que describe las interacciones fuertes en términos de quarks y gluones, poseía la propiedad de la libertad asintótica. Esto significaba que a grandes energías los quarks eran esencialmente libres, mientras que a bajas energías se encontraban confinados dentro de los hadrones en una región con radio R de valor R ≈ hc/Λ ≈ 10^{-13 cm}.

Dicho descubrimiento, que fue recompensado con la concesión del Premio Nobel de Física a sus autores en 2.004, desvió el interés de la comunidad científica hacia la Cromodinámica Cuántica como teoría de las interacciones fuertes, relegando casi al olvido a la teoría de supercuerdas.

Se habla de cuerdas abiertas, cerradas o de lazos, de p branas donde p denota su dimensionalidad (así, 1 brana podría ser una cuerda y 2.Brana una membrana) o D-Branas (si son cuerdas abiertas) Y, se habla de objetos mayores y diversos que van incorporados en esa teoría de cuerdas de diversas familias o modelos que quieren sondear en las profundidades del Universo físico para saber, como es.

En la década de los noventa se creó una versión de mucho éxito de la teoría de cuerdas. Sus autores, los físicos de Princeton David Gross, Emil Martinec, Jeffrey Harvey y Ryan Rohn, a quienes se dio en llamar el cuarteto de cuerdas de Princeton.

El de más edad de los cuatro, David Gross, hombre de temperamento imperativo, es temible en los seminarios cuando al final de la charla, en el tiempo de preguntas, con su inconfundible vozarrón dispara certeros e inquisidoras preguntas al ponente. Lo que resulta sorprendente es el hecho de que sus preguntas dan normalmente en el clavo.

Gross y sus colegas propusieron lo que se denomina la cuerda heterótica. Hoy día, de todas las variedades de teorías tipo Kaluza-Klein que se propusieron en el pasado, es precisamente la cuerda heterótica la que tiene mayor potencial para unificar todas las leyes de la naturaleza en una teoría. Gross cree que la teoría de cuerdas resuelve el problema de construir la propia materia a partir de la geometría de la que emergen las partículas de materia y también la gravedad en presencia de las otras fuerzas de la naturaleza.

El caso curioso es que, la Relatividad de Einstein, subyace en la Teoría de cuerdas, y, si eliminamos de esta a aquella y su geometría de la Gravedad…todo resulta inútil. El gran Einstein está presente en muchos lugares y quizás, más de los que nos podamos imaginar.

Es curioso constatar que si abandonamos la teoría de la gravedad de Einstein como una vibración de la cuerda, entonces la teoría se vuelve inconsistente e inútil. Esta, de hecho, es la razón por la que Witten se sintió atraído inicialmente hacia la teoría de cuerdas. En 1.982 leyó un artículo de revisión de John Schwarz y quedó sorprendido al darse cuenta de que la gravedad emerge de la teoría de supercuerdas a partir solamente de los requisitos de auto consistencia. Recuerda que fue “la mayor excitación intelectual de mi vida”.

Gross se siente satisfecho pensando que Einstein, si viviera, disfrutaría con la teoría de supercuerdas que sólo es válida si incluye su propia teoría de la relatividad general, y amaría el hecho de que la belleza y la simplicidad de esa teoría proceden en última instancia de un principio geométrico, cuya naturaleza exacta es aún desconocida.atividad general de Einstein. Nos ayuda a estudiar las partes más grandes del Universo, como las estrellas y las galaxias. Pero los elementodiminutoso los átomos y las partículas subatómicas se rigen por unas leyes diferentes denominadas mecánica cuántica.

Claro que, como todos sabemos, Einstein se pasó los últimos treinta años de su vida tratándo de buscar essa teoría unificada que nunca pudo encontrar. No era consciente de que, en su tiempo, ni las matemáticas necesarias existían aún. En la historia de la física del siglo XX muchos son los huesos descoloridos de teorías que antes se consideraban cercanas a esa respuesta final que incansables buscamos.

Hasta el gran Wolfgang Pauli había colaborado con Heisenberg en la búsqueda de una teoría unificada durante algún tiempo, pero se alarmó al oir en una emisión radiofónica como Heisenberg decía: “Está a punto de ser terminada una Teoría unificada de Pauli-Heisenserg, en la que sólo nos queda por elaborar unos pocos detalles técnicos.”

            Wolfgang Pauli

Enfadado por lo que consideraba una hipérbole de Heisenberg que se extralimitó con aquellas declaraciones en las que lo inviolucraba sin su consentimiento,  Pauli envió a Gamow y otros colegas una simple hija de papel en blanco en la que había dibujado una caja vacía. Al pie del dibujo puso estas pablabras: “Esto es para demostrar al mundo que yo puedo pintar con Tiziano. Sólo faltan algunos detalles técnicos.”

Los críticos del concepto de supercuerdas señalaron que las afirmaciones sobre sus posibilidades se basaban casi enteramente en su belleza interna. La teoría aún  no había repetido siquiera los logros del Modelo Estándar, ni había hecho una sola predicción que pudiera someterse a prueba mediante el experimento. La Supersimetría ordenaba que el Universo debería estar repleto de familias de partículas nuevas, entre ellas los selectrones (equivalente al electrón supersimétrico) o el fotino (equivalente al fotón).

Lo cierto es que, nada de lo predicho ha podido ser comprobado “todavía” pero, sin embargo, la belleza que conlleva la teoría de cuerdas es tal que nos induce a creer en ella y, sólo podemos pensar que no tenemos los medios necesarios para comprobar sus predicciones, con razón nos dice E. Witten que se trata de una teoría fuera de nuestro tiempo, las supercuerdas pertenecen al futuro y aparecieron antes por Azar.

Y, a todo esto, ¿Dónde están esas otras dimensiones?

emilio silvera