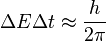Sep
18
¿La Mecçanica Cuántica? ¡Una “gran” Disciplina!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Mecánica cuántica ~
Clasificado en Mecánica cuántica ~
 Comments (0)
Comments (0)
Universo, Ciencia, Consciencia…¡Futuro!

Nos gusta especular con lo que hubiera sudo en el caso de que algunos sucesos no hubieran existidos, y, nuestra calenturienta imaginación, incluso ha pensado en que podríamos vivir en un mundo del revés.
¿Qué hubiera pasado sin la caída en la península del Yucatan de aquel meteorito que acabó con la vida de los dinosaurios, hubiéramos prosperado nosotros? Ese supuesto escenario te hace pensar que, de la misma manera, otros acontecimientos como la erupción e volcanes (por ejemplo), aunque ha causado desastres a nivel local, también ha regenerado la zona y ha sembrado la región de nueva sabia de la que, más tarde, floreció la vida.
El “principio antrópico”

¿Estaría programada la presencia de los seres vivos inteligentes en el Universo?
Por fuerza la cosmología conduce a cuestiones fronterizas entre ciencia experimental, filosofía y religión. No es solo el caso de los sabios antiguos. También los físicos de hoy se plantean preguntas de esa clase, sobre todo a propósito del llamado “principio antrópico”. A partir de los conocimientos actuales, este principio señala que las leyes y magnitudes físicas fundamentales parecen cuidadosamente afinadas para que la formación y el desarrollo del universo pudieran dar lugar a la vida en la Tierra y en otros planetas idóneos para acogerla.
Sep
12
Aportacion a la IX edición del Carnaval de Física
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Mecánica cuántica ~
Clasificado en Mecánica cuántica ~
 Comments (0)
Comments (0)

“La Teoría cuántica, una aproximación al Universo probable”
La teoría cuántica es un ejemplo de talento que debemos al físico alemán Max Planck (1.858 – 1.947) que, en el año 1.900 para explicar la emisión de radiación de cuerpo negro de cuerpos calientes, dijo que la energía se emite en cuantos, cada uno de los cuales tiene una energía igual a hv, donde h es la constante de Planck (E = hv o ħ = h/2π) y v es la frecuencia de la radiación. Esta teoría condujo a la teoría moderna de la interacción entre materia y radiación conocida como mecánica cuántica, que generaliza y reemplaza a la mecánica clásica y a la teoría electromagnética de Maxwell. En la teoría cuántica no relativista se supone que las partículas no son creadas ni destruidas, que se mueven despacio con respecto a la velocidad de la luz y que tienen una masa que no cambia con la velocidad. Estas suposiciones se aplican a los fenómenos atómicos y moleculares y a algunos aspectos de la física nuclear. La teoría cuántica relativista se aplica a partículas que viajan cerca de la velocidad de la luz, como por ejemplo, el fotón.
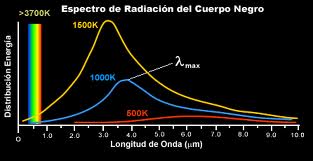
Por haberlo mencionado antes me veo obligado a explicar brevemente el significado de “cuerpo negro”, que está referido a un cuerpo hipotético que absorbe toda la radiación que incide sobre él. Tiene, por tanto, una absortancia y una emisividad de 1. Mientras que un auténtico cuerpo negro es un concepto imaginario, un pequeño agujero en la pared de un recinto a temperatura uniforme es la mejor aproximación que se puede tener de él en la práctica.
La radiación de cuerpo negro es la radiación electromagnética emitida por un cuerpo negro. Se extiende sobre todo el rango de longitudes de onda y la distribución de energía sobre este rango tiene una forma característica con un máximo en una cierta longitud de onda, desplazándose a longitudes de onda más cortas al aumento de temperaturas (ley de desplazamiento de Wien).

No puedo continuar adelante sin explicar aquí lo que son las partículas elementales como “constituyentes fundamentales” de toda la materia del universo.
Hasta el descubrimiento del electrón por J. J. Thomson en 1.897, se pensaba que los átomos eran los constituyentes fundamentales de la materia, como había postulado 400 años a. de C. Demócrito de Abdera. Pero el hallazgo de Thomson, junto al de Rutherford del núcleo atómico y del protón en 1.911, hizo evidente que los átomos no eran elementales, en el sentido de que tienen estructura interna. El descubrimiento de Chadwick del neutrón en 1.932 completó el modelo atómico basado en el núcleo atómico consistente en protones y neutrones rodeados de un número suficiente de electrones como para equilibrar la carga nuclear.
Sin embargo, no explicaba la gran estabilidad del núcleo, que claramente no podía mantenerse unido por una interacción electromagnética, pues el neutrón no tiene carga eléctrica. En 1.935, Yukawa sugirió que la fuerza de intercambio que lo mantenía junto estaba mediada por partículas de vida corta, llamadas mesones, que saltaban de un protón a un neutrón y hacia atrás de nuevo. Este concepto dio lugar al descubrimiento de las interacciones fuertes y de las interacciones débiles, dando un total de cuatro interacciones fundamentales.
También dio lugar al descubrimiento de unas 200 partículas “elementales” de vida corta, algunas de las cuales eran claramente más elementales que las otras. En la clasificación actual existen dos clases principales de partículas
| Leptones: | Electrón, muón, tau y sus neutrinos, que interaccionan tanto con las interacciones electromagnéticas como con la interacción débil y que no tienen estructura interna aparente. | |
| Hadrones: | Bariones: | Protones, neutrones, lambda, signa, omega. |
| Mesones: | Piones, kaones, etc. | |
que interaccionan con la interacción fuerte y tienen una estructura interna compleja.
La estructura hadrónica está basada ahora en el concepto de quarks de Murray Gell-Mann, introducido en 1.964. Este modelo nos dice que los hadrones están divididos en bariones (que se desintegran en protones) y mesones, que se desintegran en leptones y fotones.
Los bariones están formados por tres quarks y los mesones por dos quarks (un quark y un antiquark). En la teoría quark, por tanto, las únicas partículas elementales realmente, son los leptones y los quarks. Al contrario que los electrones y protones, que poseen cargas exactamente iguales en valor absoluto pero de signos opuestos (positiva el protón y negativa el electrón), los quark tienen cargas que son fracciones de la carga electrónica (+ 2/3 ó -1/3 de la carga electrónica).

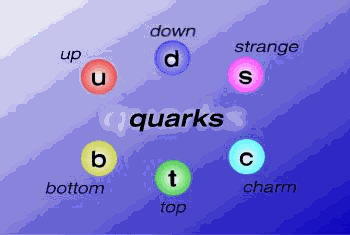
Los quarks aparecen en seis variedades distintas que generalmente se escriben mediante las letras u, d, c, s, t y b que responden a los nombres de up, down, charmed, strange, top y bottom.
El protón, siendo un barión, está constituido por tres quarks, uud (2/3 + 2/3 – 1/3 = 1) y el neutrón por udd (2/3 – 1/3 -1/3 = 0), para cada variedad de quark existen los equivalentes antiquarks que se denotan , que tienen valores exactos al quark pero con signos opuestos en su carga eléctrica.
Para evitar conflictos con el principio de exclusión de Pauli, se han añadido conceptos de carga de color a las seis variedades de quarks, cuya explicación al resultar compleja obviamos por no ser fundamental en la meta que aquí perseguimos.
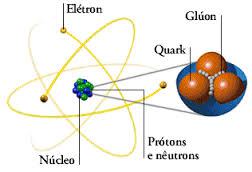
ña fuerza nuclear fuerte actúa al contrario de las otras fuerzas, es decir, aumenta con la distancia (como un muebçlle de acero que se estira), su misión es la de mantener a los Quarks juntos para dar estabilidad a los nucleones (protones y neutrones).
Las interacciones fuertes entre quarks se pueden entender por el intercambio de ocho partículas sin carga y sin masa en reposo, llamadas gluones (porque pegan a los quarks juntos). Aunque los gluones, como los fotones que realizan una función similar entre los leptones, no tienen carga eléctrica, sí que tienen una carga de color (también aquí nos paramos para no enredar demasiado y confundir al lector).
La teoría quark completamente elaborada esta ahora bien establecida por evidencias experimentales, pero como ni los quarks ni los gluones han sido identificados nunca en experimentos, la teoría no se puede decir que haya sido directamente verificada. Los quarks individuales pueden tener la curiosa propiedad de ser mucho más masivos que los hadrones que usualmente forman (debido a la enorme energía potencial que tendrían cuando se separan), y algunos teóricos creen que es, en consecuencia, imposible desde un punto de vista fundamental, que existan aislados. Sin embargo, algunos experimentales han anunciado resultados consistentes con la presencia de cargas fraccionarias, que tendrían los quarks no ligados y en estados libres.
emilio silvera
Jul
10
El enigma maravilloso de los cuantos
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Mecánica cuántica ~
Clasificado en Mecánica cuántica ~
 Comments (0)
Comments (0)
Podríamos decir sin temor a equivocarnos que la Física del siglo XX empezó exactamente en el año 1900, cuando el físico Max Planck propuso, en un artículo de ocho páginas, una posible solución a un problema que había estado intrigando a los físicos durante muchos años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menos intensidad, por los objetos más fríos.
“Todo cuerpo emite energía en forma de ondas electromagnéticas, siendo esta radiación, que se emite incluso en el vacío, tanto más intensa es más elevada la temperatura del emisor. … Los cuerpos no emiten con igual intensidad a todas las frecuencias o longitudes de onda, sino que siguen la ley de Planck.”
Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la Naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calos, la así llamada “termodinámica”, o al menos eso parecía. Pero si usamos las leyes de la termodinámica para calcular la intensidad de la radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantiodad infinita de radiación en el ultravioleta más lejano, y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para longitudes menores.
Esta longitud característica es inversamente proporcional a la temperatura absoluta del objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273 ºC bajo cero). Cuando a 1.000 ºC un objeto se pone al “rojo vivo” (arriba en la imagen), el objeto está radiando en la zona de la luz visible.
![</p>
<div class='bookmark'>
<table align='left' border='0' cellpadding='0' width='100%'>
<tr><td><span class='pushbutton'><a href='http://delicious.com/post?url=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F&title=El+enigma+maravilloso+de+los+cuantos' title='Delicious' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/delicious.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://digg.com/submit?url=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F&title=El+enigma+maravilloso+de+los+cuantos' title='Digg' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/digg.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://www.google.com/bookmarks/mark?op=edit&bkmk=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F&title=El+enigma+maravilloso+de+los+cuantos' title='Google' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/google.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://myweb2.search.yahoo.com/myresults/bookmarklet?u=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F&t=El+enigma+maravilloso+de+los+cuantos' title='Yahoo' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/yahoo.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://www.technorati.com/faves?add=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F' title='Technorati' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/technorati.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://meneame.net/submit.php?url=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F' title='Meneame' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/meneame.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://enchilame.com/submit.php?url=http://www.emiliosilveravazquez.com/blog/2020/07/10/el-enigma-maravilloso-de-los-cuantos-2/' target='_blank' rel='nofollow'><img title='Enchilame' src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/enchilame.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://www.blinklist.com/index.php?Action=Blink/addblink.php&Description=&Url=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F&title=El+enigma+maravilloso+de+los+cuantos' title='BlinkList' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/blinklist.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://reddit.com/submit?url=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F&title=El+enigma+maravilloso+de+los+cuantos' title='Reddit' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/reddit.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://www.tecnologiadiaria.com/2009/07/abrir-com-hotmail-correo.html' target='_blank' title='hotmail'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/linklove.png' alt='hotmail correo' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://bitacoras.com/votar/anotacion/externo/mini/www.emiliosilveravazquez.com/blog/2020/07/10/el-enigma-maravilloso-de-los-cuantos-2/' title='Bitacoras.com' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/bitacoras.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://www.wikio.es/vote?url=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F' title='Wikio' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/wikio.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://friendfeed.com/?url=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F&title=El+enigma+maravilloso+de+los+cuantos' title='Friend Feed' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/friendfeed.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://www.facebook.com/share.php?u=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F&t=El+enigma+maravilloso+de+los+cuantos' title='Facebook' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/facebook.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://twitter.com/home?status=El+enigma+maravilloso+de+los+cuantos: http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F' title='Twitter' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/twitter.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span class='pushbutton'><a href='http://www.feedburner.com/fb/a/emailFlare?itemTitle=El+enigma+maravilloso+de+los+cuantos&uri=http%3A%2F%2Fwww.emiliosilveravazquez.com%2Fblog%2F2020%2F07%2F10%2Fel-enigma-maravilloso-de-los-cuantos-2%2F' title='Enviar por Email' target='_blank' rel='nofollow'><img src='http://www.emiliosilveravazquez.com/blog/wp-content/plugins/knxdt-bookmarks-wordpress-plugin/images/email.png' alt='' class='book_img' border='none' style='margin:1px; padding: 0;' /></a></span><span style='font-weight:bold; padding-left: 5px;'><a href='http://wordpress.org/extend/plugins/knxdt-bookmarks-wordpress-plugin/' title='Plugin' rel='nofollow' target='_blank'>[?]</a></span></td></tr></table><br/><br/></div> </div>
<!--
<rdf:RDF xmlns:rdf=](https://www.aulafacil.com/uploads/cursos/5843/20101_cuerpnegro.es.png)
Mar
4
Más allá del Modelo Estándar
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Mecánica cuántica ~
Clasificado en Mecánica cuántica ~
 Comments (0)
Comments (0)
T. Kaluza
Las dimensiones mas altas fueron introducidas en una teoría unificada por primera vez en 1919, en Alemania, por Theodor Kaluza. Kaluza le escribió a Einstein sugiriéndole que su sueño de hallar una teoría unificada de la gravitación y el electromagnetismo podía realizarse si elaboraba sus ecuaciones en un espaciotiempo de cinco dimensiones. Einstein al principio se burlo de la idea, mas tarde, pensando y estudiando la sugerencia con mas frialdad y examen mas profundo, lo reconsideró y ayudo a Kaluza a que pudiera publicar su articulo.
Oskar Klein
Pocos años mas tarde, el físico sueco Oskar Klein publico una version del de Kaluza que lo mejoraba dejando un diseño matemático mas fino, de mas calidad y que explicaba de manera mas contundente lo que la teoría quería significar al elevar la teoría a cinco dimensiones y lograr unificar la gravedad con el magnetismo. Desde entonces, la teoría es conocida como de Kaluza-Klein y, aunque parecía muy interesante, en realidad nadie sabia que con ella hasta los años setenta, cuando resulto beneficioso trabajar en la supersimetria.
Pronto Kaluza-Klein estuvo en los labios de todo el mundo (los físicos mas destacados del hablaron de esa teoría). Aunque la teoría de cuerdas en particular y la supersimetría en general apelaban a mas dimensiones, las cuerdas tenían un modo de seleccionar su dimensionalidad requerida. Pronto se hizo evidente que la teoría de cuerdas solo seria eficaz en, diez, once y veintiséis dimensiones, y solo invocaba dos posibles grupos de simetría: SO(32) o E8 x E8. Cuando una teoría apunta algo tan tajantemente, los científicos prestan atención, y a finales de los años ochenta había muchos físicos que trabajaban en “las cuerdas”.

El Modelo estándar se nos quedó pequeño, iremos más lejos
La cuerda es cuántica y gravitatoria, de sus entrañas surge, por arte de magia, la partícula mensajera de la fuerza de gravedad: el gravitón. Funde de natural las dos teorías físicas más poderosas de que disponemos, la mecánica cuántica y la relatividad general, y se convierte en supercuerda -con mayores grados de libertad- es capaz de describir bosones y fermiones, partículas de fuerza y de materia. La simple vibración de una cuerda infinitesimal podría unificar todas la fuerzas y partículas fundamentales.
Parece que todo está hecho de cuerdas, incluso el espacio y el tiempo podrían emerger de las relaciones, más o menos complejas, cuerdas vibrantes. La materia-materia, que tocamos y nos parece tan sólida y compacta, ya sabíamos que está conformada por grandes espacios vacíos, pero no imaginábamos que era tan sutil como una cuerda de energía vibrando. Los átomos, las galaxias, los agujeros negros, todo son marañas de cuerdas y supercuerdas vibrando en diez u once dimensiones espaciotemporales.
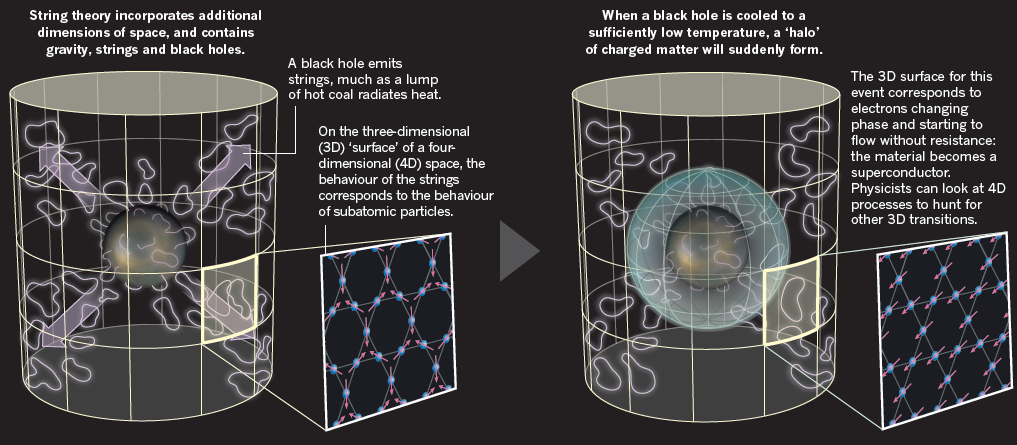
Lo cierto es que, andamos un poco perdidos y no pocos físicos (no sabemos si de forma interesada), insisten una y otra vez, en cuestiones que parecen no llevar a ninguna parte y que, según las imposibilidades que nos presentan esos caminos, ¿no sería conveniente elegir otros derroteros para indagar nuevas físicas mientras tanto?, para dejar que avanzasen las tecnologías, se adquieran más potentes y nuevas formas de energías que nos puedan permitir llegar a sondear las cuerdas y poder vislumbrar si es cierto, que puedan existir esas cuerdas vibrantes que, con sus resonancias crean las partículas y la materia.


Nos queda mucho poder oír las vibraciones de esas “cuerdas” que la física trata de encontrar, y, mientras tanto, oiremos vibrar esas otras que nos ofrece el violín en las manos expertos del músico con experiencia. Mientras tanto, esas otras cuerdas cuya existencia intuimos y soñamos, si es cierto que están ahí, seguirán silenciosas vibrando y creando materia a partir de esa ínfima sustancia que no hemos podido observar… ¡por el momento!
Quedaba mucho y duro trabajo por hacer, pero las perspectivas eran brillantes. y, de entre todos ellos, los mas destacados fueron Schwarz y sus colaboradores en supercuerdas Green y Edward Witten. Ellos fueron los artífices de un gran periodo de aventura intelectual que desembocó en la más moderna versión de la teoría de cuerdas que elaboro E. Witten con el de Teoría M. Esta teoría de más altas dimensiones nos ha llevado a una enorme profundidad matemática en el campo de la topología y, desde luego, ha dejado un panorama muy optimista en el horizonte.

Tal optimismo, luego, podría ser equivocado, ya que, de momento, solo contamos con el aparato teórico de la teoría y su verificación experimental se nos escapa al requerir disponer de la energía de Planck de 1019 GeV para comprobarla y, de momento, dicha energía fuera del alcance humano.

nadie las ha podido ver, las imaginamos de mil maneras y, de las dimensiones extra nos imaginamos modelos que quieren (pero no pueden) significar esas dimensiones que no podemos contemplar en el Universo
Einstein, como todos sabeis, dedico buena de la segunda mitad de su vida a intentar hallar una teoría de campo unificada de la gravitación y el electromagnetismo, con expectativas populares tan altas que las ecuaciones de su labor en marcha eran expuestas en escaparates a lo largo de la Quinta Avenida de Nueva York, donde eran escudriñadas por multitud de curiosos que no las entendían. En aquel tiempo, Einstein desconocía que las matemáticas precisas desarrollar una teoria asi, aun no existían. De ahi su fracaso en el intento. Él paradógicamente, había ignorado los principios cuánticos, a pesar de haber sido uno de los padres de la teoría.
, retomemos las cuerdas. Los críticos del concepto de supercuerda señalaron que las afirmaciones sobre sus posibilidades se basaban casi enteramente en su belleza interna. La teoría no había siquiera repetido los logros del Modelo Estándar, ni había hecho ni una sola predicción que pudiera someterse a prueba mediante experimentos. Una teoría así, más que teoría era una gran conjetura a la que le quedaba mucho camino por andar.

Hemos podido ver otras muchas cosas …, ni fotinos ni selectrones han aparecido nunca
puedo admirar la imagen de un púlsar o un magnetar, me siento transportado a regiones lejanas del espacio en las que, ese magnetar o magnetoestrella (que es una estrella de neutrones alimentada con un campo magnético extremadamente fuerte y, simplemente se trata de una variedad de púlsar cuya característica principal es la expulsión, en un breve período -equivalente a la duración de un relámpago-, de enormes cantidades de alta energía en de rayos X y rayos gamma. ), ha surgido a partir de una estrella masiva y se ha conformado un extraño objeto exótico que nos produce sorpresa y admiración al ver como, a partir de una cosa totalmente diferente, por medio de transiciones de fase de diversa índole, se llega a formar otro objeto totalmente distinto del que fue.

“Mucha gente opina que si la supersimetría no se observa en el LHC del CERN, el modelo estándar se convertirá en una teoría aburrida y con pocas sorpresas. Todo lo contrario, hay muchos problemas en el modelo estándar para los que la supersimetría no aporta ninguna solución. La física de precisión de baja energía, que ya dio la sorpresa al descubrir que los neutrinos tienen masa en reposo, es un portal que permitirá acceder a física más allá del modelo estándar fuera del alcance de los grandes aceleradores de partículas. Parafraseando a Feynman “There’s Plenty of Room at the Bottom.”

La supersimetría ordenaba que el Universo debía contener familias enteras dee nuevas partículas, entre ellas “selectrones” (equivalente supersimétrico del electrón) y “fotinos” (equivalentes del fotón), pero no especificaba las masas hipotéticas de tales partículas. La ausencia de pruebas aducidas en búsquedas preliminares de partículas supersimétricas, como las realizadas en el acelerador PEP de Stanford y el PETRA de Hamburgo, por lo tanto no probaban nada; siempre se podia imaginar que las partículas eran demasiado masivas para ser producidas en esas maquinas y habría que esperar a otras mas adelantadas del futuro que, como el LHC, nos pueda sacar a la luz, algunas de esas partículas supersimétricas que confirmarían la teoría.



¡Fotinos y selectrones! ¿Dónde? El LHC con sus 14 TeV ha llegado (según nos cuentan) al Bosón de Higgs pero… ¡cuerdas!
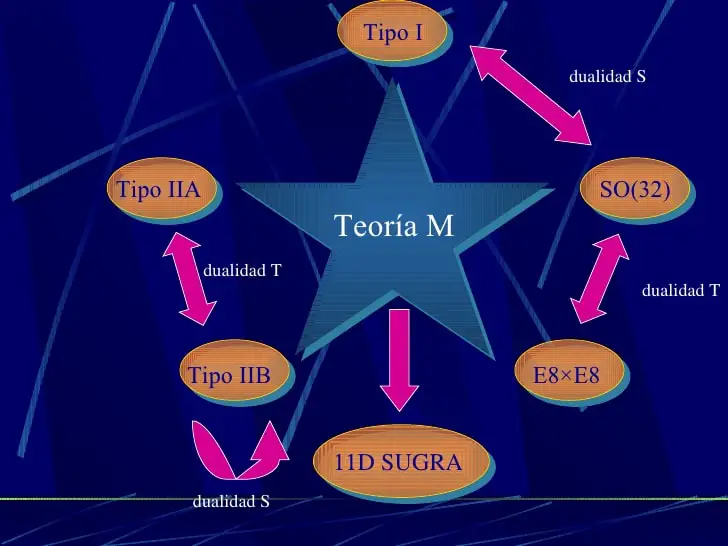
Cuando Edgar Witten expuso ante la Comunidad Científica su Teoría M, algunos escucharon extasiados sus explicaciones, otros no podían comprender lo que estaba diciendo pero, todos, sin excepción comprendieron que se había estrado en otro capítulo de la física que habría que verificar.
La Teoria M que antes mencionaba, es una version mas adelantada, en 11 dimensiones, nos ha dejado un cuadro que ilusiona y, luego, si finalmente se puede verificar lo que predice, estaríamos ante una teoría cuántica de la gravedad y, desde luego, nos explicaría el Universo como nunca antes se pudo hacer. Claro que, nosotros, pobres mortales e ignorantes, nos seguimos haciendo las mismas preguntas:
¿Donde, pues, hemos de buscar ese universo hiperdimensional de la simetría perfecta? El mundo en el que vivimos esta lleno de simetrías rotas, y solo tiene cuatro dimensiones. La respuesta llega de la Cosmología, la cual nos dice que el universo supersimétrico, si existió, pertenece al pasado. La implicación de esto es que el universo empezó en un de perfección simétrica, del que evoluciono al universo menos simétrico en el que vivimos. Si es así, la búsqueda de la simetría perfecta es la búsqueda del secreto del origen del universo, y la atención de sus acólitos puede, volverse con buenas razones, como las caras de las flores al alba, hacia la blanca luz de la génesis cósmica.
¡Nos queda tanto por saber!
emilio silvera
Jul
8
¡Fluctuaciones de vacío! ¿Que son?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Mecánica cuántica ~
Clasificado en Mecánica cuántica ~
 Comments (0)
Comments (0)
Un fuerte campo gravitatorio puede inducir un efecto desbocado en las fluctuaciones cuánticas que se producen en el espacio, aparentemente vacío, …
En física cuántica, la fluctuación cuántica es un cambio temporal en la cantidad de energía en un punto en el espacio como resultado del Principio de Incertidumbre que imaginó Werner Heisenberg. De acuerdo a una formulación de este principio energía y tiempo se relacionan de la siguiente forma:
Esto significa que la conservación de la energía puede parecer violada, pero sólo por breves lapsos. Esto permite la creación de pares partícula-antipartícula de partículas virtuales. El efecto de esas partículas es medible, por ejemplo, en la carga efectiva del electrón, diferente de su carga “desnuda”. En una formulación actual, la energía siempre se conserva, pero los estados propios del Hamiltoniano no son los mismos que los del operador del número de partículas, esto es, si está bien definida la energía del sistema no está bien definido el número de partículas del mismo, y viceversa, ya que estos dos operadores no conmutan.
Científicos lograron filmar por primera vez un electrón en movimiento gracias a una tecnología reciente que genera pulsos cortos e intensos de luz láser. A un electrón le toma 140 atosegundos
En un estudio realizado por un equipo de físicos con avanzados aparatos, han hallado un resultado del que nos dicen:
“La materia se construye sobre fundamentos frágiles. Los físicos acaban de confirmar que la materia, aparentemente sustancial, es en realidad nada más que fluctuaciones en el vació cuántico. Los investigadores simularon la frenética actividad que sucede en el interios de los protones y neutrones, que como sabéis son las partículas que aportan casi la totalidad de la masa a la materia común.
Cada protón (o neutrón) se compone de tres quarks – véase ilustración – pero las masas individuales de estos quarks apenas comprenden el 1% del total de la masa del protón¿Entonces de dónde sale el resto? La teoría sostiene que esta masa es creada por la fuerza que mantiene pegados a los quarks, y que se conoce como fuerza nuclear fuerte. En términos cuánticos, la fuerza fuerte es contenida por un campo de partículas virtuales llamadas gluones, las cuales irrumpen aleatoriamente en la existencia para desaparecer de nuevo. La energía de estas fluctuaciones del vacío debe sumarse a la masa total del neutróny del protón.”


Sus distintas formas no dejan de ser materia, y, las dudas que podamos tener sobre la luz que son fotones energéticos… ¿No dicen Einstein que la energía es materia y la materia energia (E=Mc2)?
Tiene y encierra tantos misterios la materia que estamos aún y años-luz de y conocer sobre su verdadera naturaleza. Es algo que vemos en sus distintas formas materiales que configuran y conforman todo lo material desde las partículas elementales hasta las montañas y los océanos. Unas veces está en estado “inerte” y otras, se eleva hasta la vida que incluso, en ocasiones, alcanza la consciencia de SER. Sin embargo, no acabamos de dilucidar de dónde viene su verdadero origen, su esencia, lo que era antes de “ser” materia. ¿Existe acaso una especie de sustancia cósmica anterior a la materia? Y, si realmente existe esa sustancia… ¿Dónde está?

Claro que hemos llegado a saber que las llamadas fluctuaciones del vacío son oscilaciones aleatorias, impredecibles e ineliminables de un campo de fuerza (electromagnético o gravitatorio) que son debidas a un “tira y afloja” en el que pequeñas regiones del espacio toman prestada, momentáneamente, energía de regiones adyacentes y luego las devuelven. Pero…
– ¿Qué regiones adyacentes?
Acaso universos paralelos, acaso defomraciones del espacio-tiempo a escalas microscópicas, micros agujeros negros que pasan a ser agujeros blancos salidos de estas regiones o campos de fuerza que no podemos ver pero sí sentir, y, en última instancia, ¿por qué se forman esas partículas virtuales que de inmediato se aniquilan y desaparecen antes de que puedan ser capturadas? ¿Qué sentido tiene todo eso?

No, no era este el vacío al que me quería referir
Las consecuencias de la existencia del cuanto mínimo de acción fueron revolucionarios para la comprensión del vacío. Mientras la continuidad de la acción clásica suponía un vacío plano, estable y “realmente” vacío, la discontinuidad que supone el cuanto nos dibuja un vacío inestable, en continuo cambio y muy lejos de poder ser considerado plano en las distancias atómicas y menores. El vacío cuántico es de todo menos vacío, en él la energía nunca puede quedar estabilizada en valor cero, está fluctuando sobre ese valor, continuamente se están creando y aniquilando todo tipo de partículas, llamadas por eso virtuales, en las que el producto de su energía por el tiempo de su existencia efímera es menor que el cuanto de acción. Se llaman fluctuaciones cuánticas del vacío y son las responsables de que exista un que lo inunda todo llamado campo de punto cero.

En nuestro Universo cualquier cosa puede surgir de una fluctuación de “Vacío”
Pero volvamos de nuevo a las fluctuaciones de vacío, que al igual que las ondas “reales” de energía positiva, están sujetas a las leyes de la dualidad onda/partícula; es decir, tienen tanto aspectos de onda como aspectos de partícula.
Las ondas fluctúan de forma aleatoria e impredecible, con energía positiva momentáneamente aquí, energía negativa momentáneamente allí, y energía cero en promedio. El aspecto de partícula está incorporado en el concepto de partículas virtuales, es decir, partículas que pueden nacer en pares (dos partículas a un tiempo), viviendo temporalmente de la energía fluctuacional tomada prestada de regiones “vecinas” del , y que luego se aniquilan y desaparecen, devolviendo la energía a esas regiones “vecinas”. Si hablamos de fluctuaciones electromagnéticas del vacío, las partículas virtuales son fotones virtuales; en el caso de fluctuaciones de la gravedad en el vacío, son gravitones virtuales.
De las llamadas fluctuaciones de vacío pueden surgir, partículas virtuales y quién sabe que cosas más… Hasta un nuevo Universo.

Son muchas las preguntas que no tienen respuestas
Parece que las fluctiuaciones ocurren en cualquier lugar, pero que, son tan minúsculas que ningún observador o experimentador las ha detectado de una manera franca hasta la fecha y, se sabe que están ahí por experimentos que lo han confirmado. Estas fluctuaciones son más poderosas cuanto menos escala se considera en el espacio y, por debajo de la longitud de Planck-Wheeler las fluctuaciones de vacío son tan enormes que el espacio tal como lo conocemos “pareciera estar hirviendo” para convertirse en una especie de espuma cuántica que parece que en realidad, cubre todo el espacio “vacío cuántico” que sabemos que está ahí y es el campo del que surgen esas partículas virtuales que antes menccionaba.

¿Espuma cuántica? Si profundizamos mucho en la materia… Podríamos ver otro universo distinto al nuestro. Las cosas miles de millones de veces más pequeñas que en nuestro mundo cotidiano, no parecen las mismas cosas.
Hay magnitudes asociadas con las leyes de la gravedad cuántica. La longitud de Planck-Wheeler, ![]() es la escala de longitud por debajo de la cual el tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro. ¡Qué locura!
es la escala de longitud por debajo de la cual el tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro. ¡Qué locura!

Como tantas veces hemos comentado, los trabajos que se han realizado sobre poder construir una teoría cuántica de la gravedad nos llevan a un sorprendente de implicaciones. Por un lado, sólo se ha podido conceptuar a la gravedad cuántica, siempre y cuando, el universo tenga más de cuatro dimensiones. Además, se llega a considerar que en la era de Planck, tanto el universo como la gravedad pudieron ser una sola cosa compacta estructurada por objetos cuánticos infinitamente diminutos, como los que suponemos que conforman las supercuerdas. A esta escala, el mismísimo espaciotiempo estaría sometido a imprescindibles fluctuaciones muy semejantes a las que causan las partículas al nacer y desaparecer de la existencia en el espaciotiempo ordinario. Esta noción ha conducido a los teóricos a describir el universo de la era cuántica como una especie de extremadamente densa y agitada espuma que pudo haber contenido las vibrantes cuerdecillas que propugnan los cosmólogos cuerdistas.
Los físicos especulan que el cosmos ha crecido a desde una «nada» primigenia que al nacer comenzó el principio del tiempo y que, en ese parto, contenía toda la materia y toda la energía.

En física como en todas las demás disciplinas científicas, los conocimientos avanzan y las teorías que sostuvieron los cimientos de nuestros conocimientos se van haciendo viejas y van teniendo que ser reforzadas con las nuevas y más poderosas “vigas” de las nuevas ideas y los nuevos hallazgos científicos que hacen posible ir perfeccionando lo que ya teníamos.
Recientemente se han alzado algunas voces contra el Principio de Incertidumbre de Heisenberg. He podido leer en un artíoculo de la prestigiosa Revista Nature, un artículo del premio Nobel de Física Gerald ´t Hoofft, en el que propone que la naturaleza probabilistica de la mecánica cuántica, desaparecería a la escala de Planck, en la que el comportamiento de la materia sería determinista; a longitudes mayores, energías más pequeñas.
El mundo de lo muy pequeño (el micro espacio), a nivel atómico y subatómico, es el dominio de la física cuántica, así nunca podríamos saber, de acuerdo m con el principio de incertidumbre, y, en un momento determinado, la posición y el estado de una partícula. Este estado podría ser una función de la escala espacio-temporal. A esta escala tamaños todo sucede demasiado deprisa para nosotros.

El “universo cuántico” nada es lo que parece a primera vista, allí entramos en otro mundo que en nada, se parece al nuestro.
Cuando hablamos de la mecánica cuántica, tenemos mirar un poco hacia atrás en el tiempo y podremos darnos del gran impacto que tuvo en el devenir del mundo desde que, en nuestras vidas, apareció el átomo y, más tarde, sus contenidos. Los nombres de Planck, Einstein, Bohr, Heisenberg, Schrödinger, Pauli, Bardeen, Roentgen, Dirac y muchos otros, se pudieron a la cabeza de la lista de las personas más famosas. Aquel primer premio Nobel de Física otorgado en 1900 a Roentgen por descubrir los rayos X, en el mismo año llegaría el ¡cuanto! De Planck que inspiró a Einstein para su trabajo sobre el Efecto fotoeléctrico que también, le valdría el Nobel, y, a partir de ese momento, se desencadenó una especie de alucinante por saber sobre el átomo, sus contenidos, y, de qué estaba hecha la materia.
Einstein-Podolsky-Rosen

El “entrelazamiento cuántico” es una extraña característica de la mecánica cuántica que permite determinar o modificar el estado de una partícula -a distancia y de forma instantánea- operando sobre otra. Esta correlación, que no tiene contrapartida en el mundo de nuestras experiencias cotidianas, fue abordada por físicos de la talla de Albert Einstein. Justamente, un experimento mental propuesto por el autor de la Teoría de la Relatividad dio lugar, en 1935, a la denominada “Paradoja de Einstein-Podolsky-Rosen”(o EPR).
La conocida como Paradoja EPR y los conceptos de Tiempo y , presente, pasado y futuro.
“Nadie ha resuelto la paradoja del gato de Schroedinger, ni la paradoja de Einstein-Podolsky-Rosen. El principio de incertidumbre no se ha explicado y se asume como un dogma, lo mismo pasa con el spin. El spin no es un giro pero es un giro. Aquí hay un desafío al pensamiento humano. ¡Aquí hay una aventura del pensamiento!”“El experimento planteado por EPR consiste en dos partículas que interactuaron de alguna forma en el pasado y que quedan vinculadas por este entrelazamiento cuántico. Dos observadores, alejados entre si, reciben cada una de las partículas. Si un observador mide el momento de una de ellas, sabe cuál es el momento de la otra. Si mide la posición, puede saber la posición de la otra partícula de forma instantánea, lo que contradice el sentido común y genera la paradoja EPR.Este resultado está en contradicción con la teoría de la relatividad, ya que se transmite información de forma instantánea entre las dos partículas. Hasta el año 1964, este debate se mantuvo en la órbita de la filosofía de la ciencia.Pero ese año John Bell, un físico irlandés, propuso una forma matemática para poder verificar la paradoja EPR, gracias a un refinado análisis de las sutilezas que involucra el entrelazamiento. Bell pudo deducir unas desigualdades asumiendo que el proceso de medición en mecánica cuántica obedece a leyes deterministas. Si Einstein tenía razón, las desigualdades de Bell son ciertas y la teoría cuántica es incompleta. Si la teoría cuántica es completa, entonces estas desigualdades serán violadas. Dejando de lado el enredo matemático detrás del razonamiento de Bell, lo que puso felices a los científicos fue hecho de disponer de una herramienta que les ayudaría a dilucidar esta paradoja.”
¿Qué es y en qué consiste el entrelazamiento cuántico? Esta increíble propiedad de la física más pequeña inquietó a Einstein hasta el día de su muerte. Pero también es la base de la computación y el teletransporte cuántico.
Fueron muchas las polémicas desatadas a cuenta de las aparentes incongruencias de la moderna Mecánica Cuántica. La paradoja de Einstein-Podolsky-Rosen, denominada “Paradoja EPR”, trata de un experimento mental propuesto por Albert Einstein, Boris Podolsky y Nathan Rosen en 1935. Es relevante, pues pone de manifiesto un problema aparente de la mecánica cuántica, y en las décadas siguientes se dedicaron múltiples esfuerzos a desarrollarla y resolverla.
A Einstein (y a muchos otros científicos), la idea del entrelazamiento cuántico le resultaba extremadamente perturbadora. Esta particular característica de la mecánica cuántica permite preparar estados de dos o más partículas en los cuales es imposible obtener útil sobre el estado total del sistema haciendo sólo mediciones sobre una de las partículas.

Por otro lado, en un entrelazado, manipulando una de las partículas, se puede modificar el estado total. Es decir, operando sobre una de las partículas se puede modificar el estado de la otra a distancia de manera instantánea. Esto habla de una correlación entre las dos partículas que no tiene paralaje en el mundo de nuestras experiencias cotidianas. Cabe enfatizar pues que cuando se mide el estado de una partícula, enseguida sabemos el estado de la otra, lo cual aparentemente es instantáneo, es decir, sin importar las distancias a las que se encuentren las partículas, una de la otra, ambas saben instantáneamente el estado de la otra.
El experimento planteado por EPR consiste en dos partículas que interactuaron en el pasado y que quedan en un estado entrelazado. Dos observadores reciben cada una de las partículas. Si un observador mide el momento de una de ellas, sabe cuál es el momento de la otra. Si mide la posición, gracias al entrelazamiento cuántico y al principio de incertidumbre, puede la posición de la otra partícula de forma instantánea, lo que contradice el sentido común.

Animación que muestra dos átomos de oxígeno fusionándose para formar una molécula de O2 en su estado cuántico fundamental. Las nubes de color representan los orbitales atómicos. Los orbitales 2s y 2p de cada átomo se combinan para formar los orbitales σ y π de la molécula, que la mantienen unida. Los orbitales 1s, más interiores, no se combinan y permiten distinguir a cada núcleo. Lo que ocurre a escalas tan pequeñas es fascienante.
Si nos pudiéramos convertir en electrones, por ejemplo, sabríamos dónde y cómo estamos en cada momento y podríamos ver asombrados, todo lo que estaba ocurriendo a nuestro alrededor que, entonces sí, veríamos transcurrir a un ritmo más lento del que podemos detectar en los electrones desde nuestro macroestado espacio temporal. El electrón, bajo nuestro punto de vista se mueve alrededor del núcleo atómico a una velocidad de 7 millones de km/h.
A medida que se asciende en la escala de tamaños, hasta el tiempo se va ajustando a esta escala, los objetos, a medida que se hacen mayores se mueven más despacio y, además, tienen más duración que los pequeños objetos infinitesimales del micro mundo cuántico. La vida media de un neutron es de unos 15 minutos, por ejemplo, mientras que la vida media de una estrellas se puede contar en miles de millones de años.
En nuestra macroescala, los acontecimientos y ,los objetos se mueven a velocidades que a nosotros nos parecen normales. Si se mueven con demasiada lentitud nos parece que no se mueven. Así hablamos de escala de tiempo geológico, para referirnos al tiempo y velocidad de la mayor parte de los acontecimientos geológicos que afectan a la Tierra, el tiempo transcurre aquí en millones de años y nosotros ni lo apreciamos; nos parece que todo está inmóvil. Nosotros, los humanos, funcionamos en la escala de años (tiempo biológico).

El Tiempo Cosmológico es aún mucho más dilatado y los objetos cósmicos (mundos, estrellas y galaxias), tienen una mayor duración aunque su movimiento puede ser muy rápido debido a la inmensidad del espacio universal en el que se mueven. La Tierra, por ejemplo, orbita alrededor del Sol a una velocidad media de 30 Km/s., y, el Sol, se desplaza por la Galaxia a una velocidad de 270 km/s. Y, además, se puede incrementar el tiempo y el espacio en su andadura al estar inmersos y ligados en una misma maya elñástica.
Así, el espacio dentro de un átomo, es muy pequeño; dentro de una célula, es algo mayor; dentro de un animal, mayor aún y así sucesivamente… hasta llegar a los enormes espaciosa que separan las estrellas y las galaxias en el Universo.

Distancias astronómicas separan a las estrellas entre sí, a las galaxias dentro del cúmulo, y a los cúmulos en los supercúmulos.
Las distancias que separan a los objetos del Cosmos se tienen que medir con unidades espaciales, tal es su inmensa magnitud que, nuestras mentes, aunque podamos hablar de ellas de manera cotidiana, en realidad, no han llegado a asimilarlas.Y, a todo ésto, los físicos han intentado con denuedo elaborar una teoría completa de la gravedad que incluya la mecánica cuántica. Los cálculos de la mayoría de las teorías propuesta de la «gravedad cuántica» arrojan numerosos infinitos. Los físicos no están seguros si el problema es técnico o conceptual. No obstante, incluso prescindiendo de una teoría completa de gravedad cuántica, se puede deducir que los efectos de la teoría cuántica, habrían cruciales durante los primeros 10-43 segundos del inicio del universo, cuando éste tenía una densidad de 1093 gramos por centímetro cúbico y mayor. (El plomo sólido tiene una densidad de aproximadamente diez gramos por centímetro cúbico.) Este período, que es el que corresponde a la era de Planck, y a su estudio se le llama cosmología cuántica. Como el universo en su totalidad habría estado sujeto a grandes incertidumbres y fluctuaciones durante la era de Planck o era cuántica, con la materia y la energía apareciendo y desapareciendo de un vacío en grandes cantidades, el concepto de un principio del universo podría no tener un significado bien definido. En todo caso, la densidad del universo durante este período es de tal magnitud que escapa a nuestra comprensión. Para propósitos prácticos, la era cuántica podría considerarse el estado inicial, o principio, del universo. En consecuencia, los procesos cuánticos ocurridos durante este período, cualquiera sea su naturaleza, determinaron las iniciales del universo.

Una cosa nos ha podido quedar clara: Los científicos para lograr conocer la estructura del universo a su escala más grande, deben retroceder en el tiempo, centrando sus teorías en el momento en que todo comenzó. Para ello, como todos sabeis, se han formulado distintas teorías unificadoras de las cuatro fuerzas de la naturaleza, con las cuales se han modelado acontecimiento y en el universo primitivo casi a todo lo largo del camino hasta el principio. Pero cómo se supone que debió haber habido un «antes», aparece una barrera que impide ir más allá de una frontera que se halla fijada a los 10-43 [s] después del Big Bang, un instante conocido como «momento de Planck», en homenaje al físico alemán Max Planck.
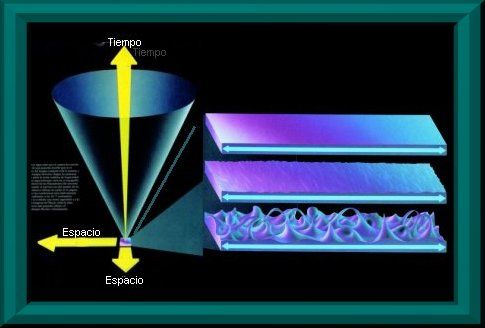
Esta barrera existe debido a que antes del momento de Planck, durante el período llamado la «era de Planck o cuántica», se supone que las cuatro fuerza fundamentales conocidas de la naturaleza eran indistinguibles o se hallaban unificadas , que era una sola fuerza. Aunque los físicos han diseñado teorías cuánticas que unen tres de las fuerzas, una por una, a través de eras que se remontan al momento de Planck, hasta ahora les ha prácticamente imposible armonizar las leyes de la teoría cuántica con la gravedad de la relatividad de Einstein, en un sólo modelo teórico ampliamente convincente y con posibilidades claras de ser contrastado en experimentos de laboratorio y, mucho menos, con observaciones.
Y después de todo ésto, sólo una caso me queda clara: ¡Lo poco que sabemos! A pesar de la mucha imaginación que ponemos en las cosas que creemos conocer.
emilio silvera
















 Totales: 69.196.397
Totales: 69.196.397 Conectados: 19
Conectados: 19