Dic
11
Creando parcelas del saber: ¡Datación!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (0)
Comments (0)
Es curioso como nuestra imaginación ha ido creando parcelas del saber para desvelar misterios bien guardados por la Naturaleza, y, uno de ellos es el tiempo de las cosas muy antiguas y fósiles del pasado profundamente enterrados a los que tenemos que buscar sus fechas de nacimiento.

Los radioisótopos son átomos inherentemente inestables que se desintegran espontáneamente en elementos descendientes estables con tasas que pueden medirse con precisión en el laboratorio. Por tanto, si determinamos la cantidad de isótopo radiactivo progenitor que ha desaparecido del mineral con el tiempo, o la cantidad de isótopo descendiente que se ha acumulado, podemos calcular la edad del mineral. Curiosamente, lo que se mantiene constante en la desintegración radiactiva es la proporción de radioisótopo que se desintegra en un intervalo de tiempo determinado, y no el número de átomos que se desintegran. Por tanto, a medida que disminuye con el tiempo la abundancia de un isótopo radiactivo en un mineral, la tasa absoluta de desaparición del elemento también disminuye. El ritmo de desintegración de un isótopo radiactivo se denomina vida media, y se define como el tiempo necesario para que la mitad del radioisótopo de un material se desintegre en otro elemento.

Fue un filósofo griego de la escuela eleática, nacido en Elea (Italia meridional). Fue discípulo de Parménides (uno de los filósofos griegos más importantes de la época y de los más señalados en la escuela eleática) y, según varios escritores, enseñó en Atenas durante algún tiempo. Zenón trató de mostrar que la realidad es una e invariable y que todo movimiento es ilusorio.
Era costumbre suya mostrar lo absurdo de algunas creencias y frecuentemente se valía de paradojas (expresión o situación que parece absurda y sin embargo es razonable), en las que viene a decir que todo movimiento es un engaño.
Contrastadas con la realidad, las pruebas de Zenón contra el movimiento, se revelan al punto como paradojas y como auténticos paralogismos (argumento o contradicción falsa). Es como ponerse a discutir el azul del cielo.

Los que conozcan bien los clásicos habrán recordado la paradoja de Zenón en la que Aquiles persigue a una liebre (¿O, era una tortuga?). Como héroe que es, Aquiles corre más rápido que su presa, y cada minuto que pasa acorta a la mitad la distancia entre ambos. ¿Cuándo alcanzará Aquiles a la liebre? La respuesta, naturalmente, es nunca, porque si la liebre se mueve a una velocidad constante, entonces Aquiles debe disminuir constantemente la suya. Si al principio lleva una desventaja de doscientos metros, puede correr doscientos metros en el primer minuto contra los cien de la liebre, pero en el segundo minuto avanzará sólo 150 metros, y en el cuarto apenas 112,5 m. Nótese que si conocemos la distancia recorrida por Aquiles y el modo como varía su velocidad de acuerdo con la distancia que media entre él y la liebre, podemos inferir cuánto tiempo lleva dedicado a esa frustrante persecución. En esencia, así es como funciona la datación radiométrica.

Lugares de alunizaje de las misiones Apolo
Por si te lo estás preguntando, la edad de estas rocas se determinó, como sucede con las muestras terrestres, utilizando la datación radiométrica , es decir, midiendo la concentración de isótopos inestables respecto a la de los productos en los que se desintegran — seguro que conoces la datación de muestras mediante el carbono-14; en el caso de las rocas el sistema es el mismo, con la diferencia de que la vida media del carbono-14 es de unos 5 700 años (de modo que sirve para datar muestras recientes), mientras que en el caso de las rocas se utilizan otros isótopos, como el uranio-235 (con una vida media de unos 700 millones de años) y el uranio-238 (cuya vida media es de unos 4 500 millones de años).
El sistema de datación radiométrica más conocido es el proporcionado por el ¹⁴C, o Carbono 14, un isótopo raro del Carbono que se produce de forma natural por acción de los rayos cósmicos y antropogénicamente por bombas nucleares. Se desintegra en Nitrógeno (¹⁴N) con una vida media de 5.730 años. Como el ¹⁴C es tan poco común (menos de uno de cada mil átomos de Carbono) y su vida media es tan corta, la Datación con radio carbono queda limitada a los últimos cien mil años, aproximadamente.



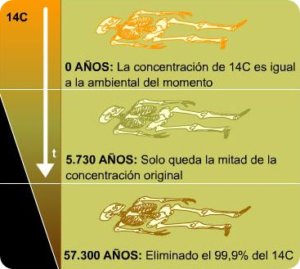
En los materiales más antiguos simplemente no queda suficiente ¹⁴C para que pueda medirse con precisión. Por consiguiente, el ¹⁴C proporciona una herramienta de datación valiosa para egiptólogos o para paleontólogos interesados en mamuts lanudos, pero no sirve para desentrañar la historia profunda de la Tierra.
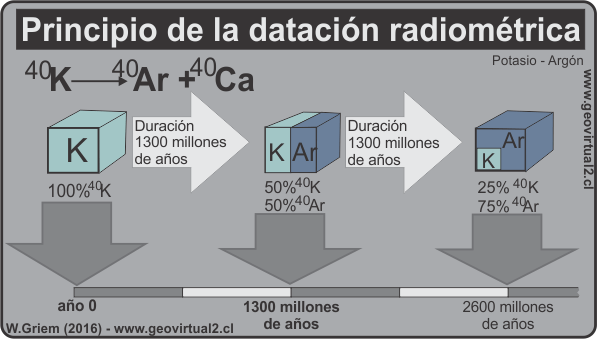
Datación Potasio-Argón
Este método se usa para datar sedimentos volcánicos y se basa en la desintegración del elemento radiactivo del Potasio 40 en el gas inerte del Argón 40. Este último es un gas que está en las rocas y que se libera al calentarlo. En el momento de una colada volcánica no hay Potasio 40, pero empieza a generarse poco después. La muestra se analiza en el laboratorio y midiendo la cantidad de Potasio 40 y de Argón 40 y estableciendo la relación entre ambas medidas, se obtiene la datación. Este método permite datar muestras de hasta 30 millones años y es muy útil en disciplinas como la arqueología.
Para datar sucesos más lejanos y arcaicos necesitamos un reloj más importante: un radioisótopo cuya vida media se mide en muchos millones de años, incluso miles de millones de años. El Potasio 40 (⁴⁰K) se identificó inicialmente como un candidato prometedor para la geocronología. Este isótopo inestable se desintegra formando o bien Calcio (⁴⁰ Ca), que desafortunadamente no puede distinguirse de los iones de calcio ya presentes en el mineral, o bien Argón (⁴⁰ Ar), que si puede distinguirse.
La vida media del ⁴⁰K es de 1.250 millones de años. Además el Potasio es abundante y está ampliamente distribuido en los minerales que forman las rocas: está presente en los feldespatos que tiñen de rosa los granitos, en los minerales microscópicos de las cenizas volcánicas y en arcillas que se forman durante la meteorización.
Pese a todas sus ventajas, el cronómetro de Potasio-Argón no es muy utilizado por los geólogos interesados en la Tierra antigua. El ⁴⁰K se comporta como un reloj, pero los procesos tectónicos y metamórficos se comportan como niños deseosos de juguetear con sus agujas.
Sucesos geológicos ocurridos mucho después de la formación del mineral pueden eliminar el Argón de éste, lo que equivale a poner el reloj a cero, y por tanto, a destruir la memoria química del tiempo transcurrido. (El Argón, un gas noble, sólo queda ligeramente ligado a las redes químicas de los minerales).
Lo que realmente necesitamos para datar las rocas muy antiguas es un sistema que funcione como las “cajas negras” de los aviones: un isótopo que no se pierda fácilmente de un mineral, y un mineral que no se altere fácilmente.

Formas de cristales de circón para rocas de edad Pérmica
Los circones, unos minerales que contienen uranio y se encuentran en los granitos y otras rocas ígneas, son las cajas negras de la geología precámbrica. De hecho, el uranio enlazado a los a los cristales de circón en el momento de su formación nos proporciona dos cronómetros fiables: el ³²⁸U se desintegra en Plomo 206 (²⁰⁶ Pb) con una vida media de más de 4.500 millones de años (la edad de la Tierra), mientras que el isótopo ²³⁵U, menos abundante, se desintegra en ²⁰⁷ Pb con una vida media de algo más de 600 millones de años. Esta peculiaridad nos permite verificar por dos métodos las edades medidas: si los dos relojes dan una edad distinta es que el circón ha sufrido alguna alteración.

Los indestructibles circones
Izquierda: Cristal de circón visto bajo el microscopio petrográfico (fuente: commons.wikimedia.org).
Derecha: Cristal de circón visto a simple vista (autor: Ángel Luis Esteban).

La Tierra tiene aproximadamente 4.600 millones de años. Entre los 3.500 y los 555 millones se estimaba que había habido únicamente bacterias, organismos unicelulares y formas de vida primitiva como la de las esponjas (de todos ellos existen rastros fósiles).
Si el circón tiene algún problema, es que es demasiado inalterable. A diferencia de otros muchos minerales, los circones pueden completar el ciclo completo de rocas –desde la cristalización en una roca ígnea hasta el metamorfismo y posterior erosión hasta formar partículas de sedimento-, sin perder un ápice de su integridad química. Tanto es así que durante su ascenso a través de la corteza de la Tierra, el magma puede arrancar circones de rocas adyacentes, incorporando minerales (y por tanto, relojes) más antiguos en rocas más recientes. Además, los circones pueden crecer durante cada tránsito por el interior de la Tierra; los circones arcaicos (anterior al Proterozoico) pueden presentar hasta media docena de capas alrededor de un núcleo central, cada una de las cuales es el producto de la acreción durante un evento geológico específico.


El método de Datación nos ha facilitado el saber la edad de los fósiles hallados
Bueno, sólo quería dejar aquí un comentario sencillo que aclarara, de alguna manera, el tema de la Datación que nos puede hablar del tiempo de determinadas rocas y de fósiles allí presentes que nos hablan de la vida primigenia en nuestro planeta desde hace miles de millones de años.
emilio silvera
Abr
1
¡El Universo y Nosotros! ¿Sabremos algún día la verdadera relación?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (1)
Comments (1)

Max Planck nos decía:
“La ciencia no puede resolver el misterio final de la Naturaleza. Y esto se debe a que, en el último análisis, nosotros somos parte del misterio que estamos tratando de resolver”.
Y, desde luego, no parece que fuese muy desencaminado, nuestra complejidad es tan grande que, llegar a comprendernos, no será nada fácil.


Las respuestas están en nuestras Mentes, sólo hay que saber buscar
¿Quién no ha tenido alguna vez, la sensación de que sabe la respuesta ? ¿De que todo está ahí, en su mente, escondido y a punto de salir a la superficie? Esas sensaciones que parecen querer hablarnos, contarnos ese secreto tan largamente perseguido por muchos y no desvelado por ninguno. Sin embargo, ese momento es efímero y, lo mismo que llegó, se fue. La frustración que deja en nosotros esa sensación de tener ese algo a mano y de que se nos esfume y desaparezca sin más, es verdaderamente…dolorosa.
Bueno, a mí me pasa continuamente, siento que de un momento a otro, mi mente, me daría respuestas a preguntas que no han sido contestadas. El tiempo inexorable pasa y, las respuestas no llegan. ¡Qué impotencia! Parece como si una gran Nebulosa ocupara nuestra mente y todo lo tuviera envuelto en una espesa niebla que no nos deja ver lo que buscamos.

Imagino que, de vez en cuando, la niebla se ve despejada por alguna especie de “viento solar” dejando ver lo que allí está presente. En algunas mentes, entonces, saltan esas respuestas (Newton, Planck, Einstein y otros) y son ofrecidas al mundo para que puedan continuar avanzando.

Los aspectos inconscientes de la actividad mental, como las rutinas motoras y cognitivas, así como los recuerdos, intenciones y expectativas inconscientes, las preocupaciones y los estados de ánimos, desempeñan un papel fundamental a la hora de conformar y dirigir nuestras experiencias conscientes. Todo está siempre estrechamente relacionado, nada ocurre en nosotros que no esté unido a lo que pasa en nuestro entorno, somos una parte de un todo que se llama Universo, y, aún cuando somos autónomos en el pensamiento y en la manera de obrar, existen condicionantes exteriores que inciden, de una u otra manera en nosotros, en lo que somos.

Sin la fuerza de Gravedad, nuestras mentes serían diferentes (o no serían), estamos estrechamente conectados a las fuerzas que rigen el Cosmos y, precisamente, somos como somos, porque las fuerzas fundamentales de la Naturaleza, son como son y hacen posible la vida y la existencia de seres pensantes y evolucionados que son capaces de tener conciencia de SER, de hacer preguntas tales como: ¿de donde venimos? ¿Hacia donde vamos?

La qualia y la discriminación, correlatos neuronales de la percepción del color, ¿un grupo neuronal, un quale?, los gualia y el núcleo dinámico, los qualia en el tiempo neuronal, el desarrollo de los qualia: referencia al propio yo, lo consciente y lo inconsciente, los puertos de entrada y de salida, los bucles largos y rutinas cognitivas, aprendizaje por el estudio y la experiencia, rupturas talamocorticales: posibilidades de núcleos escindidos, la observación, el lenguaje, el pensamiento, los mensajes exteriores, la unificación de datos y la selección lógica de respuestas, y, por fin: el significado último de las cosas (las preguntas de la filosofía), la metafísica.
Sí, por todas estas fases del estudio y del pensamiento he tenido que pasar para llegar a una simple conclusión:
No pocas veces, nuestra imaginación nos juega malas trastadas y nos hace ver… ¡Lo que ya no somos!
“No somos la imagen de nadie” y, simplemente, como seres que evolucionamos, sin que nos demos cuenta, mutamos y nos adaptamos al medio cambiante y, mientras eso ocurre, llegan mensajes que no comprendemos a la primera. No, no exagero, dentro de esa imagen de frágil físico y de escasa capacidad para poder dar respuesta a ciertas preguntas, en realidad, se esconden cualidades y potenciales que, no sabemos ni podemos medir. En realidad, somos una compleja estructura de pensamientos que puede llegar…muy lejos.
Dentro de nuestro ser están todas las respuestas y solo necesitamos tiempo para encontrarlas. Nuestra mente, es la energía del Universo, aún no sabemos utilizarla y pasaran, posiblemente, millones de años hasta que estemos preparados para saber lo que en realidad, es la conciencia.
Mientras eso llega, algunos curiosos como yo, con más voluntad que conocimientos, tratan de especular con ideas y conceptos que nos puedan dar alguna luz sobre tan complicado problema. Nuestra mente es una maravilla de la Naturaleza, algo tan grande que, a pesar de los muchos avances y conocimientos alcanzados, no podemos explicar… aún.
Está claro que, como me ha comentado un amigo, la materia tiene memoria y, es precisamente esa memoria, la que hace posible el avance de nuestros conocimientos a través de la mente que, sin duda, está directamente conectada con el resto del Universo y las fuerzas que lo gobiernan que son las que hacen posible su funcionamiento tal como acontece.

La curiosidad y la sabiduría, esas gotas del transcurrir del tiempo que salpican el río de la vida a través de la experiencia y nos hace saber… ¡Algunas cosas!
Pero nada es tan sencillo ni podemos hablar de lo sensorial sin tener en cuenta el plano más simple y cotidiano que está referido a la materia, a nuestro cuerpo, las sensaciones, las experiencias, lo que aprendemos, el estudio y la profunda observación que nos lleva de la mano de la curiosidad hasta la fuente de la que mana el agua de la sabiduría.
Entender las claves que explican el devenir de la vida sobre este planeta, con la idea en el horizonte de aspiraciones intelectuales a que nos aboca la conciencia del SER, no resulta fácil, la complejidad de la empresa exige tener en cuenta múltiples factores que no siempre estamos preparados para comprender, y, sobre todo, debemos ser muy conscientes de que formamos parte de un Universo inmenso, y, estamos supeditamos a las fuerzas que lo rigen. Lo mejor para hacer nuestras vidas más fáciles, es tratar de comprender la Naturaleza de ese Universo nuestro.
Sí, el Universo podría ser considerado como la mayor “Obra de Arte” que, a su vez, es capaz de generar otras Obras de Arte que, en alguna ocasión, dan mucho que pensar, ya que, el surgir de la vida partiendo del simple hidrógeno que evoluciona en las estrellas del cielo…es ¡Increíble! pero, sin embargo, nada más cierto hay.
¡La Vida! Siempre me llamó la atención y elevó el grado de curiosidad ese gran misterio que llamamos ¡vida!, y, cada vez que he tenido la oportunidad, no me he perdido el poder aprender alguna cosa sobre ella. Ya os he contado en otras ocasiones mi experiencia con la eminente y privilegiada mente de…
Lynn Margulis comenzó a explorar los caminos de la genética a partir de un libro escrito en el siglo XIX por Edmund B.Webs. En ese texto encontró reflexiones sobre la herencia citoplasmática y datos sobre las bacterias, entonces no muy consideradas en el estudio del origen de la vida.
Lynn Margulis fue una importante e influyente bióloga estadounidense. Además de ser una de las madres del evolucionismo, aportó notables conocimientos a la ciencia, como por ejemplo, su teoría de la aparición de las células eucariotas, o la de la simbio-génesis, por nombrar solo algunas.
La doctora Margulis fue profesora del Departamento de Geociencias de la Universidad de Massachusselts (Estados Unidos) relacionó el papel de las bacterias con la microbiología, una ciencia surgida de la medicina, de la salud pública y del procedimiento seguido para procesar los alimentos. De ahí saltó al estudio del tema que ocupa su curso magistral: Contribución de los microbios a la evolución.

El pequeño Monasterio franciscano de La Rábida en Huelva, dónde Colón fue acogido por los frailes y se fraguó el viaje a Las Américas. La zona está enclavada en un margen del Río Odiel y los terrenos de de Bosques y Pinares con senderos para pasear.

Junto al Monasterio se levanta un enorme obelisco que fue construido en conmemoración del cuarto centenario del nuevo continente y, en su interior, como podéis ver arriba, existen obras pictóricas conmemorativas de la gesta que pintó Daniel Vázquez Díaz. El monasterio tipológicamente pertenece al Gótico-Mudéjar incorporado a la Rábida desde el período Almohade.

La iglesia-Santuario es de dimensiones pequeñas y estructura compacta posee una sola nave y un hermoso artesonado de influencia mudéjar que cubre la bóveda primitiva. El ábside posee arcos apuntados. En las paredes conserva pinturas de Juan de Dios realizadas en el Siglo XVIII que tratan temas de la vida de San Francisco.

Si las piedras pudiera hablar ¿Qué nos contarían estas?
El claustro del Monasterio de la Rábida es pequeño y sigue el modelo de San Isidoro y Guadalupe: estilo mudéjar. Se amplió en el siglo XVII con un cuerpo superior y se le incorporaron almenas como protección de invasiones.
Tiene en sus paredes frescos del siglo XV que han sido restauradas. El claustro estuvo punto de desaparecer en 1855 por la desamortización, y salvado el conjunto por el Gobernador Alonso. Es uno de los monumentos mas importantes y significativos en la historia de España y de América, fue declarado primer monumento histórico de los pueblos Hispanos y en 1856 fue declarado el tercer monumento nacional y patrimonio de la humanidad.

Me desvío del tema. Muy cerca del entorno, junto al Monasterio, está la Sede de la Universidad Internacional Iberoamericana de La Rábida, en la que, se imparten Cursos de verano y se acogen a grandes personalidades en los distintos campos del saber que dan conferencias muy apreciadas. Aquí, en el pasado no muy lejano, tuve la suerte de asistir a una de Lynn Margulis y pude hablar con ella que respondió a mis preguntas con amabilidad y sabiduría.
Ella centraba el curso en la enorme importancia que tenían los microbios para nosotros, no siempre bien valorados. Los microbios pueden ser definidos como organismos que no podemos ver a simple vista y, la cultura popular dice que tan sólo sirven de agentes para canalizar enfermedades, pero esa apreciación conlleva un error muy serio. Por ejemplo: el 10% del peso del cuerpo humano en seco está compuesto por microbios, sin los cuales no podemos vivir ni siquiera un día. Ellos asumen tareas tan importantes como la de generar el oxígeno del aire que precisamos para respirar. Además, tienen un papel fundamental en la evolución de la vida: todos los seres vivos considerados simples –animales, plantas, hongos, etc.- están hechos de microbios en combinación simbiótica con otros organismos. Se trata de una historia que se aleja en el pasado hasta 3.500 millones de años en el curso de la vida sobre la superficie de nuestro planeta: La Tierra.
Los conceptos que maneja y esgrime la doctora en genética, están encuadrados en una visión totalmente contradictoria con la religión y otros muchos conceptos culturales.
Pregunté a la doctora Margulis si la mala imagen de los microbios nacía de un estudio deficiente de la microbiología, o si simplemente surgía a partir de tópicos sin fundamentos. Su contestación fue:
“La asociación de esos pequeños organismos con aspectos negativos se explica por el origen de su estudio científico, que siempre estuvo relacionado con descubrimientos ligados a la investigación en torno a enfermedades. Junto a esta idea, lo cierto es que pensamos en formas ideales que corresponden al esquema platónico de hace casi 30 siglos, cuando en realidad no existen tales ideas sino organismos que interaccionan con el medio ambiente en el que se encuentran. Esta colaboración recibe el nombre de ecología. De hecho, el concepto de independencia no tiene sentido en este campo: al margen de los microbios moriríamos inmediatamente”.
Nos creemos lo contrario pero, siempre seremos aprendices, no tenemos tiempo para más
Aquel día, como casi todos los días de mi vida, aprendí cosas nuevas y muy interesantes que me confirmaron que nuestras vidas, podrían ser cualquier cosa, menos simples. Es tal el nivel de complejidad implicado que, precisamente por eso, no somos capaces de explicarla al completo, solo vamos dominando parcelas limitadas que, algún día, al ser unidas, nos darán las respuesta.
En fin amigos, que como habréis podido deducir, aunque nuestras limitaciones nos impongan barreras, no debemos rendirnos ante ninguna de ellas y, si persistimos, finalmente encontraremos el camino de pasarlas para poder ir un poco más allá. Era Jhon Wheeler el que nos decía:
Claro que, si los conocimientos que vamos adquiriendo son continuados… Finalmente, ¿podríamos secar ese mar de ignorancia?
Pero, ¿Que tiene todo esto que ver con el título del trabajo? Bueno, lo único que puedo decir es que, nosotros… ¡También somos universo!
emilio silvera
Oct
20
El Saber del mundo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (1)
Comments (1)

No intentes ver la verdad sin conocer la mentira.

No sabrás lo que es la luz sin conocer las tinieblas.
Si no sabes de donde vienes no sabrás nunca quien eres.
Lo sé por experiencia, la dificultad, agudiza el ingenio… ¡La crisis también!

Mi padre me dijo una vez que, el respeto por la verdad es casi el fundamento de la moral.
Nada puede surgir de la “nada”, si surgió…, ¡es porque había!

A la edad de quince años, había aprendido a oír el silencio. En cualquier sitio, aunque no lo parezca, podemos “oír” lo que la Naturaleza nos dice.

La vida no es gratis, se nos da para pagarla. ¡De tantas maneras! Todos tenemos que llevar nuestra “carreta” para llegar al destino propuesto. Y, por lo general, no resulta nada fácil llegar al destino, se paga un alto precio.

Más vale un… por si acaso, que un… ¡yo creí!
¡Qué vida ésta!

En el Universo puede haber miles de millones de planetas. Si están habitados ¡Cuánto dolor y amargara! Y, si no lo están… ¡Que desperdicio de mundos!
En verdad, los seres humanos… ¡Son muy complejos! Y, hasta tal punto es así que, ni nosotros mismos llegaremos nunca a cocernos. ¿Cómo poder saber ese asombroso “milagro” de cien mil millones de neuronas gestando ideas, pensamientos y… ¡Sentimientos!

Siempre me ha llamado la atención el hecho de que, a lo largo de la historia, en cualquier parte del mundo, sin importar su condición u origen, de vez en cuando, surgieron personajes que, con sus hechos, dejaron señalado un camino que muchos siguieron y, de esa manera, ha ido caminando la Humanidad a lo largo de la Historia, influida por esas mentes que, en uno u otro ámbito del saber humano, abrieron los caminos a seguir. Muchos serían los ejemplos que podríamos poner aquí pero, hoy, dejaré una simple reseña de uno de ellos.
![]()
Pitágoras de Samos. 569 a.C. (Samos).475 a.C. (Tarento).
Pitágoras era hijo de un comerciante griego, por lo que viajó mucho de niño, acompañando a su padre. No se conocen muchos detalles de su infancia, pero es seguro que recibió buena educación. En Mileto, Tales y Anaximandro lo introdujeron en el mundo de las Matemáticas y le recomendaron ir a Egipto para profundizar en su estudio, lo que hizo en el 535 a.C. Estudió en el templo de Dióspolis.
Allí fue hecho prisionero hacia el 525 a.C. y llevado a Babilonia, de donde regresaría a Samos hacia el 520 a.C. Al regreso, fundó una escuela que llamó El Semicírculo. Al cabo de dos años se trasladó a Cretona, en el sur de Italia, donde fundó una escuela filosófica y religiosa que tuvo muchos seguidores.
Las enseñanzas principales decían que la realidad era matemática y que el estudio puede llevar a la purificación espiritual y la unión con la divino.
Creían que todo lo que existe son números y todas las relaciones podían reducirse a relaciones numéricas. Además, atribuían a cada número una propia personalidad (masculina o femenina, perfecta o incompleta, bella o fea).
Por ejemplo, el 10 era el número perfecto, pues contenía en sí mismo los cuatro primeros enteros (1 + 2 + 3 + 4 = 10).
La escuela exigía a sus miembros estricta lealtad y secretismo por lo que los conocimientos en Matemáticas producidos por ellos eran siempre atribuidos a Pitágoras, y no podemos saber qué descubrió él personalmente y qué se le atribuyó. Sin ir más lejos, el conocido teorema de Pitágoras (del que antes di un ejemplo) no lo descubrió él, sino que ya era conocido por los babilonios mil años antes, aunque puede que él fuese el primero en demostrarlo.
El objeto de estudio de esta escuela no eran las Matemáticas tal como las pensamos hoy, sino desde una perspectiva más filosófica. Se preocupaban de los principios en que se basan las Matemáticas, el significado de los conceptos número o círculo, así como qué ha de entenderse por demostración (de un teorema por ejemplo).
Son varios los teoremas debidos a Pitágoras o, más genéricamente, a los pitagóricos: el que afirma que la suma de los ángulos de un triángulo es igual a dos ángulos rectos, o el teorema de Pitágoras, esto es, que un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
También descubrieron los números irracionales –que no se pueden expresar como el cociente de dos enteros- y los cinco sólidos regulares: el tetraedro, el hexaedro o cubo, el octaedro, el dodecaedro y el icosaedro.
Aunque Pitágoras es uno de los matemáticos griegos más conocidos, a mí, no se porqué, me gusta más Euclides. Claro que a cada acontecimiento o a cada personaje, hay que valorarlo dentro del contexto de su obra en su época, en su “tiempo”.
El lenguaje, las matemáticas, la escritura,… son las cosas que nos hicieron distintos, partiendo siempre de la base de que teníamos los sentidos y la mente que requerían aquellos logros que nos separaron de los demás animales.
La lengua o el lenguaje, cuyos comienzos se limitan a sonidos guturales y sin sentido de aquellos primeros homínidos que, caminando ya erguidos, vivían más o menos en comunidad y, ello, les llevó, a inventarse un sistema arbitrario de signos que los miembros de una comunidad establecían por convención, con el fin de comunicarse, así fueron los principios del lenguaje que, en cada caso, en cada lugar, está relacionado con la psicología y antropología específica de los distintos pueblos, lo que llevó a que el lenguaje, tomado en su conjunto, sea multiforme y heteróclito, y conectado con lo físico-fisiológico-psíquico y dentro de un dominio individual y a la vez social.
El lenguaje hablado se quiso expresar mediante escritura, y, el comienzo, fueron dibujos, signos, jeroglíficos, etc., hasta alcanzar un alto nivel mediante las reglas inventadas para la escritura.
Otra forma de lenguaje
La importancia del lenguaje y la escritura para la humanidad no está bien valorada, pocos piensan en lo importante que fue el hecho ocurrido hace ya muchos miles de años, cuando aquel ser primitivo, pintó un animal en la pared de su cueva, allí, en aquel lugar, se dio el primer paso.
Mediante un conjunto de sonidos articulados podemos manifestar lo que pensamos y comunicarnos con los demás y, cada pueblo, tiene su propio lenguaje. Este hecho, el de distintas lenguas para cada región del mundo, expresa en realidad nuestro retraso en la evolución del lenguaje y en la de otros aspectos más generales que, algún día lejos aún en el futuro, nos llevarán a la unificación de todos y de todo en este planeta que pasará a ser una sola entidad ante el resto de civilizaciones que vendrán desde otros mundos pero, para que eso llegue…falta mucho.
emilio silvera
Ene
8
Alguien dijo hace mucho tiempo: “Todo es número”
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (11)
Comments (11)
¿Conocieron los antiguos constructores los secretos del Universo?

¿Conocían los antiguos egipcios hace miles de años la que hoy día se conoce como la fórmula más bella del Universo? Si esto fuera cierto representaría que los antiguos constructores debieron entender el Universo de forma geométrica, como (de hecho) apuntan todas las evidencias. Y es que la fórmula de Euler es pura geometría, y, como tal, representa el lenguaje más perfecto en que puede expresarse el Universo: el lenguaje numérico.
Déjame explicarte la ecuación de Euler en términos coloquiales para que entiendas como convergen todos los conceptos, como podemos conciliar el antiguo conocimiento con nuestra forma, radicalmente opuesta, de pensar. Para ello utilizaré un razonamiento previo que considero irrefutable, ya que se basa en la más pura lógica. Y después haremos arqueología matemática.
Una conjetura no es más que una afirmación que aún no hemos podido refutar, que no sabemos si es o no cierta. En su versión opuesta una conjetura también es una afirmación, para la que tampoco nunca hemos podido demostrar que no sea cierta. De hecho todas las evidencias en las más importantes conjeturas matemáticas, después de millones o billones de intentos o experimentos, nos hacen pensar que éstas son ciertas, pero que aún no hemos encontrado la manera de demostrarlo inequívocamente.

Todas las conjeturas que tenemos hoy día, al menos en el campo que denominamos “Teoría de Números” indican que los números siguen en su composición algún tipo de patrón organizado, que…, de alguna manera, parecen comunicarse entre ellos. La más famosa de todas, la Conjetura de Riemann establece, por ejemplo, que los números primos siguen un criterio de densidad en su comportamiento. Si esto fuera cierto denotaría que los números tendrían de forma subyacente un criterio inteligente que dictaminaría su distribución. Si todas ellas fueran correctas implicaría que los números, de forma independiente, tienen un criterio subyacente que es totalmente independiente de la manera en que nos refiramos a él. En otras palabras, dicho patrón sería incluso independiente de las matemáticas, una especie de código fuente que es intemporal o, en otras palabras, que siempre ha sido y será.
Todo en el Universo… ‘Son números!
Aunque suene antiguo decirlo, si todas esas conjeturas fueran ciertas, querría decir como pensaron los antiguos que los números son el Universo, pues siempre y en todo momento siguen un patrón organizado de comportamiento que es independiente incluso del espacio y del tiempo. Un patrón intemporal que siempre ha sido y será, y que siempre se cumplirá incluso en los extremos de nuestro Universo.
Por lo tanto si los números son intemporales e independientes de las matemáticas, podemos incluso prescindir de ellas y admirar la belleza conceptual (y visual) de la más pura identidad. Esta es la idea subyacente en este razonamiento.
La ecuación de Euler se considera (con permiso de Pitágoras) como la ecuación más bella de las matemáticas, sin ninguna duda. Keith Devlin se refirió a ella en los siguientes términos: “ Como un soneto de Shakespeare que capta la esencia del amor o un cuadro que saca a relucir la belleza de la forma, que es mucho más profundo que solo la piel, la ecuación de Euler llega a lo más profundo de la existencia”.
La ecuación de Euler “vive” en muchos mundos, es “algo” que trasciende al lenguaje matemático. Vamos a tratar de entender la ecuación de Euler desde su perspectiva más trascendente, desde una perspectiva más humana, para llegar a comprobar finalmente que la ecuación de Euler es capaz de conectar incluso nuestras conciencias, dando sentido a la existencia de un patrón espacio-temporal que nos dirá claramente que nunca podremos determinar lo que es o no real. Y es que este patrón es incluso capaz de determinar nuestra forma de pensar. Realmente se trata de una especie de “código fuente” universal.
Lo primero que hay que decir al respecto es que la ecuación de Euler no es una ecuación normal. En contra de las creencias no se trata de una fórmula ni de un teorema matemático. Todas estas ideas hacen referencia a la existencia de un criterio humano y racional, es decir algo que es consecuencia de nuestra forma de pensar. La ecuación de Euler va más allá, porque es independiente de todos nuestros criterios. Dicha ecuación es una identidad numérica que podemos calificar de universal e intemporal. Tan sólo necesitamos números (aunque sean irracionales) para describirla, no utiliza ninguna variable, ninguna x arbitraría, tan sólo utiliza números universales.
En cualquier unidad siempre podremos inscribir, por ejemplo, la divina proporción, pues este valor es totalmente independiente de cualquier unidad de medida, el gran hándicap de la física. Toda distancia unitaria puede ser siempre dividida entre la media y la extrema razón. La divina proporción hace referencia a un tipo de equilibrio matemático, pero que también podemos observar en el mundo real, en la propia naturaleza. A esta relación hicieron referencia los antiguos egipcios con el símbolo de la balanza, o… inscribiendo sus medidas en las pirámides de Egipto. Bajo este punto de vista unificado también podemos comparar a esta ecuación, incluso, con nuestra propia evolución. Es decir… ¿Conoció otra civilización anterior este patrón? Esta es la idea subyacente, establecer que la identidad de Euler se puede entender de muchas formas diferentes, porque es independiente incluso del lenguaje.

Las matemáticas reflejan conceptos, ideas mentales, ideas abstractas que tienen lugar en un espacio mental e imaginario. En este contexto el simbolismo es necesario, para mecanizar de forma más eficiente el lenguaje que empleamos. La geometría también puede ser vista como un lenguaje conceptual e imaginario. La geometría es la parte más sensitiva, la más directa de todas las ramas matemáticas y, como tal, constituye un efectivo lenguaje visual.
Los símbolos matemáticos, como sabemos, son creaciones humanas, sin embargo en algunos casos incluso su simbolismo es independiente de las matemáticas, constituyen un lenguaje por sí mismo. Se trata del lenguaje áureo, un lenguaje propio que tienen estos valores sagrados e irracionales que aparecen en la identidad de Euler.
Keith Devlin nos decía que la ecuación de Euler es como un soneto de Shakespeare. Y debe de ser correcto, sobre todo si hacemos referencia al más famoso de todos ellos: “Ser o no ser, esa es la cuestión”. A lo que añadiríamos que, en efecto, esto es correcto, sólo que incompleto, porque ser o no ser también puede ser la solución. De esta forma podríamos compatibilizar la causa con el efecto o, en otros términos, comprobar cómo el “Todo” siempre está contenido en la parte. En términos totalmente opuestos, sería algo así como admitir que los últimos serán los primeros.
Ser o no ser expresa la existencia de dos formas diferentes de entender la realidad, en esencia expresa la dualidad, la necesaria presencia de dos conceptos opuestos entre ellos. Es como si nos dijera que la existencia del mundo físico y real que podemos observar necesitara de la existencia de un mundo opuesto, un mundo material que podemos simbolizar matemáticamente y, por lo tanto, que es meramente conceptual. En otras palabras, que las ideas matemáticas pueblan el mundo del alma, como decía Platón.
La ecuación de Euler puede ser vista desde diferentes simbolismos, por lo que también es independiente incluso del simbolismo propiamente matemático. Así pues, libera tu mente, observa la Identidad de Euler de forma diferente. No la veas de forma lineal, como si de un simple teorema se tratará, vamos a ver cómo la ecuación de Euler es una ecuación multi-dimensional, la llave que abre la puerta a dimensiones diferentes, el patrón que impone un orden al ritmo de lo infinito y lo irracional. Una eterna verdad que nos dice claramente que todo está conectado como si fuera una unidad, nos dice cómo se conecta el mundo irracional y arbitrario con nuestra idea de un mundo determinado.
La esencia del problema de conectar dimensiones diferentes la Ecuación de Euler lo resuelve de una forma elegante e impecable y, a su vez, imposible de modificar, pues tan sólo se basa en la probabilidad. La ecuación de Euler nos dice que hay que apelar siempre a la regla universal: la dualidad que los opuestos representan. Piensa, por ejemplo, que un cuadro, como al que hacía referencia Devlin y la realidad sólo son dos concepciones diferentes de una misma existencia, que el cuadro no es más que el reflejo en el mundo inmaterial de las ideas, una especie de holograma, un reflejo de lo que vemos en el mundo “real”.
Los únicos valores en el infinito matemático que cumplen siempre la regla de la dualidad son los valores áureos o sagrados. Son los únicos que tienen la capacidad de moverse entre dos planos diferentes de la realidad: el plano real y el plano irracional o imaginario. Podemos decir nuevamente que sus formas siempre han sido y serán. Pongamos un ejemplo para cada uno de ellos para entenderlo mejor.
La divina proporción es el único valor matemático, cuyo valor (precisamente) coincide con el valor que representa su inversa. Realmente toda una incoherencia. Las matemáticas ocultan esta coincidencia, no le dan relevancia y relegan a una de las soluciones al plano de lo inexistente. Tan sólo la divina proporción, por tanto, es capaz de situarse a medio camino, realmente de forma equilibrada, entre el plano de lo que es real matemáticamente hablando y el plano opuesto, o el plano del (aparentemente) inexistente mundo imaginario. La divina proporción representa con exquisita perfección el concepto subyacente al número i, o número imaginario, la posibilidad de ser capaz de situarse en dos planos diferentes de la realidad.
Con pi pasa exactamente lo mismo. Pi es el único valor en el infinito matemático que puede dar lugar a la esfera tridimensional, una construcción matemática que situamos en una cuarta dimensión imaginaria.
Ricard Jiménez
Nov
16
El viaje interminable del saber
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (0)
Comments (0)
Desde nuestro pequeño mundo azul, situados en el lugar adecuado, podremos contemplar la inmensa Vía Láctea que nos alberga en un Sistema planetario donde, un Sol amarillo, es decir, una estrella corriente de la clase G2V, nos envía su luz y su calor para que, los seres vivos de la llamada Tierra, podamos continuar nuestra andadura por este pequeño mundo que nos cobija, y del que, desde tiempos inmemoriales, hemos podido obtener todo aquello que nos hizo falta para sobrevivir, no siempre en un ambiente agradable y placentero.

Pocas dudas nos pueden caber de que las dimensiones del Universo, sus escalas, no son Humanas. Nosotros comparado con nuestro propio mundo somos muy poca cosa, si lo hacemos en relación a la Vía Láctea, somo menos que un grano de arena en el desierto, y, si es el Universo el objeto de comparación… ¡Nuestra minúscula figura en ese inmenso contexto, se perdería, incluso de la vista del telescopio más potente.

Sin embargo, y a pesar de nuestra “hipotética” pequeñez, el Mundo, se nos ha quedado pequeño. Ya hace mucho tiempo desde que, nuestra especie, preparaba expediciones para conocer éste o aquel rincón del planeta, no ha quedado ninguna región por explorar y, el pie humano, ha pisado todos los terrenos firmes que imaginarnos podamos y surcado todos los mares y océanos del globo terrestre. Sólo nos queda la asignatura pendiente de los Abismos oceánicos que, por falta de tecnología, nos son desconocidos y también las maravillas que allí se esconde,
En el ámbito del Espacio Interestelar, todavía andamos muy retrasados y quizás, dentro de algunos cientos de años podamos andar entre las estrellas, lo que, por otra parte, nos será muy necesario si queremos que nuestra especie perdure.

Hemos llegado a saber con nuestros ingenios y conocimientos que, existen muchos mundos fuera de nuestro Sistema Solar, que la Vía láctea que tiene más de cien mil millones de estrellas, contiene múltiples sistemas planetarios donde infinidad de mundos, pueden, como la Tierra, tener las condiciones precisas para albergar la Vida.
Si tuviéramos una moderna nave espacial capacitada para recorrer la Galaxia, ¿qué veríamos?
Bueno, entre otras muchas maravillas nos daríamos cuenta de nuestra “pequeñez” en relación a una inmensa Galaxia que alberga más de cien mil millones de estrellas y en el que, el planeta que habitamos es menos que un granito de arena de la inmensa playa
çAh! Pero, de todas las maneras nos creemos importantes.

Pasado el Tiempo tendremos inmensos y modernos Puertos Espaciales desde los que despegarán modernas naves de tecnología inalcanzable hoy, que nos podrán llevar a efectuar recorridos de ensueño. La Humanidad depende de su entorno para la supervivencia, y, como en nuestro Universo eterno no hay nada, resulta que el Sol (la estrella que nos da la vida con su luz y su calor), tiene su fecha de caducidad antes de convertirse en una Gigante Rija primero y en una Enana Blanca después. Para cuando eso llegue, tendremos que poseer los conocimientos científicos necesarios para poder viajar a las estrellas.

No dentro de mucho tiempo, habrán pasado los tiempos en los que, en peligrosos cohetes, hicimos aquellos primeros viajes hacia el espacio exterior, cuando salir del planeta Tierra era jugarse la vida, ya que, los combustibles empleados eran rústicos y peligrosos.
Nuevos motores que consumirán energías hoy desconocidas nos llevarán a los confines del Cosmos.

Visitar los planetas y lunas de nuestro entorno no será ningún problema y, con los nuevos motores y sistemas de combustión, se habrán acabado los largos viajes de meses, y, las naves, llevarán sistemas de gravedad artificial que anulará la ingravidez, el material del que estarán hechas las naves, será inteligente y se auto reparará cuando un micrometeorito perfore el fuselaje. Estará provista de gravedad artificial, y será autosuficiente para abastecer las necesidades de cientos de viajeros.

Entonces sí, podremos acercarnos a las hermosas Nebulosas planetarias y, a pesar de su fuerte radiación, no sufriremos daño, la nave estará provista de escudos electromagnéticos impenetrables. Podremos ver a ojo desnudo las estrellas enanas blancas que llevan en su interior.
Lo que nuestra especie habrá logrado dentro de 500 años… ¡Hoy nos parecería magia!, aunque “mañana” será lo cotidiano pero, ese es el futuro que nunca podremos presenciar, es decir, el Presente de otros.
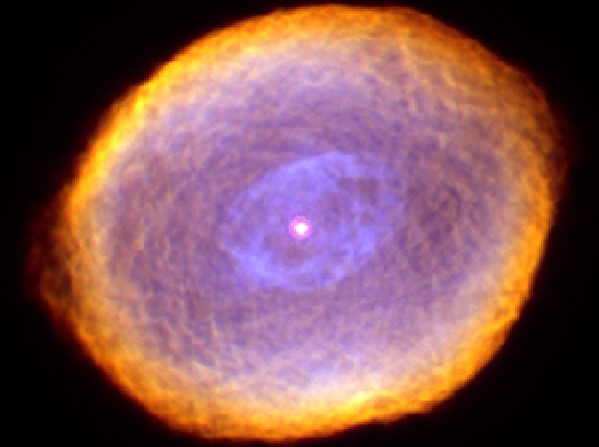
De la misma manera podremos acercarnos a lugares tan bellos como este y contemplar, maravillados como (dejando ahí los aparatos adecuados de toma de datos y grabación) a partir del gas y el polvo pueden surgir nuevas estrellas o nuevos mundos, y, con el tiempo, nuevas formas de vida.

Lugares como este que sobrepasa todo aquello que podamos imaginar, nos haría pensar y preguntarnos:
¿Quién sabe como podría ser aquella Nebulosa de la que surgió el Sistema Solar? ¿Sería como ésta que llaman, por su , del Capullo? Algunas veces me da que pensar nuestra presencia aquí, en el planeta Tierra y, con la imaginación, viajo hacia muy atrás en el tiempo, “veo” una estrella masiva que, llegado al final de su ciclo en la secuencia principal, expulsa sus capas exteriores de materia al espacio interestelar que, en ese momento, ha sido sembrado del gas y el polvo del que, millones, o miles de millones de años más tarde, surgiría nuestro Sistema Solar.
En el interior de nuestro cerebro encontramos conexiones sin fin, más de cien mil neuronas, como estrellas hay en la Vía Láctea, y, todas ellas (las neuronas) trabajan para que asimilemos los mensajes que nuestro entorno genera y que, captados por los sentidos, llegan al centro neurálgico para que los recicle y queden archivados para cuando los necesitemos.
Hay que ser conscientes de que, los seres vivos, son parte de este Universo que creó las condiciones necesarias para su presencia. La maravilla y el hecho más asombroso está, precisamente, en que a partir de la materia “inerte” se pudiera evolucionar hasta llegar a los pensamientos y sentimientos, un estado superior de consciencia que aún nadie ha podido explicar.
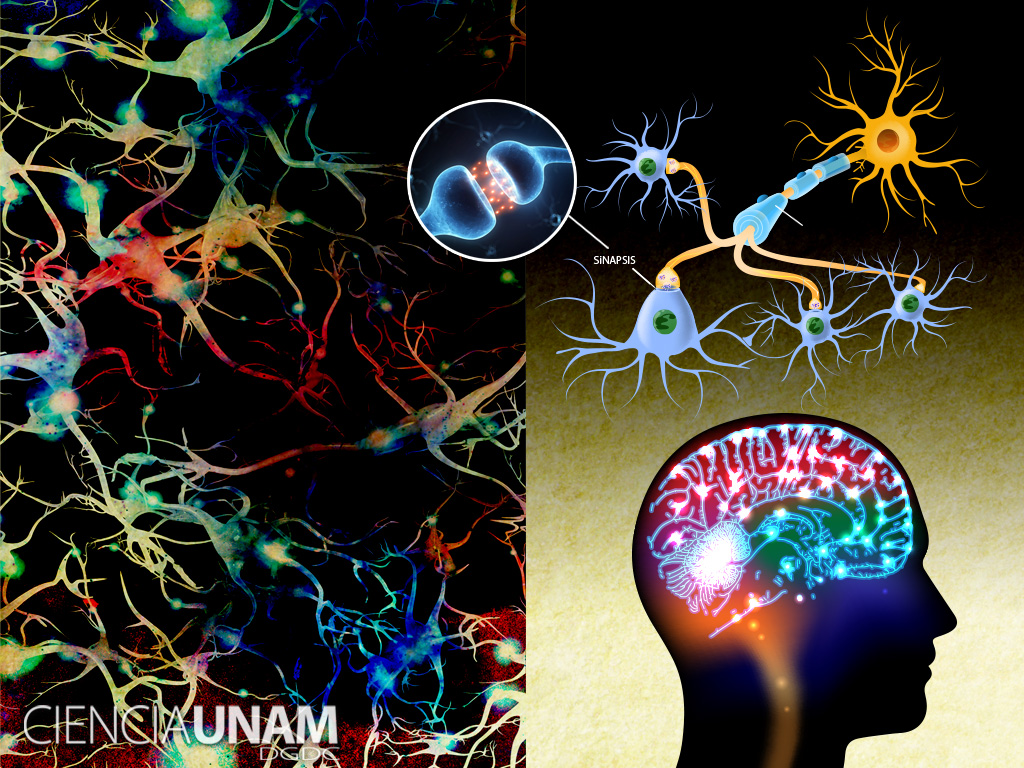
Si contáramos una sinapsis cada segundo, tardaríamos 32 millones de años en hacer el recuento. Si consideramos el número posible de circuitos neuronales, tenemos que habérnosla con cifras hiper.astronómicas: 10 seguido de al menos un millón de ceros (En comparación con el número de partículas del universo conocido que asciende a “tan sólo” 1079 es decir, es el número conocido como NEdd (Número de Eddintong), el Universo se quedará pequeño comparado con lo que nosotros llevamos dentro y podemos llegar a ser a pesar de nuestra engañosa pequeñez… ¡Lo más grande del Universo!
emilio silvera
















 Totales: 69.201.062
Totales: 69.201.062 Conectados: 47
Conectados: 47


























