Jul
24
Estructuración del Protoplasma vivo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (2)
Comments (2)
Estructuración del protoplasma de la Vida, uno de los muchos secretos que nos queda por desvelar y que la Naturaleza esconde con el celo propio de quién no quiere desvelar su intimidad más profunda y, al mismo tiempo compleja. ¿Qué podemos saber nosotros de tan maravilloso suceso?

En la Gran Nebulosa de Orión, también conocida como M42, y una de las nebulosas más famosas del cielo, podríamos encontrar ese Laboratorio natural en el que se cuecen los elementos que dan lugar a las sustancias necesarias para la aparición de la vida. Este producto de una explosión supernova, contiene todos los ingredientes necesarios para ello y, de este conglomerado de gas y polvo en el que están presentes átomos y moléculas diversas, se encuentra la fuente, no sólo de nuevas estrellas y nuevos mundos, sino que, también están ahí los materiales necesarios para el surgir de la vida.

Muchos fueron los parámetros que tuvieron que estar presentes para que, finalmente, la vida, hiciera acto de presencia en nuestro mundo, y, hasta que llegó a nuestra especie…
Muchas son las veces que aquí, en este lugar dedicado a distintas disciplinas de la Ciencia, hemos hablado de la Vida. Sin embargo, nunca nos hemos parado a explicar algunos de los procesos del origen de la vida, conociendo antes, aunque sea de manera sencilla y sin profundidad, aquellos principios básicos de la estructura del protoplasma, ese sustrato material que será la base de todos los seres vivos, sin excepción. Para poder alcanzar nuestro objetivo y así poder responder a la cuestión de la evolución y al proceso del origen de la vida, una de las fuentes que debemos conocer, es, sin duda alguna, el protoplasma y, la mejor explicación la encontré en el Libro de Alesandr Ivanovich Oparín, El Origen de la Vida que nos lo cuenta como como sigue:


Los primeros seres vivos (hasta donde sabemos), surgieron hace unos 3.800 millones de años según fósiles encontrados en las rocas más antiguas en Australia.
Desde el punto de vista evolutivo, los procariotas son el grupo de organismos más antiguos sobre la Tierra. Además, a pesar de su relativa simplicidad, los procariotas contemporáneos son los organismos más abundantes del mundo.
A finales del siglo XIX y principios del XX, había científicos que creían que los organismos sólo eran “máquinas vivientes” especiales, de estructuras muy complejas y, aseguraban que la estructura del protoplasma era algo así como una máquina, construido conforme a un determinado plan y que estaba formado por “vigas” y “tirantes” como si de un puente se tratara y que, de manera similar a éste, los lazos de unión tenían unida toda la estructura que, de esta manera, se mantenía firme, y, esa estructura de tan estricto orden en la colocación recíproca de las distintas partes del protoplasma, era precisamente, según ellos, la causa específica de la vida.

¿Será nuestro planeta como una gran célula viva con sus propias reglas biológicas?
Pero el estudio concreto del protoplasma desmintió esta teoría mecanicista. Fue probado que no existía ninguna estructura parecida a una máquina ni siquiera a las de máxima precisión, en el interior del protoplasma.
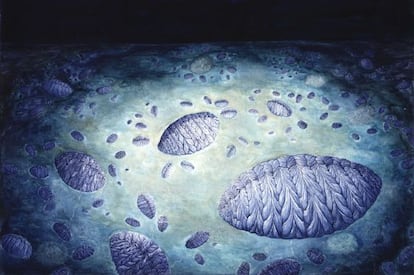
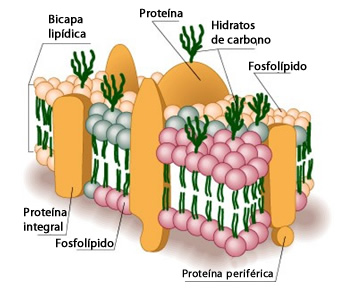
Es bien conocido que la masa básica del protoplasma es líquida; nos hallamos ante un coacervado complejo, constituido por una gran cantidad de sustancias orgánicas de un peso molecular considerable, entre estas destacan las proteínas y los lipoides. Por esta razón, se encuentran flotando a su libre albedrío en esa sustancia esencial y fundamental, partículas filamentosas coloides, quizás enormes moléculas proteínicas sueltas, y muy probablemente, auténticos enjambres de esas moléculas. El tamaño de las partículas es tan diminuto que no se distinguen ni a través de los microscopios actuales más sofisticados. Pero encontramos otros elementos visibles en el interior del protoplasma. Cuando las moléculas proteínicas y de otras sustancias se unen formando conglomerados, destacan en la masa protoplasmática en forma de pequeñas gotas, captadas a través del microscopio, o en forma de coágulos, con una determina estructura denominados elementos morfológicos. El núcleo, las plastídulas, las mitocondrias, etcétera.
Una célula es la unidad morfológica y funcional de todo ser vivo. De hecho, la célula es el elemento de menor tamaño que puede considerarse vivo. De este modo, puede clasificarse a los organismos vivos según el número de células que posean: si sólo tienen una, se les denomina unicelulares (como pueden ser los protozoos o las bacterias, organismos microscópicos); si poseen más, se les llama pluricelulares En estos últimos el número de células es variable: de unos pocos cientos, como en algunos nematodos, a cientos de billones (1014), como en el caso del ser humano.. Las células suelen poseer un tamaño de 10 μm y una masa de 1 ng, si bien existen células mucho mayores.

Estructuración del Protoplasma vivo
Estos elementos protoplasmáticos, observables a través del microscopio, son, esencialmente, una manifestación aparente y externa de determinadas relaciones de solubilidad, enormemente complejas, de las distintas sustancias que conforman el protoplasma y que se ha podido comprobar que tiene, un papel determinante, en el curso del proceso de la vida, que no se puede comparar de ningún modo con el papel que desempeña una máquina en su trabajo específico. Esto queda totalmente justificado por la sencilla razón de que una máquina y el protoplasma son dos sistemas distintos y contrarios.
Sin duda, lo que caracteriza la función de una máquina es el desplazamiento mecánico de sus diferentes partes en el espacio. Por esa razón hay que insistir que el elemento más importante de la estructura de una máquina es, precisamente, la colocación de sus piezas; mientras que el proceso vital tiene un carácter totalmente distinto. Se manifiesta esencialmente con el recambio de sustancias, o sea, con la interacción química de las diferentes partes que conforman el protoplasma. Por esto deducimos que el elemento primordial en toda la estructuración del protoplasma es el orden concreto que siguen los procesos químicos en el tiempo, la forma tan armónica en que se combinan, siempre con tendencia a conservar en su conjunto el sistema vital.
Entonces, para que las sustancias integradoras del protoplasma vivo puedan participar realmente con el metabolismo, debe combinarse con una proteína y …
Es de vital importancia para la formación del protoplasma que exista una estructura interna determinada. Pero otro factor no menos decisivo es la organización en el tiempo, o sea, que los procesos que se dan en el protoplasma lo hagan en armonía. Cualquier organismo, tanto animal, planta o microbio, vive únicamente mientras pasen por él, de forma continuada y constante, nuevas partículas de sustancias, cargadas de energía. Distintos cuerpos químicos pasan del medio ambiente al organismo; y cuando están dentro, sufren unos determinados y esenciales trastornos, mediante los cuales acaban convirtiéndose en sustancias del propio organismo invadido y serán iguales que aquellos cuerpos químicos que antes formaban parte del ser vivo. Este proceso se conoce con el nombre de asimilación. Sin embargo, de forma paralela a este proceso se da la desasimilación, que se trata precisamente del proceso contrario, es decir, las distintas sustancias que forman la parte del organismo vivo son sensibles a los cambios del propio organismo, se desintegran a menor o mayor velocidad, y son sustituidas por los cuerpos asimilados. De esta forma, los productos de la desintegración se echan al medio envolvente.

¡Y pensar que todo está formado por esas partículas infinitesimales que llamamos Quarks y Leptones!
Es muy cierto que la sustancia del organismo vivo siempre se encuentra en movimiento, desintegrándose y volviendo a formarse de manera continua en virtud de la gran cantidad de reacciones de desintegración y síntesis, que se dan guardando una fuerte relación entre ellas. Ya Heráclito, aquel gran dialéctico de la antigua Grecia, nos decía: “nuestros cuerpos fluyen como un arroyo, y de la misma manera que el agua de éste, la materia se renueva en ellos.” Está claro que una corriente o un chorro de agua pueden mantener su forma, su aspecto externo, durante un tiempo, pero su aspecto sólo es la manifestación exterior de ese proceso continuo y constante del movimiento de las partículas del agua. Incluso la misma existencia de este sistema depende, naturalmente, de que las renovadas moléculas de materia pasen constantemente, y a una velocidad determinada por el chorro de agua. Pero si interrumpimos este proceso, el chorro dejará de existir como tal. Lo mismo sucede en todos los sistemas conocidos como dinámicos, los cuales tienen un proceso concreto.

Es un hecho concreto e innegable que los seres vivos también son sistemas dinámicos. Igual que el chorro de agua al que antes hacíamos referencia, su forma y su estructura sólo forman parte de la expresión externa y aparente de un equilibrio, muy competente, formado por procesos que se dan en el ser vivo en sucesión permanente a lo largo de toda su vida. Sin embargo, el carácter de estos procesos es totalmente diferente a los que ocurre en los sistemas dinámicos de la naturaleza orgánica.

/vinilos-gotas-agua.jpg.jpg)
Las moléculas de agua llegan al chorro, ya como moléculas de agua, y lo atraviesan sin que se produzca ningún cambio. Pues el organismo toma del medio ambiente sustancias ajenas y desconocidas para él, pero a continuación, mediante procesos químicos muy complejos, son convertidos en sustancias del propio organismo, muy parecidas a los materiales que forman su cuerpo.
Precisamente esto es lo que hace posible las condiciones que mantienen constantemente la composición y estructura del organismo, ignorando este proceso continuo e ininterrumpido de desasimilación que se da en todos los organismos vivos.
![El METABOLISMO de los seres vivos [ANABOLISMO y CATABOLISMO]](https://i.ytimg.com/vi/IHJSpPpdNY0/maxresdefault.jpg)
Así pues, desde una perspectiva puramente química, el recambio de sustancias, también llamado metabolismo, es un conjunto enorme de reacciones más o menos sencillas, de oxidación, reducción, hidrólisis, condensación, etcétera. Lo que lo hace diferente del protoplasma, es que en el metabolismo, estas reacciones se encuentran organizadas en el tiempo de de cierto modo, las cuales se combinan para poder crear un sistema integral. Dichas reacciones no surgen por casualidad, y de forma caótica, sino que se dan en estricta sucesión, y en un orden armónico concreto.
Ese orden será la base de todos los fenómenos vitales conocidos. En la fermentación alcohólica, por ejemplo, el azúcar proveniente del líquido, que es fermentable, penetra en la célula de la levadura, sufriendo determinados trastornos químicos. O sea, primero se le incorpora el ácido fosfórico y luego se divide en dos partes.
Una de las cuales experimentará un proceso de reducción, mientras que la otra se oxidará, quedando convertida, finalmente, en ácido pirúvico, que más tarde se descompondrá en anhídrido carbónico y acetaldehído. Este último se reducirá, quedando transformado después en alcohol etílico. Como resultado, podemos observar que el azúcar queda convertido en alcohol y anhídrido carbónico.

Aquí podemos contemplar una célula de levadura. Se reproducen por germinación o sexualmente (…algo más interesante…). Las protuberancias de esta célula (esos círculos que parecen ojos de pescado) son las huellas de las cicatrices dejadas por las yemas al separarse. La fotografía aumenta el tamaño de la célula 12.500 veces.
Esto nos demuestra que en la célula de la levadura, lo que determina la producción de estas sustancias es el extraordinario rigor con que se dan todas estas reacciones, las cuales se suceden de forma muy ordenada. Sólo con que sustituyésemos en esta cadena de transmutaciones un único eslabón o si alterásemos en lo más mínimo el orden de dichas transmutaciones ya no tendríamos como resultado alcohol etílico, sino cualquier otra sustancia. En efecto, en las bacterias de la fermentación de la leche, el azúcar, al principio sufría los mismos cambios en la levadura, pero cuando se llega a la fermentación del ácido pirúvico, éste ya no se descompone, todo lo contrario, se reduce al instante. Esto explica que en las bacterias de la fermentación láctica el azúcar no se transforme en alcohol etílico, sino en ácido láctico.
Un estudio de la síntesis de distintas sustancias en el protoplasma demuestra que éstas no se crean de repente, y no provienen de un acto químico especial, sino que son el resultado de una cadena larguísima de trastornos químicos.

No puede constituirse un cuerpo químico complejo, propio de un ser vivo en concreto, sin que se produzcan centenares o miles de reacciones en un orden regular, constante, y ya previsto con rigurosidad, lo cual constituirá la base de la existencia del protoplasma.
Porque cuanto más compleja es la sustancia, más reacciones intervienen en su formación dentro del protoplasma y estas reacciones deben coordinarse entre sí con mayor rigor y exactitud. En efecto, investigaciones bastante recientes han demostrado que en la síntesis de las proteínas a partir de los aminoácidos toman parte gran cantidad de reacciones que se producen en una sucesión muy ordenada. Únicamente como consecuencia de esta rigurosa armonía, de esta sucesión ordenada de las reacciones, se da en el protoplasma vivo ese ritmo estructural, esa regularidad en la sucesión de los distintos aminoácidos que también podemos apreciar en las proteínas actuales.
Por consiguiente, las moléculas proteínicas, así originadas y con una estructura determinada se agrupan entre sí, y ciertas leyes las hacen tender a la formación de auténticos conglomerados moleculares que se acaban separando de la masa protoplasmática y se distinguen como elementos morfológicos, visibles a través del microscopio, como formas protoplasmáticas características por su gran movilidad. De esta manera, la composición química propia del protoplasma, como su estructura, son la manifestación del orden en que se producen estos procesos químicos que se dan de forma continua y permanente en la materia viva.
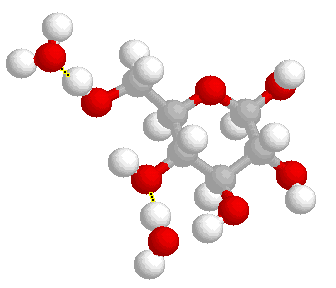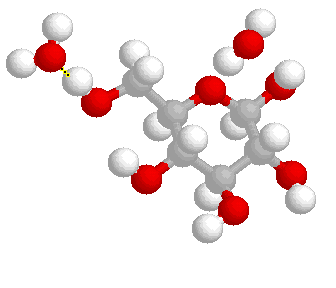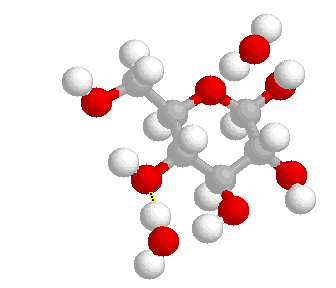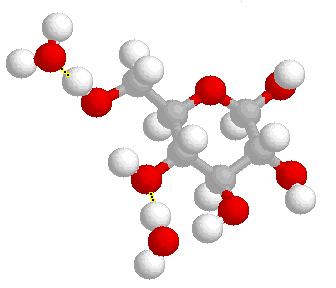
Las grandes moléculas de los sistemas vivos tienen una estructura modular mantenida mediante enlaces covalentes y formada esencialmente por tan sólo seis elementos químicos: Carbono, Hidrógeno, Nitrógeno, Oxígeno, Fósforo y Azufre. Los azúcares (moléculas formadas en torno a un anillo de carbono, oxígeno e hidrógeno) son los bloques de construcción básicos de los carbohidratos. Los almidones y la celulosa están compuestos por cadenas de azúcares (glucosa), siendo utilizados los primeros como almacenamiento de energía y la celulosa como estructura de las paredes celulares vegetales. Las diferencias entre ambas moléculas son tan sutiles como pequeñas variaciones en los enlaces intermoleculares, pero el resultado es tan diferente que nuestro organismo, por ejemplo, puede digerir el almidón y no la celulosa.
Pues bien, debemos preguntarnos de qué depende ese orden, propio de la organización del protoplasma, y cuáles son sus causas inmediatas. Un estudio minucioso sobre esta cuestión dejará demostrado que el orden indicado no es simplemente algo externo, que queda al margen de la materia viva, teoría defendida por los idealistas; en cambio, hoy día, sabemos perfectamente que la velocidad, la dirección y el encadenamiento de las diferentes reacciones, todo lo que forma el orden que estamos viendo, depende totalmente de las relaciones físicas y químicas que se establecen en el protoplasma vivo.
Las propiedades químicas de las sustancias integradoras del protoplasma, en primer lugar, y también las de las sustancias orgánicas que intervienen son las que constituyen la base de todo ello. Dichas sustancias orgánicas poseen enormes posibilidades químicas y pueden generar gran variedad de reacciones. Pero, aprovechan estas posibilidades con mucha “pereza”, lentamente, a veces a una velocidad ínfima. En muchas ocasiones, se necesitan meses e incluso años, para que llegue a producirse alguna de las reacciones efectuadas entre las mismas sustancias orgánicas. Por esto, los químicos, para acelerar el proceso de las reacciones entre las sustancias orgánicas, usan a menudo en su trabajo diferentes sustancias de acción enérgica-ácidos y álcalis fuertes, etcétera.
Para conseguir tal aceleramiento cada vez con más frecuencia, los químicos recurren a la utilización de los catalizadores. Hace ya mucho tiempo que habían notado que sólo con añadir una pequeña dosis de algún catalizador a la mezcla donde se estaba realizando una reacción, se producía un gran aceleramiento de ésta. Además, otra propiedad propia e los catalizadores es que no se destruyen durante el proceso de la reacción, y cuando esta finaliza, comprobamos que queda exactamente la misma cantidad de catalizador que añadimos a la mezcla al principio. Así que, cantidades insignificantes de catalizador son suficientes, muchas veces, pata provocar la rápida transmutación de masas considerables de diferentes sustancias. Esta cualidad, hoy día, es de gran utilidad para la industria química, que usa como catalizadores distintos metales, sus óxidos, sus sales y otros cuerpos orgánicos o inorgánicos. Las reacciones químicas dadas en animales y vegetales entre las distintas sustancias orgánicas se suceden a gran velocidad. De lo contrario, la Vida no pasaría tan rápida como en realidad pasa. Se sabe que la gran velocidad de las reacciones químicas producidas en el protoplasma es debida a la presencia constante de catalizadores biológicos especiales llamados fermentos.

Leyendo sobre el Protoplasma y sus complejos caminos, podemos llegar a comprender que, efectivamente, todos somos uno, y, sin embargo, diferentes. ¡Ese largo camino recorrido hasta llegar aquí! No sabemos mediante qué mecanismos llegan a nuestros cerebros esas ráfagas luminosas del saber que, a unos les hace comprender ciertas cuestiones complejas y, a otros no nos llegan esos fogonazos de luz que alumbren los rincones oscuros existentes en nuestras mentes. Así, para unos es el futbol y para otros las estrellas su mayor preocupación.
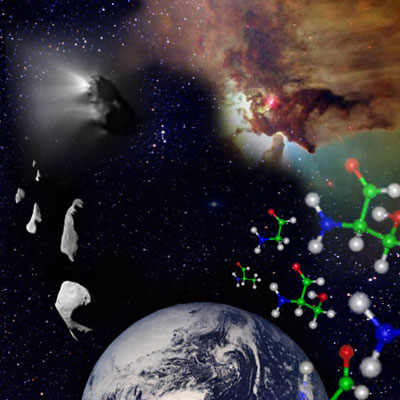


Hace tiempo que estos fermentos fueron descubiertos, y ya con anterioridad, los científicos se habían fijado en ellos. Pues resultó que los fenómenos se podían extraer del protoplasma vivo y así separarse en forma de solución acuosa o como polvo seco de fácil solubilidad. Esto me hace pensar en lo que ocurre en las Nebulosas. No hace mucho se consiguieron fermentos en forma cristalina y se resolvió su composición química. Estos resultaron ser proteínas, y muchas veces, en combinación con otras sustancias de distinta naturaleza. Estos fermentos, por el carácter de su acción, se asemejan a los catalizadores inorgánicos. Sin embargo, se diferencian de ellos por la increíble intensidad de sus efectos.

En este sentido, los fermentos superan a los catalizadores inorgánicos de acción en centenares de miles, y en ocasiones hasta en millones de veces. Así que en los fermentos de naturaleza proteínica se da un mecanismo increíblemente perfecto y racional que hace posible acelerar las reacciones químicas entre las distintas sustancias orgánicas. Los fermentos también se caracterizan por la excepcional especifidad de su acción.
Por supuesto, esto es a causa de las particularidades del efecto catalítico de las proteínas; pues la sustancia orgánica (el sustrato) que sufre alteraciones en el transcurso del proceso metabólico, forma ya al principio, una unión bastante compleja aunque de corta duración, con la correspondiente proteína-fermento. Esta fusión tan completa, no es estable, pues sufre distintos trastornos con mucha rapidez: el sustrato sufre las transformaciones correspondientes y el fermento se regenera, para poder unirse de nuevo a otras porciones del sustrato.


Entonces, para que las sustancias integradoras del protoplasma vivo puedan participar realmente con el metabolismo, debe combinarse con una proteína y constituir con ella un enlace complejo. De no ser así, sus posibilidades químicas se producirán muy lentamente y entonces perderán toda su importancia en el impetuoso proceso vital. Por esta razón el cómo se modifique una sustancia orgánica en el transcurso del metabolismo, depende, además de la estructura molecular de esta sustancia, y de las posibilidades químicas de la misma, también de la acción de fermentación de las proteínas protoplasmáticas, las cuales se encargan de llevar esa sustancia al proceso metabólico general.
Los fermentos, además de ser un poderoso acelerador de los procesos químicos sufridos por la materia viva; son también un mecanismo químico interno, el cual se encarga de que esos procesos sean conducidos por un cauce muy concreto. La gran especificidad de las proteínas-fermentos consigue que cada una de ellas forme enlaces complejos sólo con determinadas sustancias y catalice solamente algunas reacciones. Por esto, cuando se produce éste o el otro proceso vital, y con más motivo, cuando se verificas todo el proceso metabólico, actúan miles de proteínas-fermento de distintas clases. Cada una de estas proteínas puede catalizar de forma específica una sola reacción, y sólo el conjunto de acciones de todas ellas, en muy precisa combinación, hará posible ese orden regular de los fenómenos que entendemos como base del metabolismo.
¡Es tanta la diversidad de la Vida!
Con el uso de los distintos fermentos específicos que se obtienen a partir del organismo vivo, en el laboratorio, pueden reproducirse de forma aislada cada una de las reacciones químicas, y todos los eslabones que forman el proceso metabólico. Así desenredamos el ovillo tan sumamente complicado de las transmutaciones químicas producidas durante el metabolismo, donde miles de reacciones individuales se mezclan. Por este mismo procedimiento se puede descomponer el proceso metabólico en sus diferentes etapas químicas, se puede analizar las sustancias integradora de la materia viva, y además los distintos procesos realizados en ella.
De esa manera se demostró que la respiración funciona a partir de una serie de reacciones como la oxidación o la reducción, dichas reacciones se dan con muchísimo rigor en un orden estricto y cada una de éstas es catalizada por un fermento específico (S.Kóstichev, A. Liédev y otros autores).
Hoy día, ya hemos dado el salto del análisis de los procesos vitales a su reproducción, a su síntesis. De esta forma, combinando de manera precisa en una solución acuosa de azúcar, una veintena de fermentos distintos, obtenidos a partir de seres vivos, pueden reproducirse los fenómenos propios de la fermentación alcohólica. En este líquido, donde gran cantidad de proteínas distintas se hallan disueltas, los trastornos que sufre el azúcar son verificados en el mismo orden regular que siguen en la levadura viva, aunque aquí no existe ninguna estructura celular.
Todos estos procesos son, en realidad, terriblemente complejos y están expuestos a que, cualquier alteración del medio incida de manera directa en su devenir. Pero, por otra parte y en las circunstancias adecuadas, no existe ningún factor físico o químico, ni sustancia orgánica o sal inorgánica que, de alguna manera, puedan alterar el curso de las reacciones fermentativas. Cualquier aumento o disminución de la temperatura, alguna modificación de la acidez del medio, del potencial oxidativo y de la composición salina o de la presión osmótica, alterará la correlación entre las velocidades de las distintas reacciones de fermentación, y de esta forma cambia su sucesión temporal. Es aquí donde se asientan todas las premisas de esa unidad entre el organismo y el medio, tan característica de la vida.
Esta organización tan especial de la sustancia viva influye en gran manera, en las células de los organismos actuales, en el orden y la dirección de las reacciones fermentativas, las cuales son la base del proceso metabólico. Cuando se agrupan las proteínas entre sí pueden quedar aisladas de la solución general y conseguir diferentes estructuras protoplasmáticas de muy ágil movimiento. Con total seguridad, sobre la superficie de estas estructuras se encuentran concentrados gran cantidad de fermentos.

Aparato de Miller que buscaba la Actividad integradora del Origen de la vida
Está claro que el orden característico de la organización del protoplasma está basado en las distintas propiedades químicas de las sustancias integradoras de la materia viva. Esta gran variedad de sustancias existentes y su increíble capacidad de originar gran cantidad de reacciones químicas, pueden generar incalculables trastornos y cambios químicos. Pero debemos tener en cuenta que en el protoplasma vivo existen una serie de factores externos e internos que rigen estas transmutaciones, son factores como la presencia de conjuntos de fermentos; su relación cualitativa; la acidez del medio circundante; el potencial de oxido-reducción; las propiedades coloidales del protoplasma y su estructura, entre otros.
Todos estos fenómenos entrelazados entre sí y fuertemente relacionados con el orden regular de las reacciones químicas son propios del protoplasma vivo que desemboca en la muestra de estructuras morfológicas muy variadas. Pues bien, todo este orden sigue una dirección muy concreta, persigue un objetivo que al final desemboca en eso que llamamos vida y es verdaderamente importante darse cuenta de que, la dinámica del Universo, a través de las estrellas, de las explosiones supernovas, de las nebulosas y, finalmente, de los mundos, se vale de un conjunto de sucesos que vistos desde fuera pudieran parecer inmersos en un inmenso Caos pero que, en realidad, son simplemente pasos necesarios para que, la materia inerte, tome forma y evolucione hasta la vida que, de una u otra manera siempre se abrirá paso y estará presente en los lugares más insospechados que imaginar podamos, ya que, la vida, es algo irreversible en nuestro universo y está llamada a poblar miles de millones de mundos donde tomará las más variadas formas, unas veces conscientes y otras no, conformando un escenario de diversidad en el que, como ahora sabemos, prevalecerá aquella forma de vida que es consciente de SER.
¿Es la materia “inerte” que evoluciona hacia la Vida?
Ahora conocemos las leyes de la Naturaleza, sabemos cómo se forman las distintas sustancias y elementos y que es, lo que de ellas puede surgir cuando se mezclan de una manera determinada y qué es lo que puede pasar cuando todo esto ocurre en el marco adecuado y en presencia de las condiciones idóneas para que surja el orden vital y su carácter perfectamente armónico que le hace estar siempre en consonancia con las condiciones del medio ambiente.
Todo esto nos lleva a comprender que es necesario e ineludible profundizar mucho más en la evolución de la materia a lo largo de la historia del mundo, del Sistema Solar, del Universo en los que, no puede caber ninguna duda, surgió, a partir de esa materia “inerte” lo que conocemos como ¡Vida! En sus miles de formas y colores (también olores y diversa y maravillosa hermosura) que, se podría decir, sin lugar a equivocarnos que, la esencia del Universo es, precisamente la Vida.
El surgir de la vida en nuestro planeta
Todo fue posible a que, de alguna manera que no hemos llegado a comprender (aún), la vida surgió durante toda esta serie de procesos complejos inmersos en el Caos de una Complejidad que transmutaba la materia simple en otra, cada vez más compleja y organizada que seguía unos pasos que la llevaba a conseguir estructuras impensables de un orden superior y mucho más elevado de lo que, la “simple” materia, nos haría suponer que sería posible. Claro que, todo ello, sólo y únicamente fue posible gracias a la interrelación de la materia con el medio donde se dieron las bases para hacer posible la formación de sistemas individuales de orden pluri-molecular que fue el factor determinante para la aparición de la vida y su posterior desarrollo en el planeta tal como la conocemos.
En el Universo todo es energía…la Vida, también.
Emilio Silvera V.
Ene
30
Aquellos primeros momentos (?)
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (9)
Comments (9)
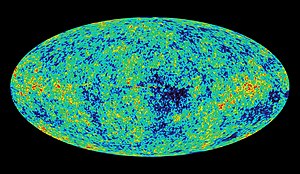


Todo en el Universo tiene un principio y un final y, el mismo universo tuvo que nacer y evolucionar para que hoy lo podamos contemplar, mediante nuestros sofisticados telescopios, un universo en expansión lleno de galaxias que contienen estrellas nuevas y viejas estrellas, muchas de ellas rodeadas de mundos que, aún no hemos podido determinar de qué criaturas estarán poblados muchos de ellos.


¡El Universo! ¿Cuántas maravillas esconde?
Antes de alrededor de un minuto y cuarenta segundos desde el comienzo del tiempo, no hay núcleos atómicos estables. El nivel de energía en el ambiente es mayor que la energía de unión nuclear. Por consiguiente, todos los núcleos que se forman, se destruyen de rápidamente.
Alrededor de un segundo desde el comienzo del tiempo, llegamos a la época de desacoplamiento de los neutrinos. Aunque en esa época el Universo es más denso que las orcas (y tan caliente como la explosión de una bomba de hidrógeno), ya ha empezado a parecer vacío a los neutrinos. Puesto que los neutrinossólo reaccionan a la fuerza débil, que tiene un alcance extremadamente corto, pueden escapar de sus garras y volar indefinidamente sin experimentar ninguna otra interacción.

Aunque parezca mentira, al día de hoy no sabemos, a ciencia cierta, como se formaron las galaxias a pesar de la expansión de Hubble ¿Qué retuvo allí la materia? ¿Sería la sustancia cósmica?
Así, emancipados, en lo sucesivo son libres de vagar por el Universo a su manera indiferente, volando a través de la mayor de la materia como sino existiese. (Diez trillones de neutrinos atravesarán sin causar daños el cerebro y el cuerpo del lector en el tiempo que le lleve leer esta frase. Y en el tiempo en que usted haya leído esta frase estarán más lejos que la Luna).
En menos de un siglo, el neutrino pasó de una partícula fantasma – propuesta en 1930 por el físico austríaco Wolfgang Pauli (1900-1958) a explicar el balance de energía en una forma de radioactividad, el llamado decaimiento beta, en una sonda capaz de escrutar el interior de estrellas y de la propia Tierra.
De esa manera, oleadas de neutrinos liberados en un segundo después del Big Bang persiste aún después, formando una radiación cósmica de fondo de neutrinos semejante a la radiación de fondo de microondas producida por el desacoplamiento de los fotones.
Si estos neutrinos “cósmicos” (como se los llama para diferenciarlos de los neutrinos liberados más tarde por las supernovas) pudiesen ser observador por un telescopio de neutrinos de alguna clase, proporcionarían una visión directa del Universo cuando sólo tenía un segundo.
A medida que retrocedemos en el tiempo, el Universo se vuelve más denso y más caliente, y el nivel de estructura que puede existir se hace cada vez más rudimentario.

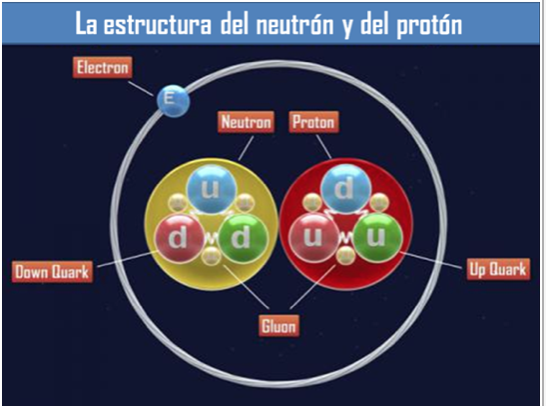
Por supuesto, en ese tiempo, no hay moléculas, ni átomos, ni núcleos atómicos, y, a 10-6 (0.000001) de segundo después del comienzo del tiempo, tampoco hay neutrones ni protones. El Universo es un océano de quarks libres y otras partículas elementales.
Si nos tomamos el de contarlos, hallaremos que por cada mil millones de antiquarks existen mil millones y un quark. asimetría es importante. Los pocos quarks en exceso destinados a sobrevivir a la aniquilación general quark-antiquark formaran todos los átomos de materia del Universo del último día. Se desconoce el origen de la desigualdad; presumiblemente obedezca a la ruptura de una simetría materia antimateria en alguna etapa anterior.

Nos aproximamos a un tiempo en que las estructuras básicas de las leyes naturales, y no sólo las de las partículas y campos cuya conducta dictaban, cambiaron a medida que evolucionó el Universo.
La primera transición semejante se produjo en los 10-11 de segundo después del comienzo del tiempo, cuando las funciones de las fuerzas débiles y electromagnéticas se regían por una sola fuerza, la electrodébil. hay bastante energía ambiente para permitir la creación y el mantenimiento de gran de bosones w y z.
El bosón Z cumple 30 años
Estas partículas – las mismas cuya aparición en el acelerador del CERN verificó la teoría electrodébil – son las mediadoras intercambiables en las interacciones de fuerzas electromagnéticas y débiles, lo que las hace indistinguibles. En ese tiempo, el Universo está gobernando sólo por tres fuerzas: la gravedad, la interacción nuclear fuerte y la electrodébil.
Más atrás de ese tiempo nos quedamos en el misterio y envueltos en una gran nebulosa de ignorancia. Cada uno se despacha a su gusto para lanzar conjeturas y teorizar sobre lo que pudo haber sido. Seguramente, en el futuro, será la teoría M (de supercuerdas) la que contestará esas preguntas sin respuestas ahora.
En los 10-35 de segundo desde el comienzo del tiempo, entramos en un ámbito en el que las fuerzas cósmicas son aún menos conocidas. Si las grandes teorías unificadas son correctas, se produjo una ruptura de la simetría por la que la fuerza electronuclear unificada se escindió en las fuerzas electrodébil y las fuertes. Si es correcta la teoría de la supersimetría, la transición puede haberse producido antes, había involucrado a la gravitación.
En el universo temprano la primera materia (hidrógeno y Helio) era llevada por la fuerza de gravedad a conformarse en grandes conglomerados de gas y polvo que interaccionan, producen calor y formaron las primeras estrellas.

Un norteamericano nacido en Tokio y dos japoneses ganan el Premio Nobel de Física
Los ganadores del Premio Nobel de Física 2008 han sido los japoneses Makoto Kobayashi y Toshihide Maskawa y el estadounidense, también de origen nipón, Yoichiro Nambu, por sus descubrimientos en el campo de la física subatómica, según ha informado hoy la Academia Real Sueca de las Ciencias de Estocolmo en un comunicado.
El universo primitivo
Elaborar una teoría totalmente unificada es tratar de comprender lo que ocurrió en ese tiempo remoto que, según los últimos estudios está situado entre 15.000 y 18.000 millones de años, cunado la perfecta simetría que, se pensaba, caracterizó el Universo, se hizo añicos para dar lugar a los simetrías rotas que hallamos a nuestro alrededor y que, nos trajo las fuerzas y constantes Universales que, paradójicamente, hicieron posible nuestra aparición para que , sea posible que, alguien como yo esté contando lo que pasó.
Pero hasta que no tengamos tal teoría no podemos esperar comprender lo que realmente ocurrió en ese Universo bebé. Los límites de nuestras conjeturas actuales cuando la edad del Universo sólo es de 10-43de segundo, nos da la única respuesta de encontrarnos ante una puerta cerrada.
Del otro lado de esa puerta está la época de Planck, un tiempo en que la atracción gravitatoria ejercida por cada partícula era comparable en intensidad a la fuerza nuclear fuerte.
- La fuerza nuclear fuerte: es la más intensa, su partícula portadora de fuerza es el gluon.
“Pero aún no se ha podido unificar la fuerza nuclear fuerte con las otras, pues la energía que se requiere para lograrlo es tan intensa que se necesitaría un acelerador de partículas tan potente que sería aun más grande que la fuerza del sistema solar. Igual cabe destacar que en teoría es posible, pues las fuerzas anteriores se hacen intensas a mayor energía, en tanto la fuerza fuerte, a mayor energía se debilita. Si se suministra energía a todas estas partículas, la fuerza electro débil aumenta de intensidad, y la nuclear fuerte reduce su intensidad, así se tendría una unificación más, pues llegaría un valor energético que seria común a todas. Tratando de explicar otros fenómenos que surgen de ella, es que a continuación hablaremos un poco de las propiedades de la fuerza nuclear fuerte. “
La fuerza nuclear fuerte hizo posible la existencia de los núcleos que atraían electrones para formar átomos
Así que, llegados a este punto podemos decir que la clave teórica que podría abrir esa puerta sería una teoría unificada que incluyese la gravitación, es decir, una teoría cuántica-gravitatoria que uniese, de una vez por todas, a Planck y Einsteins que, aunque eran muy amigos, no parecen que sus teorías (la Mecánica Cuántica) y (la Relatividad General) se lleven de maravilla.
emilio silvera
Ene
30
Teoría del proceso seguido por la Tierra en su evolución
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (0)
Comments (0)
En este Blog, una de las premisas más importante, en realidad convertida en un Principio a seguir, es dar voz al visitante y, no sólo en comentarios, sino en los posibles trabajos que puedan querer exponer para divulgar sus ideas, y, en este caso,el visitante José C. Gómez, me envía un Correo que dejo aquí reproducido:

El origen del agua y su ciclo en la naturaleza, no es entendida por los europeos hasta finales del siglo XVII. Sin embargo, en al año 500 a.C los chinos ya conocían
Veamos que nos dice sobre el tema José C. Gómez
|
Amigo José C. Gómez, es bueno que sigas pensando y mejorando tus ideas que, como decía Einstein, lo mejor para la Mente es hacerla pensar y, este que nos manda, es un buen ejercicio. Aprovecho para decir a todos los visitantes del lugar (unos 15.000/20.000 diarios) que, sus ideas también pueden ser expuestas aquí. ¡Envíenlas!
Saludos.
Ene
10
¡Las matemáticas! ¿El origen?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (2)
Comments (2)
¡Las leyes físicas! A veces sorprendentes,
Si miramos … ¿Qué veremos? La imagen de un objeto se forma en la retina de cada ojo, por tanto tendríamos dos imágenes de un mismo objeto y sin embargo, vemos una sola… Claro que no siempre lo que podemos ver está determinado por la visión de los ojos… ¡La Mente llega más lejos y ve mucho más!

Muescas en el hueso de Ishango, una herramienta de hueso que data del Paleolítico Superior, aproximadamente de unos 35.000 años a. C.
Lo que veremos es que las cosas nunca son como parecen ser a primera vista y, con el tiempo que inexorablemente transcurre, las cosas cambian sin que nada lo pueda evitar y, los saberes del mundo evolucionan tomando siempre el camino de la perfección. Es decir, cada vez se hacen las cosas mejor, se depuran más las técnicas y, con la experiencia llega el conocimiento y la sabiduría.

Los expertos occidentales, por ejemplo, dicen que la autoría del teorema de Pitágoras corresponde a éste. A pesar de que los babilonios habían creado el mismo concepto siglos antes. La razón es que Pitágoras o sus seguidores habían creado la primera demostración de este principio fundamental, mientras que los babilonios no lo hicieron. Es lo mismo que pasó (en tiempos más recientes) con Faraday y Maxwell, el primero descubrió con sus experimentos todos los fundamentos encerrados en la electricidad y el magnetismo y, al no saber exponerlo matemáticamente, tuvo que llegar Maxwell que, con sus ecuaciones vectoriales nos dejara una demostración fundamental del electromagnetismo.
Faraday Maxwell
Los críticos consideran tan la demostración al estilo griego que su inexistencia en las culturas no europeas desacredita, en su opinión, miles de años de trabajos matemáticos. Claro que, en este punto, no todos estamos de acuerdo y, por mi creo que los pueblos no occidentales sí tenían sus demostraciones, mientras que otros dudan de que sea realmente posible “demostrar” cualquier concepto para toda la eternidad y para la totalidad del Universo. Es cierto que eterno…no hay nada pero, en todo el Universo será válida la ecuación E = mc², de la misma manera que 2 + 2 = 4. Hay cosas que ni el Tiempo ni las distancias pueden variar.
La numeración egipcia (escrita) permitía la representación de números mayores que un millón. Utilizaban un sistema aditivo de decimal con jeroglíficos específicos para la unidad y una de las seis primeras potencias de 10.
En la figura podemos ver los símbolos usados para 1, 10, 100 y 1.000. El 10.000 se representaba con un dedo doblado, el 100.000 con un pez y 1.000.000 mediante una figura humana de rodillas y con los brazos alzados.
En un principio escribían los nueve primeros números colocando símbolos de la unidad, uno a continuación de otro; más tarde utilizaron la representación por desdoblamiento mientras los arameos de Egipto usaban un principio ternario (ver tabla).
La nunmeración y sus símbolos fueron variados según los pueblos
El escepticismo es oportuno en toda investigación, pero quien investigue las matemáticas no occidentales se enfrenta a menudo con un gran obstáculo. Expertos que han estudiado los sistemas de numeración de la antigua Etiopía, cuentan que los expertos occidentales se negaron en una ocasión a aceptar que esta civilización africana hubiera desarrollado sus propios números. Los números etíopes se parecen a los números egipcios, que son anteriores, y, en menor medida, a los antiguos números griegos –lo cual no es sorprendente, dada, por una la proximidad geográfica de Etiopía con Egipto y, por otra , la influencia que ejerció Egipto en las matemáticas griegas.
Una serie de cartas escritas por algunos etíopes a personajes griegos y encontradas en Grecia estaban escritas en los dos lenguajes para que las entendieran y, a pesar de ello, algunos “expertos” dudaban que los etíopes hubieran sido capaces de tal sofisticación. Sin embargo, los análisis químicos demostraron que la empleada tenía un color no habitual y los análisis químicos demostraron que la tinta se había fabricado a partir de unas bayas autóctonas de Etiopía.
Nuestro patrimonio matemático y nuestro orgullo occidentales dependen irremediablemente de los logros de la antigua Grecia. Dichos logros se han exagerado tanto que a resulta difícil distinguir qué part3e de la matemática moderna procede de los griegos y cuál es la que su origen en los babilonios, los egipcios, los hindúes, los chinos, los árabes, etc. Sin embargo, si nuestras actuales se basaran exclusivamente en Pitágoras, Euclides, Demócrito, Arquímedes y otros griegos, serían una disciplina bastante deficiente.
En 1908, el historiador de las matemáticas, Rouse Ball escribió:
“La historia de las matemáticas no se puede remontar ciertamente a ninguna ni a ningún período que sean anteriores a la etapa de los griegos jónicos”.
Matemáticas de Mesopotamia Matemática Babilónica
Matemáticas de la India Matemáticas de Egipto
Hoy sabemos que el hombre se extralimitó al ponerle fecha al conocimiento matemático del mundo humano que, como ahora sabemos, viene desde muy lejos en el Tiempo. Aunque las huellas no todas han sobrevivido, si aparecieron tablillas y otros objetos que contenían la prueba de que nuestros antepasados de Mesopotamia, Babilonia, India, Egipto… y otros fueron los precursores de la posterior matemática griega.

En 1952 el historiador Morris Kline escribió:
“Fue en el extraordinariamente propicio suelo de Gracia donde [las matemáticas] garantizaron finalmente una nueva forma de controlar la existencia humana y florecieron espectacularmente durante un breve período de tiempo… Con el declive de la civilización griega la planta quedó aletargada durante unos mil años… [hasta que] esa planta fue llevada de una manera adecuada a Europa y plantada una vez más en el terreno fértil”
De un modo esquemático, se interpreta a menudo el significado de esta afirmación entendiendo que ha habido tres etapas de la de las matemáticas:
- 1. Hacia el año 600 a. C., los antiguos griegos inventaron las matemáticas, que estuvieron desarrollando hasta aproximadamente el año 400 d. C., en el cual desaparecieron de la faz de la Tierra.
- 2. A esto siguió un período oscuro para las matemáticas, que duró más de mil años. Algunos expertos admiten que los árabes mantuvieron vivas las matemáticas griegas durante toda la Edad Media.
- 3. En la Europa del siglo XVI se produce el redescubrimiento de las matemáticas griegas que vuelven a florecer de hasta el momento actual.
Claro que este punto de es muy discutible. Nuestros números modernos -del 0 al 9- se desarrollaron en la India (como ha quedado reseñado en escritos expuestos aquí en tiempos pasados) durante la segunda etapa, el llamado período oscuro de las matemáticas. Las matemáticas existían ya mucho antes de que los griegos construyeran su primer ángulo recto.
Rouse Ball, desconocía las primeras matemáticas hindúes contenidas en los Sulbasutras (las reglas de la cuerda). Escritos en alguna comprendida entre los años 800 y 500 a. C., los Silbasutras demuestran, entre otras cosas, que los indios de este período tenían su propia versión del teorema de Pitágoras así como un procedimiento para obtener la raíz cuadrada de 2 con una precisión de hasta cinco cifras decimales. Los Sulbasutras ponen de manifiesto la existencia de un rico conocimiento geométrico que fue muy a los griegos.
Otro experto nos dice que, la afirmación de Kline es más problemática, ya que ignora un rico conjunto de matemáticas no europeas que fueron desenterradas hacia mediados del siglo XX, incluidas las matemáticas de Mesopotamia, Egipto, China, la India, el mundo árabe y la América precolombina. También existe el problema de los propios griegos –Demócrito, Aristóteles, Heródoto- prodigaron alabanzas a los egipcios, reconociéndolos como sus gurús matemáticos (aunque con distintas palabras). El hecho cierto es que, antes que los griegos fueron muchos los que aportaron su matemático para que ahora nosotros, sepamos de esa imprescindible y necesaria disciplina que nos sirve para construir puentes, para diseñar veloces trenes, para poder calcular las trayectorias de las naces espaciales que van hacia Marte, o, simplemente, para saber cómo funcionan las leyes de la Naturaleza, los átomos que conforman la materia e incluso, saber sobre densidades y energías en las estrellas.
Repasando todos estos hechos, de alguna manera, podemos llegar a entender aquel “Todo es número” de los pitagóricos.
“Relaciona los números imaginarios ( i = raíz cuadrada de ( –1)), con las potencias (número e y logaritmos neperianos ) y con las funciones trigonométricas. Nos la podemos encontrar en cualquier sitio, en cualquier expresión matemática pura o relacionada con algo tan prosaico como las relaciones de impedancias en un circuito de corriente alterna. En la función de onda de la mecánica cuántica o en cualquier expresión de naturaleza ondulatoria o periódica. En la técnica, en la física o en las matemáticas más abstractas ( Roger Penrose reflexiona– en su último libro, en el capítulo sobre las diferenciales complejas – lo que habría disfrutado Euler con todas las maravillas de su fórmula y de los números imaginarios ).”
La más famosa fórmula de Euler. Hay veces en la que no tenemos más opción que asombrarnos de lo que puede discurrir la mente humana. Sobre esta fórmula mágica, alguien dijo:
“Si una aburrida noche de invierno decidieran acudir a un restaurante de las Matemáticas y pidieran una paella con “un poco de todo” o, más precisamente, “un poco de todo lo importante”, probablemente les llevarían a la mesa la ecuación del título. Ésta, a pesar de tratarse de una pura tautología, es muy conocida en la comunidad científica por su simplicidad y casi sobrenatural completitud: contiene en una sola línea de elementos de lo más diverso y de cierta relevancia en la historia de las Matemáticas.”
Leonhard Euler
Está claro que este breve comentario no pretende ser la Historia de las matemáticas que, para ser un fiel reflejo de la realidad, tendría que estar contada en muchos volúmenes llenos de explicaciones, hallazgos y anécdotas y hechos que nos llegaron a través de los descubrimientos realizados a lo largo del tiempo. Sin embargo, si es un apunte interesante de lo que pudo ser. Para cerrar el trabajo he querido traer aquí una fórmula mágica, es debida a Leonhard Euler, nacido en Basilea en el año 1707. Una mente prodigiosa que deslumbraba desde su más tierna juventud en diversas disciplinas, especialmente en Matemáticas. Le llamaron el Rey Midas de las matemáticas.
Fue el precursor de la utilización de la letra
para denotar la base de los logaritmos neperianos.
Popularizó la utilización de la letra
para denotar la razón entre la longitud de una circunferencia y su diámetro.
Introdujo la notación
para
.
Utilizó la letra
para designar a su constante.
Notación sobre lados y ángulos y otras notaciones sobre triángulos.
- Otras notaciones en análisis. Euler también introdujo la notación moderna de las funciones trigonométricas, el símbolo
para denotar un sumatorio y
para denotar logaritmo de
.
- Funciones. Uno de los aportes más importantes (posiblemente el que más) de Euler a la notación matemática fue la utilización de
(usada en los Commentarii de San Petersburgo en 1734-35) como forma para denotar al valor de una función
al aplicarla a un valor
.
Como se puede ver las matemáticas posteriores a Euler no habrían sido las mismas sin las notaciones que nuestro protagonista introdujo, ya que éstas simplificaron de manera significativa la forma de escribir matemáticas.
En el campo de las llamadas Matemáticas Puras, Euler creó de golpe y de manera extraordinaria varias nuevas disciplinas de investigación, apartes de las ya mencionadas, y las desarrolló metódicamente: la teoría de las series infinitas, el álgebra superior y el cálculo de variaciones. Asimismo, Euler determinó, investigando la serie armónica, la constante de su nombre, siendo la más sencilla de las series infinitas que dan el valor de ella: e = 1 + 1/1! + 1/2! + …

La Poesía y la Música han sido eternas compañeras
“Podemos volar hacia el mundo de la poesía y de la música y, nos encontramos cara a cara con la cantidad y el número, en sus ritmos y octavas,…”
Alfred North Whitehead.
emilio silvera
Mar
3
La mujer en la Ciencia ha tenido su importancia
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (0)
Comments (0)

Marie Curie
La Asamblea general de las Naciones Unidas, ha declarado el día 8 de Marzo de 2.011 el Año Internacional de la Química, coincidiendo con el centenario de la concesión del Premio Nobel otorgado a Marie Curie –Marja Sklodowska- por sus aportes a la Química.
Sin embargo, se aprovechó el tirón mediático de esta célebre científica, y, el valor simbólico de su buena imagen popular, no olvidemos que es poseedora de dos Premios Nobel, por una de las personas más importes que, dedicadas a la Ciencia, se puede decir que, pasó y dedicó su vida a la investigación, haciendo posible, de alguna manera, que hoy, nosotros podamos vivir mejor gracias a sus contribuciones científicas.
Así que, los responsables, creyeron conveniente, aprovechar aquel momento para celebrar también, en el Año 2.011, el Año Internacional de la Mujer Científica, lo que, por otra parte, es muy de justicia, ya que, queramos o no, en éste (como en otros ámbitos) tenemos a la mujer un poco postergadas y, ya va siendo hora de que se le reconozcan los mismos (en algunos casos más) méritos que a las hombres.
Cuando publiqué este trabajo por ve<z primera, decía:
“En ese año Internacional de la mujer científica, entre otros muchos, ´se publicó éste reportaje de Laura Martínez Alarcón queriendo hacerles un homenaje a unas cuantas mujeres científicas como representación de todas las demás.”

Laura Martínez
Cuando hablamos de ciencia, ¿a cuántas mujeres podríamos citar? Seguro que a nuestra memoria vendrá inmediatamente el nombre de Marie Curie, pero ¿y después? Siempre pensamos en Albert Einstein o Charles Darwin cuando de ciencia se trata; sin embargo, seguimos ignorando los logros de muchas mujeres que, a lo largo de la historia, han dedicado su vida a estos menesteres.
Hoy, que estamos celebrando el Día Internacional de la Mujer, queremos recordar a 10 mujeres que se han destacado en la ciencia.
1. Hipatia de Alejandría.
Hipatia de Alejandría, matemática, astrónoma, filósofa neoplatónica y símbolo de la sabiduría antigua.
Fue la primera mujer en realizar una contribución fundamental al desarrollo de las matemáticas, una verdadera precursora y, hasta mártir, como mujer de ciencias. Nació en el año 370 D. C. en Alejandría y falleció en el 416, cuando sus trabajos en filosofía, física y astronomía fueron considerados como una herejía por un amplio grupo de cristianos que la asesinaron brutalmente. Su imagen se considera un símbolo de la defensa de las ciencias contra la irracionalidad y la estupidez de las embestidas religiosas, siempre carentes del más mínimo sentido. En 2009, el director de cine Alejandro Amenábar realizó la película “Ágora” en memoria de Hipatia.
2. Sophie Germain.

Fue una matemática autodidacta, nacida en París en las últimas décadas del Siglo de las Luces (1776-1831). Sus primeros trabajos en Teoría de Números los conocemos a través de su correspondencia con C. F. Gauss, con el que mantenía oculta su identidad bajo el pseudónimo de Monsieur Le Blanc. El teorema que lleva su nombre fue el resultado más importante desde 1753 hasta 1840 para demostrar el último teorema de Fermat. Posteriormente, sus investigaciones se orientaron a la teoría de la elasticidad y en 1816 consiguió el Premio Extraordinario de las Ciencias Matemáticas que la Academia de Ciencias de París otorgaba al mejor estudio que explicara mediante una teoría matemática el comportamiento de las superficies elásticas. En los últimos años de su corta vida, escribió un ensayo sobre filosofía de la ciencia que Augusto Comte citó y elogió en su obra.
3. Augusta Ada Byron (Condesa de Lovelace).

Mejor conocida como Ada Lovelace fue una brillante matemática inglesa. Nació en Londres en el año 1815 y falleció en 1852. Absolutamente adelantada a su tiempo, podría decirse que fue la primera científica de la computación de la historia, la primera programadora del mundo. Ella descubrió que mediante una serie de símbolos y normas matemáticas era posible calcular una importante serie de números, ella previó las capacidades que una máquina (más tarde sería la computadora) tenía para el desarrollo de los cálculos numéricos. Como curiosidad y por si su apellido te suena, ella fue la hija de uno de los poetas más grandes en la historia de la literatura universal, por supuesto: el magnífico Lord Byron.
4. Amalie Emmy Noether.

Podría considerarse como la mujer más importante en la historia de las matemáticas y, de hecho, así la consideraba Albert Einstein. Nació en Erlangen (Alemania), en 1882 y falleció en 1935 en Estados Unidos, luego de ser expulsada por los nazis unos años antes. La figura de Noether ocupa un imprescindible lugar en el ámbito de las matemáticas, especialmente en la física teórica y el álgebra abstracta, con grandes avances en cuanto a las teorías de anillos, grupos y campos. A lo largo de su vida realizó unas 40 publicaciones realmente ejemplares.
5. Lise Meitner.

Lise Meitner and Otto Hahn at the Kaiser Wilhelm Institute for Chemistry in Berlin (1928Lise Meitner and Otto Hahn at the Kaiser Wilhelm Institute for Chemistry in Berlin (1928
Nació en la Viena del Imperio Austrohúngaro, hoy Austria, en 1878 y falleció en 1968. Fue una extraordinaria física con un amplio desarrollo en el campo de la radioactividad y la física nuclear. Aunque fue parte fundamental del equipo que descubrió la fisión nuclear, solo su colega Otto Hahn obtuvo el reconocimiento. Años más tarde, el meitnerio (elemento químico de valor atómico 109) fue nombrado así en su honor.
6. Marie Curie.

La radiactividad. En 1897 Marie Curie se dispuso a preparar su tesis doctoral. El tema escogido era tan apasionante como difícil: las radiaciones de …
Química y física de origen polaco, Marie Salomea Skodowska Curie dedicó su vida entera a la radioactividad y fue la máxima pionera en este ámbito. Ella nació en 1867 y murió en 1934; es la primera persona en conseguir dos premios Nóbel para los cuales literalmente dio su vida, de hecho, hoy, muchas décadas después de su muerte, sus papeles son tan radiactivos que no pueden manejarse sin un equipo especial. Su legado y sus conocimientos en física y química impulsaron grandes avances.
7. Barbara McClintock.

Barbara McClintock in the laboratory at Cold Spring Harbor, New York, March 26,
Nació en Hartford (Estados Unidos) en 1902 y falleció en 1992, dejando un importante descubrimiento en el campo de la genética. Ella se especializó en la citogenética y obtuvo un doctorado en botánica en 1927. A pesar de que durante mucho tiempo, injustamente sus trabajos no fueron tomados en cuenta, 30 años más tarde se le otorgó el premio Nóbel por su excepcional e increíblemente adelantada investigación para su época: teoría de los genes saltarines, revelando el hecho de que los genes eran capaces de saltar entre diferentes cromosomas. Hoy, este es un concepto esencial en genética.
8. Jocelyn Bell.
Se trata de la astrofísica británica que descubrió la primera radioseñal de un púlsar. Nació en el año 1943, en Belfast (Irlanda del Norte) y su descubrimiento fue parte de su propia tesis. Sin embargo, el reconocimiento sobre este hallazgo fue para Antony Hewish, su tutor, a quien se le otorgó el premio Nobel de Física en 1974. Este injusto acto, que aunque como ya vimos no es nada nuevo, fue cuestionado durante años, siendo hasta hoy un tema de controversia.
9. Rosalind Franklin.
Nació en 1920 en Londres y falleció en 1958. Fue biofísica y cristalógrafa, y tuvo una participación crucial en la comprensión de la estructura del ADN, ámbito en el que dejó grandes contribuciones. Como suele ocurrir en la comunidad científica, uno de sus más grandes trabajos, la observación de la estructura del ADN mediante imágenes tomadas con rayos X, no le fue reconocido. Por el contrario, el crédito y el premio Nóbel en Medicina se lo llevaron Watson (quien más tarde fue cuestionado por sus polémicas declaraciones racistas y homofóbicas) y Crick.
10. Jane Goodall.

Nació en Londres, Inglaterra, en el año 1934. Ha dedicado toda su vida al estudio de los chimpancés. Jane ha realizado profundas y fructíferas investigaciones científicas sobre el comportamiento, el uso de herramientas y los modos de vida de estos primates. En 2003, sus trabajos fueron reconocidos por la comunidad científica con el Premio Príncipe de Asturias de Investigación Científica y Técnica.

Es una verdadera pena que, la verdadera contribución de la mujer científica a la Ciencia, sea poco conocida. Mujeres que han destacado en muchas de las disciplinas científicas que son importantes para la Humanidad, son totalmente desconocidas, y, el caso de la Curie, es excepcional.
Es justo que consideremos llegado el momento de otorgar a las mujeres de la Ciencia la categoría que, por méritos propios, se han ganado a lo largo de la Historia, y, no olvidemos que en la actualidad, no son pocas mujeres las que están al frente de la vanguardia en muchas de esas disciplinas que son punteras en el mundo, y, la Química o la Astronomía, pueden ser un buen ejemplo de ello. La Astronomía en España está al frente de grandes científicas Astrofísicas como Montserrat Villar o Ana Ulla entre otras muchas, y, también en otras disciplinas destacan mujeres de nuestro tiempo que han llegado a la Física, la Medicina y otras áreas de la Ciencia con una fuerza inusitada.

Lynn Margulis nació en 1938 en la ciudad de Chicago. Inició sus estudios de secundaria en el instituto público Hyde Park a lado de South Park y cuando fue trasladada por sus padres a la elitista Escuela Laboratorio de la Universidad de Chicago, regresó por su cuenta al instituto con sus antiguos amigos, lugar al que ella pensó que pertenecía. De esa época recuerda con agrado a su profesora de español, la señora Kniazza.
A los 16 años fue aceptada en el programa de adelantados de la Universidad de Chicago donde se licenció a los 20 años, adquiriendo según ella «un título, un marido (Carl Sagan) y un más duradero escepticismo crítico». Margulis diría de su paso por la Universidad de Chicago:
Allí la ciencia facilitaba el planteamiento de las cuestiones profundas en las que la filosofía y la ciencia se unen: ¿Qué somos? ¿De qué estamos hechos nosotros y el universo? ¿De dónde venimos? ¿Cómo funcionamos? No dudo de que debo la elección de una carrera científica a la genialidad de esta educación «idiosincrásica».
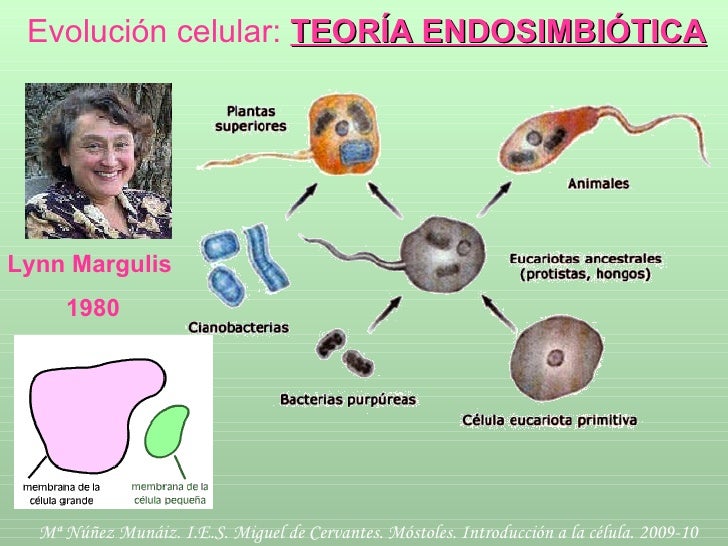
En 1958 continuó su formación en la Universidad de Wisconsin como alumna de un máster y profesora ayudante. Estudió biología celular y genética: genética general y genética de poblaciones. De su profesor de estas dos últimas, James F. Crow, diría:
“Cambió mi vida. Cuando dejé la Universidad de Chicago sabía que quería estudiar genética, pero después de las clases de Crow supe que sólo quería estudiar genética”.
Desde un principio se sintió atraída por el mundo de las bacterias, que en aquel entonces ella indica que eran consideradas solo en su dimensión de gérmenes de carácter patógeno y sin interés en la esfera del evolucionismo. Margulis investigó en trabajos ignorados y olvidados para apoyar su primera intuición sobre la importancia del mundo microbiano en la evolución. Ella misma, en sus diferentes trabajos, nos guía en lo que fue su investigación y los antecedentes de sus aportaciones. Siempre ha mostrado una especial disposición a valorar estos antecedentes, desde su recuerdo hacia la señora Kniazza, su profesora de español en el instituto; pasando por el recuerdo de sus profesores de universidad y lo que para ella significaron; y terminando por una extensa referencia de los trabajos de aquellos científicos que ella rescató del olvido para apoyar su pensamiento evolucionista.

Investidura de Margulis como doctora honoris causa por la UAM, junto a Peter David Townsend(izda.), el rector Raúl Villar y Eugenio Morales Agacino.
Se interesó por los trabajos de Ruth Sager, Francis Ryan y Gino Pontecorvo. Estos trabajos la llevan a la que ella considera obra maestra: The Cell in Developement and Heredity (La célula en el desarrollo y la herencia), escrita por E. B. Wilson en 1928. Toda esta obra relacionada con las bacterias está relacionada a su vez con los trabajos de L. E. Wallin, Konstantin Mereschkowski y A. S. Famintsyn, en los que se plantea la hipótesis de que las partes no nucleadas de las células eucariotas eran formas evolucionadas de otras bacterias de vida libre. Desde entonces su trabajo se ha centrado en desarrollar esa hipótesis que la condujo a formular su teoría de la endosimbiosis seriada, y posteriormente su visión del papel de la simbiogénesis en la evolución.
Sus aportaciones a la biología y el evolucionismo son múltiples: ha descrito paso a paso y con concreción el origen de las células eucariotas (la SET, que considera su mejor trabajo); junto a K. V. Schwartz ha clasificado la vida en la tierra en cinco reinos agrupados en dos grandes grupos: bacterias y eucariotas; formuló su teoría sobre la simbiogénesis y la importancia de esta en la evolución; apoyó desde el primer momento la hipótesis de Gaia del químico James E. Lovelock, contribuyendo a ella desde la biología e intentando que adquiriera categoría de teoría; y ha realizado una suma de trabajos concretos sobre organismos bacterianos y formas de vida simbióticas, entre otras. Actualmente trabaja profundizando en el estudio de diferentes espiroquetas y su posible protagonismo en procesos simbiogenéticos.
Ella trae una influencia espectacular porque trae la mezcla de biología con humanidades. Ella es del linaje de estos científicos: Galileo Galilei, Copérnico y Newton. Es una científica que trae ideas radicales, pero que el tiempo y la historia demuestran que son correctas.
Teoría de la endosimbiosis seriada (SET)

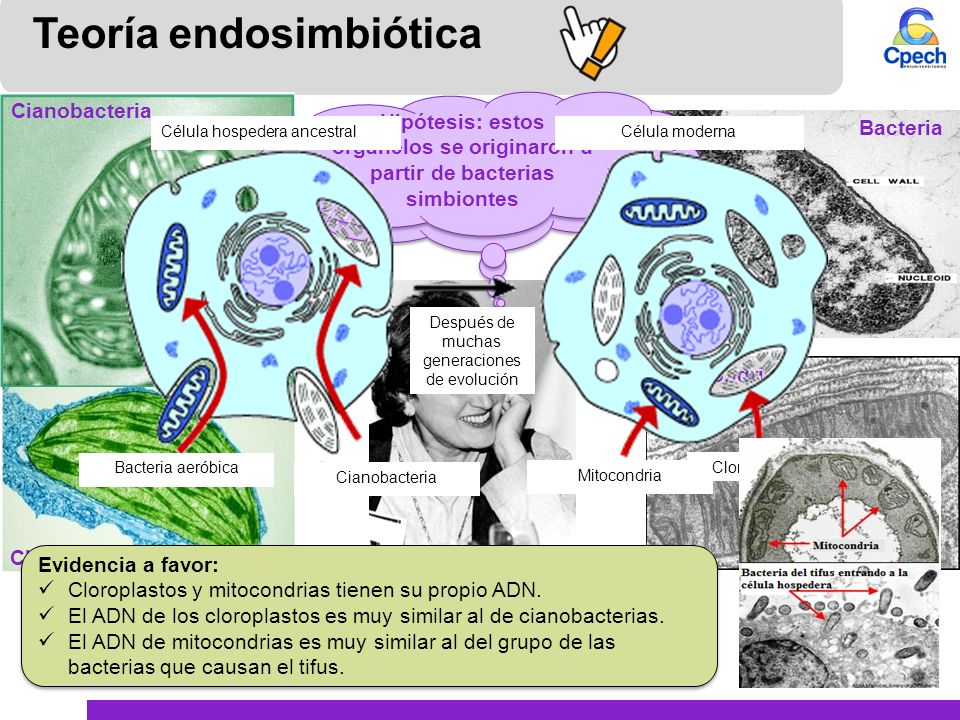
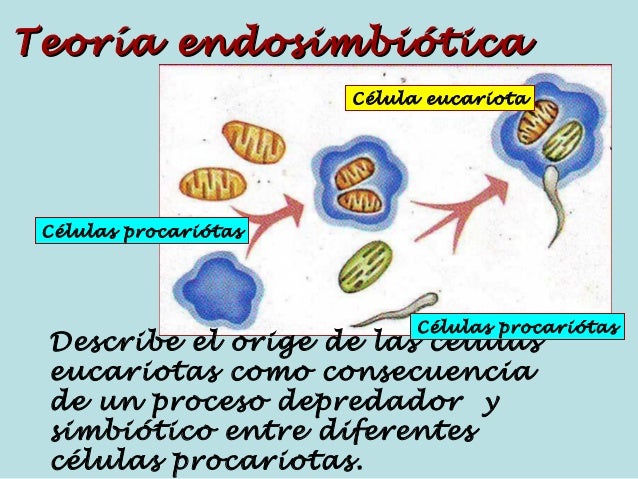
La teoría de la endosimbiosis seriada (SET) describe el origen de las células eucariotas como consecuencia de sucesivas incorporaciones simbiogenéticas de diferentes células procariotas. Margulis considera que esta teoría, en la que define ese proceso con una serie de interacciones simbióticas, es su mejor trabajo.
Tras quince intentos fracasados de publicar sus trabajos sobre el origen de las células eucariotas,en 1966 logró que la revista Journal of Theoretical Biology la aceptara y finalmente publicara a finales de 1967 su artículo Origin of Mitosing Cells (gracias, según ella misma dice, al especial interés del que fuera su editor James F. DaNelly). Max Taylor, profesor de la Universidad de la Columbia Británica especializado en protistas, fue quien la bautizó con el acrónimo SET (Serial Endosymbiosis Theory).

Margulis continuó trabajando en su teoría sobre el origen de las células eucariotas y lo que en principio fue un artículo adquirió las dimensiones de un libro. Nuevamente fracasó en sus intentos de publicar (la que entonces era su editorial, Academia Press, tras mantener el manuscrito retenido durante cinco meses le envió una carta donde le comunicaban su rechazo sin más explicaciones). Tras más de un año de intentos el libro fue publicado por Yale University Press.
El paso de procariotas a eucariotas significó el gran salto en complejidad de la vida y uno de los más importantes de su evolución. Sin este paso, sin la complejidad que adquirieron las células eucariotas, sin la división de trabajo entre membranas y orgánulos presente en estas células, no habrían sido posibles ulteriores pasos como la aparición de los pluricelulares. La vida, probablemente, se habría limitado a constituirse en un conglomerado de bacterias. De hecho, los cuatro reinos restantes procedemos de ese salto cualitativo. El éxito de estas células eucariotas posibilitó las posteriores radiaciones adaptativas de la vida que han desembocado en la gran variedad de especies que existe en la actualidad.

La idea fundamental es que los genes adicionales que aparecen en el citoplasma de las células animales, vegetales y otras células nucleadas no son «genes desnudos», sino que más bien tienen su origen en genes bacterianos. Estos genes son el legado palpable de un pasado violento, competitivo y formador de treguas. Las bacterias que hace mucho tiempo fueron parcialmente devoradas, y quedaron atrapadas dentro de los cuerpos de otras, se convirtieron en orgánulos. Las bacterias verdes que fotosintetizan y producen oxígeno, las llamadas cianobacterias, todavía existen en los estanques y arroyos, en los lodos y sobre las playas. Sus parientes cohabitan con innumerables organismos de mayor tamaño: todas las plantas y todas las algas. […] Me gusta presumir de que nosotros, mis estudiantes, mis colegas y yo, hemos ganado tres de las cuatro batallas de la teoría de la endosimbiosis seriada (SET). Ahora podemos identificar tres de los cuatro socios que subyacen al origen de la individualidad celular. Los científicos interesados en este asunto están ahora de acuerdo en que la sustancia base de las células, el nucleocitoplasma, descendió de las arqueobacterias; en concreto, la mayor parte del metabolismo constructor de proteínas procede de las bacterias termoacidófilas (“parecidas a las del género Thermoplasma»). Las mitocondrias respiradoras de oxígeno de nuestras células y otras células nucleadas evolucionaron a partir de simbiontes bacterianos ahora llamados «bacterias púrpura» o «proteobacterias». Los cloroplastos y otros plástidos de algas y plantas fueron en su tiempo cianobacterias fotosintéticas de vida libre.
En los años 1960 este paso no constituía ningún problema de comprensión, el neodarwinismo se había ya consolidado y desde este paradigma, este paso se habría dado mediante pequeños cambios adaptativos producto de mutaciones aleatorias (errores en la replicación del ADN) que la selección natural se habría encargado de fijar. También, en aquel tiempo, el evolucionismo, liderado principalmente por zoólogos, ponía su énfasis especialmente en el reino animal, las bacterias pasaban desapercibidas para ese campo de la ciencia y eran tratadas casi exclusivamente como agentes patógenos, estudiadas desde el campo de la medicina.
Con anterioridad a Margulis, principalmente a finales del siglo XIX, principios del XX, diferentes científicos intuyeron y llegaron a proponer que el paso de procariotas a eucariotas era el resultado de interacciones simbióticas. Propuestas que fueron desestimadas, incluso ridiculizadas, y que costó perder el prestigio profesional a sus proponentes. Estos trabajos permanecieron olvidados hasta que Margulis, intuyendo igualmente el origen simbiótico de las eucariotas, los rescató y se apoyó en ellos para formular su teoría simbiogenética.
La propuesta simbiogenética de Margulis chocaba (y aún hoy en día choca, aunque se haya aceptado como un hecho puntual) con el paradigma neodarwiniano: la fusión de organismos y la plasmación de esa fusión en el ADN del individuo resultante, choca con la tesis neo-darwiniana de que la evolución de los organismos y la aparición de nuevas especies tiene su origen en errores en la replicación del ADN (mutaciones aleatorias). También, la propuesta de Margulis, con las bacterias como agentes activos en un paso tan importante de la evolución, resultó exótica para el evolucionismo de la época, para el que las bacterias habían pasado desapercibidas. Margulis, para apoyar su hipótesis, reunió «gran número de hechos morfológicos, bioquímicos y paleontológicos» propios y de otros científicos.
El escepticismo y el rechazo inicial que suscitó la posibilidad de que las células eucariotas hubiesen evolucionado por simbio-génesis, tuvieron que modificarse, dando paso a la parcial aceptación de la teoría ya que aún hoy se encuentran entre nosotros los descendientes de aquellas primigenias bacterias que protagonizaron la simbiosis.
Margulis se vio gratamente sorprendida cuando durante los años 1970 su teoría bautizada con el acrónimo SET comenzó a despertar el interés del mundo académico, apareciendo trabajos de investigadores y estudiantes de doctorado que desarrollaban aspectos de su teoría. La endosimbiosis seriada fue apoyada por Rayen, Schnepf & Brown y Taylor; siendo muy atacada por otros autores, sobre todo por Alsopp, Raff & Mahler y por Bogorad.
Desde entonces, la SET se ha ido abriendo camino hasta hoy, que se considera probada la incorporación de tres de los cuatro simbiontes, o si se quiere, dos de los tres pasos propuestos por Margulis (la incorporación de las espiroquetas no se considera probada).
Afortunadamente, gracias a la genial bióloga estadounidense Lynn Margulis, hoy tenemos la solución a este desconcertante enigma: una explicación científica mucho más sensata, lúcida y creativa que la que se ha empeñado en sostener la ortodoxia neodarwinista durante los últimos 35 años, pese a tener la solución, publicada por Margulis en 1967, literalmente delante de sus narices. La ortodoxia se ha resistido con uñas y dientes —en gran medida sigue resistiéndose— a aceptar la teoría de Margulis por el sencillo hecho de que no encaja con sus prejuicios darwinistas. Pero si usted logra liberarse de ese lastre irracional y anticientífico, verá inmediatamente que la idea de Margulis no sólo es la correcta, sino que está dotada de un luminoso poder explicativo. El modelo de Margulis sobre el origen de la célula eucariota no es gradual, pero no le hace ninguna falta para ser factible. Implica un suceso brusco y altamente creativo, pero también enteramente materialista, ciego y mecánico.
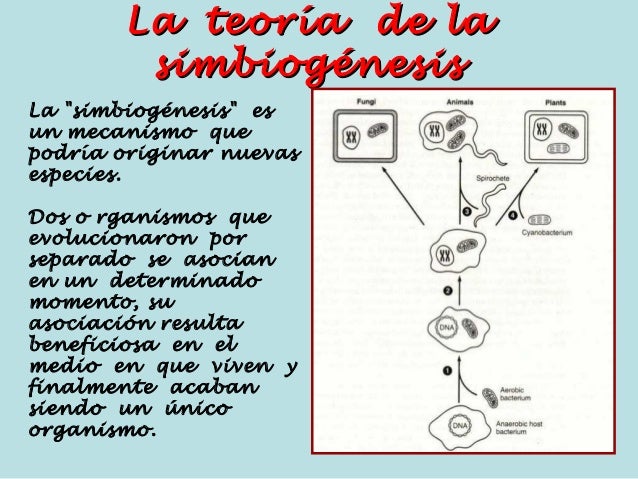
Teoría de la simbiogénesis
La biología evolutiva se centra, desde sus inicios, en el estudio de animales y plantas, a los cuales se considera actores de las innovaciones que han conducido a los máximos niveles de complejidad y especialización. Para Lynn Margulis estos organismos de una superior complejidad son comunidades de individuos menos complejos capaces de sobrevivir.
Margulis formula que son las bacterias, hasta el momento solo de interés para la bacteriología médica, las artífices de esta complejidad y de los actuales refinamientos de los diferentes organismos. A una visión de animales, plantas y, en general, de todos los pluricelulares como seres individuales, contrapone la visión de comunidades de células auto-organizadas, otorgando a dichas células la máxima potencialidad evolutiva. Las considera el motor de la evolución.

Margulis, que se caracteriza por buscar y valorar los antecedentes de sus trabajos, en lugar de diluir estos antecedentes acuñando nuevos términos, procura usar aquellos que ya usaran los autores de estos trabajos anteriores. Este es el caso del término «simbio-génesis» (Konstantin Mereschkowski, 1855-1921), que ella rescata y con el que define el núcleo central de su propuesta para la biología evolutiva.
Considera que, al igual que las células eucariotas (origen de protistas, animales, hongos y plantas) tienen su origen en la simbiogénesis, la mayoría de las adquisiciones de caracteres de los pluricelulares son producto de la incorporación simbiótica de, principalmente, bacterias de vida libre. Resta valor a las mutaciones aleatorias considerándolas sobrevaloradas por el neodarwinismo y plantea una nueva visión de la evolución por incorporación genética. Los organismos tenderíamos a organizarnos en consorcios:
La simbio-génesis reúne a individuos diferentes para crear entidades más grandes y complejas. Las formas de vida simbio-genéticas son incluso más improbables que sus inverosímiles «progenitores». Los «individuos» permanentemente se fusionan y regulan su reproducción. Generan nuevas poblaciones que se convierten en individuos simbióticos multi-unitarios nuevos, los cuales se convierten en «nuevos individuos» en niveles más amplios e inclusivos de integración.
















 Totales: 69.196.182
Totales: 69.196.182 Conectados: 13
Conectados: 13