Algunos quieren encontrar las respuestas en la religión que como todos sabemos es cosa de fe. Creer en aquello que no podemos ver ni comprobar no es precisamente el camino de la ciencia que empieza por imaginar, después conjeturar, más tarde teorizar, se comprueba una y mil veces la teoría aceptada a medias y sólo cuando todo está amarrado y bien atado, todas esas fases pasan a la categoría de una ley o norma que se utiliza para continuar investigando en la buena dirección.

Otros han sido partidarios de la teoría del caos y argumentan que a medida que el nivel de complejidad de un sistema aumenta, entran en juego nuevos tipos de leyes. Entender el comportamiento de un electrón o un quark es una cosa; utilizar este conocimiento para comprender el comportamiento de un tornado es otra muy distinta. La mayoría está de acuerdo con este aspecto. Sin embargo, las opiniones divergen con respecto a si los fenómenos diversos y a veces inesperados que pueden darse en sistemas más complejos que las partículas individuales son realmente representativos del funcionamiento de los nuevos principios de la física, o si los principios implicados son algo derivado y están basados, aunque sea de un modo terriblemente complicado, en los principios físicos que gobiernan el ingente número de componentes elementales del universo.

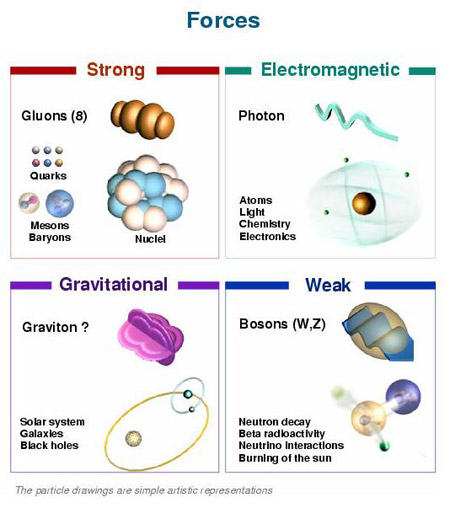
Una Teoría de Gran unificación (TGU), es una teoría que unificaría tres de las cuatro fuerzas fundamentales en la naturaleza: la fuerza nuclear débil, fuerza nuclear fuerte y la fuerza electromagnética.

Casi todo el mundo está de acuerdo en que el hallazgo de la Gran Teoría Unificada (teoría del Todo), no significaría de modo alguno que la psicología, la biología, la geología, la química, y también la física, hubieran resuelto todos sus problemas.

El Universo es un lugar tan maravilloso, rico y complejo que el descubrimiento de una teoría final, en el sentido en el que esta planteada la teoría de súper-cuerdas, no supondría de modo alguno el fin de la ciencia ni podríamos decir que ya lo sabemos todo y para todo tendremos respuestas.

¿Cómo surgió el universo? Esta pregunta equivale a plantearse de qué manera comenzó todo y por este motivo se habla de la teoría del todo. La fórmula matemática definitiva que explique el origen del universo todavía no existe.

Más bien será, cuando llegue, todo lo contrario: el hallazgo de esa “Teoría de Todo” (la explicación completa del universo en su nivel más microscópico, una teoría que no estaría basada en ninguna explicación más profunda) nos aportaría un fundamento mucho más firme sobre el que podríamos construir nuestra comprensión del mundo y, a través de estos nuevos conocimientos, estaríamos preparados para comenzar nuevas empresas de metas que, en este momento, nuestra ignorancia no nos dejan ni vislumbrar. La nueva teoría de Todo nos proporcionaría un pilar inmutable y coherente que nos daría la llave para seguir explorando un universo más comprensible y por lo tanto, más seguro, ya que el peligro siempre llega de lo imprevisto, de lo desconocido que surge sin aviso previo; cuando conocemos bien lo que puede ocurrir nos preparamos para evitar daños.

                                Algunos postulan que el Universo es un holograma

La búsqueda de esa teoría final que nos diga cómo es el universo, el tiempo y el espacio, la materia y los elementos que la conforman, las fuerzas fundamentales que interaccionan, las constantes universales y en definitiva, una formulación matemática o conjunto de ecuaciones de las que podamos obtener todas las respuestas, es una empresa nada fácil y sumamente complicada; la teoría de cuerdas es una estructura teórica tan profunda y complicada que incluso con los considerables progresos que ha realizado durante los últimos décadas, aún nos queda un largo camino antes de que podamos afirmar que hemos logrado dominarla completamente. Se podría dar el caso de que el matemático que encuentre las matemáticas necesarias para llegar al final del camino, aún no sepa ni multiplicar y esté en primaria en cualquier escuela del mundo civilizado.

            Al final de la historia… ¿No acabará todo en un inmenso agujero negro?

Muchos de los grandes científicos del mundo (Einstein entre ellos), aportaron su trabajo y conocimientos en la búsqueda de esta teoría, no consiguieron su objetivo pero sí dejaron sus ideas para que otros continuaran la carrera hasta la meta final. Por lo tanto, hay que considerar que la teoría de cuerdas es un trabajo iniciado a partir de las ecuaciones de campo de la relatividad general de Einstein, de la mecánica cuántica de Planck, de las teorías gauge de campos, de la teoría de Kaluza–Klein, de las teorías de… hasta llegar al punto en el que ahora estamos.

La armoniosa combinación de la relatividad general y la mecánica cuántica es un éxito muy importante. Además, a diferencia de lo que sucedía con teorías anteriores, la teoría de cuerdas tiene la capacidad de responder a cuestiones primordiales que tienen relación con las fuerzas y los componentes fundamentales de la naturaleza.

Igualmente importante, aunque algo más difícil de expresar, es la notable elegancia tanto de las respuestas que propone la teoría de cuerdas, como del marco en que se generan dichas respuestas. Por ejemplo, en la teoría de cuerdas muchos aspectos de la naturaleza que podrían parecer detalles técnicos arbitrarios (como el número de partículas fundamentales distintas y sus propiedades respectivas) surgen a partir de aspectos esenciales y tangibles de la geometría del universo. Si la teoría de cuerdas es correcta, la estructura microscópica de nuestro universo es un laberinto multidimensional ricamente entrelazado, dentro del cual las cuerdas del universo se retuercen y vibran en un movimiento infinito, marcando el ritmo de las leyes del cosmos.

Lejos de ser unos detalles accidentales, las propiedades de los bloques básicos que construyen la naturaleza están profundamente entrelazadas con la estructura del espacio-tiempo. Son muchos los parámetros que rigen la dinámica universal y, todos ellos, perfectamente sincronizados hacen posible que se formen átomos y galaxias… ¡Y también la Vida!

Claro que, siendo todos los indicios muy buenos, para ser serios, no podemos decir aún que las predicciones sean definitivas y comprobables para estar seguros de que la teoría de cuerdas ha levantado realmente el velo de misterio que nos impedía ver las verdades más profundas del universo, sino que con propiedad se podría afirmar que se ha levantado uno de los picos de ese velo y nos permite vislumbrar algo de lo que nos podríamos encontrar.

                    Parece que en la teoría de cuerdas subyace la Gravedad Cuántica

La teoría de cuerdas, aunque en proceso de elaboración, ya ha contribuido con algunos logros importantes y ha resuelto algún que otro problema primordial como por ejemplo, uno relativo a los agujeros negros, asociado con la llamada entropía de Bekenstein–Hawking, que se había resistido pertinazmente durante más de veinticinco años a ser solucionada con medios más convencionales. Este éxito ha convencido a muchos de que la teoría de cuerdas está en el camino correcto para proporcionarnos la comprensión más profunda posible sobre la forma de funcionamiento del universo, que nos abriría las puertas para penetrar en espacios de increíble belleza y de logros y avances tecnológicos que ahora ni podemos imaginar.

Como he podido comentar en otras oportunidades, Edward Witten, uno de los pioneros y más destacados experto en la teoría de cuerdas, autor de la versión más avanzada y certera, conocida como teoría M, resume la situación diciendo que:

“La teoría de cuerdas es una parte de la física que surgió casualmente en el siglo XX, pero que en realidad era la física del siglo XXI”.

Witten, un físico-matemático de mucho talento, máximo exponente y punta de lanza de la teoría de cuerdas, reconoce que el camino que está por recorrer es difícil y complicado. Habrá que desvelar conceptos que aún no sabemos que existen.

El hecho de que nuestro actual nivel de conocimiento nos haya permitido obtener nuevas perspectivas impactantes en relación con el funcionamiento del universo es ya en sí mismo muy revelador y nos indica que podemos estar en el buen camino revelador de la rica naturaleza de la teoría de cuerdas y de su largo alcance. Lo que la teoría nos promete obtener es un premio demasiado grande como para no insistir en la búsqueda de su conformación final.

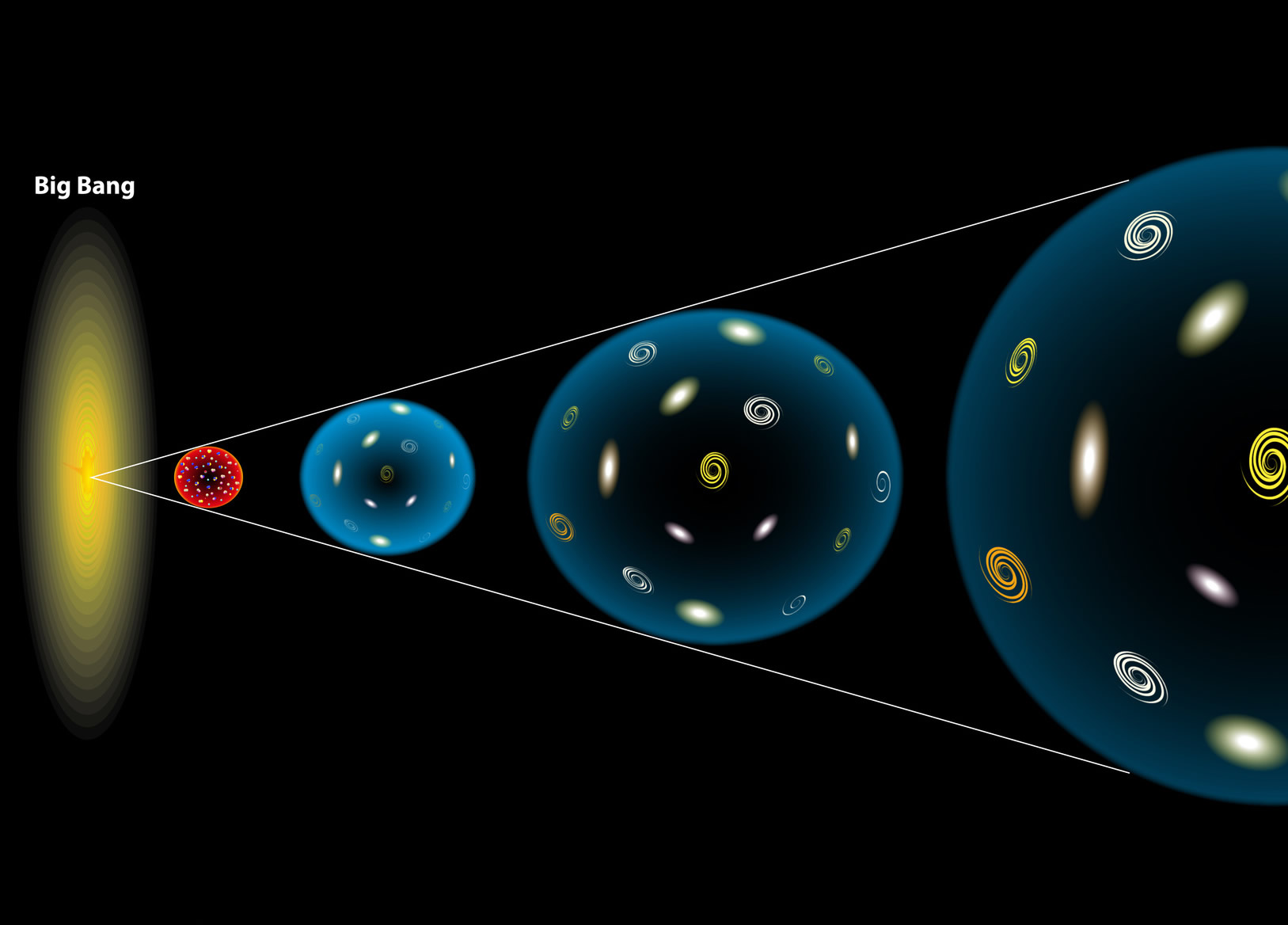
El universo, la cosmología moderna que hoy tenemos, es debida a la teoría de Einstein de la relatividad general y las consecuencias obtenidas posteriormente por Alexandre Friedmann. El Big Bang, la expansión del universo, el universo plano y abierto o curvo y cerrado, la densidad crítica y el posible Big Crunch.

Un comienzo y un final que abarcará miles y miles de millones de años de sucesos universales a escalas cosmológicas que, claro está, nos afectará a nosotros, insignificantes mortales habitantes de un insignificante planeta, en un insignificante sistema solar creado por una insignificante y común estrella.

Pero… ¿somos en verdad tan insignificantes?

Emilio Silvera V.

[?]

                                       

 

Los físicos que abordan el multiverso coinciden en que sería imposible visitar los universos vecinos, pero pueden estar ahí. / The Washington Post (Washington Post)

 

Nuestro universo, con lo inmenso que es, con centenares de miles de millones de galaxias visibles y tantos millones de estrellas en cada una de ellas, puede que no sea el único que exista. Tal vez hay otros universos, distintos del que conocemos, y alguno parecido… ¿Sería posible visitarlos? ¿Echarles un vistazo? ¿Comprobar siquiera si efectivamente están por ahí como burbujas aisladas… a no ser que entren algunas en colisión? Medio centenar de expertos estadounidenses, europeos y españoles se han reunido esta semana en un encuentro científico de alto nivel celebrado en la Universidad Autónoma de Madrid (UAM) para discutir precisamente los multiversos y las teorías en las que emerge su existencia.

El problema del Multiverso

En realidad, cuando observamos el Universo y vemos los fenómenos que ahí ocurren, las transiciones de fase que se producen en la materia, las energías desatadas que por todas partes son proyectadas en explosiones de supernovas y colisiones de estrellas de neutrones o agujeros negros, cuando dos inmensas galaxias se funden en una y se fusionan mediante un Vals de Gravedad que dura algunos millones de años… Cuando todo eso ocurre, podríamos pensar que, la Vida, no está preparada para ese entorno. Sin embargo, ¡aquí estamos!

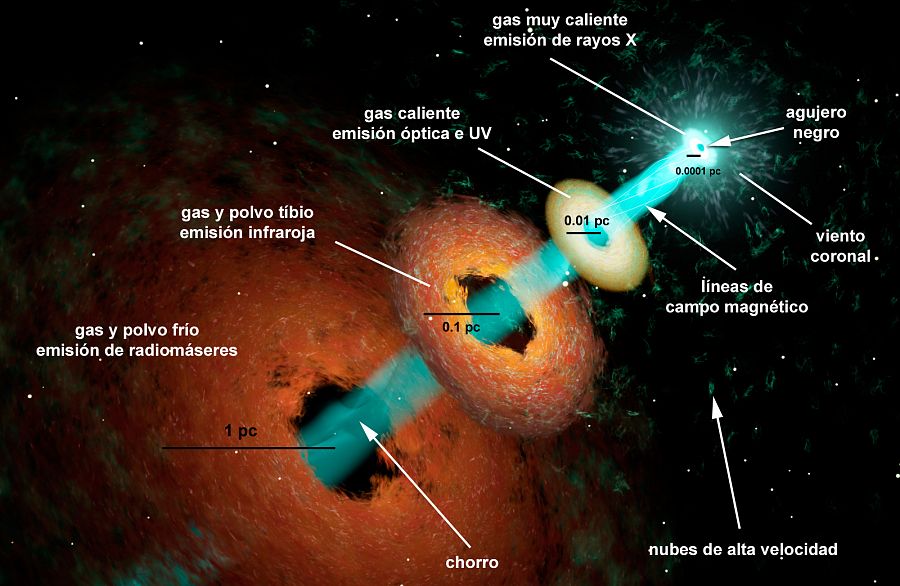
Como nos dice la filosofía, nada es como se ve a primera vista, todo depende del punto de vista desde el que miremos las cosas, de la perspectiva que nos permita nuestra posición física y, la intelectual también. No todos podemos ver las cosas de la misma manera. La imagen de abajo que es una Nebulosa como otras tantas, ¿qué te dice a tí? ¿qués es lo que ahí puedes ver? ¿qué deduces de los componentes de la nebulosa? ¿qué puede surgir de ahí y de otros lugares como este de abajo? ¿Cómo llegó a formarse tal conglomerado de gas y polvo?

De forma cotidiana denominamos masa a la cantidad de materia de un cuerpo. Prácticamente toda la masa de los átomos que componen la materia se debe a la masa de sus núcleos. La masa de los núcleos atómicos esencialmente corresponde a la de los protones y neutrones que los forman. Sin embargo, la masa de un protón o un neutrón es mucho mayor que la suma de las masas de los quarks que los forman (éstas son tan pequeñas que sólo explican el 1% de la masa total). El 99% de la masa de protones y neutrones está asociada a la energía cinética de los quarks en su interior, que se mueven a velocidades relativistas, pero que no escapan por estar confinados por la fuerza de color. Esta masa corresponde por tanto a una energía interna de las partículas compuestas.

La energía interna no puede, sin embargo, explicar la masa de las partículas elementales (como los propios quarks, los leptones o los bosones Z y W), por no estar compuestos de partículas más pequeñas.

¿Cuál es el origen de la masa de las partículas elementales?

[?]

Leibniz nos decía:

“Todo estado presente de una sustancia simple es naturalmente, una consecuencia de su estado anterior, de modo que se presente está cargado de su futuro”.

 

Y, Marco Aurelio:

“Quien ha visto las cosas presentes ha visto todo, todo lo ocurrido desde la eternidad y todo lo que ocurrirá en el tiempo sin fin; pues todas las cosas son de la misma clase y de la misma forma.”

El primero nos señalaba el camino recorrido por la evolución hasta nuestros días y, señalaba los cambios que el ritmo del universo produciría en todo lo presente que es producto del pasado, lo mismo que el futuro, lo será del presente, es decir, todo es debido a la causalidad. El segundo, más profundo, nos daba a entender que todo está hecho de la misma cosa. Desde una flor hasta una galaxia, todos son Quarks y Leptones.

A finales del siglo XIX, la física experimentó importantes avances que pavimentaron el camino para la física de partículas. El descubrimiento de fenómenos como la radiactividad, la naturaleza corpuscular de la luz y el electrón como partícula fundamental, junto con la postulación del átomo como estructura divisible, marcaron un punto de inflexión. Estos descubrimientos sentaron las bases para la comprensión de la materia a nivel subatómico y el desarrollo de la física cuántica. 

Los finales del siglo XX quizá sean recordados en la historia de la ciencia como la época en que la física de partículas, el estudio de las estructuras más pequeñas de la naturaleza, unió sus fuerzas a la cosmología, el estudio del universo como un todo. Juntas, estas dos disciplinas esbozarían el esquema de la historia cósmica, investigando el pasado de las estructuras naturales en un ámbito de escala enorme, desde los núcleos de los átomos hasta los cúmulos de las galaxias.

Fue un matrimonio apresurado de dos disciplinas muy diferentes. Los cosmólogos tienden a ser solitarios, con la mirada fija en los horizontes lejanos del espacio “infinito” y del tiempo “sin fin”, y acumulan fascinados sus datos que son, en realidad, los hilos de la antigua luz que llegaron de las estrellas lejanas situadas en los confines de ese universo presentido y lejano. Los físicos de partículas, en contraste con ellos, son relativamente gregarios -tienen que serlo, pues ni siquiera un Einstein sabe suficiente física como para hacerlo todo él solo- y físicos: son por tradición transmitida estudiosos del aquí y ahora, inclinados a curvar cosas, volar cosas y desmontar cosas. Los físicos trabajan dura y rápidamente, obsesionados por la leyenda de que es probable que tengan muchas ideas nuevas útiles después de los cuarenta, mientras que los comólogos son más a menudo jugadores de finales, adeptos a las visiones de vasto alcance, de quiénes cabe esperar que realicen investigaciones productivas cuando ya les blanquea el cabello. Si los físicos son los zorros de los que Arquíloco decía que saben muchas cosas, los cosmólogos son más afines a las centenarias tortugas que saben una sola gran cosa.

Sin embargo, a finales de los años setenta, los físicos de partículas se aventuraron a acudir a los seminarios de cosmología a estudiar las galaxias y los quásars, mientras que los cosmólogos alquilaron máquinas del CERN y el Fermilab para trabajar en la física de altas energías en las instalaciones subterráneas desde donde no se veían las estrellas. En 1985 Murray Gell-Mann declaró que “la física de partículas elementales y el estudio del universo primitivo, las dos ramas fundamentales de la ciencia de la naturaleza, se habían fundido esencialmente.”

Su terreno de encuentro fue el Big Bang. Los físicos identificaron simetrías en la naturaleza que hoy están rotas pero que estuvieron intactas en un entorno de altas energías. Los cosmólogos informaron que el universo estuvo antaño en tal estado de alta energía, en las etapas iniciales del Big Bang. Unidas ambas cosas, aparece el cuadro de un universo perfectamente simétrico cuyas simetrías se quebraron a medida que se expandió y se enfrió, creando partículas de materia y energías que encontramos hoy a nuestro alrededor y estampándoles las pruebas de su genealogía. Steven Winberg, un adalid de aquella alianza, describió la teoría electrodébil unificada en términos de su relación con el universo primitivo:

Lo que es tan especial en la teoría electrodébil es que las partículas [portadoras de fuerza] forman una familia estrechamente unida, con cuatro miembros: la W⁺, la W^– de carga opuesta, la Z neutra y el cuarto miembro es nuestro viejo amigo el fotón, portador del electromagnetismo. Son todas hermanas, estrechamente relacionadas por el principio de simetría que dice que son todas la misma cosa, pero que la simetría se ha roto. La simetría está allí, en las ecuaciones subyacentes de la teoría, pero no es evidente en las partículas mismas. Por eso las W y la Z son mucho más pesadas que el fotón.

Estas partículas – las mismas cuya aparición en el acelerador del CERN verificó la teoría electrodébil – son las mediadoras intercambiables en las interacciones de fuerzas electromagnéticas y débiles, lo que las hace indistinguibles.  En ese tiempo, el Universo está gobernando sólo por tres fuerzas: la gravedad, la interacción nuclear fuerte y la electrodébil.

Precisamente eso nos da la pista para creer que hubo un tiempo,  en el pasado, en el universdo muy temprano, en que la temperatura estaba muy por encima de algunos cientos de veces de la masa del protón, cuando la simetría aún no se había roto, y la fuerza débil y la electromagnética no sólo eran la misma matemáticamente, sino realmente la misma. Un físico que hubiera vivido por aquel entonces, lo que es difícil imaginar, no habría visto ninguna diferencia real entre las fuerzas producidas por el intercambio de estas cuatro partículas:

Las W, la Z y el fotón.

Más atrás de ese tiempo nos quedamos en el misterio y envueltos en una gran nebulosa de ignorancia.  Cada uno se despacha a su gusto para lanzar conjeturas y teorizar sobre lo que pudo haber sido.   Seguramente, en el futuro, será la teoría M (de supercuerdas) la que contestará esas preguntas sin respuestas ahora, si por fin, llegamos a ser capaces de verificarla y, si no es así, vendrá alguna otra teoría avanzada que lo hará.

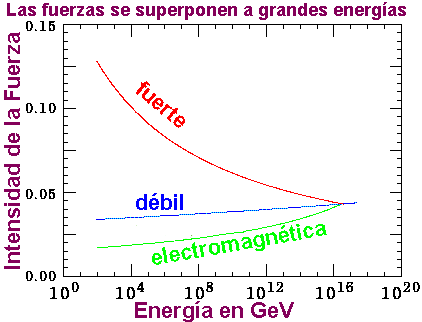
En los 10^-35 de segundo desde el comienzo del tiempo, entramos en un ámbito en el que las condiciones cósmicas son aún menos conocidas.  Si las grandes teorías unificadas son correctas, se produjo una ruptura de la simetría por la que la fuerza electronuclear unificada se escindió en las fuerzas electrodébil y las fuertes.  Si es correcta la teoría de la supersimetría, la transición puede haberse producido antes, había involucrado a la gravitación.

Elaborar una teoría totalmente unificada es tratar de comprender lo que ocurrió en ese tiempo remoto que, según los últimos estudios está situado entre 15.000 y 18.000 millones de años, cuando la perfecta simetría que, se pensaba, caracterizó el Universo, se hizo añicos para dar lugar a los simetrías rotas que hallamos a nuestro alrededor y que nos trajo las fuerzas y constantes Universales que, paradójicamente, hicieron posible nuestra aparición para que ahora, sea posible que, alguien como yo esté contando lo que pasó.

Pero hasta que no tengamos tal teoría no podemos esperar comprender lo que realmente ocurrió en ese Universo primitivo.  Los límites de nuestras conjeturas actuales cuando la edad del Universo sólo es de 10^-43 de segundo, nos da la única respuesta de encontrarnos ante una puerta cerrada.

La Era de Planck y la espuma cuántica

Del otro lado de esa puerta está la época de Planck, un tiempo en que la atracción gravitatoria ejercida por cada partícula era comparable en intensidad a la fuerza nuclear fuerte. Así que, llegados a este punto podemos decir que la clave teórica que podría abrir esa puerta sería una teoría unificada que incluyese la gravitación. La persona que llegue a esa teoría llegará a la mayor profundidad en la contemplación del alba del tiempo.

¿Qué es lo que verá?

Pero, eso sí, mientras tanto seguimos produciendo imágenes de todo tipo mediante las cuáles se nos quiere hacer ver que, la materia oscura  está ahí presente, sin embargo, nada de lo que estamos viendo es “materia oscura”  son filamentos de plasma, polvo y gas interestelar, y otros objetos y sustancias que en el Universo se producen mediante la química de la energía de las estrellas presente en esos lugares pero, “materia oscura” me parece que no. Claro que, una cosa no se puede discutir, alguna clase de “materia” o de “fuerza” desconocida (o lo quen sea) estaba allí presente para hacer posible que surgieran las primeras estrellas y galaxias.

Por supuesto, en aquel tiempo primero, no hay moléculas, ni átomos, ni núcleos atómicos, y, a 10-⁶ (0.000001) de segundo después del comienzo del tiempo, tampoco hay neutrones ni protones.  El Universo es un océano de Quarks  libres y otras partículas elementales.

 Si nos tomamos el trabajo de contarlos, hallaremos que por cada mil millones de ant-quarks existen mil millones y un quark.  Esta asimetría es importante.  Los pocos quarks en exceso destinados a sobrevivir a la aniquilación general quark-anti-quark formaran todos los átomos de materia del Universo del último día.  Se desconoce el origen de la desigualdad; presumiblemente obedezca a la ruptura de una simetría materia antimateria en alguna etapa anterior.

Nuestra indicutible ignorancia siempre nos llevó ante muchas puertas cerradas que, de alguna manera misteriosa, pudimos abrir para asombrarnos ante las maravillas que detrás de ellas existen. Hombres y mujeres de nuestra especie han sido capaces de encontrar esas llaves perdidas que posibilitaron abrir aquellas puertas, descorriendo el velo que tapaba y escondía los misterios de la naturaleza.

Creo, en mi enorme ignorancia, que se verán más puertas cerradas. En las que, en lo anto de sus dinteles habrá carteles que digan: Materia Oscura, Singularidad, Agujeros Negros, Multiversos, Fluctuaciones de vacío, Energía de punto cero, teoría luz-luz…y muchas más puertas que nos exigen encontrar las llaves que la puedan abrir para mirar dentro de sus recintos para saber….y, al entrar, ver y comprender sobre todo aquello, con sorpresa veremos que, al fondo y en penumbra, otras puertas con otros letreros nuevos…están esperando allí, para que comencemos de nuevo a buscar las llaves que las abran para mostrarnos sus secretos…Esos puertas cerradas, amigos míos, siempre estarán ahí esperándonos. O, lo que es lo mismo, siempre detrás de un nuevo conocimiento, encontraremos otras nuevas preguntas, otras puertas cerradas que esconderán más saber de cosas que ignoramos.

Emilio Silvera Vázquez

[?]

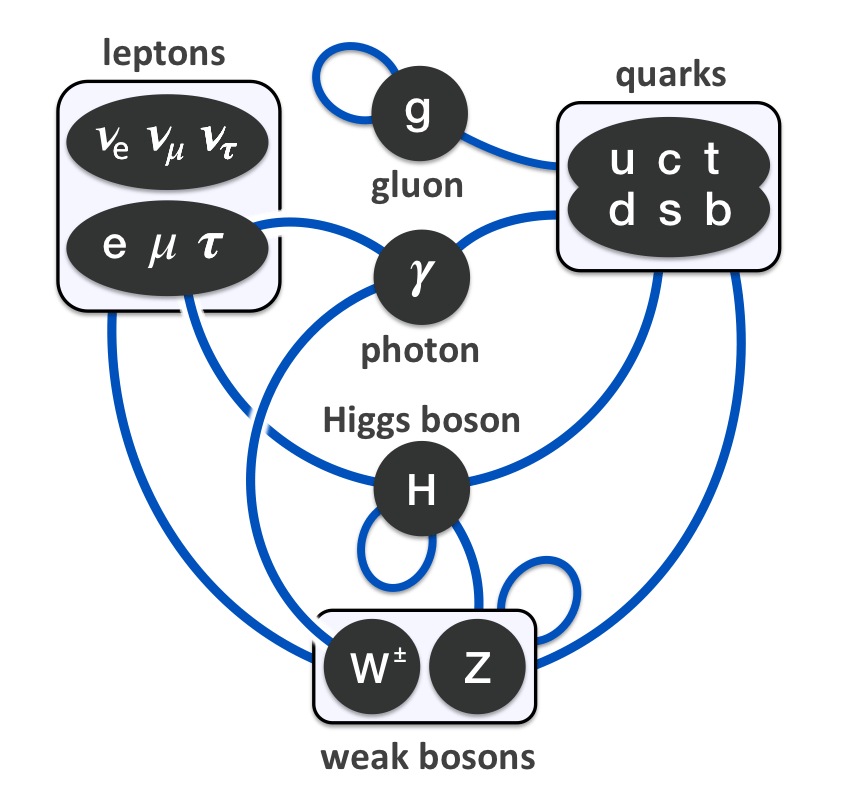
Un bosón es una partícula elemental (o estado ligado de partículas elementales, por ejemplo, un núcleo atómico o átomo) con espín entero, es decir, una partícula que obedece a la estadísitca de Bose-Einstein (estadísictica cuántica), de la cual deriva su nombre. Los bosones son importantes para el Modelo estándar de las partículas. Son bosones vectoriales de espín uno que hacen de intermediarios de las interacciones gobernadas por teorías gauge. Los Fotones, los Gluones, el hipotético Gravitón, las partículas W y Z son todos bosones mensajeros del electromagnetismo y todas las formas de radiación, de la fuerza nuclear fuerte, de la Gravedad, y, de la fuerza nuclear débil.

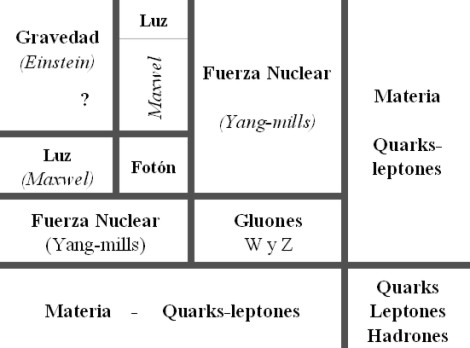
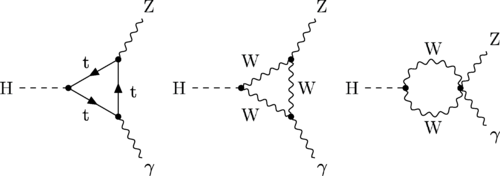
En física se ha sabido crear lo que se llama el Modelo estándar y, en él, los Bosones quedan asociados a las tres fuerzas que lo conforman, el fotón es el Bosón intermediario del electromagnetismo, los W^+, w^–y Zº son bosones gauge que transmiten la fiuerza en la teoría electrodébil, mientras que los gluones son los bosones de la fuerza fuerte, los que se encargan de tener bien confinados a los Quarks conformando protones y neutrones para que el núcleo del átomo sea estable. La Gravedad, no se ha dejado meter en el modelo y, por eso su bosón no es de gauge. El gravitón que sería la partícula mediadora de la gravitación sería el hipótetico cuanto de energía que se intercambia en la interacción gravitacional.

Ejemplos de los Bosones gauge son los fotones en electrodinámica cuántica (en física, el fotón se representa normalmente con el símbolo 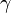, que es la letra griega gamma), los gluones en cromodinámica cuántica y los bosones W y Z en el modelo de Winberg-Salam en la teoría electrodébil que unifica el electromagnetismo con la fuerza débil. Si la simetría  gauge de la teoría no está rota, el bosón gauge es no masivo. Ejemplos de bosones gauge no masivos son el fotón y el gluón.

Si la simetría gauge de la teoría  es una simetría rota el bosón gauge tiene masa no nula, ejemplo de ello son los bosones W y Z . Tratando la Gravedad, descrita según la teoría de la relatividad general, como una teoría gauge, el bosón gauge sería el gravitón, partícula no masiva y de espín dos.

Diagrama de Feynman mostrando el intercambio de un fotón virtual (simbolizado por una línea ondulada y ) entre un positrón y un electrón.De esta manera podemos llegar a comprender la construcción que se ha hecho de las interacciones que están siempre intermediadas por un nosón mensajero de la fuerza.

En el modelo estándar, como queda explicado,  hay tres tipos de bosones de gauge: fotones, bosones W y Z y gluones. Cada uno corresponde a tres de las cuatro interacciones: fotones son los bosones de gauge de la interacciones electromagnética, los bosones W y Z traen la interacción débil, los gluones transportan la interacción fuerte.  El gravitón, que sería responsable por la interacción gravitacional, es una proposición teórica que a la fecha no ha sido detectada. Debido al confinamiento del color, los gluones aislados no aparecen a bajas energías.

Aquí, en el gráfico, quedan representadas todas las partículas del Modelo estándar, las familias de Quarks y Leptones que conforman la materia y los bones que intermedian en las interacciones o fuerzas fundamentales que están presentes en el Universo. La Gravedad no ha podido ser incluida y se ha negado a estar unida a las otras fuerzas. Así el bosón que la transnmite, tampoco está en el modelo que es incompleto al dejar fuera la fuerza que mantiene unidos los planetas en los sistemas solares, a las galaxias en los cúmulos y nuestros pies unidos a la superficie del planeta que habitamos. Se busca una teoría que permita esta unión y, los físicos, la laman gravedad cuántica pero… ¡no aparece por ninguna parte!

Llegados a este punto tendremos que retroceder, para poder comprender las cosas, hasta aquel trabajo de sólo ocho páginas que publicó  Max Planck  en 1.900 y  lo cambió todo. El mismo Planck se dió cuenta de que, todo lo que él había tenido por cierto durante cuarenta años, se derrumbaba con ese trabajo suyo que, venía a decirnos que el mundo de la materia y la nergía estaba hecho a partir de lo que el llamaba “cuantos”.

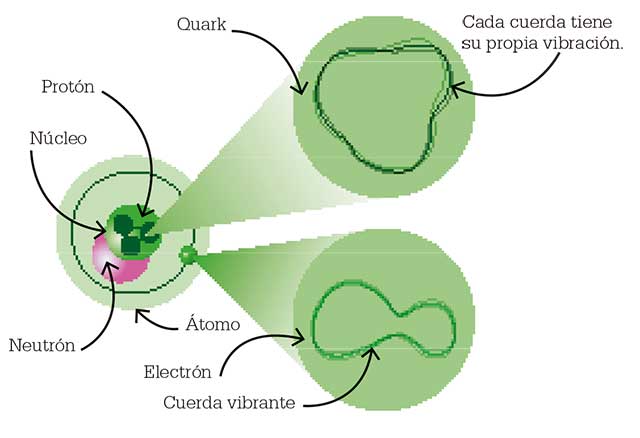
Supuso el nacimiento de la Mecánica Cuántica (MC), el fin del determinismo clásico y el comienzo de una nueva física, la Física Moderna, de la que la Cuántica sería uno de sus tres pilares junto con la Relatividad y la Teoría del Caos. Más tarde, ha aparecido otra teoría más moderna aún por comprobar, ¿las cuerdas…?

El universo según la teoría de las cuerdas sería entonces una completa extensa polícroma SINFONIA ETERNA de vibraciones, un multiverso infinito de esferas, cada una de ellas un universo independiente causalmente, en una de esas esferas nuestra vía láctea, en ella nuestro sistema solar, en él nuestro planeta, el planeta tierra en el cual por una secuencia milagrosa de hechos se dió origen a la vida autoconsciente que nos permite preguntarnos del cómo y del por qué de todas las cosas que podemos observar y, también, de las que intiuimos que están ahí sin que se dejen ver.

Claro que, cuando nos adentramos en ese minúsculo “mundo” de lo muy pequeño, las cosas difieren y se apartan de lo que nos dicta el sentido común que, por otra parte, es posible que sea el menos común de los sentidos. Nos dejamos guiar por lo que observamos, por ese mundo macroscópico que nos rodea y, no somos consciente de ese otro “mundo” que está ahí formando parte del universo y que, de una manera muy importante incide en el mundo de lo grande, sin lo que allí existe, no podría existir lo que existe aquí.

[?]

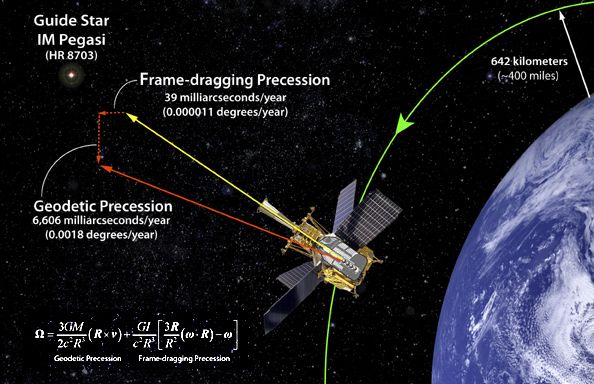
                                                                               Satélite Gravity Probe B.

Dedicado a medir la curvatura del campo gravitatorio terrestre debido a la teoría de la relatividad de Einstein. La gravedad ha sido medida y comprobada de muchas maneras pero… ¡Gravedad cuántica! ¿qué es eso? La imaginación anda más rápida que los conocimientos. Sin embargo, así hemos ido avanzando en el transcurrir del Tiempo.

La llamada gravedad cuántica trata de fundir en una sola las dos teorías físicas más soberbias con las que contamos, la relatividad general y la mecánica cuántica, que en el estado actual de nuestro conocimiento parecen incompatibles. Su estudio, ahora mismo, es en algunos aspectos análogo a la física de hace cien años, cuando se creía en los átomos, pero se ignaraban los detalles de su estructura.

Desde aquel día en que Kaluza, le escribió a Einstein una carta con su teoría de las cinco dimensiones, en la que unía la Gravedad con el Electromagnetismo, la puerta de las dimensiones más altas quedó abierta y a los teóricos se les regaló una herramienta maravillosa: el hiperespacio; todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí sí es posible encontrar esa soñada teoría de la gravedad cuántica.

Así que las teorías se han embarcado a la búsqueda de un objeto audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos; una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.

                       Hay que reconocer que nos dice mucho

Claro que saber, lo que el universo es, leyendo una ecuación, por muy ingeniosa que ésta sea y por mucho que la misma pueda abarcar… Parece poco probable. ¿Dónde radica el problema? El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el nuevo acelerador de partículas LHC, la máquina más potente del mundo hasta el momento.

La verdad es que la teoría que ahora tenemos, el modelo estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías. ¡Necesitamos algo más avanzado!

A pesar de su grandeza, se queda corto para que nos pueda decir, lo que necesitamos saber: Si nos habla del Bosón de Higgs, ya estará bien

Se ha dicho que la función de la partícula de Higgs es la de dar masa a las partículas que carecen de ella, disfrazando así la verdadera simetría del mundo. Cuando su autor lanzó la idea a la comunidad científica, resultó además de nueva, muy extraña. El secreto de todo radica en conseguir la simplicidad: el átomo resultó ser complejo, lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones. Resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún; los quarks que estaban instalados en nubes de otras partículas llamadas gluones, y ahora queremos continuar profundizando, sospechando que después de los quarks puede haber algo más.

                             Ahí las partículas toman su masa por el efecto frenado

Nos dicen que existen lugares que llaman los Océanos de Higgs, y, por ellos, circula libremente el dichoso Bosón que, también según nos dicen, proporciona la masa al resto de las partículas. Todo el Universo está permeado por esa especie de sustancia -como el viejo éter- que los griegos llamaban Ylem cósmico y que, a medida que el tiempo avanza, le vamos cambiando el nombre. Pues bien, ahí, en ese “océano” dicen que está el Bosón dador de masas.

Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes, es decir, que si miramos a las estrellas en una noche clara, estamos mirando el campo de Higgs. Las partículas influidas por este campo toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado otras veces, tales como: del campo gravitatorio o del electromagnético.

Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquirirá energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra. Como E = mc², ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein: la masa, m, tiene en realidad dos partes; una es la masa en reposo, m₀, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c) en los aceleradores, o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.

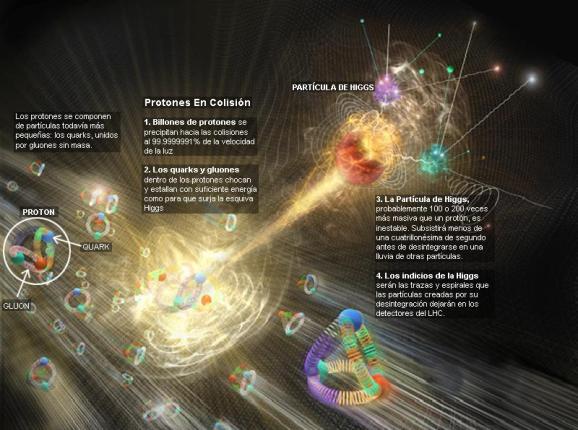
Pero la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas. Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs.

La influencia de Higgs en las masas de los quarks y de los leptones nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.

Hasta ahora no tenemos ni idea de qué reglas controlan los incrementos de masa generados por Higgs (de ahí la expectación creada por el nuevo acelerador de partículas LHC), pero el problema es irritante: ¿por qué sólo esas masas ­­- las masas de los W⁺, W^–, Z⁰, y el up, down, encanto, extraño, top y bottom, así como los leptones – que no forman ningún patrón obvio?

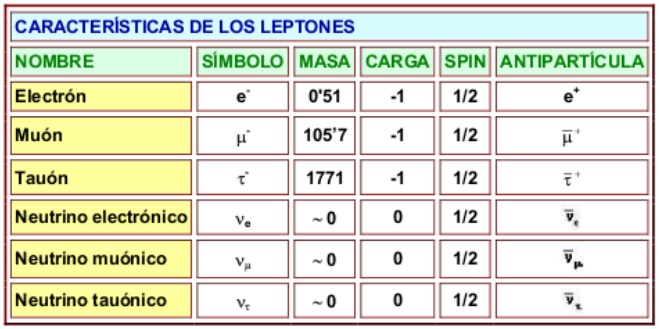
Las masas van desde la del electrón (0’0005 GeV) a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-Salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnética y débil. En la unidad hay cuatro partículas mensajeras sin masa – los W⁺, W^–, Z⁰ y el fotón – que llevan la fuerza electrodébil. Además está el campo de Higgs, y rápidamente, los W y Z absorben la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos), y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen las teorías. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa.

Tampoco el Higgs es una partícula especial porque sea una excitación del del campo de Higgs que nos permita explorar sus propiedades, porque en las teorías sin Higgs o con Higgs compuesto también hay excitaciones del vacío que nos permiten explorar el campo.”

Eso nos dicen en el magnifico Blog de Francis (th)E mule Science’s News.

Partícula	Símbolo	Masa (en GeV/c2)	Carga eléctrica	Espín	Interacción
Fotón		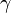0	0	1	electromagnética
Bosón W	W±	80,4	± 1	1	débil
Bosón Z	Z0	91,187	0	1	débil
Gluón	g	0	0	1	fuerte

Las masas de los W y Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil, y las relajadas sonrisas de los físicos teóricos nos recuerdan que Hooft y Veltman dejaron sentado que la teoría entera está libre de infinitos.

Todos los intentos y los esfuerzos por hallar una pista de cuál era el origen de la masa fallaron. Feynman escribió su famosa pregunta: “¿por qué pesa el muón?”. Ahora, por lo menos, tenemos una respuesta parcial, en absoluto completa. Una voz potente y segura nos dice “¡Higgs!”. Durante más de sesenta años los físicos experimentadores se rompieron la cabeza con el origen de la masa, y ahora el campo de Higgs presenta el problema en un contexto nuevo; no se trata sólo del muón. Proporciona, por lo menos, una fuente común para todas las masas. La nueva pregunta feynmaniana podría ser: ¿Cómo determina el campo de Higgs la secuencia de masas, aparentemente sin patrón, que da a las partículas de la materia?

La variación de la masa con el estado de movimiento, el cambio de masa con la configuración del sistema y el que algunas partículas (el fotón seguramente, y los neutrinos posiblemente) tengan masa en reposo nula son tres hechos que ponen en entredicho que el concepto de masa sea un atributo fundamental de la materia. Habrá que recordar aquel cálculo de la masa que daba infinito y nunca pudimos resolver; los físicos sólo se deshicieron de él “renormalizándolo”, ese truco matemático que emplean cuando no saben hacerlo bien.

                                            ¿Sabremos alguna vez cómo adquieren masa las partículas?

Ese es el problema de trasfondo con el que tenemos que encarar el problema de los quarks, los leptones y los vehículos de las fuerzas, que se diferencian por sus masas. Hace que la historia de Higgs se tenga en pie: la masa no es una propiedad intrínseca de las partículas, sino una propiedad adquirida por la interacción de las partículas y su entorno.

La idea de que la masa no es intrínseca como la carga o el espín resulta aún más plausible por la idílica idea de que todos los quarks y fotones tendrían masa cero. En ese caso, obedecerían a una simetría satisfactoria, la quiral, en la que los espines estarían asociados para siempre con su dirección de movimiento. Pero ese idilio queda oculto por el fenómeno de Higgs.

Una cosa más; hemos hablado de los bosones gauge y de su espín de una unidad. Hemos comentado también las partículas fermiónicas de la materia (espín de media unidad). ¿Cuál es el pelaje de Higgs? Es un bosón de espín cero. El espín supone una direccionalidad en el espacio, pero el campo de Higgs da masa a los objetos donde quiera que estén y sin direccionalidad. Al Higgs se le llama a veces “bosón escalar” (sin dirección) por esa razón.

La interacción débil, recordaréis, fue inventada por E. Fermi para describir la desintegración radiactiva de los núcleos, que era básicamente un fenómeno de poca energía, y a medida que la teoría de Fermi se desarrolló, llegó a ser muy precisa a la hora de predecir un enorme número de procesos en el dominio de energía de los 100 MeV. Así que ahora, con las nuevas tecnologías y energías del LHC, las esperanzas son enormes para, por fin, encontrar el bosón de Higgs origen de la masa… y algunas cosas más.

Hay que responder montones de preguntas: ¿cuáles son las propiedades de las partículas de Higgs? y, lo que es más importante, ¿cuál es su masa? (Bueno, parece que, en el último experimento apareció se localizó un bosón con ~125 GeV que, según parece, podría ser el esquivo Hihhs)¿Cómo reconoceremos una si nos la encontramos en una colisión del LHC? ¿Cuántos tipos hay? ¿Genera el Higgs todas las masas o sólo las hace incrementarse? ¿Cómo podemos saber más al respecto? Cómo es su partícula, nos cabe esperar que la veremos ahora después de gastar más de 50.000 millones de euros en los elementos necesarios para ello.

También a los cosmólogos les fascina la idea de Higgs, pues casi se dieron de bruces con la necesidad de tener campos escalares que participasen en el complejo proceso de la expansión del universo, añadiendo pues, un peso más a la carga que ha de soportar el Higgs.

El campo de Higgs, tal como se lo concibe ahora, se puede destruir con una energía grande, o temperaturas altas. Éstas generan fluctuaciones cuánticas que neutralizan el campo de Higgs. Por lo tanto, el cuado que las partículas y la cosmología pintan juntas de un universo primitivo puro y de resplandeciente simetría es demasiado caliente para Higgs. Pero cuando la temperatura cae bajo los 10^-5 grados Kelvin o 100 GeV, el Higgs empieza a actuar y hace su generación de masas. Así, por ejemplo, antes del Higgs teníamos unos W, Z y fotones sin masa y la fuerza electrodébil unificada.

                          No, esto no es el Higgs, es, simplemente, una burbuja multicolor

El universo se expande y se enfría, y entonces viene el Higgs (que “engorda” los W y Z, y por alguna razón ignora el fotón) y de ello resulta que la simetría electrodébil se rompe. Tenemos entonces una interacción débil, transportada por los vehículos de la fuerza W⁺, W^–, Z⁰, y por otra parte una interacción electromagnética, llevada por los fotones. Es como si para algunas partículas del campo de Higgs fuera una especie de aceite pesado a través del que se moviera con dificultad y que les hiciera parecer que tienen mucha masa.  Para otras partículas, el Higgs es como el agua, y para otras, los fotones y quizá los neutrinos, es invisible.

De todas formas, es tanta la ignorancia que tenemos sobre el origen de la masa que nos agarramos como a un clavo ardiendo, en este caso, a la partícula de Higgs, que algunos han llegado a llamar “la partícula divina”. Lo mismo nos pasa con la dichosa “materia oscura” para ocultar lo que no sabemos sobre la expansión del Universo.

¡Ya veremos en qué termina todo esto!

Arriba tenemos nada más y nada menos que: a John Mather, Carlo Rubbia, Martinus Veltman, Gerardus ‘t Hooft at the Lindau Nobel Meetings 2010. Si científicos  como ellos no vienen a nuestro rescate, y nos sacan del atolladero en el que estamos inmerso y hasta el cuelo de ignorancia…¡Mal irán las cosas!

Peter Higgs, de la Universidad de Edimburgo, introdujo la idea en la física de partículas. La utilizaron los teóricos Steven Weinberg y Abdus Salam, que trabajaban por separado, para comprender cómo se convertía la unificada y simétrica fuerza electrodébil, transmitida por una feliz familia de cuatro partículas mensajeras de masa nula, en dos fuerzas muy diferentes: la QED con un fotón carente de masa y la interacción débil con sus W⁺, W^– y Z⁰ de masa grande. Weinberg y Salam se apoyaron en los trabajos previos de Sheldon Glashow, quien, tras los pasos de Julian Schwinger, sabía sólo que había una teoría electrodébil unificada, coherente, pero no unió todos los detalles. Y estaban Jeffrey Goldstone y Martinus Veltman y Gerard’t Hooft. También hay otros a los que habría que mencionar, pero lo que siempre pasa, quedan en el olvido de manera injusta. Además, ¿Cuántos teóricos hacen falta para encender una bombilla? La verdad es que, casi siempre, han hecho falta muchos. Recordemos el largo recorrido de los múltiples detalles sueltos y físicos que prepararon el terreno para que llegara Einstein y pudiera, uniéndolo todo, exponer su teoría relativista.

Lo cierto es que (al menos de momento), la materia y energía oscura, las supercuerdas, y el bosón de Higss, sí son la alfonbra que decía Veltman, aquel físico serio y Premio Nobel que, no confesaba con ciertas ruedas de molino. Él, quería hablar de cosas tamgibles y, tampoco le gustaban las partículas virtuales.

Sobre la idea de Peter Higgs, Veltman, uno de sus arquitectos, dice que es una alfombra bajo la que barremos nuestra ignorancia. Glashow es menos amable y lo llamó retrete donde echamos las incoherencias de nuestras teorías actuales. La objeción principal: que no tenemos la menor prueba experimental. Ahora, por fin, la tendremos con el LHC. El modelo estándar es lo bastante fuerte para decirnos que la partícula de Higgs de menor masa (podría haber muchas) debe “pesar” menor de 1 TeV, ¿por qué?; si tiene más de 1 TeV el modelo estándar se vuelve incoherente y tenemos la crisis de la unitariedad.

Después de todo esto, llego a la conclusión de que el campo de Higgs, el modelo estándar y nuestra idea de surgió el universo dependen de que se encuentre el bosón de Higgs. Y ahora, por fin, tenemos un acelerador con la energía necesaria para que nos la muestre, y que con su potencia pueda crear para nosotros una partícula que pese nada menos que 1 TeV.

Emilio Silvera Vázquez

[?]