Dic
6
¡Cuántas maravillas!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)




No sería descabellado decir que las simetrías que vemos a nuestro alrededor, un arco iris a las flores y a los cristales, pueden considerarse en última instancia como manifestaciones de fragmentos de la teoría decadimensional original. Riemann y Einstein habían confiado en llegar a una comprensión geométrica de por qué las fuerzas pueden determinar el movimiento y la naturaleza de la materia. Por ejemplo, la fuerza de Gravedad generada por la presencia de la materia, determina la geometría del espacio-tiempo.
Dado el enorme poder de sus simetrías, no es sorprendente que la teoría de supercuerdas sea radicalmente diferente de cualquier otro de física. De hecho, fue descubierta casi por casualidad. Muchos físicos han comentado que si este accidente fortuito no hubiese ocurrido, entonces la teoría no se hubiese descubierto hasta bien entrado el siglo XXI. Esto es así porque supone una neta desviación de todas las ideas ensayadas en este siglo. No es una extensión natural de tendencias y teorías populares en este siglo que ha pasado; permanece aparte.

Por el contrario, la teoría de la relatividad general de Einstein tuvo una evolución normal y lógica. En primer lugar, su autor, postula el principio de equivalencia. Luego reformuló principio físico en las matemáticas de una teoría de campos de la gravitación basada en los campos de Faraday y en el tensor métrico de Riemann. Más tarde llegaron las “soluciones clásicas”, tales el agujero negro y el Big Bang. Finalmente, la última etapa es el intento actual de formular una teoría cuántica de la gravedad. Por lo tanto, la relatividad general siguió una progresión lógica, un principio físico a una teoría cuántica.

Geometría → teoría de campos → teoría clásica → teoría cuántica.
Contrariamente, la teoría de supercuerdas ha evolucionando hacia atrás desde su descubrimiento accidental en 1.968. Esta es la razón de que nos parezca extraña y poco familiar, estamos aún buscando un principio físico subyacente, la contrapartida del principio de equivalencia de Einstein.
La teoría nació casi por casualidad en 1.968 cuando dos jóvenes físicos teóricos, Gabriel Veneziano y Mahiko Suzuki, estaban hojeando independientemente libros de matemáticas. Figúrense ustedes que estaban buscando funciones matemáticas que describieran las interacciones de partículas fuertemente interactivas. Mientras estudiaban en el CERN, el Centro Europeo de Física Teórica en Ginebra, Suiza, tropezaron independientemente con la función beta de Euler, una función matemática desarrollada en el S. XIX por el matemático Leonhard Euler. Se quedaron sorprendidos al que la función beta de Euler ajustaba casi todas las propiedades requeridas para describir interacciones fuertes de partículas elementales.
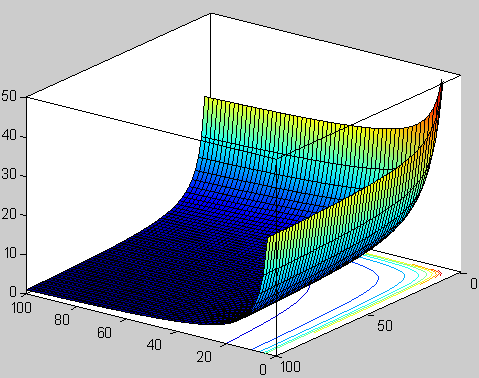
Función beta. Representación de la función valores reales positivos de x e y.
Según he leído, durante un almuerzo en el Lawrence Berkeley Laboratory en California, con una espectacular vista del Sol brillando sobre el puerto de San Francisco, Suzuki le explicó a Michio Kaku mientras almorzaban la excitación de descubrir, prácticamente por casualidad, un resultado parcialmente importante. No se suponía que la física se pudiera hacer de ese modo casual.
Tras el descubrimiento, Suzuki, muy excitado, mostró el hallazgo a un físico veterano del CERN. Tras oír a Suzuki, el físico veterano no se impresionó. De hecho le dijo a Suzuki que otro físico joven (Veneziano) había descubierto la misma función unas semanas antes. Disuadió a Suzuki de publicar su resultado. Hoy, esta función beta se conoce con el de modelo Veneziano, que ha inspirado miles de artículos de investigación iniciando una importante escuela de física y actualmente pretende unificar todas las leyes de la física.

Gabriele Veneziano es un físico italiano
En 1.970, el Modelo de Veneziano-Suzuki (que contenía un misterio), fue parcialmente explicado cuando Yoichiro Nambu, de la Universidad de Chicago, y Tetsuo Goto, de la Nihon University, descubrieron que una cuerda vibrante yace detrás de sus maravillosas propiedades. Así que, la teoría de cuerdas fue descubierta hacia atrás y por casualidad, los físicos aún no conocen el principio físico que subyace en la teoría de cuerdas vibrantes y sus maravillosas propiedades. El último paso en la evolución de la teoría de cuerdas (y el primer paso en la evolución de la relatividad general) aún está pendiente de que alguien sea capaz de darlo.
Así, Witten dice:
“Los seres humanos en el planeta tierra nunca dispusieron del marco conceptual que les llevara a concebir la teoría de supercuerdas de manera intencionada, surgió por razones del azar, por un feliz accidente. Por sus propios méritos, los físicos c del siglo XX no deberían haber tenido el privilegio de estudiar teoría muy avanzada a su tiempo y a su conocimiento. No tenían (ni tenemos ahora mismo) los conocimientos y los prerrequisitos necesarios para desarrollar dicha teoría, no tenemos los conceptos correctos y necesarios.”
Actualmente, como ha quedado dicho en este mismo , Edwar Witten es el físico teórico que, al frente de un equipo de físicos de Princeton, lleva la bandera de la teoría de supercuerdas con aportaciones muy importantes en el desarrollo de la misma. De todas las maneras, aunque los resultados y avances son prometedores, el camino por andar es largo y la teoría de supercuerdas en su conjunto es un edificio con muchas puertas cerradas de las que no tenemos las llaves acceder a su interior y mirar lo que allí nos aguarda.
Ni con colección de llaves podremos abrir la puerta que nos lleve a la Teoría cuántica de la gravedad que, según dicen, subyace en la Teoría M, la más moderna versión de la cuerdas expuesta por E. Witten y que, según contaron los que estuvieron presentes en su presentación, Witten les introdujo en un “universo” fascinante de inmensa belleza que, sin embargo, no puede ser verificado por el experimento.
El problema está en que nadie es lo suficientemente inteligente para resolver la teoría de campos de cuerdas o cualquier otro enfoque no perturbativo de esta teoría. Se requieren técnicas que están actualmente más allá de nuestras capacidades. Para encontrar la solución deben ser empleadas técnicas no perturbativas, que son terriblemente difíciles. Puesto que el 99 por ciento de lo que conocemos sobre física de altas energías se basa en la teoría de perturbaciones, esto significa que estamos totalmente perdidos a la hora de encontrar la verdadera solución de la teoría.

¿Por qué diez dimensiones?
Uno de los secretos más profundos de la teoría de cuerdas, que aún no es comprendido, es por qué está definida sólo en diez, once y veintiséis dimensiones. Si calculamos cómo se rompen y se vuelven a juntar las cuerdas en el espacio N-dimensional, constantemente descubrimos que pululan términos absurdos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos indeseados aparecen multiplicados por (N-10). Por consiguiente, para hacer que desaparezcan estas anomalías, no tenemos otra elección cuántica que fijar N = 10. La teoría de cuerdas, de hecho, es la única teoría cuántica conocida que exige completamente que la dimensión del espacio-tiempo esté fijada en un número único, el diez.

Por desgracia, los teóricos de cuerdas están, por el , completamente perdidos para explicar por qué se discriminan las diez dimensiones. La respuesta está en las profundidades de las matemáticas, en un área denominada funciones modulares.
Al manipular los diagramas de lazos1 de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el 10 aparecen en los lugares más extraños. Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del este. Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro universo actual.

nos asomamos a la Teoría de cuerdas, entramos en un “mundo” lleno de sombras en los que podemos ver brillar, a lo lejos, un resplandor cegador. Todos los físicos coinciden en el hecho de que es una teoría muy prometedora y de la que parece se podrán obtener buenos rendimientos en el futuro pero, de momento, es imposible verificarla.
El misterio de las funciones modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió de cumplir cuarenta años, y como Riemann antes que él, trabajó en total aislamiento en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.
Dispersas oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre las más extrañas jamás encontradas en matemáticas. Ellas reaparecen en las ramas más distantes e inconexas de las matemáticas. Una función que aparece una y otra vez en la teoría de las funciones modulares se denomina (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. Esta extraña función contiene un término elevado a la potencia veinticuatro.
La magia esconde una realidad
El 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente donde menos se esperan por razones que nadie entiende. Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas. En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio-tiempo debe tener 24 + 2 = 26 dimensiones espacio-temporales.

Para comprender este misterioso factor de dos (que añaden los físicos), consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista Aµ cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell. Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones. Sin embargo, dos de estos modos vibracionales pueden ser eliminados rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.
Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio-tiempo sea diez.
En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “no lo sé”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una cuánticamente autoconsistente), pero no sabemos por qué se seleccionan estos números concretos.
Godfrey Harold Hardy
G. H. Hardy, el mentor de Ramanujan, trató de estimar la capacidad matemática que poseía Ramanujan. Concedió a David Hilbert, universalmente conocido y reconocido uno de los mayores matemáticos occidentales del siglo XIX, una puntuación de 80. A Ramanujan le asignó una puntuación de 100. Así mismo, Hardy se concedió un 25.
Por desgracia, ni Hardy ni Ramanujan parecían interesados en la psicología a los procesos de pensamiento mediante los cuales Ramanujan descubría estos increíbles teoremas, especialmente cuando diluvio material brotaba de sus sueños con semejante frecuencia. Hardy señaló:
“Parecía ridículo importunarle sobre como había descubierto este o ese teorema conocido, cuando él me estaba mostrando media docena día, de nuevos teoremas”.
Ramanujan
Hardy recordaba vivamente:
-”Recuerdo una vez que fui a visitarle cuando estaba enfermo en Putney. Yo había tomado el taxi 1.729, y comenté que el numero me parecía bastante feo, y que esperaba que no fuese mal presagio.”
– No. -Replicó Ramanujan postrado en su cama-. Es un número muy interesante; es el número más pequeño expresable como una suma de dos cubos en dos formas diferentes.
(Es la suma de 1 x 1 x 1 y 12 x 12 x 12, y la suma de 9 x 9 x 9 y 10 x 10 x 10).
Era capaz de recitar en el acto teoremas complejos de aritmética cuya demostración requeriría un ordenador moderno.
En 1.919 volvió a casa, en la India, donde un año más tarde murió enfermo.
El legado de Ramanujan es su obra, que consta de 4.000 fórmulas en cuatrocientas páginas que llenan tres volúmenes de notas, todas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario o, lo que es más frustrante, sin ninguna demostración. En 1.976, sin embargo, se hizo un nuevo descubrimiento. Ciento treinta páginas de borradores, que contenían los resultados del último año de su vida, fueron descubiertas por casualidad en una caja en el Trinity Collage. Esto se conoce ahora con el de “Cuaderno Perdido” de Ramanujan.

Comentando cuaderno perdido, el matemático Richard Askey dice:
“El de este año, mientras se estaba muriendo, era el equivalente a una vida entera de un matemático muy grande”. Lo que él consiguió era increíble. Los matemáticos Jonathan Borwien y Meter Borwein, en relación a la dificultad y la ardua tarea de descifrar los cuadernos perdidos, dijeron: “Que nosotros sepamos nunca se ha intentado una redacción matemática de este alcance o dificultad”.
Por mi creo que, Ramanujan, fue un genio matemático muy adelantado a su tiempo y que pasaran algunos años hasta que podamos descifrar al cien por ciento sus trabajos, especialmente, sus funciones modulares que guardan el secreto de la teoría más avanzada de la física moderna, la única capaz de unir la mecánica quántica y la Gravedad.
Fórmula de Ramanujan determinar los decimales de pi
Las matemáticas de Ramanujan son como una sinfonía, la progresión de sus ecuaciones era algo nunca vísto, él trabajaba otro nivel, los números se combinaban y fluían de su cabeza a velocidad de vértigo y con precisión nunca antes conseguida por nadie. Tenía tal intuición de las cosas que éstas simplemente fluían de su cerebro. Quizá no los veía de una manera que sea traducible y el único lenguaje eran los números.
saben los físicos, los “accidentes” no aparecen sin ninguna razón. Cuando están realizando un cálculo largo y difícil, y entonces resulta de repente que miles de términos indeseados suman milagrosamente cero, los físicos saben que esto no sucede sin una razón más profunda subyacente. Hoy, los físicos conocen que estos “accidentes” son una indicación de que hay una simetría en juego. Para las cuerdas, la simetría se denomina simetría conforme, la simetría de estirar y deformar la hoja del Universo de la cuerda.

Nuestro mundo asimétrico hermosas simetrias
Aquí es precisamente donde entra el trabajo de Ramanujan. Para proteger la simetría conforme original contra su destrucción por la teoría cuántica, deben ser milagrosamente satisfechas cierto número de identidades matemáticas que, son precisamente las identidades de la función modular de Ramanujan. ¡Increíble , cierto.

Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan su punto más débil. Cualquier teoría, afirman, debe ser verificable. Puesto que ninguna teoría definida a la energía de Planck de 1019 miles de millones de eV es verificable, ¡La teoría de cuerdas no es realmente una teoría!
El principal problema, es teórico más que experimental. Si fuéramos suficientemente inteligentes, podríamos resolver exactamente la teoría y encontrar la verdadera solución no perturbativa de la teoría. Sin embargo, esto no nos excusa de encontrar algún medio por el que verificar experimentalmente la teoría, debemos esperar señales de la décima dimensión.

Volviendo a Ramanujan…
Es innegable lo sorprendente de su historia, un muchacho pobre con escasa preparación y arraigado pocos a sus creencias y tradiciones, es considerado como una de los mayores genios de las matemáticas del siglo XX. Su legado a la teoría de números, a la teoría de las funciones theta y a las series hipergeométricas, además de ser invaluable aún sigue estudiándose por muchos prominentes matemáticos de todo el mundo. Una de sus fórmulas más famosas es
Utilizada para realizar aproximaciones del número Pi con más de dos millones de cifras decimales. Otra de las sorprendentes fórmulas descubiertas por Ramanujan es un igualdad en que era “casi” un entero (la diferencia era de milmillonésimas). De hecho, durante un tiempo se llegó a sospechar que el número era efectivamente entero. No lo es, pero este hallazgo sirvió de base para la teoría de los “Cuasi enteros”. A veces nos tenemos que sorprender al comprobar hasta donde puede llegar la mente humana que, prácticamente de “la nada”, es capaz de sondear los misterios de la Naturaleza para dejarlos al descubierto ante nuestros asombros ojos que, se abren como platos ante tales maravillas.
Publica: emilio silvera
Dic
6
¡Una Singularidad! Extraño Objeto
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)
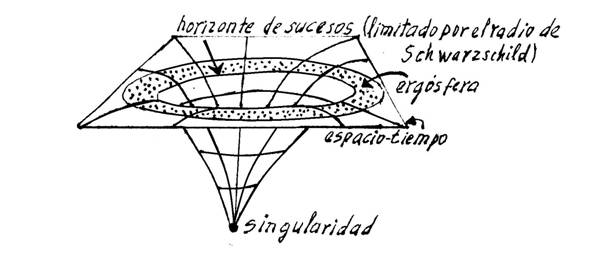

El concepto mismo de “singularidad” desagradaba a la mayoría de los físicos, pues la idea de una densidad infinita se alejaba de toda comprensión. La naturaleza humana está mejor condicionada a percibir situaciones que se caracterizan por su finitud, cosas que podemos medir y pesar, y que están alojadas dentro de unos límites concretos; serán más grande o más pequeñas pero, todo tiene un comienzo y un final pero… infinito, es difícil de digerir. Además, en la singularidad, según resulta de las ecuaciones, ni existe el tiempo ni existe el espacio. Parece que se tratara de otro universo dentro de nuestro universo toda la región afectada por la singularidad que, eso sí, afecta de manera real al entorno donde está situada y además, no es pacífica, ya que se nutre de cuerpos estelares circundantes que atrae y engulle.
La complejidad que supone la idea de una singularidad, como he dicho en otras ocasiones, deben ser dejadas a la Metafísica, la rama de la Física que estudia la naturaleza de las cosas complejas como el Ser. la Existencia, el Ente, la causalidad, el Tiempo…
La noción de singularidad empezó a adquirir un mayor crédito cuando Robert Oppenheimer, junto a Hartlan S. Snyder, en el año 1.939 escribieron un artículo anexo de otro anterior de Oppenheimer sobre las estrellas de neutrones. En este último artículo, describió de manera magistral la conclusión de que una estrella con masa suficiente podía colapsarse bajo la acción de su propia gravedad hasta alcanzar un punto adimensional; con la demostración de las ecuaciones descritas en dicho artículo, la demostración quedó servida de forma irrefutable que una estrella lo suficientemente grande, llegado su final al consumir todo su combustible de fusión nuclear, continuaría comprimiéndose bajo su propia gravedad, más allá de los estados de enana blanca o de estrella de neutrones, para convertirse en una singularidad.

Los cálculos realizados por Oppenheimer y Snyder para la cantidad de masa que debía tener una estrella para terminar sus días como una singularidad estaban en los límites másicos de M =~ masa solar, estimación que fue corregida posteriormente por otros físicos teóricos que llegaron a la conclusión de que sólo sería posible que una estrella se transformara en singularidad, la que al abandonar su fase de gigante roja retiene una masa residual como menos de 2 – 3 masas solares.

La figura de la izquierda representa a la nube de polvo en colapso de Oppenhieimer y Snyder, que ilustra una superficie atrapada.
El modelo de Oppenhieimer y Snyder posee una superficie atrapada, que corresponde a una superficie cuya área se iOppenheimer y Snyder desarrollaron el primer ejemplo explícito de una solución a las ecuaciones de Einstein que describía de manera cierta a un agujero negro, al desarrollar el planteamiento de una nube de polvo colapsante. En su interior, existe una singularidad, pero no es visible desde el exterior, puesto que está rodeada de un horizonte de suceso que no deja que nadie se asome, la vea, y vuelva para contarlo. Lo que traspasa los límites del horizonte de sucesos, ha tomado el camino sin retorno. Su destino irreversible, la singularidad de la que pasará a formar parte.
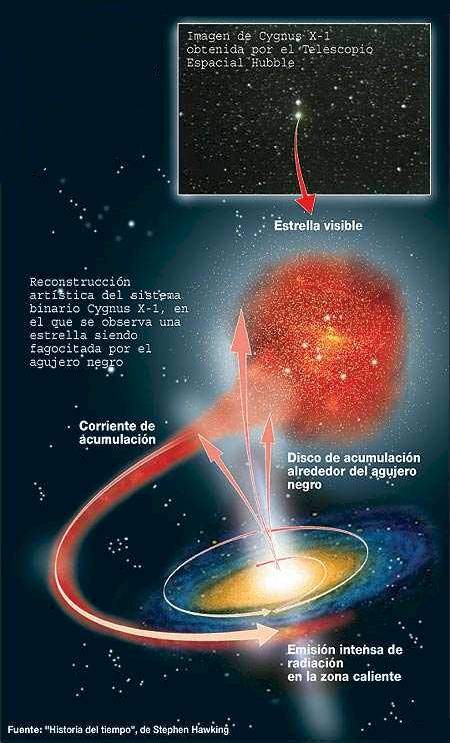
Desde entonces, muchos han sido los físicos que se han especializado profundizando en las matemáticas relativas a los agujeros negros. John Wheeler (que los bautizó como agujeros negros), Roger Penrose, Stephen Hawking, Kip S. Thorne, Kerr y muchos otros nombres que ahora no recuerdo, han contribuido de manera muy notable al conocimiento de los agujeros negros, las cuestiones que de ellas se derivan y otras consecuencias de densidad, energía, gravedad, ondas gravitacionales, etc, que son deducidas a partir de estos fenómenos del cosmos.

Se afirma que las singularidades se encuentran rodeadas por un horizonte de sucesos, pero para un observador, en esencia, no puede ver nunca la singularidad desde el exterior. Específicamente implica que hay alguna región incapaz de enviar señales al infinito exterior. La limitación de esta región es el horizonte de sucesos, tras ella se encuentra atrapado el pasado y el infinito nulo futuro. Lo anterior nos hace distinguir que en esta frontera se deberían reunir las características siguientes:

- Debe ser una superficie nula donde es pareja, generada por geodésicas nulas;
- contiene una geodésica nula de futuro sin fin, que se origina a partir de cada punto en el que no es pareja, y que
- el área de secciones transversales espaciales jamás pueden disminuir a lo largo del tiempo.
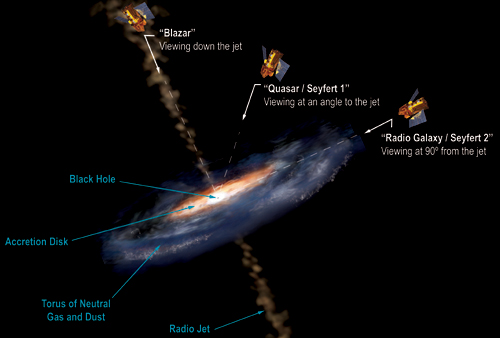
Pueden existir agujeros negros supermasivos (de 105 masas solares) en los centros de las galaxias activas. En el otro extremo, mini agujeros negros con un radio de 10-10 m y masas similares a las de un asteroide pudieron haberse formado en las condiciones extremas que se dieron poco después delBig Bang. Diminutos agujeros negros podrían ser capaces de capturar partículas a su alrededor, formando el equivalente gravitatorio de los átomos.

Todo esto ha sido demostrado matemáticamente por Israel, 1.967; Carter, 1.971; Robinson, 1.975; y Hawking, 1.978 con límite futuro asintótico de tal espaciotiempo como el espaciotiempo de Kerr, lo que resulta notable, pues la métrica de Kerr es una hermosa y exacta formulación para las ecuaciones de vacío de Einstein y, como un tema que se relaciona con la entropía en los agujeros negros.
No resulta arriesgado afirmar que existen variables en las formas de las singularidades que, según las formuladas por Oppenheimer y su colaborador Snyder, después las de Kerr y más tarde otros, todas podrían existir como un mismo objeto que se presenta en distintas formas o maneras.
Ahora bien, para que un ente, un objeto o un observador pueda introducirse dentro de una singularidad como un agujero negro, en cualquiera que fuese su forma, tendría que traspasar el radio de Schwarzschild (las fronteras matemáticas del horizonte de sucesos), cuya velocidad de escape es igual a la de la luz, aunque esta tampoco puede salir de allí una vez atrapada dentro de los límites fronterizos determinados por el radio. Este radio de Schwarzschild puede ser calculado usándose la ecuación para la velocidad de escape:

Para el caso de fotones u objeto sin masa, tales como neutrinos, se sustituye la velocidad de escape por la de la luz c2. “En el modelo de Schrödinger se abandona la concepción de los electrones como esferas diminutas con carga que giran en torno al núcleo, … Es cierto que en mecánica cuántica quedan muchos enigmas por resolver. Pero hablando de objetos de grandes masas, veámos lo que tenemos que hacer para escapar de ellos.
Podemos escapar de la fuerza de gravedad de un planeta pero, de un A.N., será imposible.
La velocidad de escape está referida a la velocidad mínima requerida para escapar de un campo gravitacional. El objeto que escapa puede ser cualquier cosa, desde una molécula de gas a una nave espacial. Como antes he reflejado está dada por , donde G es la constante gravitacional, M es la masa del cuerpo y R es la distancia del objeto que escapa del centro del cuerpo del que pretende escapar (del núcleo). Un objeto que se mueva a velocidad menor a la de escape entra en una órbita elíptica; si se mueve a una velocidad exactamente igual a la de escape, sigue una órbita parabólica, y si el objeto supera la velocidad de escape, se mueve en una trayectoria hiperbólica.
Así hemos comprendido que, a mayor masa del cuerpo del que se pretende escapar, mayor será la velocidad que necesitamos para escapar de él. Veamos algunas:
|
Objeto |
Velocidad de escape |
| La Tierra |
………….11,18 Km/s |
| El Sol |
………….617,3 Km/s |
| Júpiter |
………….59,6 Km/s |
| Saturno |
………….35,6 Km/s |
| Venus |
………….10,36 Km/s |
| Agujero negro |
…….+ de 299.000 Km/s |
Como se ve en el cuadro anterior, cada objeto celeste, en función de su masa, tiene su propia velocidad de escape para que cualquier cosa pueda salir de su órbita y escapar de él.
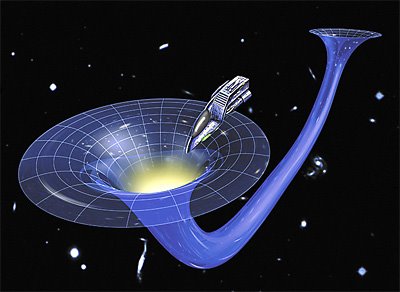
La excepción está en el último ejemplo, la velocidad de escape necesaria para vencer la fuerza de atracción de un agujero negro que, siendo preciso superar la velocidad de la luz 299.792’458 Km/s, es algo que no está permitido, ya que todos sabemos que conforme determina la teoría de la relatividad especial de Einstein, la velocidad de la luz es la velocidad límite en nuestro universo; nada puede ir más rápido que la velocidad de la luz, entre otras razones porque el objeto sufriría la transformación de Lorentz y su masa sería infinita.
Podría continuar explicando otros aspectos que rodean a los agujeros negros, pero estimo que el objetivo que perseguía de hacer conocer lo que es un agujero negro y el origen del mismo, está sobradamente cumplido.
Existen aspectos del A.N. que influyen en el mundo cuántico, y, por ejemplo, el máximo radio que puede tener un agujero negro virtual está dado aproximadamente por
![]()
que equivale a unos 10-³³ centímetros. Esta distancia se conoce como longitud de Planck y es la única unidad de distancia que se puede construir con las tres constantes fundamentales de la naturaleza: G, h y c. La longitud de Planck es tan extremadamente pequeña (10²° veces menor que el radio de un electrón) que debe ser la distancia característica de otro nivel de la naturaleza, subyacente al mundo subatómico, donde rigen las leyes aún desconocidas de la gravedad cuántica.
Así como el océano presenta un aspecto liso e inmóvil cuando se observa desde una gran distancia, pero posee fuertes turbulencias y tormentas a escala humana, el espacio-tiempo parece “liso” y estático a gran escala, pero es extremadamente turbulento en el nivel de la longitud de Planck, donde los hoyos negros se forman y evaporan continuamente. En el mundo de Planck, las leyes de la física deben ser muy distintas de las que conocemos hasta ahora.
 La estructura macroscópica del espacio-tiempo parece plana, pero éste debe ser extremadamente turbulento en el nivel de la escala de Planck. Escala en la que parece que entramos en otro mundo… ¡El de la mecánica cuántica! que se aleja de ese mundo cotidinao que conocemos en el que lo macroscópico predomina por todas partes y lo infinitesimal no se deja ver con el ojo desnudo.
La estructura macroscópica del espacio-tiempo parece plana, pero éste debe ser extremadamente turbulento en el nivel de la escala de Planck. Escala en la que parece que entramos en otro mundo… ¡El de la mecánica cuántica! que se aleja de ese mundo cotidinao que conocemos en el que lo macroscópico predomina por todas partes y lo infinitesimal no se deja ver con el ojo desnudo.
¡Existen tantos secretos!
emilio silvera















 Totales: 77.732.729
Totales: 77.732.729 Conectados: 43
Conectados: 43























