May
29
Física y algunos personajes
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
¡¡Qué Bonito es saber!!


Hubo que la historia de explorarla. Los mensajes del pasado se transmitían primero a través de las habilidades de la memoria, luego de la escritura y, finalmente, de modo explosivo, en los libros. El insospechado tesoro de reliquias que guardaba la tierra se remontaba a la prehistoria. El pasado se convirtió en algo más que un almacén de mitos y leyendas o un catálogo de lo familiar.

INAH restaura piezas mayas de Palenque que nos hablan del pasado
Nuevos mundos terrestres y marinos, riquezas de continentes remotos, relatos de viajeros aventureros que nos traían otras formas de vida de pueblos ignotos y lejanos, abrieron perspectivas de progreso y novedad. La sociedad, la vida diaria del hombre en comunidad, se convirtió en un “nuevo mundo” cambiante de nuevos escenarios y asombrosos descubrimientos.
“George Herbert Leigh Mallory (18 de junio de 1886 – 8 o 9 de junio de 1924) fue un escalador y montañero británico que tomó parte en las tres primeras expediciones que se proponían escalar el Everest (1921, 1922 y 1924). Desapareció junto con su compañero de cordada, Andrew Irvine, a más de 8000 msnm en la cara noreste de la montaña. Aún hoy persiste la duda sobre si consiguieron hacer cumbre, en cuyo caso, se habrían adelantado en 29 años al primer ascenso oficial, que llevaron a cabo Edmund Hillary y Tenzing Norgay en 1953. El cuerpo de Mallory no fue encontrado hasta 1999, 75 años después de su desaparición.”
Quizás una de las historias más maravillosas que nos han dejado los aventureros del pasado siglo XX, es la de la tercera expedición de Irvine y Mallory. Estos dos jóvenes aventuresros ingleses tenían el ardiente deseo de escalar por primera vez el pico más alto del planeta.Siempre nos ha movido una fuerza misteriosa por llegar hasta lo desconocido para contemplar lo que desde allí nos muestra la Naturaleza.
Aquí, sería imposible un recorrido por el ámbito de todos los descubrimientos de la Humanidad, me circunscribo al ámbito de la física, y, hago un recorrido breve por el mundo del átomo que es el tema de hoy, sin embargo, sin dejar de mirar al hecho cierto de que, TODA LA HUMANIDAD ES UNA, y, luego, teniendo muy presente que, todo lo que conocemos es finito y lo que no conocemos infinito. Es bueno tener presente que intelectualmente nos encontramos en medio de un océano ilimitado de lo inexplicable.

La complejidad de nuestras mentes que tienen un gran reto por delante
La tarea de generación es reclamar un poco más de terreno, añadir algo a la extensión y solidez de nuestras posesiones del saber.
decía Einstein: “El eterno misterio del mundo es su comprensibilidad.”
Amigos, hablemos del átomo. De lo Grande a lo Pequeño.
Explosión nuclear de Hiroshima
El 6 de Agosto de 1945 el mundo recibió estupefacto Hiroshima la noticia de que el hombre había desembarcado en el oscuro continente del átomo. Sus misterios habrían de obsesionar al siglo XX. Sin embargo, el “átomo” había sido más de dos mil una de las más antiguas preocupaciones de los filósofos naturales. La palabra griega átomo significa unidad mínima de materia, que se suponía era indestructible. el átomo era un término de uso corriente, una amenaza y una promesa sin precedentes.
![[leucipo.jpg]](http://1.bp.blogspot.com/_ns8_0N54PWc/Skge4dCBVhI/AAAAAAAAAEs/KmhKlua_IWU/s1600/leucipo.jpg)
Leucipo (c. 450-370 a.C.), filósofo griego. Es reconocido creador de la teoría atómica de la materia, más tarde desarrollada por su discípulo, el filósofo griego Demócrito. Según teoría, toda materia está formada por partículas idénticas e indivisibles llamadas átomos.
Así que, el primer filósofo atómico fue un griego legendario, Leucipo, que se cree vivió en el siglo V a.C., y, a Demócrito, su discípulo, que dio al atomismo su clásica filosofía: “la invisible e indivisible de la materia”, se divertía tanto con la locura de los hombres que era conocido “el filósofo risueño” o “el filósofo que ríe”. No obstante fue uno de los primeros en oponerse a la idea de la decadencia de la Humanidad a partir de una Edad de Oro mítica, y predicó sobre una base de progreso. Si todo el Universo estaba compuesto solamente por átomos y vacío, no sólo no era infinitamente complejo, sino que, de un modo u otro, era inteligible, y seguramente el poder del hombre no tenía límite.
Lucreci0 (c. 95 a. C. -c. 55 a.C.) perpetuó en De rerum natura uno de los más importantes poemas latinos, al atomismo antiguo. Con la intención de liberar al pueblo del temor a los dioses, el poeta demostró que el mundo entero estaba constituido por vacío y átomos, los cuales se movían según sus leyes propias; que el alma moría con el cuerpo y que por consiguiente no había razón en temer a la muerte o a los poderes sobrenaturales.

Lucrecio decía que comprender la Naturaleza era el único modo de hallar la paz de espíritu, y, era de esperar, los padres de la Iglesia que pregonaban la vida eterna, atacaron sin piedad a Lucrecio y fue ignorado y olvidado toda la Edad Media que, como sabéis, fue la culpable de la paralización del saber de la Humanidad. Sin embargo, Lucrecio fue, una de las figuras más influyentes del Renacimiento.
Así pues, en un principio el atomismo vino al mundo de la mano del sistema filosófico. Del mismo modo que la simetría pitagórica había proporcionado un marco a Copérnico, la geometría había seducido a Kepler y el círculo perfecto aristotélico a Harvey, así los “indestructibles” átomos de los filósofos atrajeron a los físicos y a los químicos. Francis Bacon observó que “la teoría de Demócrito referida a los átomos es, si no cierta, al aplicable con excelentes resultados al análisis de la Naturaleza”.

Descartes
Descartes (1596-1650) inventó su propia noción de partículas infinitamente pequeñas que se movían en un medio que llamó éter. Otro filósofo francés, Pierre Gassendi (1592-1655), pareció confirmar la teoría de Demócrito y presentó otra versión más del atomismo, que Robert Boyle (1627-1691) adaptó a la química demostrando que los “elementos clásicos -tierra, aire, fuego y agua- no eran en absoluto elementales.
Las proféticas intuiciones de un matemático jesuita, R.G. Boscovich (1711-1787) trazaron los caminos una nueva ciencia, la física atómica. Su atrevido concepto de “los puntos centrales” abandonaba la antigua idea de una variedad de átomos sólidos diferentes. Las partículas fundamentales de la materia, sugería Boscovich, eran todas idénticas, y las relaciones espaciales alrededor de esos puntos centrales constituían la materia… Boscovich que había llegado a estas conclusiones a partir de sus conocimientos de matemáticas y astronomía, anunció la íntima conexión la estructura del átomo y la del Universo, lo infinitesimal y lo infinito.
John Dalton
El camino experimental el átomo fue trazado por John Dalton (1766-1844). Era este un científico aficionado cuáquero y autodidacta que recogió un sugestivo concepto de Lavoisier (1743-1794). Considerado una de los fundadores de la química moderna, Lavoisier, definió un “elemento” una sustancia que no ser descompuesta en otras sustancias por medio de ningún método conocido, hizo del átomo un útil concepto de laboratorio y trajo la teoría atómica a la realidad.
Dalton había nacido en el seno de una familia de tejedores de Cumberland, localidad inglesa situada en la región de los lagos, y estuvo marcada toda su vida por su origen humilde. A los doce ya se encontraba a cargo de la escuela cuáquera de su pueblo. Después, comenzó a ejercer la enseñanza en la vecina Kendal, y en la biblioteca del colegio encontró ejemplares de los Principia de Newton, de las Obras de la Historia Natural de Buffón, así un telescopio reflectante de unos setenta centímetros y un microscopio doble. Dalton recibió allí la influencia de John Gough, un notable filósofo natural ciego que, de acuerdo a lo que Dalton escribió a un amigo, “entiende muy todas las diferentes ramas de las matemáticas…Conoce por el tacto, el sabor y el olor de casi todas las plantas que crecen a casi treinta kilómetros a la redonda”. También Wordsworth elogia a Gough en su Excursión. Dalton recibió del filósofo ciego una educación básica en latín, griego y francés, y fue introducido en las matemáticas, la astronomía y todas las ciencias “de la observación”. Siguiendo el ejemplo de Gough, Dalton comenzó a llevar un meteorológico diario, que continuó el día de su muerte.

Una ilustración de moléculas, según la teoría atómica de John Dalton. En el siglo XIX, Dalton sentó las bases de la actual teoría atómica, que luego se revelaría substancialmente correcta.
los “disidentes” fundaron su colegio propio en Manchester, Dalton fue designado profesor de matemáticas y de filosofía natural. Halló una audiencia muy receptiva para sus experimentos en la Sociedad Literaria y Filosófica de Manchester, y presentó allí sus Hechos extraordinarios concernientes a la visión de los colores, que probablemente fue el primer sistemático sobre la imposibilidad de percibir los colores, o daltonismo, enfermedad que padecían tanto John Dalton como su hermano Jonathan. “He errado tantas veces el camino por aceptar los resultados de otros que he decidido escribir lo posible y solamente lo que pueda afirmar por mi propia experiencia”.

Dalton observó la boreal, sugirió el probable origen de los vientos alisios, las causas de la formación de nubes y de la lluvia y, sin habérselo propuesto, introdujo mejoras en los pluviómetros, los barómetros, los termómetros y los higrómetros. Su interés por la atmósfera le proporcionó una visión de la química que lo condujo al átomo.
Newton había confiado en que los cuerpos visibles más pequeños siguieran las leyes cuantitativas que gobernaban los cuerpos celestes de mayor tamaño. La química sería una recapitulación de la Astronomía. , ¿Cómo podía el hombre observar y medir los movimientos y la atracción mutua de estas partículas invisibles? En los Principios Newton había conjeturado que los fenómenos de la Naturaleza no descritos en libro podrían “depender todos de ciertas fuerzas por las cuales las partículas de los cuerpos, debido a causas desconocidas, se impulsan mutuamente unas otras y se unen formando figuras regulares, o se repelen y se apartan unas de otras.”

¿Podremos ver algún día, el átomo así?
Dalton se lanzó a la búsqueda de “estas partículas primitivas” tratando de encontrar algún medio experimental que le permitiera incluirlas en un sistema cuantitativo. Puesto que los gases eran la de materia más fluida, más móvil, Dalton centró su estudio en la atmósfera, la mezcla de gases que componen el aire, el cual constituyó el punto de partida de toda su reflexión sobre los átomos.
“¿Por qué el agua no admite un volumen similar de gas?, preguntó Dalton a sus colegas de la Sociedad Literaria y Filosófica de Manchester en 1803. “Estoy casi seguro de que la circunstancia depende del peso y el de las partículas últimas de los diversos gases; aquellos cuyas partículas son más ligeras y simples se absorben con más dificultad, y los demás con mayor facilidad, según vayan aumentando en peso y en complejidad.”
Dalton había descubierto que, contrariamente a la idea dominante, el aire no era un vasto disolvente químico único sino una mezcla de gases, uno de los cuales conservaban su identidad y actuaba de manera independiente. El producto de sus experimentos fue recogido en la trascendental TABLE: Of the Relative Weights of Ultimate Particles of Gaseous and Other Bodies (“Tabla de los pesos relativos de las partículas últimas de los cuerpos gaseosos y de otros cuerpos”).
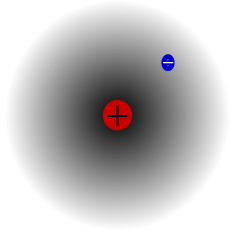
El átomo de Hidrógeno sólo 1 protón y 1 electrón
Tomando al Hidrógeno uno, Dalton detalló en esta obra sustancias. Describió las invisibles “partículas últimas” como diminutas bolitas sólidas, similares a balas pero mucho más pequeñas, y propuso que se les aplicaran las leyes newtonianas de las fuerzas de atracción de la materia. Dalton se proponía lograr “una nueva perspectiva de los primeros principios de los elementos de los cuerpos y sus combinaciones”, que “sin duda…con el tiempo, producirá importantísimos cambios en el sistema de la química y la reducirá a una ciencia de gran simplicidad, inteligible hasta los intelectos menos dotados”. Cuando Dalton mostró una “partícula de aire que descansa sobre cuatro partículas de agua como una ordenada pila de metralla” donde cada pequeño globo está en con sus vecinos, proporcionó el modelo de esferas y radio de la química del siglo siguiente.
Dalton inventó unas “señales arbitrarias como signos elegidos representar los diversos elementos químicos o partículas últimas”, organizadas en una tabla de pesos atómicos que utilizaba en sus populares conferencias. Naturalmente, Dalton no fue el primero en emplear una escritura abreviada para representar las sustancias químicas, pues los alquimistas también tenían su código. Pero él fue probablemente el primero que utilizó este de simbolismo en un sistema cuantitativo de “partículas últimas”. Dalton tomó como unidad el átomo de Hidrógeno, y a partir de él calculó el peso de las moléculas como la suma de los pesos de los átomos que la componían, creando así una sintaxis moderna para la química. Las abreviaturas actuales que utilizan la primera letra del latino (por ejemplo H2O) fueron ideadas por el químico sueco Berzelius (1779-1848).

Berzelius
La teoría del átomo de Dalton no fue recibida en un principio con entusiasmo. El gran sir Humphry Davy desestimó inmediatamente sus ideas tachándolas de “más ingeniosas que importantes”. Pero las nociones de Dalton, desarrolladas en A New System of Chemical Philosophy (1808), eran tan convincentes que en 1826 le fue concedida la medalla real. Dalton no olvidó nunca su origen plebeyo, permaneció siempre apartado de la Royal Society de Londres, pero fue elegido miembro, sin su consentimiento, en 1822. Receloso del tono aristocrático y poco profesional de la Sociedad, él se encontraba más a gusto en Manchester, donde realizó la mayor de su obra, colaboró con Charles Babage y contribuyó a fundar la Asociación Británica el Progreso de la Ciencia, cuyo objetivo era llevar la ciencia el pueblo. Los newtonianos partidarios de la ortodoxia religiosa no creían que Dios hubiera hecho necesariamente sus invisibles “partículas últimas” invariables e indestructibles. Compartían con Isaac Newton la sospecha de que Dios había utilizado su poder “ variar las leyes de la Naturaleza y crear mundos diversos en distintos lugares del Universo”.
El átomo indestructible de Dalton se convirtió en el fundamento de una naciente ciencia de la química, proporcionando los principios elementales, las leyes de composición constante y de proporciones múltiples y la combinación de elementos químicos en razón de su peso atómico. “El análisis y la síntesis química no van más allá de la separación de unas partículas de otras y su reunión”, insistió Dalton. “La creación o la destrucción de la materia no está al alcance de ningún agente químico. Sería lo mismo tratar de introducir un planeta en el Sistema Solar o aniquilar uno de los ya existentes que crear o destruir una partícula de Hidrógeno.” Dalton continuó usando las leyes de los cuerpos celestes visibles como indicios del Universo infinitesimal. El profético sir Humphry Davy, sin embargo, no se convencía, “no hay razón suponer que ha sido descubierto un principio real indestructible”, afirmó escéptico.
Humphry Davy.
Dalton no era más que un Colón. Los Vespucios aún no habían llegado, y lo hicieron trajeron consigo algunas sorpresas muy agradables y conmociones aterradoras. Entretanto, y durante medio siglo, el sólido e indestructible átomo de Dalton fue muy útil los químicos, y dio lugar a prácticas elaboraciones. Un científico francés, Gay-Lussac, demostró que cuando los átomos se combinaban no lo hacían necesariamente de dos en dos, como había indicado Dalton, sino que podían agruparse en asociaciones distintas de unidades enteras. Un químico italiano, Avogadro (1776-1856), demostró que volúmenes iguales de gases a la misma temperatura y presión contenían el mismo de moléculas. Un químico ruso, Mendeleiev, propuso una sugestiva “Ley periódica” de los elementos. Si los elementos estaban dispuestos en orden según su creciente peso atómico entonces grupos de elementos de características similares se repetirían periódicamente.
La disolución del indestructible átomo sólido provendría de dos fuentes, una conocida y la otra bastante nueva: el estudio de la luz y el descubrimiento de la electricidad. El propio Einstein describió histórico movimiento como la decadencia de una perspectiva “mecánica” y el nacimiento de una perspectiva “de campo” del mundo físico, que le ayudó a encontrar su propio camino la relatividad, explicaciones y misterios nuevos.

Albert Einstein tenía en la pared de su estudio un retrato de Michael Faraday (1791-1867), y ningún otro hubiera podido ser más apropiado, pues Faraday fue el pionero y el profeta de la gran revisión que hizo posible la obra de Einstein. El mundo ya no sería un escenario newtoniano de “fuerzas a distancias”, objetos mutuamente atraídos por la fuerza de la Gravedad inversamente proporcional al cuadrado de la distancia que hay ellos. El mundo material se convertiría en una tentadora escena de sutiles y omnipresentes “campos de fuerzas”. idea era tan radical como la revolución newtoniana, e incluso más difícil de comprender los legos en la materia.
Toda esta historia es mucho más amplia de lo que aquí podemos contar pero, en algún hay que parar y aquí lo dejamos.
emilio silvera
May
29
Recordemos a un personaje, unos hechos.
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Personajes de la Historia ~
Clasificado en Personajes de la Historia ~
 Comments (0)
Comments (0)

trabajo fue presentado en el Carnaval de la Física en homenaje a Riemann.

Recordemos aquí un extraño caso que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: la teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann que dio su célebre conferencia en la facultad de la Universidad de Göttingen en Alemania. Aquello fue como abrir de golpe todas las ventanas cerradas 2.000 años de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.
Su ensayo, de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del universo y su evolución mediante su asombrosa teoría de la relatividad general. Ciento treinta años después de su conferencia, los físicos utilizarían la geometría decadimensional para intentar unir todas las leyes del universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.

Contradictoriamente, Riemann era la persona indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria que arruinó su vida en la miseria abyecta y la tuberculosis.
Riemann nació en 1.826 en Hannover, Alemania, segundo de los seis hijos de un pobre pastor luterano que trabajó y se esforzó como humilde predicador para alimentar a su numerosa familia que, mal alimentada, tendrían una delicada salud que les llevaría a una temprana muerte. La madre de Riemann también murió de que sus hijos hubieran crecido.
A edad muy temprana, Riemann mostraba ya los rasgos que le hicieron famoso: increíble capacidad de cálculo que era el contrapunto a su gran timidez y temor a expresarse en público. Terriblemente apocado era objeto de bromas de otros niños, lo que le hizo recogerse aún más en un mundo matemático intensamente privado que le salvaba del mundo hostil exterior.
Para complacer a su padre, Riemann se propuso hacerse estudiante de teología, obtener un puesto remunerado pastor y ayudar a su familia. En la escuela secundaria estudió la Biblia con intensidad, pero sus pensamientos volvían siempre a las matemáticas. Aprendía tan rápidamente que siempre estaba por delante de los conocimientos de sus instructores, que encontraron imposible mantenerse a su altura. Finalmente, el director de la escuela dio a Riemann un pesado libro para mantenerle ocupado. El libro era la Teoría de números de Adrien-Marie Legendre, una voluminosa obra maestra de 859 páginas, el tratado más avanzado del mundo sobre el difícil tema de la teoría de números. Riemann devoró el libro en seis días.
Cuando el director le preguntó: “¿ dónde has leído?”, el joven Riemann respondió: “ es un libro maravilloso. Ya me lo sé todo”.
Sin creerse realmente la afirmación de su pupilo, el director le planteó varios meses después cuestiones complejas sobre el contenido del libro, que Riemann respondió correctamente.
Con mil sacrificios, el padre de Riemann consiguió reunir los fondos necesarios que a los 19 años pudiera acudir a la Universidad de Göttingen, donde encontró a Carl Friedrich Gauss, el aclamado por todos “Príncipe de las Matemáticas”, uno de los mayores matemáticos de todos los tiempos. Incluso hoy, si hacemos una selección por expertos para distinguir a los matemáticos más grandes de la Historia, aparecerá indudablemente Euclides, Arquímedes, Newton y Gauss.
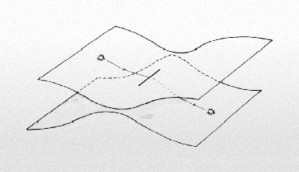
Gráfico: Un corte de Riemann, con dos hojas conectadas a lo largo de una línea. Si caminamos alrededor del corte, permanecemos dentro del mismo espacio. Pero si atravesamos el corte, pasamos de una hoja a la continua. es una superficie múltiplemente conexa
Los estudios de Riemann no fueron un camino de rosas precisamente. Alemania sacudida por disturbios, manifestaciones y levantamientos, fue reclutado en el cuerpo de estudiantes para proteger al rey en el palacio real de Berlín y sus estudios quedaron interrumpidos.
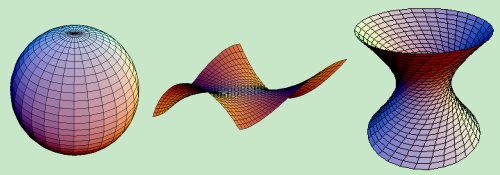
En aquel ambiente, el problema que captó el interés de Riemann fue el colapso que, según el pensaba, suponía la geometría euclidiana, que mantiene que el espacio es tridimensional y “plano” (en el espacio plano, la distancia más corta dos puntos es la línea recta; lo que descarta la posibilidad de que el espacio pueda estar curvado, como en una esfera).
Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna veía Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita. Riemann, ante aquella realidad, se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos, descubrió él, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.
Euclides nos habló de la obviedad de que un punto no tiene dimensión. Una línea tiene una dimensión: longitud. Un plano tiene dos dimensiones: longitud y anchura. Un sólido tiene tres dimensiones: longitud, anchura y altura. Y allí se detiene. Nada tiene cuatro dimensiones, incluso Aristóteles afirmó que la cuarta dimensión era imposible. En Sobre el cielo, escribió: “La línea tiene magnitud en una dirección, el plano en dos direcciones, y el sólido en tres direcciones, y más allá de éstas no hay otra magnitud porque los tres son todas”. Además, en el año 150 d. C. el astrónomo Ptolomeo de Alejandría fue más allá de Aristóteles y ofreció, en su libro sobre la distancia, la primera “demostración” ingeniosa de que la cuarta dimensión es imposible.

En realidad, lo único que Ptolomeo demostraba era que era imposible visualizar la cuarta dimensión con nuestros cerebros tridimensionales (de hecho, hoy sabemos que muchos objetos matemáticos no pueden ser visualizados, aunque demostrarse que en realidad, existen). Ptolomeo puede pasar a la Historia como el hombre que se opuso a dos grandes ideas en la ciencia: el sistema solar heliocéntrico y la cuarta dimensión.
La ruptura decisiva con la geometría euclidiana llegó Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.
Riemann desarrolló su teoría de dimensiones más altas.
Finalmente, cuando hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante dos milenios.
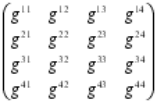
El tensor de Riemann contiene toda la información necesaria poder describir un espacio curvo en N-dimensiones. Se necesita dieciséis números para describir el tensor métrico en un espacio tetradimensional. Estos números pueden disponerse en una matriz cuadrada (seis de dichos números son realmente redundantes; de modo que el tensor métrico diez números independientes).
Riemann creó su tensor métrico que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a2 + b2 = c2. El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).
El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de supergravedad, supersimetría y, finalmente, las supercuerdas.

Para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio de que allí estaba la clave para resolver su problema. Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la relatividad general. fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc2. La reinterpretación física de la famosa conferencia de Riemann se denomina relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.
No sería justo reconocer aquí que Riemann, tiene mucho que ver en ese gran logro de Einstein (Relatividad General), y de toda la física en lo que a la geometría de espacios curvos se refiere..
emilio silvera
















 Totales: 69.205.722
Totales: 69.205.722 Conectados: 47
Conectados: 47
























