Principio de Simetria

Podemos concebir, en una muy simple definición, que el «principio de simetría» viene a ser como un intento de simplificar las cosas en términos matemáticos y abstractos. Existe, de hecho, simetría cuando se le hace algo a un objeto sin que éste cambie. Por ejemplo si usted comporta un libro de una habitación a otra de su casa, su texto no sufre ninguna variación, puede seguir siendo igual de bueno, malo o pésimo. Hay una simetría de contenido ante el desplazamiento del libro. Si lo invierte ya no se podrá leer fácilmente, pero la forma externa no ha cambiado: es una simetría de forma ante un medio giro. Si lo deja de leer ahora y lo retoma mañana, tampoco hace diferencia en el contenido, de donde se desprende una simetría con respecto a cambios en el tiempo.

Este tipo de simetrías es fácil encontrar su presencia en la naturaleza, y de ellas se desprenden leyes tan fundamentales como la conservación de la energía. De hecho, existe un antiguo e importante teorema que enunció, en 1918, Emmy Noether. Ella demostró que hay una relación entre simetrías continuas y leyes de conservación de alguna magnitud básica. Simetrías continuas son las que resultan de operaciones sin restricción de magnitud. Por ejemplo, si en vez de girar un libro que se encuentra leyendo en media vuelta lo rota un poquito, o un cuarto de vuelta, o algo diferente a media vuelta o vuelta entera, su contorno ya no se ve igual: no es una simetría continua. Importa la magnitud del ángulo de giro. Un plato, en cambio, se puede girar en cualquier ángulo, y su contorno se ve siempre igual; hay una simetría continua. La simetría de contenido que se deriva de desplazar el libro es continua, pues no importa que lo lleve al cuarto del lado, lo mueva un centímetro, o casi nada: el libro siempre sigue igual. La conservación de la energía, esa magna e inamovible ley descubierta el siglo XIX y enriquecida por Einstein con una de sus más reconocida ecuación emececuadrado es, por ejemplo, una consecuencia de la simetría continua de atrasar o adelantar (en el tiempo) todo lo que ocurre en el universo. Versiones más abstractas del teorema de Noether permiten deducir la conservación de la carga eléctrica, y la existencia de algunos mensajeros de las fuerzas.

En realidad, la simetría se encuentra en todo nuestro entorno: la simetría aproximadamente bilateral de nuestros cuerpos, la esférica de la pelota, la cilíndrica de una lata de conservas. Hay una simetría relacionada con cómo permanecen inalterados o invariantes ciertos objetos si los transformamos. Por ejemplo, si imprimimos un movimiento de rotación a una esfera perfecta alrededor de cualquier eje, o a un cilindro alrededor de su eje, permanecen invariables, lo que constituye una manifestación de su simetría específica. Se denomina a estas operaciones operaciones de simetría. Por otro lado, todo lo relacionado con simetría tiene un peso enorme en la relación de los problemas cuánticos.

En el siglo XIX, los matemáticos ya habían intentado describir matemáticamente todas las posibles operaciones de simetría de este tipo, basándose en una disciplina nueva denominada «teoría de grupo». Una idea básica de la teoría de grupo es describir simbólicamente operaciones de simetría, como las rotaciones, utilizando el álgebra. Supongamos, por ejemplo, que expresamos la rotación de un objeto alrededor de un eje concreto denominado 1, y siguiendo un ángulo concreto, por R₁, R₂ y R₃ expresarán otras rotaciones siguiendo otros ángulos distintos alrededor de ejes, denominados 2 y 3. Si expresamos luego algebraicamente el producto R₂ x R₁, esto significa: Realizar primero la rotación R₁ y luego la rotación R₂. La operación conjunta R₂ x R₁ es por sí sola una rotación. Hay que tener en cuenta que, en las rotaciones, R₂ X R₁ no es igual que R₁ x R₂. Pero supongamos que esto no se cumple aquí.

Entonces efectuemos la rotación R₃, de modo que la rotación resultante sea ya R₃ x (R₂ x R₁), lo que significa la rotación R₂ x R₁ seguida de R₃. Supongamos que empezamos otra vez y realizamos la rotación R₁ y a continuación la rotación conjunta expresada por R₃ x R₂, de modo que el resultado neto será (R₃ x R₂) x R₁ = R₃ (R₂ x R₁); vemos, pues, que en estas operaciones rotatorias se cumple la «ley asociativa». Esta norma es uno de los axiomas de la teoría de grupo.

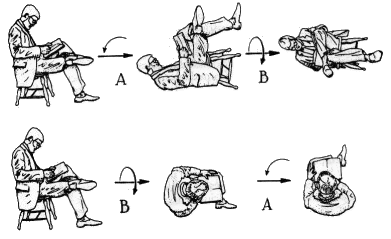
Las operaciones rotatorias no cumplen la propiedad algebraica conmutativa A x B =B x A. En este ejemplo, A corresponde a una rotación de 90 grados en sentido contrario al de las agujas del reloj, alrededor de un eje perpendicular al plano de la página; y B corresponde a una rotación de 90 grados alrededor de un eje horizontal. Si hacemos girar al lector conforme a la operación B y luego conforme a la operación A, comprobamos que el resultado final no es el mismo que el obtenido cuando las operaciones se realizan en el orden inverso.

Por otra parte, vemos que hay una rotación bastante simple del objeto que corresponde a dejarlo invariable: la operación de identidad denominada I, que equivale a no realizar ninguna rotación. Es evidente que I x R₁ = R₁ x I = R₁. La existencia de la operación de identidad I es el segundo axioma de la teoría de grupo.

Ahora, por último, supongamos que hay una operación inversa mediante la cual podemos deshacer cualquier rotación, y que equivale a girar simplemente el objeto hacia atrás. La operación inversa a la rotación R₁ se expresa mediante R₁^–1, y tiene la propiedad R₁ x R₁^–1 = I = R₁^–1 x R₁.

De estos tres axiomas engañosamente simples (la ley asociativa, la existencia de la identidad y de un inverso) brota la bella estructura de la teoría matemática de grupo, de modo muy parecido a cómo de los axiomas de Euclides surgen las maravillas de la geometría plana. Aunque hemos ejemplificado los axiomas algebraicos de la teoría de grupo valiéndonos de las rotaciones de un objeto en el espacio tridimensional, dichos axiomas son muchísimo más generales y se aplican a muchos tipos de transformaciones de simetría en espacios multidimensionales (el intercambio de objetos, las reflexiones espaciales, etc.). Pueden aplicarse métodos algebraicos formidables a partir de la noción de simetría, y los matemáticos han clasificado y estudiado todas las posibles simetrías de este tipo. Pero, ¿qué tienen que ver con la física estas ideas matemáticas abstractas?

Mucho pues. Coloquémonos un ejemplo. Imaginemos a dos físicos situados en puntos distintos del espacio, observando ambos el mismo objeto, situado a su vez en un tercer punto. Los dos físicos realizan mediciones de este objeto respecto a sus posiciones relativas y luego deciden comunicarse los resultados. Como cada uno de los físicos realizó las mediciones respecto a su propio sistema de coordenadas de cálculo, para comunicarse tales mediciones necesitan transformar o trasladar las mediciones realizadas en un sistema de coordenadas a las realizadas en el otro. La más general de estas transformaciones de coordenadas para dos físicos en reposo entre sí (como hemos supuesto aquí) es una translación (un desplazamiento en línea recta en el espacio) y una rotación alrededor de un eje. Es fácil ver que cualquiera de estas traslaciones y rotaciones obedece a los axiomas de la teoría de grupo cuando se describen algebraicamente. Vemos que la teoría de grupo y la simetría salen a colación en cuanto nos planteamos la transformación de varias mediciones realizadas en sistemas de coordenadas distintos uno de otro: las leyes generales de las transformaciones de espacio y tiempo.

Imaginemos a dos físicos, en reposo relativo en el espacio, asidos a sus respectivos sistemas de coordenadas, representados por tres flechas perpendiculares entre sí. Si desean comunicar los res resultados de las mediciones obtenidas respecto a sus sistemas de coordenadas han de saber cómo se relacionan los dos sistemas. La conversión de coordenadas más general que transformará un sistema en el otro es la traslación del punto de origen de un sistema de coordenadas al otro, seguido de una rotación.

Hay que tomar en consideración que los conceptos de simetría se aplican a las leyes generales de la física, no a configuraciones o acontecimientos específicos. En el ejemplo que di, es importante que dos sistemas cualesquiera de coordenadas (no simplemente algunos) puedan transformarse uno en otro mediante una traslación y una rotación. Además, si dos físicos cualesquiera, deducen las mismas leyes de la física utilizando distintos sistemas de coordenadas, podemos extraer la conclusión de que las leyes de la física son translativa y rotatoriamente invariantes: se aplican independientemente del lugar en que uno esté emplazado o de la orientación que se tenga en el espacio. Las simetrías de las leyes de la física expresan así una invarianza.

Hasta ahora, hemos abordado las translaciones y las rotaciones en el espacio tridimensional ordinario. Pero si reflexionamos un poco comprenderemos que esas mismas ideas deben generalizarse y aplicarse al espaciotiempo cuatridimensional de Minkowski, lo cual es importante para las leyes de transformación espaciotemporal de Einstein entre observadores en movimiento. Los físicos saben que el sentido más profundo de la teoría de la relatividad restringida o especial de Einstein es que las leyes de la física sólo son invariantes para operaciones de simetría que corresponden a rotaciones y traslaciones en el espaciotiempo cuatridimensional. Si establecemos esta condición de simetría (que es lo mismo que exigir que sea válida la relatividad especial) descubrimos algo muy notable.

Uno de los primeros que investigaron esta relación de las transformaciones de Einstein con el «grupo de simetría» y la aplicaron a las partículas cuánticas fue un físico de Princeton, Eugene Wigner. Wigner escribió en 1939 un artículo que demostraba cómo esas consideraciones puramente matemáticas de la teoría de grupo podían permitir la clasificación de las partículas cuánticas, lo que constituía un acontecimiento notable y trascendental. Lo que consiguió Wigner recuerda en varios sentidos lo que había logrado la generación anterior de científicos que clasificó todos los cristales posibles mediante el uso de grupos de simetría, los llamados «grupos cristalinos», de retículas espaciales periódicas. Si bien los cristales pueden representarse en retículas espaciales, objetos del tipo de las partículas cuánticas (o, en realidad, cualquier objeto dado que existe en espaciotiempo cuatridimensional) deben ser representaciones de las correspondientes simetrías de espaciotiempo encarnadas en las transformaciones einstianas. Wigner demostró que esto permitía clasificar las partículas cuánticas.

Demostró primero que toda partícula cuántica podía clasificarse según su masa en reposo. Si la partícula se movía y su masa en reposo no era cero, podíamos suponer que nos movíamos a la misma velocidad que la partícula, de modo que respecto a nuestro propio movimiento la partícula estuviese en reposo, y medir así con exactitud su masa en reposo. Por otra parte, sí la masa en reposo de una partícula fuese exactamente cero (como la del fotón, la partícula de luz), se movería siempre a la velocidad de la luz y jamás podríamos movernos a la misma velocidad. Así pues, todas las partículas podían clasificarse según su masa en reposo, fuese ésta cero o no.

Los trabajos de Wigner admitían también la existencia de dos «taquiones», partículas hipotéticas que se movían siempre a una velocidad superior a la de la luz. Gerald Feinberg, en 1967, propuso que quizá existan partículas con velocidades superiores a la de la luz, las llamó «taquiones». Para ellas la de la luz seguiría siendo una velocidad límite, pero un mínimo, no un máximo. Sin embargo, no sabemos si en realidad existen, ya que no se han podido detectar. Tampoco, nadie ha logrado formular jamás una teoria matemática coherente de taquiones interactuantes. Por ahora, el único lugar donde se pueden encontrar «taquiones» es en los glosarios de física y diccionarios.

El segundo principio de clasificación importante de Wigner es que toda partícula cuántica ha de tener un espín definido. Podríamos imaginarnos las partículas como peoncitas que giran. Este giro o espín en unidades especiales, sólo podía tener los valores 0, 1/2, 1, 3/2, 2, 5/2, 3… o un entero o un valor semientero; el espín era cuantificable. Si se descubriera alguna vez una partícula con un espín de 1/6 esto entrañaría una violación de la relatividad especial y seria una grave falla de las leyes físicas.

Las partículas de espín entero, 0, 1, 2… se denominan «bosones» mientras que las de espín de medio entero, 1/2, 3/2, 5/2… se denominan «fermiones», diferenciación de suma importancia, porque cada grupo de partículas en giro interactúa de modo muy distinto con otras partículas. Por ejemplo, el número total de fermiones que intervienen en una reacción tiene que ser igual al número total de fermiones resultantes… los fermiones se conservan. Pero esa ley de conservación no rige con los bosones.

El sistema de clasificación que ideó Wigner en 1939 tiene gran importancia y trascendencia, desde el punto de vista de la teoría cuántica, debido a que las diversas propiedades de que se valió para clasificar las partículas (masa, spin, etc.) no estaban sometidas al principio de incertidumbre de Heisenberg. Podemos determinar la masa y el spin de una partícula simultaneamente con absoluta precisión. De ahí que tales propiedades (pero no otras) tengan valores precisos para cada partícula; pueden considerarse los atributos de las partículas cuánticas.

Wigner se basó en la idea de que las transformaciones einstianas eran un grupo de simetría del espaciotiempo de Minkowski, una de las primeras aplicaciones fructíferas de los principios de simetría en la moderna física de partículas. Era una idea especialmente fecunda aplicada a sistemas multiparticulares, como por ejemplo el núcleo atómico, compuesto de protones y neutrones. Lo importante de la idea de Wigner era el hecho de que cuando uno aplicaba la condición algebraica del grupo de simetría en una descripción matemática del mundo, automáticamente se presuponía no sólo que se cumplirían los principios de la relatividad especial sino, además, que en ese mundo, las partículas podían clasificarse con sencillez. De una sola condición brotaba una rica estructura de deducciones.

De una u otra manera, la simetría impulsa a la física. De hecho, todas las realidades emanadas de sesudos trabajos matemáticos y descritas en literatura que hemos analizado en esta sección están relacionadas con la simetría que concebimos en aceptación general para el universo. A las que he vinculado con la conservación de la energía y, por ello, se las llama simetrías espaciotiempo, por la obvia razón de que se relacionan con las simetrías de la naturaleza asociadas con el espacio y el tiempo, y para distinguirlas de las que no lo están. Se vinculan íntegramente entonces con la teoría especial o restringida de Einstein. Como la relatividad pone al tiempo en igual condición que al espacio, hace patente una nueva simetría entre ambos. Los une en una nueva y única entidad, el espaciotiempo, que conlleva un conjunto de simetrías que no están presentes cuando se consideran el espacio y el tiempo en forma desagregada. En verdad, la invariante de la velocidad de la luz es, en sí misma, señal de una nueva simetría de la naturaleza, que conecta el espacio y el tiempo.

Texto extraído de Astrocosmo

[?]