Jul
30
¡La Luz! Esa maravilla de la Naturaleza
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

Grandes pensadores quisieron explicar la naturaleza de la luz, trataron de desentrañar sus secretos de mil maneras. Claro que tuvieron que llegar Planck y Einstein para que hablaran de fotones, los Bosones que la transmite.
Está claro que, los estudiosos de la época antigua y medieval estaban por completo a oscuras acerca de la naturaleza de la luz. Especulaban sobre que consistía en partículas emitidas por objetos relucientes o tal vez por el mismo ojo. Establecieron el hecho de que la luz viajaba en línea recta, que se reflejaba en un espejo con un ángulo igual a aquel con el que el rayo choca con el espejo, y que un rayo de luz se inclina (se refracta) cuando pasa del aire al cristal, al agua o a cualquier otra sustancia transparente.


Dicen que así fue la primera luz del universo
Cuando la luz entra en un cristal, o en alguna sustancia transparente, de una forma oblicua (es decir, en un ángulo respecto de la vertical), siempre se refracta en una dirección que forma un ángulo menor respecto de la vertical. La exacta relación entre el ángulo original y el ángulo reflejado fue elaborada por primera vez en 1.621 por el físico neerlandés Willerbrord Snell. No publicó sus hallazgos y el filósofo francés René Descartes descubrió la ley, independientemente, en 1.637.

Siempre nos gustó hacer experimentos con la luz
Los primeros experimentos importantes acerca de la naturaleza de la luz fueron llevados a cabo por Isaac Newton en 1.666, al permitir que un rayo de luz entrase en una habitación oscura a través de una grieta e las persianas, cayendo oblicuamente sobre una cara de un prisma de cristal triangular. El rayo se refracta cuando entra en el cristal y se refracta aún más en la misma dirección cuando sale por una segunda cara del prisma. (Las dos refracciones en la misma dirección se originan por que los dos lados del prisma de se encuentran en ángulo en vez de en forma paralela, como sería el caso en una lámina ordinaria de cristal.)
Newton atrapó el rayo emergente sobre una pantalla blanca para ver el efecto de la refracción reforzada. Descubrió que, en vez de formar una mancha de luz blanca, el rayo se extendía en una gama de colores: rojo, anaranjado, amarillo, verde, azul, y violeta, en este orden.
Newton dedujo de ello que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores. La amplia banda de sus componentes se denominó spectrum (palabra latina que significa “espectro”, “fantasma”).
Newton llegó a la conclusión de que la luz se componía de diminutas partículas (“corpúsculos”), que viajaban a enormes velocidades.
Le surgieron y se planteó algunas inquietudes cuestiones. ¿Por qué se refractaban las partículas de luz verde más que los de luz amarilla? ¿Cómo se explicaba que dos rayos de luz se cruzaran sin perturbase mutuamente, es decir, sin que se produjeran colisiones entre partículas?
Titán, la luna de Saturno, contempla la sonda que lleva su nombre
En 1.678, el físico neerlandés Christian Huyghens (un científico polifacético que había construido el primer reloj de péndulo y realizado importantes trabajos astronómicos) propuso una teoría opuesta: la de que la luz se componía de minúsculas ondas. Y si sus componentes fueran ondas, no sería difícil explicar los diversos difracciones de los diferentes tipos de luz a través de un medio refractante, siempre y cuando se aceptara que la luz se movía más despacio en ese medio refractante que en el aire. La cantidad de refracción variaría con la longitud de las ondas: cuanto más corta fuese tal longitud, tanto mayor sería la refracción. Ello significaba que la luz violeta (la más sensible a este fenómeno) debía de tener una longitud de onda mas corta que la luz azul, ésta, más corta que la verde, y así sucesivamente.

Lo que permitía al ojo distinguir los colores eran esas diferencias entre longitudes de onda. Y, como es natural, si la luz estaba integrada por ondas, dos rayos podrían cruzarse sin dificultad alguna. (Las ondas sonoras y las del agua se cruzan continuamente sin perder sus respectivas identidades.)
Peor la teoría de Huyqhens sobre las ondas tampoco fue muy satisfactoria. No explicaba por qué se movían en línea recta los rayos luminosos; ni por qué proyectaban sombras recortadas; ni aclaraba por qué las ondas luminosas no podían rodear los obstáculos, del mismo modo que pueden hacerlo las ondas sonoras y de agua. Por añadidura, se objetaba que si la luz consistía en ondas, ¿Cómo podía viajar por el vacío, ya que cruzaba el espacio desde el Sol y las Estrellas? ¿cuál era esa mecánica ondulatoria?

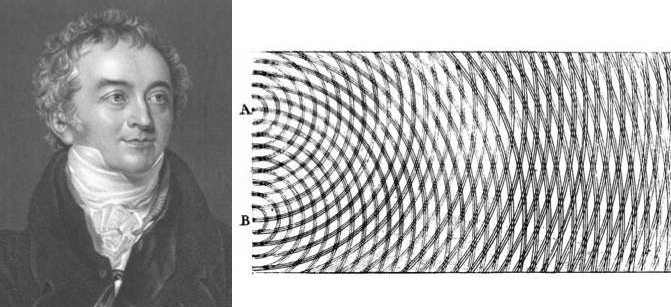
Interferencia: Sonido más sonido en algunos casos puede producir silencio. Esto sucede cuando dos ondas de sonido se superponen destructivamente, igual como se observa en las zonas nodales de una cuerda en vibración. ¿Será posible que en algún caso luz más luz produzca oscuridad? La respuesta es afirmativa. Quien lo demostrara en 1803, en un famoso experimento, fue Thomas Young (1773-1829). Éste consistió en hacer llegar un haz de luz simultáneamente a dos rendijas muy delgadas y muy cercanas, según se ilustra en el siguiente esquema.
Aproximadamente durante un siglo, contendieron entre sí estas teorías. La teoría corpuscular, de Newton, fue, con mucho, la más popular, en parte, porque la respaldó el famoso nombre de su autor. Pero hacia 1.801, un físico y médico ingles, de nombre Thomas Young, llevó a cabo un experimento que arrastró la opinión pública al campo opuesto. Proyectó un fino rayo luminoso sobre una pantalla, haciéndolo pasar antes por dos orificios casi juntos. Si la luz estuviera compuesta por partículas, cuando los dos rayos emergieran de ambos orificios, formarían presuntamente en la pantalla una región más luminosa donde se superpusieran, y regiones menos brillantes, donde no se diera tal superposición. Pero no fue esto lo que descubrió Young. La pantalla mostró una serie de bandas luminosas, separadas entre sí por bandas oscuras. Pareció incluso que, en esos intervalos de sombra, la luz de ambos rayos contribuía a intensificar la oscuridad.

Sería fácil explicarlo mediante la teoría ondulatoria. La banda luminosa representaba el refuerzo presado por las ondas de un rayo a las ondas del otro. Dicho de otra manera: Entraba “en fase” dos trenes de ondas, es decir, ambos nodos, al unirse, se fortalecían el uno al otro. Por otra parte, las bandas oscuras representaban puntos en que las ondas estaban “desfasadas” porque el vientre de una neutralizaba el nodo de la otra. En vez de aunar sus fuerzas, las ondas se interferían mutuamente, reduciendo la energía luminosa neta a las proximidades del punto cero.
Considerando la anchura de las bandas y la distancia entre los dos edificios por los que surgen ambos rayos, se pudo calcular la longitud de las ondas luminosas, por ejemplo, de la luz roja a la violeta o los colores intermedios. Las longitudes de onda resultaron ser muy pequeñas. Así, la de la luz roja era de unos 0’000075 cm. (Hoy se expresan las longitudes de las ondas luminosas mediante una unidad muy práctica ideada por Angströn. Esta unidad, denominada, en honor a su autor Ángstrom (Á), es la cienmillonésima parte de un centímetro. Así, pues, la longitud de onda de la luz roja equivale más o menos a 7.500 Á, y la de la luz violeta, a 3.900 Å, mientras que las de colores visibles en el espectro oscilan entre ambas cifras.)
La cortedad de estas ondas es muy importante. La razón de que las ondas luminosas se desplacen en línea recta y proyecten sombras recortadas se debe a que todas son incomparablemente más pequeñas que cualquier objeto; pueden contornear un obstáculo sólo si éste no es mucho mayor que la longitud de onda. Hasta las bacterias, por ejemplo, tienen un volumen muy superior de una onda luminosa y, por tanto, la luz puede definir claramente sus contornos bajo el microscopio. Sólo los objetos cuyas dimensiones se asemejan a la longitud de la onda luminosa (por ejemplo, los virus y otras partículas submicroscópicas) son lo suficientemente pequeños como para que puedan ser contorneados por las ondas luminosas.

ç
Agustín Jean Fresnel (1788 – 1827)
Photo: German Museum Munich
Un físico francés, Augustin-Jean Fresnel, fue quien demostró por vez primera, en 1.818, que si un objeto es lo suficientemente pequeño, la onda luminosa lo contorneará sin dificultad. En tal caso, la luz determina el llamado fenómeno de “difracción”. Por ejemplo, las finísimas líneas paralelas de una “reja de disfracción” actúan como una serie de minúsculos obtáculos, que se refuerzan entre si. Puesto que la magnitud de la difracción va asociada a la longitud de onda, se produce el espectro. A la inversa, se puede calcular la longitud de onda midiendo la difracción de cualquier color o porción del espectro, así como la separación de las marcas sobre el cristal.
Fraunhofer exploró dicha reja de difracción con objeto de averiguar sus finalidades prácticas, progreso que suele olvidarse, pues queda eclipsado por su descubrimiento más famoso: los rayos espectrales. El físico americano Henry Augustus Rowlane ideó la reja cóncava y desarrolló técnicas para regularlas de acuerdo con 20.000 líneas por pulgada. Ello hizo posible la sustitución del prisma por el espectroscopio.
Ante tales hallazgos experimentales, más el desarrollo metódico y matemático del movimiento ondulatorio, debido a Fresnel, pareció que la teoría ondulatoria de la luz había arraigado definitivamente, desplazando y relegando para siempre a la teoría corpuscular.
Jacques Babinet
No sólo se aceptó las existencias de ondas luminosas, sino que también se midió su longitud con una precisión cada vez mayor. Hacia 1.827, el físico francés Jacques Babinet sugirió que se empleara la longitud de onda luminosa (una cantidad física inalterable) como unidad para medir tales longitudes, en vez de las muy diversas unidades ideadas y empleadas por el hombre. Sin embargo, tal sugerencia no se llevó a la práctica hasta 1.880 cuando el físico germano-americano Albert Abraham Michelson inventó un instrumento, denominado “interferómetro”, que podía medir las longitudes de ondas luminosas con una exactitud sin precedentes. En 1.893, Michelson midió la onda de la raya roja en el espectro del cadmio y determinó que su longitud era de 1/1.553.164 m.
Pero la incertidumbre reapareció al descubrirse que los elementos estaban compuestos por isótopos diferentes, cada uno de los cuáles aportaba una raya cuya longitud de onda difería ligeramente de las restantes. En la década de 1.930 se midieron las rayas del criptón 86. Como quiera que este isótopo fuera gaseoso, se podía abordar con bajas temperaturas, para frenar el movimiento atómico y reducir el consecutivo engrosamiento de la raya.

Tubo de descarga lleno de kriptón puro
En 1.960, el Comité Internacional de Pesos y Medidas adoptó la raya del criptón 86 como unidad fundamental de longitud. Entonces se restableció la longitud de metro como 1.650.763’73 veces la longitud de onda de dicha raya espectral. Ello aumento mil veces la precisión de las medidas de longitud. Hasta entonces se había medido el antiguo metro patrón con un margen de error equivalente a una millonésima, mientras que en lo sucesivo se pudo medir la longitud de onda con un margen de error equivalente a una milmillonésima.
Ahora, después de todo esto, sabemos algo más sobre la luz. Pero…, ¿Qué pasa con su velocidad?
¡Veámoslo!

La velocidad de la luz, desde hace mucho tiempo, fue un misterio que los estudiosos de la física de la Naturaleza querían desvelar
![Cosas que pasan cuando eres Game Master en una Escape Room 2 (y Ep 3) ]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjD9-d3zWY191jBGgA2oU7fFQTVyHTT1E8d7nNRW-cSnKbXh6L6P_qMRPnaFJy5seI3ipzASui-9prZ9-_StmbVzhj_hdPNP00Acm7Wc_8B64ls_3j7P3yYx06GHM2siaROkz3H57lVL9tdfWG05ppRLScQmmesd6j9qBX4FhIuFbvRyW0I10Eq4ToeYi7-/s480/gZV7XA.gif)
Lo que sí sabemos es que la luz es muy importante para nosotros, para las plantas, para todo el Universo
Está claro que, la luz se desplaza a enormes velocidades. Si pulsamos el interruptor de apagado de la lámpara de nuestro salón, todo queda a oscuras de manera instantánea y, de la misma manera e inmediata, todo se inunda de luz si con una potente linterna encendida, apuntamos hacia un rincón oscuro.
La velocidad del sonido es más lenta, por ejemplo, si vemos a un leñador que está cortando leña en un lugar alejado de nosotros, sólo oiremos los golpes momentos después de que caiga el hacha. Así, pues, el sonido tarda cierto tiempo en llegar a nuestros oídos. En realidad es fácil medir la velocidad de su desplazamiento: unos 1.206 km/h enel aire y a nivel del mar.

Aquel sistema nunca le podría dar una respuesta fiable
Galileo fue el primero en intentar medir la velocidad de la luz. Se colocó en lo alto de una colina, mientras que su ayudante, se situaba en otro lugar alto de la colina vecina; luego sacó una linterna encendida: tan pronto como su ayudante vió la luz, hizo una señal con otra linterna. Galileo repitió el experimento a distancias cada vez mayores, suponiendo que el tiempo requerido por su ayudante para responder mantendría una uniformidad constante, por lo cual, el intervalo entre la señal de su propia linterna y la de su ayudante representaría el tiempo empleado por la luz para recorrer cada distancia. Aunque la idea era lógica, la luz viajaba demasiado aprisa como para que Galileo pudiera percibir las sutiles diferencias con un método tan rudimentario.

Ole Christensen Rømer (Århus, 25 de septiembre de 1644-Copenhague, 19 de septiembre de 1710)[1] fue un astrónomo danés, famoso por ser la primera persona en determinar la velocidad de la luz en el año 1676 con un valor inicial de 225.000 km/s.
En 1.676, el astrónomo danés Olau Roemer logró cronometrar la velocidad de la luz a escala de distancias astronómicas. Estudiando los eclipses de Júpiter en sus cuatro grandes satélites, Roemer observó que el intervalo entre eclipses consecutivos era más largo cuando la Tierra se alejaba de Júpiter, y más corto cuando se movía en su órbita hacía dicho astro. Al parecer, la diferencia entre las duraciones del eclipse reflejaba la diferencia de distancias entre la Tierra y Júpiter. Y trataba, pues, de medir la distancia partiendo del tiempo empleado por la luz para trasladarse desde Júpiter hasta la Tierra. Calculando aproximadamente el tamaño de la órbita terrestre y observando la máxima discrepancia en las duraciones del eclipse que, según Roemer, representaba el tiempo que necesitaba la luz para atravesar el eje de al órbita terrestre, dicho astrónomo computó la velocidad de la luz. Su resultado, de 225.000 km/s., parece excelente si se considera que fue el primer intento, y resultó bastante asombroso como para provocar la incredulidad de sus coetáneos.
Sin embargo, medio siglo después se confirmaron los cálculos de Roemer en un campo totalmente distinto. Allá por 1.728, el astrónomo británico James Bradley descubrió que las estrellas parecían cambiar de posición con los movimientos terrestres; y no por el paralaje, sino porque la traslación terrestre alrededor del Sol era una fracción mensurable (aunque pequeña) de la velocidad de la luz. La analogía empleada usualmente es la de un hombre que camina con el paraguas abierto bajo un temporal. Aun cuando las gotas caigan verticalmente, el hombre debe inclinar hacia delante el paraguas, porque ha de abrirse paso entre las gotas.

James Bradley descubrió la aberración estelar
Cuanto más acelere su paso, tanto más deberá inclinar el paraguas. De manera semejante la Tierra avanza entre los ligeros rayos que caen desde las estrellas, y el astrónomo debe inclinar un poco su telescopio y hacerlo en varias direcciones, de acuerdo con los cambios de la trayectoria terrestre (no olvidemos que nuestro planeta Tierra, es como una enorme nave espacial que nos lleva en un viaje eterno, alrededor del Sol, a la velocidad de 30 km/s. + -) Mediante ese desvío aparente de los astros (“aberración de la luz”), Bradley pudo evaluar la velocidad de la luz y calcularla con gran precisión.
Sus cálculos fueron de 285.000 km/s, bastante más exacto que los de Roemer, pero aún un 5’5% más bajos. Poco a poco, con medios tecnológicos más sofisticados y más conocimientos matemáticos, los científicos fueron obteniendo medidas más exactas aún, conforme se fue perfeccionando la idea original de Galileo y sus sucesores.
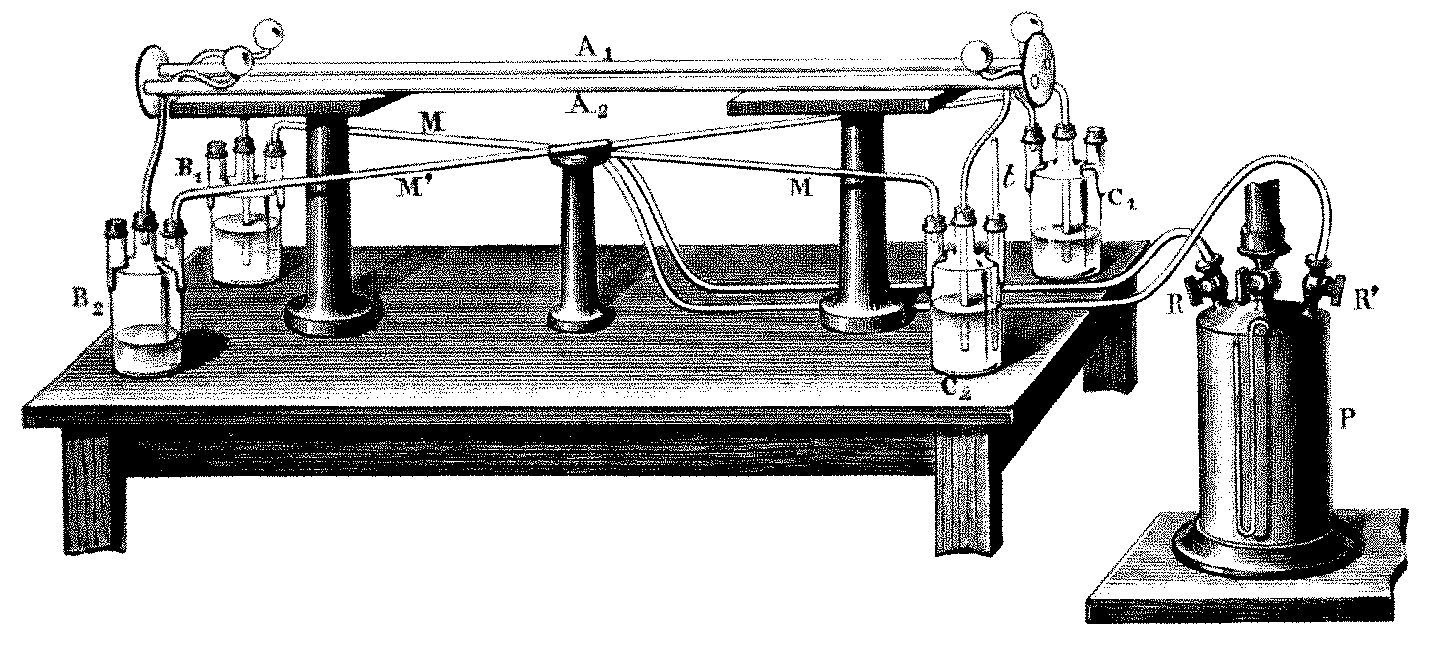
En 1.849, el físico francés Armand-Hippolyte-Louis Eizeau ideó un artificio mediante el cual se proyectaba la luz sobre un espejo situado a 8 km de distancia, que devolvía el reflejo al observador. El tiempo empleado por la luz en su viaje de ida y vuelta no rebasó apenas la 1/20.000 de segundo, por Fizeau logró medirlo colocando una rueda dentada giratoria en la trayectoria del rayo luminoso. Cuando dicha rueda giraba a cierta velocidad, regulada, la luz pasaba entre los dientes y se proyectaba contra el siguiente, al ser devuelta por el espejo; así, Fizeau, colocado tras la rueda, no pudo verla. Entonces se dio más velocidad a la rueda, y el reflejo pasó por la siguiente muesca entre los dientes, sin intercepción alguna. De esa forma, regulando y midiendo la velocidad de la rueda giratoria, Fizeau pudo calcular el tiempo transcurrido y, por consiguiente, la velocidad a que se movía el rayo de luz.
Un año más tarde, Jean Foucault (quien realizaría poco después su experimento con los péndulos) precisó más estas medidas empleando un espejo giratorio en ve de una rueda dentada. Entonces se midió el tiempo transcurrido desviando ligeramente el ángulo de reflexión mediante el veloz espejo giratorio. Foucault obtuvo un valor de la velocidad de la luz de 300.883 km/s. También, el físico francés utilizó su método para determinar la velocidad de la luz a través de varios líquidos. Averiguó que era notablemente inferior a la alcanzada en el aire. Esto concordaba también con la teoría ondulatoria de Huyghens.



Michelson y su Interferómetro
Michelson fue más preciso aún en sus medidas. Este autor, durante cuarenta años largos, a partir de 1.879, fue aplicando el sistema Fizeau-Foucault cada vez con mayor refinamiento, para medir la velocidad de la luz. Cuando se creyó lo suficientemente informado, proyectó la luz a través de vacío, en vez de hacerlo a través del aire, pues este frena ligeramente su velocidad, y, empleó para ello tuberías de acero cuya longitud era superior a 1’5 km. Según sus medidas, la velocidad de la luz en el vacío era de 299.730 km(seg. (sólo un 0’006% más bajo). Demostraría también que todas las longitudes de ondas luminosas viajan a la misma velocidad en el vacío.
En 1.972, un equipo de investigadores bajo la dirección de Kenneth M. Eveson efectuó unas mediciones aún más exactas y vio que la velocidad de la luz era de 299.727’74 km/seg. Una vez se conoció la velocidad de la luz con semejante precisión, se hizo posible usar la luz, o por lo menos formas de ella, para medir distancias.
Aunque para algunos resulte alto tedioso el tema anterior, no he podido resistirme a la tentación de exponerlo, así podrá saber algo más sobre la luz y, habrán conocido a personajes que hicieron posible el que ahora nosotros, la conozcamos mejor.
La Luz y sus múltiples aplicaciones

Paerícula y onda
Podría continuar, hasta el final de este trabajo, hablando de la luz y sus distintas formas o aplicaciones: ondas de luz a través del espacio, de cómo se transmite la luz en el “vacío”, nos llega a través del espacio desde Galaxias situadas a miles de millones de años luz; las líneas de fuerzas electromagnéticas de Faraday y Maxwell de campos eléctricos y magnéticos cambiantes (todo ello explicado en un simple conjunto de cuatro ecuaciones, que describían casi todos los fenómenos referentes a esta materia electromagnética), o de los enigmas aún por descubrir (aunque predichos).
Ahora, en Física, se dice que la luz es una forma de radiación electromagnética a la que el ojo humano es sensible y sobre la cual depende nuestra consciencia visual del universo y sus contenidos.

Aparte de todo lo que antes hemos explicado, no sería justo finalizar el trabajo sin exponer aquí que, en 1905, Albert Einstein, inspirado en el cuanto de Planck, realizó un importante avance en el conocimiento de lo que es la luz. Demostró que el Efecto fotoeléstrico sólo podía ser explicado con la hipótesis de que la luz consiste en un chorro de fotones de energía electromagnética discretos. Aquello le valió el Nobel de Física y… ¡Le hurtaron otros dos por las dos partes de su teoría de la relatividad! Una revolución que lo cambió todo y que nunca podremos pagarle.
El conflicto entre la teoría ondulatoria y corpuscular de la luz fue resuelto con la evolución de la teoría cuántica y la mecánica ondulatoria que ha dejado claro que, los electrones y las otras partículas elementales tienen propiedades duales de partículas y onda.
sería mucho más largo, pero creo que está bien con lo dicho.
El Universo fue opaco porque los fotones estaban confinados, y, cuando algún tiempo después quedaron liberados, el universo se hizo transparente, la luz lo inundaba rodo. Precisamente es ese acontecimiento el que le impide a los grandes telescopios espaciales, llegar al Fondo del Universo, si no había luz para captar imágenes… Las más lejanas en el Tiempo que se han podido captar, estaban situadas a 13.000.000 de años luz, es decir, que existe una zona más allá que es nescrutable, está en el límite de Planck, de ese lugar no podemos mpasar y, difícilmente podremos comprobar que el Bib Bang existió.
Emilio Silvera V.
Jul
30
¡El mundo de lo muy pequeño! ¿Cuántas maravillas encierra?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (2)
Comments (2)

Mi fascinación por la Ciencia en general y por la Física y la Astronomía en particular, me lleva a bucear en cuántos libros, revistas especializadas, conferencias, y seminarios caen en mis manos o puedo asistir. Tomo nota de todo en libretas que tengo para ello, y, más tarde, haciendo trabajos donde pueden ir mezclados unos con otros, disfruto al ofrecer a otros lo que grandes especialistas nos han contado sobre temas que, no sólo deben interesarnos, sino que, no en pocas ocasiones, nuestro futuro depende de ellos. Este es, uno de esos casos.
No es fácil adentrarse en este universo de lo definitivamente pequeño, o incluso hablar de ello, exige un conocimiento muy profundo de las leyes de la naturaleza que rigen el mundo y que no tenemos. Las fuerzas que encontramos allí determinan la forma en la cual se mueven las partículas pequeñísimas y también le dan sus propiedades por medio de unos mecanismos que no siempre llegamos a comprender.
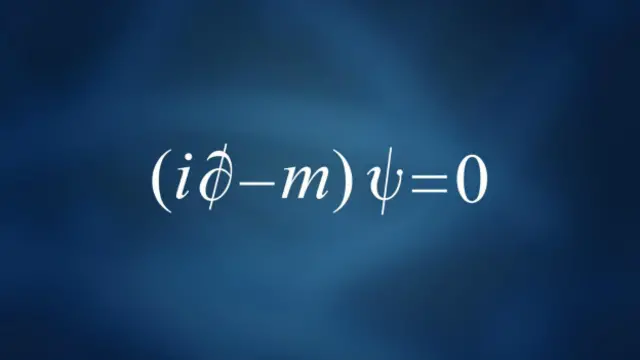
Muchos, diciendo que “saben” buscan refugio en un galimatías matemático que pocas personas “normales” pueden entender a menos que sea uno de ellos, y, sin embargo, para apreciar realmente la solidez de la lógica de las leyes físicas, no se pueden evitar las matemáticas que es, el único lenguaje que pueden explicar aquello que no podemos decir con palabras. Desde siempre, he tratado de hablar de la Física como si de cualquier otra disciplina se tratara y, he procurado soslayar ecuaciones, teoremas y funciones modulares que aterran al lector no versado y, desde luego, no siempre he conseguido transmitir lo que quería decir.
Hacer un viaje al mundo de lo muy pequeño no resulta nada comprensible para nuestros sentidos que, acostumbrados a lo “pequeño” cotidiano, cuando se adentra en lo infinitesimal, allí, las cosas se comportan de manera muy distinta a la acostumbrada en nuestro mundo real.
Jul
23
¡La Física! ¡Nos dice tántas cosas…! (Carnaval de Física)
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)


Hablamos de Física y, la constante de Planck en sus dos versiones, h y ħ; la igualdad masa-energía de Einstein; la Constante gravitacional de Newton, la constante de estructura fina (137); o, el radio del electrón.
¡ Me encantan sus mensajes !
Es verdaderamente meritorio el enorme avance que en tan poco tiempo ha dado la Humanidad, en el campo de la Física.
En poco más o menos, un siglo y medio, se ha pasado de la oscuridad a una claridad, no cegadora aún, pero sí, aceptable. Son muchos los secretos de la Naturaleza física que han sido desvelados y, el ritmo, parece que se mantiene a un nivel muy elevado.
¡ El Tiempo !, ese preciado bien, está a nuestro favor. Sólo tenemos que ir pasando el testigo para alcanzar las metas propuestas.
Pongamos nuestras esperanzas en que no seamos tan irresponsables como para estropearlo todo.
Las voces de Emi y Alicia, en una de sus innumerables discusiones, me distraen. Me concentro y consigo aislarme, ya estoy en otro lugar, todo tranquilo.

Con niños alrededor y la algarabía que generan, es difícil concentrarse en complejidades
Ahora puedo pensar en mis cosas de la Física, de la Astronomía, la Gravedad o el electromagnetismo.
Cuestiones sencillas de entender para los iniciados y, a veces, muy complejas para la gente corriente. Por tal motivo, si escribo sobre estos interesantes temas, mi primera preocupación es la de buscar la sencillez en lo que explico. No siempre lo consigo.
Jul
22
Todo lo grande está hecho de cosas pequeñas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)
Tiempo de Planck:
Es el tiempo que necesita el fotón (viajando a la velocidad de la luz, c, para moverse a través de una distancia igual a la longitud de Planck. Está dado por , donde G es la constante gravitacional (6, 672 59 (85) x 10-11 N m2 kg-2), ħ es la constante de Planck racionalizada (ħ = h/2л = 1,054589 x 10-34 Julios segundo), c, es la velocidad de la luz (299.792.458 m/s).
El valor del tiempo del Planck es del orden de 10-43 segundos. En la cosmología del Big Bang, hasta un tiempo de Planck después del instante inicial (en este punto hay que aclarar que, los grandes telescopios espaciales como el James West, alcanzan hasta llegar a los 13.500 millones de años hacia atrás, es decir, hasta el tiempo de Planck, más allá, no había luz, los fotones no se habían liberado, y, como los grandes telescopios, lo que hacen es recoger la luz que nos pueden llegar de las estrellas y las galaxias, al estar la luz ausente… ¡Nada se puede captar), es necesaria usar una teoría cuántica de la gravedad para describir la evolución del Universo. Todo, desde Einstein, es relativo. Depende de la pregunta que se formule y de quién nos de la respuesta.
¿El Tiempo? Muchos Filósofos lo quisieron explicar pero… ¡No pudieron!
Si preguntamos ¿Qué es el tiempo?, tendríamos que ser precisos y especificar si estamos preguntando por esa dimensión temporal que no deja de fluir desde el Big Bang y que nos acompaña a lo largo de nuestras vidas, o nos referimos al tiempo atómico, ese adoptado por el SI, cuya unidad es el segundo y se basa en las frecuencias atómicas, definida a partir de una línea espectral particular de átomo de cesio 133, o nos referimos a lo que se conoce como tiempo civil, tiempo coordinado, tiempo de crecimiento, tiempo de cruce, tiempo de integración, tiempo de relajación, tiempo dinámico o dinámico baricéntrico, dinámico terrestre, tiempo terrestre, tiempo de Efemérides, de huso horario, tiempo estándar, tiempo local, tiempo luz, tiempo medio, etc. etc. Cada una de estas versiones del tiempo, tiene una respuesta diferente, ya que, no es lo mismo el tiempo propio que el tiempo sidéreo o el tiempo solar, o solar aparente, o solar medio, o tiempo terrestre, o tiempo Universal. Como se puede ver, la respuesta dependerá de cómo hagamos la pregunta.
… Y que el mismo tiempo suele borrar
En realidad, para todos nosotros el único tiempo que rige es el que tenemos a lo largo de nuestras vidas, los otros tiempos, son inventos del hombre para facilitar sus tareas de medida, de convivencia o de otras cuestiones técnicas o astronómicas pero, sin embargo, el tiempo es solo uno; ese que comenzó cuando nació el Universo y que finalizará cuando este llegue a su final.
Lo cierto es que, para las estrellas supermasivas, cuando llegan al final de su ciclo y deja de brillar por agotamiento de su combustible nuclear, en ese preciso instante, el tiempo se agota para ella. Cuando una estrella pierde el equilibrio existente entre la energía termonuclear (que tiende a expandir la estrella), y, la fuerza de gravedad (que tiende a comprimirla), al quedar sin oposición esta última, la estrella supermasiva se contrae aplastada bajo su propia masa. Queda comprimida hasta tal nivel que llega un momento que desaparece, para convertirse en un Agujero Negro, una singularidad, donde dejan de existir el “tiempo” y el espacio. A su alrededor nace un horizonte de sucesos que, si se traspasa, se es engullido por la enorme gravedad del Agujero Negro.
En la singularidad no se distorsiona, se para
El tiempo, de ésta manera, deja de existir en estas regiones del Universo que conocemos como singularidad. El mismo Big Bang -dicen- surgió de una singularidad de energía y densidad infinitas que, al explotar, se expandió y creó el tiempo, el espacio y la materia.
Como contraposición a estas enormes densidades de las enanas blancas, estrellas de neutrones y Agujeros Negros, existen regiones del espacio que contienen menos galaxias que el promedio o incluso ninguna galaxia; a estas regiones las conocemos como vacío cósmico. Han sido detectados vacíos con menos de una décima de la densidad promedio del Universo en escalas de hasta 200 millones de años luz en exploraciones a gran escala. Estas regiones son a menudo esféricas. El primer gran vacío en ser detectado fue el de Boötes en 1.981; tiene un radio de unos 180 millones de años luz y su centro se encuentra aproximadamente a 500 millones de años luz de la Vía Láctea. La existencia de grandes vacíos no es sorprendente, dada la existencia de cúmulos de galaxias y supercúmulos a escalas muy grandes.
Mientras que en estas regiones la materia es muy escasa, en una sola estrella de neutrones, si pudiéramos retirar 1 cm3 de su masa, obtendríamos una cantidad de materia increíble. Su densidad es de 1017 kg/m3, los electrones y los protones están tan juntos que se combinan y forman neutrones que se degeneran haciendo estable la estrella de ese nombre que, después del agujero negro, es el objeto estelar más denso del Universo.
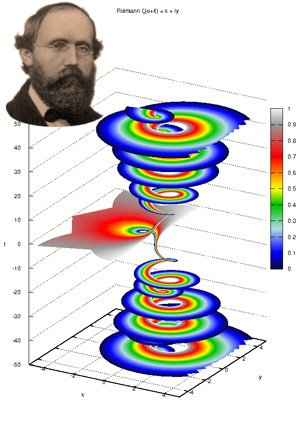
Es interesante ver cómo a través de las matemáticas y la geometría, han sabido los humanos encontrar la forma de medir el mundo y encontrar las formas del Universo. Pasando por Arquímedes, Pitágoras, Newton, Gauss o Riemann (entre otros), siempre hemos tratado de buscar las respuestas de las cosas por medio de las matemáticas.
“Magia es cualquier tecnología suficientemente avanzada”
Arthur C. Clarke
Pero también es magia el hecho de que, en cualquier tiempo y lugar, de manera inesperada, aparezca una persona dotada de condiciones especiales que le permiten ver, estructuras complejas matemáticas que hacen posible que la Humanidad avance considerablemente a través de esos nuevos conceptos que nos permiten entrar en espacios antes cerrados, ampliando el horizonte de nuestro saber.
Recuerdo aquí uno de esos extraños casos que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: La teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann dio su célebre conferencia en la facultad de la Universidad de Gotinga en Alemania. Aquello fue como abrir de golpe, todas las ventanas cerradas durante 2.000 años, de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.
Su ensayo de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la Literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del Universo y su evolución mediante su asombrosa teoría de la relatividad general Ciento treinta años después de su conferencia, los físicos utilizarían la geometría deca-dimensional para intentar unir todas las leyes del Universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.
Contradictoriamente, Riemann era la persona menos indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria que arruinó su vida en la miseria abyecta y la tuberculosis.
Riemann nació en 1.826 en Hannover, Alemania, segundo de los seis hijos de un pobre pastor luterano que trabajó y se esforzó como humilde predicador para alimentar a su numerosa familia que, mal alimentada, tendrían una delicada salud que les llevaría a una temprana muerte. La madre de Riemann también murió antes de que sus hijos hubieran crecido.
A edad muy temprana, Riemann mostraba ya los rasgos que le hicieron famoso: increíble capacidad de cálculo que era el contrapunto a su gran timidez y temor a expresarse en público. Terriblemente apocado era objeto de bromas de otros niños, lo que le hizo recogerse aún más en un mundo matemático intensamente privado que le salvaba del mundo hostil exterior.
Para complacer a su padre, Riemann se propuso hacerse estudiante de teología, obtener un puesto remunerado como pastor y ayudar a su familia. En la escuela secundaria estudió la Biblia con intensidad, pero sus pensamientos volvían siempre a las matemáticas. Aprendía tan rápidamente que siempre estaba por delante de los conocimientos de sus instructores, que encontraron imposible mantenerse a su altura. Finalmente, el director de la escuela dio a Riemann un pesado libro para mantenerle ocupado. El libro era la Teoría de números de Adrien-Marie Legendre, una voluminosa obra maestra de 859 páginas, el tratado más avanzado del mundo sobre el difícil tema de la teoría de números. Riemann devoró el libro en seis días.

Cuando el director le preguntó: “¿Hasta dónde has leído?”, el joven Riemann respondió: “Este es un libro maravilloso. Ya me lo sé todo”.
Sin creerse realmente la afirmación de su pupilo, el director le planteó varios meses después cuestiones complejas sobre el contenido del libro, que Riemann respondió correctamente.
Con mil sacrificios, el padre de Riemann consiguió reunir los fondos necesarios para que, a los 19 años pudiera acudir a la Universidad de Gotinga, donde encontró a Carl Friedrich Gauss, el aclamado por todos “Príncipe de las Matemáticas”, uno de los mayores matemáticos de todos los tiempos. Incluso hoy, si hacemos una selección por expertos para distinguir a los matemáticos más grandes de la Historia, aparecerá indudablemente Euclides, Arquímedes, Newton y Gauss.

Hannover, Alemania
Los estudios de Riemann no fueron un camino de rosas precisamente. Alemania sacudida por disturbios, manifestaciones y levantamientos, fue reclutado en el cuerpo de estudiantes para proteger al rey en el palacio real de Berlín y sus estudios quedaron interrumpidos.
En aquel ambiente el problema que captó el interés de Riemann, fue el colapso que, según el pensaba, suponía la geometría euclidiana, que mantiene que el espacio es tridimensional y “plano” (en el espacio plano, la distancia más corta entre dos puntos es la línea recta; lo que descarta la posibilidad de que el espacio pueda estar curvado, como en una esfera).
Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna parte vería Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita. Riemann, ante aquella realidad se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos., descubrió el, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.
Euclides nos habló de la obviedad de que un punto no tiene dimensión. Una línea tiene una dimensión: longitud. Un plano tiene dos dimensiones: longitud y anchura. Un sólido tiene tres dimensiones: longitud, anchura y altura. Y allí se detiene. Nada tiene cuatro dimensiones, incluso Aristóteles afirmó que la cuarta dimensión era imposible. En Sobre el cielo, escribió: “La línea tiene magnitud en una dirección, el plano en dos direcciones, y el sólido en tres direcciones, y más allá de éstas no hay otra magnitud porque los tres son todas.” Además, en el año 150 d. C. el astrónomo Ptolomeo de Alejandría fue más allá de Aristóteles y ofreció, en su libro sobre la distancia, la primera “demostración” ingeniosa de que la cuarta dimensión es imposible.
https://youtu.be/2qaJ6A1nx9M
En realidad, lo único que Ptolomeo demostraba era que, era imposible visualizar la cuarta dimensión con nuestros cerebros tridimensionales (de hecho, hoy sabemos que muchos objetos matemáticos no pueden ser visualizados, aunque puede demostrarse que en realidad, existen). Ptolomeo puede pasar a la Historia como el hombre que se opuso a dos grandes ideas en la ciencia: el sistema solar heliocéntrico y la cuarta dimensión.
La ruptura decisiva con la geometría euclidiana llegó cuando Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.
Riemann desarrolló su teoría de dimensiones más altas.
Parte real (rojo) y parte imaginaria (azul) de la línea crítica Re(s) = 1/2 de la función zeta de Riemann. Pueden verse los primeros ceros no triviales en Im(s) = ±14,135, ±21,022 y ±25,011. La hipótesis de Riemann, por su relación con la distribución de los números primos en el conjunto de los naturales, es uno de los problemas abiertos más importantes en la matemática contemporánea.
Finalmente, cuando hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, esta fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante los milenios.
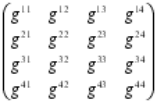
Riemann creó el tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresar a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a2 + b2 = c2. El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional.)
La Teoría de la Relatividad General aprovechó el Tensor de Riemann para su desarrollo
El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann, permitió a Einstein formular su teoría de la gravedad y, posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de super-gravedad, supersimetría y, finalmente las supercuerdas.

Para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854, que le había enviado su amigo Marcel Grossman, rápidamente se dio cuenta de que allí estaba la clave para resolver su problema. Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de a relatividad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E=mc2. La reinterpretación física de la famosa conferencia de Riemann se denomina ahora relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.
Emilio Silvera Vázquez
Jul
13
Velocidades inimaginables
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (9)
Comments (9)

El núcleo tiene dimensiones muy reducidas. Ocupa la parte central del átomo; en él reside toda la carga positiva y casi la totalidad de la masa atómica. Está formado fundamentalmente por protones y neutrones. Los protones tienen una carga positiva cuantitativamente igual a la del electrón (1,602 x 10-19 culombios).
En el centro del átomo se encuentra un pequeño grano compacto aproximadamente 100.000 veces más pequeño que el propio átomo: el núcleo atómico. Su masa, e incluso más aún su carga eléctrica, determinan las propiedades del átomo del cual forma parte. Debido a la solidez del núcleo parece que los átomos, que dan forma a nuestro mundo cotidiano, son intercambiables entre sí, e incluso cuando interaccionan entre ellos para formar sustancias químicas (los elementos). Pero el núcleo, a pesar de ser tan sólido, puede partirse. Si dos átomos chocan uno contra el otro con gran velocidad podría suceder que los núcleos llegaran a chocar entre sí y entonces, o bien se rompen en trozos, o se funden liberando en el proceso partículas subnucleares. La nueva física de la primera mitad del siglo XX estuvo dominada por los nuevos acertijos que estas partículas planteaban.

Pero tenemos la mecánica cuántica; ¿es que no es aplicable siempre?, ¿Cuál es la dificultad? Desde luego, la mecánica cuántica es válida para las partículas subatómicas, pero hay más que eso. Las fuerzas con que estas partículas interaccionan y que mantienen el núcleo atómico unido son tan fuertes que las velocidades a las que tienen que moverse dentro y fuera del núcleo están cerca de la velocidad de la luz, c, que es de 299.792’458 Km/s. Cuando tratamos con velocidades tan altas se necesita una segunda modificación a las leyes de la física del siglo XIX; tenemos que contar con la teoría de la relatividad especial de Einstein.
Esta teoría también fue el resultado de una publicación de Einstein de 1905. en esta teoría quedaron sentadas las bases de que el movimiento y el reposo son conceptos relativos, no son absolutos, como tampoco habrá un sistema de referencia absoluto con respecto al cual uno pueda medir la velocidad de la luz.

Pero había más cosas que tenían que ser relativas. En este teoría, la masa y la energía también dependen de la velocidad, como lo hacen la intensidad del campo eléctrico y del magnético. Einstein descubrió que la masa de una partícula es siempre proporcional a la energía que contienen, supuesto que se haya tenido en cuenta una gran cantidad de energía en reposo de una partícula cualquiera, como se denota a continuación:
E =mc2 La ecuación nos dice que masa y energía son la misma cosa.
Como la velocidad de la luz es muy grande, esta ecuación sugiere que cada partícula debe almacenar una cantidad enorme de energía, y en parte esta predicción fue la que hizo que la teoría de la relatividad tuviese tanta importancia para la física (¡y para todo el mundo!). Para que la teoría de la relatividad también sea auto-consistente tiene que ser holista, esto es, que todas las cosas y todo el mundo obedezcan a las leyes de la relatividad. No son sólo los relojes los que se atrasan a grandes velocidades, sino que todos los procesos animados se comportan de la forma tan inusual que describe esta teoría cuando nos acercamos a la velocidad de la luz. El corazón humano es simplemente un reloj biológico y latirá a una velocidad menor cuando viaje en un vehículo espacial a velocidades cercanas a la de la luz. Este extraño fenómeno conduce a lo que se conoce como la “paradoja de los gemelos”, sugerida por Einstein, en la que dos gemelos idénticos tienen diferente edad cuando se reencuentran después de que uno haya permanecido en la Tierra mientras que el otro ha viajado a velocidades relativistas.
Einstein comprendió rápidamente que las leyes de la gravedad también tendrían que ser modificadas para que cumplieran el principio relativista.

La formulación de newton es bien conocida, en la segunda imagen que se representan en este esquema dos partículas que se acercan entre sí siguiendo un movimiento acelerado. La interpretación newtoniana supone que el espacio-tiempo es llano y que lo que provoca la curvatura de las líneas de universo es la fuerza de interacción gravitatoria entre ambas partículas. Por el contrario, la interpretación einsteiniana supone que las líneas de universo de estas partículas son geodésicas (“rectas”), y que es la propia curvatura del espacio tiempo lo que provoca su aproximación progresiva.
Para poder aplicar el principio de la relatividad a la fuerza gravitatoria, el principio tuvo que ser extendido de la siguiente manera: no sólo debe ser imposible determinar la velocidad absoluta del laboratorio, sino que también es imposible distinguir los cambios de velocidad de los efectos de una fuerza gravitatoria.
Einstein comprendió que la consecuencia de esto era que la gravedad hace al espacio-tiempo lo que la humedad a una hoja de papel: deformar la superficie con desigualdades que no se pueden eliminar. Hoy en día se conocen muy bien las matemáticas de los espacios curvos, pero en el época de Einstein el uso de estas nociones matemáticas tan abstractas para formular leyes físicas era algo completamente nuevo, y le llevó varios años encontrar la herramienta matemática adecuada para formular su teoría general de la relatividad que describe cómo se curva el espacio en presencia de grandes masas como planetas y estrellas.
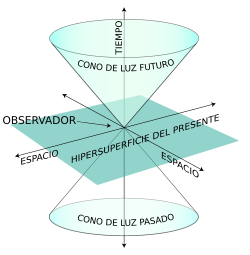
Einstein tenía la idea en su mente desde 1907 (la relatividad especial la formuló en 1905), y se pasó 8 años buscando las matemáticas adecuadas para su formulación.
Leyendo el material enviado por un amigo al que pidió ayuda, Einstein quedó paralizado. Ante él, en la primera página de una conferencia dada ante el Sindicato de Carpinteros, 60 años antes por un tal Riemann, tenía la solución a sus desvelos: el tensor métrico de Riemann, que le permitiría utilizar una geometría espacial de los espacios curvos que explicaba su relatividad general.

Desde que se puso en órbita el telescopio espacial de rayos gamma Fermi, el 11 de junio de 2008, ha detectado poblaciones enteras de objetos nunca antes vistos. El último hallazgo de Fermi afecta al púlsar J1823-3021A, avistado en 1994 con el radiotelescopio Lovell, en Inglaterra. Un equipo internacional de expertos se ha dado cuenta de que esta estrella pulsante emite rayos gamma y gracias a Fermi ha podido caracterizar sus inusuales propiedades. Los resultados de su investigación se publican en el último número de Science. Lo cierto es que han descubierto el púlsar de milisegundos más joven y con la fuerza magnética más potente

No está mal que en este punto recordemos la fuerza magnética y gravitatoria que nos puede ayudar a comprender mejor el comportamiento de las partículas subatómicas.
El electromagnetismo, decíamos al principio, es la fuerza con la cual dos partículas cargadas eléctricamente se repelen (si sus cargas son iguales) o se atraen (si tienen cargas de signo opuesto).
La interacción magnética es la fuerza que experimenta una partícula eléctricamente cargada que se mueve a través de un campo magnético. Las partículas cargadas en movimiento generan un campo magnético como, por ejemplo, los electrones que fluyen a través de las espiras de una bobina.
Las fuerzas magnéticas y eléctricas están entrelazadas. En 1873, James Clerk Maxwell consiguió formular las ecuaciones completas que rigen las fuerzas eléctricas y magnéticas, descubiertas experimentalmente por Michael Faraday. Se consiguió la teoría unificada del electromagnetismo que nos vino a decir que la electricidad y el magnetismo eran dos aspectos de una misma cosa.
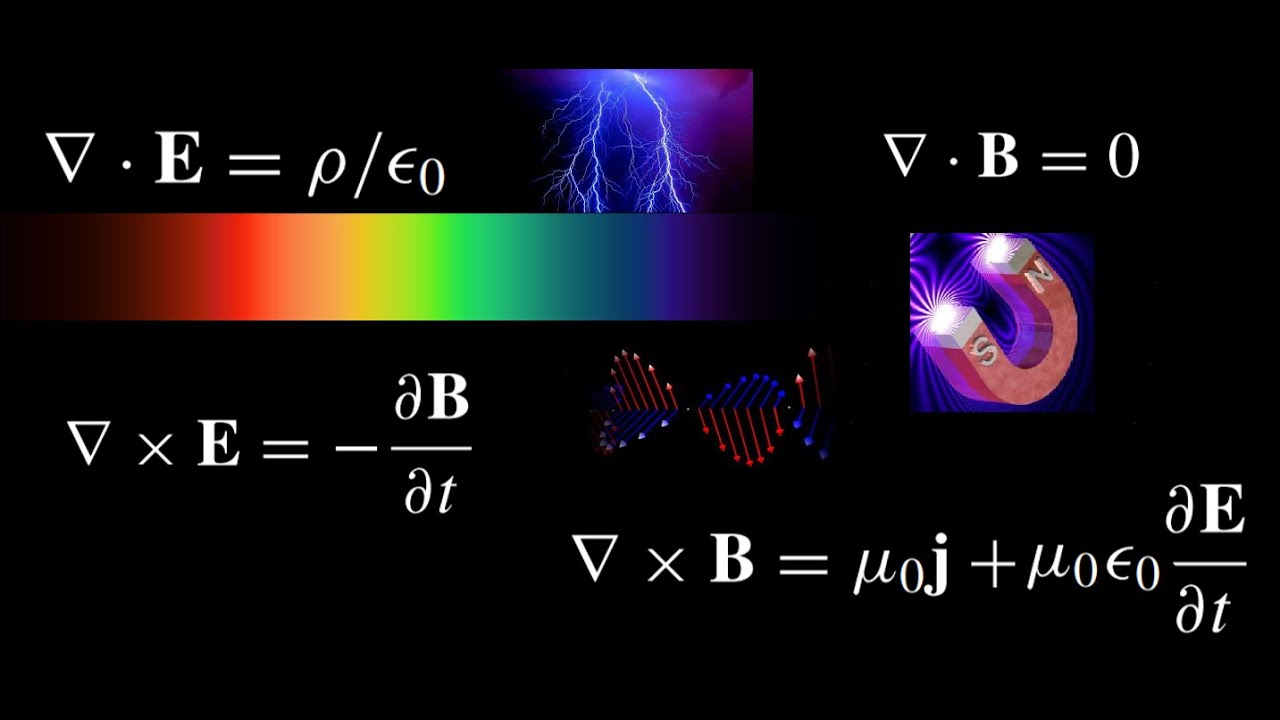
La interacción es universal, de muy largo alcance (se extiende entre las estrellas), es bastante débil. Su intensidad depende del cociente entre el cuadrado de la carga del electrón y 2hc (dos veces la constante de Planck por la velocidad de la luz). Esta fracción es aproximadamente igual a 1/137’036…, o lo que llamamos α y se conoce como constante de estructura fina.
En general, el alcance de una interacción electromagnética es inversamente proporcional a la masa de la partícula mediadora, en este caso, el fotón, sin masa.
También antes hemos comentado sobre la interacción gravitatoria de la que Einstein descubrió su compleja estructura y la expuso al mundo en 1915 con el nombre de teoría general de la relatividad, y la relacionó con la curvatura del espacio y el tiempo. Sin embargo, aún no sabemos cómo se podrían reconciliar las leyes de la gravedad y las leyes de la mecánica cuántica (excepto cuando la acción gravitatoria es suficientemente débil).

La teoría de Einstein nos habla de los planetas y las estrellas del cosmos. La teoría de Planck, Heisemberg, Schrödinger, Dirac, Feynman y tantos otros, nos habla del comportamiento del átomo, del núcleo, de las partículas elementales en relación a estas interacciones fundamentales. La primera se ocupa de los cuerpos muy grandes y de los efectos que causan en el espacio y en el tiempo; la segunda de los cuerpos muy pequeños y de su importancia en el universo atómico. Cuando hemos tratado de unir ambos mundos se produce una gran explosión de rechazo. Ambas teorías son (al menos de momento) irreconciliables.
- La interacción gravitatoria actúa exclusivamente sobre la masa de una partícula.
- La gravedad es de largo alcance y llega a los más lejanos confines del universo conocido.
- Es tan débil que, probablemente, nunca podremos detectar esta fuerza de atracción gravitatoria entre dos partículas elementales. La única razón por la que podemos medirla es debido a que es colectiva: todas las partículas (de la Tierra) atraen a todas las partículas (de nuestro cuerpo) en la misma dirección.
La partícula mediadora es el hipotético gravitón. Aunque aún no se ha descubierto experimentalmente, sabemos lo que predice la mecánica cuántica: que tiene masa nula y espín 2.
La ley general para las interacciones es que, si la partícula mediadora tiene el espín par, la fuerza entre cargas iguales es atractiva y entre cargas opuestas repulsiva. Si el espín es impar (como en el electromagnetismo) se cumple a la inversa.
Pero antes de seguir profundizando en estas cuestiones hablemos de las propias partículas subatómicas, para lo cual la teoría de la relatividad especial, que es la teoría de la relatividad sin fuerza gravitatoria, es suficiente.
Si viajamos hacia lo muy pequeño tendremos que ir más allá de los átomos, que son objetos voluminosos y frágiles comparados con lo que nos ocupará a continuación: el núcleo atómico y lo que allí se encuentra. Los electrones, que ahora vemos “a gran distancia” dando vueltas alrededor del núcleo, son muy pequeños y extremadamente robustos. El núcleo está constituido por dos especies de bloques: protones y neutrones. El protón (del griego πρώτος, primero) debe su nombre al hecho de que el núcleo atómico más sencillo, que es el hidrógeno, está formado por un solo protón. Tiene una unidad de carga positiva. El neutrón recuerda al protón como si fuera su hermano gemelo: su masa es prácticamente la misma, su espín es el mismo, pero en el neutrón, como su propio nombre da a entender, no hay carga eléctrica; es neutro.
La masa de estas partículas se expresa en una unidad llamada mega-electrón-voltio o MeV, para abreviar. Un MeV, que equivale a 106 electrón-voltios, es la cantidad de energía de movimiento que adquiere una partícula con una unidad de carga (tal como un electrón o un protón) cuando atraviesa una diferencia de potencial de 106 (1.000.000) voltios. Como esta energía se transforma en masa, el MeV es una unidad útil de masa para las partículas elementales.


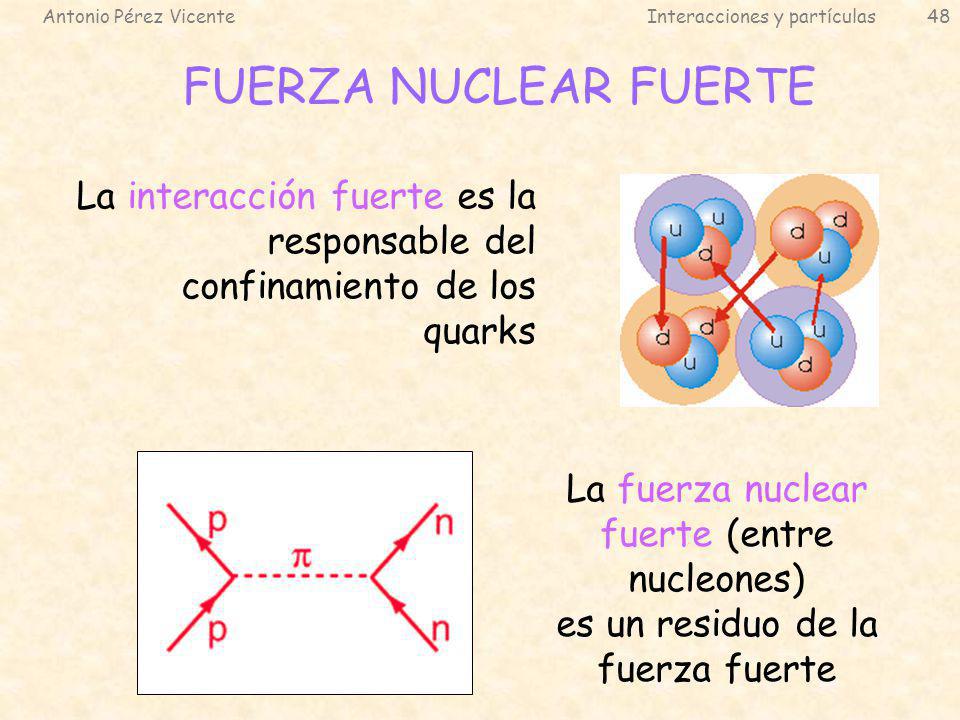
La mayoría de los núcleos atómicos contienen más neutrones que protones. Los protones se encuentran tan juntos en el interior de un núcleo tan pequeño que se deberían repeles entre sí fuertemente, debido a que tienen cargas eléctricas del mismo signo. Sin embargo, hay una fuerza que los mantiene unidos estrechamente y que es mucho más potente e intensa que la fuerza electromagnética: la fuerza o interacción nuclear fuerte, unas 102 veces mayor que la electromagnética, y aparece sólo entre hadrones para mantener a los nucleones confinados dentro del núcleo. Actúa a una distancia tan corta como 10-15 metros, o lo que es lo mismo, 0’000000000000001 metros.
La interacción fuerte está mediada por el intercambio de mesones virtuales, 8 gluones que, como su mismo nombre indica (glue en inglés es pegamento), mantiene a los protones y neutrones bien sujetos en el núcleo, y cuanto más se tratan de separar, más aumenta la fuerza que los retiene, que crece con la distancia, al contrario que ocurre con las otras fuerzas.

La luz es una manifestación del fenómeno electromagnético y está cuantizada en “fotones”, que se comportan generalmente como los mensajeros de todas las interacciones electromagnéticas. Así mismo, como hemos dejado reseñado en el párrafo anterior, la interacción fuerte también tiene sus cuantos (los gluones). El físico japonés Hideki Yukawa (1907 – 1981) predijo la propiedad de las partículas cuánticas asociadas a la interacción fuerte, que más tarde se llamarían piones. Hay una diferencia muy importante entre los piones y los fotones: un pión es un trozo de materia con una cierta cantidad de “masa”. Si esta partícula está en reposo, su masa es siempre la misma, aproximadamente 140 MeV, y si se mueve muy rápidamente, su masa parece aumentar en función E = mc2. Por el contrario, se dice que la masa del fotón en reposo es nula. Con esto no decimos que el fotón tenga masa nula, sino que el fotón no puede estar en reposo. Como todas las partículas de masa nula, el fotón se mueve exclusivamente con la velocidad de la luz, 299.792’458 Km/s, una velocidad que el pión nunca puede alcanzar porque requeriría una cantidad infinita de energía cinética. Para el fotón, toda su masa se debe a su energía cinética.
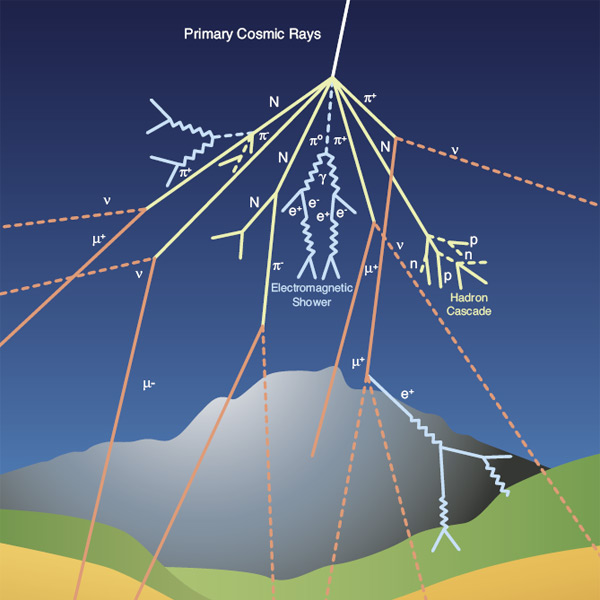
Los físicos experimentales buscaban partículas elementales en las trazas de los rayos cósmicos que pasaban por aparatos llamados cámaras de niebla. Así encontraron una partícula coincidente con la masa que debería tener la partícula de Yukawa, el pión, y la llamaron mesón (del griego medio), porque su masa estaba comprendida entre la del electrón y la del protón. Pero detectaron una discrepancia que consistía en que esta partícula no era afectada por la interacción fuerte, y por tanto, no podía ser un pión. Actualmente nos referimos a esta partícula con la abreviatura μ y el nombre de muón, ya que en realidad era un leptón, hermano gemelo del electrón, pero con 200 veces su masa.
Antes de seguir veamos las partículas elementales de vida superior a 10-20 segundos que eran conocidas en el año 1970.
| Nombre | Símbolo | Masa (MeV) | Carga | Espín | Vida media (s) |
| Fotón | γ | 0 | 0 | 1 | ∞ |
| Leptones (L = 1, B = 0) | |||||
| Electrón | e– | 0’5109990 | – | ½ | ∞ |
| Muón | μ– | 105’6584 | – | ½ | 2’1970 × 10-6 |
| Tau | τ | ||||
| Neutrino electrónico | νe | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino muónico | νμ | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino tauónico | ντ | ~ 0 | 0 | ½ | ~ ∞ |
| Mesones (L = 0, B = 0) | |||||
| Pión + | π+ | 139’570 | 2’603 × 10-8 | ||
| Pión – | π– | 139’570 | 2’603 × 10-8 | ||
| Pión 0 | π0 | 134’976 | 0’84 × 10-16 | ||
| Kaón + | k+ | 493’68 | 1’237 × 10-8 | ||
| Kaón – | k– | 493’68 | 1’237 × 10-8 | ||
| Kaón largo | kL | 497’7 | 5’17 × 10-8 | ||
| Kaón corto | kS | 497’7 | 0’893 × 10-10 | ||
| Eta | η | 547’5 | 0 | 0 | 5’5 × 10-19 |
| Bariones (L = 0, B = 1) | |||||
| Protón | p | 938’2723 | + | ½ | ∞ |
| Neutrón | n | 939’5656 | 0 | ½ | 887 |
| Lambda | Λ | 1.115’68 | 0 | ½ | 2’63 × 10-10 |
| Sigma + | Σ+ | 1.189’4 | + | ½ | 0’80 × 10-10 |
| Sigma – | Σ– | 1.1974 | – | ½ | 7’4× 10-20 |
| Sigma 0 | Σ0 | 0 | ½ | 1’48 × 10-10 | |
| Ksi 0 | Ξ0 | 1.314’9 | 0 | ½ | 2’9 × 10-10 |
| Ksi – | Ξ– | 1.321’3 | – | ½ | 1’64 × 10-10 |
| Omega – | Ω– | 1.672’4 | – | 1½ | 0’82 × 10-10 |


Para cada leptón y cada barión existe la correspondiente antipartícula, con exactamente las mismas propiedades a excepción de la carga que es la contraria. Por ejemplo, el antiprotón se simboliza con y el electrón con e+. Los mesones neutros son su propia antipartícula, y el π+ es la antipartícula del π–, al igual que ocurre con k+ y k–. El símbolo de la partícula es el mismo que el de su antipartícula con una barra encima. Las masas y las vidas medias aquí reflejadas pueden estar corregidas en este momento, pero de todas formas son muy aproximadas.
Los símbolos que se pueden ver algunas veces, como s (extrañeza) e i (iso-espín) están referidos a datos cuánticos que afectan a las partículas elementales en sus comportamientos.
Debo admitir que todo esto tiene que sonar algo misterioso. Es difícil explicar estos temas por medio de la simple palabra escrita sin emplear la claridad que transmiten las matemáticas, lo que, por otra parte, es un mundo secreto para el común de los mortales, y ese lenguaje es sólo conocido por algunos privilegiados que, mediante un sistema de ecuaciones pueden ver y entender de forma clara, sencilla y limpia, todas estas complejas cuestiones.

Si hablamos del espín (o, con más precisión, el momento angular, que es aproximadamente la masa por el radio por la velocidad de rotación) se puede medir como un múltiplo de la constante de Planck, h, dividido por 2π. Medido en esta unidad y de acuerdo con la mecánica cuántica, el espín de cualquier objeto tiene que ser o un entero o un entero más un medio. El espín total de cada tipo de partícula – aunque no la dirección del mismo – es fijo.
El electrón, por ejemplo, tiene espín ½. Esto lo descubrieron dos estudiantes holandeses, Samuel Gondsmit (1902 – 1978) y George Uhlenbeck (1900 – 1988), que escribieron sus tesis conjuntamente sobre este problema en 1972. Fue una idea audaz que partículas tan pequeñas como los electrones pudieran tener espín, y de hecho, bastante grande. Al principio, la idea fue recibida con escepticismo porque la “superficie del electrón” se tendría que mover con una velocidad 137 veces mayor que la de la luz, lo cual va en contra de la teoría de la relatividad general en la que está sentado que nada en el universo va más rápido que la luz, y por otra parte, contradice E=mc2, y el electrón pasada la velocidad de la luz tendría una masa infinita.
Hoy día, sencillamente, tal observación es ignorada, toda vez que el electrón carece de superficie.
Las partículas con espín entero se llaman bosones, y las que tienen espín entero más un medio se llaman fermiones. Consultado los valores del espín en la tabla anterior podemos ver que los leptones y los bariones son fermiones, y que los mesones y los fotones son bosones. En muchos aspectos, los fermiones se comportan de manera diferente de los bosones. Los fermiones tienen la propiedad de que cada uno de ellos requiere su propio espacio: dos fermiones del mismo tipo no pueden ocupar o estar en el mismo punto, y su movimiento está regido por ecuaciones tales que se evitan unos a otros. Curiosamente, no se necesita ninguna fuerza para conseguir esto. De hecho, las fuerzas entre los fermiones pueden ser atractivas o repulsivas, según las cargas. El fenómeno por el cual cada fermión tiene que estar en un estado diferente se conoce como el principio de exclusión de Pauli. Cada átomo está rodeado de una nube de electrones, que son fermiones (espín ½). Si dos átomos se aproximan entre sí, los electrones se mueven de tal manera que las dos nubes se evitan una a otra, dando como resultado una fuerza repulsiva. Cuando aplaudimos, nuestras manos no se atraviesan pasando la uno a través de la otra. Esto es debido al principio de exclusión de Pauli para los electrones de nuestras manos que, de hecho, los de la izquierda rechazan a los de la derecha.
En contraste con el característico individualismo de los fermiones, los bosones se comportan colectivamente y les gusta colocarse todos en el mismo lugar. Un láser, por ejemplo, produce un haz de luz en el cual muchísimos fotones llevan la misma longitud de onda y dirección de movimiento. Esto es posible porque los fotones son bosones.
Cuando hemos hablado de las fuerzas fundamentales que, de una u otra forma, interaccionan con la materia, también hemos explicado que la interacción débil es la responsable de que muchas partículas y también muchos núcleos atómicos exóticos sean inestables. La interacción débil puede provocar que una partícula se transforme en otra relacionada, por emisión de un electrón y un neutrino. Enrico Fermi, en 1934, estableció una fórmula general de la interacción débil, que fue mejorada posteriormente por George Sudarshan, Robert Marschak, Murray Gell-Mann, Richard Feynman y otros. La fórmula mejorada funciona muy bien, pero se hizo evidente que no era adecuada en todas las circunstancias.
Uno de los protones se transmuta en un neutrón por medio de la interacción débil, transformando un quark “up”, en “down”. Este proceso consume energía (el neutrón tiene ligeramente más masa que..
En 1970, de las siguientes características de la interacción débil sólo se conocían las tres primeras:
- La interacción actúa de forma universal sobre muchos tipos diferentes de partículas y su intensidad es aproximadamente igual para todas (aunque sus efectos pueden ser muy diferentes en cada caso). A los neutrinos les afecta exclusivamente la interacción débil.
- Comparada con las demás interacciones, ésta tiene un alcance muy corto.
- La interacción es muy débil. Consecuentemente, los choques de partículas en los cuales hay neutrinos involucrados son tan poco frecuentes que se necesitan chorros muy intensos de neutrinos para poder estudiar tales sucesos.
- Los mediadores de la interacción débil, llamados W+, W– y Z0, no se detectaron hasta la década de 1980. al igual que el fotón, tienen espín 1, pero están eléctricamente cargados y son muy pesados (esta es la causa por la que el alcance de la interacción es tan corto). El tercer mediador, Z0, que es responsable de un tercer tipo de interacción débil que no tiene nada que ver con la desintegración de las partículas llamada “corriente neutra”, permite que los neutrinos puedan colisionar con otras partículas sin cambiar su identidad.
A partir de 1970, quedó clara la relación de la interacción débil y la electromagnética (electrodébil de Weinberg-Salam).
La interacción fuerte (como hemos dicho antes) sólo actúa entre las partículas que clasificamos en la familia llamada de los hadrones, a los que proporciona una estructura interna complicada. Hasta 1972 sólo se conocían las reglas de simetría de la interacción fuerte y no fuimos capaces de formular las leyes de la interacción con precisión.
Como apuntamos, el alcance de esta interacción no va más allá del radio de un núcleo atómico ligero (10-13 cm aproximadamente).
La interacción es fuerte. En realidad, la más fuerte de todas.
Lo dejaré aquí, en verdad, eso que el Modelo Estándar de la Física, es feo, complejo e incompleto y, aunque hasta el momento es una buena herramienta con la que trabajar, la verdad es que, se necesita un nuevo modelo más avanzado y que incluya la Gravedad.

Veremos que nos trae la nueva etapa del LHC.
La nueva etapa del LHC, conocida como Run 3, comenzó en 2022 después de tres años de actualizaciones y mejoras.
Esta fase se centra en la exploración de nuevas fronteras de la física de partículas a energías récord y en el estudio de procesos raros. Además, se están realizando preparativos para el LHC de Alta Luminosidad (HL-LHC), que aumentará la cantidad de datos disponibles para los experimento
Emilio Silvera V.
















 Totales: 84.914.476
Totales: 84.914.476 Conectados: 79
Conectados: 79