Dic
31
La Física no duerme
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)

Lentes atómicas
Científicos del DIPC y el Centro de Física de Materiales (CSIC-UPV) y de la Universidad de Cambridge, han creado una lente que puede concentrar la luz en dimensiones inferiores a las de un átomo. Los investigadores han utilizado nanopartículas de oro para desarrollar estas lentes focalizadoras, que permiten ver enlaces químicos individuales en las moléculas.

Nuestras predicciones teóricas sugerían que esto podía ser posible, como así se ha comprobado ahora, asegura el profesor Javier Aizpurua, que lidera los esfuerzos teóricos de esta investigación, y cuyo desarrollo ha permitido entender el confinamiento y la interacción de la luz con moléculas en escalas tan pequeñas.
El equipo de investigadores experimentales de Cambridge, liderado por el profesor Jeremy Baumberg, ha utilizado oro altamente conductor para fabricar la cavidad óptica más pequeña del mundo (picocavidad), que confina la luz a una distancia inferior a una mil millonésima de metro.
Los resultados se han publicado en Science.
Fuente: Revista mensual electrónica de la Real Sociedad Española de Física.
Dic
27
Las misteriosas funciones modulares
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Rumores del saber del mundo ~
Clasificado en Rumores del saber del mundo ~
 Comments (0)
Comments (0)

Al manipular los diagramas de lazos de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el número 10 aparecen en los lugares más extraños.
Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del Este. Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro Universo actual.
El misterio de las Funciones Modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y como Riemann antes que él trabajó en total aislamiento, en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que, los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.
La función modular de Ramanujan y la teoría de cuerdas
![]()
La función de Ramanujan contiene un término elevado a la potencia veinticuatro. Ese número es el origen de las cancelaciones milagrosas que se dan en la … Pero hablemos de las cuerdas.
La teoría de cuerdas supone que cada modo o vibración de una cuerda fundamental representa una partícula elemental distinta, y puede explicar a la vez la naturaleza de la materia y del espacio-tiempo (las partículas en lugar de ser puntuales pasan a ser unidimensionales). Es la primera teoría cuántica de la gravedad: Cuando se calcularon por primera vez las ligaduras de autoconsistencia que impone la cuerda sobre el espacio-tiempo, se observó con sorpresa que las ecuaciones de Einstein ( teoría de la gravedad) emergían de la cuerda, de hecho, el gravitón o cuanto de gravedad era la menor vibración de la cuerda cerrada.
No sabemos todavía por qué la teoría de cuerdas está definida sólo en 10 y 26 dimensiones, aunque parece seguro que esta teoría no podría unificar las fuerzas fundamentales con tan solo tres dimensiones. Las cuerdas se rompen y se forman en el espacio N-dimensional arrastrando con ellas una serie de términos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos aparecen multiplicados por el factor (N-10), lo que nos obliga a elegir N=10 para eliminarlos.

Dispersas entre oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre los más extraños jamás encontradas en matemáticas. Ellos reaparecen en los ramos más distantes e inconexos de las matemáticas. Una función, que aparece una y otra vez en la teoría de las funciones modulares, se denominan (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. Esta extraña función contiene un término elevado a la potencia veinticuatro.
El número 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente, donde menos se esperan, por razones que nadie entiende. Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas. En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. (Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio -tiempo debe tener 24 + 2 = 26 dimensiones espacio – temporales.)

Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el número 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. No estará la solución final de la Teoría de cuerdas, en estas misteriosas funciones modelares.
Para comprender este misterioso factor de dos (que añaden los físicos consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada puede vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista Aµ tiene cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell. Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones. Sin embargo, dos de estos modos vibracionales pueden ser eliminados cuando rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.
Antes explicamos que cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el número 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio – tiempo sea diez.

Claro que, la Teoría de Cuerdas tiene versiones en 10, 11 y 26 dimensiones
En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “No lo se”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una forma cuánticamente autoconsistente), pero no sabemos por que se seleccionan estos números concretos.
Quizá la respuesta a todo esto esté esperando a ser descubierta cuando alguien (algún genio matemático como Perelman) sea capaz de entender el contenido de los cuadernos perdidos de Ramanujan.
Srinivasa Ramanujan nació en 1.887 en Erode, India, cerca de Madrás. Su familia de clase media alta, brahmin, la más alta de las castas Hindúes, fueron destituidos y venidos a menos, su padre trabajaba de oficinista de un comerciante de tejidos.
Con diez años, lo mismo que pasó antes con Riemann, ya destacaba y sorprendía a todos con sus enormes poderes de cálculos. Siendo niño, rederivó la identidad de Euler entre funciones trigonométricas y exponenciales.

En la vida de cada científico joven hay un punto de partida, un hecho que, sin ellos saberlo, les marca el destino. Para Einstein fue la fascinación que le causó la brújula que le regaló su tío cuando estaba enfermo siendo un niño, no podía apartar la mirada de la aguja que siempre indicaba hacia el mismo sitio, y se preguntó una y mil veces por la fuerza invisible que la obligaba a dirigirse hacia esa dirección. Para Riemann, fue la lectura del libro de matemáticas de Legendre. Para Ramanujan, fue cuando se sumergió en un oscuro y olvidado libro de matemáticas escrito por George Carr. Este libro ha quedado inmortalizado desde entonces por el hecho de que señaló la única exposición conocida de Ramanujan a los modernas matemáticas occidentales. Según su hermana: “Fue este libro el que despertó su genio. El se propuso establecer por sí mismo las fórmulas dadas allí. Como no tenía la ayuda de otros libros, cada solución era un trabajo de investigación por lo que a él concernía… Ramanujan solía decir que la diosa Namakkal le inspiraba las fórmulas en sueños”.

Con ayuda de amigos, Ramanujan consiguió un puesto de bajo nivel del puerto de Madrás. Era un trabajo servil, con una mísera paga de 20 libras al año, pero dio libertad a Ramanujan, como a Einstein antes que él en la oficina de Patentes Suiza, para seguir sus sueños en su tiempo libre. Ramanujan, en la fascinación que en él ejercían los números, era incansable, llenaba libretas enteras de cálculos y ecuaciones que antes veía florecer en su cabeza.
Así estaban las cosas cuando decidió escribir algunos de sus trabajos a las tres matemáticos más famosos de Inglaterra y Europa.
Dos de aquellos matemáticos, al tener en su poder las cartas enviadas por un miserable empleado sin instrucción formal alguna, sin haber comprobado su contenido, las arrojaron directamente a la basura. El tercero era el brillante matemático de Cambridge Godfrey Harold Hardy. Debido a su categoría en Inglaterra, Hardy estaba acostumbrado a recibir correo de chiflados proponiéndole los más peregrinos proyectos y, en un primer momento apenas prestó atención a la carta del joven Ramanujan.
Srinivasa Ramanujan trabajó principalmente en teoría de números, encontrando identidades relacionadas con el número pi y el número e o los números primos. Como decimos, en general sus fórmulas son muy enrevesadas, pero en su mayoría verdaderas (a posteriori se ha descubierto que algunos de sus resultados era incorrectos), y algunas de ellas se han convertido en potentes herramientas para calcular grandes cantidades de decimales de, principalmente, el número pi. Quizás la más conocida sea ésta:
que nos da 8 decimales exactos de pi en cada iteración. Tremendo, ¿verdad?
Entre los densos garabatos advirtió muchos teoremas matemáticos que ya eran bien conocidos. Pensando que era la obra obvia de un plagiario, el también la desechó en ese primer impulso. Pero había algo que no encajaba. Algo que inquietaba a Hardy; no podía dejar de pensar en aquella extraña carta.
Durante la cena de esa noche, 16 de enero de. 1913, Hardy y su colega John Littlewood discutieron esta carta singular y decidieron echar un segundo vistazo – repaso a su contenido. Comenzaba de forma bastante inocente, con “Me permito presentarme a usted como un empleado en el departamento de contabilidad de la oficina del puerto franco de Madrás con un salario de solo veinte libras al año”. Pero la carta del pobre empleado de Madrás contenía teoremas que eran totalmente desconocidos para los matemáticos occidentales. En total, contenía 120 teoremas. Hardy estaba atónito. Recordaba que demostrar algunos de esos teoremas “Me derrotó por completo”. “Nunca había visto nada antes que se le pareciera en lo más mínimo. Una simple ojeada a ellos es suficiente para mostrar que sólo podían estar elaborados por un matemático muy grande”.
Littlewood y Hardy alcanzaron la misma conclusión: Aquello era el trabajo de un genio empeñado en derivar de nuevo 100 años de matemáticas europeas. “Él había estado llevando a cabo una carrera imposible, un pobre y solitario hindú, completamente solo y sin ayuda, enfrentando su cerebro contra toda la sabiduría acumulada en Europa”, recordaba con asombro Hardy.

Hardy escribió a Ramanujan y, tras muchas pesquisas, uso de amistades e influencias, arregló su estancia en Cambridge en 1.914. Por primera vez, Ramanujan podía comunicarse regularmente con sus iguales, la comunidad de los matemáticos europeos. Entonces comenzó el estallido de su actividad: tres cortos e intensos años de colaboración con Hardy en el Trinity Collage en Cambridge.
Hardy trató más tarde de estimar la capacidad matemática que poseía Ramanujan. Concedió a David Hilbert, universalmente conocido y reconocido como uno de los mayores matemáticos occidentales del siglo XIX, una puntuación de 80. A Ramanujan le asignó una puntuación de 100. Así mismo, Hardy se concedió un 25.
Por desgracia, ni Hardy ni Ramanujan parecían interesados en la psicología a los procesos de pensamiento mediante los cuales Ramanujan descubría estos increíbles teoremas, especialmente cuando este diluvio material brotaba de sus sueños con semejante frecuencia. Hardy señaló: “Parecía ridículo importunarle sobre como había descubierto este o ese teorema conocido, cuando él me estaba mostrando media docena cada día, de nuevos teoremas”.
Hardy recordaba vivamente:
-”Recuerdo una vez que fui a visitarle cuando estaba enfermo en Putney. Yo había tomado el taxi número 1.729, y comenté que el numero me parecía bastante feo, y que esperaba que no fuese mal presagio.”
– No. -Replicó Ramanujan postrado en su cama-. Es un número muy interesante; es el número más pequeño expresable como una suma de dos cubos en dos formas diferentes.
(Es la suma de 1 x 1 x 1 y 12 x 12 x 12, y también la suma de 9 x 9 x 9 y 10 x 10 x 10).

Era capaz de recitar en el acto teoremas complejos de aritmética cuya demostración requeriría un ordenador moderno.
En 1.919 volvió a casa, en la India, donde un año más tarde murió enfermo.
El legado de Ramanujan es su obra, que consta de 4.000 fórmulas en cuatrocientas páginas que llenan tres volúmenes de notas, todas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario o, lo que es más frustrante, sin ninguna demostración. En 1.976, sin embargo, se hizo un nuevo descubrimiento. Ciento treinta páginas de borradores, que contenían los resultados del último año de su vida, fueron descubiertas por casualidad en una caja en el Trinity Collage. Esto se conoce ahora con el nombre de “Cuaderno Perdido” de Ramanujan.

Comentando cuaderno perdido, el matemático Richard Askey dice:
“El de este año, mientras se estaba muriendo, era el equivalente a una vida entera de un matemático muy grande”. Lo que él consiguió era increíble. Los matemáticos Jonathan Borwien y Meter Borwein, en relación a la dificultad y la ardua tarea de descifrar los cuadernos perdidos, dijeron: “Que nosotros sepamos nunca se ha intentado una redacción matemática de este alcance o dificultad”.
Por mi parte creo que, Ramanujan, fue un genio matemático muy adelantado a su tiempo y que pasaran algunos años hasta que podamos descifrar al cien por ciento sus trabajos, especialmente, sus funciones modulares que guardan el secreto de la teoría más avanzada de la física moderna, la única capaz de unir la mecánica quántica y la Gravedad.
Las matemáticas de Ramanujan son como una sinfonía, la progresión de sus ecuaciones era algo nunca vísto, él trabajaba desde otro nivel, los números se combinaban y fluían de su cabeza a velocidad de vértigo y con precisión nunca antes conseguida por nadie. Tenía tal intuición de las cosas que éstas simplemente fluían de su cerebro. Quizá no los veía de una manera que sea traducible y el único lenguaje eran los números.
Si finalmente las dos madejas se desenredan… ¡Por algo será!
Como saben los físicos, los “accidentes” no aparecen sin ninguna razón. Cuando están realizando un cálculo largo y difícil, y entonces resulta de repente que miles de términos indeseados suman milagrosamente cero, los físicos saben que esto no sucede sin una razón más profunda subyacente. Hoy, los físicos conocen que estos “accidentes” son una indicación de que hay una simetría en juego. Para las cuerdas, la simetría se denomina simetría conforme, la simetría de estirar y deformar la hoja del Universo de la cuerda.
Aquí es precisamente donde entra el trabajo de Ramanujan. Para proteger la simetría conforme original contra su destrucción por la teoría cuántica, deben ser milagrosamente satisfechas cierto número de identidades matemáticas que, son precisamente las identidades de la función modular de Ramanujan. ¡Increíble! Pero, cierto.
En resumen, he dicho que las leyes de la naturaleza se simplifican cuando se expresan en dimensiones más altas. Sin embargo, a la luz de la teoría cuántica, debemos corregir algo Este sentido básico de mirar la cuestión. El enunciado correcto sería ahora: las leyes de la naturaleza se simplifican cuando se expresan COHERENTEMENTE en dimensiones más altas. El añadido de la palabra coherente es crucial. Esta ligadura nos obliga a utilizar las funciones modulares de Ramanujan, que fijan en diez la dimensión del espacio – tiempo. Esto, a su vez, puede darnos la clave decisiva para explicar el origen del Universo.
Einstein se preguntaba a menudo si Dios tuvo alguna elección al crear el universo.

Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan como su punto más débil. Cualquier teoría, afirman, debe ser verificable. Puesto que ninguna teoría definida a la energía de Planck de 1019 miles de millones de eV es verificable, ¡La teoría de supercuerdas no es realmente una teoría!
El principal problema, es teórico más que experimental. Si fuéramos suficientemente inteligentes, podríamos resolver exactamente la teoría y encontrar la verdadera solución no perturbativa de la teoría. Sin embargo, esto no nos excusa de encontrar algún medio por el que verificar experimentalmente la teoría, debemos esperar señales de la décima dimensión.
¿La décima dimensión?
¡Qué extraño sería que la teoría final se descubriera durante nuestra vida! El descubrimiento de las leyes finales de la Naturaleza marcará una discontinuidad en la Historia del intelecto humano, la más abrupta que haya ocurrido desde el comienzo de la ciencia moderna en el siglo XVII. ¿Podemos imaginar ahora como sería?
Steven Weinberg
emilio silvera
El apunte sobre Ramanujan fue incluido en otro de mis trabajos. Sin embargo, el presente cuaderno trata temas expresamente solicitados para utilizar en unos seminarios de física, y se me pidió incluir el tema “Ramanujan”. La Fuente es diversa y precisaría una larga relación.
Dic
27
Buscando nuevas teorías
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Nuevas revoluciones científicas ~
Clasificado en Nuevas revoluciones científicas ~
 Comments (3)
Comments (3)

El holandés Erik Verlinde acaba de provocar un pequeño terremoto al decir que la materia oscura no existe y cuestionar a Einstein y su teoría de la relatividad. La propuesta de este físico teórico de la Universidad de Ámsterdam ha despertado las suspicacias entre algunos de sus colegas, mientras otros reconocen que su idea es interesante.

La inmensa mayoría de expertos piensa que las leyes formuladas por Isaac Newton hace más de tres siglos y la relatividad aportan la mejor explicación del universo, y la inmensa mayoría de observaciones y experimentos hasta la fecha, incluidas las ondas gravitacionales descubiertas este mismo año, les da la razón. Sin embargo estas teorías no sirven en el mundo de lo muy pequeño, donde las interacciones entre las partículas elementales están gobernadas por la teoría cuántica de campos, incompatible con la relatividad. También en el universo a grandes escalas, en galaxias, grupos de galaxias y los cúmulos con decenas o cientos de galaxias, la gravedad es mucho más fuerte de la que ejerce la materia visible. Para que las ecuaciones de Einstein funcionen en estos entornos es necesario añadir el empuje gravitatorio de la invisible materia oscura y la fuerza de la energía oscura, que acelera la expansión del universo. Juntos, estos dos ingredientes desconocidos suponen el 95% del universo.
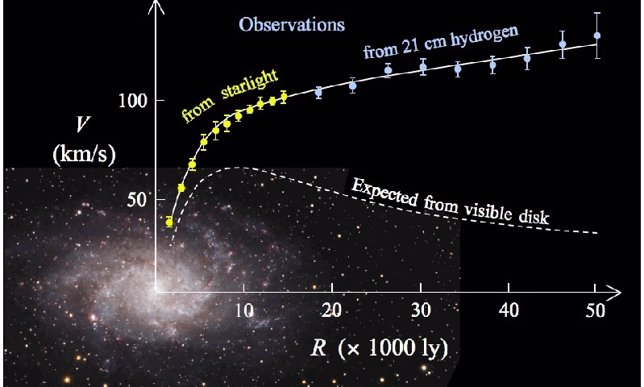
Una nueva teoría de la gravedad podría explicar la materia oscura
La nueva teoría de la gravedad emergente podría explicar el curioso movimiento de las estrellas en las galaxias, según el experto en teoría de cuerdas Erik Verlinde, de la Universidad de Amsterdam. Esta ‘segunda ley de Newton’ predice exactamente la misma desviación de los movimientos que se suele explicar cuando se inserta la materia oscura en la teoría.
La propuesta de Verlinde afirma que la fuerza de la gravedad entre dos objetos muy distantes decae menos de lo que predijeron Newton y Einstein. De esta forma, solo el empuje de la materia visible y la interacción con la energía oscura bastan para explicar el comportamiento de las galaxias.
Un equipo de astrónomos de Holanda, Alemania, Reino Unido y Australia ha puesto a prueba esta teoría en observaciones de más de 33.000 galaxias. Sus conclusiones son que tanto la teoría de Verlinde como la de Einstein sirven para explicar la curvatura de la luz por la gravedad. Pero las ecuaciones de Verlinde, resaltan los autores, explican esa distorsión sin necesidad de materia oscura.
“El resultado de esta primera prueba parece definitivamente interesante”, ha dicho Margot Brower, astrónoma del Observatorio de Leiden y coautora del estudio, publicado online en Monthly Notices of the Royal Astronomical Society. “Ahora la pregunta es si esta nueva teoría sigue adelante y si se puede probar” a mayor escala.
Árboles en medio del mar
Como teórico de cuerdas,el trabajo del holandés intenta conjugar la naturaleza cuántica de la realidad con los conceptos de espacio y tiempo de Einstein, usando una sola teoría, un logro que sería más importante que la relatividad. “Lo que propone Verlinde es que la energía oscura revela que hay un entrelazamiento cuántico de larga distancia cuyo efecto sería modificar las ecuaciones de la gravitación clásicas a grandes distancias”, explica José Luis Barbón, investigador del Instituto de Física Teórica, en Madrid. “Los físicos vemos la gravitación desde Einstein como una deformación del espacio-tiempo, pero aquí la idea es que la elasticidad intrínseca del espacio es diferente de la habitual cuando te vas a distancias muy grandes, debido a ese entrelazamiento de larga distancia”, añade.

El argentino Juan Maldacena, uno de los físicos teóricos en cuyas ideas se ha inspirado Verlinde, destruye a su colega con una analogía. “Los astrofísicos son como un navegante […] que va en el medio del océano” y de repente se encuentran ramas de árboles, señala. “La teoría de la materia oscura es análoga a concluir que debe haber una isla cerca, mientras que la teoría de Verlinde es análoga a decir: ‘Oh, hay algas con forma de ramas de árboles que crecen en el mar” . “Creo que es tan probable que su teoría sea cierta como que haya árboles que crecen en el medio del mar”, remacha este físico teórico del Instituto de Estudio Avanzado de Princeton, EE UU.

Mordehai Milgrom
Mordehai Milgrom, del Instituto Weizmann, en Israel, dice que el trabajo es “muy bienvenido”, porque ayuda a atraer a científicos de disciplinas como la teoría de cuerdas al desarrollo de alternativas a la relatividad. Pero considera que la idea de Verlinde es aún “muy preliminar” y “está muy lejos de haber resuelto el problema de la materia oscura con una teoría fundamental elegante”. Milgrom desarrolló en los 80 la dinámica newtoniana modificada (MOND, en sus siglas en inglés), que también niega que exista la materia oscura. En su opinión, la teoría de Verlinde es una derivada parcial de su propio trabajo, al que además el físico holandés no habría reconocido como debe.

Todas estas teorías alternativas “naufragan bastante” cuando intentan describir el universo a escalas mayores, como los cúmulos de galaxias, así como la estructura detallada de la radiación de fondo radiación de fondo de microondas tras el Big Bang, advierte Barbón. “Las ideas de Verlinde son interesantes, pero muy vagas”, explica. “Es enteramente posible que sean totalmente erróneas, aunque también es posible que encierren algo de verdad, en este momento son demasiado nebulosas como para emitir un veredicto”, señala.
Verlinde no ha respondido a las preguntas de Materia. En un video facilitado por la Universidad de Ámsterdam, dice que la manera de falsar su propuesta es “descubrir una partícula que describa” el comportamiento de la gravedad “en galaxias y grupos de galaxias”, algo que, por ahora, nadie ha logrado
Dic
26
Un pequeño homenaje a la presencia de la Vida en la Tierra
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo y la Vida ~
Clasificado en El Universo y la Vida ~
 Comments (0)
Comments (0)
Analizando la luz de las galaxias pequeñas y de brillo débil que orbitan a la Vía Láctea, un equipo de científicos cree haber descubierto la masa mínima para las galaxias en el universo: 10 millones de veces la masa del Sol. Esta masa podría ser el “bloque de construcción” más pequeño conocido de la sustancia misteriosa e invisible denominada “materia oscura”. Las estrellas que se forman dentro de estos bloques se agrupan y se convierten en galaxias.

¿Filametos de materia oscura? ¿Dónde?
Los científicos saben muy poco sobre las propiedades microscópicas de la “materia oscura” aunque dicen que constituye aproximadamente las cinco sextas partes de toda la materia en el universo (bueno, al menos eso es lo que se cree antes de haberlo demostrado).
Pequeñas Galaxias y Materia Oscura
La verdadera Historia de la Teoría del Caos
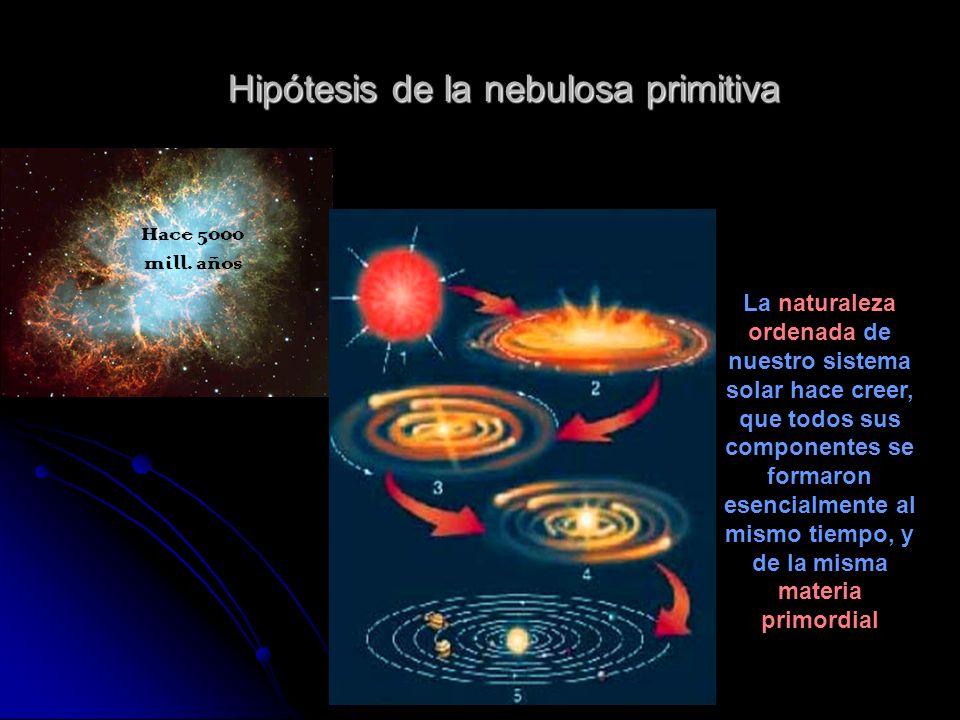
Son muchas las cosas que no sabemos y, de cada una de ellas, nosotros los humanos, creamos hipótesis y hacemos conjeturas, construimos modelos y, con los datos que hemos podido reunir, dejamos expuesta una teoría de lo que pudo ser. De esa manera hemos creado la “historia” de cómo se formó nuestro Sistema solar a partir de una explosión de supernova que creando una nebulosa sería el origen, hace algunos miles de millones de años, de todo el sistema planetario en el que está la Tierra y nos cobijamos nosotros.

Nadie pudo escribir la crónica de la Historia de la Vida
A mayor escala y viajando mucho más lejos en el Tiempo, también hemos “recreado” el escenario que suponemos que pudo existir cuando “nació” el universo, cuando dio comienzo la existencia del Tiempo y apareció el Espacio, se creó la materia y comenzaron a formarse los objetos que hoy podemos contemplar por todo el inmenso Cosmos. De todo ello, de manera “misteriosa” (nadie sabe a ciencia cierta como fue), aparecIeron los primeros signos de vida, primero en forma de rústicas criaturas y más elaboradas después, cuando con el paso de miles de millones de años, pudieron evolucionar.
A ciencia cierta (no había presente ningún cronista para poder relatar los sucesos), nadie sabe, cómo se forma´ron aquellos primeros signos de vida, primero una serie de circunstancias vinieron a conformar un protoplasma vivo del que surgirían aquellas primeras células replicantes que comenzaron la fascinante aventura de la Vida, y, más tarde, todos sabemos de las especies que han poblado nuestro mundo y las que actualmente están con nosotros. Está claro que no se conocen muchas especies desaparecidas y, de la misma manera, tampoco muchas de las que actualmente existen en lugares imposibles.
En nuestra región, situada en el interior del brazo de Orión a unos 30.000 años-luz del centro galáctico, las cosas se pudieron suceder, más o menos, como nos dicen al margen de la imagen, con algunas dudas y algunas preguntas sin contestar, así pudieron suceder, a grandes rasgos las cosas. Sin embargo, no es ese el tema que el título nos señala, nos vamos a centrar en la “vida” esa explosión de imaginación que ha tenido el universo para que, al menos en nuestro caso, haya alguien que comente sobre él y también, sobre esa maravilla que representamos: Seres Conscientes en un universo de materia, de explosiones y cambios, de energías sin fin.

Lo cierto es que, el recuerdo de los miles de millones de años de la historia de la vida, no ha podido ser inscrito en la memoria de los seres que la representan, al igual que los últimos millones de años no están grabados en la memoria de los seres humanos, los primeros naturalistas que se sintieron intrigados por los fósiles que encontraban, no pudieron presentir de qué manera aquello que estaban sacando a la luz del día, acabaría por servir para reconstruir el pasado a través de los archivos sedimentarios de la tierra.


De nada sirvieron los razonamientos poéticos y religiosos que les habían preparado para lo contrario. La realidad nos hizo descubrir un mundo distinto, una cronología distinta y una historia distinta. Resulta fácil comprender, en qué medida, los primeros descubrimientos paleontológicos les pudieron parecer (en aquellos tiempos), por tanto, maravillosos y también, desconcertantes, hasta que punto aquella extraordinaria diversidad de formas de vida desaparecidas, su frecuente extravagancia y rareza y el encadenamiento asombroso que parecían ir revelando poco a poco, les debieron fascinar, pero también confundir.

Y, de esa manera, nuestra innata curiosidad, nos llevó a descubrir muchas clases de vida que existió en el pasado, incluso de seres monstruosamente grandes que extinguidos, sirvieron para que todos, antes sus descomunales restos, dejaran volar la imaginación y pudieran construir escenarios ya desaparecidos hacia millones de años.

Claro que, todos aquellos descubrimientos, vinieron a ensanchar la mente de lo posible y la concepción de la historia de la vida en la Tierra y también, de manera paralela, hemos ido creando una historia más profunda, de unos 13.750.000 millones de años para la historia del propio universo. Pero, la historia que nos interesa, la de la vida, se remonta a unos 4.000 millones de años (al menos en nuestro planeta), que es el tiempo que tienen los fósiles más antiguo hallados en las rocas más viejas del planeta.

Los fósiles más antiguos de la Tierra tienen 3.400 millones de años y fueron hallados en Australia en rocas milenarias.
-
Se trata de bacterias que usaban el sulfuro para vivir, en lugar de oxígeno
-
Confirman que los primeros organismos de la Tierra ‘respiraban’ sulfuro
-
El descubrimiento replantea la existencia de vida en otros planetas
Los fósiles hallados son restos de bacterias, de apenas 0,01 milímetros de tamaño, que se cree usaban el sulfuro en lugar de oxígeno para subsistir según su artículo publicado en la revista Nature Geoscience.
Las marcas de los microfósiles fueron descubiertas en sedimentos de cuarzo y arena de la región de Pilbara, en el noroeste de Australia.
Se trata de una zona que presenta formaciones rocosas del Eón Arcaico, una época geológica de nuestro planeta que tuvo lugar hace 3.800 millones de años.

Ya el hombre de Neanderthal se interesaba por los fósiles.
El descubrimiento de edades anteriores a la aparición del hombre tuvo una enorme repercución, a finales del siglo XIX, mucho más allá de los círculos científicos, en buena parte porque reveló paisajes desaparecidos y poblados por criaturas extrañas, predominantemente mostruosas. Incluso en nuestros días los grandes vertebrados del pasado ejercen a menudo una especie de fascinación: ¿no se ha convertido acaso el mamut en el emblema de una cadena de supermercados y no resultan los nombres de muchos dinosaurios mucho más familiares, incluso para los niños, que los numerosos animales actuales?.
Esa familiaridad relativa con criaturas que hasta hace dos siglos, su existencia era inimaginable, es así mismo, un gran logro de la paleontología de los vertebrados sacados a la luz por la ciencia. Claro que, si hablamos de vida, no sólo de grandes animales se compone la gran relación que podríamos hacer de todas aquellas especies que poblaron nuestro planeta y de las que, el 99% están desaparecidas. Ahora, sólo el 1% de todas las especies vivientes siguen presentes y, las demás, por una u otra causa, quedaron extinguidas al no poder adaptarse, al ser eliminadas en las grandes extinciones… ¡y vaya usted a saber cómo!

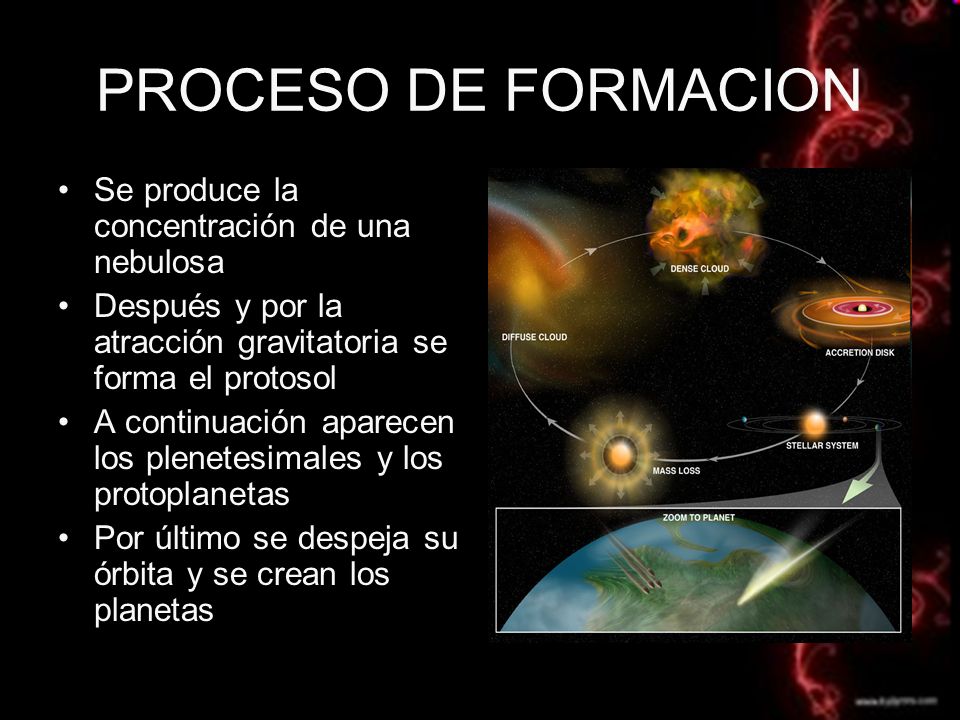
Cuentan que, durante uno de sus viajes por el Mediterráneo, san Pablo, según la leyenda que circula, naufragó ante las costas de Malta. Habiendo logrado llegar a esa isla, fue mordido por una vibora. Encolerizado, maldijo entonces a todas las serpientes maltesas, por lo que sus lenguas bífidas se transformaron en piedra. Esas lenguas petrificadas, llamadas a veces “lenguas de san pablo”, son muy comunes en Malta; no son otra cosa que los dientes de los tiburones del período mioceno, cuyas formas evocan las lenguas bífidas de las serpientes.

El relato ilustra muy bien la fascinación que han ejercido desde tiempos inmemoriales ciertos fósiles sobre la imaginación humana y la forma en que pueden ser explicados los orígenes de esos objetos misteriosos, más allá de toda hipótesis científica, en los sistemas de pensamientos tradicionales. Sin embargo, jamás conoceremos las más antiguas de esas leyendas explicativas, ya que el interés por los fósiles se remonta a la prehistoria lejana, tal como nos lo demuestran los diversos descubrimientos arqueológicos.

La cueva fue descubierta por unos jóvenes el 12 de septiembre de 1940 y tras la Segunda Guerra Mundial se facilitó la visita al público. En 1963, debido al deterioro ocasionado por la presencia del público, se cerró para proteger las pinturas. Posteriormente se restauraron las pinturas a su aspecto original .
En el transcurso de sus excavaciones en las cuevas de Arcy-sur-Cure, en Borgoña, el célebre prehistoriador francés André Leroi Gourhan descubrió en un estrato correspondiente qal paleolítico medio una pequeña pero muy antigua “colección paleontológica” ; se trataba de un polípero y de un gasterópodo fósiles, y habían sido llevados a esa cueva por un hombre de Neardenthal. Hará más de 50.000 años posiblemente, que la atención de un “hombre fósil” se vio atraida por esos objetos curiosos, hasta el punto de que se los llevó consigo. No cabe duda de que nunca sabremos cuáles eran las interpretaciones que los hombres prehistóricos daban a los fósiles que recogían. En todo caso, ciertas conchas profundamente enterradas, le pudieron recordar a sus conchas actuales, y bien pudiera ser que se hubieran preguntado en aquel entonces qué hacían sobre las rocas unos animales que se encuentran habitualmente en el agua.
Es cierto que siempre, a lo largo de la Historia, hemos tenido pensadores y naturalistas. La Historia natural es un término cuya definición es problemática, en tanto que diversas disciplinas la abordan de manera diferente. Muchas de estas concepciones incluyen el estudio de las cosas vivientes (por ejemplo, la biología, incluyendo botánica, zoología y ecología); otras concepciones extienden el término al campo de la paleontología, la geografía y la bioquímica, así como a la geología, astronomía y la física. Lo cierto es que, al final del camino, todas esas disciplinas se encuentras, es decir, están de una u otra manera relacionadas. Todo en el Universo tiene una conexión que no siempre podemos ver o comprender.

Claro que, algunos pensadores griegos ya especularon con las viejas conchas fósiles que se hallaban dentro de las piedras y que eran el orgien de especulaciones “geológicas” de algunos que, como Jenófanes o Heródoto, quiénes habían comprendido la naturaleza auténtica de ciertas conchas fósiles y habían sacado conclusiones pertinentes, aquellos restos de organismos marinos, encontrados tierra adentro, demostraba que los mares, se extendían en otras épocas mucho más allá de sus límites actuales.

Lo cierto es que, hacer historia de la vida en nuestro planeta es imposible, sólo podemos ir atando cabos a medida que se encuentran huellas de ella en las viejas rocas, y, como la vida consciente tardó mucho más en llegar… ¡Carece de historia, toda vez que no existieron cronistas para escribirla! Así, nos vemos abocados a especular juntando todos los datos que hemos podido reunir y, de esas especulaciones, hemos formado un conjunto, si no plausible en su totalidad, sí aceptable mientras no encontremos más respuestas a la gran pregunta: ¿Cómo surgió la vida en la Tierra, y, es nuestro planeta el único lugar del Universo que la contiene?

Claro que, si creemos que la vida es ciudadana del universo sin fronteras, no debemos perder de vista la Panspermia, esas esporas viajeras que llegan a los mundos y en ellos, se posan y dejan pasar el tiempo para que, las condiciones locales, las radiaciones exteriores y propias del lugar, hagan su trabajo para que, con el tiempo suficiente por delante, puedan emerger y crecer hasta llegar a conformar seres con ideas y pensamientos.
Los animales unicelulares han descubierto el método más corto para comer las plantas. La muerte y el sexo han de crearse para que los organismos pluricelulares sean capaces de envejecer y dejar de funcionar como una cooperativa colonial de células. Los animales han descubierto como comerse a otros animales. Por encima de todo, ha evolucionado una especie inteligente, una especie tan lista que ha llegado a descubrir una vía para poder salir de la Tierra y llevar todo el proceso de la evolución hasta el extremo.

Nunca nadie ha sabido explicar lo que es la Vida a pesar de que tambien siempre nos lo hemos preguntado. Cuál es su origen y cómo surgieron los seres vivos que conocemos y que tenemos a nuestro alrededor, así como aquellos que con el paso de tiempo no supieron adaptarse y se extinguieron. La especie humana, la única que en nuestro planeta alcanzó la plenitud de conciencia, siempre ha tratado de responder a esa pregunta: ¿Qué es la Vida? Pero siempre también, resultó un gran problema el poder responderla y las Ciencias Naturales nunca pudo confeccionar una respuesta plausible. Hemos podido llegar a saber que sin los materiales fabricados en las estrellas, la vida no sería posible en nuestro Universo. Así muchos, dicen que somos…
¡Polvo de estrellas!

La célula viva es un sistema dinámico, en cambio constante en el cual las sustancias químicas se tornan ordenados por un tiempo en estructuras microscópicas, tan solo para disolverse nuevamente cuando otras moléculas se juntan para formar los mismos tipos de estructuras nuevamente, o para sustituirlas nuevamente en la misma estructura. Las organelas de las cuales las células están hechas no son más estáticas que la llama de una vela. En cualquier instante, la vela exhibe un patrón dinámico de casamientos y divorcios químicos, de procesos que producen energía y procesos que la consumen, de estructuras formándose y estructuras desapareciendo. La vida es proceso no una cosa.

¿Cómo ese proceso ordenado llegó a existir? Una vez que la célula es una entidad altamente ordenada y no aleatoria (evitando, la torpe regularidad de un cristal), se puede pensar en ella como un sistema que contiene información. La información es un ingrediente que adicionado, trae a la vida lo que serían átomos no vivos. ¿Cómo –nos preguntamos- la información puede ser introducida sin una inteligencia creativa sobrenatural? Este es el problema que la Ciencia aún tiene que responderse, lo que colocaría a Dios en la categoría de completamente desempleado.
![]()
La vida, seguramente, fue el resultado de los mismos procesos químicos y físicos que formaron los océanos y la corteza continental de nuestro planeta. Sin embargo, la vida es distinta porque puede experimentar evolución darwiniana. La selección natural ha desempeñado un pepel fundamental en la evolución de plantas y animales durante los primeros tiempos de la historia de nuestro planeta, pero también dirigió la evolución química que hizo posible la propia vida. A grandes rasgos entendemos cómo pueden haber evolucionado las moléculas a partir de precursores simples presentes en la Tierra joven. Sin embargo, sigue siendo un misterio cómo las proteínas, los ácidos nucleicos y las membranas llegaron a interaccionar de forma tan compleja.

Según todos los indicios, en los primeros años del planeta, los continentes que hoy conocemos estaban todos unidos formando la denominada Pangea. El movimiento de las placas tectónicas terrestres logró que estos se separaran y, con el transcurso de millones de años, llegaron a adquirir la moderna forma que hoy conocemos. En todo ese transcurrir y, mientras tanto, una serie de condiciones nuevas aparecieron para hacer posible el surgir de la vida.
Distribución de los continentes hace 260 millones durante el Pérmico. El supercontinente con forma de “C” es Pangea; dentro de la C se localizan los océanos Paleo-Tetis al norte y Tetis al sur; separando ambos océanos se sitúa el continente Cimmeria; cerrando la “C” al noreste se sitúan los microcontinentes de China del Norte y China del Sur; mientras que el resto del globo está ocupado por el océano Panthalassa.

Microfósiles de sedimentos marinos. “Microfósil” es un término descriptivo que se aplica al hablar de plantas o animales fosilizados cuyo tamaño es menor de aquel que puede llegar a ser analizado por el ojo humano. Normalmente se utilizan dos rasgos diagnósticos para diferenciar microfósiles de eucariotas y procariotas.
A partir de todos los fragmentos que la ciencia ha podido ir acumulando, ¿qué tipo de planeta podemos recomponer y qué porcesos tuvieron que darse para que, la vida, tal como la conocemos pudiera surgir? Sin temor a equivocarnos podemos afirmar que, cuando se formó el mar de Warrawoona la Tierra ya era un planeta biológico. Además, las mediciones de isótopos de carbono indican que ya podía haber comenzado la gran liberación ecológica de la fotosíntesis. No podemos tener la certeza si entre los microorganismos de aquel entonces había cianobacterias reproductoras de oxígeno, pero la presencia de cualquier tipo de organismo fotosintético en el océano de Warrawoona es de por sí muy informativa, pues nos permite colocar un punto de calibración en el árbol de la vida.
Los estromatolitos forman parte del registro fósil y son los responsables del oxígeno de la Tierra
Son la evidencia de vida más antigua que se conoce en la Tierra. Las rocas ígneas más antiguas de la Tierra están en Groenlandia y tienen 3800 millones de años. Los estromatolitos más antiguos son de Warrawoona, Australia y tienen unos 3500 millones de años (Precámbricos – Arqueanos). La edad de la Tierra como planeta acrecionado se calcula en 4500 millones de años. La teoría dice que, dadas las condiciones en esa época, los primeros habitantes de la Tierra debieron ser organismos unicelulares, procariontes, y anaerobios. Por tanto, los estromatolitos forman parte del registro fósil más importante de la vida microbiológica temprana. Pero además, vida microscópica fototrófica.

En la nueva concepción de la evolución microbiana que simboliza el árbol, los organismos fotosintéticos aparecen relativamente tarde y se diversifican mucho después del origen de la vida y de la divergencia de los principales dominios de la biología. Si la materia orgánica de Warrawoona es producto de la fotosíntesis, hay que concluir que para entonces la evolución de la vida ya debía llevar en marcha un buen tiempo.

Las observaciones geológicas indican que hace tres mil quinientos millones de años la atmósfera de la Tierra contenía nitrógeno, dióxido de carbono y vapor de agua, pero muy poco oxígeno libre. La mayoría de las inferencias acerca de ambientes antiguos se realizan a partir de pistas sutiles que nos proporcionan la geoquímica; la signatura sedimentaria del oxígeno, sin embargo, es muy llamativa: bandas de color rojo vivo en rocas con silex ricos en hermatita (Fe2 O3), un mineral de óxido de hierro.

En la actualidad, nuestros conocimientos de la vida y ambientes arcaicos son a un tiempo frustrantes y emocionantes: frustrantes por las pocas certezas que tenemos y, sólo muchas hipótesis a partir de los datos dispersos que se van obteniendo, emocionante porque sabemos algo, por poco que esto pueda ser, es estimulante contar con un punto de partida que nos permita continuar en el estudio y la observación, seguir experimentando para que, algún día, sepamos a ciencia cierta, de donde pudo venir la vida.
Es verdad que las rocas más antiguas que podemos identificar nos indican la presencia de organismos complejos ¿qué clase de células vivían en aquellos tiempos aún más lejanos? En última instancia, ¡cuál será el verdadero origen de la vida?

Ademas de las cianobacterias, la microflora puede incluir algas (verdes y diatomeas), hongos, crustaceos, insectos, esporas, polen, rodofitas, fragmentos y sedimentos de todo tipo. La variedad biologica de cada comunidad estromatolitica dependerá de condiciones ambientales e hidrológicas: hipersalino, dulceacuicola, intermareales, submareales, fuertes corrientes, moderadas nulas, calidos, templado, altitud (afecta a la exposicion de la luz uv). En la superficie, es rugosa, porosa y cubierta por mucilago, filamentos, etc. Las particulas de carbonato van quedadonde atrapadas, hasta que la cementacion por crecimiento de cristales, forma una capa mas, de esta forma la estructura aumenta de tamaño.
La Tierra es el tercer planeta del Sistema Solar. Esta situación orbital y sus características de masa la convierten en un planeta privilegiado, con una temperatura media de unos 15º C, agua en forma líquida y una atmósfera densa que pudo evolucionar, con oxígeno y otros ingredientes, condiciones imprescindibles para el desarrollo de la vida.
La creencia general es que hace unos 4.600 millones de años la corteza de la Tierra comenzó a consolidarse y las erupciones de los volcanes empezaron a formar la atmósfera, el vapor de agua y los océanos. El progresivo enfriamiento del agua y de la atmósfera permitió el nacimiento de la vida, iniciada en el mar en forma de bacterias y algas, de las que derivamos todos los seres vivos que habitamos hoy nuestro planeta tras un largo proceso de evolución biólogica.

Aun los organismos más simples son máquinas moleculares extraordinariamente sofisticadas. Las primeras formas de vida tenían que ser muchísimo más sencillas. Necesitamos encontrar una familia de moléculas lo bastante simples como para formarse por procesos químicos y lo bastante complejas como para servir de cimiento a la evolución de las células vivas. Una molécula capaz de contener información y estructura suficientes como para replicarse a sí mismas y, al cabo, para dirigir la síntesis de otros componentes que puedan canalizar la replicación con una eficiencia cada vez mayor.
ESTRUCTURA DE LA CELULA BACTERIANA
Unas moléculas, en fin, que pudieran iniciar una trayectoria evolutiva que permitiera a la vida emanciparse de los procesos físicos que le dieron nacimiento, sintetizando las moléculas necesarias para el crecimiento en lugar de incorporarlas de su entorno y captando energía química o solar para alimentar el funcionamiento de la célula.
El descubrimiento de las enzimas de ARN, o ribosomas, realizado de forma independiente y aproximadamente al mismo tiempo por el bioquímico de Yale Sidney Altman, tuvo un efecto catalítico sobre el pensamiento acerca del origen de la vida.

Los enzimas de ARN (llamadas “ribozimas” o “aptazimas”) son moléculas de ARN capaces de autorreplicarse a temperatura constante en ausencia de proteínas. Utilizan la llamada replicación cruzada, en la que dos enzimas se catalizan el uno al otro de forma mutua. Este proceso permite entender cómo surgió la vida, pero los biotecnólogos las usan para algo mucho más prosaico. Estos enzimas de ARN pueden ser utilizados para detectar una gran variedad de compuestos, incluyendo muchos relevantes en diagnóstico médico. El compuesto orgánico se liga al aptazima, que se replica exponencialmente, amplificando exponencialmente la concentración del compuesto hasta permitir que sea fácilmente detectado.
En palabras del filósofo de la biología Iris Fry, esta extraordinaria molécula se alzó como “el huevo y la gallina al mismo tiempo” en el rompecabezas del orgien de la vida. La vida, esa misteriosa complejidad que surgió a partir de la “materia inerte” que, bajo ciertas y complejas condiciones, dio lugar a que lo sencillo se conviertiera en complejo, a que lo inerte pudiera despertar hasta los pensamientos.

Sabemos que, en ciertas condiciones prebióticas, los aminoácidos se forman fácilmente, así quedó demostrado por Stanley Miller en su gamoso experimento. Como los ácidos nucléicos, pueden unirse para formar péptidos, las cadenas de aminoácidos que se pliegan para formar proteínas funcionales.
Hay teorías para todos los gustos, y, el afamado Freeman Dyson, un renombrado físico que ha pensado profundamente sobre el origen de la vida, sugiere que en realidad la vida comenzó en dos ocasiones, una por la vía del ARN y otra vez por vía de las proteínas. Las células con proteínas y ácidos nucleicos interactivos habrían surgido más tarde en función protobiológica. Y, está claro que, la innovación por alianzas es uno de los principales temas de la evolución.

En el árbol de la vida, nosotros (“tan importantes”), sólo somos una pequeña ramita.
Hay muchos procesos que son de una importancia extrema en la vida de nuestro planeta y, dado que los organismos fotosintéticos (o quimiosinteéticos) no pueden fraccionar isótopos de carbono en más de unas treinta parte por 1.000, necesitamos invocar la participación de otros metabolismos para poder explicar los resultados de las mediciones que se han realizado. Los candidatos más probables son bacterias que se alimentan de metano en los sedimentos. Estas bacterias obtienen tanto el carbono como la energía del gas natural (CH4) y, al igual que los organismos fotosintéticos, son selectivos con los isótopos. A causa de su preferencia química por el 12CH4 frente al 13CH4, los microbios que se alimentan de metano fraccionan los isótopos de carbono en unas veinte o vejnticinco partes por 1.000 en los ambientes donde el metano es abundante. ¿Habeis pensado en la posibilidad de que esos organismos fotosintéticos estén presentes en Titán? ¡El fetín está servido!

Los océanos de metano de titán podrían ser una buena fuente de vida
La fotosíntesis anoxigénica se da en los organismos que utiliza la energía de la luz del sol, dióxido de carbono (sustrato a reducir) y sulfuro de hidrógeno (en lugar del agua) como dador de electrones que se oxida, se fabrican glúcidos y se libera azufre a el medio acuoso donde habitan o se aloja en el interior de la bacteria.


Otra característica es que los organismos fotosinteticos anoxigénicos contienen bacterioclorofila, un tipo de clorofila exclusiva de los foto-organotrofos, usan longitudes de onda de luz que no son absorbidas por las plantas. Estas bacterias contienen también carotenoides, pigmentos encargados de la absorción de la energía de la luz y posterior transmisión a la bacterioclorofila. El color de estos pigmentos dan el nombre a estas bacterias: bacterias púrpuras del azufre y bacterias verdes del azufre. En las cianobacterias los pigmentos captadores de luz son las ficobilinas, por lo tanto se les nombra, bacterias azules.

Cualquiera de estas imágenes de arriba nos cuenta una larga y compleja historia de cómo se pudieron formar cada uno de los ahí representados, y, en cualquiera de sus fases, formas y colores, es toda una gran obra de la Ingenieria de la Naturaleza que, al fin y al cabo, es la única fuente de la que debemos beber para saciar nuestra sed de sabiduría y alejar la ignorancia que nos abruma.
No pocas veces he dejado aquí constancia de que, el Universo, en todas sus regiones, por muy alejadas que estén, se rige por unas leyes que están presentes en todas parte por igual, y, así lo confirman mil observaciones y mil proyectos que a tal efecto se han llevado a buen término. Por ejemplo, mediaciones precisas de isótopos de azufre en muestras de Marte traídas a la Tierra por meteoritos demuestran que muy pronto en la historia del planeta vecino el ciclo del azufre estaba dominado por procesos atmosféricos que producían un fraccionamiento independiente de la masa.

Valles en Marte. (ESA) La región de Valles Marineris, que tiene una longitud de 4.000 kilómetros y una anchura de 600 kilómetros, es el sistema de cañones más grande conocido en el sistema solar, con profundidades que llegan a los diez kilómetros.
Basándose en este descubrimiento del fraccionamiento independiente de la masa, se dirigió la atención sobre las rocas terrestres más antiguas. Para sorpresas de muchos geoquímicos, lo que se hayó fue que el yeso y la pirita de las sucesiones sedimentarias más antiguas de la Tierra también como en Marte, han dejado constancias del fraccionamiento independiente de la masa de los isótopos de azufre. Al igual que en Marte, en la Tierra primitiva la química del azufre se encontraba al parecer influenciada por procesos fotoquímicos que sólo pueden producirse en una atmósfera pobre en oxígeno. La etapa del oxígeno comenzó en nuestra atmósfera a comienzos del eón Ptoterozoico. En suma, todos los caminos de la biogeoquímica llevan al mismo sitio, es decir, lo que pasa aquí pudo pasar allí y, al decir allí, quiero decir en cualquier planeta de cualquier galaxia. Las leyes fundamentales de la Naturaleza son, las mismas en todas partes. No existen sitios privilegiados.

Es difícil imaginarse hoy una Tierra sin oxígeno
Dos equipos independientes de investigadores descubrieron que el oxígeno gaseoso apareció en la atmósfera terrestre unos 100 millones de años antes del evento de la gran oxidación de hace 2400 millones de años. Es decir, cuando cambió la antigua atmósfera y el planeta se equipo con la que hoy conocemos.

El oxígeno es un gas muy reactivo, no existe de manera libre durante un largo período de tiempo, pues forma óxidos o reacciona con otras sustancias de manera rápida. Si está presente en la atmósfera es porque las plantas lo reponen continuamente. Antes de la invención de la fotosíntesis y durante muchos cientos de millones de años no había oxígeno libre en la Tierra.
En los estratos geológicos se pueden encontrar pruebas de la existencia de un momento en el que se produjo una gran oxidación mineral, prueba de que el oxígeno se encontraba ya libre en la atmósfera terrestre por primera vez y en gran cantidad. A este hecho se le ha denominado evento de gran oxidación, o GOE en sus siglas en inglés, y fue un hecho dramático en la historia de la Tierra. Este oxígeno permitió más tarde la aparición de vida animal compleja. Los geólogos creían que durante el GOE los niveles de oxígeno subieron rápidamente desde niveles prácticamente despreciables.

El mundo bacteriano es fascinante
Con estas bacterias es posible obtener dos tipos de celdas microbianas o baterías. Unas llamadas celdas de sedimento emplean el lodo donde habitan estos microorganismos; ahí, se produce energía simplemente conectando un electrodo en la parte donde, a cierta profundidad, no hay oxígeno, con otro electrodo que se encuentre en presencia de oxígeno.
¿Cómo respondió la vida a la revolución del oxígeno? Podemos imaginar, un “holocausto de oxígeno” que habría llevado a la muerte y la extinción a innumerables linajes de microorganismos anaeróbicos. Pero hace dos mil doscientos millones de años los ambientes anóxicos no desaparecieron; simplemente, quedaron relegados bajo una capa oxigenada de agua y sedimentos superficiales.
Aquello permitió a la Tierra dar cobijo a una diversidad biológica sin precedentes. Los microorganismos anaeróbicos mantuvieron un papel esencial en el funcionamiento de los ecosistemas, igual que en la actualidad.

En la primera fase de cualquier ejercicio aeróbico, el oxígeno se combina con la glucosa procedente del glucógeno. Al cabo de unos minutos, cuando el cuerpo nota que escasea el azúcar, empieza a descomponer las grasas. Entonces disminuye un poco el rendimiento, mientras el cuerpo se adapta al cambio de origen de su energía. Superado este punto, se vuelve a los niveles y sensaciones normales, pero se queman grasas en lugar de glucosa.
De otro lado, los organismos que utilizan, o al menos toleran el oxígeno se expandieron enormemente. La respiración aeróbica se convirtió en una de las formas principales de metabolismo en las bacterias, y las bacteria quimiosintéticas que obtienen energía de la reacción entre oxígeno e hidrógeno o iones metálicos se diversificaron a lo largo de la frontera entre ambientes ricos en oxígeno y ambientes pobres en oxígeno. Desde ese momento, la Tierra comenzó a convertirse en nuestro mundo.

Nuestro mundo, rico en agua líquida que cubre el 71% de la superficie del planeta, y, su atmósfera con un 78% (en volumen) de Nitrógeno, un 21 de Oxígeno y un 0,9 de Argón, además de dióxido de carbono, hidrógeno y otros gases en cantidades mucho menores que, permiten que nuestros organismos encuentren el medio indóneo para poder vivir. Otros muchos factores presentes en la Tierra contribuyen a que nuestra presencia aquí sea posible.

Las algas verdeazuladas también son llamadas bacterias verdeazuladas porque carecen de membrana nuclear como las bacterias. Sólo existe un equivalente del núcleo, el centroplasma, que está rodeado sin límite preciso por el cromatoplasma periférico coloreado. El hecho de que éstas se clasifiquen como algas en vez de bacterias es porque liberan oxígeno realizando una fotosíntesis similar a la de las plantas superiores. Ciertas formas tienen vida independiente, pero la mayoría se agrega en colonias o forma filamentos. Su color varía desde verdeazulado hasta rojo o púrpura dependiendo de la proporción de dos pigmentos fotosintéticos especiales: la ficocianina (azul) y la ficoeritrina (rojo), que ocultan el color verde de la clorofila.
Mientras que las plantas superiores presentan dos clases de clorofila llamadas A y B, las algas verdeazuladas contienen sólo la de tipo A, pero ésta no se encuentra en los cloroplastos, sino que se distribuye por toda la célula. Se reproducen por esporas o por fragmentación de los filamentos pluricelulares. Las algas verdeazuladas se encuentran en hábitats diversos de todo el mundo. Abundan en la corteza de los árboles, rocas y suelos húmedos donde realizan la fijación de nitrógeno. Algunas coexisten en simbiosis con hongos para formar líquenes. Cuando hace calor, algunas especies forman extensas y, a veces, tóxicas floraciones en la superficie de charcas y en las costas. En aguas tropicales poco profundas, las matas de algas llegan a constituir unas formaciones curvadas llamadas estromatolitos, cuyos fósiles se han encontrado en rocas formadas durante el precámbrico, hace más de 3.000 millones de años. Esto sugiere el papel tan importante que desempeñaron estos organismos cambiando la atmósfera primitiva, rica en dióxido de carbono, por la mezcla oxigenada que existe actualmente. Ciertas especies viven en la superficie de los estanques formando las “flores de agua”.
Sin descanso se habla de quer nosotros, con nuestro comportamiento estamos cambiando la atmósfera de la Tierra, que contaminamos y que, de seguir así, podemos acabar con la vida placentera en el planeta. Tal exageración queda anulada por la realidad de los hechos.

Gigantescas ciudades son una buena muestra de nuestra presencia aquí, y, ¿qué duda nos puede caber? Nuestro morfología nos ha convertido en el ser vivo dominante en el planeta. Sin embargo, no somos los que más hemos incidido en sus condiciones. Si se estudia la larga historia de la vida en la Tierra, podremos ver que una inmensa cantidad de especies han interactuado con la biosfera para modificar, en mayor o menor medida los ecosistemas del mundo. En realidad, la especie que cambió el planeta de manera radical, la que en verdad modificó la Tierra hasta traerla a lo que hoy es, creando una biosfera nueva a la que todas las especies se tuvieron que adaptar (también nosotros), esa especie que, aunque diminuta en su individualidad forma un gigantesco grupo, no son otras que las cianobacterias.

De esa manera, si el oxígeno trajo consigo un cambio revolucionario, las heroínas de la revolución fueron las cianobacterias. Fósiles extraordinarimente bien conservados en síles de Siberia de mil quinientos millones de años de edad demuestran que las bacterias verdeazuladas se diversificaron tempranamente y se han mantenido hasta la actualidad sin alterar de manera sustancial su forma. La capacidad de cambiar con rapidez, pero persistir indefinidamente, compendia la evolución bacteriana.
Las cianobacterias comparten con algunas otras bacterias la habilidad de tomar el N2 del aire, donde es el gas más abundante, y reducirlo a amonio (NH4), una forma que todas las células pueden aprovechar. Los autótrofos que no pueden fijar el N2, tienen que tomar nitrato (NO3-), que es una sustancia escasa. Esto les ocurre por ejemplo a las plantas. Algunas cianobacteria son simbiontes de plantas acuáticas, como los helechos del género Azolla, a las que suministran nitrógeno. Dada su abundancia en distintos ambientes las cianobacterias son importantes para la circulación de nutrientes, incorporando nitrógeno a la cadena alimentaria, en la que participan como productores primarios o como descomponedores.
La resistencia general de las bacterias a la extinción es bien conocida, las bacterias que hayan sobrevivido al cepillo de dientes, a media tarde se habrán multiplicado hasta el extremo de recubrir nuevamente el interior de la boca. Además, las bacterias saben habérselas muy bien con medios cambiantes. El aire, por ejemplo, está lleno de bacterias; un plato de leche colocado en el alfeizar de la ventana no tarda en fermentar.
Nosotros tenemos un “convenio” de simbiosis con muchas bacterias que conviven con nuestra especie que sin ellas, no podría existir. ¿Os acordáis de aquel trabajo sobre las mitocondrias? El cuerpo humano, en seco, tiene un diez por ciento de bacterias.
emilio silvera
Dic
25
Aquella triste concioncilla
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Tiempo pasa...¿O somos nosotros? ~
Clasificado en El Tiempo pasa...¿O somos nosotros? ~
 Comments (5)
Comments (5)

Hay cosas que nunca olvidamos. Cuando era un niño y vivía con mis padres y mis tres hermanos, yo dormía en una habitación que daba a la calle que podía ver por la ventana. En estas fechas navidenas, aparte del jolgorio natural de las fiestas y de las visitas a los nacimientos (eran otros tiempos), la gente acostumbraba a formar reuniones de familias y celebrar, después de la cena, la Navidad con canciones apropiadas al evento que se conmemoraba.
Recuerdo que siempre me quedaba dormido y, casi arrastras, podía llegar a la cama que cogía con tantas ganas que era llegar a ella y caer en profundo sueño. Generalmente, era despertado al amanecer por algunos que seguían la fiesta por las calles cantando a voz en grito y, una de aquellas cancioncillas, nunca me dejó, cuando llegan estos días, su recuerdo vuelve y, como cuando era pequeño, vuelvo a oir aquellas voces cantar:
Campanilleros que cantan con nostalgia:
“el año nuevo ya viene
el año viejo se va
y nosotros nos iremos
y no volveremos más”
Eran cantares muy tristes
con un fondo de verdad
no había temor a la muerte
era cosa natural
tampoco miedo a la vida
la sabían disfrutar
Se reunían en la mesa
esa mesa familiar
donde siempre había un lugar
no faltaba nunca un pan
A las doce se reunían
en la plaza principal

zambombas y panderetas
turrones y mazapán
Todo el mundo se abrazaba
se daban besos de paz
algunos se emocionaban
no dejaban de llorar
ni tampoco de cantar
El recuerdo de una pena
tal vez de felicidad

un amor que se ha perdido
un familiar que no está
El año viejo se ha ido
y nunca más volverá
Los años se van volando
las vida los ve pasar
El Nuevo año ha llegado
todo el mundo a festejar y,
cuando pasa la euforia,
todo el mundo a trabajar.

¡Feliz Año Nuevo! a todos los amigos de este lugar y, también, para todos en general. Aprovecho la oportunidad para haceros una recomendación:
Ahora que podeis, decidle a la persona amada cuánto la queréis.
No dejéis pendiente, por más tiempo, esa buena obra que puedes hacer.
Es triste mirar hacia atrás y, al recordar, decirte a tí mismo… ¡Si hubiera…! Así que remedialó.
La vida es corta, muy corta, y, si no tenemos claras las prioridades, cuando queremos darnos cuenta…¡es tarde! No siempre se puede rectificar y, algunas veces, cuando se hace a destiempo, los efectos pueden ser contrarios a los esperados. Pensad que no siempre lo mejor es lo más caro, ni la felicidad se compra con tesoros.
Si quieres te querrán y, como decimos en física, todo es causa de lo que antes pasó, es su consecuencia.
¡Sed felices!
emilio silvera
















 Totales: 69.212.164
Totales: 69.212.164 Conectados: 40
Conectados: 40

























