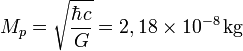Dic
31
Hoy un sueño ¿Realidad mañana?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (2)
Comments (2)


Llegará un día en el que, podremos entrar en un inmenso recinto en el que, previa elección de la programación adecuada, todo se transformará en un “mundo de fantasía”, que lo mismo podrá ser una playa luminosa con arena dorada por el un Sol que, una Selva tropical con inmensas cascadas o un desierto, dependiendo de los gustos del usuario.
Si repasamos la historia de la ciencia, seguramente encontraremos muchos motivos para el optimismo. Witten (el Físico de la Teoría M), está convencido de que la ciencia será algún día capaz de sondear hasta las energías de Planck. Como ya he contado en otras ocasiones, él dijo:
“No siempre es tan sencillo decir cuáles son las preguntas fáciles y cuáles las difíciles. En el siglo XIX, la pregunta de por qué el agua hierve a 100 grados era desesperadamente inaccesible. Si usted hubiera dicho a un físico del siglo XIX que hacia el siglo XX sería capaz de calcularlo, le habría parecido un cuento de hadas… La teoría cuántica de campos es tan difícil que nadie la creyó completamente durante 25 años.”
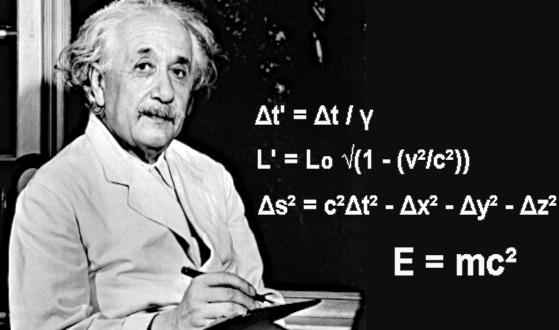
En su opinión, las buenas ideas siempre se verifican. Los ejemplos son innumerables: la gravedad de Newton, el campo eléctrico de Faraday y el electromagnetismo de Maxwell, la teoría de la relatividad de Einstein en sus dos versiones y su demostración del efecto fotoeléctrico, la teoría del electrón de Paul Dirac, el principio de incertidumbre de Heisenberg, la función de ondas de Schrödinger, y tantos otros. Algunos de los físicos teóricos más famosos, sin embargo, protestaban de tanto empeño en la experimentación. El astrónomo Arthur Eddington se cuestionaba incluso si los científicos no estaban forzando las cosas cuando insistían en que todo debería ser verificado.
Sin embargo, muchos son los ejemplos de un ingenio superior que nos llevaron a desvelar secretos de la Naturaleza que estaban profundamente escondidos, y, el trabajo de Dirac en relación al electrón, es una buena miuestra de ese ingenio humano que, de vez en cuando vemos florecer.

Siendo m la masa en reposo del electrón, c la velocidad de la luz, p el operador de momento,  la constante reducida de Planck, x y t las coordenadas del espacio y el tiempo, respectivamente; y ψ (x, t) una función de onda de cuatro componentes. La función de onda ha de ser formulada como un espinor (objeto matemático similar a un vector que cambia de signo con una rotación de 2π descubierto por Pauli y Dirac) de cuatro componentes, y no como un simple escalar, debido a los requerimientos de la relatividad especial. Los α son operadores lineales que gobiernan la función de onda, escritos como una matriz y son matrices de 4×4 conocidas como matrices de Dirac.
la constante reducida de Planck, x y t las coordenadas del espacio y el tiempo, respectivamente; y ψ (x, t) una función de onda de cuatro componentes. La función de onda ha de ser formulada como un espinor (objeto matemático similar a un vector que cambia de signo con una rotación de 2π descubierto por Pauli y Dirac) de cuatro componentes, y no como un simple escalar, debido a los requerimientos de la relatividad especial. Los α son operadores lineales que gobiernan la función de onda, escritos como una matriz y son matrices de 4×4 conocidas como matrices de Dirac.
El premio Nobel Paul Dirac incluso llegó a decir de forma más categórica:
En su famosa ecuación está presente la belleza
“Es más importante tener belleza en las ecuaciones que tener experimentos que se ajusten a ellas“, o en palabras del físico John Ellis del CERN, “Como decía en una envoltura de caramelos que abrí hace algunos años, «Es sólo el optimista el que consigue algo en este mundo».“
Yo, como todos ustedes, un hombre normal y muy curioso por saber del mundo que nos rodea, escucho a unos y a otros, después pienso en lo que dicen y en los argumentos y motivaciones que les han llevado a sus respectivos convencimientos, y finalmente, también decido según mis propios criterios mi opinión, que no obligatoriamente coincidirá con alguna de esas opiniones, y que en algún caso, hasta me permito emitirla.

Para poder verificar esta teoría, necesitamos la energía de Planck (1019 GeV), con la que no podemos contar
Suponiendo que algún físico brillante nos resuelva la teoría de campos de cuerdas y derive las propiedades conocidas de nuestro universo, con un poco de suerte, podría ocurrir en este mismo siglo, lo que no estaría nada mal considerando las dificultades de la empresa. El problema fundamental es que estamos obligando a la teoría de supercuerdas a responder preguntas sobre energías cotidianas, cuando “ámbito natural” está en la energía de Planck. Esta fabulosa energía fue liberada sólo en el propio instante de la creación, lo que quiere decir que la teoría de supercuerdas es naturalmente una teoría de la creación.

Las importantes observaciones realizadas por Planck | ESA
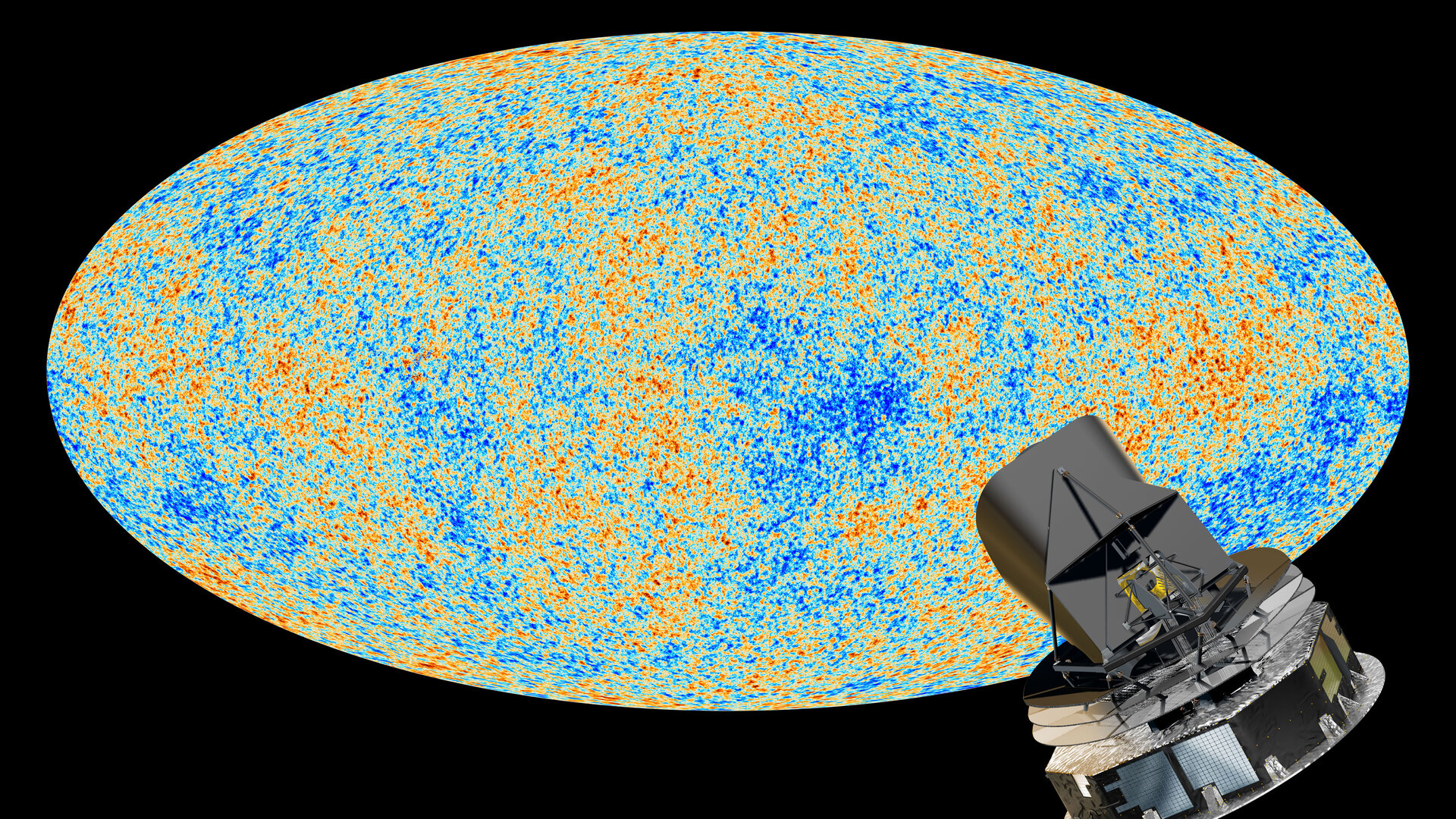
Este satélite, puesto en órbita en el año 2009, estaba diseñado para analizar los débiles restos de la radiación del Big Bang – la Radiación Cósmica de Fondo. La señal CMB nos muestra el Universo tal y como era unos 380.000 años después del Big Bang, y describe las condiciones iniciales a partir de las cuales se formó el Universo que conocemos hoy en día. El Observatorio ha dejado de prestar sus servicios después de muchos años de información, ha sido un gran proyecto para desvelar y confirmar datos que solo (antes de que llegara), solo se intuían.
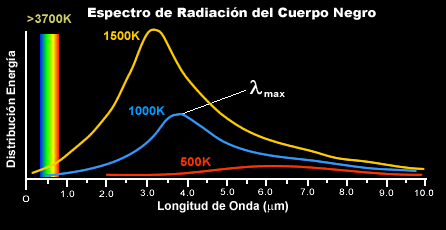
Fuimos capaces de predecir que el Big Bang produjo un “eco” cósmico reverberando en el universo y que podría ser mesurable por los instrumentos adecuados. De hecho, Arno Penzias y Robert Wilson de los Bell Telephone Laboratories ganaron el premio Nobel en 1.978 por detectar este eco del Big Bang, una radiación de microondas que impregna el universo conocido. El que el eco del Big Bang debería estar circulando por el universo miles de millones de años después del suceso fue predicho por primera vez por George Gamow y sus discípulos Ralpher y Robert Herman, pero nadie les tomó en serio. La propia idea de medir el eco de la creación parecía extravagante cuando la propusieron por primera vez poco después de la segunda guerra mundial. Su lógica, sin embargo, era aplastante. Cualquier objeto, cuando se calienta, emite radiación de forma gradual. Ésta es la razón de que el hierro se ponga al rojo vivo cuando se calienta en un horno, y cuanto más se calienta, mayor es la frecuencia de radiación que emite. Una fórmula matemática exacta, la ley de Stefan-Boltzmann, relaciona la frecuencia de la luz (o el color en este caso) con la temperatura. De hecho, así es como los científicos determinan la temperatura de la superficie de una estrella lejana; examinando su color. Esta radiación se denomina radiación de cuerpo negro.

Esta radiación, cómo no, ha sido aprovechada por los ejércitos, que mediante visores nocturnos pueden operar en la oscuridad. De noche, los objetos relativamente calientes, tales como soldados enemigos o los carros de combate, pueden estar ocultos en la oscuridad, pero continúan emitiendo radiación de cuerpo negro invisible en forma de radiación infrarroja, que puede ser captada por gafas especiales de infrarrojo. Ésta es también la razón de que nuestros automóviles cerrados se calientes en verano, ya que la luz del Sol atraviesa los cristales del coche y calienta el interior. A medida que se calienta, empieza a emitir radiación de cuerpo negro en forma de radiación infrarroja. Sin embargo, esta clase de radiación no atraviesa muy bien el vidrio, y por lo tanto queda atrapada en el interior del automóvil, incrementando espectacularmente la temperatura.
Análogamente, la radiación de cuerpo negro produce el efecto invernadero. Al igual que el vidrio, los altos niveles de dióxido de carbono en la atmósfera, causados por la combustión sin control de combustibles fósiles, pueden atrapar la radiación de cuerpo negro infrarroja en la Tierra, y de este modo calentar gradualmente el planeta.
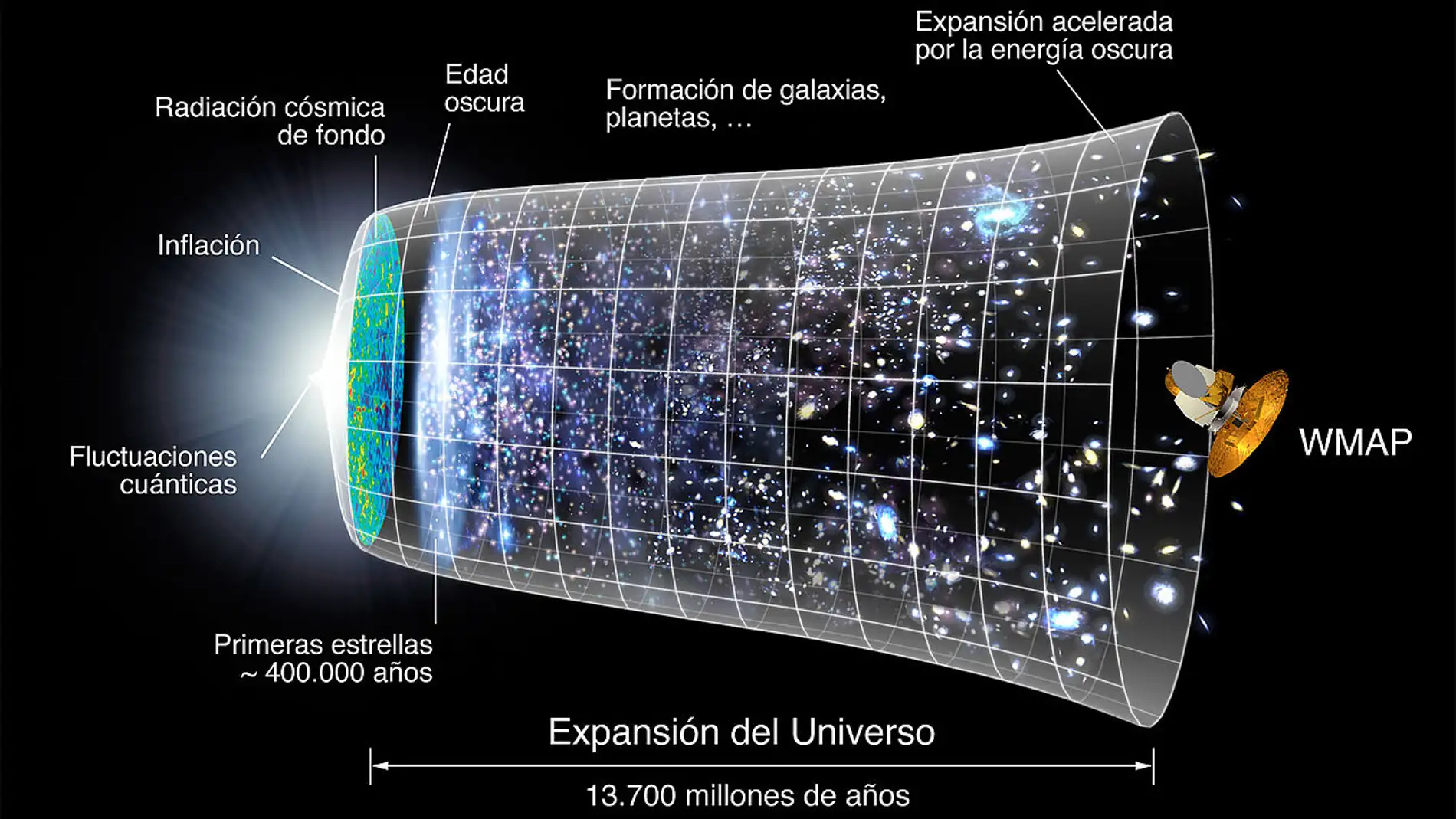
El Big Bang lo hemos adoptado porque es, el Modelo que mejor se adapta a lo que hemos podido ver
Gamow razonó que el Big Bang era inicialmente muy caliente, y que por lo tanto sería un cuerpo negro ideal emisor de radiación. Aunque la tecnología de los años cuarenta era demasiado primitiva para captar esta débil señal de la creación, Gamow pudo calcular la temperatura de dicha radiación y predecir con fiabilidad que un día nuestros instrumentos serían lo suficientemente sensibles como para detectar esta radiación “fósil”.
La lógica que había detrás de su razonamiento era la siguiente: alrededor de 300.000 años después del Big Bang, el universo se enfrió hasta el punto en el que los átomos pudieron empezar a componerse; los electrones pudieron empezar a rodear a los protones y neutrones formando átomos estables, que ya no serían destruidos por la intensa radiación que estaba impregnando todo el universo. Antes de este momento, el universo estaba tan caliente que los átomos eran inmediatamente descompuestos por esa radiación tan potente en el mismo acto de su formación. Esto significa que el universo era opaco, como una niebla espesa absorbente e impenetrable.
Pasados 300.000 años, la radiación no era tan potente; se había enfriado y por lo tanto la luz podía atravesar grades distancias sin ser dispersada. En otras palabras, el universo se hizo repentinamente negro y transparente.
Terminaré esta parte comentando que un auténtico cuerpo negro es un concepto imaginario; un pequeño agujero en la pared de un recinto a temperatura uniforme es la mejor aproximación que se puede tener de él en la práctica.
La radiación de cuerpo negro es la radiación electromagnética emitida por un cuerpo negro. Se extiende sobre todo el rango de longitudes de onda y la disminución de energías sobre este rango tiene una forma característica con un máximo en una cierta longitud de onda, desplazándose a longitudes de onda más cortas al aumentar las temperaturas*.


Hablar, sin más especificaciones, de radiación, es estar refiriéndonos a una energía que viaja en forma de ondas electromagnéticas o fotones por el universo. También nos podríamos estar refiriendo a un chorro de partículas, especialmente partículas alfa o beta de una fuente radiactiva o neutrones de un reactor nuclear.
La radiación actínida es la electromagnética que es capaz de iniciar una reacción química. El término es usado especialmente para la radiación ultravioleta y también para denotar radiación que podría afectar a las emulsiones fotográficas.
Radiación blanda, radiación cósmica, radiación de calor, radiación de fondo, de fondo de microondas, radiación dura, electromagnética, radiación gamma, infrarroja, ionizante, monocromática, policromática, de sincrotón, ultravioleta, de la teoría cuántica, de radiactividad… y, como se puede ver, la radiación en sus diversas formas es un universo en sí misma.
Siempre me llamó la atención y se ganó mi admiración el físico alemán Max Planck (1.858 – 1.947), responsable entre otros muchos logros de la ley de radiación de Planck, que da la distribución de energía radiada por un cuerpo negro. Introdujo en física el concepto novedoso de que la energía es una cantidad que es radiada por un cuerpo en pequeños paquetes discretos, en vez de una emisión continua. Estos pequeños paquetes se conocieron como cuantos y la ley formulada es la base de la teoría cuántica.
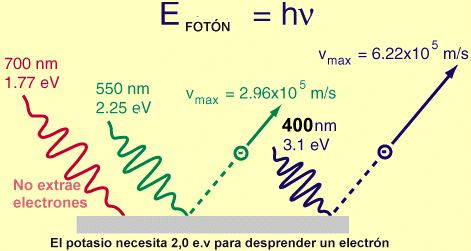
Einstein se inspiró en este trabajo para a su vez presentar el suyo propio sobre el efecto fotoeléctrico, donde la energía máxima cinética del fotoelectrón, Em, está dada por la ecuación que lleva su nombre: Em = hf – Φ.
Cada metal requiere, para que se produzca la extracción, una radiación con una frecuencia mínima (no). Cualquier otra radiación de menor frecuencia, no será capaz de arrancar electrones. Por debajo de la frecuencia mínima la intensidad de corriente -“i” (amperios)- será cero. No hay efecto fotoeléctrico.
Einstein mostró como la hipótesis de un cuanto de luz podía explicar el efecto fotoeléctrico y la presencia de una frecuencia característica para cada material por debajo de la cual no se producía ningún efecto.
Planck publicó en 1.900 un artículo sobre la radiación de cuerpo negro que sentó las bases para la teoría de la mecánica cuántica que más tarde desarrollaron otros, como el mismo Einstein, Heisenberg, Schrödinger, Dirac, Feynmann, etc. Todos los físicos son conocedores de la enorme contribución que Max Planck hizo en física: la constante de Planck, radiación de Planck, longitud de Planck, unidades de Planck, etc. Es posible que sea el físico de la historia que más veces ha dado su nombre a conceptos de física. Pongamos un par te ejemplos de su ingenio:
1. vale 10-35 metros. Esta escala de longitud (veinte órdenes de magnitud menor que el tamaño del protón, de 10-15 m) es a la que la descripción clásica de gravedad cesa de ser válida y debe ser tenida en cuenta la mecánica cuántica. En la fórmula que la describe, G es la constante gravitacional, ħ es la constante de Planck racionalizada y c en la velocidad de la luz.
2. . Es la masa de una partícula cuya longitud de onda Compton es igual a la longitud de Planck. En la ecuación, ħ es la constante de Planck racionalizada, c es la velocidad de la luz y G es la constante gravitacional. Así, Se denomina masa de Planck a la cantidad de masa (21,7644 microgramos) que, incluida en una esfera cuyo radio fuera igual a la longitud de Planck, generaría una densidad del orden de 1093 g/cm³. Según la física actual, esta habría sido la densidad del Universo cuando tenía unos
segundos, el llamado Tiempo de Planck. Su ecuación, es decir la masa de Planc se denota:
El valor de la masa de Planck  se expresa por una fórmula que combina tres constantes fundamentales, la constante de Planck, (h), la velocidad de la luz (c), y la constante de gravitación universal (G). La masa de Planck es una estimación de la masa del agujero negro primordial menos masivo, y resulta de calcular el límite donde entran en conflicto la descripción clásica y la descripción cuántica de la gravedad.
se expresa por una fórmula que combina tres constantes fundamentales, la constante de Planck, (h), la velocidad de la luz (c), y la constante de gravitación universal (G). La masa de Planck es una estimación de la masa del agujero negro primordial menos masivo, y resulta de calcular el límite donde entran en conflicto la descripción clásica y la descripción cuántica de la gravedad.
“Aunque todas estas descripciones reflejan más una abundante imaginación que un hecho existencial apoyado teóricamente con alguna hipótesis que pueda ser comprobada en el laboratorio sobre hechos que están más allá de poder ser medidos jamás en algún laboratorio construido por humanos. La única forma de confrontar la factibilidad o la posibilidad del modelo de la espuma cuántica nos lleva necesariamente a confrontar la carencia de un modelo que logre unificar exitosamente al macrocosmos con el microcosmos, a la Relatividad General con la Mecánica Cuántica, la Gravedad Cuántica. Si la energía y la materia (o mejor dicho la masa-energía) están discretizadas, se supone que también deben de estarlo el espacio y el tiempo (o mejor dicho, el espacio-tiempo), y la “partícula fundamental” del espacio-tiempo debe de serlo el gravitón, aunque de momento todo esto son especulaciones que seguirán siéndolo mientras no tengamos a la mano algo que pueda confirmar la existencia de tan exótica partícula, quizá la más exótica de cuantas hayan sido concebidas por la imaginación del hombre.”
La descripción de una partícula elemental de esta masa, o partículas que interaccionan con energías por partículas equivalentes a ellas (a través de E = mc2), requiere de una teoría cuántica de la gravedad. Como la masa de Planck es del orden de 10-8 Kg (equivalente a una energía de 1019 GeV) y, por ejemplo, la masa del protón es del orden de 10-27 Kg y las mayores energías alcanzables en los aceleradores de partículas actuales son del orden de 103 GeV, los efectos de gravitación cuántica no aparecen en los laboratorios de física de partículas. Únicamente en un laboratorio aparecieron partículas que tenían energías del orden de la masa de Planck: en el universo primitivo, de acuerdo con la teoría del Big Bang, motivo éste por el que es necesaria una teoría cuántica de la gravedad para estudiar aquellas condiciones. Esta energía de la que estamos hablando, del orden de 1019 GeV (inalcanzable para nosotros), es la que necesitamos para verificar la teoría de supercuerdas.
Siempre, desde que puedo recordar, me llamó la atención los misterios y secretos encerrados en la naturaleza, y la innegable batalla mantenida a lo largo de la historia por los científicos para descubrirlos. Muchos han sido los velos que hemos podido descorrer para que, la luz cegadora del saber pudiera entrar en nuestras mentes para hacerlas comprender cómo actuaba la Naturaleza en ciertas ocasiones y el por qué de tales comportamientos, y, sin embargo, a pesar del largo camino recorrido, es mucho más el que nos queda por andar.
Nuestro Universo es complejo, la Naturaleza nos muestra “cosas” que no comprendemos como las puede realizar, nuestra Mente ha evolucionado, pero no ha podido llegar a ese punto en el que, podamos comprender desvelando secretos que están profundamente escondidos en lugares a los que ¿nunca? podremos llegar.
¿Es el límite un Principio con el que debemos cargar para siempre?

¿Ciertamente estamos confinados en este pequeño mundo, del que nunca podremos salir? Bueno, esa “realidad” la hemos enmascarado, y, nuestro cerebro, tratando de evitar daños irreparables de que podamos caer en una peligrosa depresión, por la frustración que sentiríamos, ante la imposibilidad de viajar a otros mundos y a las estrellas, hace un ejercicio de auto-engaño y nos induce a “jugar” con cohetes y proyectos encaminados a cubrir con un tupido velo, esa realidad “que no queremos ver”. Mandamos objetos tecnológicos al Espacio y a otros mundos y lunas. Sin embargo, el que algún día podamos ir nosotros… ¡Es altamente dudoso?
El Espacio, por mucho que nos empeñemos, es un medio hostil para nosotros, seres frágiles e indefensos ante ciertas condiciones.
¿Qué existen mundos parecidos a la Tierra que nos podrían acoger? ¡Seguro!
¿Qué carecemos de los medios para vencer las distancias que nos separan, y, nuestra tecnología no es suficiente para construir naves tan avanzadas con nuevos materiales inteligentes que no está a nuestro alcance?
¡Cierto!
Pero, admitir tal escenario es muy duro, sabemos que, un día lejano en el futuro, el sol morirá y la vida en la Tierra no será posible, y también sabemos que la Vía Láctea se fusionará con Andrómeda. Sí, falta mucho para que eso llegue pero… ¡Llegará! Y, pensamos que si para entonces seguimos aquí, tendremos que buscar la manera de salvar a la especie. La imposibilidad de que podamos hacerlo… ¡Es una carga que no podemos soportar!

El cultivo espacial ha sido experimentado por la NASA
Precisamente por eso, hablamos continuamente de viajar a otros mundos, del Proyecto Aurora (un nuevo amanecer para la Humanidad), de naves ciudades en la que miles de viajeros (familias, científicos, expertos en todas las actividades humanas, filósofos, poetas, cultivo de alimentos, escuelas y hospitales…), nos llevarán a mundos parecidos a la Tierra y el viaje durará decenas, cientos, miles de años…
No quisiera herir la sensibilidad de nadie pero… ¿Cómo podrían conseguir que todo eso funcionara? Enumerar los múltiples problemas que todo eso conlleva (son tantos), es imposible, ya que, además de los conocidos, están los imprevisibles, los que determine el Azar.
Pero, mientras tanto, a vivir tan ricamente pensando que, algún día (y nos dicen que en unos años), podremos realizar ese “Proyecto” que, en realidad, sería el viaje de irás y no volverás.
Decimos que la Naturaleza es sabia, y si ha dispuesto que las estrellas estén tan separadas las unas de las otras... ¿Por qué será? Si ha puesto el límite de velocidad para viajar y mandar información… ¿Por qué será? Si nos ha constituido a los humanos con un físico frágil para no poder soportar la radiación del Espacio… ¡por qué será?
Los “Por que será” son interminables.
Entonces… ¿ Viajeros a otros mundos?
¿Cómo?
Emilio Silvera V.
Dic
24
Velocidades inimaginables
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
En el centro del átomo se encuentra un pequeño grano compacto aproximadamente 100.000 veces más pequeño que el propio átomo: el núcleo atómico. Su masa, e incluso más aún su carga eléctrica, determinan las propiedades del átomo del cual forma parte. Debido a la solidez del núcleo parece que los átomos, que dan forma a nuestro mundo cotidiano, son intercambiables entre sí, e incluso cuando interaccionan entre ellos para formar sustancias químicas (los elementos). Pero el núcleo, a pesar de ser tan sólido, puede partirse. Si dos átomos chocan uno contra el otro con gran velocidad podría suceder que los núcleos llegaran a chocar entre sí y entonces, o bien se rompen en trozos, o se funden liberando en el proceso partículas sub-nucleares. La nueva física de la primera mitad del siglo XX estuvo dominada por los nuevos acertijos que estas partículas planteaban.
Pero tenemos la mecánica cuántica; ¿es que no es aplicable siempre?, ¿Cuál es la dificultad? Desde luego, la mecánica cuántica es válida para las partículas subatómicas, pero hay más que eso. Las fuerzas con que estas partículas interaccionan y que mantienen el núcleo atómico unido son tan fuertes que las velocidades a las que tienen que moverse dentro y fuera del núcleo están cerca de la velocidad de la luz, c, que es de 299.792’458 Km/s. Cuando tratamos con velocidades tan altas se necesita una segunda modificación a las leyes de la física del siglo XIX; tenemos que contar con la teoría de la relatividad especial de Einstein.
Esta teoría también fue el resultado de una publicación de Einstein de 1905. en esta teoría quedaron sentadas las bases de que el movimiento y el reposo son conceptos relativos, no son absolutos, como tampoco habrá un sistema de referencia absoluto con respecto al cual uno pueda medir la velocidad de la luz.
Pero había más cosas que tenían que ser relativas. En este teoría, la masa y la energía también dependen de la velocidad, como lo hacen la intensidad del campo eléctrico y del magnético. Einstein descubrió que la masa de una partícula es siempre proporcional a la energía que contienen, supuesto que se haya tenido en cuenta una gran cantidad de energía en reposo de una partícula cualquiera, como se denota a continuación:

E = mc2
Como la velocidad de la luz es muy grande, esta ecuación sugiere que cada partícula debe almacenar una cantidad enorme de energía, y en parte esta predicción fue la que hizo que la teoría de la relatividad tuviese tanta importancia para la física (¡y para todo el mundo!). Para que la teoría de la relatividad también sea auto-consistente tiene que ser holista, esto es, que todas las cosas y todo el mundo obedezcan a las leyes de la relatividad. No son sólo los relojes los que se atrasan a grandes velocidades, sino que todos los procesos animados se comportan de la forma tan inusual que describe esta teoría cuando nos acercamos a la velocidad de la luz. El corazón humano es simplemente un reloj biológico y latirá a una velocidad menor cuando viaje en un vehículo espacial a velocidades cercanas a la de la luz. Este extraño fenómeno conduce a lo que se conoce como la “paradoja de los gemelos”, sugerida por Einstein, en la que dos gemelos idénticos tienen diferente edad cuando se reencuentran después de que uno haya permanecido en la Tierra mientras que el otro ha viajado a velocidades relativistas.
Einstein comprendió rápidamente que las leyes de la gravedad también tendrían que ser modificadas para que cumplieran el principio relativista.
Para poder aplicar el principio de la relatividad a la fuerza gravitatoria, el principio tuvo que ser extendido de la siguiente manera: no sólo debe ser imposible determinar la velocidad absoluta del laboratorio, sino que también es imposible distinguir los cambios de velocidad de los efectos de una fuerza gravitatoria.
Einstein comprendió que la consecuencia de esto era que la gravedad hace al espacio-tiempo lo que la humedad a una hoja de papel: deformar la superficie con desigualdades que no se pueden eliminar. Hoy en día se conocen muy bien las matemáticas de los espacios curvos, pero en el época de Einstein el uso de estas nociones matemáticas tan abstractas para formular leyes físicas era algo completamente nuevo, y le llevó varios años encontrar la herramienta matemática adecuada para formular su teoría general de la relatividad que describe cómo se curva el espacio en presencia de grandes masas como planetas y estrellas.
Einstein tenía la idea en su mente desde 1907 (la relatividad especial la formuló en 1905), y se pasó 8 años buscando las matemáticas adecuadas para su formulación.
En geometría de Riemann, el tensor métrico es un tensor de rango 2 que se utiliza para definir conceptos métricos como distancia, ángulo y volumen en un espacio localmente euclídeo. Paraboloide de Flamm (solución exterior de Schwarzschild).
Leyendo el material enviado por un amigo al que pidió ayuda, Einstein quedó paralizado. Ante él, en la primera página de una conferencia dada ante el Sindicato de Carpinteros, 60 años antes por un tal Riemann, tenía la solución a sus desvelos: el tensor métrico de Riemann, que le permitiría utilizar una geometría espacial de los espacios curvos que explicaba su relatividad general.
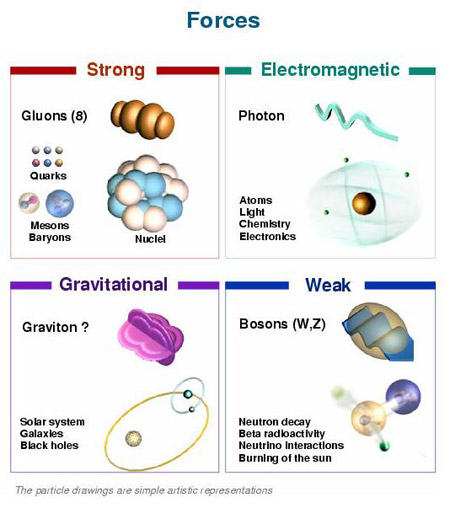
No está mal que en este punto recordemos la fuerza magnética y gravitatoria que nos puede ayudar a comprender mejor el comportamiento de las partículas subatómicas.
El electromagnetismo, decíamos al principio, es la fuerza con la cual dos partículas cargadas eléctricamente se repelen (si sus cargas son iguales) o se atraen (si tienen cargas de signo opuesto).
La interacción magnética es la fuerza que experimenta una partícula eléctricamente cargada que se mueve a través de un campo magnético. Las partículas cargadas en movimiento generan un campo magnético como, por ejemplo, los electrones que fluyen a través de las espiras de una bobina.
Las fuerzas magnéticas y eléctricas están entrelazadas. En 1873, James Clerk Maxwell consiguió formular las ecuaciones completas que rigen las fuerzas eléctricas y magnéticas, descubiertas experimentalmente por Michael Faraday. Se consiguió la teoría unificada del electromagnetismo que nos vino a decir que la electricidad y el magnetismo eran dos aspectos de una misma cosa.
¿Qué dicen?

La electricidad y el magnetismo no pueden desvanecerse sin más. Una región de un campo eléctrico girando crea un campo magnético perpendicular al giro. Una región de un campo magnético girando crea un campo eléctrico perpendicular al giro, pero en el sentido opuesto.
¿Por qué es importante?
Fue la primera unificación importante de fuerzas físicas, mostrando que la electricidad y el magnetismo están íntimamente interrelacionados, o, son dos aspectos diferentes de la misma cosa.
¿Qué provocó?
La predicción de que las ondas electromagnéticas existen, desplazándose a la velocidad de la luz, de modo que la propia luz es una de dichas ondas. Esto motivó la invención de la radio, el radar, la televisión, las conexiones inalámbricas para los ordenadores y la mayoría de las comunicaciones modernas.

La interacción es universal, de muy largo alcance (se extiende entre las estrellas), es bastante débil. Su intensidad depende del cociente entre el cuadrado de la carga del electrón y 2hc (dos veces la constante de Planck por la velocidad de la luz). Esta fracción es aproximadamente igual a 1/137’036…, o lo que llamamos Alfa (α) y se conoce como constante de estructura fina.
En general, el alcance de una interacción electromagnética es inversamente proporcional a la masa de la partícula mediadora, en este caso, el fotón, sin masa.
También antes hemos comentado sobre la interacción gravitatoria de la que Einstein descubrió su compleja estructura y la expuso al mundo en 1915 con el nombre de teoría general de la relatividad, y la relacionó con la curvatura del espacio y el tiempo. Sin embargo, aún no sabemos cómo se podrían reconciliar las leyes de la gravedad y las leyes de la mecánica cuántica (excepto cuando la acción gravitatoria es suficientemente débil).
La teoría de Einstein nos habla de los planetas y las estrellas del cosmos. La teoría de Planck, Heisenberg, Schrödinger, Dirac, Feynman y tantos otros, nos habla del comportamiento del átomo, del núcleo, de las partículas elementales en relación a estas interacciones fundamentales. La primera se ocupa de los cuerpos muy grandes y de los efectos que causan en el espacio y en el tiempo; la segunda de los cuerpos muy pequeños y de su importancia en el universo atómico. Cuando hemos tratado de unir ambos mundos se produce una gran explosión de rechazo. Ambas teorías son (al menos de momento) irreconciliables.
- La interacción gravitatoria actúa exclusivamente sobre la masa de una partícula.
- La gravedad es de largo alcance y llega a los más lejanos confines del universo conocido.
- Es tan débil que, probablemente, nunca podremos detectar esta fuerza de atracción gravitatoria entre dos partículas elementales. La única razón por la que podemos medirla es debido a que es colectiva: todas las partículas (de la Tierra) atraen a todas las partículas (de nuestro cuerpo) en la misma dirección.
El gravitón hace tiempo que se ríe de nosotros…y se oculta donde no lo podamos ver.
La partícula mediadora es el hipotético gravitón. Aunque aún no se ha descubierto experimentalmente, sabemos lo que predice la mecánica cuántica: que tiene masa nula y espín 2.
La ley general para las interacciones es que, si la partícula mediadora tiene el espín par, la fuerza entre cargas iguales es atractiva y entre cargas opuestas repulsiva. Si el espín es impar (como en el electromagnetismo) se cumple a la inversa.
Pero antes de seguir profundizando en estas cuestiones hablemos de las propias partículas subatómicas, para lo cual la teoría de la relatividad especial, que es la teoría de la relatividad sin fuerza gravitatoria, es suficiente.
Si viajamos hacia lo muy pequeño tendremos que ir más allá de los átomos, que son objetos voluminosos y frágiles comparados con lo que nos ocupará a continuación: el núcleo atómico y lo que allí se encuentra. Los electrones, que ahora vemos “a gran distancia” dando vueltas alrededor del núcleo, son muy pequeños y extremadamente robustos. El núcleo está constituido por dos especies de bloques: protones y neutrones. El protón (del griego πρώτος, primero) debe su nombre al hecho de que el núcleo atómico más sencillo, que es el hidrógeno, está formado por un solo protón. Tiene una unidad de carga positiva. El neutrón recuerda al protón como si fuera su hermano gemelo: su masa es prácticamente la misma, su espín es el mismo, pero en el neutrón, como su propio nombre da a entender, no hay carga eléctrica; es neutro.
La masa de estas partículas se expresa en una unidad llamada mega-electrón-voltio o MeV, para abreviar. Un MeV, que equivale a 106 electrón-voltios, es la cantidad de energía de movimiento que adquiere una partícula con una unidad de carga (tal como un electrón o un protón) cuando atraviesa una diferencia de potencial de 106 (1.000.000) voltios. Como esta energía se transforma en masa, el MeV es una unidad útil de masa para las partículas elementales.


La mayoría de los núcleos atómicos contienen más neutrones que protones. Los protones se encuentran tan juntos en el interior de un núcleo tan pequeño que se deberían repeles entre sí fuertemente, debido a que tienen cargas eléctricas del mismo signo. Sin embargo, hay una fuerza que los mantiene unidos estrechamente y que es mucho más potente e intensa que la fuerza electromagnética: la fuerza o interacción nuclear fuerte, unas 102 veces mayor que la electromagnética, y aparece sólo entre hadrones para mantener a los nucleones confinados dentro del núcleo. Actúa a una distancia tan corta como 10-15 metros, o lo que es lo mismo, 0’000000000000001 metros.
La interacción fuerte está mediada por el intercambio de mesones virtuales, 8 gluones que, como su mismo nombre indica (glue en inglés es pegamento), mantiene a los protones y neutrones bien sujetos en el núcleo, y cuanto más se tratan de separar, más aumenta la fuerza que los retiene, que crece con la distancia, al contrario que ocurre con las otras fuerzas.
La luz es una manifestación del fenómeno electromagnético y está cuantizada en “fotones”, que se comportan generalmente como los mensajeros de todas las interacciones electromagnéticas. Así mismo, como hemos dejado reseñado en el párrafo anterior, la interacción fuerte también tiene sus cuantos (los gluones). El físico japonés Hideki Yukawa (1907 – 1981) predijo la propiedad de las partículas cuánticas asociadas a la interacción fuerte, que más tarde se llamarían piones. Hay una diferencia muy importante entre los piones y los fotones: un pión es un trozo de materia con una cierta cantidad de “masa”. Si esta partícula está en reposo, su masa es siempre la misma, aproximadamente 140 MeV, y si se mueve muy rápidamente, su masa parece aumentar en función E = mc2. Por el contrario, se dice que la masa del fotón en reposo es nula. Con esto no decimos que el fotón tenga masa nula, sino que el fotón no puede estar en reposo. Como todas las partículas de masa nula, el fotón se mueve exclusivamente con la velocidad de la luz, 299.792’458 Km/s, una velocidad que el pión nunca puede alcanzar porque requeriría una cantidad infinita de energía cinética. Para el fotón, toda su masa se debe a su energía cinética.

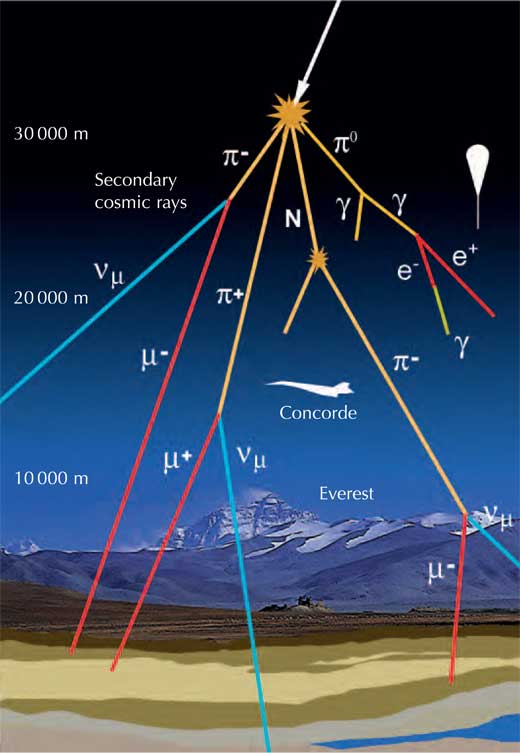
Fotones en los rayos cósmicos que llegan a la Tierra
En el estudio de los rayos cósmicos, las trazas de luz y los fotones son elementos clave tanto en la composición como en los métodos utilizados para su detección en la Tierra.
- Fotones Primarios: Aunque la gran mayoría de los rayos cósmicos son protones y núcleos atómicos, una pequeña fracción está compuesta por fotones de alta energía (rayos gamma). Estos viajan en línea recta desde su fuente (como supernovas o agujeros negros), a diferencia de las partículas cargadas que son desviadas por campos magnéticos.
- Fotones Secundarios: Cuando un rayo cósmico primario choca con la atmósfera, crea una cascada atmosférica extensa (EAS). En este proceso se generan miles de millones de partículas secundarias, incluyendo grandes cantidades de fotones, electrones y piones.
- Luz de Fluorescencia: Al atravesar la atmósfera, las partículas de la cascada excitan las moléculas de nitrógeno, las cuales emiten una tenue luz ultravioleta al desexcitarse. Detectores como los del Observatorio Pierre Auger captan estas trazas para reconstruir la energía y trayectoria del rayo.
- Radiación Cherenkov: Si las partículas viajan más rápido que la luz en el aire (o en el agua de un detector), producen un “destello” azulado llamado luz Cherenkov.
- Trazas en detectores: En laboratorios o globos aerostáticos, se utilizan cámaras de niebla o sensores CCD para visualizar las trazas de ionización (caminos de burbujas o señales eléctricas) que dejan las partículas al pasar.
Los físicos experimentales buscaban partículas elementales en las trazas de los rayos cósmicos que pasaban por aparatos llamados cámaras de niebla. Así encontraron una partícula coincidente con la masa que debería tener la partícula de Yukawa, el pión, y la llamaron mesón (del griego medio), porque su masa estaba comprendida entre la del electrón y la del protón. Pero detectaron una discrepancia que consistía en que esta partícula no era afectada por la interacción fuerte, y por tanto, no podía ser un pión. Actualmente nos referimos a esta partícula con la abreviatura μ y el nombre de muón, ya que en realidad era un leptón, hermano gemelo del electrón, pero con 200 veces su masa.
Antes de seguir veamos las partículas elementales de vida superior a 10-20 segundos que eran conocidas en el año 1970.
Nombre Símbolo Masa (MeV) Carga Espín Vida media (s) Fotón γ 0 0 1 ∞ Leptones (L = 1, B = 0) Electrón e– 0’5109990 – ½ ∞ Muón μ– 105’6584 – ½ 2’1970 × 10-6 Tau τ Neutrino electrónico νe ~ 0 0 ½ ~ ∞ Neutrino muónico νμ ~ 0 0 ½ ~ ∞ Neutrino tauónico ντ ~ 0 0 ½ ~ ∞ Mesones (L = 0, B = 0) Pión + π+ 139’570 2’603 × 10-8 Pión – π– 139’570 2’603 × 10-8 Pión 0 π0 134’976 0’84 × 10-16 Kaón + k+ 493’68 1’237 × 10-8 Kaón – k– 493’68 1’237 × 10-8 Kaón largo kL 497’7 5’17 × 10-8 Kaón corto kS 497’7 0’893 × 10-10 Eta η 547’5 0 0 5’5 × 10-19 Bariones (L = 0, B = 1) Protón p 938’2723 + ½ ∞ Neutrón n 939’5656 0 ½ 887 Lambda Λ 1.115’68 0 ½ 2’63 × 10-10 Sigma + Σ+ 1.189’4 + ½ 0’80 × 10-10 Sigma – Σ– 1.1974 – ½ 7’4× 10-20 Sigma 0 Σ0 0 ½ 1’48 × 10-10 Ksi 0 Ξ0 1.314’9 0 ½ 2’9 × 10-10 Ksi – Ξ– 1.321’3 – ½ 1’64 × 10-10 Omega – Ω– 1.672’4 – 1½ 0’82 × 10-10
Para cada leptón y cada barión existe la correspondiente antipartícula, con exactamente las mismas propiedades a excepción de la carga que es la contraria. Por ejemplo, el antiprotón se simboliza con y el electrón con e+. Los mesones neutros son su propia antipartícula, y el π+ es la antipartícula del π–, al igual que ocurre con k+ y k–. El símbolo de la partícula es el mismo que el de su antipartícula con una barra encima. Las masas y las vidas medias aquí reflejadas pueden estar corregidas en este momento, pero de todas formas son muy aproximadas.
Los símbolos que se pueden ver algunas veces, como s (extrañeza) e i (isoespín) están referidos a datos cuánticos que afectan a las partículas elementales en sus comportamientos.
Debo admitir que todo esto tiene que sonar algo misterioso. Es difícil explicar estos temas por medio de la simple palabra escrita sin emplear la claridad que transmiten las matemáticas, lo que, por otra parte, es un mundo secreto para el común de los mortales, y ese lenguaje es sólo conocido por algunos privilegiados que, mediante un sistema de ecuaciones pueden ver y entender de forma clara, sencilla y limpia, todas estas complejas cuestiones.
Si hablamos del espín (o, con más precisión, el momento angular, que es aproximadamente la masa por el radio por la velocidad de rotación) se puede medir como un múltiplo de la constante de Planck, h, dividido por 2π. Medido en esta unidad y de acuerdo con la mecánica cuántica, el espín de cualquier objeto tiene que ser o un entero o un entero más un medio. El espín total de cada tipo de partícula – aunque no la dirección del mismo – es fijo.
El electrón, por ejemplo, tiene espín ½. Esto lo descubrieron dos estudiantes holandeses, Samuel Gondsmit (1902 – 1978) y George Uhlenbeck (1900 – 1988), que escribieron sus tesis conjuntamente sobre este problema en 1972. Fue una idea audaz que partículas tan pequeñas como los electrones pudieran tener espín, y de hecho, bastante grande. Al principio, la idea fue recibida con escepticismo porque la “superficie del electrón” se tendría que mover con una velocidad 137 veces mayor que la de la luz, lo cual va en contra de la teoría de la relatividad general en la que está sentado que nada en el universo va más rápido que la luz, y por otra parte, contradice E=mc2, y el electrón pasada la velocidad de la luz tendría una masa infinita.
Hoy día, sencillamente, tal observación es ignorada, toda vez que el electrón carece de superficie.
La familia de los Bosones son partículas elementales que4 se caracterizan por tener espín entero (0, 1, 2, …),, lo que les permite ocupar el mismo estado cuántico simultáneamente, a diferencia de los fermiones (con espín semi-entero) que obedecen el Principio de Exclusión de Pauli y no pueden hacerlo. Ejemplos de bosones son los fotones, el bosón de Higgs y los gluones, y son cruciales para mediar las fuerzas de la naturaleza.
Las partículas con espín entero se llaman bosones, y las que tienen espín entero más un medio se llaman fermiones. Consultado los valores del espín en la tabla anterior podemos ver que los leptones y los bariones son fermiones, y que los mesones y los fotones son bosones. En muchos aspectos, los fermiones se comportan de manera diferente de los bosones. Los fermiones tienen la propiedad de que cada uno de ellos requiere su propio espacio: dos fermiones del mismo tipo no pueden ocupar o estar en el mismo punto, y su movimiento está regido por ecuaciones tales que se evitan unos a otros. Curiosamente, no se necesita ninguna fuerza para conseguir esto. De hecho, las fuerzas entre los fermiones pueden ser atractivas o repulsivas, según las cargas. El fenómeno por el cual cada fermión tiene que estar en un estado diferente se conoce como el principio de exclusión de Pauli. Cada átomo está rodeado de una nube de electrones, que son fermiones (espín ½). Si dos átomos se aproximan entre sí, los electrones se mueven de tal manera que las dos nubes se evitan una a otra, dando como resultado una fuerza repulsiva. Cuando aplaudimos, nuestras manos no se atraviesan pasando la uno a través de la otra. Esto es debido al principio de exclusión de Pauli para los electrones de nuestras manos que, de hecho, los de la izquierda rechazan a los de la derecha.
En contraste con el característico individualismo de los fermiones, los bosones se comportan colectivamente y les gusta colocarse todos en el mismo lugar. Un láser, por ejemplo, produce un haz de luz en el cual muchísimos fotones llevan la misma longitud de onda y dirección de movimiento. Esto es posible porque los fotones son bosones.
Cuando hemos hablado de las fuerzas fundamentales que, de una u otra forma, interaccionan con la materia, también hemos explicado que la interacción débil es la responsable de que muchas partículas y también muchos núcleos atómicos exóticos sean inestables. La interacción débil puede provocar que una partícula se transforme en otra relacionada, por emisión de un electrón y un neutrino. Enrico Fermi, en 1934, estableció una fórmula general de la interacción débil, que fue mejorada posteriormente por George Sudarshan, Robert Marschak, Murray Gell-Mann, Richard Feynman y otros. La fórmula mejorada funciona muy bien, pero se hizo evidente que no era adecuada en todas las circunstancias.
¿Cuál es la diferencia entre el protón y el neutrón?
Basta con cambiar un quark tipo U a uno tipo D.
Pues justamente esto es lo que ocurre en la naturaleza cuando entra en acción la fuerza nuclear débil. Un quark tipo U cambia a uno tipo D por medio de la interacción débil así
Las otras dos partículas que salen son un anti-electrón y un neutrino.
Este mismo proceso es el responsable del decaimiento radiactivo de algunos núcleos atómicos. Cuando un neutrón se convierte en un protón en el decaimiento radiactivo de un núcleo, aparece un electrón y un neutrino. Este es el origen de la radiación beta (electrones).
En 1970, de las siguientes características de la interacción débil sólo se conocían las tres primeras:
- La interacción actúa de forma universal sobre muchos tipos diferentes de partículas y su intensidad es aproximadamente igual para todas (aunque sus efectos pueden ser muy diferentes en cada caso). A los neutrinos les afecta exclusivamente la interacción débil.
- Comparada con las demás interacciones, ésta tiene un alcance muy corto.
- La interacción es muy débil. Consecuentemente, los choques de partículas en los cuales hay neutrinos involucrados son tan poco frecuentes que se necesitan chorros muy intensos de neutrinos para poder estudiar tales sucesos.
- Los mediadores de la interacción débil, llamados W+, W– y Z0, no se detectaron hasta la década de 1980. al igual que el fotón, tienen espín 1, pero están eléctricamente cargados y son muy pesados (esta es la causa por la que el alcance de la interacción es tan corto). El tercer mediador, Z0, que es responsable de un tercer tipo de interacción débil que no tiene nada que ver con la desintegración de las partículas llamada “corriente neutra”, permite que los neutrinos puedan colisionar con otras partículas sin cambiar su identidad.
A partir de 1970, quedó clara la relación de la interacción débil y la electromagnética (electrodébil de Weinberg-Salam).
La interacción fuerte (como hemos dicho antes) sólo actúa entre las partículas que clasificamos en la familia llamada de los hadrones, a los que proporciona una estructura interna complicada. Hasta 1972 sólo se conocían las reglas de simetría de la interacción fuerte y no fuimos capaces de formular las leyes de la interacción con precisión.
Como apuntamos, el alcance de esta interacción no va más allá del radio de un núcleo atómico ligero (10-13 cm aproximadamente).
En 1963, cuando se supo que protones y neutrones (los llamados nucleones) están formados por Quarks, se pensó que la fuerza fuerte actúa realmente entre los Quarks.
En la teoría cuántica de campos, a cada tipo de interacción le corresponde una familia de partículas portadoras de la interacción.Las partículas que transportan la fuerza fuerte nuclear que interactúa entre los quarks se denominan gluones.
La fuerza nuclear fuerte se deduce del requisito de que las ecuaciones que describen a los quarks deben ser las mismas, independientemente de cómo se elija la definición de los colores de los quarks.

La interacción es fuerte. En realidad, la más fuerte de todas.
Lo dejaré aquí, en verdad, eso que el Modelo Estándar de la Física, es feo, complejo e incompleto y, aunque hasta el momento es una buena herramienta con la que trabajar, la verdad es que, se necesita un nuevo modelo más avanzado y que incluya la Gravedad.
Veremos que más descubre el LHC.
Emilio Silvera V.
Dic
17
Todo tiene límite, las teorías… También
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (3)
Comments (3)
Poco a poco vamos pudiendo explicar las cosas que hoy no sabemos y, los adelantos continuados, en todas las disciplinas, del saber humano, hace posible que las teorías de hoy, no sean las del mañana, toda vez que, cuando se descubren nuevos datos y nuevos sucesos, nos hacen tomar también, caminos nuevos que nos llevan a la búsqueda de nuevas teorías. Lo cierto es que siempre andamos a vueltas con las teorías, y, tenemos que ser conscientes que las teorías tienen unos límites que están bien determinados.
Veamos:

Unas nos hablan del “universo” de lo muy pequeño y otras, del “universo” de lo muy grande, pero… ¿Cuáles son los límites de la teoría cuántica y de la teoría de la relatividad general de Einstein? Afortunadamente, hay una respuesta simple y las unidades de Planck nos dicen cuales son.
Supongamos que tomamos toda la masa del universo visible y determinamos su longitud de onda cuántica. Podemos preguntarnos en qué momento esta longitud de onda cuántica del universo visible superará su tamaño. La respuesta es: cuando el universo sea más pequeño en tamaño que la longitud de Planck, es decir, 10-33 centímetros, más joven que el tiempo de Planck 10ˉ⁴³ segundos y supere la temperatura de Planck de 1032 grados. Las unidades de Planck marcan la frontera de aplicación de nuestras teorías actuales. Para comprender en que se parece el mundo a una escala menor que la longitud de Planck tenemos que comprender plenamente cómo se entrelaza la incertidumbre cuántica con la gravedad. Para entender lo que podría haber sucedido cerca del suceso que estamos tentados a llamar el principio del universo, o el comienzo del tiempo, tenemos que penetrar la barrera de Planck. Las constantes de la naturaleza marcan las fronteras de nuestro conocimiento existente y nos dejan al descubierto los límites de nuestras teorías.
En los intentos más recientes de crear una teoría nueva para describir la naturaleza cuántica de la gravedad ha emergido un nuevo significado para las unidades naturales de Planck. Parece que el concepto al que llamamos “información” tiene un profundo significado en el universo. Estamos habituados a vivir en lo que llamamos “la edad de la información”. La información puede ser empaquetada en formas electrónicas, enviadas rápidamente y recibidas con más facilidad que nunca antes. Nuestra evolución en el proceso rápido y barato de la información se suele mostrar en una forma que nos permite comprobar la predicción de Gordon Moore, el fundador de Intel, llamada ley de Moore, en la que, en 1.965, advirtió que el área de un transistor se dividía por dos aproximadamente cada 12 meses. En 1975 revisó su tiempo de reducción a la mitad hasta situarlo en 24 meses. Esta es “la ley de Moore” cada 24 meses se obtiene una circuitería de ordenador aproximadamente el doble, que corre a velocidad doble, por el mismo precio, ya que, el coste integrado del circuito viene a ser el mismo, constante.
![]()
Los procesamiento de información vienen impuestos por las constantes de la naturaleza. Día a día la computación cuántica se va acercando a la realidad.

Jacob David Bekenstein
Los límites últimos que podemos esperar para el almacenamiento y los ritmos de procesamiento de la información están impuestos por las constantes de la naturaleza. En 1981, el físico israelí, Jacob Bekenstein, hizo una predicción inusual que estaba inspirada en su estudio de los agujeros negros. Calculó que hay una cantidad máxima de información que puede almacenarse dentro de cualquier volumen. Esto no debería sorprendernos. Lo que debería hacerlo es que el valor máximo está precisamente determinado por el área de la superficie que rodea al volumen, y no por el propio volumen. El número máximo de bits de información que puede almacenarse en un volumen viene dado precisamente por el cómputo de su área superficial en unidades de Planck. Supongamos que la región es esférica. Entonces su área superficial es precisamente proporcional al cuadrado de su radio, mientras que el área de Planck es proporcional a la longitud de Planck al cuadrado, 10-66 cm2. Esto es muchísimo mayor que cualquier capacidad de almacenamiento de información producida hasta ahora
máximo de bits de información que puede almacenarse en un volumen viene dado precisamente por el cómputo de su área superficial en unidades de Planck. Supongamos que la región es esférica. Entonces su área superficial es precisamente proporcional al cuadrado de su radio, mientras que el área de Planck es proporcional a la longitud de Planck al cuadrado, 10-66 cm2. Esto es muchísimo mayor que cualquier capacidad de almacenamiento de información producida hasta ahora . Asimismo, hay un límite último sobre el ritmo de procesamiento de información que viene impuesto por las constantes de la naturaleza.
. Asimismo, hay un límite último sobre el ritmo de procesamiento de información que viene impuesto por las constantes de la naturaleza.
Stoney Planck
No debemos descartar la posibilidad de que seamos capaces de utilizar las unidades de Planck-Stoney para clasificar todo el abanico de estructuras que vemos en el universo, desde el mundo de las partículas elementales hasta las más grandes estructuras astronómicas. Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias. Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y mprotón.
el mundo de las partículas elementales hasta las más grandes estructuras astronómicas. Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias. Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y mprotón.
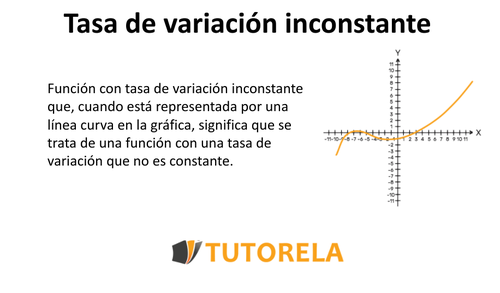

El valor más preciso de la constante de estructura fina, resultado de las últimas mediciones.
“Tras medir alfa en unas 300 galaxias lejanas, vimos un patrón constante: este número , que nos dice la fuerza del electromagnetismo, no es igual en otras partes que en la Tierra, y parecer variar de forma continua a lo largo de un eje”. Algunos se empeñan en variar la constante de estructura fina y, si eso llegara a producirse… las consecuencias serían funestas para nosotros. Otros estudios nos dicen que esa constante, no ha variado a lo largo de los miles de millones de años del Universo y, así debe ser, o, si varió, lo hizo en una escala ínfima.
, que nos dice la fuerza del electromagnetismo, no es igual en otras partes que en la Tierra, y parecer variar de forma continua a lo largo de un eje”. Algunos se empeñan en variar la constante de estructura fina y, si eso llegara a producirse… las consecuencias serían funestas para nosotros. Otros estudios nos dicen que esa constante, no ha variado a lo largo de los miles de millones de años del Universo y, así debe ser, o, si varió, lo hizo en una escala ínfima.
| α = 2πe2 / hc ≈ 1/137 |
| αG = (Gmp2)2 / hc ≈ 10-38 |
Si varian algunas de las dos en sólo una diezmillonésima, muchas de las cosas que conforman el Universo serían imposible y, la consecuencia sería, la ausencia de vida. La identificación de constantes adimensionales de la naturaleza como a (alfa) y aG, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro. Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala. La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.
en mundos diferentes del nuestro. Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala. La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.

La identificación de constantes adimensionales de la naturaleza como a (alfa) y aG, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro. Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala. La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.
Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck). Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.
en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck). Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.
Cuando surgen comentarios de números puros y adimensionales, de manera automática aparece en mi mente el número 137. Ese número encierra más de lo que estamos preparados para comprender; me hace pensar y mi imaginación se desboca en múltiples ideas y teorías. Einstein era un campeón en esta clase de ejercicios mentales que él llamaba “libre invención de la mente”. El gran físico creía que no podríamos llegar a las verdades de la naturaleza sólo por la observación y la experimentación. Necesitamos crear conceptos, teorías y postulados de nuestra propia imaginación que posteriormente deben ser explorados para averiguar si existe algo de verdad en ellos.
137. Ese número encierra más de lo que estamos preparados para comprender; me hace pensar y mi imaginación se desboca en múltiples ideas y teorías. Einstein era un campeón en esta clase de ejercicios mentales que él llamaba “libre invención de la mente”. El gran físico creía que no podríamos llegar a las verdades de la naturaleza sólo por la observación y la experimentación. Necesitamos crear conceptos, teorías y postulados de nuestra propia imaginación que posteriormente deben ser explorados para averiguar si existe algo de verdad en ellos.
Para poner un ejemplo de nuestra ignorancia poco tendríamos que buscar, tenemos a mano miles de millones.
El gran Físico León Lederman nos decía:
“Todos los físicos del mundo, deberían tener un letrero en el lugar más visible de sus casas, para que al mirarlo, les recordara lo que no saben. En el cartel sólo pondría esto: 137. Ciento treinta y siete es el inverso de algo que lleva el nombre
de constante de estructura fina”.

Este número puro y adimensional, esconde los secretos del electromagnetismo, el electrón (e˜), de la velocidad de la luz (c), y, de los cuentos de Planck (h).
Este número guarda relación con la posibilidad de que un electrón emita un fotón o lo absorba. La constante de estructura fina responde también al nombre de “alfa” y sale de dividir el cuadrado de la carga del electrón, por el producto de la velocidad de la luz y la constante de Planck. Tanta palabrería y numerología no significan otra cosa sino que ese solo numero, 137, encierra los misterios del electromagnetismo (el electrón, e–), la relatividad (la velocidad de la luz, c), y la teoría cuántica (la constante de Planck, h).
La tensión superficial
Sus dimensiones y masa le permiten ¡lo imposible! para nosotros. La tensión superficial es una consecuencia de que todas las moléculas y los átomos se atraen unos a otros con una fuerza que nosotros llamamos fuerza de Van der Vaalls. esta fuerza tiene un alcance muy corto. para ser más precisos, diremos que la intensidad de esta fuerza a una distancia r es aproximadamente proporcional a 1/r7. Esto significa que si se reduce la distancia entre dos átomos a la mitad, la fuerza de Van der Vaalls con la que se atraen uno a otro se hace 2 x 2 x 2 x 2 x 2 x 2 x 2 = 128 veces más intensa. Cuando los átomos y las moléculas se acercan mucho unos a otros quedan unidos muy fuertemente a través de esta fuerza.
La mecánica cuántica domina en el micro-mundo de los átomos y de las partículas “elementales”. Nos enseña que en la naturaleza cualquier masa, por sólida o puntual que pueda parecer, tiene un aspecto ondulatorio. Esta onda no es como una onda de agua. Se parece más a una ola de histeria que se expande: es una onda de información. Nos indica la probabilidad de detectar una partícula. La longitud de onda de una partícula, la longitud cuántica, se hace menor cuanto mayor es la masa de esa partícula.


Por el contrario, la relatividad general era siempre necesaria cuando se trataba con situaciones donde algo viaja a la velocidad de la luz, o está muy cerca o donde la gravedad es muy intensa. Se utiliza para describir la expansión del universo o el comportamiento en situaciones extremas, como la formación de agujeros negros.
Sin embargo, la gravedad es muy débil comparada con las fuerzas que unen átomos y moléculas y demasiado débil para tener cualquier efecto sobre la estructura del átomo o de partículas subatómicas, se trata con masas tan insignificantes que la incidencia gravitatoria es despreciable. Todo lo contrario que ocurre en presencia de masas considerables como planetas, estrellas y galaxias, donde la presencia de la gravitación curva el espacio y distorsiona el tiempo.
Como resultado de estas propiedades antagónicas, la teoría cuántica y la teoría relativista gobiernan reinos diferentes, muy dispares, en el universo de lo muy pequeño o en el universo de lo muy grande. Nadie ha encontrado la manera de unir, sin fisuras, estas dos teorías en una sola y nueva de Gravedad-Cuántica.
La velocidad de la luz en el vacío es por definición una constante universal de valor 299.792.458 m/s (suele aproximarse a 3·108 m/s), o lo que es lo mismo 9,46·1015 m/año; la segunda cifra es la usada para definir al intervalo llamado año luz. La información se transmitirá a esa velocidad como máximo, nuestro Universo, no permite mayor rapidez, al menos, por los métodos convencionales. Lo cierto es que algún día nos daremos cuenta y descubriremos que la luz tiene más importancia de la que ahora le podemos dar, toda vez que no conocemos, la realidad de su naturaleza y todo lo que significa en nuestro Universo. Nosotros mismos, en última instancia… ¡Somos luz!
definir al intervalo llamado año luz. La información se transmitirá a esa velocidad como máximo, nuestro Universo, no permite mayor rapidez, al menos, por los métodos convencionales. Lo cierto es que algún día nos daremos cuenta y descubriremos que la luz tiene más importancia de la que ahora le podemos dar, toda vez que no conocemos, la realidad de su naturaleza y todo lo que significa en nuestro Universo. Nosotros mismos, en última instancia… ¡Somos luz!
Estamos hechos de polvo de estrellas, somos Seres de LUZ
De átomos que se juntan para formar moléculas y sustancias que tienen sus origen en las estrellas, y, que por unas inexplicables transformaciones, ese conjunto evolucionada y puede llegar, a convertirse en pensamientos.
El año 2.015 fue el Año Internacional de la Luz, ese fenómeno natural del que tenemos muchos secretos que desvelar. Creo que, el día que sepamos, lo es realmente la luz,la inmensa ignorancia que llevamos acuesta, será más llevadera.
¡Sabemos aun tan poco!
Emilio Silvera V.
Dic
16
¡Qué misterio esconde la materia? ¿Qué es la luz? ¿Las radiaciones?...
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
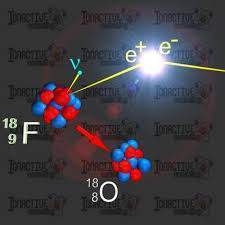
Decaimiento β– de un núcleo. Se ilustra cómo uno de los neutrones se convierte en un protón a la vez que emite un electrón(β–) y un antineutrino electrónico. La desintegración beta se debe a la interacción nuclear débil, que convierte un neutrón en un protón (desintegración β–), o viceversa (β+), y crea un par leptón–antileptón. Así se conservan los números bariónico(inicialmente 1) y leptónico (inicialmente 0). Debido a la aparente violación al principio de conservación de la energía, estas reacciones propiciaron precisamente que se propusiera la existencia del neutrino. Precisamente de eso hablamos aquí.
Una vez escenificados los conceptos, diremos que, los físicos se vieron durante mucho tiempo turbados por el hecho de que a menudo, la partícula beta emitida en una desintegración del núcleo no alberga energía suficiente para compensar la masa perdida por el núcleo. En realidad, los electrones no eran igualmente deficitarios. Emergían con un amplio espectro de energías, y el máximo (conseguido por muy pocos electrones), era casi correcto, pero todos los demás no llegaban a alcanzarlo en mayor o menor grado. Las partículas alfa emitidas por un nucleido particular poseían iguales energías en cantidades inesperadas. En ese caso, ¿Qué era errónea en la emisión de partículas beta? ¿Qué había sucedido con la energía perdida?
En 1.922, Lise Maitner se hizo por primera vez esta pregunta, y, hacia 1.930, Niels Bohr estaba dispuesto a abandonar el gran principio de conservación de la energía, al menos en lo concerniente a partículas subatómicas. En 1.931, Wolfgang Pauli sugirió una solución para el enigma de la energía desaparecida.
La radiación alfa está compuesta por un núcleo de helio y puede ser detenida por una hoja de papel. La radiación beta, compuesta por electrones, es detenida por una hoja de papel de aluminio. La radiación gamma es absorbida cuando penetra en un material denso
Digamos que la solución de Pauli para explicar la masa perdida, era muy simple: junto con la partícula beta del núcleo se desprendía otra, que se llevaba la energía desaparecida. Esa misteriosa segunda partícula tenía propiedades bastante extrañas. No poseía carga ni masa. Lo único que llevaba mientras se movía a la velocidad de la luz era cierta cantidad de energía. A decir verdad, aquello parecía un cuerpo ficticio creado exclusivamente para equilibrar el contraste de energías.
Sin embargo, tan pronto como se propuso la posibilidad de su existencia, los físicos creyeron en ella ciegamente. Y esta certeza se incrementó al descubrirse el neutrón y al saberse que se desintegraba en un protón y se liberaba un electrón, que, como en la decadencia beta, portaba insuficientes cantidades de energía. Enrico Fermi dio a esta partícula putativa el nombre de “neutrino”, palabra italiana que significa “pequeño neutro”.
Primera observación de un neutrino en una cámara de burbujas, en 1970 en el Argonne National Laboratory de EE. UU., la observación se realizo gracias a las líneas observadas en la Cámara de burbujas basada en hidrógeno líquido. Siempre hemos tenido imaginación para idear aparatos que nos ayudaran a desvelar los secretos de la Naturaleza. Más tarde, la cámara de burbujas, fue sustituida por la cámara de chispas.
El neutrón dio a los físicos otra prueba palpable de la existencia del neutrino. Como ya he comentado otras veces, casi todas las partículas describen un movimiento rotatorio. Esta rotación se expresa, más o menos, en múltiplos de una mitad según la dirección del giro. Ahora bien, el protón, el neutrón y el electrón tienen rotación de una mitad. Por tanto, si el neutrón con rotación de una mitad origina un protón y un electrón, cada uno con rotación de una mitad, ¿qué sucede con la ley sobre conservación del momento angular? Aquí hay algún error. El protón y el electrón totalizan una mitad con sus rotaciones (si ambas rotaciones siguen la misma dirección) o cero (si sus rotaciones son opuestas); pero sus rotaciones no pueden sumar jamás una mitad. Sin embargo, por otra parte, el neutrino viene a solventar la cuestión.
Supongamos que la rotación del neutrón sea +½. Y admitamos también que la rotación del protón sea +½ y la del electrón -½, para dar un resultado neto de cero. Demos ahora al neutrino una rotación de +½, y la balanza quedará equilibrada.
+½(n) = +½(p) – ½(e) + ½(neutrino)

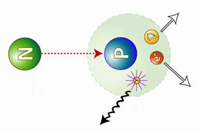
Pero aun queda algo por equilibrar. Una sola partícula (el neutrón) ha formado dos partículas (el protón y el electrón), y, si incluimos el neutrino, tres partículas. Parece más razonable suponer que el neutrón se convierte en dos partículas y una antipartícula. En otras palabras: lo que realmente necesitamos equilibrar no es un neutrino, sino un antineutrino.
El propio neutrino surgiría de la conversación de un protón en un neutrón. Así, pues, los productos serían un neutrón (partícula), un positrón (antipartícula) y un neutrino (partícula). Esto también equilibra la balanza. En otras palabras, la existencia de neutrinos y antineutrinos debería salvar no una, sino tres, importantes leyes de conservación: la conservación de la energía, la de conservación del espín y la de conservación de partícula/antipartícula.
Para un electrón, protón o neutrón la cantidad de espín es siempre 1/2 del valor mínimo de momento permitido (ħ).

Es importante conservar esas leyes puesto que parece estar presentes en toda clase de reacciones nucleares que no impliquen electrones o positrones, y sería muy útil si también se hallasen presentes en reacciones que incluyesen esas partículas.

Las más importantes conversiones protón-neutrón son las relaciones con las reacciones nucleares que se desarrollan en el Sol y en los astros. Por consiguiente, las estrellas emiten radiaciones rápidas de neutrinos, y se calcula que tal vez pierdan a causa de esto el 6 u 8 % de su energía. Pero eso, sería meternos en otra historia y, por mi parte, con la anterior explicación solo trataba de dar una muestra del ingenio del hombre que, como habréis visto, no es poco.
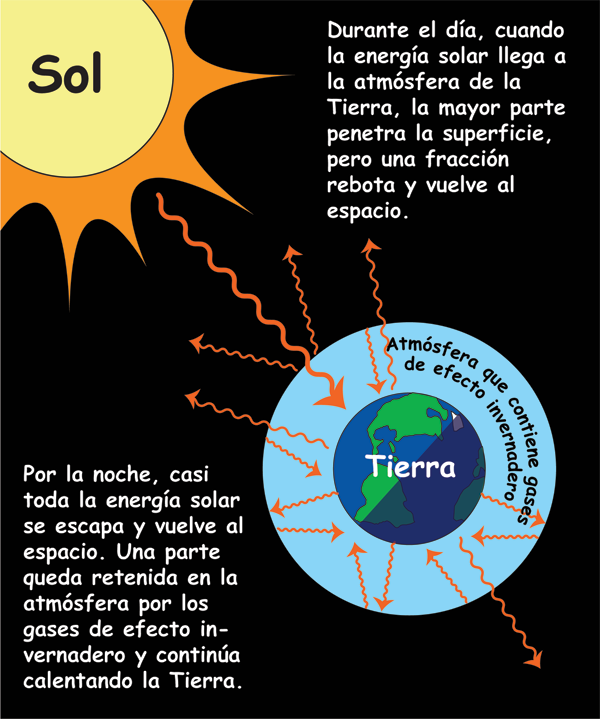
Aunque sólo una cinco mil millonésima de la luz solar llega a la Tierra, ha sido suficiente para dar a esta calor y vida, así como bípedos bastante listos para calcular al detalle su deuda con el Sol que, si pusiera intereses, nunca podríamos pagar.
Desde que puedo recordar, he sido un amante de la Física. Me asombran cuestiones como la luz, su naturaleza de un conglomerado de colores, ondas y partículas, su velocidad que nos marca el límite máximo que se puede desplazar cualquier cosa en nuestro Universo, y en fin, muchos otros misterios que encierra esa maravilla cotidiana que nos rodea y lo inunda todo haciendo posible que podamos ver por donde vamos, que las plantas vivan y emitan oxígeno o que nos calentemos. Realmente, sin luz, nuestra vida no sería posible.
Me gustaría que alguien contestara: ¿Qué es realmente la luz?
Muchos (casi todos) opinan que es algo inmaterial. Los objetos materiales, grandes o muy pequeños como las galaxias o los electrones, son materia. La luz, sin embargo, se cree que es inmaterial, dos rayos de luz se cruzan sin afectarse el uno al otro. Sin embargo, yo que deberíamos profundizar un poco más y, sabiendo que la luz está formada por fiotones, que los fotones son energía, que la energía es un aspecto de la masa… ¿Qué es realmente la luz? Nosotros mismos, el última instancia ¿No seremos luz?
Está claro que los estudiosos de la época antigua y medieval estaban por completo a oscuras acerca de la naturaleza de la luz. Especulaban sobre que consistía en partículas emitidas por objetos relucientes o tal vez por el mismo ojo. Establecieron el hecho de que la luz viajaba en línea recta, que se reflejaba en un espejo con un ángulo igual a aquel con el que el rayo choca con el espejo, y que un rayo de luz se inclina (se refracta) cuando pasa del aire al cristal, al agua o a cualquier otra sustancia transparente.
Cuando la luz entra en un cristal, o en alguna sustancia transparente, de una forma oblicua (es decir, en un ángulo respecto de la vertical), siempre se refracta en una dirección que forma un ángulo menor respecto de la vertical. La exacta relación entre el ángulo original y el ángulo reflejado fue elaborada por primera vez en 1.621 por el físico neerlandés Willerbrord Snell. No publicó sus hallazgos y el filósofo francés René Descartes descubrió la ley, independientemente, en 1.637.

Los primeros experimentos importantes acerca de la naturaleza de la luz fueron llevados a cabo por Isaac Newton en 1.666, al permitir que un rayo de luz entrase en una habitación oscura a través de una grieta e las persianas, cayendo oblicuamente sobre una cara de un prisma de cristal triangular. El rayo se refracta cuando entra en el cristal y se refracta aún más en la misma dirección cuando sale por una segunda cara del prisma. (Las dos refracciones en la misma dirección se originan por que los dos lados del prisma de se encuentran en ángulo en vez de en forma paralela, como sería el caso en una lámina ordinaria de cristal.)
Newton atrapó el rayo emergente sobre una pantalla blanca para ver el efecto de la refracción reforzada. Descubrió que, en vez de formar una mancha de luz blanca, el rayo se extendía en una gama de colores: rojo, anaranjado, amarillo, verde, azul, y violeta, en este orden. Newton dedujo de ello que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores. La amplia banda de sus componentes se denominó spectrum (palabra latina que significa “espectro” fantasma).

Newton llegó a la conclusión de que la luz se componía de diminutas partículas (“corpúsculos”), que viajaban a enormes velocidades.
Le surgieron y se planteó algunas inquietantes cuestiones. ¿Por qué se refractaban las partículas de luz verde más que los de luz amarilla? ¿Cómo se explicaba que dos rayos de luz se cruzaran sin perturbase mutuamente, es decir, sin que se produjeran colisiones entre partículas?
En 1.678, el físico neerlandés christian Huyghens (un científico polifacético que había construido el primer reloj de péndulo y realizado importantes trabajos astronómicos) propuso una teoría opuesta: la de que la luz se componía de minúsculas ondas. Y si sus componentes fueran ondas, no sería difícil explicar los diversos difracciones de los diferentes tipos de luz a través de un medio refractante, siempre y cuando se aceptara que la luz se movía más despacio en ese medio refractante que en el aire. La cantidad de refracción variaría con la longitud de las ondas: cuanto más corta fuese tal longitud, tanto mayor sería la refracción. Ello significaba que la luz violeta (la más sensible a este fenómeno) debía de tener una longitud de onda mas corta que la luz azul, ésta, más corta que la verde, y así sucesivamente.

Se encuentra la galaxias más lejana nacida después del Big Bang
Gracias a las radiaciones electromagnéticas podemos ver el Universo como fue hace ahora miles de millones de años. Cuando la luz, nos trae la imagen de galaxias situadas a distancias inconmensurables. ¿Quién podría haber pensado, en el pasado, que tal cosa fuese posible?
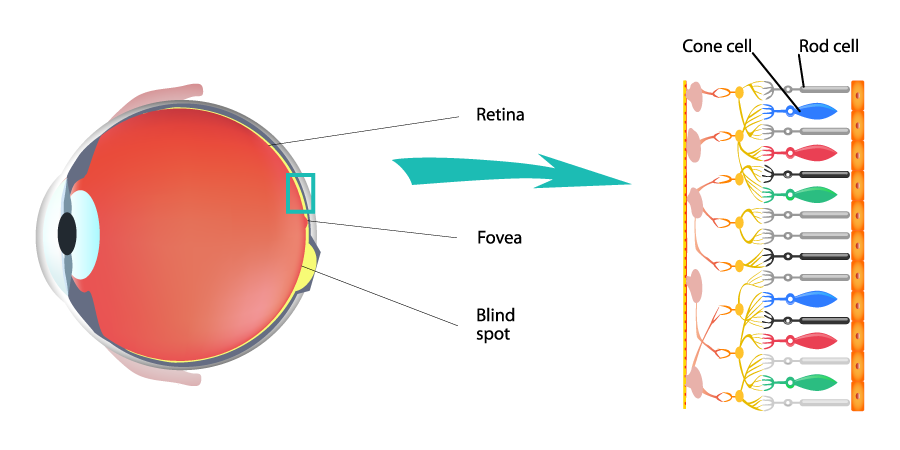
El ojo humano percibe los colores porque sus células fotorreceptoras (conos) son sensibles a diferentes longitudes de onda dentro del espectro visible, y el cerebro interpreta la combinación de estas señales, interpretando una longitud de onda como azul, otra como verde, y otras como variaciones de rojo, o mezclas de ellas, permitiéndonos ver un vasto abanico de tonos.
Lo que permitía al ojo distinguir los colores eran esas diferencias entre longitudes de onda. Y, como es natural, si la luz estaba integrada por ondas, dos rayos podrían cruzarse sin dificultad alguna. (Las ondas sonoras y las del agua se cruzan continuamente sin perder sus respectivas identidades.)
Pero la teoría de Huyqhens sobre las ondas tampoco fue muy satisfactoria. No explicaba por qué se movían en línea recta los rayos luminosos; ni por qué proyectaban sobras recortadas; ni aclaraba por qué las ondas luminosas no podían rodear los obstáculos, del mismo modo que pueden hacerlo las ondas sonoras y las ondas marinas. Por añadidura, se objetaba que si la luz consistía en ondas, ¿Cómo podía viajar por el vacío, ya que cruzaba el espacio desde el Sol y las Estrellas? ¿Cuál era esa mecánica ondulatoria?

Así que, la vieja idea de Newton de que la luz estaba formada por partículas, en contra de la teoría ondulatoria de su contemporáneo Huygens corroborada por posteriores experimentos en el siglo XIX y por la teoría electromagnética de Maxwell, volvía a ser vigente en parte. La radiación electromagnética estaba formada por paquetes de energía llamados fotones, tenía una doble naturaleza: ondulatoria y corpuscular. La doble naturaleza ondulatoria y corpuscular de la luz, hizo pensar al físico francés Louis de Broglie que el resto de partículas podían disfrutar de esa cualidad y estableció que cualquier partícula lleva asociada una onda de longitud igual al cuanto de acción (h) dividido por su masa y por su velocidad (cualquier objeto macroscópico también tiene su onda asociada, pero debido al valor tan pequeño del cuanto de acción su efecto es despreciable). De hecho, cuando se diseña un experimento, dependiendo de las restricciones que se impongan a la partícula se pone de manifiesto su naturaleza ondulatoria o corpuscular pero, esa es, otra historia.

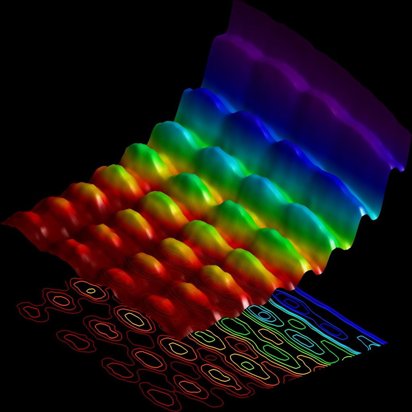
Hace tiempo que se saber que la luz tiene una dualidad onda-partícula, y se comporta como una onda (propagación, interferencia, difracción) y como una partícula (fotones, efecto fotoeléctrico) a la vez, una característica fundamental de la mecánica cuántica que depende de cómo la observes o interactúes con ella.
Primera foto de la luz como onda y partícula a la vez
Todo esto me lleva a pensar que lo que hace la Naturaleza para conseguir sus fines… ¡Es maravilloso!
¿En qué clase de universo estaríamos sin la presencia de la Luz?
El fotón en sí mismo es una maravilla, una partícula sin masa en reposo y que es la que consigue moverse a la mayor velocidad permitida en nuestro universo. ¿Es sólo energía? Pero, si es solo energía y la ecuación de E = mc2 nos dice que masa y energía son dos aspectos de la misma cosa, tendríamos que concluir que el fotón también es masa ¿No?
Planteada esta duda, me dicen:
“¡Excelente pregunta que toca el corazón de la física relativista! Sí un fotón es energía pura, pero la ecuación =2 se refiere a la energía en reposo. Un fotón tiene masa en reposo nula, por lo que toda su energía es cinética y no puede estar quieto; viaja a la velocidad de la luz (c) y su energía se define por su frecuencia, no por 2, aunque sí se cumple la equivalencia masa-energía, pero para el fotón es una masa que se manifiesta en movimiento, no en reposo, ¡una partícula sin masa intrínseca pero con una tremenda energía y momento!.
Todo esto puede ser fascinante, para nosotros es como viajar a otro “universo” sin salir de este.
Si tienes tiempo….
Emilio Silvera V.
Dic
1
¿Qué es un bosón? ¿y que es un bosón gauge?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)


Las partículas elementales de la familia de los bosones son los mediadores de las interacciones fundamentales, Se dividen en el bosón de Higgs (escalar) y cuatro bosones vectoriales o de gauge:

Fotones ( Las radiaciones electromagnéticas transportadas por fotones son ondas de energía que abarcan un amplio espectro, incluyendo la luz visible, los rayos gamma, los rayos X, la radiación ultravioleta, el infrarrojo, las microondas y las ondas de radio. Estas radiaciones no necesitan un medio material para propagarse y se mueven a través del vacío a la velocidad de la luz.
El Gluon es el Bosón que transmite la fuerza nuclear fuerte, la cual mantiene confinados a los Quarks dentro de los Protones y los Neutrones (que son nucleones en el núcleo atómico). Es una partícula sin masa y sin carga eléctrica, pero con carga de color, que le permite interactuar consigo misma.


Decaimiento β– de un núcleo. Se ilustra cómo uno de los neutrones se convierte en un protón a la vez que emite un electrón (β–) y un anti-neutrino electrónico.


Las partículas que transmiten la fuerza nuclear débil son los bosones W± y Zº. Esta fuerza es responsable de fenómenos como la desintegración beta, que permite que una partícula cambie su “sabor”, como cuando un neutrón se transforma en un protón. El bosón W está cargado y el bosón Z es neutro y al ser partículas muy masivas, su alcance es extremadamente corto, solo dentro del núcleo atómico.


Un bosón es una partícula elemental (o estado ligado de partículas elementales, por ejemplo, un núcleo atómico o átomo) con espín entero, es decir, una partícula que obedece a la estadística de Bose-Einstein (estadística cuántica), de la cual deriva su nombre. Los bosones son importantes para el Modelo estándar de las partículas. Son bosones vectoriales de espín uno que hacen de intermediarios de las interacciones gobernadas por teorías gauge.
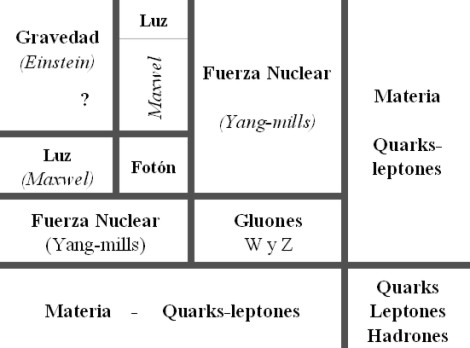
En física se ha sabido crear lo que se llama el Modelo estándar y, en él, los Bosones quedan asociados a las tres fuerzas que lo conforman, el fotón es el Bosón intermediario del electromagnetismo, los W+, w– y Zº son bosones gauge que transmiten la fuerza en la teoría electrodébil, mientras que los gluones son los bosones de la fuerza fuerte, los que se encargan de tener bien confinados a los Quarks conformando protones y neutrones para que el núcleo del átomo sea estable. La Gravedad, no se ha dejado meter en el modelo y, por eso su bosón no es de gauge. El gravitón que sería la partícula mediadora de la gravitación sería el hipotético cuanto de energía que se intercambia en la interacción gravitacional.
Ejemplos de los Bosones gauge son los fotones en electro-dinámica cuántica (en física, el fotón se representa normalmente con el símbolo 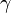 , que es la letra griega gamma), los gluones en cromodinámica cuántica y los bosones W y Z en el modelo de Weinberg-Salam en la teoría electrodébil que unifica el electromagnetismo con la fuerza débil. Si la simetría gauge de la teoría no está rota, el bosón gauge es no masivo. Ejemplos de bosones gauge no masivos son el fotón y el gluon.
, que es la letra griega gamma), los gluones en cromodinámica cuántica y los bosones W y Z en el modelo de Weinberg-Salam en la teoría electrodébil que unifica el electromagnetismo con la fuerza débil. Si la simetría gauge de la teoría no está rota, el bosón gauge es no masivo. Ejemplos de bosones gauge no masivos son el fotón y el gluon.
Si la simetría gauge de la teoría es una simetría rota el bosón gauge tiene masa no nula, ejemplo de ello son los bosones W y Z . Tratando la Gravedad, descrita según la teoría de la relatividad general, como una teoría gauge, el bosón gauge sería el gravitón, partícula no masiva y de espín dos.
Diagrama de Feynman mostrando el intercambio de un fotón virtual (simbolizado por una línea ondulada y  ) entre un positrón y un electrón.De esta manera podemos llegar a comprender la construcción que se ha hecho de las interacciones que están siempre intermediadas por un nosón mensajero de la fuerza.
) entre un positrón y un electrón.De esta manera podemos llegar a comprender la construcción que se ha hecho de las interacciones que están siempre intermediadas por un nosón mensajero de la fuerza.
En el modelo estándar, como queda explicado, hay tres tipos de bosones de gauge: fotones, bosones W y Z y gluones. Cada uno corresponde a tres de las cuatro interacciones: fotones son los bosones de gauge de la interacciones electromagnética, los bosones W y Z traen la interacción débil, los gluones transportan la interacción fuerte. El gravitón, que sería responsable por la interacción gravitacional, es una proposición teórica que a la fecha no ha sido detectada. Debido al confinamiento del color, los gluones aislados no aparecen a bajas energías.
Aquí, en el gráfico, quedan representadas todas las partículas del Modelo estándar, las familias de Quarks y Leptones que conforman la materia y los bones que intermedian en las interacciones o fuerzas fundamentales que están presentes en el Universo. La Gravedad no ha podido ser incluida y se ha negado a estar unida a las otras fuerzas. Así el bosón que la transnmite, tampoco está en el modelo que es incompleto al dejar fuera la fuerza que mantiene unidos los planetas en los sistemas solares, a las galaxias en los cúmulos y nuestros pies unidos a la superficie del planeta que habitamos. Se busca una teoría que permita esta unión y, los físicos, la laman gravedad cuántica pero… ¡no aparece por ninguna parte!
Llegados a este punto tendremos que retroceder, para poder comprender las cosas, hasta aquel trabajo de sólo ocho páginas que publicó Max Planck en 1.900 y lo cambió todo. El mismo Planck se dio cuenta de que, todo lo que él había tenido por cierto durante cuarenta años, se derrumbaba con ese trabajo suyo que, venía a decirnos que el mundo de la materia y la nergía estaba hecho a partir de lo que el llamaba “cuantos”.
de que, todo lo que él había tenido por cierto durante cuarenta años, se derrumbaba con ese trabajo suyo que, venía a decirnos que el mundo de la materia y la nergía estaba hecho a partir de lo que el llamaba “cuantos”.
Supuso el nacimiento de la Mecánica Cuántica (MC), el fin del determinismo clásico y el comienzo de una nueva física, la Física Moderna, de la que la Cuántica sería uno de sus tres pilares junto con la Relatividad y la Teoría del Caos. Más tarde, ha aparecido otra teoría más moderna aún por comprobar, ¿las cuerdas…?

El universo según la teoría de las cuerdas sería entonces una completa extensa polícroma SINFONIA ETERNA de vibraciones, un multiverso infinito de esferas, cada una de ellas un universo independiente causalmente, en una de esas esferas nuestra Vía Láctea, en ella nuestro sistema solar, en él nuestro planeta, el planeta tierra en el cual por una secuencia milagrosa de hechos se dio origen a la vida autoconsciente que nos permite preguntarnos del cómo y del por qué de todas las cosas que podemos observar y, también, de las que intuimos que están ahí sin que se dejen ver.
una de ellas un universo independiente causalmente, en una de esas esferas nuestra Vía Láctea, en ella nuestro sistema solar, en él nuestro planeta, el planeta tierra en el cual por una secuencia milagrosa de hechos se dio origen a la vida autoconsciente que nos permite preguntarnos del cómo y del por qué de todas las cosas que podemos observar y, también, de las que intuimos que están ahí sin que se dejen ver.
Claro que, cuando nos adentramos en ese minúsculo “mundo” de lo muy pequeño, las cosas difieren y se apartan de lo que nos dicta el sentido común que, por otra parte, es posible que sea el menos común de los sentidos. Nos dejamos guiar por lo que observamos, por ese mundo macroscópico que nos rodea y, no somos consciente de ese otro “mundo” que está ahí formando parte del universo y que, de una manera muy importante incide en el mundo de lo grande, sin lo que allí existe, no podría existir lo que existe aquí.
común de los sentidos. Nos dejamos guiar por lo que observamos, por ese mundo macroscópico que nos rodea y, no somos consciente de ese otro “mundo” que está ahí formando parte del universo y que, de una manera muy importante incide en el mundo de lo grande, sin lo que allí existe, no podría existir lo que existe aquí.
Interacciones en la naturaleza
Albert Einstein habría dicho que “es más importante la imaginación que el conocimiento”, el filósofo Nelson Goodman ha dicho que “las formas y las leyes de nuestros mundos no se encuentran ahí, ante nosotros, listas para ser descubiertas, sino que vienen impuestas por las versiones-del-mundo que nosotros inventamos – ya sea en las ciencias, en las artes, en la percepción y en la práctica cotidiana-.”
ser descubiertas, sino que vienen impuestas por las versiones-del-mundo que nosotros inventamos – ya sea en las ciencias, en las artes, en la percepción y en la práctica cotidiana-.”
Sin embargo yo, humilde pensador, me decanto por el hecho cierto de que, nuestra especie, siempre llegó al conocimiento a través de la imaginación y la experiencia primero, a la que más tarde, acompañó largas secciones de estudio y muchas horas de mediatación y, al final de todo eso, llego la experimentación que hizo posible llegar a lugarés ignotos que antes nunca, habían podido ser visitados. De todo ello, pudieron surgir todos esos “nuevos mundos” que, como la Mecanica Cuántica y la Relatividad, nos describían el propio mundo que antes nos era desconocido.
nos era desconocido.
Cuando comencé éste trabajo sólo quería dar una simple explicación de los bosones y su intervención en el mundo de lo muy pequeño pero…

Demócrito de Abdera
No estaría mal echar una mirada hacia atrás en el tiempo y recordar, en este momento, a Demócrito que, con sus postulados, de alguna manera venía a echar un poco de luz sobre el asunto, dado que él decía que para determinar si algo era un á-tomo habría que ver si era indivisible. En el modelo de los quarks, el protón, en realidad, un conglomerado pegajoso de tres quarks que se mueven rápidamente. Pero como esos quarks están siempre ineludiblemente encadenados los unos a los otros, experimentalmente el protón aparece indivisible.
Acordémonos aquí de que Boscovich decía que, una partícula elemental, o un “á-tomo”, tiene que ser puntual. Y, desde luego, esa prueba , no la pasaba el protón. El equipo del MIT y el SLAC, con la asesoría de Feynman y Bjorken, cayó en la cuenta de que en este caso el criterio operativo era el de los “puntos” y no el de la indivisibilidad. La traducción de sus datos
, no la pasaba el protón. El equipo del MIT y el SLAC, con la asesoría de Feynman y Bjorken, cayó en la cuenta de que en este caso el criterio operativo era el de los “puntos” y no el de la indivisibilidad. La traducción de sus datos a un modelo de constituyentes puntuales requería una sutileza mucho mayor que el experimento de Rutherford.
a un modelo de constituyentes puntuales requería una sutileza mucho mayor que el experimento de Rutherford.
Precisamente por eso era tan conveniente fue tan conveniente para Richard Edward Taylor y su equipo, tener a dos de los mejores teóricos del mundo en el equipo aportando su ingenio, agudeza e intuición en todas las fases del proceso experimental. El resultado fue que los datos indicaron, efectivamente, la presencia de objetos puntuales en movimiento dentro del protón.
indicaron, efectivamente, la presencia de objetos puntuales en movimiento dentro del protón.
En 1990 Taylor, Friedman y Kendall recogieron su premio Nobel por haber establecido la realidad de los quarks. Sin embargo, a mí lo que siempre me ha llamado más la atención es el hecho cierto de que, este descubrimiento como otros muchos (el caso del positrón de Dirac, por ejemplo), han sido posible gracias al ingenio de los teóricos que han sabido vislumbrar cómo era en realidad la Naturaleza.
posible gracias al ingenio de los teóricos que han sabido vislumbrar cómo era en realidad la Naturaleza.
A todo esto, una buena pregunta sería: ¿Cómo pudieron ver este tipo de partículas de tamaño infinitesimal, si los quarks no están libres y están confinados -en este caso- dentro del protón? Hoy, la respuesta
sería: ¿Cómo pudieron ver este tipo de partículas de tamaño infinitesimal, si los quarks no están libres y están confinados -en este caso- dentro del protón? Hoy, la respuesta tiene poco misterio sabiendo lo que sabemos y hasta donde hemos llegado con el LHC que, con sus inmensas energías “desmenuza” un protón hasta dejar desnudos sus más íntimos secretos.
tiene poco misterio sabiendo lo que sabemos y hasta donde hemos llegado con el LHC que, con sus inmensas energías “desmenuza” un protón hasta dejar desnudos sus más íntimos secretos.
Este es, el resultado ahora de la colisión de protones en el LHC
Lo cierto es que, en su momento, la teoría de los Quarks hizo muchos conversos, especialmente a medida que los teóricos que escrutaban los datos fueron imbuyendo a los quarks una realidad creciente, conociendo mejor sus propiedades y convirtiendo la incapacidad de ver quarks libres en una virtud. La palabra
fueron imbuyendo a los quarks una realidad creciente, conociendo mejor sus propiedades y convirtiendo la incapacidad de ver quarks libres en una virtud. La palabra de moda en aquellos momentos era “confinamiento”. Los Quarks están confinados permanentemente porque la energía requerida para separarlos aumenta a medida que la distancia entre ellos crece. Esa es, la fuerza nuclear fuerte que está presente dentro del átomo y que se encarga de transmitir los ocho Gluones que mantienen confinados a los Quarks.
de moda en aquellos momentos era “confinamiento”. Los Quarks están confinados permanentemente porque la energía requerida para separarlos aumenta a medida que la distancia entre ellos crece. Esa es, la fuerza nuclear fuerte que está presente dentro del átomo y que se encarga de transmitir los ocho Gluones que mantienen confinados a los Quarks.
Así, cuando el intento de separar a los Quarks es demasiado intenso, la energía se vuelve lo bastante grande para crear un par de quark-anti-quark, y ya tenemos cuatro quarks, o dos mesones. Es como intentar conseguir un cabo de cuerda. Se corta y… ¡ya tenemos dos!
un cabo de cuerda. Se corta y… ¡ya tenemos dos!
¿Cuerdas? Me parece que estoy confundiendo el principal objetivo de este trabajo y, me quiero situar en el tiempo futuro que va, desde los quarks de Gell-Mann hasta las cuerdas de Veneziano y John Schwarz y más tarde Witten. Esto de la Física, a veces te juega malas pasadas y sus complejos caminos te llevan a confundir conceptos y momentos que, en realidad, y de manera individualizada, todos han tenido su propio tiempo y lugar.
¿Cuántas veces no habré pensado, en la posibilidad de tomar el elixir de la sabiduría para poder comprenderlo todo? Sin embargo, esa pócima mágica no existe y, si queremos saber , el único camino que tenemos a nuestro alcance es la observación, el estudio, el experimento… ¡La Ciencia!, que en definitiva, es la única que nos dirá como es, y como se producen los fenómenos que podemos contemplar en la Naturaleza y, si de camino, podemos llegar a saber el por qué de su comportamiento… ¡mucho mejor!
, el único camino que tenemos a nuestro alcance es la observación, el estudio, el experimento… ¡La Ciencia!, que en definitiva, es la única que nos dirá como es, y como se producen los fenómenos que podemos contemplar en la Naturaleza y, si de camino, podemos llegar a saber el por qué de su comportamiento… ¡mucho mejor!
El camino será largo y, a veces, penoso pero… ¡llegaremos!
Nuestra insaciable curiosidad nos llevará lejos en el saber del “mundo”. llegaremos al corazón mismo de la materia para comprobar si allí, como algunos imaginan, habitan las cuerdas vibrantes escondidas tan profundamente que no se dejan ver. Sabremos de muchos mundos habitados y podremos hacer ese primer contacto tantas veces soñado con otros seres que, lejos de nuestro región del Sistema solar, también, de manera independiente y con otros nombres, descubrieron la cuántica y la relatividad. Sabremos al fín qué es la Gravedad y por qué no se dejaba juntar con la cuántica. Podremos realizar maravillas que ahora, aunque nuestra imaginación es grande, ni podemos intuir por no tener la información necesaria que requiere la imaginación.
En fin, como decía Hilbert: ¡”Tenemos que saber, sabremos”!
Emilio Silvera V.
















 Totales: 84.912.152
Totales: 84.912.152 Conectados: 79
Conectados: 79