Sep
22
Buscando la Gravedad-Cuántica
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
Entre los teóricos, el casamiento de la relatividad general y la teoría cuántica es el problema central de la física moderna. A los esfuerzos teóricos que se realizan con ese propósito se les llama “supergravedad”, “súpersimetría”, “supercuerdas” “teoría M” o, en último caso, “teoría de todo o gran teoría unificada”.

Ahí tenemos unas matemáticas exóticas que ponen de punta hasta los pelos de las cejas de algunos de los mejores matemáticos del mundo (¿y Perelman? ¿Por qué nos se ha implicado?). Hablan de 10, 11 y 26 dimensiones, siempre, todas ellas espaciales menos una que es la temporal. Vivimos en cuatro: tres de espacio (este-oeste, norte-sur y arriba-abajo) y una temporal. No podemos, ni sabemos o no es posible instruir, en nuestro cerebro (también tridimensional), ver más dimensiones. Pero llegaron Kaluza y Klein y compactaron, en la longitud de Planck las dimensiones que no podíamos ver. ¡Problema solucionado!
¿Quién puede ir a la longitud de Planck para verlas?

Ni vemos la longitud de Planck ni las dimensiones extra
La puerta de las dimensiones más altas quedó abierta y, a los teóricos, se les regaló una herramienta maravillosa. En el Hiperespacio, todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí si es posible encontrar esa soñada teoría de la Gravedad cuántica.
Así que, los teóricos, se han embarcado a la búsqueda de un objetivo audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos, una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.
¿Dónde radica el problema?

Nuestro universo es tridimensional y no podemos ver otro más allá… ¡si existe!
El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el nuevo acelerador de partículas LHC que con sus 14 TeV no llegaría ni siquiera a vislumbrar esas cuerdas vibrantes de las que tanto se habla.
La verdad es que, la teoría que ahora tenemos, el Modelo Estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías.

Con sus 20 parámetros aleatorios (parece que uno de ellos ha sido hallado -el bosón de Higgs-), el Modelo estándar de la f´çisica de partículas que incluye sólo tres de las interacicones fundamentales -las fuerzas nucleares débil y fuerte y el electromagnetismo-, ha dado un buen resultado y a permitido a los físicos trabajar ampliamente en el conocimiento del mundo, de la Naturaleza, del Universo. Sin embargo, deja muchas preguntas sin contestar y, lo cierto es que, se necesitan nuevas maneras, nuevas formas, nuevas teorías que nos lleven más allá.
¡Necesitamos algo más avanzado!
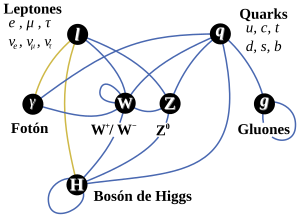
Se ha dicho que la función de la partícula de Higgs es la de dar masa a las partículas que conocemos y están incluidas en el Modelo estándar, se nos ha dicho que ha sido encontrada pero, nada se ha dicho de cómo ésta partícula transmite la masa a las demás. Faltan algunas explicaciones.
El secreto de todo radica en conseguir la simplicidad: el átomo resulto ser complejo lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones, resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún, los quarks que estaban instalados en nubes de otras partículas llamadas gluones y, ahora, queremos continuar profundizando, sospechamos, que después de los quarks puede haber algo más.
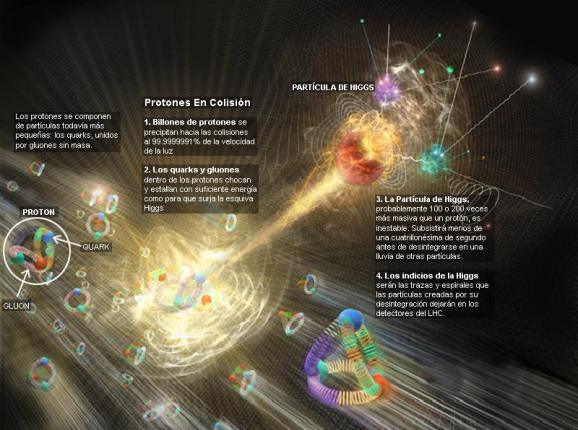
¿Acaso las partículas circulan por el campo de Higgs y se ven frenadas por éste que les adosa la masa?
Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes. Es decir, que si miramos a las estrellas en una noche clara estamos mirando el campo de Higgs. Las partículas influidas por este campo, toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado, del campo gravitatorio o del electromagnético. Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquiriría energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra.

Como E=mc2, ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del Sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein. La masa, m, tiene en realidad dos partes. Una es la masa en reposo, m0, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c) o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.
Pero la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas.
Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs.

La influencia de Higgs en las masas de los quarks y de los leptones, nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.
Hasta ahora no tenemos ni idea de que reglas controlan los incrementos de masa generados por el Higgs (de ahí la expectación creada cuando se estrenó el nuevo acelerador de partículas LHC). Pero el problema es irritante: ¿por qué sólo esas masas –Las masas de los W+, W–, y Zº, y el up, el down, el encanto, el extraño, el top y el bottom, así como los leptones – que no forman ningún patrón obvio? Y, desde luego, aunque hace algún tiempo que nos dijeron que la tal partícula de Higgs había sido encontrada, no nos han explicado muchas cosas más que faltan en esa fiesta para que la podamos celebrar.

No dejamos de experimentar para saber ccómo es nuestro mundo, la Naturaleza, el Universo que nos acoge
Las masas van de la del electrón 0’0005 GeV, a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnéticas y débiles. En la unidad hay cuatro partículas mensajeras sin masa –los W+, W–, Zº y fotón que llevan la fuerza electrodébil. Además está el campo de Higgs, y, rápidamente, los W y Z chupan la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos) y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen los teóricos. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa. Claro que nadie ha explicado cómo lo hace.
Las masas de los W y el Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil. Y las relajadas sonrisas de los físicos teóricos nos recuerdan que Gerard ^t Hooft y Veltman dejaron sentado que la teoría entera esta libre de infinitos.

En esta última dirección ha publicado numerosos libros y artículos, donde aborda la asignatura pendiente de la unificación de la mecánica cuántica y la teoría del campo gravitatorio. El camino que ha seguido Penrose es encontrar una base común a ambas.
Para ello ha introducido dos modelos: los “spin networks” y los “twistors”, el primero discreto, con una métrica intrínseca, no relativista, previo al concepto de espacio, el segundo continuo, con una métrica extrínseca, relativista e inmerso en un espacio-tiempo dado.
Claro que son varias las corrientes que quieren abrirse camino hacia otras físicas nuevas.

Cuando no sabemos de qué estamos hablando, lo representamos de cualquier manera y, no siempre acertamos
La teoría de supercuerdas tiene tantas sorpresas fantásticas que cualquiera que investigue en el tema reconoce que está llena de magia. Es algo que funciona con tanta belleza… Cuando cosas que no encajan juntas e incluso se repelen, si se acerca la una a la otra alguien es capaz de formular un camino mediante el cual, no sólo no se rechazan, sino que encajan a la perfección dentro de ese sistema, como ocurre ahora con la teoría M que acoge con naturalidad la teoría de la relatividad general y la teoría mecánico-cuántica; ahí, cuando eso se produce, está presente la belleza.
Lo que hace que la teoría de supercuerdas sea tan interesante es que el marco estándar mediante el cual conocemos la mayor parte de la física es la teoría cuántica y resulta que ella hace imposible la gravedad. La relatividad general de Einstein, que es el modelo de la gravedad, no funciona con la teoría cuántica. Sin embargo, las supercuerdas modifican la teoría cuántica estándar de tal manera que la gravedad no sólo se convierte en posible, sino que forma parte natural del sistema; es inevitable para que éste sea completo.
¿Por qué es tan importante encajar la gravedad y la teoría cuántica? Porque no podemos admitir una teoría que explique las fuerzas de la naturaleza y deje fuera a una de esas fuerzas. Así ocurre con el Modelo Estándar que deja aparte y no incluye a la fuerza gravitatoria que está ahí, en la Naturaleza.
La teoría de supercuerdas se perfila como la teoría que tiene implicaciones si tratamos con las cosas muy pequeñas, en el microcosmos; toda la teoría de partículas elementales cambia con las supercuerdas que penetra mucho más; llega mucho más allá de lo que ahora es posible.

La topología es, el estudio de aquellas propiedades de los cuerpos geométricos que permanecen inalteradas por transformaciones continuas. La topología es probablemente la más joven de las ramas clásicas de las matemáticas. En contraste con el álgebra, la geometría y la teoría de los números, cuyas genealogías datan de tiempos antiguos, la topología aparece en el siglo diecisiete, con el nombre de analysis situs, ésto es, análisis de la posición.
De manera informal, la topología se ocupa de aquellas propiedades de las figuras que permanecen invariantes, cuando dichas figuras son plegadas, dilatadas, contraídas o deformadas, de modo que no aparezcan nuevos puntos, o se hagan coincidir puntos diferentes. La transformación permitida presupone, en otras palabras, que hay una correspondencia biunívoca entre los puntos de la figura original y los de la transformada, y que la deformación hace corresponder puntos próximos a puntos próximos. Esta última propiedad se llama continuidad, y lo que se requiere es que la transformación y su inversa sean ambas continuas: así, trabajarnos con homeomorfismos.

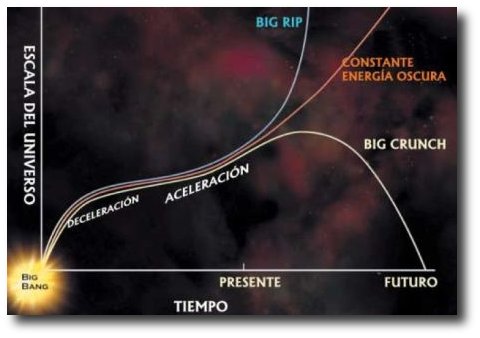
En cuanto a nuestra comprensión del universo a gran escala (galaxias, el Big Bang…), creo que afectará a nuestra idea presente, al esquema que hoy rige y, como la nueva teoría, el horizonte se ampliará enormemente; el cosmos se presentará ante nosotros como un todo, con un comienzo muy bien definido y un final muy bien determinado.
Para cuando eso llegue, sabremos lo que es, como se genera y dónde están situados los orígenes de esa “fuerza”, “materia”, o, “energía” que ahora no sabemos ver para explicar el movimiento de las galaxias o la expansión del espacio mismo.
emilio silvera
Sep
21
De la vida y la muerte de las partículas y…otros
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
Por aquel tiempo pudimos leer en la prensa de todo el mundo: ESTOCOLMO, Suecia.- El premio Nobel de Física (2.008) fue atribuido hoy al norteamericano Yoichiro Nambu y a los japoneses Makoto Kobayashi y Toshihide Maskawa por sus trabajos separados sobre la física de las partículas que mejoraron la comprensión de la materia, Demos un repaso hoy aquí a esos componentes de la materia, y, profundicemos en sus propiedades., en sus “vidas”.

Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida media, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.

También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.
Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, ksi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales manera de desintegración, veríamos como difieren las unas de las otras.
| Quarks | Antiquarks | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Nombre | Símbolo[1] | Generación | Carga eléctrica (e) |
Masa en reposo (MeV/c²) |
Nombre | Símbolo | Generación | Carga eléctrica (e) |
Masa en reposo (MeV/c²) |
| Arriba | 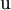 |
Primera | 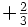 |
— | Antiarriba | 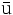 |
Primera | 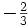 |
— |
| Abajo |  |
Primera | 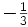 |
— | Antiabajo | 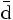 |
Primera |  |
— |
| Encanto |  |
Segunda | 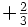 |
— | Antiencanto | 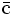 |
Segunda | 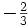 |
— |
| Extraño | 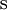 |
Segunda | 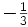 |
— | Antiextraño | 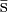 |
Segunda |  |
— |
| Cima | 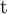 |
Tercera | 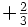 |
— | Anticima | 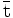 |
Tercera | 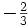 |
— |
| Fondo | 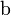 |
Tercera | 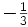 |
— | Antifondo | 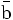 |
Tercera |  |
— |
- Las iniciales de los símbolos los toma del inglés: u: up, arriba; d: down, abajo; c: charmed, encantado; s: strange, extraño; t: top, alto, superior, cima; b: bottom bajo, fondo.
Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.

Todas las partículas elementales vistas hasta ahora en esta serie, incluido el neutrino. Claro que, aquí no está todavía el Bosón de Higgs que será confirmado en breve…al parecer. Esas son las últimas noticias, el Bosón de Higgs está “casi” localizado y sólo está a la espera de confirmar el hallazgo no una, sino miles de veces.
 |
| The CMS detector.Image © CERN |
 |
| The ATLAS detector. Image © CERN |
Por fin, los físicos empiezan a recoger los frutos de una búsqueda que dura ya casi cincuenta años. Dos de los principales detectores del LHC, el gran acelerador europeo de partículas (el Atlas y el muones“>CMS) han encontrado señales que podrían delatar la presencia del esquivo Higgs“>bosón de Higgs, la última particula subatómica que queda por descubrir para completar el Modelo Estandar de la Física y la que encierra, además, el secreto de por qué las demás partículas tienen masa.
Pero sigamos. ¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

Una colisión entre un prtón y un antiprotón registrada mediante una cámara de chispas del experimento UA5 del CERN.
Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.
| Leptones cargados | Neutrinos | |||||||
|---|---|---|---|---|---|---|---|---|
| Nombre | Símbolo | Carga | Masa en reposo | Nombre | Símbolo | Carga | Masa en reposo | |
| 1ª generación | Electrón | 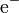 |
−1 | 0,511 |  |
0 | < 3·10−6 | |
| Positrón | 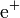 |
+1 | Neutrino electrónico |
 |
0 | |||
| 2ª generación | Muón | 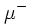 |
−1 | 105,658 | Neutrino muónico | 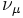 |
0 | < 0,19 |
| Antimuón |  |
+1 | Antineutrino muónico | 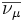 |
0 | |||
| 3ª generación | Tauón |  |
−1 | 1776,99 | Neutrino tauónico |  |
0 | < 18,2 |
| Antitauón |  |
+1 | Antineutrino tauónico | 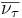 |
0 | |||
En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su carta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas, Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.

Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.
Bariones
| Partícula | Símbolo[1] | Quarks[2] | Spin | Masa en reposo (MeV/c²) |
S | C | B | Vida media (s) |
Desintegraciones más importantes |
|---|---|---|---|---|---|---|---|---|---|
| Protón | 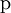 |
 |
 |
938,27 | 0 | 0 | 0 | Estable [3] | — |
| Neutrón |  |
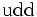 |
 |
939,56 | 0 | 0 | 0 | 885,7 [4] |  |
| Delta doble positiva | 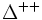 |
 |
 |
≈1.232 | 0 | 0 | 0 | 6·10-24 | 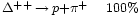 |
| Delta positiva |  |
 |
 |
≈1.232 | 0 | 0 | 0 | 6·10-24 | 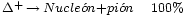 |
| Delta neutra | 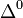 |
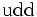 |
 |
≈1.232 | 0 | 0 | 0 | 6·10-24 |  |
| Delta negativa |  |
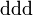 |
 |
≈1.232 | 0 | 0 | 0 | 6·10-24 |  |
| Lambda neutra |  |
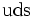 |
 |
1.115,68 | −1 | 0 | 0 | 2,63·10-10 |  |
| Sigma positiva | 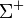 |
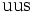 |
 |
1.189,37 | −1 | 0 | 0 | 8,01·10-11 |  |
| Sigma neutra |  |
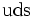 |
 |
1.192,64 | −1 | 0 | 0 | 7,4·10-20 |  |
| Sigma negativa | 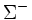 |
 |
 |
1.197,45 | −1 | 0 | 0 | 1,48·10-10 | 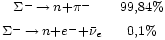 |
| Xi neutra | 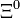 |
 |
 |
1.314,83 | −2 | 0 | 0 | 2,90·10-10 | 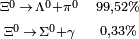 |
| Xi negativa | 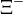 |
 |
 |
1.321,31 | −2 | 0 | 0 | 1,64·10-10 | 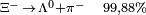 |
| Omega |  |
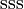 |
 |
1.672,45 | −3 | 0 | 0 | 8,21·10-11 | 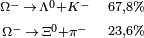 |
| Omega encantada |  |
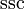 |
 |
2.697,5 | −2 | +1 | 0 | 6,90·10-14 |  |
| Xi positiva encantada | 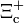 |
 |
 |
2.468 | −1 | +1 | 0 | 4,42·10-13 |  |
| Xi neutra encantada | 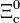 |
 |
 |
2.471 | −1 | +1 | 0 | 1,12·10-13 |  |
| Lambda encantada | 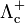 |
 |
 |
2.284,9 | 0 | +1 | 0 | 2,00·10-13 |  |
| Xi doble encantada | 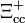 |
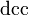 |
 |
3.519 | 0 | +2 | 0 | <3,30·10-14 | — |
| Lambda inferior |  |
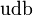 |
 |
5.624 | 0 | 0 | −1 | 1,23·10-12 | 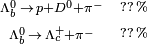 |
- [1] El símbolo de los antibariones es el mismo pero con una barra superpuesta.
- [2] Los antibariones están formados por los respectivos antiquarks.
- [3] Debe ser superior a 1030 años.
- [4] Vida media de los neutrones libres. En los núcleos atómicos son estables.
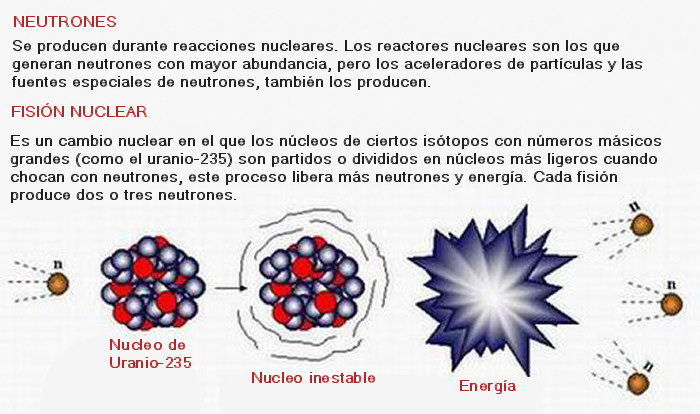
- Se ha conseguido observar por primera vez la desintegración radiactiva del neutrón. Dentro de los núcleos de los átomos hay neutrones y protones. En condiciones normales y mientras que están ahí los neutrones son estables. Sin embargo los neutrones libres son inestables, tienen una vida media de unos 10 minutos, y se desintegran produciendo un protón un electrón y un antineutrino. Pero los físicos nucleares teóricos predijeron que una de cada mil veces los neutrones decaerían en todas esas partículas y además en un fotón.
Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.
Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.
Bosones
| Nombre | Símbolo | Carga eléctrica (e) |
Carga de color | Spin | Masa en reposo (GeV/c²) |
Existencia | Vida media | Desintegraciones más importantes |
|---|---|---|---|---|---|---|---|---|
| Fotón |  |
Neutra | Neutra | 1 | Nula | Confirmada | Estable | — |
| Bosón W | 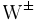 |
± 1 | Neutra | 1 | 80,425 | Confirmada | 3·10-25 |  [1] [1] |
| Bosón Z |  |
Neutra | Neutra | 1 | 91,187 | Confirmada | 3·10-25 | — |
| Gluón |  |
Neutra | Color + Anticolor | 1 | Nula | Confirmada | Estable | — |
| Gravitón |  |
Neutra | Neutra | 2 | Nula | Hipotética | Estable | — |
| Higgs“>Bosón de Higgs |  |
Neutra | Neutra | 0 | > 114 | Hipotética | Inestable |  |
Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”
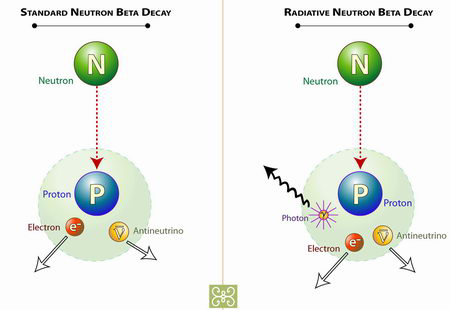
Típicamente el neutrón decae en un protón, un antineutrino y un electrón. Muy raramente lo hace radiativamente emitiendo además un fotón. Diagrama: Zina Deretsky, National Science Foundation. Fue difícil observar los fotones porque el haz está contaminado con fotones que fondo que producen mucho “ruido” en las medidas, por lo que era como buscar una aguja en un pajar. El decaimiento radiativo del neutrón es importante porque conecta directamente con el modelo estándar de partículas.
Si la vida de una partícula es tan corta como 10ˉ²³ segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.
Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.
Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).

En el Universo existen muchas clases de resonancias…inesperadas
Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.
Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:
∆⁺⁺→р + π⁺; ∆⁰→р + πˉ; o п+π⁰
En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.

El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (materia), es aún limitado. Los cuadros que aparecen arriba, están referidos a las partículas más usuales como los Quarks y los Leptones (verdaderos componentes de la materia) que a su vez, son: Los Quarks los que forman a los Hadrones y los Leptones los que completan el núcleo atómico de la materia para conformar los átomos. He dejado a los mesones y a las supuestas partículas supersimétricas centrándome en las que me parecen principales en la conformación de la materia.
emilio silvera
Sep
7
La vida de las partículas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)
La Mente: Ese misterio

La mente humana es tan compleja que no todos ante la misma cosa vemos lo mismo. Nos enseñan figuras y dibujos y nos piden que digamos (sin pensarlo) la primera cosa que nos sugiere. De entre diez personas, sólo coinciden tres, los otros siete divergen en la apreciación de lo que el dibujo o la figura les sugiere. Un paisaje puede ser descrito de muy distintas maneras según quién lo pueda contar.

Solo el 1% de las formas de vida que han vivido en la Tierra están ahora presentes, el 99%, por una u otra razón se han extinguido. Sin embargo, ese pequeño tanto por ciento de la vida actual, supone unos cinco millones de especies según algunas estimaciones. La Tierra acoge a todas esas especies u palpita de vida que prolifera por doquier. Hay seres vivos por todas partes y por todos los rincones del inmenso mosaico de ambientes que constituye nuestro planeta encontramos formas de vida, cuyos diseños parecen hechos a propósito para adaptarse a su hábitat, desde las profundidades abisales de los océanos hasta las más altas cumbres, desde las espesas selvas tropicales a las planicies de hielo de los casquetes polares. Se ha estimado la edad de 3.800 millones de años desde que aparecieron los primeros “seres vivos” sobre el planeta (dato de los primeros microfósiles). Desde entonces no han dejado de aparecer más y más especies, de las que la mayoría se han ido extinguiendo. Desde el siglo XVIII en que Carlos Linneo propuso su Systema Naturae no han cesado los intentos por conocer la Biodiversidad…, de la que por cierto nuestra especie, bautizada como Homo sapiens por el propio Linneo, es una recién llegada de apenas 200.000 años.

Ahora, hablaremos de la vida media de las partículas elementales (algunas no tanto). Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida media, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.
También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.

Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, psi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales maneras de desintegración, veríamos como difieren las unas de las otras.

Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.
¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.

Una colisión entre un prtón y un antiprotón registrada mediante una cámara de chispas del experimento UA5 del CERN.
En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su carta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas, Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.
Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.

Se habla de ondas cuánticas y también, de ondas gravitacionales. Las primeras han sido localizadas y las segundas están siendo perseguidas.
Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.

Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.
Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”

Si la vida de una partícula es tan corta como 10ˉ²³ segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.

Bariones Delta. Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.
Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).
Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.
Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:
∆⁺⁺→р + π⁺; ∆⁰→р + πˉ; o п+π⁰
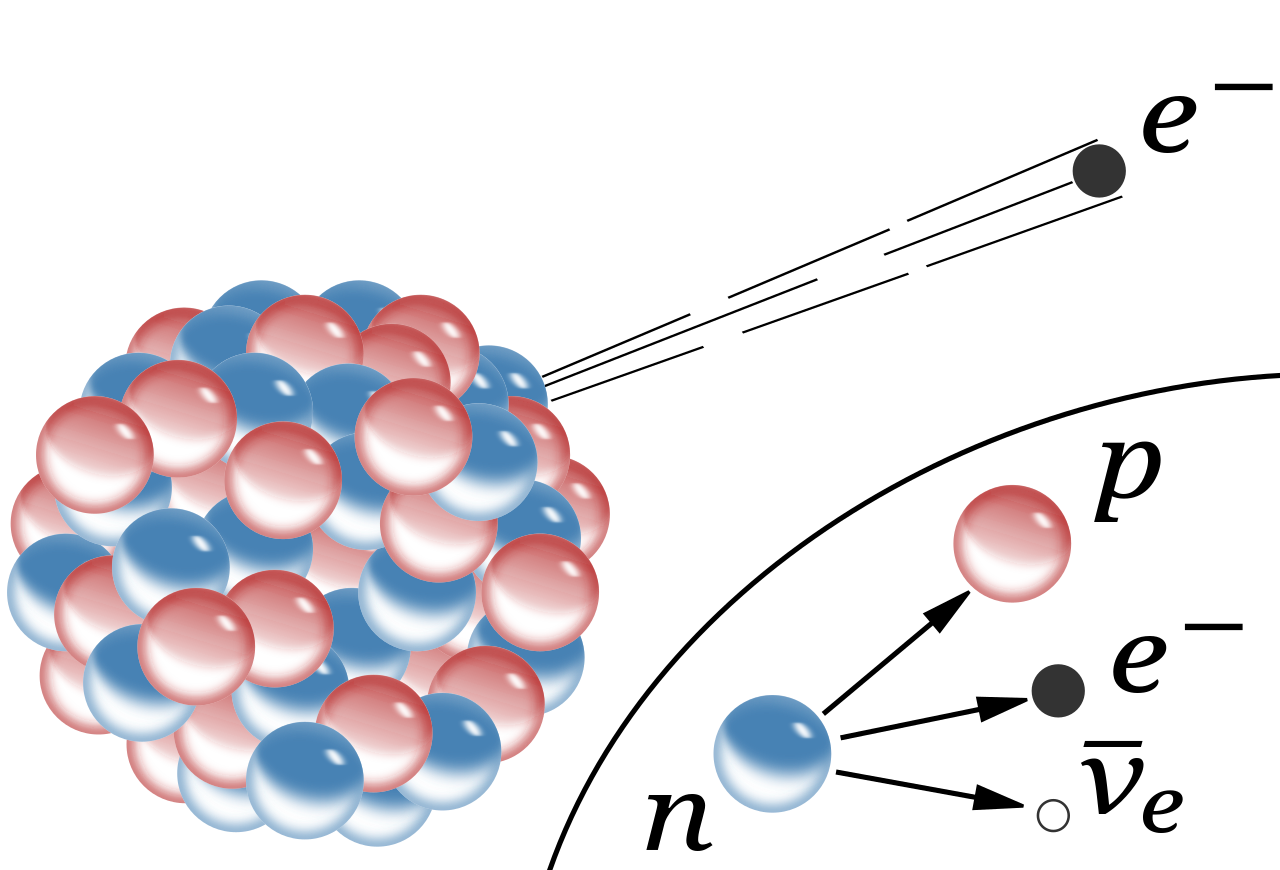
En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.
El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (aunque nos parezca lo contrario), son aún bastante limitados, nos queda mucho por descubrir antes de que podamos decir que dominamos la materia y sabemos de todos sus componentes. Antes de que eso llegue, tendremos que conocer, en profundidad, el verdadero origen de la Luz que esconde muchos secretos que tendremos que desvelar.
Esperemos que con los futuros experimentos del LHC y de los grandes Aceleradores de partículas del futuro, se nos aclaren algo las cosas y podamos avanzar en el perfeccionamiento del Modelo Estándar de la Física de Partículas que, como todos sabemos es un Modelo incompleto que no contiene a todas las fuerzas de la Naturaleza y, cerca de una veintena de sus parámetros son aleatorios y no han sido explicados. Uno de ellos, el Bosón de Higgs, dicen que ha sido encontrado. Sin embargo, a mí particularmente me quedan muchas dudas al respecto.
emilio silvera
Ago
24
¿Dos verdades incompatibles? La Cuántica y la Relatividad
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (2)
Comments (2)

El mundo de la Física tiene planteado un gran problema y los físicos son muy conscientes de ello, conocen su existencia desde hace décadas. El problema es el siguiente:

Existen dos pilares fundamentales en los cuales se apoya toda la física moderna. Uno es la relatividad general de Albert Einstein, que nos proporciona el marco teórico para la comprensión del universo a una escala máxima: estrellas, galaxias, cúmulos (o clusters) de galaxias, y aún más allá, hasta la inmensa expansión del propio universo.
El otro pilar es la mecánica cuántica, que en un primer momento vislumbro Max Planck y posteriormente fue desarrollada por el mismo Einstein, W. Heisemberg, Schrödinger, Dirac, Feynman, Niels Bohr y otros, que nos ofrece un marco teórico para comprender el universo en su escala mínima: moléculas, átomos, y así hasta las partículas subatómicas, como los electrones y quarks.

Durante años de investigación, los físicos han confirmado experimentalmente, con una exactitud casi inimaginable, la practica totalidad de las predicciones que hacen las dos teorías. Sin embargo, estos mismos instrumentos teóricos nos llevan a una conclusión inquietante: tal como se formulan actualmente, la relatividad general y la mecánica cuántica no pueden ser ambas ciertas a la vez.
Nos encontramos con que las dos teorías en las que se basan los enormes avances realizados por la física durante el último siglo (avances que han explicado la expansión de los cielos y la estructura fundamental de la materia) son mutuamente incompatibles. Cuando se juntan ambas teorías, aunque la formulación propuesta parezca lógica, aquello explota; la respuesta es un sinsentido que nos arroja un sin fin de infinitos a la cara.

Así que si tú, lector, no has oído nunca previamente hablar de este feroz antagonismo, te puedes preguntar a que será debido. No es tan difícil encontrar la respuesta. Salvo en algunos casos muy especiales, los físicos estudian cosas que son o bien pequeñas y ligeras (como los átomos y sus partes constituyentes), o cosas que son enormes y pesadas (como estrellas de neutrones y agujeros negros), pero no ambas al mismo tiempo. Esto significa que sólo necesitan utilizar la mecánica cuántica, o la relatividad general, y pueden minimizar el problema que se crea cuando las acercan demasiado; las dos teorías no pueden estar juntas. Durante más de medio siglo, este planteamiento no ha sido tan feliz como la ignorancia, pero ha estado muy cerca de serlo.

No obstante, el universo puede ser un caso extremo. En las profundidades centrales de un agujero negro se aplasta una descomunal masa hasta reducirse a un tamaño minúsculo. En el momento del Bing Bang, la totalidad del universo salió de la explosión de una bolita microscópica cuyo tamaño hace que un grano de arena parezca gigantesco. Estos contextos son diminutos y, sin embargo, tienen una masa increíblemente grande, por lo que necesitan basarse tanto en la mecánica cuántica como en la relatividad general.
Por ciertas razones, las fórmulas de la relatividad general y las de la mecánica cuántica, cuando se combinan, empiezan a agitarse, a traquetear y a tener escapes de vapor como el motor de un viejo automóvil. O dicho de manera menos figurativa, hay en la física preguntas muy bien planteadas que ocasionan esas respuestas sin sentido, a que me referí antes, a partir de la desafortunada amalgama de las ecuaciones de las dos teorías.

Siempre hemos querido saber qué pasa dentro de un Agujero Negro. Sin embargo, nadie entró nunca y regresó para poder contarlo. Según todos los indicios, lo que pueda caer dentro del agujero negro, una vez pasado el límite de irás y no volverás del horizonte de sucesos, quedará allí “triturado” hasta densidades inimaginables. No sabemos qué clase de materia es la que pueda confiormar una singularidad y qué es lo que pasa con las partículas de materia que allí pudieron llegar atraídas por la inmensa fuerza gravitatoria que el A.N. genera.
Aunque se desee mantener el profundo interior de un agujero negro y el surgimiento inicial del universo envueltos en el misterio, no se puede evitar sentir que la hostilidad entre la mecánica cuántica y la relatividad general está clamando por un nivel más profundo de comprensión.
¿Puede ser creíble que para conocer el universo en su conjunto tengamos que dividirlo en dos y conocer cada parte por separado? Las cosas grandes una ley, las cosas pequeñas otra.
No creo que eso pueda ser así. Mi opinión es que aún no hemos encontrado la llave que abre la puerta de una teoría cuántica de la gravedad, es decir, una teoría que unifique de una vez por todas las dos teorías más importantes de la física: mecánica cuántica + relatividad general.

La teoría de supercuerdas ha venido a darme la razón. Los intensos trabajos de investigación llevada a cabo durante las últimas décadas demuestran que puede ser posible la unificación de las dos teorías cuántica y relativista a través de nuevas y profundas matemáticas topológicas que han tomado la dirección de nuevos planteamientos más avanzados y modernos, que pueden explicar la materia en su nivel básico para resolver la tensión existente entre las dos teorías.
En esta nueva teoría de supercuerdas se trabaja en 10, 11 ó en 26 dimensiones, se amplía el espacio ahora muy reducido y se consigue con ello, no sólo el hecho de que la mecánica cuántica y la relatividad general no se rechacen, sino que por el contrario, se necesitan la una a la otra para que esta nueva teoría tenga sentido. Según la teoría de supercuerdas, el matrimonio de las leyes de lo muy grande y las leyes de lo muy pequeño no sólo es feliz, sino inevitable.

Esto es sólo una parte de las buenas noticias, porque además, la teoría de las supercuerdas (abreviando teoría de cuerdas) hace que esta unión avance dando un paso de gigante. Durante 30 años, Einstein se dedicó por entero a buscar esta teoría de unificación de las dos teorías, no lo consiguió y murió en el empeño; la explicación de su fracaso reside en que en aquel tiempo, las matemáticas de la teoría de supercuerdas eran aún desconocidas. Sin embargo, hay una curiosa coincidencia en todo esto, me explico:
Cuando los físicos trabajan con las matemáticas de la nueva teoría de supercuerdas, Einstein, sin que nadie le llame, allí aparece y se hace presente por medio de las ecuaciones de campo de la relatividad general que, como por arte de magia, surgen de la nada y se hacen presentes en la nueva teoría que todo lo unifica y también todo lo explica; posee el poder demostrar que todos los sorprendentes sucesos que se producen en nuestro universo (desde la frenética danza de una partícula subatómica que se llama quark hasta el majestuoso baile de las galaxias o de las estrellas binarias bailando un valls, la bola de fuego del Big Bang y los agujeros negros) todo está comprendido dentro de un gran principio físico en una ecuación magistral.

Esta nueva teoría requiere conceptos nuevos y matemáticas muy avanzados y nos exige cambiar nuestra manera actual de entender el espacio, el tiempo y la materia. Llevará cierto tiempo adaptarse a ella hasta instalarnos en un nivel en el que resulte cómodo su manejo y su entendimiento. No obstante, vista en su propio contexto, la teoría de cuerdas emerge como un producto impresionante pero natural, a partir de los descubrimientos revolucionarios que se han realizado en la física del último siglo. De hecho, gracias a esta nueva y magnifica teoría, veremos que el conflicto a que antes me refería existente entre la mecánica cuántica y la relatividad general no es realmente el primero, sino el tercero de una serie de conflictos decisivos con los que se tuvieron que enfrentar los científicos durante el siglo pasado, y que fueron resueltos como consecuencia de una revisión radical de nuestra manera de entender el universo.
El primero de estos conceptos conflictivos, que ya se había detectado nada menos que a finales del siglo XIX, está referido a las desconcertantes propiedades del movimiento de la luz.

Isaac Newton y sus leyes del movimiento nos decía que si alguien pudiera correr a una velocidad suficientemente rápida podría emparejarse con un rayo de luz que se esté emitiendo, y las leyes del electromagnetismo de Maxwell decían que esto era totalmente imposible. Einstein, en 1.905, vino a solucionar el problema con su teoría de la relatividad especial y a partir de ahí le dio un vuelco completo a nuestro modo de entender el espacio y el tiempo que, según esta teoría, no se pueden considerar separadamente y como conceptos fijos e inamovibles para todos, sino que por el contrario, el espacio-tiempo era una estructura maleable cuya forma y modo de presentarse dependían del estado de movimiento del observador que lo esté midiendo.
El escenario creado por el desarrollo de la relatividad especial construyó inmediatamente el escenario para el segundo conflicto. Una de las conclusiones de Einstein es que ningún objeto (de hecho, ninguna influencia o perturbación de ninguna clase) puede viajar a una velocidad superior a la de la luz. Einstein amplió su teoría en 1915 – relatividad general – y perfeccionó la teoría de la gravitación de Newton, ofreciendo un nuevo concepto de la gravedad que estaba producida por la presencia de grandes masas, tales como planetas o estrellas, que curvaban el espacio y distorsionaban el tiempo. También la Luz acusa los efectos gravitatorios.

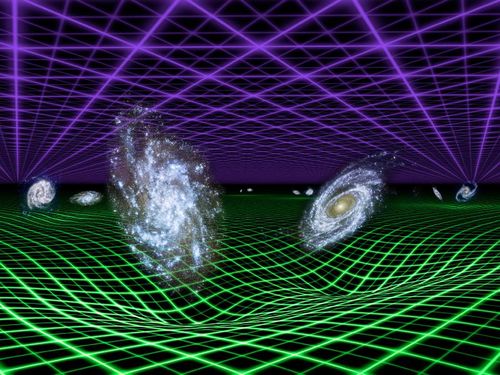
Tales distorsiones en la estructura del espacio y el tiempo transmiten la fuerza de la gravedad de un lugar a otro. La luna no se escapa y se mantiene ahí, a 400.000 Km de distancia de la Tierra, porque está influenciada por la fuerza de gravedad que ambos objetos crean y los mantiene unidos por esa cuerda invisible que tira de la una hacia la otra y viceversa. Igualmente ocurre con el Sol y la Tierra que, separados por 150 millones de kilómetros, están influidos por esa fuerza gravitatoria que hace girar a la Tierra (y a los demás planetas del Sistema Solar) alrededor del Sol.
Así las cosas, no podemos ya pensar que el espacio y el tiempo sean un telón de fondo inerte en el que se desarrollan los sucesos del universo, al contrario; según la relatividad especial y la relatividad general, son actores que desempeñan un papel íntimamente ligado al desarrollo de los sucesos.

En el “universo” infinitesimal de las partículas ocurren cosas muy extrañas que no vemos en la vida cotidiana
El descubrimiento de la relatividad general, aunque resuelve un conflicto, nos lleva a otro. Durante tres décadas desde 1.900, en que Max Planck publicó su trabajo sobre la absorción o emisión de energía de manera discontinua y mediante paquetes discretos a los que él llamo cuantos, los físicos desarrollaron la mecánica cuántica en respuesta a varios problemas evidentes que se pusieron de manifiesto cuando los conceptos de la física del siglo XIX se aplicaron al mundo microscópico. Así que el tercer conflicto estaba servido, la incompatibilidad manifiesta entre relatividad general y mecánica cuántica.
La forma geométrica ligeramente curvada del espacio que aparece a partir de la relatividad general, es incompatible con el comportamiento microscópico irritante y frenético del universo que se deduce de la mecánica cuántica, lo cual era sin duda alguna el problema central de la física moderna.
Las dos grandes teorías de la física, la relatividad general y la mecánica cuántica, infalibles y perfectas por separado, no funcionaban cuando tratábamos de unirlas resulta algo incomprensible, y, de todo ello podemos deducir que, el problema radica en que debemos saber como desarrolar nuevas teorías que modernicen a las ya existentes que, siendo buenas herramientas, también nos resultan incompletas para lo que, en realidad, necesitamos.
emilio silvera
Ago
12
La Fisica, ¡que maravilla!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

En el mundo de los seres vivos, la escala o tamaño crea importantes diferencias. En muchos aspectos, la anatomía de un ratón es una copia de la de un elefante, pero mientras que un ratón puede trepar por una pared prácticamente vertical sin mucha dificultad (y se puede caer desde una altura varias veces mayor que su propio tamaño sin hacerse daño), un elefante no sería capaz de realizar tal hazaña. Con bastante generalidad se puede afirmar que los efectos de la gravedad son menos importantes cuanto menores sean los objetos que consideremos (sean vivos o inanimados).

Cuando llegamos a los seres unicelulares, se ve que para ellos no hay distinción entre arriba y abajo. Para ellos, la tensión superficial del agua es mucho más importante que la fuerza de la gravedad a esa escala.
La tensión superficial es una consecuencia de que todas las moléculas y los átomos se atraen unos a otros con una fuerza que nosotros llamamos de Van der Waals. Esta fuerza tiene un alcance muy corto; para ser precisos, diremos que la intensidad de esta fuerza a una distancia r es aproximadamente 1/r7. Esto significa que si se reduce la distancia entre dos átomos a la mitad de la fuerza de Van der Waals con la que se atraen uno a otro se hace 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128 veces más intensa. Cuando los átomos y las moléculas se acercan mucho unos a otros quedan unidos muy fuertemente a través de esta fuerza. El conocimiento de esta fuerza se debe a Johannes Diderik Van der Waals (1837 – 1923) con su tesis sobre la continuidad del estado líquido y gaseoso que le haría famoso, ya que en esa época (1873), la existencia de las moléculas y los átomos no estaba completamente aceptado.
La tensión superficial del agua, es el efecto físico (energía de atracción entre las moléculas) que “endurece” la capa superficial del agua en reposo y permite a algunos insectos, como el mosquito y otros desplazarse por la superficie del agua sin hundirse.

El famoso físico inglés James Clerk Maxwell, que formuló la teoría del electromagnetismo de Faraday, quedó muy impresionado por este trabajo de Van der Waals.
Los tamaños de los seres uniceculares, animales y vegetales, se miden en micrómetros o “micras”, donde 1 micra es 1/1.000 de milímetro, aproximadamente el tamaño de los detalles más pequeños que se pueden observar con un microscopio ordinario. El mundo de los microbios es fascinante, pero no es el objeto de este trabajo, y continuaremos el viaje emprendido hacia las partículas elementales que forman núcleos, átomos, células y materia, así como las fuerzas que intervienen en las interacciones fundamentales del universo y que afecta a todo lo que existe.
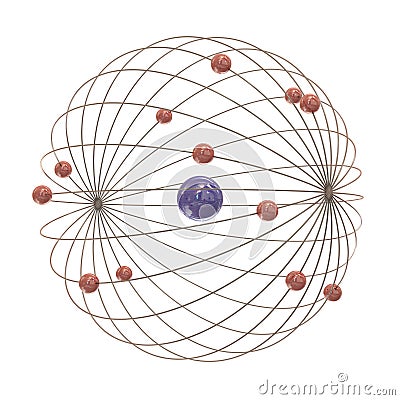
Hemos hablado del electrón que rodea el núcleo, de su carga eléctrica negativa que complementa la positiva de los protones y hace estable al átomo; tiene una masa de solamente 1/1.836 de la del núcleo más ligero (el del hidrógeno). La importancia del electrón es vital en el universo.
Pero busquemos los “cuantos”. La física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menor intensidad, por los objetos más fríos (radiación de cuerpo negro).

Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si utilizamos las leyes de la termodinámica para calcular la intensidad de una radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para menores. Esta longitud de onda característica es inversamente proporcional a la temperatura absoluta de objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273º bajo cero). Cuando a 1.000º C un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.
Radiación de Cuerpo Negro
Un cuerpo negro es un objeto teórico o ideal que absorbe toda la luz y toda la energía radiante que incide sobre él. Nada de la radiación incidente se refleja o pasa a través del cuerpo negro. A pesar de su nombre, el cuerpo negro emite luz y constituye un modelo ideal físico para el estudio de la emisión de radiación electromagnética. El nombre Cuerpo negro fue introducido por Gustav Kirchhoff en 1862.
La luz emitida por un cuerpo negro se denomina radiación de cuerpo negro. Todo cuerpo emite energía en forma de ondas electromagnéticas, siendo esta radiación, que se emite incluso en el vacío, tanto más intensa cuando más elevada es la temperatura del emisor. La energía radiante emitida por un cuerpo a temperatura ambiente es escasa y corresponde a longitudes de onda superiores a las de la luz visible (es decir, de menor frecuencia). Al elevar la temperatura no sólo aumenta la energía emitida sino que lo hace a longitudes de onda más cortas; a esto se debe el cambio de color de un cuerpo cuando se calienta. Los cuerpos no emiten con igual intensidad a todas las frecuencias o longitudes de onda, sino que siguen la ley de Planck.
Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda, y por tanto, proporcional a la frecuencia de radiación emitida. La fórmula es E = hν, donde E es la energía del paquete, ν es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.
Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: él sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck. El príncipe francés Louis-Victor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta región del espacio, y que la frecuencia ν de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilantes de campos de fuerza, pero esto lo veremos más adelante.
El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de de Broglie. Poco después, en 1926, Edwin Schrödinger descubrió cómo escribir la teoría ondulatoria de de Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de ondas cuánticas”.
Está bien comprobado que la mecánica cuántica funciona de maravilla…, pero, sin embargo, surge una pregunta muy formal: ¿qué significan realmente estas ecuaciones?, ¿qué es lo que están describiendo? Cuando Isaac Newton, allá en 1867 formuló cómo debían moverse los planetas alrededor del Sol, estaba claro para todo el mundo qué significaban sus ecuaciones: que los planetas estaban siempre en una posición bien definida des espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades en el tiempo.
Pero para los electrones todo es diferente. Su comportamiento parece estar envuelto en misterio. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?
Niels Bohr consiguió responder a esta pregunta de forma tal que con su explicación se pudo seguir trabajando, y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la interpretación de Copenhague de la mecánica cuántica.

Cosas extrañas están presentes por todas partes. Nosotros estamos invadidos por una ingente cantidad de bacterias a las que no prestamos atención, y, sin embargo, sin ellas nos sería imposible vivir. Hace mucho tiempo ya que hicimos “ese convenio” con ellas y, formamos un binomio que nos permite seguir adelante con la mutua ayuda. ¿Os acordáis del trabajo que puse aquí sobre las mitocondrias?
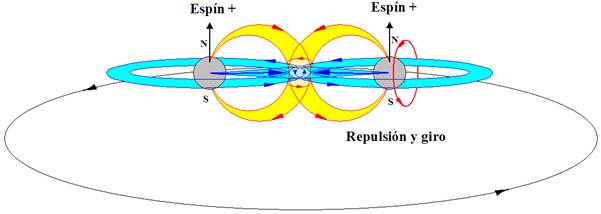
Si la mecánica cuántica tiene cosas extrañas y el espín es una de ellas. Y si uno piensa que la intuición le ayudará a comprender todo esto, pues no lo hará, o es poco probable que lo haga. Las partículas tienen un espín fundamental. Al igual que la carga eléctrica o la masa, el espín ayuda a definir que tipo de partícula es cada una.
Las leyes de la mecánica cuántica han sido establecidas con mucha precisión; permite cómo calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas de manera simultánea. Por ejemplo, podemos determinar la velocidad de una partícula con mucha precisión, pero entonces no sabremos exactamente dónde se encuentra; o a la inversa, podemos determinar la posición con precisión, pero entonces su velocidad queda mal definida. Si una partícula tiene espín (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.
Existe una relación directa entre el espín de una partícula y la estadística que obedece en un sistema colectivo de muchas de ellas. Esta relación, conocida empíricamente, es demostrable en teoría cuántica de campos relativista.
La colisión de un quark (la esfera roja) desde un protón (la esfera naranja) con un gluon (la esfera verde) desde otro protón con espín opuesto. El espín está representado por las flechas azules alrededor de los protones y del quark. Los signos de interrogación azules alrededor del gluon representan la pregunta: ¿Están los gluones polarizados? Las partículas expulsadas de la colisión son una lluvia de quarks y un fotón (la esfera púrpura).

No es fácil explicar de forma sencilla de dónde viene esta incertidumbre, pero existen ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar. Para afinar un instrumento musical se debe escuchar una nota durante un cierto intervalo de tiempo y compararla, por ejemplo, con un diapasón que debe vibrar también durante un tiempo. Notas muy breves no tienen bien definido el tono.
Para que las reglas de la mecánica cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuando más grande y más pesado es un objeto, más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica. Me gustaría referirme a esta exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por holismo, y que podría definir como “el todo es más que la suma de sus partes”. Si la física nos ha enseñado algo es justo lo contrario. Un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (partículas); basta que sepamos sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes. Por ejemplo, la constante de Planck, h, que es igual a 6’626075… × 10-34 Julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.

El principio de incertidumbre de Heisenberg representa uno de los pilares fundamentales de la mecánica cuántica por no decir el principal nuevos estudios señalan una estrecha relación entre este principio y otro principio de la mecánica cuántica el entrelazamiento cuántico.
La mecánica cuántica es muy extraña a nuestro “sentido común”, sabemos que se desenvuelve en ese “universo” de lo muy pequeño, alejado de nuestra vida cotidiana en el macrocosmos tetradimensional que, no siempre coincide con lo que, en aquel otro ininitesimal acontece.
Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisemberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros como Erwin Schrödinger siempre presentaron serias objeciones a esta interpretación. Quizá funcione bien, pero ¿dónde está exactamente el electrón?, ¿en el punto x o en el punto y? En pocas palabras, ¿dónde está en realidad?, y ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.
Es cierto que, existe otro universo dentro de este nuestro del que, aún, nos queda mucho por aprender.

La mecánica cuántica puede ser definida o resumida así: en principio, con las leyes de la naturaleza que conocemos ahora se puede predecir el resultado de cualquier experimento, en el sentido que la predicción consiste en dos factores: el primer factor es un cálculo definido con exactitud del efecto de las fuerzas y estructuras, tan riguroso como las leyes de Isaac Newton para el movimiento de los planetas en el Sistema Solar; el segundo factor es una arbitrariedad estadística e incontrolable definida matemáticamente de forma estricta. Las partículas seguirán una distribución de probabilidades dadas, primero de una forma y luego de otra. Las probabilidades se pueden calcular utilizando la ecuación de Schrödinger de función de onda (Ψ) que, con muchas probabilidades nos indicará el lugar probable donde se encuentra una partícula en un momento dado.
Muchos estiman que esta teoría de las probabilidades desaparecerá cuando se consiga la teoría que explique, de forma completa, todas las fuerzas; la buscada teoría del todo, lo que implica que nuestra descripción actual incluye variables y fuerzas que (aún) no conocemos o no entendemos. Esta interpretación se conoce como hipótesis de las variables ocultas.
Fuente: Partículas de Gerard ´t Hofft
emilio silvera
















 Totales: 85.715.169
Totales: 85.715.169 Conectados: 78
Conectados: 78






















