May
11
La mujer debe ser reconocida como una igual
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
Recuerdo allá por el 2.011, en la sede de la UNESCO, en París, la 13ª Ceremonia de entrega de los Premios L’Oréal-UNESCO “FOR WOMEN IN SCIENCE”. La Ceremonia fue presidida por el Profesor Ahmed Zewail, galardonado con el Premio Nobel de Química en 1999. De este modo, cinco investigadoras de ciencias físicas que han contribuido a afrontar los importantes desafíos globales planteados a la humanidad han sido recompensadas con el Premio L’Oréal-UNESCO. El galardón fue entregado por Irina Bokova, Directora General de la UNESCO y por Lindsay Owen-Jones, Presidente de L’Oréal y de la Fundación Empresarial L’Oréal
.
Este premio honra a cinco mujeres excepcionales por su excelencia científica:

-Profesora Faiza Al-Kharafi (Kuwait), Galardonada por África y Estados Árabes. Profesora de química de la Universidad de Kuwait (Safat, Kuwait). Recompensada por sus trabajos sobre la corrosión, un problema de esencial importancia para el tratamiento del agua y la industria del petróleo. Declaraciones:
“La ciencia es un lenguaje universal y un viaje lleno de descubrimientos. Es para mí un honor recibir este premio excepcional en nombre de mi país y también en nombre de todas las mujeres de los cinco continentes del mundo que buscan la excelencia en sus investigaciones.”
Vivian Wing-Wah Yam
-Profesora Vivian Wing-Wah Yam (China), Galardonada por Asia y el Pacífico. Profesora de química energética en el Departamento de química de la Universidad de Hong Kong (China). Recompensada por sus trabajos sobre materiales emisores de luz y métodos innovadores para captar la energía solar. Declaraciones:
“No creo que haya diferencia entre hombres y mujeres en términos de capacidad intelectual. Independientemente del sexo o de la raza, siempre que una persona tenga pasión, dedicación y determinación podrá destacar y conseguir un trabajo de alta calidad.”
Nacida en Francia, Anne L’Huillier se doctoró en Ciencias Físicas por la Universidad de París.
-Profesora Anne L’Huillier. Galardonada por Europa. Profesora de física atómica en la Universidad de Lund (Lund, Suecia). Recompensada por sus trabajos sobre la creación de un aparato fotográfico extremadamente rápido que puede captar fenómenos en el lapso de un attosegundo (una milmillonésima de milmillonésima de segundo). Declaraciones:
“¿Que por qué me convertí en física? Mi abuelo era ingeniero; me enseñó la importancia de la ciencia para la Humanidad. Es la misma filosofía que me sigue motivando día a día. Después de esta semana, volveré a casa imaginando un futuro optimista para las científicas, para la ciencia en general y para los hombres y mujeres de todo el mundo.”
Silvia Torres-Peimbert, Profesora emérita del Instituto de Astronomía de la Universidad Nacional Autónoma de México (UNAM) (México).
-Profesora Silvia Torres-Peimbert (México), Galardonada por América Latina. Profesora emérita del Instituto de Astronomía de la Universidad Nacional Autónoma (UNAM) de México D.F. (México). Recompensada por sus trabajos sobre la composición química de las Nebulosas Planetarias, que es fundamental para comprender el origen del Universo. Declaraciones:
“Vengo de un país en desarrollo; considero que los países en desarrollo necesitan realizar más esfuerzos e invertir más dinero en Educación y Ciencia. Es algo caro, pero creo que resulta más caro todavía no hacerlo.”
-Profesora Jillian Banfield (Estados Unidos), Galardonada por América del Norte. Profesora de ciencias planetarias, terrestres y ambientales en el Departamento de ciencias e ingeniería material de la Universidad de California (Berkeley, Estados Unidos). Recompensada por sus trabajos sobre el comportamiento de las bacterias y la materia en condiciones extremas así como por sus repercusiones en el medioambiente terrestre. Declaraciones:
“Me gustaría decir a los jóvenes científicos: no tengáis nunca miedo a admitir que no sabéis algo, a preguntar, o cambiar de dirección apara buscar nuevos retos y oportunidades.”
“El mundo, ahora más que nunca, necesita ciencia, y la ciencia necesita mujeres; también necesita pasión y dedicación. Hoy, nuestro programa “Por las Mujeres en la Ciencia” es un gran éxito. De entre todas las iniciativas que he tenido la oportunidad de desarrollar, se trata de la que más satisfacción me produce y de la que más orgulloso me siento.”
Irina Bokova, Directora General de la UNESCO, señala:
“Tan sólo el 10% de los profesores universitarios y menos del 5% de los académicos científicos son mujeres; se desperdicia mucho talento porque a las jóvenes no se les permite acceder a estos campos. Al promover a las mujeres del mundo de la ciencia y de la tecnología esperamos cambiar el rostro de la investigación.”
Compromiso a largo plazo con el progreso científico.
El pasado 3 de marzo de 2011, Silvia Torres Castilleja, profesora emérita del Instituto de Astronomía de la Universidad Nacional Autónoma de México (UNAM), obtuvo el Premio Internacional L’Oreal-Unesco “For Women in Science 2011.
En la edición de este año, el premio buscó reconocer las aportaciones a la química con motivo del centenario de la concesión del Premio Nobel de Química a Marie Curie.

NGC 6543 Nebulosa Planetaria
En palabras del jurado, la mexicana fue “recompensada por sus trabajos sobre la composición química de las nebulosas planetarias, que es fundamental para comprender el origen del universo”. Sobre el galardón, Silvia Torres manifiesta su alegría:
“Es una enorme satisfacción, me parece lindísimo que instancias extranjeras nos reconozcan. Es fabuloso, estoy muy contenta y orgullosa, pero tampoco me lo debo de creer mucho”.
Con sencillez, la científica intenta describir sus investigaciones y los términos astrofísicos: “Estudio los gases alrededor de las estrellas que éstas acaban de arrojar al espacio y determino, midiendo la luz con espectros, de qué están hechos y cuánto material tienen de cada uno de los elementos químicos que se dejan ver, entonces se puede medir carbón, nitrógeno, oxígeno, neón, cloro, azufre, etcétera para ver si son iguales o distintos entre sí, lo que nos lleva a entender cómo son las estrellas que dieron origen a estos gases”.

Saber sobre la química de las Nebulosas nos lleva a saber sobre el Universo y cómo se forman los objetos que pueblan. Silvia Torres ha hecho una gran contribución a la Astrofísica y ha señalado el camino a seguir para avanzar en el conocimiento del Cosmos.
Es decir, resume, “los astrónomos tratamos de entender cómo se ha formado la galaxia, cómo son las estrellas, cómo cambian, o sea las diferencias y las semejanzas entre ellas”.
Silvia Torres es una de las pocas mujeres mexicanas que han incursionado en la ciencia y al cuestionársele por qué tomó esa decisión explica: “Porque es padrísima, porque el conocimiento es interesante, indagar más y más. Los astros o el universo siempre han sido objeto de gran curiosidad humana y pocas personas se dedican a ello, pero no es una carrera exclusiva de hombres, también cabemos ahí las mujeres y podemos hacer una aportación equivalente, no digo mejor ni peor”.
Sin embargo, asegura que no fue tan difícil como se puede pensar: los maestros le dieron tantas oportunidades como a los hombres, le abrieron las puertas, le dieron una beca, “pero sí hubo algunas sutilezas, como que a mi esposo, que también se dedica a la astronomía, le dieron una oficina y a mí me dijeron que me fuera a la oficina de mi esposo, lo que no acepté y tuve que irme al fondo de una bodega”.
Silvia Torres sostiene que por parte de su esposo también recibió siempre mucho apoyo para desarrollar sus actividades científicas, pero esa ayuda no se transmitió a las labores de la casa, en donde “he recibido apoyo espiritual, pero él no me ayuda en nada ahí”.
La ciencia, comenta, demanda mucho tiempo durante periodos prolongados, por lo que para muchas personas es difícil tener una relación de pareja: con frecuencia, las mujeres que se dedican a las ciencias tienen problemas, ya que sus parejas no las comprenden cuando tienen que viajar constantemente o dedicar mucho tiempo a sus investigaciones.
Considera que la escasa participación femenina en las ciencias es algo histórico, aunque no todas las ramas tienen el mismo grado de ausencia de las mujeres. En este punto ejemplifica: hay mucho más participación en las ciencias biológicas, químicas y de la salud, posiblemente porque es una tradición y más fácil que a la mujer se le acepte como doctora, médica o química. Donde sí es ampliamente notoria la ausencia femenina es en las ciencias exactas y en las ingenierías.
Ante ello, Silvia Torres subraya que se debe buscar la igualdad de oportunidades, pero desde la familia, porque en el núcleo de la sociedad tratan de manera diferente a las hijas y a los hijos. Mientras a los hijos les dicen ve a cambiar el foco, a las hijas las mandan a arreglar la mesa.
En la actualidad las cosas van cambiando
No son pocas las ocasiones en que, mujeres valiosas, han renunciado a su triunfo personal para dedicarse a su familia. Muchas buenas científicas se han perdido por causa de la doble obligación de la mujer de tener que llevar sobre sus hombros tantas responsabilidades.
Con sentido del humor, sostiene que hay muchos aspectos que tienen igual grado de dificultad y pueden atenderse tanto por hombres como por mujeres, pero hay otros donde los hombres son mucho más fuertes, “como para abrir un frasco de mayonesa”.
Existen muchas diferencias desde las familias, insiste, ya que a las niñas no las ponen a jugar con carritos ni a los niños con muñecas, por lo que se les forma de manera distinta. Lo mismo pasa en sus habilidades matemáticas o de razonamiento, los tratan de manera diferente.
Silvia Torres considera que se debe cambiar a la sociedad para que exista la igualdad de oportunidades: “No busco que las mujeres tengan más oportunidades, sino que tengan las mismas que los hombres en realidad, no que los dados ya están cargados”.
Recuerda que cuando estudiaba era impensable que una mujer escogiera ingeniería, ya que los propios estudiantes eran muy hostiles y agredían a las compañeras de manera verbal, ya que siempre ha existido una cultura machista.
![]()
Los aspectos, el mundo sigue siendo machista, y, los cambios son lentos.
Hoy tenemos mujeres camioneros, mineros, marineras… ¡El Mundo está cambiando para mejor!
Por ello, la astrónoma mexicana envía un mensaje a todas las mujeres que quieren participar en ámbitos donde la mayoría es masculina: “Mi consejo es que insistan si ese es su deseo, su voluntad, su sueño. Que insistan en el sueño, que no lo suelten, que continúen pensando en eso y que no dejen que otros les roben su sueño y sus oportunidades”.
Silvia Torres Escamilla
La Ciudad de México

Nació en la Ciudad de México, posee estudios en física en la Facultad de Ciencias de la UNAM y un doctorado en astronomía en la Universidad de California, en Berkeley. Fue directora y ahora es investigadora emérita del Instituto de Astronomía de la UNAM e integrante de la Sociedad Americana de Astronomía, de la Academia de Ciencias para el Mundo en Desarrollo.
Hay que procurar una buena educación a las niñas de hoy para que sean mujeres de provecho en el mañana. Siento que se me encoje el Alma cuando veo escenas de niños y niñas abandonados por esos mundos en los que no encontraran oportunidades para desarrollar sus intelectos por falta de medios.
La joven Silvia Torres
Además del premio L’Oreal-Unesco, ha sido galardonada con la Medalla Guillaume Bude, del College de France, el Premio Universidad Nacional en el área de Ciencias Exactas; la Medalla Académica de la Sociedad Mexicana de Física; la Medalla Heberto Castillo del Instituto de Ciencia y Tecnología del Distrito Federal. En 2007 obtuvo el Premio Nacional de Ciencias y Artes.
Fue editora de la Revista Mexicana de Astronomía y Astrofísica. Asimismo, ha publicado en revistas internacionales de prestigio más de 100 artículos.
¡Felicidades a todas las mujeres científicas! en particular, y, a todas las mujeres en general.
May
10
Todo está relacionado… De una u otra manera
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (2)
Comments (2)
“En 1900 Planck formuló que la energía se radia en unidades pequeñas separadas que llamamos cuantos. De ahí surge el nombre teoría cuántica. La ley de Planck establece que la energía de cada cuanto es igual a la frecuencia de la radiación multiplicada por la constante universal.En 1900 Planck formuló que la energía se radia en unidades pequeñas separadas que llamamos cuantos. De ahí surge el nombre teoría cuántica.”
Avanzando en el desarrollo de esta teoría, descubrió una constante de naturaleza universal que se conoce como la constante de Planck. La ley de Planck establece que la energía de cada cuanto es igual a la frecuencia de la radiación multiplicada por la constante universal. Sus descubrimientos, sin embargo, no invalidaron la teoría de que la radiación se propagaba por ondas. Los físicos en la actualidad creen que la radiación electromagnética combina las propiedades de las ondas y de las partículas.
Los descubrimientos de Planck, que fueron verificados posteriormente por otros científicos, fueron el nacimiento de un campo totalmente nuevo de la física, conocido como mecánica cuántica y proporcionaron los cimientos para la investigación en campos como el de la energía atómica. Reconoció en 1905 la importancia de las ideas sobre la cuantificación de la radiación electromagnética expuestas por Albert Einstein, con quien colaboró a lo largo de su carrera.
El Efecto Foto eléctrico de Einstein
El propio Planck nunca avanzó una interpretación significativa de sus quantums. En 1905 Einstein, basándose en el trabajo de Planck, publicó su teoría sobre el fenómeno conocido como efecto fotoeléctrico. Dados los cálculos de Planck, Einstein demostró que las partículas cargadas absorbían y emitían energías en cuantos finitos que eran proporcionales a la frecuencia de la luz o radiación. En 1930, los principios cuánticos formarían los fundamentos de la nueva física.
Planck recibió el Nobel de Física de 1918
Albert Einstein dijo sobre Max Planck: “Era un hombre a quien le fue dado aportar al mundo una gran idea creadora”. De esa idea creadora nació la física moderna.
Radiación de cuerpo negro
En 1900 Planck formuló que la energía se radia en unidades pequeñas separadas que llamamos cuantos. De ahí surge el nombre teoría cuántica.
Avanzando en el desarrollo de esta teoría, descubrió una constante de naturaleza universal que se conoce como la constante de Planck. La ley de Planck establece que la energía de cada cuanto es igual a la frecuencia de la radiación multiplicada por la constante universal. Sus descubrimientos, sin embargo, no invalidaron la teoría de que la radiación se propagaba por ondas. Los físicos en la actualidad creen que la radiación electromagnética combina las propiedades de las ondas y de las partículas.
Los descubrimientos de Planck, que fueron verificados posteriormente por otros científicos, fueron el nacimiento de un campo totalmente nuevo de la física, conocido como mecánica cuántica y proporcionaron los cimientos para la investigación en campos como el de la energía atómica. Reconoció en 1905 la importancia de las ideas sobre la cuantificación de la radiación electromagnética expuestas por Albert Einstein, con quien colaboró a lo largo de su carrera.


“Hay una leyenda urbana sobre el eclipse de 1919 que popularizó el best-seller de Stephen Hawking, «Historia del tiempo» Crítica (1988). La verificación de la teoría de Einstein sería resultado del sesgo de confirmación por parte de Eddington. Pero en 1979 se realizó un análisis con técnicas modernas de las placas fotográficas originales que confirmó los resultados de 1919; más aún, ya en 1919 su precisión era comparable a la que se logró con el eclipse de 1973. Por tanto, los resultados del eclipse de 1919 confirmaron a más de cinco sigmas la teoría de Einstein. La leyenda urbana es solo un bulo.”Fuente del párrafo: La Ciencia de la Mula Francis
“Un excitón es una cuasipartícula de los sólidos formada por un electrón y un hueco ligados a través de la interacción coulombiana. Se da únicamente en semiconductores y aislantes.”
Silicio purificado.
Semiconductor es un elemento que se comporta como un conductor o como un aislante dependiendo de diversos factores, por ejemplo: el campo eléctrico o magnético, la presión, la radiación que le incide, o la temperatura del ambiente en el que se encuentre. Los elementos químicos semiconductores de la tabla periódica se indican en la tabla adjunta.”

Gustav Mie
“La teoría de Mie, también llamada teoría de Lorenz-Mie o teoría de Lorenz-Mie-Debye, es una solución completamente analítica a las ecuaciones de Maxwell para la dispersión de la radiación electromagnética por partículas esféricas.”

“En física se denomina dispersión al fenómeno de separación de las ondas de distinta frecuencia al atravesar un material. Todos los medios materiales son más o menos dispersivos, y la dispersión afecta a todas las ondas; por ejemplo, a las ondas sonoras que se desplazan a través de la atmósfera, a las ondas de radio que atraviesan el espacio interestelar o a la luz que atraviesa el agua, el vidrio o el aire.”
Ese ha sido uno de las grandes esfuerzos realizados por desarrollar una teoría que diera cuenta del equilibrio de la electricidad que constituye el electrón y, los trabajos de Mie, han sido apoyados por toda la comunidad de los físicos teóricos, él se basa principalmente en la introducción de un tensor- energía de términos suplementarios que dependen de las componentes del potencial electromagnético, además de los términos de energía de la teoría de Maxwell-Lorentz. Estos nuevos términos que en el espacio exterior no son importantes, son sin embargo efectivos en el interior de los electrones al mantener el equilibrio frente a la repulsión eléctrica.
A pesar de la belleza de la estructura formal de esta teoría, erigida por Mie, Hilbelt y Weyl, sus resultados físicos hasta ahora han sido insatisfactorios. Por una parte, la multiplicidad de posibilidades es desalentadora, y por otra parte dichos términos adicionales no han podido ser formulados de una manera tan simple que la solución pudiera ser satisfactoria,
El poder predictivo de esta ecuación. Aquí Gμν es el tensor de Einstein que depende de la métrica gμν y de sus primeras y segundas derivadas con respecto a las coordenadas del espacio-tiempo. El tensor de Einstein contiene solamente magnitudes geométricas y su cálculo explícito se obtiene a partir de la curvatura del espacio-tiempo. La parte derecha de las ecuaciones contiene el tensor de energía-momento Tμν que depende directamente de magnitudes físicas como la masa, presión, volumen, etc. Consecuentemente, las ecuaciones de Einstein tienen un sentido físico muy profundo ya que se pueden interpretar conceptualmente como
Hasta ahora la Teoría de la Relatividad General no ha realizado ningún cambio en este estado de la cuestión. Si por el momento no consideramos el término cosmológico
Gμν = ½δμν G = KT μν
Donde G denota el Tensor de curvatura de Riemann contraído, G es el escalar de curvatura formado por contracción repetida, y Tμν el Tensor de energía de “materia”. En fin, explicar toda la ecuación puede llegar a ser engorroso y es toda una larga historia que no siempre entretiene al personal. Así que, lo dejamos.
Muchos son los conceptos que tendríamos que explicar aquí para dilucidar todas estas cuestiones que, implicadas en estas teorías, nos llevan a la cinemática, la simultaneidad, transformaciones de coordenadas, relatividad de longitudes y tiempos, adición de velocidades, lo que nos dijo Maxwell y Lorentz. transformación de energía en rayos luminosos, la gravedad y la propagación de la luz, la naturaleza física de los campos gravitatorios… y un sin fin de cuestiones que, hacen necesario un gran volumen y, también, un amplio dominio de conocimientos de los que carezco.
Adición de Velocidades
Por ejemplo: Un niño que viaja con su padre en el Tren, juega con una pelota y, al pasar frente a la Estación (donde se encuentra observando el Jefe de estación), lanza una pelota en el sentido de la marcha del tren a 20 Km/h. El Trén viaja a la velocidad de 120 KIm/h.
El padre del Niño lleva una máquina que mide la velocidad de la pelota que marca 20 Km/h. El Jefe de Estación tiene una máquina similar que le marca 140 Km/h la velocidad de la pelota.
¿Como entendemos eso: Muy fácil, la máquina del padre que viaja también a 120 Km/h, no registra la velocidad del Tren. Sin embargo, el Jefe de Estación parado en el Anden, mide la velocidad del Tren y a ella le suma la de la pelota.
Lo cierto es que, la Teoría de la Gravedad, nos lleva a imaginar situaciones que podrían ser y, en alguna ocasión, se nos puede presentar como posibles caminos para solucionar cuestiones que, en el mundo físico que conocemos, nos parecen irresolubles pero… En física, amigos míos, lo imposible parece posible.
¡Encontrar la solución para burlar la velocidad de la luz, y, atravesando portales mágicos, ir a otras galaxias! Es cierto que la mente está muy delante de los hechos pero… Cuando se piensa en algo, ahí queda la posibilidad de plasmarlo en una realidad.

Al menos por el momento, no podemos saber si nuestro Universo es único. Sin embargo, hemos pensado en la posibilidad de que pudiera ser uno de tantos. Como nunca nadie pudo estar en otro Universo, tenemos que imaginarlos y basados en la realidad del nuestro, realizamos conjeturas y comparaciones con otros que podrían ser. ¿Quién puede asegurar que nuestro Universo es único?
/cloudfront-eu-central-1.images.arcpublishing.com/larazon/TV7XIUIBVVGWRDNCERH6V4V3BE.png)
Realmente nadie puede afirmar tal cosa e incluso, estando limitados a un mundo de cuatro dimensiones espacio-temporales, no contamos con las condiciones físicas necesarias para poder captar (si es que lo hay), ese otro universo paralelo o simbiótico que presentimos junto al nuestro y que sospechamos que está situado en ese “vacío” que no hemos llegado a comprender. Sin embargo, podríamos conjeturar que, ambos universos, se necesitan mutuamente, el uno sin el otro no podría existir y, de esa manera, estaríamos en un universo dual dentro de la paradoja de no poder conocernos mutuamente, al menos de momento, al carecer de los conocimientos necesarios para ello.
emilio silvera
May
9
La verdadera Historia de la Teoría del Caos
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
Los Medios de Comunicación, no siempre son fieles “comunicadores” y, para realzar las noticias, las expresan con un grado extra de exaltación, o, licencia poética que, distorsiona la realidad de lo que realmente deberían comunicar, y, no pocas veces, tal hecho se debe a que (sobre todo en noticias relativas a cuestiones científicas) no se elige a la persona debidamente preparada y adecuada a la noticia que se quiere ofrecer al público.

La supueta aparición del Bosón de Higgs
Escribo esto a partir de un artículo leído en la prensa diaria que, tratando de hablar de exóticos objetos que existen en el Universo, llegan a hablarnos de estrellas masivas con 400 veces la masa del Sol, y, tal barbaridad, nos lleva a pensar que, para hacer un reportaje o comentario de estos temas, los diferentes medios, deberían acudir a personas versadas en los temas tratados, y, de esa manera, además de quedar mucho mejor, evitarían el ridículo de publicar las cosas alejadas de la realidad.
Buscando en mi documentación, un buen ejemplo de lo que digo, por suerte, me encuentro con un artículo escrito por Don Carlos Miguel Madrid Casado del Departamento de Lógica y Filosofía de la Ciencia en la Facultad de Filosofía de la Universidad Complutense de Madrid, dónde nos deja un claro ejemplo de lo que no debiera ser. Aquí os lo dejo.

Nubes moleculares en Orión que son los materiales primigenios para complejidades futuras
“Edward Lorenz (1917-2008): ¿Padre de la Teoría del Caos?

El miércoles de 16 de abril de 2008, a los 90 años de edad, moría Edward Norton Lorenz. Los periódicos de medio mundo pronto se hicieron eco de la noticia. Todos los obituarios recogieron que había muerto “el Padre de la Teoría del Caos”. Lorenz, escribían, fue el primero en reconocer el comportamiento caótico de ciertos sistemas dinámicos, como el atmosférico. El estudio de este comportamiento altamente inestable y errático le condujo, continuaban, a formular una de las principales características de lo que hoy se llama “caos determinista”: la dependencia sensible a las condiciones iniciales, popularmente conocida como “efecto mariposa”. Lorenz, concluían, fue el artífice de la tercera revolución científica del siglo XX, después de la Teoría de la Relatividad y la Mecánica Cuántica.



James Yorke
Pero, alto ahí, ¿ha sido realmente Edward Lorenz el “creador” de la Teoría del Caos? ¿O acaso su papel de estrella protagonista se debe más bien a una inusitada alianza entre mérito y fortuna? El propósito de esta nota es ofrecer una panorámica de la Historia de la Teoría del Caos que complique su nacimiento y enriquezca su evolución, sacando a la luz la figura de ciertos científicos que el gran talento de Lorenz ha ensombrecido y ocultado. Comenzamos nuestra panorámica retrocediendo hasta los tiempos de la Revolución Científica. El intento por comprender las trayectorias planetarias observadas por Kepler condujo a Newton a modelarlas matemáticamente, siguiendo la estela de Galileo. Newton formuló sus leyes de una forma matemática que relacionaba entre sí las magnitudes físicas y sus ritmos de cambio. Las leyes físicas quedaron expresadas como ecuaciones diferenciales. Estudiar un fenómeno físico y hallar las ecuaciones diferenciales que las gobernaban eran las dos caras de la misma moneda.
Desde el siglo XVII, toda la naturaleza –sólidos, fluidos, sonido, calor, luz, electricidad- fue modelada mediante ecuaciones diferenciales. Ahora bien, una cosa era dar con las ecuaciones del fenómeno en cuestión y otra, bien distinta, resolverlas. La teoría de las ecuaciones diferenciales lineales fue desarrollada por completo en poco tiempo. No así la teoría gemela, la teoría de las ecuaciones diferenciales no lineales.

Uno de los problemas no lineales que trajo de cabeza a físicos y matemáticos fue el problema de los n cuerpos de la Mecánica Celeste: dados n cuerpos de distintas masas bajo atracción gravitacional mutua, se trataba de determinar el movimiento de cada uno de ellos en el espacio. Newton resolvió geométricamente el problema de los dos cuerpos en los Principia. Posteriormente, Bernoulli y Euler lo resolvieron analíticamente con todo detalle. Sin embargo, no ocurrió así con el problema de los tres cuerpos. Newton sabia que, cuando un tercer cuerpo entraba en escena, el problema no era fácilmente resoluble, y que esto traía serias consecuencias para la cuestión de la estabilidad del Sistema Solar (que, a fin de cuentas, en la época, pasaba por ser un sistema de siete cuerpos). Aunque débiles en comparación con la fuerza de atracción del Sol, las fuerzas gravitatorias entre los planetas no eran ni mucho menos despreciables, por cuanto a la larga podían desviar algún planeta de su órbita e incluso, en el límite, expulsarlo fuera del Sistema Solar.

El matemático suizo Leonhard Euler
Las fuerzas interplanetarias podían estropear las bellas elipses keplerianas, sin que fuera posible predecir el comportamiento del Sistema Solar en un futuro lejano. En Motu corporum in gyrum, Newton afirmaba que los planetas no se mueven exactamente en elipses ni recorren dos veces la misma órbita, y reconocía que definir estos movimientos para todo futuro excedía con mucho la fuerza entera del intelecto humano. Si el Sistema Solar se iba desajustando, era necesaria una solución drástica: la Mano de Dios tenía que reconducir cada planeta a su elipse, reestableciendo la armonía. Este Deus ex machina newtoniano provocó, como es bien sabido, la ira de Leibniz, para quien Dios no podía ser un relojero tan torpe.
Tiempo después, Laplace creyó explicar las anomalías orbitales que preocuparon a Newton como meras perturbaciones que sólo dependían de la Ley de Gravitación y tendían a compensarse en el transcurso del tiempo. Así, al presentar su Mecánica Celeste a Napoleón, exclamó que Dios no era una hipótesis necesaria en su sistema del mundo. Sin embargo, en sus ecuaciones del sistema Sol-Júpiter-Saturno (problema de los tres cuerpos), Laplace despreció un término matemático que creía muy pequeño pero que, en contra de lo por él supuesto, podía crecer rápidamente y sin límite, hasta desestabilizar el Sistema Solar.
Muchos físicos y matemáticos decimonónicos dedicaron sus esfuerzos a dar una respuesta completa al problema de los tres cuerpos y a la cuestión de la estabilidad del Sistema Solar. Entre ellos, uno de los personajes clave en la configuración de la Teoría del Caos: Henri Poincaré.
Henri Poincaré
En 1855, los matemáticos europeos tuvieron noticia de que un importante concurso internacional iba a ser convocado bajo el auspicio de Oscar II, rey de Suecia y Noruega, para celebrar su sesenta aniversario en el trono. Se ofrecía un sustancioso premio al matemático capaz de resolver el problema de los tres cuerpos y, de este modo, avanzar en el estudio de la estabilidad del Sistema Solar. Alentado por la competencia, Poincaré procedió a sintetizar muchas de sus ideas acerca del estudio cualitativo o topológico de las ecuaciones diferenciales no lineales. El Jurado declaró ganador a Poincaré por una compleja resolución del problema restringido de los tres cuerpos, en que un planeta ligero se mueve bajo la atracción gravitatoria de dos estrellas iguales que giran una alrededor de la otra describiendo dos elipses confinadas en un mismo plano. Sin embargo, el artículo de Poincaré contenía un error y una tirada completa de la prestigiosa revista Acta Mathemática hubo de ser destruida.
A toda prisa, Poincaré revisó su trabajo y descubrió que, en verdad, no podía probarse la estabilidad del sistema, porque su dinámica no seguía pauta regular alguna. Su revisión del problema contiene una de las primeras descripciones del comportamiento caótico en un sistema dinámico. Poincaré fue, desde luego, el abuelo de la Teoría del Caos. Además, a partir de entonces, Poincaré contribuyó como pocos, a popularizar la idea de que existen sistemas deterministas cuya predicción a largo plazo resulta imposible. En Ciencia y Método, escribía: “Puede suceder que pequeñas diferencias en las condiciones iniciales produzcan algunas muy grandes en los estados finales. Un pequeño error al inicio engendrará un enorme error al final. La predicción se vuelve imposible”.
¡Caramba! Medio siglo antes que Lorenz, Poincaré se había topado con… ¡el efecto mariposa! Aún más: el genial matemático francés señaló que el tiempo meteorológico hacía gala de esta clase de inestabilidad y apuntó qué dificultades se derivarían para la predicción meteorológica. En su labor divulgadora no estuvo solo: su compatriota Pierre Duhem difundió las investigaciones de Poincaré y, también, de Jacques Hadamard, quien fue pionero en demostrar matemáticamente que, para cierto sistema dinámico hoy conocido como el Billar de Hadamard, un pequeño cambio en las condiciones iniciales provoca un notable cambio en la posterior evolución del sistema.

Durante el primer cuarto del siglo XX, la influencia de Poincaré no desapareció y se dejó notar en los trabajos de George David Birkhoff a propósito de las características cualitativas y topológicas de los sistemas dinámicos. Tampoco puede olvidarse el papel de Stephen Smale, que ganaría la Medalla Fields –el Premio Nobel de los matemáticos- en 1966 por sus contribuciones a la Teoría de los Sistemas Dinámicos. Mediado el siglo XX, este topólogo continuó la senda trazada por Poincaré t Birkhoff, y descubrió la Herradura de Smale, que pasa por ser el mecanismo topológico que da lugar al caos (efecto mezcla).

George David Birkhoff
Simultáneamente, cruzando el telón de acero, existía otra fértil tradición: la Escuela Rusa. En la U. R. S. S., los físicos y matemáticos habían heredado de Alexander Liapunov sus influyentes nociones acerca de la estabilidad del movimiento de los sistemas dinámicos. Si Poincaré se había ocupado de la teoría de la estabilidad desde una perspectiva cualitativa, Liapunov lo hizo cuantitativamente (exponentes de Liapunov). Recogiendo el testigo de ambos, Kolmogorov y Arnold se concentraron en el estudio de la estabilidad de los sistemas dinámicos de la Dinámica Celeste. Durante la guerra fría, los principales resultados de los matemáticos soviéticos fueron traducidos al inglés y dados a conocer al resto de matemáticos, europeos y norteamericanos, gracias al providencial trabajo de Solomon Lefschetz.
Y en éstas, apareció Lorenz… En 1963, este matemático y meteorólogo, antiguo alumno de Birkhoff en Harvard, estaba trabajando en el pronóstico del tiempo en el MIT. Estudiando la convección en la atmósfera, Lorenz planteó un modelo matemático formado por tres ecuaciones diferenciales ordinarias para describir el movimiento de un fluido bajo la acción de un gradiente térmico. Mientras buscaba soluciones numéricas con la ayuda de una computadora, se encontró –al volver de tomar una taza de café- con que se producía un dramático comportamiento inestable, caótico. Lorenz se había topado por casualidad con el fenómeno de la sensibilidad a las condiciones iniciales, que hacía de su sistema algo en la práctica impredecible. En efecto, tras establecer las propiedades básicas del flujo, Lorenz reparó en que una pequeña variación en las condiciones iniciales ocasionaba estados finales completamente diferentes. Lorenz había descubierto, tomando prestada la indeleble metáfora que forjaría más tarde, el efecto mariposa: el aleteo de una mariposa en Brasil puede ocasionar un tornado en Texas. Ahora bien, sería el matemático norteamericano Guckenheimer el que, allá por los años 70, acuñara la expresión “dependencia sensible a las condiciones iniciales”.

Lorenz publicó su hallazgo en una revista de meteorología, en un artículo titulado Deterministic Nonperiodic Flow, en que citaba expresamente a Poincaré y Birkhoff (aunque desconocía las ideas del primero sobre predicciones meteorológicas), pero que pasó prácticamente desapercibido. Sólo Stephen Smale y James Jorke –el introductor del término caos en la literatura científica- reconocieron las repercusiones filosóficas de la investigación de Lorenz y la dieron a conocer. Si Edward Lorenz ofreció a la comunidad científica el paradigma de sistema dinámico caótico continuo, el zoólogo Robert May dio a conocer en su artículo Simple Mathematical Models with Complicated Dynamics el paradigma del sistema dinámico caótico discreto: la aplicación logística.
A finales de los 70 y principios de los 80, la exploración de aplicaciones de la Teoría del Caos comenzó a dar sus frutos más allá de las simulaciones en las pantallas de ordenador. Entre los fenómenos físicos estudiados destaca, sin duda, la transición a la turbulencia en los fluidos, cuyo estudio contaba con el precedente que suponía el artículo On the nature of turbulence de David Ruelle y Floris Takens, quiénes introdujeron la noción de atractor extraño. Paralelamente, el físico Mitchell Feigenbaum descubrió heurísticamente ciertas constantes universales que caracterizan la transición del movimiento periódico al movimiento caótico, dando inicio a una de las ramas más prometedoras de la Teoría del Caos a día de hoy: la Teoría de la Bifurcación.

En resumidas cuentas, a comienzos del siglo XXI, la Teoría del Caos se nos aparece como la ciencia fisicomatemática que estudia el comportamiento aperiódico e inestable en sistemas deterministas no lineales. Mientras que la revolución relativista fue, prácticamente, fruto de un único hombre (Albert Einstein), y la revolución cuántica lo fue de apenas un puñado (Planck, Bhor, Heisenberg, Schrödinger, Dirac), la revolución del caos determinista es, en cambio, obra de múltiples. La Teoría del Caos es hija tanto de matemáticos (Poincaré, Hadamard, Birkhoff, Smale, Yorke…) como de físicos, biólogos y otros tantos científicos de campos dispares (Lorenz, May, Feigenbaum…). Atribuir su paternidad únicamente a un hombre, aun cuando sea Lorenz, es una simplificación excesiva. Lorenz fue, por así decirlo uno de los muchos padres.”
Hasta aquí el artículo que el Señor Madrid Casado escribió y fue publicado en el número 3 del volumen 22 de la Revista Española de Física en 2008.
Mach Maxwell Lorentz
Riemann
El trabajo está bien y nos introduce en la historia de la Teoría del Caos desde sus raíces, y, lo único en lo que podemos disentir del autor es, en el hecho cierto de que, Einstein, autor de la relatividad, también se apoyó en muchos (Mach, Maxwell, Lorentz, -en la primera parte, y, sobre todo en Riemann, en la segunda), aunque eso no le quita ni una pizca del mérito que tiene como científico que supo aunar muchos conocimientos dispersos, unirlos en una sola entidad y hacer ver al mundo lo que allí había. Y, por otra parte, al hablar de la Mecánica Cuántica, excluye a Einstein que, en verdad (aunque la combatió) fue uno de sus padres en aquellos primeros momentos, su trabajo sobre el Efecto Fotoeléctrico (que le dio el Nobel de Física) así lo demuestra. Por otra parte, no habría estado de más y de pasada, comentar que Poincaré fue el autor de la “Conjetura” que lleva su nombre y que ha estado ahí 100 años sin que nadie la resolviera hasta que llegó, un matemático extraño, llamado Perelman (ruso) que sin tener el premio que ofrecían al ganador, puso en Internet la solución. Este personaje, no acudió a la cita en Madrid, donde se celebraba el Año Internacional de las Matemáticas y el rey le entregaría la Medalla Field. Todos se quedaron esperando y él, que vicía con su madre en un apartamento de 65 m2, estaba con su cestita al brazo cogiendo setas en el campo.
De todo esto podemos obtener la consecuencia de que, todo tiene otra historia detrás, y, si profundizamos, la podemos descubrir para conocer de manera completa y precisa, el transcurso de los hechos y los personajes que en ellos tomaron parte.
emilio silvera
May
8
Engañosa perfección
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (1)
Comments (1)
El modelo estándar es una poderosa herramienta pero no cumple todas las expectativas; no es un modelo perfecto. En primer lugar, podríamos empezar por criticar que el modelo tiene casi veinte constantes que no se pueden calcular. Desde luego, se han sugerido numerosas ideas para explicar el origen de todos estos parámetros o números inexplicables y sus valores, pero el problema de todas estas teorías es que los argumentos que dan nunca han sido enteramente convincentes. ¿Por qué se iba a preocupar la naturaleza de una fórmula mágica si en ausencia de tal fórmula no hubiera contradicciones? Lo que realmente necesitamos es algún principio fundamental nuevo, tal como el principio de la relatividad, pero no queremos abandonar todos los demás principios que ya conocemos. Ésos, después de todo, han sido enormemente útiles en el descubrimiento del modelo estándar. El mejor lugar para buscar un nuevo principio es precisamente donde se encuentran los puntos débiles de la presente teoría.

Una regla universal en la física de partículas es que para partículas con energías cada vez mayores, los efectos de las colisiones están determinados por estructuras cada vez más pequeñas en el espacio y en el tiempo.
El modelo estándar es una construcción matemática que predice sin ambigüedad cómo debe ser el mundo de las estructuras aún más pequeñas. Pero existen varias razones para sospechar que sus predicciones pueden, finalmente (cuando podamos emplear más energía en un nivel más alto), resultar equivocadas.

Vistas a través del microscopio, las constantes de la naturaleza parecen estar cuidadosamente ajustadas sin ninguna otra razón aparente que hacer que las partículas parezcan lo que son. Hay algo muy erróneo aquí. Desde un punto de vista matemático no hay nada que objetar, pero la credibilidad del modelo estándar se desploma cuando se mira a escalas de tiempo y longitud extremadamente pequeñas, o lo que es lo mismo, si calculamos lo que pasaría cuando las partículas colisionan con energías extremadamente altas. ¿Y por qué debería ser el modelo válido hasta aquí?
Podrían existir muchas clases de partículas súper pesadas que no han nacido porque se necesitan energías aún inalcanzables. ¿Dónde está la partícula de Higgs? ¿Cómo se esconde de nosotros el gravitón?

Si deseamos evitar la necesidad de un delicado ajuste de las constantes de la naturaleza, creamos un nuevo problema: ¿Cómo podemos modificar el modelo estándar de tal manera que el ajuste fino no sea necesario? Está claro que las modificaciones son necesarias, lo que implica que muy probablemente haya un límite más allá del cual el modelo tal como está deja de ser válido. El modelo estándar no será nada más que una aproximación matemática que hemos sido capaces de crear, de forma que todos los fenómenos que hemos observado hasta el presente están reflejados en él, pero cada vez que se pone en marcha un aparato más poderoso, tenemos que estar dispuestos a admitir que puedan ser necesarias algunas modificaciones del modelo para incluir nuevos datos que antes ignorábamos.
Más allá del modelo estándar habrá otras respuestas para preguntas que, en este momento, no sabemos ni plantear.
Quedó abandonado con miles de dolores enterrados
El gobierno de Estados Unidos, después de llevar gastados miles de millones de dólares, suspendió la construcción del supercolisionador superconductor de partículas asestando un duro golpe a la física de altas energías, y se esfumó la oportunidad para obtener nuevos datos de vital importancia para el avance de este modelo, que de momento es lo mejor que tenemos.

Se han estado inventando nuevas ideas, como la supersimetría y el technicolor. Los astrofísicos estarán interesados en tales ideas porque predicen una gran cantidad de nuevas partículas superpesadas, y también varios tipos de partículas que interaccionan ultradébilmente, los technipiones. Éstas podrían ser las WIMP’s (Weakly Interacting Massive Particles, o Partículas Masivas Débilmente Interactivas) que pueblan los huecos entre las galaxias, y serían así las responsables de la masa perdida que los astrofísicos siguen buscando y llaman materia oscura.
Paul Dirac se sintió muy incómodo cuando en 1931 dedujo, a partir de su ecuación del electrón, que debería existir una partícula con carga eléctrica opuesta. Esa partícula no había sido descubierta y le daba reparo perturbar la paz reinante en la comunidad científica con una idea tan revolucionaria, así que disfrazó un poco la noticia: “Quizá esta partícula cargada positivamente, tan extraña, sea simplemente el protón”, sugirió. Cuando poco después se identificó la auténtica antipartícula del electrón (el positrón) se sorprendió tanto que exclamó: “¡Mi ecuación es más inteligente que su inventor!”. Este último comentario es para poner un ejemplo de cómo los físicos trabajan y buscan caminos matemáticos mediante ecuaciones de las que, en cualquier momento (si están bien planteadas), surgen nuevas ideas y descubrimientos que ni se podían pensar. Así pasó también con las ecuaciones de Einstein de la relatividad general, donde Schwarzschild dedujo la existencia de los agujeros negros.
Se piensa que al principio del comienzo del tiempo, cuando surgió el Big Bang, las energías eran tan altas que allí reinaba la simetría total; sólo había una sola fuerza que todo lo englobaba. Más tarde, a medida que el universo se fue expandiendo y enfriando, surgieron las cuatro fuerzas que ahora conocemos y que todo lo rigen.
Tenemos los medios, en los super-colisionadores de partículas, para viajar comenzando por 1.000 MeV, hasta finalizar en cerca de 1019 MeV, que corresponde a una escala de longitudes de aproximadamente 10–30 cm. Howard Georgi, Helen Quinn y Steven Weinberg descubrieron que ésta es la región donde las tres constantes de acoplamiento gauge se hacen iguales (U(1), SU(2) y SU(3)); resultan ser lo mismo. ¿Es una coincidencia que las tres se hagan iguales simultáneamente? ¿Es también una coincidencia que esto suceda precisamente en esa escala de longitud? Faltan sólo tres ceros más para alcanzar un punto de retorno que ya comentaremos. Howard Georgi y Sheldon Glashow descubrieron un modelo genuinamente unificado en el dominio de energías de 1019 MeV tal que, cuando se regresa de allí, espontáneamente surgen las tres fuerzas gauge tal como las conocemos. De hecho, ellos encontraron el modelo; la fórmula sería SU(5), que significa que el multiplote más pequeño debe tener cinco miembros.
El boson X predicho por Georgi-Glashow daría lugar a transiciones a través de masa que deben estar en la región de 1019 MeV. Una peculiaridad de este bosón X es que puede transformar los quarks en leptones e incluso en anti-quarks.
Y, a todo esto, ¿dónde está esa energía oculta? ¿Y donde la materia? Podemos suponer que la primera materia que se creo en el Universo fue la que llamamos “Materia Oscura” (mejor sería llamarla invisible), ya que, de no ser así, difícil sería explicar cómo se pudieron formar las primeras estrellas y galaxias de nuestro Universo, ¿dónde está el origen de la fuerza de Gravedad lo hizo posible, sino en esa materia escondida?
¡Lo dicho! Necesitamos saber, y, deseo que de una vez por todas, se cumpla lo que dejó dicho Hilbert en su tumba de Gotinga (Alemania).
¡Que sea pronto!
emilio silvera
May
8
La Tecnología de Vacío en la simulación Espacial
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
De Jesús Manuel Sobrado y José Ángel Martín-Gago
La Tierra está rodeada, esencialmente, de vacío. Por tanto, una de las formas de profundizar en el conocimiento del espacio es mediante la utilización de equipos de vacío. No sólo se trata de comprender el funcionamiento de los cuerpos celestes o de los procesos que ocurren en el espacio sino también en la superficie de muchos de los planetas, incluyendo las capas altas de la atmósfera terrestre. Un sistema de vacío puede ser un entorno adecuado donde recrear diferentes ambientes espaciales controlando algunos de los parámetros físicos del sistema (como presión total, composición de los gases, radiación, temperatura…). La simulación espacial utilizando equipos de vacío es una poderosa herramienta para preparar misiones espaciales, interpretar datos de las mismas o simplemente para investigar cómo se comporta la materia en esas condiciones.
1. Introducción
Con el lanzamiento del primer satélite Sputnik [1] comienza una nueva era tecnológica que ha permitido a la humanidad explorar el universo físicamente [2]. Este año se ha cumplido el 40 aniversario de la llegada del hombre a la Luna. Del fruto de este empeño y de otros de la misma naturaleza, como fue el primer la puesta en marcha del proyecto internacional común para la construcción de la estación espacial internacional, la sociedad ha obtenido un elevado beneficio tecnológico.
Podemos afirmar que la frase pronunciada por Neil Armstrong cuando pisó Luna se ha hecho realidad: “Este es un pequeño paso para el hombre, pero un gran paso para la humanidad”.
La ventana abierta hacia el espacio nos acerca al conocimiento que tenemos sobre nosotros mismos. No olvidemos que formamos parte del sistema solar en el planeta Tierra y que estamos, por tanto, rodeados de vacío, en medio de fuerzas gravitatorias y electromagnéticas, que convierten nuestro planeta en una maravillosa perla azul en un vasto territorio negro. (En 1990, en la misión “Voyager”, Carl Sagan, insistió antes de que la sonda abandonase el sistema solar, que tomase fotografías de la tierra vista desde el exterior.

Las imágenes tardaban 5 horas y media en ser recibidas en la Tierra) [3]. Fruto de esta necesidad de conocimiento surge el planteamiento de buscar nuevas formas de conocer el espacio que nos rodea. El espacio está esencialmente vacío.
Parece por tanto evidente, que los avanzados sistemas de vacío actuales puedan ayudarnos a comprender mejor los procesos y mecanismos que ocurren fuera de la atmósfera terrestre.
No sólo en el espacio interestelar, sino también sobre la superficie de muchos de los planetas y objetos celestes en los que su presión atmosférica sea menor que la terrestre. Así, un sistema de vacío puede ser un entorno adecuado donde recrear diferentes ambientes espaciales, controlando algunos de los parámetros físicos del sistema para poder aprender sin necesidad de desplazarnos materialmente.
15 años mostrando la belleza de Marte
“La sonda espacial ha contribuido significativamente en el estudio del planeta rojo; sus hallazgos sentaron las bases para las misiones de detección de signos de vida, como las dos misiones del programa ExoMars de la ESA.”
Las misiones espaciales presentan un número elevado de inconvenientes. Una de las principales críticas que han recibido siempre es su elevado coste. Por ejemplo, una misión “económica” a Marte, como pudo ser la Mars Express, tuvo un costo aproximado de unos 1000 millones de euros. Otro inconveniente es el largo tiempo necesario para realizarlas, ya que desde que una misión se concibe en los despachos hasta que se concluye pasa más de una década. Parece por tanto necesario asegurar todos los parámetros y, para ello, probar y calibrar lo mejor posible y en las mismas condiciones de operación, la instrumentación de la misión. Este es el marco en el que hay que entender la simulación en sistemas de vacío. Como una plataforma que nos permita reproducir condiciones planetarias e interestelares. Esta simulación tiene, por tanto, un doble objetivo. Por una parte preparar las misiones espaciales y, por otra, ayudar a entender los resultados obtenidos por las mismas.
La simulación de un problema complejo permite acotar y separar de forma controlada las variables relevantes de un sistema aislado. Es una manera de resolver pequeños problemas obteniendo valiosa información sobre el funcionamiento de sistemas en condiciones muy especificas. De este modo se van creando parámetros o esquemas de comportamiento que son fácilmente reproducibles, si se respetan todas las variables iníciales. Es importante conocer las limitaciones de la simulación. Al realizar la simulación en la Tierra, son dos normalmente los factores limitantes, las dimensiones de la cámara de vacío y la gravedad [4]. Este último es el menos relevante, ya que en la simulación de atmósferas o superficies planetarias, la gravedad es un factor existente que no determina las condiciones climatológicas de la atmósfera.
Sin embargo las dimensiones si son importantes, ya que limitan las diferentes gradientes de presión y temperatura, así como los niveles de radiación en función de la altura a la superficie. El volumen interno de una cámara así como la superficie interna limitan la transferencia de energía (calor), y por tanto la homogeneidad del sistema. En este trabajo vamos a describir como recrear distintos ambientes espaciales y planetarios mediante el uso de entornos de vacío. Daño del ADN por la radiación espacial, estabilidad de fases cristalinas de minerales en la superficie de Marte, comportamiento de sensores frente al polvo marciano o supervivencia de esporas en un viaje especial o superficie planetaria, son algunos ejemplos de una interminable lista de temas interdisciplinar que se pueden estudiar en equipos de simulación.

Veremos cuáles son los parámetros importantes para reproducir una atmósfera planetaria en un laboratorio, o para poder estudiar los hielos que se forman en el medio interestelar denso. Estas ideas se han materializado en la creación de una serie de máquinas de vacío que describiremos y que están operativas dentro de la unidad de simulación de ambientes planetarios y microscopía del Centro de Astrobiología [5]. 2. La simulación espacial y de atmósferas planetarias Planetas con atmósferas singulares, residuos de explosión de estrellas, espacio profundo o la entrada de meteoritos en una atmósfera planetaria, son algunos de los objetos y procesos que ocurren en el espacio. Un entorno espacial se puede caracterizar en función de muchos parámetros, que cruzados dan como resultado la recreación de un sistema concreto. Las principales variables que definen un sistema de simulación en un entorno espacial son la presión total, la composición de gases, la temperatura local o en la superficie de objetos planetarios, la temperatura ambiental, y la radiación recibida.
Estas variables son muy generales. Para poder implementar una instrumentación adecuada que responda a un determinado problema, es necesario conocer su rango de variación [6]. A partir de este dato se desarrolla la tecnología necesaria para poder controlar y monitorizar estas variables en un entorno de vacío. Vamos a hacer un repaso de los rangos de cada una de ellas y del tipo de instrumentación que deberíamos utilizar en cada caso.
Planetas con atmósferas singulares, residuos de explosión de estrellas, espacio profundo o la entrada de meteoritos en una atmósfera planetaria, son algunos de los objetos y procesos que ocurren en el espacio. Un entorno espacial se puede caracterizar en función de muchos parámetros, que cruzados dan como resultado la recreación de un sistema concreto. Las principales variables que definen un sistema de simulación en un entorno espacial son la presión total, la composición de gases, la temperatura local o en la superficie de objetos planetarios, la temperatura ambiental, y la radiación recibida.
Estas variables son muy generales. Para poder implementar una instrumentación adecuada que responda a un determinado problema, es necesario conocer su rango de variación [6]. A partir de este dato se desarrolla la tecnología necesaria para poder controlar y monitorizar estas variables en un entorno de vacío. Vamos a hacer un repaso de los rangos de cada una de ellas y del tipo de instrumentación que deberíamos utilizar en cada caso.
Puesto que vamos a utilizar para la simulación sistemas de vacío, la presión total debe de ser menor que la presión atmosférica. Esta es la primera limitación, que excluye automáticamente el estudio de planetas como Venus, cuya presión en la superficie es unas 90 veces mayor que la de la Tierra [7]. Estos planetas, así como el interior de océanos y mares de hielo que puedan existir en objetos planetarios como Europa (luna de Júpiter), deben de estudiarse mediante cámaras de alta presión, que incorporan una tecnología completamente distinta.
Es muy difícil dar valores precisos para la presión total en diferentes entornos planetarios o interestelares, y de hecho se encuentra frecuentemente bibliografía contradictoria. No obstante intentaremos dar algunas estimaciones y sobre todo, los rangos aproximados de estos parámetros para algunos entornos espaciales.
En el espacio interplanetario, por ejemplo, la presión viene determinada por el viento solar y por moléculas provenientes de las atmósferas de los distintos cuerpos celestes que lo pueblan, como cometas, o planetas. En física del espacio se suele utilizar la presión dinámica, que se define como:
Esta fórmula, aplicada para el viento solar en las inmediaciones de la Tierra, que tiene un número de partículas aproximadas de 4 por cm como del orden de vacío es el Pascal, 1 mbar se empleaba el Torr, como homenaje a Evangelista Torricelli. 1 mbar = 0,75 Torr [mm Hg]. Nosotros en este trabajo utilizaremos el mbar, que aunque no es la unidad en el sistema internacional, es la utilizada mayoritariamente por la comunidad científico-tecnológica en equipos de alto y ultra alto vacío).

El viento solar lo forman protones, partículas alfa, iones pesados y electrones, que fluyen desde la superficie del Sol con velocidades de hasta 800 Km/s. Como el viento solar es un plasma, este lleva consigo parte del campo magnético solar, por lo que las partículas de viento solar que son atrapadas en el campo magnético terrestre provocan entre otras cosas las auroras boreales y australes cuando chocan con la atmósfera terrestre cerca de los polos. Sabemos que el borde del sistema solar lo forma la burbuja del viento solar en el medio interestelar.
En el punto en el que el viento solar no ejerce presión para desplazar el medio interestelar, se considera que es el borde más exterior del sistema solar [8].
Si nos acercamos a algún cuerpo celeste, es la emisión de gases del mismo la que limita la presión total. Así, por ejemplo, cerca de la estación espacial internacional la presión viene determinada por los propios gases de la estación y otras partículas atrapadas por el campo gravitatorio de la misma, siendo esta del orden de Fuera del espacio interplanetario, en donde las temperaturas son muy bajas y la densidad molecular prácticamente inexistente, el concepto de presión deja de tener sentido. Sin embargo, encontramos zonas del espacio interestelar, las llamadas nubes de polvo, en las que se detecta acumulación de material.
Así, en el llamado medio interestelar difuso, (aquel cuya densidad es menor que el principal componente gaseoso es el hidrógeno atómico.
A causa de la gran cantidad de fotones y rayos cósmicos la temperatura típica del polvo en el medio interestelar difuso es de 100 K y sus principales componentes, según se deduce de las observaciones por absorción en el infrarrojo, son el hidrógeno, silicatos amorfos y carbono amorfo hidrogenado.

Su presión, puede ser estimada entonces como del orden de medio denso (nubes moleculares con densidades entre 103 – 106 partículas $ cm-3), cuyo principal componente gaseoso es el hidrógeno molecular. Aunque la densidad molecular en este caso es mucho mayor, la temperatura es muy baja en su interior, hasta unos 10 K, debido al apantallamiento de la radiación UV en las capas externas de la nube.
Las partículas de polvo, como las presentes en el medio difuso, se cubren de mantos de hielo con espesores del orden de 0.01 micras. Por tanto la presión total puede ser del orden de 10 -12 – 10 -18 mbar.
Laboratorio de presión de alto vacío
Se ha dicho en algunas ocasiones que las presiones del medio interestelar no son alcanzables en un laboratorio. Esto no es del todo cierto. En realidad no son medibles. En algunas líneas criogénicas de He líquido, se estima que la presión residual puede ser de 10-30 mbar, y es debida exclusivamente a la desorción por rayos cósmicos de los gases de las paredes del recipiente. El problema reside en que no existe actualmente tecnología para medir el vacío por debajo de 10-14 – 10-15 mbar. En el CERN, con manómetros modificados del tipo Bayard-Alpert se han podido medir presiones de hasta 2 $ 10-14 mbar [9].
En el caso de la mayor parte de los planetas la presión si es una magnitud alcanzable y con sentido físico. Así la presión media en la superficie de Marte es de unos 7 mbar, o en Tritón de 10-2 mbar. Las atmósferas planetarias de la mayoría de los cuerpos del sistema solar son conocidas por observaciones de IR. Sin embargo, no hay que olvidar que la presión total en un planeta depende de la altura. Por ejemplo, en la tierra a 86.000 m de altura la presión es de 10-2 mbar. (100.000 veces menor que la atmosférica). Por tanto debemos tener en cuenta esta dependencia cuando queramos simular la presión en la atmósfera marciana o la superficie marciana.
Existen gráficas en la que se resumen los distintos rangos del vacío junto con las bombas necesarias para alcanzarlos. En la figura vemos que las presiones interplanetarias y del medio interestelar son sólo reproducibles en sistemas trabajando en las llamadas de vacío extremo (XHV-del inglés, extreme high vacuum). Sin embargo, experimentos que se realicen en la estación espacial internacional, pueden simularse utilizando una bomba turbo molecular.
No sólo es necesario elegir el tipo de bombas adecuado para llegar a una u otra presión. También es necesario contar con distintos tipos de sensores, desde el Pirani y el piezoresistivo, para vacío bajo, capacitivo para vacíos medios y terminando en sensores tipo Penning o Bayard-Alpert para alto vacío y ultra alto vacío y vacío extremo.
La composición atmosférica
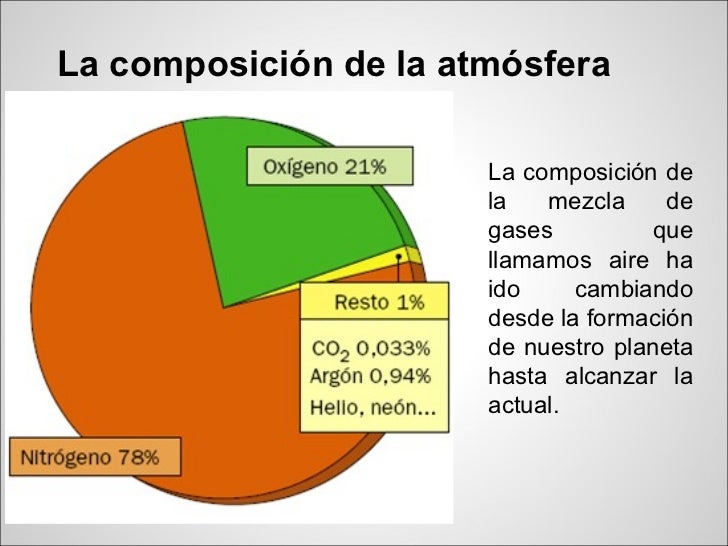
El siguiente parámetro relevante para controlar en una cámara de simulación es la composición de los gases de la atmósfera. De nuevo la primera división es entre composición de gases en medio interestelar denso y superficies planetarias. La principal fuente de información para la composición atmosférica son espectros de infrarrojo tomados por telescopios orbitales o por satélites. Por ejemplo en el caso de Marte la atmósfera es muy compleja. Se han detectado composiciones medias de 95% CO2, 2,7% N2, 1.6% Ar y 0.6% H2O.
En el caso de otros planetas como Europa, luna Galileana de Júpiter, la presión está formada en más de un 95% de O2 y en el caso del interior de una cámara de vacío a 10-11– mbar en el laboratorio, casi el 100% es hidrógeno.
La composición atmosférica según el medio interestelar denso es esencialmente hidrógeno tanto en forma molecular como gaseosa. En estos medios existen también una densidad no despreciable de otras moléculas, de composición orgánica y mineral, que se recombinan entre ellas dando lugar a lo que se conoce como Astro-química. Por ejemplo, en el interior de la nube situada tras la nebulosa de Orión, el gas adquiere la densidad suficiente y la baja temperatura necesaria para que los átomos se enlacen y formen moléculas, en las que predomina el hidrógeno molecular y hay trazas de monóxido de carbono, cianógeno y amoniaco [10], entre otras moléculas.
El control de la composición de gases en el sistema de simulación se realiza mediante la inclusión de detectores de masa cuadrupolares. Estos detectores ionizan el gas separando cada molécula según su relación carga/masa.Sabiendo la masa molecular podemos, identificarla en muchos casos y cuantificar su número. Este instrumento, mediante bombeo diferencial, puede operarse desde presión atmosférica. Sin embargo, a presiones inferiores de 10-5 mbar puede utilizarse con mayor resolución.
Para estar seguros de la composición de la atmósfera es preciso primero hacer el mejor vacío posible, y luego introducir la composición de gases deseada. Es por tanto importante controlar la composición de la presión residual en el sistema de simulación. En un sistema de alto-vacío con cierres KF, y bombeado con una bomba turbomolecular la presión residual parcial de cada uno de los gases está determinada por la velocidad efectiva de bombeo de la bomba turbomolecular (es distinta para cada composición gaseosa), y por la tasa de fugas en cierres de juntas de vitón (KF y LF), situándose en 10-8 mbar. Por tanto, planetas como Europa no pueden simularse utilizando este tipo de cierres. En un sistema con cierres de UHV (ultra alto vacío), la presión mínima está determinada por la permeabilidad del hidrogeno en cámaras de vacío de acero inoxidable 316 L o aluminio, que está en el orden de 10-13– mbar.
 Para introducir atmósferas complejas, como por ejemplo la de Marte, en el interior de las cámaras de vacío o sistema de simulación, se han desarrollado mezcladores (y evaporadores para el caso del agua) en los que se controla la presión parcial de cada uno de ellos mediante un espectrómetro de masas cuadrupolar antes de introducirlos en el sistema. Estos mezcladores pueden incorporar caudalímetros para experimentos en los que se requiera un control más preciso sobre alguno de los componentes atmosféricos. La mezcla de los gases en los sistemas de simulación se realiza mediante válvulas de fugas o sistemas de capilar controlados por válvulas de aguja. Las válvulas de fuga permiten una entrada de gas controlada hasta 2 $ 10-10 mbar litro/s, mediante el ajuste cónico de dos piezas metálicas una de cobre (metal blando) y la otra de acero (metal duro), de este modo la pieza de cobre se garantiza la estanqueidad ya que recupera su forma original después de cada cierre. En cuanto a los capilares permiten, o bien introducir o extraer gas desde el punto exacto donde comienza el capilar, esto permite además generar flujos en el interior de la cámara de simulación.
Para introducir atmósferas complejas, como por ejemplo la de Marte, en el interior de las cámaras de vacío o sistema de simulación, se han desarrollado mezcladores (y evaporadores para el caso del agua) en los que se controla la presión parcial de cada uno de ellos mediante un espectrómetro de masas cuadrupolar antes de introducirlos en el sistema. Estos mezcladores pueden incorporar caudalímetros para experimentos en los que se requiera un control más preciso sobre alguno de los componentes atmosféricos. La mezcla de los gases en los sistemas de simulación se realiza mediante válvulas de fugas o sistemas de capilar controlados por válvulas de aguja. Las válvulas de fuga permiten una entrada de gas controlada hasta 2 $ 10-10 mbar litro/s, mediante el ajuste cónico de dos piezas metálicas una de cobre (metal blando) y la otra de acero (metal duro), de este modo la pieza de cobre se garantiza la estanqueidad ya que recupera su forma original después de cada cierre. En cuanto a los capilares permiten, o bien introducir o extraer gas desde el punto exacto donde comienza el capilar, esto permite además generar flujos en el interior de la cámara de simulación.
La temperatura
Compatibilidad cromatográfica versátil
“El detector SQ 2, diseñado para una compatibilidad óptima con múltiples técnicas de separación cromatográfica, está indicado para ayudarle a obtener más conocimiento a partir de sus análisis.
El detector SQ 2 es compatible con UPLC, UPC2, HPLC, GC, HPLC preparativo y SFC preparativo, así como con análisis directos con la sonda ASAP.”
El concepto de temperatura es de difícil aplicación, ya que es un concepto termodinámico que se aplica a sistemas en equilibrio. En el espacio, el campo de temperaturas es quizá más amplio que el de las presiones. En planetas cercanos al Sol, puede superar varios cientos de grados y en los hielos de los cometas llega a pocos Kelvin.
La temperatura en la superficie de los objetos planetarios es fácilmente controlable con un criostato refrigerado con He líquido, en el que se pueden realizar ciclos de temperatura simulando por ejemplo, variaciones estacionales o diarias. Para ello, una vez enfriado el material que queremos estudiar en condiciones espaciales, un pequeño filamento nos permite aumentar la temperatura y ajustarla mediante un controlador PID a los valores deseados. Como ya hemos indicado, la temperatura en nubes densas de gas del medio interestelar viene determinada por la interacción de la materia con la radiación UV y rayos cósmicos. Esta temperatura es del orden de 10 K en el interior de la nube. Sin embargo en planetas con atmósfera muy ligera o prácticamente inexistente puede oscilar entre la noche y el día entre 400 K y 100 K,como puede ser el caso de la Luna, o entre 300 K y 135 K en los polos de Marte. La temperatura sobre un cristalito de hielo, por ejemplo de dióxido de carbono, que se pueda crear en el espacio interestelar, puede simularse depositando el gas.
Sobre una ventana transparente de un criostato, que a través de un dedo frío, permite enfriar a 4 K.
Para las medidas de bajas temperaturas se emplean diodos de germanio y silicio, y para el resto de temperaturas hay un espectro amplísimo, que va desde distintos tipos de termopares, pasando por hilos de platino y acabando en Pirómetros ópticos.
Controlar la temperatura ambiental es un proceso más difícil de controlar de manera estable, aunque es relativamente sencillo monitorizarla. La temperatura como manifestación de la energía se transfiere mediante conducción, convección y radiación.
En entornos interplanetarios como en ultra alto vacío y vacío extremo sólo se transfiere mediante radiación, y en atmósferas planetarias normalmente mediante convección y radiación. Solamente se le añade la conducción en la superficie de los planetas. En una cámara de simulación juega un papel muy importante las dimensiones, ya que estas condicionan el volumen interno y la superficie de radiación, con lo que se convierte en el factor determinante a la hora de poder cambiar la temperatura ambiental de la atmósfera en función de la temperatura del contenedor, en este caso las paredes de la cámara de vacío.
En los sistemas de simulación es realmente complejo establecer una temperatura homogénea para un volumen relativamente pequeño (50 l), como en una cámara destinada a la verificación de sensores, por lo que se suele emplear es un intercambiador de calor interno refrigerado por nitrógeno líquido, acompañando una resistencia externa que recubre todas la paredes de la cámara y utilizando un gas con una alta movilidad como es el helio. De este modo se consigue una cierta homogeneidad de la temperatura ambiental en detrimento de la composición gaseosa original de la atmósfera planetaria.
Simulando la atmósfera de Marte con la cámara de la UMA
La NASA cuenta con la UMA para explorar Marte
Los sistemas desarrollados para medir la temperatura ambiental están basados en conjuntos de sensores repartidos por todo el volumen de la cámara, y a la vez aislados térmicamente, para poder crear un mapa tridimensional de temperaturas en el interior de la cámara de vacío. Así, por ejemplo, la figura 2 representa una simulación mediante ordenador mostrando un diagrama de temperaturas de la cámara MARTE, cuando se resuelve la ecuación del calor en dos dimensiones mediante elementos finitos. Este estudio previo es necesario para poder entender cómo se comporta la temperatura ambiental antes de realizar una prueba experimental. En el caso de la figura 2 todas las paredes externas así como los anillos interiores se encuentran a temperatura ambiental de 300 K, la parte inferior del porta muestras a 77 K (refrigerado por nitrógeno líquido), y la superior a 150 K (controlado térmicamente mediante un controlador PID, Proporcional Integral Diferencial), en un ambiente a 7 mbar en atmósfera de Marte. La figura 2 muestra el gradiente de temperatura ambiental en función de la distancia, en un plano medio de la cámara, que cuenta con simetría cilíndrica en el eje central vertical.
“El clima de Marte es bastante más extremo que el que encontramos en la Tierra. Al estar mucho más lejos del sol, el frío es mucho mayor, con una temperatura en Marte media de -63 grados. Sin embargo, las mínimas nocturnas pueden alcanzar fácilmente los -80 °C. Por contra, las máximas diurnas, en el ecuador y en verano pueden superar los 20 grados. Como vemos, lo más destacable es la variación de temperatura, que ronda desde los -140 grados hasta los 30ºC.
Un dato curioso y muy similar a la Tierra es la duración de los días, siendo en Marte de solo 37 minutos más. Sin embargo, las estaciones duran diferente, teniendo un año marciano 687 días.”










No la pude trasladar aquí




















 Fig.2.
Fig.2.
Representación de la temperatura, en el interior de la cámara
MARTE, en el plano central de la misma. (La cámara MARTE presenta
simetría cilíndrica en el eje central vertical).
Las fuentes de irradiación
Para concluir esta revisión de parámetros relevantes para la simulación de entornos espaciales, nos falta añadir la radiación. En el sistema solar la mayor parte de la radiación recibida en la superficie de los planetas es UV (ultravioleta), que es generada en el laboratorio normalmente mediante una fuente de xenón. En el caso de vacío inter-planetario, tenemos además electrones, iones y rayos X, que son generados en el laboratorio por fuentes de radiación específicas. Aunque las fuentes más comunes de electrones e iones tienen energías muy inferiores a las producidas por el viento solar pueden ayudar a hacerse una idea del tipo de alteraciones químicas que ocasionan.
Como hemos dicho cruzando todas estas variables generamos un entorno espacial. Entorno sobre el que podemos realizar multitud de estudios científicos y tecnológicos, apoyados en instrumentación específica como es el caso de interferómetros de Fourier en el infrarrojo FTIR y espectroscopia Raman, que nos permitan seguir en tiempo real los cambios químico-físicos que se producen.
La unidad de simulación de ambientes planetarios del CAB
Un ejemplo de aplicación de las ideas expuestas anteriormente lo podemos encontrar en la Unidad de Simulación de Ambientes Planetarios y Microscopia, del Centro de Astrobiología (centro mixto INTA-CSIC). El principal objetivo de la unidad es el de prestar apoyo técnico y tecnológico a los científicos usuarios del CAB y cualquier otro investigador interesado en la realización de experimentos
relacionados con el vacío y la simulación espacial.





 No la pude trasladar
No la pude trasladar
Fig.3. Fotografía de la Unidad de Simulación de Ambientes Planetarios
y Microscopia en el centro de Astrobiología (INTA-CSIC).
La unidad cuenta actualmente con diversas máquinas de vacío dedicadas a la simulación de diferentes sistemas espaciales. Cada una de ellas está concebida para estudiar distintas facetas de diferentes entornos. En este sentido, las más importantes y representativas son: PASC (Planetary Atmospheres Simulation Chamber), ISAC (Interstellar Astrochemistry Chamber), MARTE (Mars Simulation Chamber) y TUNEL (Túnel de viento en vacío). Pasaremos a describir las más representativas tecnológicamente en la simulación de ambientes planetarios e interplanetarios [11].
ISAC (InterstellarAstrochemistry Chamber)

La primera aplicación de simulación espacial la encontramos en la simulación de ambientes interestelares y circunestelares.
Uno de los objetivos científicos principales es el estudio de la naturaleza (las propiedades físico-químicas), el origen y la evolución de las partículas de polvo, de composición carbonácea/orgánica y/o mineral, en su periplo desde las atmósferas estelares, pasando por el medio interestelar hasta la nebulosa solar, para dar lugar a la formación de cometas, asteroides y planetas. Además se estudian las implicaciones astrobiológicas de dicha materia. Para tal fin es necesario entender la relación entre la materia observada en el espacio (radioastronomía y astronomía en el infrarrojo), la materia orgánica producida por procesos primarios (procesamiento fotónico e iónico de hielos) y simulaciones experimentales del procesamiento de hielos (annealing térmico e irradiación). ISAC ha sido diseñada para tal efecto.
Describiremos la tecnología y las aplicaciones de ISAC [12], que cuenta con el diseño y la tecnología adecuados para trabajar en presiones por debajo de 10-10 mbar. Combinando bombas de absorción sin evaporación (NEG), y sublimadoras de Ti podemos alcanzar presiones de 2 $ 10-11 mbar. Esta máquina incorpora un criostato que permite bajar la temperatura hasta 7 K. A esta temperatura, una mezcla de gases que se introduce en el sistema, como los que se han detectado en las nubes de polvo interestelar, forman una capa de hielo en el criostato. El hielo de composición análoga a los mantos de hielo interestelares se puede irradiar con una fuente de ultravioleta de vacío y espectro parecido a la radiación presente en el medio difuso interestelar. Al mismo tiempo, tanto la composición química del hielo como su alteración debida a la irradiación pueden estudiarse in situ mediante espectroscopia infrarroja (FTIR) en transmisión y Raman. Las moléculas que desorden del hielo durante el calentamiento (desorción térmica) o la irradiación ultravioleta (foto-desorción) son detectadas por QMS. El avance en nuevas bombas de absorción no evaporables, bombas NEG (Non Evaporable Getter), combinado con una optimización del volumen y una correcta disposición de las bombas de vacío así como una desgasificación de la misma en un horno de vacío en el proceso de fabricación, hace posible pasar de UHV a XHV, permitiendo, alcanzar presiones en torno a 10-11 mbar, en tan sólo 48 horas desde su puesta en marcha. Otro punto muy destacable y tecnológicamente viable pero complejo, es el de la preparación de mezclas de gases con una resolución en ppm (partes por millón), gracias al innovador diseño de una línea de gases que funciona con electroválvulas en condiciones de flujo laminar, mezcladores en vacío, monitorizados por un espectrómetro de masas o cuadru-polo en RF (radio frecuencia), que permiten una vez obtenida la composición deseada del gas, depositarlo por medio de una válvula de aguja en la cámara principal para formar el hielo de interés astrofísico. De este modo, es posible controlar el número de mono-capas que se desea depositar. PASC (Planetary Atmosphere Simulation Chamber)
La máquina de simulación PASC, [13,14], es un entorno de simulación para las condiciones de objetos planetarios con atmósferas. La característica principal de esta máquina es la versatilidad, de manera que el investigador puede definir cada uno de los parámetros para simular el entorno que desee. Esta máquina reproduce la presión atmosférica, composición gaseosa, temperatura e irradiación de la mayor parte de los planetas sólidos del sistema solar o en un entorno ficticio. La presión puede regularse entre 5 y 5 $ 10-9 mbar y la temperatura desde 4 a 325 K. El porta muestras está concebido para permitir introducir diferentes tipos de muestras y de diferentes tamaños, que vayan desde regolitos marcianos o terrestres, esporas, hielos o materiales utilizados en aeronáutica. La irradiación (UV) se realiza mediante una lámpara de deuterio. Uno de los principales retos tecnológicos de este diseño es que permite el encendido de fuentes de irradiación de electrones e iones a presiones de 10-2 mbar. Para ello se ha diseñado una cámara interior en la que se realizan dosetapas de bombeo diferencial, como se indica en la figura 5. Así, se puede enviar electrones sobre la muestra en estudio, por ejemplo, mientras que en la presión total es 10-2 mbar. Las aplicaciones científicas de la misma tienen mucho que ver con el comportamiento de muestras de origen biológico y geológico, en condiciones similares a las de Marte, Triton o Europa, algunos ejemplos pueden ser el comportamiento de absorción y desorción de CO2 en muestras minerales bajo ciclos de temperatura y radiación estacionales, disorción de vapor de agua en jarositas, estabilidad de fases minerales en Marte, estudio de resistencia radiactiva UV de biosensores, son algunos de los proyectos de investigaciónes recientes realizados en esta máquina.
4. MARTE
Veinte años ha tardado la NASA en volver a mostrar interés por Marte, este es el periodo de tiempo que hay entre las sondas Viking y el Mars Pathfinder (MPf). Durante este tiempo los científicos han estudiado las 57.000 imágenes de la Viking, que han permitido conocer la geología del planeta rojo con bastante exactitud. Sin lugar a dudas no hay planeta del sistema solar con mejores condiciones para albergar vida, extinta o actual, que Marte. Se parece a la Tierra en muchos aspectos; El proceso de su formación, la historia climática de sus primeros tiempos, sus reservas de agua y fenómenos geológicos como los volcanes [15,16]. Las misiones desde la MPf tienen un carácter de exploración física y ambiental del entorno, para lo cual la exploración no sólo se realiza con satélites y sondas como la Viking, sino también con rovers(pequeños vehículos todoterreno) que son capaces de recorrer la superficie marciana, cada vez con mayor autonomía. En las futuras misiones a Marte, no sólo por la NASA sino también por la ESA, se desea caracterizar la climatología, así como la búsqueda de vida primigenia, en la que mediante una tecnologíabasada en biosensores, se puedan analizar muestras in situ y de enviar los resultados a la Tierra en tiempo real.

La cámara de simulación de MARTE, está especialmente diseñada para estudiar condiciones marcianas e introducir muestras electrónicas reales. Para ello, se puede modificar la temperatura en el porta muestras en un rango entre 80 K y 450 K, y además es capaz de modificar la temperatura ambiental entre 200 K y 400 K y de generar “tormentas de polvo” en su interior. El principal objetivo de esta cámara es la de probar nuevos dispositivos electromecánicos “sensores”, por lo que su ámbito de aplicación se destina principalmente a la calibración de sensores e instrumentación ambiental que serán enviados al espacio en futuras misiones espaciales. El principal reto, está en poder combinar rangos de temperatura en el porta muestras distintos a los de la atmósfera, y cruzar esto con cambios bruscos de presión, mientras se mantiene la composición gaseosa de Marte. El porta muestras de MARTE, está diseñado para poder soportar dispositivos electromecánicos de grandes dimensiones usando la misma geometría de las mesas ópticas, y pudiendo ser enfriado y calentado desde el interior. En cuanto a la atmósfera el interior, de MARTE cuenta con unos anillos refrigeradores de nitrógeno líquido
que en función de la presión y la composición de la atmósfera permite enfriar la misma no sólo por radiación sino también por conducción y convección.
Además la cámara, está diseñada y construida para poder generar tormentas de polvo en su interior mediante un ingenioso sistema de deposición, que mediante la combinación de un tamiz vibratorio, la gravedad y la diferencia de presiones es capaz de producir una niebla de polvo de partículas de hierro, similar a las de Marte. Sobre todo este conjunto de posibilidades también hay unos pasamuros, en los que se pueden adaptar fuentes de luz halógenas y de xenón, siguiendo el esquema del movimiento del Sol en el hemisferio norte de Marte, de este modo simulamos la incidencia de la luz solar en función de la dependencia angular. Todo este complejo sistema se ha desarrollado para testear los sensores de la estación meteorológica REMS (Rover Environmental Monitoring Station), de lamisión MSL (Mars Science Laboratory) de la NASA, así como otros proyectos para la ESA, como ExoMars. El proyecto REMS, lo compone una estación meteorológica formada por sensores de radiación ultravioleta, sensor de presión, sensor de temperatura del suelo, sensor de temperatura ambiental, y sensor de viento. En cuanto al vacío, la cámara MARTE puede trabajar en dinámico o en estático, en dinámico cuando las condiciones de temperatura tanto del porta muestras como del interior modifican las condiciones de presión, y en estático cuando lo que interesa es cambiar el volumen sin modificar las condiciones de temperatura, como ocurre cuando se desea verificar la resolución del sensor de presión (calibración y tiempo de respuesta) en incrementos de presión a partir de 0.05 mbar.
Conclusión
El avance en la tecnología del vacío, dado por la consecución de presiones cada vez menores, es debido no sólo a las mejoras de las bombas, sino también al avance en materiales contenedores de vacío, “cámaras”, con presiones de vapor y permeabilidades cada vez más bajas. Este desarrollo unido a sistemas de medida más precisos y fiables en rangos extremos, ha permitido que sea posible estudiar la
materia condicionada por fenómenos atmosféricos, que ocurren en objetos planetarios con un gran interés científico, y que están situados a cientos de miles de kilómetros de la Tierra, y de dar credibilidad a los resultados en los sistemas experimentales. La experiencia ha demostrado que la simulación no es sólo un recurso de innovación tecnológica, sino también una herramienta útil, que permite validar la responsabilidad de las misiones espaciales, que debido al alto coste de las mismascondicionan su propia viabilidad. Del fruto de la simulación de algo tan complejo y tan vasto como es un sistema climático, en el que una mínima variación de un parámetro condiciona el comportamiento global del sistema, estamos obteniendo un gran provecho tecnológico, que nos permitirá en un futuro cada vez más cercano verificar nuestros propios resultados, y realizarnos preguntas sobre fenómenos que ni siquiera podemos conocer.
6. Agradecimientos
Queremos agradecer a las empresas Tecnovac SL y Maques SL el gran esfuerzo técnico y tecnológico, así como su colaboración desinteresada, realizado durante la construcción de algunos de los sistemas de simulación que se describen en este artículo. También agradecemos a José Flores del ICMM-CSIC, por su tiempo, experiencia y dedicación en la construcción de cámaras y componentes de vacío, a Andrés Buendía de la UAM por sus consejos en criogenia y principalmente, a nuestros compañeros Eva Mateo Martí, Pablo Merino, Guillermo Muñóz Caro, Antonio Jimeneéz, Elena López, y Celia Rogero por su dedicación y responsabilidades la explotación de las máquinas de la unidad de simulación de ambientes planetarios y microscopia de CAB.
Referencias bibliográficas
[1] Física y Sociedad. nº18, Especial sobre Astronáutica: 50 años
después del Sputnik
[2] GILES SPARROW. Astronáutica, La historia desde el Sputnik
al transbordador y más allá, Editorial Akal.
ISBN: 9788446029472.
[3] CARL SAGAN. Un punto azul pálido: Una visión del futuro
humano en el espacio. Editorial Planeta. 2006.
ISBN: 9788408059073.
[4] LORI C. WALTERS. To Create Space on Earth: The Space
Environment Simulation Laboratory and Project Apollo.
NASA/CR-2003-208933.
[5] http://www.cab.inta.es
[6] JOHN F. O´HANLON. A user´s guide to vacuum technology.
Editorial Wiley, Third Edition. ISBN: 9780471270522.
[7] ROMAN SMOLUCHOWSKI. El sistema solar. Biblioteca Scientifi c
American, ISBN: 9788475930138.
[8] La NASA dispone de datos sobre el viento solar en tiempo
real a través del satélite ACE, lanzado en 1997. La variación
del viento solar en tiempo real puede encontrarse en la página
web del satélite.
[9] KARL JOUSTEN. Pressure Measurement with ionization
Gauges. Physikalisch-Technische Bundesanstalt. Berlin.
[10] NICK SCOVILLE Y JUDITH S. YOUNG, Nubes moleculares,
formación de estrellas y estructura galáctica. La vida
de las estrellas, TEMAS 7 de Investigación y Ciencia.
ISBN: 9778411355668-0007.
[11] http://www.electronvoltio.com
[12] G.M. MUÑOZ-CARO, J.A. MARTÍN-GAGO, C. ROGERO,
J.M. SOBRADO, C. ATIENZA, S. PUERTAS. The Interstellar
Astrochemistry Chamber (ISAC). WSPC – September 9, 2008
[13] E. MATEO-MARTÍ, O. PRIETO-BALLESTEROS, J.M. SOBRADO,
J. GÓMEZ-ELVIRA AND J.A. MARTÍN-GAGO. A chamber for
studying planetary environments and its applications to
astrobiology. Meas. Sci. Technol. 17 (2006) 2274–2280.
[14] MARTIN REES. Universo, La guía visual defi nitiva. Editorial
Pearson de Alhambra. ISBN: 8420551414.
[15] PHILIP R. CHRISTENSEN, Estratigrafía y relieve de Marte.
Planetas. TEMAS 53 de, Investigación y Ciencia, Tercer
trimestre del 2008. ISBN: 9778411355668-00053
[16] TIM BEARDSLEY, Paseo Planetario, Marte. Sistemas Solares.
TEMAS 15 de Investigación y Ciencia, Primer trimestre de
1999. ISBN: 9778411355668-00015.
Jesús Manuel Sobrado
Centro de Astrobiología. CSIC-INTA
Unidad de Simulación de Ambientes Planetarios y Microscopía
(sobradovj@inta.es)
José Ángel Martín-Gago
Instituto de Ciencia de Materiales de Madrid. CSIC,
(gago@icmm.csic.es)
Nota: Si quieren leer el original y verlos gráficos, sólo tienen que poner en Google el Título de arriba y pulsar buscar. Enlace




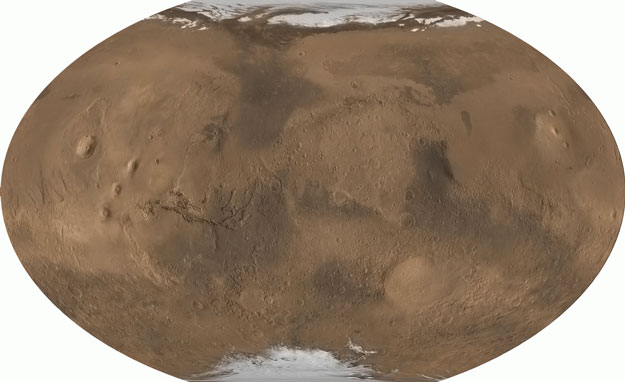











 Totales: 85.986.846
Totales: 85.986.846 Conectados: 41
Conectados: 41