Feb
2
¡Las Matemáticas! ¿Dónde radica su origen?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (0)
Comments (0)
Nuestro patrimonio matemático y nuestro orgullo occidentales depende irremediablemente de los logros de la antigua Grecia. Dichos logros se han exagerado tanto que a menudo resulta difícil distinguir qué parte de la matemática moderno procede de los griegos y cuál es la que tiene su origen en los babilonios, los egipcios, los hindúes, los chinos, los árabes, etc. Las matemáticas de los griegos eran muy imaginativas y es grande la deuda que tenemos con ellos.
Sin duda alguna la obra cumbre de la Matemática griega, que aún hoy levanta pasiones entre los matemáticos y científicos en general es sin duda Los Elementos de Euclides. Generalmente se cree, erróneamente, que los Los Elementos de Euclides contienen únicamente un resumen sumario y y exhaustivo de toda la Geometría griega.

En realidad los Los Elementos supusieron la gran síntesis no sólo de la producción geométrica griega hasta el siglo III a. C. sino también de un compendio, usando el lenguaje geométrico, de toda la Matemática elemental: Geometría plana y espacial, Aritmética y Álgebra.
A este respecto escribió Proclos: «Son singularmente admirales sus Elementos de Geometría (de Euclides) por el orden que reina en ellos, la selección de los teoremas y problemas tomados como elementos y también la variedad de los razonamientos desarrollados de todas las maneras y que conducen a la convicción» y más adelante expresa «Los Elementos son una guía segura y completa para la consideración científica de los objetos geométricos».
Sin embargo, si nuestras matemáticas actuales se basaran exclusivamente en Pitágoras, Euclides, Demócrito, Arquímes y otros griegos, sería una disciplina muy deficiente. Claro que, la realidad es que la historia de las matemáticas en occidente no se puede remontar a ninguna escuela y a ningún período que sean anteriores a la etapa de los griegos jónicos.

Euclides se le considera el gran sistematizador y maestro de la matemática griega, ésta alcanza su cenit con la figura de Arquímedes: uno de los más grandes matemáticos y científicos de todos los tiempos. A Arquímedes se le deben innumerables cálculos de áreas y volúmenes; algunos tan importantes y difíciles como el área de la superficie esférica o una vuelta de espiral. A partir del siglo XIII se recuperó su obra en Europa Occidental, pero no fue hasta el XVI cuando los matemáticos volvieron a adquirir la suficiente capacidad para entenderla.

Arquímedes era natural de Siracusa pero se formó en Alejandría bajo la correspondiente influencia de la ideología platónica de una matemática esencialmente teórica y abstracta. No obstante a ello, la actividad de este genio fue tremendamente original y diferente de la ciencia alejandrina ya que mezcló, enfrentándose contra todos los prejuicios platónicos, técnicas extraídas de la Mecánica, de lo infinitesimal, lo operativo. No obstante si bien ese era su modus operandi, lo escondía deliberadamente al escribir sus obras, ya que, todas ellas tienen la estructura euclidiana: comienza por las hipótesis para pasar a proposiciones impecablemente demostradas usando generalmente el método de exhaución de Eudoxo -para lo cual debía conocer de antemano la solución-. Esto último dio pie a las sospechas de muchos matemáticos -Wallis y Barrow entre ellos- de que Arquímedes tenía un método.
Teorema de Pitágoras
Busto de Pitágoras y su teorema
En 1952 Kline escribió: “Fue en el extraordinariamente propicio suelo de Grecia donde [las matemáticas] garantizaron finalmente una nueva forma de controlar la existencia humana y florecieron espectacularmente durante un breve período de tiempo…Con el declive de la civilización griega la planta quedó aletargada durante unos mil años…[hasta que] esa planta fue llevada de manera adecuada a Europa y plantada una vez más en terreno fértil”.
La Escuela de Atenas. Pintura de Rafael Sanzio
La escuela jónica, con Tales de Mileto (cuyo nombre lleva un importante teorema de geometría elemental, (el Teorema de Tales), fue la primera en comenzar la deducción matemática, hacia el año 600 a. C.
De un modo esquemático, se interpreta a menudo el significado de esta afirmación entendiendo que ha habido tres etapas en la historia de las matemáticas.
1. Hacia el año 6oo a. C., los antiguos griegos inventaron las matemáticas, que estuvieron desarrollándose hasta aproximadamente el año 400 d. C., momento en el cual desaparecieron de la faz de la Tierra.
2. A esto siguió un período oscuro para las matemáticas, que duró más de mil años. Algunos expertos admiten que los árabes mantuvieron vivas las matemáticas griegas durante la Edad Media.
3. En la Europa del siglo XVI se produce el redescubrimiento de las matemáticas griegas y esta disciplina vuelve a florecer de nuevo hasta el momento actual.

Pappus, es considerado como el último gran geómetra griego. A él debemos La Colección Matemática, obra de un inmenso valor histórico gracias a la cual conocemos hoy los trabajos de muchos matemáticos griegos -como por ejemplo Apolonio-. Incluimos aquí la primera impresión de esta importante obra editada por Federico Commandino en Venecia en 1589. Fue a partir de ella que resurge el interés a mediados del siglo XIX por la historia de la matemática griega y que daría como fruto impresionantes ediciones de las obras de Euclides, Arquímedes, Apolonio, Diofanto, Pappus, etc.

Tras Pappus ya sólo encontramos comentaristas como Teón, su hija Hipatia o Proclo. El final de la Matemática y, en general, de la ciencia griega lo simboliza la terrible muerte de Hipatia en Alejandría: fue brutalmente torturada y asesinada por un grupo de cristianos exaltados por Cirilo -después San Cirilo- en marzo del año 415 d. C. Cuenta un historiador de la época «la encerraron en una iglesia llamada Caesium; la desnudaron; le arrancaron la piel y le desgarraron la carne de su cuerpo utilizando conchas afiladas, hasta que su último aliento salió de su cuerpo; la descuartizaron; llevaron sus trozos hasa un lugar llamado Cinaron y los quemaron hasta reducirlos a cenizas». Fueron tiempos complicados para los científicos y, terribles, si además de científico se era mujer. Como colofón a esta sección de nuestra exposición incluimos un manuscrito griego del siglo XVI que contiene los comentarios de Teón, padre de Hipatia, a las Hármonicas.

Nuestros números modernos -del 0 al 9- se desarrollaron en la India durante la segunda etapa, el llamado período oscuro de las matemáticas. Las matemáticas existían ya mucho antes de que los griegos construyeran su primer ángulo recto. Otras veces hemos hablado aquí de las matemáticas hindúes contenidas en los Sulbasutras (las reglas de la cuerda). Escritos en alguna fecha comprendida entre los años 800 y 500 a. C., los Sulbasutras demuestran, entre otras cosas, que los indios de este período tenían su propia visión del teorema de Pitágoras así como un procedimiento para obtener la raíz cuadrada de 2 con una precisión de hasta cinco cifras decimales. Los Sulbasutras ponen de manifiesto la existencia de un rico conocimiento geométrico que fue anterior a los griegos.
 En el papiro Ahmes vemos que el cálculo de áreas tendía a emplear la conversión de la figura a analizar en “algo parecido a una figura conocida” que permita llegar al área buscada. Un sistema de cálculos parciales cuya suma permita obtener el área de la figura inicial. Veremos este método en el cálculo del área del círculo. Es quizá un primer paso hacia la demosción geométrica y un intento de encontrar las relaciones mutuas entre figuras geométricas, pero que se quedó ahí, en un primer paso, y al que nunca se le ha dado la importancia que tiene. Por este método se justifica el cálculo del área de un triángulo isósceles.
En el papiro Ahmes vemos que el cálculo de áreas tendía a emplear la conversión de la figura a analizar en “algo parecido a una figura conocida” que permita llegar al área buscada. Un sistema de cálculos parciales cuya suma permita obtener el área de la figura inicial. Veremos este método en el cálculo del área del círculo. Es quizá un primer paso hacia la demosción geométrica y un intento de encontrar las relaciones mutuas entre figuras geométricas, pero que se quedó ahí, en un primer paso, y al que nunca se le ha dado la importancia que tiene. Por este método se justifica el cálculo del área de un triángulo isósceles.
Existe un conjunto de matemáticas no europeas que fueron desenterradas hacia mediados del siglo XX, incluidas las matemáticas de Mesopotamia, Egipto, China, la India, el mundo árabe y la América precolombina. De todos es bien conocido que los propios griegos, entre ellos Demócrito, Aristóteles, Herodoto y otros, prodigaron alabanzas a los egipcios, reconociéndolos como sus gurús matemáticos (aunque no con estas palabras). El hecho es que fueron muchos antes que los griegos.
Merece la pena comenzar este artículo con la misma cita de Laplace que usamos en el artículo en el que dimos una primera revisión de las matemáticas indias.

Laplace escribió:
“El ingenioso método de expresar cada número posible utilizando un conjunto de diez símbolos (cada uno de ellos con un valor en su posición y un valor absoluto), surgió en la India. La idea parece hoy en día tan simple que su significado y profundidad no son apreciados en su justa medida. Su simplicidad subyace en el modo en el que facilitó el cálculo y colocó la aritmética en la primera posición entre las invenciones más útiles. La importancia del invento se aprecia con más facilidad cuando se considera que estaba mucho más allá que las ideas de dos de los mayores hombres de la antigüedad, Arquímedes y Apolonio.”

CIVILIZACIÓN SUMERIA Y BABILONICA.- Hacia el año 4000 a.C. en el sudeste de la mesopotámica se instalaron los sumerios y su capital fue Ur, posteriormente en el año 2500 a.C. este pueblo fue dominado por los acadios, un pueblo semita cuya capital era Acad, gobernados en esa época por Sargón, de esta forma la brillante cultura sumeria quedó fusionada con la acadia. Posteriormente este imperio cayó en poder de los babilonios hacia el año de 2270 a.C., gobernando el rey Hammurabi y haciendo de Babilonia su capital, durante su reinado floreció un período de alto nivel cultural.
Los babilonios fueron los primeros en contribuir al desarrollo de las matemáticas, la aritmética alcanzó su más alto nivel de desarrollo. En los restos arqueológicos de las Tablas de Senkreh, llamadas así por el lugar donde fueron descubiertas a orillas del Éufrates en 1854, se encontraron otras referencias literarias antiguas de esta civilización. En otros restos arqueológicos de Nuffar, existían tablas de multiplicar grabadas con caracteres cuneiformes, de números enteros dispuestos en columnas con valores superiores a 180 000.
Los primeros símbolos escritos de estas culturas, representaban los números con marcas en forma de cuña de acuerdo a su escritura cuneiforme. Los babilonios tenían un método de contar un poco complicado, su sistema numérico era en base sesenta (60), o sea, contaban de sesenta en sesenta, llamadas sesentenas babilónicas, Su aritmética se basaba en dos números ejes, el 10 y 60, teniendo en cuenta el posicionamiento de estos caracteres así mismo se leían e interpretaban, en la figura de arriba.
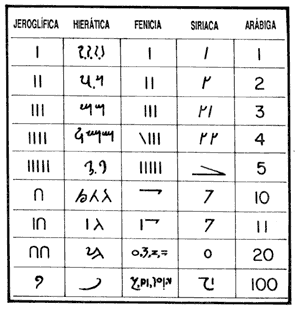
Resulta difícíl o imposible encontrar o hablar de una cultura que no tuviera alguna forma de contar, es decir, algún método para establecer la comparación entre un conjunto de objetos y una serie de números, marcadores u otros símbolos que sirvieran para registrar una cantidad estableciendo una correspondencia, ya fuera con símbolos escritos o en forma de cuentas, nudos o muescas realizadas en una madera, una piedra o en un hueso. Contar es hacer matemáticas y, en todas las cuturas existieron individuos capaces de hacerlo.
El sistema de numeración egipcio, era un sistema decimal de base 10.

La historia de las matemáticas en Egipto es larga, ya que comienza hacia el año 3200 a. C., cuando se inventó un sistema de escritura, y se alarga hasta el año 332 a. C., cuando Alejandro Magno conquistó y helenizó Egipto. Nuestras fuentes son escasas, porque el papiro se deteriora en un medio ambiente húmedo. Los únicos documentos legibles son los hallados en cementerios y templos de la franja desértica situada a lo largo del Nilo o en su delta. La mayoría data del Imperio Medio, entre 2000 y 1700 a. C. En total no hay más que cinco papiros, un par de tablillas de madera con ejercicios y una laja de piedra. Sin embargo, encontramos en estos documentos una rica tradición matemática. ¿Quién sabe lo que estaban haciendo con los números en las grandes ciudades?

Arriba Papiro de Rhind.
De los Babilonios: Los registros que se tienen son de naturaleza arqueológica, en arcilla, y, por supuesto, se encuentran limitados de muchas maneras. No nos permiten una visión exacta de las características en que se desarrollaron cultural y matemáticamente. En relación con Mesopotamia, los registros más antiguos datan del 3 500 a.C. y terminan en el 539 a.C, fecha en la que estos territorios fueron conquistados por Persia.
Hay alrededor de 500 000 tablillas de arcilla que constituyen las fuentes principales de la cultura babilónica, y entre ellas unas 500 son de interés para las matemáticas. La mayoría de los registros de que se dispone son del periodo llamado Antiguo, más o menos alrededor del 2 500 a.C.
El sistema cuneiforme de escritura fue descifrado a mediados del siglo XIX por George Frederick Grotefend y Henry Creswicke Rawlinson.
La aritmética más desarrollada en la civilización Mesopotámica fue la Acadiana. Dos de las características más importantes de su sistema numérico fueron la base 60 y la notación posicional. No obstante, debe señalarse que los babilonios no usaban solamente la base 60. En ocasiones, aparecía la base 10, pero otras bases también. Al igual que sucede con otras culturas y sistemas numéricos, con los babilonios se dio una forma combinada de sistemas numéricos determinados por circunstancias históricas o incluso regionales. En lo que sí parece haber consenso es que se dio el uso bastante sistemático de la base 60 para todos los cálculos relacionados con la astronomía. Esto debe subrayarse.

Tanto el sistema sexagesimal como el sistema del valor del lugar han permanecido en posesión permanente de la humanidad. Nuestra división presente de la hora en 60 minutos y 3 600 segundos data de los sumerios, al igual que nuestra división del círculo en 360 grados, cada grado en 60 minutos y cada minuto en 60 segundos. Hay razón para creer que esta opción de 60 en lugar de 10 como una unidad ocurrió en un esfuerzo por unificar sistemas de medida, aunque el hecho de que 60 tiene muchos divisores también puede haber jugado un papel. Acerca del sistema del valor posicional, su importancia permanente se ha comparado con el alfabeto (ambas invenciones reemplazaron un simbolismo complejo por un método fácilmente entendible por muchas personas). Es razonable suponer que hindúes y griegos obtuvieron las rutas de las caravanas hacia Babilonia; también sabemos que los académicos musulmanes lo describieron como una invención india. La tradición babilónica, sin embargo, puede haber influido en la aceptación tardía del sistema posicional.” (Struik, A Concise History of Mathematics, p. 26].
No poseían sin embargo el cero, ni tampoco algún símbolo para expresar la diferencia entre la parte entera y la fraccionaria de un número. Estos problemas implicaban cierto nivel de ambigüedad en el sistema numérico. De hecho, se afirma que -aunque lo usaban- no se trataba de un sistema posicional absoluto.
Para los babilonios, los símbolos fundamentales eran del 1 al 10 y los números del 1 al 59 se formaban combinando algunos de estos símbolos.
De las tablilas babilónicas, unas 300 son dedicadas a las matemáticas y hablan de cuentas y préstamos con interés, de multiplicaciones y otros problemas cotidianos. Otras, sin embargo, nos hablan de problemas mucho más avanzados con la superficie de la circunferencia, o, ¡el teorema de Pitágoras! y las propiedades de los triaángulos. Problemas de segundo, tercero y hasta de cuarto grado. También resolvían sistemas de ecuaciones. ¡Aspmbroso para aquellos tiempos!
Este problema de los Babilonios se basa en el Teorema de Pitágoras porque:
Bueno amigos, en un repaso tan superficial de lo que fueron las matemáticas, no puede extenderme tanto como para dejar una relación pormenorizada de todas las civilizaciones y personajes que merecen estar aquí reflejados. Sin embargo, el corto repaso, deja una muestra de lo que fueron aquellos primeros principios matemáticos y que dejan bien claro que, de ninguna manera, fuimos nosotros los que las inventamos en aquelos primeros principios.
emilio silvera
Feb
2
La relatividad especial
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
En cualquier parte que podamos buscar información nos dirán:
“Henri Poincqaré, matemático francés, sugirió a finales del siglo XIX que el principio de relatividad establecido desde Galileo (la invariancia galileana) se mantiene para todas las leyes de la naturaleza. Joseph Larmor y Hendrik Lorentz descubrieron que las ecuaciones de Maxwell, la piedra angular del electromagnetismo, eran invariantes solo por una variación en el tiempo y una cierta unidad longitudinal, lo que produjo mucha confusión en los físicos, que en aquel tiempo estaban tratando de argumentar las bases de la teoría del éter, la hipotética substancia sutil que llenaba el vacío y en la que se transmitía la luz. El problema es que este éter era incompatible con el principio de relatividad.”
En su publicación de 1905 en electrodinámica, Henri Poincaré y Albert Einstein explicaron que, con las transformaciones hechas por Lorentz, este principio se mantenía perfectamente invariable. La contribución de Einstein fue el elevar a este axioma a principio y proponer las transformaciones de Lorentz como primer principio. Además descartó la noción de tiempo absoluto y requirió que la velocidad de la luz en el vacío sea la misma para todos los observadores, sin importar si éstos se movían o no. Esto era fundamental para las ecuaciones de Maxwell, ya que éstas necesitan de una invarianza general de la velocidad de la luz en el vacío.

Como en otras ocasiones, aquí dejamos una muestra de la velocidad de la luz cuando viaja desde la Tierra a la Luna
La aparición de la Teoría de la relatividad fue tan poco convencional como su autor. El ya famoso artículo que escribió en 1905 (con el apoyo de los trabajos de los arriba mencionados) y que enunciaba por primera vez la teoría, era algo rústico y sencillo y no mencionaba o contenía cita científico-literaria alguna, tampoco mencionaba ayuda de ninguna persona a excepción de su amigo Besso, que dicho sea de paso no era científico (él, por aquel entonces, no conocía a científico alguno). La primera conferencia de Einstein explicando la Teoría, en Zurich, no fue dada en ninguna universidad sino en el salón del Sindicato de Carpinteros, duró más de una hora, y luego repentinamente se interrumpió para preguntar la hora, explicando que no tenía reloj. Sin embargo, a pesar de los modestos comienzos, allí comenzó a reformarse los conceptos del espacio y del tiempo.

Lo cierto es que, con su teoría de la relatividad, Einstein finalmente resolvió la paradoja que se había presentado a los dieciseis años, por la que las ecuciaones de Maxwell pierden su validez si uno atrapa un haz de luz a la velocidad de la luz. Lo hizo mediante la conclusión de que no se puede acelerar la velocidad de la luz, de que la velocidad de la luz es la misma para todos los observadores, cualquiera que sea su movimiento relativo. Si un astronáuta que vuela hacia la estrella más cercana a una velocidad del cincuenta por ciento de la de la luz, , midiera la velocidad de la luz a bordo de la nave, el resultado sería exactamente igual que el que daría la medición de otro colega suyo situado en la Tierra.

Podrían ocurrir fenómenos que ni podemos imaginar pero, quedándonos en lo que más llama la atención al público en general, podríamos conseguir que el tiempo … ¡Se ralentizara y pasara más despacio para el viajero relativista! Si miráis el diagrama del Minkouski os hablará de los fenómenos que se pueden producir al viajar a la velocidad de la luz, cuando el Tiempo se ralentiza.
Diferentes sistemas de referencia para el mismo fenómeno. Claro que, en la teoría están presentes factores y trabajos que no se mencionan y, la fórmula
siguiente:  es el llamado factor de Lorentz donde
es el llamado factor de Lorentz donde  es la velocidad de la luz en el vacío. Contrario a nuestro conocimiento actual, en aquel momento esto era una completa revolución, debido a que se planteaba una ecuación para transformar al tiempo, cosa que para la época era imposible. En la mecánica clásica, el tiempo era un invariante. Y para que las mismas leyes se puedan aplicar en cualquier sistema de referencia se obtiene otro tipo de invariante a grandes velocidades (ahora llamadas relativistas), la velocidad de la luz. Los sucesos que se realicen en el sistema en movimiento S’ serán más largos que los del S. La relación entre ambos es esa
es la velocidad de la luz en el vacío. Contrario a nuestro conocimiento actual, en aquel momento esto era una completa revolución, debido a que se planteaba una ecuación para transformar al tiempo, cosa que para la época era imposible. En la mecánica clásica, el tiempo era un invariante. Y para que las mismas leyes se puedan aplicar en cualquier sistema de referencia se obtiene otro tipo de invariante a grandes velocidades (ahora llamadas relativistas), la velocidad de la luz. Los sucesos que se realicen en el sistema en movimiento S’ serán más largos que los del S. La relación entre ambos es esa  . Este fenómeno se lo conoce como dilatación del tiempo. Si se dice que el tiempo varía a velocidades relativistas, la longitud también lo hace.
. Este fenómeno se lo conoce como dilatación del tiempo. Si se dice que el tiempo varía a velocidades relativistas, la longitud también lo hace.
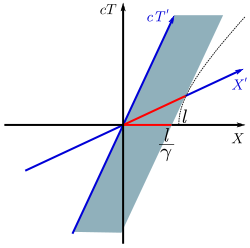
En el gráfico se escenifica la contracción de Lorentz
Para cuantificar aquella extraña situación, Einstein se vio obligado a emplear la contracción de Lorentz (En aquel momento no conocía a Lorentz al que más tarde consideraría “el hombre más grande y más noble de nuestro tiempo… una obrta de arte viviente.)” En manos de Einstein, las ecuciones de Lorentz esopecifican que, cuando aumenta la velocidad a la que se desplaza un observador, sus dimensiones, y la de la nave espacial y todo aparato de medición que haya a bordo, se contrae a lo largo de su movimiento en la cantidad requerida para hacer que la medición de la velocidad de la luz sea siempre la misma.
Esta era la razón de que Michelson y Morley no hallasen ningún rastrodel “arrastre del éter”. En verdad, el éter es superfluo, al igual que el espacio y el tiempo absolutos de Newton, pues no hay ninguna necesidad de un marco de referencia inmóvil. “Al concepto de reposo absoluto no le corresponde ninguna propiedad de los fenómenos, ni en la mecánica ni en la electromecánica.” Lo importante son los sucesos observables, y no puede observarse ningún suceso hasta que la luz (o las ondas de radio o cualquier otra forma de radiación electromagnética) que lleve noticias de él no llegue al observador. Einstein reemplazó el espacio de Newton por una red de haces de luz; la de ellos era una red absoluta dentro de la cual el espacio mismo se vuelve flexible.

Los observadores en movimiento experimentan también una lentificación del paso del tiempo. Un astronáuta que viaje al 90 por 100 de la velocidad de la luz sólo envejecerá a la mitad de rápido que su colega de la Tierra. Ya conocéis la paradoja de los gemelos en la que se explica tal fenómeno.

También en aquel primer artículo Einstein nos habló sobre la igualdad entre la masa y la energía. Él demostró que la masa de un cuerpo aumenta cuando absorbe energía. Se sigue de ello que su masa disminuye cuando irradia energía. Esto es verdadero no sólo para una nave espacial que se desplaza hacia las estrellas, sino también para un objeto en reposo. Una máquina fotográfica pierde algo (muy poco) de masa cuando el flash se dispara, y la gente cuya fotografía se saca se vuelve también, un poco más masiva al absorber sus cuerpos aquella radiación perdida por la máquina. Masa y energía son intercambiables.
m = E/c2
donde m es la masa del objeto, E su energía y c la velocidad de la luz. Al formular esta ecuación particularmente sencilla, que unifica los conceptos de energía y materia, y relaciona ambos con la velocidad de la luz, Einstein inicialmente estaba interesado en la masa. En cambio, si despejamos la energía, adquiere una forma más familiar y presagiosa:
en la Isla de los Museos (Berlín). Festejando el Año mundial de la Física en 2005, en el centenario de la publicación de la ecuación más famosa del mundo. Contemplada desde esta perspectiva, la teoría dice que la materia es energía congelada. Esto, por supuesto, es la clave de la fuerza nuclear y, en manos de los astrofísicos, la ecuación sería usada para descubrir los procesos termonucleares en el corazón de las estrellas.
Pero pese a todos sus variados logros, la relatividad especial no decía nada de la gravitación y, su autor, la veía incompleta. Aquella teoría sin la presencia de la otra gran fuerza más conocida del universo se veíoa desvalída: Había que vincularla con la masa inercial. La resistencia al cambio que ofrecen los objetos en estado de movimiento, su “peso” por decirlo así. La gravitación actúa sobre los objetos según su masa gravitacional, esto es, su “peso”. Todos sabem,os lo que es la masa inercial y de ella, tendremos que hablar cuando acometamos la p´çagina sobre la relatividad general. Dejemos aquí el apunte de que, la masa inercial y la gravitación de cualquier objeto son iguales. También se podría decir que, es la masa de los cuerpos que pueblan el universo, la que moldea y modela la geometría del del Cosmos, del espacio-tiempo.

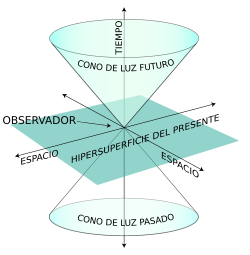
Terminemos con la misma imagen del comienzo. Causalidad e imposibilidad de movimientos más rápidos que la luz. Previo a esta teoría, el concepto de causalidad estaba determinado: para una causa existe un efecto. Anteriormente, gracias a los postulados de Laplace, se creía que para todo acontecimiento se debía obtener un resultado que podía predecirse. La revolución en este concepto es que se “crea” un cono de luz de posibilidades (Véase gráfico adjunto).
Se observa este cono de luz y ahora un acontecimiento en el cono de luz del pasado no necesariamente nos conduce a un solo efecto en el cono de luz futuro. Desligando así la causa y el efecto. El observador que se sitúa en el vértice del cono ya no puede indicar qué causa del cono del pasado provocará el efecto en el cono del futuro.
Asumiendo el principio de causalidad obtenemos que ninguna partícula de masa positiva puede viajar más rápido que la luz. A pesar que este concepto no es tan claro para la relatividad general. Pero no solo el principio de causalidad imposibilita el movimiento más rápido que el de la luz. Ya hablaremos de ello.
emilio silvera
Feb
2
Nuevas ideas, ideas viejas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)
Cuando Einstein irrumpió en la Física, nadie le conocía y sólo era un oscuro empleado de la Oficina de Patentes de Berna en Suiza. Él, sin embargo, no había dejado de estar al día y seguí todo aquello que se pudiera mover en relñación a su pasión: La Física. Los escritos de Mach, de Lorentz, de Maxwell, de Planck… Todo ello le llevó a elaborar su famosa teoría relativista que convulsionó el mundo de la ciencia y, si me apuras mucho, hasta el ámbito filosófico cambió a partir de la relatividad. Una teoría que venía a decir cosas increibles como que la masa era energía congelada, que la luz marcaba el límite de la velocidad del universo, o, que el tiempo se ralentizaba si se marcha a velocidades cercanas a c. Esos estraños postulados no fueron, en un principio, bien entendidos por la física del momento.

Manuscrito de Einstein con la fórmula de la Teoría de la Relatividad. Cuando esto se dio a conocer al mundo, muchos miraron excépcicos la fórmula y las implicaciones que de ella se podrían derivar, aquello podría cambiar lo firmemente establecido: ¡sacrilegio! ¿qué será de la Física si hacemos caso a lo que diga cualquiera?
Siempre ha sido así, el Status Institucional establecido, bien acomodado en los sillones de las academias y corporaciones, hacen la señal de la cruz, como para espantar al diablo, cada vez que aparecen nuevas ideas que, en realidad, les aterra, toda vez que les puede remover de sus asientos y prebendas, ya que, generalmente, dejan al descubierto que todo lo que predomina, está asentado en una falsa base de criterios y teorías que no siempre, son las correctas ni pueden ser demostradas y, mientras tanto eso ocurre, ellos, ¡a vivir que son dos días!

En el trabajo “No siempre la Física se puede explicar con palabras”, el amigo Tom Vood nos deja el siguiente comentario que, al parecerme de interés aquí os lo inserrto para que todos, podais pensar en lo que aquí expone: Creo que sí, deben ser divulgadas.
!”Te dejo una entre muchas “revelaciones” reciente, calentitas solo para ti; que no quisiera que se divulgaran. Pero le dejo a su responsabilidad, si borrarlas, si usted cree que debo seguir como guerrillero de la ciencia o debe ser conocidas estas ideas por toda la comunidad científica. Disculpa, pero no logro discernir eso. Pero como admiras tanto a Einstein y yo soy tan tonto, te la insinúo por arribita: (Según el modelo de la interacción Luz-Luz).
http://www.emiliosilveravazquez.com/blog/2012/05/31/acercarse-a-la-velocidad-de-la-luz-trae-consecuencias/
¿Sabes por que las energíasmasas (partículas, o electromagnéticos confinados) no pueden superar la velocidad de la luz?

Bueno Einstein se moriría por explicárselo; a pesar de que para los modernos físicos esas preguntas ilegales no se le hacen a la física; recuerda el famoso: ¡no preguntes y calcula! Como diciendo, no eres físico, sino físico-matemático. O lo que no se, o no me puedo explicar, no lo puedes preguntar, es de mal gusto hacerlo, o de ignorantes. ¡Que daño Dios!
Bueno, pues una partícula según mi modelo es energíacampo confinada o electromagnético confinado en forma de energíamasa y por lo tanto cuando alcanza la velocidad de la luz, ocurre la ruptura de simetría que lo regresa a ser de nuevo energíacampo.
Más riguroso: Si una energíamasa alcanza la velocidad de la luz, se convierte en energíacampo.
De aquí se extraen miles de corolarios:
-Las energíasmasas (partículas) si alcanzan la velocidad de la luz, solo que una vez que la alcanzan, se rompe su topología de confinación, de energíasmasas y se liberan de nuevo como energíascampos. Algo que nunca dejaron de ser. Es que eso nunca las cinco física anteriores lo prohibían; por algo era. Mi modelo no mutila, incorpora,… Son los físicos, los que al no tener un buen modelo, medio que lo veían implícito así en la teoría; que eso no podía suceder. Pero si sucede, solo que nunca pueden sostenerse así.

Tom parece tener en sus manos las respuesto pero… se les escapa entre los dedos
-Nunca una energíamasa (partícula con masa) podrá superar la velocidad de la luz. La conclusión Eisteniana que nadie se ha podido explicar. Vez que fácil es todo, una vez que se va ha la física.
-La velocidad de la luz no es una barrera, la barrera es la ley que confina la energíacampo, en forma de energíamasa. Esa topología, geometría; o relaciona geometrías/energía.
-Toda aniquilación, desintegración y explosión tipo Big Bang (odio, o no creo lo del Big Bang) de los cuerpos del macrocosmo, es por la misma causa.
-De esto se extrae (del modelo también) la ley universal permitibilidad máxima de energía por unidad de espaciotiempo… El VICEVERSA; porque si no todo fuera energíascampos y la naturaleza no ocurre así: Toda energíacampo (luz,…) se confina como energíamasa, cuando su velocidad se hace cero.
-O lo que es lo mismo, ninguna partícula sin masa puede llegar a alcanzar el estado de reposo. Otra cosa que ningún modelo ha explicado, aunque es evidente que es un principio natural. Como todo lo que les explico. ¡Total, si eso es ilegal para el establishment!
De aquí se infieren muchas preguntas, conclusiones, paradojas, o explicaciones más racionales, a muchas cosas que decimos explicadas o que no hemos explicado todavía.

también nosotros estamos inmersos en un campo de energía-masa
La energíascampos (ustedes siempre piensen en la luz como yo al principio, para que no se pierdan) nunca puede estar en reposo (que la energía no puede estar en reposo es conocido, por eso es energía), pero como si existen circunstancias físicas muy especiales, donde esta puede ir disminuyendo su velocidad hasta que sea cero; la naturaleza resuelve esta paradoja, confinando las energíascampos, en diferentes topologías que donde se conserva como energíascampos (mas fácil verlo si piensan en luz); pero exteriormente se manifiesta como un ente, que puede estar en reposo o moverse como un todo; como lo que llamamos partículas con masa ( para mi energíasmasas).
Otra idea que puede ayudarlos a digerir esto: la energíacampo oscila, están acotadas entre la velocidad cero y la velocidad “c”. Esa oscilación, tipo superficie de agua hirviente, es lo que ocurre en la superficie de un agujero negro. Otra revelación de la riqueza física que despliega el modelo.

Te explico mejor: Cuando una energíacampo (luz) cae en un campo tan intenso como el de un agujero negro, su velocidad comienza a disminuir, llegado al “horizonte” (concepto que hay que ampliar) donde su velocidad seria cero; según mi modelo se confina como una energíamasa y trataría de moverse como un todo. Y aquí pueden ocurrir varias cosas que no te he explicado. Según la geometría que adopte la confinación, podrá ser un fermión izquierdo o derecho (una partícula o una antipartícula); así que puede ocurrir aniquilación…
También podría ocurrir que esa partícula (o energíamasa) alcance la velocidad de la luz; es decir regrese ha ser energíacampo, ya te explique por que. Ahora, la gravitación es energíacampo también, y aquí ocurre que ella penetra a la partícula (el mismo proceso de la aniquilación, todo es lo mismo, hay una regularidad natural entre el micromundo y el macromundo, que nadie ve), satura la estabilidad de su topología, y esta se desintegra (aquí tienes la explicación de todos los procesos de desintegración y con el, los tiempos de vida). Pero desintegración en mi razonamientos, en el modelo; es decaer en otra topología de menor energía y cuando esas topologías estables, quedan agotadas por las leyes naturales, que los físicos llamamos de conservación (carga, spin, Isoespin, CP, CPT,…); no le queda otro remedio a la energíamasa; que volver ha ser una energíacampo.

Estaría bien que Tom pudiera, por fín, atrapar con los dedos de la Mente, su teoría Luz-Luz (débil-fuerte) para asombrar al mundo.
Bueno espero haberte complacido en algo, “tuvisteis la exclusividad”, lo dejo ahí porque para que lo digieran y porque tengo muchos problemas que resolver. Tampoco tengo tiempo de leer lo que escribí (como ya es costumbre); pero ustedes son inteligentes como para no crucificarme, así que corrígeme ha tus Dones. Pueden divulgar a su antojo, como siempre les digo, “mi física de café con leche”. Tómense su tiempo para digerirlo, para acostumbrarse a estas nuevas concepciones físicas, esto párese merecerlo, parece novedoso.
Gracias amigo, te agradecemos las revelaciones que, si al fin se abren camino, nos podrían llevar a terrenos más cercanos a la realidad física del mundo. Daríamos un paso adelante en la comprensión del Universo y, como pasa siempre que obtenemos alguna nueva respuesta…¡Podríamos seguir planteando neuvas preguntas! que por cierto, ahora no podemos hacer por no tener ese conocimiento que tú tratas de entregar al mundo.

Sigamos con la Gravedad Cuántica
La física será incompleta y conceptualmente insatisfactoria en tanto no se disponga de una teoría adecuada de la gravedad cuántica. Todos hemos oido hablar de la incompatibilidad de las dos teorías que sustentan hoy por hoy toda la Física y que, todosm también sabemos que, son teorías incompletas que necesitan de una reunificación en un todo poderoso que todo lo puesda explicar.
Durante el siglo XX, la física se fundamentó, en general, sobre dos grandes pilares: la mecánica cuántica y la teoría de relatividad. Sin embargo, a pesar de los enormes éxitos logrados por cada una de ellas, las dos aparecen ser incompatibles. Esta embarazosa contradicción, en el corazón mismo de física teórica, se ha transformado en uno de los grandes desafíos permanentes en la ciencia.
La teoría de la relatividad general da cuenta a la perfección de la gravitación. Por su parte, la aplicación a la gravedad de la mecánica cuántica requiere de un modelo específico de gravedad cuántica. A primera vista, parecería que la construcción de una teoría de gravedad cuántica no sería más problemático que lo que resultó la teoría de la electrodinámica cuántica (EDC), que ya lleva más de medio siglo con aplicaciones más que satisfactorias.

En lo medular, la EDC describe la fuerza electromagnética en términos de los cambios que experimentan las llamadas partículas virtuales, que son emitidas y rápidamente absorbidas de nuevo; el principio de incertidumbre de Heisenberg nos dice que ellas no tienen que conservar la energía y el movimiento. Así la repulsión electrostática entre dos electrones puede ser considerada como la emisión, por parte de un electrón, de fotones virtuales y que luego son absorbidos por el otro.

La misma mecánica, pero a través de los cambios de la partícula virtual de la gravedad el «gravitón» (el quantum del campo gravitacional), podría considerarse para estimar la atracción gravitacional entre dos cuerpos. Pero gravitones nunca se han visto. La gravedad es tan débil que puede obviarse a escala molecular, donde los efectos cuánticos son importantes. Ahora, si los cambios que podrían realizarse en los gravitones sólo se producen en la interacción entre dos puntos de masa, es posible, entonces, que en los cuerpos masivos se ignore los efectos cuánticos. El principio de incertidumbre de Heisenberg nos señala que no podemos medir simultáneamente la posición y la velocidad de una partícula subatómica, pero esta indeterminación es imperceptible para los planetas, las estrellas o las galaxias.
Sí, pero, ¿qué me dices del gravitón?
Pero el principal obstáculo, sin embargo, es la cantidad de complicados procesos que implica examinar un gran número de gravitones. La gravedad se diferencia crucialmente del electromagnetismo al no ser lineal. Esta inlinealidad surge porque la gravedad posee la energía, y ésta tiene la masa, que gravita. En el lenguaje cuántico, esto implica que gravitones interactúan recíprocamente con otro gravitones, a diferencia de los fotones, que interactúan sólo con cargas y corrientes eléctricas y no con otros fotones. Ahora, como los gravitones interactúan el uno con el otro, las partículas de materia son rodeadas por complejas redes de gravitones virtuales que forman «lazos cerrados», muy semejante a «árboles bifurcados».
En la teoría de campo cuántica, los lazos cerrados son un signo de problema; ellos normalmente producen respuestas infinitas en los cálculos de procesos físicos. En EDC, tales lazos ocurren cuando un electrón emite y absorbe de nuevo su propio fotón. En ese caso, los infinitos son soslayados a través de un procedimiento matemático conocido como renormalización. Si éste es hecho correctamente, se obtienen razonables respuestas. La QED es lo que se llama una teoría renormalizable porque todos los infinitos pueden ser soslayados sistemáticamente; en efecto, solo un conjunto de operaciones matemáticas es suficiente para eliminar los infinitos.

Parece que aquí puede estar la solución
Lamentablemente, tal procedimiento sistemático no es operativo cuando la mecánica cuántica es aplicada a la relatividad general; la teoría es, por lo tanto, «no-renormalizable». Cada proceso que implique progresivamente más lazos cerrados de gravitones introduce nuevas variantes de términos infinitos. Lo anterior, coarta la investigación para muchísimos fenómenos de interés, y sugiere que puede que haya básicamente algo que esté errado en la relatividad general, en la mecánica cuántica, o en ambas.
Pero miremos más allá del problema de renormalización, ¿qué pasaría si nos remontáramos a un momento en que todo lo que podemos ver, y hasta lo que hay más allá de nuestro «horizonte» de 13.000 millones de años luz, estaba comprimido hasta un volumen menor que el de un núcleo atómico? A estas densidades descomunales, que se dieron durante los primeros 10-43 segundos del universo (lo que se conoce como «tiempo de Planck»), tanto los efectos cuánticos como la gravedad habrían sido importantes. ¿Qué pasa cuando los efectos cuánticos convulsionan todo un universo?

Por ello, la física será incompleta y conceptualmente insatisfactoria en tanto no se disponga de una teoría adecuada de la gravedad cuántica. Algunos teóricos creen que ya es tiempo de explorar las leyes físicas que prevalecían en el tiempo de Planck, y han propuesto algunas hipótesis interesantes. Sin embargo, no hay consenso sobre qué ideas hay que descartar. Lo que es seguro es que debemos rechazar nuestras queridas concepciones del espacio y el tiempo basadas en el sentido común: el espaciotiempo a muy pequeña escala podría tener una estructura caótica, espumosa, sin ninguna flecha temporal bien definida; puede que haya una generación y fusión continua de agujeros negros primores y minúsculos. La actividad podría ser lo bastante violenta para generar nuevos dominios espaciotemporales que evolucionarían como universos independientes. Eventos más tardíos (en particular la fase inflacionaria que se describe en el capítulo XVI) podrían haber borrado cualquier rastro de la era cuántica inicial. El único lugar donde podrían observarse efectos cuántico-gravitatorios sería cerca de las singularidades centrales de los agujeros negros (de donde ninguna señal puede escapar). Una teoría sin consecuencias evidentes fuera de estos dominios tan exóticos e inaccesibles no es verificable. Para que se la tome en serio debe estar íntimamente insertada o, en su efecto, articulada en alguna teoría con fundamento empírico, o bien debe percibirse como una conclusión inevitable y convincente.
Durante las últimas décadas, varias tentativas han sido hechas para buscarle una solución al problema de la no-renormalización de la gravedad cuántica y caminar hacia la unificación de todas las fuerzas. La aproximación más esperanzadora para alcanzar ese viejo anhelo de los físicos es la teoría de las «supercuerdas», que ya anteriormente vimos.

Sin embargo, recordemos aquí que en la teoría de las supercuerdas se presume una escala natural energética determinada por la energía de Planck, alrededor de unos 1019 GeV. Esto es 1017 veces más alto que los tipos de energías que pueden ser producidos en los aceleradores de partículas más grandes, lo que imposibilita contrastar con la teoría la existencia misma de las supercuerdas. No obstante, los teóricos esperan que a escala de energía accesible tanto la física, la relatividad general, el electromagnetismo, las fuerzas nucleares débiles y fuertes, las partículas subatómicas surjan de la teoría de las supercuerdas como una aproximación. Así, se espera conseguir con ese modelo de cuerdas no sólo una ajustada descripción de la gravedad cuántica, sino que también intentar con ella la anhelada unificación de las fuerzas.
Lamentablemente, no hay un único límite de baja energía para la teoría de las supercuerdas como tampoco un sólo modelo de la teoría. Por un tiempo, lo anterior pareció como una barrera infranqueable, pero en años recientes, y a través de una mayor abstractación matemática, se ha construido un nuevo modelo de supercuerdas conocido como «la teoría M» que amalgama dentro de ella otras teorías de supercuerdas.
Por ahora, es demasiado pronto para pronunciarse si la teoría M es finalmente el medio que reconciliará la gravitación y la mecánica cuántica, pero sí debería poder cumplir con algunas expectativas, como ser las de explicar algunos hechos básicos sobre el mundo físico. Por ejemplo, el espaciotiempo de cuatro dimensional tendría que surgir de la teoría, más bien que ser insertado en ella. Las fuerzas y las partículas de naturaleza también deberían ser descritas, preferentemente incluyendo sus propiedades claves, como fuerzas de interacción y masas. Sin embargo, a no ser que la teoría M, o una variante futura, pueda ser proyectada a la baja energía de los laboratorio de física para poder ser contrastada, corre el riesgo de empezar a ser olvidada y finalmente archivada como uno más de los muchos y elegantes ejercicios matemáticos que se han elaborado para la física en los últimos tiempos.
Cuerdas o filamentos vibrantes en el corazón de la materia
Si la teoría de supercuerda es una pérdida de tiempo o no, ello está por verse. Por ahora, el desafío más duro a superar por la teoría es entender por qué el espacio de 9 dimensiones más el tiempo se «comprime» bajo el aspecto de nuestro espacio habitual tetradimensional (el tiempo más las tres dimensiones espaciales), en vez de hacerlo en tres o cinco dimensiones, y ver cómo sucede esto. Aún hay un espacio infranqueable entre la teoría de supercuerdas y los fenómenos observables. La teoría de supercuerdas plantea problemas demasiado difíciles ahora mismo para los matemáticos. En este aspecto, es muy diferente de la mayor parte de teorías físicas: normalmente, el aparato matemático de las teorías se desarrolla antes que éstas. Por ejemplo, Einstein utilizó conceptos geométricos desarrollados en el siglo XIX, no tuvo que partir de cero para construir las matemáticas que necesitaba.
Por su parte, los físicos cuerdistas se acorralan en lo que es fácil de comprobar, es difícil de calcular y lo que es fácil de calcular, es difícil comprobar. En consecuencia, pareciera que el camino que se está siguiendo es pretender desarrollar la teoría más y más, y hacer cálculos cada vez más difíciles de manera de poder predecir cosas que sean fáciles de observar. ¿El camino tendrá tiempo y final? Nadie tiene por ahora la respuesta.
El físico Eugene Wigner escribió un célebre artículo sobre este particular que llevaba por título «La irrazonable efectividad de la matemática en las ciencias físicas». También es un hecho notable que el mundo exterior muestre tantas estructuras susceptibles de descripción en «lenguaje» matemático (sobre todo cuando tales estructuras se alejan mucho de las experiencias cotidianas que moldearon la evolución de nuestros cerebros). Edward Witten, el principal experto en supercuerdas, describe dicha teoría como «una física del siglo XXI que cayó en el siglo XX». Sin embargo, sería más extraordinario que seres humanos de cualquier siglo llegaran a desarrollar una teoría tan «final» y general como pretenden ser las supercuerdas.
Salvo mejor parecer
















 Totales: 77.895.919
Totales: 77.895.919 Conectados: 98
Conectados: 98


























