Ago
1
¿La Naturaleza? ¡Simetría dentro de la Diversidad!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Simetrías ~
Clasificado en Simetrías ~
 Comments (0)
Comments (0)


Nuestro planeta visto desde el Espacio
Nuestro mundo, aunque en la Galaxia existan muchos como él (que no los hemos podido encontrar), es un lugar privilegiado que conforma un Ecosistema superior en su conjunto formado por muchos ecosistemas locales aislados los unos de los otros y sin embargo, todos conexionados. La Diversidad de regiones diferentes que existen dentro del mismo planeta es asombrosa y, lo mismo nos podemos encontrar en un lugar como ese que vemos arriba, o en una isla paradisíaca, una selva, un desierto, o perdidos en un inmenso y embravecido océano, en la ventisca de nieve de inmensas montañas y, también, en grutas enormes en las profundidades del planeta.
“”La posición de la Tierra en el sistema solar también es privilegiada, ya que tiene un cuerpo gigante, Júpiter, que la protege de cometas y asteroides. Tiene, además, una atmósfera casi única que hace posible la vida, un efecto invernadero y un campo magnético que la protege de las radiaciones.”
Pero todos esos climas diferentes son el resultado de la diversidad y, en cada uno de esos lugares ocurren cosas y, la vida, aunque parezca imposible, está allí presente. Es la consecuencia de que el planeta Tierra esté situado en la zona habitable del Sol, ni demasiado cerca para que la vida perezca achicharrada, ni demasiado lejos para que resulte congelada por el frío. Aquí el agua discurre líquida y cantarina por multitud de lugares y hace posible que, entre el preciado líquido y los rayos del Sol que nos envían la luz y el calor necesarios para la fotosíntesis y la vida… ¡Podamos estar aquí!
“El electromagnetismo es la rama de la física que estudia las relaciones entre los fenómenos eléctricos y magnéticos, es decir, entre el campo magnético y la corriente eléctrica.”
Fuente: https://concepto.de/electromagnetismo/#ixzz5sIhuRCgE
Todos sabemos que la materia en nuestro Universo adopta muchas formas distintas: Galaxias de estrellas y mundos que, en alguna ocasión, pueden incluso tener seres vivos y algunos han podido evolucionar hasta adquirir la consciencia. Sin embargo, no me quería referir a eso que es bien sabido por todos, sino que, trato de pararme un poco sobre una curiosa propiedad que la materia tiene en algunas ocasiones y que, la Naturaleza se empeña en repetir una y otra vez: ¡La Simetría!
Las Galaxias espirales, la redondez de los mundos, las estrellas del cielo, los árboles y las montañas, los ríos y los océanos, las especies animales (incluida la nuestra) que, se repiten una y otra vez y, en general, salvando particularidades, todas repiten un patrón de simetría.
Recuerdo aquí aquel pensamiento de Paul Valery en el que nos decía:
“El Universo está construido según un plan cuya profunda simetría está presente de algún modo en la estructura interna de nuestro intelecto.”

La Naturaleza está llena de simetrías
La simetría es una propiedad universal tanto en la vida corriente, como desde un punto de vista matemático desde el quehacer de la Física Teórica. En realidad, lo que observamos en la vida corriente es siempre lo repetitivo, lo simétrico, lo que se puede relacionar entre sí por tener algo común. Es siempre lo mismo dentro de una inmensa diversidad formada por grupos iguales.
En un sentido dinámico, la simetría podemos entenderla como lo que se repite, lo reiterativo, lo que tiende a ser igual. Es decir, los objetos que, por mantener la misma geometría, son representativos de otros objetos. En el Caos matemático encontramos concepción de la simetría en el mundo los fractales. Sin embargo, la simetría es mucho más. Hay distintas maneras de expresarla: “Conjunto de invariancias de un sistema”, podría ser una de ellas. Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado, la simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y las rotaciones en las moléculas y las translaciones en las redes cristalinas.

Aquí hay mucho más de lo que a simple vista parece.

La divina proporción aurea, el nñume3ro de oro (PHI)
Los físicos teóricos también se guían en sus investigaciones por motivaciones estéticas tanto como racionales. Poincaré escribió: “Para hacer ciencia, es necesario algo más que la pura lógica”. Él identificó ese elemento adicional como la intuición, que supone “el sentido de la belleza matemática”. Heisenberg hablaba de “la simplicidad y belleza de los esquemas matemáticos que la Naturaleza nos presenta”.

La simetría está presente por todas partes y, cada objeto, tiene la suya que siempre, está relacionada con la de otro de la misma especie. Hay simetrías que en física incluye todos los rasgos de un sistema físico que exhibe propiedades de la simetría – eso es, que bajo ciertas transformaciones, aspectos de esos sistemas son “incambiables”, de acuerdo a una observación particular. Una simetría de un sistema físico es un rasgo físico o matemático de un sistema que es preservado sobre cierto cambio.
En matemática, una transformación es un operador aplicado a una función tal que bajo esa transformación, ciertas operaciones sean simplificadas. En ejemplo, en la aritmética cuando se busca un algoritmo de números, el proceso de búsqueda es reducido a la suma de los algoritmos de cada factor.

Por ejemplo, veamos la invariancia de escala: En un recipiente con agua a punto de hervor, las burbujas de vapor, nucleadas en el fondo del recipiente, crecen, se liberan, y fluctúan hasta la superficie de donde se escapan para la atmósfera. A la temperatura de ebullición, el agua existe al mismo tiempo en dos fases distintas – líquido y gas – y a medida que las burbujas se forman las dos fases se separan en el espacio. Si cerramos el recipiente la temperatura de ebullición aumenta, como en una olla a presión. A medida que la presión aumenta, el sistema llega al punto crítico, donde las propiedades del líquido y del gas se vuelven idénticas. Por encima de esa temperatura, en el régimen supercrítico, dejan de existir dos fases distintas y existe apenas un fluido homogéneo.

Cerca del punto crítico, la materia fluctúa sin límites. Burbujas y gotas, unas tan pequeñas como unos cuantos átomos, otras tan grandes como el recipiente, aparecen y desaparecen, se unen y se separan. Exactamente en el punto crítico la escala de las mayores fluctuaciones divergen, pero el efecto de las fluctuaciones en escalas menores no es despreciable. La distribución de las fluctuaciones es invariable para transformaciones de escala.
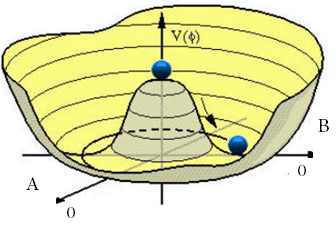
De la figura se deduce que la teoría tiene una “simetría interna”: la figura no cambia cuando hacemos rotaciones en el plano definido por A y B. La invariancia es definida matemáticamente por transformaciones que dejan magnitudes sin cambio. Por ejemplo, la distancia entre dos puntos de un sólido que se mueve, pero no se deforma.
Simetrías locales y globales
Una simetría global es una simetría que sostiene todos los puntos en el tiempo-espacio bajo consideración, a diferencia de la simetría local que solo sostiene a un subconjunto de puntos.
Un lagrangiano

La mayoría de las teorías físicas son descritas por lagrangianos (En física, un lagrangiano es una función matemática a partir del cual se pueden derivar la evolución temporal, las leyes de conservación y otras propiedades importantes de un sistema físico) que son invariantes bajo ciertas transformaciones, cuando las transformaciones son realizadas en diferentes puntos del espacio-tiempo y están relacionadas linealmente – ellas tienen simetría global.
Por ejemplo, en toda teoría cuántica la fase global de una función de onda es arbitraria y no representa algo físico. Consecuentemente, la teoría es invariante bajo a cambio global de fases (Agregando una constante a la fase de todas las funciones de onda, en todos lados); esto es una simetría global. En la electrodinámica quántica, la teoría es también invariante bajo un cambio local de fase, es decir, que se puede alterar la fase de todas las funciones de onda tal que la alteración sea diferente en cada punto del espacio-tiempo. Esto es una simetría local.

También se habla de ruptura de simetrías temporales en la física de partículas.
Los físicos creen también que están en el camino correcto porque, de algún modo que no pueden explicar, tienen la convicción de que son correctas, y las ideas de simetría son esenciales para esa intuición. Se presiente que es correcto que ningún lugar del Universo es especial comparado con cualquier otro lugar del Universo, así que los físicos tienen la confianza de que la simetría de traslación debería estar las simetrías de las leyes de la Naturaleza. Se presiente que es correcto que ningún movimiento a velocidad constante es especial comparado con cualquier otro. De modo que los físicos tienen confianza en que la relatividad especial, al abrazar plenamente la simetría entre todos los observadores con velocidad constante, es una parte esencial de las leyes de la Naturaleza.
Se dice que esta ecuación de Euler es la más bella conocida. Aunque son muchas las ecuaciones que podríamos traer aquí y que son de todos conocidas y han quedado como símbolos en la historia de las matemáticas, la de Euler, es posible que por su elegancia y simplicidad, le pueda ganar a las demás en belleza. Ahí, en ese sencillo conjunto, los números más significativos de las matemáticas se abrazan: o, 1, e, π, y la unidad imaginaria i .
Si se fijan en la fórmula, en ella aparecen los 5 números más importantes en la historia de las matemáticas. El 0 y el 1 que, entre otras aportaciones a esta disciplina, son famosos por ser elementos neutros y, por lo tanto, indispensables en las operaciones de suma y producto; los números π y e, posiblemente, los dos irracionales más famosos (junto con φ, la razón aúrea) que existen (y que nos permiten hacer el chiste aquel de que la parte más irracional de nuestro cuerpo es el pi-e); y la unidad imaginaria, i, cuyo valor es
La BBC Earth le preguntó a matemáticos y físicos qué ecuaciones piensan que son las más hermosas. ¡Aquí las 12 elegidas! las ecuaciones que ellos piensan son las más bonitas.

La ecuación de Dirac arriba. La ecuación fue descubierta a finales de los años 20 por el físico Paul Dirac, y juntó dos de las ideas más importantes de la ciencia: la mecánica cuántica, que describe el comportamiento de objetos muy pequeños; y la teoría especial de Einstein de la relatividad, que describe el comportamiento de objetos en movimiento rápido.
La ecuación fue descubierta por el físico Paul Dirac a finales de los años 20 y junta la mecánica cuántica y la teoría especial de Einstein de la relatividad, que describe el comportamiento de objetos en movimiento rápido. En otras palabras, explica cómo las partículas se comportan cuando viajan a casi la velocidad de la luz.
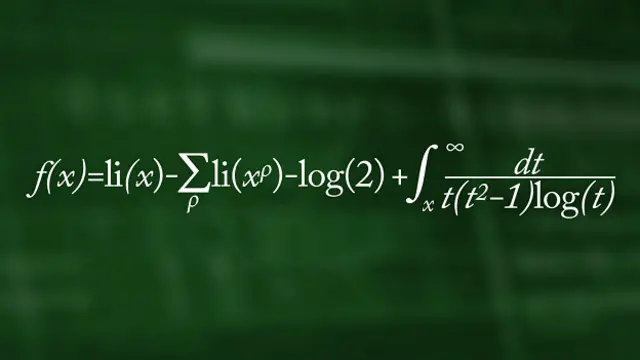
El matemático Bernhard Riemann publicó esta ecuación en 1859
Permite calcular los números primos por debajo de un número dado. “Son los números más básicos e importantes en el corazón del mundo de la matemática. Pero sorprendentemente, a pesar de más de 2000 años de investigación, todavía no los entendemos”, explica Marcus du Sautoy de la universidad de Oxford.
Pi
Pi es la ecuación de la circunferencia, la relación entre la circunferencia y el diámetro de un círculo. Además es un número irracional, lo que significa que los dígitos pueden continuar indefinidamente sin que se repitan.
En uno de los artículos científicos revolucionarios de Albert Einstein publicado en 1905, se introdujo el concepto de E=mc2, donde “E” es energía, “m” es masa y “c” es la velocidad de la luz en el vacío.[1]Desde entonces, E=mc2 se ha convertido en una las ecuaciones más famosas del mundo. Incluso las personas que no tienen conocimiento de física al menos han oído sobre esta ecuación y saben la enorme influencia que tiene en el mundo en que vivimos. Sin embargo, la mayoría de las personas no saben exactamente qué es lo que significa. En términos simples, la ecuación representa la equivalencia entre la masa y la energía; básicamente indica que ambas son solo dos formas diferentes de la misma cosa.[2]Esta simple ecuación ha alterado la forma en la que pensamos sobre la energía y nos ha permitido crear un gran número de avances tecnológicos.
“La ecuación de Euler-Lagrange fue desarrollada en 1750 por Euler y Lagrange como solución al problema de la tautócrona (caso general de la braquistócrona): consiste en determinar la curva de la trayectoria que describiría el descenso en la que una partícula con masa cae a cierto punto, en un tiempo dado, independiente de su posición inicial.
Lagrange resolvería el problema en 1755 y enviaría la solución a Euler. Ambos desarrollarían aún más el método de Lagrange y lo aplicarían a problemas de mecánica; cosa que a su vez conduciría a formular por vez primera la mecánica lagrangiana. Dicha correspondencia también desembocaría en el desarrollo del cálculo de variaciones, un término acuñado por el mismo Euler en 1766.”
Esta ecuación se utiliza para analizar todo. “Más que una ecuación, es una receta para generar una infinita variedad de posibles leyes de física”, comenta Andrew Pontzen de la University College London.
La entidad de
En matemáticas, la identidad de Euler es la igualdad: Función exponencial ez puede definirse como el límite de una secuencia (1 + z/N)N, con N tendiendo a infinito, y así e iπ es el límite de (1 + iπ/N)N.
La ecuación de onda.
El autor de la ecuación matemática más famosa es Leonhard Euler, de ahí que lleve su nombre: la identidad de Euler, llamada «identidad» porque en ella solo existen números. Aunque en la fórmula veamos letras, estas representan en realidad números.
La identidad más famosa de las matemáticas. La Identidad de Euler es la fórmula más famosa de las matemáticas, ya que liga los cinco números más famosos de la matemática e, i, π , 1 y 0. ¡Sólo falta Φ
Demostró el último teorema de Fermat para n = 3, donde introdujo cálculo con números algebraicos. Se puede afirmar que el análisis matemático comienza con Euler.
La fórmula de Euler es eⁱˣ=cos(x)+i⋅sin(x), y la identidad de Euler es e^(iπ)+1=0. Observa cómo se obtienen estas relaciones por medio de las series de Maclaurin de cos(x), sin(x) y eˣ. ¡Estos son algunos de los resultados más sorprendentes de las matemáticas!
“La belleza de la ecuación de la onda se manifiesta de muchas formas”, explica Ian Stewart de la universidad de Warwick del Reino Unido. Se aplica a todo tipo de ondas, desde las de agua a las de sonido y vibraciones. Incluso a las ondas de luz y radio.
Este teorema tiene más usos de los que uno se imagina, calcula la probabilidad que un evento (A) sea real, dado que otro evento (B) también lo es. Tiene muchos usos, como para detectar fallas de vigilancia, defensa militar, operaciones de búsqueda y rescate, en escáneres médicos en incluso para filtros de correos electrónicos no deseados.
Pasamos a la ecuación de campo de Einstein
Tensor de curvatura de Einstein, que se forma a partir de derivadas segundas del tensor métrico gμν
Tensor momento-energía c Velocidad de la luz G Constante de la gravitación universal
Esta ecuación es en realidad un sumario de diez ecuaciones. Katie Mack, de la universidad de Melbourne en Australia, explica que estas fórmulas cambiaron completamente cómo entendemos la naturaleza y evolución del Universo. La ecuación de Einstein nos puede decir cómo nuestro universo ha cambiado con el tiempo, y ofrece un vistazo de los primeros momentos de la creación.
Es un prodigio de la Mente humana
Dirac nos hablaba de ecuaciones bellas. La estética es, evidentemente, subjetiva, y la afirmación de que los físicos buscan la belleza en sus teorías tiene sentido sólo si podemos definir la belleza. Afortunadamente, esto se puede , en cierta medida, pues la estética científica está iluminada por el sol central de la simetría.
La Naturaleza nos la muestra por todas partes
La simetría es un concepto venerable y en modo alguno inescrutable y no podemos negar que tiene muchas implicaciones en la Ciencia, en las Artes y sobre todo, ¡en la Naturaleza! que de manera constante nos habla de ella. Miremos donde miremos…¡allí está!

El físico chino-norteamericano Chen Ning Yang ganó el Nóbel de Física por su en el desarrollo de una teoría de campos basada en la simetría y, aún afirmaba: “No comprendemos todavía el alcance del concepto de simetría”. Es lógico pensar que, si la Naturaleza emplea la simetría en sus obras, la razón debe estar implicada con la eficacia de los sistemas simétricos.
En griego, la palabra simetría significa “la misma medida” (syn significa “juntos”, como en sinfonía, una unión de sonidos, y metrón, “medición”); así su etimología nos informa que la simetría supone la repetición de una cantidad medible. Pero la simetría los griegos, también significaba la “la debida proporción”, lo que implicaba que la repetición involucrada debía ser armoniosa y placentera, como de hecho, resultan ser en las imágenes que arriba contemplamos. Asi, la Naturaleza nos está indicando que una relación simétrica debe ser juzgada por un criterio estético superior.

Humo simétrico
Muchos de nosotros, la mayoría, conocimos la simetría en sus manifestaciones geométricas de aquellas primeras clases en la Escuela Elemental, más tarde en el arte y, finalmente, la pudimos percibir en la Naturaleza, en el Universo y en nosotros mismos que, de alguna manera, somos de ese Universo de simetría.
Los planetas son esféricos y, por ejemplo, tienen simetría de rotación. Lo que quiere indicar es que poseen una característica -en caso, su perfil circular- que permanece invariante en la transformación producida cuando la Natuiraleza los hace rotar. Las esferas pueden Hacerse rotar en cualquier eje y en cualquier grado sin que cambie su perfil, lo cual hace que sea más simétrica.

La clave de la belleza está en la simetría
La simetría por rotación se encuentra en los pétalos de una flor o en los tentáculos de una medusa: aunque sus cuerpos roten, permanecen iguales. La simetría bilateral que hace que los lados derecho e izquierdo sean iguales y se presenta en casi todos los animales, incluido nosotros. Pero es uniendo estos aspectos se obtienen figuras realmente armoniosas. Si se trata de desplazamiento y rotación en un mismo plano hablamos de una espiral, mientras que en el espacio sería una hélice, aunque ambas se encuentran por todas partes en la naturaleza.
Las simetrías se generan mediante las fuerzas que actúan sobre los cuerpos, descritas por leyes rigurosas e inequívocas, como una fórmula matemática y dependen de la existencia de fuerzas distintas que actúan en diversas direcciones. Si éstas permanecen en equilibrio, no hay preferencia alguna hacia arriba o abajo, a la derecha o a la izquierda, y los cuerpos tenderán a ser perfectamente esféricos, como suele ocurrir en el caso de virus y bacterias, las estrellas y los mundos… las galaxias. Además, cuando el aspecto no es el de una esfera perfecta, la Naturaleza hará todo lo posible para acercarse a esta.

La simetría también están presentes en nuestros cerebros
¿Sería posible que la simetría material tuviera un paralelismo en la abstracción intelectual que son las leyes físicas? luego hace falta un esfuerzo mental considerable para pasar de lo material a lo intelectual, pero cuando se profundiza en ellla, la conexión aparece. En la naturaleza existen muchas cosas que nos pueden llevar a pensar en lo complejo que puede llegar a resultar entender cosas que, a primera vista, parecían sencillas.
Me explico:

Fijémonos, por ejemplo, en una Flor de Girasol y en las matemáticas que sus semillas conllevan. Forman una serie de números en la que cifra es la suma de las dos precedentes (por ejemplo 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…) se denomina, en términos matemáticos, sucesión de Fibonacci, una ley que se cumple incluso en el mundo vegetal, como hemos podido comprobar en las semillas del girasol, dispuestas en espiral y que respetan ésta fórmula. La podemos ver por todas partes.

Lo mismo ocurre con otros ejemplares de la diversidad del mundo de las plantas
En el mundo inorgánico las leyes de la cristalización del agua congelada, determinadas por las fuerzas que actúan entre las moléculas, hacen que los cristales adopten formas que son infinitas y varían con respecto a un tema común: la estrella de seis puntas. Sin embargo, los planetas son esféricos porque han nacido en la primordial que rodeaba al Sol, atrayendo materia indiferentemente de todas partes.





Claro que, en la Naturaleza, nada ocurre porque sí, todo tiene su por qué, y, todo lo que en ella podemos contemplar posee una funcionalidad que está directamente relacionada con su mecánica, con el medio en el que habita, con lo que el Universo espera que haga en su medio y, para ello, dota a figura con aquellos “trajes” que mejor les permita realizar aquello para lo que están destinados.
Vamos a generalizar un paso más el concepto de simetría, planteándonos si es posible que una ley física se cumpla en cualquier lugar. ¿En cualquier lugar… de dónde?, ¿de nuestra ciudad?, ¿de nuestro planeta? No: del universo. Una ley que fuera válida en cualquier lugar del universo sería una ley simétrica respecto al espacio. Se cumpliría dondequiera que se hiciese un experimento para comprobarla.

La simetría de las galaxias espirales
Fíjense que nuestra idea de simetría se va haciendo más compleja y más profunda. no nos detenemos en ver si la forma material de un objeto es simétrica, ni de si la escritura de una fórmula matemática es simétrica. Ahora nos preguntamos si una ley física es válida en todo el Universo.
La otra simetría interesante para una ley física es la que se refiere al tiempo. Cierta ley física se cumple ; ¿antes también?, ¿se cumplirá pasado algún tiempo? Una ley que fuera cierta en cualquier instante de la historia del universo sería una ley simétrica respecto al tiempo.

Lo que nos preguntamos es: ¿son simétricas o no las leyes de la física?
Hasta donde alcanzan nuestras medidas, las leyes físicas (y, por tanto, la interacción gravitatoria) sí son simétricas respecto al espacio y respecto al tiempo. En cualquier lugar y momento temporal del universo, la Naturaleza se comporta igual que aquí y ahora en lo que se refiere a estas leyes.

Todas las especies son simétricas entre sí
Esta simetría es un arma muy poderosa para investigar hacia el pasado y hacia el futuro, ya que nos permite suponer (y, en la medida en que confiemos en la seguridad de la simetría, conocer) locales donde jamás podremos llegar por la distancia espacial y temporal que nos separa de muchas partes del universo. Así, por ejemplo, gracias a esta simetría, podemos calcular que el Sol lleva 5.000 millones de años produciendo energía y que le quedan, probablemente, otros 5.000 millones hasta que consuma toda su masa. Esto lo podemos aventurar suponiendo que en ese enorme tramo de 5.000 + 5.000 = 10.000 millones de años las leyes físicas que determinan los procesos mediante los cuales el Sol consume su propia masa como combustible (las reacciones nucleares que le permiten producir energía), fueron, son y serán las mismas aquí en el Brazo de Orión donde nos encontramos como en los arrabales de la Galaxia Andrómeda donde luce una estrella como nuestro Sol que, también envía luz y calor a sus planetas circundantes, y, por muy lejos que podamos mirar, siempre veremos lo mismo.
Por tanto, en cierto modo, la simetría se vuelve tan importante o más que la propia ley física.

La regularidad de las formas de la Naturaleza se refleja incluso en la cultura humana, que desde siempre intenta inspirarse en el mundo natural conformar su propio mundo. Existen hélices en las escaleras de palacios, castillos y minaretes y en las decoraciones de esculturas y columnas. Las espirales abundan en los vasos, en los bajorrelieves, en los cuadros, en las esculturas en los collares egipcios, griegos, celtas, precolombinos e hindúes e, incluso, en los tatuajes con los que los maoríes neozelandeses se decoran el rostro.

¿Tenía en mente Leonardo la proporción áurea a la hora de realizar su obra maestra? Afirmarlo resultaría aventurado. Menos polémico es aseverar que el genio florentino concedía gran importancia a la relación entre la estética y la matemática. Dejaremos la cuestión en el aire por el momento, no sin antes mencionar que Leonardo realizó las ilustraciones de una obra de contenido estrictamente matemático, escrita por su buen amigo Luca Pacioli, llamada “De divina proportione”, es decir, “La divina proporción”.
La proporción aurea
La búsqueda de la perfección geométrica y de las propiedades matemáticas pueden ser una guía importante en el estudio científico del mundo. Paul Dirac, una de los padres de la moderna mecánica cuántica, solía decir que “si una teoría es bella desde el punto de vista matemático, muy probablemente es también verdadera”.
A todo esto, no debemos olvidar que todo, sin excepción, en nuestro Universo, está sometido a la Entropía que nos trae el paso inexorable de eso que llamamos “Tiempo”, y que, convierte perfectas simetrias de joven belleza, en deteriorados objetos o entidades que, nos viene a recordar que nada es perpetuo, que todo pasa y se transforma. Claro que, de alguna manera, todo vuelve a resurgir.

La Belleza más valiosa no la podemos ver. ¡Vive en el interior!
Un dolor que llevo dentro de mí es el no poder contemplar la verdadera belleza que estando presente en los seres vivos inteligentes, en la mayoría de los casos, se nos queda oculta a nuestra percepción, toda vez que esa clase de belleza, que no podemos ver pero sí percibir, sólo la podemos captar con el trato y la convivencia y, verdaderamente, tengo que admitir que, algunas bellezas que he tenido la suerte de poder “ver con los ojos del espíritu”, llegan a ser segadoras, deslumbrantes, su esplendor es muy superior al de la estrella más brillante del cielo, y, seguramente (estoy seguro) como a muchos de ustedes les pasa, tengo la suerte de tenerla junto a mí desde hace muchos años. y, si pienso en ello en profundidad y detenimiento, no tengo más remedio que concluir que es ese brillo y esplendor el que me da la fuerza para seguir cada dia en la dura lucha que nos ha participar.
¡Sí que es importante la Belleza! Dirac tenía toda la razón. Y, no digamos las Simetrías que nos señala el dedo de la Naturaleza el camino a seguir a muchos físicos que quieren desvelar sus secretos.
Emilio Silvera V.
Ago
1
El transcurrir del Tiempo hace que todo cambie
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo cambiante ~
Clasificado en El Universo cambiante ~
 Comments (0)
Comments (0)
La casualidad quiso que la órbita de la Estación Espacial Internacional pasara por encima de la isla rusa de Matua, hev een el archipiélago de las Kuriles, instantes después de que el estratovolcán Sarycntrara en erupción. Las imágenes que fueron tomando los astronautas desde 350 Km de altura son impresionantes:
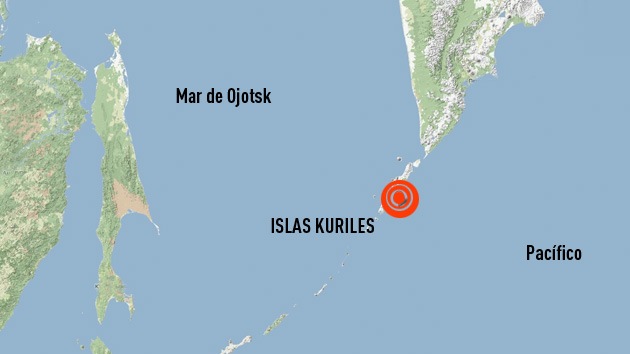
El Caos y la destrucción que nos puede dar la variedad de colores, olores y sabores que junto con la belleza destruida o construida cambiará el paisaje del lugar donde puedan ocurrir acontecimientos como este que observan los tripulantes de la Estación Espacial Internacional, como bien se dice, desde su privilegiada atalaya.
Los volcanes han existido desde los inicios de la Tierra hace 4.500 millones de años. Si bien las erupciones volcánicas pueden destruir la flora y la fauna en su entorno, la lava enriquece el suelo con variados minerales. La mayor parte de los volcanes están situados a lo largo de los límites activos de las placas continentales. Los volcanes submarinos se hallan en regiones donde tienen lugar nueva formación de corteza terrestre, como en la dorsal oceánica. Estos volcanes pueden formar islas.
Los volcanes terrestres se encuentran, por lo general, en zonas de subducción, que se hallan especialmente en el Océano Pacifico. Los volcanes situados en las regiones costeras están distribuidos como una “sarta de perlas” y constituyen el anillo de fuego del Pacífico., en el que se encuentran más del 80% de los volcanes actuales. Además, los “puntos calientes” donde la fusión interna de la corteza crea magma, producen volcanes que son independientes de las placas continentales y sus limites. Un ejemplo de de este grupo lo constituyen los volcanes de Hawai.
Los volcanes se alimentan de las cámaras magmáticas, una especie de bolsas de rocas fundidas, a más de 1 km bajo la corteza terrestre. Si la presión en la cámara sobrepasa un determinado nivel (que es que parece que ha ocurrido en el de la imagen), el magma asciende por fisuras y grietas y forma una chimenea volcánica.

En el interior de esas montañas están activos materiales en forma de gases, líquidos y sólidos, todo a altas temperatura y presión. Cuando se producen las explosiones las zonas circundantes son bombardeadas con materiales y enterradas bajo una gruesa capa de ceniza en poco tiempo. Es la erupción denominada piroclástica (como la ocurrida en el año 79 a.C. que sepultó la ciudad de Pompeya bajo una capa de cenizas de 25 cm. de espesor) y los materiales pueden llegar a formar una nube piroplástica de 1.000 Cº de temperatura que puede desplazarse a 1.000 Km/h.
Hay diferentes tipos de explosiones volcánicas y en cada una de ellas se producen diferentes acontecimientos pero, como sólo se trata de dejar una leve y sencilla reseña de lo que estamos viendo en la imagen, creo que con la explicación dada queda bien.
Hasta hace muy poco no podía predecir este tipo de fenómenos naturales y, la gente que vivía en poblaciones situadas cercas de las laderas volcánicas estaban en peligro auque raramente, se producían erupciones espontáneas sin avisos previos como los terremotos, los volcanes y sus actividades son controladas por sismógrafos.



Los cráteres volcánicos, como parece ser el caso, están frecuentemente llenos de agua de lluvia y freáticas, formando lagos. Suele ocurrir que, tras una erupción volcánica, sean destruidos miles de kilómetros cuadrados de terreno a su alrededor y cambien por completo la orografía de la zona. Parece imposible pensar que la Naturaleza pueda recuperarse tras un acontecimiento de este tipo, sin embargo, las primeras muestras de vida vegetal aparecen a unos escasos tres meses del acontecimiento en los campos cubiertos por las cenizas ricas en minerales. Poco tiempo después, vuelven los animales y la vida, se reanuda, como si allí, nada hubiese pasado.
Así es la Naturaleza, y, como tantas veces se dijo aquí, algo se destruye para que algo surja a la vida. ¿Esperanza después de la muerte?
Emilio Silvera V.
Jul
31
¡Qué historias! ¡Qué personajes! ¡Qué tiempos!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Rumores del Saber ~
Clasificado en Rumores del Saber ~
 Comments (0)
Comments (0)
Es una hermosa y terrible historia esta de la navegación. Bella y espantosa como el mar mismo. Porque frente a las notables proezas de los marinos de todos los tiempos, a sus descubrimientos, a sus maravillosas leyendas y tradiciones, al colorido de los piratas, corsarios y bucaneros, se oponen la sórdida condición de los marineros antes del advenimiento del vapor, los galeotes encadenados a los remos, las estremecedoras historias de los barcos devorados por el mar, los cientos de batallas despiadadas que se libraron en sus aguas y, en último análisis, el universo desconocido y ominoso que vive subyacente en las entrañas del océano.

La tempestad
“Escrito en 1611 y estrenado el mismo año, este drama en cinco actos en verso y prosa de William Shakespeare se publicó en el in-folio de 1623, donde precede a todas las demás piezas. La fuente de esta obra debe buscarse en la commedia dell’arte italiana; algunas intrigas análogas a la suya han sido descritas por diversos estudiosos. Shakespeare combinó con estos elementos italianos detalles del naufragio en las Bermudas de sir George Somers (25 de julio de 1609). Otros eruditos consideran como fuente probable de la tragedia la novela castellana La gran conquista de Ultramar.”
La gran conquista de Ultramar


Los navegantes, tal como narraba Shakespeare, gustaban de exagerar sus experiencias y hablaban de hombres cuyas cabezas nacían abajo de los hombros, o que no tenían cabeza, o de aquellos que, como los patagones, sólo tenían un pie muy grande, o los de Labrador, que tenían cola. Todo esto originó un “renacimiento de la superstición”. Aquellos viajeros crearon en sus mentes escenarios fantásticos, que los situaban más allá del tiempo y del espacio, en mundos ignotos donde nuevos órdenes de razas monstruosas de animales fantásticos existían. Dado que es casi tan difícil inventarse un animal nuevo como descubrirlo, a las criaturas míticas y folklóricas conocidas se les añadieron otros rasgos imaginarios.
como descubrirlo, a las criaturas míticas y folklóricas conocidas se les añadieron otros rasgos imaginarios.
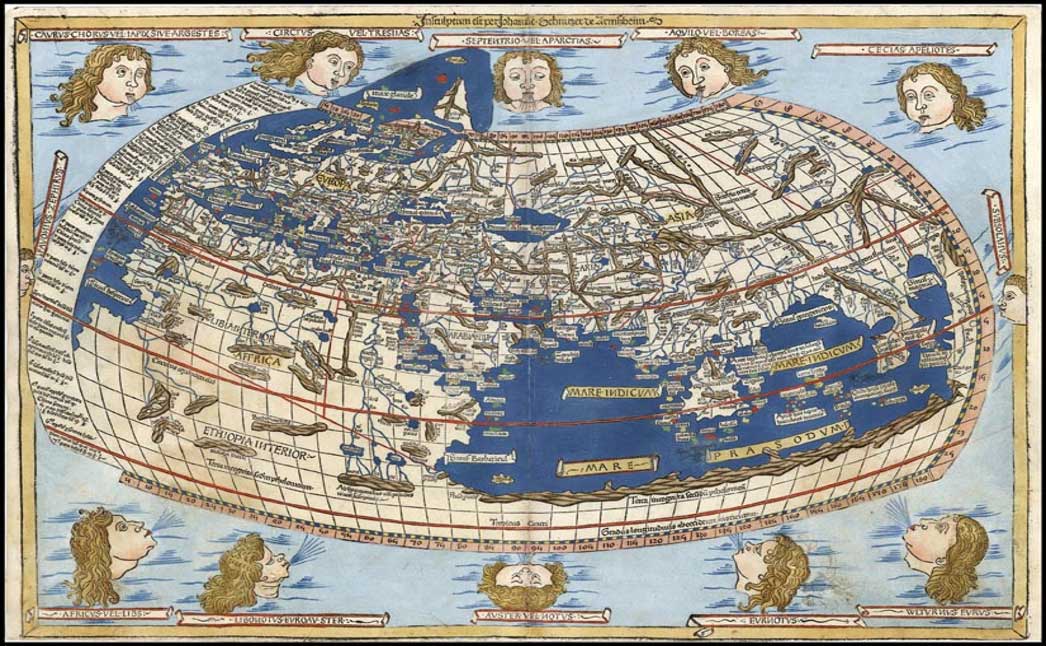
Así, la era del descubrimiento trajo consigo un renacimiento de la fábula. Las serpientes marinas de ciento cincuenta metros de largo se multiplicaron como nunca, y, era raro el marinero que habiendo viajado a lejanos horizontes de nuevas tierras, no contaba, a su regreso, fantásticas historias de animales que sobrepasaban la fantasía de la imaginación más creadora: Sirenas y Tritones, Unicornios y hasta bellas mujeres de larga cabellera que andaban suavemente por encima del agua de maravillosos lagos de cascadas de increíble belleza.
bellas mujeres de larga cabellera que andaban suavemente por encima del agua de maravillosos lagos de cascadas de increíble belleza.


La imaginación desmesurada de los marines aventureros
Las leyendas dudosas eran ahora confirmadas por jesuitas misioneros, por adinerados plantadores de azúcar y por sobrios capitanes de barcos. A las quimeras de la fantasía medieval se añadían ahora criaturas reales cuyas noticias llegaban con cada viaje procedente de las Américas, de China y de otros lejanos horizontes. Los que no leían latín podían disfrutar de las numerosas ilustraciones que acompañaban a los textos que abundaban para deleite de los más soñadores.
confirmadas por jesuitas misioneros, por adinerados plantadores de azúcar y por sobrios capitanes de barcos. A las quimeras de la fantasía medieval se añadían ahora criaturas reales cuyas noticias llegaban con cada viaje procedente de las Américas, de China y de otros lejanos horizontes. Los que no leían latín podían disfrutar de las numerosas ilustraciones que acompañaban a los textos que abundaban para deleite de los más soñadores.
Imágenes como esas de arriba, eran las que adornaban aquellas pioneras publicaciones en las que se contaban las historias de marineros-aventureros que, viniendo de lugares lejanos, siempre traían consigo narrativas de leyendas que dejaban boquiabiertos a los lectores u oyentes de las mismas.

Todo aquello inspiró el surgir de una nueva generación de enciclopedistas de la Naturaleza. El más destacado de todos ellos, Konrad Gesner (1516-1565), tenía habilidad para combinar lo nuevo con lo antiguo. Gesner, que conocía extraordinariamente bien varias lenguas, se debatía entre lo que había leído y lo que veía.
con lo antiguo. Gesner, que conocía extraordinariamente bien varias lenguas, se debatía entre lo que había leído y lo que veía.


Gesnerus y sus criaturas
A los 20 años escribió un diccionario Griego-Latin. Durante los treinta años que siguieron produjo treinta violúmes sobre todos los temas imaginables. Su monumental Biblioteca Universal en cuatro volúmes (1545-1555) pretendía ser un catálogo de todos los escritos producidos en griego, latín y hebreo a lo largo de la historia.

Gesner clasificó mil ochocientos autores y los títulos de sus obras manuscritas e impresas, acompañadas de un resumen de su contenido. De este modo ganó el título de “padre de la bibliografía”. La bibliografía sería para las Bibliotecas lo que la cartografía para los exploradores de la tierra y de los mares.
En la Biblioteca de los Fugger, Gesner encontró un manuscrito griego enciclopédico del siglo II que le inspiró para convertirse en un Plinio moderno. Por fin, su Historia Animalium, que seguía la disposición de Aristóteles, recogíam todo lo que se conocía, especulaba, imaginaba o contaba de cada uno de los animales conocidos. Como Plinio, Gesner produjo una miscelánea, pero añadió los datos que se habían acumulado en el milenio y medio transcurrido desde entonces. Sin bien era algo más crítico que Plinio, él tampoco desmintió las leyendas increíbles, y mostró una serpiente marina de noventa metros de largo. Pero describió la caza de ballenas e incorporó la primera ilustración de una ballena que estaba siendo despellejada para obtener la grasa.
que se habían acumulado en el milenio y medio transcurrido desde entonces. Sin bien era algo más crítico que Plinio, él tampoco desmintió las leyendas increíbles, y mostró una serpiente marina de noventa metros de largo. Pero describió la caza de ballenas e incorporó la primera ilustración de una ballena que estaba siendo despellejada para obtener la grasa.

Unicornios montados por bellas y misteriosas amazonas y otras fantásticas criaturas llenaban las mentes con la única libertad que se nos ha dado ¡El Pensamiento! ¿Quién no ha pensado alguna vez en fantásticos mundos poblados por criaturas de inimaginable belleza, o, también, de fealdad indescriptible.


La duradera influencia de la obra de Gesner emanaba de su sentido del folklore y de su capacidad para presentar la fantasía y la realidad con la misma convincente veracidad. Cuando alguien escribe con pasión y plasma en el papel lo que siente, de alguna manera, es más fácil que pueda llegar al lector que, presiente, el mensaje que el autor le quiere hacer llegar.
Al cabo de un siglo, el lector inglés ya tenía acceso a la popular enciclopedia de Gesner gracias a la traducción de Edward Topsell, que éste tituló Historias de las bestias de cuatro patas, de las serpientes y de los insectos, 1658. Allí podemos saber con respecto a la gorgona que…

La gorgona, flanqueada por leonas y mostrando su cinturón de serpientes, tal como aparece en el pedimento del templo del siglo VII a. C. expuesto en el Museo arqueológico de Corfú. Todos estos mitos y leyendas han llegado a nuestro tiempo de las maneras más diversas cuando, aquellos personajes del pasado querían escenificar todas aquellas “historias” y las plasmaban en dibujos y relieves o quedaban escritas hasta en las piedras.
gorgona
“En la mitología griega, una gorgona (en griego antiguo γοργώ gorgō o γοργών gorgōn, terrible’) era un despiadado monstruo femenino a la vez que una deidad protectora procedente de los conceptos religiosos más antiguos. Su poder era tan grande que cualquiera que intentase mirarla quedaba petrificado, por lo que su imagen se ubicaba en todo tipo de lugares, desde templos a cráteras de vino, para propiciar su protección. La gorgona llevaba un cinturón de serpientes, entrelazadas como una hebilla y confrontadas entre sí”.
Górgonas y Medusas
…se planteó la cuestión de si el veneno que había emitido procedía de su aliento o de los ojos. Es más probable que, como el basilisco, matara con la mirada y también lo hiciera con el aliento de su boca, lo cual no es comparable con ninguna otra bestia del mundo… Al considerar esa bestia, se demostró de modo evidente la divina sabiduria y providencia del Creador, que había vuelto los ojos de esta criatura hacia la tierra, como si así enterrara su veneno y evitara que dañara al hombre, y los había ensombrecido con un cabello fuerte, largo y áspero, para que los rayos envenenados no pudieran dirigirse hacia arriba, hasta que la bestia se viera azuzada por el miedo o la ira…
criatura hacia la tierra, como si así enterrara su veneno y evitara que dañara al hombre, y los había ensombrecido con un cabello fuerte, largo y áspero, para que los rayos envenenados no pudieran dirigirse hacia arriba, hasta que la bestia se viera azuzada por el miedo o la ira…

Tras recurrir al indiscutible testimonio del salmo nonagésimo segundo, Gesner declara que los Unicornios son sagrados porque “reverencian a las vírgenes y a las jóvenes doncellas” y muchas veces al verlas se vuelven mansos y se acercan a dormir a su lado… ocasión que los cazadores indios y etíopes aprovechan para apoderarse de la bestia. Toman a un hombre joven, fuerte y hermoso, lo visten de mujer y lo adornan con diversas flores y especias olorosas”.

de la obra de Gesner
Pese a la fantasía de su texto, el millar de grabados de Gesner contribuyó a que la biología tomara un rumbo distinto. Al igual que los padres alemanes de la botánica, Gesner colaboró con los artistas y presentó los dibujos más realistas hechos hasta el momento de todos los tipos de criaturas, desde el “vulgar ratoncillo” al sátiro, la esfinge, el gato, el topo y el elefante. Durero fue el autor de su ilustración del rinoceronte, “la segunda maravilla de la naturaleza…como el elefante era la primera”. Estos incunables de la ilustración biológica empezaron a liberar a los lectores de los herbarios y los bestiarios.
el “vulgar ratoncillo” al sátiro, la esfinge, el gato, el topo y el elefante. Durero fue el autor de su ilustración del rinoceronte, “la segunda maravilla de la naturaleza…como el elefante era la primera”. Estos incunables de la ilustración biológica empezaron a liberar a los lectores de los herbarios y los bestiarios.
![]()
La obra de Gesner, reimpresa, traducida y resumida, dominó la zoología post-aristotélica hasta los innovadores estudios modernos de Ray y Linneo, que no estaban ilustrados. Sus notas inéditas fueron la base, el el siglo siguiente, del primer tratado completo que se escribió sobre los insectos. Para su Opera Botánica recogió cerca de un millar de dibujos, algunos realizados por él mismo, pero no llegó a terminar su gran trabajo sobre las plantas, que habían sido su primer amor.
sobre las plantas, que habían sido su primer amor.

Enemigo implacable de Roma
Gesner nunca se liberó completamente de su obsesión filológica. En su libro de 158 páginas Mitrídates, u observaciones sobre las diferencias existentes entre las lenguas que han estado o están en uso en las diversas naciones del mundo entero (1555), intentó hacer con las lenguas lo que ya estaba haciendo con los animales y las plantas. Tomando como base su traducción del padrenuestro, Gesner describió y comparó “la totalidad” de las ciento treinta lenguas del mundo. Por vez primera, incluyó un vocabulario del lenguaje de los gitanos.
o están en uso en las diversas naciones del mundo entero (1555), intentó hacer con las lenguas lo que ya estaba haciendo con los animales y las plantas. Tomando como base su traducción del padrenuestro, Gesner describió y comparó “la totalidad” de las ciento treinta lenguas del mundo. Por vez primera, incluyó un vocabulario del lenguaje de los gitanos.


Nadie nunca se hubiera atrevido a querer visitar las misteriosas cumbres de las montañas
Al revelar públicamente su intención de explorar las altas montañas, que hasta entonces habían inspirado pasmo y terror, Gesner halló un modo típicamente suizo de descubrir la naturaleza. La Europa renacentista había presenciado un breve y prematuro surgir de la fascinación por la aventura de las montañas. Petrarca (1304-1374) había sido el precursor, con su ascensión al monte Ventoux, cerca de Avignon, en 1336. En la cumbre leyó en un ejemplar de las confesiones de san Agustín que se sacó del bolsillo una advertencia dirigida a los hombres que “van a admirar las altas montañas y la inmensidad del océano y el curso de los astros… y se olvidan de sí mismos”. Leonardo Da Vinci exploró el monte Bo en 1511 con ojos de artista y naturalista. El reformista y humanista suizo Joachim Vadian (1484-1551), amigo de Lutero y defensor de Zwinglio, llegó a la cumbre de Gnepfstein, cerca de Lucerna, en 1555, escribió su pequeña obra clásica.
la naturaleza. La Europa renacentista había presenciado un breve y prematuro surgir de la fascinación por la aventura de las montañas. Petrarca (1304-1374) había sido el precursor, con su ascensión al monte Ventoux, cerca de Avignon, en 1336. En la cumbre leyó en un ejemplar de las confesiones de san Agustín que se sacó del bolsillo una advertencia dirigida a los hombres que “van a admirar las altas montañas y la inmensidad del océano y el curso de los astros… y se olvidan de sí mismos”. Leonardo Da Vinci exploró el monte Bo en 1511 con ojos de artista y naturalista. El reformista y humanista suizo Joachim Vadian (1484-1551), amigo de Lutero y defensor de Zwinglio, llegó a la cumbre de Gnepfstein, cerca de Lucerna, en 1555, escribió su pequeña obra clásica.

“Si deseáis ampliar vuestro campo de visión, dirigid la mirada a vuestro alrededor y contemplad todas las cosas que hay a lo largo y a lo ancho. No faltan atalayas y riscos, desde
donde os parecerá que tenéis la cabeza en la nubes. Si, por otra parte, preferís reducir la visión, podéis mirar los prados y los verdes bosques, o adentraros en ellos; y si la queréis reducir todavía más, podéis observar los oscuros valles, las sombrías rocas y las oscuras cavernas… En verdad, en ningún otro lugar se encuentran tal variedad en tan reducido espacio con en las montañas, en las cuales… en un solo día se puede contemplar y sentir las cuatro estaciones del año, verano, otoño, primavera e invierno. Además, desde los picos más altos de las montañas, la cúpula entera de nuestro cielo se tenderá audazmente abierta ante nuestra mirada, y podréeis presenciar la salida y la puesta de las constelaciones sin ningún estorbo, y comprobareis que el Sol se pone mucho después y sale mucho antes.”
El Mont Blanc
Pero resultaba tan difícil vencer los temores primitivos que tendrían que transcurrir dos siglos entre las excursiones de Gesner y los verdaderos comienzos del montañismo moderno. El Mont Blanc (4.810 m), el pico más alto de Europa aparte del Cáucaso, no fue escalado hasta 1786 por un montañero que se proponía cobrar la recompensa que había ofrecido un geólogo suizo, Horace-Bénedict de Saussure (1740-1779), veinticinco años antes.
En tanto los naturalistas dispusieran las plantas y los animales por orden alfabético, el estudio de la naturaleza estaba condenado a seguir siendo teórico…Pero, ¡esa es otra historia que no toca hoy!
Lo cierto es que, leyendo estas historias del pasado nos podemos situar en aquel tiempo y llegar a comprender cómo la gente tenían aquellos pensamientos, el desconocimiento del mundo y de las cosas y los seres que lo pueblan hacen que la imaginación desbocada vague por caminos que, en la mayoría de los casos, están aconsejados por la ignorancia. Pero, el tiempo pasa y las sociedades y sus gentes evolucionan, los descubrimientos no cesan y la ciencia avanza. Ahora, todo aquello ¡nos queda tan lejano!
Emilio Silvera V-
Historias como estas son contadas por Daniel J. Boorstin en sus libros titulados Los Descubridores…La Naturaleza. Los podeis encontrar en la Biblioteca de Divulgación Científica (1986 Editorial Crítica, S.A.) ISBN (Obra completa): 84-873-0174-5. Cuatro Caminos s/n. Sant Vicentç dels Hirts (Barcelona).
Jul
30
El Principio antrópico, el gato de Schrödinger
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (4)
Comments (4)
¡¡Viajar en el Tiempo!!
El físico Alan Harvey Guth dijo
:
“El principio antrópico es algo que la gente propone si no pueden pensar en algo mejor que hacer.”
Para Richard Feynman, el objetivo de un físico teórico es “demostrarse a sí mismo que está equivocado en cuanto sea posible”. Sin embargo, el principio antrópico es estéril y no puede ser refutado. Weinberg dijo: “aunque la ciencia es claramente imposible sin científicos, no está claro que el universo sea imposible sin ciencia.

En cosmología el principio antrópico establece que cualquier teoría válida sobre el universo tiene que ser consistente con la existencia del ser humano.
El debate sobre el principio antrópico (y por consiguiente sobre Dios) estuvo en letargo durante muchos años, aunque fue reactivado recientemente por la función de onda del universo de Hawking. Si Hawking está en lo cierto, entonces existen en realidad un número infinito de universos paralelos, muchos de ellos con diferentes constantes físicas. En algunos de ellos, quizá los protones se desintegran con demasiada rapidez, o las estrellas no pueden fabricar los elementos pesados por encima del hierro, o el Big Crunch tiene lugar demasiado deprisa porque su densidad crítica sobrepasa en mucho a la ideal y no da tiempo a que pueda comenzar la germinación de la vida, y así sucesivamente. De hecho, un número infinito de estos universos paralelos están muertos, sin las leyes físicas que puedan hacer posible la vida tal como la conocemos.


Hace tiempo ya que muchos piensan en la existencia de universos paralelos. Muchas estrellas y galaxias, muchos mundos, y, también, muchos universos. Claro que, es tan grande el nuestro que sería impensable poder salir de él para visitar otros universos vecinos, cuando la realidad es que, ni podemos visitar las galaxias más cercanos o los mundos que nos rodean en el propio Sistema solar. ¡Qué atrasados estamos todavía!

En tal universo paralelo (el nuestro), las leyes de la física eran compatibles con la vida que conocemos. La prueba es que nosotros estamos aquí para tratar esta cuestión. Si esto es cierto, entonces quizá no haya que invocar a Dios para explicar por qué la vida, por preciosa que sea, es posible en nuestro universo. Sin embargo, esto reabre la posibilidad del principio antrópico débil, es decir, que coexistimos con nuestros universos muertos y que el nuestro sea el único compatible para vida.
La segunda controversia estimulada por la función de onda del universo de Hawking es mucho más profunda y, de hecho, aun está sin resolver. Se denomina el Gato de Schrödinger.

La teoría cuántica, recordémoslo, afirma que para todo objeto existe una función de onda que mide la probabilidad de encontrar dicho objeto en un cierto punto del espacio y del tiempo. La teoría cuántica afirma también que nunca se conoce realmente el estado de una partícula hasta que se haya hecho una observación. Antes de que haya una medida, la partícula puede estar en uno de entre una diversidad de estados, descritos por la función de onda de Schrödinger. Por consiguiente, antes de que pueda hacerse una observación o medida, no se puede conocer realmente el estado de la partícula. De hecho, la partícula existe en un estado ultramundano, una suma de todos los estados posibles, hasta que se hace una medida.

Cuando esta idea fue propuesta por primera vez por Niels Bohr y Werner Heisemberg, Einstein se revolvió contra ella. “¿Existe la luna sólo porque la mira un ratón?”, le gustaba preguntar. Según la teoría cuántica, en su más estricta interpretación, la Luna, antes de que sea observada, no existe realmente tal como la conocemos. “La Luna puede estar, de hecho, en uno cualquiera de entre un número infinito de estados, incluyendo el estado de estar en el cielo, de estar explotando, o de no estar allí en absoluto. Es el proceso de medida que consiste en mirarla el que decide que la Luna está girando realmente alrededor de la Tierra”. Decía Einstein con ironía.

De la resolución de la ecuación de onda de Schrödinger se obtiene una serie de funciones de onda (ó probabilidades de distribución de los electrones) para los diferentes niveles energéticos que se denominan orbitales atómicos.
Edwin Schrödinger, autor de la ecuación con su función de onda, se disgustó con estas interpretaciones de su ecuación. Para demostrar lo absurdo de la situación creada, Schrödinger colocó un gato imaginario en una caja cerrada. El gato estaba frente a una pistola, que está conectada a un contador Geiger, que a su vez está conectado a un fragmento de uranio. El átomo de uranio es inestable y sufrirá una desintegración radiactiva. Si se desintegra un núcleo de uranio, será detectado por el contador Geiger que entonces disparará la pistola, cuya bala matará al gato.
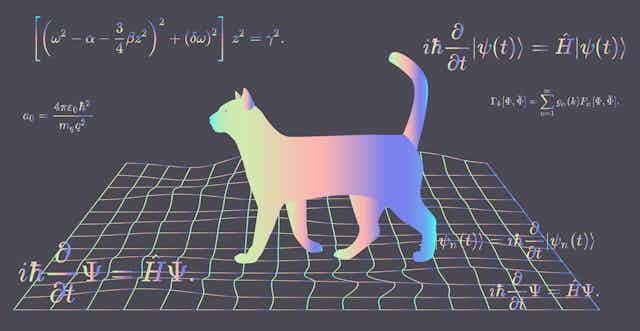
Para decidir si el gato está vivo o muerto, debemos abrir la caja y observar al gato. Sin embargo, ¿cuál es el estado del gato antes de que abramos la caja? Según la teoría cuántica, sólo podemos afirmar que el gato esta descrito por una función de onda que describe la suma de un gato muerto y un gato vivo.
Para Schrödinger, la idea de pensar en gatos que no están ni muertos ni vivos era el colmo del absurdo, pero la confirmación experimental de la mecánica cuántica nos lleva inevitablemente a esta conclusión. Hasta el momento, todos los experimentos han verificado, favorablemente, la teoría cuántica.

La paradoja del gato de Schrödinger es tan extraña que uno recuerda a menudo la reacción de Alicia al ver desaparecer el gato de Cheshire en el centro del cuento de Lewis Carroll: “Allí me verás”, dijo el Gato, y desapareció, lo que no sorprendió a Alicia que ya estaba acostumbrada a observar cosas extrañas en aquel lugar fantástico. Igualmente, los físicos durante años se han acostumbrados a ver cosas “extrañas” en la mecánica cuántica.
Existen varias maneras de abordar esta dificultad de lo incomprensible en mecánica cuántica. En primer lugar, podemos suponer que Dios existe. Puesto que todas las “observaciones” implican un observador, entonces debe haber alguna “conciencia” en el universo. Algunos físicos como el premio Nobel Eugene Wigner, han insistido en que la teoría cuántica prueba la existencia de algún tipo de conciencia cósmica universal.
La segunda forma de tratar la paradoja es la preferida por la gran mayoría de los físicos en activo: ignorar el problema.
El físico Richard Feynman dijo en cierta ocasión:
“Creo que es justo decir que nadie comprende la mecánica cuántica. No siga diciéndose a sí mismo, si puede evitarlo, “¿pero cómo puede ser así?” porque usted se meterá “hasta el fondo” en un callejón sin salida del que nadie ha escapado. Nadie sabe como puede ser eso.”
De hecho, a menudo se ha dicho que de todas las teorías propuestas en el siglo XX, la más absurda es la teoría cuántica. Algunos dicen que la única cosa que la teoría tiene a su favor es que “es indudablemente correcta”.
Sin embargo, existe una tercera forma de tratar esta paradoja, denominada teoría de los muchos universos. Esta teoría (como el principio antrópico) no gozó de mucho favor en la última década, pero está siendo revitalizada por la función de onda del universo de Stephen Hawking.

Existe un principio de la física denominado Navaja de Occam, que afirma que siempre deberíamos tomar el camino más sencillo posible e ignorar las alternativas más complicadas, especialmente si las alternativas no pueden medirse nunca.

Para seguir fielmente el consejo contenido en la navaja de Occam, primero hay que tener el conocimiento necesario para poder saber elegir el camino más sencillo, lo que en la realidad, no ocurre. Nos faltan los conocimientos necesarios para hacer las preguntas adecuadas.
Hugo Everett, Bryce DeWitt y ahora Hawking (también otros), han propuesto la teoría de los universos múltiples. En unos universos los protones se desintegran antes haciendo inestable la materia, en otros, el átomo de uranio se desintegra mediante un proceso sin radiaciones, y en otros universos las constantes universales que existen en el nuestro, son totalmente diferentes y no dan posibilidad alguna para la existencia de seres vivos. Está claro que cualquier variación que en principio pudiera parecer sin importancia, como por ejemplo la carga del electrón, podría transformar radicalmente nuestro universo.

Como apuntó el físico Frank Wilczek:
“Se dice que la historia del mundo sería totalmente distinta si Helena de Troya hubiera tenido una verruga en la punta de su nariz.”
Hasta el momento, se han celebrado varias conferencias internacionales sobre la función de onda del universo. Sin embargo, como ocurre en la teoría de supercuerdas, las matemáticas implicadas en la función de onda del universo, parecen estar más allá de la capacidad de cálculo que cualquier humano en este planeta pudiera resolver, y tendríamos que esperar años antes de que aparezca un individuo genial que pudiera encontrar una solución rigurosa a las ecuaciones de Hawking.
Emilio Silvera V.
Jul
30
¡Increible planeta Tierra!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Nuestro increíble planeta ~
Clasificado en Nuestro increíble planeta ~
 Comments (1)
Comments (1)




















Con el título de paisajes alucinógenos, el Diario el País, publicó estas imágenes que, verdaderamente son dignas de asombro al poder comprobar de lo que es capaz la Naturaleza en nuestro planeta. Lo asombroso del caso es que, en la mayoría de esos lugares, aunque nos parezca mentira, está presente la vida que, según vamos comprobando día a día, es imparable en nuestro Universo.
Por las pruebas que de la Tierra tenemos en relación a la vida, por las probabilidades que realmente existen, por el hecho cierto de que, el Universo es igual en todas partes, por la innegable realidad de que el Universo está regido por las cuatro fuerzas fundamentales y las constantes universales, por todo ello, sabemos que la vida, puede estar presente en cualquier mundo que, como el nuestro, tenga las adecuadas condiciones.
Emilio Silvera V.















 Totales: 84.662.704
Totales: 84.662.704 Conectados: 53
Conectados: 53














































