https://youtu.be/z3r5lnogwq8

https://www.emiliosilveravazquez.com/blog/wp-admin/post.php?post=28750&action=edit

Lo cierto es que viajamos hacia el futuro de manera imparable. Nuevos descubrimientos en tecnologías revolucionarias, posibilitan viajar con metano líquido a mayor velocidad de la que ahora podemos alcanzar.

Viajar al Espacio, hasta el momento, es sólo un sueño. No tenemos los medios para alcanzar las lejanas estrellas y los planetas que las orbitan. Finalmente, aunque eso pasará dentro de mucho, mucho, muchísimo Tiempo, el Sol llegará a su final y nuestro mundo perderá la fuente que le suministra la luz y el calor que necesita la vida.  Siendo así (que lo es), tenemos que buscar nuevas maneras de viajar a mayores velocidades (sería el primer paso), para vencer ese escollo. Mas adelante, vendrán los descubrimientos del Hiperespacio y los Agujeros de Gusano u otras similares que nos lleven lejos en poco Tiempo.

[?]

                                                   

                                          Viajar – África

Danakil, el «valle extraterrestre» de la Tierra

Este desierto de África es conocido como el «lugar más cruel de la Tierra» por su terreno y altas temperaturas.

Si hay un lugar en la Tierra que se asemeje a la vida extraterrestre ese es sin duda el desierto de Danakil. Esta enorme extensión de tierra situada en el Cuerno de África, -en la depresión de Afar-, es conocido por su calor extremo con temperaturas que superan los 40 grados centígrados durante el día y donde formaciones de sulfuro, sal y azufre brotan de la tierra otorgando al terreno un color amarillento más propio de otro planeta.

 

           

                                                                                    Erta Ale

La región, situada a unos 60 metros por debajo del nivel del mar, es conocida además por la presencia de volcanes como el Erta Ale o el Dabbahu. El primero es todo un espectáculo al que los habitantes locales no se acercan por la creencia de que en ese lugar habitan espíritus malignos que se pasean en caballo. Lo cierto es que su cima está bañada por un lago de lava, una de las más duraderas del planeta, que ocasionalmente se desborda hacia la falda meridional.

 

     

 

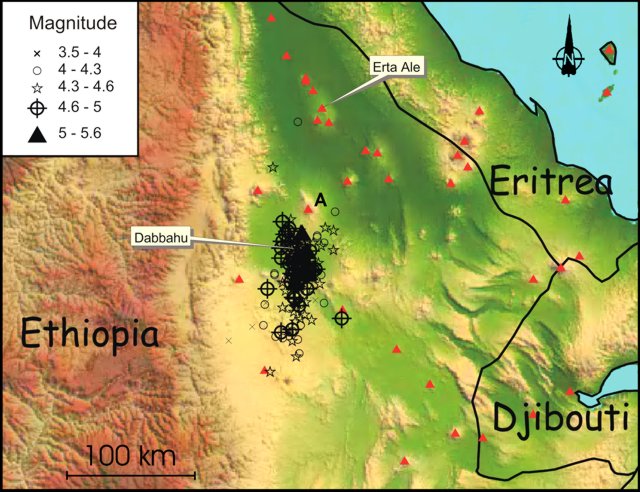
El Dabbahu, por su parte, ha entrado una única vez en erupción en 2005 pero al hacerlo creó una gran grieta en el suelo, conocida como la «fisura Dabbahu».

 

                 

                                                                  Manantiales de azufre y sal

                                                     

Pero si algo caracteriza el paisaje del desierto de Danakil es el volcán Dallol, un cráter situado a 45 metros por debajo del nivel del mar y cuyas corrientes ascendentes crean asombrosos manantiales de azufre y sal.

 

                                     Inhóspita zona imposible para la vida

 

         

       Infierno en la Tierra

Los intrépidos turistas que se atreven a entrar en esta inhóspita zona por sus temperaturas -este es el lugar que tiene el récord de media más alta en un lugar habitado en la Tierra- así como peligrosa por la situación política en Etiopía, descubrirán un impresionante paisaje donde la arena del desierto es sustituida por las fuentes de azufre y minerales que otorgan tonos amarillos, verdes o blanco al terreno.

  Paisajes que en la oscuridad de la noche ejercen una extraña fascinación

                 

               El pueblo nómada afar,  que transita por el desierto de arena y sal en  Danakil

 

En esta amplia zona de Etiopía conocida como el infierno en la tierra y a la que National Geographic nombró el «lugar más cruel» la vida se antoja muy complicada sin embargo es la patria del pueblo nómada afar conocidos por su capacidad para soportar el intenso calor y los vientos abrasadores y dedicados al comercio de la sal como forma de vida.

[?]

“Como la cola de un pavo real, como la gema en la cabeza de una serpiente, así están las matemáticas a la cabeza de todo el conocimiento”.

“El trabajo matemático que contienen estos cuadernos que ha realizado Ramanujan durante el último año de su vida, es mucho más que lo que haría el mejor matemático del mundo durante toda su vida. Tardaremos mucho en desvelar los secretos matemáticos que aquí se expresan, y, un ejemplo son sus funciones modulares y su trabajo sobre el número Pi (π).

•  Los Hindúes desarrollaron el uso del cero y los números negativos quizá unos mil años antes de que estos conceptos fueran aceptados en Europa.  Los mayas inventaron su propio cero -de hecho, una gran cantidad de ellos- más o menos al mismo tiempo que los hindúes.

El famoso teorema de Pitágoras, en realidad se encontró en una tablilla de 3.500 años, lo que pone en duda la autoría de Pitágoras en el mismo. Así se escribe la Historia, y, no siempre se le ha dado el mérito a quien lo tenía. Aristarco de Samos predijo que el Sol era el centro del Sistema planetario en el que estaba la Tierra, y, nadie le prestó atención, 700 años años más tarde, llegó Nicolás Copérnico y se apuntó el mérito.

La Tablilla Plimpton 322: La resolución del Teorema de Pitágoras antes de Pitágoras. (o lo que los griegos no contaron :Donde lo habían conocido. Llamándolo por su nombre: El “plagio  que Pitágoras hizo de conocimientos  sumerio-babilonios más de mil años anteriores).

“Aproximadamente medio millón de tablillas paleobabilónicas de barro, escritas en cuneiforme, se han encontrado en las excavaciones de Mesopotamia desde mediado del  pasado siglo XIX d.C.

 De ellas, una 400 contienen listas de problemas matemáticos y  tablas matemáticas y muchas de ellas se pueden ver en los museos de  Paris, Berlín  y Londres así como en las colecciones de la Universidades de  Yale, Columbia y la  Universidad de  Pennsylvania.

Los  Babilonios, ya desde la I Dinastía ( su sexto rey fue Hammurabi) , usaban, como sus antepasados sumerios más de 1500 años antes, el sistema sexagesimal , es decir, de base 6. Así, si vemos unos números escritos 

La tablilla babilónica  322  en la colección de G A Plimpton , en la  Columbia University, conocida como Plimpton 322,  escrita en cinco columnas , es un magnífico ejemplo de una tablilla matemática escrita por los babilonios.”

Se puede ver http://www.sciences-en-ligne.com/momo/chronomath/anx3/plimpton.html

•  Ciertas tablillas de barro escritas unos mil años antes de la civilización griega revelan indicios de la existencia de un álgebra bastante sofisticada entre los sumerios. Existen papiros del siglo XVIII a. C., y también anteriores a esa fecha, en los que se ve que los egipcios utilizaban ecuaciones simples para abordar problemas relativos a la distribución de alimentos y otros suministros.

Los egipcios sabían que, la trigonometría es una rama de las matemáticas que significa “medición de triángulos”.

Los antiguos egipcios y babilonios conocían los teoremas sobre los lados de los triángulos semejantes. Las sociedades pre-helénicas carecían de estos conocimientos, por lo que estudiaban los lados en su medida, la trilaterometría, que es un término que, si bien no es tan común como “trigonometría”, se refiere a la medición de los lados de un triangulo,  en contraste con la trigonometría, que se ocupa tanto de los lados como de los ángulos.. En el segundo milenio a.C, los egipcios utilizaban la trigonometría para la construcción de pirámides.

Esta imagen muestra el Papiro de Ahmes que contiene el siguiente problema de trigonometría:  ” Si una pirámide es de 250 codos de alto y al lado de su base de 360 codos de largo, ¿Cúal es su Seked?”  Solución: la cantidad para la Seked es la cotangente del ángulo que forman la base de la pirámide y su cara.

•  En el tercer milenio a. C. los babilonios desarrollaron un sistema de numeración que contemplaba el principio del valor según la posición. (En nuestro sistema de base 10, por ejemplo, 348 significa 8 unidades, 4 decenas y 3 centenas.) El Sistema de numeración Sexagesimal (base 60) de los babilonios puede parecer incómodo en un principio, pero Copérnico utilizó fracciones sexagesimales para construir su modelo del sistema solar y nosotros utilizamos este sistema para medir el tiempo y los ángulos (la hora tiene 60 minutos y cada minuto se divide en 60 segundos).

                         Sistema Sexagesimal Babilónico

•  Los escribas que trabajaban en los templos de Egipto conocían la fórmula que se usa para calcular el volumen del cilindro mucho antes de que existieran griegos que supiesen leer y escribir, por lo que conocieron la existencia del misterioso factor π mucho antes que los griegos. Los egipcios inventaron también el concepto de mínimo común denominador, así como una tabla de fracciones cuya preparación, según estimaciones de expertos modernos, requirió la realización de veintiocho mil tediosos cálculos.

Sí, el conocimiento de los números y las matemáticas se pierde en la noche de los tiempos y, desde hace milenios están alojados en la Mente de la Humanidad que, los tiene en sus manos para hacer el uso requerido en cada caso y lugar para hacernos más comprensible y fácil la vida. ¿Qué sería de nosotros sin las matemáticas?

•  En el año 2000 a. C., los sacerdotes en Mesopotamia (una región de la que hemos hablado hace muy poco tiempo, y, donde la Civilización sumeria desarrolló todo su talento e inventiva para el progreso), desarrollaron unas extensas tablas de cuadrados. Sabemos esto por las tablillas de barro con textos en escritura cuneiforme que han sido halladas en las bibliotecas de los templos. Hay que recordar que los europeos en el siglo XIV ni siquiera tenían Tablas de multiplicar.

•  Gottfried Leibniz, el coinventor del cálculo, afrimaba haber descubierto el secreto del modo de descifrar los diagramas del sabio chino de la antigüedad Fu Hsi. Leibniz sostenía que los diagramas de Fu Hsi se correspondían  con su propio sistema binario moderno de aritmética.

•  Los hindúes inventaron una incipiente forma de cálculo siglos antes de que Leibniz inventara el cálculo en Europa.

Mohammed Ibn Musa abu Djafar Al-Khwarizmi.  Murió: hacia el 850 en Bagdad (hoy Irak)

        Matemático, astrónomo y geógrafo musulmán, Mohammed Ibn Musa abu Djafar Al-Khwarizmi, nació probablemente en la ciudad persa de Khwarizm (actual Khiva, en Uzbekistan), situada al sudeste del mar de Aral, en la vieja ruta de la seda, que había sido conquistada 70 años antes por los árabes. Su nombre significa “Mohamed, hijo de Moisés, padre de Jafar, el de Khwarizm”.

https://commons.wikimedia.org/w/index.php?curid=587146

Hacia el 820, Al’Khwarizmi fue llamado a Bagdad por el califa abasida Al Mamun, segundo hijo de Harun ar Rashid,  conocido por todos gracias a las “Mil y una noches”. Al Mamun continuó el enriquecimiento de la ciencia árabe y de la Academia de Ciencias creada por su padre, llamada la Casa de la Sabiduría. Se tradujeron al árabe obras científicas y filosóficas griegas e hindúes, y contaba con observatorios astronómicos. En este ambiente científico y multicultural se educó y trabajó Al-Khwarizmi, el cual dedicó sus tratados de álgebra y astronomía al propio califa. Todo este florecimiento traería importantes consecuencias en el desarrollo de la ciencia en Europa, principalmente a través de España.

La casa de la Sabiduría

•  Así, los árabes acuñaron el término álgebra e inventaron las fracciones decimales: 0,25 para ¼, etc. Los europeos, antes de sacar pecho cuando de matemáticas se habla, debemos mirar hacia atrás en el tiempo y hacia otros pueblos que, antes que nosotros, hicieron bien su trabajo.

Aristóteles supo reconocer el mérito de los egipcios a los que otorgó la autoría de haber desarrollado las matemáticas antes de que sus paisanos lo hicieran, aunque los expresó de una forma un poco ambigua: “Las ciencias matemáticas nacieron en el entorno de Egipto porque allí la clase sacerdotal disfrutaba de tiempo de ocio”.

De todas las maneras, es de justicia reconocer las cosas y el historiador de matemáticas Morris Kline, el más prominente de América, nos dice:

“Comparar las matemáticas de los egipcios y los babilonios con los logros de sus sucesores inmediatos, los griegos, es como comparar los grabados de los niños que aprenden a escribir con la gran literatura”.

Esto, sin dejar de reconocer que sumerios, babilonios y egipcios fueron los pioneros, junto a los hindúes y chinos, de las matemáticas que más tarde, fueron desarrolladas por griegos…, sin olvidar a los matemáticos árabes que tienen una gran tradición matemática en su historia.

La historia es más extensa pero, el tiempo se me acaba y el trabajo me espera, otro día seguiremos desarrollando este tema fascinante de las matemáticas que, junto con la escritura y el lengujae, viene a ser uno de los mayores logros de la Humanidad.

Emilio Silvera Vázquez

[?]

Esta región contiene muchas maravillas y es un lugar ideal para investigar cómo surgió la vida en el planeta. También encierra una caldera volcánica que el día que salga a la superficie…

Pero veamos el video y disfrutemos,

[?]

                 Agua, luz y calor, sustancia cósmica… ¡El surgir de la vida!

                        Pero no está muerto lo que duerme eternamente

¿Cómo es posible que, a partir de la materia “inerte”, hayan podido surgir seres vivos e incluso, algunos que, como nosotros, puedan pensar? Que cosa mágica se pudo producir en el corazón de las estrellas para que, materiales sencillos como el Hidrógeno se convirtieran a miles de millones de grados de calor en otros que, como el Carbono, Oxigeno y Nitrógeno, muchos miles de Millones de años más tardes, en mundos perdidos en sistemas planetarios como el nuestro, dieran lugar a la formación de Protoplasma vivo del que surgieron aquellos infinitesimales seres que llamamos bacterias y que, posibilitaron la evolución hacia formas de vida superiores?

“La generación de una nueva especie a partir de una especie anterior es un proceso que necesita centenares de miles de años de evolución. Desde una perspectiva evolutiva se piensa que la biodiversidad es la respuesta de los seres vivos, mediante la evolución adaptativa de las especies, a la multitud de ambientes que han ido apareciendo a lo largo de la historia de la vida en la Tierra. Cada especie tiene una serie de características, muchas veces únicas, que los humanos, en ocasiones, hemos sabido aprovechar para nuestra alimentación o para curar nuestras enfermedades. Por todo ello vale la pena mantener amplios espacios naturales dónde puedan continuar viviendo todas las especies.”

        Los sentidos: las herramientas que utiliza el cerebro para estar comunicado con el exterior

La percepción, los sentidos y los pensamientos… Para poder entender la conciencia como proceso es preciso que entendamos cómo funciona nuestro cerebro, su arquitectura y desarrollo con sus funciones dinámicas. Lo que no está claro es que la conciencia se encuentre causalmente asociada a ciertos procesos cerebrales pero no a otros.

El cerebro humano ¿es especial?,  su conectividad, su dinámica, su forma de funcionamiento, su relación con el cuerpo y con el mundo exterior, no se parece a nada que la ciencia conozca. Tiene un carácter único y ofrecer una imagen fidedigna del cerebro no resulta nada fácil; es un reto tan extraordinario que no estamos preparados para cumplir en este momento. Estamos lejos de ofrecer esa imagen completa, y sólo podemos dar resultados parciales de esta enorme maravilla de la Naturaleza.

Nuestro cerebro adulto, con poco más de 1.300 gr de peso, contiene unos ochenta y seis mil mil millones de células nerviosas o neuronas. La parte o capa ondulada más exterior o corteza cerebral, que es la parte del cerebro de evolución más reciente, contiene alrededor de treinta millones de neuronas y un billón de conexiones o sinapsis. Si contáramos una sinapsis cada segundo, tardaríamos 32 millones de años en acabar el recuento. Si consideramos el número posible de circuitos neuronales, tendremos que habérnoslas con cifras hiper-astronómicas. Un 10 seguido de, al menos, un millón de ceros (en comparación, el número de partículas del universo conocido asciende a “tan sólo” un 10 seguido de 79 ceros). ¡A que va a resultar que no somos tan insignificantes!

El suministro de datos que llega en forma de multitud de mensajes procede de los sentidos, que detectan el entorno interno y externo, y luego envía el resultado a los músculos para dirigir lo que hacemos y decimos. Así pues, el cerebro es como un enorme ordenador que realiza una serie de tareas basadas en la información que le llega de los sentidos. Pero, a diferencia de un ordenador, la cantidad de material que entra y sale parece poca cosa en comparación con la actividad interna. Seguimos pensando, sintiendo y procesando información incluso cuando cerramos los ojos y descansamos.

Con tan enorme cantidad de circuitos neuronales, ¿Cómo no vamos a ser capaces de descifrar todos los secretos de nuestro universo? ¿De qué seremos capaces cuando podamos disponer de un rendimiento cerebral del 80 ó 90 por ciento? Algunas veces hemos oido comentar: “Sólo utilizamos un diez por ciento del cerebro…” En realidad, la frase no indica la realidad, se refiere al hecho de que, aunque utilizamos el cerebro en su totalidad, se estima que está al diez por ciento de su capacidad real que, será una realidad a medida que evolucione y, en el futuro, esa capacidad de hoy será un 90 por ciento mayor.

Aún no conocemos bien la direccionalidad de los circuitos neuronales

El límite de lo que podremos conseguir tiene un horizonte muy lejano. Y, llega un momento en el cual, se puede llegar a pensar que no existen limites en lo que podemos conseguir: Desde hablar sin palabras sonoras a la auto-transportación. Si -como pienso- somos pura energía pensante, no habrá límite alguno; el cuerpo que ahora nos lleva de un lugar a otro, ya no será necesario, y como los fotones que no tienen masa, podremos desplazarnos a velocidades lumínicas.

Creo que estoy corriendo demasiado en el tiempo, volvamos a la realidad. A veces mi mente se dispara. Lo mismo visito mundos extraordinarios con mares luminosos de neón líquido poblados por seres transparentes, que viajo a galaxias muy lejanas pobladas de estrellas de fusión fría circundadas por nubes doradas compuestas de antimateria en la que, los positrones medio congelados, se mueven lentamente formando un calidoscopio de figuras alucinantes de mil colores. ¡La mente, qué tesoro!

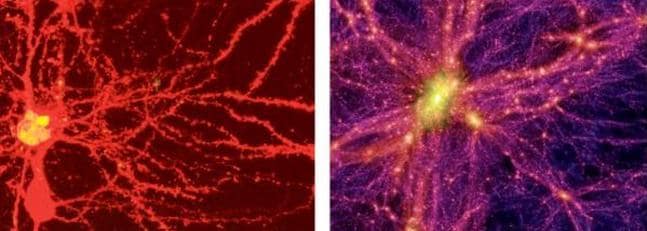
   ¿Quién podría decir, si no se les explicara, que son “universos diferentes”

La unidad a partir de la cual se configuran todas las fabulosas actividades del cerebro es una célula del mismo, la neurona. Las neuronas son unas células fantásticamente ramificadas y extendidas, pero diminutas que, sin embargo y en sentido figurado,  podríamos decir que son tan grandes como el universo mismo.

Cuando seamos capaces de convertir en realidad todo aquello en lo que podamos pensar, entonces, habremos alcanzado la meta. Para que eso pueda llegar a ocurrir, aún falta mucho tiempo. Sin embargo, si el Universo no lo impide y nuestro transcurrir continúa, todo lo que podamos imaginar… podrá ser posible. Incluso imposibilidades físicas de hoy, dejarán de existir mañana y, ¡la Mente! posiblemente (al igual que hoy ordena a las distintas partes del cuerpo que realice esta o aquella función), se encargará de que todo funcione bien, erradicará cualquier enfermedad que nos pueda atacar y, tendrá el conjunto del “sistema” en perfectas condiciones de salud, lo cual me lleva a pensar que, para cuando eso llegue, los médicos serán un recuerdo del pasado.

Es curioso y sorprendente la evolución alcanzada por la Mente Humana. El mundo físico se representa gobernado de acuerdo a leyes matemáticas. Desde este punto de vista, todo lo que hay en el universo físico está realmente gobernado en todos sus detalles por principios matemáticos, quizá por ecuaciones tales que aún no hemos podido llegar a comprender y, ni que sabemos que puedan existir.

Lo más seguro es que la descripción real del mundo físico esté pendiente de matemáticas futuras, aún por descubrir, fundamentalmente distintas de las que ahora tenemos. Llegarán nuevos Gauss, Riemann, Euler, o, Ramanujans… que, con sus nuevas ideas transformarán el pensamiento matemático para hacer posible que podamos, al fin, comprender lo que realmente somos.

Son nuestras Mentes, productos de la evolución del Universo que, a partir de la materia inerte, ha podido alcanzar el estadio bio-químico de la consciencia y, al ser conscientes, hemos podido descubrir que existen “números misteriosos” dentro de los cuales subyacen mensajes que tenemos que desvelar.

Antes tendremos que haber descifrado las funciones modulares de los cuadernos perdidos de Ramanujan, o por ejemplo, el verdadero significado del número 137, ése número puro adimensional que encierra los misterios del electrón (e) – electromagnetismo -, de la constante de Planck (h) – el cuando te acción – y de la luz (c) – la relatividad -.

       Las primeras proto-estrellas, grandes grumos e gas y polvo

Los resultados son lentos, no se avanza con la rapidez que todos deseamos. Sin embargo, eso ocurre por algo, el ritmo del Universo considerado como Naturaleza, podríamos decir que es “sabio” y, si actúa de esa manera…Por algo será. Deja que de vez en cuando, sobresalgan algunas mentes y se eleven por encima del común, de ejemplos tenemnos la historia llena. Esos “saltos” de la conciencia son los tiempos que marca el Universo para que, poco a poco, se produzca nuestra evolución, es la única forma de que todo se haga de manera correcta y de que, los nuevos pensamientos se vayan asentando debidamente en las Mentes futuras. Pongamos un ejemplo: Poincaré expuso su conjetura y, más de un siglo después, Perelman la resolvió. Riemann expuso su geometría del espacio curvo, y hasta 60 años más tarde no fue descubierta por Einstein para hacer posible su formulación de la relatividad general, donde describe cómo las grandes masas distorsionan el espacio y el tiempo por medio de la fuerza de gravedad que generan. El conocimiento humano avanza al ritmo que le impone la Naturaleza.

¡Son tantos los secretos que nos quedan por desvelar! la Naturaleza es la portadora de todas las respuestas…Observémosla con atención y, aprendamos de ella y, de ser posible, procuremos no molestarla, “Ella” nos permite estar aquí para que evolucionemos y, algún día, cuando seamos mayores…quizás nos deje formar parte de algo más…¿mental?

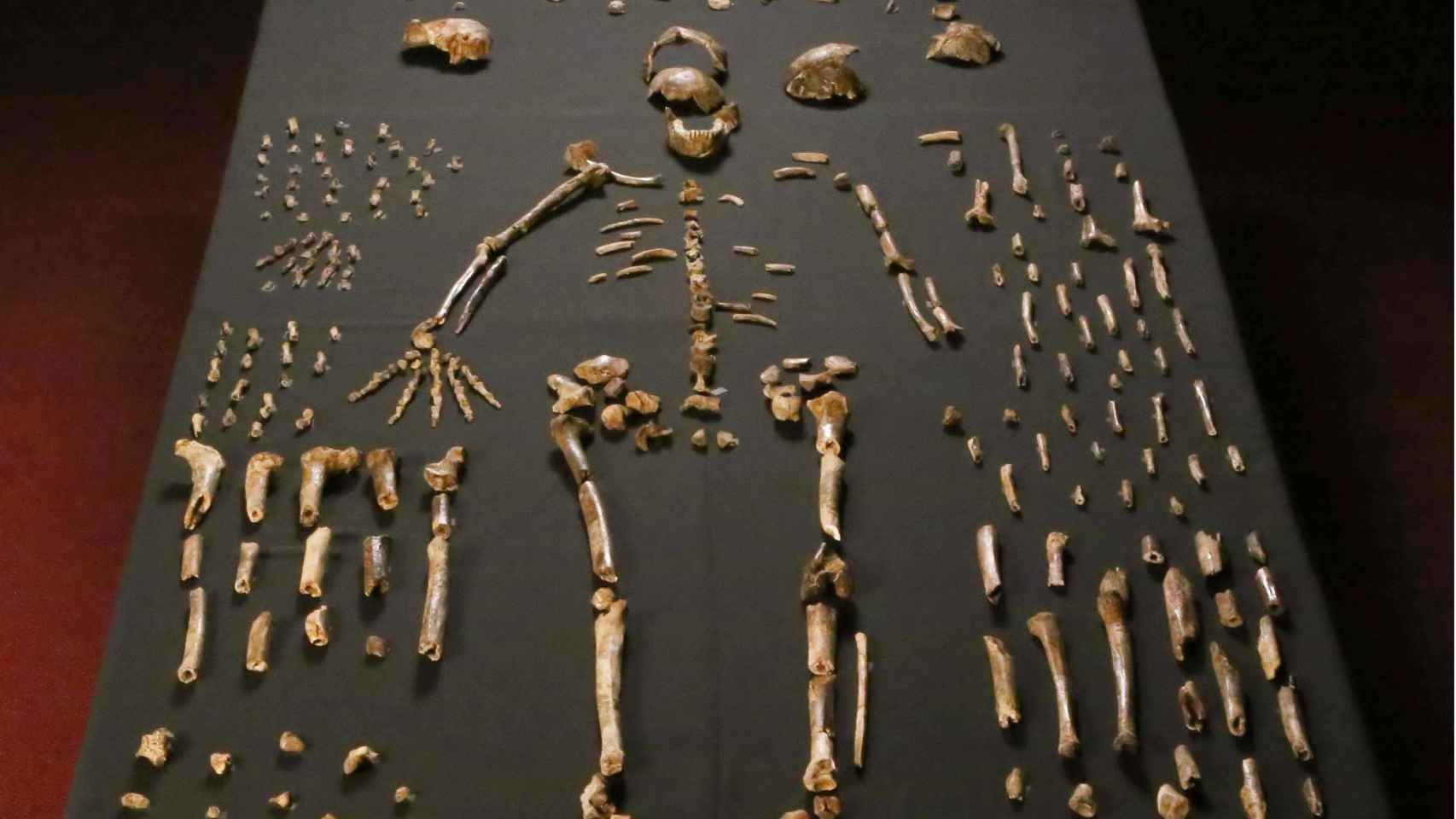
                                Visto así…. ¡No parece que seamos gran cosa!

No, no será nada fácil imitar a la Naturaleza…¡Esa perfección! Sin embargo, llegados a ese punto, debemos pensar que nosotros también formamos parte de ella, la parte que piensa y, si es así, ¿Qué cometido tendremos asignado en este Universo? Esa es la pregunta que ninguno de los grandes pensadores de la Historia, han podido contestar.

Pensar, por ejemplo, en las complejas matemáticas topológicas requeridas por la teoría de supercuerdas puede producir incomodidad en muchas personas que, aún siendo físicos, no están tan capacitados como para entender tan profundas ideas (me incluyo).

Bernhard Riemann introdujo muchas nuevas ideas y fue uno de los más grandes matemáticos. En su corta vida (1.826 – 1.866) propuso innumerables propuestas matemáticas que cambiaron profundamente el curso del pensamiento de los números en el planeta Tierra, como el que subyace en la teoría relativista en su versión general de la gravedad, entre otras muchas (superficie de Riemann, etc.). Riemann les enseñó a todos a considerar las cosas de un modo diferente.

 La geometría de las espacios curvos. Superficie de Riemann que aparece al extender el dominio de la función .

La superficie de Riemann asociada a la función holomorfa “tiene su propia opinión” y decide por sí misma cuál debería ser el, o mejor, su dominio, con independencia de la región del plano complejo que nosotros podamos haberle asignado inicialmente.

Podríamos encontrar otros muchos tipos de superficies de Riemann.

Este bello concepto desempeña un papel importante en algunos de los intentos modernos de encontrar una nueva base para la física matemática (muy especialmente en la teoría de cuerdas), y al final, seguramente se descubrirá el mensaje que encierra.

El caso de las superficies de Riemann es fascinante, aunque desgraciadamente sólo es para iniciados. Proporcionaron los primeros ejemplos de la noción general de variedad, que es un espacio que puede pensarse “curvado” de diversas maneras, pero que localmente (por ejemplo, en un entorno pequeño de cualquiera de sus puntos), parece un fragmento de espacio euclídeo ordinario.

	fig.1: Proyección estereográfica del plano complejo extendido sobre la “esfera de Riemann”.
	fig.2: La “esfera de Riemann” puede ser visualizada como el plano complejo envuelto alrededor de una esfera.

En matemática, la esfera de Riemann (o plano complejo extendido), llamado en honor al matemático del siglo XIX del mismo nombre, es una esfera obtenida del plano complejo mediante la adición de un punto del infinito. La esfera es la representación geométrica de los números complejos extendidos , (véase fig.1 y fig.2), la cual consiste en los números complejos ordinarios en conjunción con el símbolo para representar el infinito.

La esfera de Riemann, superficie de Riemann compacta, el teorema de la aplicación de Riemann, las superficies de Riemann y aplicaciones complejas… He tratado de exponer en unas líneas la enorme importancia de este personaje para las matemáticas en general y la geometría y para la física en particular. Es uno de esos casos a los que antes me refería. Después de él, la Humanidad ha tenido un parón en el desarrollo de las ideas hasta que asimilaron las suyas y, después, llegó Einstein y otros que supieron aplicarlas. Einstein, sin el Tensor métrico de Riemann, nunc habría podido finalizar su Teoría de la Relatividad General.

             La Geometría de Riemann de los espacios curvos que Einstein aprovechó

Tenemos que convenir que todo, sin excepción, es relativo y resulta ya evidente la gran crisis de la noción de realidad “veritas” que el mundo padece, la ciencia BASE, la matemática, sufrió el varapalo a partir de la matemática topológica de Poincaré, y el desarrollo sorpresivo de la matemática del caos; de pronto el idealismo de la ecuación diferencial queda derribado : el mundo que funciona como un reloj de Tolomeo queda finiquitado; ¿donde puñetas está la materia perdida?; de pronto nuestras consciencias “comprenden” que la “verdad” no existe, es decir, que no existe nuestra realidad del mundo.

Y, mientras tanto, nuestras mentes siguen su camino, siempre queriendo ir más allá y siempre profundizando en los secretos de la Naturaleza de lo que tenemos muchos ejemplos, tales como nuestras consideraciones sobre los dos aspectos de la relatividad general de Einstein, a saber, el principio de la relatividad, que nos dice que las leyes de la física son ciegas a la distinción entre reposo y movimiento uniforme; y el principio de equivalencia, que nos dice de qué forma sutil deben modificarse estas ideas para englobar el campo gravitatorio.

Todo es finito, es decir, que tiene un fin, y la velocidad de la luz no podía ser una excepción

Ahora hay que hablar del tercer ingrediente fundamental de la teoría de Einstein, que está relacionada con la finitud de la velocidad de la luz. Es un hecho notable que estos tres ingredientes básicos puedan remontarse a Galileo; en efecto, parece que fue también Galileo el primero que tuvo una expectativa clara de que la luz debería viajar con velocidad finita, hasta el punto de que intentó medir dicha velocidad. El método que propuso (1.638), que implica la sincronización de destellos de linternas entre colinas distantes, era, como sabemos hoy, demasiado tosco (otro ejemplo de la evolución que, con el tiempo, se produce en nuestras mentes). Él no tenía forma alguna de anticipar la extraordinaria velocidad de la luz.

Parece que tanto Galileo como Newton tenían poderosas sospechas respecto a un profundo papel que conecta la naturaleza de la luz con las fuerzas que mantienen la materia unida y, si consideramos que esa fuerza que hace posible la unión de la materia reside en el corazón de los átomos (en sus núcleos), podemos hacernos una clara idea de lo ilimitado que puede ser el pensamiento humano que, ya en aquellos tiempos -en realidad mucho anters- pudo llegar a intuir las fuerzas que están presentes en nuestro Universo.

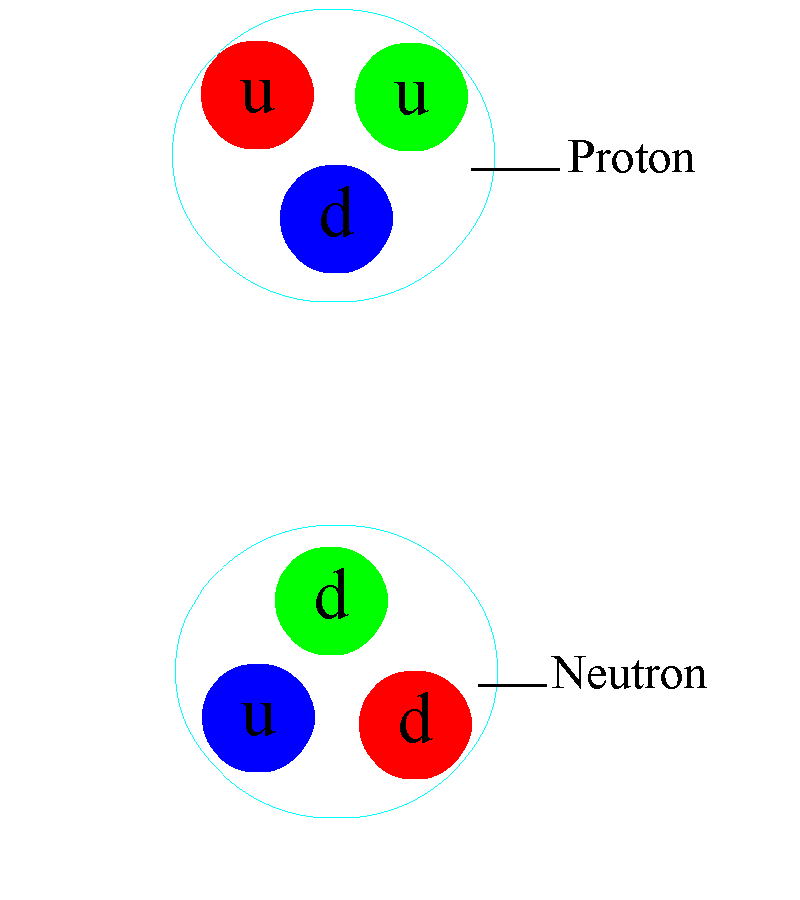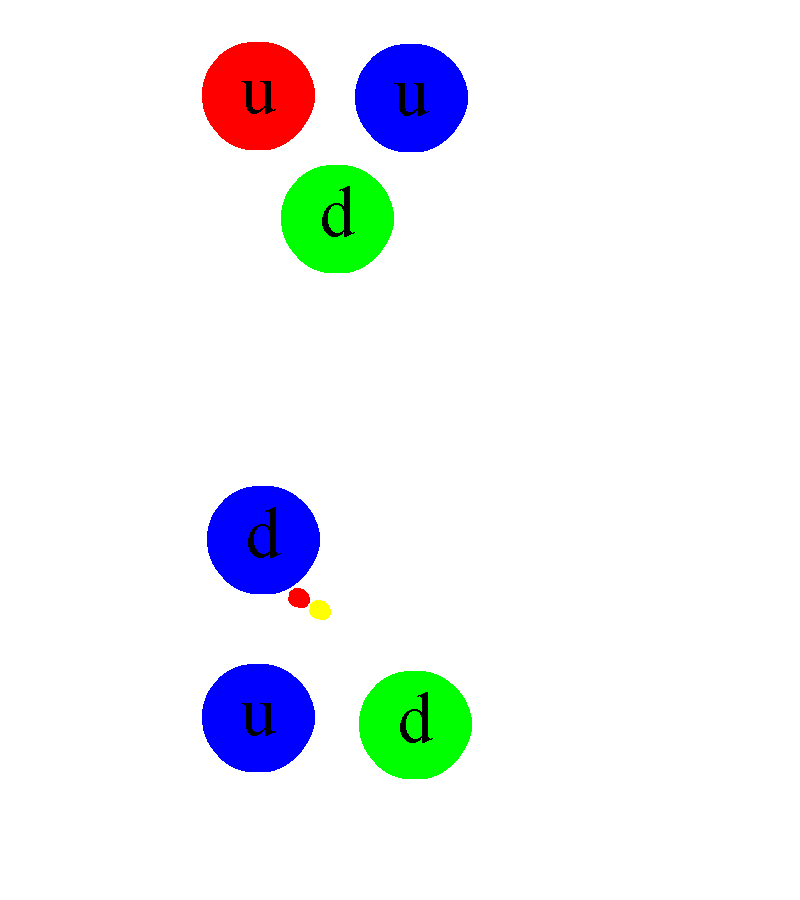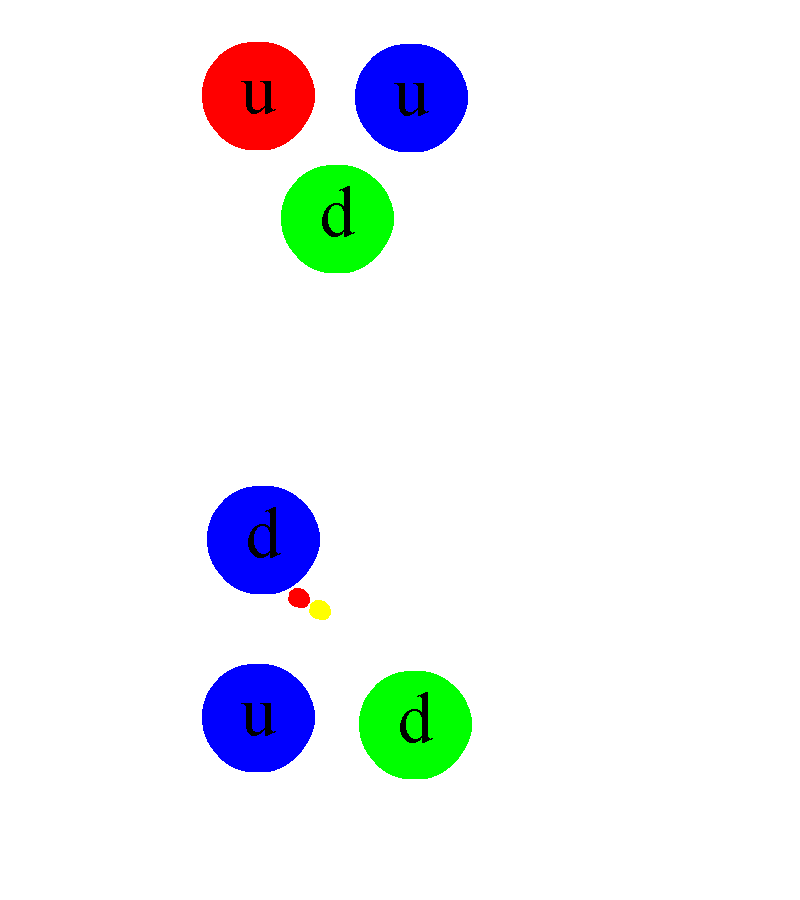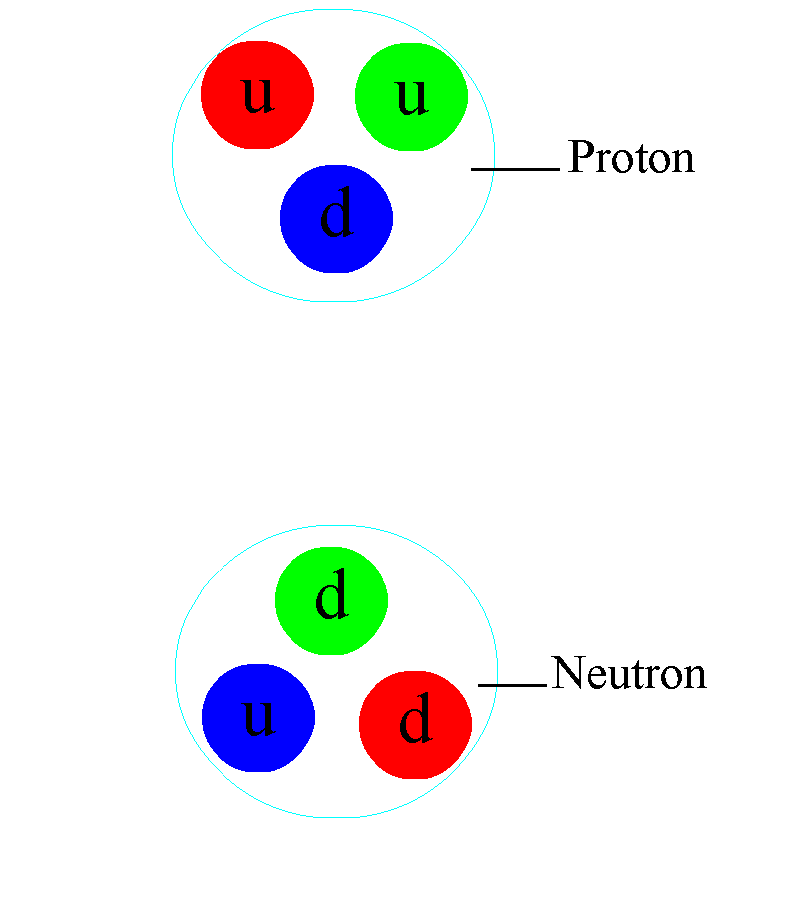
Los Quarks están confinados dentro de los nucleones (protones y neutrones)

En los núcleos atómicos reside la fuerza (nuclear fuerte) que hace posible la existencia de la materia que comienza por los átomos que, al juntarse y formar células, hace posible que éstas se junten y formen moléculas que a su vez, se reunen para formar sustancias y cuerpos.

Pero la comprensión adecuada de estas ideas tuvo que esperar hasta el siglo XX, cuando se reveló la verdadera naturaleza de las fuerzas químicas y de las fuerzas que mantienen unidos los átomos individuales. Ahora sabemos que tales fuerzas tienen un origen fundamentalmente electromagnético (que vincula y concierne a la implicación del campo electromagnético con partículas cargadas) y que la teoría del electromagnetismo es también la teoría de la luz.

Para entender los átomos y la química se necesitan otros ingredientes procedentes de la teoría cuántica, pero las ecuaciones básicas que describen el electromagnetismo y la luz fueron propuestas en 1.865 por el físico escocés James Clark Maxwell, que había sido inspirado por los magníficos descubrimientos experimentales de Michael Faraday unos treinta años antes y que él plasmó en una maravillosa teoría.

El escudo magnético de la tierra nos defiende de los campos magnéticos del Sol

El electromagnetismo es una rama de la Física que estudia y unifica los fenómenos eléctricos y magnéticos en una sola teoría. El electromagnetismo es una teoría de campos; es decir, las explicaciones y predicciones que provee se basan en magnitudes físicas vectoriales dependientes de la posición en el espacio y del tiempo.

Esta teoría del electromagnetismo de Maxwell tenía la particularidad de que requería que la velocidad de la luz tuviera un valor fijo y definido, que normalmente se conoce como c, y que en unidades ordinarias es aproximadamente 3 × 10⁸ metros por segundo. Maxwell, guiado por los experimentos de Faraday, hizo posible un hecho que cambió la historia de la humanidad para siempre. Un hecho de la misma importancia que el descubrimiento del fuego, la rueda o los metales. El matemático y poeta escocés unificó los campos eléctrico y magnético a través de unas pocas ecuaciones que describen como estos campos se entretejen y actúan sobre la materia.

Claro que, estos importantísimos avances han sido simples escalones de la “infinita” escalera que tenemos que subir y, la misma relatividad de Einstein no ha sido (después de un siglo) aún comprendido en su plenitud y muchos de sus mensajes están escondidos en lo más profundo de nuestras mentes que, ha sabido parcialmente descubrir el mensaje de Einstein pero, seguimos buscando.

Sin embargo, esto nos presenta un enigma si queremos conservar el principio de relatividad. El sentido común nos diría que si se mide que la velocidad de la luz toma el valor concreto c en el sistema de referencia del observador, entonces un segundo observador que se mueva a una velocidad muy alta con respecto al primero medirá que la luz viaja a una velocidad diferente, aumentada o disminuida, según sea el movimiento del segundo observador.

Estaría bueno que, al final se descubriera que alfa (α) tuviera un papel importante en la compleja teoría de cuerdas, ¿Por qué no? En realidad alfa, la constante de estructura fina, nos habla del magnetismo, de la constante de Planck y de la relatividad especial, es decir, la velocidad de la luz y, todo eso, según parece, emergen en las ecuaciones topológicas de la moderna teoría de cuerdas. ¡Ya veremos!

Pero el principio de relatividad exigiría que las leyes físicas del segundo observador (que definen en particular la velocidad de la luz que percibe el segundo observador) deberían ser idénticas a las del primer observador. Esta aparente contradicción entre la constancia de la velocidad de la luz y el principio de relatividad condujo a Einstein (como de hecho, había llevado previamente al físico holandés Hendrick Antón Lorentz y muy en especial al matemático francés Henri Poincaré) a un punto de vista notable por el que el principio de relatividad del movimiento puede hacerse compatible con la constancia de una velocidad finita de la luz.

¿Cómo funciona esto? Sería normal que cualquier persona creyera en la existencia de un conflicto irresoluble entre los requisitos de una teoría como la de Maxwell, en la que existe una velocidad absoluta de la luz, y un principio de relatividad según el cual las leyes físicas parecen las mismas con independencia de la velocidad del sistema de referencia utilizado para su descripción.

¿No podría hacerse que el sistema de referencia se moviera con una velocidad que se acercara o incluso superara a la de la luz? Y según este sistema, ¿no es cierto que la velocidad aparente de la luz no podría seguir siendo la misma que era antes? Esta indudable paradoja no aparece en una teoría, tal como la originalmente preferida por Newton (y parece que también por Galileo), en la que la luz se comporta como partículas cuya velocidad depende de la velocidad de la fuente. En consecuencia, Galileo y Newton podían seguir viviendo cómodamente con un principio de relatividad.

La velocidad de la luz en el vacío es una constante de la Naturaleza y, cuando cientos de miles de millones de millones salen disparados de esta galaxia hacia el vacío espacial, su velocidad de 299.792.450 metros por segundo, es constante independientemente de la fuente que pueda emitir los fotones y de si ésta está en reposo o en movimiento.

Así que, la antigua imagen de la naturaleza de la luz entró en conflicto a lo largo de los años, como era el caso de observaciones de estrellas dobles lejanas que mostraban que la velocidad de la luz era independiente de la de su fuente. Por el contrario, la teoría de Maxwell había ganado fuerza, no sólo por el poderoso apoyo que obtuvo de la observación (muy especialmente en los experimentos de Heinrich Hertz en 1.888), sino también por la naturaleza convincente y unificadora de la propia teoría, por la que las leyes que gobiernan los campos eléctricos, los campos magnéticos y la luz están todos subsumidos en un esquema matemático de notable elegancia y simplicidad.

Las ondas luminosas como las sonoras, actúan de una u otra manera dependiendo del medio en el que se propagan.

En la teoría de Maxwell, la luz toma forma de ondas, no de partículas, y debemos enfrentarnos al hecho de que en esta teoría hay realmente una velocidad fija a la que deben viajar las ondas luminosas.

El punto de vista geométrico-espaciotemporal nos proporciona una ruta particularmente clara hacia la solución de la paradoja que presenta el conflicto entre la teoría de Maxwell y el principio de relatividad.

Este punto de vista espaciotemporal no fue el que Einstein adoptó originalmente (ni fue el punto de vista de Lorentz, ni siquiera, al parecer, de Poincaré), pero, mirando en retrospectiva, podemos ver la potencia de este enfoque. Por el momento, ignoremos la gravedad y las sutilezas y complicaciones asociadas que proporciona el principio de equivalencia y otras complejas cuestiones, que estimo aburrirían al lector no especialista, hablando de que en el espacio-tiempo se pueden concebir grupos de todos los diferentes rayos de luz que pasan a ser familias de íneas de universo.

                                  La maravilla de los cuantos llamados fotones

Baste saber que, como quedó demostrado por Einstein, la luz, independientemente de su fuente y de la velocidad con que ésta se pueda mover, tendrá siempre la misma velocidad en el vacío, c, o 299.792.458 metros por segundo. Cuando la luz atraviesa un medio material, su velocidad se reduce. Precisamente, es la velocidad c el límite alcanzable de la velocidad más alta del universo. Es una constante universal y, como hemos dicho, es independiente de la velocidad del observador y de la fuente emisora.

El Universo está dentro de nuestras Mentes

¡La Mente! Qué caminos puede recorrer y, sobre todo ¿Quién la guía? Comencé este trabajo con la imagen del ojo humano y hablando de los sentidos y de la consciencia y mira donde he finalizado…Sí, nos falta mucho camino por recorrer para llegar a desvelar los misterios de la Mente que, en realidad, es la muestra más alta que el Universo nos puede mostrar de lo que puede surgir a partir de la sencillez de los átomos de hidrógeno que, evolucionados, primero en las entrañas de las estrellas y después en los circuitos de nuestras mentes, llega hasta los pensamientos y la imaginación que…son palabras mayores de cuyo alcance, aún no tenemos una idea que realmente refleje su realidad.

Todo en nuestro universo ambia, comienza siendo una cosa y finaliza siendo otra

Pero, ¿existe alguna realidad?, o, por el contrario todo es siempre cambiante y lo que hoy es mañana no existirá, si “realmente” es así, ocurre igual que con el tiempo. La evolución es algo que camina siempre hacia adelante, es inexorable, nunca se para y, aunque como el tiempo pueda ralentizarse, finalmente sigue su camino hacia esos lugares que ahora, sólo podemos imaginar y que, seguramente, nuestros pensamientos no puedan (por falta de conocimientos) plasmar en lo que será esa realidad futura.

Emilio Silvera Vázquez

[?]