Dic
27
Sobre el Modelo Estándard de la Física
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)
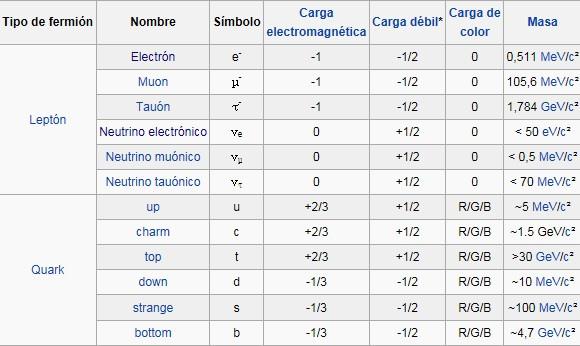
Puedo ver los átomos, los protones y neutrones y, en su interior, los diminutos quarks enfangados en un mar de gluones. Pensar que esas pequeñas cositas son capaces (con la ayuda de las fuerzas fundamentales de la Naturaleza) de construir todo lo que podemos ver…

Me resulta, siempre sorprendente. ¡Qué maravilla!
Dic
21
La Libertad Asintótica en El Carnaval de la Física
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
La fuerza nuclear fuerte actúa al contrario de las otras fuerzas, con la distancia se fortalece y en la cercanía es más débil. Así, los Bosones que llamamos Gluones actúan como muelles de acero, cuanto más los estiramos más resistencia oponen.
Los Quarks están confinados dentro de los protones y neutrones que, son llamados nucleones dentro del núcleo atómico.
Podríamos poner aquí miles de ejemplos de idas brillantes salidas de mentes humanas. Sin embargo, me viene a la memoria un titular: “Los descubridores del PEGAMENTO que une la materia ganan el Nobel de Física” (decía un periódico allá por el último trimestre de 2.004).
La noticia se refería a David Gross, David Politzer y Frank Wilczek, los descubridores del funcionamiento de la fuerza que cohesionan a los quarks, las partículas más elementales.
Cualquiera que haya leído sobre temas de ciencia de la materia, sabe que desde los tiempos de la antigua Grecia hasta el de Einstein, el gran sueño de todos los sabios que han estudiado la naturaleza ha sido una descripción precisa y completa de nuestro Universo, las constantes de la Naturaleza y las fuerzas fundamentales, algo que ya está más cerca gracias al trabajo de estos tres científicos estadounidenses.
Hace más de treinta años que Gross, Politzer y Wilczek desvelaron el enigmático funcionamiento de la llamada interacción fuerte, una de las cuatro fuerzas fundamentales que rigen el Universo, y que actúa como un pegamento cósmico para mantener unida la materia. Su trabajo reveló como los quarks, las diminutas partículas que forman los nucleones de los átomos, interaccionan entre sí para mantenerse unidos.
Las fuerzas que podemos sentir en la vida cotidiana, es decir, la Gravedad y el electromagnetismo, aumentan con la cercanía: así, cuando más cerca está un clavo de un imán o una manzana del suelo, más se verán atraídos.
Dic
18
La simetría CP y otros aspectos de la Física
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

.. “Nature publica una recreación del experimento E122 de hace 35 años,” LCMF, 06 Feb 2014; “Los quarks se mueven al otro lado del espejo,” Agencia SINC,

Los quarks al otro lado del espejo. También un Equipo de Científicos del Laboratorio Nacional Jefferson Lab (EEUU) han verificado la rotura de la simetría de paridad (también llamada simetría del espejo) en los quarks mediante el bombardeo de núcleos de deuterio con electrones de alta energía. Los núcleos de deuterio están formados por un protón y un neutrón, es decir, por tres quarks arriba y tres quarks abajo. La dispersión inelástica entre un electrón y un quark, es decir, su colisión, está mediada por la interacción electrodébil, tanto por la fuerza electromagnética como por la fuerza débil. Esta última es la única interacción fundamental que viola la simetría de paridad.

Tenemos que saber cómo la violación de la simetría CP (el proceso que originó la materia) aparece, y, lo que es más importante, hemos de introducir un nuevo fenómeno, al que llamamos campo de Higgs, para preservar la coherencia matemática del modelo estándar. La idea de Higgs, y su partícula asociada, el bosón de Higgs, cuenta en todos los problemas que he mencionado antes. Parece, con tantos parámetros imprecisos (19) que, el modelo estándar se mueve bajo nuestros pies.
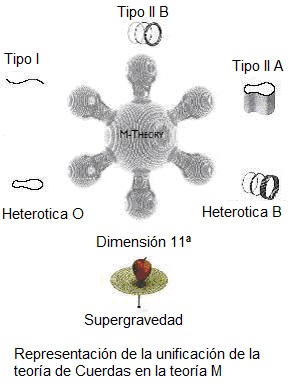
Entre los teóricos, el casamiento de la relatividad general y la teoría cuántica es el problema central de la física moderna. A los esfuerzos teóricos que se realizan con ese propósito se les llama “super-gravedad”, “súpersimetría”, “supercuerdas” “teoría M” o, en último caso, “teoría de todo o gran teoría unificada”.
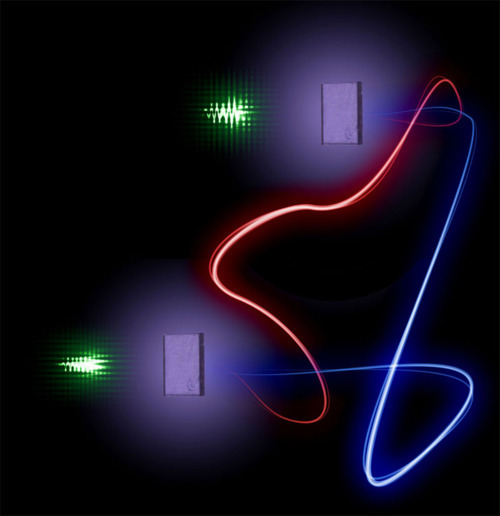
La Física nos lleva de vez en cuando a realizar viajes alucinantes. Se ha conseguido relacionar y vibrar a dos diamantes en el proceso conocido como entrelazamiento cuántico. El misterioso proceso, al que el propio Eisntein no supo darle comprensión completa, supone el mayor avance la fecha y abre las puertas de la computación cuántica. que nos hagamos una idea del hallazgo, en 1935 Einstein lo llegó a denominar la “acción fantasmal a distancia”. Un efecto extraño en donde se conecta un objeto con otro de manera que incluso si están separados por grandes distancias, una acción realizada en uno de los objetos afecta al otro.

Ahí tenemos unas matemáticas exóticas que ponen de punta hasta los pelos de las cejas de algunos de los mejores matemáticos del mundo (¿y Perelman? ¿Por qué nos se ha implicado?). Hablan de 10, 11 y 26 dimensiones, siempre, todas ellas espaciales menos una que es la temporal. Vivimos en cuatro: tres de espacio (este-oeste, norte-sur y arriba-abajo) y una temporal. No podemos, ni sabemos o no es posible instruir, en nuestro cerebro (también tridimensional), ver más dimensiones. Pero llegaron Kaluza y Klein y compactaron, en la longitud de Planck las dimensiones que no podíamos ver. ¡Problema solucionado! Pero se sigue hablando de partículas super-simétricas.
¿Quién puede ir a la longitud de Planck para verlas?
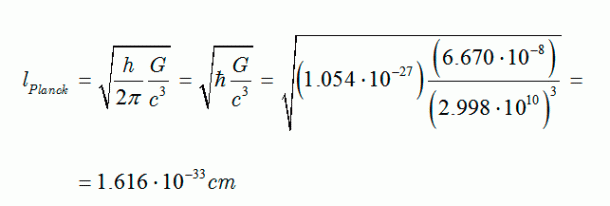

La puerta de las dimensiones más altas quedó abierta y, a los teóricos, se les regaló una herramienta maravillosa. En el Hiperespacio, todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí si es posible encontrar esa soñada teoría de la Gravedad cuántica.
Así que, los teóricos, se han embarcado a la búsqueda de un objetivo audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intento calor del universo en sus primeros tiempos, una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.
¿Dónde radica el problema?
El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni la nueva capacidad energético del acelerador de partículas LHC . Ni sumando todos los aceleradores de partículas de nuestro mundo, podríamos lograr una energía de Planck (1019 GeV), que sería necesaria para poder llegar hasta las cuerdas vibrantes de la Teoría. Ni en las próximas generaciones seremos capaces de poder utilizar tal energía.
La verdad es que, la teoría que ahora tenemos, el Modelo Estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías. Sabemos sobre las partíoculas elementales que conforman la materia bariónica, es decir, los átomos que se juntan para formar moléculas, sustancias y cuerpos… ¡La materia! Pero, no sabemos si, pudiera haber algo más elemental aún más allá de los Quarks y, ese algo, pudieran ser esas cuerdas vibrantes que no tenemos capacidad de alcanzar.
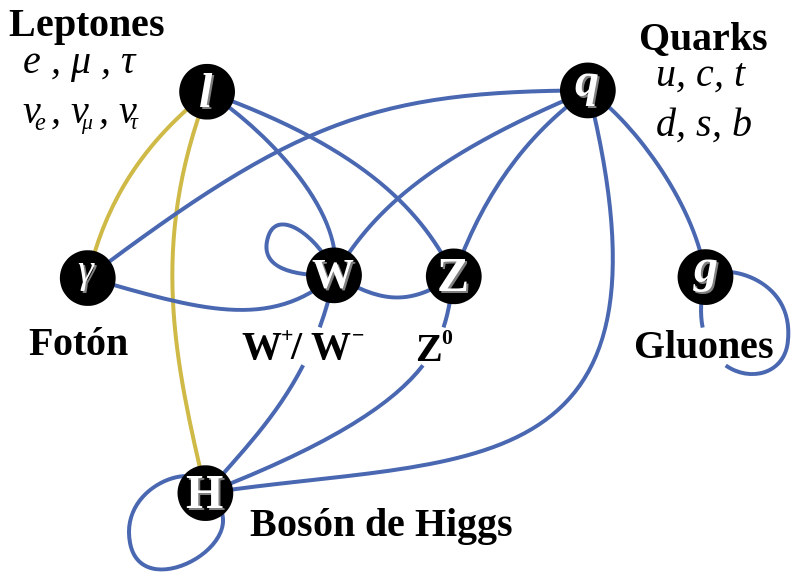
¡Necesitamos algo más avanzado!
Se ha dicho que la función de la partícula de Higgs es la de dar masa a las Cuando su autor lanzó la idea al mundo, resultó además de nueva muy extraña. El secreto de todo radica en conseguir la simplicidad: el átomo resulto ser complejo lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones, resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún, los quarks que estaban instalados en nubes de otras partículas llamadas gluones y, ahora, queremos continuar profundizando, sospechamos, que después de los quarks puede haber algo más.


Con 7 TeV ha sido suficiente para encontrar la famosa partícula de Higgs pero…
Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes. Es decir, que si miramos a las estrellas en una noche clara estamos mirando el campo de Higgs. Las partículas influidas por este campo, toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado, del campo gravitatorio o del electromagnético. Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquiriría energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra.
Si viajamos muy rápido la masa aumenta
Como E=mc2, ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del Sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein. La masa, m, tiene en realidad dos partes. Una es la masa en reposo, m0, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c) o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.
Peor la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas.

Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs (podría ser el efecto frenado de Ramón Márquez).
La influencia de Higgs en las masas de los quarks y de los leptones, nos recuerda el descubrimiento por Pietez Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.
Hasta ahora no tenemos ni idea de que reglas controlan los incrementos de masa generados por el Higgs (de ahí la expectación creada por el nuevo acelerador de partículas LHC). Pero el problema es irritante: ¿por qué sólo esas masas -Las masas de los W+, W–, y Zº, y el up, el down, el encanto, el extraño, el top y el bottom, así como los leptones – que no forman ningún patrón obvio?
Las masas van de la del electrón 0’0005 GeV, a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electro-débil (Weinberg-Salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnéticas y débiles. En la unidad hay cuatro partículas mensajeras sin masa -los W+, W–, Zº y fotón que llevan la fuerza electro-débil. Además está el campo de Higgs, y, rápidamente, los W y Z chupan la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electro-débil se fragmenta en la débil (débil porque los mensajeros son muy gordos) y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen los teóricos. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa.
Las masas de los W y el Z se predijeron con éxito a partir de los parámetros de la teoría electro-débil. Y las relajadas sonrisas de los físicos teóricos nos recuerdan que ^t Hooft y Veltman dejaron sentado que la teoría entera esta libre de infinitos.

Todos los intentos y los esfuerzos por hallar una pista del cuál era el origen de la masa fallaron. Feynman escribió su famosa pregunta: “¿Por qué pesa el muón?”. Ahora, por lo menos, tenemos una respuesta parcial, en absoluto completa. Una vez potente y segura nos dice: “!Higgs¡” Durante más de 60 años los físicos experimentadores se rompieron la cabeza con el origen de la masa, y ahora el campo Higgs presenta el problema en un contexto nuevo; no se trata sólo del muón. Proporciona, por lo menos, una fuente común para todas las masas. La nueva pregunta feynmaniana podría ser: ¿Cómo determina el campo de Higgs la secuencia de masas, aparentemente sin patrón, que da a las partículas de la materia?
La variación de la masa con el estado de movimiento, el cambio de masa con la configuración del sistema y el que algunas partículas (el fotón seguramente y los neutrinos posiblemente) tengan masa en reposo nula son tres hechos que ponen entre dicho que el concepto de masa sea una tributo fundamental de la materia. Habrá que recordar aquel cálculo de la masa que daba infinito y nunca pudimos resolver; los físicos sólo se deshicieron del “renormalizándolo”, ese truco matemático que emplean cuando no saben hacerlo bien.
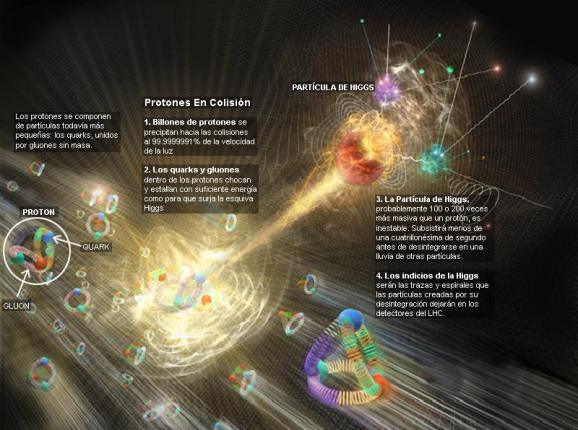
En los alrededores de Ginebra (Suiza), en las entrañas de las montañas del Jura construyeron un túnel de 27 Km. de circunferencia. Es el Acelerador más grande del mundo, el LHC. Allí mismo se está planeando construir uno mayor aún con el que, utilizando energías inusitadas e impensables hasta hace unos pocos años, se tratará de buscar el origen de la masa.
Ese es el problema de trasfondo con el que tenemos que encarar el problema de los quarks, los leptones y los vehículos de las fuerzas, que se diferencian por sus masas. Hace que la historia de Higgs se tenga en pie: la masa no es una propiedad intrínseca de las partículas, sino una propiedad adquirida por la interacción de las partículas y su entorno.
La idea de que la masa no es intrínseca como la carga o el espín resulta aún más plausible por la idílica idea de que todos los quarks y fotones tendrían masa cero. En ese caso, obedecerían a una simetría satisfactoria, la quiral, en laque los espines estarían asociados para siempre con su dirección de movimiento. Pero ese idilio queda oculto por el fenómeno de Higgs.
¡Ah, una cosa más! Hemos hablado de los bosones gauge y de su espín de una unidad; hemos comentado también las partículas fermiónicas de la materia (espín de media unidad). ¿Cuál es el pelaje de Higgs? Es un bosón de espin cero. El espín supone una direccionalidad en el espacio, pero el campo de Higgs de masa a los objetos dondequiera que estén y sin direccionalidad. Al Higgs se le llama a veces “bosón escalar” [sin dirección] por esa razón.
Basta con cambiar un quark tipo U a uno tipo D.
Pues justamente esto es lo que ocurre en la naturaleza cuando entra en acción la fuerza nuclear débil. Un quark tipo U cambia a uno tipo D por medio de la interacción débil así
Las otras dos partículas que salen son un anti-electrón y un neutrino. Este mismo proceso es el responsable del decaimiento radiactivo de algunos núcleos atómicos. Cuando un neutrón se convierte en un protón en el decaimiento radiactivo de un núcleo, aparece un electrón y un neutrino. Este es el origen de la radiación beta (electrones).
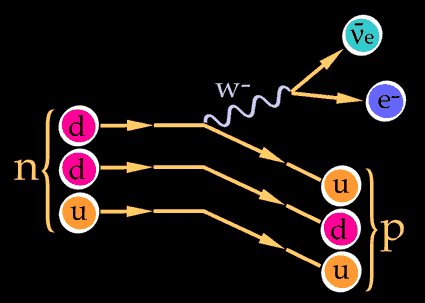
La interacción débil, recordareis, fue inventada por E. Fermin para describir la desintegración radiactiva de los núcleos, que era básicamente un fenómeno de poca energía, y a medida que la teoría de Fermi se desarrolló, llegó a ser muy precisa a la hora de predecir un enorme número de procesos en el dominio de energía de los 100 MeV. Así que ahora, con las nuevas tecnologías y energías del LHC, las esperanzas son enormes para, por fin, encontrar el bosón Higgs origen de la masa… y algunas cosas más.
Hay que responder montones de preguntas. ¿Cuáles son las propiedades de las partículas de Higgs y, lo que es más importante, cuál es su masa? ¿Cómo reconoceremos una si nos la encontramos en una colisión de LHC? ¿Cuántos tipos hay? ¿Genera el Higgs todas las masas, o solo las hace incrementarse? ¿Y, cómo podemos saber más al respecto? Como s su partícula, nos cabe esperar que la veamos ahora después de gastar más de 50.000 millones de euros en los elementos necesarios para ello.

También a los cosmólogos les fascina la idea de Higgs, pues casi se dieron de bruces con la necesidad de tener campos escalares que participasen en el complejo proceso de la expansión del Universo, añadiendo, pues, un peso más a la carga que ha de soportar el Higgs.
El campo de Higgs, tal y como se lo concibe ahora, se puede destruir con una energía grande, o temperaturas altas. Estas generan fluctuaciones cuánticas que neutralizan el campo de Higgs. Por lo tanto, el cuadro que las partículas y la cosmología pintan juntas de lo que un universo primitivo puso y de resplandeciente simetría es demasiado caliente para Higgs. Pero cuando la temperatura cae bajo los 10′5 grados kelvin o 100 GeV, el Higgs empieza a actuar y hace su generación de masas. Así por ejemplo, antes de Higgs teníamos unos W, Z y fotones sin masa y la fuerza electro-débil unificada.
El Universo se expande y se enfría, y entonces viene el Higgs (que engorda los W y Z, y por alguna razón ignora el fotón) y de ello resulta que la simetría electro-débil se rompe.
Tenemos entonces una interacción débil, transportada por los vehículos de la fuerza W+, W–, Z0, y por otra parte una interacción electromagnética, llevada por los fotones. Es como si para algunas partículas del campo de Higgs fuera una especie de aceite pesado a través del que se moviera con dificultad y que las hiciera parecer que tienen mucha masa. Para otras partículas, el Higgs es como el agua, y para otras, los fotones y quizá los neutrinos, es invisible.
De todas las maneras, es tanta la ignorancia que tenemos sobre el origen de la masa que, nos agarramos como a un clavo ardiendo el que se ahoga, en este caso, a la partícula de Higgs que, algunos, han llegado a llamar, de manera un poco exagerada:
¡La partícula Divina! (Como la llamó Lederman en su libro).

¡Ya veremos en que termina todo esto! Y que explicación se nos ofrece desde el CERN en cuanto al auténtico escenario que según ellos, existe en el Universo para que sea posible que las partículas tomen su masa de ese oceáno de Higgs, en el que, según nuestro amigo Ramón Márquez, las partículas se frenan al interaccionar con el mismo y toman su masa, el lo llama el “efecto frenado”.
Peter Higgs, de la Universidad de Edimburgo, introdujo la idea en la física de partículas. La utilizaron los teóricos steven Weinberg y Abdus Salam, que trabajaban por separado, para comprender como se convertía la unificada y simétrica fuerza electrodébil, transmitida por una feliz familia de cuatro partículas mensajeras de masa nula, en dos fuerzas muy diferentes: la QED con un fotón carente de masa y la interacción débil con sus W+, W– y Z0 de masa grande. Weinberg y Salám se apoyaron en los trabajos previos de Sheldon Glasgow, quien tras los pasos de Julian Schwinger, sabía sólo que había una teoría electrodébil unificada, coherente, pero no unió todos los detalles. Y estaban Jeffrey Goldstone y Martines Veltman y Gerard’t Hooft. También hay otras a los que había que mencionar, pero lo que siempre pasa, quedan en el olvido de manera muy injusta. Además, ¿Cuántos teóricos hacen falta para encender una bombilla?
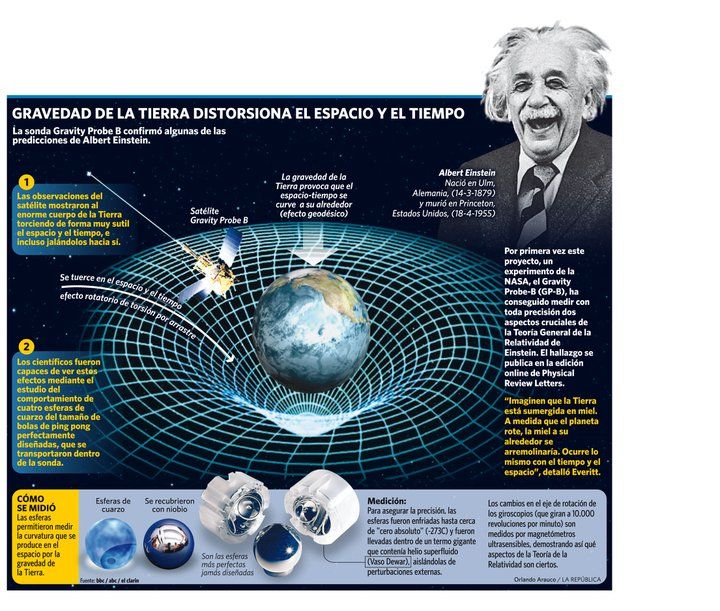
La verdad es que, casi siempre, han hecho falta muchos. Recordemos el largo recorrido de los múltiples detalle sueltos y físicos que prepararon el terreno para que, llegara Einstein y pudiera, uniéndolo todos, exponer su teoría relativista. (Mach, Maxwell, Lorentz… y otros).
Sobre la idea de Peter Higgs, Veltman, uno de sus arquitectos, dice que es una alfombra bajo la que barremos nuestra ignorancia. Glasgow es menos amable y lo llamó retrete donde echamos las incoherencias de nuestras teorías actuales. La objeción principal: que no tenemos la menor prueba experimental.

Ahora, por fin la tenemos con el LHC, y ésta pega, se la traspasamos directamente a la teoría de supercuerdas y a la materia oscura que, de momento, están en la sombra y no brillan con luz propia, toda vez que ninguna de ellas ha podido ser verificada, es decir, no sabemos si el Universo atiende a lo que en ellas se predice.
El modelo estándar es lo bastante fuerte para decirnos que la partícula de Higgs de menor masa (podría haber muchas) debe “pesar” menos de 1 TeV. ¿Por qué? Si tiene más de 1 TeV, el modelo estándar se vuelve incoherente y tenemos la crisis de la unitariedad.
Después de todo esto, llego a la conclusión de que, el campo de Higgs, el modelo estándar y nuestra idea de cómo pudo surgir el Universo no dependen de que se encuentre el bosón de Higgs o se averigüe si realmente existe la materia oscura, Aunque sepamos llegar al fondo de la Teoría de Cuerdas y confirmarla, Poder crear esa Teoría cuántica de la Gravedad…Y, en fin, seguir descubriendo los muchos misterios que no nos dejan saber lo que el Universo es. Ahora, por fin, tenemos grandes aceleradores y Telescopios con la energía necesaria y las condiciones tecnológicas suficientes para que nos muestre todo eso que queremos saber y nos digan dónde reside esa verdad que incansables perseguimos. Sin embargo, siempre seguiremos haciendo preguntas y siempre, también, serán insuficientes, los aparatos que podamos construir para que nos digan como es el Universo y cómo funciona la Naturaleza. Saberlo todo, nunca sabremos.
¡La confianza en nosotros mismos, no tiene límites! Pero, no siempre ha estado justificada.
emilio silvera
Dic
14
Nada en el Universo podrá ir más rápido que la Luz
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Relativista ~
Clasificado en Física Relativista ~
 Comments (14)
Comments (14)

¿Por qué la materia no puede moverse más deprisa que la velocidad de la luz?
Para contestar esta pregunta hay que advertir al lector que la energía suministrada a un cuerpo puede influir sobre él de distintas maneras. Si un martillo golpea a un clavo en medio del aire, el clavo sale despedido y gana energía cinética o, dicho de otra manera, energía de movimiento. Si el martillo golpea sobre un clavo, cuya punta está apoyada en una madera dura e incapaz de moverse, el clavo seguirá ganando energía, pero esta vez en forma de calor por rozamiento al ser introducido a la fuerza dentro de la madera.
Albert Einstein demostró en su teoría de la relatividad especial que la masa cabía contemplarla como una forma de energía (E = mc2, la bomba atómica lo confirmó). Al añadir energía a un cuerpo, esa energía puede aparecer en la forma de masa o bien en otra serie de formas.
En condiciones ordinarias, la ganancia de energía en forma de masa es tan increiblemente pequeña que sería imposible medirla. Fue en el siglo XX (al observar partículas subatómicas que, en los grandes aceleradores de partículas, se movían a velocidades de decenas de miles de kilómetros por segundo) cuando se empezaron a encontrar aumentos de masa que eran suficientemente grandes para poder detectarlos. Un cuerpo que se moviera a unos 260.000 Km por segundo respecto a nosotros mostraría una masa dos veces mayor que cuando estaba en reposo (siempre respecto a nosotros).
Dic
10
Creemos cosas que…, ¿serán ciertas?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
La verdadera Historia de la Teoría del Caos

Diagrama de la trayectoria del sistema de Lorenz para los valores r = 28, σ = 10, b = 8/3.
Teoría del caos es la denominación popular de la rama de las matemáticas, la física y otras disciplinas científicas que trata ciertos tipos de sistemas dinámicos muy sensibles a las variaciones en las condiciones iniciales. Pequeñas variaciones en dichas condiciones iniciales pueden implicar grandes diferencias en el comportamiento futuro, imposibilitando la predicción a largo plazo. Esto sucede aunque estos sistemas son en rigor determinísticos, es decir; su comportamiento puede ser completamente determinado conociendo sus condiciones iniciales.
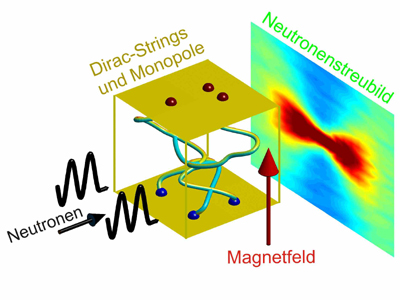
Montaje experimental. Foto: HZB, D.J.P. Morris y A. Tennant. Monopolos magneticos .
Hubo un tiempo, el el Universo muy temprano, en el que la temperatura estaba encima de algunos cientos de veces la masa del protón, cuando la simetría aún no se había roto, y la fuerza débil y electromagnética no sólo eran la misma matemáticamente, sino realmente la misma. Un físico que hibiera podido estar allí presente, en aquellos primeros momento, no habría podido observar ninguna diferencia real entre las fuerzas producidas por el intercambio de estas cuatro partículas: las W, la Z y el Fotón.

Muchas son las sorpresas que nos podríamos encontrar en el universo primitivo, hasta la presencia de agua ha sido detectada mediante la técnica de lentes gravitacionales en la galaxia denominada MG J0414+0534 que está situada en un tiempo en el que el Universo sólo tenía dos mil quinientos millones de años de edad. El equipo investigador pudo detectar el vapor de agua presente en los chorros de emisión de un agujero negro super-masivo. Este tipo de objeto es bastante raro en el universo actual. El agua fue observada en forma de mases, una emisión de radiación de microondas provocada por las moléculas (en este caso de agua) al ser amplificadas por una onda o un campo magnético.
Siguiendo con el trabajo, dejemos la noticia de más arriba (sólo insertada por su curiosidad y rareza), y, sigamos con lo que hemos contado repetidas veces aquí de las fuerzas y la simetría antes de que, el universo se expandiera y enfriara para que, de una sola, surgieran las cuatro fuerzas que ahora conocemos: Gravedad que campa sola y no quiere juntarse con las otras fuerzas del Modelo Estándar, el electromagnetismo y las nucleares débil y fuerte.
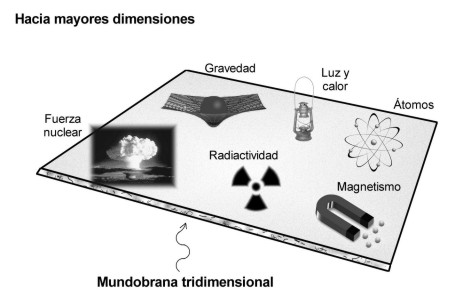
Las fuerzas de la naturaleza que gobiernan la electricidad, el magnetismo, la radiactividad y las reacciones nucleares están confinadas a un “mundo-brana” tridimensional, mientras que la gravedad actúa en todas las dimensiones y es consecuentemente más débil. Seguramente ese será el motivo por el cual, encontrar al Bosón mediador de la fuerza, el Gravitón, resulta tan difícil.
De manera similar, aunque menos clara, las teorías de supersimetrías conjeturaban que las cuatro fuerzas tal vez estaban ligadas por una simetría que se manifestaba en los niveles de energía aún mayores que caracterizaban al universo ya antes del Big Bang. La introducción de un eje histórico en la cosmología y la física de particulas (como decía ayer en uno de los trabajos), beneficio a ambos campos. Los físicos proporcionaron a los cosmólogos una amplia gama de herramientas útiles para saber cómo se desarrolló el universo primitivo. Evidentemente, el Big Bang no fue una muralla de fuego de la que se burló Hoyle, sino un ámbito de sucesos de altas energías que muy posiblemente pueden ser comprensibles en términos de teoría de campo relativista y cuántica.

La cosmología, por su parte, dio un tinte de realidad histórica a las teorías unificadas. Aunque ningún acelerador concebible podrían alcanzar las titánicas energías supuestas por las grandes teorías unificadas y de la supersimetría, esas exóticas ideas aún pueden ser puestas a prueba, investigando su las partículas constituyentes del universo actual son compatibles con el tipo de historia primitiva que implican las teorías.
Gell-Mann, el premio Nobel de física, al respeto de todo esto decía: “Las partículas elementales aparentemente proporcionan las claves de algunos de los misterios fundamentales de la Cosmología temprana… y resulta que la Cosmología brinda una especia de terreno de prueba para alguna de las ideas de la física de partículas elementales.” Hemos podido llegar a descubrir grandes secretos de la naturaleza mediante los pensamientos que, surgidos de la mente desconocida y misteriosa de algunos seres humanos, han podido ser intuidos mediante ráfagas luminosas que nunca sabremos de dónde pudieron surgir )Lorentz, Planck, Einstein, Heisenberg, Dirac, Eddigton, Feymann, Wheeler… Y, una larga lista de privilegiados que pudieron ver, lo que otros no podían.
Moléculas, átomos y conexiones para formar pensamientos
Hemos llegado a poder discernir la relación directa que vincula el tamaño, la energía de unión y la edad de las estructuras fundamentales de la Naturaleza. Una molécula es mayor y más fácil de desmembrar que un átomo; lo mismo podemos decir de un átomo respecto al núcleo atómico, y de un núcleo con respecto a los quarks que contiene. La cosmología sugiere que esta relación resulta del curso de la historia cósmica, que los quarks se unieron primero en las energías extremadamente altas del big bang original y que a medida que el Universo se expandió, los protones y neutrones compuestos de quarks se unieron para formar núcleos de átomos, los cuales, cargados positivamente, atrajeron a los electrones cargados con electricidad negativa estableciéndose así como átomos completos, que al unirse formaron moléculas.
Si es así (que lo es), cuanto más íntimamente examinemos la Naturaleza, tanto más lejos hacia atrás vamos en el tiempo. Alguna vez he puesto el ejemplo de mirar algo que no es familiar, el dorso de la mano, por ejemplo, e imaginemos que podemos observarlo con cualquier aumento deseado.
Con un aumento relativamente pequeño, podemos ver las células de la piel, cada una con un aspecto tan grande y complejo como una ciudad, y con sus límites delineados por la pared celular. Si elevamos el aumento, veremos dentro de la célula una maraña de ribosomas serpenteando y mitocondrias ondulantes, lisosomas esféricos y centríolos, cuyos alrededores están llenos de complejos órganos dedicados a las funciones respiratorias, sanitarias y de producción de energía que mantienen a la célula.
Ya ahí tenemos pruebas de historia. Aunque esta célula particular solo tiene unos pocos años de antigüedad, su arquitectura se remonta a más de mil millones de años, a la época en que aparecieron en la Tierra las células eucariota o eucarióticas como la que hemos examinado.
Para determinar dónde obtuvo la célula el esquema que le indicó como formarse, pasemos al núcleo y contemplemos los delgados contornos de las macromoléculas de ADN segregadas dentro de sus genes. Cada una contiene una rica información genética acumulada en el curso de unos cuatro mil millones de años de evolución.
Almacenado en un alfabeto de nucleótidos de cuatro “letras”- hecho de moléculas de azúcar y fosfatos, y llenos de signos de puntuación, reiteraciones para precaver contra el error, y cosas superfluas acumuladas en los callejones sin salida de la historia evolutiva-, su mensaje dice exactamente cómo hacer un ser humano, desde la piel y los huesos hasta las células cerebrales.
Si elevamos más el aumento veremos que la molécula de ADN está compuesta de muchos átomos, con sus capas electrónicas externas entrelazadas y festoneadas en una milagrosa variedad de formas, desde relojes de arena hasta espirales ascendentes como largos muelles y elipses grandes como escudos y fibras delgadas como puros. Algunos de esos electrones son recién llegados, recientemente arrancados a átomos vecinos; otros se incorporaron junto a sus núcleos atómicos hace más de cinco mil millones de años, en la nebulosa de la cual se formó la Tierra.
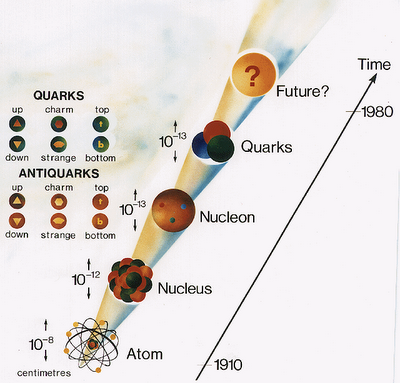
Una molécula es mayor y más fácil de desmembrar que un átomo; lo mismo podemos decir de un átomo respecto al núcleo atómico, y de un núcleo con respecto a los quarks que contiene. Sion embargo, nos queda la duda de: ¿qué podrá haber más allá de los Quarks?
¿Qué no podremos hacer cuando conozcamos la naturaleza real del átomo y de la luz? El fotón, ese cuánto de luz que parece tan insignificante, nos tiene que dar muchas satisfacciones y, en él, están escondidos secretos que, cuando sean revelados, cambiará el mundo. Esa imagen de arriba que está inmersa en nosotros en en todo el Universo, es la sencilles de la complejidad. A partir de ella, se forma todo: la muy pequeño y lo muy grande.
Si elevamos el aumento cien mil veces, el núcleo de un átomo de carbono se hinchará hasta llenar el campo de visión. Tales núcleos y átomos se formaron dentro de una estrella que estalló mucho antes de que naciera el Sol. Si podemos aumentar aún más, veremos los tríos de quarks que constituyen protones y neutrones. Los quarks han estado unidos desde que el Universo sólo tenía unos pocos segundos de edad.
Al llegar a escalas cada vez menores, también hemos entrado en ámbitos de energías de unión cada vez mayores. Un átomo puede ser desposeído de su electrón aplicando sólo unos miles de electrón-voltios de energía. Sin embargo, para dispersar los nucleones que forman el núcleo atómico se requieren varios millones de electrón-voltios, y para liberar los quark que constituyen cada nucleón.

Uno de los misterios de la naturaleza, están dentro de los protones y neutrones que, conformados por Quarks, resulta que, si estos fueran liberados, tendrían independientemente, más energía que el protón que conformaban. ¿Cómo es posible eso?
Introduciendo el eje de la historia, esta relación da testimonio del pasado de las partículas: las estructuras más pequeñas, más fundamentales están ligadas por niveles de energía mayores porque las estructuras mismas fueron forjadas en el calor del Big Bang. Esto implica que los aceleradores de partículas, como los telescopios, funcionen como máquinas del tiempo. Un telescopio penetra en el pasado en virtud del tiempo que tarda la luz en desplazarse entre las estrellas; un acelerador recrea, aunque sea fugazmente, las condiciones que prevalecían en el Universo primitivo. El acelerador de 200 Kev diseñado en los años veinte por Cockroft y Walton reproducía algunos de los sucesos que ocurrieron alrededor de un día después del comienzo del Big Bang. Los aceleradores construidos en los años cuarenta y cincuenta llegaron hasta la marca de un segundo. El Tevatrón del Fermilab llevó el límite a menos de una milmillonésima de segundo después del comienzo del Tiempo. El nuevo LHC proporcionara un atisbo del medio cósmico cuando el Universo tenía menos de una billonésima de segundo de edad.
El Tevatrón del Fermilab y el LHC
Esta es una edad bastante temprana: una diez billonésima de segundo es menos que un pestañeo con los párpados en toda la historia humana registrada. A pesar de ello, extrañamente, la investigación de la evolución del Universo recién nacido indica que ocurrieron muchas cosas aún antes, durante la primera ínfima fracción de un segundo.
Todos los teóricos han tratado de elaborar una explicación coherente de los primeros momentos de la historia cósmica. Por supuesto, sus ideas fueron esquemáticas e incompletas, muchas de sus conjeturas, sin duda, se juzgaran deformadas o sencillamente erróneas, pero constituyeron una crónica mucho más esclarecedora del Universo primitivo que la que teníamos antes.
A los cien millones de años desde el comienzo del tiempo, aún no se habían formado las estrellas, si acaso, algunas más precoces. Aparte de sus escasas y humeantes almenaras, el Universo era una sopa oscura de gas hidrógeno y helio, arremolinándose aquí y allá para formar protogalaxias.

He aquí la primera imagen jamás obtenida de antimateria, específicamente un “anti-átomo” de anti-hidrógeno. Este experimento se realizó en el Aparato ALPHA de CERN, en donde los anti-átomos fueron retenidos por un récord de 170 milisegundos (se atraparon el 0.005% de los anti-átomos generados).
A la edad de mil millones de años, el Universo tiene un aspecto muy diferente. El núcleo de la joven Vía Láctea arde brillantemente, arrojando las sobras de cumulonimbos galácticos a través del oscuro disco; en su centro brilla un quasar blanco-azulado. El disco, aún en proceso de formación, es confuso y está lleno de polvo y gas; divide en dos partes un halo esférico que será oscuro en nuestros días, pero a la sazón corona la galaxia con un brillante conjunto de estrellas calientes de primera generación.
Para determinar dónde obtuvo la célula es esquema que le indicó como formarse, pasemos al núcleo y contemplemos los delgados contornos de las macromoléculas de ADN segregadas dentro de sus genes. Cada una contiene una rica información genética acumulada en el curso de unos cuatro mil millones de años de evolución.
Claro que, nuestra historia está relacionada con todo lo que antes de llegar la vida al Universo pudo pasar. ¡Aquella primera célula! Se replicó en la sopa primordial llamada Protoplasma vivo y, siguió evolucionando hasta conformar seres de diversos tipos y, algunos, llegaron a adquirir la conciencia.
Macromolécula
Almacenado en un alfabeto de nucleótidos de cuatro “letras”- hecho de moléculas de azúcar y fosfatos, y llenos de signos de puntuación, reiteraciones para precaver contra el error, y cosas superfluas acumuladas en los callejones sin salida de la historia evolutiva-, su mensaje dice exactamente cómo hacer un ser humano, desde la piel y los huesos hasta las células cerebrales.
célula cerebral
Si elevamos más el aumento veremos que la molécula de ADN está compuesta de muchos átomos, con sus capas electrónicas externas entrelazadas y festoneadas en una milagrosa variedad de formas de una rareza y de una incleible y extraña belleza que sólo la Naturaleza es capaz de conformar.
Molécula de ADN
Si elevamos el aumento cien mil veces, el núcleo de un átomo de carbono se hinchará hasta llenar el campo de visión. Tales núcleos átomos se formaron dentro de una estrella que estalló mucho antes de que naciera el Sol. Si podemos aumentar aún más, veremos los tríos de quarks que se constituyen en protones y neutrones.

Átomo de Carbono
Los quarks han estado unidos desde que el Universo sólo tenía unos pocos segundos de edad. Una vez que fueron eliminados los anti-quarks, se unieron en tripletes para formar protones y neutrones que, al formar un núcleo cargado positivamente, atrajeron a los electrones que dieron lugar a formar los átomos que más tarde, conformaron la materia que podemos ver en nuestro universo.
Al llegar a escalas cada vez menores, también hemos entrado en ámbitos de energías de unión cada vez mayores. Un átomo puede ser desposeído de su electrón aplicando sólo unos miles de electrón-voltios de energía. Sin embargo, para dispersar los nucleones que forman el núcleo atómico se requieren varios millones de electrón-voltios, y para liberar los quarks que constituyen cada nucleón se necesitaría cientos de veces más energía aún.
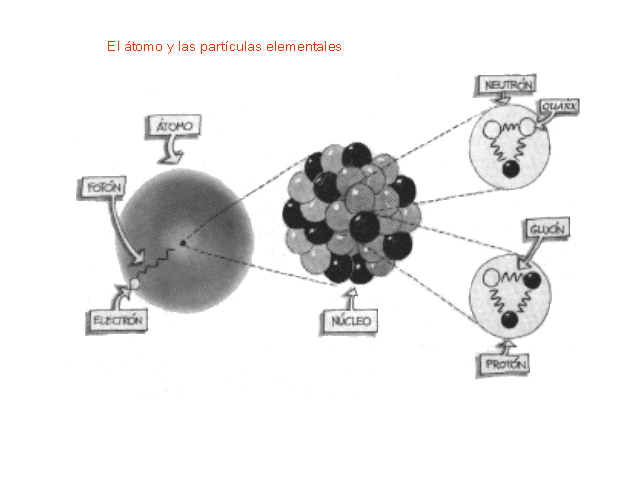
Los Quarks dentro del núcleo están sometidos a la Interacción fuerte, es decir, la más potente de las cuatro fuerzas fundamentales del Universo, la que mantiene a los Quarks confinados dentro del núcleo atómico por medio de los Gluones.
Introduciendo el eje de la historia, esta relación da testimonio del pasado de las partículas: las estructuras más pequeñas, más fundamentales están ligadas por niveles de energía mayores porque las estructuras mismas fueron forjadas en el calor del Big Bang.

Haces de protones que chocan cuando viajan a velocidad relativista en el LHC
Esto implica que los aceleradores de partículas, como los telescopios, funcionen como máquinas del tiempo. Un telescopio penetra en el pasado en virtud del tiempo que tarda la luz en desplazarse entre las estrellas; un acelerador recrea, aunque sea fugazmente, las condiciones que prevalecían en el Universo primitivo.
El acelerador de 200 Kev diseñado en los años veinte por Cockroft y Walton reproducía algunos de los sucesos que ocurrieron alrededor de un día después del comienzo del Big Bang.
Aquel acelerador nada tenía que ver con el LHC de ahora, casi un siglo los separa
Los aceleradores construidos en los años cuarenta y cincuenta llegaron hasta la marca de un segundo. El Tevatrón del Fermilab (como antes decía) llevó el límite a menos de una milmillonésima de segundo después del comienzo del Tiempo. El nuevo super-colisionador superconductor proporcionara un atisbo del medio cósmico cuando el Universo tenía menos de una billonésima de segundo de edad.
El Tevatrón del Fermilab ya estaba en el camino de la modernidad en los avances de la Física
Esta es una edad bastante temprana: una diez billonésima de segundo es menos que un pestañeo con los párpados en toda la historia humana registrada. A pesar de ello, extrañamente, la investigación de la evolución del Universo recién nacido indica que ocurrieron muchas cosas aún antes, durante la primera ínfima fracción de un segundo.
Todos los teóricos han tratado de elaborar una explicación coherente de los primeros momentos de la historia cósmica. Por supuesto, sus ideas fueron esquemáticas e incompletas, muchas de sus conjeturas, sin duda, se juzgaran deformadas o sencillamente erróneas, pero constituyeron una crónica mucho más aclaradora del Universo primitivo que la que teníamos antes.
Recreación del Universo primitivo
Bueno amigos, el trabajo era algo más extenso y entrábamos a explicar otros aspectos y parámetros implicados en todo este complejo laberinto que abarca desde lo muy grande hasta la muy pequeño, esos dos mundos que, no por ser tan dispares, resultan ser antagónicos, porque el uno sin el otro no podría exisitir. Otro día, seguiremos abundando en el tema apasionante que aquí tratamos.
emilio silvera
















 Totales: 85.893.483
Totales: 85.893.483 Conectados: 53
Conectados: 53

























