Jun
25
¿Qué es un bosón? y ¿qué es un bosón gauge?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

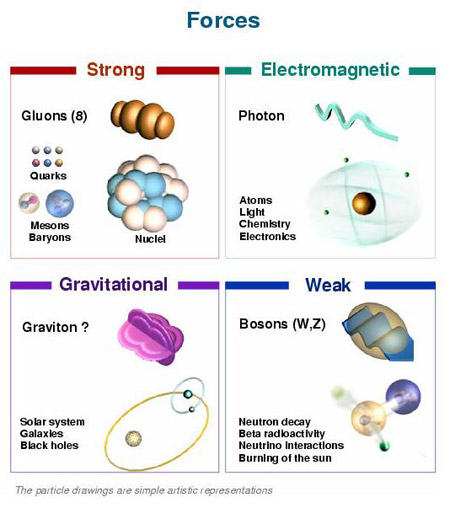
Un bosón es una partícula elemental (o estado ligado de partículas elementales, por ejemplo, un núcleo atómico o átomo) con espín entero, es decir, una partícula que obedece a la estadísitca de Bose-Einstein (estadísictica cuántica), de la cual deriva su nombre. Los bosones son importantes para el Modelo estándar de las partículas. Son bosones vectoriales de espín uno que hacen de intermediarios de las interacciones gobernadas por teorías gauge. Los Fotones, los Gluones, el hipotético Gravitón, las partículas W y Z son todos bosones mensajeros del electromagnetismo y todas las formas de radiación, de la fuerza nuclear fuerte, de la Gravedad, y, de la fuerza nuclear débil.
En física se ha sabido crear lo que se llama el Modelo estándar y, en él, los Bosones quedan asociados a las tres fuerzas que lo conforman, el fotón es el Bosón intermediario del electromagnetismo, los W+, w–y Zº son bosones gauge que transmiten la fiuerza en la teoría electrodébil, mientras que los gluones son los bosones de la fuerza fuerte, los que se encargan de tener bien confinados a los Quarks conformando protones y neutrones para que el núcleo del átomo sea estable. La Gravedad, no se ha dejado meter en el modelo y, por eso su bosón no es de gauge. El gravitón que sería la partícula mediadora de la gravitación sería el hipótetico cuanto de energía que se intercambia en la interacción gravitacional.

Ejemplos de los Bosones gauge son los fotones en electrodinámica cuántica (en física, el fotón se representa normalmente con el símbolo 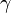 , que es la letra griega gamma), los gluones en cromodinámica cuántica y los bosones W y Z en el modelo de Winberg-Salam en la teoría electrodébil que unifica el electromagnetismo con la fuerza débil. Si la simetría gauge de la teoría no está rota, el bosón gauge es no masivo. Ejemplos de bosones gauge no masivos son el fotón y el gluón.
, que es la letra griega gamma), los gluones en cromodinámica cuántica y los bosones W y Z en el modelo de Winberg-Salam en la teoría electrodébil que unifica el electromagnetismo con la fuerza débil. Si la simetría gauge de la teoría no está rota, el bosón gauge es no masivo. Ejemplos de bosones gauge no masivos son el fotón y el gluón.

Si la simetría gauge de la teoría es una simetría rota el bosón gauge tiene masa no nula, ejemplo de ello son los bosones W y Z . Tratando la Gravedad, descrita según la teoría de la relatividad general, como una teoría gauge, el bosón gauge sería el gravitón, partícula no masiva y de espín dos.

Diagrama de Feynman mostrando el intercambio de un fotón virtual (simbolizado por una línea ondulada y  ) entre un positrón y un electrón.De esta manera podemos llegar a comprender la construcción que se ha hecho de las interacciones que están siempre intermediadas por un nosón mensajero de la fuerza.
) entre un positrón y un electrón.De esta manera podemos llegar a comprender la construcción que se ha hecho de las interacciones que están siempre intermediadas por un nosón mensajero de la fuerza.
En el modelo estándar, como queda explicado, hay tres tipos de bosones de gauge: fotones, bosones W y Z y gluones. Cada uno corresponde a tres de las cuatro interacciones: fotones son los bosones de gauge de la interacciones electromagnética, los bosones W y Z traen la interacción débil, los gluones transportan la interacción fuerte. El gravitón, que sería responsable por la interacción gravitacional, es una proposición teórica que a la fecha no ha sido detectada. Debido al confinamiento del color, los gluones aislados no aparecen a bajas energías.
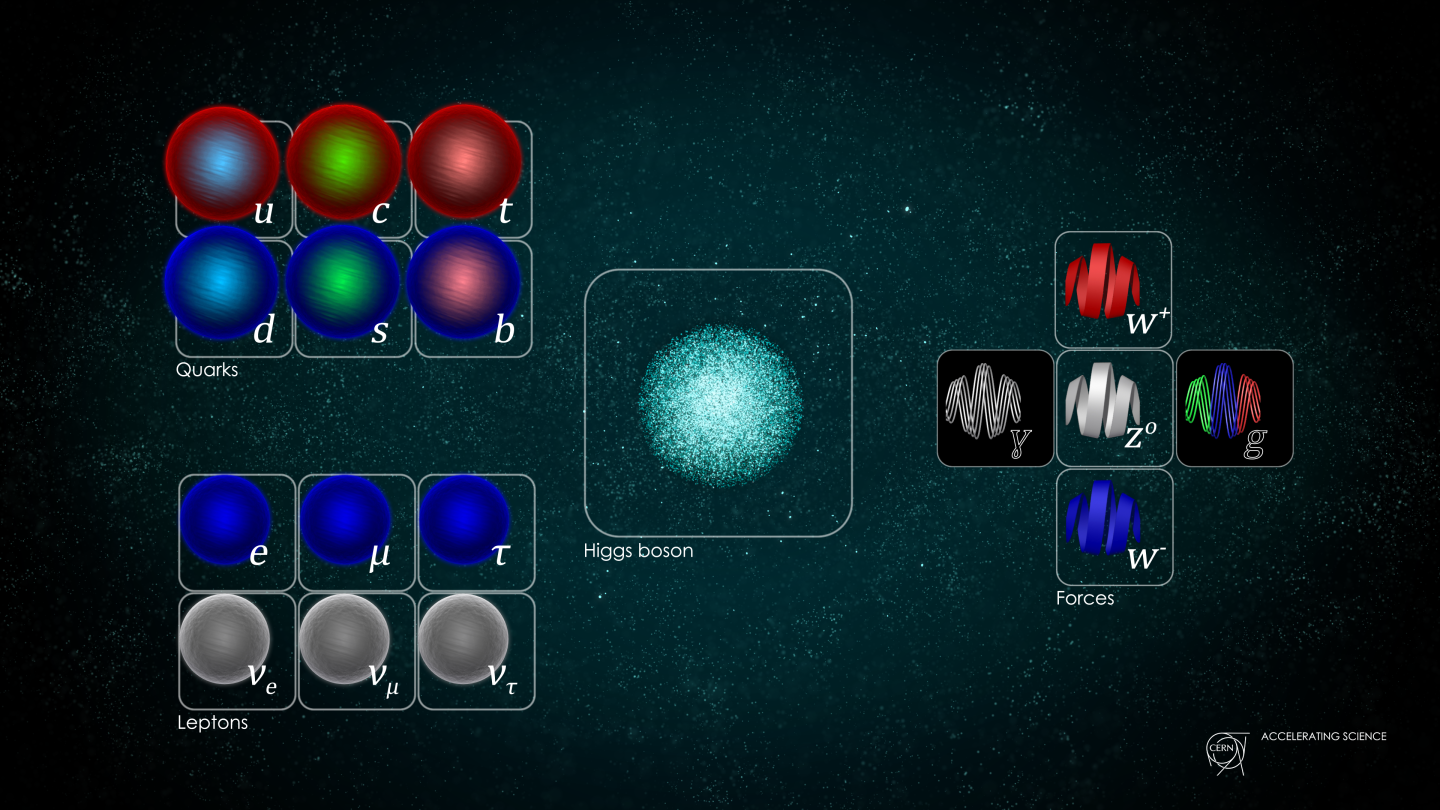
Aquí, en el gráfico, quedan representadas todas las partículas del Modelo estándar, las familias de Quarks y Leptones que conforman la materia y los bones que intermedian en las interacciones o fuerzas fundamentales que están presentes en el Universo. La Gravedad no ha podido ser incluida y se ha negado a estar unida a las otras fuerzas. Así el bosón que la transnmite, tampoco está en el modelo que es incompleto al dejar fuera la fuerza que mantiene unidos los planetas en los sistemas solares, a las galaxias en los cúmulos y nuestros pies unidos a la superficie del planeta que habitamos. Se busca una teoría que permita esta unión y, los físicos, la laman gravedad cuántica pero… ¡no aparece por ninguna parte!

Llegados a este punto tendremos que retroceder, para poder comprender las cosas, hasta aquel trabajo de sólo ocho páginas que publicó Max Planck en 1.900 y lo cambió todo. El mismo Planck se dió cuenta de que, todo lo que él había tenido por cierto durante cuarenta años, se derrumbaba con ese trabajo suyo que, venía a decirnos que el mundo de la materia y la nergía estaba hecho a partir de lo que el llamaba “cuantos”.
Supuso el nacimiento de la Mecánica Cuántica (MC), el fin del determinismo clásico y el comienzo de una nueva física, la Física Moderna, de la que la Cuántica sería uno de sus tres pilares junto con la Relatividad y la Teoría del Caos. Más tarde, ha aparecido otra teoría más moderna aún por comprobar, ¿las cuerdas…?
El universo según la teoría de las cuerdas sería entonces una completa extensa polícroma SINFONIA ETERNA de vibraciones, un multiverso infinito de esferas, cada una de ellas un universo independiente causalmente, en una de esas esferas nuestra vía láctea, en ella nuestro sistema solar, en él nuestro planeta, el planeta tierra en el cual por una secuencia milagrosa de hechos se dió origen a la vida autoconsciente que nos permite preguntarnos del cómo y del por qué de todas las cosas que podemos observar y, también, de las que intiuimos que están ahí sin que se dejen ver.

Claro que, cuando nos adentramos en ese minúsculo “mundo” de lo muy pequeño, las cosas difieren y se apartan de lo que nos dicta el sentido común que, por otra parte, es posible que sea el menos común de los sentidos. Nos dejamos guiar por lo que observamos, por ese mundo macroscópico que nos rodea y, no somos consciente de ese otro “mundo” que está ahí formando parte del universo y que, de una manera muy importante incide en el mundo de lo grande, sin lo que allí existe, no podría existir lo que existe aquí.
Interacciones en la naturaleza
Albert Einstein habría dicho que “es más importante la imaginación que el conocimiento”, el filósofo Nelson Goodman ha dicho que “las formas y las leyes de nuestros mundos no se encuentran ahí, ante nosotros, listas para ser descubiertas, sino que vienen impuestas por las versiones-del-mundo que nosotros inventamos – ya sea en las ciencias, en las artes, en la percepción y en la práctica cotidiana-.”
ser descubiertas, sino que vienen impuestas por las versiones-del-mundo que nosotros inventamos – ya sea en las ciencias, en las artes, en la percepción y en la práctica cotidiana-.”
Sin embargo yo, humilde pensador, me decanto por el hecho cierto de que, nuestra especie, siempre llegó al conocimiento a través de la imaginación y la experiencia primero, a la que más tarde, acompañó largas secciones de estudio y muchas horas de mediatación y, al final de todo eso, llego la experimentación que hizo posible llegar a lugarés ignotos que antes nunca, habían podido ser visitados. De todo ello, pudieron surgir todos esos “nuevos mundos” que, como la Mecanica Cuántica y la Relatividad, nos describían el propio mundo que antes nos era desconocido.
Cuando comencé éste trabajo sólo quería dar una simple explicación de los bosones y su intervención en el mundo de lo muy pequeño pero…

Demócrito de Abdera
No estaría mal echar una mirada hacia atrás en el tiempo y recordar, en este momento, a Demócrito que, con sus postulados, de alguna manera venía a echar un poco de luz sobre el asunto, dado que él decía que para determinar si algo era un á-tomo habría que ver si era indivisible. En el modelo de los quarks, el protón, en realidad, un conglomerado pegajoso de tres quarks que se mueven rápidamente. Pero como esos quarks están siempre ineludiblemente encadenados los unos a los otros, experimentalmente el protón aparece indivisible.
Acordémonos aquí de que Boscovich decía que, una partícula elemental, o un “á-tomo”, tiene que ser puntual. Y, desde luego, esa prueba, no la pasaba el protón. El equipo del MIT y el SLAC, con la asesoría de Feynman y Bjorken, cayó en la cuenta de que en este caso el criterio operativo era el de los “puntos” y no el de la indivisibilidad. La traducción de sus datos a un modelo de constituyentes puntuales requería una sutileza mucho mayor que el experimento de Rutherford.

Precisamente por eso era tan conveniente fue tan conveniente para Richard Edward Taylor y su equipo, tener a dos de los mejores teóricos del mundo en el equipo aportando su ingenio, agudeza e intuición en todas las fases del proceso experimental. El resultado fue que los datos indicaron, efectivamente, la presencia de objetos puntuales en movimiento dentro del protón.

En 1990 Taylor, Friedman y Kendall recogieron su premio Nobel por haber establecido la realidad de los quarks. Sin embargo, a mí lo que siempre me ha llamado más la atención es el hecho cierto de que, este descubrimiento como otros muchos (el caso del positrón de Dirac, por ejemplo), han sido posible gracias al ingenio de los teóricos que han sabido vislumbrar cómo era en realidad la Naturaleza.
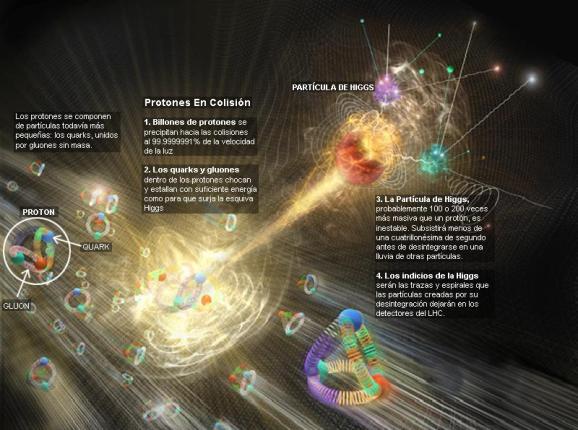
A todo esto, una buena pregunta sería: ¿cómo pudieron ver este tipo de partículas de tamaño infinitesimal, si los quarks no están libres y están confinados -en este caso- dentro del protón? Hoy, la respuesta tiene poco misterio sabiendo lo que sabemos y hasta donde hemos llegado con el LHC que, con sus inmensas energías “desmenuza” un protón hasta dejar desnudos sus más íntimos secretos.

Este es, el resultado ahora de la colisión de protones en el LHC
Lo cierto es que, en su momento, la teoría de los Quarks hizo muchos conversos, especialmente a medida que los teóricos que escrutaban los datos fueron imbuyendo a los quarks una realidad creciente, conociendo mejor sus propiedades y convirtiendo la incapacidad de ver quarks libres en una virtud. La palabra de moda en aquellos momentos era “confinamiento”. Los Quarks están confinados permanentemente porque la energía requerida para separarlos aumenta a medida que la distancia entre ellos crece. Esa es, la fuerza nuclear fuerte que está presente dentro del átomo y que se encarga de transmitir los ocho Gluones que mantienen confinados a los Quarks.
Así, cuando el intento de separar a los Quarks es demasiado intenso, la energía se vuelve lo bastante grande para crear un par de quark-anti-quark, y ya tenemos cuatro quarks, o dos mesones. Es como intentar conseguir un cabo de cuerda. Se corta y… ¡ya tenemos dos!
¿Cuerdas? Me parece que estoy confundiendo el principal objetivo de este trabajo y, me quiero situar en el tiempo futuro que va, desde los quarks de Gell-Mann hasta las cuerdas de Veneziano y John Schwarz y más tarde Witten. Esto de la Física, a veces te juega malas pasadas y sus complejos caminos te llevan a confundir conceptos y momentos que, en realidad, y de manera individualizada, todos han tenido su propio tiempo y lugar.
¿Cuántas veces no habré pensado, en la posibilidad de tomar el elixir de la sabiduría para poder comprenderlo todo? Sin embargo, esa pósima mágica no existe y, si queremos saber , el único camino que tenemos a nuestro alcance es la observación, el estudio, el experimento… ¡La Ciencia!, que en definitiva, es la única que nos dirá como es, y como se producen los fenómenos que podemos contemplar en la Naturaleza y, si de camino, podemos llegar a saber el por qué de su comportamiento… ¡mucho mejor!
, el único camino que tenemos a nuestro alcance es la observación, el estudio, el experimento… ¡La Ciencia!, que en definitiva, es la única que nos dirá como es, y como se producen los fenómenos que podemos contemplar en la Naturaleza y, si de camino, podemos llegar a saber el por qué de su comportamiento… ¡mucho mejor!

El camino será largo y, a veces, penoso pero… ¡llegaremos!
Nuestra insaciable curiosidad nos llevará lejos en el saber del “mundo”. llegaremos al corazón mismo de la materia para conmprobar si allí, como algunos imaginan, habitan las cuerdas vibrantes escondidas tan profundamente que no se dejan ver. Sabremos de muchos mundos habitados y podremos hacer ese primer contacto tantas veces soñado con otros seres que, lejos de nuestro región del Sistema solar, también, de manera independiente y con otros nombres, descubrieron la cuántica y la relatividad. Sabremos al fín qué es la Gravedad y por qué no se dejaba juntar con la cuántica. Podremos realizar maravillas que ahora, aunque nuestra imaginación es grande, ni podemos intuir por no tener la información necesaria que requiere la imaginación.
En fín, como decía Hilbert: ¡”Tenemos que saber, sabremos”!
Emilio Silvera
Jun
19
La Imaginación: ¡Mucho más rápida que la Luz!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (8)
Comments (8)
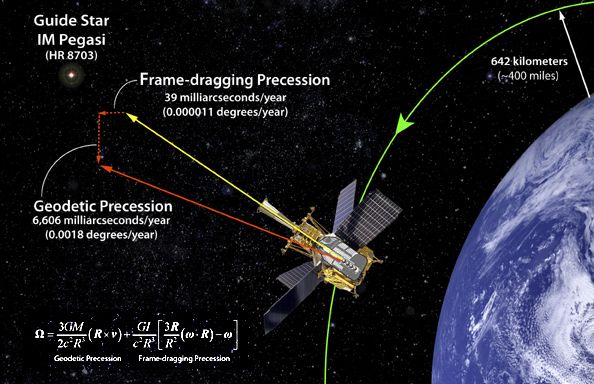
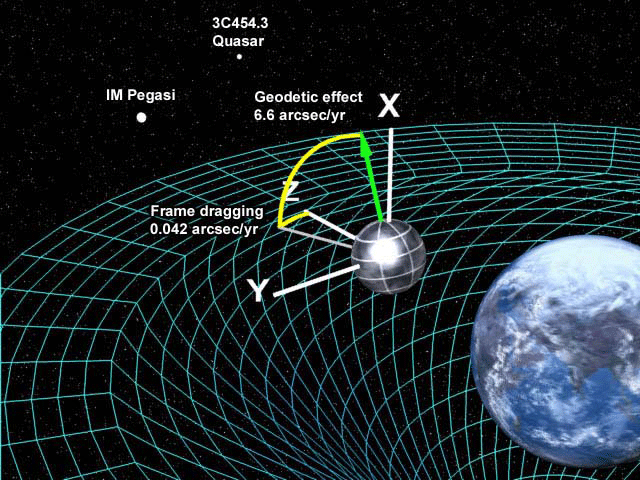
Satélite Gravity Probe B.
Dedicado a medir la curvatura del campo gravitatorio terrestre debido a la teoría de la relatividad de Einstein. La gravedad ha sido medida y comprobada de muchas maneras pero… ¡Gravedad cuántica! ¿qué es eso? La imaginación anda más rápida que los conocimientos. Sin embargo, así hemos ido avanzando en el transcurrir del Tiempo.
La llamada gravedad cuántica trata de fundir en una sola las dos teorías físicas más soberbias con las que contamos, la relatividad general y la mecánica cuántica, que en el estado actual de nuestro conocimiento parecen incompatibles. Su estudio, ahora mismo, es en algunos aspectos análogo a la física de hace cien años, cuando se creía en los átomos, pero se ignaraban los detalles de su estructura.
Desde aquel día en que Kaluza, le escribió a Einstein una carta con su teoría de las cinco dimensiones, en la que unía la Gravedad con el Electromagnetismo, la puerta de las dimensiones más altas quedó abierta y a los teóricos se les regaló una herramienta maravillosa: el hiperespacio; todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí sí es posible encontrar esa soñada teoría de la gravedad cuántica.
Así que las teorías se han embarcado a la búsqueda de un objeto audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos; una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.
![59 - Curso de Relatividad General [Ecuaciones de Campo & Constante Cosmológica] - YouTube](https://i.ytimg.com/vi/HI3m80zLo24/maxresdefault.jpg)
Hay que reconocer que nos dice mucho
Claro que saber, lo que el universo es, leyendo una ecuación, por muy ingeniosa que ésta sea y por mucho que la misma pueda abarcar… Parece poco probable. ¿Dónde radica el problema? El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el nuevo acelerador de partículas LHC, la máquina más potente del mundo hasta el momento.
La verdad es que la teoría que ahora tenemos, el modelo estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías. ¡Necesitamos algo más avanzado!

A pesar de su grandeza, se queda corto para que nos pueda decir, lo que necesitamos saber: Si nos habla del Bosón de Higgs, ya estará bien
Se ha dicho que la función de la partícula de Higgs es la de dar masa a las partículas que carecen de ella, disfrazando así la verdadera simetría del mundo. Cuando su autor lanzó la idea a la comunidad científica, resultó además de nueva, muy extraña. El secreto de todo radica en conseguir la simplicidad: el átomo resultó ser complejo, lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones. Resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún; los quarks que estaban instalados en nubes de otras partículas llamadas gluones, y ahora queremos continuar profundizando, sospechando que después de los quarks puede haber algo más.
Ahí las partículas toman su masa por el efecto frenado
Nos dicen que existen lugares que llaman los Océanos de Higgs, y, por ellos, circula libremente el dichoso Bosón que, también según nos dicen, proporciona la masa al resto de las partículas. Todo el Universo está permeado por esa especie de sustancia -como el viejo éter- que los griegos llamaban Ylem cósmico y que, a medida que el tiempo avanza, le vamos cambiando el nombre. Pues bien, ahí, en ese “océano” dicen que está el Bosón dador de masas.
Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes, es decir, que si miramos a las estrellas en una noche clara, estamos mirando el campo de Higgs. Las partículas influidas por este campo toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado otras veces, tales como: del campo gravitatorio o del electromagnético.

Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquirirá energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra. Como E = mc2, ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein: la masa, m, tiene en realidad dos partes; una es la masa en reposo, m0, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c) en los aceleradores, o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.
Pero la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas. Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs.
La influencia de Higgs en las masas de los quarks y de los leptones nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.

Hasta ahora no tenemos ni idea de qué reglas controlan los incrementos de masa generados por Higgs (de ahí la expectación creada por el nuevo acelerador de partículas LHC), pero el problema es irritante: ¿por qué sólo esas masas - las masas de los W+, W–, Z0, y el up, down, encanto, extraño, top y bottom, así como los leptones – que no forman ningún patrón obvio?
Las masas van desde la del electrón (0’0005 GeV) a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-Salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnética y débil. En la unidad hay cuatro partículas mensajeras sin masa – los W+, W–, Z0 y el fotón – que llevan la fuerza electrodébil. Además está el campo de Higgs, y rápidamente, los W y Z absorben la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos), y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen las teorías. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa.
Tampoco el Higgs es una partícula especial porque sea una excitación del del campo de Higgs que nos permita explorar sus propiedades, porque en las teorías sin Higgs o con Higgs compuesto también hay excitaciones del vacío que nos permiten explorar el campo.”
Eso nos dicen en el magnifico Blog de Francis (th)E mule Science’s News.
| Partícula | Símbolo | Masa (en GeV/c2) | Carga eléctrica | Espín | Interacción |
|---|---|---|---|---|---|
| Fotón |  |
0 | 0 | 1 | electromagnética |
| Bosón W | W± | 80,4 | ± 1 | 1 | débil |
| Bosón Z | Z0 | 91,187 | 0 | 1 | débil |
| Gluón | g | 0 | 0 | 1 | fuerte |
Las masas de los W y Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil, y las relajadas sonrisas de los físicos teóricos nos recuerdan que Hooft y Veltman dejaron sentado que la teoría entera está libre de infinitos.
Todos los intentos y los esfuerzos por hallar una pista de cuál era el origen de la masa fallaron. Feynman escribió su famosa pregunta: “¿por qué pesa el muón?”. Ahora, por lo menos, tenemos una respuesta parcial, en absoluto completa. Una voz potente y segura nos dice “¡Higgs!”. Durante más de sesenta años los físicos experimentadores se rompieron la cabeza con el origen de la masa, y ahora el campo de Higgs presenta el problema en un contexto nuevo; no se trata sólo del muón. Proporciona, por lo menos, una fuente común para todas las masas. La nueva pregunta feynmaniana podría ser: ¿Cómo determina el campo de Higgs la secuencia de masas, aparentemente sin patrón, que da a las partículas de la materia?
La variación de la masa con el estado de movimiento, el cambio de masa con la configuración del sistema y el que algunas partículas (el fotón seguramente, y los neutrinos posiblemente) tengan masa en reposo nula son tres hechos que ponen en entredicho que el concepto de masa sea un atributo fundamental de la materia. Habrá que recordar aquel cálculo de la masa que daba infinito y nunca pudimos resolver; los físicos sólo se deshicieron de él “renormalizándolo”, ese truco matemático que emplean cuando no saben hacerlo bien.

¿Sabremos alguna vez cómo adquieren masa las partículas?
Ese es el problema de trasfondo con el que tenemos que encarar el problema de los quarks, los leptones y los vehículos de las fuerzas, que se diferencian por sus masas. Hace que la historia de Higgs se tenga en pie: la masa no es una propiedad intrínseca de las partículas, sino una propiedad adquirida por la interacción de las partículas y su entorno.
La idea de que la masa no es intrínseca como la carga o el espín resulta aún más plausible por la idílica idea de que todos los quarks y fotones tendrían masa cero. En ese caso, obedecerían a una simetría satisfactoria, la quiral, en la que los espines estarían asociados para siempre con su dirección de movimiento. Pero ese idilio queda oculto por el fenómeno de Higgs.

Una cosa más; hemos hablado de los bosones gauge y de su espín de una unidad. Hemos comentado también las partículas fermiónicas de la materia (espín de media unidad). ¿Cuál es el pelaje de Higgs? Es un bosón de espín cero. El espín supone una direccionalidad en el espacio, pero el campo de Higgs da masa a los objetos donde quiera que estén y sin direccionalidad. Al Higgs se le llama a veces “bosón escalar” (sin dirección) por esa razón.
La interacción débil, recordaréis, fue inventada por E. Fermi para describir la desintegración radiactiva de los núcleos, que era básicamente un fenómeno de poca energía, y a medida que la teoría de Fermi se desarrolló, llegó a ser muy precisa a la hora de predecir un enorme número de procesos en el dominio de energía de los 100 MeV. Así que ahora, con las nuevas tecnologías y energías del LHC, las esperanzas son enormes para, por fin, encontrar el bosón de Higgs origen de la masa… y algunas cosas más.
Hay que responder montones de preguntas: ¿cuáles son las propiedades de las partículas de Higgs? y, lo que es más importante, ¿cuál es su masa? (Bueno, parece que, en el último experimento apareció se localizó un bosón con ~125 GeV que, según parece, podría ser el esquivo Hihhs)¿Cómo reconoceremos una si nos la encontramos en una colisión del LHC? ¿Cuántos tipos hay? ¿Genera el Higgs todas las masas o sólo las hace incrementarse? ¿Cómo podemos saber más al respecto? Cómo es su partícula, nos cabe esperar que la veremos ahora después de gastar más de 50.000 millones de euros en los elementos necesarios para ello.
También a los cosmólogos les fascina la idea de Higgs, pues casi se dieron de bruces con la necesidad de tener campos escalares que participasen en el complejo proceso de la expansión del universo, añadiendo pues, un peso más a la carga que ha de soportar el Higgs.
El campo de Higgs, tal como se lo concibe ahora, se puede destruir con una energía grande, o temperaturas altas. Éstas generan fluctuaciones cuánticas que neutralizan el campo de Higgs. Por lo tanto, el cuado que las partículas y la cosmología pintan juntas de un universo primitivo puro y de resplandeciente simetría es demasiado caliente para Higgs. Pero cuando la temperatura cae bajo los 10-5 grados Kelvin o 100 GeV, el Higgs empieza a actuar y hace su generación de masas. Así, por ejemplo, antes del Higgs teníamos unos W, Z y fotones sin masa y la fuerza electrodébil unificada.

No, esto no es el Higgs, es, simplemente, una burbuja multicolor
El universo se expande y se enfría, y entonces viene el Higgs (que “engorda” los W y Z, y por alguna razón ignora el fotón) y de ello resulta que la simetría electrodébil se rompe. Tenemos entonces una interacción débil, transportada por los vehículos de la fuerza W+, W–, Z0, y por otra parte una interacción electromagnética, llevada por los fotones. Es como si para algunas partículas del campo de Higgs fuera una especie de aceite pesado a través del que se moviera con dificultad y que les hiciera parecer que tienen mucha masa. Para otras partículas, el Higgs es como el agua, y para otras, los fotones y quizá los neutrinos, es invisible.
De todas formas, es tanta la ignorancia que tenemos sobre el origen de la masa que nos agarramos como a un clavo ardiendo, en este caso, a la partícula de Higgs, que algunos han llegado a llamar “la partícula divina”. Lo mismo nos pasa con la dichosa “materia oscura” para ocultar lo que no sabemos sobre la expansión del Universo.
¡Ya veremos en qué termina todo esto!


Arriba tenemos nada más y nada menos que: a John Mather, Carlo Rubbia, Martinus Veltman, Gerardus ‘t Hooft at the Lindau Nobel Meetings 2010. Si científicos como ellos no vienen a nuestro rescate, y nos sacan del atolladero en el que estamos inmerso y hasta el cuelo de ignorancia…¡Mal irán las cosas!
Peter Higgs, de la Universidad de Edimburgo, introdujo la idea en la física de partículas. La utilizaron los teóricos Steven Weinberg y Abdus Salam, que trabajaban por separado, para comprender cómo se convertía la unificada y simétrica fuerza electrodébil, transmitida por una feliz familia de cuatro partículas mensajeras de masa nula, en dos fuerzas muy diferentes: la QED con un fotón carente de masa y la interacción débil con sus W+, W– y Z0 de masa grande. Weinberg y Salam se apoyaron en los trabajos previos de Sheldon Glashow, quien, tras los pasos de Julian Schwinger, sabía sólo que había una teoría electrodébil unificada, coherente, pero no unió todos los detalles. Y estaban Jeffrey Goldstone y Martinus Veltman y Gerard’t Hooft. También hay otros a los que habría que mencionar, pero lo que siempre pasa, quedan en el olvido de manera injusta. Además, ¿Cuántos teóricos hacen falta para encender una bombilla? La verdad es que, casi siempre, han hecho falta muchos. Recordemos el largo recorrido de los múltiples detalles sueltos y físicos que prepararon el terreno para que llegara Einstein y pudiera, uniéndolo todo, exponer su teoría relativista.

Lo cierto es que (al menos de momento), la materia y energía oscura, las supercuerdas, y el bosón de Higss, sí son la alfonbra que decía Veltman, aquel físico serio y Premio Nobel que, no confesaba con ciertas ruedas de molino. Él, quería hablar de cosas tamgibles y, tampoco le gustaban las partículas virtuales.
Sobre la idea de Peter Higgs, Veltman, uno de sus arquitectos, dice que es una alfombra bajo la que barremos nuestra ignorancia. Glashow es menos amable y lo llamó retrete donde echamos las incoherencias de nuestras teorías actuales. La objeción principal: que no tenemos la menor prueba experimental. Ahora, por fin, la tendremos con el LHC. El modelo estándar es lo bastante fuerte para decirnos que la partícula de Higgs de menor masa (podría haber muchas) debe “pesar” menor de 1 TeV, ¿por qué?; si tiene más de 1 TeV el modelo estándar se vuelve incoherente y tenemos la crisis de la unitariedad.
Después de todo esto, llego a la conclusión de que el campo de Higgs, el modelo estándar y nuestra idea de surgió el universo dependen de que se encuentre el bosón de Higgs. Y ahora, por fin, tenemos un acelerador con la energía necesaria para que nos la muestre, y que con su potencia pueda crear para nosotros una partícula que pese nada menos que 1 TeV.
Emilio Silvera Vázquez
Jun
16
Observan la ruptutura de simetría en el Tiempo en las leyes de la Física
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
Hace unos años que pude leer este artículo

“Una investigación liderada por el Instituto de Física Corpuscular (centro mixto del Consejo Superior de Investigaciones Científicas y la Universidad de Valencia) ha obtenido evidencias de la ruptura de la simetría en el tiempo en las leyes de la Física.
El hallazgo, que se publica esta semana en la revista Physical Review Letters, ha sido realizado por la colaboración internacional BABAR, del laboratorio SLAC (Stanford Linear Accelerator Center, de sus siglas en inglés) del Departamento de Energía de Estados Unidos en la Universidad de Stanford (California).”
El tiempo discurre inexorablemente. En la historia del universo y en los sistemas complejos, la evolución temporal está asociada al aumento de entropía. Dicho de otro modo, con el paso del tiempo, el desorden siempre crece a partir de una situación inicial más ordenada.
Para explicarlo, podemos imaginar que vemos hacia atrás una película en la que un jarrón cae al suelo y se rompe en pedazos. Nos percataríamos muy rápido de que lo que observamos es imposible desde el punto de vista de las leyes físicas, porque sabemos que no es posible que los pedazos vuelen del suelo y se ordenen formando un jarrón. Y eso es porque desde nuestro punto de vista, “la flecha del tiempo” transcurre sin interrupción desde el pasado al futuro.

Ahora bien, para una partícula aislada, el paso del tiempo parece el mismo hacia delante y hacia atrás, es decir, su movimiento es reversible o temporalmente simétrico. Imaginemos que ahora vemos una película en la que aparece una bola de billar que choca contra una banda. Si no nos lo dicen, no seríamos capaces de saber si la proyección de la película va hacia delante o hacia atrás. Esto se debe a que, en ambos sentidos temporales, el movimiento de la bola de billar cumple las mismas leyes físicas.
Este concepto se conoce como simetría bajo inversión temporal y nos dice que, en el mundo de las partículas, las teorías físicas son válidas tanto para un sentido de su movimiento como para su inverso, lo que equivale a decir que funcionan igual hacia delante como hacia atrás en el tiempo.
El tiempo tiene una dirección preferente
Las leyes de Newton, la mecánica cuántica, el electromagnetismo y la relatividad general de Einstein son exactamente las mismas en un universo el que el tiempo fluyese en la dirección contraria. El hecho de que nosotros tengamos la impresión de que exista una diferencia entre el pasado y el futuro, ¿sólo una ilusión subjetiva? Diferentes hechos objetivos de la física indican que sí que existe una flecha del tiempo y que probablemente tengan algo en común que permita explicar la existente asimetría del tiempo.
José Bernabéu explica que “la ruptura de la simetría temporal o simetría T en física de partículas está relacionada con la asimetría CP existente entre materia y antimateria, necesaria para generar el universo actual de materia en algún momento de su historia. La simetría C afirma que, sabiendo que a cada partícula de la naturaleza le corresponde una antipartícula con carga opuesta, las leyes de la física serían las mismas al intercambiar las partículas con carga positiva con las de carga negativa”.
“La simetría CP se basa en la composición de la simetría C y la simetría P. La simetría C o simetría de carga afirma que las leyes de la Física serían las mismas si se pudiesen intercambiar las partículas con carga positiva con las de carga negativa. La simetría P o simetría de paridad dice que las leyes de la física permanecerían inalteradas bajo inversiones especulares, es decir, el universo se comportaría igual que su imagen en un espejo. La simetría CP es el producto de ambas.”
La simetría P señala que las leyes de la física permanecerían inalteradas bajo inversiones especulares, es decir, el universo se comportaría igual que su imagen en un espejo. Estas dos simetrías combinadas dan lugar a la simetría carga-paridad o simetría CP. Experimentos previos con partículas conocidas como mesones K y B han observado que no se cumple la simetría CP. Y el teorema CPT indica que, para cualquier sistema de partículas, las simetrías deben mantenerse equilibradas. O lo que es lo mismo, si la simetría CP no se cumple, la simetría T tampoco.
El investigador Fernando Martínez-Vidal añade:
“el experimento BABAR, que fue diseñado para el estudio en profundidad de la asimetría entre materia y antimateria, nos ha permitido ahora observar directamente por primera vez la ruptura de la simetría T”.
Correlación cuántica
Entre 1999 y 2008, se produjeron más de 500 millones de mesones B en el acelerador de partículas del SLAC, y sus contrapartidas de antimateria, llamados B-bar. Así, los científicos observaron cómo estas partículas incumplían la simetría CP. El problema para observar la ruptura de la simetría T residía en que los mesones B se desintegran irreversiblemente en pocas billonésimas de segundo, impidiendo invertir su situación inicial y final.
La solución se ha encontrado mediante la correlación cuántica entre los dos B, que permite que la información de la partícula que se desintegra primero se utilice en ese momento para determinar el estado de su partícula compañera que aún vive. Los investigadores han descubierto que el estado de este último mesón B se transforma en otro unas seis veces más a menudo en un sentido que en el inverso.
Bernabéu aclara que “este hecho demuestra inequívocamente la ruptura de la simetría bajo inversión temporal en las leyes fundamentales de la Física”. Estos resultados son tan contundentes que la probabilidad de que sean una casualidad es similar a la de obtener la misma cara de un dado al lanzarlo 55 veces seguidas, 14 sigma en lenguaje estadístico. Los físicos de partículas consideran que a partir de 5 sigma se trata de un descubrimiento.
La investigación cuenta con el apoyo del Ministerio de Economía y Competitividad (MINECO), a través del Programa Nacional de Física de Partículas, y de la Generalitat Valenciana, a través del Programa de Excelencia PROMETEO.
En los medios:
“Observan la ruptura de la simetría en el tiempo en las leyes de la Física“, Europa Press (19/11/2010)
“El CSIC se topa con el tiempo asimétrico“, La Razón (19/11/2012)
“Time-reversal asymmetry in particle physics has finally been clearly seen“, Physics Today (noviembre 2012)
“Backward ran sentences…“, The Economist (septiembre 2012)

Jun
4
El “universo” de las partículas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)

Solo el 1% de las formas de vida que han vivido en la Tierra están ahora presentes, el 99%, por una u otra razón se han extinguido. Sin embargo, ese pequeño tanto por ciento de la vida actual, supone unos cinco millones de especies según algunas estimaciones. La Tierra acoge a todas esas especies u palpita de vida que prolifera por doquier. Hay seres vivos por todas partes y por todos los rincones del inmenso mosaico de ambientes que constituye nuestro planeta encontramos formas de vida, cuyos diseños parecen hechos a propósito para adaptarse a su hábitat, desde las profundidades abisales de los océanos hasta las más altas cumbres, desde las espesas selvas tropicales a las planicies de hielo de los casquetes polares. Se ha estimado la edad de 3.800 millones de años desde que aparecieron los primeros “seres vivos” sobre el planeta (dato de los primeros microfósiles). Desde entonces no han dejado de aparecer más y más especies, de las que la mayoría se han ido extinguiendo. Desde el siglo XVIII en que Carlos Linneo propuso su Systema Naturae no han cesado los intentos por conocer la Biodiversidad…, de la que por cierto nuestra especie, bautizada como Homo sapiens por el propio Linneo, es una recién llegada de apenas 200.000 años.

Ahora, hablaremos de la vida media de las partículas elementales (algunas no tanto). Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida media, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.
También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.
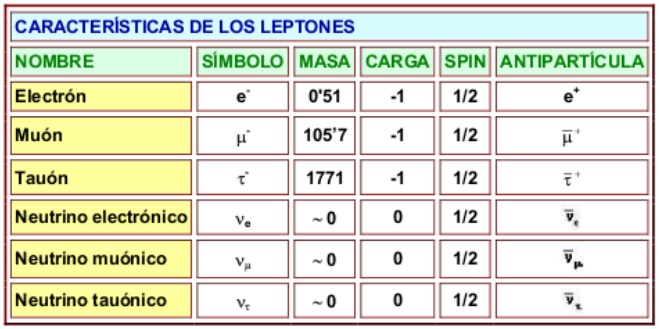
Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, psi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales maneras de desintegración, veríamos como difieren las unas de las otras.”
Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.

¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.

Una colisión entre un protón y un antiprotón registrada mediante una cámara de chispas del experimento UA5 del CERN.
En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su carta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas, Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.
¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, …
Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.
Se habla de ondas cuánticas y también, de ondas gravitacionales. Las primeras han sido localizadas y las segundas están siendo perseguidas.
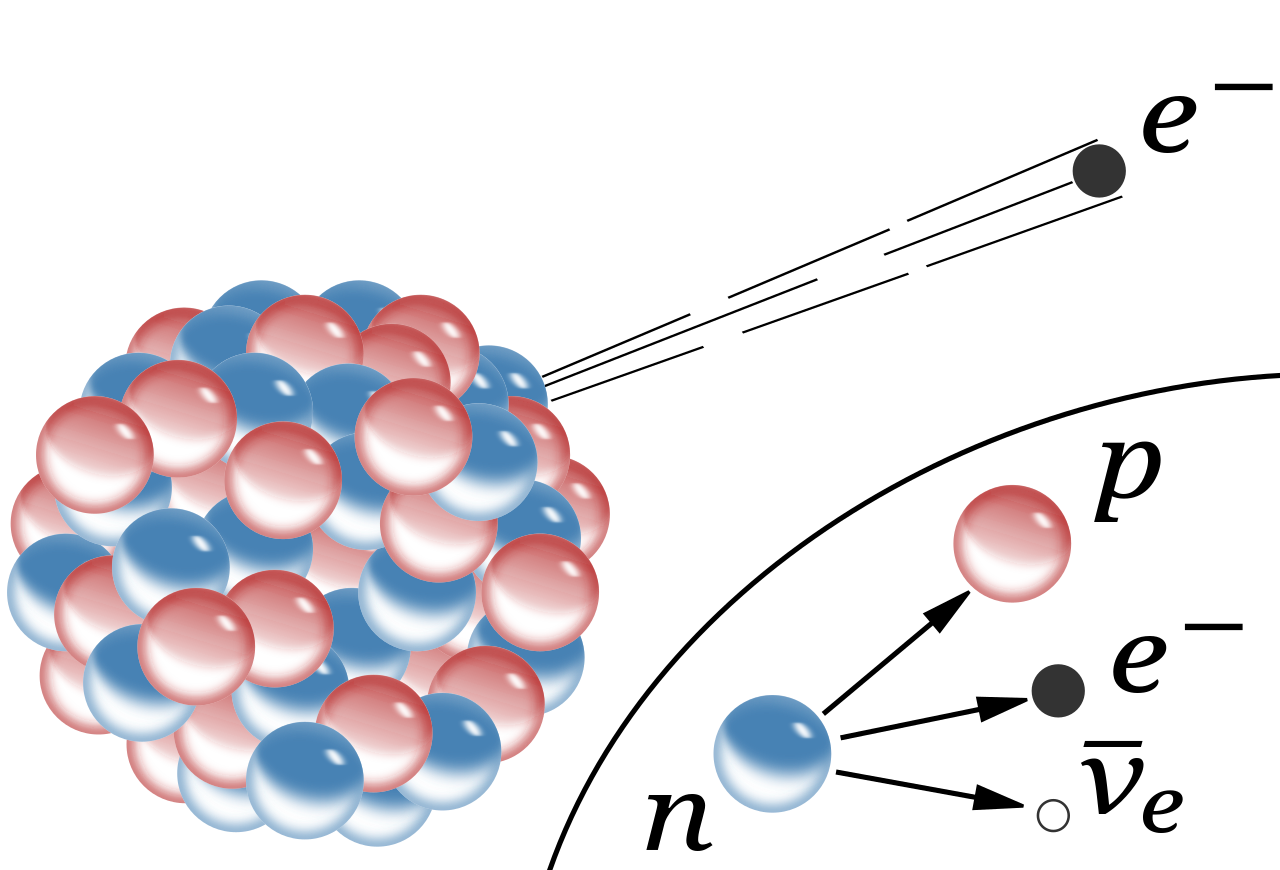
Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.
Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.
Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”

Si la vida de una partícula es tan corta como 10ˉ²³ segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.
Bariones Delta. Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.
Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).
Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.
Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:
∆⁺⁺→р + π⁺; ∆⁰→р + πˉ; o п+π⁰
En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.
El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (aunque nos parezca lo contrario), son aún bastante limitados, nos queda mucho por descubrir antes de que podamos decir que dominamos la materia y sabemos de todos sus componentes. Antes de que eso llegue, tendremos que conocer, en profundidad, el verdadero origen de la Luz que esconde muchos secretos que tendremos que desvelar.
Esperemos que con los futuros experimentos del LHC y de los grandes Aceleradores de partículas del futuro, se nos aclaren algo las cosas y podamos avanzar en el perfeccionamiento del Modelo Estándar de la Física de Partículas que, como todos sabemos es un Modelo incompleto que no contiene a todas las fuerzas de la Naturaleza y, cerca de una veintena de sus parámetros son aleatorios y no han sido explicados. Uno de ellos, el Bosón de Higgs, dicen que ha sido encontrado. Sin embargo, a mí particularmente me quedan muchas dudas al respecto.
Emilio Silvera Vázquez
Jun
3
Física, la era cuántica y otros fascinantes conceptos
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (8)
Comments (8)

Los científicos para lograr conocer la estructura del universo a su escala más grande, deben retroceder en el tiempo, centrando sus teorías en el momento en que todo comenzó. Para ello, como todos sabéis, se han formulado distintas teorías unificadoras de las cuatro fuerzas de la Naturaleza, con las cuales se han modelado acontecimiento y condiciones en el universo primitivo casi a todo lo largo del camino hasta el principio. Pero cómo se supone que debió haber habido un «antes», aparece una barrera que impide ir más allá de una frontera que se halla fijada a los 10-44 [s] después del Big Bang, un instante conocido como «momento de Planck», en homenaje al físico alemán Max Planck.
Esta barrera existe debido a que antes del momento de Planck, durante el período llamado la «era de Planck o cuántica», se supone que las cuatro fuerza fundamentales conocidas de la naturaleza eran indistinguibles o se hallaban unificadas , que era una sola fuerza. Aunque los físicos han diseñado teorías cuánticas que unen tres de las fuerzas, una por una, a través de eras que se remontan al momento de Planck, hasta ahora les ha sido prácticamente imposible armonizar las leyes de la teoría cuántica con la gravedad de la relatividad general de Einstein, en un sólo modelo teórico ampliamente convincente y con posibilidades claras de ser contrastado en experimentos de laboratorio y, mucho menos, con observaciones.

Si hablamos de singularidades en agujeros negros, debemos dejar la R.G. y acudir a la M.C. “…según las leyes de la Relatividad, el eje más horizontal siempre es espacio, mientras que el más vertical siempre es tiempo. Por tanto, al cruzar el horizonte lo que nosotros entendemos por tiempo y espacio ¡habrán intercambiado sus papeles! Puede sonar raro y, definitivamente, es algo completamente anti intuitivo, pero es la clave de que los agujeros negros sean como son y jueguen el papel tan importante que juegan en la física teórica actual. Al fin y al cabo, dentro no es lo mismo que fuera…”

Parece que una Teoría cuántica de la Gravedad subyace en la Teoría de cuerdas, allí, cuando los físicos trabajan con las ecuaciones de ésta adelantada teoría, como por arte de magia, sin que nadie las llame, aparecen los ecuaciones de campo de la Relatividad General de Einstein… ¿Por qué será?
Si ahora queremos cuantizar, es decir encontrar la versión cuántica, la gravedad escrita como RG lo que tenemos que hacer es encontrar la teoría cuántica para la métrica. Sin embargo, esto no conduce a una teoría apropiada, surgen muchos problemas para dar sentido a esta teoría, aparecen infinitos y peor que eso, muchos cálculos no tienen ni tan siquiera un sentido claro. Así que hay que buscar otra forma de intentar llegar a la teoría cuántica.

El sueño de unir lo grande y lo pequeño en una teoría
Como tantas veces hemos comentado, los trabajos que se han realizado sobre poder construir una teoría cuántica de la gravedad nos llevan a un número sorprendente de implicaciones. Por un lado, sólo se ha podido conceptuar a la gravedad cuántica, siempre y cuando, el universo tenga más de cuatro dimensiones. Además, se llega a considerar que en la era de Planck, tanto el universo como la gravedad pudieron ser una sola cosa compacta estructurada por objetos cuánticos infinitamente diminutos, como los que suponemos que conforman las supercuerdas. A esta escala, el mismísimo espaciotiempo estaría sometido a imprescindibles fluctuaciones muy semejantes a las que causan las partículas al nacer y desaparecer de la existencia en el espacio-tiempo ordinario. Esta noción ha conducido a los teóricos a describir el universo de la era cuántica como una especie de extremadamente densa y agitada espuma que pudo haber contenido las vibrantes cuerdecillas que propugnan los cosmólogos cuerdistas.
Los físicos especulan que el cosmos ha crecido a desde una «nada» primigenia que al nacer comenzó el principio del tiempo y que, en ese parto, contenía toda la materia y toda la energía.

Según los primeros trabajos sobre la teoría cuántica de la gravedad, el propio espacio-tiempo varió en su topografía, dependiendo de las dimensiones del universo niño. Cuando el universo era del tamaño de un núcleo atómico (ver imagen de abajo), las condiciones eran relativamente lisas y uniformes; a los 10-30cm (centro) es evidente una cierta granulidad; y a la llamada longitud de Planck, todavía unas 1.000 veces más pequeño (abajo), el espacio tiempo fluctúa violentamente.

La teoría cuántica de la gravedad, especialmente la Gravedad Cuántica de Bucles (GCB), plantea que el espacio-tiempo no es continuo, sino que tiene una estructura granular a la escala de Planck (aproximadamente 10-35 metros). En esta visión, el espacio-tiempo se conceptualiza como una red de lazos, o bucles, que se entrecruzan y forman una estructura espumosa.
No parece sencillo para los físicos poder conseguir esa unión (Cuántica y Gravedad) en una teoría

Los físicos han intentado con denuedo elaborar una teoría completa de la gravedad que incluya la mecánica cuántica. Los cálculos de la mayoría de las teorías propuesta de la «gravedad cuántica» arrojan numerosos infinitos. Los físicos no están seguros si el problema es técnico o conceptual. No obstante, incluso prescindiendo de una teoría completa de gravedad cuántica, se puede deducir que los efectos de la teoría cuántica, habrían sido cruciales durante los primeros 10-43 segundos del inicio del universo, cuando éste tenía una densidad de 1093 gramos por centímetro cúbico y mayor. (El plomo sólido tiene una densidad de aproximadamente diez gramos por centímetro cúbico.) Este período, que es el que corresponde a la era de Planck, y a su estudio se le llama cosmología cuántica. Como el universo en su totalidad habría estado sujeto a grandes incertidumbres y fluctuaciones durante la era de Planck o era cuántica, con la materia y la energía apareciendo y desapareciendo de un vacío en grandes cantidades, el concepto de un principio del universo podría no tener un significado bien definido. En todo caso, la densidad del universo durante este período es de tal magnitud que escapa a nuestra comprensión. Para propósitos prácticos, la era cuántica podría considerarse el estado inicial, o principio, del universo. En consecuencia, los procesos cuánticos ocurridos durante este período, cualquiera sea su naturaleza, determinaron las condiciones iniciales del universo.

Observaciones astronómicas indican que el universo tiene una edad de 13,73 ± 0,12 millardos de años (entre 13 730 y 13 810 millones de años) y por lo menos … Sin embargo…
El universo estaba a 3.000° Hace doce mil quinientos millones de años; a 10 mil millones de grados (1010° K) un millón de años antes, y, tal vez, a 1028° K un par de millones más temprano. Pero, y antes de ese tiempo ¿qué pasaba? Los fósiles no faltan, pero no sabemos interpretarlos. Mientras más elevada se va haciendo la temperatura del universo primigenio, la situación se va complicando para los científicos. En la barrera fatídica de los 1033° K –la temperatura de Planck–, nada funciona. Nuestros actuales conocimientos de la física dejan de ser útiles. El comportamiento de la materia en estas condiciones tan extremas deja de estar a nuestro alcance de juicio. Peor aún, hasta nuestras nociones tradicionales pierden su valor. Es una barrera infranqueable para el saber de la física contemporánea. Por eso, lo que se suele decir cómo era el universo inicial en esos tempranos períodos, no deja de tener visos de especulación.
Los progresos que se han obtenido en física teórica se manifiestan a menudo en términos de síntesis de campos diferentes. Varios son los ejemplos que de ello encontramos en diversos estudios especializados, que hablan de la unificación de las fuerzas fundamentales de la naturaleza.
En física se cuentan con dos grandes teorías de éxito: la cuántica y la teoría de la relatividad general.

Cada una de ellas ha demostrado ser muy eficiente en aplicaciones dentro de los límites de su ámbito propio. La teoría cuántica ha otorgado resultados más que satisfactorios en el estudio de las radiaciones, de los átomos y de sus interacciones. La ciencia contemporánea se presenta como un conjunto de teorías de campos, aplicables a tres de las grandes interacciones: electromagnética, nuclear fuerte, nuclear débil. Su poder predictivo es bastante elocuente, pero no universal. Esta teoría es, por ahora, incapaz de describir el comportamiento de partículas inmersas en un campo de gravedad intensa. Ahora, no sabemos si esos fallos se deben a un problema conceptual de fondo o falta de capacidad matemática para encontrar las ecuaciones precisas que permitan la estimación del comportamiento de las partículas en esos ambientes.
La teoría de la relatividad general, a la inversa, describe con gran precisión el efecto de los campos de gravedad sobre el comportamiento de la materia, pero no sabe explicar el ámbito de la mecánica cuántica. Ignora todo acerca de los campos y de la dualidad onda-partícula, y en ella el «vacío» es verdaderamente vacío, mientras que para la física cuántica hasta la «nada» es «algo»…
¿El vacío? No existe. Si surgió es porque había
Claro está, que esas limitaciones representativas de ambas teorías no suelen tener mucha importancia práctica. Sin embargo, en algunos casos, esas limitantes se hacen sentir con agresividad frustrando a los físicos. Los primeros instantes del universo son el ejemplo más elocuente.
El científico investigador, al requerir estudiar la temperatura de Planck, se encuentra con un cuadro de densidades y gravedades extraordinariamente elevadas. ¿Cómo se comporta la materia en esas condiciones? Ambas teorías, no dicen mucho al respecto, y entran en serias contradicciones e incompatibilidades. De ahí la resistencia de estas dos teorías a unirse en una sólo teoría de Gravedad-Cuántica, ya que, cada una de ellas reina en un universo diferente, el de lo muy grande y el de lo muy pequeño.

Esta es la primera imagen de un electrón dentro de un excitón y podría suponer un gran avance para la mecánica cuántica.
Científicos suecos han logrado filmar por primera vez en la historia un electrón en movimiento. La película muestra cómo un electrón se mueve sobre una onda de luz en el instante inmediatamente posterior a haber sido arrancado de un átomo. Hasta la fecha un experimento semejante había sido imposible de realizar, ya que los electrones se mueven a velocidades extremadamente altas y las fotografías realizadas siempre tenían un carácter muy impreciso.
La primera imagen de un electrón en acción se logró utilizando tecnología de ottos-egundos, impulsos de láser muy cortos, y microscopios de efecto túnel. Esta imagen, aunque no es una foto tradicional, permite visualizar la distribución espacial de un electrón dentro de un excitón, lo que abre nuevas posibilidades para la investigación en mecánica cuántica.
Todo se desenvuelve alrededor de la noción de localización. La teoría cuántica limita nuestra aptitud para asignar a los objetos una posición exacta. A cada partícula le impone un volumen mínimo de localización. La localización de un electrón, por ejemplo, sólo puede definirse alrededor de trescientos fermis (más o menos un centésimo de radio del átomo de hidrógeno). Ahora, si el objeto en cuestión es de una mayor contextura másica, más débiles son la dimensión de este volumen mínimo. Se puede localizar un protón en una esfera de un décimo de fermi, pero no mejor que eso. Para una pelota de ping-pong, la longitud correspondiente sería de unos 10-15 cm, o sea, bastante insignificante.La física cuántica, a toda partícula de masa m le asigna una longitud de onda Compton: lc = h / 2p mc
Por su parte, la relatividad general igualmente se focaliza en la problemática del lugar que ocupan los objetos. La gravedad que ejerce un cuerpo sobre sí mismo tiende a confinarlo en un espacio restringido. El caso límite es aquel del agujero negro, que posee un campo de gravedad tan intenso que, salvo la radiación térmica, nada, ni siquiera la luz, puede escapársele. La masa que lo constituye está, según esta teoría, irremediablemente confinada en su interior.
En lo que hemos inmediatamente descrito, es donde se visualizan las diferencias entre esos dos campos del conocimiento. Uno localiza, el otro localiza. En general, esta diferencia no presenta problemas: la física cuántica se interesa sobre todo en los micro-objetos y la relatividad en los macro-objetos. Cada cual en su terreno.
Sin embargo, ambas teorías tienen una frontera común para entrar en dificultades. Se encuentran objetos teóricos de masa intermedia entre aquella de los micro-objetos como los átomos y aquella de los macro-objetos como los astros: las partículas de Planck. Su masa es más o menos la de un grano de sal: 20 microgramos. Equivale a una energía de 1028 eV o, más aún, a una temperatura de 1033° K. Es la «temperatura de Planck».
Ahora bien, si queremos estimar cuál debería ser el radio en que se debe confinar la masita de sal para que se vuelva un agujero negro, con la relatividad general la respuesta que se logra encontrar es de que sería de 10-33 cm, o sea ¡una cien mil millonésima de mil millonésima de la dimensión del protón! Esta dimensión lleva el nombre de «radio de Planck». La densidad sería de ¡1094 g/cm3! De un objeto así, comprimido en un radio tan, pero tan diminuto, la relatividad general sólo nos señala que tampoco nada puede escapar de ahí. No es mucha la información.
Si recurrimos a la física cuántica para estimar cuál sería el radio mínimo de localización para un objeto semejante al granito de sal, la respuesta que encontramos es de un radio de 10-33 cm. Según esta teoría, en una hipotética experiencia se lo encontrará frecuentemente fuera de ese volumen. ¡Ambos discursos no son coincidentes! Se trata de discrepancias que necesitan ser conciliadas para poder progresar en el conocimiento del universo. ¿Se trata de entrar en procesos de revisión de ambas teoría, o será necesaria una absolutamente nueva? Interrogantes que solamente el devenir de la evolución de la física teórica las podrá responder en el futuro.
De todas las maneras, en lo que se refiere a una Teoría cuántica de la Gravedad, tendremos que esperar a que se confirmen las teorías de super-gravedad, supersimetría, cuerdas, la cuerda heterótica, supercuerdas y, la compendiada por Witten Teoría M. Aquí, en estas teorías (que dicen ser del futuro), sí que están apaciblemente unidas las dos irreconciliables teorías: la cuántica y la relativista, no sólo no se rechazan ni emiten infinitos, sino que, se necesitan y complementan para formar un todo armónico y unificador.
¡Si pudiéramos verificarla!
Pero, contar con la energía de Planck (1019 GeV), no parece que, al menos de momento, sea de este mundo. Ni todos los aceleradores de partículas del mundo unidos, podrían llegar a conformar una energía semejante.

Aunque de extraña y atípica figura, también, esta galaxia, está hecha de materia
Tiene y encierra tantos misterios la materia que estamos aún q años-luz de saber y conocer sobre su verdadera naturaleza. Es algo que vemos en sus distintas formas materiales que configuran y conforman todo lo material desde las partículas elementales hasta las montañas y los océanos. Unas veces está en estado “inerte” y otras, se eleva hasta la vida que incluso, en ocasiones, alcanza la consciencia de SER. Sin embargo, no acabamos de dilucidar de dónde viene su verdadero origen y que era antes de “ser” materia. ¿Existe acaso una especie de sustancia cósmica anterior a la materia? Y, si realmente existe esa sustancia… ¿Dónde está? Aristóteles la llamaba Ylem, la sustancia o materia cósmica antes de la materia, a partir del Ylem llegaría la materia bariónica, la que conocemos y de la que todo está hecho.

Nos podríamos preguntar miles de cosas que no sabríamos contestar. Nos maravillan y asombran fenómenos naturales que ocurren ante nuestros ojos pero que tampoco sabemos, en realidad, a que son debidos. Sí, sabemos ponerles etiquetas como, por ejemplo, la fuerza nuclear débil, la fisión espontánea que tiene lugar en algunos elementos como el protactinio o el torio y, con mayor frecuencia, en los elementos que conocemos como transuránicos.
A medida que los núcleos se hacen más grandes, la probabilidad de una fisión espontánea aumenta. En los elementos más pesados de todos (einstenio, fermio y mendelevio), esto se convierte en el método más importante de ruptura, sobrepasando a la emisión de partículas alfa.
¡Parece que la materia está viva!

Son muchas las cosas que desconocemos y, nuestra curiosidad nos empuja continuamente a buscar esas respuestas.
El electrón y el positrón son notables por sus pequeñas masas (sólo 1/1.836 de la del protón, el neutrón, el antiprotón o antineutrón), y, por lo tanto, han sido denominados leptones (de la voz griega lepto que significa “delgado”).

Lo que veis en esta imagen es la primera imagen directa que la ciencia ha logrado obtener de la órbita de un electrón alrededor del núcleo de un átomo
Aunque el electrón fue descubierto en 1.897 por el físico británico Josepth John Thomson (1856-1940), el problema de su estructura, si la hay, no está resuelto. Conocemos su masa y su carga negativa que responden a 9,1093897 (54)x10-31kg la primera y, 1,602 177 33 (49)x10-19 culombios, la segunda, y también su radio clásico. No se ha descubierto aún ninguna partícula que sea menos masiva que el electrón (o positrón) y que lleve una carga eléctrica, sea lo que fuese (sabemos como actúa y cómo medir sus propiedades, pero aun no sabemos qué es), tenga asociada un mínimo de masa, y que esta es la que se muestra en el electrón.
Lo cierto es que, el electrón, es una maravilla en sí mismo. El Universo no sería como lo conocemos si el electrón (esa cosita “insignificante”), fuese distinto a como es, bastaría un cambio infinitesimal para que, por ejemplo, nosotros no pudiéramos estar aquí ahora.
(“Aunque no se trata propiamente de la imagen real de un electrón, un equipo de siete científicos suecos de la Facultad de Ingeniería de la Universidad de Lund consiguieron captar en vídeo por primera vez el movimiento o la distribución energética de un electrón sobre una onda de luz, tras ser desprendido previamente del átomo correspondiente.

Previamente dos físicos de la Universidad Brown habían mostrado películas de electrones que se movían a través de helio líquido en el International Symposium on Quantum Fluids and Solids del 2006. Dichas imágenes, que mostraban puntos de luz que bajaban por la pantalla fueron publicadas en línea el 31 de mayo de 2007, en el Journal of Low Temperature Physics.
En el experimento que ahora nos ocupa y dada la altísima velocidad de los electrones el equipo de investigadores ha tenido que usar una nueva tecnología que genera pulsos cortos de láser de luz intensa (“Attoseconds Pulses”), habida cuenta que un attosegundo equivalente a la trillonésima parte de un segundo”.)
¡No por pequeño, se es insignificante! Recordémoslo, todo lo grande está hecho de cosas pequeñas.
Louis de Broglie
En realidad, existen partículas que no tienen en absoluto asociada en ellas ninguna masa (es decir, ninguna masa en reposo). Por ejemplo, las ondas de luz y otras formas de radiación electromagnéticas se comportan como partículas (Einstein en su efecto fotoeléctrico y De Broglie en la difracción de electrones.)

Imagen ilustrativa de la dualidad onda-partícula, en el cual se puede ver cómo un mismo fenómeno puede tener dos percepciones distintas. Esta manifestación en forma de partículas de lo que, de ordinario, concebimos como una onda se denomina fotón, de la palabra griega que significa “luz”.
El fotón tiene una masa de 1, una carga eléctrica de 0, pero posee un espín de 1, por lo que es un bosón. ¿Cómo se puede definir lo que es el espín? Los fotones toman parte en las reacciones nucleares, pero el espín total de las partículas implicadas antes y después de la reacción deben permanecer inmutadas (conservación del espín). La única forma que esto suceda en las reacciones nucleares que implican a los fotones radica en suponer que el fotón tiene un espín de 1. El fotón no se considera un leptón, puesto que este termino se reserva para la familia formada por el electrón, el muón y la partícula Tau con sus correspondientes neutrinos: Ve, Vu y VT.

Existen razones teóricas para suponer que, cuando las masas se aceleran (como cuando se mueven en órbitas elípticas en torno a otra masa o llevan a cabo un colapso gravitacional), emiten energía en forma de ondas gravitacionales. Esas ondas pueden así mismo poseer aspecto de partícula, por lo que toda partícula gravitacional recibe el nombre de gravitón.
La fuerza gravitatoria es mucho, mucho más débil que la fuerza electromagnética. Un protón y un electrón se atraen gravitacionalmente con sólo 1/1039 de la fuerza en que se atraen electromagnéticamente. El gravitón (aún sin descubrir) debe poseer, correspondientemente, menos energía que el fotón y, por tanto, ha de ser inimaginablemente difícil de detectar.
De todos modos, el físico norteamericano Joseph Weber emprendió en 1.957 la formidable tarea de detectar el gravitón. Llegó a emplear un par de cilindros de aluminio de 153 cm. De longitud y 66 de anchura, suspendidos de un cable en una cámara de vacío. Los gravitones (que serían detectados en forma de ondas), desplazarían levemente esos cilindros, y se empleó un sistema para detectar el desplazamiento que llegare a captar la cienmillonésima parte de un centímetro.
Joseph Weber
El interferómetro funciona enviando un haz de luz que se separa en dos haces; éstos se envían en direcciones diferentes a unos espejos donde se reflejan de regreso, entonces los haces al combinarse presentarán interferencia.
Las débiles ondas de los gravitones, que producen del espacio profundo, deberían chocar contra todo el planeta, y los cilindros separados por grandes distancias se verán afectados de forma simultánea. En 1.969, Weber anunció haber detectado los efectos de las ondas gravitatorias. Aquello produjo una enorme excitación, puesto que apoyaba una teoría particularmente importante (la teoría de Einstein de la relatividad general). Desgraciadamente, nunca se pudo comprobar mediante las pruebas realizadas por otros equipos de científicos que duplicaran el hallazgo de Weber.
De todas formas, no creo que, a estas alturas, nadie pueda dudar de la existencia de los gravitones, el bosón mediador de la fuerza gravitatoria. La masa del gravitón es cero, su carga es cero, y su espín de 2. Como el fotón, no tiene antipartícula, ellos mismos hacen las dos versiones.
Tenemos que volver a los que posiblemente son los objetos más misteriosos de nuestro Universo: Los agujeros negros. Si estos objetos son lo que se dice (no parece que se pueda objetar nada en contrario), seguramente serán ellos los que, finalmente, nos faciliten las respuestas sobre las ondas gravitacionales y el esquivo gravitón.

Imagen de un agujero negro en el núcleo de una galaxia arrasando otra próxima- NASA

La onda gravitacional emitida por el agujero negro produce una ondulación en la curvatura del espacio-temporal que viaja a la velocidad de la luz transportada por los gravitones. Tenemos varios proyectos en marcha de la NASA y otros Organismos oficiales que buscan las ondas gravitatorias de los agujeros negros, de colisiones entre estrellas de neutrones y de otras fuentes análogas que, según se cree, nos hablará de “otro universo”, es decir, nos dará información desconocida hasta ahora y sabremos “ver” un universo distinto al reflejado por las ondas elecromagnéticas que es el que ahora conocemos.

¿Espuma cuántica? Si profundizamos mucho en la materia…
Hay aspectos de la física que me dejan totalmente sin habla, me obligan a pensar y me transporta de este mundo material nuestro a otro fascinante donde residen las maravillas del Universo. Hay magnitudes asociadas con las leyes de la gravedad cuántica. La longitud de Planck-Wheeler, ![]() es la escala de longitud por debajo de la cual el espacio tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro.
es la escala de longitud por debajo de la cual el espacio tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro.

“Una investigación ha llevado a pensar que, la materia se construye sobre fundamentos frágiles. Los físicos acaban de confirmar que la materia, aparentemente sustancial, es en realidad nada más que fluctuaciones en el vació cuántico. Los investigadores simularon la frenética actividad que sucede en el interior de los protones y neutrones, que como sabéis son las partículas que aportan casi la totalidad de la masa a la materia común. Estas dos partículas, protones y neutrones, se comportan como si en su interior, los quarks de los que están hechas ambas partículas, lucharan por escapar del confinamiento a que se ven sometidos por la fuerza nuclear fuerte por medio de los Gluones que forman un océano en el que se ven confinados sin remedio. De hecho, nunca nadie ha podido ver a un quark libre.
Podría ser algo así lo que veríamos si alcanzamos el “vacío” cuántico
Así que, si estudiamos el vacío cuántico, parece que eso permitirá a los físicos someter a prueba a la Cromo Dinámica Cuántica y buscar sus efectos más allá de la física conocida. Por ahora, los cálculos demuestran que la QCD describe partículas basadas en quarks de forma precisa, y que la mayor parte de nuestra masa viene de quarks virtuales y gluones que burbujean en el vacío cuántico.
Se cree que el campo de Higgs hace también su pequeña contribución, dando masa a los quarksindividuales, así como a los electrones y a otras varias partículas. El campo de Higgs también crea masa a partir del vacío cuántico, en forma de bosones virtuales de Higgs. De modo que si el LHC confirma la existencia del bosón de Higgs, eso significará que toda la realidad es virtual, es menos virtual de lo que se pensaba. No creo que hasta el momento, y, a pesar de las declaraciones salidas desde el CERN, se tenga la seguridad de haber detectado el Bosón de Higgs.
De todo lo anterior, no podemos obtener una respuesta cierta y científicamente probada de que todo eso sea así, más bien, los resultados indican que todo eso “podría ser así”, lo que ocurre es que, los científicos, a veces se dejan llevar por las emociones. Al fin y al cabo, ellos como el común de los mortales, también son humanos.

Ya nos gustaría saber cómo es, ese vacío cuántico y qué pasa allí
Me llama poderosamente la atención lo que conocemos como las fluctuaciones de vacío, esas oscilaciones aleatorias, impredecibles e ineliminables de un campo (electromagnético o gravitatorio), que son debidas a un tira y afloja en el que pequeñas regiones del espacio toman prestada momentáneamente energía de regiones adyacentes y luego la devuelven. Hace un par de días que hablamos de ello.
Ordinariamente, definimos el vacío como el espacio en el que hay una baja presión de un gas, es decir, relativamente pocos átomos o moléculas. En ese sentido, un vacío perfecto no contendría ningún átomo o molécula, pero no se puede obtener, ya que todos los materiales que rodean ese espacio tienen una presión de vapor finita. En un bajo vacío, la presión se reduce hasta 10-2 pascales, mientras que un alto vacío tiene una presión de 10-2-10-7 pascales. Por debajo de 10-7 pascales se conoce como un vacío ultra-alto.

No puedo dejar de referirme al vacío-theta (vació θ) que, es el estado de vacío de un campo gauge no abeliano (en ausencia de campos fermiónicos y campos de Higgs). En el vacío theta hay un número infinito de estados degenerados con efecto túnel entre estos estados. Esto significa que el vacío theta es análogo a una funciónn de Bloch en un cristal.
Se puede derivar tanto como un resultado general o bien usando técnicas de instantón. Cuando hay un fermión sin masa, el efecto túnel entre estados queda completamente suprimido. Cuando hay campos fermiónicos con masa pequeña, el efecto túnel es mucho menor que para campos gauge puros, pero no está completamente suprimido.

¡Es tanto lo que hay pero que no podemos ver!
Si buscamos por ahí podremos leer explicaciones como esta: “En la Teoría cuántica de campos, el vacío cuántico (también llamado el vacío) es el estado cuántico con la menor energía posible. Generalmente no contiene partículas físicas. El término “Energía de punto cero” es usado ocasionalmente como sinónimo para el vacío cuántico de un determinado campo cuántico.
De acuerdo a lo que se entiende actualmente por vacío cuántico o “estado de vacío”, este “no es desde ningún punto de vista un simple espacio vacío” , y otra vez: “es un error pensar en cualquier vacío físico como un absoluto espacio vacío.” De acuerdo con la mecánica cuántica, el vacío cuántico no está verdaderamente vacío sino que contiene ondas electromagnéticas fluctuantes y partículas que saltan adentro y fuera de la existencia.
Según las modernas teorías de las partículas elementales, el vacío es un objeto físico, se puede cargar de energía y se puede convertir en varios estados distintos. Dentro de su terminología, los físicos hablan de vacíos diferentes. El tipo de partículas elementales, su masa y sus interacciones están determinados por el vacío subyacente. La relación entre las partículas y el vacío es similar a la relación entre las ondas del sonido y la materia por la que se propagan. Los tipos de ondas y la velocidad a la que viajan varía dependiendo del material.”

Como nos dicen en este anuncio del Kybalion, nada es estático en el Universo y, todo está en continuo movimiento o vibración. Habreis oido hablar de la energía de punto cero que permanece en una sustancia en el cero absoluto (cero K). Está de acuerdo con la teoría cuántica, según la cual, una partícula oscilando con un movimiento armónico simple no tiene estado estacionario de energía cinética nula. Es más, el Principio de Incertidumbre no permite que esta partícula esté en reposo en el punto central exacto de sus oscilaciones. Del vacío surgen sin cesar partículas virtuales que desaparecen en fracciones de segundo, y, ya conoceis, por ejemplo, el Efecto Casimir en el que dos placas pueden producir energía negativa surgidas del vacío.
De todas las maneras, en este momento sabemos tanto de la espuma cuántica como de nuestra presencia en el Universo, es decir, nada. Todo son conjeturas, suposiciones e hipótesis que nos hacen imaginar lo que pueda existir a la distancia de Planck. Claro que en una longitud de 10-35 metros, sí que es fácil imaginar que lo que podamos ver allí sería simplemente una especie de espuma cuántica asociada a lo que estimamos que sería la gravedad cuántica.
Emilio Silvera Vázquez















 Totales: 85.840.294
Totales: 85.840.294 Conectados: 43
Conectados: 43