Ya me gustaría contemplar, como contemplo la de arriba, a nuestra Galaxia, La Vía Láctea

Sólo en nuestra Galaxia existen más de 100.000 millones de estrellas. El Universo está poblado por cientos de miles de millones de Galaxias cuyo promedio es de 100 mil millones de estrellas cada una. En cada galaxia existen miles de miles de millones de soles con sus planetas, lo que supone una cantidad enorme de mundos. ¿Podemos pensar que de entre cientos y cientos de miles de millones de planetas, solo la Tierra alberga la vida inteligente? Parece algo pretencioso, ¿no te parece?

Si nos asomamos al pasado y al presente, veremos que múltiples formas de vida han poblado el planeta. Ahora, solo el 1 por 100 de todas las especies que vivieron en nuestro planeta existen y, son millones las que disfrutan de este planeta con nosotros ¿cuántos miles de millones habrán desaparecido? El registro fósil no puede facilitarnos la respuesta a esa pregunta.

El Universo está lleno de vida que se aparece en mil formas diferentes, unas inteligentes y otras vegetativas, de distintas morfologías e incluso distintas en sus componentes básicos que, a diferencia de la nuestra, basada en el carbono, aquellas podrán tener u origen vital en el silicio o vaya usted a saber de qué componentes podrían estar formadas y si han dado origen a civilizaciones inteligentes que ni podemos imaginar.

No tenemos que asombrarnos de nada, nosotros mismos, de seguro asombraríamos a una raza inteligente que nos pudiera observar y viera que la patente n° 6.754.472, ha sido concedida a Microsoft y ampara los mecanismos o procedimientos para “transmitir datos y energía utilizando el cuerpo humano”. Se trata, según aparece, de aprovechar la conductividad de la piel para conectar una serie de dispositivos electrónicos por todo el cuerpo.

EL MICROCHIP EN EL CUERPO HUMANO Por más prácticas que sean las tarjetas comunes al microchip pueden ser siempre robadas, perdidas o dañadas. Ahora los grandes financieros presentaron la última solución: ligar físicamente a la persona con su carta, de modo que no haya posibilidad alguna de perderla. El microchip no estará más inserto en una tarjeta plástica, sino implantado directamente en el cuerpo humano, bajo la piel, como se hace actualmente con los animales con fines identificatorios. Se puede así saber a cada momento dónde se encuentra el animal, gracias a los satélites y a las antenas celulares. Pero, si esto sigue así, ¿dónde queda nuestra supuesta libertad?

Además, muchos tratan de apagar esta llama de la libertad y del libre pensamiento. Hay que dejar transcurrir, dentro de una dinámica lógica del pensamiento que, las ideas fluyan y los proyectos se plasmen.

Con certeza no sabemos hasta dónde podremos llegar. Sin embargo, por el camino emprendido…da un poco de miedo pensarlo.

Me viene a la mente una escena futurista en la cual, una raza avanzada, conecta un dispositivo metálico en la sien de un humano y, en una pantalla, aparecen las imágenes de sus recuerdos. Sí, pueden parecer exageraciones, pero a mí particularmente, me parecen escenas cotidianas de cualquier día del siglo XXIII.

[?]

 ESTOCOLMO, Suecia.- El premio Nobel de Física (2.008) fue atribuido hoy al norteamericano Yoichiro Nambu y a los japoneses Makoto Kobayashi y Toshihide Maskawa por sus trabajos separados sobre la física de las partículas que mejoraron la comprensión de la materia, Demos un repaso hoy aquí a esos componentes de la materia, y, profundicemos en sus propiedades., en sus “vidas”.

Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida medio, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.

[?]

La Imagen especular (simetría)

La ley conocida como Interacción débil, no cumple con ciertas “leyes de la Física” tales como la conservación de la extrañeza y del isospín, aunque hay otras muchas leyes de conservación que sí respeta.

Los físicos hablan muy a menudo de la conservación de la simetría. Una simetría muy importante, aunque simple, es la “simetría especular” oficialmente llamada “paridad”.

No, esta no es, la imagen especular de un neutrino, de hecho, ellos no tienen imagen especular.

Antes de 1956, siempre se había supuesto que cualquier fenómeno  respetaba las mismas leyes físicas que su imagen especular. En consecuencia uno podría esperar que las partículas o haces de partículas chocan entre ellas de una forma que sea especularmente simétrica, la simetría especular se preservaría.

                                   Los neutrinos siempre nos han dado dolor de cabeza. Su ponemos nuestras manos delante un espejo, ahí las veremos reflejadas. Si de la misma manera, pudiéramos poner dos neutrinos delante del espejo de al lado, eso veríamos: NADA.

El descubrimiento de que muchas partículas no se parecían en nada a sus respectivas imágenes especulares fue realizado por dos físicos chinos, Tsung Dao Lee y Chen Ning Yang, algún tiempo después de haber emigrado a los EE UU. Resultó que la Interacción débil distinguía entre derecha e izquierda. Esto es más claro en el caso del neutrino.

Los neutrinos v_e y v_µ como el fotón, no tienen masa en reposo y, por lo tanto, se mueven siempre a la velocidad de la luz. Los neutrinos también rotan con un espín ½. Si definimos el “polo norte” y el “polo sur” igual que se definen en la Tierra. Los neutrinos son especiales porque siempre tienen el polo sur enfrente de ellos y el polo norte detrás. Nunca se han observados neutrinos para los cuales esto no sea así.

La física sueca Cecilia Jarlskog comparó a los neutrinos con los vampiros porque no tienen imagen especular. Su imagen especular es un imposible físico.

Hace unos días, con ocasión del “hallazgo” del Bosón de Higgs, hablamos aquí del “Mecanismo Higgs”. Pero, ¿es correcto? ¿Nos conducirá hacia una buena teoría? ¿Qué es lo que está permitido y lo que no para describir las partículas elementales y por qué?

El Instituto de Cargèse, en la Isla de Córcega, fue fundado por el físico francés Maurice Lèvy. Desde 1960. Allí, construido en un precioso terreno con una pequeña playa, se realizaban (ahora no se si continúan) escuelas de verano.

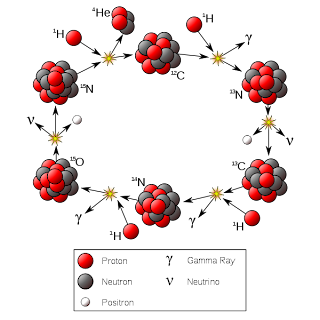
La de 1970 era sobre las interacciones fuertes. Junto con Gell-Mann, Lévy había desarrollado un modelo para la interacción fuerte. Aunque no esperaban que representase toda la verdad, tenía la característica de que se reproducían todas las simetrías de las interacciones fuertes de una forma muy interesante. Pero, debido a que las interacciones son tan fuertes, las partículas no se mueven ni siquiera aproximadamente en línea recta y esto hacía que no se pudiera utilizar el esquema aproximativo habitual, el llamado “desarrollo perturbativo”. A pesar de las dificultades fundamentales que presentaba el modelo con su interminable serie de aproximaciones que no convergían en nada, las discusiones de aquel curso de verano, terminaron dedicándose de forma predominante a intentar extraer de aquel modelo, resultados con algún sentido.

El modelo era interesante. Era un modelo renormalizable en el cual, protones, neutrones y tres clases de piones jugaban un papel muy importante. Pero hacía falta un cuarto acompañante de los piones que se llamó “sigma” (σ). La simetría el modelo requería que los protones “desnudos” y los neutrones no tuvieran masa. Sólo en ese caso se podía entender cómo funcionan las cirrientes sobre las que actúa la interacción débil.

Y, aquí está la parte interesante: se suponía que las partículas sigmas sufrían una condensación Bose y, por lo tanto, aquí también tenemos una “rotura espontánea de simetría”. Los protones y los neutrones, que no tendrían masa en un ambiente simétrico, son entonces frenados por esas partículas sigmas que pueblan el vacío, y adquieren así la masa de la rotura de la simetría. En este sistema se verificaba el teorema de Goldstone, y por lo tanto perdían su masa en reposo.

Aquello no estaba tan mal después de todo. Ya se sabía que los piones eran, con diferencia, los hadrones más ligeros. En la mayoría de las teorías, lo que se tenía que comparar era el cuadrado de las masas de las partículas, y el cuadrado de la masa del pión es aproximadamente catorce veces menor que la masa de la siguiente partícula, el kaón. Una aproximación en la que la masa del pión fuera nula no era, pues, ninguna locura. En una versión mejorado del modelo sigma, podríamos suponer que la masa del pión proviene de una pequeña perturbación. Más tarde, cuando se utilizó el modelo Quarks, se consideró que tanto los piones de Goldstone como la partícula sigma estaban formados por un quark y un anti-quark. La “pertubación” que da la masa al pión resultará ser la pequeña masa de los quarks u y d del interior del hadrón.

 ¡Aquien se le diga que aquí está concentrado todo lo que vemos!

Dos autoridades en el tema de la renormalización, el corenao Benjamin Lee y el alemán Kurt Symanzik, estuvieron en Cargèse, en aquella escuela de verano, para explicar cómo se podía renormalizar en el modelo sigma sin que se perdiera su propiedad más importante, , la rotira espontánea de simetría.

Pero “¿se puede hacer lo mismo si hay un campo de Yang-Mills?”. Gerard ´t Hooft, uno de los alumnos de aquella escuela de verano, le preguntó a Lee y a Symanzik. Ambos le dieron la misma respuesta: “Si yo fuera un estudiante de Veltman le preguntaría a él.” Ellos no habían estuidiado los campos de Yang-Mills, pero a ´t Hooft le pareció que el procedimiento de Lee y Symanzik para el modelo sigma también sería aplicable a cualquier sistema en el que la simetría esté afectada por una condensación de Bose, incluyendo la teoría de Higgs-Kibble. Aquí estaba presente el semillero de una nueva teoría y, ´t Hooft, pensó de inmediato en cómo podía hacerlo crecer.

Esa será otra historia que trataré de contaramos y, de seguro, os interesará.ç

emilio silvera

[?]

¿Es la Física una mercancía?

Leyendo el comentario de nuestro contertulio Tom Wood, termina uno la lectura con la impresión de que, al fin y al cabo, el esfuerzo de los físicos no sirve para mucho aparte de descubrir, de vez en cuando, alguna nueva partícula para añadir al Modelo y, que más o menos accidentalmente, se ha llegado a una descripción que representa adecuadamente todo lo que conocemos hasta el presente y que ha sido aportado a eso que se ha dado en llamar “modelo estándar de la Fisica de Partículas en el que se recogen tres de las cuatro fuerzas y se explican las propuedades de las partícuals y sus interacciones pero, a pesar de todo, deja algunos cabos sueltos.

Después de un buen rato, he tenido que dejar de buscar la situación del gravitón en este cuadro, y, de pronto caí en la cuanta de que, en el Modelo estándar, sólo se incluyen tres de las cuatro fuerzas, por lo tanto, nunca podría encontrar aquí el Gravitón.

Pero, realmente ¿se podrían concluir cosas nuevas de él, algo que no hubiera sido posible conocer por adelantado, una predicción de algo realmente nuevo? Hay veces en las que, toda la fanfarria y parafernalia con la que se presentan algunos “logros”, nos pueden llevar a pensar que, se está tratando de vender algo y, en alguna ocasión, ¡algo que no se tiene!

Las partículas que tenemos hasta ahora empiezan siendo de masa nula. Luego, añadimos una partícula con espín 0, la partícula de Higgs, que hace todo el trabajo pesado. Todas las partículas –Bosones gauge, fermiones y, desde luego, la propia Higgs- deben su masa a la interacción con la Higgs. Hasta hace muy poco tiempo nunca se había detectado la Higgs y, para evitarlo, se construyó esa inmensa máquina de muchos miles de millones de dolores, ya que, todos decían que, el “Campo de Higgs” se sentía por todas partes y, si la partícula de Higgs no estuviera ahí, nuestro modelo sería tan simétrico que todas las partículas parecerían iguales; habría demasiada poca diferenciación. Para que las partículas obtengan sus masas, las simetrías deben ser suficientemente reducidas.

Esto tiene que ver con la conservación de la helicidad, el espín a lo largo del eje paralelo a su movimiento, pero los detalles son demasiado matemáticos y aquí queremos evitar las ecuaciones que no todos comprendemos. Lo que es importante recordar es que todas las partículas deben su masa a las interacciones con el Campo de Higgs.

Pero no es sólo la masa, otras estructuras también surgen en la teoría debido a las muchas formas en la que los fermiones interaccionan con el Campo de Higgs. Esto significa que las masas serán todas diferentes. Además, habiendo tres generaciones, hay sitio suficiente para interacciones que violen la simetría PC, de manera que en el Modelo también se explican las extrañas desintegraciones de la partícula K_L en dos piones.

Todos hemos podido ver alguna Tabla de partículas a la que, para completar la serie, añaden una partícula más, la llamada gravitón, que se cree que transmite la interacción gravitatoria. Parece ser una consecuencia inevitable de las teorías de la gravedad y de la mecánica cuántica, y su espín tendrá que ser igual a dos. Nunca ha sido detectada y no esperamos verla en un futuro cercano.

                                                                                   Violación de la Simetría PC

La teoría no predice la masa de las partículas ni la intensidad de sus interacciones básicas, que tienen que ser determinadas experimentalmente. Esto se debe a que los parámetros básicos del modelo son constantes de la Naturaleza no relacionadas.

Si hacemos una lista completa de las constantes, nos encontramos con que hay veinte números que tienen que ser especificados en cualquier descripción matemática del modelo estándar. Muchos de ellos corresponden a las masas, otros describen aspectos de sus interacciones mutuas, tales como las tres constantes de acoplamiento gauge: Tenemos tres tipos de Campo de Yang-Mills gauge, cada uno con sus propias “constantes de interacción”, no los predice la teoría y todos tienen que ser medidos con gran precisión de manera experimental. Por otra parte, unos pocos parecen ser exactamente cero (tales como la “constante cosmológica de acoplamiento”, que describe la extensión a la cual el espacio vacío emite un campo gravitacional). Estos han sido, sin embargo, incluidos en la lista porque, por lo que sabemos, no hay nada en el modelo que las obligue a ser cero.

Independientemente del hecho irrefutable, de que el modelo estándar contiene veinte números de los que no sabemos porque toman los valores que tienen y, en consecuencia, no sepamos cómo obtenerlos a partir de primeros principios, lo cierto es que, el modelo para los físicos, ha resultado ser una herramienta extraordinaria que, a pesar de sus carencias, ha servido y sirve para el trabajo diario y resolver, muchos de los problemas que se plantean y surgen cuando se profundiza en ese mundo microscópico del que aún (y a pesar de lo que digan algunos), sabemos más bien poco que, bien mirado, y, si tenemos en cuenta que la única herramienta inicial para descubrirlo era nuestra Mente, en realidad, tampoco se puede decir que sea poco el avance conseguido desde Demócrito y Empédocles con sus átomos indivisibles y sus cuatro elementos.

                         Los cuatro elemetos de Empédocles

Todas las propiedades de las partículas fundamentales, los hadrones, núcleos atómicos, átomos, moléculas, sustancias, tejidos, plantas, animales, personas, planetas, sistemas solares, galaxias y quizá incluso el universo entero son consecuencia directa del modelo estándar. Y lo que es más, para la mayoría de las propiedades generales no tienen mucha importancia cual sea el valor exacto de esas constantes que aún no se conocen muy bien, tales como la masa de Higgs. Por ejemplo, el efecto de la interacción débil en las propiedades químicas de los átomos que es extremadamente difícil de detectar (debería dar una estructura helicoidal a los átomos de manera que puedan distinguir la derecha de la izquierda).

Claro que, alguna vez le oí a Tom Wood referirse a algunas de estas cuestiones, haciéndonos ver que, algunos, las mencionan como si sus significados sólo fueran cuestiones filosóficas enunciadas de cara al público, cuando, en realidad, en algunas ocasiones, tienen poca importancia práctica que se quiere enmascarar con aquella otra presentación subliminal o metafísica que, desde luego, caen lejos del campos estricto y muy serio (por cierto) de la Física.

       La dualidad onda-partícula, en el que se aprecia cómo un mismo fenómeno puede ser percibido de dos modos distintos, fue uno de los problemas filosóficos que planteó la mecánica cuántica. Tratándo sobre mecánica cuántica podríamos hablar de la filosofía de la física pero, nunca de la Física como filosofía.

Nosotros no somos capaces de deducir las propiedades de un escarabajo utilizando el modelo estándar y esto nunca va a cambiar. Imaginemos un examen de la siguiente cuestión:

Calcula el número de segmentos del Aselluz aquaticus a partir del modelo estándar. Se puede utilizar la lista adjunta para la masa de Higgs y los parámetros que violan la CP…

Nunca se podrá resolver tal tipo de problemas, ni es la intención de los Físicos Teóricos sugerir que ellos pueden hacer la labor de los Biólogos o la de los miembros de cualquier otra disciplina que no sea la Física. Lo que afirman es que las fuerzas de la Naturaleza responsables del número de segmentos de esas criaturas son conocidas, pero que el efecto es incalculable. A duras penas somos capaces de calcular los efectos de las fuerzas fundamentales en un simple hadrón tal como el protón (¡los resultados están a menudo desviados más de un cincuenta por ciento!), así que imagínese cuan imposible se hace la complejidad de un sistema formado por los 10²² átomos con la forma de un escarabajo.

Por primera vez, la ciencia logró fotografiar dos átomos vibrando juntos dentro de una molécula mediante un procedimiento en el cual se convirtió a un electrón en un “flash” para la mencionada foto. Ya de por sí el haber podido controlar el electrón para un fin específico abre perspectivas esperanzadoras con respecto a la posibilidad futura de poder controlar los productos químicos y sus reacciones a escala atómica.

Siguiendo las leyes de la mecánica cuántica, resulta que el cálculo de las propiedades de dos átomos juntos es muchísimo más complicado que el de un solo átomo y que las propiedades de la mayoría de los átomos son enormemente más difíciles de calcular que las del átomo más sencillo, el del hidrógeno.

Entender las fuerzas involucradas en nuestro Modelo Estándar es importante porque entonces también sabremos cuales son las leyes generales a las que obedecen estrictamente. Tenemos las leyes de conservación de la energía, de conservación del momento e incluso de conservación de la información; ésta última implica que los llamados fenómenos paranormales tendrán que ser explicados en términos de la física ordinaria, biología, psicología y así sucesivamente, pero si no se dan explicaciones realistas, estos temas no podrán ser de ninguna forma compatibles con todo lo que sabemos del modelo estándar, del que por cierto, nos que ¡tanto por saber!

No pocas veces la física nos puede parecer similar a uno de esos cuadros abstractos en los que, en un revoltujo incomprensible, aparecen figuras y colores que, la gente corriente no sabe como encajar y, tampoco alcanzar a poder ver la belleza allí presente, si, en realidad hay alguna.

Amargamente, y algo desalentado y hasta con una pizca de desesperación, oímos los lamentos de nuestro amigo Tom Woos que, comienza su largo comentario con:

“Introducir masa desde afuera; masa impropia como digo yo, no es nada nuevo y cada época lo ha hecho con los conocimientos físicos que poseía. Y lo desecho al entrar en contradicciones insalvables, con los nuevos conocimientos que vinieron. Primero para explicar la masa inercial de un cuerpo ordinario, los que tropezamos a diario, los que se usan para las demostraciones escolares. Después para explicar la masa y la interacción de los cuerpos del sistema solar. Posteriormente cuando ya no había discusión sobre la existencia del sistema solar y su mecánica de movimiento y se generalizaron los conocimientos físicos a todo el universo; tampoco en hombre se pudo explicar racionalmente, desde la física, físicamente, que era la masa, que es la inercia, que relaciona en lo profundo la masa y la gravedad.

El problema es el desespero, la enorme frustración científica que esto provoca en la sicología de un físico. Por eso tanta euforia, tanto fanatismo, por nada; es el deseo acumulado por anos. Por la normal aparición de un animal mas en el zoológico. Que los científicos dicen que es el traficante de masa y los periodistas informaron todo los que les vino en gana. Se vendieron como pan caliente, casi un complot científico-mediático.”

En mucho de lo que dice, lleva toda la razón…

emilio silvera

[?]

Ayer finalizábamos así la primera parte de este trabajo:

Por su parte, el científico británico Peter Higgs, de 80 años, que dio su nombre a la llamada “partícula divina” en 1964, afirmó que cree que su Bosón seríaá hallado gracias al Gran Colisionador. “Creo que es bastante probable” dijo pocas horas después de que entrara en funcionamiento el gigantesco acelerador. Y, según parece, se está saliendo con la suya.

De todas las maneras,  estaría bien saber, a ciencia cierta, cómo es el campo de Higgs del que toman la masa todas las partículas, y conocer, mediante que sistema se transfieren la masa, o, si cuando las partículas entran en el campo de Higgs e interracionan con él, es el efecto frenado el que les otorga la masa.

Claro que, esa, como otras conjeturas sobre los Océanos de Higgs y su dichosa Partícula “repartidora de masa”, no son más que conjeturas que, más adelante, debemos ir comprobando para poder escribirlas con letras de oro en el Libro de la Física, o, por el contrario, desecharlas como se ha hecho con tántas otras ideas y teorías frustradas que nunca llegaron a ninguna parte.

¡Los fotones de Yang-Mills adquieren su masa y el proncipio gauge se sigue cimpliendo! Al principio esta visión no mereció la atención que merecía. Por una parte, la gente penso que el modelo era feo. El principio gauge estaba ahí, pero ya no era el tema central. El “Campo de Higgs” había sido puesto ahí “a propósito” y la “partícula de Higgs”, en sí misma, no era una “partícula gauge”. Si se admitía esto, ¿por qué no introducir más partículas y campos arbitrarios? Estas ideas se consideraron como simples modelos con los que jugart, sin mucho significado fundamental al que ahora se quiere llegar con el LHC pretendiendo hacer bueno todo aquello y, al menos los físicos, insisten en que, el campo y la partícula están ahí…¡ya veremos en qué queda todo esto! Son muchos los cabos sueltos y las cosas sin explicar.

En segundo lugar estaba lo que se llamó “teorema de Goldstone”. Ya se habían priducido antes modelos de partículas con “rotura espontánea de simetría”, pero para la mayoría de esos modelos, Jeoffrey Goldstone habia probado que siempre contenían partículas sin masa y sin espín. Muchos investigadores, por lo tanto, pensaron que la teoría de Higgs también debía contener esa partícula de Goldstone, sin masa y que esto era un inconveniente porque entre las partículas conocidas no había ninguna partícula de Goldstone. Incluso el propio Goldstone había advertido que el Modelo de Higgs no satisfaccía las condiciones para su demostración, así que no tenía que ser válido para este caso, pero todo el mundo estaba tan impresionado con las matemáticas del teorema que el Modelo de Huggs-Kibble no tuvo éxito durante mucho tiempo.

El bosón de Higgs pretende ser una parte integral de nuestra comprensión de la Naturaleza. Se trata de una partícula que es una excitación de lo que se llama el campo de Higgs. El campo de Higgs impregna todo el espacio y cuando algunas de las partículas fundamentales que viajan a través de este campo adquieren masa (al interaccionar con el Campo dónde, probablemente, ve frenada su marcha y su desplazamiento es más lento debido al medio por el que discurre su viaje). La cantidad de masa que adquieren depende de la fuerza en que interactúan con el campo de Higgs. Algunas particulas, como el electrón adquieren una pequeña masa, mientras que otras adquieren una masa mucho mayor.

Y así, el teorema de Goldstone se utilizó como un “teorema de imposibilidad”: si el espacio vacío no es simétrico, entonces no se puede evitar la presencia de partículas sin masa y sin espín. Ahora sabemos que, en nuestro caso, la letra pequeña invalida el teorema; las partículas de Goldstone se hacen incisibles debido a la invariancia gauge y no son más que las “partículas fantasmas” que encontró Feynman en sus cáculos. Además, debemos recordar que el Mecanismo Higgs no es una auténtica rotura de simetría.

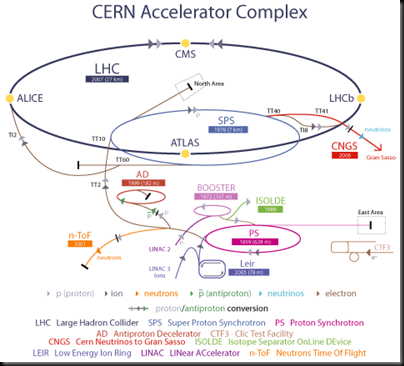
        Ingenios que quieren entrar en los campos de Higgs

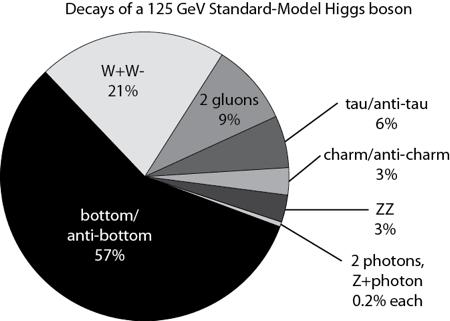
Un aspecto peculiar de esto es que este campo de Higgs que impregna en todo el espacio es parte de lo que llamamos espacio vacío o el vacío. Es sólo su impacto sobre las partículas que viajan a través de él y el bosón de Higgs que podemos observar en el laboratorio. El bosón de Higgs vive por un lapso muy corto de tiempo, así que no lo observan directamente, sino que más bien se observa que las partículas se descompone en y tienen que inferir su existencia a partir de eso. En la teoría actual que tenemos para comprender la naturaleza podemos hacer afirmaciones precisas acerca de qué fracción del tiempo que se desintegra en dos fotones en comparación con dos quarks abajo.

Claro que, algunos, me piden más profundidad en las explicaciones y, no se conforman con pasar por encima de las cuestiones, hay que entrar más en materia y dejar sentados algunos de los parámetros maemáticos que en todo esto están presente, y, para ellos…

Los físicos han buscado al bosón de Higgs por cerca de 50 años porque su descubrimiento completaría el Modelo Estándar de la física de partículas. El bosón de Higgs y su campo asociado explican cómo la simetría electrodébil se rompió justo después del Big Bang, lo que le dio a ciertas partículas elementales la propiedad de la masa. Sin embargo del Modelo Estándar no predice la masa de Higgs, y varios programas experimentales en el LEP del CERN, en el Tevatron de Fermilab y ahora el LHC del CERN habían intentado medir la masa de la partícula.

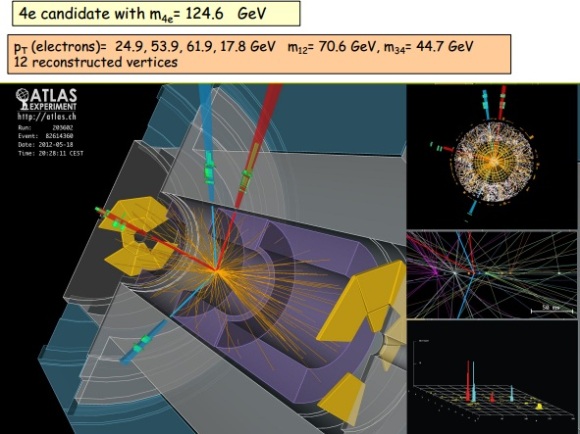
En el seminario llevado a cabo hoy en CERN como preludio a la mayor conferencia de física de partículas de este año, el ICHEP2012 en Melbourne, los experimentos ATLAS y CMS presentaron sus resultados preliminares en la búsqueda del Bosón de Higgs. Ambos experimentos observaron una nueva partícula en la región de masa entre 125-126 GeV.

“Observamos en nuestros datos claras señales de una nueva partícula, al nivel de 5 sigma, en la región de masa alrededor de 126 GeV. El impresionante rendimiento del LHC y ATLAS y el gran esfuerzo de mucha gente nos trajo a esta excitante etapa”, dijo la presentadora del experimento ATLAS Fabiola Gianotti, “pero se necesita más tiempo para preparar estos resultados para su publicación”

“Los resultados son preliminares pero la señal 5 sigma alrededor de 125 Gev que estamos viendo es dramática. Ésta es de hecho una nueva partícula. Sabemos que tiene que ser un bosón y es el bosón más pesado que hemos encontrado hasta ahora,” dijo el presentador del experimento CMS Joe Incandela. “Las implicaciones son muy significantes y es precisamente por esta razón que debemos ser extremadamente diligentes en todos nuestros estudios.”

¿Donde aparece el Higgs en todo esto?

Pues pasemos a hablar de teoría cuántica de campos, en ese tendremos unas densidades lagrangianas que dependerán del campo de cada partícula, dependiendo de su spin será un lagrangiano o otro, por ejemplo para N (a = 1,….N) campos escalares(omito fórmula).

.Al buscar el mínimo del potencial (en realidad un extremal de la acción, pero para lo que nos interesa a nosotros serán mínimos) resulta que hay varios posibles (con el mismo valor) pero para que la energía se minimice hace falta fijar un vacío (debido a que el Hamiltoniano depende del potencial y de unos términos positivos que van con las derivadas del campo). Ahora bien, inicialmente nuestra acción podría tener una simetría gauge global, es decir que al efectuar una transformación de un grupo sobre los campos la acción no cambia, al fijar el vacío la simetría se reduce a un subgrupo y algunos campos obtienen masa (originalmente ninguno tiene masa), pues bien el teorema de Goldstone lo que dice es que campos se quedan sin masa, estos son los bosones de Goldstone.

¿Y el higgs? ¬¬

Ya llegamos, en el apartado anterior hemos considerado transformaciones globales, pero por ejemplo en electromagnetismo tenemos transformaciones locales, así que hay que mirar lo que pasa en las transformaciones locales. Lo primero que pasa es que la derivada parcial no preserva los vectores (lo que hemos llamado antes ) igual que pasa en relatividad general, al hacer una transformación que depende de las coordenadas la derivada ya no es covariante, así que hay que buscar una covariante para seguir con lo que sabemos (en este caso la transformación se debe a un grupo gauge arbitrario, que no tiene porque ser el de difeomorfismos como en relatividad general. En este contexto aparecen los campos gauge que jugaran un papel similar al de la conexión en relatividad general y en el caso del electromagnetismo el campo gauge es el potencial electromagnético). Ahora al ser transformaciones locales, aparecen campos gauge que por similitud con el electromagnetismo escribiremos el lagrangiano de Yang-Mills igual que en el electromagnetismo F depende de los campos gauge, pero debido a que no es abeliano hay un termino extra que tiene que ver con las constantes de estructura del álgebra de Lie, . Ahora ya vien lo bueno, aparte del lagrangiano de la partícula también tenemos el de Yang-Mills, resulta que debido a la simetría local:

1. Los bosones de Goldstone desaparecen, es decir no son partículas físicas.
2. campos gauge obtienen masa

Pues eso es el efecto Higgs. Ahora para llegar ya al famoso bosón, en el modelo estandar no se pueden construir terminos de masa para las partículas debido a que no se pueden acoplar adecuadamente para ese propósito los campos de Yang-Mills y las partículas, debido a las simetrías que deben satisfacer (en general el famoso aunque cada campo tendrá una simetría concreta) y ahí es donde entra el bosón de Higgs, ya que el modelo más sencillo para añadir masa es justamente ese, añadir un doblete de campos escalares complejos y al romper la simetría …….. Higgs !!!!

Dos prestigiosos investigadores habñían sugerido de forma independiente que se podían construir modelos realistas dde partículas en los cuales, el sistema de Yang-Mills fuera responsable de la interacción débil y el mecanismo de Higgs-Kibble la causa de su corto alcance. Uno de ellos era el paquistaní Abdus Salam que estaba buscando modelos estéticos de partículas y pensó que la belleza de la idea de Yan-Mills era razón suficiente para intentar construir con ella un modelo de interacción débil. La partícula mediadora de la interacción débil tenía que ser un fotón de Yang-Mills y el mecanismo de Higgs-Kibble la única explicación aceptable para que esta partícula tuviera una cierta cantidad de masa en reposo.

Una simetría puede ser perfecta en el plano de las ecuaciones y resultar rota en el plano de las soluciones. Como decía Weinberg: «Aunque una teoría postule un alto grado de simetría, no es necesario que los estados de las partículas muestren la simetría. Nada me parece tan halagüeño en física como la idea de que una teoría puede tener un alto grado de simetría que se nos oculta en la vida ordinaria».

La teoría que unifica las interacciones electromagnéticas y débil se debe a Glashow, Salam y Weinberg que obtuvieron por ella el Premio Nobel de física de 1979. La dificultad esencial de esta teoría es que los bosones del estado inicial simétrico debían ser de masa nula (masa nula de los bosones de interacción origina una fuerza a gran distancia), mientras que se necesitan bosones intermedios (partículas que originan la fuerza) muy masivos para justificar la interacción débil (corto alcance) . El mecanismo de Higgs, permite resolver esa dificultad, mediante la ruptura espontánea de simetría hace masivos los bosones W y Z (interacción débil) y mantiene nula la masa del fotón (interacción electromagnética).

Los famosos diagramas de Feynaman, nos explican algunos mecanismos de los que se pueden producir (de hecho se producen) en ese misterioso campo de las partículas elementales cuando están presentes en cuertos lugares y se juntas con otros individuos de la especie.

Salam que estaba muy cerca de poder alcanzar la gloria…no llegaba a poder explicar y aplicar las reglas de Feynman y tuvo quer admitir que la teoría parecía estar llena de partículas fantasmas que estaban a punto de estropearlo todo. En estas, llegó el otro investigador, Steven Weinberg, que supo dar un paso más al formular con mucho más detalle un modelo sencillo en el cual indicaba con precisión los campos que existían y cómo podían interactuar. Pero se limitó a los leptones. Weinberg comprendió que, junto al fotón ordinario tenía que haber tres fotones de Yang-Mills pesados::

– Uno cargado positivamente.

– Otro cargado negativamente.

– Otro Neutro.

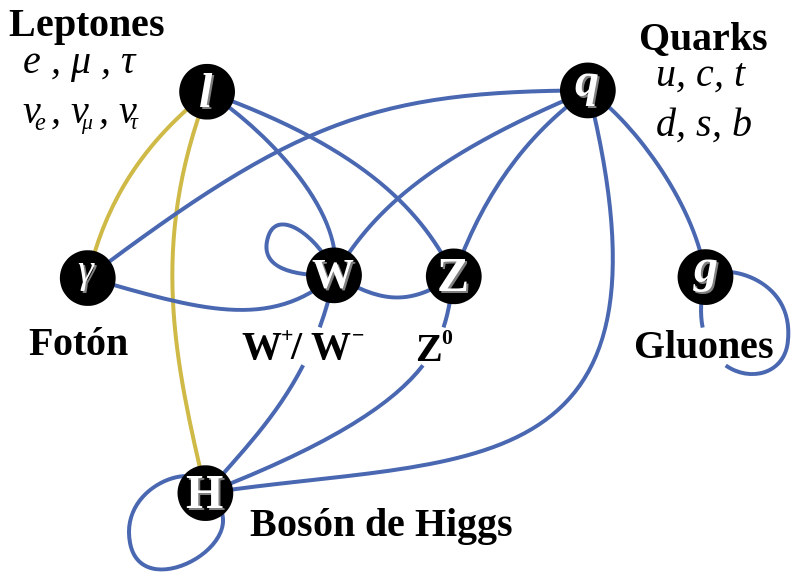
El panorama completo

En lo que se refiere a los fotones cargados, todo el mundo estaba de acuerdo en que estos se necesitarían para describir la interacción débil: serían los famoso bosones vectoriales intermediarios, W⁺ y W^–. De acuierdo con Weinberg, sus masas tenían que ser mayores de 60.000 MeV. Pero solos, estos bosones, vectoriales cargados eran suficientes para explicar todos los procesos de interacción débil que conocían en aquella época.  Que aparte de ellos y del fotón ordinario, y, también se necesita otro componente neutro (Weinberg le llamó Zº) no era evidente en absoluto. Se encontró que la masa del Zº tenía que ser un poco mayor que la de los bosones cargados.

De todo aquello surgió una tería para las interacciones débiles en las cuales jugaban un papel dominante distintos diagramas de Feynman, de los que se podían plasmar un número infinito para mostrar, de manera gráfica, los sucesos que acontecían en aquellos fenómenos de la radiación producida en la interacción débil. Pasado el tiempo y mirado con una mejor perspectiva, es fácil comprender todo aquello pero, en aquellos momentos en que se estaba gestando, las cosas no resultaban tan fáciles.

Después de todo aquello, se prestó más atención al mecanismo Higgs-Kibble y, algunos, como Veltman fueron muy escépticos con aquellas ideas, y, desde luego, no fue fácil converlo de que pudiéramos llamar vacío a algo lleno de partículas invisibles. ¿No delatarían dijo, su presencia por sus campos gravitatorios? La teoría puede ser formulada de tal manera que esos campos gravitatorios se compensen exactamente con otras partículas invibles o por una contribución misteriosa del propio espacio vacío.

Cómo consigue la Naturaleza enmascarar tan exacta y eficientemente esos factores de la gravedad que no podemos notar nada, es un misterio que continua siendo muy debatido hoy en día. Claro que, todo esto dejará de ser un misterio cuando un día (lejos aún en el futuro), podamos comprender la Gravedad Cuántica.

Miehntras todo esto sucede… ¡Dejémos volar nuestra imaginación! con ideas y teorías como la de los ¡Campos de Higgs! ¡Bosones que, generosos ellos, regalan masas a otras partículas! ¡Materia que no podemos ver pero que, dem manera acérrima, nos empeñamos en que sí está! ¡Fluctiaciones de vacío que rasgan el espacio-tiempo, y, que de vez en cuando, hace surgir nuevos universos! ¡Universos paralelos que nacieron sin vida! ¡Ciclos eternos en el que las cosas se repetin una y otra vez hasta el infinito! ¡Nuevos Big Bangs después del nuestro! ¡Agujeros negros en nuestro universo y, blancos al otro lado, en otro universo. Aquí recoge materia y, allú, la expulsa por el contrario, un Agujero Blanco! ¡Agujeros de Gusano que nos podrían llevar a otras galaxias! ¡El sueño de vencer (mejor burlar) a la velocidad de la luz, ese muro que nos tiene confinados en nuestro pequeño mundo, el Sistema Solar!

Después de leer todo esto, ¿por qué no dedicais aunque sólo sea una hora para pensar sobre ello?

emilio silvera

[?]