¿Los campos de Higgs? Hablemos un poco del tema Higgs.

Por su parte, el científico británico Peter Higgs, de 80 años, que dio su nombre a la llamada “partícula divina” (de Lederman), afirmó creer que su Bosón sería hallado gracias al Gran Colisionador. “Creo que es bastante probable” dijo pocas horas después de que entrara en funcionamiento el gigantesco acelerador. Y, según parece (al menos eso afirman algunos),  se está saliendo con la suya.

De todas las maneras,  estaría bien saber, a ciencia cierta, cómo es el campo de Higgs del que toman la masa todas las partículas, y conocer, mediante que sistema se transfieren la masa, o, si cuando las partículas entran en el campo de Higgs e interaccionan con él, es el efecto frenado el que les otorga la masa.

Claro que, esa, como otras conjeturas sobre los Océanos de Higgs y su dichosa Partícula “repartidora de masa”, no son más que conjeturas que, más adelante, debemos ir comprobando para poder escribirlas con letras de oro en el Libro de la Física, o, por el contrario, desecharlas como se ha hecho con tántas otras ideas y teorías frustradas que nunca llegaron a ninguna parte.

¡Los fotones de Yang-Mills adquieren su masa y el proncipio gauge se sigue cimpliendo! Al principio esta visión no mereció la atención que merecía. Por una parte, la gente penso que el modelo era feo. El principio gauge estaba ahí, pero ya no era el tema central. El “Campo de Higgs” había sido puesto ahí “a propósito” y la “partícula de Higgs”, en sí misma, no era una “partícula gauge”. Si se admitía esto, ¿por qué no introducir más partículas y campos arbitrarios? Estas ideas se consideraron como simples modelos con los que jugart, sin mucho significado fundamental al que ahora se quiere llegar con el LHC pretendiendo hacer bueno todo aquello y, al menos los físicos, insisten en que, el campo y la partícula están ahí…¡ya veremos en qué queda todo esto! Son muchos los cabos sueltos y las cosas sin explicar.

En segundo lugar estaba lo que se llamó “teorema de Goldstone”. Ya se habían priducido antes modelos de partículas con “rotura espontánea de simetría”, pero para la mayoría de esos modelos, Jeoffrey Goldstone habia probado que siempre contenían partículas sin masa y sin espín. Muchos investigadores, por lo tanto, pensaron que la teoría de Higgs también debía contener esa partícula de Goldstone, sin masa y que esto era un inconveniente porque entre las partículas conocidas no había ninguna partícula de Goldstone. Incluso el propio Goldstone había advertido que el Modelo de Higgs no satisfaccía las condiciones para su demostración, así que no tenía que ser válido para este caso, pero todo el mundo estaba tan impresionado con las matemáticas del teorema que el Modelo de Huggs-Kibble no tuvo éxito durante mucho tiempo.

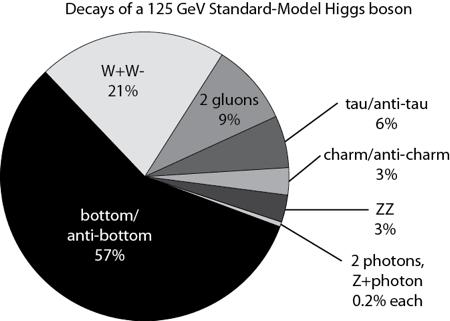
El bosón de Higgs pretende ser una parte integral de nuestra comprensión de la Naturaleza. Se trata de una partícula que es una excitación de lo que se llama el campo de Higgs. El campo de Higgs impregna todo el espacio y cuando algunas de las partículas fundamentales que viajan a través de este campo adquieren masa (al interaccionar con el Campo dónde, probablemente, ve frenada su marcha y su desplazamiento es más lento debido al medio por el que discurre su viaje). La cantidad de masa que adquieren depende de la fuerza en que interactúan con el campo de Higgs. Algunas particulas, como el electrón adquieren una pequeña masa, mientras que otras adquieren una masa mucho mayor.

Y así, el teorema de Goldstone se utilizó como un “teorema de imposibilidad”: si el espacio vacío no es simétrico, entonces no se puede evitar la presencia de partículas sin masa y sin espín. Ahora sabemos que, en nuestro caso, la letra pequeña invalida el teorema; las partículas de Goldstone se hacen incisibles debido a la invariancia gauge y no son más que las “partículas fantasmas” que encontró Feynman en sus cáculos. Además, debemos recordar que el Mecanismo Higgs no es una auténtica rotura de simetría.

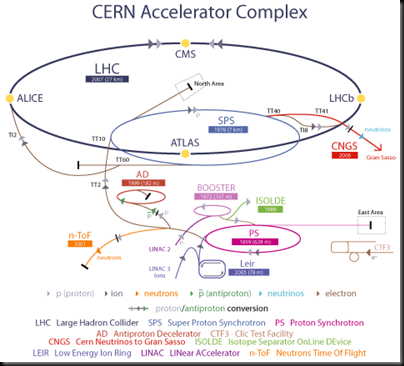
        Ingenios que quieren entrar en los campos de Higgs

Un aspecto peculiar de esto es que este campo de Higgs que impregna en todo el espacio es parte de lo que llamamos espacio vacío o el vacío. Es sólo su impacto sobre las partículas que viajan a través de él y el bosón de Higgs que podemos observar en el laboratorio. El bosón de Higgs vive por un lapso muy corto de tiempo, así que no lo observan directamente, sino que más bien se observa que las partículas se descompone en y tienen que inferir su existencia a partir de eso. En la teoría actual que tenemos para comprender la naturaleza podemos hacer afirmaciones precisas acerca de qué fracción del tiempo que se desintegra en dos fotones en comparación con dos quarks abajo.

Claro que, algunos, me piden más profundidad en las explicaciones y, no se conforman con pasar por encima de las cuestiones, hay que entrar más en materia y dejar sentados algunos de los parámetros maemáticos que en todo esto están presente, y, para ellos…

Los físicos han buscado al bosón de Higgs por cerca de 50 años porque su descubrimiento completaría el Modelo Estándar de la física de partículas. El bosón de Higgs y su campo asociado explican cómo la simetría electrodébil se rompió justo después del Big Bang, lo que le dio a ciertas partículas elementales la propiedad de la masa. Sin embargo del Modelo Estándar no predice la masa de Higgs, y varios programas experimentales en el LEP del CERN, en el Tevatron de Fermilab y ahora el LHC del CERN habían intentado medir la masa de la partícula.

 

 

 

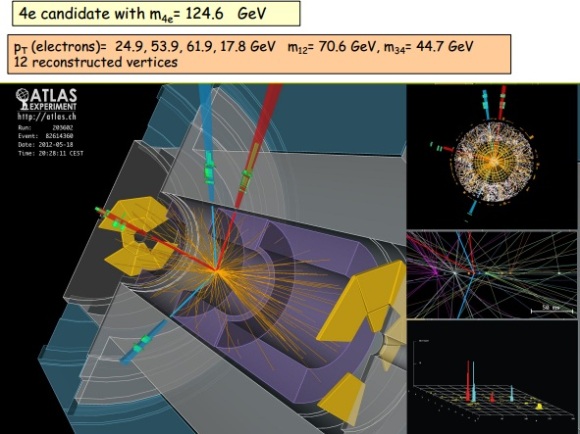
En el seminario llevado a cabo hoy en CERN como preludio a la mayor conferencia de física de partículas de este año, el ICHEP2012 en Melbourne, los experimentos ATLAS y CMS presentaron sus resultados preliminares en la búsqueda del Bosón de Higgs. Ambos experimentos observaron una nueva partícula en la región de masa entre 125-126 GeV.

“Observamos en nuestros datos claras señales de una nueva partícula, al nivel de 5 sigma, en la región de masa alrededor de 126 GeV. El impresionante rendimiento del LHC y ATLAS y el gran esfuerzo de mucha gente nos trajo a esta excitante etapa”, dijo la presentadora del experimento ATLAS Fabiola Gianotti, “pero se necesita más tiempo para preparar estos resultados para su publicación”

“Los resultados son preliminares pero la señal 5 sigma alrededor de 125 Gev que estamos viendo es dramática. Ésta es de hecho una nueva partícula. Sabemos que tiene que ser un bosón y es el bosón más pesado que hemos encontrado hasta ahora,” dijo el presentador del experimento CMS Joe Incandela. “Las implicaciones son muy significantes y es precisamente por esta razón que debemos ser extremadamente diligentes en todos nuestros estudios.”

                                            ¿Donde aparece el Higgs en todo esto?

Pues pasemos a hablar de teoría cuántica de campos, en ese tendremos unas densidades lagrangianas que dependerán del campo de cada partícula, dependiendo de su spin será un lagrangiano o otro, por ejemplo para N (a = 1,….N) campos escalares . Al buscar el mínimo del potencial (en realidad un extremal de la acción, pero para lo que nos interesa a nosotros serán mínimos) resulta que hay varios posibles (con el mismo valor) pero para que la energía se minimice hace falta fijar un vacío (debido a que el Hamiltoniano depende del potencial y de unos términos positivos que van con las derivadas del campo). Ahora bien, inicialmente nuestra acción podría tener una simetría gauge global, es decir que al efectuar una transformación de un grupo sobre los campos la acción no cambia, al fijar el vacío la simetría se reduce a un subgrupo y algunos campos obtienen masa (originalmente ninguno tiene masa), pues bien el teorema de Goldstone lo que dice es que campos se quedan sin masa, estos son los bosones de Goldstone.

                                                                    ¿Y el higgs? ¬¬

Ya llegamos, en el apartado anterior hemos considerado transformaciones globales, pero por ejemplo en electromagnetismo tenemos transformaciones locales, así que hay que mirar lo que pasa en las transformaciones locales. Lo primero que pasa es que la derivada parcial no preserva los vectores (lo que hemos llamado antes ) igual que pasa en relatividad general, al hacer una transformación que depende de las coordenadas la derivada ya no es covariante, así que hay que buscar una covariante para seguir con lo que sabemos (en este caso la transformación se debe a un grupo gauge arbitrario, que no tiene porque ser el de difeomorfismos como en relatividad general. En este contexto aparecen los campos gauge que jugaran un papel similar al de la conexión en relatividad general y en el caso del electromagnetismo el campo gauge es el potencial electromagnético). Ahora al ser transformaciones locales, aparecen campos gauge que por similitud con el electromagnetismo escribiremos el lagrangiano de Yang-Mills igual que en el electromagnetismo F depende de los campos gauge, pero debido a que no es abeliano hay un termino extra que tiene que ver con las constantes de estructura del álgebra de Lie, . Ahora ya vien lo bueno, aparte del lagrangiano de la partícula también tenemos el de Yang-Mills, resulta que debido a la simetría local:

1. Los bosones de Goldstone desaparecen, es decir no son partículas físicas.
2. campos gauge obtienen masa

Pues eso es el efecto Higgs. Ahora para llegar ya al famoso bosón, en el modelo estandar no se pueden construir terminos de masa para las partículas debido a que no se pueden acoplar adecuadamente para ese propósito los campos de Yang-Mills y las partículas, debido a las simetrías que deben satisfacer (en general el famoso aunque cada campo tendrá una simetría concreta) y ahí es donde entra el bosón de Higgs, ya que el modelo más sencillo para añadir masa es justamente ese, añadir un doblete de campos escalares complejos y al romper la simetría …….. Higgs !!!!

Dos prestigiosos investigadores habían sugerido de forma independiente que se podían construir modelos realistas dde partículas en los cuales, el sistema de Yang-Mills fuera responsable de la interacción débil y el mecanismo de Higgs-Kibble la causa de su corto alcance. Uno de ellos era el paquistaní Abdus Salam que estaba buscando modelos estéticos de partículas y pensó que la belleza de la idea de Yan-Mills era razón suficiente para intentar construir con ella un modelo de interacción débil. La partícula mediadora de la interacción débil tenía que ser un fotón de Yang-Mills y el mecanismo de Higgs-Kibble la única explicación aceptable para que esta partícula tuviera una cierta cantidad de masa en reposo.

Una simetría puede ser perfecta en el plano de las ecuaciones y resultar rota en el plano de las soluciones. Como decía Weinberg: «Aunque una teoría postule un alto grado de simetría, no es necesario que los estados de las partículas muestren la simetría. Nada me parece tan halagüeño en física como la idea de que una teoría puede tener un alto grado de simetría que se nos oculta en la vida ordinaria».

La teoría que unifica las interacciones electromagnéticas y débil se debe a Glashow, Salam y Weinberg que obtuvieron por ella el Premio Nobel de física de 1979. La dificultad esencial de esta teoría es que los bosones del estado inicial simétrico debían ser de masa nula (masa nula de los bosones de interacción origina una fuerza a gran distancia), mientras que se necesitan bosones intermedios (partículas que originan la fuerza) muy masivos para justificar la interacción débil (corto alcance) . El mecanismo de Higgs, permite resolver esa dificultad, mediante la ruptura espontánea de simetría hace masivos los bosones W y Z (interacción débil) y mantiene nula la masa del fotón (interacción electromagnética).

Los famosos diagramas de Feynaman, nos explican algunos mecanismos de los que se pueden producir (de hecho se producen) en ese misterioso campo de las partículas elementales cuando están presentes en cuertos lugares y se juntas con otros individuos de la especie.

Salam que estaba muy cerca de poder alcanzar la gloria…no llegaba a poder explicar y aplicar las reglas de Feynman y tuvo quer admitir que la teoría parecía estar llena de partículas fantasmas que estaban a punto de estropearlo todo. En estas, llegó el otro investigador, Steven Weinberg, que supo dar un paso más al formular con mucho más detalle un modelo sencillo en el cual indicaba con precisión los campos que existían y cómo podían interactuar. Pero se limitó a los leptones. Weinberg comprendió que, junto al fotón ordinario tenía que haber tres fotones de Yang-Mills pesados::

– Uno cargado positivamente.

– Otro cargado negativamente.

– Otro Neutro.

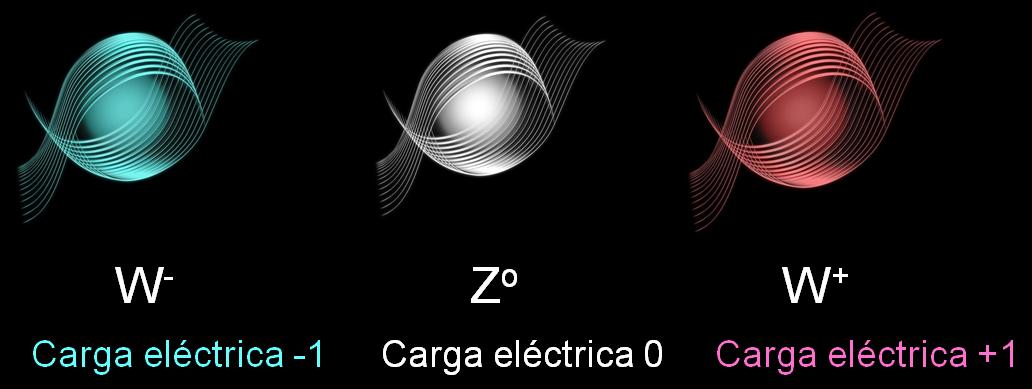
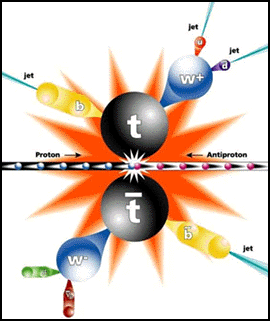
    La carga de la  W⁺ se nos puerde a la derecha de la imagen pero, como rodos habeis supuesto, es carga + 1

En lo que se refiere a los fotones cargados, todo el mundo estaba de acuerdo en que estos se necesitarían para describir la interacción débil: serían los famoso bosones vectoriales intermediarios, W⁺ y W^–. De acuierdo con Weinberg, sus masas tenían que ser mayores de 60.000 MeV. Pero solos, estos bosones, vectoriales cargados eran suficientes para explicar todos los procesos de interacción débil que conocían en aquella época.  Que aparte de ellos y del fotón ordinario, y, también se necesita otro componente neutro (Weinberg le llamó Zº) no era evidente en absoluto. Se encontró que la masa del Zº tenía que ser un poco mayor que la de los bosones cargados.

De todo aquello surgió una tería para las interacciones débiles en las cuales jugaban un papel dominante distintos diagramas de Feynman, de los que se podían plasmar un número infinito para mostrar, de manera gráfica, los sucesos que acontecían en aquellos fenómenos de la radiación producida en la interacción débil. Pasado el tiempo y mirado con una mejor perspectiva, es fácil comprender todo aquello pero, en aquellos momentos en que se estaba gestando, las cosas no resultaban tan fáciles.

Después de todo aquello, se prestó más atención al mecanismo Higgs-Kibble y, algunos, como Veltman fueron muy escépticos con aquellas ideas, y, desde luego, no fue fácil converlo de que pudiéramos llamar vacío a algo lleno de partículas invisibles. ¿No delatarían dijo, su presencia por sus campos gravitatorios? La teoría puede ser formulada de tal manera que esos campos gravitatorios se compensen exactamente con otras partículas invibles o por una contribución misteriosa del propio espacio vacío.

Cómo consigue la Naturaleza enmascarar tan exacta y eficientemente esos factores de la gravedad que no podemos notar nada, es un misterio que continua siendo muy debatido hoy en día. Claro que, todo esto dejará de ser un misterio cuando un día (lejos aún en el futuro), podamos comprender la Gravedad Cuántica.

Miehntras todo esto sucede… ¡Dejémos volar nuestra imaginación! con ideas y teorías como la de los ¡Campos de Higgs! ¡Bosones que, generosos ellos, regalan masas a otras partículas! ¡Materia que no podemos ver pero que, dem manera acérrima, nos empeñamos en que sí está! ¡Fluctiaciones de vacío que rasgan el espacio-tiempo, y, que de vez en cuando, hace surgir nuevos universos! ¡Universos paralelos que nacieron sin vida! ¡Ciclos eternos en el que las cosas se repetin una y otra vez hasta el infinito! ¡Nuevos Big Bangs después del nuestro! ¡Agujeros negros en nuestro universo y, blancos al otro lado, en otro universo. Aquí recoge materia y, allú, la expulsa por el contrario, un Agujero Blanco! ¡Agujeros de Gusano que nos podrían llevar a otras galaxias! ¡El sueño de vencer (mejor burlar) a la velocidad de la luz, ese muro que nos tiene confinados en nuestro pequeño mundo, el Sistema Solar!

Después de leer todo esto, ¿por qué no dedicais aunque sólo sea una hora para pensar sobre ello?

emilio silvera

[?]

La mayoría de las partículas subatómicas que son producidas en los aceleradores de partículas, tiene una existencia muy breve, pero aun así ha producido asombro que una,  como el quark top – cima en español-, puede vivir tan efimero espacio de tiempo. Los experimentos realizados han permitido a los físicos determinar el tiempo de vida del quark top que es apenas de 3 x 10^-25 segundos.  Una fracción de tiempo asombrosamente pequeña.

Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida medio, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.

También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.

Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, ksi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales manera de desintegración, veríamos como difieren las unas de las otras.

Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.

¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.

En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su carta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas, Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas  experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.

Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.

Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según  la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.

Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.

Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”

Si la vida de una partícula  es tan corta como 10ˉ²³ segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.

Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.

Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).

Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.

Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:

∆⁺⁺→р + π⁺;  ∆⁰→р + πˉ; o п+π⁰

En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.

El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (materia), es aún limitado.

emilio silvera

[?]

Algunas veces, cuando nos adentramos en teorías muy avanzadas de la Física que pretende “desnudar” al Universo para conocerlo en su más absoluta desnudez, uno no puede dejar de generar la idea de que, estamos volviendo de nuevo a escenarios mitológicos en los que, la imaginaciónn del hombre dibujaba escenarios que ahora nos pueden parecer demenciales, y, sin embargo, acercarse a ésta nueva Teoria que llaman de supercuerdas… No estámucho más alejado de todo aquello guardando las distancias entre ambas imaginaciones.

Esta “nueva teoría” la de Supercuerdas, nos dice que el Universo consta de diez dimensiones de espacio y una de tiempo que están creadas por delgadas cuerdas que, al mismo modo que si se trataran de las cuerdas de una lira, pueden vibrar, y, al vibrar, van creando partículas con las resonancias o notas que se generan de sus vibraciones.

En la Mitología muchos dioses tocan instrumentos musicales formados por cuerdas que al ser rasgadas suavemente van generando melódicos sonidos y, las diosas tejedoras van hilando el destino del mundo. La lira de Apolo o el Arpa de Orfeo se me vienen a la mente recordando escenas que la mitología nos dejó.

Claro que, llegó Tales de Mileto el antiguos  filósofo griego que nació en Mileto en la Jonia griega. Él fue, la fuente principal para la filosofía y la ciencia. Identificado como la primera persona que investigó los principios básicos, la cuestión de las sustancias procedentes de la materia y, por tanto, como el fundador de la escuela de filosofía natural. Thales estaba interesado en casi todo, la investigación de casi todas las áreas del conocimiento, la filosofía, la historia, la ciencia, las matemáticas, la ingeniería, la geografía y la política.

Propuso teorías para explicar muchos de los eventos de la naturaleza, la sustancia primordial, la importancia que tenía el agua para la vida, el apoyo de la tierra, y las causas de los cambios. Thales estaba muy involucrado en los problemas de la astronomía y formuló una serie de explicaciones de los acontecimientos cosmológicos en los que, (se decía) que tradicionalmente participan entidades sobrenaturales.

Su enfoque cuestionador a la comprensión de los fenómenos celestes fue el comienzo de la astronomía griega. Las hipótesis de Thales eran nuevas y audaces, el fue el que liberó a los fenómenos naturales de la intervención divina, el que allanó el camino hacia la empresa científica. Fundó la escuela de Mileto de la filosofía natural, desarrolló el método científico que más tarde y pasado el tiempo iniciaó la iluminación occidental en el campo científico. Una serie de anécdotas está estrechamente relacionada con las investigaciones de Thales sobre el Cosmos. Tales fue muy apreciado en la antigüedad, y una carta citada por Diógenes Laercio, y que pretendía ser de Anaxímenes a Pitágoras, informó “…que todo nuestro discurso debe comenzar con una referencia a Thales.” Fue el primero que dejó la mitología para emplear la lógica.

Claro que el relato sobre Mileto, aunque irremediablemente relacionado con el presente, es cosa del pasado. Ahora, como entonces, nos seguimos haciendo las mismas preguntas de ¿dónde estamos?, ¿qué hacemos aquí? ¿qué es la materia? y ¿de qué manera se rige el Universo en realidad? Estas y mil preguntas más son las que nuestra curiosidad nos hace formular con la esperanza de que alguien… nos pueda ofrecer alguna respuesta.

La Física del último siglo ha sido asombrosa y los avances a la vista están. Hemos llegado con la Mecánica Cuántica y la Relatividad hasta un Universo dosdoblado en dos partes: Uno que nos cuenta como es el microcosmos, ese “mundo de lo muy pequeño” y, el otro, nos habla de lo macroscópico, lo muy grande. Partículas infinitesimales y supercúmulos de galaxias conforman nuestro saber del Cosmos y, queriendo desentrañar los secretos que nos esconde, imaginamos teorías que pretenden ir encaminadas a desvelarlos.

         Aquí, en la figura, dicen que hay 7 dimensiones

Y, mientras tanto buscamos y procuramos indagar en lo más profundo de la Naturaleza, por el camino, podemos encontrarnos con gente que dicen cosas: “Detectan huellas de otras siete dimensiones en nuestro Universo Un mapa alternativo de la energía cósmica en el big bang corroboraría la teoría de las supercuerdas.” Es entonces cuando uno, no sabe si reir o llorar, al ver la osadía que algunos tienen que, por buscar un poco de notoriedad y algunos minutos de “gloria”, no se recatan en decir sandeces que no tienen ninguna base científica. Pero, los medios de comunicación ¡lo soportan todo!

Quiero recordar que lfue la Revista Time la que vino a poner la guinda en el léxico de la Física de partículas al proclamar la teoría de las Supercuerdas a bombo y platillo, lanzando a los cuatro vientos la noticia de una Teoria de Tdo. Una teoría que proponía una descripción unificada de todas las fuerzas de la Naturaleza, hasta la Gravedad, tan díscola ella negándose a entrar en el Modelo Estándar de la Física de Partículas, estaría allí incluída y cómodamente instalada en una Teoría libre de parámetros aleatorios e infinitos. ¡Qué maravilla!

La premisa básica de la nueva teoría era que reemplazaba a las familiares partículas puntuales por otras que eran segmentos cortos “de cuerda”. La teoría de cuerdas se caracteriza por una estructura que empuja las fronteras de las matemáticas (como la física ya ha hecho en alguna otra ocasión en el pasado) y las limitaciones conceptuales de la imaginación humana hasta extremos antes nunca experimentados.

Como todo en este mundo, la creación de esta teoría tiene su propia historia y sus propios héroes: Gabrielle Veneziano, Johon Schwartz, André Neveu, Pierre Ramond, Jeff Harvey, Joel Sherk, Michael Green, David Gross y un  dotado flutista de Hamelin que responde al nombre de Edward Witten y cuya flauta, etá hecha de increibles ecuaciones de tal complijidad topológica que, hasta a los más afamados físicos, se les ponen de punta los pelos de las cejas al enfrentarse a ellas.

Hablamos y hablamos de un universo hecho con  dimensiones extra que, pueden ser 10, 11 o 26 y, lo curioso del caso es que, aparte de una temporal que está presente en todas esas variantes, con el resto siempre hacemos el mismo reparto: tres de espacio (que es en el que nos movemos y no podemos renegar de su existencia) y, el resto -no importa el número- son dimensiones compactadas en el límite de Planck, al que, naturalemte, no tenemos manera de llegar.

Los tiempos cambian, y, con los cambios llegan las nuevas doctrinas o creencias, y, ¿por qué no? nuevas teorías. Desde hace algún tiempo venimos dando vueltas y vueltas, en el campo de la Física, a estas avanzadas teorías que no podemos demostrar, toda vez que, al contrario del Modelo Estándar, no son -por ahora- verificables sus predicciones. Me estoy refiriendo, como habeis podido suponer a la Teoría de supercuerdas, La cuerdad Heterótica, la Supergravedad y Supersimetría, y, finalmente, la última versión que viene a ser un compendio de todas las demás, la Teoría M.

Como nos dice Brian Greene en uno de los capítulos del libro El tejido del cosmos, que él titula: “Especulaciones sobre el espacio y el tiempo en la teoría M”, hoy, tres décadas después de la articulación de la teoría de cuerdas,la mayoría de los que trabajan en ella, creen que aún no tenemos una respuesta general para la pregunta fundamental: ¿qué es la teoría de cuerdas? A pesar de que sabemos bastante de la teoría, sus características más elementales son familiares y, a estas alturas, casi cercanas. Tampoco debemos despreciar los éxitos que ha cosechado y, desde luego, es bien sabido todo lo que nos promete y también ¿cómo no? los desafíos que suponen lograr todas esas promesas que en ella están encerradas.

La relatividad especial tiene la constancia de la Velocidad de la luz, la relatividad general tiene el principio de Equivalencia, la mecánica cuántica tiene, el principio de Incertidumbre y, sin embargo, los teóricos de cuerdas aún siguen buscando algo de lo que carece la teoría de cuerdas que, precisamente es: el tipo de principio nuclear que se encontraron en aquellas otras teorías y le dan razón de ser y la sólida base que toda teoría necesita para ser…¡una auténtica teoría!

Esa nueva teorías quiere explicarlo todo. Nada puede estar fuera de ella: ¡El Universo que  es, todo lo que existe, ahí estará!

La Teoría de Cuerdas nos habla de un lugar muy distante, casi tan distante como Hoz o la Atlántida (no, no sonrías Kike, que hablo en serio). Esta Teoría nos quiere llevar hasta los dominios de Planck, un lugar que nadie ha visitado nunca. Ni con un LHC que tuviera un millón de veces la potencia de energía del que ahora busca el Bosón de Higgs, podríamos ir allí. Tan lejano está ese lugar que, cuando los científicos tratan de llegar a él, situado en los primeros instantes después del comienzo del Tiempo, no saben, las matemáticas no responden a sus planteamientos y, de esa manera, nunca hemos podido llegar a saber que sucedió en aquellas primeras fracciones de segundo en el nacimiento del Big Bang, donde, supuestamente, se encuentra el límite de Planck.

¿Será tan difícil encontrar las “cuerdas” como localizar el mundo perdido de la Atlántida? Bueno, por aquí cerca de mi casa, en las costas de Doñana, en el mismo epicentro del Golfo de Cádiz, un equipo de científicos están buscando, afanosamente esa Ciudad perdida que nadie sabe si es leyenda o fue realidad alguna vez. Queda un atisbo de esperanza de poder encontrarla. Algunos textos antiguos la mencionan. Sin embargo, de las cuerdas ¿qué tenemos? ¡La Imaginación de algunos! ¡Las esperanzas de muchos!

Ni observando con una lupa podremos descubrir más de tres dimensiones de espacio en nuestro mundo cotidiano, la otra que completa el cuadro en el que estamos inmersos, según Einstein, es el Tiempo que siempre nos acompaña. Hasta ahí todo está -más o menos- conforme. Sin emnbargo, cuando se nos habla de 11 dimensiones de las que quitamos las cuatro antes mencionada y nos quedan siete compactadas o enrolladas…pero,  enrollada ¿dónde y cómo? Bueno, la teoría arranca de la Gravedad, que se basa en la geometría, así que cabe visualizar que algunas de esas dimensiones estén enrolladas en una bola minúscula. El tamaño de la bola es el característico del régimen de Planck, 10^-33 centímetrtos que viene a ser el tamaño de la cuerda que reemplaza a la partícula puntual.

Así, las partículas que conocemos, surgen en la forma de vibraciones de esas cuerdas, es decir, sus resonancias producen las partículas y, esas cuerdas tensadas, tendrían un número infinito de modos vibración (ese es, el fundamento del violín o del laud -si os acordáis de lo que os conté aquí de aquel viejo músico Italiano llamado Galileo (sí, el padre del astrónomo)-. Las vibraciones de las cuerdas reales se clasifican a partir de la nota fundamental y de sus armónicos o modos de frecuencia, Las matemáticas de las microcuerdas son similares. Nuestras partículas salen de los modos de frecuencia menor.

No, no será fácil llegar a las respuestas de éstas difíciles preguntas que la física tiene planteadas. Y, sin embargo, ¿cómo podríamos describir lo que en esta teoría ha llegado a causar tanta pasión en esos físicos que llevan años luchando con ella? Recuerdo haber leído aquella conferencia apasionante que dio E. Witten en el Fermilab. Su pasión y forma de encausar los problemas, sus explicaciones, llevaron a todos los presentes a hacerse fervientes y apasionados fans de aquella maravillosa teoría. Todos hablaban subyugados mucho después de que el evento hubiera terminado. Según contó León Lederman, que asistió a aquella conferencia: “Yo nunca había visto nada igual, cuando Witten concluyó su charla, hubo muchos segundos de silencio -¿es mucho?- antes de los aplausos.

Claro que, a medida que la teoría fue topándose con unas matemáticas cada vez más difíciles y una proliferación de direcciones posibles, el progreso y la intensidad que rodeaban a las supercuerdas disminuyeron hasta un nivel más sensato, y ahora, sólo podemos seguir insistiendo y esperar para observar que nos puede traer el futuro de esta teoría que, es posible (y digo sólo posible) que se pueda beneficiar, de alguna manera, de las actividades del LHC que, en algunas de sus incursiones a ese mundo fantasmagórico de lo infinitesimal, podría -y digo podría- atisvar la sombra que puedan producir las supercuerdas.

No son pocos los físicos capaces que están empeñados en demostrar esa teoría. Por ejemplo, Físicos de SLAC desarrollan una prueba de marco de trabajo dependiente para la Teoría de Cuerdas Crítica. La Teoría de Cuerdas resuelve muchas de las cuestiones que arruinan la mente de los físicos, pero tiene un problema importante — no hay actualmente ningún método conocido para comprobarla y, si las energías requeridas para ello, es la de Planck  (10¹⁹ GeV), la cosa se pone fea.

                              ¿Cómo llegsar hasta la energía de Planck?

Lo cierto es que, de momento, sólo es un sueño y, la energía de Planck está muy lejos de nuestro alcance. Poder contar con la energía de Planck, por el momento y durante mucho, mucho, muchísimo tiempo, será sólo un sueño que algunos físicos tienen en la mente. Una regla universal en la física de partículas es que para partículas con energías cada vez mayores, los efectos de las colisiones están determinados por estructuras cada vez más pequeñas en el espacio y en el tiempo. El modelo estándar es una construcción matemática que predice sin ambigüedad cómo debe ser el mundo de las estructuras aún más pequeñas. Pero existen varias razones para sospechar que sus predicciones pueden, finalmente (cuando podamos emplear más energía en un nivel más alto), resultar equivocadas.

¡Un universo de Supercuerdas! El sueño de Einstein comienza a tomar realidad, a través de un nuevo paradigma de la ciencia que viene a romper con la toda la visión del mundo y del universo que teníamos hasta ahora, más allá de lo imaginable. Si la Teoría de cuerdas, finalmente resultase ser cierta, ese descubrimiento llevaría al mundo y a la humanidad hasta una nueva dimensión de su propia conciencia.

Habrá que tener paciencia con la Teoría de cuerdas y con el hallazgo tan esperado del Gravitón que nos confirmará, al fín, que la Gravedad como las demás interacciones, también está cuantizada y tiene su Bosón transmisor. De lo que no acabo de estar seguro es…del hecho en sí, de que podamos unir la Gravedad con la Cuántica…¡son tan dispares! y ¡habitan en reinos tan diferentes!

Aunque, ¿qué puedo saber yo?

emilio silvera

[?]

He dicho muchas veces que: “Adentrarse en el universo de las partículas que componen los elementos de la Tabla Periódica, y en definitiva, la materia conocida, es verdaderamente fantástico”. Esos pequeños objetos que no podemos ver, de dimensiones infinitesimales, son, en definitiva, los componentes de todo lo que contemplamos a nuestro alrededor: Las montañas, ríos, Bosques, océanos, los más exoticos animales y, hasta nosotros mismos, estamos hechos de Quarks y Leptones que, en nuestro caso, han podido evolucionar hasta llegar…¡A los pensamientos!

Estas dos familias de partículas conforman todo lo que podemos ver a nuestro alrededor, la materia del Universo y, si la “materia oscura” en realidad existe, no sabemos de qué pueda estar hecha y las clases de partículas que la puedan conformar. Habrá que esperar y, de momento, hablaremos de lo que conocemos.

[?]