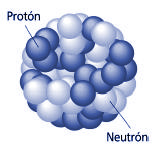
El núcleo desnudo

Si bien existe confusión e intriga acerca de su uso y factibilidad, la computación cuántica no es un sueño. De hecho, muchos expertos la ven como inevitable. En los computadores tradicionales, el procesamiento paralelo divide una tarea en partes y las delega a procesadores separados. La computación cuántica hace mas o menos lo mismo, solo que el procesamiento ocurre a nivel subatómico, donde rigen las leyes de la mecánica cuántica.

Mientras que un bit magnético tradicional puede representar solo un 1 o un 0, los bits cuánticos, o “qubits”, consistentes de atomos y partículas subatómicas ofrecen una gama de posibilidades exóticas. Un computador cuántico puede guardar datos en el espín de los electrónes, o en la posición de un cierto electrón. Un qubit, por ejemplo, puede ser 0, 1 y 0 y 1 al mismo tiempo, permitiendo la construcción de procesadores inmensamente más rápidos que los procesadores tradicionales.

En el centro del átomo se encuentra un pequeño grano compacto aproximadamente 100.000 veces más pequeño que el propio átomo: el núcleo atómico. Su masa, e incluso más aún su carga eléctrica, determinan las propiedades del átomo del cual forma parte. Debido a la solidez del núcleo parece que los átomos, que dan forma a nuestro mundo cotidiano, son intercambiables entre sí, e incluso cuando interaccionan entre ellos para formar sustancias químicas (los elementos). Pero el núcleo, a pesar de ser tan sólido, puede partirse. Si dos átomos chocan uno contra el otro con gran velocidad podría suceder que los núcleos llegaran a chocar entre sí y entonces, o bien se rompen en trozos, o se funden liberando en el proceso partículas subnucleares. La nueva física de la primera mitad del siglo XX estuvo dominada por los nuevos acertijos que estas partículas planteaban.

Pero tenemos la mecánica cuántica; ¿es que no es aplicable siempre?, ¿cuál es la dificultad? Desde luego, la mecánica cuántica es válida para las partículas subatómicas, pero hay más que eso. Las fuerzas con que estas partículas interaccionan y que mantienen el núcleo atómico unido son tan fuertes que las velocidades a las que tienen que moverse dentro y fuera del núcleo están cerca de la velocidad de la luz, c, que es de 299.792’458 Km/s. Cuando tratamos con velocidades tan altas se necesita una segunda modificación a las leyes de la física del siglo XIX; tenemos que contar con la teoría de la relatividad especial de Einstein.

Esta teoría también fue el resultado de una publicación de Einstein de 1905. en esta teoría quedaron sentadas las bases de que el movimiento y el reposo son conceptos relativos, no son absolutos, como tampoco habrá un sistema de referencia absoluto con respecto al cual uno pueda medir la velocidad de la luz.

Pero había más cosas que tenían que ser relativas. En este teoría, la masa y la energía también dependen de la velocidad, como lo hacen la intensidad del campo eléctrico y del magnético.

Einstein descubrió que la masa de una partícula es siempre proporcional a la energía que contienen, supuesto que se haya tenido en cuenta una gran cantidad de energía en reposo de una partícula cualquiera, como se denota a continuación:

E = mc²

[?]

Algunos se empeñan en que, las leyes de la física se simplifican en dimensiones más altas. Y, lo cierto es que, al no haberlas visto nunca -no están en nuestro plano de universo-, nos inventamos mil y una imagen pretendiendo que las representen pero, en realidad, no lo hace, Simplemente son figuras extrañas y espacios curvos de Riemann de enrevesado diseño que son…, otra cosa.

En una de las teorías de cuerdas, la conocida como la, se tiene que desarrollar en el espacio 26–dimensional de las vibraciones de sentido contrario a las agujas del reloj de la cuerda heterótica que tiene espacio suficiente para explicar todas las simetrías encontradas en la teoría de Einstein y en la teoría cuántica. Así, por primera vez, la geometría pura ha dado una simple explicación de por qué el mundo subatómico debería exhibir necesariamente ciertas simetrías que emergen del enrollamiento del espacio de más dimensiones: Las simetrías del dominio subatómico no son sino remanentes de la simetría del espacio de más dimensiones.

Las galaxias, las estrellas y los mundos… Y muchas más cosas, respetan patrónes simétricos que hacen de cada una de sus figuras, una misma estructuración que las hacen similares en un plano general, independientemente de que cada objeto tenga sus propias peculiaridades.

Esto significa que la belleza y simetrías encontradas en la naturaleza pueden ser rastreadas en última instancia hasta el espacio multidimensional.  Por ejemplo, los copos de nieve crean bellas figuras hexagonales, ninguna de las cuales es exactamente igual a otra, han heredado sus estructuras de las formas en que sus moléculas han sido dispuestas geométricamente, determinada básicamente por las cortezas electrónicas de estas moléculas, que a su vez nos llevan de nuevo a las simetrías rotacionales de la teoría cuántica, dadas por O (3).

Del bonito arcoiris ?quién no tiene la experiencia de contemplarlo?             También aquí hay una bella simetría

Podemos concluir diciendo que las simetrías que vemos a nuestro alrededor, desde un arco iris a las flores y a los cristales, pueden considerarse en última instancia como manifestaciones de fragmentos de la teoría decadimensional original. Riemann y Einstein habían confiado en llegar a una comprensión geométrica de por qué las fuerzas pueden determinar el movimiento y la naturaleza de la materia.

Dado el enorme poder de sus simetrías, no es sorprendente que la teoría de supercuerdas sea radicalmente diferente de cualquier otro tipo de física.  De hecho, fue descubierta casi por casualidad. Muchos físicos han comentado que si este accidente fortuito no hubiese ocurrido, entonces la teoría no se hubiese descubierto hasta bien entrado el siglo XXI. Esto es así porque supone una neta desviación de todas las ideas ensayadas en el pasado siglo XX. No es una extensión natural de tendencias y teorías populares en este siglo que ha pasado; permanece aparte.

       Las supercuerdas van más lejos que todo esto

Por el contrario, la teoría de la relatividad general de Einstein tuvo una evolución normal y lógica. En primer lugar, su autor, postula el principio de equivalencia. Luego reformuló este principio físico en las matemáticas de una teoría de campos de la gravitación basada en los campos de Faraday y en el tensor métrico de Riemann. Más tarde llegaron las “soluciones clásicas”, tales como el agujero negro y el Big Bang. Finalmente, la última etapa es el intento actual de formular una teoría cuántica de la gravedad. Por lo tanto, la relatividad general siguió una progresión lógica, desde un principio físico a una teoría cuántica.

Geometría → teoría de campos → teoría clásica → teoría cuántica.

Contrariamente, la teoría de supercuerdas ha estado evolucionando hacia atrás desde su descubrimiento accidental en 1.968. Esta es la razón de que nos parezca extraña y poco familiar, estamos aún buscando un principio físico subyacente, la contrapartida del principio de equivalencia de Einstein.

    Suponemos que las cuerdas están más allá de los Quarks

Uno de los secretos más profundos de la teoría de cuerdas, que aún no es bien comprendido, es por qué está definida solo en diez , once y veintiséis dimensiones. De todas las maneras, como nos dice Michiu Kaku, ese Físico que mira hacia el futuro, habría que tener presente las funciones modulares del Ramanujan para ver sí, dentro de ellas, están las respuestas de esas preguntas que, por ahora, nadie ha sabido contestar.

Gran parte de este trabajo es original del libro Hiperespacio de Michio Kaku, y, desde luego, como él nos anuncia, la Física tiene muchas de las respuestas que buscamos, sin embargo, también como nos dice la misma Física, algunas veces esas respuestas están situadas en la parte más simple de lo que estamos estudiando y, sin embargo, nos empeñamos en ahondar, de manera innecesaria hacia lo más profundo e incomprensible para buscar lo que tenemos delante de nuestras propias narices.

Si el límite de todas las teorías están marcados por las unidades de Planck, ya sabemos hasta dónde podemos llegar y, desde luego, la verificación de la Teoría de cuerdas, si como dicen los expertos necesita de la energía de Planck (10¹⁹ GeV) para ser verificada, entonces, nos queda mucho que esperar porque, ¿cuándo podrán tener los humanos esa energía a su disposición?

Existen límites a los que aún no han podido llegar nuestras teorías, y, el Límite de Planck es el que marca las fronteras de las teorías actuales que, nunca han podido llegar tan lejos como lo que nos dice esta simple ecuación:

            Gabriele Veneziano es un físico italiano          Mahiko Suzuki

La teoría nació casi por casualidad en 1.968 cuando dos jóvenes físicos teóricos, Gabriel Veneziano y Mahiko Suzuki, estaban hojeando independientemente libros de matemáticas. Figúrense ustedes que estaban buscando funciones matemáticas que describieran las interacciones de partículas fuertemente interactivas. Mientras estudiaban en el CERN, el Centro Europeo de Física Teórica en Ginebra, Suiza, tropezaron independientemente con la función beta de Euler, una función matemática desarrollada en el S. XIX por el matemático Leonhard Euler. Se quedaron sorprendidos al descubrir que la función beta de Euler ajustaba casi todas las propiedades requeridas para describir interacciones fuertes de partículas elementales.

Según he leído, durante un almuerzo en el Lawrence Berkeley Laboratory en California, con una espectacular vista del Sol brillando sobre el puerto de San Francisco, Suzuki le explicó a Michio Kaku mientras almorzaban la excitación de descubrir, prácticamente por casualidad, un resultado parcialmente importante. No se suponía que la física se pudiera hacer de ese modo casual.

Tras el descubrimiento, Suzuki, muy excitado, mostró el hallazgo a un físico veterano del CERN. Tras oír a Suzuki, el físico veterano no se impresionó. De hecho le dijo a Suzuki que otro físico joven (Veneziano) había descubierto la misma función unas semanas antes. Disuadió a Suzuki de publicar su resultado. Hoy, esta función beta se conoce con el nombre de modelo Veneziano, que ha inspirado miles de artículos de investigación iniciando una importante escuela de física y actualmente pretende unificar todas las leyes de la física.

En 1970, el Modelo de Veneziano-Suzuki (que contenía un misterio), fue parcialmente explicado cuando Yoichiro Nambu, de la Universidad de Chicago, y Tetsuo Goto, de la Nihon University, descubrieron que una cuerda vibrante yace detrás de sus maravillosas propiedades.

Así que, como la teoría de cuerdas fue descubierta hacia atrás y por casualidad, los físicos aún no conocen el principio físico que subyace en la teoría de cuerdas vibrantes y sus maravillosas propiedades.

El último paso en la evolución de la teoría de cuerdas (y el primer paso en la evolución de la relatividad general) aún está pendiente de que alguien sea capaz de darlo.

     Así, Witten dice:

“Los seres humanos en el planeta tierra nunca dispusieron del marco conceptual que les llevara a concebir la teoría de supercuerdas de manera intencionada, surgió por razones del azar, por un feliz accidente. Por sus propios méritos, los físicos del siglo XX no deberían haber tenido el privilegio de estudiar esta teoría muy avanzada a su tiempo y a su conocimiento. No tenían (ni tenemos ahora mismo) los conocimientos y los prerrequisitos necesarios para desarrollar dicha teoría, no tenemos los conceptos correctos y necesarios.”

Actualmente, Edwar Witten es el físico teórico que, al frente de un equipo de físicos de Princeton, lleva la bandera de la teoría de supercuerdas con aportaciones muy importantes en el desarrollo de la misma. De todas las maneras, aunque los resultados y avances son prometedores, el camino por andar es largo y la teoría de supercuerdas en su conjunto es un edificio con muchas puertas cerradas de las que no tenemos las llaves para acceder a su interior y mirar lo que allí nos aguarda.

Ni con esta colección podremos abrir la puerta que nos lleve a la Teoría cuántica de la gravedad que, según dicen, subyace en la teoría M

El problema está en que nadie es lo suficientemente inteligente para resolver la teoría de campos de cuerdas o cualquier otro enfoque no perturbativo de esta teoría. Se requieren técnicas que están actualmente más allá de nuestras capacidades. Para encontrar la solución deben ser empleadas técnicas no perturbativas, que son terriblemente difíciles. Puesto que el 99 por ciento de lo que conocemos sobre física de altas energías se basa en la teoría de perturbaciones, esto significa que estamos totalmente perdidos a la hora de encontrar la verdadera solución de la teoría.

Nosotros, como el gato, estamos ante un enredo que no sabemos como solucionar. Nos faltan los conocimientos para ello. Y, como nuestras mentes evolucionan al ritmo que tiene impuesto el Universo, tendremos esas respuestas cuando llegue el momento, cuando estémos preparados para ello. Sobre todo, el conocimiento necesario para manejar las implicaciones que de tales conocimientos se pueden derivar.

¿Por qué diez dimensiones?

Uno de los secretos más profundos de la teoría de cuerdas, que aún no es bien comprendido, es por qué está definida sólo en diez, once y veintiséis dimensiones. Si calculamos cómo se rompen y se vuelven a juntar las cuerdas en el espacio N-dimensional, constantemente descubrimos que pululan términos absurdos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos indeseados aparecen multiplicados por (N-10). Por consiguiente, para hacer que desaparezcan estas anomalías, no tenemos otra elección cuántica que fijar N = 10. La teoría de cuerdas, de hecho, es la única teoría cuántica conocida que exige completamente que la dimensión del espacio-tiempo esté fijada en un número único, el diez.

Por desgracia, los teóricos de cuerdas están, por el momento, completamente perdidos para explicar por qué se discriminan las diez dimensiones.  La respuesta está en las profundidades de las matemáticas, en un área denominada funciones modulares.

Al manipular los diagramas de lazos de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el número 10 aparecen en los lugares más extraños.

Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del este. Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro universo actual.

El misterio de las funciones modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y como Riemann antes que él, trabajó en total aislamiento en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.

En los cuardenos perdidos de Ramanujan podrían estar las respuestas. Dispersas entre oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre las más extrañas jamás encontradas en matemáticas. Ellas reaparecen en las ramas más distantes e inconexas de las matemáticas. Una función que aparece una y otra vez en la teoría de las funciones modulares se denomina (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. Esta extraña función contiene un término elevado a la potencia veinticuatro.

El número 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente donde menos se esperan por razones que nadie entiende.   Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas.  En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio-tiempo debe tener 24 + 2 = 26 dimensiones espacio-temporales.

               Reflejos de luz polarizada sobre una superficie de un disco

Para comprender este misterioso factor de dos (que añaden los físicos), consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada puede vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista A_µ tiene cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell.  Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones.  Sin embargo, dos de estos modos vibracionales pueden ser eliminados cuando rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.

Es posible que, en las matemáticas de Ramanujan estén algunas respuestas

Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el número 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio-tiempo sea diez.

En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “no lo sé”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una forma cuánticamente autoconsistente), pero no sabemos por qué se seleccionan estos números concretos.

¡Son tantas las cosas que no sabemos!

Publica: emilio silvera

PD. Le damos las gracias a Michio Kaku por sus ideas y su manera futurista de ver la Física.

[?]

LA MARAVILLA DE LOS CUANTOS

Aunque la semilla la puso Planck en 1900, fue a partir de 1930 cuando la mecánica cuántica se aplicó con mucho éxito a problemas relacionados con núcleos atómicos, moléculas y materia en estado sólido. La mecánica cuántica hizo posible comprender un extenso conjunto de datos, de otra manera enigmáticos. Sus predicciones han sido de una exactitud notable. Ejemplo de ésto último es la increíble precisión de diesciciete cifras significativas del momento magnético del electrón calculadas por la EDC (Electrodinámica Cuántica) comparadas con el experimento.

Si viajamos hacia lo muy pequeño tendremos que ir más allá de los átomos, que son objetos voluminosos y frágiles comparados con lo que nos ocupará a continuación: el núcleo atómico y lo que allí se encuentra. Los electrones, que ahora vemos “a gran distancia” dando vueltas alrededor del núcleo, son muy pequeños y extremadamente robustos. El núcleo está constituido por dos especies de bloques: protones y neutrones. El protón (del griego πρώτος, primero) debe su nombre al hecho de que el núcleo atómico más sencillo, que es el hidrógeno, está formado por un solo protón. Tiene una unidad de carga positiva. El neutrón recuerda al protón como si fuera su hermano gemelo: su masa es prácticamente la misma, su espín es el mismo, pero en el neutrón, como su propio nombre da a entender, no hay carga eléctrica; es neutro.

La masa de estas partículas se expresa en una unidad llamada mega-electrón-voltio o MeV, para abreviar. Un MeV, que equivale a 10⁶ electrón-voltios, es la cantidad de energía de movimiento que adquiere una partícula con una unidad de carga (tal como un electrón o un protón) cuando atraviesa una diferencia de potencial de 10⁶ (1.000.000) voltios. Como esta energía se transforma en masa, el MeV es una unidad útil de masa para las partículas elementales.

La mayoría de los núcleos atómicos contienen más neutrones que protones. Los protones se encuentran tan juntos en el interior de un núcleo tan pequeño que se deberían repeles entre sí fuertemente, debido a que tienen cargas eléctricas del mismo signo. Sin embargo, hay una fuerza que los mantiene unidos estrechamente y que es mucho más potente e intensa que la fuerza electromagnética: la fuerza o interacción nuclear fuerte, unas 10² veces mayor que la electromagnética, y aparece sólo entre hadrones para mantener a los nucleones confinados dentro del núcleo. Actúa a una distancia tan corta como 10^–15 metros, o lo que es lo mismo, 0’000000000000001 metros.

La interacción fuerte está mediada por el intercambio de mesones virtuales, 8 gluones que, como su mismo nombre indica (glue en inglés es pegamento), mantiene a los protones y neutrones bien sujetos en el núcleo, y cuanto más se tratan de separar, más aumenta la fuerza que los retiene, que crece con la distancia, al contrario que ocurre con las otras fuerzas.

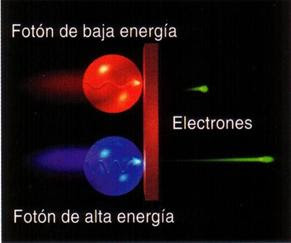
La luz es una manifestación del fenómeno electromagnético y está cuantizada en “fotones”, que se comportan generalmente como los mensajeros de todas las interacciones electromagnéticas. Así mismo, como hemos dejado reseñado en el párrafo anterior, la interacción fuerte también tiene sus cuantos (los gluones). El físico japonés Hideki Yukawa (1907 – 1981) predijo la propiedad de las partículas cuánticas asociadas a la interacción fuerte, que más tarde se llamarían piones. Hay una diferencia muy importante entre los piones y los fotones: un pión es un trozo de materia con una cierta cantidad de “masa”. Si esta partícula está en reposo, su masa es siempre la misma, aproximadamente 140 MeV, y si se mueve muy rápidamente, su masa parece aumentar en función E = mc². Por el contrario, se dice que la masa del fotón en reposo es nula. Con esto no decimos que el fotón tenga masa nula, sino que el fotón no puede estar en reposo. Como todas las partículas de masa nula, el fotón se mueve exclusivamente con la velocidad de la luz, 299.792’458 Km/s, una velocidad que el pión nunca puede alcanzar porque requeriría una cantidad infinita de energía cinética. Para el fotón, toda su masa se debe a su energía cinética.

La Física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menos intensidad, por los objetos más fríos.

Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía.

Pero si usamos las leyes de la termodinámica para calcular la intensidad de la radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano, y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico o una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para longitudes menores. Esta longitud característica es inversamente proporcional a la temperatura absoluta del objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273 ºC bajo cero). Cuando a 1.000 ºC un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de la luz visible.

Poco a poco vamos avanzando y llegará el momento en el que, los más profundos secretos de la Naturaleza hayan sido desvelados

Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda y, por lo tanto, proporcional a la frecuencia de la radiación emitida. La fórmula es:

E = h x v

Donde E es la energía del paquete, v es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.

Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: el sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck.

El príncipe francés Louis Victor de Broglie, dándole otra vuelta a la teoría, que no sólo cualquier cosa que oscila tiene una energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta dirección del espacio, y que la frecuencia, v, de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilatorias de campos de fuerza.

Es curioso el comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de De Broglie. Poco después, en 1926, Edwin Schrödinger descubrió como escribir la teoría ondulatoria de De Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar los cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de onda cuántica”.

No hay duda de que la Mecánica Cuántica funciona maravillosamente bien. Sin embargo, surge una pregunta muy formal: ¿qué significan realmente esas ecuaciones?, ¿qué es lo que están describiendo? Cuando Isaac Newton, allá por el año 1687, formuló cómo debían moverse los planetas alrededor del Sol, estaba claro para todo el mundo lo que significaban sus ecuaciones: que los planetas están siempre en una posición bien definida en el espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades con el tiempo.

Pero para los electrones todo esto es muy diferente. Su comportamiento parece estar envuelto en la bruma. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?

Niels Bohr consiguió responder a esta pregunta de forma tal que con su explicación se pudo seguir trabajando y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la “interpretación de Copenhague” de la Mecánica Cuántica. En vez de decir que el electrón se encuentra en el punto x o en el punto y, nosotros hablamos del estado del electrón. Ahora no tenemos el estado “x” o el estado “y”, sino estados “parcialmente x” o “parcialmente y. Un único electrón puede encontrarse, por lo tanto, en varios lugares simultáneamente. Precisamente lo que nos dice la Mecánica Cuántica es como cambia el estado del electrón según transcurre el tiempo.

           El detector ATLAS funcionó, y rastrearon las partículas subatómicas…

Un “detector” es un aparato con el cual se puede determinar si una partícula está o no presente en algún lugar pero, si una partícula se encuentra con el detector su estado se verá perturbado, de manera que sólo podemos utilizarlo si no queremos estudiar la evolución posterior del estado de la partícula. Si conocemos cuál es el estado, podemos calcular la probabilidad de que el detector registre la partícula en el punto x.

Las leyes de la Mecánica Cuántica se han formulado con mucha precisión. Sabemos exactamente como calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas simultáneamente. Por ejemplo, podemos determinar la velocidad de una partícula con mucha exactitud, pero entonces no sabremos exactamente dónde se encuentra; o, a la inversa. Si una partícula tiene “espín” (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.

                      Explorar el misterio del espín de los protones ha sido uno de los objetivos clave de la investigación científica en el RHIC

No es fácil explicar con sencillez de dónde viene esta incertidumbre, pero hay ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar.

Para que las reglas de la Mecánica Cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuanto más grande y más pesado es un objeto más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica.

Me gustaría referirme a esta exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por “holismo”, y que se podría definir como “el todo es más que la suma de las partes”.

Bien, si la Física nos ha enseñado algo, es justamente lo contrario: un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (las partículas): basta que uno sepa sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que yo entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes.

Por ejemplo, la constante de Planck, h = 6,626075…x 10 exp. -34 julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.

Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisenberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros tales como Edwin Schrödinger, siempre presentaron serias objeciones a esta interpretación.

                  ¡Y pensar que todo esto está formado por pequeñas partículas infinitesimales!

Quizá funcione bien, pero ¿dónde está exactamente el electrón, en el punto x o en el punto y? Em pocas palabras, ¿dónde está en realidad?, ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.

Hasta hoy, muchos investigadores coinciden con la actitud pragmática de Bohr. Los libros de historia dicen que Bohr demostró que Einstein estaba equivocado. Pero no son pocos,  incluyéndome a mí, los que sospechamos que a largo plazo el punto de vista de Einstein volverá: que falta algo en la interpretación de Copenhague. Las objeciones originales de Einstein pueden superarse, pero aún surgen problemas cuando uno trata de formular la mecánica cuántica para todo el Universo (donde las medidas no se pueden repetir) y cuando se trata de reconciliar las leyes de la mecánica cuántica con las de la Gravitación.

La mecánica cuántica y sus secretos han dado lugar a grandes controversias, y la cantidad de disparates que ha sugerido es tan grande que los físicos serios ni siquiera sabrían por donde empezar a refutarlos. Algunos dicen que “la vida sobre la Tierra comenzó con un salto cuántico”, que el “libre albedrío” y la “conciencia” se deben a la mecánica cuántica: incluso fenómenos paranormales han sido descritos como efectos mecanocuánticos.

Yo sospecho que todo esto es un intento de atribuir fenómenos “ininteligibles” a causas también “ininteligibles” (como la mecánica cuántica) dónde el resultado de cualquier cálculo es siempre una probabilidad, nunca una certeza.

Claro que, ahí están esas teorías más avanzadas y modernas que vienen abriendo los nuevos caminos de la Física y que, a mi no me cabe la menor duda, más tarde o más temprano, podrá explicar con claridad esas zonas de oscuridad que ahora tienen algunas teorías y que Einstein señalaba con acierto.

¿No es curioso que, cuando se formula la moderna Teoría M, surjan, como por encanto, las ecuaciones de Einstein de la Relatividad General? ¿Por qué están ahí? ¿Quiere eso decir que la Teoría de Einstein y la Mecánica Cuántica podrán al fin unirse en pacifico matrimonio sin que aparezcan los dichosos infinitos?

Bueno, eso será el origen de otro comentario que también, cualquier día de estos, dejaré aquí para todos ustedes.

emilio silvera

[?]

Sí, a veces la Física, es un Carnaval.

Las teorías de cuerdas [TC’s] no son una invención nueva, ni mucho menos. La primera TC se inventó a finales de los años sesenta del siglo XX en un intento para encontrar una teoría para describir la interacción fuerte. La idea medular consistía en que partículas como el protón y el neutrón podían ser consideradas como ondas de «notas de una cuerda de violín». La interacción fuerte entre las partículas correspondería a fragmentos de cuerda que se extenderían entre pequeños pedacitos de cuerda, como las telas que forman algunos simpáticos insectos. Para que esta teoría proporcionase el valor observado para la interacción fuerte entre partículas, las cuerdas tendrían que ser semejantes a las de un violín, pero con una tensión de alrededor de unas diez toneladas.

La primera expresión de las TC’s fue desarrollada por Jöel Scherk, de París, y John Schwuarz, del Instituto de Tecnología de California, quienes en el año 1974 publicaron un artículo en el que demostraban que la TC podía describir la fuerza gravitatoria, pero sólo si la tensión en la cuerda se tensiometrara alrededor de un trillón de toneladas métricas. Las predicciones de la teoría de cuerdas serían las mismas que las de la relatividad general a escala de longitudes normales, pero diferirían a distancias muy pequeñas, menores que una trillonésima de un cm. Claro está, que en esos años, no recibieron mucha atención por su trabajo.

[?]

Los físicos de más edad dejan volar a menudo sus pensamientos hacia aquellos tiempos gloriosos en los que, durante mucho tiempo, ha sido la era de los grandes descubrimientos de la primera mitad del siglo XX: La mecánica cuántica, la relatividad especial y general, la electrodinámica cuántica y los descubrimientos de las primeras partículas elementales.

El Zoo de las partículas llegó a ser tan exótico y numeroso que, Entico Fermi dejó caer aquella famosa frase: “Si tengo que saber de memoria el nombre de todas las partículas que existen,  hubiera sido  botánico”.

Fermi (abajo a la izquierda), Szilárd (segundo desde la derecha abajo), y el resto del equipo de la pila atómica

Claro que, días gloriosos también lo fueron en la década de los 70 cuando fueron colocadas en su sitio muchas piezas del gran puzzle de las interacciones débil, electromagnética y fuerte. El descubrimiento en 1974 de la J/Ψ fue el clímax. Antes de que este se produjera, aún quedaba alguna duda de que la teoría de la interacción débil fuera correcta y se consideraba la teoría de la intertacción fuerte simplemente como una idealización de algo que podría muy bien ser más complicado e insondable.

Pero, pasado algún tiempo, los experimentos llevaron a la convicción de que ambas teorías eran correctas, incluso en sus detalles. Según continuaban los experimentos las sorpresas iban en aumento a medida que surgían detalles más precisos de lo que muchos de aquellos físicos habrían esperado. Una cosa estaba muy clara: vivíamos en un mundo que obedecía meticulosamente a las leyes de las matemáticas, y las matemáticas son difíciles, pero se pueden llegar a entender completamente para poder llegar a esos misteriosos secretos que la Naturaleza trata de esconder y nosotros, de desvelar.

Antes os mencionaba la J/Ψ.  Cuando una partícula J/Ψ se desintegra (o decae), por lo general produce un par de muones. Observa atentamente los dos eventos mostrados a continuación. ¿Hay pruebas de pares de muones (trayectorias en rojo) en uno de estos eventos o en ambos? ¿Podría ser cualquiera de estos eventos un candidato para J/Ψ? ¿Es esta evidencia débil o fuerte? ¿Está seguro de tus conclusiones?

Un evento debe pasar dos pruebas antes de que pueda ser considerado como un candidato para J/Ψ. Usarás un sistema de evaluación para hacer un seguimiento de que tan confidentes eres en tu conclusión. Tú—y tu compañero estudiarán 100 eventos. Corresponderá a los estudiantes, en colaboración con los mentores y con los maestros, determinar el peso que asignaran a cada uno de los criterios y evaluaciones usadas. Vas a escribir tus evaluaciones en una hoja de datos.

Para ser una posible candidato a J/Ψ, el evento debe contener dos trayectorias de muones de cargas eléctricas opuestas.

Seguir hasta el final el proceso sería tedioso y, con este esbozo, sólo he querido significar que, llegar a conclusiopnes finales nunca ha sido fácil y se han necesitado de muchos experimentos, desechar todo aquello que no implican sucesos importantes paras lo que se busca, y un sin fin de cuestiones que hay que tener en cuenta antes de dar por bueno éste o aquel experimento de cuyos resultados veremos, finalmente, si coincide con la teoría.

Mucho tendríamos que aprender sobre los mecanimso misteriosos que rigen ese objeto que arriba vemos para poder entender que hayamos podido llegar a saber sobre el mundo físico de la materia y las fuerzas que lo rigen. Es una maravilla que tardaremos mucho tiempo en poder explicar.

Claro que, durante cualquiera de estos procesos, por el camino, nos encontramos con maravillas que nos invitan a la reflexión. ¿Cómo puede ser el cerebro humano capaz de entender totalmente el extraño mundo de las partículas subatómicas más exóticas y con tanto detalle? ¿Es que nuestro cerebro ha evolucionado al margen y más rápidamente que lo que tendría que haber sido conforme a la evolcuioón natural? Si lo pensamos bien, hasta ayaer mismo estábamos atareados con arcos y flechas y, hoy, tratamos de desentrañar los más recóndidos misterios de la Naturaleza de la materia queriendo desvelar sus componentes y como se comportan y por qué lo hace de esa manera.

La partícula J/Ψ se desintegra cuando dos quarks se aniquilan entre sí produciendo tres gluones, Estos gluones a su vez, se desintegran en piones, kaones o lo que sea, pero es la primera interacción, que se produce muy lentamente, la que determina la duración de su vida total. Sustituyendo los números, se encontró que se ajustaban razonablemente a las observaciones y no se tardó mucho en lograr que esta explicación fuera aceptada por la comunidad científica.

Ahora que las propiedades del quark c se podía determinar con muchio más detalle, los experimentadores sabían exactamente donde podían buscar más. Calculándo las masas de estas partículas paracía razonable deducir que la Ψ´´,  más pesada, podría desintegrarse directamente en mesones con encanto. esta desintegración se produce mucho más rápidamente que la desimtegración de J/Ψ, porque no requiere que se aniquilen antes entre sí un quark y un antiquark con encanto.  Esta es la razón por la que Ψ´´,es menor estable, pero es también la razón por la que el sitio ideal para buscar mesones con encanto sea entre los productos entre los que se descompone, donde, emn efecto, pronto se descubrierom.

En realidad, la partícula J/Ψ fue una pieza que vino a univer varias partes sueltas de nuestro gran puzzle. Por una parte teníamos el perdido quark encanto, necesario para completar la teoría de la interacción débil a través del mecanismo GIM; por otra parte, la cromodinñamica cuántica, con su libertad asintótica, se comportaba tan de acuerdo con las leyes teóruicas, que a muchos les cogió por sorpresa. Al parecer la cromodinámica cuántica no era únicamente un miodelo amplificado: los detalles que hasta aquel momento sólo unos pocos habían tomado en serio, se ajustaban perfectamente a todas las observaciones.

La QCD   es una parte  integral del modelo atómico estándar. El nombre cromodinámica viene del hecho de que las partículas que interactúan a través de la fuerza fuerte tienen una propiedad denominada color, que puede ser dicha como un análogo de carga eléctrica.

Es universalmente aceptada como la teoría fundamental de las interacciones fuertes. La estructura de esa teoría guarda relación con la electrodinámica cuántica (QED). Las interacciones electromagnéticas no diferencian partículas que tengan la misma carga eléctrica. Así, un electrón es un antiprotón –ambos negativos – parecerían ser la misma partícula desde el punto de vista de un fotón, si no fuese por su diferencia de masa entre ambas partículas.

Veltman que era un excéptico empedernido, si se tiene una teoría,  decía, se debería predecir algo y no sólo decir retrospectivamente que todo encaja perfectamente.  Lo cierto era que, para las partículas descubiertas por aquel entonces, se tenía un esquema bastante detallado de las interacciones débil, electromagnética y fuerte. Había una sola cosa que no estaba del todo bien en el esquema: Que por término medio , tres de cada mil mesones K_L se desintegraban en piones, violando así, la conservación de la simetría PC. ¿Qué fuerza sería la responsable de ese fenómeno?

El modelo estándar es una jungla de constantes por determinar: las masas de las partículas, las cargas eléctricas y otros valores. Sin embargo, gracias al modelo estándar podemos conocer casi todas las reacciones que tienen lugar en los aceleradores de partículas. Es adoptar un punto de vista pragmático y conseguir avanzar mientras la física teórica trabaja para encontrar las razones profundas. Por eso es muy habitual en este mundo encontrarse con la constante búsqueda de simetrías y leyes de conservación, porque sencillamente, simplifican mucho las cosas.

En este caso tratamos con una simetría llamada simetría de carga-paridad. Viene a decir que si tenemos una cierta interacción física, si cogemos las ecuaciones que la describen, cambiamos de signo las cargas eléctricas (+q por -q) y cambiamos izquierda por derecha y viceversa (+x por -x, o lo que es lo mismo, ver nuestro sistema en un espejo) nos encontramos con el mismo escenario físico. Vale, las partículas han cambiado y tal, pero la física que ocurrirá ahí es la misma. Dicho así parece muy ad hoc, pero esta simetría la cumplen tanto la interacción fuerte, como la electromagnética como la gravedad (en este caso, la masa no tiene signo y la gravedad no distingue izquierda de derecha, por lo que trivialmente se cumple siempre).

Se propuso la simetría CP al descubrirse en los años 50 que la paridad no era una simetría fundamental. Pero cuando se testeó esta simetría en una interacción débil, la cosa se vino abajo. El primer experimento fue en un núcleo de Cobalto 60 en el año 1956 donde se vió que la interacción débil rompe la simetría de paridad. Esto quiere decir que las reacciones que ocurren con cierta frecuencia en un lado del espejo, no ocurren con tanta frecuencia en el otro.

Por este motivo, se supuso que habría una simetría más general y en 1957 Lev Landau propuso la simetría CP, para hacer que los dos lados del espejo volvieran a ser equivalentes.

El Premio Nobel de Física de 2008 para Makoto Kobayashi y Toshihide Maskawa por el descubrimiento de la conexión entre violación de la simetría CP y la masa en reposo de los quarks más ligeros nos dejó cierto mal sabor de boca. ¿Por qué la asimetría CP es más pequeña de lo necesario? Aparentemente el Modelo Estándar no nos daba la respuesta, aunque ahora Gary Gibbons y sus colaboradores de la Universidad de Cambridge han logrado obtener la respuesta. Es tan pequeña porque las masas de los quarks son pequeñas. ¿Por qué las masas de los quarks más ligeros son tan pequeñas? Nadie lo sabe. Unos misterios se aclaran, otros siguen esperando respuesta.

Pero volvamos a lo que estábamos tratando. La alegría no duró mucho, pues en los años 60 se demostró que era posible romper la simetría CP y esto llevó a ganar el premio Nobel en los años 80 (ya que la teoría suele anteceder a la experimentación).

La violación directa de la simetría CP se observó en una partícula descubierta a finales de los 40 y que trajo al mundo además el descubrimiento de un nuevo tipo de quarks: el extraño (s). Esta partícula (o más bien, familia de partículas) es el kaón. El kaón es un mesón (es decir, una partícula constituida por un quark y un antiquark) formado a partir del quark “up” o el quark “down” y el quark “antiestraño”. Existen de hecho 3 kaones, con carga neutra (down, antistrange + strange, antidown), carga positiva (up, antistrange) y carga negativa (strange, antiup).

El problema es que hace falta una nueva simetría: La Simetría COP en la que se añade un nuevo protagonista: el tiempo. Según esta simetría, además de invertir espacialmente y cambiar la carga por su opuesta, se ve el sistema pulsando el botón de rebobinar. Un espejo de lo más curioso, pero lo cierto es que la simetría CPT tiene todas las papeletas para ser la simetría fundamental, ya que es cumplida por todas las interacciones, que sepamos.

Más aún desde que en 2002 se demostrase (“Data Tables for Lorenztz and CPT Ciolatión”),  Ene 2010, arXiv;) que violar la simetría CPT implica cargarse la invariancia (o covariancia) de Lorentz,  Esta invariancia es uno de los pilares que deben cumplir todas las teorías que pretendan tener sentido físico, aunque luego pueda haber casos de ruptura espontánea de la simetría. Pero la teoría viola Lorentz de entrada, no puede ser válida. Esto es un puntal muy fuerte para la teoría CPT.

Hubo que esperar 40 años, hasta los años 80, en que se relacionara directamente a los kaones con la simetría CP y el problema de la bariogénesis en el universo. Es decir, ¿por qué si hay simetrías por todas partes, el universo está constituido de materia y no de materia y antimateria por partes iguales? ¿Por qué el universo no es una aburrida sopa de fotones?

Claro, si en el inicio del universo se hubiera encontrado la misma cantidad de materia que de antimateria, todo se habría aniquilado haciendo que el universo fuera un gas de fotones de lo más aburrido. Nada de lo que existe, existiría. Pero como de hecho existe, hay que encontrarle explicación. Y en eso consiste el problema de la bariogénesis asimétrica.

Como sea que ocurriera, aunque de hecho hubiera mucha materia y antimateria que se aniquilara, al final la materia venció esta batalla épica que se libró durante la época de Planck.

Pero resulta que no es posible modificar nuestro modelo invocando otro campo de Yang . Mills, Las partículas de espín 1 siempre preservan la simetría PC (¿Podría ser esta la razón por la que la que la simetría PC es tan tenue?.

Se han detectado nuevas partículas que nacen dentro de las enanas blancas de Helio

Podríamos imaginar el efercto que tendría otra partícula de espìn cero, preferiblemente que también sufriera algún tipo de condensación Bose, el resultado sería lo que llamamos la “violación espontánea de PC”. Sin embargo, los modelos resultantes que se obtienen así no son muy populares. Deseamos evitar partículas de espín cero tanto como sea posible, porque añaden muchos parámetros arbitrarios a la interacción. Los modelkos con tales partículas parecen muy artificiales. En si mismo, un argumento de este tipo no es, desde luego, suficiente para escluir una posibilidad, pero ducede que existen alternativas más interesantes.

 Gloshosow            Iliopoulos         Maiani

Recordaréis que Glashow, Iliopoulos y Maiani habían introducido el quarks encanto para entender la estructura simétrica de la interacción débil. Bien, lo que se propuso fue hacerlo de nuevo. Esta vez necesitamos introducir dos quarks más. Los cuatro primeros habían formado pares ( u y d, c y s), con cargas eléctricas + 2/3 y – 1/3. El nuevo par se tenía que parecer a este, pero los nuevos quark podrían fácilmente ser mucho más pesados. Siendo quarks análogos a los “arriba” y “abajo” se llamaron “cima” (t) y “fondo” (b), respectivamente. Pero a veces las mismas letras se utilizan pa<ra darles nombres más poéticos: “verdad” y “belleza”.

Era inevitablemente necesaria una partícula de espín cero para que la interacción débil tuviera las simetrías que tiene a través del mecanismo de Higgs-Kibble. Esta partícula de Higgs se acopla ahora con los quarks y a los leptones para dotarlos de masa. Pero la misma partícula de Higgs también puede producir transiciones entre varios tipos de quarks. Si no existiera interacción débil en absoluto, los qu quarks podrían permanecer en todas clases de estados estables. Es pues, una conspiración entre la interacción débil  y la interacción de Higgs lo que permite muchos tipos de desintegración de los hadrones extraños y con encanto.

Cuanto mayor sea el número de fermiones introducido, más tipos de interacción  puede experimentar el campo de Higgs con esos quarks. Los físicos japoneses Kobayashi y Maskawa escribieron la expresión matemática más general que se puede obtener para las fuerzas. Resultó que uno de los términos de sus ecuaciones no tienen simetría PC, y que ese término sólo aparece si hay, al menos, seis tipos de quarks. Esto hizo que comezaran a buscarse partículas que contuvieran otras especies de quarks.

Podríamos seguir por este camino que hoy he tomado (no muy convencido), sin ver nunca el final de donde podríamos acabar. Hay cuestiones de la Física que me resultan farragosas, espesas, poco diáfanas y que, por mucho que me empeñe, no puedo explicar de manera amena y sencilla que la gente, el posible lector, se involucre en el tema.

Ahora, parece que están anunciando en el LHC que, sobre los primeros días de Julio, se hará el anuncio tan esperado sobre el Bosón de Higgs y, ya veremos en que termina todo esto. La verdad es que, no tengo nada claro muchos de los conceptos que los físicos manejan en la mecánica cuántica y que, no en pocas ocasiones, me dan la sensación de ser, “trucos” ingeniosos que, apoyados por las matemáticas, nos quieren convencer de que el “mundo” es así.

¡Ya veremos en qué queda todo esto!

emilio silvera

[?]