Los ordenadores cuánticos serán «los más seguros» del mercado

marta moreiraabc_es / Valencia

El premio Príncipe de Asturias, Ignacio Cirac, cree que podrán comercializarse en un plazo entre 10 y 50 años

 

 

ROBER SOLSONA

El Premio Príncipe de Asturias, Ignacio Cirac, afirma, sin embargo, que los avances en esta materia están «a un nivel muy fundamental»

Las investigaciones teóricas sobre física cuántica van por buen camino, pero todavía están muy lejos de traducirse en aplicaciones prácticas en el campo de la informática. La comunidad científica ha depositado grandes esperanzas en los ordenadores cuánticos, que permitirán realizar cálculos que no pueden resolverse con los ordenadores actuales –los que trabajan según las leyes clásicas de los ceros y unos-. Sin embargo, su comercialización podría tardar entre diez y cincuenta años. «Estoy convencido de que va a suceder, lo que no sé es si voy a vivir para verlo», añade Ignacio Cirac, director de la División Teórica Max-Plank de Óptica Cuántica de Garching (Alemania).

Así lo defendió en el marco de la 34 Bienal de la Real Sociedad de Física Española, que se celebra estos días en Valencia. Renuente a lanzar promesas cortoplacistas de difícil cumplimiento, este científico recordó que los avances en esta matería están todavía «a un nivel muy fundamental».

Uno de los aspectos más interesantes de los sistemas de compuitación basados en mecánica cuántica es la seguridad. «La física cuántica permite codificar la información de manera que se destruya en el momento en que cualquier persona no autorizada quiera leer el mensaje», explica. La diferencia con respecto a los sistemas actuales es que la información no puede interceptarse porque no pasa por ningún lugar. «Desaparece una vez lo envía el emisor y aparece de nuevo en el aparato del receptor, como por arte de magia». Se abre por tanto un nuevo reto para los «hackers».

[?]

Comentando, sobre Ramanuján y su cuaderno perdido, recordé lo que dijo el matemático Richard Askey:

“El trabajo de este año, mientras se estaba muriendo, era el equivalente a una vida entera de un matemático muy grande”.  Lo que él consiguió era increíble.  Los matemáticos Jonathan Borwien y Meter Borwein, en relación a la dificultad y la ardua tarea de descifrar los cuadernos perdidos, dijeron: “Que nosotros sepamos nunca se ha intentado una redacción matemática de este alcance o dificultad”.

Por mi parte creo que, Ramanujan, fue un genio matemático muy adelantado a su tiempo y que pasaran algunos años hasta que podamos descifrar al cien por ciento sus trabajos, especialmente, sus funciones modulares que guardan el secreto de la teoría más avanzada de la física moderna,   la única capaz de unir la mecánica quántica y la Gravedad.

Las matemáticas de Ramanujan son como una sinfonía, la progresión de sus ecuaciones era algo nunca visto, él trabajaba desde otro nivel, los números se combinaban y fluían de su cabeza a velocidad de vértigo y con precisión nunca antes conseguida por nadie.   Tenía tal intuición de las cosas que éstas simplemente fluían de su cerebro.   Quizá no los veía de una manera que sea traducible y el único lenguaje eran los números.

Como saben los físicos, los ” accidentes” no aparecen sin ninguna razón.  Cuando están realizando un cálculo largo y difícil, y entonces resulta de repente que miles de términos indeseados suman milagrosamente cero, los físicos saben que esto no sucede sin una razón más profunda subyacente.  Hoy, los físicos conocen que estos “accidentes” son una indicación de que hay una simetría en juego.  Para las cuerdas, la simetría se denomina simetría conforme, la simetría de estirar y deformar la hoja del Universo de la cuerda.

Aquí es precisamente donde entra el trabajo de Ramanujan.  Para proteger la simetría conforme original contra su destrucción por la teoría cuántica, deben ser milagrosamente satisfechas cierto número de identidades matemáticas que, son precisamente las identidades de la función modular de Ramanujan.  ¡Increíble!   Pero, cierto.

En resumen, he dicho que las leyes de la naturaleza se simplifican cuando se expresan en dimensiones más altas.   Sin embargo, a la luz de la teoría cuántica, debemos corregir algo Este sentido básico de mirar la cuestión.   El enunciado correcto sería ahora:   las leyes de la naturaleza se simplifican cuando se expresan  COHERENTEMENTE en dimensiones más altas.  El añadido de la palabra coherente es crucial.   Esta ligadura nos obliga a utilizar las funciones modulares de Ramanujan, que fijan en diez la dimensión del espacio – tiempo.   Esto, a su vez, puede darnos la clave decisiva para explicar el origen del Universo.

Einstein se preguntaba a menudo si Dios tuvo alguna elección al crear el universo.   Según los teóricos de supercuerdas, una vez que exigimos una unificación de la teoría cuántica y la relatividad general, Dios no tenía elección.  La auto consistencia por sí sola, afirman ellos, debe haber obligado a Dios a crear el universo como lo hizo.

Existen teorías muy bonita pero ¿existen algunas evidencias? En realidad la respuesta la hallamos en el contexto de la teoría de cuerdas. Que sabemos que no se puede comprobar experimentalmente por el momento. En concreto, la respuesta es la correspondencia AdS/CFT de la que hablé  aquí. Por recordarlo brevemente, esta es una herramienta matemática desarrollada enteramente en la teoría de cuerdas afirma que un espacio anti-de Sitter de cinco dimensiones tiene una frontera de 4 que en cierto límite se parece al espaciotiempo plano con 1 dimensión temporal y 3 espaciales. Esta reducción de una dimensión nos lleva a relacionar inmediatamente la correspondencia AdS/CFT con el principio holográfico y de hecho, la correspondencia es da tratamiento matemático riguroso al principio holográfico.

Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan como su punto más débil.  Cualquier teoría, afirman, debe ser verificable.   Puesto que ninguna teoría definida a la energía de Planck de 10¹⁹ miles de millones de eV es verificable, ¡La teoría de supercuerdas no es realmente una teoría! Y, de momento, parece que la debemos colocar en la estantería de las hipótesis o en la de los Hermosos Sueños.

El principal problema, es teórico más que experimental.  Si fuéramos suficientemente inteligentes, podríamos resolver exactamente la teoría y encontrar la verdadera solución no perturbativa de la teoría. Así lo cree un amigo mío llamado Armando que nos viene a decir que, lo de las altas energías de Planck para verificar la teoría de cuerdas, es una excusa ordenada por la ignorancia. Sin embargo, esto no nos excusa de encontrar algún medio por el que verificar experimentalmente la teoría, debemos esperar señales de la décima dimensión.

¿La décima dimensión? Pero, ¿No eran once?

¡Qué extraño sería que la teoría final se descubriera durante nuestra vida! El descubrimiento de las leyes finales de la Naturaleza marcará una discontinuidad en la Historia del intelecto humano, la más abrupta que haya ocurrido desde el comienzo de la ciencia moderna en el siglo XVII. ¿Podemos imaginar ahora como sería?

Steven Weinberg

 

Pienso en lo que sería una cuerda, esos filamentos que están más allá de los quarks y no me puedo abstraer de pensar en el electrón y el positrón que son notables por sus pequeñas masas (sólo 1/1.836 de la del protón, el neutrón, el antiprotón o antineutrón), y, por lo tanto, han sido denominados leptones (de la voz griega lentos, que significa “delgado”).

Aunque el electrón fue descubierto en 1.897 por el físico británico Josepth John Thomson (1856-1940), el problema de su estructura, si la hay, no está resuelto.  Conocemos su masa y su carga negativa que responden a 9,1093897 (54)x10^-31kg la primera y, 1,602 177 33 (49)x10^-19 culombios, la segunda, y también su radio clásico: r₀ = e²/(mc²) = 2’82×10^-13 cm no se ha descubierto aún ninguna partícula que sea menos cursiva que el electrón (o positrón) y que lleve  una carga eléctrica, sea lo que fuese (sabemos como actúa y cómo medir sus propiedades, pero aun no sabemos qué es), tenga asociada un mínimo de masa, y que esta es la que se muestra en el electrón.

Lo cierto es que, el electrón, es una maravilla en sí mismo.  El Universo no sería como lo conocemos si el electrón (esa cosita “insignificante”), fuese distinto a como es, bastaría un cambio infinitesimal para que, por ejemplo, nosotros no pudiéramos estar aquí ahora.

¡No por pequeño, se es insignificante! Recordémoslo, todo lo grande está hecho de cosas pequeñas.

En realidad, existen partículas que no tienen en absoluto asociada en ellas ninguna masa (es decir, ninguna masa en reposo).  Por ejemplo, las ondas de luz y otras formas de radiación electromagnéticas se comportan como partículas (Einstein en su efecto fotoeléctrico y De Broglie en la difracción de electrones.

Esta manifestación en forma de partículas de lo que, de ordinario, concebimos como una onda se denomina fotón, de la palabra griega que significa “luz”.

El fotón tiene una masa de 1, una carga eléctrica de 0, pero posee un espín de 1, por lo que es un bosón. ¿Cómo se puede definir lo que es el espín? Los fotones toman parte en las reacciones nucleares, pero el espín total de las partículas implicadas antes y después de la reacción deben permanecer inmutadas (conservación del espín).  La única forma que esto suceda en las reacciones nucleares que implican a los fotones radica en suponer que el fotón tiene un espín de 1. El fotón no se considera un leptón, puesto que este termino se reserva para la familia formada por el electrón, el muón y la partícula Tau con sus correspondientes neutrinos.

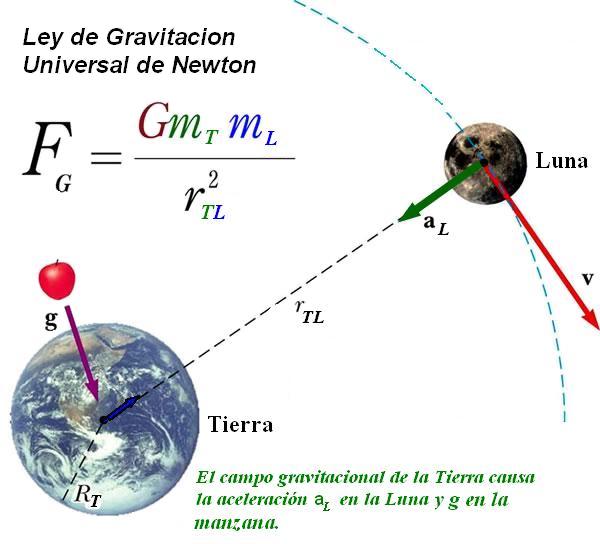
Existen razones teóricas para suponer que, cuando las masas se aceleran (como cuando se mueven en órbitas elípticas en torno a otra masa o llevan a cabo un colapso gravitacional), emiten energía en forma de ondas gravitacionales.  Esas ondas pueden así mismo poseer aspecto de partícula, por lo que toda partícula gravitacional recibe el nombre de gravitón.

La fuerza gravitatoria es mucho, mucho más débil que la fuerza electromagnética.  Un protón y un electrón se atraen gravitacionalmente con sólo 1/10³⁹ de la fuerza en que se atraen electromagnéticamente. El gravitón (aún sin descubrir) debe poseer, correspondientemente, menos energía que el fotón y, por tanto, ha de ser inimaginablemente difícil de detectar.

De todos modos, el físico norteamericano Joseph Weber emprendió en 1.957 la formidable tarea de detectar el gravitón.  Llegó a emplear un par de cilindros de aluminio de 153 cm. De longitud y 66 de anchura, suspendidos de un cable en una cámara de vacío.  Los gravitones (que serían detectados en forma de ondas), desplazarían levemente esos cilindros, y se empleó un sistema para detectar el desplazamiento que llegare a captar la cienmillonésima parte de un centímetro.

Las débiles ondas de los gravitones, que producen del espacio profundo, deberían chocar contra todo el planeta, y los cilindros separados por grandes distancias se verán afectados de forma simultánea.  En 1.969, Weber anunció haber detectado los efectos de las ondas gravitatorias.  Aquello produjo una enorme excitación, puesto que apoyaba una teoría particularmente importante (la teoría de Einstein de la relatividad general).  Desgraciadamente, nunca se pudo comprobar mediante las pruebas realizadas por otros equipos de científicos que duplicaran el hallazgo de Weber.

De todas formas, no creo que, a estas alturas, nadie pueda dudar de la existencia de los gravitones, el bosón mediador de la fuerza gravitatoria.  La masa del gravitón es cero, su carga es cero, y su espín de 2.  Como el fotón, no tiene antipartícula, ellos mismos hacen las dos versiones. Si todas las fuerzas tienen una partícula mensajera, ¿por qué la Gravedad no la tendría?

¿Cómo será el dichoso y esquivo gravitòn?

Tenemos que volver a los que posiblemente son los objetos más misteriosos de nuestro Universo: Los agujeros negros.  Si estos objetos son lo que se dice (no parece que se pueda objetar nada en contrario), seguramente serán ellos los que, finalmente, nos faciliten las respuestas sobre las ondas gravitacionales y el esquivo gravitón.

La onda gravitacional emitida por el agujero negro produce una ondulación en la curvatura del espacio-temporal que viaja a la velocidad de la luz transportada por los gravitones.

Hay aspectos de la física que me dejan totalmente sin habla, me obligan a pensar y me transporta de este mundo material nuestro a otro fascinante donde residen las maravillas del Universo.  Hay magnitudes asociadas con las leyes de la gravedad cuántica. La longitud de Planck-Wheeler, es la escala de longitud por debajo de la cual el espacio tal como lo conocemos deja de existir y se convierte en espuma cuántica.  El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10^-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2’61×10^-66 cm²) juega un papel clave en la entropía de un agujero negro.

Me llama poderosamente la atención lo que conocemos como las fluctuaciones de vacío, esas oscilaciones aleatorias, impredecibles e ineliminables de un campo (electromagnético o gravitatorio), que son debidas a un tira y afloja en el que pequeñas regiones del espacio toman prestada momentáneamente energía de regiones adyacentes y luego la devuelven.

Ordinariamente, definimos el vacío como el espacio en el que hay una baja presión de un gas, es decir, relativamente pocos átomos o moléculas.  En ese sentido, un vacío perfecto no contendría ningún átomo o molécula, pero no se puede obtener, ya que todos los materiales que rodean ese espacio tienen una presión de vapor finita.  En un bajo vacío, la presión se reduce hasta 10^-2 pascales, mientras que un alto vacío tiene una presión de 10^-2-10^-7 pascales.  Por debajo de 10^-7 pascales se conoce como un vacío ultraalto.

No puedo dejar de referirme al vacío theta (vació θ) que, es el estado de vacío de un campo gauge no abeliano (en ausencia de campos fermiónicos y campos de Higgs). En el vacío theta hay un número infinito de estados degenerados con efecto túnel entre estos estados.  Esto significa que el vacío theta es análogo a una fundón de Bloch en un cristal. Se puede derivar tanto como un resultado general o bien usando técnicas de instantón.  Cuando hay un fermión sin masa, el efecto túnel entre estados queda completamente suprimido. Cuando hay campos fermiónicos con masa pequeña, el efecto túnel es mucho menor que para campos gauge puros, pero no está completamente suprimido.

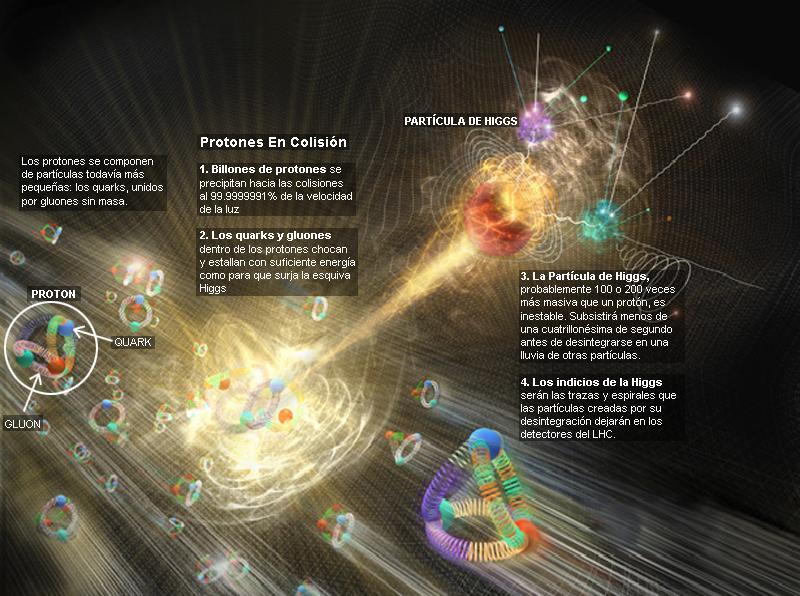
Pero, a todo esto, no perdamos de vista los campos de Higgs, ahí se espera que esté escondida la gran sorpresa de la Física de éste siglo que, según dicen, llegará de la mano del LHC. ¿Será eso cierto?

emilio silvera

[?]

La infinitud de la creación es suficientemente grande como para hacer que un mundo, o una Vía Láctera de mundos, parezca, en comparación con ella, lo que una flor o un insecto en comparación con la Tierra,

Immanuel Kant

Una simple región de nuestro Grupo Local de Galaxias ya resulta de una inmensidad que, nuestras mentes tridimensionales, difícilmente llegan a comprender. La infinitud de las distancias espaciales nos han obligado a crear medidas especiales para poder controlar las enormes distancias a las que están situados los objetos celestes.

Al mencionar dimensiones más altas (ahora trabajamos con tres de espacio y una temporal), se me ocurre, como ejemplo cotidiano y sencillo, el referirme al general que, escondido con su ejército en la profundidad de un enorme valle, no sabía qué estrategia emplear para vencer a sus enemigos. Pensando en cómo resolver el problema, ascendió con sus capitanes a lo alto de la montaña, y con sorpresa vio desde aquella altura todas las posiciones enemigas. Así, de aquel nuevo conocimiento, adquirido al subir más alto, pudo extraer consecuencias de lo que vio para preparar la estrategia adecuada y alcanzar la meta, en este caso, la victoria.

El enemigo bien localizado desde arriba no presiente lo que le espera

Pues, de la misma manera, nosotros también estamos obligados a subir a la montaña que nos permita ver más allá de las matemáticas topológicas, más allá de las fluctuaciones de vacío, más allá de los quarks, más allá de las singularidades y… ¿por qué no decirlo?, más allá de nuestro propio universo. No podemos olvidarnos de que dentro de varios eones, nuestro universo podría morir. Estamos obligados a buscar la manera (si existe) de escapar de ese destino fatal.

Lo cierto es que, en este mundo nuestro y con nuestra conformación y percepciones, no será nada fácil acceder a ese otro mundo (si en verdad existe) de más dimensiones, ya que, aparte de las tres espaciales y la temporal que añadió la relatividad general de Einstein, por muchos esfuerzos que hemos realizados, las otras dimensiones extras sólo han aparecido en las matemáticas.

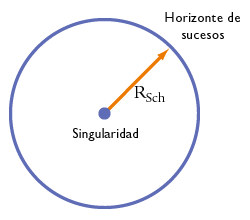
Si el universo finalmente se convierte en una singularidad que es una región donde (según las leyes de la relatividad general) la curvatura del espacio-tiempo se hace infinitamente grande, y el espacio-tiempo deja de existir, toda vez que la singularidad es también una región de gravedad de marea infinita, es decir, una región donde la gravedad ejerce un tirón infinito sobre todos los objetos a lo largo de algunas direcciones y una compresión infinita a lo largo de otras.

Región de una densidad inusitada donde se concentra la masa en una fase más alla de la neutrónica, desconocida, que se reduce y reduce hasta desaparecer, sólo deja a su alrededor un disco de acreción de extrema energía que marca el horizonte de suscesos, la linea de irás y no volveras. A partir de ese momento, el Agujero negro engullirá todo lo que por sus dominios pueda pasar y la singularidad, se hará más y más densa cada vez.

[?]

¿Podrá el magnetismo y la Gravedad estar unidos en un universo de más dimensiones? Cuando Einstein oyó hablar de esta idea se entusiasmó con ella,  pero pronto comprendió que con esa teoría no se podía predecir nada y la abandonó. Cuando recibió la carta de Kaluza en la que le mostraba que en cinco dimensiones se podían unir el magnetismo y la Gravedad, se quedó perplejo y, aunque el abandonó pronto la idea, años más tarde, daría lugar a la teoría de cuerdas.

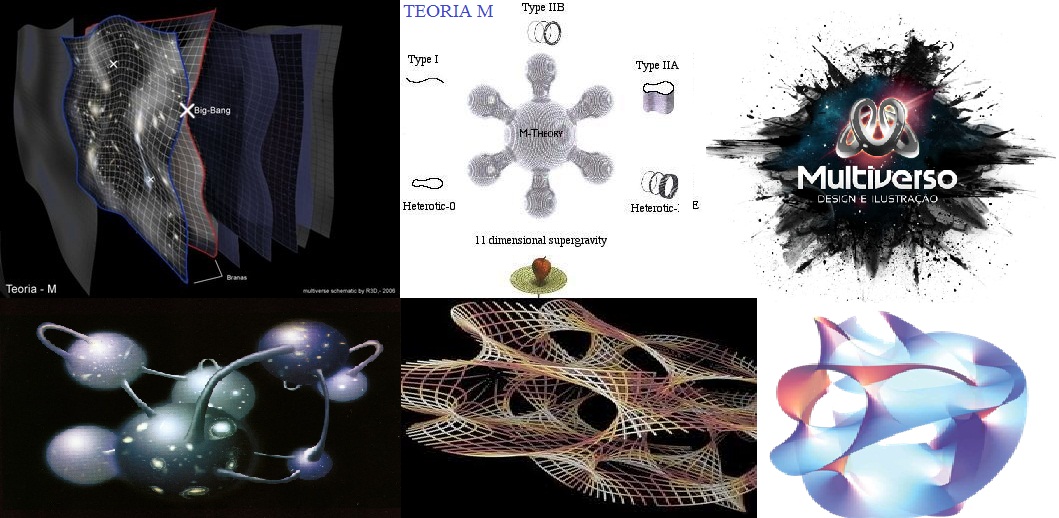
La característica esencial del diagrama que vemos más abajo es que la materia, junto con las ecuaciones de Yang-Mills y de Einstein, está ahora incluida en el mismo campo de supergravedad de 11 dimensiones. Veámoslo así:

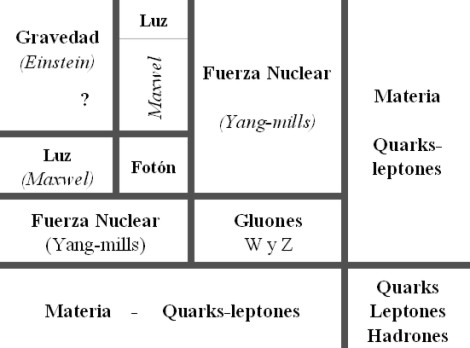
La materia con todas las fuerzas fundamentales de la naturaleza. Los bosones intermediarios o partículas portadoras de las fuerzas como el fotón para el electromagnetismo, los gluones para la fuerza nuclear fuerte, las partículas W y Z para la nuclear débil y, en la partícula portadora de la gravedad, el gravitón, ponemos el signo de interrogación, ya que se sabe que esta ahí en algún sitio pero hasta la fecha no ha sido detectado.

Los expertos en supergravedad redescubrieron esta idea de Kaluza y Klein.Una vez que hemos empezado a considerar muchas dimensiones extra, entramos en una especie de Valhalla de las matemáticas donde podemos enrollar las cosas de muchas maneras diferentes. Las componentes de los campos de fuerza gravitatorias en las direcciones enrolladas actúan como diferentes campos gauge. Obtenemos así, prácticamente por nada, no sólo electromagnetismo sino también otras fuerzas gauge. El número mágico de dimensiones es 11, tres de las cuales forman el espacio ordinario, una el tiempo y las siete restantes están enrolladas. Haciendo ciertos trucos con los números, este sistema resulta tener una simetría mayor que nuestro viejo sistema espacio-temporal de cuatro dimensiones. Los campos y las partículas observadas ahora pueden ser fácilmente acomodados, ya que una simetría mayor significa que los indeseados infinitos se cancelan unos a otros con mayor perfección que antes.

Ciertamente esta idea, esta idea parece ser la contraria a la noción de que el espacio y el tiempo sean nada más que puntos aislados, ya que entonces la noción de “dimensión” deja de tener sentido. Pero los matemáticos no se sienten amenazados por tales contracciones aparentes. De acuerdo con ellos,  hay todo tipo de relaciones entre los espacios enrollados y la matemática de los números enteros, “sueltos” (uno podría indicar los puntos aislados del espaciotiempo con enteros). ¿Podría ser que exitieran diferentes formas de describir nuestro espacio y el tiempo que todas fueran matemáticamente equivalentes? Simplemente no lo sabemos.

Lo que sospecho es que la Supergravedad de dimensión once puede que sólo sea, en el mejor de los casos, la punta de un amravilloso Iceberg que nosotros podemos intuir pero, también es simplemente posible  que sea errónea. Los caminos de la Mente no son bien entendidos y resultan demasiado complejos. He hecho, se han podido lograr conocimientos que la Naturaleza mantenía profundamente escondidos y, sin embargo, ahí están al descubierto y desnudos por medio de nuestros pensamientos que fueron capaces de llegar, hasta las entrañas mismas del Universo.

                                          No siempre podemos ver todo lo que hay

En cuanto a las teorías físicas más avanzadas, no deberíamos olvidar en este  momento que estamos tratando de suposiciones y que los argumentos teóricos que la sustentan son aún, extremadamente débiles. ¿Por qué supersimetría? ¿Por qué Once Dimensiones? ¿Por qué en este mundo todo debería ser maravillosamente simétrico? Y, sobre todo, ¿por qué un continuo, si ya sabemos que el espacio y el tiempo han perdido su significado habitual a distancias ultracortas? Además está la dificultad persistente en esta clase de teorías de que las interacciones entre partículas son siempre tratadas como perturbaciones que afectan a sus trayectorias las cuales, de otra manera, serían perfectamente rectilineas.

Pero entonces habrá nuevas (y diferentes) perturbaciones sobre esas trayectorias perturbadas, y perturbaciones sobre ellas, y así sucesivamente. esta serie de perturbaciones no acaba nunca y este es un problema que se impone en cualquier proceso de formulación exacta.

Es cierto que este problema también afecta al viejo “modelo estándar”, pero al menos allí se podría argüir que, donde realmente importaba, las fuerzas podrían mantenerse pequeñas  y que la serie de perturbaciones convergía rápidamente. Esto no se puede mantener así en nuestra teoría de la (super)  Gravedad, ya que a distancias pequeñas las interacciones se hacen fuertes.

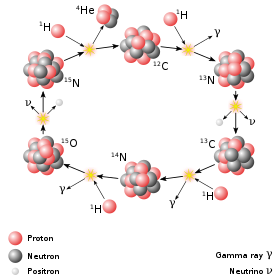
Los Quarks permacen confinados dentro del núcleo formando protones y neutrones y, cuando tratan de separase, la fuerza nuclear fuerte aumenta, en cambio, cuando los Quarks están juntos, se mueven con facilidad y la fuerza disminuye: Libertad asintótica de los Quarkas.

Es cierto que fue un alivio descubrir aquellas primeras dificultades serias en esta teoría, y resultó que no era posible tener infinitos que se cancelasen en diagramas con más de siete lazos cerrados. La teoría, o mejor dicho, la especulación de que esto fuese una “teoría de todo” se abandonó (como otras veces ocurrió) porque algo más interesante apareció en el horizonte de la Física. ¡Las Supercuerdas!

Aunque hemos hablado mucho de ellas, creo que debemos profundizar algo más en esta prometedora teoría y, aunque de momento es sólo una especulación avanzada…¿quién sabe? lo que nos podrían traer esas ideas avanzadas que han dado lugar a matemáticas profundas de un 2universo topológico” incomprensible para muchos y fascinantes para unos pocos.

Los tiempos cambian, y, con los cambios llegan las nuevas doctrinas o creencias, o, ¿por qué no? nuevas teorías. Desde hace algún tiempo venimos dando vueltas y vueltas, en el campo de la Física, a esas avanzadas teorías que no podemos demostrar, toda vez que, al contrario del Modelo Estándar, no son (por ahora) verificables sus predicciones. Me estoy refiriendo, como habeis podido suponer a la Teoría de supercuerdas, La cuerdad Heterótica, la Supergravedad y Supersimetría, y, finalmente, la última versión que viene a ser un compendio de todas las demás, la Teoría M.

Como nos dice Brian Greene en uno de los capítulos del libro El tejido del cosmos, que él titula: “Especulaciones sobre el espacio y el tiempo en la teoría M”, hoy, tres décadas después de la articulación de la teoría de cuerdas,la mayoría de los que trabajan en ella, creen que aún no tenemos una respuesta general para la pregunta fundamental: ¿qué es la teoría de cuerdas? A pesar de que sabemos bastante de la teoría, sus características más elementales son familiares y, a estas alturas, casi cercanas. Tampoco debemos despreciar los éxitos que ha cosechado y, desde luego, es bien sabido todo lo que nos promete y también ¿cómo no? los desafíos que suponen lograr todas esas promesas que en ella están encerradas.

La relatividad especial tiene la constancia de la Velocidad de la luz, la relatividad general tiene el principio de Equivalencia, la mecánica cuántica tiene, el principio de Incertidumbre y, sin embargo, los teóricos de cuerdas aún siguen buscando algo de lo que carece la teoría de cuerdas que, precisamente es: el tipo de principio nuclear que se encontraron en aquellas otras teorías y le dan razón de ser y la sólida base que toda teo´ria necesita para ser.

Esa nueva teorías quiere explicarlo todo. Nada puede estar fuera de ella: El Universo que es, todo lo que existe, ahí estará

Un universo de Supercuerdas. El sueño de Einstein comienza a tomar realidad, a través de un nuevo paradigma de la ciencia que viene a romper con la toda la visión del mundo y del universo que teníamos hasta ahora, más allá de lo imaginable. Si la Teoría de cuerdas, finalmente resultase ser cierta, ese descubrimiento llevaría al mundo y a la conciencia humana hasta una nueva dimensión de su propia conciencia.

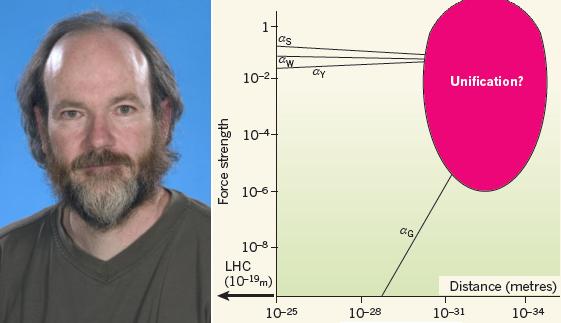
El sueño de Einstein es el sueño de la física teórica moderna: unificar la gravedad con las otras interacciones fundamentales de la naturaleza. Un artículo publicado en Nature estudia cómo se ve afectado el electromagnetismo (una teoría gauge abeliana) debido a la existencia de la gravedad. Las constantes de acoplamiento que caracterizan la “fuerza” de las interacciones fundamentales cambian con la energía. A energías muy altas, o distancias muy cortas, las tres constantes convergen entre sí (de forma aproximada en el modelo estándar y de forma exacta en las teorías supersimétricas). Sin embargo, el comportamiento de la gravedad a distancias ultracortas, en el rango entre 10^-32 m y 10^-35 m, influye o afecta a las constantes de acoplamiento incluso aunque no se conoce la teoría cuántica correcta de la gravedad, ya que dicha teoría solo es necesaria a distancias menores de 10^-35 m. El nuevo análisis indica que el efecto de la gravedad sobre las otras interacciones fundamentales podría ser observado a distancias entre 10^-33 m y 10^-35 m; en concreto se observaría  un cambio en el fenómeno llamado libertad asintótica de las constantes de acoplamiento.

La Libertad Asintótica nos habla de que las fuerzas entre partículas como los Quarks se hacen más débiles a distancias más cortas (es decir, a altas energías) y se anulan a medida que las distancias entre las  partículas tienden a cero. Este fenómeno se puede observar en la fuerza nuclear fuerte, entre los quarks que si se alejan los unos de los otros aumenta la fuerza y, cuando se juntan, esta disminuye.

Lo primero que debemos entender es la inevitabilidad de la gravitación en la Teoría de Cuerdas. Una vez conjugamos efectos cuánticos con el carácter extenso de la cuerda aparece inevitablemente en el espectro un gravitón, y es esta inevitabilidad de la gravitación la que nos aporta una comprensión nueva de la escala de longitud de la cuerda. En breves palabras, si parametrizamos por g la amplitud cuántica de que una cuerda se divida en dos y por  L la escala de longitud de la misma, nos encontramos conque gL es precisamente la longitud de Planck:

Dicho de otra manera, la constante de Newton  G, que define la intensidad gravitatoria, ¡es simplemente (gL)! Y, este hecho, tiene importantísimas consecuencias. En efecto, si la longitud de Planck está definida de manera intrínseca, podemos asociar, sin salirnos de la propia teoría, con cualquier modo de vibración de la cuerda de masa M su radio gravitacional, o, si se prefiere, su tamaño gravitatorio: R(M) = MG. Una vez hacemos esto aparece de manera inmediata una masa o energía crítica por encima de la cual el modo de vibración de la cuerda adquiere un tamaño gravitacional mayor que su propia longitud.

Este modo de vibración se ha convertido en ¡un agujero negro! Dicho con otras palabras, cuando profundizamos en el ultravioleta llega un momento en el que las excitaciones de la cuerda no nos desvelan una estructura de constituyentes más elementales sino algo completamente nuevo, a saber: agujeros negros cuyo tamaño en vez de disminuir con la energía aumenta. El paradigma de teoría cuántica de campos Wilsoniana caracterizado por la libertad asintótica, en suma por unos constituyentes casi libres, se transforma, en la Teoría de Cuerdas, en una oscuridad asintótica controlada por agujeros negros. En otras palabras, la cuerda, de manera inevitable, se completa en el ultravioleta gravitacionalmente sin desvelar una subestructura Wilsoniana de constituyentes más fundamentales regidos por alguna teoría conforme.

Es importante que apreciemos que la manera en la que la teoría se completa en el ultravioleta no es en término de un espectro nuevo, como podrían ser los quarks y gluones en el caso de la QCD, sino en término de objetos, como son los agujeros negros, cuya definición no nos exige en ningún momento invocar nuevos grados de libertad, sino tan solo la propia dinámica de la teoría.

Así, la Teoría de Cuerdas es una teoría cuántica cuya física en el ultravioleta profundo, a distancias más pequeñas que la propia longitud de la cuerda, está dominada por agujeros negros clásicos. ¿Cómo derivar estos comentarios a un principio rector y definitorio de la Teoría?

Lo cierto es que hemos creado enormes aceleradores de partículas para poder llegar hasta las entrañas de la materia y, estamos tratándo de “ver” si al menos, podemos atisbar aunque sólo sea las sombras de las cuerdas vibrantes que, con sus resonancias, crean contiunuamente nuevas partículas. Pero no, la potencia utilizada en estas colisiones, no dejan ver las cuerdas que están mucho más allá de las energías que ahora podemos utilizar, se necesitaría la energía de Planck para poder acercarnos a ese mundo soñado de las cuerdas que residen en el pais de las once dimensiones.

Hay que conseguir que se puedan hacer consistentes los principios de la Mecánica Cuántica con nuevos postulados: el de la existencia de una longitud mínima. Cuando intentamos combinar estos dos principios de una manera consistente nos encontramos con una teoría en el ultravioleta, es decir, más allá de la longitud mínima, debe poder ser descrita no en términos de constituyentes más primitivos sino necesariamente en términos de configuraciones o entidades de la propia teoría cuyo tamaño efectivo es necesariamente mayor que la longitud mínima. Esta descripción “infrarroja” (grandes distancias) del mundo ultravioleta es lo que se conoce como correspondencia UV/IR y es el corazón de la celebradísima e importantísima correspondencia descubierta hace ya más de diez años por Juan Maldacena.

Todo esto es fascinante pero, no todos lo podemos comprender.

emilio silvera

[?]

 Cuando hablamos de la mecánica cuántica, tenemos mirar un poco hacia atrás en el tiempo y podremos darnos cuenta del gran impacto que tuvo en el devenir del mundo desde que, en nuestras vidas, apareció el átomo y, más tarde, sus contenidos. Los nombres de Planck, Einstein, Bohr, Heisenberg, Schrödinger, Pauli, Bardeen, Roentgen, Dirac y muchos otros, se pudieron a la cabeza de la lista de las personas más famosas. Aquel primer premio Nobel de Física otorgado en 1900 a Roentgen por descubrir los rayos X, en el mismo año llegaría el ¡cuanto! De Planck que inspiró a Einstein para su trabajo sobre el Efecto fotoeléctrico que también, le valdría el Nobel, y, a partir de ese momento, se desencadenó una especie de carrera alucinante por saber sobre el átomo, sus contenidos, y, de qué estaba hecha la materia.

      La conocida como Paradoja EPR y los conceptos de Tiempo y Espacio, presente, pasado y futuro

Fueron muchas las polémicas desatadas a cuenta de las aparentes incongruencias de la moderna Mecánica Cuántica. La paradoja de Einstein-Podolsky-Rosen, denominada “Paradoja EPR”, trata de un experimento mental propuesto por Albert Einstein, Boris Podolsky y Nathan Rosen en 1935. Es relevante, pues pone de manifiesto un problema aparente de la mecánica cuántica, y en las décadas siguientes se dedicaron múltiples esfuerzos a desarrollarla y resolverla.

A Einstein (y a muchos otros científicos), la idea del entrelazamiento cuántico le resultaba extremadamente perturbadora. Esta particular característica de la mecánica cuántica permite preparar estados de dos o más partículas en los cuales es imposible obtener información útil sobre el estado total del sistema haciendo sólo mediciones sobre una de las partículas.

Por otro lado, en un estado entrelazado, manipulando una de las partículas, se puede modificar el estado total. Es decir, operando sobre una de las partículas se puede modificar el estado de la otra a distancia de manera instantánea. Esto habla de una correlación entre las dos partículas que no tiene paralaje en el mundo de nuestras experiencias cotidianas. Cabe enfatizar pues que cuando se mide el estado de una partícula, enseguida sabemos el estado de la otra, lo cual aparentemente es instantáneo, es decir, sin importar las distancias a las que se encuentren las partículas, una de la otra, ambas saben instantáneamente el estado de la otra.

El experimento planteado por EPR consiste en dos partículas que interactuaron en el pasado y que quedan en un estado entrelazado. Dos observadores reciben cada una de las partículas. Si un observador mide el momento de una de ellas, sabe cuál es el momento de la otra. Si mide la posición, gracias al entrelazamiento cuántico y al principio de incertidumbre, puede saber la posición de la otra partícula de forma instantánea, lo que contradice el sentido común.

La paradoja EPR está en contradicción con la teoría de la relatividad, ya que aparentemente se transmite información de forma instantánea entre las dos partículas. De acuerdo a EPR, esta teoría predice un fenómeno (el de la acción a distancia instantánea) pero no permite hacer predicciones deterministas sobre él; por lo tanto, para todos los físicos de esa época, la mecánica cuántica es una teoría incompleta.

Esta paradoja critica dos conceptos cruciales: la no localidad de la mecánica cuántica (es decir, la posibilidad de acción a distancia) y el problema de la medición. En la física clásica, medir un sistema, es poner de manifiesto propiedades que se encontraban presentes en el mismo, es decir, que es una operación determinista. En mecánica cuántica, constituye un error asumir esto último. El sistema va a cambiar de forma incontrolable durante el proceso de medición, y solamente podemos calcular las probabilidades de obtener un resultado u otro.

Hoy nos enteramos que un grupo de físicos ha logrado modificar desde el presente un evento que ya había sucedido con anterioridad. La hazaña se ha conseguido aprovechando una extraña capacidad de las partículas subatómicas que nunca hasta ahora había podido ser demostrada.Lo cierto es que, el entrelazamiento cuántico, descrito como esa barrera invisiblñe entre la física moderna y la clásica, parece servir como un cordón inmaterial que conecta todas las cosas del universo y tiende un puente entre lo materialy lo metafísico.

El experimento recién realizado plantea paradojas más perturbadoras. ¿Cómo es posible que una partícula que desapareció en el pasado esté entrelazada con otra que ya no existe? ¿Es que acaso hay estados que tienen que ver con la flecha del tiempo que no entendemos? ¿qué tal que toda la percepción del espacio-tiempo no sea el adecuado? ¿No hay otra alternativa? ¿Podemos finalmente ser capaces de entender -y tal vez, sacar provecho- de este extrañísimo fenómeno?

Lo cierto es que la mecánica cuántica ha tenido siempre una cierta especie de fascinación atrayente para todos aquellos que, aunque no iniciados en ciencia física,  cuando se les habla del principio de incertidumbre, del efecto túnel, o, incluso del contenido de los átomos y de lo que pasa dentro ellos, están situados ante escenarios tan extraños y maravilloso a la vez que, no pueden dejar de sentir atracción hacia todo aquello que no comprenden.

Esas partículas de luz que llamamos fotones, pueden transformar un lóbrego y oscuro lugar en algo inesperado. El Universo de lo infinitesimal, de lo muy pequeño, nos lleva hasta la realidad de hasta donde resulta para nosotros incomprensible ese micro mundo de la mecánica cuántica, ese “universo” misterioso, donde ocurren cosas que no llegamos a comprender.

La mecánica cuántica domina en el micromundo de los átomos y de las partículas “elementales”. Nos enseña que en la naturaleza cualquier masa, por sólida o puntual que pueda parecer, tiene un aspecto ondulatorio. Esta onda no es como una onda de agua.  Es una onda de información. Nos indica la probabilidad de detectar una partícula. La longitud de onda de una partícula, la longitud cuántica, se hace menor cuanto mayor es la masa de esa partícula.

La física cuántica empezó a enseñarnos que no debemos estar tan seguros de las reglas del espacio y del tiempo, que hasta ese entonces parecían muy confiables e invariables”. Cuando nos sumergimos en las profundas aguas de la mecánica cuántica, lo que allí podemos encontrar, no son “criaturas” de este mundo nuestro, en aquel espacio-tiempo infinitamente pequeño, ocurren cosas extrañas que no vemos en nuestras vidas cotidianas, en nuestro macromundo. Allí, una partícula puede desaparecer de pronto y, de manera instantánea, apaerecer en otro lugar sin haber realizado el recorrido entre los dos lugares, se transportó sin recorrer la distancia.

Por el contrario, la relatividad general era siempre necesaria cuando se trataba con situaciones donde algo viaja a la velocidad de la luz, o está muy cerca o donde la gravedad es muy intensa. Se utiliza para describir la expansión del universo o el comportamiento en situaciones extremas, como la formación de agujeros negros. Sin embargo, la gravedad es muy débil comparada con las fuerzas que unen átomos y moléculas y demasiado débil para tener cualquier efecto sobre la estructura del átomo o de partículas subatómicas, se trata con masas tan insignificantes que la incidencia gravitatoria es despreciable. Todo lo contrario que ocurre en presencia de masas considerables como planetas, estrellas y galaxias, donde la presencia de la gravitación curva el espacio y distorsiona el tiempo.

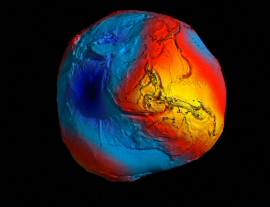
La Gravedad hace que la Tierra se vea como un mapa. Es una vista altamente exagerada, pero ilustra a las claras cómo la atracción gravitatoria que se manifiesta desde la masa de roca bajo nuestros pies no es la misma en todo lugar. La gravedad es más fuerte en áreas amarillas y más débil en las azules. (Imagen tomada por el satélite Goce). Lo cierto es que se ha podido comprobar como la Gravedad, distorsiona el espacio y ralentiza el Tiempo.

Como resultado de estas propiedades antagónicas, la teoría cuántica y la teoría relativista gobiernan reinos diferentes, muy dispares, en el universo de lo muy pequeño o en el universo de lo muy grande. Nadie ha encontrado la manera de unir, sin fisuras, estas dos teorías en una sola y nueva de Gravedad-Cuántica.

¿Cuáles son los límites de la teoría cuántica y de la teoría de la relatividad general de Einstein? Afortunadamente, hay una respuesta simple y las unidades de Planck nos dicen cuales son. Nunca hemos podido ir más allá del Tiempo de Planck para saber, qué pasó en aquellos primeros momentos del Big Bang, tampoco podemos disponer de la Energía de Planck para comprobar de manera experimental la Teoría de Cuerdas, y así, podríamos seguir enumerando todo lo que no está a nuestro alcance y el límite lo marcan las unidades de Planck.

Supongamos que tomamos toda la masa del universo visible y determinamos su longitud de onda cuántica. Podemos preguntarnos en qué momento esta longitud de onda cuántica del universo visible superará su tamaño.  La respuesta es: cuando el universo sea más pequeño en tamaño que la longitud de Planck, es decir, 10^-33  centímetros, más joven que el Tiempo de Planck, 10^-43 segundos y supere la temperatura de Planck de 10³² grados.  Las unidades de Planck marcan la frontera de aplicación de nuestras teorías actuales. Para comprender en que se parece el mundo a una escala menor que la longitud de Planck tenemos que comprender plenamente cómo se entrelaza la incertidumbre cuántica con la gravedad. Para entender lo que podría haber sucedido cerca del suceso que estamos tentados a llamar el principio del universo, o el comienzo del tiempo, tenemos que penetrar la barrera de Planck. Las constantes de la naturaleza marcan las fronteras de nuestro conocimiento existente y nos dejan al descubierto los límites de nuestras teorías.

En los intentos más recientes de crear una teoría nueva para describir la naturaleza cuántica de la gravedad ha emergido un nuevo significado para las unidades naturales de Planck. Parece que el concepto al que llamamos “información” tiene un profundo significado en el universo. Estamos habituados a vivir en lo que llamamos “la edad de la información”.  La información puede ser empaquetada en formas electrónicas, enviadas rápidamente y recibidas con más facilidad que nunca antes.

        ¿Por qué circuitos es más rápida la informaciòn, el natural o el artificial?

Los tiempos cambian y la manera de informar también, lejos nos queda ya aquellos toscos aparatos impresores del pasado, ahora, en espacios muy reducidos, tenemos guardada más información que antes había en una colección de libros. Las ondas transmiten información a la velocidad de la luz y, ningún rincón del mundo queda fuera de “ese milagro” de la técnica. De hecho, nuestro planeta se queda chico y enviamos ingenios a otros mundos desde donde nos envían información que recibimos en poco tiempo, el que tarda la luz en traernos las nuevas y sorprendentes noticias.

Como he referido otras veces, nuestra evolución en el proceso rápido y barato de la información se suele mostrar en una forma que nos permite comprobar la predicción de Gordon Moore, el fundador de Intel, llamada ley de Moore, en la que, en 1.965, advirtió que el área de un transistor se dividía por dos aproximadamente cada 12 meses. En 1.975 revisó su tiempo de reducción a la mitad hasta situarlo en 24 meses. Esta es “la ley de Moore” cada 24 meses se obtiene una circuiteria de ordenador aproximadamente el doble, que corre a velocidad doble, por el mismo precio, ya que, el coste integrado del circuito viene a ser el mismo, constante.

Los límites últimos que podemos esperar para el almacenamiento y los ritmos de procesamiento de la información están impuestos por las constantes de la naturaleza. En 1.981, el físico israelí, Jacob Bekenstein, hizo una predicción inusual que estaba inspirada en su estudio de los agujeros negros.  Calculó que hay una cantidad máxima de información que puede almacenarse dentro de cualquier volumen. Esto no debería sorprendernos. Lo que debería hacerlo es que el valor máximo está precisamente determinado por el área de la superficie que rodea al volumen, y no por el propio volumen. El número máximo de bits de información que puede almacenarse en un volumen viene dado precisamente por el cómputo de su área superficial en unidades de Planck. Supongamos que la región es esférica. Entonces su área superficial es precisamente proporcional al cuadrado de su radio, mientras que el área de Planck es proporcional a la longitud de Planck al cuadrado, 10^-66 cm².  Esto es muchísimo mayor que cualquier capacidad de almacenamiento de información producida hasta ahora. Asimismo, hay un límite último sobre el ritmo de procesamiento de información que viene impuesto por las constantes de la naturaleza.

No debemos descartar la posibilidad de que seamos capaces de utilizar las unidades de Planck-Stoney para clasificar todo el abanico de estructuras que vemos en el universo, desde el mundo de las partículas elementales hasta las más grandes estructuras astronómicas.  Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias.

             Lo grande y lo pequeño inmersos en un inmenso recorrido de espacio-tiempo en un Universo “infinito” que contiene todo lo que existe

Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y m_protón.

α = 2πe² / hc ≈ 1/137

α_G = (Gm_p2)² / hc ≈ 10^-38

La identificación de constantes adimensionales de la naturaleza como a (alfa) y α_G, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro.

Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala.  La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.

Pero esas constantes universales son las que han propiciado que nuestro universo tenga la vida

Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck).  Si se duplica el valor de todas las masas no se puede llegar a saber, por qué todos los números puros definidos por las razones de cualquier par de masas son invariables.

Cuando surgen comentarios de números puros y adimensionales, de manera automática aparece en mi mente el número 137. Ese número encierra más de lo que estamos preparados para comprender. Este número guarda relación con la posibilidad de que un electrón emita un fotón o lo absorba. La constante de estructura fina responde también al nombre de “alfa” y sale de dividir el cuadrado de la carga del electrón, por el producto de la velocidad de la luz y la constante de Planck. Tanta palabrería y numerología no significan otra cosa sino que ese solo numero, 137, encierra los misterios del electromagnetismo (el electrón, e-), la relatividad (la velocidad de la luz, c), y la teoría cuántica (la constante de Planck, h). α = 2πe2 hc =  137.

Lo más notable de este número es su dimensionalidad. La velocidad de la luz, c, es bien conocida y su valor es de 299.792.458 m/segundo; la constante de Planck racionalizada, ћ, es h/2π = 1’054589×10 julios segundo; todo viene con sus dimensiones. Pero resulta que cuando uno combina las magnitudes que componen alfa ¡se borran todas las unidades! El 137 está solo: se escribe desnudo a donde va.

Esto quiere decir que los científicos del undécimo planeta de una estrella lejana situada en un sistema solar de la galaxia Andrómeda, aunque utilicen quién sabe qué unidades para la carga del electrón y la velocidad de la luz y qué versión utilicen para la constante de Planck, también les saldrá el 137.

Es un número puro. No lo inventaron los hombres. Está en la naturaleza, es una de sus constantes naturales, sin dimensiones. La física se ha devanado los sesos con el 137 durante décadas. Werner Heisember (el que nos regaló el Principio de Incertidumbre en la Mecánica Cuántica), proclamó una vez que todas las fuentes de perplejidad que existen en la mecánica cuántica se secarían si alguien explicara de una vez el 137.

¿Por qué alfa es igual a 1 partido por 137?

Es uno de esos misterios de la Naturaleza que nos queda por desvelar y esperemos que algún día aparezca alguien que, con la intuición, el talento y el ingenio de Newton o Einstein, nos pueda por fin aclarar el misterioso número y las verdades que encierra. Menos perturbador sería que la relación de todos estos importantes conceptos (e-, h y c) hubieran resultado ser 1 ó 3 o un múltiplo de pi… pero ¿137?

El Universo es muy grande, inmensamente grande y, probablemente, todo lo que nuestras mentes puedan imaginar podrá exisitr en alguna parte de esas regiones perdidas en las profundidades cósmicas, en los confines del Espacio- Tiempo, en lugares ignotos de extraña belleza en los que otros mundos y otras criaturas tendrán, su propio habitat que, siendo diferente al nuestro, también, sus criaturas, estarán buscando el significado de las leyes del Universo.

emilio silvera

[?]