Mar
3
¿Los cuántos? ¡Una maravilla de la Naturaleza!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)

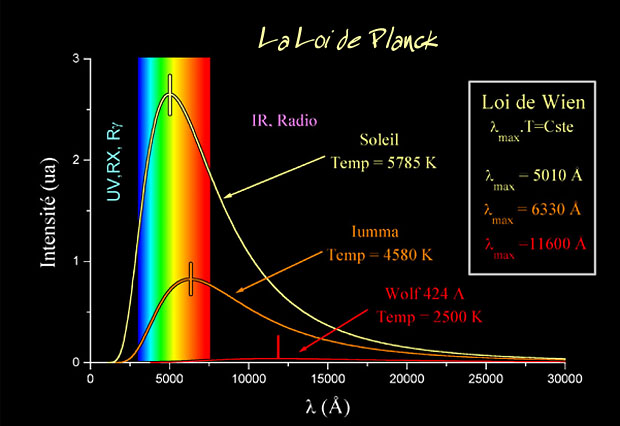
La Física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menos intensidad, por los objetos más fríos. Planck escribió un artículo de ocho páginas y el resultado fue que cambió el mundo de la física y aquella páginas fueron la semilla de la futura ¡mecánica cuántica! que, algunos años más tardes, desarrollarían físicos como Einstein (Efecto fotoeléctrico), Heisenberg (Principio de Incertidumbre), Feynman, Bhor, Schrödinger, Dirac…
Figura animada que representa un rayo de luz incidiendo sobre un cuerpo negro hasta su total absorción. l nombre cuerpo negro fue introducido por Gustav Kirchhoff en 1862 y su idea deriva de la siguiente observación: toda la materia emite radiación electromagnética cuando se encuentra a una temperatura por encima del cero absoluto. La radiación electromagnética emitida por un cuerpo a una temperatura dada es un proceso espontáneo y procede de una conversión de su energía térmica en energía electromagnética. También sucede a la inversa, toda la materia absorbe radiación electromagnética de su entorno en función de su temperatura.
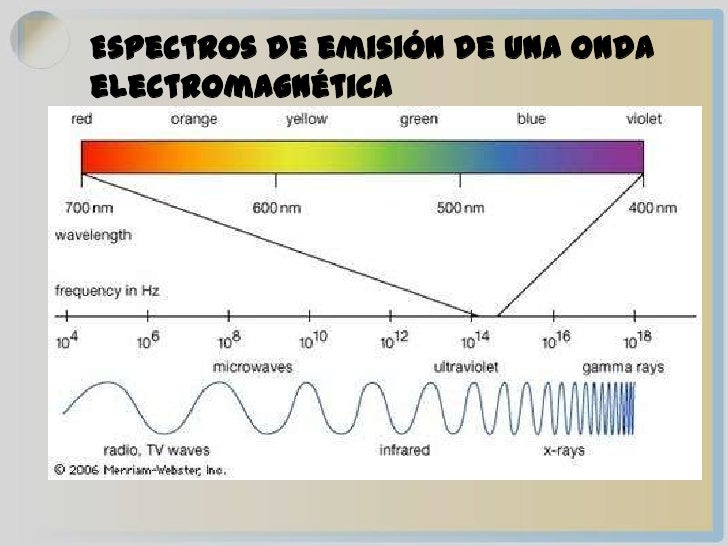
La expresión radiación se refiere a la emisión continua de energía de la superficie de todos los cuerpos. Los portadores de esta energía son las ondas electromagnéticas producidas por las vibraciones de las partículas cargadas que forman parte de los átomos y moléculas de la materia. La radiación electromagnética que se produce a causa del movimiento térmico de los átomos y moléculas de la sustancia se denomina radiación térmica o de temperatura.

Ley de Planck para cuerpos a diferentes temperaturas.
Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía.

Pero si usamos las leyes de la termodinámica para calcular la intensidad de la radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano, y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico o una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para longitudes menores. Esta longitud característica es inversamente proporcional a la temperatura absoluta del objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273 ºC bajo cero). Cuando a 1.000 ºC un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de la luz visible.

Acero al “rojo vivo”, el objeto está radiando en la zona de la luz visible.

Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda y, por lo tanto, proporcional a la frecuencia de la radiación emitida. La sencilla fórmula es:
E = hv
Donde E es la energía del paquete, v es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.
Ni que decir tiene que, desde entonces, la fórmula ha sido mejorada y, como siempre pasa, los avances que son imparables van modificando las teorías originales para perfeccionarlas y que se ajusten mucho más a la realidad que la Naturaleza nos muestra cuando somos capaces de descubrir sus secretos.

Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: el sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck.
El príncipe francés Louis Victor de Broglie, dándole otra vuelta a la teoría, que no sólo cualquier cosa que oscila tiene una energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta dirección del espacio, y que la frecuencia, v, de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilatorias de campos de fuerza.


En mecánica cuántica, el comportamiento de un electrón en un átomo se describe por un orbital, que es una distribución de probabilidad más que una órbita. El electrón (e−), es una partícula subatómica con una carga eléctrica elemental negativa.Un electrón no tiene componentes o subestructura conocidos, en otras palabras, generalmente se define como una partícula elemetal.

En la Teoría de cuerdas subyace la Gravedad cuántica
En la Teoría de cuerdas se dice que un electrón se encuentra formado por una subestructura (cuerdas). Tiene una masa que es aproximadamente 1836 veces menor con respecto a la del protón. El miomento angular (espín) intrínseco del electrón es un valor semientero en unidades de ħ, lo que significa que es un fermión. Su antipartícula es denominada positrón: es idéntica excepto por el hecho de que tiene cargas —entre ellas, la eléctrica— de signo opuesto. Cuando un electrón colisiona con un positrón, las dos partículas pueden resultar totalmente aniquiladas y producir fotones y rayos gamma.
Los electrones, que pertenecen a la primera generación de la familia de partículas de los leptones y participan en las interacciones fundamentales, tales como la Gravedad, el electromagnetismo y la fuerza nuclear débil. Como toda la materia, posee propiedades mecánico cuánticas tanto de partículas como de onmdas, de tal manera que pueden colisionar con otras partículas y pueden ser difractadas como la luz. Esta dualidad se demuestra de una mejor manera en experimentos con electrones a causa de su ínfima masa. Como los electrones son fermiones, dos de ellos no pueden ocupar el mismo estado cuántico, según el Principio de exclusión de Pauli. Por este motivo se forman las estrellas enanas blancas y de neutrones al final de la vida de las estrellas de poca masa.
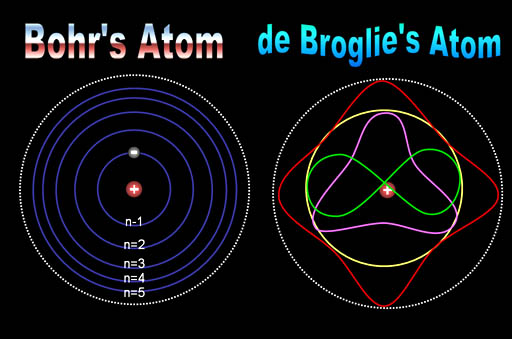
Es curioso el comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de De Broglie. Poco después, en 1926, Edwin Schrödinger descubrió como escribir la teoría ondulatoria de De Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar los cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de onda cuántica”.


No hay duda de que la Mecánica Cuántica funciona maravillosamente bien. Sin embargo, surge una pregunta muy formal: ¿qué significan realmente esas ecuaciones?, ¿qué es lo que están describiendo? Cuando Isaac Newton, allá por el año 1687, formuló cómo debían moverse los planetas alrededor del Sol, estaba claro para todo el mundo lo que significaban sus ecuaciones: que los planetas están siempre en una posición bien definida en el espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades con el tiempo.
Pero para los electrones todo esto es muy diferente. Su comportamiento parece estar envuelto en la bruma. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?
Niels Bohr consiguió responder a esta pregunta de forma tal que con su explicación se pudo seguir trabajando y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la “interpretación de Copenhague” de la Mecánica Cuántica. En vez de decir que el electrón se encuentra en el punto x o en el punto y, nosotros hablamos del estado del electrón. Ahora no tenemos el estado “x” o el estado “y”, sino estados “parcialmente x” o “parcialmente y. Un único electrón puede encontrarse, por lo tanto, en varios lugares simultáneamente. Precisamente lo que nos dice la Mecánica Cuántica es como cambia el estado del electrón según transcurre el tiempo.
Un “detector” es un aparato con el cual se puede determinar si una partícula está o no presente en algún lugar pero, si una partícula se encuentra con el detector su estado se verá perturbado, de manera que sólo podemos utilizarlo si no queremos estudiar la evolución posterior del estado de la partícula. Si conocemos cuál es el estado, podemos calcular la probabilidad de que el detector registre la partícula en el punto x.

Las leyes de la Mecánica Cuántica se han formulado con mucha precisión. Sabemos exactamente como calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas simultáneamente. Por ejemplo, podemos determinar la velocidad de una partícula con mucha exactitud, pero entonces no sabremos exactamente dónde se encuentra; o, a la inversa. Si una partícula tiene “espín” (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.
No es fácil explicar con sencillez de dónde viene esta incertidumbre, pero hay ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar.

¿Onda o partícula? ¡Ambas a la vez! ¿Cómo es eso?
Para que las reglas de la Mecánica Cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuanto más grande y más pesado es un objeto más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica.
Me gustaría referirme a esta exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por “holismo”, y que se podría definir como “el todo es más que la suma de las partes”.
Bien, si la Física nos ha enseñado algo, es justamente lo contrario: un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (las partículas): basta que uno sepa sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que yo entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes.
Por ejemplo, la constante de Planck, h = 6,626075…x 10 exp. -34 julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal. Así, los extraterrestres del cuarto planeta a partir de la estrella SIL, cuando descubran esa constante, el resultado sería exactamente el mismo que le dio a Plancl, es decir, el Universo, funciona igual en todas partes.
Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisenberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros tales como Edwin Schrödinger, siempre presentaron serias objeciones a esta interpretación.
Quizá funcione bien, pero ¿dónde está exactamente el electrón, en el punto x o en el punto y? Em pocas palabras, ¿dónde está en realidad?, ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.

Hasta hoy, muchos investigadores coinciden con la actitud pragmática de Bohr. Los libros de historia dicen que Bohr demostró que Einstein estaba equivocado. Pero no son pocos, incluyéndome a mí, los que sospechamos que a largo plazo el punto de vista de Einstein volverá: que falta algo en la interpretación de Copenhague. Las objeciones originales de Einstein pueden superarse, pero aún surgen problemas cuando uno trata de formular la mecánica cuántica para todo el Universo (donde las medidas no se pueden repetir) y cuando se trata de reconciliar las leyes de la mecánica cuántica con las de la Gravitación… ¡Infinitos!
La mecánica cuántica y sus secretos han dado lugar a grandes controversias, y la cantidad de disparates que ha sugerido es tan grande que los físicos serios ni siquiera sabrían por donde empezar a refutarlos. Algunos dicen que “la vida sobre la Tierra comenzó con un salto cuántico”, que el “libre albedrío” y la “conciencia” se deben a la mecánica cuántica: incluso fenómenos paranormales han sido descritos como efectos mecanocuánticos.

Yo sospecho que todo esto es un intento de atribuir fenómenos “ininteligibles” a causas también “ininteligibles” (como la mecánica cuántica) dónde el resultado de cualquier cálculo es siempre una probabilidad, nunca una certeza.
Claro que, ahí están esas teorías más avanzadas y modernas que vienen abriendo los nuevos caminos de la Física y que, a mi no me cabe la menor duda, más tarde o más temprano, podrá explicar con claridad esas zonas de oscuridad que ahora tienen algunas teorías y que Einstein señalaba con acierto.

¿No es curioso que, cuando se formula la moderna Teoría M, surjan, como por encanto, las ecuaciones de Einstein de la Relatividad General? ¿Por qué están ahí? ¿Quiere eso decir que la Teoría de Einstein y la Mecánica Cuántica podrán al fin unirse en pacifico matrimonio sin que aparezcan los dichosos infinitos?
Bueno, eso será el origen de otro comentario que también, cualquier día de estos, dejaré aquí para todos ustedes.
emilio silvera
Feb
21
¿Qué es un bosón? y ¿qué es un bosón gauge?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

Un bosón es una partícula elemtal (o estado ligado de partículas elementales, por ejemplo, un núcleo atómico o átomo) con espín entero, es decir, una partícula que obedece a la estadísitca de Bose-Einstein (estadísictica cuántica), de la cual deriva su nombre. Los bosones son importantes para el Modelo estándar de las partículas. Son bosones vectoriales de espín uno que hacen de intermediarios de las interacciones gobernadas por teorías gauge.
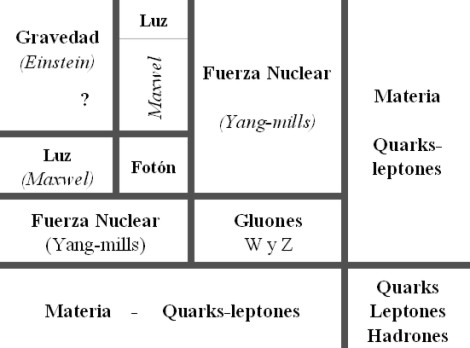
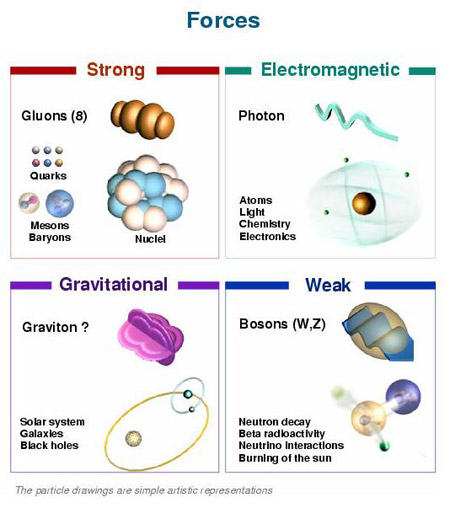
En física se ha sabido crear lo que se llama el Modelo estándar y, en él, los Bosones quedan asociados a las tres fuerzas que lo conforman, el fotón es el Bosón intermediario del electromagnetismpo, los W+, w– y Zº son bosones gauge que transmiten la fiuerza en la teoría electrodébil, mientras que los gluones son los bosones de la fuerza fuerte, los que se encargan de tener bien confinados a los Quarks conformando protones y neutrones para que el núcleo del átomo sea estable. La Gravedad, no se ha dejado meter en el modelo y, por eso su bosón no es de gauge. El gravitón que sería la partícula mediadora de la gravitación sería el hipótetico cuanto de energía que se intercambia en la interacción gravitacional.

Ejemplos de los Bosones gauge son los fotones en electrodinámioca cuántica (en física, el fotón se representa normalmente con el símbolo 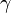 , que es la letra griega gamma), los gluones en cromodinámica cuántica y los bosones W y Z en el modelo de Winberg-Salam en la teoría electrodébil que unifica el electromagnetismo con la fuerza débil. Si la simetría gauge de la teoría no está rota, el bosón gauge es no masivo. Ejemplos de nbosones gauge no masivos son el fotón y el gluón.
, que es la letra griega gamma), los gluones en cromodinámica cuántica y los bosones W y Z en el modelo de Winberg-Salam en la teoría electrodébil que unifica el electromagnetismo con la fuerza débil. Si la simetría gauge de la teoría no está rota, el bosón gauge es no masivo. Ejemplos de nbosones gauge no masivos son el fotón y el gluón.

Si la simetría gauge de la teoría es una simetría rota el bosón gauge tiene masa no nula, ejemplo de ello son los bosones W y Z . Tratando la Gravedad, descrita según la teoría de la relatividad general, como una teoría gauge, el bosón gauge sería el gravitón, partícula no masiva y de espín dos.

Diagrama de Feynman mostrando el intercambio de un fotón virtual (simbolizado por una línea ondulada y  ) entre un positrón y un electrón.De esta manera podemos llegar a comprender la construcción que se ha hecho de las interacciones que están siempre intermediadas por un nosón mensajero de la fuerza.
) entre un positrón y un electrón.De esta manera podemos llegar a comprender la construcción que se ha hecho de las interacciones que están siempre intermediadas por un nosón mensajero de la fuerza.
En el modelo estándar, como queda explicado, hay tres tipos de bosones de gauge: fotones, bosones W y Z y gluones. Cada uno corresponde a tres de las cuatro interacciones: fotones son los bosones de gauge de la interacciones electromagnética, los bosones W y Z traen la interacción débil, los gluones transportan la interacción fuerte. El gravitón, que sería responsable por la interacción gravitacional, es una proposición teórica que a la fecha no ha sido detectada. Debido al confinamiento del color, los gluones aislados no aparecen a bajas energías.
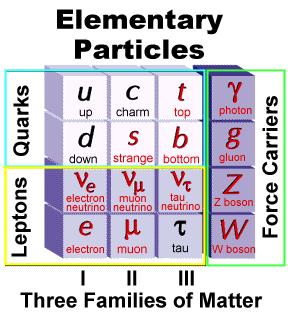
Aquí, en el gráfico, quedan representadas todas las partículas del Modelo estándar, las familias de Quarks y Leptones que conforman la materia y los bones que intermedian en las interacciones o fuerzas fundamentales que están presentes en el Universo. La Gravedad no ha podido ser incluida y se ha negado a estar unida a las otras fuerzas. Así el bosón que la transnmite, tampoco está en el modelo que es incompleto al dejar fuera la fuerza que mantiene unidos los planetas en los sistemas solares, a las galaxias en los cúmulos y nuestros pies unidos a la superficie del planeta que habitamos. Se busca una teoría que permita esta unión y, los físicos, la laman gravedad cuántica pero… ¡no aparece por ninguna parte!

Llegados a este punto tendremos que retroceder, para poder comprender las cosas, hasta aquel trabajo de sólo ocho páginas que publicó Max Planck en 1.900 y lo cambió todo. El mismo Planck se dio de que, todo lo que él había tenido por cierto durante cuarenta años, se derrumbaba con ese trabajo suyo que, venía a decirnos que el mundo de la materia y la nergía estaba hecho a partir de lo que el llamaba “cuantos”.
Supuso el nacimiento de la Mecánica Cuántica (MC), el fin del determinismo clásico y el comienzo de una nueva física, la Física Moderna, de la que la Cuántica sería uno de sus tres pilares junto con la Relatividad y la Teoría del Caos. Más tarde, ha aparecido otra teoría más moderna aún por comprobar, ¿las cuerdas…?

El universo según la teoría de las cuerdas sería entonces una completa extensa polícroma SINFONIA ETERNA de vibraciones, un multiverso infinito de esferas, una de ellas un universo independiente causalmente, en una de esas esferas nuestra vía láctea, en ella nuestro sistema solar, en él nuestro planeta, el planeta tierra en el cual por una secuencia milagrosa de hechos se dió origen a la vida autoconsciente que nos permite preguntarnos del cómo y del por qué de todas las cosas que podemos observar y, también, de las que intiuimos que están ahí sin que se dejen ver.

Claro que, cuando nos adentramos en ese minúsculo “mundo” de lo muy pequeño, las cosas difieren y se apartan de lo que nos dicta el sentido común que, por otra parte, es posible que sea el común de los sentidos. Nos dejamos guiar por lo que observamos, por ese mundo macroscópico que nos rodea y, no somos consciente de ese otro “mundo” que está ahí formando parte del universo y que, de una manera muy importante incide en el mundo de lo grande, sin lo que allí existe, no podría existir lo que existe aquí.
Interacciones en la naturaleza
Albert Einstein habría dicho que “es más importante la imaginación que el conocimiento”, el filósofo Nelson Goodman ha dicho que “las formas y las leyes de nuestros mundos no se encuentran ahí, ante nosotros, listas ser descubiertas, sino que vienen impuestas por las versiones-del-mundo que nosotros inventamos – ya sea en las ciencias, en las artes, en la percepción y en la práctica cotidiana-.”
Sin embargo yo, humilde pensador, me decanto por el hecho cierto de que, nuestra especie, siempre llegó al conocimiento a través de la imaginación y la experiencia primero, a la que más tarde, acompañó largas secciones de estudio y muchas horas de mediatación y, al final de todo eso, llego la experimentación que hizo posible llegar a lugarés ignotos que antes nunca, habían podido ser visitados. De todo ello, pudieron surgir todos esos “nuevos mundos” que, como la Mecanica Cuántica y la Relatividad, nos describían el propio mundo que nos era desconocido.
Cuando comencé éste trabajo sólo quería dar una simple explicación de los bosones y su intervención en el mundo de lo muy pequeño pero…

Demócrito de Abdera
No estaría mal echar una mirada hacia atrás en el tiempo y recordar, en este momento, a Demócrito que, con sus postulados, de alguna manera venía a echar un poco de luz sobre el asunto, dado que él decía que para determinar si algo era un á-tomo habría que ver si era indivisible. En el modelo de los quarks, el protón, en realidad, un conglomerado pegajoso de tres quarks que se mueven rápidamente. Pero como esos quarks están siempre ineludiblemente encadenados los unos a los otros, experimentalmente el protón aparece indivisible.
Acordémonos aquí de que Boscovich decía que, una partícula elemental, o un “á-tomo”, tiene que ser puntual. Y, desde luego, esa , no la pasaba el protón. El equipo del MIT y el SLAC, con la asesoría de Feynman y Bjorken, cayó en la cuenta de que en este caso el criterio operativo era el de los “puntos” y no el de la indivisibilidad. La traducción de sus a un modelo de constituyentes puntuales requería una sutileza mucho mayor que el experimento de Rutherford.

Precisamente por eso era tan conveniente fue tan conveniente para Richard Edward Taylor y su equipo, tener a dos de los mejores teóricos del mundo en el equipo aportando su ingenio, agudeza e intuición en todas las fases del proceso experimental. El resultado fue que los indicaron, efectivamente, la presencia de objetos puntuales en movimiento dentro del protón.

En 1990 Taylor, Friedman y Kendall recogieron su premio Nobel por haber establecido la realidad de los quarks. Sin embargo, a mí lo que siempre me ha llamado más la atención es el hecho cierto de que, este descubrimiento como otros muchos (el caso del positrón de Dirac, por ejemplo), han posible gracias al ingenio de los teóricos que han sabido vislumbrar cómo era en realidad la Naturaleza.
A todo esto, una buena sería: ¿cómo pudieron ver este tipo de partículas de tamaño infinitesimal, si los quarks no están libres y están confinados -en este caso- dentro del protón? Hoy, la tiene poco misterio sabiendo lo que sabemos y hasta donde hemos llegado con el LHC que, con sus inmensas energías “desmenuza” un protón hasta dejar desnudos sus más íntimos secretos.

Este es, el resultado ahora de la colisión de protones en el LHC
Lo cierto es que, en su momento, la teoría de los Quarks hizo muchos conversos, especialmente a medida que los teóricos que escrutaban los fueron imbuyendo a los quarks una realidad creciente, conociendo mejor sus propiedades y convirtiendo la incapacidad de ver quarks libres en una virtud. La de moda en aquellos momentos era “confinamiento”. Los Quarks están confinados permanentemente porque la energía requerida para separarlos aumenta a medida que la distancia entre ellos crece. Esa es, la fuerza nuclear fuerte que está presente dentro del átomo y que se encarga de transmitir los ocho Gluones que mantienen confinados a los Quarks.
Así, cuando el intento de separar a los Quarks es demasiado intenso, la energía se vuelve lo bastante grande para crear un par de quark-anti-quark, y ya tenemos cuatro quarks, o dos mesones. Es como intentar un cabo de cuerda. Se corta y… ¡ya tenemos dos!

¿Cuerdas? Me parece que estoy confundiendo el principal objetivo de este trabajo y, me quiero situar en el tiempo futuro que va, desde los quarks de Gell-Mann hasta las cuerdas de Veneziano y John Schwarz y más tarde Witten. Esto de la Física, a veces te juega malas pasadas y sus complejos caminos te llevan a confundir conceptos y momentos que, en realidad, y de manera individualizada, todos han tenido su propio tiempo y lugar.
¿Cuántas veces no habré pensado, en la posibilidad de tomar el elixir de la sabiduría para poder comprenderlo todo? Sin embargo, esa pósima mágica no existe y, si queremos , el único camino que tenemos a nuestro alcance es la observación, el estudio, el experimento… ¡La Ciencia!, que en definitiva, es la única que nos dirá como es, y como se producen los fenómenos que podemos contemplar en la Naturaleza y, si de camino, podemos llegar a saber el por qué de su comportamiento… ¡mucho mejor!

El camino será largo y, a veces, penoso pero… ¡llegaremos!
Nuestra insaciable curiosidad nos llevará lejos en el saber del “mundo”. llegaremos al corazón mismo de la materia para conmprobar si allí, como algunos imaginan, habitan las cuerdas vibrantes escondidas tan profundamente que no se dejan ver. Sabremos de muchos mundos habitados y podremos hacer ese primer contacto tántas veces soñado con otros seres que, lejos de nuestro región del Sistema solar, también, de manera independiente y con otros nombres, descubrieron la cuántica y la relatividad. Sabremos al fín qué es la Gravedad y por qué no se dejaba juntar con la cuántica. Podremos realizar maravillas que ahora, aunque nuestra imaginación es grande, ni podemos intuir por no tener la información necesaria que requiere la imaginación.
En fín, como decía Hilbert: ¡”Tenemos que saber, sabremos”!
emilio silvera
Feb
18
El Micro Mundo de los Átomos
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (4)
Comments (4)
Cuando por primera vez se puso este trabajo, dio lugar a comentarios que nos llevan hasta la realidad de hasta donde, resulta para nosotros incomprensible ese micro mundo de la cuántica, ese “universo” infinitesimal donde ocurren cosas que, no llegamos a comprender.


Sí, existe otro mundo que no vemos pero, ¡está en éste!
La mecánica cuántica domina en el micromundo de los átomos y de las partículas “elementales”. Nos enseña que en la naturaleza cualquier masa, por sólida o puntual que pueda parecer, tiene un aspecto ondulatorio. Esta onda no es como una onda de agua. Es una onda de información. Nos indica la probabilidad de detectar una partícula. La longitud de onda de una partícula, la longitud cuántica, se hace menor cuanto mayor es la masa de esa partícula.
Por el contrario, la relatividad general era siempre necesaria cuando se trataba con situaciones donde algo viaja a la velocidad de la luz, o está muy cerca o donde la gravedad es muy intensa. Se utiliza para describir la expansión del universo o el comportamiento en situaciones extremas, como la formación de agujeros negros. Sin embargo, la gravedad es muy débil comparada con las fuerzas que unen átomos y moléculas y demasiado débil para tener cualquier efecto sobre la estructura del átomo o de partículas subatómicas, se trata con masas tan insignificantes que la incidencia gravitatoria es despreciable. Todo lo contrario que ocurre en presencia de masas considerables como planetas, estrellas y galaxias, donde la presencia de la gravitación curva el espacio y distorsiona el tiempo.

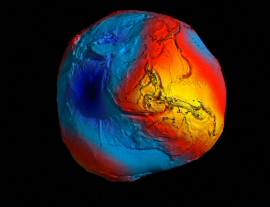
La Gravedad hace que la Tierra se vea como un mapa. Es una vista altamente exagerada, pero ilustra a las claras cómo la atracción gravitatoria que se manifiesta desde la masa de roca bajo nuestros pies no es la misma en todo lugar. La gravedad es más fuerte en áreas amarillas y más débil en las azules. (Imagen tomada por el satélite Goce)
Como resultado de estas propiedades antagónicas, la teoría cuántica y la teoría relativista gobiernan reinos diferentes, muy dispares, en el universo de lo muy pequeño o en el universo de lo muy grande. Nadie ha encontrado la manera de unir, sin fisuras, estas dos teorías en una sola y nueva de Gravedad-Cuántica.
¿Cuáles son los límites de la teoría cuántica y de la teoría de la relatividad general de Einstein? Afortunadamente, hay una respuesta simple y las unidades de Planck nos dicen cuales son.

Supongamos que tomamos toda la masa del universo visible y determinamos su longitud de onda cuántica. Podemos preguntarnos en qué momento esta longitud de onda cuántica del universo visible superará su tamaño. La respuesta es: cuando el universo sea más pequeño en tamaño que la longitud de Planck, es decir, 10-33 centímetros, más joven que el Tiempo de Planck, 10-43 segundos y supere la temperatura de Planck de 1032 grados. Las unidades de Planck marcan la frontera de aplicación de nuestras teorías actuales. Para comprender en que se parece el mundo a una escala menor que la longitud de Planck tenemos que comprender plenamente cómo se entrelaza la incertidumbre cuántica con la gravedad. Para entender lo que podría haber sucedido cerca del suceso que estamos tentados a llamar el principio del universo, o el comienzo del tiempo, tenemos que penetrar la barrera de Planck. Las constantes de la naturaleza marcan las fronteras de nuestro conocimiento existente y nos dejan al descubierto los límites de nuestras teorías.
En los intentos más recientes de crear una teoría nueva para describir la naturaleza cuántica de la gravedad ha emergido un nuevo significado para las unidades naturales de Planck. Parece que el concepto al que llamamos “información” tiene un profundo significado en el universo. Estamos habituados a vivir en lo que llamamos “la edad de la información”. La información puede ser empaquetada en formas electrónicas, enviadas rápidamente y recibidas con más facilidad que nunca antes.

Los tiempos cambian y la manera de informar también, lejos nos queda ya aquellos toscos aparatos impresores del pasado, ahora, en espacios muy reducidos, tenemos guardada más información que antes había en una colección de libros.
Nuestra evolución en el proceso rápido y barato de la información se suele mostrar en una forma que nos permite comprobar la predicción de Gordon Moore, el fundador de Intel, llamada ley de Moore, en la que, en 1.965, advirtió que el área de un transistor se dividía por dos aproximadamente cada 12 meses. En 1.975 revisó su tiempo de reducción a la mitad hasta situarlo en 24 meses. Esta es “la ley de Moore” cada 24 meses se obtiene una circuiteria de ordenador aproximadamente el doble, que corre a velocidad doble, por el mismo precio, ya que, el coste integrado del circuito viene a ser el mismo, constante.

Los límites últimos que podemos esperar para el almacenamiento y los ritmos de procesamiento de la información están impuestos por las constantes de la naturaleza. En 1.981, el físico israelí, Jacob Bekenstein, hizo una predicción inusual que estaba inspirada en su estudio de los agujeros negros. Calculó que hay una cantidad máxima de información que puede almacenarse dentro de cualquier volumen. Esto no debería sorprendernos. Lo que debería hacerlo es que el valor máximo está precisamente determinado por el área de la superficie que rodea al volumen, y no por el propio volumen. El número máximo de bits de información que puede almacenarse en un volumen viene dado precisamente por el cómputo de su área superficial en unidades de Planck. Supongamos que la región es esférica. Entonces su área superficial es precisamente proporcional al cuadrado de su radio, mientras que el área de Planck es proporcional a la longitud de Planck al cuadrado, 10-66 cm2. Esto es muchísimo mayor que cualquier capacidad de almacenamiento de información producida hasta ahora. Asimismo, hay un límite último sobre el ritmo de procesamiento de información que viene impuesto por las constantes de la naturaleza.

La información llega a todos los rincones del Mundo
No debemos descartar la posibilidad de que seamos capaces de utilizar las unidades de Planck-Stoney para clasificar todo el abanico de estructuras que vemos en el universo, desde el mundo de las partículas elementales hasta las más grandes estructuras astronómicas. Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias.
Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y mprotón.
α = 2πe2 / hc ≈ 1/137
αG = (Gmp2)2 / hc ≈ 10-38
La identificación de constantes adimensionales de la naturaleza como a (alfa) y aG, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro.

Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala. La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.
Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck). Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.
Cuando surgen comentarios de números puros y adimensionales, de manera automática aparece en mi mente el número 137. Ese número encierra más de lo que estamos preparados para comprender; me hace pensar y mi imaginación se desboca en múltiples ideas y teorías. Einstein era un campeón en esta clase de ejercicios mentales que él llamaba “libre invención de la mente”. El gran físico creía que no podríamos llegar a las verdades de la naturaleza sólo por la observación y la experimentación. Necesitamos crear conceptos, teorías y postulados de nuestra propia imaginación que posteriormente deben ser explorados para averiguar si existe algo de verdad en ellos. Con los adelantos actuales, estudiando la luz lejana de cuásares muy antiguos, se estudia si la constante de estructura fina (α) ha variado con el paso del tiempo.
El Universo es muy grande, inmensamente grande y, probablemente, todo lo que nuestras mentes puedan imaginar podrá exisitr en alguna parte de esas regiones perdidas en las profundidades cósmicas, en los confines del Espacio- Tiempo, en lugares ignotos de extraña belleza en los que otros mundos y otras criaturas tendrán, su propio habitat que, siendo diferente al nuestro, también, sus criaturas, estarán buscando el significado de las leyes del Universo.
emilio silvera
Feb
10
La Vida de las Partículas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
La Mente: Ese misterio

La mente humana es tan compleja que no todos ante la misma cosa vemos lo mismo. Nos enseñan figuras y dibujos y nos piden que digamos (sin pensarlo) la primera cosa que nos sugiere. De entre diez personas, sólo coinciden tres, los otros siete divergen en la apreciación de lo que el dibujo o la figura les sugiere. Un paisaje puede ser descrito de muy distintas maneras según quién lo pueda contar.

Solo el 1% de las formas de vida que han vivido en la Tierra están ahora presentes, el 99%, por una u otra razón se han extinguido. Sin embargo, ese pequeño tanto por ciento de la vida actual, supone unos cinco millones de especies según algunas estimaciones. La Tierra acoge a todas esas especies u palpita de vida que prolifera por doquier. Hay seres vivos por todas partes y por todos los rincones del inmenso mosaico de ambientes que constituye nuestro planeta encontramos formas de vida, cuyos diseños parecen hechos a propósito para adaptarse a su hábitat, desde las profundidades abisales de los océanos hasta las más altas cumbres, desde las espesas selvas tropicales a las planicies de hielo de los casquetes polares. Se ha estimado la edad de 3.800 millones de años desde que aparecieron los primeros “seres vivos” sobre el planeta (dato de los primeros microfósiles). Desde entonces no han dejado de aparecer más y más especies, de las que la mayoría se han ido extinguiendo. Desde el siglo XVIII en que Carlos Linneo propuso su Systema Naturae no han cesado los intentos por conocer la Biodiversidad…, de la que por cierto nuestra especie, bautizada como Homo sapiens por el propio Linneo, es una recién llegada de apenas 200.000 años.

Ahora, hablaremos de la vida media de las partículas elementales (algunas no tanto). Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida media, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.
También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.

Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, psi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales maneras de desintegración, veríamos como difieren las unas de las otras.

Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.
¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.

Una colisión entre un protón y un anti-protón registrada mediante una cámara de chispas del experimento UA5 del CERN.
En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su carta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas, Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.
Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.

Se habla de ondas cuánticas y también, de ondas gravitacionales. Las primeras han sido localizadas y las segundas están siendo perseguidas.
Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.

Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.
Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”

Si la vida de una partícula es tan corta como 10ˉ²³ segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.

Bariones Delta. Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.
Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).
Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.
Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:
∆⁺⁺→р + π⁺; ∆⁰→р + πˉ; o п+π⁰
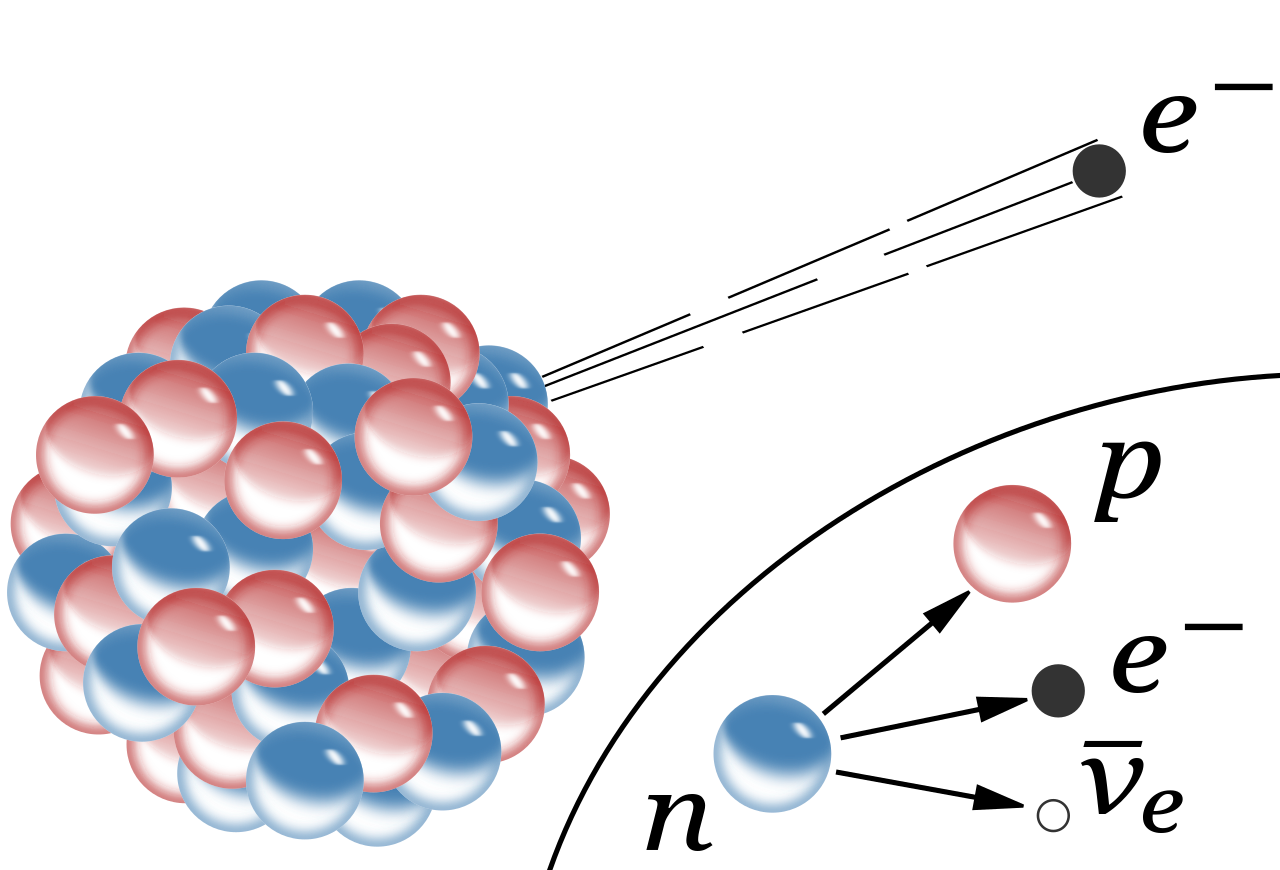
En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.
El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (aunque nos parezca lo contrario), son aún bastante limitados, nos queda mucho por descubrir antes de que podamos decir que dominamos la materia y sabemos de todos sus componentes. Antes de que eso llegue, tendremos que conocer, en profundidad, el verdadero origen de la Luz que esconde muchos secretos que tendremos que desvelar.
Esperemos que con los futuros experimentos del LHC y de los grandes Aceleradores de partículas del futuro, se nos aclaren algo las cosas y podamos avanzar en el perfeccionamiento del Modelo Estándar de la Física de Partículas que, como todos sabemos es un Modelo incompleto que no contiene a todas las fuerzas de la Naturaleza y, cerca de una veintena de sus parámetros son aleatorios y no han sido explicados.(Bueno, ahora son 19 después del descubrimiento del Bosón de Higgs).
Sin embargo, a mí particularmente me quedan muchas dudas al respecto.
emilio silvera
Ene
27
La Ciencia no duerme
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
Ciencia ABC
Hallan, por vez primera, la forma de teletransportar un organismo vivo. Científicos proponen cómo pasar la memoria de un microorganismo a otro en un experimento que parece sacado de Star Trek

La investigación puede ser un espectacuar primer avance en el teletransporte de seres vivos completos – Archivo
Nunca hasta ahora habíamos estado tan cerca de Star Trek y el impresionante teletransportador que permitía a la tripulación de la nave Enterprise desmaterializarse en un punto y reaparecer instantaneamente en otro. Un equipo mixto de investigadores de las Universidades de Purdue, en Estados Unidos, y Tsinghua, en China, ha elaborado, en efecto, el primer esquema realizado hasta ahora para teletransportar el estado cuántico interno (la memoria) de un microorganismo vivo a otro. La investigación constituye un espectacular avance en el camino, hoy propio de la ciencia ficción, del teletransporte de seres vivientes completos.
El esquema propuesto por Tongcan Li y Zhang-qi Yin prevé el uso de osciladores electromecánicos y circuitos superconductores para lograr su ambicioso objetivo. En un artículo publicado en Science Bulletin, los investigadores proponen también un esquema para crear un estado de “Gato de Schrodinger” en el que un microorganismo puede estar en dos lugares al mismo tiempo.

En 1935, Erwin Schroedinger propuso un experimento imaginario que consistía en encerrar un gato vivo dentro de una caja en la que se había introducido también una probeta con gas venenoso y un dispositivo, de una sola partícula radiactiva y que tenía una probabilidad del 50% de desintegrarse en un tiempo dado. Al desintegrarse la partícula, el veneno quedaría liberado y el gato moriría sin remedio. Una vez pasado el tiempo establecido, tendríamos un 50% de probabilidades de que la partícula se haya desintegrado y encontrar que el gato está muerto, y otro 50% de que no haya sido así y el gato siga vivo. En el idioma de la Física Cuántica, estaríamos ante una superposición de dos estados posibles (vivo o muerto) que no se concretará hasta el instante en que se abra la caja. Hasta ese momento, en efecto, podríamos decir sin miedo a equivocarnos que el gato está vivo y muerto al mismo tiempo. Sólo abriendo la caja modificaremos el estado de Superposición y haremos que se concrete una de las dos posibilidades.
Realidades «imposibles»
La idea de Schroedinger sirvió para revelar por primera vez al gran público las profundas implicaciones de la Mecánica Cuántica, en cuyo reino la superposición de estados de las partículas está a la orden del día y es pura rutina para los investigadores, que han tenido que acostumbrarse a realidades “imposibles”, como electrones que están en varios lugares a la vez, partículas que se comunican de forma instantánea sin importar la distancia o que, incluso, son capaces de viajar en el tiempo. Desde el hipotético experimento de Schroedinger, los físicos han dedicado décadas de estudio y esfuerzo para tratar de averiguar si las extrañas leyes que rigen en el universo cuántico pueden trasladarse también al mundo macroscópico. Y es que, después de todo, tanto nosotros como todo lo que nos rodea está hecho de partículas.

Por supuesto, se han hecho ya importantes avances. Y en las últimas dos décadas diversos grupos de investigadores han conseguido cada vez mejores resultados a la hora de “teletransportar” estados cuánticos, primero de partículas individuales (un único fotón, en 1997), después de átomos completos, y últimamente de conjuntos cada vez más numerosos de átomos. Recientemente, por ejemplo, un equipo de la Universidad de Colorado logró llevar al estado cuántico toda una membrada de aluminio de 15 micrómetros de diámetro (un micrómetro es la milésima parte de un milímetro), y “teletransportar” sus características y su movimiento a una serie de fotones aislados.
Pero nadie ha conseguido hacer lo mismo con un organismo vivo. Y todos los experimentos llevados a cabo hasta ahora están aún muy lejos de conseguir teletransportar un organismo, o su estado cuántico.
Bacteria cuántica
En su estudio, Tongcang Li y Zhang-qi Yin proponen colocar una bacteria sobre un oscilador electromecánico integrado en un circuito superconductor para conseguir un estado cuántico de superposición en el organismo y teletransportar después ese estado. En principio, el microorganismo es mucho más pequeño que la membrana del oscilador y no debería, por lo tanto, afectar a su funcionamiento. La bacteria, junto a la membrana, serían llevados a un estado cuántico. Después de lo cual, ese estado se podría teletransportar hasta otro organismo distante por medio de circuitos superconductores de microondas. Dado que los estados internos del organismo contienen información, la propuesta de los investigadores supone, en realidad, un esquema para teletransportar esa información, o memoria, de un organismo vivo a otro.

La configuración propuesta por Tongcang Li y Zhang-qi Yin constituye también un poderoso microscopio, ya que no solo es capaz de detectar la existencia del spin de electrones individuales (que puede asociarse a determinados defectos genéticos), sino que puede también manipular y detectar sus estados cuánticos, permitiendo su uso como “memorias cuánticas”.
En palabras de Li, “proponemos un método sencillo para poner un microorganismo en dos lugares al mismo tiempo, y facilitamos un esquema para teletransportar el estado cuántico de un organismo completo. Espero que nuestro trabajo inspire a otros investigadores para que piensen seriamente sobre la posibilidad de la teleportación cuántica de microorganismos y en sus posibilidades futuras. Nuestro trabajo también proporciona pistas para futuros estudios sobre los efectos de las reacciones bioquímicas en los estados de superposición cuántica de los organismos vivientes”.
















 Totales: 85.700.552
Totales: 85.700.552 Conectados: 45
Conectados: 45