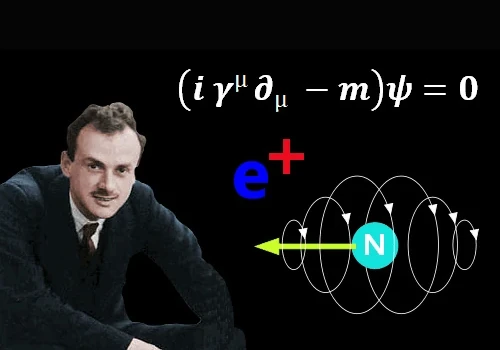Jul
13
¿El Misterio? Persistirá, ¡como el Tiempo!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Naturaleza misteriosa ~
Clasificado en Naturaleza misteriosa ~
 Comments (1)
Comments (1)

Los habitantes de este mundo hemos, hemos conseguido construir un cuadro plausible del Universo, de la Naturaleza que tratamos de comprender. Hemos llegado a ser conscientes de que, en ella, en la Naturaleza, están todas las respuestas que buscamos y, nosotros mismos no hemos llegado a conocernos por ese mismo hecho de que formando parte de la Naturaleza, también somos parte del enigma que tratamos de desvelar.
somos parte del enigma que tratamos de desvelar.
Parece que ahora estamos entrando en la edad adulta, quiero significar que después de siglos y milenios de esporádicos esfuerzos, finalmente hemos llegado a comprender algunos de los hechos fundamentales del Universo, conocimiento que, presumiblemente, es un requisito de la más modesta pretensión de nuestra madurez cosmológica.
estamos entrando en la edad adulta, quiero significar que después de siglos y milenios de esporádicos esfuerzos, finalmente hemos llegado a comprender algunos de los hechos fundamentales del Universo, conocimiento que, presumiblemente, es un requisito de la más modesta pretensión de nuestra madurez cosmológica.

¿ Porqué sabemos que vivimos dentro de una galaxia espiral?


“Las velocidades de las estrellas en la Vía Láctea suele ser de miles de kilómetros por hora

Así sabemos dónde estamos, que vivimos en un planeta que gira alrededor de una estrella situada en el borde de la Galaxia espiral a la que llamamos Vía Láctea, cuya posición ha sido determinada con respecto a varios cúmulos vecinos que, en conjunto, albergan a unas cuarenta mil galaxias extendidas a través de un billón de años-luz cúbicos de espacio.

También sabemos más o menos, cuando hemos entrado en escena, hace unos cinco mil millones de años que se formaron el Sol y los planetas de nuestro Sistema Solar , en un Universo en expansión que probablemente tiene una edad entre dos y cuatro veces mayor. Hemos determinado los mecanismos básicos de la evolución de la Tierra, hallado prueba también de evolución química a escala cósmica y hemos podido aprender suficiente física como para comprender e investigar la Naturaleza en una amplia gama de escalas desde los Quarks saltarines en el “mundo” microscópico hasta el vals de las galaxias.
los Quarks saltarines en el “mundo” microscópico hasta el vals de las galaxias.

El Tiempo inexorable nunca dejó de fluir y mientras eso pasaba, nuestra especie evolucionaba, aprendía al observar los cielos y cómo y por qué pasaban las cosas. Hay realizaciones humanas de las que, en verdad, podemos sentirnos orgullosos. Aquellos habitantes de Sumer y Babilonia, de Egipto o China y también de la India y otros pueblos que dejaron una gran herencia de saber a los Griegos que pusieron al mundo occidental en el camino de la ciencia, nuestra medición del pasado se ha profundizado desde unos pocos miles de años a más de diez mil millones de años, y la del espacio se ha extendido desde un cielo de techo bajo no mucho mayor que la distancia que nos separa de la Luna hasta el radio de más de diez mil millones de años-luz del universo observable.
unos pocos miles de años a más de diez mil millones de años, y la del espacio se ha extendido desde un cielo de techo bajo no mucho mayor que la distancia que nos separa de la Luna hasta el radio de más de diez mil millones de años-luz del universo observable.
Tenemos razones para esperar que nuestra época sea recordada (si por ventura queda alguien para recordarlo) por sus contribuciones al supremo tesoro intelectual de toda la Humanidad unida al contexto del Universo en su conjunto por unos conocimientos que, aunque no suficiente, sí son los necesarios para saber dónde estamos y, ahora , debemos buscar la respuesta a esa pregunta: ¿Hacia dónde vamos?
, debemos buscar la respuesta a esa pregunta: ¿Hacia dónde vamos?

Claro que, el futuro es incierto
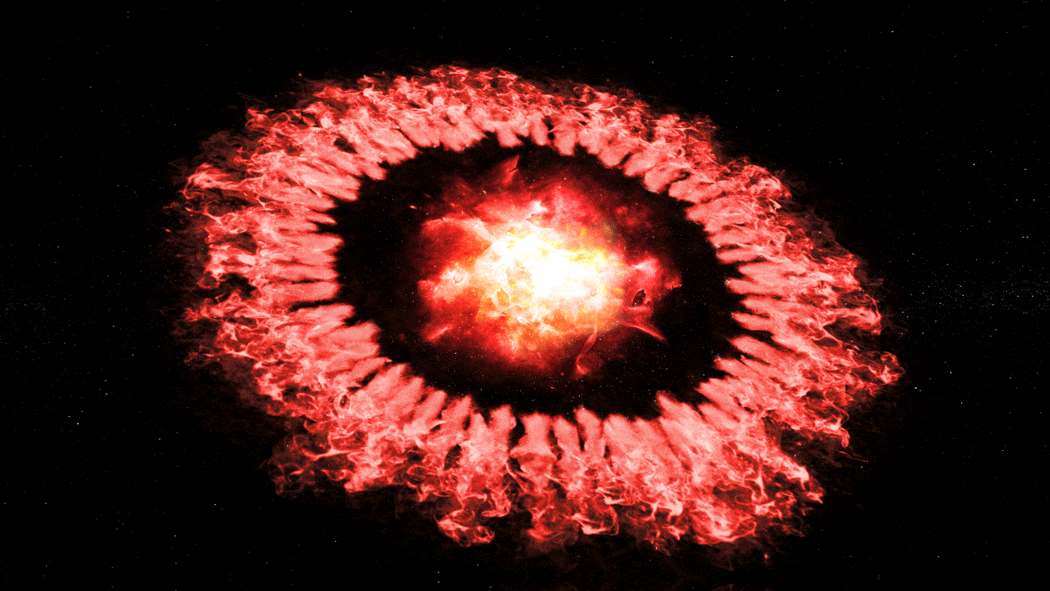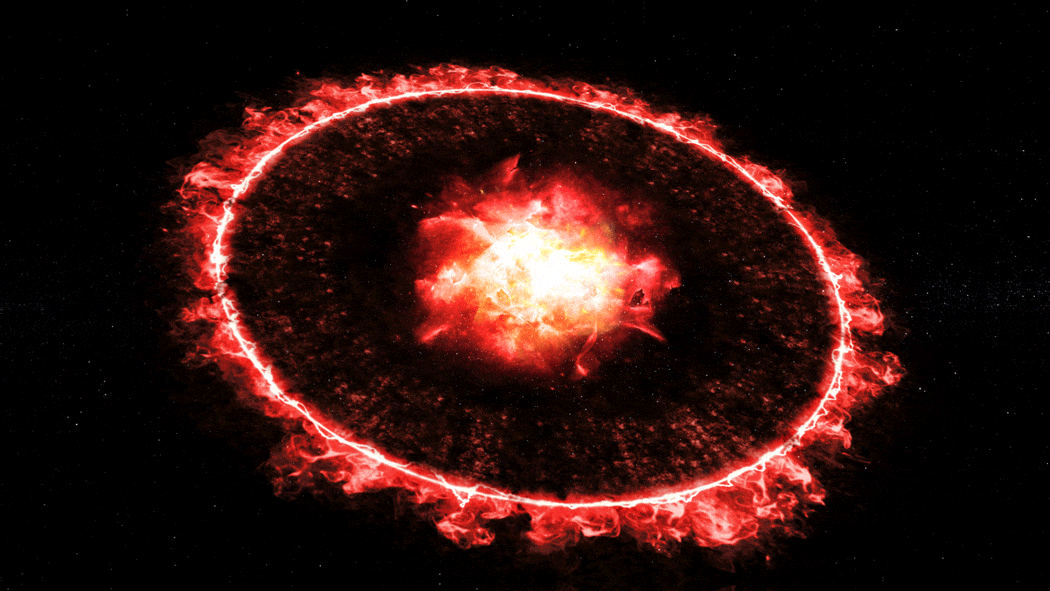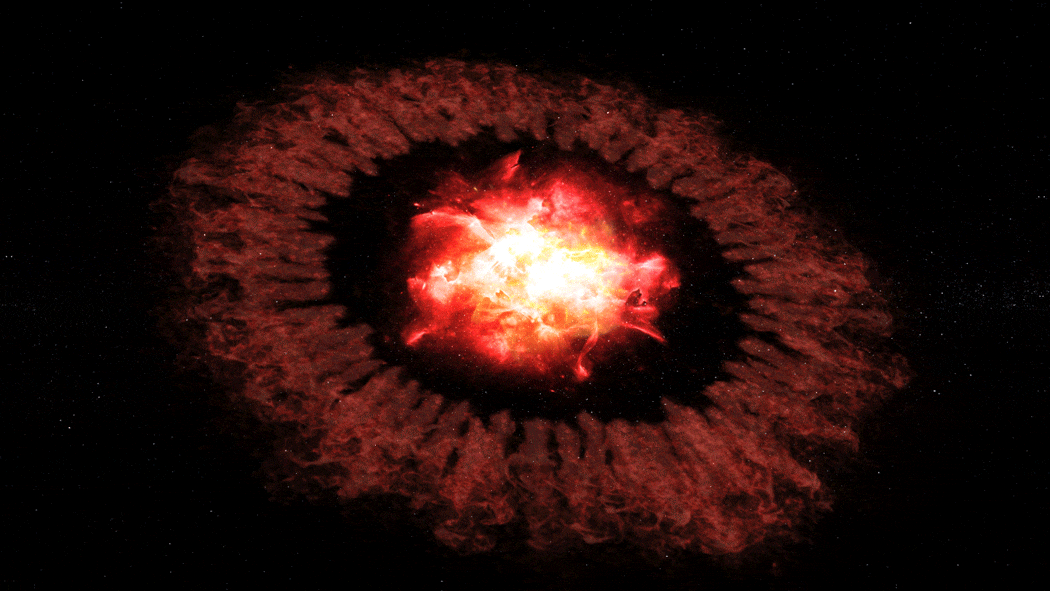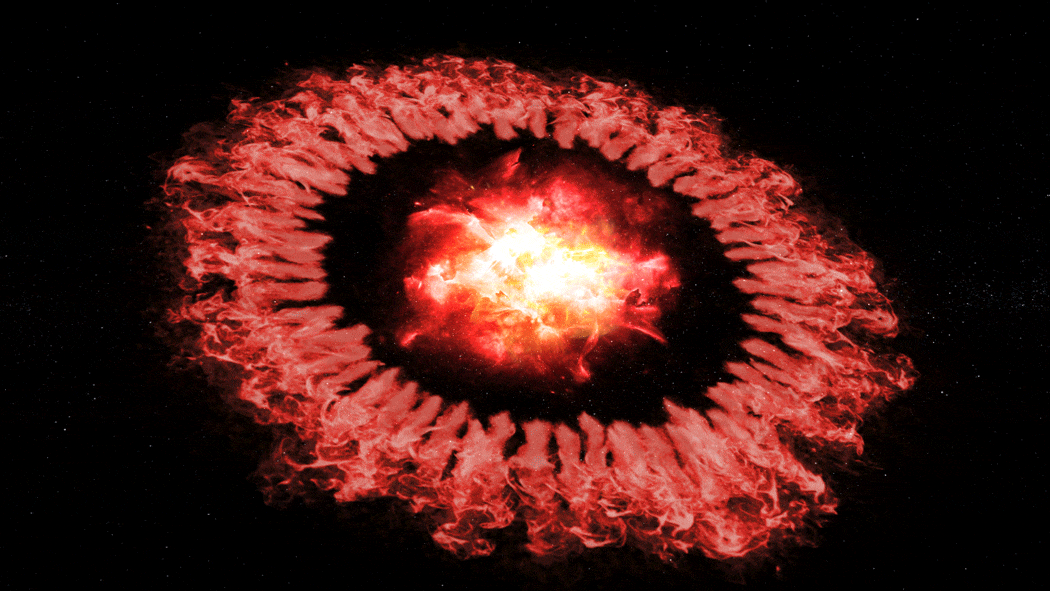
Como en la física, en el mundo y en nuestras vidas, también está presente el principio de incertidumbre y, de ninguna manera, podemos saber del mañana. Sin embargo, cuanto más sabemos del universo, tanto más claramente comprendemos lo poco que sabemos de él. La vastedad del Universo nos lleva a poder comprender algunas estructuras cósmicas y mecanismos que se producen y repiten como, el caso de la destrucción que nos lleva a la construcción. Es decir, una estrella masiva vieja explota y siembre el Caos y la destrucción en una extensa región del espacio, y, es precisamente ese hecho el que posibilita que, nuevas estrellas y nuevos mundos surgan a la vida. Sin embargo, la grandeza, la lejanía, esa inmensidad que se nos escapa a nuestra comprensión terrestre, nunca nos dejará comprender el universo en detalle y, siendo así, siempre tendremos secretos que desvelar y misterios que resolver.
en la física, en el mundo y en nuestras vidas, también está presente el principio de incertidumbre y, de ninguna manera, podemos saber del mañana. Sin embargo, cuanto más sabemos del universo, tanto más claramente comprendemos lo poco que sabemos de él. La vastedad del Universo nos lleva a poder comprender algunas estructuras cósmicas y mecanismos que se producen y repiten como, el caso de la destrucción que nos lleva a la construcción. Es decir, una estrella masiva vieja explota y siembre el Caos y la destrucción en una extensa región del espacio, y, es precisamente ese hecho el que posibilita que, nuevas estrellas y nuevos mundos surgan a la vida. Sin embargo, la grandeza, la lejanía, esa inmensidad que se nos escapa a nuestra comprensión terrestre, nunca nos dejará comprender el universo en detalle y, siendo así, siempre tendremos secretos que desvelar y misterios que resolver.
https://www.google.com/search?newwindow=1&sca_esv=90fe3ab6b3a05dbb&rlz=1C1FHFK_enES1150ES1150&
Hasta llegar aquí, hicimos un largo recorrido
Si añadimos a todo eso que, si poseyésemos un atlas de nuestra propia Galaxia y que dedicase una sola página a cada sistema estelar de la Vía Láctea (de modo que el Sol y sus planetas estuviesen comprimidos en una página), tal atlas tendría más de dies mil millones de volúmenes de diez mil páginas cada uno. Se necesitaría una biblioteca del tamaño de la de Harvard para alojar el Atlas, y solamente ojearlo al ritmo de una página por segundo nos llevaría más de diez mil años. Podemos añadir los detalles de la cartografía planetaria, la potencial biología extraterrestre, las sutilezas de los principios científicos involucrados y las dimensiones históricas del cambio, y se nos hará claro que nunca aprenderemos más que una diminuta fracción de la historia de nuestra Galaxia solamente, y hay cien mil millones de galaxias más.
sistema estelar de la Vía Láctea (de modo que el Sol y sus planetas estuviesen comprimidos en una página), tal atlas tendría más de dies mil millones de volúmenes de diez mil páginas cada uno. Se necesitaría una biblioteca del tamaño de la de Harvard para alojar el Atlas, y solamente ojearlo al ritmo de una página por segundo nos llevaría más de diez mil años. Podemos añadir los detalles de la cartografía planetaria, la potencial biología extraterrestre, las sutilezas de los principios científicos involucrados y las dimensiones históricas del cambio, y se nos hará claro que nunca aprenderemos más que una diminuta fracción de la historia de nuestra Galaxia solamente, y hay cien mil millones de galaxias más.
Sabiendo todo todo esto, siendo consciente de que, realmente, es así, tendremos que convenir con el físico Lewis Thomas cuando dijo:
dijo:
“El mayor de todos los logros de la ciencia del siglo XX ha sido el descubrimiento de la ignorancia humana”.
La ignorancia, como todo en el Universo, es relativa. Nuestra ignorancia, por supuesto, siempre ha estado con nosotros, y siempre seguirá estando, es una compañera con la que cargamos toda nuestra vida y que nos pesa. Algunos procuramos que pese lo menos posible para hacer más llevadero el viaje. Lo nuevo está en nuestras consciencias y de ellas, ha surgido nuestro despertar al comprender de sus abismales dimensiones, y es eso más que otro cosa, lo que señala la madurez de nuestra especie. El espacio puede tener un horizonte y el tiempo un final pero la aventura del aprendizaje siempre será interminable y eterno, quizá (no me he parado a pensarlo) pueda ser esa la única forma de eternidad que pueda existir.
con nosotros, y siempre seguirá estando, es una compañera con la que cargamos toda nuestra vida y que nos pesa. Algunos procuramos que pese lo menos posible para hacer más llevadero el viaje. Lo nuevo está en nuestras consciencias y de ellas, ha surgido nuestro despertar al comprender de sus abismales dimensiones, y es eso más que otro cosa, lo que señala la madurez de nuestra especie. El espacio puede tener un horizonte y el tiempo un final pero la aventura del aprendizaje siempre será interminable y eterno, quizá (no me he parado a pensarlo) pueda ser esa la única forma de eternidad que pueda existir.

La ciencia tiene límites
La dificultad de explicarlo todo no se debe a nuestra debilidad mental, sino a la estructura misma del universo. En los últimos siglos hemos descubierto que la trama del cosmos puede abordarse en varios niveles diferentes. Mientras no se descubre el siguiente nivel, lo que ocurre en el anterior no se puede explicar, sólo puede describirse. En consecuencia, para el último nivel que se conoce en cada momento nunca hay explicaciones, sólo puede haber descripciones.
La Ciencia es intrínsicamente abierta y exploratoria, y comete errores todos los días. En verdad, ese será siempre su destino, de acuerdo con la lógica esencial del segundo teorema de incompletitud de Kurt Gödel. El teorema demuestra que la plena validez de cualquier sistema, inclusive un sistema científico, no puede demostrarse dentro del sistema. Es decir, tiene que haber algo fuera del marco de cualquier teoría para poder comprobarla. La lección que podemos haber aprendido es que, no hay ni habrá nunca una descripción científica completa y comprensiva del universo cuya validez pueda demostrarse.
demostrarse dentro del sistema. Es decir, tiene que haber algo fuera del marco de cualquier teoría para poder comprobarla. La lección que podemos haber aprendido es que, no hay ni habrá nunca una descripción científica completa y comprensiva del universo cuya validez pueda demostrarse.
No es que pertenezcamos al Universo, formamos parte de él
de él
Y, a todo esto, debemos alegrarnos de que así sea, de que no podamos comprender el Universo en toda su inmensa dimensión y diversidad. Nuestras mentes necesitan que así sea y, tendrán, de esa manera, el escenario perfecto para seguir creciendo a medida que busca todas esas respuestas que nos faltan y, lo bueno del caso es que, cada respuesta que encontramos, viene acompañada de un montón de nuevas preguntas y, de esa manera, esa historia interminable de nuestra aventura del saber…llegará hasta la eternidad de nuestro tiempo que, necesariamente, no tiene por que ser el tiempo del universo.
respuesta que encontramos, viene acompañada de un montón de nuevas preguntas y, de esa manera, esa historia interminable de nuestra aventura del saber…llegará hasta la eternidad de nuestro tiempo que, necesariamente, no tiene por que ser el tiempo del universo.
Emilio Silvera Vázquez
Jul
13
¿La Naturaleza? ¡Simetría dentro de la Diversidad!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (1)
Comments (1)
Nuestro mundo, aunque en la Galaxia existan muchos como él (que no los hemos podido encontrar), es un lugar privilegiado que conforma un Ecosistema superior en su conjunto formado por muchos ecosistemas locales aislados los unos de los otros y sin embargo, todos conexionados. La Diversidad de regiones diferentes que existen dentro del mismo planeta es asombrosa y, lo mismo nos podemos encontrar en un lugar como ese que vemos arriba, o en una isla paradisíaca, una selva, un desierto, o perdidos en un inmenso y embravecido océano, en la ventisca de nieve de inmensas montañas y, también, en grutas enormes en las profundidades del planeta.
Pero todos esos climas diferentes son el resultado de la diversidad y, en cada uno de esos lugares ocurren cosas y, la vida, aunque parezca imposible, está allí presente. Es la consecuencia de que el planeta Tierra esté situado en la zona habitable del Sol, ni demasiado cerca para que la vida perezca achicharrada, ni demasiado lejos para que resulte congelada por el frío. Aquí el agua discurre líquida y cantarina por multitud de lugares y hace posible que, entre el preciado líquido y los rayos del Sol que nos envían la luz y el calor necesarios para la fotosíntesis y la vida… ¡Podamos estar aquí!
El electromagnetismo es la rama de la física que estudia las relaciones entre los fenómenos eléctricos y magnéticos, es decir, entre el campo magnético y la corriente eléctrica.
Fuente: https://concepto.de/electromagnetismo/#ixzz5sIhuRCgE





Todos sabemos que la materia en nuestro Universo adopta muchas formas distintas: Galaxias de estrellas y mundos que, en alguna ocasión, pueden incluso tener seres vivos y algunos han podido evolucionar hasta adquirir la consciencia. Sin embargo, no me quería referir a eso que es bien sabido por todos, sino que, trato de pararme un poco sobre una curiosa propiedad que la materia tiene en algunas ocasiones y que, la Naturaleza se empeña en repetir una y otra vez: ¡La Simetría!
La bella galaxia espiral NGC 6744 tiene casi 175.000 años luz de diámetro, es decir, es mayor que la Vía Láctea. Se encuentra a unos 30 millones de años luz de distancia en la constelación austral Pavo y con un pequeño telescopio aparece como un objeto tenue y alargado.
Las Galaxias espirales, la redondez de los mundos, las estrellas del cielo, los árboles y las montañas, los ríos y los océanos, las especies animales (incluida la nuestra) que, se repiten una y otra vez y, en general, salvando particularidades, todas repiten un patrón de simetría.
:format(jpg)/f.elconfidencial.com%2Foriginal%2F872%2F20f%2Fe77%2F87220fe777fdb6c009104f34e8752845.jpg)

Recuerdo aquí aquel pensamiento de Paul Valery en el que nos decía:
“El Universo está construido según un plan cuya profunda simetría está presente de algún modo en la estructura interna de nuestro intelecto.”

La Naturaleza está llena de simetrías
La simetría es una propiedad universal tanto en la vida corriente, como desde un punto de vista matemático desde el quehacer de la Física Teórica. En realidad, lo que observamos en la vida corriente es siempre lo repetitivo, lo simétrico, lo que se puede relacionar entre sí por tener algo común. Es siempre lo mismo dentro de una inmensa diversidad formada por grupos iguales.

En un sentido dinámico, la simetría podemos entenderla como lo que se repite, lo reiterativo, lo que tiende a ser igual. Es decir, los objetos que, por mantener la misma geometría, son representativos de otros objetos. En el Caos matemático encontramos concepción de la simetría en el mundo los fractales. Sin embargo, la simetría es mucho más. Hay distintas maneras de expresarla: “Conjunto de invariancias de un sistema”, podría ser una de ellas. Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado, la simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y las rotaciones en las moléculas y las translaciones en las redes cristalinas.
Aquí hay mucho más de lo que a simple vista parece
Los físicos teóricos también se guían en sus investigaciones por motivaciones estéticas tanto como racionales. Poincaré escribió: “Para hacer ciencia, es necesario algo más que la pura lógica”. Él identificó ese elemento adicional como la intuición, que supone “el sentido de la belleza matemática”. Heisenberg hablaba de “la simplicidad y belleza de los esquemas matemáticos que la Naturaleza nos presenta”.

La simetría está presente por todas partes y, cada objeto, tiene la suya que siempre, está relacionada con la de otro de la misma especie. Hay simetrías que en física incluye todos los rasgos de un sistema físico que exhibe propiedades de la simetría – eso es, que bajo ciertas transformaciones, aspectos de esos sistemas son “incambiables”, de acuerdo a una observación particular. Una simetría de un sistema físico es un rasgo físico o matemático de un sistema que es preservado sobre cierto cambio.
En matemática, una transformación es un operador aplicado a una función tal que bajo esa transformación, ciertas operaciones sean simplificadas. En ejemplo, en la aritmética cuando se busca un algoritmo de números, el proceso de búsqueda es reducido a la suma de los algoritmos de cada factor.

Por ejemplo, veamos la invariancia de escala: En un recipiente con agua a punto de hervor, las burbujas de vapor, nucleadas en el fondo del recipiente, crecen, se liberan, y fluctúan hasta la superficie de donde se escapan para la atmósfera. A la temperatura de ebullición, el agua existe al mismo tiempo en dos fases distintas – líquido y gas – y a medida que las burbujas se forman las dos fases se separan en el espacio. Si cerramos el recipiente la temperatura de ebullición aumenta, como en una olla a presión. A medida que la presión aumenta, el sistema llega al punto crítico, donde las propiedades del líquido y del gas se vuelven idénticas. Por encima de esa temperatura, en el régimen supercrítico, dejan de existir dos fases distintas y existe apenas un fluido homogéneo.

Cerca del punto crítico, la materia fluctúa sin límites. Burbujas y gotas, unas tan pequeñas como unos cuantos átomos, otras tan grandes como el recipiente, aparecen y desaparecen, se unen y se separan. Exactamente en el punto crítico la escala de las mayores fluctuaciones divergen, pero el efecto de las fluctuaciones en escalas menores no es despreciable. La distribución de las fluctuaciones es invariable para transformaciones de escala.
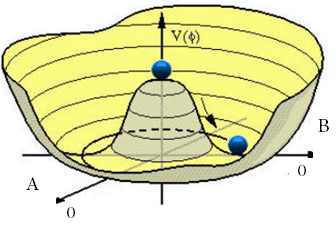
De la figura se deduce que la teoría tiene una “simetría interna”: la figura no cambia cuando hacemos rotaciones en el plano definido por A y B. La invariancia es definida matemáticamente por transformaciones que dejan magnitudes sin cambio. Por ejemplo, la distancia entre dos puntos de un sólido que se mueve, pero no se deforma.
Simetrías locales y globales
Una simetría global es una simetría que sostiene todos los puntos en el tiempo-espacio bajo consideración, a diferencia de la simetría local que solo sostiene a un subconjunto de puntos.
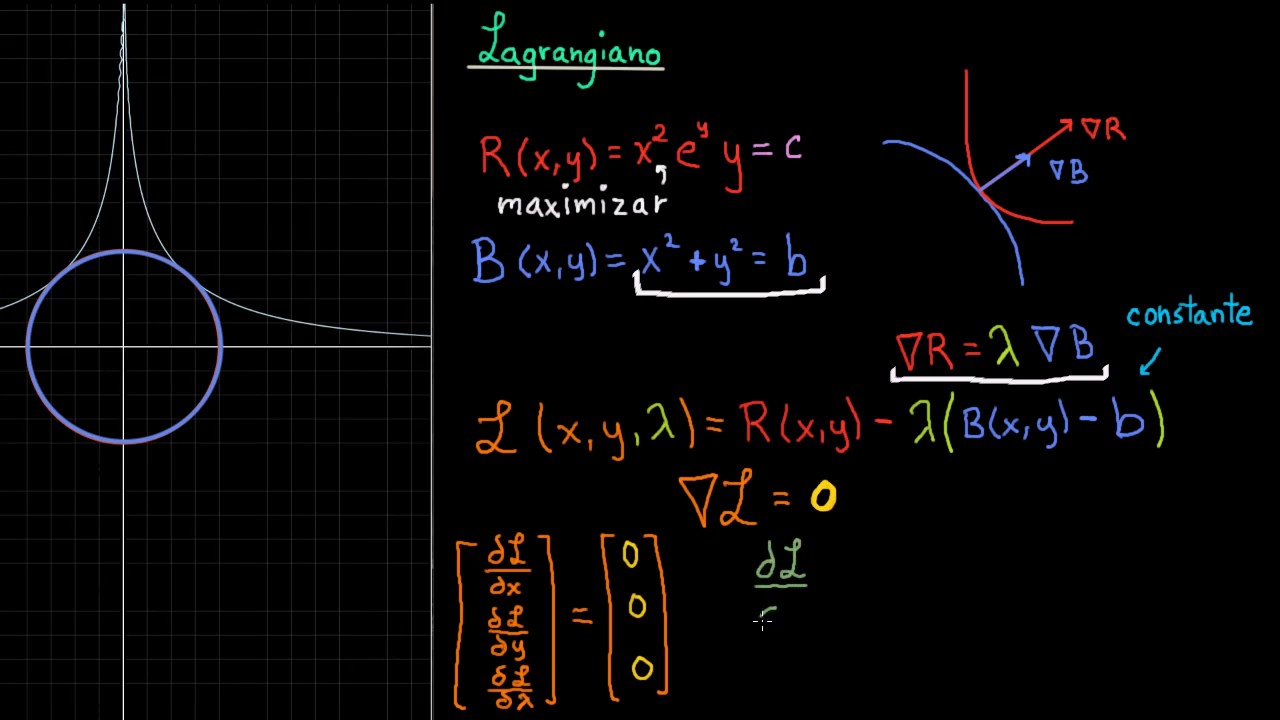
La mayoría de las teorías físicas son descritas por lagrangianos (En física, un lagrangiano es una función matemática a partir del cual se pueden derivar la evolución temporal, las leyes de conservación y otras propiedades importantes de un sistema físico) que son invariantes bajo ciertas transformaciones, cuando las transformaciones son realizadas en diferentes puntos del espacio-tiempo y están relacionadas linealmente – ellas tienen simetría global.
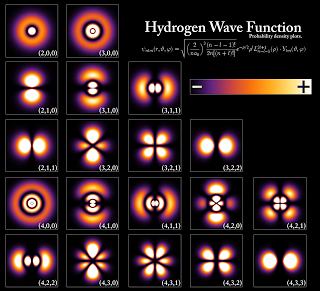

Por ejemplo, en toda teoría cuántica la fase global de una función de onda es arbitraria y no representa algo físico. Consecuentemente, la teoría es invariante bajo a cambio global de fases (Agregando una constante a la fase de todas las funciones de onda, en todos lados); esto es una simetría global. En la electrodinámica quántica, la teoría es también invariante bajo un cambio local de fase, es decir, que se puede alterar la fase de todas las funciones de onda tal que la alteración sea diferente en cada punto del espacio-tiempo. Esto es una simetría local.
También se habla de ruptura de simetrías temporales en la física de partículas
Los físicos creen también que están en el camino correcto porque, de algún modo que no pueden explicar, tienen la convicción de que son correctas, y las ideas de simetría son esenciales para esa intuición. Se presiente que es correcto que ningún lugar del Universo es especial comparado con cualquier otro lugar del Universo, así que los físicos tienen la confianza de que la simetría de traslación debería estar las simetrías de las leyes de la Naturaleza. Se presiente que es correcto que ningún movimiento a velocidad constante es especial comparado con cualquier otro. De modo que los físicos tienen confianza en que la relatividad especial, al abrazar plenamente la simetría entre todos los observadores con velocidad constante, es una parte esencial de las leyes de la Naturaleza.
“Sí, la identidad de Euler, expresada como e^(iπ) + 1 = 0, es ampliamente considerada una de las ecuaciones más bellas de las matemáticas. Esta afirmación se debe a que relaciona de manera elegante cinco de las constantes matemáticas más fundamentales: el número de Euler (e), la unidad imaginaria (i), el número pi (π), el número 1 y el número 0. “
Se dice que esta ecuación de Euler es la más bella conocida. Aunque son muchas las ecuaciones que podríamos traer aquí y que son de todos conocidas y han quedado como símbolos en la historia de las matemáticas, la de Euler, es posible que por su elegancia y simplicidad, le pueda ganar a las demás en belleza. Ahí, en ese sencillo conjunto, los números más significativos de las matemáticas se abrazan: o, 1, e, π, y la unidad imaginaria i .
Si se fijan en la fórmula, en ella aparecen los 5 números más importantes en la historia de las matemáticas. El 0 y el 1 que, entre otras aportaciones a esta disciplina, son famosos por ser elementos neutros y, por lo tanto, indispensables en las operaciones de suma y producto; los números π y e, posiblemente, los dos irracionales más famosos (junto con φ, la razón áurea) que existen (y que nos permiten hacer el chiste aquel de que la parte más irracional de nuestro cuerpo es el pi-e); y la unidad imaginaria, i, cuyo valor es:
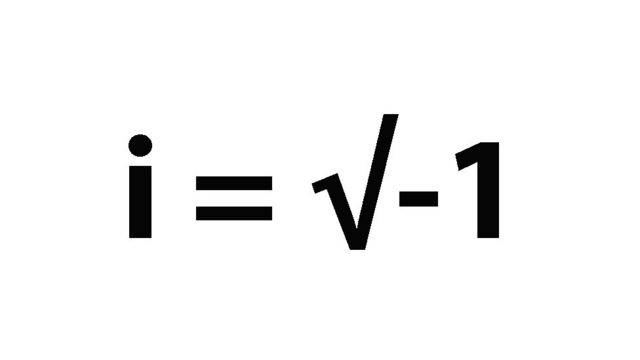
La BBC Earth le preguntó a matemáticos y físicos qué ecuaciones piensan que son las más hermosas. ¡Aquí las 12 elegidas! las ecuaciones que ellos piensan son las más bonitas.
La ecuación de Dirac arriba
La ecuación fue descubierta por el físico Paul Dirac a finales de los años 20 y junta la mecánica cuántica y la teoría especial de Einstein de la relatividad, que describe el comportamiento de objetos en movimiento rápido. En otras palabras, explica cómo las partículas se comportan cuando viajan a casi la velocidad de la luz.
La fórmula de Riemann
La fórmula de Riemann permite calcular los números primos por debajo de un número dado.Permite calcular los números primos por debajo de un número dado. “Son los números más básicos e importantes en el corazón del mundo de la matemática. Pero sorprendentemente, a pesar de más de 2000 años de investigación, todavía no los entendemos.

Pi es la ecuación de la circunferencia, la relación entre la circunferencia y el diámetro de un círculo. Además es un número irracional, lo que significa que los dígitos pueden continuar indefinidamente sin que se repitan.
Euler-Lagrange
Esta ecuación se utiliza para analizar todo. “Más que una ecuación, es una receta para generar una infinita variedad de posibles leyes de física”, comenta Andrew Pontzen de la University College London.
La entidad de Euler explicada más arriba
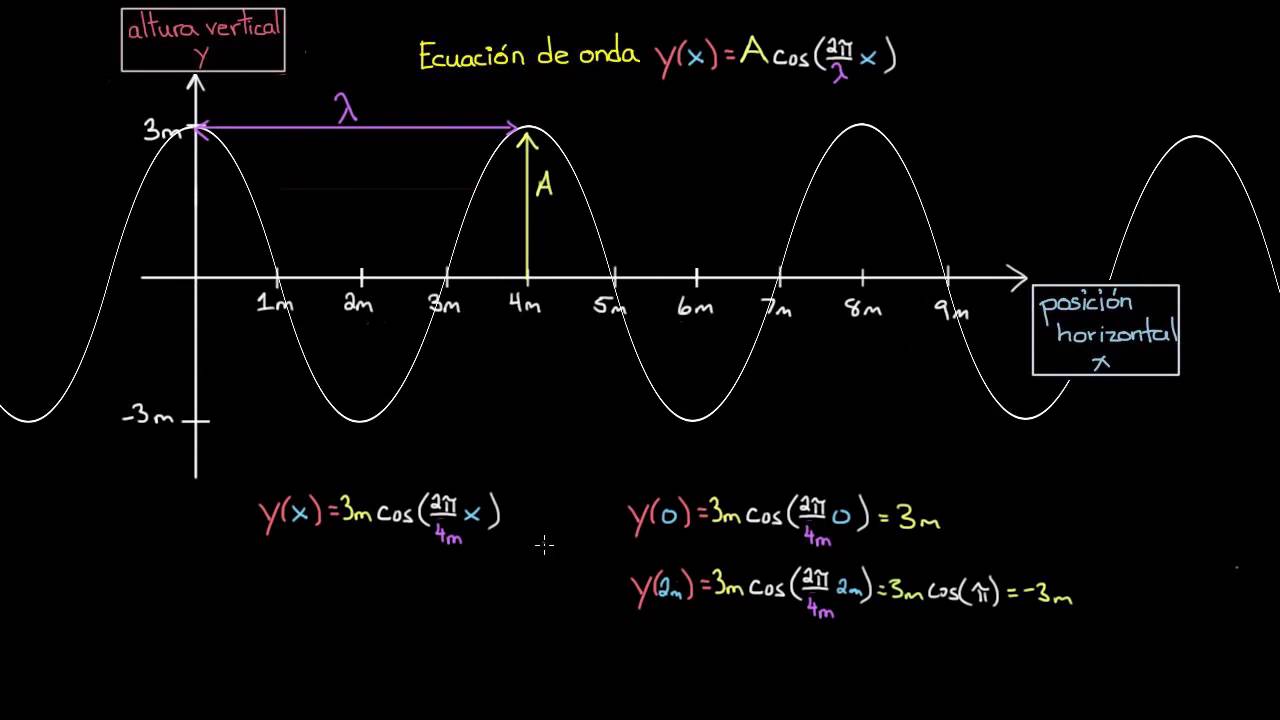
“La belleza de la ecuación de la onda se manifiesta de muchas formas”, explica Ian Stewart de la universidad de Warwick del Reino Unido. Se aplica a todo tipo de ondas, desde las de agua a las de sonido y vibraciones. Incluso a las ondas de luz y radio.
Este teorema tiene más usos de los que uno se imagina, calcula la probabilidad que un evento (A) sea real, dado que otro evento (B) también lo es. Tiene muchos usos, como para detectar fallas de vigilancia, defensa militar, operaciones de búsqueda y rescate, en escáneres médicos en incluso para filtros de correos electrónicos no deseados.
Pasamos a la ecuación de campo de Einstein
La materia le dice al Espacio como curvarse y el Espacio le dice a la materia como moverse
Estas ecuaciones son en realidad un sumario de diez ecuaciones. Katie Mack, de la universidad de Melbourne en Australia, explica que estas fórmulas cambiaron completamente cómo entendemos la naturaleza y evolución del Universo. La ecuación de Einstein nos puede decir cómo nuestro universo ha cambiado con el tiempo, y ofrece un vistazo de los primeros momentos de la creación
La Naturaleza nos la muestra por todas partes
La simetría es un concepto venerable y en modo alguno inescrutable y no podemos negar que tiene muchas implicaciones en la Ciencia, en las Artes y sobre todo, ¡en la Naturaleza! que de manera constante nos habla de ella. Miremos donde miremos…¡allí está!
El físico chino-norteamericano Chen Ning Yang ganó el Nóbel de Física por su en el desarrollo de una teoría de campos basada en la simetría y, aún afirmaba: “No comprendemos todavía el alcance del concepto de simetría”. Es lógico pensar que, si la Naturaleza emplea la simetría en sus obras, la razón debe estar implicada con la eficacia de los sistemas simétricos.
En griego, la palabra simetría significa “la misma medida” (syn significa “juntos”, como en sinfonía, una unión de sonidos, y metrón, “medición”); así su etimología nos informa que la simetría supone la repetición de una cantidad medible. Pero la simetría los griegos, también significaba la “la debida proporción”, lo que implicaba que la repetición involucrada debía ser armoniosa y placentera, como de hecho, resultan ser en las imágenes que arriba contemplamos. Así, la Naturaleza nos está indicando que una relación simétrica debe ser juzgada por un criterio estético superior.
Muchos de nosotros, la mayoría, conocimos la simetría en sus manifestaciones geométricas de aquellas primeras clases en la Escuela Elemental, más tarde en el arte y, finalmente, la pudimos percibir en la Naturaleza, en el Universo y en nosotros mismos que, de alguna manera, somos de ese Universo de simetría.
Los planetas son esféricos y, por ejemplo, tienen simetría de rotación. Lo que quiere indicar es que poseen una característica -en caso, su perfil circular- que permanece invariante en la transformación producida cuando la Natuiraleza los hace rotar. Las esferas pueden Hacerse rotar en cualquier eje y en cualquier grado sin que cambie su perfil, lo cual hace que sea más simétrica.

La clave de la belleza está en la simetría
La simetría por rotación se encuentra en los pétalos de una flor o en los tentáculos de una medusa: aunque sus cuerpos roten, permanecen iguales. La simetría bilateral que hace que los lados derecho e izquierdo sean iguales y se presenta en casi todos los animales, incluido nosotros. Pero es uniendo estos aspectos se obtienen figuras realmente armoniosas. Si se trata de desplazamiento y rotación en un mismo plano hablamos de una espiral, mientras que en el espacio sería una hélice, aunque ambas se encuentran por todas partes en la naturaleza.

Asimetría facial
Arquitectura asimétrica
La asimetría, la falta de simetría, a menudo se considera una fuente de belleza y singularidad. Aunque la simetría es un ideal en muchas áreas, la asimetría puede añadir carácter, individualidad, y un atractivo muy particular de alguien o de alguna cosa, veamos en el arte y en la arquitectura cuanta asimetría está presente en algunas obras, y, no digamos en el rostro humano.


Las simetrías se generan mediante las fuerzas que actúan sobre los cuerpos, descritas por leyes rigurosas e inequívocas, como una fórmula matemática y dependen de la existencia de fuerzas distintas que actúan en diversas direcciones. Si éstas permanecen en equilibrio, no hay preferencia alguna hacia arriba o abajo, a la derecha o a la izquierda, y los cuerpos tenderán a ser perfectamente esféricos, como suele ocurrir en el caso de virus y bacterias, las estrellas y los mundos… las galaxias. Además, cuando el aspecto no es el de una esfera perfecta, la Naturaleza hará todo lo posible para acercarse a esta.

La simetría también están presentes en nuestros cerebros
¿Sería posible que la simetría material tuviera un paralelismo en la abstracción intelectual que son las leyes físicas? luego hace falta un esfuerzo mental considerable para pasar de lo material a lo intelectual, pero cuando se profundiza en ellla, la conexión aparece. En la naturaleza existen muchas cosas que nos pueden llevar a pensar en lo complejo que puede llegar a resultar entender cosas que, a primera vista, parecían sencillas.
Me explico:

Fijémonos, por ejemplo, en una Flor de Girasol y en las matemáticas que sus semillas conllevan. Forman una serie de números en la que cifra es la suma de las dos precedentes (por ejemplo 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…) se denomina, en términos matemáticos, sucesión de Fibonacci, una ley que se cumple incluso en el mundo vegetal, como hemos podido comprobar en las semillas del girasol, dispuestas en espiral y que respetan ésta fórmula. La podemos ver por todas partes.

Lo mismo ocurre con otros ejemplares de la diversidad del mundo de las plantas
En el mundo inorgánico las leyes de la cristalización del agua congelada, determinadas por las fuerzas que actúan entre las moléculas, hacen que los cristales adopten formas que son infinitas y varían con respecto a un tema común: la estrella de seis puntas. Sin embargo, los planetas son esféricos porque han nacido en la primordial que rodeaba al Sol, atrayendo materia indiferentemente de todas partes.

Claro que, en la Naturaleza, nada ocurre porque sí, todo tiene su por qué, y, todo lo que en ella podemos contemplar posee una funcionalidad que está directamente relacionada con su mecánica, con el medio en el que habita, con lo que el Universo espera que haga en su medio y, para ello, dota a figura con aquellos “trajes” que mejor les permita realizar aquello para lo que están destinados.
Vamos a generalizar un paso más el concepto de simetría, planteándonos si es posible que una ley física se cumpla en cualquier lugar. ¿En cualquier lugar… de dónde?, ¿de nuestra ciudad?, ¿de nuestro planeta? No: del universo. Una ley que fuera válida en cualquier lugar del universo sería una ley simétrica respecto al espacio. Se cumpliría dondequiera que se hiciese un experimento para comprobarla.
Fíjense que nuestra idea de simetría se va haciendo más compleja y más profunda. no nos detenemos en ver si la forma material de un objeto es simétrica, ni de si la escritura de una fórmula matemática es simétrica. Ahora nos preguntamos si una ley física es válida en todo el Universo.
La otra simetría interesante para una ley física es la que se refiere al tiempo. Cierta ley física se cumple ; ¿antes también?, ¿se cumplirá pasado algún tiempo? Una ley que fuera cierta en cualquier instante de la historia del universo sería una ley simétrica respecto al tiempo.

Lo que nos preguntamos es: ¿son simétricas o no las leyes de la física?
Hasta donde alcanzan nuestras medidas, las leyes físicas (y, por tanto, la interacción gravitatoria) sí son simétricas respecto al espacio y respecto al tiempo. En cualquier lugar y momento temporal del universo, la Naturaleza se comporta igual que aquí y ahora en lo que se refiere a estas leyes.
Esta simetría es un arma muy poderosa para investigar hacia el pasado y hacia el futuro, ya que nos permite suponer (y, en la medida en que confiemos en la seguridad de la simetría, conocer) locales donde jamás podremos llegar por la distancia espacial y temporal que nos separa de muchas partes del universo. Así, por ejemplo, gracias a esta simetría, podemos calcular que el Sol lleva 5.000 millones de años produciendo energía y que le quedan, probablemente, otros 5.000 millones hasta que consuma toda su masa. Esto lo podemos aventurar suponiendo que en ese enorme tramo de 5.000 + 5.000 = 10.000 millones de años las leyes físicas que determinan los procesos mediante los cuales el Sol consume su propia masa como combustible (las reacciones nucleares que le permiten producir energía), fueron, son y serán las mismas aquí en el Brazo de Orión donde nos encontramos como en los arrabales de la Galaxia Andrómeda donde luce una estrella como nuestro Sol que, también envía luz y calor a sus planetas circundantes, y, por muy lejos que podamos mirar, siempre veremos lo mismo.
Por tanto, en cierto modo, la simetría se vuelve tan importante o más que la propia ley física.

La regularidad de las formas de la Naturaleza se refleja incluso en la cultura humana, que desde siempre intenta inspirarse en el mundo natural conformar su propio mundo. Existen hélices en las escaleras de palacios, castillos y minaretes y en las decoraciones de esculturas y columnas. Las espirales abundan en los vasos, en los bajorrelieves, en los cuadros, en las esculturas en los collares egipcios, griegos, celtas, precolombinos e hindúes e, incluso, en los tatuajes con los que los maoríes neozelandeses se decoran el rostro.

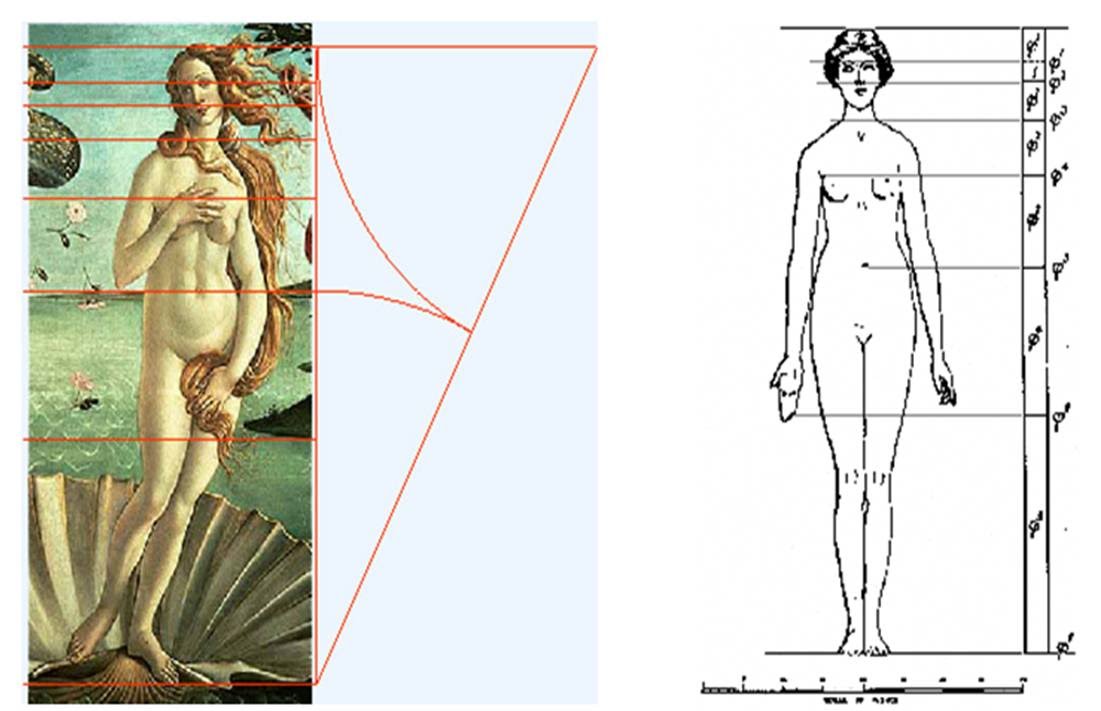
¿Tenía en mente Leonardo la proporción áurea a la hora de realizar su obra maestra? Afirmarlo resultaría aventurado. Menos polémico es aseverar que el genio florentino concedía gran importancia a la relación entre la estética y la matemática. Dejaremos la cuestión en el aire por el momento, no sin antes mencionar que Leonardo realizó las ilustraciones de una obra de contenido estrictamente matemático, escrita por su buen amigo Luca Pacioli, llamada “De divina proportione”, es decir, “La divina proporción”.
La búsqueda de la perfección geométrica y de las propiedades matemáticas pueden ser una guía importante en el estudio científico del mundo. Paul Dirac, una de los padres de la moderna mecánica cuántica, solía decir que “si una teoría es bella desde el punto de vista matemático, muy probablemente es también verdadera”.

A todo esto, no debemos olvidar que todo, sin excepción, en nuestro Universo, está sometido a la Entropía que nos trae el paso inexorable de eso que llamamos “Tiempo”, y que, convierte perfectas simetrías de joven belleza, en deteriorados objetos o entidades que, nos viene a recordar que nada es perpetuo, que todo pasa y se transforma. Claro que, de alguna manera, todo vuelve a resurgir.

La Belleza más valiosa no la podemos ver. ¡Vive en el interior!
Un dolor que llevo dentro de mí es el no poder contemplar la verdadera belleza que estando presente en los seres vivos inteligentes, en la mayoría de los casos, se nos queda oculta a nuestra percepción, toda vez que esa clase de belleza, que no podemos ver pero sí percibir, sólo la podemos captar con el trato y la convivencia y, verdaderamente, tengo que admitir que, algunas bellezas que he tenido la suerte de poder “ver con los ojos del espíritu”, llegan a ser segadoras, deslumbrantes, su esplendor es muy superior al de la estrella más brillante del cielo, y, seguramente (estoy seguro) como a muchos de ustedes les pasa, tengo la suerte de tenerla junto a mí desde hace muchos años. y, si pienso en ello en profundidad y detenimiento, no tengo más remedio que concluir que es ese brillo y esplendor el que me da la fuerza para seguir cada día en la dura lucha que nos ha participar.
¡Sí que es importante la Belleza! Dirac tenía toda la razón. Y, no digamos las Simetrías que nos señala el dedo de la Naturaleza el camino a seguir a muchos físicos que quieren desvelar sus secretos.
Emilio Silvera V.
Jul
13
Velocidades inimaginables
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (9)
Comments (9)

El núcleo tiene dimensiones muy reducidas. Ocupa la parte central del átomo; en él reside toda la carga positiva y casi la totalidad de la masa atómica. Está formado fundamentalmente por protones y neutrones. Los protones tienen una carga positiva cuantitativamente igual a la del electrón (1,602 x 10-19 culombios).
En el centro del átomo se encuentra un pequeño grano compacto aproximadamente 100.000 veces más pequeño que el propio átomo: el núcleo atómico. Su masa, e incluso más aún su carga eléctrica, determinan las propiedades del átomo del cual forma parte. Debido a la solidez del núcleo parece que los átomos, que dan forma a nuestro mundo cotidiano, son intercambiables entre sí, e incluso cuando interaccionan entre ellos para formar sustancias químicas (los elementos). Pero el núcleo, a pesar de ser tan sólido, puede partirse. Si dos átomos chocan uno contra el otro con gran velocidad podría suceder que los núcleos llegaran a chocar entre sí y entonces, o bien se rompen en trozos, o se funden liberando en el proceso partículas subnucleares. La nueva física de la primera mitad del siglo XX estuvo dominada por los nuevos acertijos que estas partículas planteaban.

Pero tenemos la mecánica cuántica; ¿es que no es aplicable siempre?, ¿Cuál es la dificultad? Desde luego, la mecánica cuántica es válida para las partículas subatómicas, pero hay más que eso. Las fuerzas con que estas partículas interaccionan y que mantienen el núcleo atómico unido son tan fuertes que las velocidades a las que tienen que moverse dentro y fuera del núcleo están cerca de la velocidad de la luz, c, que es de 299.792’458 Km/s. Cuando tratamos con velocidades tan altas se necesita una segunda modificación a las leyes de la física del siglo XIX; tenemos que contar con la teoría de la relatividad especial de Einstein.
Esta teoría también fue el resultado de una publicación de Einstein de 1905. en esta teoría quedaron sentadas las bases de que el movimiento y el reposo son conceptos relativos, no son absolutos, como tampoco habrá un sistema de referencia absoluto con respecto al cual uno pueda medir la velocidad de la luz.

Pero había más cosas que tenían que ser relativas. En este teoría, la masa y la energía también dependen de la velocidad, como lo hacen la intensidad del campo eléctrico y del magnético. Einstein descubrió que la masa de una partícula es siempre proporcional a la energía que contienen, supuesto que se haya tenido en cuenta una gran cantidad de energía en reposo de una partícula cualquiera, como se denota a continuación:
E =mc2 La ecuación nos dice que masa y energía son la misma cosa.
Como la velocidad de la luz es muy grande, esta ecuación sugiere que cada partícula debe almacenar una cantidad enorme de energía, y en parte esta predicción fue la que hizo que la teoría de la relatividad tuviese tanta importancia para la física (¡y para todo el mundo!). Para que la teoría de la relatividad también sea auto-consistente tiene que ser holista, esto es, que todas las cosas y todo el mundo obedezcan a las leyes de la relatividad. No son sólo los relojes los que se atrasan a grandes velocidades, sino que todos los procesos animados se comportan de la forma tan inusual que describe esta teoría cuando nos acercamos a la velocidad de la luz. El corazón humano es simplemente un reloj biológico y latirá a una velocidad menor cuando viaje en un vehículo espacial a velocidades cercanas a la de la luz. Este extraño fenómeno conduce a lo que se conoce como la “paradoja de los gemelos”, sugerida por Einstein, en la que dos gemelos idénticos tienen diferente edad cuando se reencuentran después de que uno haya permanecido en la Tierra mientras que el otro ha viajado a velocidades relativistas.
Einstein comprendió rápidamente que las leyes de la gravedad también tendrían que ser modificadas para que cumplieran el principio relativista.

La formulación de newton es bien conocida, en la segunda imagen que se representan en este esquema dos partículas que se acercan entre sí siguiendo un movimiento acelerado. La interpretación newtoniana supone que el espacio-tiempo es llano y que lo que provoca la curvatura de las líneas de universo es la fuerza de interacción gravitatoria entre ambas partículas. Por el contrario, la interpretación einsteiniana supone que las líneas de universo de estas partículas son geodésicas (“rectas”), y que es la propia curvatura del espacio tiempo lo que provoca su aproximación progresiva.
Para poder aplicar el principio de la relatividad a la fuerza gravitatoria, el principio tuvo que ser extendido de la siguiente manera: no sólo debe ser imposible determinar la velocidad absoluta del laboratorio, sino que también es imposible distinguir los cambios de velocidad de los efectos de una fuerza gravitatoria.
Einstein comprendió que la consecuencia de esto era que la gravedad hace al espacio-tiempo lo que la humedad a una hoja de papel: deformar la superficie con desigualdades que no se pueden eliminar. Hoy en día se conocen muy bien las matemáticas de los espacios curvos, pero en el época de Einstein el uso de estas nociones matemáticas tan abstractas para formular leyes físicas era algo completamente nuevo, y le llevó varios años encontrar la herramienta matemática adecuada para formular su teoría general de la relatividad que describe cómo se curva el espacio en presencia de grandes masas como planetas y estrellas.
Einstein tenía la idea en su mente desde 1907 (la relatividad especial la formuló en 1905), y se pasó 8 años buscando las matemáticas adecuadas para su formulación.
Leyendo el material enviado por un amigo al que pidió ayuda, Einstein quedó paralizado. Ante él, en la primera página de una conferencia dada ante el Sindicato de Carpinteros, 60 años antes por un tal Riemann, tenía la solución a sus desvelos: el tensor métrico de Riemann, que le permitiría utilizar una geometría espacial de los espacios curvos que explicaba su relatividad general.

Desde que se puso en órbita el telescopio espacial de rayos gamma Fermi, el 11 de junio de 2008, ha detectado poblaciones enteras de objetos nunca antes vistos. El último hallazgo de Fermi afecta al púlsar J1823-3021A, avistado en 1994 con el radiotelescopio Lovell, en Inglaterra. Un equipo internacional de expertos se ha dado cuenta de que esta estrella pulsante emite rayos gamma y gracias a Fermi ha podido caracterizar sus inusuales propiedades. Los resultados de su investigación se publican en el último número de Science. Lo cierto es que han descubierto el púlsar de milisegundos más joven y con la fuerza magnética más potente

No está mal que en este punto recordemos la fuerza magnética y gravitatoria que nos puede ayudar a comprender mejor el comportamiento de las partículas subatómicas.
El electromagnetismo, decíamos al principio, es la fuerza con la cual dos partículas cargadas eléctricamente se repelen (si sus cargas son iguales) o se atraen (si tienen cargas de signo opuesto).
La interacción magnética es la fuerza que experimenta una partícula eléctricamente cargada que se mueve a través de un campo magnético. Las partículas cargadas en movimiento generan un campo magnético como, por ejemplo, los electrones que fluyen a través de las espiras de una bobina.
Las fuerzas magnéticas y eléctricas están entrelazadas. En 1873, James Clerk Maxwell consiguió formular las ecuaciones completas que rigen las fuerzas eléctricas y magnéticas, descubiertas experimentalmente por Michael Faraday. Se consiguió la teoría unificada del electromagnetismo que nos vino a decir que la electricidad y el magnetismo eran dos aspectos de una misma cosa.
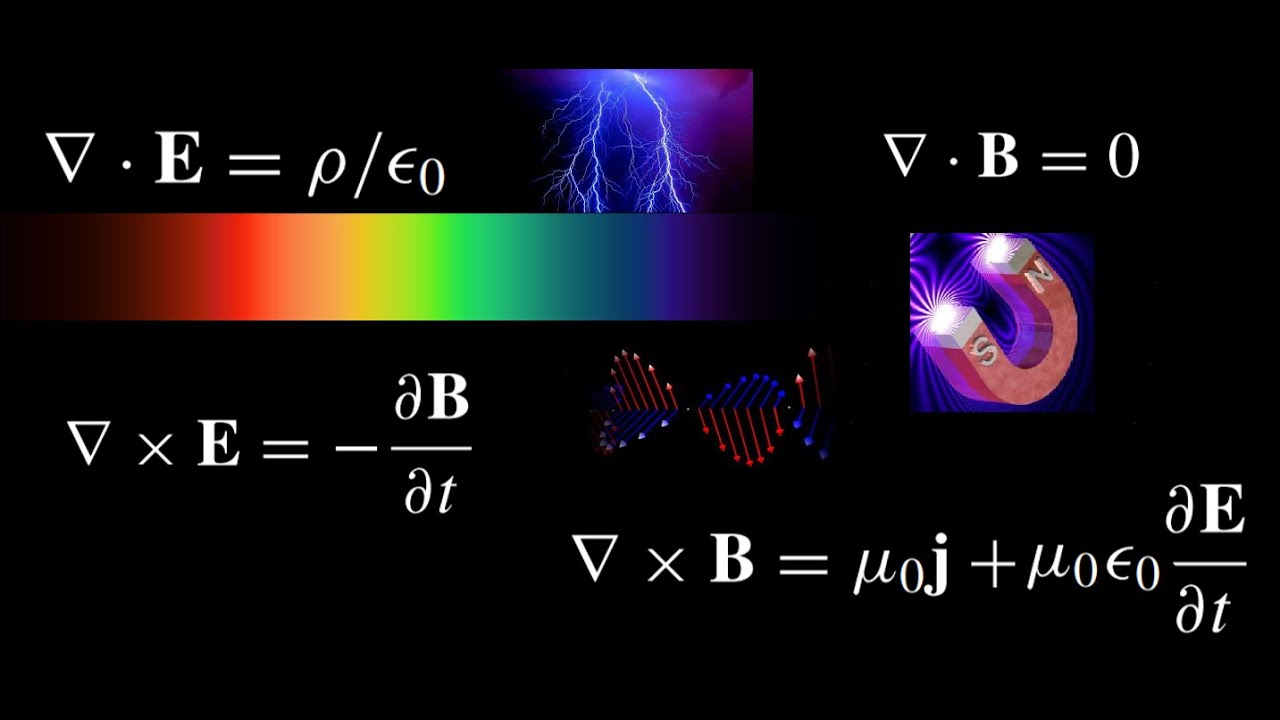
La interacción es universal, de muy largo alcance (se extiende entre las estrellas), es bastante débil. Su intensidad depende del cociente entre el cuadrado de la carga del electrón y 2hc (dos veces la constante de Planck por la velocidad de la luz). Esta fracción es aproximadamente igual a 1/137’036…, o lo que llamamos α y se conoce como constante de estructura fina.
En general, el alcance de una interacción electromagnética es inversamente proporcional a la masa de la partícula mediadora, en este caso, el fotón, sin masa.
También antes hemos comentado sobre la interacción gravitatoria de la que Einstein descubrió su compleja estructura y la expuso al mundo en 1915 con el nombre de teoría general de la relatividad, y la relacionó con la curvatura del espacio y el tiempo. Sin embargo, aún no sabemos cómo se podrían reconciliar las leyes de la gravedad y las leyes de la mecánica cuántica (excepto cuando la acción gravitatoria es suficientemente débil).

La teoría de Einstein nos habla de los planetas y las estrellas del cosmos. La teoría de Planck, Heisemberg, Schrödinger, Dirac, Feynman y tantos otros, nos habla del comportamiento del átomo, del núcleo, de las partículas elementales en relación a estas interacciones fundamentales. La primera se ocupa de los cuerpos muy grandes y de los efectos que causan en el espacio y en el tiempo; la segunda de los cuerpos muy pequeños y de su importancia en el universo atómico. Cuando hemos tratado de unir ambos mundos se produce una gran explosión de rechazo. Ambas teorías son (al menos de momento) irreconciliables.
- La interacción gravitatoria actúa exclusivamente sobre la masa de una partícula.
- La gravedad es de largo alcance y llega a los más lejanos confines del universo conocido.
- Es tan débil que, probablemente, nunca podremos detectar esta fuerza de atracción gravitatoria entre dos partículas elementales. La única razón por la que podemos medirla es debido a que es colectiva: todas las partículas (de la Tierra) atraen a todas las partículas (de nuestro cuerpo) en la misma dirección.
La partícula mediadora es el hipotético gravitón. Aunque aún no se ha descubierto experimentalmente, sabemos lo que predice la mecánica cuántica: que tiene masa nula y espín 2.
La ley general para las interacciones es que, si la partícula mediadora tiene el espín par, la fuerza entre cargas iguales es atractiva y entre cargas opuestas repulsiva. Si el espín es impar (como en el electromagnetismo) se cumple a la inversa.
Pero antes de seguir profundizando en estas cuestiones hablemos de las propias partículas subatómicas, para lo cual la teoría de la relatividad especial, que es la teoría de la relatividad sin fuerza gravitatoria, es suficiente.
Si viajamos hacia lo muy pequeño tendremos que ir más allá de los átomos, que son objetos voluminosos y frágiles comparados con lo que nos ocupará a continuación: el núcleo atómico y lo que allí se encuentra. Los electrones, que ahora vemos “a gran distancia” dando vueltas alrededor del núcleo, son muy pequeños y extremadamente robustos. El núcleo está constituido por dos especies de bloques: protones y neutrones. El protón (del griego πρώτος, primero) debe su nombre al hecho de que el núcleo atómico más sencillo, que es el hidrógeno, está formado por un solo protón. Tiene una unidad de carga positiva. El neutrón recuerda al protón como si fuera su hermano gemelo: su masa es prácticamente la misma, su espín es el mismo, pero en el neutrón, como su propio nombre da a entender, no hay carga eléctrica; es neutro.
La masa de estas partículas se expresa en una unidad llamada mega-electrón-voltio o MeV, para abreviar. Un MeV, que equivale a 106 electrón-voltios, es la cantidad de energía de movimiento que adquiere una partícula con una unidad de carga (tal como un electrón o un protón) cuando atraviesa una diferencia de potencial de 106 (1.000.000) voltios. Como esta energía se transforma en masa, el MeV es una unidad útil de masa para las partículas elementales.


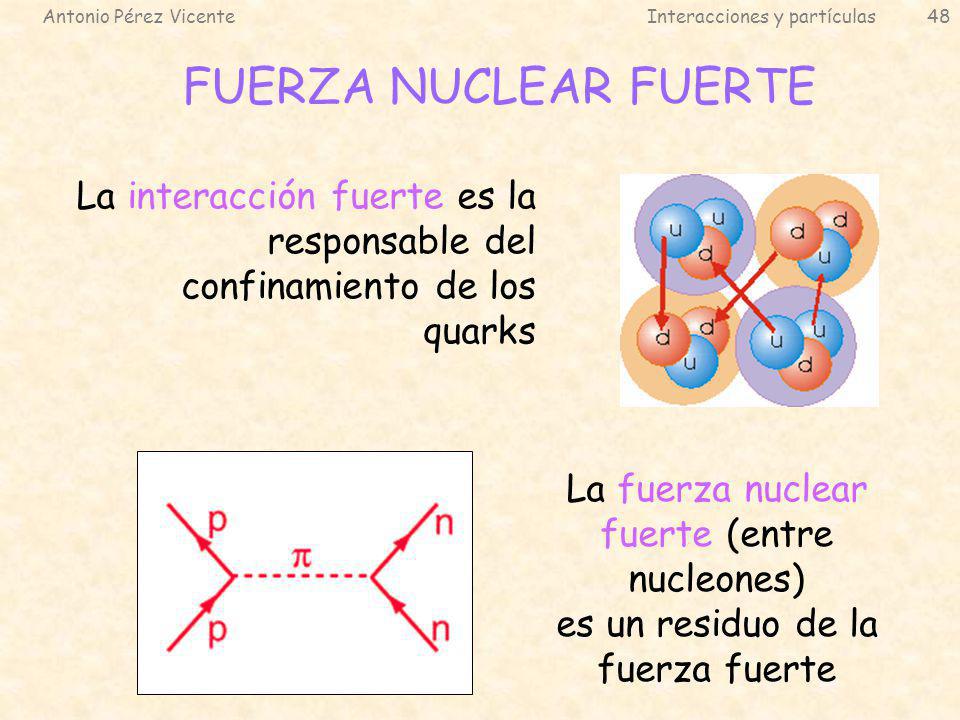
La mayoría de los núcleos atómicos contienen más neutrones que protones. Los protones se encuentran tan juntos en el interior de un núcleo tan pequeño que se deberían repeles entre sí fuertemente, debido a que tienen cargas eléctricas del mismo signo. Sin embargo, hay una fuerza que los mantiene unidos estrechamente y que es mucho más potente e intensa que la fuerza electromagnética: la fuerza o interacción nuclear fuerte, unas 102 veces mayor que la electromagnética, y aparece sólo entre hadrones para mantener a los nucleones confinados dentro del núcleo. Actúa a una distancia tan corta como 10-15 metros, o lo que es lo mismo, 0’000000000000001 metros.
La interacción fuerte está mediada por el intercambio de mesones virtuales, 8 gluones que, como su mismo nombre indica (glue en inglés es pegamento), mantiene a los protones y neutrones bien sujetos en el núcleo, y cuanto más se tratan de separar, más aumenta la fuerza que los retiene, que crece con la distancia, al contrario que ocurre con las otras fuerzas.

La luz es una manifestación del fenómeno electromagnético y está cuantizada en “fotones”, que se comportan generalmente como los mensajeros de todas las interacciones electromagnéticas. Así mismo, como hemos dejado reseñado en el párrafo anterior, la interacción fuerte también tiene sus cuantos (los gluones). El físico japonés Hideki Yukawa (1907 – 1981) predijo la propiedad de las partículas cuánticas asociadas a la interacción fuerte, que más tarde se llamarían piones. Hay una diferencia muy importante entre los piones y los fotones: un pión es un trozo de materia con una cierta cantidad de “masa”. Si esta partícula está en reposo, su masa es siempre la misma, aproximadamente 140 MeV, y si se mueve muy rápidamente, su masa parece aumentar en función E = mc2. Por el contrario, se dice que la masa del fotón en reposo es nula. Con esto no decimos que el fotón tenga masa nula, sino que el fotón no puede estar en reposo. Como todas las partículas de masa nula, el fotón se mueve exclusivamente con la velocidad de la luz, 299.792’458 Km/s, una velocidad que el pión nunca puede alcanzar porque requeriría una cantidad infinita de energía cinética. Para el fotón, toda su masa se debe a su energía cinética.
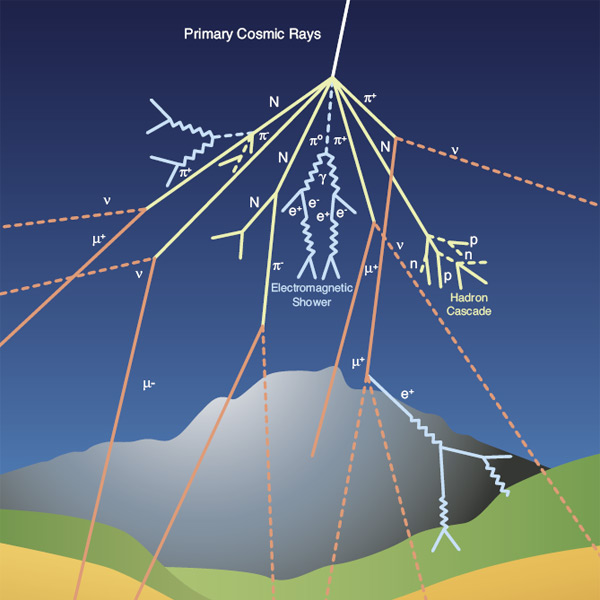
Los físicos experimentales buscaban partículas elementales en las trazas de los rayos cósmicos que pasaban por aparatos llamados cámaras de niebla. Así encontraron una partícula coincidente con la masa que debería tener la partícula de Yukawa, el pión, y la llamaron mesón (del griego medio), porque su masa estaba comprendida entre la del electrón y la del protón. Pero detectaron una discrepancia que consistía en que esta partícula no era afectada por la interacción fuerte, y por tanto, no podía ser un pión. Actualmente nos referimos a esta partícula con la abreviatura μ y el nombre de muón, ya que en realidad era un leptón, hermano gemelo del electrón, pero con 200 veces su masa.
Antes de seguir veamos las partículas elementales de vida superior a 10-20 segundos que eran conocidas en el año 1970.
| Nombre | Símbolo | Masa (MeV) | Carga | Espín | Vida media (s) |
| Fotón | γ | 0 | 0 | 1 | ∞ |
| Leptones (L = 1, B = 0) | |||||
| Electrón | e– | 0’5109990 | – | ½ | ∞ |
| Muón | μ– | 105’6584 | – | ½ | 2’1970 × 10-6 |
| Tau | τ | ||||
| Neutrino electrónico | νe | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino muónico | νμ | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino tauónico | ντ | ~ 0 | 0 | ½ | ~ ∞ |
| Mesones (L = 0, B = 0) | |||||
| Pión + | π+ | 139’570 | 2’603 × 10-8 | ||
| Pión – | π– | 139’570 | 2’603 × 10-8 | ||
| Pión 0 | π0 | 134’976 | 0’84 × 10-16 | ||
| Kaón + | k+ | 493’68 | 1’237 × 10-8 | ||
| Kaón – | k– | 493’68 | 1’237 × 10-8 | ||
| Kaón largo | kL | 497’7 | 5’17 × 10-8 | ||
| Kaón corto | kS | 497’7 | 0’893 × 10-10 | ||
| Eta | η | 547’5 | 0 | 0 | 5’5 × 10-19 |
| Bariones (L = 0, B = 1) | |||||
| Protón | p | 938’2723 | + | ½ | ∞ |
| Neutrón | n | 939’5656 | 0 | ½ | 887 |
| Lambda | Λ | 1.115’68 | 0 | ½ | 2’63 × 10-10 |
| Sigma + | Σ+ | 1.189’4 | + | ½ | 0’80 × 10-10 |
| Sigma – | Σ– | 1.1974 | – | ½ | 7’4× 10-20 |
| Sigma 0 | Σ0 | 0 | ½ | 1’48 × 10-10 | |
| Ksi 0 | Ξ0 | 1.314’9 | 0 | ½ | 2’9 × 10-10 |
| Ksi – | Ξ– | 1.321’3 | – | ½ | 1’64 × 10-10 |
| Omega – | Ω– | 1.672’4 | – | 1½ | 0’82 × 10-10 |


Para cada leptón y cada barión existe la correspondiente antipartícula, con exactamente las mismas propiedades a excepción de la carga que es la contraria. Por ejemplo, el antiprotón se simboliza con y el electrón con e+. Los mesones neutros son su propia antipartícula, y el π+ es la antipartícula del π–, al igual que ocurre con k+ y k–. El símbolo de la partícula es el mismo que el de su antipartícula con una barra encima. Las masas y las vidas medias aquí reflejadas pueden estar corregidas en este momento, pero de todas formas son muy aproximadas.
Los símbolos que se pueden ver algunas veces, como s (extrañeza) e i (iso-espín) están referidos a datos cuánticos que afectan a las partículas elementales en sus comportamientos.
Debo admitir que todo esto tiene que sonar algo misterioso. Es difícil explicar estos temas por medio de la simple palabra escrita sin emplear la claridad que transmiten las matemáticas, lo que, por otra parte, es un mundo secreto para el común de los mortales, y ese lenguaje es sólo conocido por algunos privilegiados que, mediante un sistema de ecuaciones pueden ver y entender de forma clara, sencilla y limpia, todas estas complejas cuestiones.

Si hablamos del espín (o, con más precisión, el momento angular, que es aproximadamente la masa por el radio por la velocidad de rotación) se puede medir como un múltiplo de la constante de Planck, h, dividido por 2π. Medido en esta unidad y de acuerdo con la mecánica cuántica, el espín de cualquier objeto tiene que ser o un entero o un entero más un medio. El espín total de cada tipo de partícula – aunque no la dirección del mismo – es fijo.
El electrón, por ejemplo, tiene espín ½. Esto lo descubrieron dos estudiantes holandeses, Samuel Gondsmit (1902 – 1978) y George Uhlenbeck (1900 – 1988), que escribieron sus tesis conjuntamente sobre este problema en 1972. Fue una idea audaz que partículas tan pequeñas como los electrones pudieran tener espín, y de hecho, bastante grande. Al principio, la idea fue recibida con escepticismo porque la “superficie del electrón” se tendría que mover con una velocidad 137 veces mayor que la de la luz, lo cual va en contra de la teoría de la relatividad general en la que está sentado que nada en el universo va más rápido que la luz, y por otra parte, contradice E=mc2, y el electrón pasada la velocidad de la luz tendría una masa infinita.
Hoy día, sencillamente, tal observación es ignorada, toda vez que el electrón carece de superficie.
Las partículas con espín entero se llaman bosones, y las que tienen espín entero más un medio se llaman fermiones. Consultado los valores del espín en la tabla anterior podemos ver que los leptones y los bariones son fermiones, y que los mesones y los fotones son bosones. En muchos aspectos, los fermiones se comportan de manera diferente de los bosones. Los fermiones tienen la propiedad de que cada uno de ellos requiere su propio espacio: dos fermiones del mismo tipo no pueden ocupar o estar en el mismo punto, y su movimiento está regido por ecuaciones tales que se evitan unos a otros. Curiosamente, no se necesita ninguna fuerza para conseguir esto. De hecho, las fuerzas entre los fermiones pueden ser atractivas o repulsivas, según las cargas. El fenómeno por el cual cada fermión tiene que estar en un estado diferente se conoce como el principio de exclusión de Pauli. Cada átomo está rodeado de una nube de electrones, que son fermiones (espín ½). Si dos átomos se aproximan entre sí, los electrones se mueven de tal manera que las dos nubes se evitan una a otra, dando como resultado una fuerza repulsiva. Cuando aplaudimos, nuestras manos no se atraviesan pasando la uno a través de la otra. Esto es debido al principio de exclusión de Pauli para los electrones de nuestras manos que, de hecho, los de la izquierda rechazan a los de la derecha.
En contraste con el característico individualismo de los fermiones, los bosones se comportan colectivamente y les gusta colocarse todos en el mismo lugar. Un láser, por ejemplo, produce un haz de luz en el cual muchísimos fotones llevan la misma longitud de onda y dirección de movimiento. Esto es posible porque los fotones son bosones.
Cuando hemos hablado de las fuerzas fundamentales que, de una u otra forma, interaccionan con la materia, también hemos explicado que la interacción débil es la responsable de que muchas partículas y también muchos núcleos atómicos exóticos sean inestables. La interacción débil puede provocar que una partícula se transforme en otra relacionada, por emisión de un electrón y un neutrino. Enrico Fermi, en 1934, estableció una fórmula general de la interacción débil, que fue mejorada posteriormente por George Sudarshan, Robert Marschak, Murray Gell-Mann, Richard Feynman y otros. La fórmula mejorada funciona muy bien, pero se hizo evidente que no era adecuada en todas las circunstancias.
Uno de los protones se transmuta en un neutrón por medio de la interacción débil, transformando un quark “up”, en “down”. Este proceso consume energía (el neutrón tiene ligeramente más masa que..
En 1970, de las siguientes características de la interacción débil sólo se conocían las tres primeras:
- La interacción actúa de forma universal sobre muchos tipos diferentes de partículas y su intensidad es aproximadamente igual para todas (aunque sus efectos pueden ser muy diferentes en cada caso). A los neutrinos les afecta exclusivamente la interacción débil.
- Comparada con las demás interacciones, ésta tiene un alcance muy corto.
- La interacción es muy débil. Consecuentemente, los choques de partículas en los cuales hay neutrinos involucrados son tan poco frecuentes que se necesitan chorros muy intensos de neutrinos para poder estudiar tales sucesos.
- Los mediadores de la interacción débil, llamados W+, W– y Z0, no se detectaron hasta la década de 1980. al igual que el fotón, tienen espín 1, pero están eléctricamente cargados y son muy pesados (esta es la causa por la que el alcance de la interacción es tan corto). El tercer mediador, Z0, que es responsable de un tercer tipo de interacción débil que no tiene nada que ver con la desintegración de las partículas llamada “corriente neutra”, permite que los neutrinos puedan colisionar con otras partículas sin cambiar su identidad.
A partir de 1970, quedó clara la relación de la interacción débil y la electromagnética (electrodébil de Weinberg-Salam).
La interacción fuerte (como hemos dicho antes) sólo actúa entre las partículas que clasificamos en la familia llamada de los hadrones, a los que proporciona una estructura interna complicada. Hasta 1972 sólo se conocían las reglas de simetría de la interacción fuerte y no fuimos capaces de formular las leyes de la interacción con precisión.
Como apuntamos, el alcance de esta interacción no va más allá del radio de un núcleo atómico ligero (10-13 cm aproximadamente).
La interacción es fuerte. En realidad, la más fuerte de todas.
Lo dejaré aquí, en verdad, eso que el Modelo Estándar de la Física, es feo, complejo e incompleto y, aunque hasta el momento es una buena herramienta con la que trabajar, la verdad es que, se necesita un nuevo modelo más avanzado y que incluya la Gravedad.

Veremos que nos trae la nueva etapa del LHC.
La nueva etapa del LHC, conocida como Run 3, comenzó en 2022 después de tres años de actualizaciones y mejoras.
Esta fase se centra en la exploración de nuevas fronteras de la física de partículas a energías récord y en el estudio de procesos raros. Además, se están realizando preparativos para el LHC de Alta Luminosidad (HL-LHC), que aumentará la cantidad de datos disponibles para los experimento
Emilio Silvera V.
Jul
13
Hay que recorrer un largo camino para saber
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (1)
Comments (1)
El Universo: Cometa lleno de Galaxias




“En cuanto al máximo, el límite está en lo que la naturaleza sea capaz de producir. Hasta hace poco se creía que este límite estaba en torno a monstruos de 150 masas solares, aunque recientes trabajos lo elevan hasta 300. No obstante, no es un dato seguro ya que, cuanto más masiva es una estrella, menos vive, con lo cual estrellas más grandes serían difíciles de observar.”

Verdaderamente si pudiéramos contemplar de cerca, el comportamiento de una estrella cuando llega el final de su vida, veríamos como es, especialmente intrigante las transiciones de fase de una estrella en implosión observada desde un sistema de referencia externo estático, es decir, vista por observadores exteriores a la estrella que permanecen siempre en la misma circunferencia fija en lugar de moverse hacia adentro con la materia de la estrella en implosión. La estrella, vista desde un sistema externo estático, empieza su implosión en la forma en que uno esperaría. Al igual que una pesada piedra arrojada desde las alturas, la superficie de la estrella cae hacia abajo (se contrae hacia adentro), lentamente al principio y luego cada vez más rápidamente. Si las leyes de gravedad de Newton hubieran sido correctas, esta aceleración de la implosión continuaría inexorablemente hasta que la estrella, libre de cualquier presión interna, fuera aplastada en un punto de alta velocidad.
Pero no era así según las fórmulas relativistas que aplicaron Oppenheimer y Snyder. En lugar de ello, a medida que la estrella se acerca a su circunferencia crítica su contracción se frena hasta hacerse a paso lento. Cuanto más pequeña se hace la estrella, más lentamente implosiona, hasta que se congela exactamente en la circunferencia crítica y, dependiendo de su masa, explosiona como supernova para formar una inmensa nebulosa o, se transforma en nebulosa planetaria, más pequeña.
Ahí podemos observar a una estrella muy joven, de dos o tres millones de años que, en un futuro lejano será una gran Supernova. Los procesos que podríamos observar al final de la vida de una estrella gigante… ¡Son fascinantes!

En la escena que antes explicábamos, por mucho tiempo que nos quedemos esperando y contemplando el suceso, si uno está en reposo fuera de la estrella (es decir, en reposo en el sistema de referencia externo estático), uno nunca podrá ver que la estrella implosiona a través de la circunferencia crítica. Ese fue el mensaje inequívoco que Oppenheimer y Snyder nos enviaron. Para poder ver eso, habría que estar dentro de la estrella, instalado en la materia que está sufriendo la contracción y, no sabemos porque eso es así.


¿Se debe esta congelación de la implosión a alguna fuerza inesperada de la relatividad general en el interior de la estrella? No, en absoluto, advirtieron Oppenheimer y Snyder. Más bien se debe a la dilatación gravitatoria del tiempo (el frenado del flujo del tiempo) cerca de la circunferencia crítica. Tal como lo ven los observadores estáticos, el tiempo en la superficie de la estrella en implosión debe fluir cada vez más lentamente cuando la estrella se aproxima a la circunferencia crítica; y, consiguientemente, cualquier cosa que ocurre sobre o en el interior de la estrella, incluyendo su implosión, debe aparecer como si el movimiento se frenara poco a poco hasta congelarse.
Por extraño que esto pueda parecer, aún había otra predicción más extrañas de las fórmulas de Oppenheimer y Snyder: si bien es cierto que vista por observadores externos estáticos la implosión se congela en la circunferencia crítica, no se congela en absoluto vista por los observadores que se mueven hacia adentro con la superficie de la estrella. Si la estrella tiene una masa de algunas masas solares y empieza con un tamaño aproximado al del Sol, entonces vista desde su propia superficie implosiona hacia la circunferencia crítica en aproximadamente una hora, y luego sigue implosionando más allá de la criticalidad hacia circunferencias más pequeñas.
Allá por el año 1939, cuando Oppenheimer y Snyder descubrieron estas cosas, los físicos ya se habían acostumbrados al hecho de que el tiempo es relativo; el flujo del tiempo es diferente medido en diferentes sistemas de referencia que se mueven de diferentes formas a través del Universo. Claro que, nunca antes había encontrado nadie una diferencia tan extrema entre sistemas de referencia. Que la implosión se congele para siempre medida en el sistema externo estático, pero continúe avanzando rápidamente superando al punto de congelación medida en el sistema desde la superficie de la estrella era extraordinariamente difícil de comprender. Nadie que estudiara las matemáticas de Oppenheimer y Snyder se sentía cómodo con semejante distorsión extrema del tiempo. Pero ahí estaba, en sus fórmulas. Algunos podían agitar sus brazos con explicaciones heurísticas, pero ninguna explicación parecía muy satisfactoria. No sería completamente entendido hasta finales de los cincuenta.
Fue Wheeler el que discrepó del trabajo de Oppenheimer y Snyder, alegando, con toda la razón que, cuando ellos habían realizado su trabajo, habría sido imposible calcular los detalles de la implosión con una presión realista (presión térmica, presión de degeneración y presión producida por la fuerza nuclear), y con reacciones nucleares, ondas de choque, calor, radiación y expulsión de masa. Sin embargo, los trabajos desde las armas nucleares de los veinte años posteriores proporcionaron justamente las herramientas necesarias.

Presión, reacciones nucleares, ondas de choque, calor radiación y expulsión de masa eran todas ellas características fundamentales de una bomba de hidrógeno; sin ellas, una bomba no explosionaría. A finales de los años cincuenta, Stirling Colgate quedó fascinado por el problema de la implosión estelar. Con el apoyo de Edward Teller, y en colaboración con Richard White y posteriormente Michael May, Colgate se propuso simular semejante implosión en un ordenador. Sin embargo, cometieron un error, mantuvieron algunas de las simplificaciones de Oppenheimer al insistir desde el principio en que la estrella fuera esférica y sin rotación, y, aunque tuvieron en cuenta todos los argumentos que preocupaban a Wheeler, aquello no quedó perfeccionado hasta después de varios años de esfuerzo y, a comienzo de los años sesenta ya estaban funcionando correctamente.
Un día a principio de los años sesenta, John Wheeler entró corriendo en la clase de relatividad de la Universidad de Princeton. Llegaba un poco tarde, pero sonreía con placer. Acababa de regresar de una visita a Livermore donde había visto los resultados de las simulaciones recientes de Colgate y su equipo. Con excitación en su voz dibujó en la pizarra un diagrama tras otro explicando lo que sus amigos de Livermore habían aprendido.
Cuando la estrella en implosión tenía una masa pequeña, desencadenaba una implosión de supernova y formaba una estrella de neutrones precisamente en la forma que Fritz Wicky había especulado treinta años antes. Sin embargo, si la estrella original era más masiva lo que allí se producía (aparte de la explosión supernova) era un agujero negro notablemente similar al altamente simplificado modelo que veinticinco años calcularon Oppenheimer y Snyder. Vista desde fuera, la implosión se frenaba y se quedaba congelada en la circunferencia crítica, pero vista por alguien en la superficie de la estrella, la implosión no se congelaba en absoluto. La superficie de la estrella se contraía a través de la circunferencia crítica y seguía hacia adentro sin vacilación.

Lo cierto fue que allí, por primera vez, se consiguió simular por ordenador la implosión que debía producir agujeros negros. Está claro que la historia de todo esto es mucho más larga y contiene muchos más detalles que me he saltado para no hacer largo el trabajo que, en realidad, sólo persigue explicar a ustedes de la manera más simple posible, el trabajo que cuesta obtener los conocimientos que no llegan (casi nunca) a través de ideas luminosas, sino que, son el resultado del trabajo de muchos.
Hoy, sabemos mucho más de cómo finaliza sus días una estrella y, dependiendo de su masa, podemos decir de manera precisa que clase de Nebulosa formará, que clase de explosión (si la hay) se producirá, y, finalmente, si el resultado de todo ello será una estrella enana blanca que encuentra su estabilidad final por medio del Principio de exclusión de Pauli (en mecánica cuántica)que se aplica a los fermiones pero no a los Bosones (son fermiones los quarks, electrones, protones y neutrones), en virtud del cual dos partículas idénticas en un sistema, como los electrones en un átomo o quarks en un hadrón (protón o neutrón, por ejemplo), no pueden poseer un conjunto idéntico de números cuánticos.


La estrella gigante Zeta Ophiuchi está teniendo un efecto «impactante» en las nubes de polvo circundantes a la estrella. Los vientos estelares que fluyen de esta estrella están haciendo ondulaciones en el polvo interestelar a medida que se aproxima a este, creando un arco de choque precioso. Zeta Ophiuchi es una estrella joven.
La estrella azul cerca del centro de esta imagen es Zeta Ophiuchi. Cuando se ve en luz visible aparece como una estrella roja relativamente débil rodeada de otras estrellas tenues y sin polvo. Sin embargo, en esta imagen infrarroja tomada con campo amplio por el Explorador Infrared Survey de la NASA, o WISE, un punto de vista completamente diferente emerge. Zeta Ophiuchi es en realidad una muy masiva y caliente estrella azul, brillante que traza su camino a través de una gran nube de polvo y gas interestelar.
Una estrella masiva alejándose de su antiguo compañero se manifiesta haciendo un imponente surco a través de polvo espacial, como si se tratase de la proa de un barco. La estrella, llamada Zeta Ophiuchi, es enorme, con una masa de cerca de 20 veces la de nuestro Sol. En esta imagen, en los que se ha traducido la luz infrarroja a colores visibles que vemos con nuestros ojos, la estrella aparece como el punto azul en el interior del arco de choque. Zeta Ophiuchi orbitó una vez alrededor de una estrella aún más grande. Pero cuando la estrella explotó en una supernova, Zeta Ophiuchi se disparó como una bala. Viaja a la friolera velocidad de 24 kilómetros por segundo arrastrando con ella un conglomerado de polvo que distorsiona la región por la que pasa.
Mientras la estrella se mueve través del espacio, sus poderosos vientos empujan el gas y el polvo a lo largo de su camino en lo que se llama un arco de choque. El material en el arco de choque está tan comprimido que brilla con luz infrarroja que WISE puede captar. El efecto es similar a lo que ocurre cuando un barco cobra velocidad a través del agua, impulsando una ola delante de él. Esta onda de choque queda completamente oculta a la luz visible. Las imágenes infrarrojas como esta son importantes para arrojar nueva luz sobre lo que ocurre en situaciones similares.
Pero, siguiendo con el tema de las implosiones de las estrellas, ¿Cuál es la razón por la que la materia no se colapsa, totalmente, sobre sí misma? El mismo principio que impide que las estrellas de neutrones y las estrellas enanas blancas implosionen totalmente y que, llegado un momento, en las primeras se degeneran los neutrones y en las segundas los electrones, y, de esa manera, se frena la compresión que producía la gravedad y quedan estabilizadas gracias a un principio natural que hace que la materia normal sea en su mayor parte espacio vacio también permite la existencia de los seres vivos. El nombre técnico es: El Principio de Exclusión de Pauli y dice que dos fermiones (un tipo de partículas fundamentales) idénticos y con la misma orientación no pueden ocupar simultáneamente el mismo lugar en el espacio. Por el contrario, los bosones (otro tipo de partículas, el fotón, por ejemplo) no se comportan así, tal y como se ha demostrado recientemente por medio de la creación en el laboratorio de los condensados de Bose-Einstein.
¿Cuál es la diferencia?
En la Estación Espacial se ha generado el Condensado de Bose-Einstein (5º estado de la materia)
Los bosones son sociables; les gusta estar juntos. Como regla general, cualquier átomo con un número par de electrones + protones + neutrones es un bosón. Así, por ejemplo, los átomos del sodio ordinario son bosones, y pueden unirse para formar condensados Bose-Einstein.
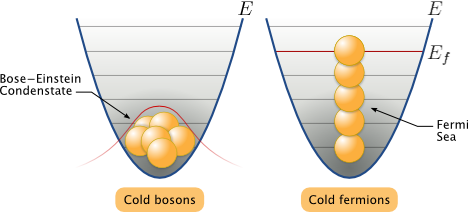
Izquierda: Los bosones son sociables; los fermiones son antisociale
La afirmación es una forma metafórica de describir la diferencia entre bosones y fermiones en física cuántica. Los Bosones pueden ocupar el mismo lugar cuántico (agruparse), los Fermiones no pueden como nos dice el Principio de Exclusión de Pauli.
Los fermiones, por otro lado, son antisociales. No pueden juntarse en el mismo estado cuántico (por el Principio de Exclusión de Pauli de la mecánica cuántica). Cualquier átomo con un número impar de electrones +protones +neutrones, como el potasio-40, es un fermión.
Pero, estábamos diciendo: “…no pueden poseer un conjunto idéntico de números cuánticos.” A partir de ese principio, sabemos que, cuando una estrella como nuestro Sol deja de fusionar Hidrógeno en Helio que hace que la estrella deje de expandirse y quede a merced de la Gravedad, ésta implosionará bajo el peso de su propia masa, es decir, se contraerá sobre sí misma por la fuerza gravitatoria pero, llegará un momento en el cual, los electrones, debido a ese principio de exclusión de Pauli que les impide estar juntos, se degeneran y se moverán de manera aleatoria con velocidades relativista hasta el punto de ser capaces de frenar la fuerza provocada por la gravedad, y, de esa manera, quedará estabilizada finalmente una estrella enana blanca.

Si hablamos de una estrella super-masiva, su produce la implosión arrojando las capas externas al espacio interestelar mientras que el grueso de la estrella se comprime más y más sin que nada la pueda frenar, aquí no sirve el Principipo de exclusión de Pauli para los fermiones y, es tal la fuerza gravitatoria que se desencadena como consecuencia de que la estrella supergigante no puede seguir fusionando y queda a merce4d de una sola fuerza: La Gravedad, que ésta, la comprime hasta lo inimaginable para convertir toda aquella ingente masa en una singularidad, es decir, un punto de densidad y energía “infinitas” que ni la luz puede escapar de allí, y, el tiempo se ralentiza y el espacio se curva a su alrededor.

Si la estrella original es más masiva, la degeneración de los electrones no será suficiente para frenar la fuerza gravitatoria y, los electrones se fusionaran con los protones para convertirse en neutrones que, bajo el mismo principio de exclusión sufrirán la degeneración que frenará la fuerza de gravedad quedando entonces una estrella de neutrones. Por último, si la estrella es, aún más masiva, ni la degeneración de los neutrones será suficiente para frenar la inmensa fuerza gravitatoria generada por la masa de la estrella que, continuará la implosión contrayéndose cada vez más hasta desaparecer de nuestra vista convertida en un agujero negro.
¿Qué forma adoptará, qué transición de fase se produce en la materia dentro de una Singularidad?
¡Resulta todo tan complejo!
Emilio Silvera V.
















 Totales: 85.888.540
Totales: 85.888.540 Conectados: 2
Conectados: 2