Los neutrinos están por todas partes y andamos a la caza de sus variedades diferentes para estudiarlos y saber

En 1.930, el físico Wolfgang Pauli propuso la hipótesis de una nueva e invisible partícula denominada neutrino para dar cuenta de la energía pérdida en ciertos experimentos sobre radiactividad que parecían violar la conservación de la materia y la energía. Pauli comprendió, no obstante, que los neutrinos serían casi imposibles de observar experimentalmente, porque interaccionarían muy débilmente y, por consiguiente, muy raramente con la materia.

          En el Sistema triple Alpha Centauri se ha descubierto el exoplaneta más cercano. También las tres estrellas más cercanas están ahí

Por ejemplo, si pudiéramos construir un bloque sólido de plomo de varios años-luz de extensión desde nuestro Sistema Solar hasta Alpha Centaury y lo pusiéramos en el camino de un haz de neutrinos, aun saldrían algunos por el extremo opuesto.  Pueden atravesar la Tierra como si ni siquiera existiese y, de hecho, billones de neutrinos emitidos por el Sol están atravesando continuamente nuestros cuerpos, tanto de día como de noche.  Pauli admitió: “He cometido el pecado más grave, he predicho la existencia de una partícula que nunca puede ser observada.”

Los neutrinos han sido objeto de grandes proyectos para su localización, y, escondidos en las profundidades de la Tierra, en minas abandonadas, han sido instalados grandes depósitos de agua pesada que, detectaban a los neutrinos que allí interaccionaban y que eran detectados por ordenador. Hay empresas que parecen descabelladas y, sin embargo, son las que nos traen los mayores éxitos.

Si repasamos la historia de la Ciencia, seguramente encontraremos muchos motivos para el optimismo.  Witten con su Teoría M,  está convencido de que la ciencia será algún día capaz de sondear hasta las energías de Planck. Como ya he contado en otras ocasiones, él dijo:

“No siempre es tan fácil decir cuáles son las preguntas fáciles y cuáles las difíciles.  En el siglo XIX, la pregunta de por qué el agua hierve a 100 grados era desesperadamente inaccesible.  Si usted hubiera dicho a un físico del siglo XIX que hacia el siglo XX sería capaz de calcularlo, le habría parecido un cuento de hadas…  La teoría cuántica de campos es tan difícil que nadie la creyó completamente durante veinticinco años.”

En su opinión Las buenas ideas siempre se verifican.

Los ejemplos son innumerables: La Gravedad de Newton, el campo eléctrico de Faraday y el electromagnetismo de Maxwell, la teoría de la relatividad de Einstein en sus dos versiones y su demostración del efecto fotoeléctrico, la teoría del electrón de Paul Dirac, el principio incertidumbre de Heisemberg, la función de ondas de Schrödinger, y tantos y tantos otros.

Algunos de los físicos teóricos más famosos, sin embargo, protestaban de tanto empeño en la experimentación.

El astrónomo Arthur Eddington (ya lo hemos nombrado antes) se cuestionaba incluso si los científicos no estaban forzando las cosas cuando insistían en que todo debería ser verificado.

El premio Nóbel Paul Dirac incluso llegó a decir de forma más categórica:

”Es más importante tener belleza en las ecuaciones que tener experimentos que se ajusten a ellas.”

Claro que, sin bellas y se ajustan a la Naturaleza…

Yo, como todos ustedes, un hombre normal y corriente de la calle, escucho a unos y a otros, después pienso en lo que dicen y en los argumentos y motivaciones que les han llevado a sus respectivos convencimientos, y, finalmente, también como todos ustedes, decido según mi propio criterio, que no obligatoriamente, coincidirá con alguna de esas opiniones, y, en algún caso, hasta me permito emitir, la mía propia.

Suponiendo que algún físico brillante nos resuelva la teoría de campos de cuerdas y derive las propiedades conocidas de nuestro universo, con un poco de suerte, podría ocurrir en este mismo siglo, lo que no estaría nada mal considerando las dificultades de la empresa.

El problema fundamental es que estamos obligando a la teoría de supercuerdas a responder preguntas sobre energías cotidianas, cuando su “ámbito natural” está en la energía de Planck.  Esta fabulosa energía fue liberada sólo en el propio instante de la creación. Lo que quiere decir, que la teoría de supercuerdas es naturalmente una teoría de la Creación.

                       Inventamos los más sofisticados artilugios para llegar al corazón de la materia y poder desvelar los secretos del Universo

Fuimos capaces de predecir que el big bang produjo un “eco” cósmico reverberando en el Universo y que podría ser medido por los instrumentos adecuados.   De hecho, Arno Penzias y Robert Wilson de los Bell telephone Laboratories ganaron el premio Nóbel en 1978 por detectar este eco del big bang, una radiación de microondas que impregna el Universo conocido. El que el eco del big bang debería estar circulando por el Universo miles de millones de años después del suceso fue predicho por primera vez por George Gamow y sus discípulos Ralpher y Robert Herman, pero nadie les tomó en serio.

La propia idea de medir el Eco de la Creación parecía extravagante cuando la propusieron por primera vez poco después de la segunda guerra mundial.

Su lógica, sin embargo, era aplastante.  Cualquier objeto, cuando se calienta, emite radiación de forma gradual.  Esta es la razón de que el hierro se ponga al rojo vivo cuando se calienta en un horno y, cuanto más se calienta, mayor es la frecuencia de radiación que emite.  Una fórmula matemática exacta, la ley de Stefan-Boltzmann, relaciona la frecuencia de la luz (o el color en este caso) con la temperatura.  (De hecho, así es como los científicos determinan la temperatura de la superficie de una estrella lejana, examinando su color).  Esta radiación se denomina RADIACIÓN DE CUERPO NEGRO.

Todo cuerpo emite energía en forma de ondas electromagnéticas, siendo esta radiación, que se emite incluso en el vacío, tanto más intensa cuando más elevada es la temperatura del emisor. La energía radiante emitida por un cuerpo a temperatura ambiente es escasa y corresponde a longitudes de onda superiores a las de la luz visible (es decir, de menor frecuencia). Al elevar la temperatura no sólo aumenta la energía emitida sino que lo hace a longitudes de onda más cortas; a esto se debe el cambio de color de un cuerpo cuando se calienta. Los cuerpos no emiten con igual intensidad a todas las frecuencias o longitudes de onda, sino que siguen la ley de Planck.

Esta radiación (como no), ha sido aprovechada por los ejércitos que mediante visores nocturnos pueden operar en la oscuridad.  De noche, los objetos relativamente calientes, tales como soldados enemigos o los carros de combate, pueden estar ocultos en la oscuridad, pero continúan emitiendo radiación de cuerpo negro invisible en forma de radiación infrarroja, que puede ser captada por gafas especiales de infrarrojos.  Esta es también la razón de que nuestros automóviles cerrados se calienten en verano, ya que, la luz del Sol atraviesa los cristales del automóvil y calienta el interior. A medida que se calienta, empieza a emitir radiación de cuerpo negro en forma de radiación infrarroja.  Sin embargo, esta clase de radiación, no atraviesa muy bien el vidrio, y por lo tanto queda atrapada en el interior del automóvil, incrementando espectacularmente la temperatura.

Análogamente, la radiación de cuerpo negro produce el efecto invernadero. Al igual que el vidrio, los altos niveles de dióxido de carbono en la atmósfera, causados por la combustión sin control de combustibles fósiles, pueden atrapar la radiación de cuerpo negro infrarroja en la Tierra y, de este modo, calentar gradualmente el planeta.

Gamow razonó que el big bang era inicialmente muy caliente, y que por lo tanto sería un cuerpo negro ideal emisor de radiación.  Aunque la tecnología de los años cuarenta era demasiado primitiva para captar esta débil señal de la Creación, Gamow pudo calcular la temperatura de dicha radiación y predecir con fiabilidad que un día nuestros instrumentos serían lo suficientemente sensibles para detectar esta radiación “fósil”.

La lógica que había detrás de su razonamiento era la siguiente: alrededor de 300.000 años después del big bang, el Universo se enfrió hasta el punto en el que los átomos pudieron empezar a componerse; los electrones pudieron empezar a rodear a los protones y neutrones formando átomos estables, que ya no serían destruidos por la intensa radiación que esta impregnando todo el Universo.  Antes de este momento, el Universo estaba tan caliente que los átomos eran inmediatamente descompuestos por esa radiación tan potente en el mismo acto de su formación.  Esto significa que el Universo era opaco, como una niebla espesa absorbente e impenetrable.

Pasados 300.000 años, la radiación no era tan potente, se había enfriado, y por lo tanto la luz podía atravesar grandes distancias sin ser dispersada.  En otras palabras, el Universo se hizo repentinamente mayor y transparente.

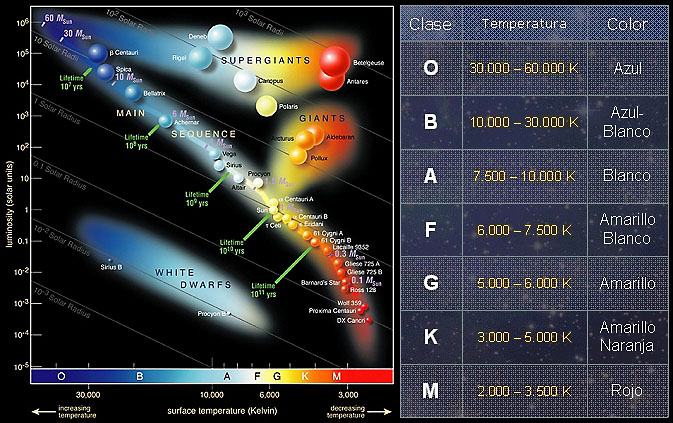
La radiación emitida por las estrellas nos hablan de qué materiales están hechas y de su temperatura

Terminaré esta parte comentando que un auténtico cuerpo negro es un concepto imaginario, un pequeño agujero en la pared de un recinto a temperatura uniforme es la mejor aproximación que se puede tener de él en la práctica.

La radiación de cuerpo negro es la radiación electromagnética emitida por un cuerpo negro.  Se extiende sobre todo el rango de longitud de onda y la distribución de energías sobre este rango tiene una forma característica con un máximo en una cierta longitud de onda, desplazándose a longitudes de onda más cortas al aumentar las temperaturas.*

Hablar, sin más especificaciones, radiación, es estar refiriéndonos a una energía que viaja en forma de ondas electromagnéticas o fotones por el Universo.  También nos podríamos estar refiriendo a un chorro de partículas, especialmente partículas alfa o beta de una fuente radiactiva o neutrones de un reactor nuclear.

La radiación actínida es la electromagnética que es capaz de iniciar una reacción química.  El término es usado específicamente para la radiación ultravioleta y también para denotar radiación que podría afectar a las emulsiones fotográficas.

Radiación blanda, radiación cósmica, radiación de calor, radiación de fondo, de fondo de microondas, radiación dura, electromagnética, radiación gamma, infrarroja, ionizante, monocromática, poli cromática, de sincrotrón, ultravioleta, de la teoría cuántica, de radiactividad…    y, como se puede ver, la radiación en sus diversas formas, es, un Universo en sí misma.

Siempre me llamó la atención y se ganó mi admiración el físico alemán Max Planck (1858-1947), responsable, entre otros muchos logros, de la ley de radiación de Planck que, da la distribución de energía radiada por un cuerpo negro.  Introdujo en Física el concepto novedoso de que la energía es una entidad que es radiada por un cuerpo en pequeños paquetes discretos, en vez de una emisión continua. Estos pequeños paquetes se conocieron como cuantos y la ley formulada es la base de la teoría cuántica.

                                                               En la naturaleza el efecto fotoeléctrico está presente de muchas maneras

Einstein se inspiró en este trabajo para a su vez, presentar el suyo propio sobre el efecto fotoeléctrico donde la energía máxima cinética del fotoelectrón, Em’ esta dada por la ecuación que lleva su nombre:

Planck publicó en 1.900, un artículo sobre la radiación de cuerpo negro que, sentó las bases para la teoría de la mecánica cuántica que más tarde desarrollaron otros, como el mismo Einstein, Heisemberg, Schrördinger, Dirac, Feymann, etc.

Todos los físicos son conocedores de la enorme contribución que Max Planck hizo en física: la constante de Planck, radiación de Planck, longitud de Planck, unidades de Planck, etc.  Es posible que sea el físico de la historia que más veces ha dado su nombre a conceptos de la física.

Pongamos un par de ejemplos de su ingenio con la fórmula de lo que se conoce como longitud de Planck:

Esta escala de longitud (veinte ordenes de magnitud menor que el tamaño del protón 10^-15  m) es a la que la descripción clásica de la gravedad cesa de ser válida y debe ser tenida en cuenta la mecánica cuántica. En la formula que la describe, G es la constante gravitacional, ħ es la constante de Planck racionalizada y c es la velocidad de la luz.

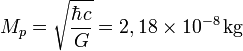
Es la masa de una partícula cuya longitud de onda Compton es igual a la longitud de Planck.  Está dada por la ecuación 2), donde ħ es la constante de Planck racionalizada, c es la velocidad de la luz y G es la constante gravitacional (los mismos términos de la ecuación 1), pero intercambiándolos de manera que tienen otro significado).

La descripción de una partícula elemental de esta masa, o partículas que interaccionan con energías por partículas equivalentes a ella (a través de ), requiere una teoría cuántica de la gravedad.  Como la masa de Planck es del orden de 10^{-8 Kg (equivalente a una energía de 10 exp.19} GeV) y, por ejemplo, la masa del protón es del orden de 10^{-27 kg y las mayores energías alcanzables en los aceleradores de partículas actuales son del orden de 10 exp.3} GeV, los efectos de gravitación cuántica no aparecen en los laboratorios de física de partículas.

Únicamente, en un laboratorio aparecieron partículas que tenían energías del orden de la masa de Planck: en el Universo primitivo, de acuerdo con la teoría del Big Bang, motivo este por el que es necesaria una teoría cuántica de la gravedad para estudiar aquellas condiciones.

Esta energía de la que estamos hablando, del orden de 10¹⁹ GeV (inalcanzable para nosotros), es la que necesitamos para verificar la teoría de supercuerdas.

Siempre, desde que puedo recordar, me llamó la atención los misterios y secretos encerrados en la Naturaleza y, la innegable batalla mantenida, a lo largo de la historia, por los científicos para descubrirlos.

emilio silvera

* Mirar Ley de Stefan y Ley de desplazamiento de Wiey.

[?]

Durante mucho tiempo se creyó que los protones y neutrones que conforman el núcleo de los átomos eran partículas “elementales”, pero experimentos en los aceleradores de partículas en los que colisionaban protones con otros protones o con electrones a velocidades cercanas a la de la luz indicaron que, en realidad, estaban formados por partículas aun más pequeñas.  Estas partículas fueron llamadas quarks por el físico de Caltech, el norteamericano, Murray Gell–Mann, que ganó el Nobel en 1.969 por su trabajo sobre dichas partículas y el modelo del óctuple camino.

Desde que Max Planck sembrara aquella primera semilla, la teoría cuántica ha avanzado hasta cotas de icreíble perfección en simetría y resultados, procurando al hombre/mujer una máquina muy valiosa para el conocimiento de la Naturaleza del Universo y la materia que lo puebla.

[?]

¡La Mecánica Cuántica! ¡Qué dolor de cabeza! No, no es fácil sumergirse en ese “universo” de los microscópico y llegar a entender del todo. ¡Son tantos los enigmas que están presente! Más de una vez he llegado a pensar sobre el hecho de que, aunque todo esté en el mismo Universo (lo micro y lo macroscópico), algunas veces nos puede dar la sensación de que son, “dos mundos diferentes” tal es la complejidad que encontramos cuando nos queremos acercar a esas distancias subatómicas donde viven e interaccionan las partículas elementales. Ese mundo, es totalmente ajeno a lo que podemos ver en nuestras vidas cotididianas, y, sin embargo, forma parte de este mundo nuestro. De hecho, todo lo grande está hecho de cosas pequeñas.

               Imágenes fractales y la belleza matemática que las describen

Algunos buenos físicos, desde siempre, han hablado de la belleza implícita en las matemáticas y, generalmente, se refieren a que con una gran economía de números nos pueden hablar de muchas cosas y además profundas. Como ejemplo de lo que digo, podríamos recordar la fórmula de Einstein de la Relatividad especial que a todos nos es familiar E = mc² y, la que nos describe la más compleja Relatividad general que no llena ni una línea de este comentario y que, sin embargo, nos habla de uno de los pensamientos más profundos que el ser humano haya podido tener. De hecho, a partir de esa ecuación de campo de la R.G., comenzó realmente la historia de lo que hoy conocemos como cosmología, tantos son sus mensajes sobre el Universo.

En la teoría de la Supersimetría, las matemáticas son realmente bellas y lo mismo podríamos decir de la teoría de Yang-Mills. La primera nos habla de una simetría que puede ser aplicada a las partículas elementales con el fin de transformar un Bosón en un fermión y viceversa. En las teorías supersimétricas más simples, cada Bosón tiene un compañero fermiónico y cada fermión tiene un compañero bosónico. Los compañeros bosónicos de los fermiones tienen nombres formados añadiendo “s” al principio del nombre del fermión, por ejemplo, selectrón, squark y sleptón.

                                                                                                                          ¿Supersimetría?

Los compañeros fermiónicos de los Bosones tienen nombres formados reemplazando el “on” del final del nombre del Bosón por “ino” o añadiendo “-ino”, por ejemplo gluino, fotino, wino, y zino.

Los infinitos que causan problemas en las teorías cuánticas de campo relativistas (obligando a la renormalización) son menos severos en las teorías supersimétricas, porque las contribuciones a los infinitos de los Bosones y los fermiones se pueden cancelar unos a otros.

Si la supersimetría es realmente una simetría de la Naturaleza, debe ser una simetría rota, aunque por el momento no hay evidencias concluyentes que muestren a qué energía debe romperse. No hay, de hecho, ninguna evidencia experimental para la teoría, aunque se piensa que puede ser un ingrediente especial en una teoría unificada de las interacciones. Esta no debe ser necesariamente una teoría de campo unificado; la idea de cuerdas con supersimetría es hasta el momento la mejor teoría para unificar a las cuatro fuerzas fundamentales de la Naturaleza y, en ella, los objetos básicos son unidimensionales (supercuerdas) que tienen una escala de longitud de unos 10 exp. 35 metros y, como distancias muy cortas están asociadas a energías muy altas, tiene una escala de energía del orden de 10 exp. 19 GeV, que está muy por encima de cualquier acelerador que, por ahora, pudiera construirse.

      Experimentos insuficientes para llegar a las cuerdas

Las cuerdas asociadas con los Bosones sólo son consistentes como teorías cuánticas en un espacio-tiempo de 26 dimensiones; aquellas asociadas a los fermiones sólo lo son en un espacio tiempo de 10 dimensiones. Se piensa que las dimensiones microscópicas surgen por el mecanismo de Kaluza-Klein, estando las restantes dimensiones “enrolladas” para ser muy pequeñas. Una de las características más atractivas de la teoría de supercuerdas es que dan lugar a partículas de espín 2, que son identificadas con los gravitones. Por tanto, una teoría de supercuerdas automáticamente contiene una teoría cuántica de la gravedad.

Una propiedad general de modelos con dimensiones extra que los hace especialmente atractivos es la localidad en la dimensión extra. Campos cuatridimensionales (los modos de KK) pueden estar localizados en puntos diferentes de la dimensión extra, lo que automáticamente suprime, en ocasiones exponencialmente, los acoplamientos entre ellos. Esto nos permite por ejemplo explicar de forma sencilla la gran diferencia de masas entre unos fermiones y otros o sus patrones de mezcla. La localidd en la dimensión extra, combinada con la fuerte curvatura en el modelo de RS produce un patrón de nueva física extremadamente interesante. En estos modelos, los primeros modos de KK -los más accesibles experimentalmente- están localizados cerca de la brana infrarroja, en la que también se produce la rotura de simetría electro débil y por tanto la masa de los fermiones. Los fermiones ligeros, cuyas propiedades han sido estudiadas experimentalmente con gran detalle sin observar ninguna anomalía, son ligeros porque están localizados lejos de la brana infrarroja y acomplan por tanto débilmente a los primeros modos de KK. Esto explica que sus propiedades no se vean modificadas apreciablemente por las dimensiones extra. El quark top, por contra, es mucho más pesado porque está localizado cerca de la brana infrarroja y por tanto su acomplamiento a los modos de KK es mucho myor. Como resultado, una predicción de estos modelos es que las propiedades del quark top -que aún no han sido medidas con precisión pero que serán objeto de profundo estudio en el LHC- serán modificadas por las dimensiones extra y que los modos de KK asociados a dichas dimensiones se mostrarán fundamentalmente en forma de producción anómala de quarks top.

Todas estas propiedades hacen los modelos con dimensiones extra alabeadas muy atractivos, pero cobran una relevancia aún mayor cuando nos damos cuenta de que la famosa conjetura de Maldacena, aplicada a modelos con dimensiones extra alabeadas implica que estos modelos son duales a teorías cuatri-dimensionales fuertemente acopladas. Esto quiere decir que, incluso si las dimensiones extra no existiesen realmente, modelos tipo RS o sus generalizaciones aún pueden serútiles. En efecto, debido a la dualidad nos permiten hacer cálculos cuantitativos que aplican a toerías cuatri-dimensionales en las que, debido al acoplamiento fuerte, no resulta sencillo calcular de otra forma. Usando esta dualidad se han hecho estudios relevantes tanto para cromodinámica cuántica como para teorías de rotura de la simetría electrodébil mediante acoplamiento fuerte, como para modelos de tecnicolor o de Higgs compuesto, por ejemplo.

Es fácil intuir que, si estos modelos están relacionados con modelos fuertemente acoplados, sus restricciones experimentales serán bastante estrictas. Efectivamente, un estudio cuidadoso muestra que, aun usando ciertas simetrías que protegen los observables más sensibles, los modos de KK de los bosones de gauge (las partículas que median las interacciones) tienen que tener una masa del orden de 3500 GeV o mayor, haciéndolos más dificilmente observables en el LHC de lo que originalmente se pensó. Los modos de KK de los fermiones,  por otro lado, pueden ser mucho más ligeros y fácilmente observables en el LHC.

Se piensa que las supercuerdas están libres de infinitos que no pueden ser eliminados por renormalización, que plagan todos los intentos de construir una teoría cuántica de campos que incorpore la gravedad. Hay algunas evidencias de que la teoría de supercuerdas está libre de infinitos, pero no hay una prueba definitiva. Aunque no existan evidencias directas de las supercuerdas, algunas de sus características son compatibles con los hechos experimentales observados en las partículas elementales, como la probabilidad de que las partículas no respeten paridad, lo que en efecto ocurre en las interacciones débiles.

Cuando hablamos de supergravedad lo hacemos de otra teoría aspirante a unificar todas las interacciones fundamentales conocidas que incorpora la supersimetría. La supergravedad se formula de forma más natural como una teoría de Kaluza-Klein en once dimensiones.

La teoría contiene partículas de espín 2, espín 3/2, espín 1, espín ½ y espín 0. Esta teoría, parece que contiene infinitos que no pueden ser renormalizados, es decir, no pueden ser eliminados. Muchos físicos piensan que para obtener una teoría cuántica de la gravitación consistente uno tiene que abandonar las teorías cuánticas de campos, pues se ocupan de objetos puntuales, y pasar a teorías cuyos objetos fundamentales sean extensos, como las supercuerdas y las supermembranas y, en consecuencia, la supergravedad no sería una teoría completa de las interacciones fundamentales.

Todas estas versiones de las teorías que tratan de unificar a las cuatro fuerzas de la Naturaleza han sido unificadas de forma magistral por W. Witten en su Teoría M que, sin embargo, y a pesar de su belleza descriptiva, aún no consigue el objetivo buscado, ya que, las matemáticas necesarias para su desarrollo final aún no son conocidas y las energías que exigen la experimentación no está en este mundo nuestro, estamos hablando de energías que sólo existieron en el momento de la creación.

Muchos han imaginado un agujero negro microscópico que contiene tanto las leyes de la gravedad como las de la mecánica cuántica y, la pregunta sería ¿cómo se debe describir su comportamiento? La pregunta tiene su lógica en que ese hipotético agujero negro se debería comportar como un átomo o molécula que obedecería a las leyes de la mecánica cuántica.

Cuando se hicieron cálculos en esa dirección, la sorpresa fue mayúscula, ya que las matemáticas que surgían eran las de la teoría de cuerdas. La fórmula para la captura y emisión de partículas por un agujero negro es exactamente igual a la fórmula de Veneziano. Lo cual resultaba extraño ya que no era un tema de cuerdas. Todo esto nos dice que la teoría de cuerdas está inacabada y, de manera formal, no podemos decir (aún) que algún día pueda ser compatible con la Gravedad.

Pero en la mecánica cuántica existen otros escenarios muy atractivos para nuestra imaginación. Sabemos que los átomos están formados por pequeños constituyentes, los protones, neutrones y electrones. Luego descubrimos que esos constituyentes, a su vez, tienen una subestructura: están formados de quarks y gluones. ¿Por qué, como probablemente todos hayamos pensado, el proceso no puede continuar así? ¿Quizá esos quarks y gluones, e igualmente los electrones y todas las demás partículas aún llamadas “elementales” en el modelo estándar, están a su vez construidas de unos gránulos de materia aún menores que no hemos sido capaces de observar en nuestros aceleradores de partículas?

Miremos a los quarks de un protón. La mecánica cuántica, la teoría maravillosa que controla todo el micromundo con increíble precisión, exige que el producto de la masa por la velocidad, el llamado “momento”, debe ser inversamente proporcional al tamaño de la “caja” en la cual ponemos nuestro sistema. El protón puede ser considerado como una de tales cajas y es tan pequeño que los quarks en su interior tendrían que moverse con una velocidad cercana a la de la luz. Debido a esto, la masa efectiva de los dos quarks más pequeños, up y dowm, es aproximadamente de 300 MeV, lo que explica porque la masa del protón es de 900 MeV, mucho mayor que la suma de la masa en reposo de los quarks y gluones.

En contraste con el protón, los propios quarks y también los leptones y todas las demás partículas en el modelo estándar parecen ser “puntuales”. Con esto quiero decir que sus propiedades no cambiarían ni siquiera cuando se colocaran en una caja mil veces más pequeñas que un protón. Aquí está nuestra dificultad: supongamos que estas partículas estuvieran compuestas de constituyentes aún más pequeños, estos tendrían que estar empaquetados más estrechamente y, por lo tanto, tendrían mucha más energía cinética (energía debida a sus rápidos movimientos) que habría que añadir a su propia masa. Pero entonces, ¿por qué son los quarks y los electrones tan ligeros?

Esto lo puedo explicar de forma más complicada. Los quarks dentro de los protones tienen tres clases de “masas”. Primero la que llamamos “masa libre”, o la masa que tendría si el objeto estuviera aislado. Pero para aislar un quarks fuera de un protón se necesita una cantidad infinita de energía y, por tanto, la masa libre de un quark es infinita. Esto es un concepto sin sentido y consecuentemente inútil. En segundo lugar, tenemos la masa efectiva de un quark dentro de un protón, que debido a las leyes de la mecánica cuántica está obligado a moverse de un lado para otro con gran velocidad. Ésta se llama “masa constituyente” tiene un valor de 300 MeV que es 1/3 de la masa del protón. La tercera clase de masa es la “masa algebraica”. Ésta es un parámetro que determina las propiedades del objeto llamado “término de masa” en sus ecuaciones. Para otras partículas, este término de masa corresponde a su masa real; para los quarks u y d esta cantidad es sólo de unos 10 MeV. El problema que tenemos es que los hipotéticos nuevos ladrillos constitutivos tendrían una masa constituyente muy grande, que es muchas veces mayor que la masa del objeto que forman. Es como si te pidieran construir una casa ligera como las briznas de algodón pero con sus pilares y estructura hechos de un material tan compacto como el acero macizo.

Claro que (como se suele decir), la esperanza es lo último que podemos perder, la Naturaleza misma nos ha dado un ejemplo de cómo se pueden conseguir cosas como esta. El pión también está formado por quarks y, como no es mucho más grande que el protón sería de esperar que ahí los quarks también tengan masas constituyentes de unos 300 MeV. Sin embargo, el pión, en vez de 600 MeV, solamente pesa 135 MeV. Esto se debe a que la masa del pión está protegida por una simetría: el pión es (aproximadamente) un Bosón de Goldstone.

Esto significa que quizá halla una forma de ver partículas tan ligeras como el electrón y que estén formadas por ladrillos constitutivos “más pesados”. Para ello se deben introducir simetrías, quizá tantas como partículas haya en el modelo estándar y, así, se podría explicar que todas las partículas conocidas son tan ligeras porque sus masas están protegidas por una simetría. Sin embargo, resulta que convertir esta idea en una receta matemática precisa es una tarea difícil.

Pocos son los casos en los que una partícula compuesta, de una manera espontánea, ha roto la simetría: uno sería el viejo modelo sigma de Gell-Mann y Lévy (la partícula Sigma compuesta realmente por quarks) y el otro es la teoría BCS de la superconductividad, donde aparece un fenómeno similar al mecanismo de Higgs debido a un estado ligado de dos electrones (el par de Cooper). Pero en el Modelo estándar se conocen con precisión muchas de las propiedades de las partículas de Higgs porque son responsables de las masas de las partículas conocidas.

Quizá el nuevo acelerador Large Hadrón Collider (LHC), que ya está en marcha, nos pueda desvelar algunos de los fenómenos asociados a tales esquemas, algunos incluso tienen la esperanza de que aparezcan, además del Bosón de Higgs, algunas otras partículas predichas en la teoría supersimétrica  que ellos denominan WIMP y que, según dicen, pueblan los huecos de las galaxias y son, así responsables de la masa perdida que los astrofísicos no dejan de buscar.

Eso sería otra historia y, como el comentario tiene que finalizar, la dejaremos para contarla en otro próximo en el cual hablemos de esa “hipotética” materia y energía oscura que, en realidad, no sabemos con certeza ni que pueda existir y, de momento, parece más un artilugio de los cosmólogos para que las cuentas del Universo cuadren.

emilio silvera

[?]

Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida medio, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.

También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.

Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, ksi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales manera de desintegración, veríamos como difieren las unas de las otras.

Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.

                       Lo que resulta de una colisión de haces de partículas en el LHC

¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.

En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su carta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas, Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas  experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.

Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.

Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según  la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.

Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.

Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”

Si la vida de una partícula  es tan corta como 10ˉ²³ segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.

Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.

Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).

Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.

Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:

∆⁺⁺→р + π⁺;  ∆⁰→р + πˉ; o п+π⁰

En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.

Masa atómica

Una de las formas como los científicos miden el tamaño de algo es a través de su masa. Los científicos pueden incluso medir cosas muy minúsculas como los átomos. Una medida del tamaño de un átomo es su “masa atómica”. Casi toda la masa de un átomo (más del 99%) está en su núcleo, de manera que la “masa atómica” es realmente una medida del tamaño del núcleo de un átomo.

Los protones son practicamente del mismo tamaño que los neutrones, y ambos son mucho más grandes que los electrones. Un protón tiene una masa aproximadamente 1.836 veces mayor que la masa del electrón, pero las masas de los protones y neutrones se diferencian menos de uno por ciento. Un protón tiene una masa de 1.6726 x 10^-24gramos. Los protones tienen una carga eléctrica positiva, conocida a veces como carga elemental, carga fundamental o carga de +1. Los electrones tienen una carga del mismo valor pero de polaridad opuesta, -1. La carga fundamental tiene un valor de 1.602 x 10^-19 coulombios.

Núcleo atómico

El núcleo de un átomo contiene protones y neutrones. Cada elemento (como el carbono, oxígeno o el oro) tiene diferente número de protones en sus átomos. Los científicos tienen un nombre especial para el número de protones en un átomo. Lo llaman “número atómico”.

¿Por qué es importante el número atómico? Los átomos normales tienen el mismo número de electrones que protones. El número de electrones es lo que hace que cada elemento se comporte de cierta manera en reacciones químicas. De manera que el número atómico, que es el número de protones y electrones, es lo que hace que un elemento sea diferente a otro.

Hace algunos años ya que los físicos se preguntaban: ¿Podrían los protones ser puntos? Y, tratándo de saberlo, comenzaron a golpear los protones con otros protones de una energía muy baja (al principio) con el objeto de explorar la fuerza electromagnética entre los dos objetos cargados.

El Acelerador Lineal de Stanford. El SLAC, ubicado al sur de San Francisco, acelera electrones y positrones a lo largo de sus 2 millas de longitud (algo mas de tres kilómetros), hacia varios blancos, anillos y detectores ubicados en su finalización. Este acelerador hace colisionar electrones y positrones, estudiando las partículas resultantes de estas colisiones. Construido originalmente en 1962, se ha ido ampliando y mejorando para seguir siendo uno de los centros de investigación de física de partículas mas avanzados del mundo. El Centro ha ganado el premio Nobel en tres ocasiones.

El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (materia), es aún limitado.

Generalmente las llamamos partículas elementales pero, lo cierto es que, algunas son más elementales que otras. Los físicos experimentadores hicieron un buen trabajo en aquellos antiguos aceleradores de partículas por despejar la incognita y saber, de una vez por todas, de qué estava hecha la materia.

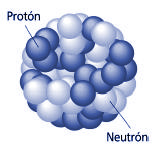
Los núcleos de los átomos están formados por protones y neutrones, alrededor de los cuales orbitan los electrones. Estos tres elementos (protones, neutrones y electrones) constituyen prácticamente toda la materia de la Tierra. Mientras que el electrón se considera como una partícula “sin tamaño”, el protón, que está compuesto de quarks, es un objeto con tamaño específico. Hasta ahora, sólo dos métodos se han utilizado para medir su radio. Basándose en el estudio de las interacciones entre un protón y un electrón, ambos métodos se centran en las colisiones entre uno y otro o sobre el átomo de hidrógeno (constituido por un electrón y un protón). El valor obtenido y que es el utilizado por los físicos, es 0,877 (+ / – 0,007) femtómetros.

Si los físicos experimentales de la década de los 60 hubieran podido tener a su disposición el moderno LHC… ¿Dónde estaríamos ahora?

La interacción fuerte es cien veces más intensa que la fuerza eléctrica de Coulomb, pero, al contrario que ésta, su alcance no es en absoluto infinito. Se extiende sólo hasta una distancia de unos 10^-13 centímetros, y luego cae deprisa a cero. Al incrementar la energía de colisión, los experimentos desenterraron más y más detalles desconocidos de la interacción fuerte. A medida que aumenta la energía, la longitud de onda de los protones (acordémonos de De Broglie y Schrödinger) se encoge. Y, como se pudo ver, cuanto menor sea la longitud de onda , más detalles cabe discernir en la partícula que se estudie.

Robert Hofstadter, de la Universidad de Stantanford, tomó en los años cincuenta algunas de las mejores “imágenes” del protón. En vez de un haz de protones, la “luz” que utilizó fue un haz de electrones de 800 MeV que apuntó a un pequeño recipiente de hidrógeno líquido. Los electrones bombardearon los protones del hidrógeno y el resultado fue un patrón de dispersión, el de los electrones que salían en una variedad de direcciones con respecto a su movimiento original. No era muy diferente a lo que hizo Rutherford. Al contrario que el protón, el electrón no responde a la interacción nuclear fuerte. Responde sólo a la carga eléctrica del protón, y por ello los científicos de Stanford pudieron explorar la forma de la distribución de carga del protón. Y esto, de hecho, reveló el tamaño del protón. Claramente no era un punto.

Se midió que el radio del protón era de 2,8 x 10^-13 centímetros; la carga se acumula en el centro, y se desvanece en los bordes de lo que llamamos el protón. Los experimentos se repitieron muchas veces y los resultados, siempre fueron parecidos al hacerlos con haces de muones, que también ignoran la interacción fuerte al ser leptones como los electrones.  (Medidas más precisas llevadas a cabo en nuestro tiempo, han podido detectar, diminutos cambios en el radio del protón que tienen enormes implicaciones. El protón parece ser 0,00000000000003 milímetros más pequeño de lo que los investigadores habían pensado anteriormente, de hecho, y según han comentados los físicos del equipo que hizo el trabajo,  las nuevas medidas podrían indicar que hay un hueco en las teorías existentes de la mecánica cuántica y algo falla en alguna parte.)

La imágen tomada en el SLAC, nos choca, todos tenemos en la mente las del LHC

Pero sigamos con la historia. Hallá por el año 1968, los físicos del Centro del Acelerador Lineal Stanford (SLAC), bombarderon los protones con electrones de mucha energía -de 8 a 15 GeV- y obtuvieron un conjunto muy diferente de patrones de dispersión. A esta “luz dura”, el protón presentaba un aspecto completamente distinto. Los electrones de energía relativamente baja que empleó Hofstadter podían ver sólo un protón “borroso”, una distribución regular de carga que hacía que el electrón pareciése una bolita musgosa. Los electrones del SLAC pudieron sondear con mayor dureza y dieron con algunos “personajillos” que “correteaban” dentro del protón. Aquella fue la primera indicación de la existencia real de los Quarks.

Hablando de partículas y de física cuántica nos podríamos llevar muchos días, meses y años y escribir todo lo que hasta el momento se ha descubierto en este campo sería una tarea imposible en un lugar como éste en el que los trabajos, son indicativos y particularmente sencillos para que, los lectores visitantes, tengan una sencilla idea de los temas que se comentan, así que, en relaciòn a éste, aquí lo dejamos.

emilio silvera

[?]

Los ordenadores cuánticos serán «los más seguros» del mercado

marta moreiraabc_es / Valencia

El premio Príncipe de Asturias, Ignacio Cirac, cree que podrán comercializarse en un plazo entre 10 y 50 años

 

 

ROBER SOLSONA

El Premio Príncipe de Asturias, Ignacio Cirac, afirma, sin embargo, que los avances en esta materia están «a un nivel muy fundamental»

Las investigaciones teóricas sobre física cuántica van por buen camino, pero todavía están muy lejos de traducirse en aplicaciones prácticas en el campo de la informática. La comunidad científica ha depositado grandes esperanzas en los ordenadores cuánticos, que permitirán realizar cálculos que no pueden resolverse con los ordenadores actuales –los que trabajan según las leyes clásicas de los ceros y unos-. Sin embargo, su comercialización podría tardar entre diez y cincuenta años. «Estoy convencido de que va a suceder, lo que no sé es si voy a vivir para verlo», añade Ignacio Cirac, director de la División Teórica Max-Plank de Óptica Cuántica de Garching (Alemania).

Así lo defendió en el marco de la 34 Bienal de la Real Sociedad de Física Española, que se celebra estos días en Valencia. Renuente a lanzar promesas cortoplacistas de difícil cumplimiento, este científico recordó que los avances en esta matería están todavía «a un nivel muy fundamental».

Uno de los aspectos más interesantes de los sistemas de compuitación basados en mecánica cuántica es la seguridad. «La física cuántica permite codificar la información de manera que se destruya en el momento en que cualquier persona no autorizada quiera leer el mensaje», explica. La diferencia con respecto a los sistemas actuales es que la información no puede interceptarse porque no pasa por ningún lugar. «Desaparece una vez lo envía el emisor y aparece de nuevo en el aparato del receptor, como por arte de magia». Se abre por tanto un nuevo reto para los «hackers».

[?]