Decaimiento β^– de un núcleo. Se ilustra cómo uno de los neutrones se convierte en un protón a la vez que emite un electrón (β^–) y un antineutrino electrónico.  La desintegración beta se debe a la interacción nuclear débil, que convierte un neutrón en un protón (desintegración β^–), o viceversa (β⁺), y crea un par leptón–antileptón. Así se conservan los números bariónico (inicialmente 1) y leptónico (inicialmente 0). Debido a la aparente violación al principio de conservación de la energía, estas reacciones propiciaron precisamente que se propusiera la existencia del neutrino. Precisamente de eso hablamos aquí.

Una vez escenificados los conceptos, diremos que, los físicos se vieron durante mucho tiempo turbados por el hecho de que a menudo, la partícula beta emitida en una desintegración del núcleo no alberga energía suficiente para compensar la masa perdida por el núcleo.  En realidad, los electrones no eran igualmente deficitarios.  Emergían con un amplio espectro de energías, y el máximo (conseguido por muy pocos electrones), era casi correcto, pero todos los demás no llegaban a alcanzarlo en mayor o menor grado.  Las partículas alfa emitidas por un nucleido particular poseían iguales energías en cantidades inesperadas.  En ese caso, ¿qué era errónea en la emisión de partículas beta? ¿Qué había sucedido con la energía perdida?

En 1.922, Lise Maitner se hizo por primera vez esta pregunta, y, hacia 1.930, Niels Bohr estaba dispuesto a abandonar el gran principio de conservación de la energía, al menos en lo concerniente a partículas subatómicas.  En 1.931, Wolfgang Pauli sugirió una solución para el enigma de la energía desaparecida.

La radiación alfa está compuesta por un núcleo de helio y puede ser detenida por una hoja de papel. La radiación beta, compuesta por electrones,  es detenida por una hoja de papel de aluminio. La radiación gamma es absorbida cuando penetra en un material denso

Digamos que la solución de Pauli para explicar la masa perdida, era muy simple: junto con la partícula beta del núcleo se desprendía otra, que se llevaba la energía desaparecida.  Esa misteriosa segunda partícula tenía propiedades bastante extrañas.  No poseía carga ni masa.  Lo único que llevaba mientras se movía a la velocidad de la luz era cierta cantidad de energía.  A decir verdad, aquello parecía un cuerpo ficticio creado exclusivamente para equilibrar el contraste de energías.

Sin embargo, tan pronto como se propuso la posibilidad de su existencia, los físicos creyeron en ella ciegamente. Y esta certeza se incrementó al descubrirse el neutrón y al saberse que se desintegraba en un protón y se liberaba un electrón, que, como en la decadencia beta, portaba insuficientes cantidades de energía.  Enrico Fermi dio a esta partícula putativa el nombre de “neutrino”, palabra italiana que significa “pequeño neutro”.

Primera observación de un neutrino en una cámara de burbujas, en 1970 en el Argonne National Laboratory de EE. UU., la observación se realizo gracias a las líneas observadas en la Cámara de burbujas  basada en hidrógeno líquido. Siempre hemos tenido imaginación para idear aparatos que nos ayudaran a desvelar los secretos de la Naturaleza. Más tarde, la cámara de burbujas, fue sustituida por la cámara de chispas.

El neutrón dio a los físicos otra prueba palpable de la existencia del neutrino.  Como ya he comentado otras veces, casi todas las partículas describen un movimiento rotatorio. Esta rotación se expresa, más o menos, en múltiplos de una mitad según la dirección del giro.  Ahora bien, el protón, el neutrón y el electrón tienen rotación de una mitad. Por tanto, si el neutrón con rotación de una mitad origina un protón y un electrón, cada uno con rotación de una mitad, ¿qué sucede con la ley sobre conservación del momento angular? Aquí hay algún error. El protón y el electrón totalizan una mitad con sus rotaciones (si ambas rotaciones siguen la misma dirección) o cero (si sus rotaciones son opuestas); pero sus rotaciones no pueden sumar jamás una mitad. Sin embargo, por otra parte, el neutrino viene a solventar la cuestión.

Supongamos que la rotación del neutrón sea +½. Y admitamos también que la rotación del protón sea +½ y la del electrón -½, para dar un resultado neto de cero. Demos ahora al neutrino una rotación de +½, y la balanza quedará equilibrada.

+½(n) = +½(p) – ½(e) + ½(neutrino)

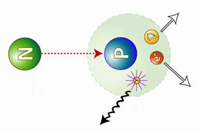
Pero aun queda algo por equilibrar.  Una sola partícula (el neutrón) ha formado dos partículas (el protón y el electrón), y, si incluimos el neutrino, tres partículas.  Parece más razonable suponer que el neutrón se convierte en dos partículas y una antipartícula.  En otras palabras: lo que realmente necesitamos equilibrar no es un neutrino, sino un antineutrino.

El propio neutrino surgiría de la conversación de un protón en un neutrón.  Así, pues, los productos serían un neutrón (partícula), un positrón (antipartícula) y un neutrino (partícula). Esto también equilibra la balanza. En otras palabras, la existencia de neutrinos y antineutrinos debería salvar no una, sino tres, importantes leyes de conservación: la conservación de la energía, la de conservación del espín y la de conservación de partícula/antipartícula.

 

 

Para un electrón, protón o neutron la cantidad de espín es siempre 1/2 del valor mínimo de momento permitido (ħ).

 

 

Cada partícula conocida tiene una antipartícula. Si se encuentran entre sí, se aniquilan y producen dos rayos gamma. Las energías cuánticas de los rayos gamma es igual a la suma de las energías de masas de las dos partículas (incluyendo sus energías cinéticas). También es posible que un fotón en su interacción con la materia,  ceda su energía cuántica para la formación de un par de partícula-antipartícula,. La energía de masa en reposo de un electrón es 0,511 MeV, por lo que el umbral para la producción de pares electrón-positrón es de 1,02 MeV. Para las energías de rayos x t rayos gamma muy superiores a 1 MeV, esta producción de pares se convierte en una de las más importantes clases de interacciones con la materia. A energías aún más altas, se producen muchos tipos de pares partícula-antipartícula.

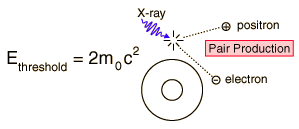
Es importante conservar esas leyes puesto que parece estar presentes en toda clase de reacciones nucleares que no impliquen electrones o positrones, y sería muy útil si también se hallasen presentes en reacciones que incluyesen esas partículas.

Las más importantes conversiones protón-neutrón son las relaciones con las reacciones nucleares que se desarrollan en el Sol y en los astros.  Por consiguiente, las estrellas emiten radiaciones rápidas de neutrinos, y se calcula que tal vez pierdan a causa de esto el 6 u 8 % de su energía.  Pero eso, sería meternos en otra historia y, por mi parte, con la anterior explicación solo trataba de dar una muestra del ingenio del hombre que, como habréis visto, no es poco.

Aunque sólo una cinco mil millonésima de la luz solar llega a la Tierra, ha sido suficiente para dar a esta calor y vida, así como bípedos bastante listos para calcular al detalle su deuda con el Sol que, si pusiera intereses, nunca podríamos pagar.

Desde que puedo recordar, he sido un amante de la Física. Me asombran cuestiones como la luz, su naturaleza de un conglomerado de colores, ondas y partículas, su velocidad que nos marca el límite máximo que se puede desplazar cualquier cosa en nuestro Universo, y en fin, muchos otros misterios que encierra esa maravilla cotidiana que nos rodea y lo inunda todo haciendo posible que podamos ver por donde vamos, que las plantas vivan y emitan oxígeno o que nos calentemos.  Realmente, sin luz, nuestra vida no sería posible.

   Me gustaría que alguien contestara: ¿Qué es realmente la luz?

Muchos (casi todos) opinan que es algo inmaterial. Los objetos materiales, grandes o muy pequeños como las galaxias o los electrones, son materia.  La luz, sin embargo, se cree que es inmaterial, dos rayos de luz se cruzan sin afectarse el uno al otro. Sin embargo, yo que deberíamos profundizar un poco más y, sabiendo que la luz está formada por fiotones, que los fotones son energía, que la energía es un aspecto de la masa… ¿Qué es realmente la luz? Nosotros mismos, el última instancia ¿No serémos luz?

Está claro que los estudiosos de la época antigua y medieval estaban por completo a oscuras acerca de la naturaleza de la luz. Especulaban sobre que consistía en partículas emitidas por objetos relucientes o tal vez por el mismo ojo. Establecieron el hecho de que la luz viajaba en línea recta, que se reflejaba en un espejo con un ángulo igual a aquel con el que el rayo choca con el espejo, y que un rayo de luz se inclina (se refracta) cuando pasa del aire al cristal, al agua o a cualquier otra sustancia transparente.

Cuando la luz entra en un cristal, o en alguna sustancia transparente, de una forma oblicua (es decir, en un ángulo respecto de la vertical), siempre se refracta en una dirección que forma un ángulo menor respecto de la vertical.  La exacta relación entre el ángulo original y el ángulo reflejado fue elaborada por primera vez en 1.621 por el físico neerlandés Willerbrord Snell.  No publicó sus hallazgos y el filósofo francés René Descartes descubrió la ley, independientemente, en 1.637.

Los primeros experimentos importantes acerca de la naturaleza de la luz fueron llevados a cabo por Isaac Newton en 1.666, al permitir que un rayo de luz entrase en una habitación oscura a través de una grieta e las persianas, cayendo oblicuamente sobre una cara de un prisma de cristal triangular. El rayo se refracta cuando entra en el cristal y se refracta aún más en la misma dirección cuando sale por una segunda cara del prisma. (Las dos refracciones en la misma dirección se originan por que los dos lados del prisma de se encuentran en ángulo en vez de en forma paralela, como sería el caso en una lámina ordinaria de cristal.)

Newton atrapó el rayo emergente sobre una pantalla blanca para ver el efecto de la refracción reforzada.  Descubrió que, en vez de formar una mancha de luz blanca, el rayo se extendía en una gama de colores: rojo, anaranjado, amarillo, verde, azul, y violeta, en este orden. Newton dedujo de ello que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores.  La amplia banda de sus componentes se denominó spectrum (palabra latina que significa “espectro” fantasma).

Newton llegó a la conclusión de que la luz se componía de diminutas partículas (“corpúsculos”), que viajaban a enormes velocidades.

Le surgieron y se planteó algunas inquietantes cuestiones. ¿Por qué se refractaban las partículas de luz verde más que los de luz amarilla? ¿Cómo se explicaba que dos rayos de luz se cruzaran sin perturbase mutuamente, es decir, sin que se produjeran colisiones entre partículas?

En 1.678, el físico neerlandés christian Huyghens (un científico polifacético que había construido el primer reloj de péndulo y realizado importantes trabajos astronómicos) propuso una teoría opuesta: la de que la luz se componía de minúsculas ondas. Y si sus componentes fueran ondas, no sería difícil explicar los diversos difracciones de los diferentes tipos de luz a través de un medio refractante, siempre y cuando se aceptara que la luz se movía más despacio en ese medio refractante que en el aire.  La cantidad de refracción variaría con la longitud de las ondas: cuanto más corta fuese tal longitud, tanto mayor sería la refracción.   Ello significaba que la luz violeta (la más sensible a este fenómeno) debía de tener una longitud de onda mas corta que la luz azul, ésta, más corta que la verde, y así sucesivamente.

                   Se encuentra la galaxias más lejana nacida después del big bang

Gracias a las radiaciones electromagnéticas podemos ver el Universo como fue hace ahora miles de millones de años. Cuando la luz, nos trae la imágen de galaxias situadas a distancias inconmensurables. ¿Quién podría haber pensado, en el pasado, que tal cosa fuese posible? hace

Lo que permitía al ojo distinguir los colores eran esas diferencias entre longitudes de onda.  Y, como es natural, si la luz estaba integrada por ondas, dos rayos podrían cruzarse sin dificultad alguna.  (Las ondas sonoras y las del agua se cruzan continuamente sin perder sus respectivas identidades.)

Pero la teoría de Huyqhens sobre las ondas tampoco fue muy satisfactoria. No explicaba por qué se movían en línea recta los rayos luminosos; ni por qué proyectaban sobras recortadas; ni aclaraba por qué las ondas luminosas no podían rodear los obstáculos, del mismo modo que pueden hacerlo las ondas sonoras y las ondas marinas.  Por añadidura, se objetaba que si la luz consistía en ondas, ¿cómo podía viajar por el vacío, ya que cruzaba el espacio desde el Sol y las Estrellas? ¿Cuál era esa mecánica ondulatoria?

Así que, la vieja idea de Newton de que la luz estaba formada por partículas, en contra de la teoría ondulatoria de su contemporáneo Huygens corroborada por posteriores experimentos en el siglo XIX y por la teoría electromagnética de Maxwell, volvía a ser vigente en parte. La radiación electromagnética estaba formada por paquetes de energía llamados fotones, tenía una doble naturaleza: ondulatoria y corpuscular. La doble naturaleza ondulatoria y corpuscular de la luz, hizo pensar al físico francés Louis de Broglie que el resto de partículas podían disfrutar de esa cualidad y estableció que cualquier partícula lleva asociada una onda de longitud igual al cuanto de acción (h) dividido por su masa y por su velocidad (cualquier objeto macroscópico también tiene su onda asociada, pero debido al valor tan pequeño del cuanto de acción su efecto es despreciable). De hecho, cuando se diseña un experimento, dependiendo de las restricciones que se impongan a la partícula se pone de manifiesto su naturaleza ondulatoria o corpuscular pero, esa es, otra historia.

emilio silvera

[?]

                  ¿Os acordais? ¿Cuántos niños no habrán soñado con escenas como estas?

Cuando hablo de lo muy pequeño, puedo llegar a entender muy bien lo que es, lo que son, “licencias literarias” el papel de nada se queja y el lápiz puede escribir lo que quiera y pience el que lo sostiene, según le dicte su imaginación. Claro que, cuando comparamos ese mundo de ilusiones e imaginación y lo comparamos con el mundo real, todo el edificio se viene abajo. ¡Lástima!

Todos los niños pequños juegan con pequeños muñecos que son soldados, guerreros o seres de otras galaxias con poderes mágicos y,ellos, en su inocente mundo sin maldad, los dirigen con sus manitas gordezuelas al desarrollo de luchas y aventuras sin fin. Jonathan Swift, nos deleitó con aquellas aventuras de Gulliver, un aventurero que llegó a las tierras de Lilliput: Allí, todo era muy pequeño, la naturaleza, las plantas, los habitantes del lugar y sus casas y palacios, embarcaciones y todos los animales.

Gulliver era allí un gigante de proporciones inmensas: Incluso llegó a extinguir un fuego con una simple chorrada (es decir, hizo pipí) y acabço de inmediato con el (para ellos) enorme fuego.

Su tamaño podía, sin dificultad alguna, decidir el resultado de una guerra entre aquellos pequeñísimos seres que, ante un gigante como él, no tenían defensa alguna y, sus armas, resultaban ridículas para poder causarle algún daño. Dormido lo tucieron que coger para poder atarlo.

Durante otro viaje, las fuerzas ignotas del destino llevaron a Gulliver a un pais llamado  Brobdingnag, donde la gente y todos los seres animados e inanimados eran mucho más grandes que él. Allí era un enano, mimado por una niña pequeña llamada Glumdalclitch. Al final, Gulliver es recogido en una jaula por un águila que lo deja caer en el mar de donde lo rescataron unos marineros a los que, al contarles esas historias, pusieron incrédulas caras de asombro.

Claro que, cuando nos trasladamos al mundo real, las cosas no suelen ser de esa manera. Poco importa lo fascinantes que las historias de este tipo nos puedan resultar. Las cosas no funcionan de esa manera. Todos sabemos, por ejemplo que la llama de una vela pequeña y la de una vela grande, son aproximadamente del mismo tamaño. ¿De qué tamaño serían las llamas de las velas de Lilliput? Y, desde luego, si pensamos un poco, más cuestiones nos surgen: ¿Cómo serían las gotas de lluvia en Lilliput y en Brobdingnag?, ¿eran las leyes físicas para el agua diferentes allí que en nuestro propio mundo? Y, finalmente, los físicos se preguntarían: ¿De qué tamaño eran los átomos en esos lugares?, ¿qué clase de reacciones químicas podrían tener lugar con los átomos del cuerpo de Gulliver?

Claro que, con esas preguntas esas historias fallan. La verdadera razón por la que los mundos de Los Viajes de Gulliver no pueden existir es que las leyes de la Naturaleza no permanecen exactamente iguales cuando se cambian las escalas. A veces, esto es evidente en las películas de desastres, donde quizá se ha construído una maqueta a escala para simular una gran ola o un rascacielos en llamas.

El ojo experto puede, sin problemas, distinguir entre la maqueta y la realidad. Los mejores resultados se obtienen cuando el factor de esacala para el tiempo se elige igual a la raíz cuadrada de la escala espacial. Así, si el rascacielos de turno se construye a escala 1:9, hay que rodar la película a un 1/3 de su velocidad real. Pero incluso así, como antes señalo, el ojo entrenado distingue la diferencia entre lo que sucede en la película y lo que se observaría en el mundo real.

En resumen, las leyes que gobiernan el mundo físico tienen dos características importantes: muchas leyes de la naturaleza permanecen inalterables, no se alteran cuando cambia la escala, pero hay otros fenómenos, tales como una vela encendida o las gotas de agua, que no cambian del mismo modo. La implicación final es que el mundo de los objetos muy pequeños será completamente diferente del mundo ordinario.

Justamente en el mundo de los seres vivos la escala crea importantes diferencias. En muchos aspectos, la anatomía de un ratón se podría consuiderar (más o menos y, guardando las distancias) como una copia de la de un elefante, pero mientras que un ratón puede trepar por una pared de piedra prácticamente vertical sin mucha dificultad (incluso se puede caer desde una altura varias veces mayor que su tamaño sin hacerse gran daño), un elefante sería incapaz de realizar tal hazaña. Así llegamosm a comprender que la Gravedad, se deja sentir en menor grado a medida que los objetos disminuyen de tamaño.

Cuando llegamos a los seres unicelulares, se ve que para ellos no hay distinción entre arriba y abajo. Para ellos, la tensión superficial del agua es mucho más importante que la fuerza de gravedad. Basta observar que la tensión superficial es la fuerza que da forma a una gota de agua y comparar el tamaño de esa gota con los seres unicelulares, muchísimo menores, para que sea evidente que la tensión superficial es muy importante a esta escala.

La tensión superficial es una consecuencia de que todas las moléculas y los átomos se atraen unos a otros con una fuerza que nosotros llamamos fuerza de Van der Vaalls. esta fuerza tiene un alcance muy corto. para ser más precisos, diremos que la intensidad de esta fuerza a una distancia r es aproximadamente proporcional a 1/r⁷. Esto significa  que si se reduce la distancia entre dos átomos a la mitad, la fuerza de Van der Vaalls con la que se atraen uno a otro se hace 2 x 2 x 2 x 2 x 2 x 2 x 2 = 128 veces más intensa. Cuando los átomos y las moléculas se acercan mucho unos a otros quedan unidos muy fuertemente a través de esta fuerza.

Ahora tendríamos que hablar algo de la mecánica cuántica y, en ese ámbito, las reglas de la mecánica cuántica funcionan tan bien que resultaría realmente difícil refutarlas.

Acordaos de los trucos ingeniosos descubiertos por Werner Hesinberg, Paul Dirac, o, Schrödinger que vinieron a mejorar y completar  las reglas generales. Sin embargo, algunos de aquellos pioneros (Einstein y el mismo Schrödinger), sin embargo, presentaron serias objeciones a dicha interpretación de la naturaleza de lo muy pequeño.

Podríamos formular una simple pregunta que pondría en un brete a más de uno: ¿Dónde está realmente el electrón, en el punto x o en el punto y? En pocas palabras, ¿dónde está en realidad? Si prestamos ate4nción a Bohr, no tiene ningún sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores serían las únicas realidades a las que deberíamos prestar atención y de las que podemos hablar.

Muchas veces me sorprende oír a muchos “científicos” que hablan con una seguridad de lo que dicen como si, de una verdad inamovible se tratara. Ellos (en realidad) creen que saben y, no llegan a darse cuenta de que están hablando de un Modelo que ha sido construído matemáticamente hablando, para poder explicar eso que, nosotros, los humanos, creemos que es la realidad del mundo. Sin embargo, más de una vez hemos tenido que cambiar esos modelos y rectificar esa “realidad” por otra que, resultó ser “más real”.

¡Sabemos tan poco

emilio silvera

[?]

Ahora todos hablamos del LHC. Sin embargo, la historia de los aceleradores no comenzó con éste moderno y complejo conglomerado de sofisticadas estructuras que hacen posible que visitemos lugares muy lejanos en el corazón de la materia. Tendríamos que recordar al acelerador lineal también llamado LINAC (linear accelerator) es un tipo de acelerador que le proporciona a la partícula subatómica cargada pequeños incrementos de energía cuando pasa a través de una secuencia de campos eléctricos alternos.

Mientras que el generador de Van de Graaff proporciona energía a la partícula en una sola etapa, el acelerador lineal y el ciclotrón proporcionan energía a la partícula en pequeñas cantidades que se van sumando. El acelerador lineal, fue propuesto en 1924 por el físico sueco Gustaf Ising. El ingeniero noruego Rolf Wideröe construyó la primera máquina de esta clase, que aceleraba iones de potasio hasta una energía de 50.000 eV.

Durante la Segunda Guerra Mundial se construyeron potentes osciladores de radio frecuencia, necesarios para los radares de la época. Después se usaron para crear aceleradores lineales para protones que trabajaban a una frecuencia de 200 MHz, mientras que los aceleradores de electrones trabajan a una frecuencia de 3000 MHz.

El acelerador lineal de protones diseñado por el físico Luis Alvarez en 1946, tenía 875 m de largo y aceleraba protones hasta alcanzar una energía de 800 MeV (800 millones). El acelerador lineal de la universidad de Stanford es el más largo entre los aceleradores de electrones, mide 3.2 km de longitud y proporciona una energía de 50 GeV (50 billones). En la industria y en la medicina se usan pequeños aceleradores lineales, bien sea de protones o de electrones.

El SLAC, ubicado al sur de San Francisco, acelera electrones y positrones a lo largo de algo más de tres kilómetros hacia varios blancos, anillos y detectores ubicados en su finalización. Este acelerador hace colisionar electrones y positrones, estudiando las partículas resultantes de estas colisiones. Construido originalmente en 1962, se ha ido ampliando y mejorando para seguir siendo uno de los centros de investigación de física de partículas mas avanzados del mundo. El centro ha ganado el premio nobel en tres ocasiones. Y, una vez recordada de manera breve la historia, pasaremos directamente al tema que en realidad nos ha tríado aquí: ¡El descubrimiento de los Quarks!

Ahora los medios con los que cuentan los físicos del LHC son inmensamente más eficaces y están más adelantados que aquellos viejos aceleradores que, sin embargo, fueron los pioneros y los que hicieron posible adquirir conocimientos que nos han traído hasta el moderno LHC.

En 1967 se emprendió una serie de experimentos de dispersión mediante los nuevos haces de electrones del SLAC. El objetivo era estudiar más incisivamente la estructura del protón. Entra el electrón de gran energía, golpea un protón en un blanco de hidrógeno y sale un electrón de energía mucho menor, pero en una dirección que forma un ángulo grande con respecto a su camino original. La estructura puntual dentro del protón actúa, en cierto sentido, como el núcleo con las partículas alfa de Rutherford. Pero el problema era aquí más sutíl.

Richard Edward Taylor

“Richard Edward Taylor fue uno de los veintidós científicos que trabajó intensamente en el acelerador lineal de Stanford (SLAC), en una serie de pruebas experimentales que vinieron a demostrar que los protones y los neutrones son poseedores de una estructura interna, lo que a su vez confirma las predicciones teóricas del neoyorquino Murray Gell-Mann (1929- ), acerca de la existencia de los denominados quarks.

Junto con sus colegas de Stanford junto con Jerome I. Friedman y Henry W. Kendall -con los que luego habría de compartir el Nobel-, Taylor investigó sobre la estructura interna de la materia, en su mínima expresión, para lo que partió del modelo teórico de los quarks, postulado por Gell-Mann y -de forma independiente- G. Zweig. Tras sus descubrimientos experimentales en el acelerado lineal de Stanford, Taylor perfeccionó dicho modelo añadiéndole la existencia de unas subpartículas desconocidas hasta entonces, que luego fueron denominadas leptones; además, introdujo en el modelo teórico de Gell-Mann otras partículas no estructurales, sino de intercambio de fuerza, a las que en Stanford comenzaron a llamar bosones.”

James Bjorken.

Richard Feynman

Los dos últimos párrafos los he tomado prestados de www.mcnbiografias.com., que es lo que se explica de este tema en casi todas partes. Sin embargo, pocos cuentan que, el equipo de Stanford, dirigido por el físico del SLAC por Richard Taylor y los otros dos físicos del MIT, Jerome Friedman y Henry Kendall, tuvieron la gran suerte de que, Richard Feynman y James Bjorken, metieran sus narices en el proyecto llevados por la curiosidad y como habían prestado  su energía y su imaginación a las interacciones fuertes  y se preguntaban: ¿que habrá dentro del protón?

Amnos, Feynman y Bjorken visitaban con frecuencia Stanford desde su base en el  Cal Tech, en Pasadena. Bjorken, teórico de Stanford, estaba muy interesado en el proyecto experimental y en las reglas que regían unos datos aparentemente incompletos. Estas reglas, razonaba Bjorken, serían indicadoras de las leyes básicas (dentro de la “caja negra”) que controlaba la estructura de los hadrones.

No estaría mal echar una mirada hacia atrás en el tiempo y recordar, en este momento, a Demócrito que, con sus postulados, de alguna manera venía a echar un poco de luz sobre el asunto, dado que él decía que  para determinar  si algo era un á-tomo habría que ver si era indivisible. En el modelo de los quarks, el protón, en realidad, un conglomerado pegajoso de tres quarks que se mueven rápidamente. Pero como esos quarks están siempre ineludiblemente encadenados los unos a los otros, experimentalmente el protón aparece indivisible.

Acordémonos aquí de que Boscovich decía que, una partícula elemental, o un “á-tomo”, tiene que ser puntual. Y, desde luego, esa prueba, no la pasaba el protón. El equipo del MIT y el SLAC, con la asesoría de Feynman y Bjorken, cayó en la cuenta de que en este caso el criterio operativo era el de los “puntos” y no el de la indivisibilidad. La traducción de sus datos a un modelo de constituyentes puntuales requería una sutileza mucho mayor que el experimento de Rutherford.

Precisamente por eso era tan conveniente fue tan conveniente para Richard Edward Taylor y su equipo, tener a dos de los mejores teóricos del mundo en el equipo aportando su ingenio, agudeza e intuición en todas las fases del proceso experimental. El resultado fue que los datos indicaron, efectivamente, la presencia de objetos puntuales en movimiento dentro del protón.

En 1990 Taylor, Friedman y Kendall recogieron su premio Nobel por haber establecido la realidad de los quarks. Sin embargo, a mí lo que siempre me ha llamado más la atención es el hecho cierto de que, este descubrimiento como otros muchos (el caso del positrón de Dirac, por ejemplo), han sido posible gracias al ingenio de los teóricos que han sabido vislumbrar cómo era en realidad la Naturaleza.

A todo esto, una buena pregunta sería: ¿cómo pudieron ver este tipo de partículas de tamaño infinitesimal, si los quarks no están libres y están confinados -en este caso- dentro del protón?  Hoy, la respuesta tiene poco misterio sabiendo lo que sabemos y hasta donde hemos llegado con el LHC que, con sus inmensas energías “desmenuza” un protón hasta dejar desnudos sus más íntimos secretos.

                    Este es, el resultado ahora de la colisión de protones en el LHC

Lo cierto es que, en su momento, la teoría de los Quarks hizo muchos conversos, especialmente a medida que los teóricos que escrutaban los datos fueron imbuyendo a los quarks una realidad creciente, conociendo mejor sus propiedades y convirtiendo la incapacidad de ver quarks libres en una virtud. La palabra de moda en aquellos momentos era “confinamiento”. Los Quarks están confinados permanentemente porque la energía requerida para separarlos aumenta a medida que la distancia entre ellos crece. Esa es, la fuerza nuclear fuerte que está presente dentro del átomo y que se encarga de transmitir los ocho Gluones que mantienen confinados a los Quarks.

Así, cuando el intento de separar a los Quarks es demasiado intenso, la energía se vuelve lo bastante grande para crear un par de quark-anti-quark, y ya tenemos cuatro quarks, o dos mesones. Es como intentar conseguir un cabo de cuerda. Se corta y… ¡ya tenemos dos!

¿Cuerdas? Me parece que estoy confundiendo el principal objetivo de este trabajo y, me quiero situar en el tiempo futuro que va, desde los quarks de Gell-Mann hasta las cuerdas de Veneziano y John Schwarz y más tarde Witten. Esto de la Física, a veces te juega malas pasadas y sus complejos caminos te llevan a confundir conceptos y  momentos que, en realidad, y de manera individualizada, todos han tenido su propio tiempo y lugar.

¿Cuántas veces no habré pensado, en la posibilidad de tomar el elixir de la sabiduría para poder comprenderlo todo? Sin embargo, esa pósima mágica no existe y, si queremos saber, el único camino que tenemos a nuestro alcance es la observación, el estudio, el experimento… ¡La Ciencia!, que en definitiva, es la única que nos dirácomo es, y como se comporta la Naturaleza y, si de camino podemos llegar a saber, por qué lo hace así…¡mucho mejor!

emilio silvera

[?]

Por aquel tiempo pudimos leer en la prensa de todo el mundo:  ESTOCOLMO, Suecia.- El premio Nobel de Física (2.008) fue atribuido hoy al norteamericano Yoichiro Nambu y a los japoneses Makoto Kobayashi y Toshihide Maskawa por sus trabajos separados sobre la física de las partículas que mejoraron la comprensión de la materia, Demos un repaso hoy aquí a esos componentes de la materia, y, profundicemos en sus propiedades., en sus “vidas”.

Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida media, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.

También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.

Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, ksi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales manera de desintegración, veríamos como difieren las unas de las otras.

Quarks					Antiquarks
Nombre	Símbolo[1]	Generación	Carga eléctrica (e)	Masa en reposo (MeV/c²)	Nombre	Símbolo	Generación	Carga eléctrica (e)	Masa en reposo (MeV/c²)
Arriba		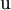Primera		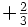—	Antiarriba		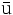Primera		—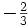
Abajo		Primera		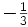—	Antiabajo		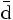Primera		—
Encanto		Segunda		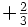—	Antiencanto		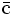Segunda		—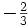
Extraño		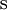Segunda		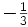—	Antiextraño		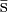Segunda		—
Cima		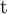Tercera		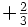—	Anticima		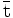Tercera		—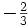
Fondo		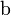Tercera		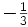—	Antifondo		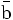Tercera		—

Las iniciales de los símbolos los toma del inglés: u: up, arriba; d: down, abajo; c: charmed, encantado; s: strange, extraño; t: top, alto, superior, cima; b: bottom bajo, fondo.

Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.

Todas las partículas elementales vistas hasta ahora en esta serie, incluido el neutrino. Claro que, aquí no está todavía el Bosón de Higgs que será confirmado en breve…al parecer. Esas son las últimas noticias, el Bosón de Higgs está “casi” localizado y sólo está a la espera de confirmar el hallazgo no una, sino miles de veces.

Por fin, los físicos empiezan a recoger los frutos de una búsqueda que dura ya casi cincuenta años. Dos de los principales detectores del LHC, el gran acelerador europeo de partículas (el Atlas y el CMS) han encontrado señales que podrían delatar la presencia del esquivo bosón de Higgs, la última particula subatómica que queda por descubrir para completar el Modelo Estandar de la Física y la que encierra, además, el secreto de por qué las demás partículas tienen masa.

Pero sigamos. ¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.

	Leptones cargados				Neutrinos
	Nombre	Símbolo	Carga	Masa en reposo	Nombre	Símbolo	Carga	Masa en reposo
1ª generación	Electrón		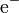−1	0,511			0	< 3·10−6
	Positrón		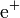+1		Neutrino electrónico		0
2ª generación	Muón		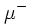−1	105,658	Neutrino muónico		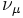0	< 0,19
	Antimuón		+1		Antineutrino muónico		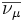0
3ª generación	Tauón		−1	1776,99	Neutrino tauónico		0	< 18,2
	Antitauón		+1		Antineutrino tauónico		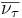0

En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su carta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas, Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas  experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.

Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.

Bariones

Partícula	Símbolo[1]	Quarks[2]	Spin	Masa en reposo (MeV/c²)	S	C	B	Vida media (s)	Desintegraciones más importantes
Protón		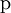		938,27	0	0	0	Estable [3]	—
Neutrón				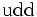939,56	0	0	0	885,7 [4]
Delta doble positiva		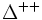		≈1.232	0	0	0	6·10-24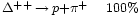
Delta positiva				≈1.232	0	0	0	6·10-24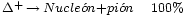
Delta neutra		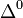		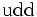≈1.232	0	0	0	6·10-24
Delta negativa				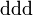≈1.232	0	0	0	6·10-24
Lambda neutra				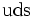1.115,68	−1	0	0	2,63·10-10
Sigma positiva		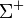		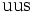1.189,37	−1	0	0	8,01·10-11
Sigma neutra				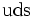1.192,64	−1	0	0	7,4·10-20
Sigma negativa		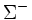		1.197,45	−1	0	0	1,48·10-10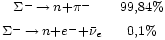
Xi neutra		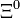		1.314,83	−2	0	0	2,90·10-10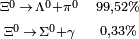
Xi negativa		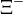		1.321,31	−2	0	0	1,64·10-10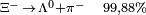
Omega				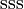1.672,45	−3	0	0	8,21·10-11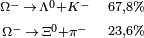
Omega encantada				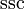2.697,5	−2	+1	0	6,90·10-14
Xi positiva encantada		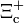		2.468	−1	+1	0	4,42·10-13
Xi neutra encantada		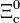		2.471	−1	+1	0	1,12·10-13
Lambda encantada		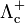		2.284,9	0	+1	0	2,00·10-13
Xi doble encantada		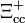		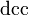3.519	0	+2	0	<3,30·10-14	—
Lambda inferior				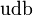5.624	0	0	−1	1,23·10-12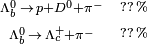

^[1] El símbolo de los antibariones es el mismo pero con una barra superpuesta.

^[2] Los antibariones están formados por los respectivos antiquarks.

^[3] Debe ser superior a 10³⁰ años.

^[4] Vida media de los neutrones libres. En los núcleos atómicos son estables.

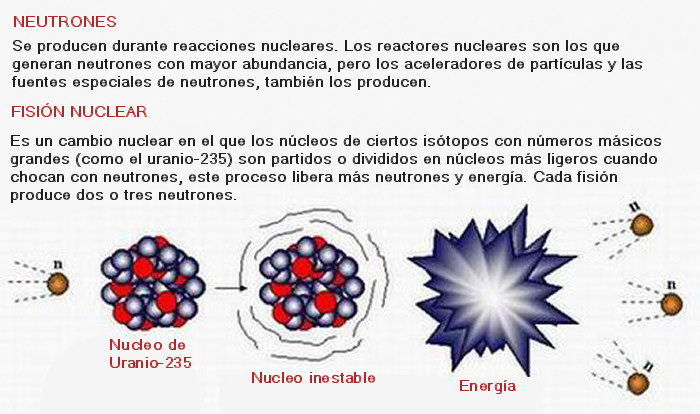
Se ha conseguido observar por primera vez la desintegración radiactiva del neutrón. Dentro de los núcleos de los átomos hay neutrones y protones. En condiciones normales y mientras que están ahí los neutrones son estables. Sin embargo los neutrones libres son inestables, tienen una vida media de unos 10 minutos, y se desintegran produciendo un protón un electrón y un antineutrino. Pero los físicos nucleares teóricos predijeron que una de cada mil veces los neutrones decaerían en todas esas partículas y además en un fotón.

Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según  la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.

Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.

Bosones

Nombre	Símbolo	Carga eléctrica (e)	Carga de color	Spin	Masa en reposo (GeV/c²)	Existencia	Vida media	Desintegraciones más importantes
Fotón		Neutra	Neutra	1	Nula	Confirmada	Estable	—
Bosón W		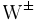± 1	Neutra	1	80,425	Confirmada	3·10-25	[1]
Bosón Z		Neutra	Neutra	1	91,187	Confirmada	3·10-25	—
Gluón		Neutra	Color + Anticolor	1	Nula	Confirmada	Estable	—
Gravitón		Neutra	Neutra	2	Nula	Hipotética	Estable	—
Bosón de Higgs		Neutra	Neutra	0	> 114	Hipotética	Inestable

Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”

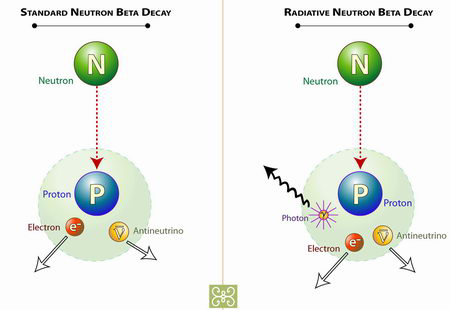
Típicamente el neutrón decae en un protón, un antineutrino y un electrón. Muy raramente lo hace radiativamente emitiendo además un fotón. Diagrama: Zina Deretsky, National Science Foundation.  Fue difícil observar los fotones porque el haz está contaminado con fotones que fondo que producen mucho “ruido” en las medidas, por lo que era como buscar una aguja en un pajar. El decaimiento radiativo del neutrón es importante porque conecta directamente con el modelo estándar de partículas.

Si la vida de una partícula  es tan corta como 10ˉ²³ segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.

Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.

Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).

            En el Universo existen muchas clases de resonancias…inesperadas

Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.

Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:

∆⁺⁺→р + π⁺;  ∆⁰→р + πˉ; o п+π⁰

En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.

El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (materia), es aún limitado. Los cuadros que aparecen arriba, están referidos a las partículas más usuales como los Quarks y los Leptones (verdaderos componentes de la materia) que a su vez, son: Los Quarks los que forman a los Hadrones y los Leptones los que completan el núcleo atómico de la materia para conformar los átomos. He dejado a los mesones y a las supuestas partículas supersimétricas centrándome en las que me parecen principales en la conformación de la materia.

emilio silvera

[?]