Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida media, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.

También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.

Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, psi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales maneras de desintegración, veríamos como difieren las unas de las otras.

Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.

[?]

           Curvatura del Espacio-Tiempo

Hay que entender que el espaciotiempo es la descripción en cuatro dimensiones del universo en la que la posición de un objeto se especifica por tres coordenadas en el espacio y una en el tiempo.

De acuerdo con la relatividad especial, no existe un tiempo absoluto que pueda ser medido con independencia del observador, de manera que eventos simultáneos para un observador ocurren en instantes diferentes vistos desde otro lugar. El tiempo puede ser medido, por tanto, de manera relativa, como lo son las posiciones en el espacio (Euclides) tridimensional, y esto puede conseguirse mediante el concepto de espaciotiempo. La trayectoria de un objeto en el espaciotiempo se denomina por el nombre de línea de universo. La relatividad general nos explica lo que es un espaciotiempo curvo con las posiciones y movimientos de las partículas de materia. La relatividad especial nos explica otras cosas, complementando así, una teoría completa y precisa de la Naturaleza del Universo.

Nuestra línea de universo resume toda nuestra historia, desde que nacemos hasta que morimos.  Cuanto más rápido nos movemos más se inclina la línea de Universo.  Sin embargo, la velocidad más rápida a la que podemos viajar es la velocidad de la luz.  Por consiguiente, una parte de este diagrama  espacio – temporal está “prohibida”; es decir, tendríamos que ir a mayor velocidad que la luz para entrar en esta zona prohibida por la relatividad especial de Einstein que, nos dice que nada en nuestro Universo puede viajar a velocidades superiores a C.

La curvatura del espaciotiempo es la propiedad del espaciotiempo en la que las leyes familiares de la geometría no son aplicables en regiones donde los campos gravitatorios son intensos. La relatividad general de Einstein, nos explica y demuestra que el espaciotiempo está íntimamente relacionado con la distribución de materia en el universo, y nos dice que el espacio se curva en presencia de masas considerables como planetas, estrellas o galaxias (entre otros).

Einstein lo dedujo en una fórmula matemática que relaciona la geometría del espaciotiempo con la distribución de masa y energía: esta fórmula se conoce como ecuación de Einstein y es el centro medular de la teoría de la relatividad general.

[?]

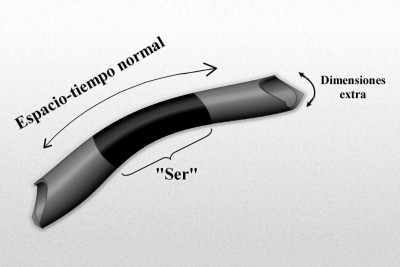
El gráfico representa un modelo de manguera de un espacio-tiempo de dimensiones más altas de tipo Kaluza-Kleim donde la longitud, o mejor, la dimensión a lo largo de la longitud de la manguera representa el 4-espacio-tiempo normal, y la dimensión alrededor de la manguera representa la dimensión extra “pequeñas” (quizá escala de Planck). Imaginemos un “ser” que habite en este mundo, que rebasa estas dimensiones extra “pequeñas”, y por ello no es realmente consciente de ellas.

Nuestras Mentes están conformadas de forma tridimensional, nuestro mundo es de tres dimensiones espaciales. La cuarta dimensión de nuestro mundo, el Tiempo, incide en la posible alteración evolutiva que podríamos experimentar para poder vislumbrar más altas dimensiones pero…, ¿podrán alterarse las percepciones?

Para ver cómo dimensiones más altas simplifican las leyes de la Naturaleza, recordemos que un objeto tiene longitud, anchura y altura.  Puesto que tenemos libertad para girar un objeto 90º, podemos transformar su longitud en anchura y su anchura en altura.   Mediante una simple rotación, podemos intercambiar cualquiera de las tres dimensiones espaciales.

Ahora bien, si el tiempo es la cuarta dimensión, entonces es posible hacer “rotaciones” que convierten el espacio en tiempo y el tiempo en espacio.  Estas rotaciones tetradimensionales son precisamente las distorsiones del espacio y del tiempo exigidas por la relatividad especial. En otras palabras, espacio y tiempo se mezclan de una forma esencial, gobernada por la relatividad.  El significado del tiempo como la cuarta dimensión es que pueden hacerse relaciones entre el tiempo y el espacio de una forma matemáticamente precisa.  A partir de entonces, deben ser tratados como dos aspectos de la misma magnitud: el espacio-tiempo. Así han quedado unificadas las leyes de la Naturaleza al pasar de tres a cuatro dimensiones.

             Posiblemente, el magnetismo, también pueda alterar el espacio-tiempo

La discusión de la unificación de las leyes de la Naturaleza fue más bien abstracta, y lo habría seguido siendo si Einstein no hubiese dado el siguiente paso decisivo.  Él comprendió que si el espacio y el tiempo pueden unificarse en una sola entidad, llamada espaciotiempo, entonces quizá la materia y la energía pueden unirse también en una relación dialéctica.  Si las reglas pueden contraerse y los relojes pueden frenarse, razonó, entonces cualquier cosa que midamos con regla y relojes también debe cambiar.

Sin embargo, casi todo en el laboratorio de un físico se mide con regla y relojes. Esto significa que los físicos tendrán que recalibrar todas las magnitudes del laboratorio que una vez dieron por hecho que eran constantes.

En concreto, la energía es una cantidad que depende de cómo midamos las distancias y los intervalos de tiempo.  Un automóvil de prueba que choca a gran velocidad contra una pared de ladrillos tiene obviamente energía.  No obstante, si el veloz automóvil se aproxima a la velocidad de la luz, sus propiedades se distorsionan.  Se contrae como un acordeón y los relojes en su interior se frenan.

Lo que es más importante, Einstein descubrió que la masa del automóvil también aumenta cuando reacelera. Pero  ¿de dónde procede este exceso de masa?  Y él concluyó que procedía de la energía.

Esto tuvo consecuencias perturbadoras.  Dos de los grandes descubrimientos de la física del siglo XIX fueron la conversación de la masa y la conservación de la energía; es decir, la masa total y la energía total de un sistema cerrado, tomadas por separado, no cambian.  Por ejemplo, si el coche veloz choca contra el muro de ladrillos, la energía del automóvil no desaparece, sino que se convierte en energía sonora del choque, energía cinética de los fragmentos de ladrillo que vuelan por los aires, energía calorífica, y así sucesivamente.  La energía total (y la masa total) antes y después del choque es la misma.

                                                                               Energía calorífica

Sin embargo, Einstein decía ahora que la energía del automóvil podía convertirse en masa (un nuevo principio de conservación que decía que la suma total de la masa y la energía debe siempre permanecer constante.  La materia no desaparece repentinamente, ni la energía brota de la nada.  En este sentido, la materia desaparece sólo para liberar enormes cantidades de energía o viceversa.

Cuando Einstein tenía 26 años, calculó exactamente cómo debía cambiar la energía si el principio de la relatividad era correcto, y descubrió la relación E=mc².  Puesto que la velocidad de la luz al cuadrado (C²) es un número astronómicamente grande, una pequeña cantidad de materia puede liberar una enorme cantidad de energía.  Dentro de las partículas más pequeñas de materia hay un almacén de energía, más de un millón de veces la energía liberada en una explosión química.  La materia, en cierto sentido, puede verse como un depósito casi inagotable de energía; es decir, la materia es en realidad, energía condensada.

Einstein supo ver que las dimensiones más altas tienen un propósito: unificar los principios de la Naturaleza.  Al añadir dimensiones más altas podía unir conceptos físicos que, en un mundo tridimensional, no tienen relación, tales como la materia y la energía o el espacio y el tiempo que, gracias a la cuarta dimensión de la relatividad especial, quedaron unificados.

Y, a todo esto, no podemos dejar de asombrarnos de nuestra presencia aquí, de todo lo que hemos sido capaces de entender en la configuración del mundo, y, como decía Eintein: “lo incomprensible del Universo es, que lo podamos comprender”.

Desde entonces, estos conceptos, los tenemos que clasificar, no por separado, sino siempre juntos como dos aspectos de un mismo ente materia-energía por una parte y espacio-tiempo por la otra.  El impacto directo del trabajo de Einstein sobre la cuarta dimensión fue, por supuesto, la bomba de hidrógeno, que se ha mostrado la más poderosa creación de la ciencia del siglo XX.  Claro que, en contra del criterio de Einstein que era un pacifista y nunca quiso participar en proyectos de ésta índole.

  ¿Dónde estará la puerta de la Quinta Dimensión? ¿Existirán en realidad las dimensiones más altas?

Einstein completó su teoría de la relatividad con una segunda etapa que, en parte, estaba inspirada por lo que se conoce como principio de Mach, la guía que utilizó Einstein para crear esta parte final y completar su teoría de relatividad general.

Einstein enunció que, la presencia de materia-energía determina la curvatura del espacio-tiempo a su alrededor.  Esta es la esencia del principio físico que Riemann no logró descubrir: la curvatura del espacio está directamente relacionada con la cantidad de energía y materia contenida en dicho espacio.

La masa del planeta curva el espacio-tiempo a su alrededor y configura la geometría local de esa región que está bajo el dominio de la Gravedad.

Albert Einstein realizó una verdadera hazaña intelectual y nos legó su teoría General de la Relatividad, una teoría construida desde la pura geometría, excediéndose en elegancia y efectiva en su espacio de aplicación. La relación entre el cuerpo y la curvatura del espacio-tiempo, es equivalente (Gµv). Significa, la manifestación visible o invisible de la energía [m=e/c2], y en este caso, manifestada en la forma masiva del cuerpo, curva el espació-tiempo.

Esto, a su vez, puede resumirse en la famosa ecuación de Einstein, que esencialmente afirma:

Materia-energía determina la curvatura del espacio-tiempo y se denota 

Esta ecuación engañosamente corta es uno de los mayores triunfos de la mente humana (me he referido a ella en otras muchas ocasiones).  De ella emergen los principios que hay tras los movimientos de las estrellas y las galaxias, los agujeros negros, el big bang, y seguramente el propio destino del Universo.

Es curiosa la similitud que se da entre la teoría del electromagnetismo y la relatividad general, mientras que Faraday experimentó y sabía los resultados, no sabía expresarlos mediante las matemáticas y, apareció Maxwell que, finalmente formuló la teoría.

Einstein, al igual que Faraday, había descubierto los principios físicos correctos, pero carecía de un formulismo matemático riguroso suficientemente potente para expresarlo (claro que Faraday no era matemático y Einstein si lo era).  Carecía de una versión de los campos de Faraday para la Gravedad.  Irónicamente, Riemann tenía el aparato matemático, pero no el principio físico guía, al contrario que Einstein.  Así que, finalmente, fue Einstein el que pudo formular la teoría con las matemáticas de Riemann.

“¡Qué extraño sería que la teoría final se descubriera durante nuestra vida!  El descubrimiento de las leyes finales de la Naturaleza marcará una discontinuidad en la Historia del intelecto humano, la más abrupta que haya ocurrido desde el comienzo de la ciencia moderna del siglo XVII.  ¿Podemos imaginar ahora como sería?”

STEVEN WEINBERG

 

 

                                                                                                            ¿Son tántas las clases de belleza en el Universo?

¿Es la belleza un principio Físico? Bueno, podríamos decir que también, pudiera ser un principio del Sentimiento de la Mente Humana, aunque, en Física, por ejmplo, el concepto de belleza tenga otras connotaciones.

La teoría de supercuerdas nos da una formulación convincente de la teoría del Universo, sin embargo, el problema fundamental radica en que una comprobación de dicha teoría, está más allá de nuestras posibilidades actuales.  De hecho, la misma teoría predice que la unificación de todas las fuerzas ocurre a la energía de Planck, o 10¹⁹ miles de millones de electronvoltios, que como sabéis, es alrededor de mil billones de veces mayor que las energías actualmente disponibles en nuestros aceleradores de partículas, se denota por la ecuación:

Como la masa de Planck es del orden de 10^-8 kg (equivalente a una energía de 10¹⁹ GeV), y, por ejemplo, la masa el protón es del orden de 10^-27 kg y las mayores energías alcanzables en los aceleradores de partículas actuales son de un orden muy inferior, los efectos de la gravitación cuántica no aparecen en los laboratorios de física de partícula (ni el LHC ni en el Fermilab). Sin embargo, en el universo primitivo las partículas tenían energías del orden de la masa de Planck, de acuerdo con la teoría el big bang, y es, por tanto, necesaria una teoría cuántica de la gravedad para estudiar las condiciones en la época conocida como Tiempo de Planck.

          David Gross

Ya he comentado otras veces que el físico David Gross (el de más edad de los miembros conocidos como el “cuarteto de cuerdos” y autores de la teoría llamada la cuerda heterótica) dijo en una ocasión: “El coste de generar esta fantástica energía, necesitaría el dinero de las tesorerías de todos los países del mundo juntos, y quizá, no llegara.  Es verdaderamente astronómico.”

Siendo así, de momento estamos condenados a no poder verificar experimentalmente este motor (parado) que haría marchar el vehículo de la Física.  La teoría decadimensional está paralizada en dos sentidos: el económico y el técnico – matemático.  El primero por falta de dinero que  nos pudiera construir aceleradores tan potentes como para descubrir la partícula de Higgs, los quarks e incluso las cuerdas vibrantes, esos previsibles y minúsculos objetos primordiales que conforman la materia.  En segundo lugar, las formulaciones matemáticas complejas que, según parece, aún no se han inventado.  Parece que hoy, ni siquiera Witten o Perelman, conocen el secreto de los números mágicos que nos puedan llevar hasta el final del camino iniciado con Einstein y Kaluza-Klein.

Estaría bueno que, al final se descubriera que alfa (α) tuviera un papel importante en la compleja teoría de cuerdas, ¿Por qué no? En realidad alfa, la constante de estructura fina, nos habla del magnetismo, de la constante de Planck y de la relatividad especial, es decir, la velocidad de la luz y, todo eso, según parece, emergen en las ecuaciones topológicas de la moderna teoría de cuerdas. ¡Ya veremos!

Sí, es cierto, que la teoría tiene muchos detractores y algunos han llegado a denominarla Física de Circo pero, particularmente opino que la teoría de cuerdas nos dará muchas alegrías y que en ella están las respuestas a muchas preguntas que no sabemos contestar. Simplemente se trata (como nos dice E. Eitten) de una teoría adelantada a su tiempo.

Dentro del mundo de la Física, los hay de todas las opiniones: en contra y a favor.  Es famosa la postura detractora del Nóbel Sheldoy Glasgow de Harvard, no quiere ni oír hablar de la teoría de supercuerdas a la que califica de física de Teatro.

Otros muchos, la mayoría, como Murray Gell-Marn, Steven Weinberg (ambos Premios Nóbel) o el mismo  E. Witten (Medalla Field), opinan lo contrario y ven en esta teoría de dimensiones más altas el futuro de la Física.

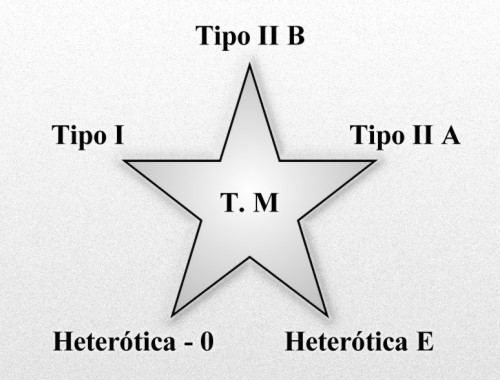
 Todas las versiones de las diversas Teorías de cuerdas han sido unificadas en una, la Teoría M de E. Witte, y, esperemos que no se quede ahí estancada y que, aparezca algún genio matemático como Ramanujan o Riemman y nos saque del agujero en el que actualmente estamos metidos y del que no podemos salir, no existen ideas que la hagan avanzar ni matemáticas complejas que la puedan hacer andar.

         La recreación del mundo no parece cosa fácil, y, en estas teorías queremos recrear mucho más

Ya sabemos que en física toda teoría debe ser verificada, una y otra vez, en uno y en otro lugar, experimentalmente, obteniendo siempre el mismo resultado, es la única manera de que sea aceptada por la comunidad científica, mientras tanto, la teoría no es fiable y queda a la espera de ser comprobada, verificada sin ningún lugar para la duda.

Pero, ¿Se puede recrear la creación?

La teoría de supercuerdas trata de eso.  Quiere explicarnos todos los misterios del Universo a partir de ese primer momento, ¡la creación!

emilio silvera

[?]

¡Preludio a la relatividad! -Las ecuaciones de Lorentz-Fitzgerald- Éste último pensaba y decía cosas comos estas:

              George FitzGerald

“…telegrafía debe mucho a Euclides y otros geómetras puro, al griego y árabe matemáticos que inventó nuestra escala de numeración y álgebra, de Galileo y Newton, quien fundó la dinámica, para que Newton y Leibniz inventó el cálculo, para que Volta descubrió la galvánica bobina, a Oersted quien descubrió la acción magnética de las corrientes, que a Ampère descubrió las leyes de su acción, a Ohm que descubrió la ley de la resistencia de los cables, a Wheatstone, de Faraday, a Lord Kelvin, a Clerk Maxwell, Hertz a .Sin los descubrimientos, invenciones, y las teorías científicas resumen de estos hombres telegrafía, ya que ahora es, sería imposible.”

“La función de la Universidad es, sobre todo, enseñar a la humanidad...en todo momento los más grandes hombres siempre han sostenido que su deber principal es el descubrimiento de nuevos conocimientos, la creación de nuevas ideas para toda la humanidad, y no la instrucción de los pocos que encuentran conveniente a residir en su vecindad inmediata.…Åre las Universidades de dedicar las energías de los intelectuales más avanzados de la edad a la instrucción de toda la nación, o en las instrucciones de los pocos cuyos padres pueden pagar a uno – en algunos lugares de lujo – la educación que en la naturaleza de las cosas sólo al alcance de los ricos?”

    Hendrik Antoon Lorentz

Se le deben importantes aportaciones en los campos de la termodinámica, la radiación, el magnetismo, la electricidad y la refracción de la luz.  Formuló conjuntamente con George Francis FitzGerald una teoría sobre el cambio de forma de un cuerpo como resultado de su movimiento; este efecto, conocido como “contracción de Lorentz-FitzGerald”, cuya representación matemática de ella es conocida con el nombre de transformación de Lorentz,  fue una más de las numerosas contribuciones realizadas por Lorentz al desarrollo de la teoría de la relatividad.

Fue, al igual que Henri Poincaré,  uno de los primeros en formular las bases de la teoría de la relatividad (frecuentemente atribuida primaria o solamente a Albert Einstein).  Fue ganador del Premio Nobel de Física en 1902, junto con su pupilo Pieter Zeeman,  por su investigación conjunta sobre la influencia del magnetismo en la radiación, originando la radiación electromagnética.  También fue premiado con la Medalla Rumford en 1908 y la Medalla Coplay en 1918. Lorentz era hombre humilde y sencillo y le gustaba resaltar los logros de los demás:

“Como es probable que sepas, gran parte de nuestro conocimiento sobre la electricidad y el magnetismo se basa en los experimentos ingeniosísimos realizados por Michael Faraday en la primera parte del siglo XIX. Faraday era un experimentador genial, y descubrió numerosos fenómenos desconocidos hasta entonces, como la inducción mutua. Estableció diversas leyes, pero no pudo elaborar una teoría global acerca del electromagnetismo porque sus conocimientos matemáticos no iban más allá de la trigonometría: hacía falta un teórico capaz de amalgamar el conocimiento adquirido por Faraday y otros experimentadores, como Hans Christian Ørsted, en una teoría general.

Ese teórico era otro genio, James Clerk Maxwell, que estableció un conjunto de cuatro ecuaciones diferenciales bellísimas que describían de una manera extraordinariamente precisa los resultados de casi todos los experimentos de Faraday, Ørsted y compañía. Lo más sorprendente, para el propio Maxwell y sus contemporáneos, fue una de las consecuencias inevitables de sus ecuaciones: la existencia de perturbaciones del campo eléctrico y el magnético que se propagaban por el espacio.”

A la contracción, Einstein le dio un marco teórico en la teoría especial de la relatividad. En esta teoría, un objeto de longitud l₀ en reposo en un sistema de referencia parecerá, para un observador en otro sistema de referencia que se mueve con velocidad relativa v con respecto al primero, tener longitud , donde c es la velocidad de la luz. La hipótesis original atribuía esta contracción a una contracción real que acompaña al movimiento absoluto del cuerpo. La contracción es en cualquier caso despreciable a no ser que v sea del mismo orden o cercana a c.

Un objeto que se moviera a 11,2 Km/s (la velocidad de escape de nuestro planeta) experimentaría sólo una contracción equivalente a 2 partes por cada 1.000 millones en el sentido del vuelo. Pero a velocidades realmente elevadas, tal contracción sería sustancial. A unos 150.000 Km/s (la mitad de la velocidad de la luz) sería del 15%; a 262.000 Km/s (7/8 de la velocidad de la luz), del 50%. Es decir, que una regla de 30 cm que pasara ante nuestra vista a 262.000 Km/s nos parecería que mide sólo 15’24 cm, siempre y cuando conociéramos alguna manera para medir su longitud en pleno vuelo. Y a la velocidad de la luz, es decir, 300.000 Km/s en números redondos, su longitud en la dirección del movimiento sería cero. Puesto que, presuntamente, no puede existir ninguna longitud inferior a cero, se deduce que la velocidad de la luz en el vacío es la mayor que puede imaginarse el universo.

                                                                                 experimento conocido de Michelson-Morley

Todo aquello fue posible gracia a que en 1893, el físico irlandés George Francis FitzGerald emitió una hipótesis para explicar los resultados negativos del experimento conocido de Michelson-Morley.  Adujo que toda materia se contrae en la dirección del movimiento, y que esa contracción es directamente proporcional al ritmo (velocidad) del movimiento.

Según tal interpretación, el interferómetro se quedaba corto en la dirección del “verdadero” movimiento terrestre, y lo hacía precisamente en una cantidad que compensaba con toda exactitud la diferencia de distancias que debería recorrer el rayo luminoso.  Por añadidura, todos los aparatos medidores imaginables, incluyendo los órganos sensoriales humanos, experimentarían ese mismo fenómeno.

Parecía como si la explicación de FitzGerald insinuara que la Naturaleza conspiraba con objeto de impedir que el hombre midiera el movimiento absoluto, para lo cual introducía un efecto que anulaba cualquier diferencia aprovechable para detectar dicho movimiento.

Este asombroso fenómeno recibió el nombre de “contracción de FitzGerald”, y su autor formuló una ecuación para el mismo que, referido a la contracción de un cuerpo móvil, fue predicha igualmente, y de manera independiente, por H.A.Lorentz (1853-1928) de manera que, finalmente, se quedaron unidas como “Contracción de Lorentz-Fitz Gerald”.

El efecto Fitzgerald sobre longitudes y el efecto Lorentz sobre masas mantuvieron una conexión tan estrecha que aparecieron a menudo agrupadas como las ecuaciones Lorentz-Fitzgerald.

Después llegó Einstein que se apropió de aquella idea y, además, la amplió al contraer también el Tiempo. La contracción de la longitud ha sido verificada en el diseño, por ejemplo, del acelerador lineal de la Universidad de Stanford. Las partículas salen con una velocidad v = 0,999975c, por tanto, cada metro de tubo acelerador es “visto” por los electrones como 144 metros. Si, según la expresión anterior, un cuerpo con masa se moviera a la velocidad c desaparecería por contracción de su longitud para un observador en reposo, lo cual refuerza el carácter inalcanzable de esta velocidad. Si los objetos con masa alcanzan este límite de velocidad la estructura básica de la realidad se desvanece. Por otra parte, vemos que cualquier influencia que afecte al tiempo también lo hará con el espacio. Esto no nos debe de extrañar, ya que ambas magnitudes se encuentran íntimamente relacionadas por lo único que se nos mantiene invariable: la velocidad de la luz. En relatividad hablamos de espacio-tiempo ya que son inseparables.

A la contracción, Einstein, le dio un marco teórico en la teoría especial de la relatividad. En esta teoría, un objeto de longitud /0 en reposo en un sistema de referencia parecerá, para un observador en otro sistema de referencia que se mueve con velocidad relativa v con respecto al primero, tener longitud /0 , donde c es la velocidad de la luz. La hipótesis original atribuía esta contracción a una contracción real que acompaña al movimiento absoluto del cuerpo. La contracción es en cualquier caso despreciable a no ser que v sea del mismo orden o cercana a c.

Un objeto que se moviera a 11 km/s (la velocidad de escape de nuestro planeta) experimentaría sólo una contracción equivalente a 2 partes por cada 1.000 millones en el sentido del vuelo. Pero a velocidades realmente elevadas, tal contracción sería sustancial. A unos 150.000 km/seg. (la mitad de la velocidad de la luz, c), sería del 15%; a 262.000 km/seg. (7/8 de la velocidad de la luz), del 50% Es decir, que una regla de 30 cm. que pasara ante nuestra vista a 262.000 km (seg., nos parecería que mide sólo 15’54 cm…, siempre y cuando conociéramos alguna manera para medir su longitud en pleno vuelo. Y a la velocidad de la luz, es decir, 300.000 km/seg., en números redondos, su longitud, en la dirección del movimiento, sería cero.  Puesto que, presuntamente, no puede existir ninguna longitud inferior a cero, se deduce que la velocidad de la luz en el vacío es la mayor que puede imaginarse en el Universo. (Pero ¿existir también?).

El físico holandés Hendrik Antón Lorentz, como hemos dicho, promovió ésta idea pensando en los rayos catódicos (que ocupaban su actividad por aquellas fechas), se hizo el siguiente razonamiento: si se comprimiera la carga de una partícula para reducir su volumen, aumentaría su masa.  Por consiguiente, una partícula voladora, escorzada en la dirección de su desplazamiento por la contracción de Fitz Gerald, debería crecer en términos de masa.

          Un objeto que corra a velocidades cercanas a la de la luz, verá incrementada su masa

Lorentz presentó una ecuación sobre el acrecentamiento de la masa, que resultó muy similar a la ecuación FitzGerald sobre el acortamiento. A 149.637 kilómetros por segundo, la masa de un electrón aumentaría en un 15%; a 262.000 km/seg., en un 100% (es decir, la masa se duplicaría); y a la velocidad de la luz, su masa sería infinita.  Una vez más pareció que no podría haber ninguna velocidad superior a la de la luz, pues, ¿cómo podría ser una masa mayor que infinita? El efecto FitzGerald sobre longitudes y el efecto Lorentz sobre masas mantuvieron una conexión tan estrecha que aparecieron a menudo agrupadas como las “ecuaciones Lorentz-FitzGerald.”

Mientras que la contracción FitzGerald no podía ser objeto de mediciones, el efecto Lorentz sobre masas si podía serlo…, aunque indirectamente. De hecho, el muón, tomó 10 veces su masa original cuando fue lanzado, a velocidades relativistas, en el acelerador de partículas, lo que confirmó la ecuación de Lorentz. Los experimentos posteriores, han confirmado las ecuaciones de ambos: a velocidades relativistas, las longitudes se contraen y las masas se incrementan.

                        Nada puede viajar a la velocidad de la luz

Como es conocido por todos, Einstein adoptó estos descubrimientos y los incorporó a su teoría de la relatividad especial que, aunque mucho más amplia, recoge la contracción de FitzGerald y el aumento de la masa de Lorentz cuando se alcanzan grandes velocidades.

¡Qué cosas!

Algunas veces pienso que, los artistas en general, y los poetas en particular, tendrían que adaptar e incluir a sus esquemas artísticos y poéticos, los adelantos científicos, para asimilarlos en las diversas expresiones y sentimientos que serán después puestos al servicio del consumo humano.

Estos adelantos científicos serían así coloreados con las pasiones humanas y transformadas, de alguna forma, en la sangre, y por qué no, los sentimientos de la naturaleza humana.

Posiblemente, de haberlo hecho así, el grado general de conocimiento sería mayor.

emilio silvera

[?]