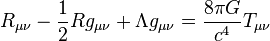Abr
1
Nos adentramos en la Física con el Tiempo de Planck
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)
Tiempo de Planck
Es el tiempo que necesita el fotón (viajando a la velocidad de la luz, c, para moverse a través de una distancia igual a la longitud de Planck. Está dado por ![]() , donde G es la constante gravitacional (6, 672 59 (85) x 10-11 N m2 kg-2), ħ es la constante de Planck racionalizada (ħ = h/2л = 1,054589 x 10-34 Julios segundo), c, es la velocidad de la luz (299.792.458 m/s).
, donde G es la constante gravitacional (6, 672 59 (85) x 10-11 N m2 kg-2), ħ es la constante de Planck racionalizada (ħ = h/2л = 1,054589 x 10-34 Julios segundo), c, es la velocidad de la luz (299.792.458 m/s).
El valor del tiempo del Planck es del orden de 10-44 segundos. En la cosmología del Big Bang, hasta un tiempo Tp después del instante inicial, es necesaria usar una teoría cuántica de la gravedad para describir la evolución del Universo.
Expresado en números corrientes que todos podamos entender, su valor 0,000.000.000.000.000.000.000.000.000.000.000.000.000.0010 de 1 segundo que es el tiempo que necesita el fotón para recorrer la longitud de Planck, de 10-35 metros (veinte ordenes de magnitud menor que el tamaño del protón de 10-15 metros). El límite de Planck es ![]()
Todo, desde Einstein, es relativo. Depende de la pregunta que se formule y de quién nos de la respuesta.
Mar
26
¡La Física! Siempre nos sorprende
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (2)
Comments (2)


Diagrama de un microscopio de fuerza atómica
Las veloces computadoras cuánticas hechas con átomos atrapados por haces de luz pueden estar un poco más cerca, gracias a las primeras imágenes de átomos individuales obtenidas en una de estas grillas.

La velocidad de las computadoras cuánticas tiene que ver con el hecho de que sus componentes pueden ocupar una serie de estados en lugar de sólo dos como ocurre en una computadora binaria. Ciertos algoritmos especiales podrían explotar estos estados cuánticos para resolver problemas que derrotarían a una computadora convencional.

Una candidata a computadora de este tipo es la llamada “rejilla óptica”, en la que haces de rayos láser estratégicamente ubicados hacen que los átomos ultrafríos se coloquen en forma de grilla, como si fueran huevos en su envase de cartón. Pero antes de que uno pudiera leer o escribir sobre estos átomos, algo indispensable si la rejilla fuera a actuar como una computadora cuántica, haría falta determinar las posiciones exactas de los mismos.
Ahora dos equipos de investigadores, uno conducido por Stefan Kuhr del Instituto Max Planck de Óptica Cuántica de Garching, Alemania, y el otro por Markus Greiner de la Universidad de Harvard, han dado el primer paso al obtener imágenes de átomos individuales de rubidio en una rejilla óptica. Este es un reto no sólo porque los átomos son pequeños, sino también porque los fotones de los átomos cercanos pueden interferir unos con otros, enturbiando cualquier patrón.

Para superar esto, los equipos estudiaron el patrón de luz de un solo átomo. Luego crearon un algoritmo capaz de generar una combinación de este patrón a partir de diferentes disposiciones de una grilla de átomos. Cotejando estas simulaciones con el modelo real observado, el algoritmo podía determinar cuál era la distribución de los átomos.
Cada átomo en la grilla actúa como un bit cuántico. Kuhr dice que la rejilla óptica tiene muchos más de estos “qubits” que otros sistemas enfocados en la computación cuántica, por lo que puede ofrecer mayor velocidad.


Los láseres pueden volver reales las partículas virtuales. Los láseres de última generación tienen el poder de crear materia por medio de la captura de partículas fantasmales que, de acuerdo a la mecánica cuántica, permean el espacio aparentemente vacío
El principio de incertidumbre de la mecánica cuántica implica que el espacio nunca puede estar realmente vacío. En cambio, las fluctuaciones aleatorias causan el nacimiento de un caldero hirviente de partículas, como electrones y sus homólogos de antimateria, los positrones.
Las llamadas “partículas virtuales” normalmente se aniquilan entre sí demasiado rápido para que las veamos. Pero los físicos predijeron en los años 30 que un campo eléctrico muy fuerte transformaría las partículas virtuales en reales, y entonces las podríamos observar. El campo las impulsa en direcciones opuestas, porque tienen cargas eléctricas que se oponen, y las separándolos de modo que no puede destruirse mutuamente.


Los láseres son ideales para esta tarea, porque su luz posee campos eléctricos fuertes. En 1997, los físicos del Stanford Linear Accelerator Center (SLAC), en Menlo Park, California, utilizaron luz láser para crear unas pocas parejas de electrón-positrón. Ahora, nuevos cálculos indican que los láser de nueva generación serán capaces de crear pares por millones.
Reacción en cadena


En el experimento de SLAC, sólo se creó un par electrón-positrón a la vez. Pero con los láseres más potentes, es probable que se produzca una reacción en cadena.
El primer par es acelerado a gran velocidad por el láser, haciendo que emita luz. Esta luz, junto con la del láser, genera aún más pares, dice Alexander Fedotov de la Dirección Nacional de Investigaciones Nucleares de la Universidad de Moscú y sus colegas en un estudio que aparecerá en Physical Review Letters.
“Surgirá una gran cantidad de partículas del vacío”, dice John Kirk del Instituto Max Planck de Física Nuclear en Heidelberg, Alemania, que no participó en el estudio.
En los láseres que pueden concentrar cerca de 1026 vatios en un centímetro cuadrado, esta reacción desatada debería convertir de manera eficiente la luz del láser en millones de pares de electrones positrones, calcula el equipo.
Fábrica de antimateria

Ese nivel de intensidad lo podría alcanzar un láser que será construido por el proyecto Extreme Light Infrastructure en Europa. La primera versión del láser se podría construir en 2015, pero podría llevar un año más completar las actualizaciones necesarias para llegar a 1026 vatios por centímetro cuadrado, dice el coautor del estudio Georg Korn del Instituto Max Planck de Óptica Cuántica en Garching , Alemania.
La capacidad de generar una gran cantidad de positrones podría ser útil para los colisionadores de partículas, como el propuesto del Colisionador Lineal Internacional, que impactará electrones y positrones, dice Kirk McDonald de la Universidad de Princeton en Nueva Jersey.
Pero Pisin Chen, de la Universidad Nacional de Taiwan en Taipei, dice que el costo de los poderosos láseres puede hacer que este método sea más caro que el alternativo. En la actualidad, la manera estándar de crear una gran cantidad de positrones es disparar un haz de electrones de alta energía a una pieza de metal, para producir pares electrón-positrón. Vean la publicación siguiente:
La materia supera a la antimateria en un experimento que imita a la creación

El desequilibrio en el acelerador de partículas de Illinois podría presagiar grandes avances en Física
A menos de una billonésima de segundo después del Big Bang ocurrió otro evento tumultuoso. Aunque el Cosmos nació con partes iguales de materia y antimateria, que se destruyeron una a la otra al entrar en contacto, de alguna forma la materia comenzó a predominar. Los físicos han descubierto una nueva pista sobre la causa de este desequilibrio fortuito, que condujo a la existencia de galaxias, planetas y personas.

Circunferencia de 4 kilómetros de diámetro del Acelerador de Partículas del Laboratorio Fermi de Chicago
El nuevo hallazgo se basa en ocho años de estudio de la desintegración de partículas de vida corta, llamadas mesones B, que se produce durante las colisiones de alta energía en el acelerador de partículas Tevatrón del Laboratorio Fermi (Fermilab), ubicado en Batavia, Illinois. Los científicos del experimento DZero del Tevatrón han descubierto que los mesones B, cuando se desintegran, producen cerca del 1 % más de pares de muones (una versión pesada del electrón) que de pares de sus antipartículas, los antimuones. Los físicos se refieren a este fenómeno como una violación CP.
El desequilibrio, reportado el 14 de mayo en un seminario del Fermilab y publicado en Internet el 18 de mayo, podría servir para entender cómo fue que la materia superó a la antimateria en el Universo. También aumenta las posibilidades de que el Gran Colisionador de Hadrones, el acelerador de Suiza que sustituyó al Tevatrón como el colisionador de partículas más poderoso del mundo, encuentre nuevas partículas elementales o una nueva física. Hablamos del LHC que, de hecho, las ha encontrado.

El acelerador de partículas Tevatróndel Laboratorio Fermi (Fermilab),ubicado en Batavia, Illinois. Fue el primero en producir antimateria
“Aunque pequeño, este excedente del 1% es 50 veces más grande que la asimetría entre materia y antimateria prevista para la desintegración de mesones B por el modelo estándar de la Física de Partículas”, señala el portavoz del DZero, Stefan Söldner-Rembold, de la Universidad de Manchester en Inglaterra.
“Se nos puso la piel de gallina”, cuenta Söldner-Rembold acerca del momento en el que él y los 500 colaboradores del DZero comprendieron lo que habían descubierto. “Estábamos muy contentos porque significa que hay una nueva Física más allá del modelo estándar que tiene que estar a nuestro alcance para que la asimetría sea tan grande”.
“Aunque hay una probabilidad de menos del 0,1 % de que los resultados del DZero sean una casualidad, de acuerdo con las normas de la Física de Partículas hay que considerarlos como indicios aún por confirmar”, advierte el teórico Yuval Grossman de la Universidad de Cornell. Söldner-Rembold señala que los hallazgos del DZero son similares a una asimetría en la producción de materia-antimateria descubierta hace un año por otro experimento llevado a cabo en el Tevatrón, el CDF, pero los nuevos resultados tienen una precisión mayor.
“Las teorías que podrían explicar las observaciones del DZero incluyen la supersimetría, que supone que cada partícula elemental en el modelo estándar de la Física de Partículas tiene una superpareja más pesada todavía por descubrir”, explica la teórica del Fermilab Marcela Carena, que no pertenece al equipo descubridor. “Otras teorías posibles incluyen un modelo en el que la gravedad y otras fuerzas operan en otras dimensiones ocultas, y la noción de que hay una cuarta familia de quarks más allá de las tres generaciones (arriba y abajo, encanto y extraño, y cima y fondo) que sirven como bloques de construcción de los núcleos atómicos y otras partículas.
“En los modelos que consideran una cuarta familia de quarks, la presencia de quarks nuevos y pesados y su interacción con las tres familias conocidas podrían dar lugar a un desequilibrio mayor entre materia y antimateria que el que se encuentra en el modelo estándar”, señala Carena. Y agrega: “En la teoría de la supersimetría, las superparejas pesadas jugarían un rol similar al de los quarks pesados, creando interacciones que podrían favorecer la producción de materia sobre la antimateria”.
No siempre la física lo puede explicar todo. Sin embargo… ¡Lo va consiguiendo!
En la teoría de las dimensiones extra, nuevas partículas mensajeras (portadoras de fuerzas previamente desconocidas) se moverían en dimensiones ocultas. Estas partículas transportadoras podrían alterar la carga y otra propiedad, llamada “sabor”, de las partículas elementales, causando el desequilibrio adicional entre materia y antimateria.
Carena añade: “Sin embargo, es difícil encontrar una teoría que pueda explicar esta asimetría sin contradecir otros resultados experimentales”.

La materia superó a la antimateria en el comienzo
Ulrich Nierste, de la Universidad de Karlsruhe en Alemania, advierte: “La conexión del resultado del DZero con el excedente de materia que existe en el Universo es vaga. Si bien el hallazgo insinúa una nueva fuente de asimetría en las propiedades del mesón B y de su antipartícula, el proceso que creó más partículas que antipartículas en el Universo primitivo podría involucrar un mecanismo físico muy diferente”.
“Sin embargo”, dice Carena, “hace falta alguna nueva fuente de asimetría para explicar el desequilibrio que hay entre la materia y la antimateria en el Universo, y, por lo tanto, nuestra existencia”. En cualquiera de los modelos propuestos “el Gran Colisionador de Hadrones debería ser la ventana directa para observar nuevas partículas”.
Uno de los experimentos más pequeños del Colisionador, diseñado para estudiar los mesones B, podría confirmar los hallazgos del DZero dentro de uno o dos años”, dice Yuval Grossman. Y agrega: “Los experimentos más grandes podrían entonces buscar nuevas partículas que serían el origen del desequilibrio cósmico entre materia y antimateria y determinar sus masas”.

El experimento Beauty (Belleza) es la matriz de investigación para la creación de antimateria. El choque de dos protones contra otro a la velocidad de la luz, ha tenido como resultado una partícula con 5 veces más masa que sus protones originales. A esa exótica partícula se le ha llamado B+ y está compuesta por un quark b-anti y un quark u. La partícula B+ se desintegra a una altísima velocidad pero le da tiempo a recorrer ¡¡2 mm!! antes de desintegrarse en dos partículas, el mesón J / ? y el Kaon K+. Esta distancia, comparada con los minúsculos tamaños que estamos tratando, es una auténtica pasada. Hemos tenido antimateria pura moviéndose a lo largo de dos extensos milímetros de “nuestro” espacio. Impresionante.
Lo revolucionario sin embargo es que de esta forma, los investigadores habrían demostrado la teoría de Albert Einstein. “Sí, podemos crear masa a partir de energía usando la famosa fórmula de Einstein, E=mc2, dicen los responsables del CERN. Aunque también hay que destacar que la confirmación de que existe la antimateria plantea muchas preguntas de difícil resolución puesto que esa sustancia no existe en nuestro universo. “Ya que la desaparición de antimateria primordial no puede ser explicada por el modelo tradicional, tendremos que comenzar a pensar en algo nuevo”, afirman los investigadores. “Los científicos están evaluando diferentes posibilidades pero, dado que sólo podemos observar un 4% de la energía y materia total del universo, podemos inferir que la respuesta al misterio de la antimateria se encuentra en la parte desconocida del mismo”, concluyen.


Como podéis ver, las preguntas son muchas y, las respuestas, son más escasas. Sin embargo, no dejamos de insistir y buscar con todos medios a nuestro alcance para saber sobre la Naturaleza no ya de la materia y la antimateria, sino sobre los muchos enigmas que tenemos planteados y a los que no sabemos dar una adecuada explicación. Parece que a lo lejos vemos una luz cegadora que nos inyecta la esperanza necesaria para seguir la búsqueda y tratar de llegar al corazón de todos esos secretos que el Universo esconde.
Hay cosas que… más que sorprendentes son… ¡Inclreibles! He leído por ahí que…
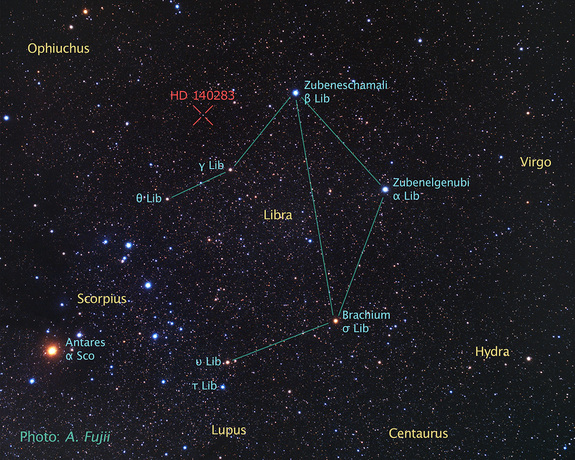
“Un grupo de astrónomos, usando datos del telescopio espacial Hubble, ha determinado la edad de la que es la estrella más vieja cuya edad puede medirse con precisión. El resultado ha sido que la edad de la estrella es de 14.500 ± 800 millones de años, mayor que la estimación de la edad del universo, unos 13.800 millones de años. La estrella en cuestión (HD 140283), también llamada “estrella Matusalén,” una gigante roja que se encuentra a una distancia de 190,1 años luz en la constelación de Libra (distancia medida con precisión mediante la técnica de paralaje). En el año 2000 se dató su edad en 16.000 millones de años. Sin embargo, existen algunas cuestiones que podrían aclarar la extrema edad de esta estrella. Nuevos modelos sobre la difusión de helio en el núcleo indican que la penetración del mismo podría ser mayor de la que se piensa, lo que provocaría un menor ritmo de combustión. También la relación oxígeno-hierro en esta estrella es anómala, demasiado grande, por lo que se cree que futuras observaciones que puedan determinar con mayor grado de precisión la abundancia de oxígeno podrían reducir nuevamente la estimación de la edad de la estrella.”

Mar
8
Gravedad cuántica, fluctuaciones de vacío…
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física, Física... ¡Y mucho más! ~
Clasificado en Física, Física... ¡Y mucho más! ~
 Comments (1)
Comments (1)

Las partículas recorren todos los caminos posibles para ir de un punto a otro. Así lo dice la hipótesis de múltiples historias. Dos partículas alejadas por miles de años luz pueden estar conectadas, otras se trasladan de un punto a otro del espacio sin recorrer las distancias que separan esos dos puntos (Efecto túnel) y, así, podríamos contar jistorias cuánticas alucinantes.

Por otra parte, existen hipótesis de todo tipo sobre lo que pudo pasar en aquellos primeros momentos.
“La hipótesis de la dimensión transicional que explica la gravitación y la materia oscura no conceptúa la hipótesis del Big-Bang en el sentido que el universo se crea a través de la explosión de un super-átomo, que crea la materia y el tiempo a partir de un punto único en el Universo. Y que ésta materia y tiempo se expanden en el espacio a partir de éste punto, en todas direcciones.
Esta hipótesis sólo puede conceptuar el Big-Bang como un evento simultáneo de creación de materia y tiempo en todo el Universo. Es decir, que no hubo ninguna explosión focal y dispersión de materia y energía en todas direcciones, sino que la materia y energía se creó instantáneamente en infinitos puntos del Universo. ( Un Big-Bang Multiple y simultaneo.).
Casi inmediatamente, por la acción de las fuerzas de la gravedad y el tiempo, se crearon los elementos y la materia como tal, así como la formación de Galaxias, Soles, Planetas y otros cuerpos celestes.
Todos los fenómenos que se dieron en ese momento y que aún se dan, obedecen a las Leyes de la Física Clásica, incluyendo la Expansión o Contracción de sectores del Universo, y no están directamente relacionados con el Big-Bang.”
Hay aspectos de la física que me dejan totalmente sin habla y quedan fuera de nuestra realidad inmersa en lo cotidiano de un mundo macroscópico que nos aleja de ese otro mundo misterioso e invisible donde residen los cuantos que, con su comportamiento, me obligan a pensar y me transportan de
En el mundo cuántico se pueden contemplar cosas más extrañas
Hay magnitudes asociadas con las leyes de la gravedad cuántica. La longitud de Planck

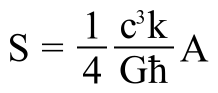
De todas las maneras, en este
Como nos dicen en este anuncio del Kybalion, nada es estático en el Universo y, todo está en continuo movimiento o vibración. Habreis oido hablar de la energía de punto cero que permanerce en una sustancia en el cero absoluto (cero K). Está de acuerdo con la teoría cuántica, según la cual, una partícula oscilando con un movimiento armónico simple no tiene
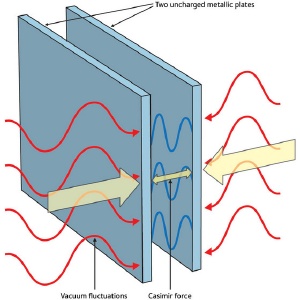
Efecto Casimir
Me llama poderosamente la atención lo que conocemos
Algunos han postulado que el Universo pudo surgir de una fluctuación del vacío que rasgó el espacio tiempo de otro universo.
Ordinariamente, definimos el vacío como el espacio en el que hay una baja presión de un gas, es decir, relativamente pocos átomos o moléculas. En ese sentido, un vacío perfecto no contendría ningún átomo o molécula, pero no se vacío theta
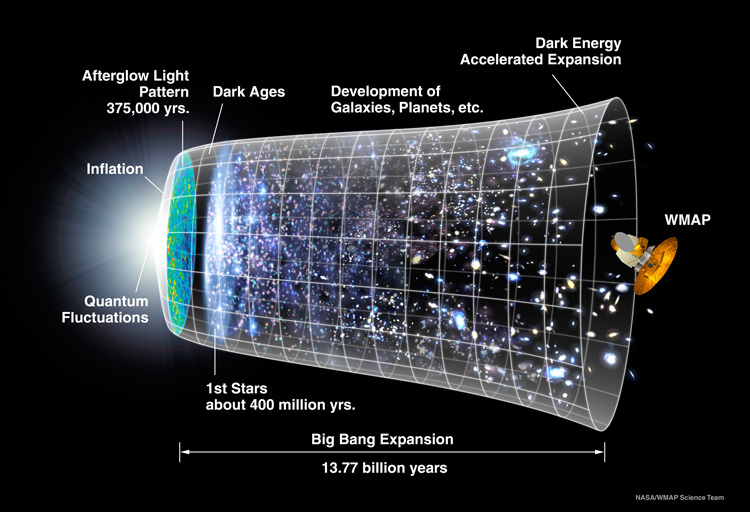

En astronomía, el vacío está referido a regiones del espacio con
El primer gran vacío en ser detectado fue el de Boötes en 1.981; tiene un radio de
La RAE reconoce los nombres hercio (hertz), julio (joule), vatio (watt), culombio (coulomb), voltio (volt), faradio (farad), ohmio (ohm) para las correspondientes unidades entre paréntesis. (a) El estereorradián (sr) no es una unidad SI base. Sin embargo, en fotometría se mantiene el estereorradián en expresiones para unidades.
Sabemos referirnos al producto o cociente de las unidades físicas básicas, elevadas a las potencias adecuadas, en una cantidad física derivada. Las cantidades físicas básicas de un sistema mecánico son habitualmente la masa (m), la longitud (l) y el tiempo (t). Utilizando estas dimensiones, la velocidad, que es una unidad física derivada, tendrá dimensiones l/t, y la aceleración tendrá dimensiones l/t2. SI
Las ondas fluctúan de forma aleatoria e impredecible, con energía positiva momentáneamente aquí, energía negativa momentáneamente allí, y energía cero en promedio. El aspecto de partícula está incorporado en el concepto de partículas virtuales, es decir, partículas que pueden nacer en pares (dos partículas a un tiempo), viviendo temporalmente de la energía fluctuacional tomada prestada de regiones “vecinas” del espacio, y que luego se aniquilan y desaparecen, devolviendo la energía a esas regiones “vecinas”. Si hablamos de fluctuaciones electromagnéticas del vacío, las partículas virtuales son fotones

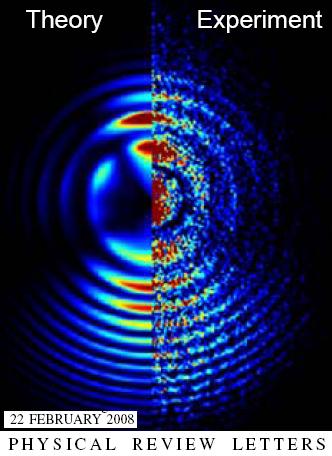
Claro que, en realidad, sabemos poco de esas regiones vecinas de las que tales fluctuaciones toman la energía. ¿Qué es lo que hay allí? ¿Está en esa región la tan buscada partícula de Higgs? Sabemos que las fluctuaciones de vacío son, para las ondas electromagnéticas y gravitatorias, lo que los movimientos de degeneración claustrofóbicos son para los electrones. Si confinamos un electrón a una pequeña región del espacio, entonces, por mucho que uno trate de frenarlo y detenerlo, el electrón está obligado por las leyes de la mecánica cuántica a continuar moviéndose aleatoriamente, de forma impredecible. Este movimiento de degeneración claustrofóbico que produce la presión mediante la que una estrella enana blanca se mantiene contra su propia compresión gravitatoria o, en el mismo caso, la degeneración de neutrones mantiene estable a la estrella de neutrones, que obligada por la fuerza que se genera de la degeneración de los neutrones, es posible frenar la enorme fuerza de gravedad que está comprimiendo la estrella.

La degeneración de los electrones impide que la gravedad continúe comprimiendo a una estrella electrones se degeneran y, “protestan” porque no quieren estar tan juntos (son fermiones), y, es la fuerza de esa degeneración la única que frena la implosión de la estrella y queda convertida en una enana blanca que, en el centro de la nueva Nebulosa radia con fuerza
De manera similar ocurre cuando la estrella es más masiva que nuestro Sol. Entonces, llegado el final de su vida y quedando a merced de la fuerza de Gravedad, ésta trata de comprimir la masa estelar al máximo. protones y electrones se fusionan neutrones que, al verse tan comprimidos “protestan” y se degeneran para neutrones estable. Si la estrella es demasiado masivo, ni el Principio de exclusión de Pauli para los fermiones, puede frenar la inmensa gravedad que genera y, el final del proceso es un Agujero Negro. De la misma
Hace tiempo que sabemos (Einstein Decir lo que pueda haber en ese “espacio vacío, no será nada fácil, sin embargo, parece que no sería un disparate pensar en la existencia allí de alguna clase de materia que, desde luego, al igual que la bariónica que sí podemos ver, genera energía y ondas gravitacionales que, de alguna manera que aún se nos oculta, escapa a nuestra vista y sólo podemos constatar sus efectos al medir las velocidades a las que se alejan las galaxias unas de otras: velocidad de expansión del universo, que no se corresponde en absoluto con la masa y la energía que podemos ver. Hay que seguir atando cabos sueltos, uniendo piezas y buscando algunas que están perdidas de tal manera que,
¡Quién sabe! Quizá sea el LHC el que, con sus resultados, nos pueda dar una respuesta de lo que realmente existe en ese mal llamado vacío y que, según parece, está lleno a rebosar. Sí, pero ¿de qué está lleno? Ya veremos. De Higgs
Estamos en un momento crucial de la física, las matemáticas y la cosmología, y debemos, para poder materia oscura




Mar
7
¿Qué habrá más allá del Modeo Estándar de la Física de Partículas?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)

“Inicialmente, se presenta, de modo simplificado, el Modelo Estándar como una teoría sofisticada que identifica las partículas elementales y sus interacciones. Después, en el ámbito de esa teoría, se enfocan aspectos –el vacuo no es vacío; partículas desnudas y vestidas; materia oscura y viento oscuro; materia y antimateria; el campo y el bosón de Higgs; neutrinos oscilantes– que pueden ser motivadores desde el punto de vista de la enseñanza y del aprendizaje de la Física. Finalmente, se discute la probable superación de esa teoría por otra más completa.”

“… el Modelo Estándar es, en la historia, la más sofisticada teoría matemática sobre la naturaleza. A pesar de la palabra “modelo” en su nombre, el Modelo Estándar es una teoría comprensiva que identifica las partículas básicas y especifica cómo interactúan. Todo lo que pasa en nuestro mundo (excepto los efectos de la gravedad) es resultado de las partículas del Modelo Estándar interactuando de acuerdo con sus reglas y ecuaciones.”
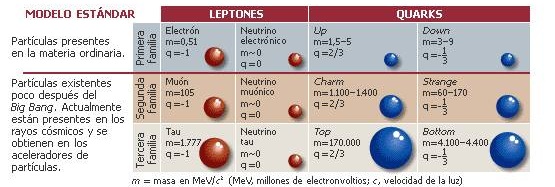



La Física actual busca una teoría más amplia que el modelo estándar . Una teoría que dé una descripción completa, unificada y consistente de la estructura fundamental del universo. ¿Será la compleja Teoría de cuerdas,que integra también la interacción gravitaroria?
El modelo estándar es una poderosa herramienta pero no cumple todas las expectativas; no es un modelo perfecto. En primer lugar, podríamos empezar por criticar que el modelo tiene casi veinte constantes que no se pueden calcular. Desde luego, se han sugerido numerosas ideas para explicar el origen de todos estos parámetros o números inexplicables y sus valores, pero el problema de todas estas teorías es que los argumentos que dan nunca han sido enteramente convincentes. ¿Por qué se iba a preocupar la naturaleza de una fórmula mágica si en ausencia de tal fórmula no hubiera contradicciones? Lo que realmente necesitamos es algún principio fundamental nuevo, tal como el principio de la relatividad, pero no queremos abandonar todos los demás principios que ya conocemos. Ésos, después de todo, han sido enormemente útiles en el descubrimiento del modelo estándar. El mejor lugar para buscar un nuevo principio es precisamente donde se encuentran los puntos débiles de la presente teoría y, construímos máquinas como el LHC para que nos diga lo que no sabemos.
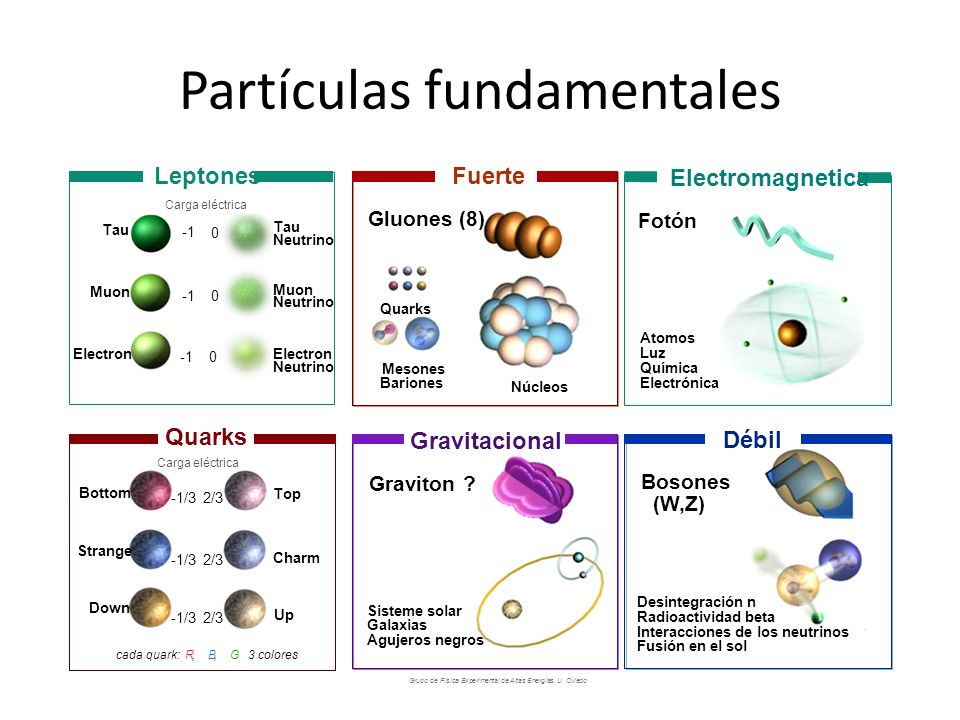
Una regla universal en la física de partículas es que para partículas con energías cada vez mayores, los efectos de las colisiones están determinados por estructuras cada vez más pequeñas en el espacio y en el tiempo. El modelo estándar es una construcción matemática que predice sin ambigüedad cómo debe ser el mundo de las estructuras aún más pequeñas. Pero existen varias razones para sospechar que sus predicciones pueden, finalmente (cuando podamos emplear más energía en un nivel más alto), resultar equivocadas.
Vistas a través del microscopio, las constantes de la naturaleza parecen estar cuidadosamente ajustadas sin ninguna otra razón aparente que hacer que las partículas parezcan lo que son. Hay algo muy erróneo aquí. Desde un punto de vista matemático no hay nada que objetar, pero la credibilidad del modelo estándar se desploma cuando se mira a escalas de tiempo y longitud extremadamente pequeñas, o lo que es lo mismo, si calculamos lo que pasaría cuando las partículas colisionan con energías extremadamente altas. ¿Y por qué debería ser el modelo válido hasta aquí? Podrían existir muchas clases de partículas súper pesadas que no han nacido porque se necesitan energías aún inalcanzables. ¿Dónde está la partícula de Higgs? ¿Cómo se esconde de nosotros el gravitón?

Parece que el Modelo estándar no admite la cuarta fuerza y tendremos que buscar más profundamente, en otras teorías que nos hablen y describan además de las partículas conocidas de otras nuevas que están por nacer y que no excluya la Gravedad. Ese es el Modelo que necesitamos para conocer mejor la Naturaleza.
Claro que las cosas no son tan sencilla y si deseamos evitar la necesidad de un delicado ajuste de las constantes de la naturaleza, creamos un nuevo problema: ¿cómo podemos modificar el modelo estándar de tal manera que el ajuste fino no sea necesario? Está claro que las modificaciones son necesarias, lo que implica que muy probablemente haya un límite más allá del cual el modelo tal como está deja de ser válido. El modelo estándar no será nada más que una aproximación matemática que hemos sido capaces de crear, de forma que todos los fenómenos que hemos observado hasta el presente están reflejados en él, pero cada vez que se pone en marcha un aparato más poderoso, tenemos que estar dispuestos a admitir que puedan ser necesarias algunas modificaciones del modelo para incluir nuevos datos que antes ignorábamos.
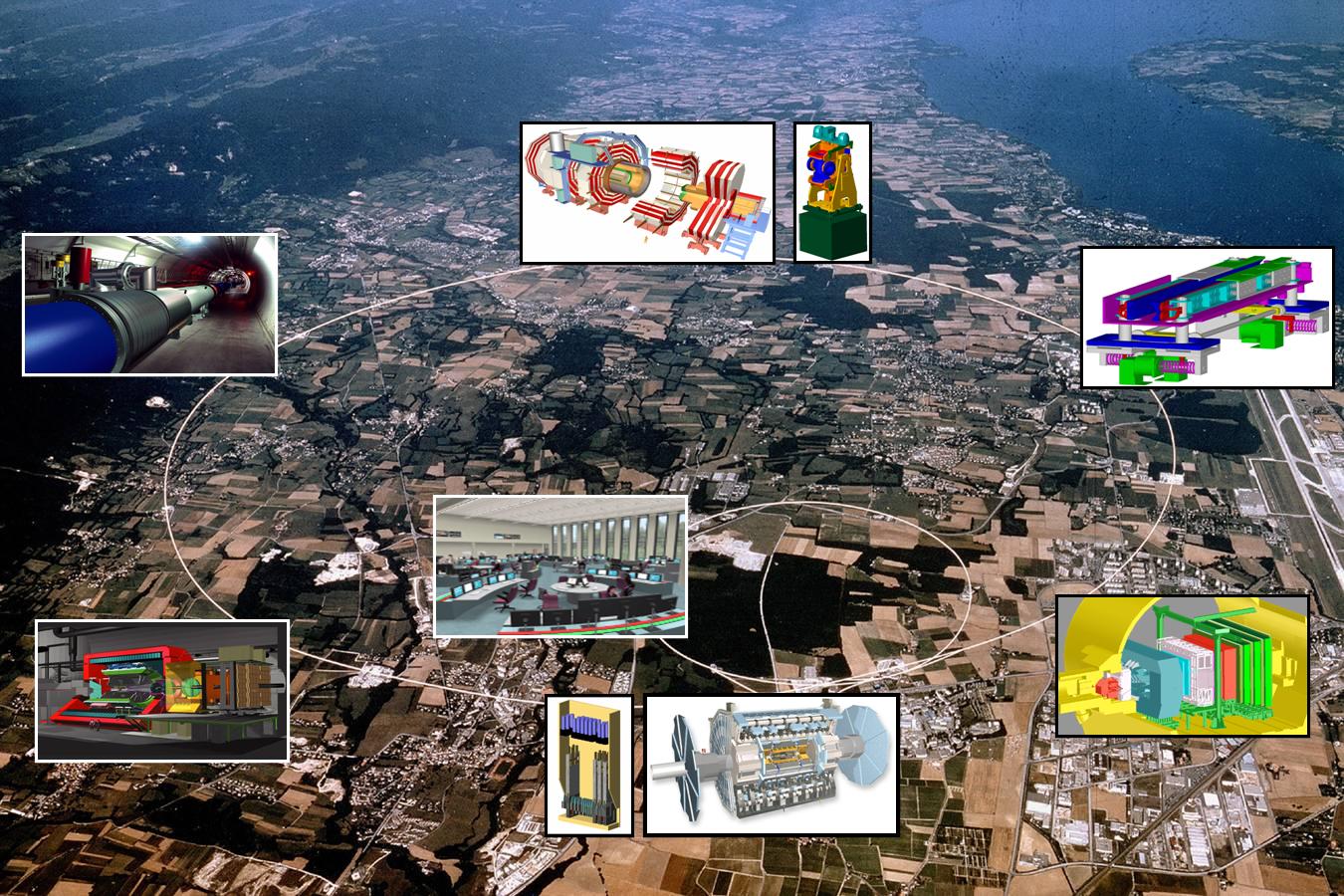
Más allá del modelo estándar habrá otras respuestas que nos lleven a poder hacer otras preguntas que en este momento, no sabemos ni plantear por falta de conocimientos. Si no conociéramos que los protones están formados por Quarks, ¿cómo nos podríamos preguntar si habrá algo más allá de los Quarks?
El gobierno de Estados Unidos, después de llevar gastados miles de millones de dólares, suspendió la construcción del supercolisionador superconductor de partículas asestando un duro golpe a la física de altas energías, y se esfumó la oportunidad para obtener nuevos datos de vital importancia para el avance de este modelo, que de momento es lo mejor que tenemos.
Se han estado inventando nuevas ideas, como la supersimetría y el technicolor. Los astrofísicos estarán interesados en tales ideas porque predicen una gran cantidad de nuevas partículas superpesadas, y también varios tipos de partículas que interaccionan ultradébilmente, los technipiones. Éstas podrían ser las WIMP’s (Weakly Interacting Massive Particles, o Partículas Masivas Débilmente Interactivas) que pueblan los huecos entre las galaxias, y serían así las responsables de la masa perdida que los astrofísicos siguen buscando y llaman “materia oscura”.

Que aparezcan “cosas” nuevas y además, imaginarlas antes, no es fácil. Recordemos cómo Paul Dirac se sintió muy incómodo cuando en 1931 dedujo, a partir de su ecuación del electrón, que debería existir una partícula con carga eléctrica opuesta. Esa partícula no había sido descubierta y le daba reparo perturbar la paz reinante en la comunidad científica con una idea tan revolucionaria, así que disfrazó un poco la noticia: “Quizá esta partícula cargada positivamente, tan extraña, sea simplemente el protón”, sugirió. Cuando poco después se identificó la auténtica antipartícula del electrón (el positrón) se sorprendió tanto que exclamó: “¡Mi ecuación es más inteligente que su inventor!”. Este último comentario es para poner un ejemplo de cómo los físicos trabajan y buscan caminos matemáticos mediante ecuaciones de las que, en cualquier momento (si están bien planteadas), surgen nuevas ideas y descubrimientos que ni se podían pensar. Así pasó también con las ecuaciones de Einstein de la relatividad general, donde Schwarzschild dedujo la existencia de los agujeros negros.
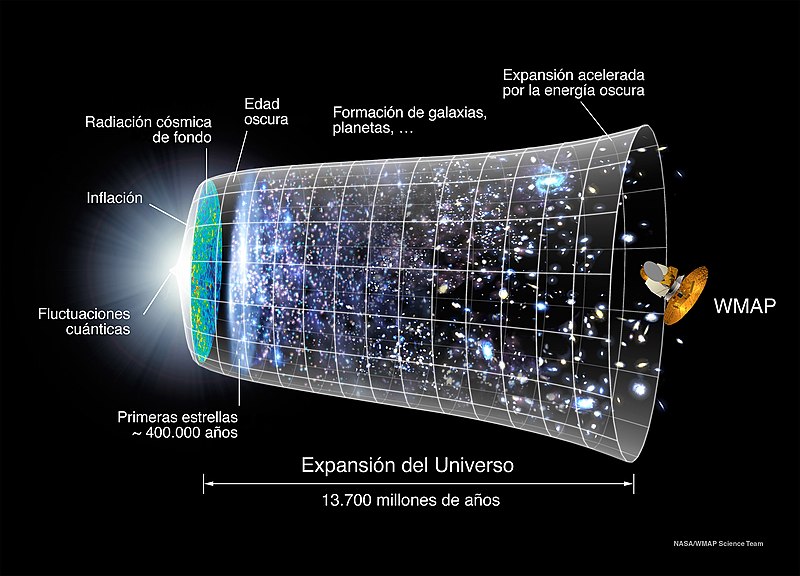
Se piensa que al principio del comienzo del tiempo, cuando surgió el Big Bang, las energías eran tan altas que allí reinaba la simetría total; sólo había una sola fuerza que todo lo englobaba. Más tarde, a medida que el universo se fue expandiendo y enfriando, surgieron las cuatro fuerzas que ahora conocemos y que todo lo rigen. Tenemos los medios, en los supercolisionadores de partículas, para viajar comenzando por 1.000 MeV, hasta finalizar en cerca de 1019 MeV, que corresponde a una escala de longitudes de aproximadamente 10–30 cm. Howard Georgi, Helen Quinn y Steven Weinberg descubrieron que ésta es la región donde las tres constantes de acoplamiento gauge se hacen iguales (U(1), SU(2) y SU(3)); resultan ser lo mismo. ¿Es una coincidencia que las tres se hagan iguales simultáneamente? ¿Es también una coincidencia que esto suceda precisamente en esa escala de longitud? Faltan sólo tres ceros más para alcanzar un punto de retorno. Howard Georgi y Sheldon Glashow descubrieron un modelo genuinamente unificado en el dominio de energías de 1019 MeV tal que, cuando se regresa de allí, espontáneamente surgen las tres fuerzas gauge tal como las conocemos. De hecho, ellos encontraron el modelo; la fórmula sería SU(5), que significa que el multiplote más pequeño debe tener cinco miembros.


Materia y Energía Oscura… Un Misterio…Sin resolver.
Y, a todo esto, ¿dónde está esa energía oculta? ¿Y donde la materia? Podemos suponer que la primera materia que se creo en el Universo fue la que llamamos (algún nom,bre había que ponerle) “Materia Oscura”, esa clase de Ilem o sustancia primera del Universo que mejor sería llamarla invisible, ya que, de no ser así, difícil sería explicar cómo se pudieron formar las primeras estrellas y galaxias de nuestro Universo, ¿dónde está el origen de la fuerza de Gravedad que lo hizo posible, sino en esa materia escondida?
¡Lo dicho! Necesitamos saber, y, deseo que de una vez por todas, se cumpla lo que dejó dicho Hilbert en su tumba de Gotinga (Alemania): “Tenemos que saber, ¡sabremos!. Pero…
¡Que sea pronto!
emilio silvera
Mar
2
La Física relativista, la cuántica y… ¡El futuro!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)
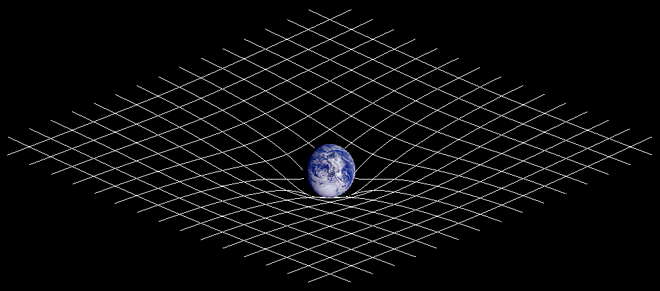
Esta es una analogía bidimensional de la distorsión del espacio-tiempo debido a un objeto de gran masa
Hay que entender que el espacio-tiempo es la única descripción en cuatro dimensiones del Universo en la que la posición de un objeto se especifica por tres coordenadas en el espacio y una en el tiempo. De acuerdo con la relatividad especial, no existe un tiempo absoluto que pueda ser medido con independencia del observador, de manera que sucesos simultáneos para un observador ocurren en instantes diferentes vistos desde otro lugar.
El tiempo puede ser medido, por tanto, de manera relativa, como los son las posiciones en el espacio tridimensional, y esto puede conseguirse mediante el concepto de espacio-tiempo. La trayectoria de un objeto en el espacio-tiempo se denomina por el nombre de línea de Universo. La relatividad general, nos explica lo que es un espacio-tiempo curvo con las posiciones y movimientos de las partículas de materia.

Presencia de materia y curvatura
La densidad de energía-momentum en la teoría de la relatividad se representa por cuadritensor energía-impulso. Las componentes de dicho tensor representan entre otras la densidad de energía y la densidad de momentum y dichas componentes están relacionadas localmente con las componentes del curvatura. La relación entre la presencia de materia y la curvatura debida a dicha materia viene dada por la ecuación de campo de Einstein:
Es una fuerza atractiva que en la comunidad científica actual es concebida como la pensó Einstein: como un efecto de la curvatura del espacio-tiempo en presencia de de objetos masivos y, cuanto más masa tenga el objeto más se curvará el espacio a su alrededor.
donde:
 , es el tensor de curvatura de Ricci
, es el tensor de curvatura de Ricci es el escalar de curvatura de Ricci
es el escalar de curvatura de Ricci , es el tensor de energía-impulso
, es el tensor de energía-impulso
Ejemplos
 Así, la curvatura del espacio tiempo es la propiedad del espacio-tiempo en la que las leyes familiares de la geometría no son aplicables en regiones donde los campos gravitatorios son intensos. La relatividad general de Einstein, nos explica y demuestra que el espacio-tiempo está íntimamente relacionado con la distribución de materia en el Universo y, nos dice que, el espacio se curva en presencia de masas considerables como planetas, estrellas o Galaxias…
Así, la curvatura del espacio tiempo es la propiedad del espacio-tiempo en la que las leyes familiares de la geometría no son aplicables en regiones donde los campos gravitatorios son intensos. La relatividad general de Einstein, nos explica y demuestra que el espacio-tiempo está íntimamente relacionado con la distribución de materia en el Universo y, nos dice que, el espacio se curva en presencia de masas considerables como planetas, estrellas o Galaxias…
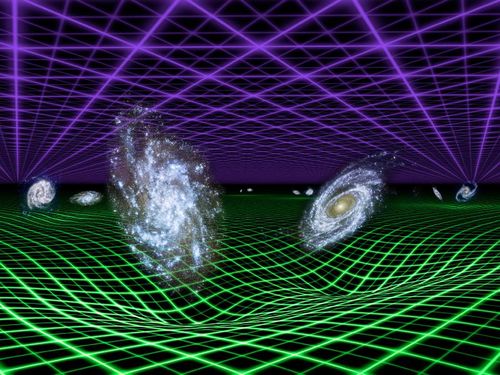
En realidad, es la presencia de la materia la que determina la geometría del espacio-tiempo
En un espacio de sólo dos dimensiones, como una lámina de goma plana, la geometría de Euclides se aplica de manera que la suma de los ángulos internos de un triángulo en la lámina es de 180º. Si colocamos un objeto masivo sobre la lámina de goma, la lámina se distorsionará y los caminos de los objetos que se muevan sobre ella se curvaran. Esto es en esencia, lo que ocurre en relatividad general.
Lo cierto es que, desde que llegó Einstein con sus versiones de la teoría relativista, muchas fueron las cosas que cambiaron y, nuestros conceptos del mundo…, también. Fenómenos que se crean en la naturaleza y que son la consecuencia de la presencia de masas o de velocidades muy grandes.
¡Los efectos de c -la velocidad de la luz en el espacio vacío-! Recordad la paradoja de los gemelos: Uno de ellos, que es astronauta, hace un viaje a la velocidad de la luz hasta Alfa de Centauri y regresa, cuando baja de la nave espacial, tiene 8,6 años más que cuando partió de la Tierra. Sin embargo, su hermano gemelo que le esperó en el planeta Tierra, era ya un anciano jubilado. El tiempo transcurrido había pasado más lento para el gemelo viajero. La velocidad ralentiza el transcurrir del tiempo.

El Universo es todo energía que se manifiesta de distintas maneras: bien como masa, o, bien como radiación.
Otra curiosidad de la relatividad especial es la que expresó Einstein mediante su famosa fórmula de E= mc2 que, nos viene a decir que masa y energía son dos aspectos de una misma cosa. Podríamos considerar que la masa (materia), es energía congelada. Todos sabemos lo que ocurre cuando se desintegra un átomo de materia y la enorme cantidad de energía que tiene concentrada.
Hay otras implicaciones dentro de esta maravillosa teoría de la relatividad especial, ahí está presente también la contracción de Lorentz. Un objeto que se mueve a velocidad de cercana a c, se achata o contrae en el sentido de la marcha, y, además, a medida que se acerca a la velocidad de la luz (299.752,458 Km/s), su masa va aumentando y su velocidad disminuyendo.
Así se ha demostrado con muones en los aceleradores de particulas que, lanzados a verlocidades relativista, han alcanzado una masa en 10 veces superior a la suya. Esto quiere decir que la fuerza de inercia que se le está transmitiendo a una nave (por ejemplo), cuando se acerca a la velocidad de la luz, se convierte en masa.
Así queda demostrado que, masa y energía son dos aspectos de la misma cosa E=mc2. Pero no olvidemos que…
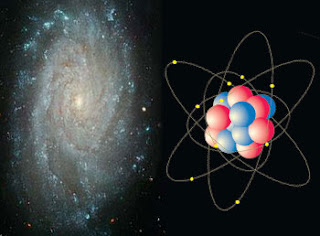
Todos hemos llegado a comprender que, todo lo grande está hecho de cosas pequeñas. Sin emnbargo hay cosas que aún no tenemos claras, y, un ejemplo de ello es, ¡El Hiperespacio!
Esta idea interesante ha sido utilizada en diversas teorías físicas prometedoras que han recurrido formalmente a la introducción de nuevas dimensiones formales para dar cuenta de fenómenos físicos. Así Kaluza y Klein trataron de crear una teoría unificada (clásica) de la gravedad y del electromagnetismo, introduciendo, a las cuatro dimensiones de la teoría relativista, una quinta dimensión adicional. En esta teoría la carga podía relacionarse con la quinta componente de la “pentavelocidad” de la partícula, y otra serie de cuestiones interesantes. El enfoque de varias teorías de supercuerdas es aún más ambicioso y se han empleado esquemas inspirados remotamente en la ideas de Einstein, Kaluza y Klein que llegan a emplear hasta diez y once dimensiones, de las cuales seis o siete estarían compactificadas y no serían detectables más que indirectamente.
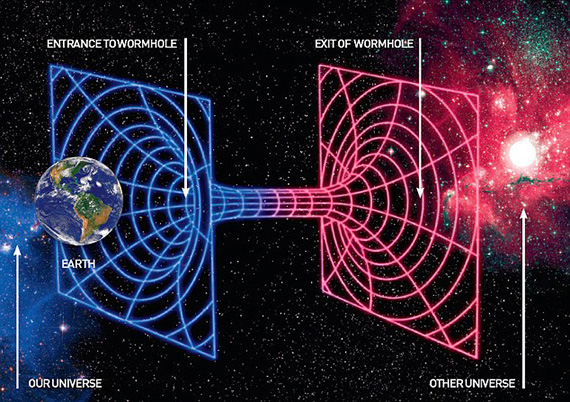

Nuestra inemsa imaginación nos ha llevado a buscar teorías que no podemos comprobar de manera experimental y, dentro de esas teorías, están, o, pudieran estar, las claves para viajar a otras regiones del espacio muy distantes de la nuestra por ese medio que intuimos, que pudiera ser accesible para nosotros y que hemos llamado Hiperespacio, que estaría situado en la quinta dimensión.

Mecánica cuántica, relatividad, átomos, el genóma, agujeros negros, la constante cosmológica, la constante de Planck racionalizada… Sabemos representar muchas otras cosas y estamos a la búsqueda de otras que intuimos como la “materia oscura”, o, ¿por qué no? la quinta dimensióny el hiperespacio. No cejamos en el desarrollo de la “imposible” teoría de cuerdas y también, buscamos bosones dadores de masa en un espacio profundo, de cuyo contenido sabemos poco.

Con los conocimientos de la mecánica cuántica que tenemos, hemos conseguido teletransportar las propiedades de la materia. Las películas de ciencia ficción -desde Star Trek hasta La Mosca- nos han mostrado un futuro donde las personas pueden teletransportarse sin problemas. Y aunque los científicos aún no logran transferir materia… Creo que, ¡todo se andará!
La teleportación cuántica no consiste en transportar instantáneamente objetos, sino de transferir el “estado” de una o varias partículas, los constituyentes íntimos de la materia, de un lugar a otro y sin necesidad de enviar físicamente la partícula a través del espacio. Este sorprendente logro es posible gracias al “entrelazamiento cuántico”, una extraña y aún poco comprendida propiedad de las partículas subatómicas que permite que dos -o más-, partículas unan sus destinos de tal forma que cualquier cambio de estado que se produzca en una de ellas se refleje de forma instantánea también en la otra, sin importar la distancia que las separe.No sabemos de qué manera, esas partículas permanecen “unidas” y la física clásica no puede darnos una explicación. Sin embargo, siendo conocedores de tal fenómeno, los científicos llevan veinte años intentando sacar rendimiento a esa realidad extraordinaria que nos envía la promesa de que, con ella, podemos traer una nueva revolución al campo de las comunicaciones por satélite, la informática y… ¿quién sabe qué más?
Sí, es cierto que, tanto la teletransportación de personas, como el viaje por el Hiperespacio es -todavía- cosa de la ciencia ficción pero… Acordáos de cuando Arthur Clarke nos hablaba de satélites que orbitaban la Tierra para recoger y enviarnos datos de alto interés en los diversos campos de la actividad humana. Aquello, parecía una fantasía y, sin embargo ahora, es lo cotidiano.


¿Quién puede decir ahora qué mundo futuro nos espera? Conforme a los conocimientos que actualmente tenemos, podemos intuir el devenir tecnologíco que los avances de la ciencia nos pueden proporcionar y, entre los muchos que están ahí, en ese horizonte futuro, están todos estos de los que hablamos y, seguramente, muchos más que ni podemos imaginar. Seguramente, como tambioén ahora mismo está pasando, no todos los aspectos de la tecnología futura nos gustarán.

La mejor manera de no equivocarse es tener la mente abierta a todo. Negar la existencia de universos paralelos, o, la certeza de la teoría de cuerdas…, ¿A dónde nos lleva? ¡A ninguna parte! Así pues, mantengamos la confianza en nosotros mismos, en lo que nuestras mentes llegan a intuir, y, dejémos, que nuestra “infinita” imaginación siga haciendo su trabajo y dibujando en nuestras mentes esos escenarios de mundos que podrían ser… ¡Una realidad futura!
emilio silvera
















 Totales: 83.589.896
Totales: 83.589.896 Conectados: 50
Conectados: 50