sábado, 27 de julio del 2024 Fecha
Ir a la página principal Ir al blog

IMPRESIÓN NO PERMITIDA - TEXTO SUJETO A DERECHOS DE AUTOR



 

«
»

May

29

Entropía

Autor por Emilio Silvera    ~    Archivo Clasificado en General    ~    Comentarios Comments (2)

RSS de la entrada Comentarios Trackback Suscribirse por correo a los comentarios

 

Variación de entropía del universo

Desde el punto de vista de la Termodinámica, el universo es el conjunto constituido por un sistema y sus alrededores. Es, por tanto, un sistema aislado (no hay nada fuera de él). De la misma manera en que se puede calcular la variación de entropía de un sistema termodinámico entre dos estados, puede calcularse la variación de entropía de sus alrededores (todo lo que ha interaccionado con nuestro sistema). La suma de ambas magnitudes se denomina variación de entropía del universo.

Como el universo es un sistema aislado, utilizando el teorema de Clausius se tiene que, para el universo:

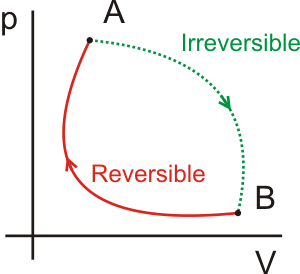
Donde el signo igual es aplicable para una transformación reversible y el signo menor que cuando dicha transformación es irreversible. A continuación se analiza cada caso por separado.

Transformación irreversible

En el siguiente diagrama p – V se ha representado un ciclo irreversible.

Está constituido por dos transformaciones: la AB (representada en verde en la figura), que es irreversible, y la BA (en rojo) que es reversible. Como el ciclo en su conjunto es irreversible, debemos aplicar el teorema de Clausius con el signo menor:

La integral de línea que aparece en la ecuación anterior puede ser descompuesta en la suma de las integrales evaluadas en cada etapa del ciclo, quedando:

Ya que la integral evaluada a lo largo del tramo reversible es precisamente la variación de entropía entre los estados B y A. Por tanto,

Expresión conocida como desigualdad de Clausius.

El significado físico de esta ecuación es que la variación de entropía entre dos estados cualesquiera será siempre mayor que la integral del calor intercambiado irreversiblemente entre los dos estados partido por la temperatura.

Como aplicación de esta expresión, la variación de entropía en la expansión libre de Joule ha de ser mayor que cero (como efectivamente lo es) ya que el calor intercambiado en esta transformación irreversible es cero.

Como el universo es un sistema aislado, cuando en el universo se produce una transformación cualquiera AB irreversible el calor intercambiado es cero, por lo que:

Es decir, la entropía del universo siempre crece para cualquier transformación irreversible que se produzca.

Transformación reversible

Cuando en el universo tiene lugar una transformación reversible, debemos tomar el signo igual:

Agrupando ambos resultados:

Esta afirmación constituye un nuevo enunciado del Segundo Principio:

La entropía es una función de estado que, evaluada para todo el universo, aumenta en una transformación irreversible y permanece constante en una transformación reversible.

Salvo mejor parecer.
hotmail correo[?]


Esta entrada fue publicada el miércoles, 29 de mayo de 2024 a las 20:28 y está clasificada bajo: General. Puede hacer un seguimiento de los comentarios de esta entrada gracias al feed RSS 2.0. Puede dejar un comentario, o enviar un trackback desde su sitio.
 

  1. 1
    Pedro
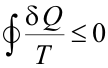
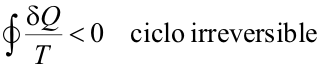
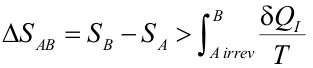
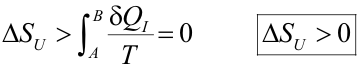
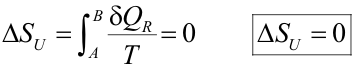
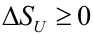
    el 31 de mayo del 2024 a las 5:29

    Vaya con el video de Javier Garcia, si hasta ahora definían la entropia como el grado de desorden de un sistema.
    Si nos preguntarán cual es el grado de entropia de un sujeto disciplinado frente a otro no disciplinado, la respuesta resultaría muy obvia. Mayor entropia aquel sujeto menor disciplinado ya que trabajo útil si logra alguno muy restringido u limitado, sin sorprender a nadie por ello .

    Ahora viendo el video, resulta que definen la entropia como la capacidad que tiene un sistema de hacer lo más improbable, ya que subyace detrás mayor información que hasta entonces no se había considerado.

    Cara y cruz de la entropia, un sistema puede tener mucha o poca entropia, un sistema puede tener mucha o poca información, o un sistema puede tener mucha o poca sorpresa, esta no es la cuestión sino, la cuestión que no terminan de resolver es ¿Que pasa con un sistema que tiene muy poca informacion, sin embargo esta resultar muy relevante? Aún más ¿Relevante, para que o para quien?.
    .

    ¿Hay ecuación que cuantifique lo relevante de esto u aquello?

    Conclusion:”¿La matematizacion de esto u aquello es lo relevante o bien lo más relevante es como nos desvivimos por esto u aquello?.

    Responder
    • 1.1
      emilio silvera
      el 31 de mayo del 2024 a las 8:25

      ¡Estos Físicos!

      Responder
.:: Subir ::.

Deja un comentario



Comentario:

XHTML

Subscribe without commenting