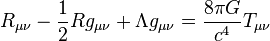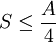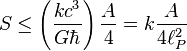Feb
8
Surgieron pensamientos… ¡Que nunca dejaran de asombrarnos!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (19)
Comments (19)

Ludwig Boltzmann será el protagonista de hoy
Hay ecuaciones que son aparentemente insignificantes por su reducido número de exponentes que, sin embargo, ¡dicen tantas cosas…! En la mente de todos están las sencillas ecuaciones de Einstein y de Planck sobre la energía-masa y la radiación de cuerpo negro. Esa es la belleza de la que hablan los físicos cuando se refieren a “ecuaciones bellas”.

Maxwell

Las ecuaciones de Maxwell…, “y se hizo la luz”
La identidad de Euler: Algunos dijeron de su ecuación: “la expresión matemática más profunda jamás escrita”, “misteriosa y sublime”, “llena de belleza cósmica”, “una explosión cerebral”.

Newton y su segunda ley que, aunque no funcione cuando nos acercamos a velocidades relativistas, rompió la marcha hacia la Gravedad.

Pitágoras y “su” teorema, también debe estar presente como lo está su teorema en las construcciones de todo el mundo y… mucho más.

Schrödinger y su función de onda que tampoco se queda atrás (aunque como la ecuación de Newton, si hablamos de velocidades relativistas…)
Bueno, E = mc2, nos lleva a profundidades de la materia antes jamás vistas y nos permite sacar conclusiones como que, en un gramo de materia está encerrada toda la energía consumida por la Humanidad durante un minuto. ¡Masa y Energía son la misma cosa!
Einstein, con esa ecuación de arriba de la relatividad general, vino a cambiar el mundo y, a partir de entonces, nació la verdadera cosmología. ¡Nos habla de tantas cosas!
¿Qué decir de la maravillosa fórmula de la entropía de Boltzman?
S = k log W
Creo que hoy, hablaremos de ella. Boltzman con su trabajo e ingenio, le dio a la Humanidad la herramienta para que pudiera seguir avanzando en el difícil laberinto de la Ciencia, fue, sin duda, uno de los físicos más ilustres del siglo XIX.
El trabajo científico desarrollado por Boltzmann en su época crítica de transición que puso el colofón a la física “clásica” –cuya culminación podríamos situar en Maxwell– y antecedió (en pocos años) a la “nueva” física, que podemos decir que comenzó con Max Planck y Einstein. Aunque ciertamente no de la importancia de los dos últimos, la labor científica de Boltzmann tiene una gran relevancia, tanto por sus aportaciones directas (creador junto con “su amigo” Maxwell y Gibbs de la mecánica estadística, aunque sea el formulismo de éste último el que finalmente haya prevalecido; esclarecedor del significado de la entropía, etc.) como por la considerable influencia que tuvo en ilustres físicos posteriores a los que sus trabajos dieron la inspiración, como es el caso de los dos mencionados, Planck y Einstein.
El principio, como suele pasar en todas las cosas, es siempre tosco y, con el tiempo, se van perfeccionando las cosas, la evolución va mejorando las formas
Boltzmann fue un defensor a ultranza del atomismo, polemizando sobre todo con Mach y Ostwald, antiatomistas partidarios de la energética y claros exponentes de la corriente idealista de la física alemana. Tuvo que abandonar su ambiciosa idea de explicar exactamente la irreversibilidad en términos estrictamente mecánicos; pero esta “derrota”, no ocultaré que dolorosa desde el punto de vista personal, le fue finalmente muy productiva, pues de alguna manera fue lo que le llevó al concepto probabilista de la entropía. Estas primeras ideas de Boltzmann fueron reivindicadas y extendidas, en el contexto de la teoría de los sistemas dinámicos inestables, sobre todo por la escuela de Prigogine, a partir de la década de 1970.
La personalidad de Boltzmann era bastante compleja. Su estado de ánimo podía pasar de un desbordante optimismo al más negro pesimismo en cuestión de unas pocas horas. Era muy inquieto; él decía – medio en serio, medio en broma – que eso se debía a haber nacido en las bulliciosas horas finales de los alegres bailes del Martes de Carnaval, previas a los “duelos y quebrantos” (entonces) del Miércoles de Ceniza.

Ludwig Boltzmann and co-workers in Graz, 1887. (standing, from the left) Nernst, Streintz, Arrhenius, Hiecke, (sitting, from the left) Aulinger, Ettingshausen, Boltzmann, Klemenčič, Hausmanninger
Su lamentable final, su suicidio en Duino (Trieste) el 5 de septiembre de 1906, muy probablemente no fue ajeno a esa retorcida personalidad, aunque su precaria salud física fue seguramente determinante a la hora de dar el trágico paso hacia el lado oscuro.
Uno de los problemas conceptuales más importantes de la física es cómo hacer compatible la evolución irreversible de los sistemas macroscópicos (el segundo principio de la termodinámica) con la mecánica reversible (las ecuaciones de Hamilton o la ecuación de Schrödinger) de las partículas (átomos o moléculas) que las constituyen. Desde que Boltzmann dedujo su ecuación en 1872, este problema ha dado lugar a muy amplios debates, y el origen de la irreversibilidad es, aún hoy en día, controvertido.

En una de sus primeras publicaciones, Boltzmann obtuvo en 1866 una expresión de la entropía, que había sido definida un año antes por Clausius, basado en conceptos mecánicos. Las limitaciones de este trabajo eran que su aplicación se restringía al estudio de los gases y que el sistema era periódico en el tiempo. Además, Boltzmann no pudo deducir de su definición de entropía la irreversibilidad del segundo principio de la termodinámica de Clausius. En 1868, basándose en las ideas probabilísticas de Maxwell, obtuvo la distribución de equilibrio de un gas de partículas puntuales bajo la acción de una fuerza que deriva de un potencial (distribución de Maxwell-Boltzmann).

En el Universo, considerado como sistema cerrado, la entropía crece y…
En 1.872 publicó la denominada ecuación de Boltzmann para cuya deducción se basó, aparentemente, en ideas mecánicas. Esta ecuación contiene, sin embargo, una hipótesis no mecánica (estadística) o hipótesis del caos molecular, que Boltzmann no apreció como tal, y cuya mayor consecuencia es que, cualquiera que sea la distribución inicial de velocidad de un gas homogéneo diluido fuera del equilibrio, ésta evoluciona irreversiblemente hacia la distribución de velocidad de Maxwell. A raíz de las críticas de Loschmidt (paradoja de la reversibilidad) y Zermelo (paradoja de la recurrencia), Boltzmann acabó reconociendo el carácter estadístico de su hipótesis, y en 1877 propuso una relación entre la entropía S de un sistema de energía constante y el número de estados dinámicos W accesibles al sistema en su espacio de fases; esto es, la conocida ecuación S = kB ln W, donde kB es la constante de Boltzmann. En esta nota, se hace una breve descripción de la ecuación de Boltzmann y de la hipótesis del caos molecular.

El comportamiento de los gases siempre dio a los físicos en qué pensar
La ecuación de Boltzmann describe la evolución temporal de un gas diluido de N partículas puntuales de masa m contenidas en un volumen V que interaccionan a través de un potencial de par central repulsivo V(r) de corto alcance a. Como simplificación adicional, considérese que sobre las partículas no actúan campos externos. Si f1(r,v,t) indica la densidad de partículas que en el tiempo t tienen un vector de posición r y velocidad v, que está normalizada en forma:
∫dr ∫dvƒ1(r,v,t) = N
Su evolución temporal es la suma de dos contribuciones. En ausencia de interacción, las partículas que en el tiempo t tienen vector de posición r y velocidad v se encuentran, después de un intervalo de tiempo Δt, en r + v Δt y tiene la misma velocidad. Como
f1(r + vΔt,v,t + Δt) = f1(r,v,t)
en el límite Δt → 0 (2) se escribe:
∂1 f1(r,v,t) = – v∂r f1(r,v,t)
Que es una ecuación invariante bajo el cambio t → – t y v → – v. La evolución es, por tanto, mecánica.
Se cumplieron más de cien años desde la muerte de Boltzmann y su trabajo sigue siendo recordado. No pienso que Boltzmann creyera en la existencia real de los átomos, pero sí en su utilidad e incluso en su necesidad para comprender las leyes macroscópicas y la evolución irreversible de los fenómenos macroscópicos desde una base más fundamental que el nivel fenomenológico. Pero había quien (con autoridad) no creía ni en la existencia ni en su utilidad. Este debate no era ajeno a las tendencias ideológicas, religiosas y usos sociales de aquella época porque, en general, la ciencia es parte de la cultura y depende del momento histórico que viven los científicos, al fin y al cabo, seres humanos como los demás, influenciables por su entorno en una gran medida.
Por el siglo XIX, e incluso antes, ya se hablaba de “átomos”* y una rudimentaria teoría cinética de los gases gozaba de aceptación y utilidad científica (recordemos los trabajos de Benoulli, Dalton, Laplace, Poisson, Cauchy, Clausius, Krönig… y Maxwell). Pero fue Boltzmann quien definitivamente profundizó en la cuestión, para el estudio del equilibrio y, sobre todo, intentando explicar mecánicamente (mecano-estadísticamente) la evolución termodinámica irreversible y la descripción de los procesos de transporte ligados a ella. Y, nuevamente (por su enorme importancia) no podemos dejar de mencionar la muy singular labor que hicieron Gibbs, Einstein, Planck, Fermi y otros. Sin la motivación ideológica de Boltzmann, Gibbs elaboró una bellísima, útil y hoy dominante formulación (cuerpo de doctrina) de la termodinámica y física estadística.
Lorentz
Fue Lorentz quien primero utilizó la ecuación de Boltzmann y lo hizo para describir la corriente eléctrica en sólidos dando un paso significativo por encima del pionero Drude. Lorentz introdujo un modelo opuesto al browniano donde partículas ligeras como viento (electrones) se mueven chocando entre sí y con árboles gordos (tales como iones en una red cristalina); un modelo del que se han hecho estudios de interés tanto físico como matemático. Enskog (inspirándose en Hilbert) y Chapman (inspirándose en Maxwell) enseñaron cómo integrar la ecuación de Boltzmann, abriendo vías a otras diversas aplicaciones (hidrodinámica, propagación del sonido, difusión másica, calor, fricción viscosa, termoelectricidad, etc.). Recordemos que Boltzmann encontró como solución de equilibrio de su ecuación una distribución de velocidades antes descubierta por Maxwell (hoy, como reseñé anteriormente, de Maxwell-Boltzmann), por lo que concluyó que así daba base microscópica mecánica (teorema H mecano-estadístico) al segundo principio de la termodinámica (estrictamente, evolución de un sistema aislado hacia su “desorden”máximo).
El físico austríaco Ludwig Boltzmann sentó las bases estadísticas de la entropía, su trabajo fue tan importante que el gran físico Max Planck sugirió que su versión de la fórmula de Boltzmann fuera grabada en la lápida de Boltzmann de Viena.
Está claro que ningún físico que se precie de serlo puede visitar Viena sin visitar el parque Zentralfriedhof para ver la tumba de Boltzmann. Yo sí me pasé por allí. Me senté junto a la tumba; el lugar estaba desierto, y cerrando los ojos traté de conectar con la conciencia del genio. La sensación, extraña y agradable, seguramente fue creada por mi imaginación, pero creo que charlé con él en el interior de mi mente – la fuerza más potente del universo– y aquellos sentimientos, aquel momento, compensaron el esfuerzo del viaje.
En la tumba, sobre una gran lápida de mármol de color blanco con los nombres Ludwig Boltzmann y de los familiares enterrados con él, sobre el busto de Boltzmann, se puede leer la inscripción, a modo de epitafio:
En esta breve ecuación se encierra la conexión entre el micromundo y el macromundo, y por ella se reconoce a Boltzmann como el padre de la rama de la física conocida como mecánica estadística. Esta sencilla ecuación es la mayor aportación de Boltzmann y una de las ecuaciones más importantes de la física. El significado de las tres letras que aparecen (aparte la notación del logaritmo) es el siguiente:
- S es la entropía de un sistema.
- W es el número de microestados posibles de sus partículas elementales.
- k es una constante de proporcionalidad que hoy recibe el nombre de Constante de Boltzmann, de valor 1’3805 × 10-23 J/K (si el logaritmo se toma en la base natural).
En definitiva, la ecuación describe la estrecha relación entre la entropía (S) y las miles de formas de partículas que en un sistema se pueden arreglar (k log W). La última parte es difícil. K es la constante de Boltzmann y W es el número de elementos microscópicos de un sistema (por ejemplo, el impulso y la posición de los átomos individuales de gas) en un sistema macroscópico en un estado de equilibrio (por ejemplo, el gas de sellado en una botella). Parece que la naturaleza ama el caos cuando empuja a los sistemas hacia el desequilibrio y Boltzmann le llamó entropía a este fenómeno.

Cuando profundizamos un poco en lo que el cerebro humano ha sido capaz de generar, los pensamientos que ha llegado a generar bien sea en forma de ecuaciones matemáticas o expresados con palabras, no podemos dejar de sorprendernos y maravillarnos al ver que, ¡todo el universo parece estar dentro de nuestras mentes! ¿Qué secretos se encierran allí? ¿Cómo nos lleva a estos pensamientos tan profundos?
Como todas las ecuaciones sencilla de gran trascendencia en la física (como la famosa E = mc2), hay un antes y un después de su formulación: sus consecuencias son de un calado tan profundo que cambiaron la forma de entender el mundo, y en particular, de hacer física a partir de ellas. De hecho, la sutileza de la ecuación es tal que hoy, cien años después de la muerte de su creador, se siguen investigando sus nada triviales consecuencias. Creo que lo mismo ocurrirá con α = 2πe2/ħc que, en tan reducido espacio y con tan pocos símbolos, encierra los misterios del electromagnetismo (el electrón), de la constante de Planck(la mecánica cuántica), y de la luz (la relatividad de Einstein), todo ello enterrado profundamente en las entrañas de un número: 137.
Bueno, a pesar de todo lo anterior, Schrödinger nos decía:
“La actitud científica ha de ser reconstruida, la ciencia ha de rehacerse de nuevo”

¡Lo grande y lo pequeño! ¡Son tantos los secretos de la Naturaleza! Pero no podemos olvidar que todo lo grande… ¡Está hecho de “cositas” pequeñas.
Siempre hemos tenido consciencia de que en física, había que buscar nuevos paradigmas, nuevos caminos que nos llevaran más lejos. Es bien conocida la anécdota de que a finales del siglo XIX un destacado físico de la época William Thomson (1824-1907) conocido como Lord Kelvin, se atrevió a decir que solo dos pequeñas “nubecillas” arrojaban sombras sobre el majestuoso panorama de conocimiento que había construido la física clásica desde Galileo y Newton hasta ese momento: el resultado del experimento de Michelson-Morley, el cual había fallado en detectar la existencia del supuesto éter luminífero; y la radiación del cuerpo negro, i.e la incapacidad de la teoría electromagnética clásica de predecir la distribución de la energía radiante emitida a diferentes frecuencias emitidas por un radiador idealizado llamado cuerpo negro. Lo que Lord Kelvin no puedo predecir es que al tratar de disipar esas dos “nubecillas”, la física se vería irremediablemente arrastrada a una nueva física: la física moderna fundada sobre dos revoluciones en ciernes: la revolución relativista y la revolución cuántica con dos científicos como protagonistas: Planck y Albert Einstein. Sin embargo, ha pasado un siglo y seguimos con esas dos únicas guías para continuar el camino y, resultan insuficientes para llegar a la meta que… ¡Está tan lejos!
emilio silvera
Feb
5
La Física relativista, la cuántica y… ¡El futuro!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (3)
Comments (3)
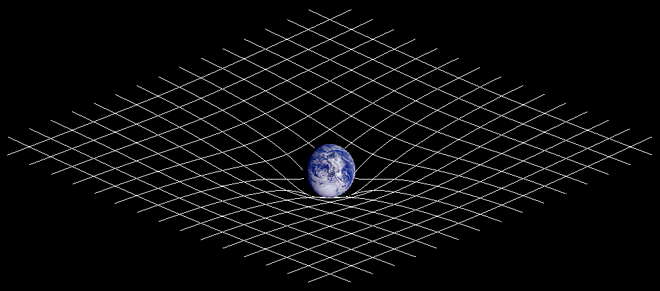
Esta es una analogía bidimensional de la distorsión del espacio-tiempo debido a un objeto de gran masa
Hay que entender que el espacio-tiempo es la única descripción en cuatro dimensiones del Universo en la que la posición de un objeto se especifica por tres coordenadas en el espacio y una en el tiempo. De acuerdo con la relatividad especial, no existe un tiempo absoluto que pueda ser medido con independencia del observador, de manera que sucesos simultáneos para un observador ocurren en instantes diferentes vistos desde otro lugar.
El tiempo puede ser medido, por tanto, de manera relativa, como los son las posiciones en el espacio tridimensional, y esto puede conseguirse mediante el concepto de espacio-tiempo. La trayectoria de un objeto en el espacio-tiempo se denomina por el nombre de línea de Universo. La relatividad general, nos explica lo que es un espacio-tiempo curvo con las posiciones y movimientos de las partículas de materia.

Presencia de materia y curvatura
La densidad de energía-momentum en la teoría de la relatividad se representa por cuadritensor energía-impulso. Las componentes de dicho tensor representan entre otras la densidad de energía y la densidad de momentum y dichas componentes están relacionadas localmente con las componentes del curvatura. La relación entre la presencia de materia y la curvatura debida a dicha materia viene dada por la ecuación de campo de Einstein:
Es una fuerza atractiva que en la comunidad científica actual es concebida como la pensó Einstein: como un efecto de la curvatura del espacio-tiempo en presencia de de objetos masivos y, cuanto más masa tenga el objeto más se curvará el espacio a su alrededor-
donde:
 , es el tensor de curvatura de Ricci
, es el tensor de curvatura de Ricci es el escalar de curvatura de Ricci
es el escalar de curvatura de Ricci , es el tensor de energía-impulso
, es el tensor de energía-impulso
Ejemplos
 Así, la curvatura del espacio tiempo es la propiedad del espacio-tiempo en la que las leyes familiares de la geometría no son aplicables en regiones donde los campos gravitatorios son intensos. La relatividadgeneral de Einstein, nos explica y demuestra que el espacio-tiempo está íntimamente relacionado con la distribución de materia en el Universo y, nos dice que, el espacio se curva en presencia de masas considerables como planetas, estrellas o Galaxias…
Así, la curvatura del espacio tiempo es la propiedad del espacio-tiempo en la que las leyes familiares de la geometría no son aplicables en regiones donde los campos gravitatorios son intensos. La relatividadgeneral de Einstein, nos explica y demuestra que el espacio-tiempo está íntimamente relacionado con la distribución de materia en el Universo y, nos dice que, el espacio se curva en presencia de masas considerables como planetas, estrellas o Galaxias…
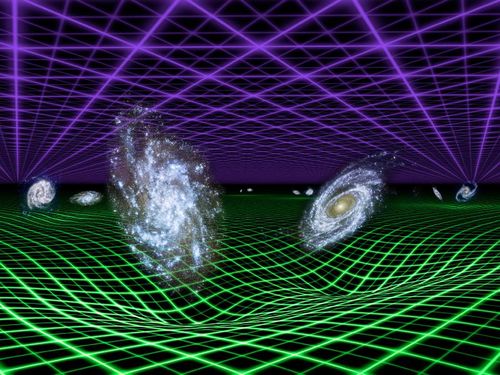
En realidad, es la presencia de la materia la que determina la geometría del espacio-tiempo
En un espacio de sólo dos dimensiones, como una lámina de goma plana, la geometría de Euclides se aplica de manera que la suma de los ángulos internos de un triángulo en la lámina es de 180º. Si colocamos un objeto masivo sobre la lámina de goma, la lámina se distorsionará y los caminos de los objetos que se muevan sobre ella se curvaran. Esto es en esencia, lo que ocurre en relatividad general.
Lo cierto es que, desde que llegó Einstein con sus versiones de la teoría relativista, muchas fueron las cosas que cambiaron y, nuestros conceptos del mundo…, también. Fenómenos que se crean en la naturaleza y que son la consecuencia de la presencia de masas o de velocidades muy grandes.
¡Los efectos de c -la velocidad de la luz en el espacio vacío-! Recordad la paradoja de los gemelos: Uno de ellos, que es astronauta, hace un viaje a la velocidad de la luz hasta Alfa de Centauri y regresa, cuando baja de la nave espacial, tiene 8,6 años más que cuando partió de la Tierra. Sin embargo, su hermano gemelo que le esperó en el planeta Tierra, era ya un anciano jubilado. El tiempo transcurrido había pasado más lento para el gemelo viajero. La velocidad ralentiza el transcurrir del tiempo.

El Universo es todo energía que se manifiesta de distintas maneras: bien como masa, o, bien como radiación
Otra curiosidad de la relatividad especial es la que expresó Einstein mediante su famosa fórmula de E= mc2 que, nos viene a decir que masa y energía son dos aspectos de una misma cosa. Podríamos considerar que la masa (materia), es energía congelada. Todos sabemos lo que ocurre cuando se desintegra un átomo de materia y la enorme cantidad de energía que tiene concentrada.
Hay otras implicaciones dentro de esta maravillosa teoría de la relatividad especial, ahí está presente también la contracción de Lorentz. Un objeto que se mueve a velocidad de cercana a c, se achata o contrae en el sentido de la marcha, y, además, a medida que se acerca a la velocidad de la luz (299.752,458 Km/s), su masa va aumentando y su velocidad disminuyendo.
Así se ha demostrado con muones en los aceleradores de particulas que, lanzados a verlocidades relativista, han alcanzado una masa en 10 veces superior a la suya. Esto quiere decir que la fuerza de inercia que se le está transmitiendo a una nave (por ejemplo), cuando se acerca a la velocidad de la luz, se convierte en masa.
Así queda demostrado que, masa y energía son dos aspectos de la misma cosa E=mc2. Pero no olvidemos que…
Todos hemos llegado a comprender que, todo lo grande está hecho de cosas pequeñas. Sin emnbargo hay cosas que aún no tenemos claras, y, un ejemplo de ello es, ¡El Hiperespacio!
Esta idea interesante ha sido utilizada en diversas teorías físicas prometedoras que han recurrido formalmente a la introducción de nuevas dimensiones formales para dar cuenta de fenómenos físicos. Así Kaluza y Klein trataron de crear una teoría unificada (clásica) de la gravedad y del electromagnetismo, introduciendo, a las cuatro dimensiones de la teoría relativista, una quinta dimensión adicional. En esta teoría la carga podía relacionarse con la quinta componente de la “pentavelocidad” de la partícula, y otra serie de cuestiones interesantes. El enfoque de varias teorías de supercuerdas es aún más ambicioso y se han empleado esquemas inspirados remotamente en la ideas de Einstein, Kaluza y Klein que llegan a emplear hasta diez y once dimensiones, de las cuales seis o siete estarían compactificadas y no serían detectables más que indirectamente.
Nuestra inmensa imaginación nos ha llevado a buscar teorías que no podemos comprobar de manera experimental y, dentro de esas teorías, están, o, pudieran estar, las claves para viajar a otras regiones del espacio muy distantes de la nuestra por ese medio que intuimos, que pudiera ser accesible para nosotros y que hemos llamado Hiperespacio, que estaría situado en la quinta dimensión.
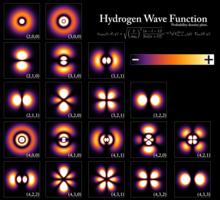

Mecánica cuántica, relatividad, átomos, el genóma, agujeros negros, la constante cosmológica, la constante de Planck racionalizada… Sabemos representar muchas otras cosas y estamos a la búsqueda de otras que intuimos como la “materia oscura”, o, ¿por qué no? la quinta dimensión y el hiperespacio. No cejamos en el desarrollo de la “imposible” teoría de cuerdas y también, buscamos bosones dadores de masa en un espacio profundo, de cuyo contenido sabemos poco y que el LHC encontró por nosotros sin saber muy bien de dónde vino y que “mundo” es ese en el que vive y que llaman océanos de Higgs.

Con los conocimientos de la mecánica cuántica que tenemos, hemos conseguido teletransportar las propiedades de la materia. Las películas de ciencia ficción -desde Star Trek hasta La Mosca- nos han mostrado un futuro donde las personas pueden teletransportarse sin problemas. Y aunque los científicos aún no logran transferir materia… Creo que, ¡todo se andará!

La teleportación cuántica no consiste en transportar instantáneamente objetos, sino de transferir el “estado” de una o varias partículas, los constituyentes íntimos de la materia, de un lugar a otro y sin necesidad de enviar físicamente la partícula a través del espacio. Este sorprendente logro es posible gracias al “entrelazamiento cuántico”, una extraña y aún poco comprendida propiedad de las partículas subatómicas que permite que dos -o más-, partículas unan sus destinos de tal forma que cualquier cambio de estado que se produzca en una de ellas se refleje de forma instantánea también en la otra, sin importar la distancia que las separe.No sabemos de qué manera, esas partículas permanecen “unidas” y la física clásica no puede darnos una explicación. Sin embargo, siendo conocedores de tal fenómeno, los científicos llevan veinte años intentando sacar rendimiento a esa realidad extraordinaria que nos envía la promesa de que, con ella, podemos traer una nueva revolución al campo de las comunicaciones por satélite, la informática y… ¿quién sabe qué más?
Sí, es cierto que, tanto la teletransportación de personas, como el viaje por el Hiperespacio es -todavía- cosa de la ciencia ficción pero… Acordaos de cuando Arthur Clarke nos hablaba de satélites que orbitaban la Tierra para recoger y enviarnos datos de alto interés en los diversos campos de la actividad humana. Aquello, parecía una fantasía y, sin embargo ahora, es lo cotidiano.


¿Quién puede decir ahora qué mundo futuro nos espera? Conforme a los conocimientos que actualmente tenemos, podemos intuir el devenir tecnológico que los avances de la ciencia nos pueden proporcionar y, entre los muchos que están ahí, en ese horizonte futuro, están todos estos de los que hablamos y, seguramente, muchos más que ni podemos imaginar. Seguramente, como también ahora mismo está pasando, no todos los aspectos de la tecnología futura nos gustarán.

La mejor manera de no equivocarse es tener la mente abierta a todo. Negar la existencia de universos paralelos, o, la certeza de la teoría de cuerdas…, ¿A dónde nos lleva? ¡A ninguna parte! Así pues, mantengamos la confianza en nosotros mismos, en lo que nuestras mentes llegan a intuir, y, dejémos, que nuestra “infinita” imaginación siga haciendo su trabajo y dibujando en nuestras mentes esos escenarios de mundos que podrían ser… ¡Una realidad futura!
emilio silvera
Feb
5
Cosas de la Física
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

¡La Física! Esa maravilla que está presente en todo lo que podemos ver y en aquello donde la vista no llega. La infinitud de las partículas elementales que forman todo cuanto existe en la Naturaleza, no siempre se dejan ver ni hacen posible que podamos observar las maravillas que pueden llevar a cabo,
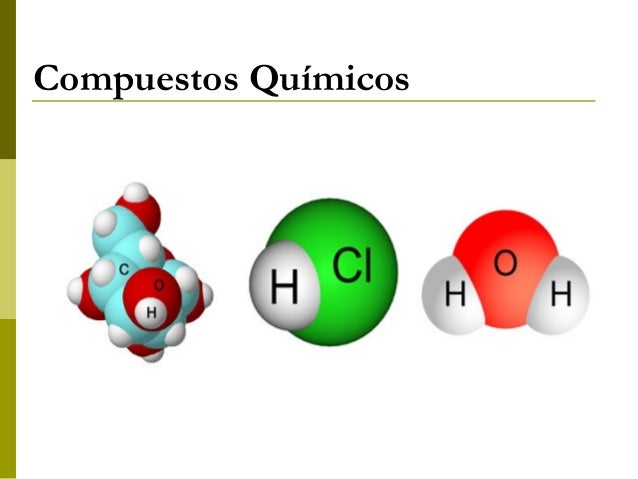
Las sustancias formadas por una sola clase de átomos se llaman elementos químicos, y, si está conformada por distintos átomos, son compuestos. La palabra “átomo” procede del griego ατομος, que significa “indivisible” y el uso de la palabra “elemento” sugiere que se ha llegado a los ladrillos básicos con los que está formada la materia. De hecho, esta es la imagen que se tenía a mediados del siglo XIX cuando se acuñaron estos términos. Sin embargo, hoy sabemos que todo esto es falso, que los átomos se pueden dividir y que, de esta manera, los elementos han dejado de ser verdaderamente elementales. Los físicos continúan con esta nomenclatura aunque sea formalmente incorrecta, ya que, la costumbre, como dicen los juristas, no pocas veces rigen la jerga de las leyes.
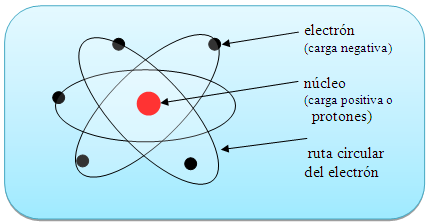
A todo esto y hablando de los átomos, por fuerza, nos tenemos que acordar del electrón que da al átomo su forma esférica. Son partículas cargadas eléctricamente que se mueven alegremente alrededor del núcleo. El electrón es muy ligero: su masa es solamente 1/1.8836 de la del núcleo más ligero (el hidrógeno). La carga eléctrica del electrón es de signo opuesto a la del núcleo, de manera que los electrones están fuertemente atraídos hacia el núcleo y se repelen mutuamente. Si la carga eléctrica total de los electrones en un átomo iguala a la del núcleo, para lo que generalmente se necesitan varios electrones, se dice que el átomo está en equilibrio o que es eléctricamente neutro.

Claro que, no debemos olvidarnos de que, ¡Todo lo grande está hecho de cosas pequeñas! Una inmensa galaxia se conforma de un conjunto inmenso de átomos inifinitesimales que juntos, hace ese gran todo.

La fuerza a la que obedecen los electrones, la denominada fuerza electrostática o de Coulomb, es matemáticamente bastante sencilla y, sin embargo, los electrones son los responsables de las importantes propiedades de los “enlaces químicos”. Esto se debe a que las leyes de movimiento de los electrones están regidas completamente por la “mecánica cuántica”, teoría que se completó a principios del siglo XX. Es una teoría paradójica y difícil de entender y explicar, pero al mismo tiempo es muy interesante, fantástica y revolucionaria. Cuando uno se introduce en las maravillas de la mecánica cuántica es como si hiciera un viaje a un universo que está situado fuera de este mundo nuestro, ya que, las cosas que allí se ven, desdicen todo lo que dicta nuestro sentido común de cómo tiene que ser el mundo que nos rodea.

La perfecta sincronía Está en la Naturaleza
No solamente los electrones, sino también los núcleos atómicos y los átomos en su conjunto obedecen y se rigen por la mecánica cuántica. La Física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck, escribió un artículo de ocho páginas y allí propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menos intensidad, por los objetos más fríos.

Estaban bien aceptados entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si usamos las leyes de la termodinámica para calcular la intensidad de la radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano, y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para las longitudes mayores como para las longitudes menores. Esta longitud característica es inversamente proporcional a la temperatura absoluta del objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273 ºC bajo cero). Cuando a 1.000 ºC un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.

Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de la onda y, por lo tanto, proporcional a la frecuencia de la radiación emitida. La sencilla fórmula es:
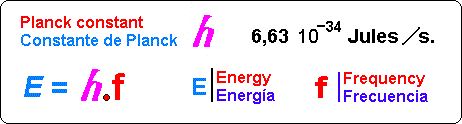
Donde E es la energía del paquete, v la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.

Los cuantos de energía están presentes en todos los objetos de materia que los emiten o absorben
Poco tiempo después, en 1905, Einstein formuló esta teoría de una forma mucho más tajante: el sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos de los paquetes de energía de Planck. El príncipe francés Louis-Victor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene una energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta región del espacio, y que la frecuencia, v, de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilatorias de campos de fuerza.

El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de De Broglie. Poco después, en 1926, Erwin Schrödinger descubrió como escribir la teoría ondulatoria de Debroglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños estaban exactamente determinados por la recién descubiertas “ecuaciones de onda cuánticas”.
Pocas dudas nos pueden caber a estas alturas de que la mecánica cuántica (de Planck) y, la Relatividad –tanto especial como general- (de Einstein), además de ser las dos teorías más importantes de la Física de nuestro tiempo, funcionan de tal forma que uno, cuando profundiza en sus predicciones y las compara con lo que ocurre en el Universo, no puede por menos que, asombrarse, al comprobar como unas mentes humanas han sido capaces de llegar a estos profundos pensamientos que nos acerca a la realidad de la Naturaleza.
emilio silvera
Feb
4
¿La Física? ¡Una maravilla! Nos dice cómo funciona la Naturaleza
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)
Ylia Prigogine ¡Qué personaje!
El Universo y la Vida… ¡Nuestra imaginación!
En su Libro Partículas, Gerard ´t Hofft, Premio Nobel de Física, nos cuenta:
“En el mundo de los seres vivos, la escala o tamaño crea importantes diferencias. En muchos aspectos, la anatomía de un ratón es una copia de la de un elefante, pero mientras que un ratón trepar por una pared prácticamente vertical sin mucha dificultad (y se puede caer desde una altura varias veces mayor que su propio tamaño sin hacerse daño), un elefante no sería capaz de realizar tal hazaña. Con bastante generalidad se puede afirmar que los efectos de la gravedad son menos importantes cuanto menores sean los objetos que consideremos (sean vivos o inanimados).”


Cuando llegamos a los seres unicelulares, se ve que ellos no hay distinción entre arriba y abajo. Para ellos, la tensión superficial del agua es mucho más importante que la fuerza de la gravedad a esa escala. Tranquilamente se pueden mover y desplazar por encima de una superficie acuática. Los pluricelulares no pueden hacer tal cosa.
Estas imágenes la hemos visto muchas veces en fuentes y charcos formados por la de la lluvia
La tensión superficial es una consecuencia de que todas las moléculas y los átomos se atraen unos a otros con una fuerza que nosotros llamamos de Van der Waals. fuerza tiene un alcance muy corto; para ser precisos, diremos que la intensidad de esta fuerza a una distancia r es aproximadamente 1/r7. Esto significa que si se reduce la distancia dos átomos a la mitad de la fuerza de Van der Waals con la que se atraen uno a otro se hace 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128 veces más intensa. Cuando los átomos y las moléculas se acercan mucho unos a otros quedan unidos muy fuertemente a través de esta fuerza. El conocimiento de esta fuerza se debe a Johannes Diderik Van der Waals (1837 – 1923) con su tesis sobre la continuidad del líquido y gaseoso que le haría famoso, ya que en esa época (1873), la existencia de las moléculas y los átomos no estaba completamente aceptado.
La tensión superficial del agua, es el efecto físico (energía de atracción entre las moléculas) que “endurece” la capa superficial del agua en reposo y permite a algunos insectos, como el mosquito y otros desplazarse por la superficie del agua sin hundirse.

El famoso físico inglés James Clerk Maxwell, que formuló la teoría del electromagnetismo de Faraday, quedó muy impresionado por este de Van der Waals.
Los tamaños de los seres unicelulares, animales y vegetales, se miden en micrómetros o “micras”, donde 1 micra es 1/1.000 de milímetro, aproximadamente el tamaño de los detalles más pequeños que se pueden observar con un microscopio ordinario. El mundo de los microbios es fascinante, pero no es el objeto de este trabajo, y continuaremos el viaje emprendido las partículas elementales que forman núcleos, átomos, células y materia, así como las fuerzas que intervienen en las interacciones fundamentales del universo y que afecta a todo lo que existe.

Hemos hablado del electrón que rodea el núcleo, de su carga eléctrica negativa que complementa la positiva de los protones y hace estable al átomo; una masa de solamente 1/1.836 de la del núcleo más ligero (el del hidrógeno). La importancia del electrón es vital en el universo.
Pero busquemos los “cuantos”. La física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menor intensidad, por los objetos más fríos (radiación de cuerpo negro).

Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si utilizamos las leyes de la termodinámica para calcular la intensidad de una radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano y, luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para menores. Esta longitud de onda característica es inversamente proporcional a la temperatura absoluta de objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273º bajo cero). Cuando a 1.000º C un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.
Radiación de Cuerpo Negro
Un cuerpo negro es un objeto teórico o ideal que absorbe toda la luz y toda la energía radiante que incide sobre él. Nada de la radiación incidente se refleja o pasa a través del cuerpo negro. A pesar de su , el cuerpo negro emite luz y constituye un modelo ideal físico para el estudio de la emisión de radiación electromagnética. El nombre Cuerpo negro fue introducido por Gustav Kirchhoff en 1862.

La luz emitida por un cuerpo negro se denomina radiación de cuerpo negro. Todo cuerpo emite energía en de ondas electromagnéticas, siendo esta radiación, que se emite incluso en el vacío, tanto más intensa cuando más elevada es la temperatura del emisor. La energía radiante emitida por un cuerpo a temperatura ambiente es escasa y corresponde a longitudes de onda superiores a las de la luz visible (es decir, de menor frecuencia). Al elevar la temperatura no sólo aumenta la energía emitida sino que lo hace a longitudes de onda más cortas; a esto se debe el cambio de color de un cuerpo cuando se calienta. Los cuerpos no emiten con igual intensidad a todas las frecuencias o longitudes de onda, sino que siguen la ley de Planck.
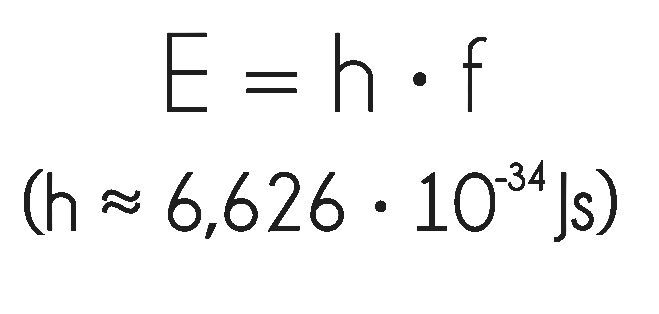
La onda electromagnética se puede entender como un grupo de “paquetes” ( cuantos) de muy poca energía que, juntos determinan la energía de la onda.
Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda, y por tanto, proporcional a la frecuencia de radiación emitida. La fórmula es E = h?, donde E es la energía del paquete, ? es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo nueva condición, el resultado coincidió perfectamente con las observaciones.
Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: él sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck. El príncipe francés Louis-Victor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene energía, sino que cualquier cosa con energía se debe comportar una “onda” que se extiende en una cierta región del espacio, y que la frecuencia ? de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilantes de campos de fuerza, esto lo veremos más adelante.
El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de de Broglie. Poco después, en 1926, Edwin Schrödinger descubrió cómo escribir la teoría ondulatoria de de Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de ondas cuánticas”.
Está bien comprobado que la mecánica cuántica funciona de maravilla…, pero, sin embargo, surge una pregunta muy formal: ¿qué significan realmente estas ecuaciones?, ¿qué es lo que están describiendo? Isaac Newton, allá en 1867 formuló cómo debían moverse los planetas alrededor del Sol, estaba claro todo el mundo qué significaban sus ecuaciones: que los planetas estaban siempre en una posición bien definida des espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades en el tiempo.
Pero los electrones todo es diferente. Su comportamiento parece estar envuelto en misterio. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?
Niels Bohr consiguió responder a esta pregunta de tal que con su explicación se pudo seguir trabajando, y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la interpretación de Copenhague de la mecánica cuántica.

Si la mecánica cuántica tiene cosas extrañas y el espín es una de ellas. Y si uno piensa que la intuición le ayudará a comprender todo esto, pues no lo hará, o es poco probable que lo haga. Las partículas tienen un espín fundamental. Al igual que la carga eléctrica o la masa, el espín ayuda a definir que de partícula es cada una.
Las leyes de la mecánica cuántica han sido establecidas con mucha precisión; permite cómo calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas de manera simultánea. Por ejemplo, podemos determinar la velocidad de una partícula con mucha precisión, pero entonces no sabremos exactamente dónde se encuentra; o a la inversa, podemos determinar la posición con precisión, pero entonces su velocidad queda mal definida. Si una partícula tiene espín (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.

La posición y el momento de una partícula nunca lo podremos saber con precisión ilimitada.
No es fácil explicar de forma sencilla de dónde viene esta incertidumbre, pero existen ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar. Para afinar un instrumento se debe escuchar una nota durante un cierto intervalo de tiempo y compararla, por ejemplo, con un diapasón que debe vibrar también durante un tiempo. Notas muy breves no tienen bien definido el tono.
Para que las reglas de la mecánica cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuando más grande y más pesado es un objeto, más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica. Me gustaría referirme a exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por holismo, y que podría definir como “el todo es más que la suma de sus partes”. Si la física nos ha enseñado algo es justo lo contrario. Un objeto compuesto de un gran de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (partículas); basta que sepamos sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes. Por ejemplo, la constante de Planck, h, que es igual a 6’626075… × 10-34 Julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.

La mecánica cuántica es muy extraña a nuestro “sentido común”, sabemos que se desenvuelve en ese “universo” de lo muy pequeño, alejado de nuestra vida cotidiana en el macrocosmos tetradimensional que, no siempre coincide con lo que, en aquel otro infinitesimal acontece.
Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisemberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros como Erwin Schrödinger siempre presentaron serias objeciones a interpretación. Quizá funcione bien, pero ¿dónde está exactamente el electrón?, ¿en el punto x o en el punto y? En pocas palabras, ¿dónde está en realidad?, y ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.
Es cierto que, existe otro universo dentro de nuestro del que, aún, nos queda mucho por aprender.

La mecánica cuántica puede ser definida o resumida así: en principio, con las leyes de la naturaleza que conocemos se puede predecir el resultado de cualquier experimento, en el sentido que la predicción consiste en dos factores: el primer factor es un cálculo definido con exactitud del efecto de las fuerzas y estructuras, tan riguroso como las leyes de Isaac Newton para el movimiento de los planetas en el Sistema Solar; el segundo factor es una arbitrariedad estadística e incontrolable definida matemáticamente de estricta. Las partículas seguirán una distribución de probabilidades dadas, primero de una forma y luego de otra. Las probabilidades se pueden calcular utilizando la ecuación de Schrödinger de función de onda (?) que, con muchas probabilidades nos indicará el lugar probable donde se encuentra una partícula en un dado.
Muchos estiman que esta teoría de las probabilidades desaparecerá cuando se consiga la teoría que explique, de forma completa, todas las fuerzas; la buscada teoría del todo, lo que implica que nuestra descripción actual incluye variables y fuerzas que (aún) no conocemos o no entendemos. Esta interpretación se conoce como hipótesis de las variables ocultas.”

También Gerard ‘t Hooft es el autor de lo que han dado en llamar l principio holográfico es una conjetura especulativa acerca de las teorías de la Gravedad Cuántica propuesta en 1993 por este autor, y mejorada y promovida por Leonard Susskin en 1995. Postula que toda la información contenida en cierto volumen de un espacio concreto se puede conocer a partir de la información codificable sobre la frontera de dicha región. Una importante consecuencia es que la cantidad máxima de información que puede contener una determinada región de espacio rodeada por una superficie diferenciable está limitada por el área total de dicha superficie.
Por ejemplo, se pueden modelar todos los eventos que ocurran en un cuarto o una habitación creando una teoría en la que sólo tome en cuenta lo que suceda en sus paredes. En el principio holográfico también se afirma que por cada cuatro Unidades de Planck existe al menos un grado de libertad (o una unidad constante de Bolttzmann k de máxima entropía). Esto se conoce como frontera de Bekenstein:
donde S es la entropía y A es la unidad de mensura considerada. En unidades convencionales la fórmula anterior se escribe:
donde:
 , es la constante de Boltzmann.
, es la constante de Boltzmann.
 , es la vecolcidad de la luz.
, es la vecolcidad de la luz.
 , es la constante gravitacional universal.
, es la constante gravitacional universal.
 , es la constante de Planck racionalizada.
, es la constante de Planck racionalizada. , es la longitud de Planck.
, es la longitud de Planck.
Claro que esta… ¡Es otra Historia!
emilio silvera
Feb
4
Viajando al Corazón de la Materia
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)


Después del Gran Colisionador de Hadrones (LHC) del CERN, situado en Suiza, otro gran experimento internacional promete sacudir la ciencia y nuestro conocimiento de la naturaleza. Hablamos de la Fuente Europea de Neutrones por Espalación (ESS, por sus siglas en inglés) un gran acelerador lineal de partículas que, como un poderoso microscopio, permitirá observar el interior de los materiales que componen nuestro mundo para así ser capaces de estudiar cómo se mueven e interactúan sus átomos por dentro y conocer los más variados fenómenos y propiedades donde nuestros ojos no llegan.

Tras un arduo período de selección del lugar de instalación del proyecto –en la que compitieron las ciudades de Bilbao y Debrecen (Hungría)–, la construcción comenzó en 2014. Las primeras pruebas están previstas para 2019 y, si todo sale como se espera, se empezará a trabajar a pleno rendimiento en 2025.
“Nuestra vida tecnológica cada vez depende más de la ciencia básica –señala a Sinc la bioquímica sueca Sindra Petersson Arsköld, que forma parte de los 400 investigadores del proyecto–. La ESS funcionará como un gran microscopio. Pero a diferencia de los microscopios convencionales no utilizará luz o lentes. Usaremos neutrones, partículas presentes en el núcleo del átomo, para ver a través de las cosas. Los neutrones atraviesan el metal como la luz atraviesa el cristal”.

Resultado de la imagen de la fuente europea de neutrones por Espalación (ESS)
Petersson comenta que “al poder estudiar como nunca las propiedades estructurales de la materia y sus dinámicos procesos internos, como los intercambios de energía, con este nuevo experimento podremos desarrollar baterías de litio más eficientes para los coches eléctricos. Además, se podrá mejorar el desarrollo de medicamentos y el funcionamiento de los trenes magnéticos. Y también podremos penetrar la piedra y ver dentro de huevos fosilizados de titanosaurios hallados en Mongolia sin necesidad de romperlos”, subraya.
Las instalaciones de la ESS ocuparán unas 10 hectáreas (equivalente a 14 canchas de fútbol). Actualmente, la construcción –cuyas obras ha tenido la oportunidad de visitar Sinc– está al 30%.
![[Img #45912]](http://noticiasdelaciencia.com/upload/img/periodico/img_45912.jpg)
Vista aérea del pasado mes de julio del estado de las obras de construcción de la Fuente Europea de Neutrones por Espalación en Lund (Suecia). (Foto: Perry Nordeng / ESS)
Caminar por su interior –con chaleco, casco, gafas y guantes protectores, después de haber suministrado datos personales y firmado una planilla por si sucede algún accidente– implica prestar atención a cada paso.
Por ejemplo, a lo largo del silencioso y por ahora vacío túnel subterráneo de 537 metros de largo por el que dentro de unos años circularán miles millones de protones generados por dos fuentes de iones. Acelerados por campos magnéticos al 96% de la velocidad de la luz, los pulsos de protones impactarán al final de su viaje por este túnel sobre un blanco, una rueda giratoria de tungsteno.
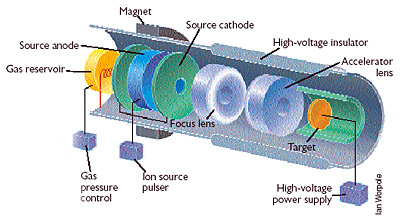
Será en estas colisiones en las que se producirá el proceso de espalación que le da el nombre a este proyecto: tras una reacción nuclear, por cada protón se generarán 30 neutrones, los verdaderos protagonistas de esta nueva ‘catedral’ de la ciencia moderna, que serán luego distribuidos en 16 instrumentos donde se analizarán las muestras.
“La tecnología necesaria para realizar estos experimentos es tan cara que varios países han tenido que unirse –detalla Petersson–. Suecia podría haberlo hecho sola pero hubiéramos tardado mucho más”.
A un coste de 1.843 millones de euros, no se trata de un proyecto de la UE sino de varios países europeos: 17 hasta el momento. Suecia y Dinamarca –los países anfitriones– pagan el 47,5 % de la construcción mientras que el resto de países que integran este consorcio –entre ellos Francia, Alemania, Italia, Reino Unido– se hace cargo del 52,5% restante. España fue el primer país socio de la ESS que firmó la carta oficial de intenciones en la que asumió un compromiso de aportar el 5% para su construcción.
La elección de Suecia como sede de la construcción de la ESS en mayo de 2009 significó una gran decepción para Bilbao, que desde 2006 anhelaba convertirse en un lugar de referencia en el mapa de la investigación y la ciencia.

Aun así, desempeña un rol importante: pese a una serie de recortes presupuestarios, en el centro estratégico de tecnologías neutrónicas ESS Bilbao (en Zamudio, Vizcaya), su plantilla de 60 trabajadores se encuentra diseñando y fabricando siete piezas clave de este proyecto: entre ellas una sección del acelerador (Medium Beam Energy Transport o MEBT), un gran espectrómetro llamado Miracles y en especial el ‘corazón’ de la ESS, el target o blanco de choque contra el que se dispararán los protones.
“El diseño desarrollado por ESS Bilbao consiste en unas 7.000 piezas de un material conocido como Wolframio colocados dentro de una rueda de 2,5 metros de diámetro, comenta a Sinc Sira Cordón, responsable de comunicación de este centro de investigación.

“La refrigeración del circuito será por gas helio. Los desarrollos de los trabajos evolucionan favorablemente –añade Cordón–. La comunidad científica española se verá beneficiada por las múltiples aplicaciones que la Fuente Europea de Neutrones por Espalación va a ofrecer para sus investigaciones con materiales en los más diversos sectores: desde el estudio de la eficacia de un detergente a la resistencia de materiales por ejemplo en transportes, la eficacia de las baterías, nuevas terapias contra el cáncer o dosificadores de medicamentos”.
Se espera además la visita de unos 2.000 científicos al año por lo que se está construyendo la Science Village Scandinavia, un pequeño pueblo de 17 hectáreas justo al lado de los límites de la instalación.
“Irónicamente, para visualizar los objetos más pequeños de la naturaleza necesitamos construir las instalaciones científicas más grandes del mundo, dice en un vídeo promocional el actor Patrick Stewart, el recordado capitán Picard de Star Trek y una de las caras famosas que buscan darle visibilidad al proyecto.
“ESS es el Hubble de la física de neutrones. Así como el telescopio espacial nos permite ver en las profundidades del espacio, con la ESS podremos explorar el espacio interior, abriendo una nueva frontera científica y tecnológica y conduciéndonos a descubrimientos que cambiarán la manera en que vemos nuestro mundo y que aún no somos capaces de imaginarnos”.

Aún sin haber comenzado a funcionar esta instalación ya ha deparado la primera gran sorpresa: el descubrimiento inesperado de un antiguo asentamiento de la Edad de Piedra, evidencia de que la gente ha estado viviendo en esta zona de Escandinavia más tiempo de lo que se creía anteriormente.
Durante el otoño de 2013, unos meses antes de la colocación de la primera piedra, 40 arqueólogos rastrillaron el amplio terreno deshabitado de unos 100.000 metros cuadrados, al noreste de Lund. Con paciencia, los investigadores del Museo de Historia Sueca inspeccionaron cada afloramiento que llamaba su atención.
El pasado no tardó en resurgir: como cuenta el director del proyecto, Magnus Andersson, encontraron restos de los primeros granjeros que habitaron el sur de Suecia entre los años 4000 y 3300 a.C. “Durante la excavación, pudimos discernir las huellas de dos casas de unos 13 metros de largo por seis de ancho –señala el arqueólogo–. Una sobre la otra, indicación de que no existieron al mismo tiempo”.
Los investigadores sospechan que varias generaciones habitaron en estas granjas. Cerca de estas cabañas redondas u ovaladas con una chimenea en el centro se encontraron también restos de unas 14 pequeñas chozas, miles de granos carbonizados –en especial cebada–, huesos de ganado, ovejas, cerdos y ciervos, un cementerio y fragmentos de cerámica con trazas de productos lácteos.

En este sitio, los arqueólogos hallaron también huellas de personas que vivieron en otro período posterior, durante la Edad de Hierro: restos de casas de madera, pozos y unos diez hornos. El asentamiento al parecer tuvo varios ocupantes porque hay indicaciones de que estuvo ocupado entre los años 500 a.C. hasta la era de los Vikingos, alrededor del 1050.
También encontraron unas 12 tumbas pero debido a las duras condiciones de conservación del suelo no se pudo recuperar mucho salvo dientes, anillos de oro y collares con cuentas de ámbar.
Los arqueólogos cuentan los días. Están ansiosos: desean que la construcción de la ESS termine lo antes posible para que todos estos tesoros recolectados y prolijamente catalogados, en especial los granos de hace casi 6.000 años, sean analizados por este súpermicroscopio nórdico, el futuro gigante de la ciencia europea. (Fuente: SINC)
















 Totales: 83.428.775
Totales: 83.428.775 Conectados: 35
Conectados: 35