Subir Sachdev

“Hace algunos años me hallé a mi mismo en un lugar completamente inesperado: una conferencia sobre teoría de cuerdas. Mi campo de investigación es la materia condensada, el estudio de materiales como metales y superconductores a tewmperaturas próximas al cero absoluto. disciplina se halla todo lo lejos de la teoría de cuerdas como podría estarlo sin salirse de la física. La Teoría de cuerdas intenta describir la Naturaleza a energía muhco mayores a las que puedan alcanzarse en los laboratorios terrestres o, de hecho, en cualquier lugar del universo conocido. Quines a ella se dedican estudian las exóticas leyes que gobiernan los agujeros negros y postulan que el universo posee otras dimensiones espaciales, además de las tres que podemos ver. ellos, la Gravedad constituye la interacción dominante de la Naturaleza. Para mí, no desempaña ningún papel.”

La mecánica cuántica fue desarrollada en el siglo XX describir el movimiento de un electrón en un átomo de hidrógeno. Más tarde, Einstein y otros señalaron que la teoría cuántica de un par de electrones no tenía funciones intuitivas que encontraron difícil de aceptar: dos separatedelectrons bien pueden tener sus estados cuánticos “enredado”, indicando que hablan el uno al otro la mecánica cuántica, incluso a pesar de que están muy separados. Hoy en día, el entrelazamiento cuántico no es visto como un sutil efecto microscópico de interés sólo unos pocos físicos, sino como un ingrediente crucial necesaria para una comprensión completa de las muchas fases de la materia. Un cristal puede tener unos billones de billones de electrones entrelazados unos con otros, y los diferentes patrones de entrelazamiento conducir a fases que son imanes, metales, o superconductores. Voy a dar una simple discusión de estas y otras características notables de la mecánica cuántica de un trillón de trillones de electrones, y de su importancia para una variedad de materiales tecnológicamente importantes. La teoría también tiene conexiones sorprendentes e inesperados a la teoría de cuerdas: notablemente, esto se conecta el movimiento de los electrones dentro de un plano de un cristal en el laboratorio, a la teoría de los agujeros negros astrofísicos similares a los estudiados por Chandrasekhar

Si hay algo que le gusta a la ciencia es estudiar los extremos de la naturaleza, incluso a veces forzarlos un poco. Cada vez construimos telescopios ver más lejos, naves para viajar más rápido, combustibles de mayor rendimiento, etc. Y uno de los aspectos de la naturaleza que no se escapa de está búsqueda de los límites extremos es la temperatura.

Efectivamente, porque en el año 1997 el premio Nobel de física fue a parar a tres investigadores: Steven Chu (Universidad de Standford, California), Claude Cohen (Collage de France and Ecole Normale, Paris) y william D. Phillips (National Institute of Standards an Technology, Maryland), por el desarrollo de técnicas para lograr las temperaturas más bajas jamás alcanzadas.

Esta investigación abrió la puerta a todo un campo de investigación. Gracias a ella estamos conociendo mejor la estructura más íntima de la materia, y lo que es más importante comenzando a controlarla.

Vórtices cuánticos en un condensado rotante de átomos de sodio. Pero sigamos con el Profesor Sachdev que, nos sigue contando:

“Estas diferencias entre los físicos de cuerdas y los de la materia condensada, se plasman en un abismo cultural. Los investigadores de teorías de cuerdas gozán de una excelente reputación, por lo que asistí a aquella conferencia con un temor casi reverencial a su pericia matemática. Había invertido meses en la lectura de artículos y libros sobre el tema, a menudo quedándome empantanado. Estsaba seguro de que sería rechazado como un advenedizo ignorante. Por su parte, los teóricos de cuerdas tenían dificultades con algunos de los conceptos más simples de mi campo. Llegué a verme dibujando esquemas que con anterioridad solo había empleado con mis estudiantes de doctorado primerizos.

Varios científicos encabezados por el físico de Oxford Ian Walmsley han conseguido relacionar y vibrar a dos diamantes en el proceso conocido como entrelazamiento cuántico. El misterioso proceso, al que el propio Eisntein no supo darle comprensión completa, supone el mayor avance hasta la y abre las puertas de la computación cuántica.

Así pues, ¿porque había asistido? Durante los últimos años, los expertos en materia condensada hemos observado que algunos materiales pueden comportarse de un modo que hasta juzgábamos imposible.  Se trata de fases marcadamente cuánticas de la materia cuya estructura se caracteriza por la aparición de uno de los fenómenos más chocantes de la naturaleza: el entrelazamiento cuántico. En un célebre artículo escrito en 1935, Albert Einstein, Boris Podolski y Nathan Rosen señalaron que la teoría cuántica implicaba  la existencia de ciertas conexiones “espeluzmantes” entre partículas. Cuando aparecen, las partículas se coordinan sin que haya entre ellas una acción física directa. Einstein y sus colaboradores consideraron el caso de dos electrones, pero un metal o un superconductor contienen muchísimos más: del orden de 10²³, en una muestra de laboratorio típica. La complejidad que exhiben algunos materiales resulta sobrecogedora, y a ella he dedicado gran parte de mi carrera. Pero el problema no se reduce a lo meramente académico:

    Se con superconductores de baja y de alta temperatura. Bueno, al menos se está intentando saber más de ambos métodos. Los superconductores revisten una enorme importancia técnica, por lo que se han dedicado ingentes esfuerzos a entender sus propiedades y su potencial.

Hace unos años descubrimos que la Teoría de cuerdas nos brindaba una manera completamnete inesperada de enfocar el problema. En su camino una formulación que unifique las interacciones cuánticas entre partículas y la Teoría de la Gravedad de Einstein, los físicos de cuerdas se han topado con lo que ellos denominan “dualidades”: relaciones ocultas entre áreas de la física muy apartadas entre sí. Las dualidades que nos interesan relacionan dos tipos de teorías: por un lado, las que funcionan bien cuando los fenómenos cuánticos no resultan significativos pero la gravedad es muy intensa; por otro lado, aquellas que describen efectos cuánticos fuertes en situaciones con campos gravitatorios débiles [vease “El Espacio, ¿una ilusión”, por Juan Maldacena; Investigación y Ciencia, enero 2006]. equivalencia permite traducir los hallazgos hallados en un campo al otro. Gracias a ella, descubrimos que podíamos expresar nuestras preguntas sobre el entrelazamiento en términos de un problema gravitatorio para, después, servirnos de los descubrimientos que los físicos de cuerdas habían realizado sobre las matemáticas de los agujeros negros. Un ejemplo de epnsamiento refinado al máximo.

                                                                        Fases Ocultas

Para entender ese círculo de ideas debemos volver por un momento a la física del bachillerato. Según esta, las fases de la materia corresponden a los estados sólidos, líquido y gaseoso. Un sólido posee tamaño y fijos; un líquido toma la forma del recipiente que lo contiene;, aunque se parecen en este último aspecto a los líquidos, pueden alterar su volumen con facilidad. Aunque se trata de conceptos simples, hasta principios del siglo XX carecíamos de un entendimiento preciso de las fases de la materia. Los átomos se disponen de manera ordenada en los sólidos cristalinos, pero pueden moverse en líquidos y gases.

Sin embargo, las tres fases anteriores no bastan en absoluto describir todos los aspectos de la materia. Un sólido no se compone solo de una red de átomos, sino también de un emjanbre de electrones. átomo libera unos pocos electrones que pueden pulular por todo el cristal. Cuando conectamos una bateria a un pedazo de metal, la corriente eléctrica fluye por él.

Casi todos los metales obedecen la ley de Ohm: la intensidad de la corriente es igual al voltaje aplicado dividido por la resistencia del material. Los aislantes, como el teflón, presentan una resistencia muy elevada; en los metales, la resistencia es baja. Los superconductores destacan por poseer una resistencia inconmensurablemente pequeña. En 1911, Helke Kamerlingh Onnes descubrió el fenómeno al refrigerar mercurio sólido a 4 grtados Kelvin (269 grados Celcius bajo cero). Hoy conocemos materiales en los que la superconductividad aparece a temperaturas mucho mayores ( 138 grados Celcius bajo cero).

Aunque tal vez no resulte obvio, aislantes y superconductores representan fases diferentes de la materia. El enjambre de electrones que los caracteriza adquiere en cada caso propiedades distintas. Durante las dos últimas décadas, hemos descubierto que los sólidos poseen fases electrónicas adicionales. Entre ellas, una especialmente interesante que, de tan insólita, ni siquiera tiene : los físicos hemos dado en llamarla “metal extraño”. Se caracteriza por una dependencia inusual entre su resistencia eléctrica y su temperatura.”

Durante décadas, los físicos han tratando de conciliar las dos teorías principales que describen el comportamiento físico. La primera, la teoría de Einstein de la relatividad general, utiliza la gravedad – Las fuerzas de atracción – explicar el comportamiento de los objetos con masas grandes, tales como la caída de los árboles o los planetas en órbita. Sin embargo, a nivel atómico y subatómico, las partículas con masas despreciables se describen mejor con otra teoría: la mecánica cuántica.

Una “teoría del todo” que unificara a la relatividad general con la mecánica cuántica abarcaría todas las interacciones físicas, sin importar el tamaño del objeto. Uno de los candidatos más populares una teoría unificada es la teoría de cuerdas, desarrollada por primera vez a finales de 1960 y principios de 1970.

La teoría de cuerdas explica que los electrones y los quarks (los bloques de construcción de las partículas más grandes) son cadenas unidimensionales oscilantes, no objetos sin dimensiones como tradicionalmente se pensaba.

Los físicos están divididos sobre si la teoría de cuerdas es una teoría viable del todo, pero muchos están de acuerdo que ofrece una nueva manera de mirar a los fenómenos físicos que han demostrado ser de otro modo difíciles de describir. En la última década, los físicos han usado la teoría de cuerdas construir una conexión entre la gravedad y la mecánica cuántica, conocida como “Gauge / dualidad gravedad”.

Hace unos 20 años que los científicos encontraron un inexplicable vacío en la estructura electrónica de ciertos supeconductores de alta temperatura. , una nueva investigación realizada por un equipo liderado por el físico Zhi-Xun Shen podría haber descubierto las razones de este misterio: la brecha podría evidenciar la existencia de un nuevo estado de la materia. El descubrimiento podría servir para conseguir materiales que presenten superconductividad a temperatura ambiente, algo que seguramente cambiaría nuestras vidas.

Es posible que uno de los misterios más antiguos que poseen los materiales superconductores haya sido resuelto. Desde hace unos 20 años que los científicos saben que, a determinadas temperaturas, los materiales superconductores presentan un vacío inexplicable en sus estructuras electrónicas. Este fenómeno podría ser explicado por la presencia de un nuevo -previamente desconocido- de la materia. O al menos, esta conclusión es a la que ha llegado un equipo de científicos liderado por el físico Zhi-Xun Shen, del Instituto de Stanford para la Ciencia de los materiales y energía (SIMES), que es una empresa conjunta del Departamento de energía (DOE) SLAC National Accelerator Laboratory y la Universidad de Stanford.

Zhi-Xun Shen está convencido que este proporciona la más fuerte evidencia encontrada hasta la fecha de la existencia de un nuevo estado de la materia. Además, la investigación podría brindar las claves necesarias para lograr materiales superconductores capaces de funcionar a temperatura ambiente.

                Zhi-Xun Shen

Los supeconductores no presentan resistencia al paso de la energía eléctrica, permitiendo la construcción de electroimanes extremadamente potentes, como los utilizados en trenes de levitación magnética o aceleradores de partículas como el LHC. Sin embargo, estos materiales solo mantienen sus propiedades a temperaturas muy bajas, a menudo cercanas al cero absoluto. Los detalles del trabajo de Zhi-Xun Shen fueron publicados en el 25 de marzo de la revista Science, y en él se destaca que uno de los obstáculos más importante que impiden el desarrollo de superconductores a altas temperaturas es el hecho de que aún los que poseen esa propiedad a temperaturas bastante mayores que cero absoluto deben ser refrigerados a mitad de camino a 0 grados Kelvin antes de que funcionen. Conseguir que un material presenten superconductividad a temperatura ambiente sin necesidad de enfriamiento previo haría posible la distribución de electricidad sin pérdidas y muchos otros adelantos que, en conjunto, cambiarían nuestras vidas.

los principios físicos de la superconductividad no se comprendieron hasta 1957, cuando los físicos estadounidenses John Bardeen, Leon N. Cooper y John R. Schrieffer propusieron una teoría que se conoce como teoría BCS por las iniciales de sus apellidos, y por la que sus autores recibieron el Premio Nobel de Física en 1972. La teoría BCS describe la superconductividad como un fenómeno cuántico, en el que los electrones de conducción se desplazan en pares, que no muestran resistencia eléctrica. teoría explicaba satisfactoriamente la superconducción a altas temperaturas en los metales, pero no en los materiales cerámicos. En 1962, el físico británico Brian Josephson estudió la naturaleza cuántica de la superconductividad y predijo la existencia de oscilaciones en la corriente eléctrica que fluye a través de dos superconductores separados por una delgada capa aislante en un campo eléctrico o magnético. Este fenómeno, conocido como efecto Josephson, fue posteriormente confirmado experimentalmente.

Los científicos han usado electroimanes para generar campos magnéticos hace mucho tiempo. Haciendo fluir corriente eléctrica por un anillo conductor se induce campo magnético. Sustituyendo el conductor por un superconductor y enfriándolo a la temperatura necesaria, podría ser posible generar campos magnéticos mucho mas potentes debido a la falta de resistencia, y por tanto de generación de calor en el anillo. Sin embargo, esto no pudo hacerse en un principio. Cuando el campo magnético alcanzaba una determinada intensidad, el superconductor perdía sus propiedades y se comportaba como un conductor ordinario. Hasta la década de los cuarenta no se resolvieron los problemas de los campos magnéticos y solo muy recientemente se ha superado el problema de las bajas temperaturas.

John Bardeen, Leon N. Cooper y John R. Schrieffer

Otras veces hemos explicado aquí que los Bosones no obedecen al Principio de exclusión de Pauli, por lo que todos los pares de electrones de un superconductor pueden englobarse en el de mínima energía, lo que da lugar a un fenómeno conocido como condensación de Bose-Eintein. Vendría a ser como verter agua en un vaso y observar que, en vez de llenarse, se forma una fina capa de hielo en el fondo que absorbe tanta agua como tenemos sin aumentar su espesor.

Si a un material de tales características le aplicamos un voltaje, veremos que promociona los pares de electrones hacia un que posee una diminuta cantidad de energía adicional, con lo que se genera una corriente eléctrica. Dicho estado de energía superior se encuentra por lo demás vacío, por lo que nada impide el flujo de pares y el superconductor transmite la corriente sin oponer resistencia.

Puntos Críticos

A principio de los ochenta, el éxito de la mecánica cuántica a la hora de explicar las propiedades de los metales, aislantes, superconductores y otros materiales, como los semiconductores (la base de la electrónica moderna) generó -la engañosa- sensación de que ya no quedaban grandes descubrimientos que . Esa convicción se vino abajo cuando aparecieron los superconductores de altas temperaturas.

Un ejemplo nos lo proporciona el arseniuro de hierro y bario cuando una fracción del arsénico ha sido reemplazada por fósforo.  A bajas temperaturas este material se comporta como un superconductor. Se cree que obedece a una teoría similar a la propuesta por BCS, pero en la que los pares de electrones no se crean por las vibraciones de la red cristalina, sino por efectos debidos a la física del espín.

Seguir ahondando en este tema de la superconductividad, nos llevaría muy lejos hasta comprobar, que no conocemos esencialmente lo que la materia es y, lo que de ella podemos espewrar en circunstancias especiales. Nada es lo que parece a primera vista y, cuando conozcamos bien ese mundo extraño y misterioso que llamamos mecánica cuántica… ¿Qué podremos encontrar? Seguramente, allí estarán esos fantásticos y maravillosos “mundos” largamente buscados por los físicos y en los que, ¡Oh! ¡sorpresa! aparecerán las predicciones de la Teoría de cuerdas a la que no podemos llegar por no disponer de la energía necesaria.

El trabajo tiene varias fuentes pero, de manera muy especial, señaló aquí la Revista Investigación y ciencia en su artículo sobre el reportaje de  Subir Sachdev que, entre otros recogidos al azar, conforman el presente trabajo que, de mi parte, contiene sólo algunos apuntes que tratan de conexionar el conjunto.

Publica: emilio silvera

[?]

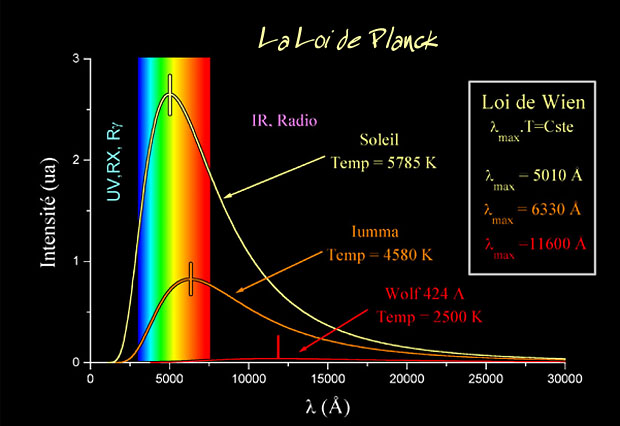
La Física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menos intensidad, por los objetos más fríos.

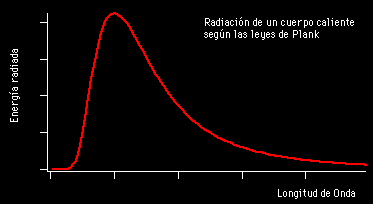
 La expresión radiación se refiere a la emisión continua de energía de la superficie de todos los cuerpos. Los portadores de esta energía son las ondas electromagnéticas  producidas por las vibraciones de las partículas cargadas  que forman parte de los átomos y moléculas de la materia. La radiación electromagnética que se produce a causa del movimiento térmico de los átomos y moléculas de la sustancia se denomina radiación térmica o de temperatura.

 Ley de Planck para cuerpos a diferentes temperaturas.

Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía.

Pero si usamos las leyes de la termodinámica para calcular la intensidad de la radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano, y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico o una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para longitudes menores. Esta longitud característica es inversamente proporcional a la temperatura absoluta del objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273 ºC bajo cero). Cuando a 1.000 ºC un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de la luz visible.

            Acero al  “rojo vivo”, el objeto está radiando en la zona de la luz visible.

Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda y, por lo tanto, proporcional a la frecuencia de la radiación emitida. La sencilla fórmula es:

E = hv

Donde E es la energía del paquete, v es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.

Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: el sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck.

El príncipe francés Louis Victor de Broglie, dándole otra vuelta a la teoría, que no sólo cualquier cosa que oscila tiene una energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta dirección del espacio, y que la frecuencia, v, de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilatorias de campos de fuerza.

Es curioso el comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de De Broglie. Poco después, en 1926, Edwin Schrödinger descubrió como escribir la teoría ondulatoria de De Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar los cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de onda cuántica”.

No hay duda de que la Mecánica Cuántica funciona maravillosamente bien. Sin embargo, surge una pregunta muy formal: ¿qué significan realmente esas ecuaciones?, ¿qué es lo que están describiendo? Cuando Isaac Newton, allá por el año 1687, formuló cómo debían moverse los planetas alrededor del Sol, estaba claro para todo el mundo lo que significaban sus ecuaciones: que los planetas están siempre en una posición bien definida en el espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades con el tiempo.

Pero para los electrones todo esto es muy diferente. Su comportamiento parece estar envuelto en la bruma. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?

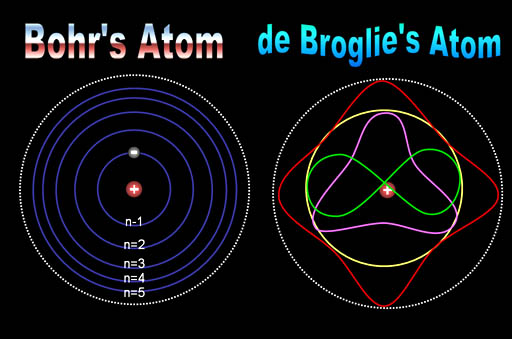
Niels Bohr consiguió responder a esta pregunta de forma tal que con su explicación se pudo seguir trabajando y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la “interpretación de Copenhague” de la Mecánica Cuántica. En vez de decir que el electrón se encuentra en el punto x o en el punto y, nosotros hablamos del estado del electrón. Ahora no tenemos el estado “x” o el estado “y”, sino estados “parcialmente x” o “parcialmente y. Un único electrón puede encontrarse, por lo tanto, en varios lugares simultáneamente. Precisamente lo que nos dice la Mecánica Cuántica es como cambia el estado del electrón según transcurre el tiempo.

Un “detector” es un aparato con el cual se puede determinar si una partícula está o no presente en algún lugar pero, si una partícula se encuentra con el detector su estado se verá perturbado, de manera que sólo podemos utilizarlo si no queremos estudiar la evolución posterior del estado de la partícula. Si conocemos cuál es el estado, podemos calcular la probabilidad de que el detector registre la partícula en el punto x.

Las leyes de la Mecánica Cuántica se han formulado con mucha precisión. Sabemos exactamente como calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas simultáneamente. Por ejemplo, podemos determinar la velocidad de una partícula con mucha exactitud, pero entonces no sabremos exactamente dónde se encuentra; o, a la inversa. Si una partícula tiene “espín” (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.

No es fácil explicar con sencillez de dónde viene esta incertidumbre, pero hay ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar.

           ¿Onda o partícula? ¡Ambas a la vez! ¿Cómo es eso?

Para que las reglas de la Mecánica Cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuanto más grande y más pesado es un objeto más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica.

Me gustaría referirme a esta exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por “holismo”, y que se podría definir como “el todo es más que la suma de las partes”.

Bien, si la Física nos ha enseñado algo, es justamente lo contrario: un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (las partículas): basta que uno sepa sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que yo entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes.

Por ejemplo, la constante de Planck, h = 6,626075…x 10 exp. -34 julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.

Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisenberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros tales como Edwin Schrödinger, siempre presentaron serias objeciones a esta interpretación.

Quizá funcione bien, pero ¿dónde está exactamente el electrón, en el punto x o en el punto y? Em pocas palabras, ¿dónde está en realidad?, ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.

Hasta hoy, muchos investigadores coinciden con la actitud pragmática de Bohr. Los libros de historia dicen que Bohr demostró que Einstein estaba equivocado. Pero no son pocos,  incluyéndome a mí, los que sospechamos que a largo plazo el punto de vista de Einstein volverá: que falta algo en la interpretación de Copenhague. Las objeciones originales de Einstein pueden superarse, pero aún surgen problemas cuando uno trata de formular la mecánica cuántica para todo el Universo (donde las medidas no se pueden repetir) y cuando se trata de reconciliar las leyes de la mecánica cuántica con las de la Gravitación… ¡Infinitos!

La mecánica cuántica y sus secretos han dado lugar a grandes controversias, y la cantidad de disparates que ha sugerido es tan grande que los físicos serios ni siquiera sabrían por donde empezar a refutarlos. Algunos dicen que “la vida sobre la Tierra comenzó con un salto cuántico”, que el “libre albedrío” y la “conciencia” se deben a la mecánica cuántica: incluso fenómenos paranormales han sido descritos como efectos mecanocuánticos.

Yo sospecho que todo esto es un intento de atribuir fenómenos “ininteligibles” a causas también “ininteligibles” (como la mecánica cuántica) dónde el resultado de cualquier cálculo es siempre una probabilidad, nunca una certeza.

Claro que, ahí están esas teorías más avanzadas y modernas que vienen abriendo los nuevos caminos de la Física y que, a mi no me cabe la menor duda, más tarde o más temprano, podrá explicar con claridad esas zonas de oscuridad que ahora tienen algunas teorías y que Einstein señalaba con acierto.

¿No es curioso que, cuando se formula la moderna Teoría M, surjan, como por encanto, las ecuaciones de Einstein de la Relatividad General? ¿Por qué están ahí? ¿Quiere eso decir que la Teoría de Einstein y la Mecánica Cuántica podrán al fin unirse en pacifico matrimonio sin que aparezcan los dichosos infinitos?

Bueno, eso será el origen de otro comentario que también, cualquier día de estos, dejaré aquí para todos ustedes.

emilio silvera

[?]

Especulan con que un ruido en un interferómetro para la detección de ondas gravitacionales sea debido a un efecto del principio holográfico que amplificaría la escala de Planck del espacio-tiempo.

Hace ya unos cincuenta años Wheeler propuso la existencia de la “espuma cuántica”. Según él el espacio-tiempo a la escala de Planck debería de tener una textura de tal modo que las fronteras entre izquierda-derecha, arriba-abajo o pasado-futuro estarían desdibujadas. El espacio presentaría “montañas”, “valles” e incluso agujeros de gusano cambiantes en el tiempo a esa escala del orden de 10^-35 m. Pero esta idea especulativa no ha producido modelos concretos y cuantitativos sobre este espacio-tiempo a esas escalas diminutas. La razón es que esta predicción proviene de la idea de juntar la Relatividad General, que explica la gravedad a través de la geometría del espacio-tiempo, con los principios de la Mecánica Cuántica, que trata los sistemas pequeños que son definidos por sus funciones de onda, y hasta ahora no contamos con una teoría cuántica de la gravedad válida y terminada que funcione. Contamos, eso sí con varios candidatos aún en desarrollo que pretenden hacerlo: gravedad cuántica de lazos, triangulación causal dinámica, e incluso la teoría de cuerdas entre otras aún más exóticas.

Las primeras dos proporcionan cierta idea sobre esta espuma cuántica. La última asume un espacio-tiempo fijo cuatrimensional sobre el cual a cada punto se le asocia un complicada geometría multidimensional compacta.

Tampoco hay esperanzas de observar esta “espuma cuántica” con los actuales o futuros aceleradores de partículas, porque se daría a una escala tan pequeña que, en la práctica, es imposible de alcanzar la energía necesaria para ello.

[?]

Llegará un día en el que, podremos entrar en una inmensa habitación en la que, previa elección de la  programación adecuada, todo se transformará en un “mundo fisciticio” que, lo mismo podrá ser una playa luminosa con arena dorada por el un Sol que, una Selva tropical o un desierto, dependiendo de los gustos del usuario.

Si repasamos la historia de la ciencia, seguramente encontraremos muchos motivos para el optimismo. Witten (el Físico de la Teoría M),  está convencido de que la ciencia será algún día capaz de sondear hasta las energías de Planck. Como ya he contado en otras ocasiones, él dijo:

“No siempre es tan fácil decir cuáles son las preguntas fáciles y cuáles las difíciles. En el siglo XIX, la pregunta de por qué el agua hierve a 100 grados era desesperadamente inaccesible. Si usted hubiera dicho a un físico del siglo XIX que hacia el siglo XX sería capaz de calcularlo, le habría parecido un cuento de hadas… La teoría cuántica de campos es tan difícil que nadie la creyó completamente durante 25 años.”

En su opinión, las buenas ideas siempre se verifican. Los ejemplos son innumerables: la gravedad de Newton, el campo eléctrico de Faraday y el electromagnetismo de Maxwell, la teoría de la relatividad de Einstein en sus dos versiones y su demostración del efecto fotoeléctrico, la teoría del electrón de Paul Dirac, el principio de incertidumbre de Heisenberg, la función de ondas de Schrödinger, y tantos otros. Algunos de los físicos teóricos más famosos, sin embargo, protestaban de tanto empeño en la experimentación. El astrónomo arthur Eddington se cuestionaba incluso si los científicos no estaban forzando las cosas cuando insistían en que todo debería ser verificado.

Sin embargo, muchos son los ejemplos de un ingenio superior que nos llevaron a desvelar secretos de la Naturaleza que estaban profundamente escondidos, y, el trabajo de Dirac en relación al electrón, es una buena miuestra de ese ingenio humano que, de vez en cuando vemos florecer.

Siendo m la masa en reposo del electrón, c la velocidad de la luz,  p el operador de momento, la constante reducida de Planck,  x y t las coordenadas del espacio y el tiempo,  respectivamente; y ψ (x, t) una función de onda de cuatro componentes. La función de onda ha de ser formulada como un espinor (objeto matemático similar a un vectorque cambia de signo con una rotación de 2π descubierto por Pauli y Dirac) de cuatro componentes, y no como un simple escalar,  debido a los requerimientos de la relatividad especial. Los α son operadores lineales que gobiernan la función de onda, escritos como una matriz y son matrices de 4×4 conocidas como matrices de Dirac.

El premio Nobel Paul dirac incluso llegó a decir de forma más categórica: “Es más importante tener belleza en las ecuaciones que tener experimentos que se ajusten a ellas“, o en palabras del físico John Ellis del CERN, “Como decía en una envoltura de caramelos que abrí hace algunos años, «Es sólo el optimista el que consigue algo en este mundo».“

Yo, como todos ustedes, un hombre normal y corriente de la calle, escucho a unos y a otros, después pienso en lo que dicen y en los argumentos y motivaciones que les han llevado a sus respectivos convencimientos, y finalmente, también decido según mis propios criterios mi opinión, que no obligatoriamente coincidirá con alguna de esas opiniones, y que en algún caso, hasta me permito emitirla.

Suponiendo que algún físico brillante nos resuelva la teoría de campos de cuerdas y derive las propiedades conocidas de nuestro universo, con un poco de suerte, podría ocurrir en este mismo siglo, lo que no estaría nada mal considerando las dificultades de la empresa. El problema fundamental es que estamos obligando a la teoría de supercuerdas a responder preguntas sobre energías cotidianas, cuando “ámbito natural” está en la energía de Planck. Esta fabulosa energía fue liberada sólo en el propio instante de la creación, lo que quiere decir que la teoría de supercuerdas es naturalmente una teoría de la creación.

    Las primeras observaciones realizadas por Planck | ESA y Axel Mellinger.

Fuimos capaces de predecir que el Big Bang produjo un “eco” cósmico reverberando en el universo y que podría ser mesurable por los instrumentos adecuados. De hecho, Arno Penzias y Robert Wilson de los Bell Telephone Laboratories ganaron el premio Nobel en 1.978 por detectar este eco del Big Bang, una radiación de microondas que impregna el universo conocido. El que el eco del Big Bang debería estar circulando por el universo miles de millones de años después del suceso fue predicho por primera vez por George Gamow y sus discípulos Ralpher y Robert Herman, pero nadie les tomó en serio. La propia idea de medir el eco de la creación parecía extravagante cuando la propusieron por primera vez poco después de la segunda guerra mundial. Su lógica, sin embargo, era aplastante. Cualquier objeto, cuando se calienta, emite radiación de forma gradual. Ésta es la razón de que el hierro se ponga al rojo vivo cuando se calienta en un horno, y cuanto más se calienta, mayor es la frecuencia de radiación que emite. Una fórmula matemática exacta, la ley de Stefan-Boltzmann, relaciona la frecuencia de la luz (o el color en este caso) con la temperatura. De hecho, así es como los científicos determinan la temperatura de la superficie de una estrella lejana; examinando su color. Esta radiación se denomina radiación de cuerpo negro.

Esta radiación, cómo no, ha sido aprovechada por los ejércitos, que mediante visores nocturnos pueden operar en la oscuridad. De noche, los objetos relativamente calientes, tales como soldados enemigos o los carros de combate, pueden estar ocultos en la oscuridad, pero continúan emitiendo radiación de cuerpo negro invisible en forma de radiación infrarroja, que puede ser captada por gafas especiales de infrarrojo. Ésta es también la razón de que nuestros automóviles cerrados se calientes en verano, ya que la luz del Sol atraviesa los cristales del coche y calienta el interior. A medida que se calienta, empieza a emitir radiación de cuerpo negro en forma de radiación infrarroja. Sin embargo, esta clase de radiación no atraviesa muy bien el vidrio, y por lo tanto queda atrapada en el interior del automóvil, incrementando espectacularmente la temperatura.

Análogamente, la radiación de cuerpo negro produce el efecto invernadero. Al igual que el vidrio, los altos niveles de dióxido de carbono en la atmósfera, causados por la combustión sin control de combustibles fósiles, pueden atrapar la radiación de cuerpo negro infrarroja en la Tierra, y de este modo calentar gradualmente el planeta.

Gamow razonó que el Big Bang era inicialmente muy caliente, y que por lo tanto sería un cuerpo negro ideal emisor de radiación. Aunque la tecnología de los años cuarenta era demasiado primitiva para captar esta débil señal de la creación, Gamow pudo calcular la temperatura de dicha radiación y predecir con fiabilidad que un día nuestros instrumentos serían lo suficientemente sensibles como para detectar esta radiación “fósil”.

La lógica que había detrás de su razonamiento era la siguiente: alrededor de 300.000 años después del Big Bang, el universo se enfrió hasta el punto en el que los átomos pudieron empezar a componerse; los electrones pudieron empezar a rodear a los protones y neutrones formando átomos estables, que ya no serían destruidos por la intensa radiación que estaba impregnando todo el universo. Antes de este momento, el universo estaba tan caliente que los átomos eran inmediatamente descompuestos por esa radiación tan potente en el mismo acto de su formación. Esto significa que el universo era opaco, como una niebla espesa absorbente e impenetrable.

Pasados 300.000 años, la radiación no era tan potente; se había enfriado y por lo tanto la luz podía atravesar grades distancias sin ser dispersada. En otras palabras, el universo se hizo repentinamente negro y transparente.

Terminaré esta parte comentando que un auténtico cuerpo negro es un concepto imaginario; un pequeño agujero en la pared de un recinto a temperatura uniforme es la mejor aproximación que se puede tener de él en la práctica.

La radiación de cuerpo negro es la radiación electromagnética emitida por un cuerpo negro. Se extiende sobre todo el rango de longitudes de onda y la disminución de energías sobre este rango tiene una forma característica con un máximo en una cierta longitud de onda, desplazándose a longitudes de onda más cortas al aumentar las temperaturas*.

Hablar, sin más especificaciones, de radiación, es estar refiriéndonos a una energía que viaja en forma de ondas electromagnéticas o fotones por el universo. También nos podríamos estar refiriendo a un chorro de partículas, especialmente partículas alfa o beta de una fuente radiactiva o neutrones de un reactor nuclear.

La radiación actínida es la electromagnética que es capaz de iniciar una reacción química. El término es usado especialmente para la radiación ultravioleta y también para denotar radiación que podría afectar a las emulsiones fotográficas.

Radiación blanda, radiación cósmica, radiación de calor, radiación de fondo, de fondo de microondas, radiación dura, electromagnética, radiación gamma, infrarroja, ionizante, monocromática, policromática, de sincrotón, ultravioleta, de la teoría cuántica, de radiactividad… y, como se puede ver, la radiación en sus diversas formas es un universo en sí misma.

Siempre me llamó la atención y se ganó mi admiración el físico alemán Max Planck (1.858 – 1.947), responsable entre otros muchos logros de la ley de radiación de Planck, que da la distribución de energía radiada por un cuerpo negro. Introdujo en física el concepto novedoso de que la energía es una cantidad que es radiada por un cuerpo en pequeños paquetes discretos, en vez de una emisión continua. Estos pequeños paquetes se conocieron como cuantos y la ley formulada es la base de la teoría cuántica.

Einstein se inspiró en este trabajo para a su vez presentar el suyo propio sobre el efecto fotoeléctrico, donde la energía máxima cinética del fotoelectrón, E_m, está dada por la ecuación que lleva su nombre: E_m = hf – Φ.

Cada metal requiere, para que se produzca la extracción, una radiación con una frecuencia mínima (n_o). Cualquier otra radiación de menor frecuencia, no será capaz de arrancar electrones. Por debajo de la frecuencia mínima la intensidad de corriente -“i” (amperios)- será cero. No hay efecto fotoeléctrico.

Planck publicó en 1.900 un artículo sobre la radiación de cuerpo negro que sentó las bases para la teoría de la mecánica cuántica que más tarde desarrollaron otros, como el mismo Einstein, Heisenberg, Schrödinger, Dirac, Feymann, etc. Todos los físicos son conocedores de la enorme contribución que Max Planck hizo en física: la constante de Planck, radiación de Planck, longitud de Planck, unidades de Planck, etc. Es posible que sea el físico de la historia que más veces ha dado su nombre a conceptos de física. Pongamos un par te ejemplos de su ingenio:

1.      vale 10^-35 metros. Esta escala de longitud (veinte órdenes de magnitud menor que el tamaño del protón, de 10^-15 m) es a la que la descripción clásica de gravedad cesa de ser válida y debe ser tenida en cuenta la mecánica cuántica. En la fórmula que la describe, G es la constante gravitacional, ħ es la constante de Planck racionalizada y c en la velocidad de la luz.

2.      . Es la masa de una partícula cuya longitud de onda Compton es igual a la longitud de Planck. En la ecuación, ħ es la constante de Planck racionalizada, c es la velocidad de la luz y G es la constante gravitacional. Así, Se denomina masa de Planck a la cantidad de masa (21,7644 microgramos) que, incluida en una esfera cuyo radio fuera igual a la longitud de Planck,  generaría una densidad del orden de 10⁹³ g/cm³. Según la física actual, esta habría sido la densidad del Universo cuando tenía unos segundos, el llamado Tiempo de Planck. Su ecuación, es decir la masa de Planc se denota:

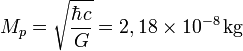
El valor de la masa de Planck se expresa por una fórmula que combina tres constantes fundamentales, la constante de Planck,  (h), la velocidad de la luz (c),  y la constante de gravitación universal (G). La masa de Planck es una estimación de la masa del agujero negro primordial menos masivo, y resulta de calcular el límite donde entran en conflicto la descripción clásica y la descripción cuántica de la gravedad.

“Aunque todas estas descripciones reflejan más una abundante imaginación que un hecho existencial apoyado teóricamente con alguna hipótesis que pueda ser comprobada en el laboratorio sobre hechos que están más allá de poder ser medidos jamás en algún laboratorio construído por humanos. La única forma de confrontar la factibilidad o la posibilidad del modelo de la espuma cuántica nos lleva necesariamente a confrontar la carencia de un modelo que logre unificar exitosamente al macrocosmos con el microcosmos, a la Relatividad General con la Mecánica Cuántica, la Gravedad Cuántica. Si la energía y la materia (o mejor dicho la masa-energía) están discretizadas, se supone que también deben de estarlo el espacio y el tiempo (o mejor dicho, el espacio-tiempo), y la “partícula fundamental” del espacio-tiempo debe de serlo el gravitón, aunque de momento todo esto son especulaciones que seguirán siéndolo mientras no tengamos a la mano algo que pueda confirmar la existencia de tan exótica partícula, quizá la más exótica de cuantas hayan sido concebidas por la imaginación del hombre.”

La descripción de una partícula elemental de esta masa, o partículas que interaccionan con energías por partículas equivalentes a ellas (a través de E = mc²), requiere de una teoría cuántica de la gravedad. Como la masa de Planck es del orden de 10^-8 Kg (equivalente a una energía de 10¹⁹ GeV) y, por ejemplo, la masa del protón es del orden de 10^-27 Kg y las mayores energías alcanzables en los aceleradores de partículas actuales son del orden de 10³ GeV, los efectos de gravitación cuántica no aparecen en los laboratorios de física de partículas. Únicamente en un laboratorio aparecieron partículas que tenían energías del orden de la masa de Planck: en el universo primitivo, de acuerdo con la teoría del Big Bang, motivo éste por el que es necesaria una teoría cuántica de la gravedad para estudiar aquellas condiciones. Esta energía de la que estamos hablando, del orden de 10¹⁹ GeV (inalcanzable para nosotros), es la que necesitamos para verificar la teoría de supercuerdas.

Siempre, desde que puedo recordar, me llamó la atención los misterios y secretos encerrados en la naturaleza, y la innegable batalla mantenida a lo largo de la historia por los científicos para descubrirlos. Muchos han sido los velos que hemos podido descorrer para que, la luz cegadora del saber pudiera entrar en nuestras mentes para hacerlas comprender cómo actuaba la Naturaleza en ciertas ocasiones y el por qué de tales comportamientos, y, sin embargo, a pesar del largo camino recorrido, es mucho más el que nos queda por andar.

emilio silvera

[?]