Ene
21
¿Viajar por el Tiempo? ¡Otro sueño de la Humanidad?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Viajar al pasado ~
Clasificado en Viajar al pasado ~
 Comments (1)
Comments (1)
Una versión de la máquina del tiempo de Thorne consiste en dos cabinas, cada una de las cuales contiene dos placas de metal paralelas. Los intensos cambios eléctricos creados entre cada par de placas de metal paralelas (mayores que cualquier cosa posible con la tecnología actual) rizan el tejido del espacio-tiempo, creando un agujero en el espacio que une las dos cabinas. Una cabina se coloca entonces en una nave espacial y es acelerada a velocidades próximas a la de la luz, mientras que la otra cabina permanece en la Tierra. Puesto que un agujero de gusano puede conectar dos regiones des espacio con tiempos diferentes, un reloj en la cabina de la nave marcha más despacio que un reloj en la cabina de la Tierra. Debido a que el tiempo transcurriría a diferentes velocidades en los dos extremos del agujero de gusano, cualquiera que entrase en un extremo del agujero de gusano sería instantáneamente lanzado al pasado o al futuro.


Crear materia exótica mediante el efecto Casimir
Parece que la función de las placas metálicas paralelas consiste en generar la materia o energía exótica necesaria para que las bocas de entrada y salida del agujero de gusano permanezcan abiertas y, como la materia exótica genera energía negativa, los viajeros del tiempo no experimentarían fuerzas gravitatorias superiores a 1g, viajando así al otro extremo de la galaxia e incluso del universo o de otro universo paralelo de los que promulga Stephen Hawking. En apariencia, el razonamiento matemático de Thorne es impecable conforme a las ecuaciones de Einstein.

Normalmente, una de las ideas básicas de la física elemental es que todos los objetos tienen energía positiva. Las moléculas vibrantes, los vehículos que corren, los pájaros que vuelan, los niños jugando tienen todos energía positiva. Por definición, el espacio vacío tiene energía nula. Sin embargo, si podemos producir objetos con “energías negativas” (es decir, algo que tiene un contenido de energía menor que el vacío), entonces podríamos ser capaces de generar configuraciones exóticas de espacio y tiempo en las que el tiempo se curve en un circulo.

Este concepto más bien simple se conoce con un nombre que suena complicado: la condición de energía media débil (average weak energy condition, o AWEC). Como Thorne tiene cuidado en señalar, la AWEC debe ser violada; la energía debe hacerse temporalmente negativa para que el viaje en el tiempo tenga éxito. Sin embargo, la energía negativa ha sido históricamente anatema para los relativistas, que advierten que la energía negativa haría posible la antigravedad y un montón de otros fenómenos que nunca se han visto experimentalmente.
Pero Thorne señala al momento que existe una forma de obtener energía negativa, y esto es a través de la teoría cuántica.

En 1.948, el físico holandés Hendrik Casimir demostró que la teoría cuántica puede crear energía negativa: tomemos simplemente dos placas de metal paralelas y descargadas ordinariamente, el sentido común nos dice que estas dos placas, puesto que son eléctricamente neutras, no ejercen ninguna fuerza entre sí. Pero Casimir demostró que, debido al principio de incertidumbre de Werner Heisenberg, en el vacío que separa estas dos placas existe realmente una agitada actividad, con billones de partículas y antipartículas apareciendo y desapareciendo constantemente. Aparecen a partir de la “nada” y vuelven a desaparecer en el “vacío”. Puesto que son tan fugaces, son, en su mayoría, inobservables, y no violan ninguna de las leyes de la física. Estas “partículas virtuales” crean una fuerza neutra atractiva entre estas dos placas que Casimir predijo que era medible.

Crear puertas de entrada hacia otras regiones del Universo
Cuando Casimir publicó el artículo, se encontró con un fuerte escepticismo. Después de todo, ¿cómo pueden atraerse dos objetos eléctricamente neutros, violando así las leyes normales de la electricidad clásica? Esto era inaudito. Sin embargo, en 1.985 el físico M. J. Sparnaay observó este efecto en el laboratorio, exactamente como había predicho Casimir. Desde entonces (después de un sin fin de comprobaciones), ha sido bautizado como el efecto Casimir.
Una manera de aprovechar el efecto Casimir mediante grandes placas metálicas paralelas descargadas, sería el descrito para la puerta de entrada y salida del agujero de gusano de Thorne para poder viajar en el tiempo.

La mayoría de los físicos que han estudiado seriamente y a fondo las ecuaciones de Einstein de la Relatividad General, lo que piensan de viajar por el Tiempo se transforma en una carcajada de burla.
Por el momento, al no ser una propuesta formal, no hay veredicto sobre la máquina del tiempo de Thorne. Su amigo, Stephen Hawking, dice que la radiación emitida en la entrada del agujero sería suficientemente grande como para contribuir al contenido de materia y energía de las ecuaciones de Einstein. Esta realimentación de las ecuaciones de Einstein distorsionaría la entrada del agujero de gusano, incluso cerrándolo para siempre. Thorne, sin embargo, discrepa en que la radiación sea suficiente para cerrar la entrada.
Aquí es donde interviene la teoría de supercuerdas. Puesto que la teoría de supercuerdas es una teoría completamente mecanocuántica que incluye la teoría de la relatividad general de Einstein como un subconjunto, puede ser utilizada para calcular correcciones a la teoría del agujero de gusano original.
En principio nos permitiría determinar si la condición AWEC es físicamente realizable, y si la entrada del agujero de gusano permanece abierta para que los viajeros del tiempo puedan disfrutar de un viaje al pasado.
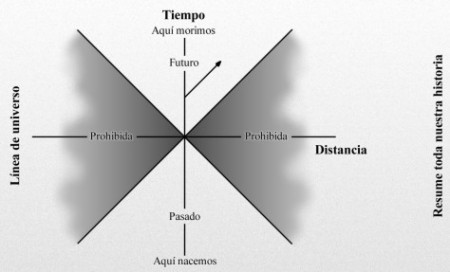
Nuestra línea de universo resume toda nuestra historia, desde que nacemos hasta que morimos. Cuanto más rápido nos movemos más se inclina la línea de universo. Sin embargo, la velocidad más rápida a la que podemos viajar es la velocidad de la luz. Por consiguiente, una parte de este diagrama espacio-temporal está “prohibida”; es decir, tendríamos que ir a mayor velocidad que la luz para entrar en esta zona prohibida por la relatividad especial de Einstein, que nos dice que nada en nuestro universo puede viajar a velocidades superiores a c.

Lo que sí tenemos claro es que, si alguna vez conseguimos realizar esos viajes… ¡No sería con esta máquina!
Antes comentaba algo sobre disfrutar de un viaje al pasado pero, pensándolo bien, no estaría yo tan seguro. Rápidamente acuden a mi mente múltiple paradojas que, de una u otra especie han sido narradas, principalmente por escritores de ciencia-ficción que, por lo general, no pocas veces son los precursores del futuro.
emilio silvera
Ene
20
Nuestro entorno, la vida, el futuro
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Futuro incierto ~
Clasificado en El Futuro incierto ~
 Comments (8)
Comments (8)

Somos, eminentemente, seres sociales, y, aprendemos con los demás y de los demás. Observamos nuestro entorno, sentimos curiosidad por el por qué de las cosas, nos planteamos preguntas y tratamos de contestarlas.
Los seres humanos, durante toda la vida están aprendiendo y desarrollando su inteligencia. Sin embargo, generalmente, la mayor actividad intelectual se desarrolla desde niño hasta los 35-40 años. Después remite para perder interés y continuar avanzando más pausadamente que en la juventud.
Claro que me estoy refiriendo a los casos de las personas estudiosas y comprometidas con el saber que, en muchos casos, no son todos los que quisieran. Hay muchos de los seres de la Tierra que por sus condiciones sociales, su lugar de nacimiento e incluso el seno de la familia en la que el destino lo trajo a este mundo, aun queriendo, no tendrá nunca la oportunidad de saber, de prepararse, de conocer sobre aspectos de la naturaleza que le inquietan o de poder acceder al conocimiento científico de las cosas.

Emon Hawlader tiene 13 años y trabaja nueve horas diarias reparando motores desde hace dos años. Seguramente se hará un hombre de provecho y estará fuera del foco de la droga y otros ámbitos que pudren nuestro mundo. Sin embargo… ¿Por qué no ha tenido la oportunidad de elegir lo que quería ser?
Estamos en un claro caso (de los millones que existen en nuestro injusto mundo) de desigualdad. No respetamos un mínimo de dignidad para que todos, de partida, tengan las mismas posibilidades de demostrar su valía.

El ser humano es curioso por naturaleza y su curiosidad le empujó siempre a preguntar y tratar de saber por qué ocurrían las cosas, tales como:

- ¿Por qué la Luna se sostenía en el aire y no caía?
- ¿Qué eran los rayos y cómo se producían los truenos?
- ¿Cuál era el origen de la lluvia?
- ¿Quién encendía aquella inmensa “lámpara” que llamamos Sol que nos daba el día, la luz y el calor?
- ¿Cómo se formaban las estrellas y de qué estaban hechas?
Nunca se dejó de hacer preguntas que la falta de conocimiento contestaba valiéndose de las divinidades, inventándose un dios o una diosa para cada situación y, claro está, la falta de conocimiento les producía temor que les llevaba a los sacrificios a los dioses para procurar tenerlos satisfechos y evitar su furor.

Así, la Humanidad caminó por el planeta Tierra durante milenios. El tiempo inexorable pasaba, y con él las generaciones, las distintas culturas y sociedades humanas.
Empédocles nos habló de elementos, y, la tierra, el aire, el agua y el fuego, mezclados en la debido proporción formaban todas las cosas. Está claro que las cosas no eran de esa manera pero… ¡Qué intuición!
Como el hombre no cejaba en su empeño de saber, lo observaba todo y procuraba aprender de todo lo que acontecía, de tal forma que, un día, dejó de lado la mitología y a los dioses para comenzar a emplear la lógica y darse cuenta de que todo cuanto ocurría, tanto en la Tierra como allá arriba en los cielos, era la consecuencia de algo que ocurrió con anterioridad.

Cuando el cielo se oscurecía y se llenaba de nubarrones, la lluvia y la tormenta no tardaban en aparecer. La noche les traía la oscuridad, el frío y el peligro, mientras que el día les llenaba de la luz y el calor del Sol fulgurante. Los ríos arrastraban las piedras y la arena del lecho fluvial y formaban las playas en las orillas. Una fuerza invisible se llevaba el agua del mar y la volvía a traer seis horas más tarde.
Poco a poco, aquellos misterios se fueron desvelando y se encontró el origen de todos los fenómenos que, en un principio, sólo eran insondables misterios.

Tales de Mileto, en la antigua Grecia, fue el primero en descubrir la importancia que tenía el agua para la vida; él también empleó la lógica para explicar las cosas.
Empédocles, otro pensador griego de aquella época floreciente del saber, nos dijo que todo lo que vemos, todas las cosas estaban formadas por cuatro elementos: agua, aire, tierra y fuego, que mezclados en la debida proporción lo podría conformar todo. Aunque algo rústico no deja de ser una buena intuición el hablar de elementos.

En realidad no fue Demócrito el que lo descubrio pero, habló de su existencia antes de saber que existía, el hombre intuyó que la materia estaba hecha de infinitesimales objetos.
Demócrito de Abdera, otro sabio de Grecia, nos adelantó (muchos años antes de Cristo) que todas las cosas estaban hechas por partículas diminutas, invisibles e indivisibles, a las que llamó átomos.
Pitágoras y Euclides con las matemáticas, Galeno con la medicina, Sócrates, Platón o Aristóteles en filosofía, matemáticas y astronomía… todos ellos y muchos otros abrieron el camino para que la Humanidad pudiera tomar un camino muy distinto y más racional que el del resto de los seres vivos del planeta.

La distancia que nos separa del Sol hace que el planeta Tierra sea habitable, el agua líquida es abundante, la atmósfera nos permite respirar, el ozono impide la entrada de partículas nosivas, y, los polos magnéticos con el cinturón electromagnético no dejan entrar la radiación ultravioleta y gamma, la vida puede desarrollarse sin problemas
Está claro que hemos tenido el privilegio de venir a caer en uno de los planetas que reúne condiciones para la vida. El Universo es tan grandioso que alberga a cientos de miles de millones de galaxias, y el número de las estrellas que las conforman es de tal magnitud que sería una temeridad creer que sólo en el Sistema Solar al que pertenecemos existe la vida inteligente.

Una inmensa bola de plasma a millones de grados de temperatura donde se fusionan elementos simples en otros más complejos. Enviamos a sus cercanías ingenios que lo observen y nos “hablen” de su comportamiento. El Sol contiene el 99,99% de Todo el Sistema solar.
Nuestro Sol, estrella de segunda generación, es en realidad una estrella mediana clasificada como G2V, amarilla, con una temperatura efectiva de 5.770 K (tipo espectral G2), formada en su mayor parte de hidrógeno (71% en masa), con algo de helio (27%) y elementos más pesados (2%). Su edad se estima en unos 4.500 millones de años y se encuentra en la mitad de su vida como estrella antes de agotar el combustible nuclear y convertirse en gigante roja que, finalmente, explotará lanzando las capas exteriores al vacío estelar y se contraerá bajo el peso de su propia masa (la gravedad sin ninguna fuerza que la contrarreste) para convertirse en una estrella enana blanca.
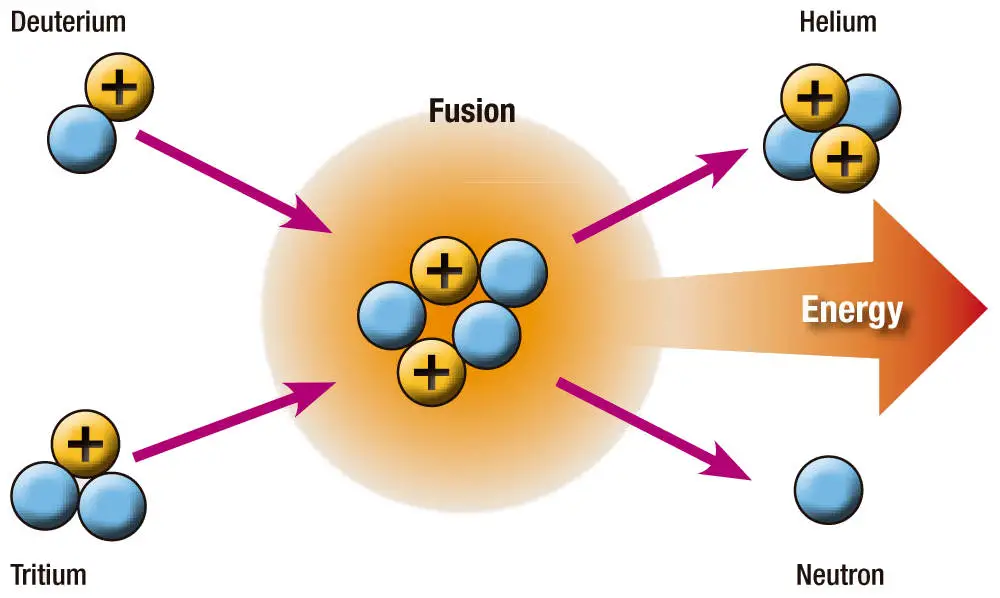
En el centro de nuestro Sol la temperatura se calcula próxima a los 15’6 millones de K y la densidad en el núcleo de 148.000 Kg/m3. Ahí se produce la fusión de los elementos.
El Sol tiene un diámetro de 1.392.530 Km, su masa total es de 1’989×1030 Kg y su velocidad de escape está cifrada en 617’3 Km/s; si no se alcanza no se puede escapar de él.
El Sol fusiona cada segundo 4.654.600 toneladas de hidrógeno en 4.650.000 toneladas de helio. Las 4.600 toneladas restantes son enviadas al espacio en forma de luz y de calor, energía de la que una pequeña parte llega al planeta Tierra, y gracias a ello es posible la vida tal como la conocemos.
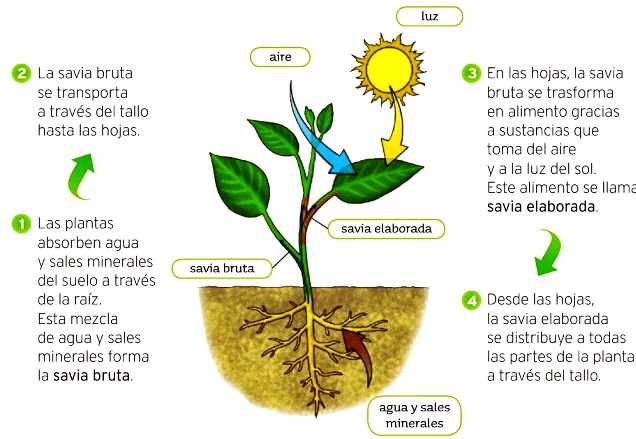
Los seres fotosintéticos son la base de la cadena trófica. De la luz del Sol a la Tierra sólo llegan dos mil millonésimas que son suficientes para que el proceso de la vida sea posible.
Como antes mencioné, la evolución de nuestro Sol, con el paso del tiempo, lo llevará de manera irremediable a expandirse para convertirse en una gigante roja primero y contraerse después hasta alcanzar el tamaño de la Tierra y volverse tan denso como para evitar su propio colapso por la presión de degeneración de los electrones. La densidad que alcanza es de 5×108 Kg/m3. Será una enana blanca y, las capas exteriores eyectadas al espacio interestelar formará una nebulosa planetaria de material ionizado.
En su fase anterior, la de gigante roja, crece muchas veces su tamaño original, y en el caso de nuestro Sol su órbita sobrepasará al planeta Mercurio, al planeta Venus y probablemente al planeta Tierra, que para entonces, por lo elevado de las temperaturas reinantes, habrá visto evaporarse el agua de los ríos y océanos hasta dejarlo seco y yermo, sin posibilidad de vida.

Para cuando todo eso ocurra, ¿quién estará aquí?; faltan varios miles de millones de años y, si la Humanidad no se ha destruido a sí misma, espero que para entonces tenga preparado todos los medios necesarios para instalarse en otros mundos, preferiblemente fuera de nuestro Sistema Solar, ya que los planetas vecinos, una vez desaparecido el Sol, no creo que reúnan las condiciones idóneas para acoger la vida, y las lunas de esos planetas tampoco parecer suficientemente acogedoras: Io, el tercer satélite más grande de Júpiter, sólo tiene un diámetro de 3.630 Km y es una caldera volcánica donde la radiante lava fluye de sus muchos volcanes. Toda la superficie de Io tiene un color amarillento debido a los depósitos de azufre u óxido de azufre. Existen extensas llanuras y regiones montañosas en Io, aunque no cráteres de impacto, indicando que su superficie es muy joven geológicamente.
La densidad de Io, 3’57 g/cm3, sugiere que tiene un núcleo de hierro-azufre de unos 1.500 Km de radio y un manto de silicatos. Las actividades volcánicas de Io son el resultado del calor liberado por las fuerzas de marea, que distorsionan el satélite a medida que se acerca o se aleja de Júpiter en su órbita.
Europa, el cuarto satélite más grande de Júpiter y el segundo de los cuatro satélites galileanos en distancia al planeta, conocido también como Júpiter II, tiene un diámetro de 3.138 Km, ligeramente menor que nuestra Luna. La densidad de Europa es de 2’97 g/cm3 indicando que está compuesta fundamentalmente por rocas de silicio, mezcladas con, al menos, un 5% de agua.
La superficie es brillante y helada con un albedo de 0’64, dominada por redes de fracturas oscuras y lineales, algunas de más de 1.000 Km de longitud. Se han identificado en Europa al menos una docena de cráteres de impacto. Se han detectado que en su interior, Europa puede albergar un océano salado y, de ahí a encontrar en ese océano, alguna forma de vida, sólo va un paso.
Ganímedes, el satélite más grande de Júpiter y el mayor del Sistema Solar, con un diámetro de 5.262 Km, conocido como Júpiter III y es el más brillante de los satélites galileanos.

El primer mapa global de Ganímedes ayudará a buscar vida en la luna de Júpiter
La densidad de este satélite es de 1’94 g/cm3 y posee una superficie helada llena de contrastes con regiones de alto y bajo albedo, cubiertos por complejos sistemas de surcos, indicando la existencia de varias fases de actividad en la corteza en el pasado. Algunos de los cráteres de impacto más grandes sobre la superficie se han convertido en palimpsestos debido al lento flujo del hielo, como en un glaciar.
Con sus océanos de metano y su espesa atmósfera parece la Tierra hace miles de millones de años
Titán, el satélite más grande de Saturno y el segundo más grande del Sistema Solar, con un diámetro de 5.150 Km; también conocido como Saturno VI. Fue descubierto en 1.655 por C. Huygens. La composición más probable de Titán es rocas e hielo en partes iguales aproximadamente. Es el único satélite del Sistema Solar que tiene una atmósfera sustancial. La atmósfera está compuesta principalmente por nitrógeno, con un 2/10% de metano, un 0’2% de hidrógeno (porcentajes moleculares) y trazas de etano, propano, etino, cianuro de hidrógeno y monóxido de carbono. Su temperatura es de -180 ºC y pueden existir lloviznas de metano en la superficie y posiblemente nieve de metano. A unos 200 Km de altura abundan espesas nubes anaranjadas de hidrocarburos y existen además capas de neblina atmosférica hasta los 500 Km.

Las sondas Voyager revelaron un casquete polar norte en las nubes de Titán, con un collar ligeramente más oscuro a su alrededor. Además, el hemisferio norte era marcadamente más oscuro que el sur. Ambos son probablemente efectos estacionales.
Otras muchas lunas acompañan a nuestros planetas vecinos: Phobos y Deimos en Marte; Callisto, Amalthea, Leda, etc. en Júpiter; Pan, Atlas, Prometheus, Pandora, etc. en Saturno; Cordelia, Ophelia, Bianca, Ariel, etc. en Urano; Galatea, Larissa, Tritón, Nereid, etc. en Neptuno; Charon en Plutón… hasta formar un conjunto aproximado de más de 60 lunas.

De los planetas vecinos, Mercurio y Venus están descartados para la vida, y Marte con su delgada atmósfera compuesta (en volumen) por alrededor del 95% de dióxido de carbono, 2’7% de nitrógeno, 1’6% de argón, 0’1% de monóxido de carbono y pequeñas trazas variables de vapor de agua, con unas temperaturas superficiales de entre 0 y -125 ºC, siendo la media de -50 ºC.
Es relativamente frecuente la presencia de vapor de agua en nubes blancas o de dióxido de carbono en dichas nubes cerca de latitudes polares. Existen dos casquetes de hielo de agua permanentes en los polos, que nunca se funden y que en invierno aumentan de tamaño al convertirse en casquetes de dióxido de carbono congelado, hasta alcanzar los 60º de longitud.
Ocurren esporádicamente tormentas de polvo, pudiendo extenderse hasta cubrir la totalidad del planeta con una neblina amarilla, oscureciendo los accidentes superficiales más familiares.

La superficie de Marte es de basalto volcánico con un alto contenido en hierro, que le da al planeta el color característico por el que se le denomina “el planeta rojo”.
Existen muchas áreas de dunas de arena rodeando los casquetes polares que constituyen los mayores campos de dunas del Sistema Solar.

La actividad volcánica fue intensa en el pasado. Tharsis Montes es la mayor región volcánica, estando Olympus Monts situado en el noroeste, y la vasta estructura colapsada Alba Patera, en el norte. Juntas, estas áreas volcánicas constituyen casi el 10% de la superficie del planeta. No hay volcanes activos en Marte, aunque en el pasado produjeron llanuras de lava que se extendieron cientos de kilómetros.
Muchos de los cráteres de impacto más recientes, como cráteres de terraplén, tienen grandes pendientes en los bordes de sus mantas de proyecciones, sugiriendo que la superficie estaba húmeda o llena de barro cuando se produjo el impacto.

Es un gran enigma el por qué Marte perdió sus océanos y la atmósfera
Aunque las sondas allí enviadas nos han demostrado la existencia de agua líquida en Marte que parece estar el el subsuelo, hay fuertes indicios de que antiguamente tuvo ríos y lagos cuando existía una atmósfera más densa, caliente y húmeda. Uno de los canales secos es Ma’adim Vallis, de unos 200 Km de longitud y varios kilómetros de ancho.
Internamente, Marte probablemente tiene una litosfera de cientos de kilómetros de espesor (grosor), una astenosfera rocosa y un núcleo metálico de aproximadamente la mitad del diámetro del planeta.
Marte no posee un campo magnético importante; su diámetro ecuatorial es de 6.794 Km, su velocidad de escape de 5,02 Km/s y su densidad media de 3’94 g/cm3. Dista del Sol 1’524 UA.. Si acaso Marte, podría albergar alguna clase de vida bacteriana que, según su historia pasada, sería lo más lógico si se tienen en cuenta todos los factores presentes en el planeta.
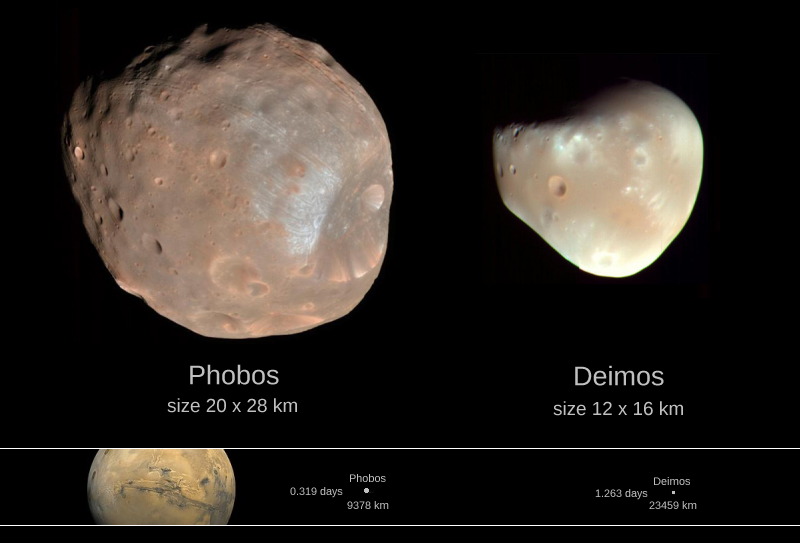
Las lunas de marte
Tanto las lunas antes mencionadas como el planeta Marte son objetos de interesantes estudios que nos facilitarán importantes conocimientos de los objetos que pueblan el espacio exterior y de cómo serán muchos de los planetas y lunas que nos encontraremos más allá de nuestro Sistema Solar.
Pero todo de queda ahí, en una interesante experiencia.

Una colonia en Marte sería vivir en la precariedad, y, sólo se puede pensar en ella como base hacia otros planetas lejanos más habitables.
Sin embargo, como lugares para vivir e instalarse no parecen, por sus condiciones físico-ambientales, los más idóneos. Si acaso, en algunos de estos objetos celestes se podrán instalar bases intermedias para el despegue hacia otros mundos más lejanos, para aprovechar sus recursos de materiales minerales, hidrocarburos, etc. que poseen en abundancia pero, desgraciadamente, no son lugares aptos para instalar a la Humanidad que necesitaría crear, artificialmente, costosas instalaciones que simularan las condiciones terrestres, y tal empresa ni económica, ni tecnológicamente es tarea fácil.

Aunque el planeta “habitable más cercano parece estar en Próxima Centauri… No es muy seguro. La radiación fulgurante de esa estrella podría impedir la habitabilidad. Está a 4,2 años luz de la Tierra.
Construidas de material inteligente, datadas de Gravedad artificial… Y muchas otras tecnologías
Así las cosas, el único camino posible para el futuro de la Humanidad será avanzar en la exploración del espacio exterior, construir naves espaciales mejor dotadas en todos los sentidos, sobre todo: aislante de radiaciones nocivas y peligrosas para la salud de los tripulantes, dispositivo antiflotabilidad que imite la gravedad terrestre, espacios hidropónicos que produzcan cosechas continuas de verduras y tubérculos, plantas de reciclaje que depuren de manera continuada el agua de toda la nave, motones lumínicos de fotones, antimateria, etc. que de alguna manera imite la velocidad relativista, laboratorios con instalaciones tecnológicas de última generación con potentes y sofisticados ordenadores que avancen y mejoren continuamente sobre el conocimiento científico de la física, la química y la biología, y, en fin y sobre todo, una conciencia colectiva de todos los gobiernos del mundo para comprender que su principal cometido es mirar y tratar de conseguir el mayor bienestar y la seguridad de todos los ciudadanos y, de entre otras cuestiones, una importante es la de destinar una parte importante de los recursos para investigar, explorar y preparar el futuro de las generaciones futuras.

Si no comenzamos ya a prepararnos para lo que tiene que venir… ¡Mal nos irá!
No podemos descansar pensando que aún falta mucho para que nuestro Sol deje de prestarnos sus servicios, ya que el reto que tendremos que superar cuando eso llegue es tal que necesitaremos todo ese tiempo sin dejar de trabajas para estar preparados cuando el momento llegue.
¡La desaparición del Sol!
Mucho antes, las condiciones atmosféricas y las temperaturas serán insoportables para el ser humano, que el único camino que tendrá será buscar otros mundos parecidos al planeta Tierra para instalarse.
Según algunos estudios realizados, la posibilidad más cercana de encontrar sistemas solares que tengan algún planeta similar a la Tierra, está situada entre 12 y 15 años-luz de nosotros: 15×9’4607×1012Km ó 15×63.240 unidades astronómicas (1 UA = 150.000.000 Km).

Muchos son los percances que nuestra especie tendrá en la búsqueda de otros alojamientos. La aventura que le espera a la Humanidad… ¡Es inimaginable!
Ante tal inmensidad de espacio a recorrer, consiguiendo naves tan veloces como la luz, se tardarían 15 años en llegar, lo que nos puede dar una idea de la complejidad de esas naves, que tendrían que alojar familias enteras y disponer de complejos industriales, de fabricación de productos, de producción de alimentos, centros de enseñanzas, viviendas o habitáculos reducidos pero suficientes con casi todos los servicios colectivos, etc.
¿Cuántas de estas naves harían falta para desalojar a toda la Humanidad? ¿Cómo se hará la selección de los primeros colonos?

Todos querrán su plaza y serán miles de millones de criaturas. El desplazamiento se hará por etapas y con destinos diferentes. Unos tendrán más suerte que otros pero…. ¡Si la Humanidad se salva… habrá valido la pena!

Encontraremos cualquier mundo que podamos imaginar
Si todo eso se consigue, los primeros terrícolas que pongan el pie en esos nuevos mundos, contarán con una avanzada tecnología para adaptar un mundo totalmente salvaje.
Pero la segunda parte, y más peliaguda, será otra muy distinta: si el nuevo planeta es apto para la vida tal como la conocemos, quién puede asegurarnos que no encontrarán allí a los propios habitantes del planeta.
En mi libreta 37, dejé un amplio comentario sobre la posibilidad de vida inteligente en nuestra propia galaxia; y en libretas anteriores aparecen estudios más profundos y documentados sobre la vida extraterrestre, por lo que no me volcaré aquí en ello, al no ser el tema que nos ocupa, puesto que hablamos de cosas más generales y diversas.
emilio silvera
Ene
19
El Universo es dinámico y fascinante
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo dinámico ~
Clasificado en El Universo dinámico ~
 Comments (0)
Comments (0)
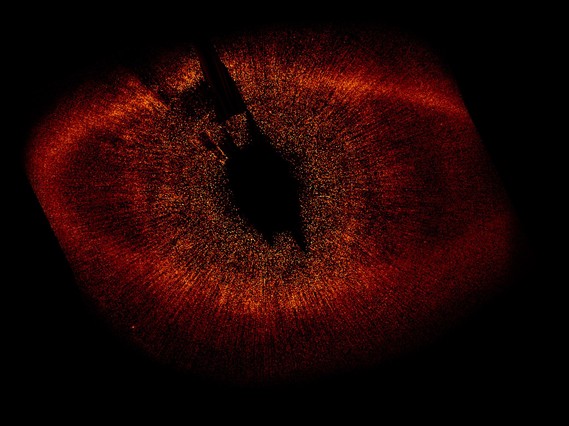
El Hubble captó el nacimiento de una estrella en el Espacio lejano. Le llaman renacuajo
En muchos de los trabajos aquí presentados he procurado explicaros lo que son las estrellas las, como se forman, como evolucionan y finalmente mueren para convertirse en otro objeto distinto. Durante sus vidas, durante miles de millones de años, las estrellas hacen posible que mediante el proceso de fusión, unos elementos se conviertan en otros cada vez más complejos para que sea posible, como ahora sabemos, la existencia de todos esos elementos que hemos relacionado en la Tabla Periódica, los más complejos formados en explosiones de Supernovas.

En nuestro Universo, el Plasma es el estado más común de la materia
Las estrellas son cuerpos celestes compuestos de materia del plasma, o de materia degenerada, que se concentra en un solo lugar por la fuerza de la gravedad. Están formadas principalmente por hidrógeno y helio. Estrella a lo largo de su vida produce la radiación electromagnética en forma de luz visible a través de los procesos de fusión de átomos de hidrógeno en el núcleo.
“Hoy en día, es muy fácil poder ver y disfrutar de hermosas imágenes astronómicas con mucho muy coloridas, que realmente parecen unas verdaderas obras de arte. Sin embargo, cuando tenemos la oportunidad de mirar estos objetos a través de un telescopio, se ven en “blanco y negro” lo que puede representar una decepción mayúscula para alguien que esperaba ver a todo locos un objeto del cielo profundo.”
“¿Sera acaso que los astrónomos nos mienten mostrándonos imágenes falsas? La respuesta es la siguiente, los instrumentos actuales para fotografiar el cielo, son tan sensibles a la luz, que pueden captar el color real de los objetos que se encuentran a millones de años luz, almacenándola en medios digitales e interpretando el color, pero nuestros ojos, no son capaces de almacenar luz, como lo hacen los aparatos electrónicos, y debido a la poca cantidad de luz que nos llega a nuestra vista, solo vemos con los “bastones” de nuestros ojos, células que son más sensibles a la luz, pero que no captan el color.”

Esta es la Nebulosa Roseta. NGC 7635
¿Cómo estan formadas las estrellas? están formadas en las nubes de materia interestelar, compuesta principalmente de hidrógeno. Una cuarta parte se compone de helio, mientras que el 1% restante es una mezcla de polvo y otros átomos. Esta nube es densa, y los átomos de hidrógeno mismo se combinan para hidrógeno molecular. Nube molecular se forma en fase terminal, lo que aumenta su tamaño y peso. La densidad de la nube está a unos pocos millones de partículas por centímetro cúbico, y el peso de 100 000 a 10 000 000 masas solares. El tamaño es enorme, de 50 a 300 años luz. Como una nube fría y fina, y el proceso de su creación, dura un tiempo relativamente corto.

El Colapso gravitatorio del Gas y el Polvo hace que nazcan nuevas estrellas

Estrellas masivas
“Cuando una estrella sobrepasa en masa el valor límite de Chandrasekhar, gasta rápidamente su combustible y empieza a comprimirse. No hay nada que detenga su colapso: la fuerza de compresión gravitacional es tan intensa que las partículas materiales que la conforman ya no obedecen el principio de exclusión y todas terminan por estar en la misma posición y con la misma velocidad, justamente, un punto sin masa, en el espacio.
Ese punto es una singularidad, con una densidad de cientos miles de millones toneladas por centímetros cúbicos. En este caso, la masa no se habría destruido porque sería una violación al principio de conservación de la materia, sino mas bien, transformada en energía gravitacional de acuerdo a la ecuación de Einstein E= mc2.”

El recorrido que hacen las estrellas desde que “nacen” en la Nebulosa, hasta que consumen su combustible nuclear de fusión, es fascinante. Y, según la masa que puedan contener, finalizarán sus vidas como enanas blancas, estrella de neutrones o agujeros negros.
¿Qué sucede a una estrella, cuando se “quema”? Núcleo de la estrella comienza a colapsar bajo su propio peso, mientras que las capas exteriores son violentamente expulsados. En función del peso que la estrella estaba en el principio, se puede transformar en una enana blanca (con aproximadamente el mismo tamaño de la Tierra), que después del enfriamiento se convierte en un enano negro. Si la masa de la estrella es de 8 masas solares, entonces tras el derrumbe ocurre erupción, y una explosión crea supernova. Pero cuando la masa de la estrella supera las 10 masas solares, cuando colapsa forma un agujero negro.
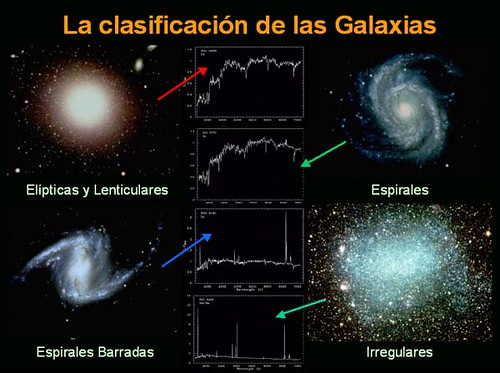
También hemos hablado aquí, de las galaxias y sus diferentes tipos, de radiogalaxias y de los cuásares, además de otras cuestiones de interés que, en todo momento, he tratado de explicar de manera muy sencilla con el objeto de que su comprensión sea fácil para las personas no versadas en Astronomía.
Es preciso que todos sepais que, en cualquier región del Universo, por muchos años luz que de nuestra Galaxia esté alejada, las leyes que rigen son las mismas que aquí, en nuestra región, interaccionan con la materia. Todo el Cosmos es lo mismo en cualquier lugar. Los Cúmulos de Galaxias y los espacios “vacíos” que existen entre ellos, las Nebulosas, los Agujeros Negros que ocupan el corazón de las Galaxias, el gas y el polvo interestelar que forman nuevas estrellas, y, en fin, todas las maravillas que a través de los procesos nucleares, forman la materia compleja a partir del Hidrógeno y del Helio.

Simulación computacional del gas pristino. Cuando salió la noticia del descubrimiento, se pudo leer:
“Astrónomos de la Universidad de California en Santa Cruz han encontrado, por primera vez, restos de la materia prima original del Universo en nubes de gas que datan de la noche de los tiempos. Estas nubes contienen remanentes absolutamente intactos del gas «limpio» que apareció en los primeros minutos después del Big Bang y que nunca llegó a formar parte de las estrellas. El hallazgo, que aparece publicado en la revista Science, coincide con las predicciones teóricas sobre los orígenes de los elementos en el Cosmos.
Solo los elementos más ligeros, principalmente hidrógeno y helio, se crearon en el Big Bang. A continuación, tuvieron que pasar varios cientos de millones de años para que grupos de este gas primordial se condensaran para formar las primeras estrellas, momento en el que los elementos más pesados se forjaron. Hasta ahora, los astrónomos han detectado siempre «metales» (término para referirse a todos los elementos más pesados que el hidrógeno y el helio) en cualquier lugar que buscaran en el Universo.”
Antes de que se formaran las primeras estrellas, el 75% del material era Hidrógeno
Hidrógeno y Helio es el material primario del Universo y, a partir de ellos, se forman las estrellas que convierten ese material en una especie de plasma a altas temperaturas que en la superficie de la estrella puede ser de 6.000 grados y en el núcleo de 15 millones.
La fusión nuclear, convierte el hidrógeno en helio, el helio en carbono, el carbono en oxígeno, y, de esta manera hasta llegar al hierro. Otros materiales más complejos se producen cuando las estrellas supermasivas explotan en supernovas sembrando el espacio con una nueva Nebulosa y, su núcleo se convierte en una estrella de neutrones o en un agujero negro.
Pero veamos algún objeto más de los que pueblan el inmenso espacio del Universo.
La luz está compuesta por fotones y precisamente ya se ha dicho que es la luz la que tiene el record de velocidad del universo al correr a unos 300.000 Km/s, exactamente 299.792’458 Km/s.
¿Y los neutrinos?

Casi todos los tipos de materia en el universo mantiene sus mismas cualidades básicas, no importa donde esté en el espacio, o donde esté en el tiempo. Las cosas no cambian espontáneamente en otra cosa al azar. Pero hay una excepción: los neutrinos. Estas minúsculas partículas se comportan principalmente de acuerdo con las leyes de la mecánica cuántica, y como resultado se comportan de una manera bastante extraña.
Existen tres tipos de neutrinos: el neutrino de electrones, el neutrino de muón y el neutrino de tau. Los Neutrinos se crean en las interacciones de las partículas, y los tres tipos de neutrinos se nombran según la partícula que es responsable de crearlos. Los científicos creen poco probable que haya algún otro «sabor», a menos que tenga propiedades muy diferentes a las de los encontrados. Estos se asocian con distintas partículas cargadas y de allí se derivan sus nombres: Están asociados al electrón (neutrino electrónico), al muón (neutrino muónico) y a la partícula Tau (neutrino tauónico).

Existen grandes detectores de neutrinos
Un grupo de investigadores del Consejo Superior de Investigaciones Científicas (CSIC) determinó que la masa de los neutrinos no excede de 0,26 electronvoltios, dos millones de veces inferior a la masa del electrón. El equipo ha descubierto que la suma de las masas de los tres tipos de neutrinos que existen (electrónicos, muónicos y tauónicos) no representa más del 6 por mil del total de la masa-energía del cosmos.
Los neutrinos se forman en ciertas reacciones nucleares y ningún físico atómico ha sido hasta ahora capaz de medir su masa. Es probable que los neutrinos, como los fotones, tengan una masa en reposo nula, aunque en realidad el neutrino nunca podrá estar en reposo y, como el fotón, siempre se está moviendo a velocidades cercanas a los 299.792’458 Km/s, casi como los fotones pero, algo menor al tener algo de masa.

Los fotones son los cuantos de la luz y transmisores del electromagnetismo y de cualquier clase de radiación en el Universo.
Pero los neutrinos no son fotones, porque ambos tienen propiedades muy distintas. Los fotones interaccionan fácilmente con las partículas de materia y son retardados y absorbidos al pasar por la materia. Los neutrinos, por el contrario, apenas interaccionan con las partículas de materia y pueden atravesar un espesor de años luz de plomo sin verse afectados.
Parece claro, por tanto, que si los neutrinos tienen una masa en reposo nula, no son materia. Por otro lado, hace falta energía para formarlos, y al alejarse se llevan algo de ella consigo, de modo que son una forma de energía.

Para capturarlos, han ideado grandes depósitos de agua pesada en las profundidades de la Tierra.
Los neutrinos atraviesan cualquier espesor de materia sin interaccionar apenas, de modo que prácticamente no efectúan trabajo. Lo cual les distingue de cualquier otra forma de energía. En su momento se habló de que los neutrinos podían ser la energía oscura que tanto fascina a todos los físicos, astrofísicos y astrónomos, sin embargo, al no haber detectado la masa de los neutrinos, se desechó la idea.
El neutrino es de la familia de los leptones y existe en tres formas. Una asociada al electrón y se conoce como neutrino electrónico (Ve), otra al muón y es el neutrino múonico (Vµ) y por último el que está asociado con la partícula tau, que es el neutrino tauónico (Vt). Cada forma tiene su propia antipartícula.
El neutrino fue postulado en 1.931 para explicar la energía “perdida” en la desintegración beta. Fue identificado de forma tentativa en 1.953, y definitivamente en 1.956, dando la razón a Wolfgang Pauli que presintió su existencia.
Los neutrinos no tienen carga y como dijimos antes, tampoco tienen masa; son pura energía que viaja siempre por el espacio a la velocidad de la luz. En algunas teorías de gran unificación se predice que los neutrinos tienen masa no nula, pero no hay evidencia concluyente para eso.
Cuando Pauli propuso su existencia para justificar la energía perdida en la desintegración beta, Enrico Fermi lo bautizó con el nombre de neutrino. La ley de conservación de la energía prohíbe que ésta se pierda, y en la desintegración beta, que es un tipo de interacción débil en la que un núcleo atómico inestable se transforma en un núcleo de la misma masa atómica pero de distinto número atómico, hace que en el proceso un neutrón se convierta en un protón con la emisión de un electrón, o de un protón en un neutrón con la emisión de un positrón. Pero la cuenta no salía, allí faltaba algo, no se completaba en la transformación la energía original, así que Pauli añadió en la primera un antineutrino electrónico y la segunda la completó con un neutrino electrónico.
Evitamos fórmulas y explicaciones complejas.
Así fue como se dio a conocer al mundo la existencia de neutrinos.
Ahora para ir conociendo mejor el Universo, dejemos aquí explicados algunos conceptos:

Asteroide.
(Planetas menores; planetoides)
Pequeños cuerpos que giran alrededor del Sol entre las órbitas de Marte y Júpiter en una zona alejada entre 1’7 y 4’0 Unidades astronómicas del Sol (cinturón de asteroides). El tamaño de estos objetos varía desde el más grande, Ceres (con un diámetro de 933 km.), a los objetos con menos de 1 km. De diámetro. Se estima que hay alrededor de 10 cuerpos con diámetro mayor de 250 km. Y unos 120 cuerpos con diámetros por encima de 130 km.
Aunque son millones, su masa total es apenas una pequeña fracción de la Tierra, aunque no por ello dejan de ser preocupantes en el sentido del peligro que pueda suponer para nuestro planeta, la colisión con uno de estos pedruscos enormes del espacio estelar. La desaparición de los Dinosaurios podría ser una prueba de los efectos devastadores de una colisión de este calibre. Según algunos creen uno de estos cuerpos enormes cayó en Mexico y arrasó con la vida de los grandes reptiles.
Astrofísica.
Ciencia que estudia la física y la química de objetos extraterrestres. La alianza de la física y la astronomía, que comenzó con la creación de la espectroscopia, permitió investigar lo que son los objetos celestes, y no solo donde están. Es una de las ciencias más antiguas, cuyo objetivo es explicar los fenómenos del Universo apoyándose en los conocimientos de la Física y otras ciencias afines. Asi también la astrofísica pretende determinar el origen, la formación y la evolución de los planetas, estrellas y galaxias.
Esta ciencia nos permite saber la composición de elementos que tiene un objeto estelar situado a miles de años-luz de la tierra, y, de momento, se confirma que el material existente en el Universo entero, es igual en todas partes.
El Universo primitivo era un plasma, cuando se enfrió se convirtió en Hidrógeno y algo de Helio (los dos elementos más simples) y más tarde, cuando se formaron las primeras estrellas y galaxias, se pudo fabricar, en los hornos termonucleares de las estrellas, el resto de elementos más complejos y pesados, tales como litio, carbono, oxigeno, nitrógeno, todos los gases nobles como argón, kriptón, neón, etc., el hierro, mercurio… uranio y se completó la tabla periódica de elementos naturales que están, de una u otra forma dispersos por el Universo.
Nosotros mismos, la especie humana, estamos hechos de un material que solo se puede producir en las estrellas, así qué, sin lugar a ninguna duda, el material que nos formó se fabricó hace miles de millones de años en estrellas situadas a miles o cientos de miles de años-luz de nuestro Sistema Solar. ¡Qué insignificante somos comparados con la enormidad del Universo! Sin embargo, el hecho de pertenecer a él nos da cierta importancia, y, además, somos conscientes de Ser.

Astronomía invisible.
Estudio de objetos celestes observados mediante la detección de su radiación o longitudes de onda diferentes de las de la luz visible.
Mediante este método se ha detectado, por ejemplo, una fuente emisora de rayos X, Cygnus X-I, que consiste en una estrella supergigante que rota alrededor de un pequeño compañero invisible con una masa unas diez veces mayor que la del Sol y, por tanto, por encima del límite de Chandrasekhar y que todos los expertos le conceden su voto para que, en realidad sea un agujero negro situado en el corazón de nuestra Galaxia a 30.000 años-luz de la Tierra.

Astronómica, unidad.
Distancia media de la Tierra al Sol, igual a 149.600 millones de km., ó 499,012 segundos-luz, ó 8’316 minutos-luz. Cuando se utiliza para medir distancias entre Galaxias, se redondea en 150 millones de km.

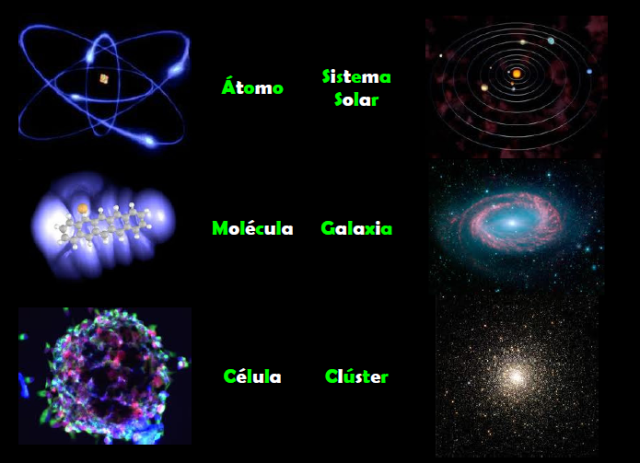
Átomo.
La parte más pequeña que puede existir de un elemento. Los átomos constan de un pequeño núcleo muy denso de protones y neutrones rodeado de electrones situados por capas o niveles y moviéndose. El número de electrones es igual al de protones y, siendo la carga de estas positivas y la carga de aquellas negativa, pero equivalentes, el resultado final del total de la carga es cero y procura la estabilidad entre cargas opuestas pero iguales.
La estructura electrónica de un átomo se refiere a la forma en la que los electrones están dispuestos alrededor del núcleo y, en particular, a los niveles de energía que ocupan. Cada electrón puede ser caracterizado por un conjunto de cuatro números cuánticos: el núm. Cuántico principal, el orbital, el magnético y el número cuántico de espín.
De acuerdo con el principio de exclusión de Pauli, dos electrones en un átomo no pueden tener el mismo conjunto de números cuánticos. Los números cuánticos definen el estado cuántico del electrón y explicar como son las estructuras electrónicas de los átomos.
En el núcleo reside casi por completo, la masa del átomo que esta compuesta, como se ha dicho por protones y neutrones que, a su vez, están hechos por quarks.
Se puede dar el caso de que, en ocasiones, se encuentren átomos exóticos en el que un electrón ha sido reemplazado por otra partícula cargada negativamente, como un muón o mesón. En este caso, la partícula negativamente cargada finalmente colisiona con el núcleo con la emisión de fotones de rayos X. Igualmente, puede suceder que sea el núcleo de un átomo el que sea reemplazado por un mesón positivamente cargado. Ese átomo exótico tiene que ser creado artificialmente y es inestable.

Big Bang.
Teoría cosmológica en la que toda la materia y energía del Universo se originó a partir de un estado de enorme densidad y temperatura que explotó en un momento finito en el pasado hace unos 15 mil millones de años. Esta teoría explica de forma satisfactoria la expansión del Universo, la radiación de fondo de microondas observada, característica de la radiación de cuerpo negro a una temperatura de 3 K y la abundancia observada de helio en el Universo, formado por los primeros 100 segundos después de la explosión a partir del denterio a una temperatura de 10.000.000.000 K. Ahora es considerada generalmente como más satisfactoria que la teoría de estado estacionario de un Universo quieto e inamovible. La teoría del Big Bang fue desarrollada por primera vez en 1.927 por A.G.E. Lamaitre (1894-1966) y retomada y revisada en 1.946 por George Camow (1904-1968). Han sido propuestas varias variantes de ella.
La teoría de la relatividad general predice la existencia de una singularidad en el comienzo, cuando la temperatura y la densidad eran infinitas. La mayoría de los cosmólogos interpretan esta singularidad como una indicación de que la relatividad general deja de ser válida en el Universo muy primitiva, y que el comienzo mismo debe ser estudiado utilizando una teoría cosmológica cuántica.
Con el conocimiento actual de la física de partículas de altas energías, podemos hacer avanzar el reloj, hacia atrás y a través de las eras Leptónica y la hadrónica hasta una millonésima de segundo después del Big Bang cuando la temperatura era de 1013 k. Utilizando una teoría más especulativa los cosmólogos han intentado llevar el modelo hasta 10-35 segundos después de la singularidad, cuando la temperatura estaba en 1018 K.

En el instante del Big Bang comenzó la expansión del Universo y en ese mismo momento, nació el espacio-tiempo. En un principio la simetría lo dominaba todo y reinaba una sola fuerza unificada. Más tarde, a medida que el Universo se enfriaba, la simetría se rompió y surgió la materia y las 4 fuerzas fundamentales que rigen hoy, la opacidad desapareció y todo fue transparencia, surgieron los fotones que transportaron la luz a todos los rincones del cosmos. Doscientos mil años más tarde surgieron las primeras estrellas, se formaron las Galaxias y, partir de la materia inerte, nosotros, la especie humana que, hoy, tan pretenciosa, quiere explicar como ocurrió todo.
Todo esto quedó bien explicado en días anteriores, sin embargo, se deja aquí un resumen como recordatorio para que todos, sin excepción, se familiaricen con estos conceptos del Cosmos.

Carbono, reacción de.
Importante proceso de fusión nuclear que se produce en las estrellas. Lo inicia, el carbono 12 y, después de interacciones con núcleos de nitrógeno, hidrógeno, oxígeno y otros elementos, reaparece al final. Este es el fenómeno que hace posible que las estrellas estén brillando en los cielos.

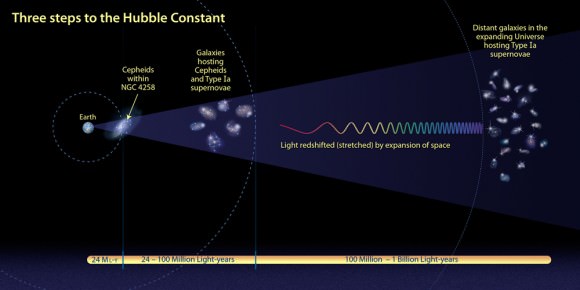
Cefeida variable.

Ahí la tenéis. Se trata de una de las estrellas más importantes del cielo. La estrella pulsante RS Puppis es el astro más brillante en el centro de la imagen. Es aproximadamente diez veces más masiva que el Sol y, en promedio, quince mil veces más luminosa.
De hecho, RS Puppis es una estrella Cefeida, es decir, una estrella cuyo brillo varia de manera regular y por esto mismo se la utiliza para estimar la distancia a las galaxias cercanas. Este es uno de los primeros pasos para establecer las escalas de las distancias cósmicas, y, este tipo de estrellas se denominan estrellas variables Cefeidas.
Una estrella variable pulsante cuya periodicidad (esto es, el tiempo que su brillo tarde en variar) está directamente relacionada con su magnitud absoluta. Esta correlación entre el brillo y el período hace útiles las cefeidas para medir distancias intergalácticas.

Se han combinados datos sobre las curvas de luz de estrellas variables como Delta Cephei y Beta Lyrae
Uno de los grupos importantes de gigantes o supergigantes amarillas variables pulsantes, llamadas así por su prototipo, Delta Cephei. Este término general y aplicado comúnmente a más de un tipo estelar, en particular a los cefeadas clásicas antes mencionadas Delta Cephei, y a los menos numerosas estrellas conocidas como W virginia. En su tamaño máximo, los Cefeidas son típicamente un 7-15% mayores que en su tamaño mínimo.

Centauros A.
Intensa radiofuente o fuente de rayos X situada en la constelación Centauros, identificada con la Galaxia elíptica gigante de una magnitud 7 NGC 5128. Centauros A es una radio galaxia clásica con dos pares de lóbulos radioemisores, el mayor de los cuales extendiéndose hasta a 1’5 millones de a.l. y con un chorro que unos 10.000 a.l. de longitud. Estando situada a 15 millones de a.luz, se trata de la radiogalaxia más cercana al Sol. Aunque la Galaxia madre se identifica como eliptica, tiene una banda de polvo poco característica cruzándola, que se cree es el resultado de la unión de una galaxia eliptica en otra espiral.
Esta situada entre el Grupo Local y el centro del supercúmulo de Virgo.

Colapso gravitacional
Fenómeno predicho por la teoría de la relatividad general en el que la materia comprimida más allá de una densidad crítica se colapsa como consecuencia de la atracción gravitacional hasta que aparece una singularidad puntual.
La singularidad resultante del colapso gravitacional puede ser interpretada como una indicación de que se ha llegado al límite de la teoría de la relatividad general y de la necesidad de construir una gravedad cuántica.
La hipótesis de la censura cósmica sugiere que el punto final del colapso gravitacional debe ser un agujero negro, pues las singularidades están siempre ocultas en astrofísica, pues suministra una evidencia indirecta de la existencia de los Agujeros negros.
También, dependiendo de la masa de la estrella, cuándo finalmente agotan su combustible nuclear de fusión (hidrógeno, helio, oxigeno, carbono, etc.) y la gravedad no encuentra oposición para realizar su trabajo, las estrellas colapsan bajo su propio peso, no siempre hasta agujeros negros, como nuestro Sol un día en el futuro, podrán colapsar a estrellas enanas blancas o estrellas de neutrones y los supermasivas, estas así, serán agujeros negros.

Cometas
Miembros secundarios del Sistema Solar que, según se cree, son montones de suciedad y hielo que son residuos de la formación del sistema solar. Se cree que hay millones de cometas en la Nube de Oort, una región esférica con un radio de treinta mil a cien mil unidades astronómicas con centro en el Sol. Los cometas que llegan de la Nube de Oort son calentados por el Sol y desarrollan colas brillantes que los hacen visibles en los cielos de la Tierra.
Figura ilustrando el corrimiento al rojo de tipo gravitacional.
Corrimiento al rojo.
Desplazamiento de las líneas espectrales en la luz proveniente de las estrellas de las galaxias distantes, que se considera producido por la velocidad de alejamiento de las galaxias en un universo en expansión (ley de Hubble). Cuando las galaxias en lugar de alejarse se acercan (caso de Andrómeda), el corrimiento es hacia el azul.
Cósmica, densidad de la materia. (Densidad crítica)
Densidad de materia que se obtendría si toda la materia contenida en las Galaxias fuera distribuida uniformemente a lo largo de todo el Universo. Aunque las estrellas y los planetas tienen densidades mayores que la densidad del agua (alrededor 1 gr/cm3), la densidad media cosmológica es extremadamente baja (menos de 10-29 gr/cm3, o 10-5 átomos/cm3 ), ya que el Universo está formado casi exclusivamente por espacio virtualmente vacío entre galaxias. La densidad media de materia determina si el Universo continuará expandiéndose o no.

La llamada densidad crítica, es la densidad media de materia requerida para que la Gravedad detenga la expansión del Universo. Un Universo con una densidad muy baja se expandirá por siempre, mientras que uno con una densidad muy alta colapsará finalmente. Un Universo con exactamente la densidad crítica, alrededor de 10-29 gr/cm3, es descrito por el modelo Einstein- de Sitter, que se encuentra en la línea divisoria de estos dos extremos.
La densidad media de materia que puede ser observada directamente en nuestro Universo representa sólo el 20% del valor crítico. Puede haber, sin embargo, una gran cantidad de materia oscura que elevaría la densidad hasta el valor crítico. Las teorías de universo inflacionario predicen que la densidad presente debería ser muy próxima a la densidad crítica; estas teorías requieren la existencia de materia oscura que, hoy por hoy, es el misterio más grande de la Astrofísica.
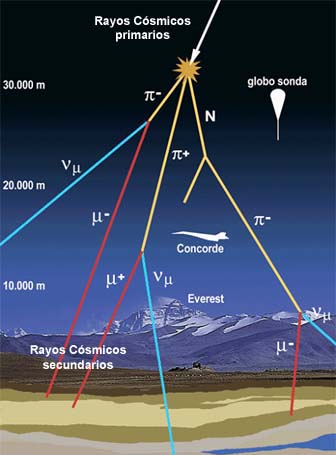
Cósmicos, rayos.
Partículas subatómicas, principalmente protones, que atraviesan velozmente el espacio y chocan con la Tierra. El hecho de que sean masivas sumado a sus altas velocidades, hace que contengan considerable energía: de 108 a más de 1022 eV (electrón-voltios).
El 90% de los rayos cósmicos son protones (núcleos de hidrógeno) y partículas alfa (núcleos de helio) la mayor parte del resto. Los núcleos más pesados son muy raros. También están presentes un pequeño número de electrones, positrones, antiprotones y neutrinos y rayos gamma.
Los rayos cósmicos fueron detectados por primera vez durante el vuelo de un globo en 1.912 por V.F.Hess, y el término fue acuñado en 1.925 por el físico norteamericano Robert Andrews Millikan (1868-1953).
Cosmología.
- Ciencia que se ocupa de estudiar la estructura y la composición del Universo como un todo. Combina la astronomía, la astrofísica y la física de partículas y una variedad de enfoques matemáticos que incluyen la geometría y la topología.
- Teoría cósmica particular.

Cosmología constante.
Un término empleado a veces en cosmología pasa expresar una fuerza de “repulsión” o “repulsión cósmica”, como la energía liberada por el falso vacío que los modelos del Universo inflacionario consideran que potenció exponencialmente la expansión del universo. Que exista tal repulsión cósmica o que haya desempeñado alguna vez un papel en la historia cósmica es un problema aún no resuelto, como ocurre con la constante cosmológica de Einstein.

Cúmulo de estrellas.
Conjunto de estrellas unidas por la Gravitación, más pequeños y menos masivos que las Galaxias. Los cúmulos “globulares” son más abundantes; son viejos y pueden contener de cientos de miles de millones de estrellas; se les encuentra dentro y lejos del disco Galactico.
Se extienden sobre un radio de unos pocos megaparsecs (también existen pequeños Grupos de Galaxias, como nuestro Grupo Local de solo unas pocas Galaxias.)
Este apartado final del trabajo de hoy, es debido a una petición de un profesor amigo que, me lo ha pedido para introducir a sus alumnos en el mundo de la Astronomía y que tomen conciencia del lugar en el que se encuentra,.
emilio silvera
Ene
19
Caer en un Agujero Negro es la muerte
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)

Kip Thorne (Logan, EE UU, 1940) es uno de los mayores expertos mundiales en agujeros negros. Últimamente también se ha convertido en una estrella de la divulgación como asesor de Interstellar, la película que plantea una expedición humana a un agujero de gusano, seguida de una caída en un agujero negro, seguida de un viaje hacia la quinta dimensión. La semana pasada, este físico teórico del Instituto Tecnológico de California acudió a Londres para la presentación de la medalla Stephen Hawking, impulsada por el Festival Starmus. Después de la ceremonia, el físico explicó a Materia sus próximos proyectos.

Pregunta. ¿Por qué cree que los agujeros negros son tan atractivos para la gente?
Respuesta. Bueno, son misteriosos, son extraños, llevan la marca personal de Stephen Hawking… Para los científicos, son únicos. Aunque se crearon por la implosión de una estrella, la materia desaparece en la singularidad en el centro del agujero negro. Por eso están hechos solo de tiempo y espacio curvos, no tienen materia, son completamente diferentes de ti y de mí.
P. Para Interstellar hizo cálculos reales de qué sucede si caes en un agujero negro. ¿Qué es lo más interesante que descubrió?
R. Lo más excitante fue ver cuál sería el aspecto de Gargantúa, el agujero negro. Es maravillosa, con ese halo alrededor y el disco que lo cruza. Otra cosa muy interesante es cuando Cooper [Matthew McConaughey] entra en el agujero negro. En ese momento dice: estoy cruzando el horizonte de sucesos [el punto de no retorno en un agujero negro]. Claro, nada escapa de un agujero negro, ni siquiera la luz, por lo que de frente no verías nada, pero, si miras atrás y ya estás dentro de él, sí verías el universo exterior. Y es una imagen maravillosa en la que el disco de gas caliente en torno al agujero negro es un anillo en el cielo que contiene al universo.

Los agujeros negros están hechos de tiempo y espacio curvo, no tienen materia, son completamente diferentes de ti y de mí”
P.¿Y qué pasa después?
R. Pues sabemos que hay tres singularidades diferentes dentro de un agujero negro. Una singularidad es un punto en el que la curvatura del espacio-tiempo se hace infinitamente fuerte. Hay una singularidaddescubierta por tres físicos teóricos rusos alrededor de 1970. Si caes en esa, estás totalmente destruido, te haces trizas de forma caótica y salvaje. Una segunda singularidad está hecha de todas las cosas que caen al agujero negro después de ti. Este material cae durante miles de millones de años, pero el tiempo va tan lento dentro de un agujero negro que todo ese material se te cae encima en una fracción de segundo, como si fuera una plancha. No me gustaría que eso me pasase. Cooper encuentra la tercera singularidad, que es la más débil de todas. Esta singularidad la causa todo lo que cayó al agujero negro antes que tú. Una fracción pequeña de todo ese material rebotará como si fuera una piedra que da saltos sobre el agua de un estanque. Esa pequeña fracción de toda la materia que cayó al agujero negro sale despedida y saca con él a Cooper en una fracción de segundo. Así que hay una posibilidad de que sobrevivas a un agujero negro.
P. ¿Qué será lo siguiente para usted en este campo?

Las leyes de la gravedad cuántica nos dirán si es posible viajar en el tiempo”
R. Stephen Hawking, Lynda Obst, una productora de Hollywood, y yo, hemos escrito nueve borradores de una nueva película. Es muy diferente de Interstellar. Estamos empezando a hablar con posibles guionistas y estudios sobre ella. Es aún en un momento inicial del proyecto
P. ¿De qué tratará?
R. Algo que aprendí de Christopher Nolan es que no dices nada a la gente sobre una película antes de tiempo. Vas filtrando la información en el momento adecuado para aumentar la expectación, así que por ahora solo puedo decir esto. Y que tendrá física interesante.
P. ¿Cuál es el próximo gran reto en la física de los agujeros negros?

R. Hay algo que nunca hemos visto: cómo se comportan dos agujeros negros que chocan y crean una tormenta en el espacio-tiempo. La colisión hace que, por un breve periodo, el paso del tiempo acelere, desacelere, vuelva a acelerar… todo de una forma salvaje, caótica. Esto deforma el espacio en una dirección y otra, que gire en el sentido de las agujas del reloj y después al revés, crea vórtices que curvan el espacio y que luchan unos con otros. Hemos visto esto muy recientemente en simulaciones por ordenador y empezamos a entender cómo se comporta una tormenta en la que el tiempo y el espacio oscilan de forma salvaje. Nunca lo hemos observado, pero lo vamos a hacer muy pronto.
P. ¿Cómo?
R. Cuando estos agujeros negros chocan crean ondas en el tejido del espacio-tiempo que se llaman ondas gravitacionales. Estas nos darán suficiente información como para ir hacia atrás en el tiempo partiendo de la onda que vemos y las simulaciones y probar si estas predicen de forma correcta lo que está pasando.
P. ¿Cuándo esperan captarlas?

Vista aérea del detector LIGO en Hanford, Washington.
R. Para hacerlo hemos construido los detectores LIGO. El equipo comenzó su primera tanda de búsquedas de ondas gravitacionales con los detectores avanzados en septiembre de 2015 y seguirá haciéndolo hasta enero de 2016. Estos detectores, incluso en la primera búsqueda, son tan sensibles que pueden captar un choque de agujeros negros a 1.000 millones de años luz de la Tierra, es decir, un décimo de la distancia hasta el límite del universo observable. Si tenemos suerte, captaremos algo en la primera búsqueda.
P. ¿Cuál es la próxima gran frontera de la física?

Es muy probable que haya civilizaciones más avanzadas que las nuestras”
R. Entender las leyes de la gravedad cuántica que derivan de combinar la Relatividad General con la física cuántica. No entendemos esas leyes bien, podría ser alguna variante de la teoría de cuerdas o la teoría M. Si tuviera que hacer una predicción diría que ese es el camino por el que iremos. Una vez entendamos esas leyes nos contarán de una forma muy clara el nacimiento del universo, qué pasa en la singularidad dentro de un agujero negro y si es posible retroceder en el tiempo.

P. ¿Cree que eso abrirá los viajes en el tiempo?
R. Abrirá una puerta a los viajes en el tiempo… o la cerrará [risas].
P. En uno de sus libros especulaba que si la humanidad quiere sobrevivir debería irse a un agujero negro¿Cree que es es nuestro futuro?

R. Hará falta mucho tiempo hasta que los humanos podamos explorar un agujero negro. Pero es verdad que en el giro de un agujero negro hay una enorme cantidad de energía rotacional que la naturaleza extrae para producir los gigantes brotes que salen de los núcleos de las galaxias. Los humanos de una civilización avanzada podrían usarlos como una descomunal fuente de energía mucho más potente que la fusión nuclear que sucede en el interior de las estrellas.
P. ¿Piensa que hay otras formas de vida inteligente en el universo?
R. Es muy probable que haya vida inteligente en el universo, civilizaciones más avanzadas que las nuestras. Pero las distancias entre las estrellas son tan enormes que el viaje interestelar es cada vez más difícil. Dudo mucho que otra civilización haya visitado la Tierra, pero creo que es muy probable que nos comuniquemos con ellos algún día, quizás antes de que yo muera, quizás no. Buscar señales de civilizaciones extraterrestres es uno de los empeños científicos más importantes que hay.

P. ¿Qué fue lo más importante que nos dejó Albert Einstein, de cuya Relatividad General se cumplen ahora 100 años?
R. Nos dio una ley que controla las leyes de la naturaleza. Es el principio de relatividad, que dice que sean cuales sean las leyes de la naturaleza, tienen que ser la mismas vistas por cualquier persona en cualquier lugar del universo si se están moviendo libremente. Creo que ese puede ser el mayor logro intelectual de todos los tiempos.
En todas las regiones del Universo, por muy alejadas que estén… pasan las mismas cosas y rigen las mismas leyes. Ocurre aquello que tiene que suceder conforme a los objetos y energías que allí estén presentes.
Hasta aquí aquella entrevista. A partir de ahora, con el descubrimiento publicado, comenzaremos una nueva etapa sobre el conocimiento del Universo que, de seguro., nos traerá muchas sorpresas.
Publica: emilio silvera
Ene
19
Moléculas vivas sorprendentes
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Biologia ~
Clasificado en Biologia ~
 Comments (0)
Comments (0)
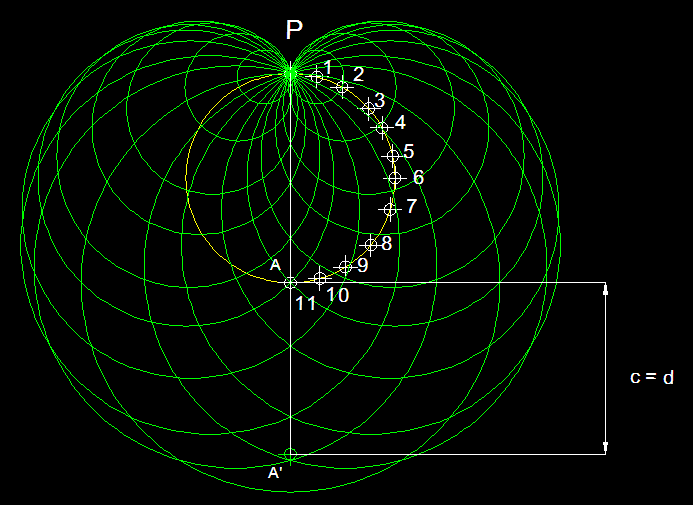
En matemáticas se pueden trazar líneas precisas y concretas que dividan en dos clases entes de naturaleza matemática. Una estructura geométrica se puede suporponer o no a su imagen especular. Una estructura asimétrica puede tener una lateralidad a la derecha o bien a la izquierda.
Cualquier número entero positivo es par o impar, y no hay ninguno de tales números para el cual su situación a este respecto ofrezca la menor duda. Pero en el mundo, si exceptuamos el nivel subatómico de la teoría cuántica, las lineas divisortias son casi siempre difusas. El alquitrán, ¿es sólido o líquido?. Lo cierto es que, la mayoría de las propiedades físicas se “mueven” en un espectro continuo que hace que vayan cambiando de manera imperceptible de un extremo a otro del mismo.

El paso del tiempo convierte en líquido, gas o sólido algunos materiales y, a otros, los deforma hasta perder su estructura original para convertirnos en lo que antes no eran. Nada permanece, todo cambia. Sea cual fuere la línea de división, habrá algunos casos en los que no podamos definirla y, en otros, habrá objetos tan próximos a ella que el lenguaje ordinario no será lo suficientemente preciso como para poder afirmar a qué lado pertenece. Y, la propiedad de la vida, está, precisamente, en uno de esos continuos.
Para porbar esto basta que consideremos los virus: son las estructuras biológicas más pequeñas que se conocen con la propiedad de poder “comer” (absorber sustancias situadas en sus proximidades), crecer y fabricar copias exactas de sí mismas.
Son mucho más pequeños que una bacteria (en realidad, algunos virus infectan las bacterias) y pasan sin dificultad a través de un filtro de porcelana fina que, aunque a nosotros nos parezca que está completamente sellada y su superficie es totalmente hermética y lisa, para ellos, tan “infinitamente” pequeños, ofrece miles de huecos por los que poder colarse.
Nuevas grabaciones en vídeo de un virus que infecta a las células sugiere que los virus se expanden mucho más rápido de lo que pensábamos. El descubrimiento de este mecanismo permitirá crear nuevos fármacos para hacer frente a algunos virus. En la punta de un alfiler caben millones de ellos. De hecho, los virus tienen el tamaño de una décima de micrómetro (diezmillonésima parte del metro).
El mundo de lo muy pequeño es fascinante y, por ejemplo, si hablamos de átomos, se necesitarían aproximadamente una cantidad para nosotros inconmensurable de átomos (602.300.000.000.000.000.000.000) para lograr un solo gramo de materia. Fijáos que hablamos de lo pequeño que pueden llegar a ser los virus y, sin embargo, el Hidrógeno con un sólo protón es el átomo más ligero y su masa es 400.000 veces menor que la masa de un virus, como antes dije, el organismo vivo más pequelo que se conoce. El virus más diminuto conocido mide unos o,00000002 m; su tamaño es 2.000 veces mayor que el del átomo. Y, en la punta del algiler que antes mencionamos cabrían 60.000.000.000 (sesenta mil millones) de átomos.


Como los virus son menores que la longitud de onda de la luz, no pueden observarse con un microscopio luminoso ordinario, pero los bioquímicos disponen de métodos ingeniosos que les permiten deducir su estructura, ya que pueden verlos mediante bombardeos con rayos X u otras partículas elementales.
En ralidad, se puede decir que un cristal “crece”, pero lo hace de un modo ciertamente trivial. Cuando se encuentra en una solución que contiene un compuesto semejante a él, dicho compuesto se irá depositando sobre su superficie; a medida que esto ocurre, el cristal se va haciendo mayor, pero el virus, igual que todos los seres vivos, crece de una manera más asombrosa: toma elementos de su entorno, los sintetiza en compuestos que no están presentes en el mismo y hace que se combinen unos con otros de tal manera que lleguen a dar una estructura compleja, réplica del propio virus.

Los virus sólo se multiplican en células vivientes. La célula huésped debe proporcionar la energía y la maquinaria de síntesis, también los precursores de bajo peso molecular para la síntesis de las proteínas virales y de los ácidos nucleicos. El ácido nucleico viral transporta la especificidad genética para cifrar todas las macromoléculas específicas virales en una forma altamente organizada.

El poder que tienen los virus de infectar, e incluso matar, un organismo, se debe precisamente a esto. Invade las células del organismo anfitrión, detiene su funcionamiento y lo sustituye, por decirlo de alguna manera, por otros nuevos. Ordena a la célula que deje de hacer lo que normalmente hace para que comience a fabricar las sustancias necesarias para crear copias de sí mismo, es decir, del virus invasor.
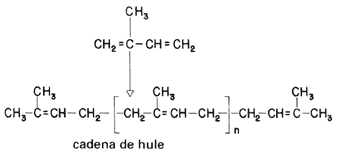
El primer virus que se descubrió, y uno de los más estudiados, es el virus sencillo que produce la “enfermedad del mosaico” en la planta del tabaco. Cristaliza en forma de barras finas que pueden observarse a través del microsopio electrónico. Recientemente se ha descubierto que cada barra es, en realidad, una estructura helicoidal orientada a la derecha, formada por unas 2.000 moléculas idénticas de proteína, cada una de las cuales contiene más de 150 subunidades de aminoácidos.


















 Totales: 85.981.906
Totales: 85.981.906 Conectados: 47
Conectados: 47