Oct
21
¡La Física! ¿Estará perdiendo el Norte?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)

¿Queremos imitar el salto cuántico y viajar más rápido sin tener recorrer el espacio que separan el punto de partida y el de llegada?
A finales del siglo XIX y principios del XX algunos podían creer que los secretos de la Naturaleza estaban todos descubiertos gracias a los hallazgos que en el pasado hicieran Newton y otros y más recientemente Maxwell, Planck, Einstein y otros muchos que, con sus trabajos nos desvelaron cómo funcionaba la gravedad, qué era en realidad la electricidad y el magnetismo y también, nos llevaron el fascinante mundo de lo muy pequeño con el cuanto de acción, h, de Planck que nos trajo poco más tarde, la mecánica cuántica.
La mecánica, la óptica, la electricidad… todo estaba descubierto y explicado. Los científicos de la época pansaban que sus futuros colegas sólo se dedicarían a realizar medidas para obtener las constantes con mayor precisión vez. Después de todo aquello, se siguió avanzando y continuamos haciéndonos preguntas creyendo que nos llevarían a las respuestas últimas.
Si, por ejemplo, las supercuerdas nos conducen a las respuestas últimas, entonces, ¿en qué dirección debemos nuestra investigación?, ¿es que nos hemos introducido tanto en el mundo de lo desconocido y lo ininteligible que estamos a punto de ahogarnos en un mar de lo absurdo?, ¿estamos enterrados bajo tántas preguntas de los imposibles que deberíamos considerarnos perdidos?, ¿tiene algún sentido especular acerca de la “Teoria de Todo” en un mundo extraño de las unidades de Planck?

Bueno, si queremos ser sinceros…, podemos discrepar de algunas de las cuestiones que hoy se están debatiendo y ser críticos con otras. Sin embargo, no podremos negar los avances que realmente se están logrando en el mundo de las nuevas tecnologías que, gracias a la Física, ya están en el futuro y, en nuestras vidas cotidianas lo estamos viendo continuamente.
Por otra , nada despierta más nuestra curiosidad que lo ininteligible y, precisamente por eso, tiene tanto éxito y llama la atención teorías como la de las supercuerdas. Miremos, por ejemplo, lo que es tan curioso en el mundo de la longitud de Planck es que no podemos encontrar absolutamente ningún modelo que nos pueda dar una descripción razonablemente autoconsistente de partículas que interaccionan entre sí con fuerzas gravitatorias tan intensas y que, al mismo tiempo, obedezcan a las leyes de la mecánica cuántica. Por tanto, incluso si hubiéramos sido capaces de realizar experimentos con choques de partículas con energías planckianas, no hubiéramos sabido como comparar los resultados con una teoría. Aquí hay para los físicos: hacer una teoría. No nos importa demasiado como describa esa teoría la interacción gravitatoria, pero tenemos suficientes requisitos en la lista como para que encontrar esa candidata a ser la teoría sea una labor extremadamente difícil. La Teoría de Supercuerdas parecía estar a punto de conseguirlo, pero falló en los últimos momentos. Dicen que necesitamos la energía de Planck para poder verificarla y, si es así, nos queda espera para rato.

Mientras buscamos esas teorías que están más allá de nuestras posibilidades reales de hoy, la Ciencia no se para y sigue avanzando en otros muchos campos que, como antes decía, nos están llevando a pasos agigantados un futuro que ya está con nosotros y, lo está haciendo con tal rapidez que ni nos hemos percatado de ello.
En cuanto a esa soñada Teoria de Todo, en primer lugar debe ser matemáticamente exacta y tiene que permitirnos calcular con extrema precisión el comportamiento de las partículas bajo todas las circunstancias imaginables. Por ahí circulan una y mil “teorías” que exponen las ideas más variopintas que imaginarnos podamos pero, desgraciadamente, son inútiles para los físicos porque sus descripciones no reúnen el rigor ni la prcisión que deben estar presentes en toda buena teoría. Por otra , los físicos prefieren que la teoría trate la fuerza gravitatoria de tal manera que esté de acuerdo con la obtenida en la formulación de la teoría de la relatividad general de Einstein. Sabemos que la fuerza gravitatoria cuerpos pesados como las estrellas y los planetas obedece a esta teoría con gran exactitud (como ha sido confirmado espectacularmente en las observaciones de los púlsares, estrellas compactas que rotan a gran velocidad. Nuestra teoría candidata debería explicar estas observaciones).

No digamos de los intrincados caminos que la Física ha sobrevolado cuando se ha querido meter en la posibilidad de viajes en el Tiempo y, los físicos se encontraron con una y mil paradojas extrañas. Además, como nos ocurre con la Teoría de cuerdas, al meternos en un sendero desconocido y de intrincados peligros…nunca hemos podido llegar al final después de largos y costosos recorridos. ¿Servirá para algo los muchos esfuerzos realizados?
Por otra somos conscientes y conocedores de que las leyes de la mecánica cuántica son inexorables y, por tanto, queremos que nuestra teoría sea formulada en términos de la mecánica cuántica. Tanto la mecánica cuántica como la teoría de la relatividad tienen la propiedad de que, tan pronto como uno admita la más pequeña desviación de esos principios, ambas darían lugar a una teoría totalmente diferente, que de ninguna manera se parecería al mundo que conocemos (o pensamos conocer). “Un poco relativista” o “un poco mecanicuántico” tan poco sentido como “un poco embarazado”. Podríamos imaginar, por otra parte, que la mecánica cuántica o la relatividad general, o ambas, serían marcos demasiado restrictivos nuestra avanzada teoría, de manera que habría que extender sus principios, llegar más lejos.


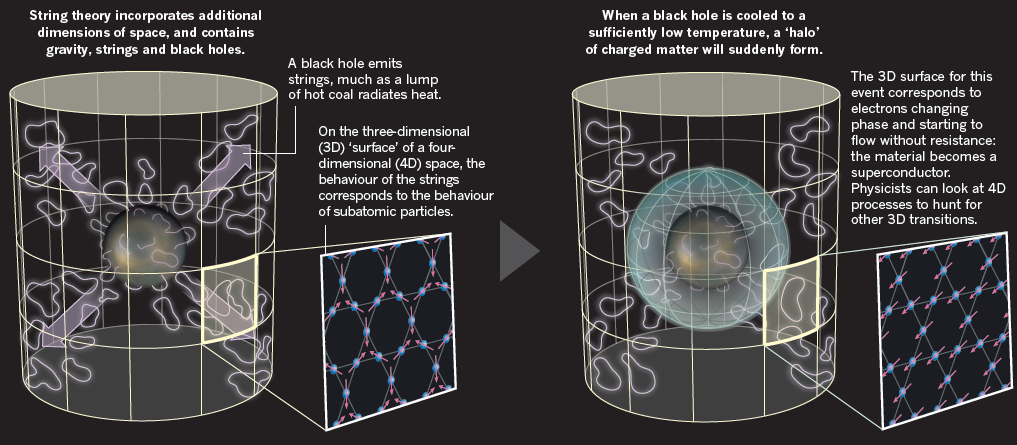
La cuerda es cuántica y gravitatoria, de sus entrañas surge, por arte de magia, la partícula mensajera de la fuerza de gravedad: el gravitón. Funde de natural las dos teorías físicas más poderosas de que disponemos, la mecánica cuántica y la relatividad general, y se convierte en supercuerda -con mayores grados de libertad- es capaz de describir bosones y fermiones, partículas de fuerza y de materia. La simple vibración de una cuerda infinitesimal podría unificar todas la fuerzas y partículas fundamentales.
Parece que todo está hecho de cuerdas, incluso el espacio y el tiempo podrían emerger de las relaciones, más o menas complejas, cuerdas vibrantes. La materia-materia, que tocamos y nos parece tan sólida y compacta, ya sabíamos que está casi vacía, pero no imaginábamos que era tan sutil como una cuerda de energía vibrando. Los átomos, las galaxias, los agujeros negros, todo son marañas de cuerdas y supercuerdas vibrando en diez u once dimensiones espaciotemporales.
Está claro que no trato de explicar aquí una teoría que no comprendo y, el tratar el tema se debe a la curiosidad de tratar de indicar el camino, o, los caminos, por los que se podría llegar más lejos, al , algo más allá. De una cosa si que estoy seguro: ¡Las cuatro fuerzas fundamentales del Universo, un día fueron una sola fuerza!

En el universo existen numerosas estrellas cuyas masas son considerablemente mayores que las del Sol, debido a lo cual, la fuerza gravitotoria en su superficie es considerablemente más intensa que sobre la Tierra o sobre el Sol. La enorme cantidad de materia de una de esas estrellas causa una presión inimaginablemente alta en su interior, pero como las tenperaturasd en el interior de las estrellas es también altísima, se produce una presión contraria que evita que la estrella se colapse. La estrella, sin embargo, pierde calor continuamente. Al proncipio de su vida, en las estrellas se producen todo de reacciones nucleares que mantienen su temperatura alta y que incluso la pueden elevar, pero antes o después el combustible nuclear se acaba. Cuanto más pesada sea la estrella, mayor es la prsión y la temperatura, y más rápidamente se consume su combustible. La contrapresión disminuye progresivamente y la estrella se va colapsando bajo la presión, según dismunye el tamaño de la estrella, la fuerza gravitatoria aumenta hasta que finalmente se produce una implosión -un colapso repentino y completo- que no puede ser evitado por más tiempo: ¡ha nacido un agujero negro!

Según todos los indicios, cuando la estrella es muy masiva, la Improsión finaliza convirtiendo toda la inmensa masa de la estrella en un A. N., pero antes, explota como supernova y llena el espacio de los materiales coplejos que han sido fabricados en sus nucleares, siembra el espacio con una Nebulosa de la que, años más tarde, nacerán nuevas estrellas y nuevos mundos…Y, ¿quién sabe? ¡Si nuevas formas de Vida!
A menudo implosión libera tanto calor que las capas exteriores de la estrella explotan por la presión de la radiación, y la implosión queda interrumpida produciéndose una esfera extremadamente compacta de “material nuclear” que conocemos como una estrella de neutrones. Algunas veces, estas estrellas de neutrones rotan con una tremenda velocidad (más de 500 revoluciones/segundo), y, debido a irregularidades en la superficie, emiten una señal de radio que pulsa con esa velocidad.
Si todos estos sucesos pudieran ser observados una distancia segura, las señales emitidas por el material durante la implosión pronto serían demasiado débiles para ser detectadas y, en el caso de un afgujero negro, el objeto se vuelve de ese color y desaparece de nuestra vista convertido en una “bola de gravedad pura”, se pueden calcular sus propiedades con precisión matemática. Sólo se necesitan tres parámetros para caracterizar completamente al agujero negro: su masa, su movimiento angular (cantidad de movimiento de rotación) y su carga eléctrica.
También se calcular como se comportan los chorros de partículas cuando se aventuiran cerca del agujero negro. Hawking ya nos habló de ello y explicó con suficiente claridad, lo que pasaba era que, en contra de lo que pudiéramos pensar, el agujero emite un débil flujo de partículas en ciertas circunstancias. ¿Esas partículas son reales! Agujero Negro está emitiendo un flujo constante de partículas de todas las especies concebibles.

El Telescopio Espacial Hubble y Chandra han captado la imagen de un impresionante anillo de Agujeros negros. La fotografía corresponde al conjunto Arp 147, en el que aparecen 2 galaxias interactuando entre sí y que se ubican a una distancia de 430 millones de años luz de la Tierra. La NASA combinó datos del Chandra con imágenes del Hubble. Mientras los tonos rojos, azules y verdes fueron resultado del trabajo del Hubble; los de color magenta, del Chandra. La captura muestra un anillo formado por estrellas masivas que evolucionaron rápidamente y explotaron en supernovas, como consecuencia de una colisión galáctica. Es así como dejaron densas estrellas de neutrones y posiblemente, también agujeros negros.
En el Universo ocurren sucesos que no podemos ni imaginar, tales son las fuerzas y energías que ahí están presentes y que dan lugar a maravillas que desembocan en transiciones de fase que convierten unas cosas en otras muy distintas haciendo que la diversidad exista, que la belleza permanezca, que la monotonía no sea el camino.

Es cierto que nunca hemos podido estar tan cerca de un agujero negro como poder comprobar, in situ, la radiación Hawking que, para su formulación, sólo utilizó leyes bien establecidas de la naturaleza y que, por tanto, el resultado debería ser incuestionable, pero no es del todo cierto por dos razones:
La primera razón es que nunca ( he dicho) hemos sido capaces de observar un agujero negro de cerca y mucho de un tamaño tan pequeño que su radiación Hawking pueda ser detectada. Ni siquiera sabemos si tales miniagujeros negros existen en nuestro universo, o si sólo forman una minoría extremadamente escasa entre los objetos del cielo. Aunque pensemos conocer la teoría, no nos habría hecho ningún daño haber podido comprobar sus predicciones de una o de otra. ¿Sucede todo exactamente como pensamos actualmente que debería suceder?
Otros, como Gerald ´t Hooft, consiguieron construir otro de teorías alternativas y le dieron resultados distintos a los de Hawking, en la que el Agujero Negro podia radiar con una intensidad considerablemente mayor que la que la teoría de Stephen predecía.

Hay un aspecto relacionado con la radiación Hawking mucho más importante. El agujero negro disminuye su tamaño al emitir partículas, y la intensidad de su radiación crece rápidamente según se reduce su tamaño. Justo de llegar a los estadios finales, el tamaño del agujero negro se hará comparable a la longitud de Planck y toda la masa llegará a ser sólo un poco mayor que la masa de Planck, Las energías de las partículas emitidas corresponderan a la masa de Planck.
¡Solamente una teoría completa de la Gravedad Cuántica podrá predecir y describir exactamente lo que sucede al agujero negro en ese ! es la importancia de los Agujeros Negros la teoría de partículas elementales en la Longitud de Planck. Los agujeros negros serían un laboratorio ideal para experimentos imaginarios. Todos alcanzan, por sí mismos, el régimen de energía de los números de Planck, y una buena teoría debe ser capaz de decirnos como calcular en ese caso. casi una década, Gerad ´t Hoofft ha resaltando esa objeción en la teoría de supercuerdas: no nos dice nada de los agujeros negros y mucho de cómo un agujero negro comenzar su vida como un agujero negro de tamaño “astronómico” y acabar su vida explosivamente.
Lo cierto es que, andamos un poco perdidos y no pocos físicos (no sabemos si de manera interesada), insisten una y otra vez, en cuestiones que parecen no llevar a ninguna parte y que, según las imposibilidades que nos presentan esos caminos, no sería conveniente elegir otros derroteros para indagar nuevas físicas mientras tanto, avanzan las tecnologías, se adquieren más potentes y nuevas formas de energías que nos puedan permitir llegar a sondear las cuerdas y poder vislumbrar si es cierto, que pueda existir alguna “materia oscura”, o, si existen bosones dadores de masa, o…¡tántas cosas más que, la lista, sería interminable! de las cosas que no sabemos. De hecho, el Modelo Estándar de la física de partículas ha tenido que dejar fuera a una de las fuerzas fundamentales, la Gravedad, no quiere cuentas con las otras fuerzas, y, además, una veintena de parámetros aleatorios conforman esa teroía que, habiendo sido (y lo sigue siendo) una buena herramienta de trabajo para los físicos, tiene muchas dudas pendientes de despejar. Aunque parece que el Bosón de Higgs, una de ellas, ha sido despejada y, esperamos que nos den muchas más explicaciones de su encuentro y de cómo ejerce sus funciones o cometidos de dar mas a las demás partículas.
emilio silvera
Oct
21
¡El Origen de la Vida! ¿Quién puede saber eso?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo y la Vida ~
Clasificado en El Universo y la Vida ~
 Comments (0)
Comments (0)
Sospecharlo sí, pero saberlo…





Los seres unicelulares han descubierto el método más corto para comer las plantas. La muerte y el sexo han de crearse para que los organismos pluricelulares sean capaces de envejecer y dejar de funcionar como una cooperativa colonial de células. Los animales han descubierto como comerse a otros animales. Por encima de todo, ha evolucionado una especie inteligente, una especie tan lista que ha llegado a descubrir una vía para poder salir de la Tierra y llevar todo el proceso de la evolución hasta el extremo.

Claro que, si creemos que la vida es ciudadana del universo sin fronteras, no debemos perder de vista la Panspermia, esas esporas viajeras que llegan a los mundos y en ellos, se posan y dejan pasar el tiempo para que, las condiciones locales, las radiaciones exteriores y propias del lugar, hagan su trabajo para que, con el tiempo suficiente por delante, puedan emerger y crecer hasta llegar a conformar seres con ideas y pensamientos.
emilio silvera.
Oct
21
¿Cómo sujetar los pensamientos?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo y los pensamientos ~
Clasificado en El Universo y los pensamientos ~
 Comments (0)
Comments (0)
El cerebro es ese “universo” que no hemos llegado a comprender, ese lugar de inmensa complejidad del que surgen las ideas y donde se crean los pensamientos sin fin. Es un conjunto de conexiones sin fin, de sinagsis y neuronas que crean en su conjunto un Ente inmaterial al que llamamos mente y que, al contrario que su parte material, puede “volar” hacia donde quiera y lo mismo visita galaxias y mundos que se puede dar una vuelta por confines del Universo. La Mente es una “herramienta” mágica que lo mismo realiza viajes en el tiempo al pasado que imagina, ese futuro que está por llegar.
Dentro de nuestras mentes se crean torbellinos de pensamientos que debemos ordenar. Andamos sumergidos en la espesa niebla de nuestra ignorancia y no siempre, sabemos “ver” con la claridad sificiente y necesaria cómo es el mundo. En escritos míos anteriores, me he referido a la teoría expuesta de manera magistral por el reconocido físico teórico Kip S. Thorne. Él cree firmemente que en el futuro será posible viajar al pasado a través de un agujero de gusano. Para que las bocas de entrada aquí, y la de salida “allí” -pongamos por ejemplo, que el allí está en Andrómeda- se mantengan abiertas, es necesario que dispongamos de energía exótica como la que se produce en las placas del Efecto Casimir.
Lo malo de esa teoría es que, para que la energía exótica de “allí” impida que la puerta de llegada se cierre, primero tendríamos que llegar hasta Andrómeda y ponerla de la manera adecuada para que el experimento funcione. Pero, ¿cómo podemos llegar hasta Andrómeda, situada a 2,3 años-luz de nosotros? ¡Estos pensadores! Casi siempre, cuando se habla de cosas así, se deja volar la imaginación y se toman licencias que permiten redondear los pensamientos pero… ¡lejos de la realidad!

De la manera que vemos avanzar la ciencia, negar cualquier posibilidad futura, me parece al menos arriesgado y de tal maravilla, podría ser posible algún día muy lejos en el futuro, ¿quién sabe? si puede llegar a ser realidad. Sin embargo, hay que puntualizar algunas cosas.
- Todos hemos oído contar, hemos leído o hemos visionado alguna película en la que el personaje principal viaja al pasado, se encuentra con su abuelo, se pelea con él y lo mata, y así, ni su padre ni él mismo pudieron nacer.
- También se podría viajar al pasado, matar a Hitler y evitar el holocausto judío.
- O impedir la crucifixión de Cristo.
- O…

¡Pues va a ser que no! Los mecanismos del universo no permitirían tales acciones que cambiarían el curso de una historia que ya tuvo muchas consecuencias, y, como decía Hawking, alguna clase de censura cósmica, lo impedirá.
Si Thorne tiene razón y alguna vez vamos al pasado, a un mundo que fue y que no es el nuestro, creo que las leyes de la física impedirán que nuestra presencia fuese material y que nuestras acciones pudieran incidir en los hechos para cambiar su curso; eso es imposible. Cuando el suceso pasó no estábamos allí, y, por eso pasó de esa manera y, ahora, por mucho que queramos, no podremos cambiar ese hecho pasado. El Jarrón roto y hecho añicos nunca se podrá recomponer.

El Tiempo, eso que no sabemos explicar lo que es, tiene mucho que decir en todo esto de ir al pasado
Nuestra presencia allí sería incorpórea, holográfica, o, de cualquier otra manera en la que podríamos ver, observar, mirar con fascinación de manera directa lo que allí pasó, ser testigos de hechos históricos (seguramente sería una forma de turismo del futuro), pero no nos estaría permitido intervenir. Además, si eso algún día fuese posible, también es dudoso que las personas de aquel lugar de época remota, pudieran vernos, ya que, en realidad, nosotros en aquel momento no estábamos allí.

Lo que ya pasó es irreversible. No podemos físicamente retrotraer el tiempo para borrar lo que pasó. Cuando una estrella muere por haber agotado su combustiblre nuclear de fusión, explota como Supernova y crea una Nebulosa y un Agujero negro… ¿Cómo podríamos cambiar eso un millón de años más tarde, aunque consiguiéramos viajar al pasado?
Cuando un astrofísico mira una galaxia que está a 1.000 millones de años-luz de nosotros, está mirando el pasado. La galaxia que ve es la galaxia que fue hace 1.000 millones de años, que es el tiempo que ha tardado su imagen en llegar a nosotros viajando a la velocidad de la luz. No estamos capacitados de ninguna manera para poder observar esa galaxia tal y como es ahora; la distancia que la separa de nosotros tiene que ser recorrida, y el viaje duró mil millones de años, así que cuando lleguemos allí, la galaxia habrá evolucionado y será muy diferente a como era cuando iniciamos el viaje.
Los astrónomos creen haber hallado el objeto más lejano jamás divisado en el universo: una galaxia muy distante en el tiempo y en el espacio. Semioculto en una foto captada por el Telescopio Espacial Hubble y dado a conocer este año, se encuentra un corpúsculo de luz que los astrónomos europeos calculan es una galaxia de hace 13.100 millones de años. Es un momento en que el universo era muy joven, de apenas 600 millones de años. De confirmarse, será el objeto más antiguo y más distante hallado hasta la fecha y, la galaxia, probablemente ni exista ya.

El rayo de luz que es atraído por un agujero negro y desaparece en la singularidad, no puede volver para que lo podamos ver de nuevo. Allí, en ese lugar extraño y desconocido, se pierde toda la información y, si no explota y esparce todo su contenido, la información se perderá para siempre.
La entropía del universo es irreversible; el deterioro de los sistemas cerrados es imparable. Todo se transforma para convertir las cosas en otras diferentes. Son las leyes del universo, y a nosotros, simples mortales, sólo nos queda tratar de comprenderlas para obtener de ellas “tal como son” el mayor beneficio posible. Cuando la ambición o la inconsciencia nos lleva a querer cambiar las leyes del universo y de su naturaleza, el resultado no puede ser bueno. Somos nosotros los que tenemos que adaptarnos al medio y no al revés (excepto cuando por medios artificiales preparamos el medio para nuestro beneficio, pero simplemente adaptándolo y no cambiándolo).
Todas estas razones y muchas más que podrían exponerse aquí son las que impedirán algún día muy lejano de nuestro futuro, cambiar el pasado que, según mi opinión, es inamovible. ¡Ah!, y en contra de lo que dice en su libro Jean Bouchart, creo que todo lo que ocurre está causado por lo que ocurrió. Es lo que los físicos llaman causalidad. Nada ocurre porque sí, todo tiene su causa.

- Si de verdad amas, te amarán.
- Si estudias, aprenderás.
- Si eres un vago, te llegará la miseria y la degradación.
- Si haces lo que te gusta, serás más feliz.
Todo es la consecuencia de lo que hacemos. Igualmente, en nuestro mundo y en nuestro universo, rige la misma ley: si contaminas el planeta, se deteriorará el medio ambiente y morirá la atmósfera que ahora nos da la vida. Si una estrella agota su combustible nuclear, morirá, dejará de brillar y se convertirá en un objeto diferente. Todo es así.
Mi consejo: que nuestro comportamiento no sea nunca causante de males ajenos; que nos conformemos y sepamos valorar lo que tenemos; que tratemos cada día de ser mejores adquiriendo nuevos conocimientos, el verdadero sustento del ser. Cuanto más sabemos, más podemos ofrecer a los demás y a nuestro propio “espíritu”.

Seguramente, el verdadero amor es el único que nos salvará. En el último momento, surgirá en nosotros esa llama interior que llevamos dentro en la que se concentra todo lo bueno. El mal será rechazado y estaremos en un Universo mejor, más igual para todos, más justo y en el que, la dignidad de las personas estará asegurada. Quien trata de humillar a otro y despojarle de su dignidad, no es consciente de que en realidad, es su dignidiad la que se verá resentida por tan vil acción.
En mi transcurrir cotidiano, por mi trabajo, veo con mucha pena cómo las personas tratan de engañarse las unas a las otras. Es la forma general, y lo excepcional es el encontrar, muy de tarde en tarde, personas decentes y honradas, mejor o peor preparadas (qué más da) pero nobles de espíritu y limpias de corazón; cuando eso ocurre, es como una ráfaga de aire fresco y perfumado que inunda los sentidos.
Como lo normal es todo lo contrario, la fealdad interior, el engaño, la ausencia de moralidad y de ética, la traición de los “amigos” o familiares, etc., mi remedio es bien sencillo: me encierro en mi mundo particular de la física, la astronomía y, en definitiva, de cualquier rama del saber que esté presente en ese momento en mis pensamientos, y de esa forma, por unos momentos, me olvido de la fea verdad que nos rodea. La bondad y el amor sólo aparecen en efímeras ráfagas que rápidamente se esfuman y desaparecen, excepto en ámbitos como el seno famliar. Ahí, dentro de la familia -la esposa, los hijos, nietos hermanos y los padres… se desencadena un alto índice de ternura que hace florecer lo lo mejor de nosotros. En el seno familiar podemos sentir las bocanadas de aire puro y perfumado inexistentes en otro lugar. En algunos casos, ese estado de amor y de ternura se extiende hacia todos los demás.
Estamos en un mundo frío, cada cual campa a lo suyo y, por lo general, los demás sólo son instrumentos para conseguir nuestros objetivos. Nuestro mundo está cambiando, ya está regido por Ordenadores personalizados que atienden a nuestras instrucciones y se ocupan de necesidades cotidianas en la casa, en la oficina, en la fábrica y que son capaces de realizar planteamientos matemáticos en minutos, cosa que los seres vivos no pueden hacer a pesar de ser ellos los inventores del prodigio. No veo nada claro el devenir de la Humanidad.
Pasemos a otras cuestiones. En enero de 2.007, comenzó y se celebró en la India el 20 International Joint Conference of Artificial Intelligence, un encuentro en el que se pusieron al día todos los avances en inteligencia artificial, y donde fue celebrado el 50 cumpleaños de su creación.
El incremento de los resultados en este campo (mucho hemos hablado aquí de ello), ha sido asombroso. Internet es una buena prueba de ello en la búsqueda de información por contenido, comercio electrónico, sistemas de recomendación, web semántica, etc. el futuro de Internet, de la industria y del comercio, de las ciudades futuras, de los viajes espaciales, de la medicina, etc., etc., etc., dependerán de los progresos que se realicen en el ámbito de la inteligencia artificial y en la nanotecnología; ahí parecen estar el progreso del futuro.

Hemos llegado a fabricar “clones” artificiales que cuesta identificar de los originales y… ¡Esto no ha hecho más que empezar! ¿Dónde acabará todo?
La inteligencia artificial, entre otras cosas, podrá llevar y facilitar información a países subdesarrollados que, de esta manera, podrá ofrecer educación a sus habitantes, mejorará la salud de la población, su agricultura, etc. la calidad de vida, en definitiva.
Ya se están desarrollando en Japón los ordenadores inteligentes (los llamados de quinta generación), y el entusiasmo de empresas informáticas japonesas y estadounidenses por la inteligencia artificial aconsejó a Europa no quedarse atrás y acometer sus propios proyectos mediante programas de investigación en estas nuevas tecnologías del futuro.
Todo ese movimiento tecnológico dirigido a crear en el “universo” de la computación dentro del ámbito de lo que se ha dado en llamar Inteligencia Artificial… ¡No está mal si se es consciente de sus peligros y tenemos mucho cuidado con los límites que no debemos sobrepasar!

El término de inteligencia artificial, si no me falla la memoria, se acuñó en la reunión de Dartmouth en 1.956, que fue un evento único e histórico. Único porque no se volvió a celebrar, es decir, no fue el primero de una serie como ocurre con los congresos internacionales de lo que, se llevan celebrandos 20; y fue histórico por el hecho de que allí se acuñó el término que ha prevalecido de inteligencia artificial.
En DartMouth se presentó un único resultado: un programa llamado Logic Theorist, capaz de demostrar teoremas de lógica proporcional contenidos (según leí) en la famosa obra “Principia Matematica” de Bertrand Russell y Alfred Whitehead (la obra más famosa de Newton lleva el mismo título). El programa lo desarrollaron Herbert Simón (que en 1.978 recibió el premio Nobel de Economía), Alan Newell y Clifford Shaw. Sin embargo, en éste de enero en la India, se presentaron 470 resultados seleccionados entre los casi 1.400 que recibieron.
Estatua de Alan Turing y su retrato de fondo
Desde aquella reunión del 56, los hitos alcanzados en el campo de la IA han sido extraordinarios: desde jugar al ajedrez hasta diagnosticar enfermedades, comprender textos sobre temas concretos que implican conocimientos especializados… No obstante, el objetivo de desarrollar las inteligencias artificiales generales que los pioneros de esta ciencia, reunidos en 1.956, propusieron para ser alcanzados, quedan aún muy lejanos. Pero, todo llegará; todo es cuestión de ¡tiempo!
Esta ciencia le debe mucho a las matemáticas. Alan Turing es un ejemplo. Fue un gran matemático que formalizó conceptos tan básicos para la informática como el concepto de algoritmo y el concepto de calculabilidad mediante la denominada Máquina de Turing, lo que nos lleva a considerar a Turing como a uno de los “padres” de la informática y, más concretamente, de la informática teórica. En 1.950 publicó un ensayo, “Computing Machinery and Intelligence”, donde describió su famoso Test de Turing, según el cual se podría determinar si una máquina es o no inteligente. La IA le debe pues el test que lleva su nombre, pero la informática le debe más.


Estamos tratando de crear cerebros positrónicos en los que se desarrollen los pensamientos propios y… ¡hasta los sentimientos! ¿No estaremos queriendo ir demasiado lejos? Está claro que la IA se aliará y formará equipo con la biología y la nanotecnología, y de esta unión surgirán avances que ahora ni podemos imaginar en nuestra actual comprensión (limitada) de la inteligencia artificial.
Como siempre me ocurre, cuando me pongo a escribir mis pensamientos vuelan, parece que estoy estableciendo una conversación conmigo mismo y traslado lo que se ella surge a la pantalla del ordenador, donde quedan plasmados todos los pensamientos presentes en mi cerebro en ese momento. En esas líneas de letras quiero expresar lo que recuerdo, lo que he leído, lo que he estudiado del tema que en ese momento ocupa mi atención, y así ocurre que, no siendo infalible, los errores pueden ser muchos y algunas explicaciones o comentarios poco documentados (consulto muy poco escribiendo y me dejo llevar), por lo que pido disculpas. Sin embargo, mis lectores -que son buenos amigos-, ganan en frescura y espontaneidad; el texto es más natural y en él están ausentes las artificialidades. Creo que salen ganando.

Imaginar otros mundos es fácil… ¡Todos están en este! ¿Cuántas veces habré visitado yo mundos, estrellas, galaxias, o, los mismos confines del Universo? Mentalmente son innumerables los viajes que hice a todos esos lugares de mágica visión, allí donde en grandes nubulosas surgen los mundos y brillan estrellas masivas nuevas de radiación ultravioleta que inundan e ionizan toda la región.
Lo que quería decir antes -como otras veces me he ido por las ramas-, es que puedo comenzar hablando de una cuestión y terminar hablando de otra muy distinta. Me vienen a la mente temas diversos, y de manera natural, sigo mis pensamientos y así lo reflejo en la blanca pantalla.
¿No resulta más ameno? De todas formas, siempre trato de finalizar los temas. Básicamente soy un insaciable buscador de la razón de ser de las cosas; todo me parece interesante. Mi curiosidad es ilimitada y mi vehemencia y pasión me llevan, a veces, a olvidarme de comer o (más grave aún), de recoger a mi mujer, que en un pueblo cercano espera mi llegada como habíamos quedado. Son cosas corrientes de mi manera de ser, que cuando emprendo una tarea, una lectura, o un proyecto, lo quiero tener terminado antes de… ¡haberlo comenzado!

Leo cualquier titular en un periódico: “Instalan un observatorio bajo el hielo para estudiar los confines del cosmos. Cuando esté en marcha, los científicos esperan que detecte 1.000 colisiones diarias de neutrinos, partículas minúsculas que nos traen información del universo.” No puedo, a partir de ahí, evitar el comprar el periódico o la revista para leer todo el reportaje completo, aunque sé que no dirán nada que ya no sepa sobre los neutrinos y la manera de cazarlos en las profundidades de la Tierra, en profundas minas abandonadas en las que colocan tanques de agua pesada que, conectados a potentes ordenadores, detectan la presencia de estas diminutas partículas -al parecer- carentes de masa que pertenecen a la familia de los leptones.
Cada segundo que pasa, billones de estas minúsculas partículas invisibles llamadas neutrinos, atraviesan nuestros cuerpos, en muchos casos, después de haber recorrido de un confín a otro todo el universo. Sin que nos demos cuenta estamos conectados con el otro extremo del Cosmos por medio de las conexiones invisibles que su Naturaleza impone. De hecho, somos parte de ese inmenso Universo que tratamos de conocer.

En un depósito de agua pesada, en las profundidades de una vieja mina de niquel. El detector del Observatorio de Neutrinos de Sudbury (SNO), situado en Canadá, un exclusivo y avanzado laboratorio de física de partículas alojado en una cavidad excavada junto a una de las galerías de la mina, a 2.070 metros de profundidad para detectar neutrinos.
Los neutrinos, al contrario que los fotones, viajan sin cesar de un lado a otro del universo sin que ningún campo magnético los desvíe de su camino, y sin ser destruidos tras colisionar con otras partículas, ya que apenas poseen carga eléctrica ni interaccionan con la materia. Por ello, estudiar de cerca un neutrino permitiría descubrir su procedencia y aportaría a los científicos una valiosa información sobre los rincones del universo de los que provienen.
El problema que se plantea es que agarrar un neutrino no es tarea nada fácil, y aunque se cree que el neutrino puede ser el mensajero cósmico ideal, primero habrá que retenerlo para poder hacer la comprobación. Esta partícula fue anunciada o prevista su existencia por Wolfgan Pauli, y su nombre, neutrino (pequeño neutro en italiano), se lo puso el físico Enrico Fermi. Pauli quiso quiso así, con la existencia del neutrino, explicar dónde estaba la masa perdida en la fusión nuclear de la materia, en los fenómenos producidos por la radiación inducida por la fuerza nuclear débil. El neutrino era la explicación: La masa “perdida” se eyectaba al espacio en forma de energía representada por los neutrinos.

Aunque parezca no venir a cuento, me viene a la mente que el fin de la Edad de Hielo, hace 300 millones de años fue precedido por bruscos cambios en el nivel de dióxido de carbono (CO2), alteraciones violentas del clima y efectos drásticos sobre la vegetación del planeta. Pero, ¡¿qué estamos haciendo ahora?! La irresponsabilidad de algunos seres humanos es ilimitada.
Hace 300 millones de años, el hemisferio sur del planeta estaba casi totalmente cubierto por el hielo; los océanos del norte eran una sola masa gélida y los trópicos estaban dominados por espesas selvas, pero 40 millones de años después, el hielo había desaparecido; el mundo era un lugar ardiente y árido. La vegetación era escasa y los vientos secos soplaban sobre una superficie donde casi no había vegetación. Sólo un reptil podría sobrevivir en aquellas condiciones.
Ahora parece que estamos decididos a repetirlo. ¿Qué hará Gaia para defenderse? Creo que hará lo que estime necesario para preservar su integridad, y si para ello es preciso eliminar a los molestos “bichitos” que causaron el mal, no creo que dude en hacerlo, ya que los acogió, les ofreció todos los recursos necesarios para la supervivencia, y el pago no fue, precisamente, el más adecuado. Lo peor de todo esto es que el comportamiento, el egoísmo de unos pocos lo pagaremos todos. Es como cuando un niño molesta en el colegio y el maestro castiga a toda la clase.

Franz Liszt dijo una vez la hermosa frase siguiente:
“Nuestras vidas son preludios; preludios de una desconocida canción cuya primera nota es la muerte.”
Claro que él se refería a un nuevo comienzo después de que nuestro paso por este mundo finalizara. Él se refería a que, nuestro paso efímero por el mundo era sólo el preludio de lo que estaba por llegar. ¡Si eso le reconfortaba…, no tengo nada que oponer a su pensamiento!
El final es volver al origen… ¡Fundirnos con el Universo!
Liszt encabezó su referencia a un poema de Lamartine, en uno de sus más conocidos poemas sinfónicos, con esta memorable definición. Y se hizo la pregunta ¿Será verdad que la muerte es el comienzo? Bueno, es mejor ser respetuoso con ciertos pensamientos. Hay ciertos temas sobre los que la ciencia no tiene potestades ni puede legislar. Yo, en este sentido, me parapeto tras mi ignorancia para no pronunciarme sobre lo que desconozco, y sobre temas que la ciencia no está en condiciones de explicar. Claro que, no por ello y para mi intimidad, no dejo de tener mi propio criterio sobre lo que vendrá luego de ese último momento por el que tenemos que pasar todos.

Hay que reconocer el mérito de la mente Humana… ¡Haber ideado este lenguaje maravilloso!
Llegados a este punto, recuerdo las palabras de mi hija María, pianista y clavecinista, que tiene una personal y artística interpretación de las cosas a través de argumentos musicales. Para ella, la música es algo más que un arte; es el todo, una manera de interpretar la vida y de ver las cosas. La música es para ella su esencia, su materia revelada y el camino elegido para vivir en un mundo aparte, de colores, lleno de notas musicales que forman melodías de una belleza infinita. Cuando habla de su música, se transporta y vive dentro de una suerte poética que la eleva a un plano superior y filosófico, casi místico o religioso, que la revitaliza, le da una fuerza especial y, sobre todo, le hace feliz al estar haciendo aquello que más le gusta. El que puede conseguir eso, es un elegido -yo no pude elegir-. Claro que, a veces pienso: ¿No será que María se sumerge en su música para no ver la fealdad del mundo?
emilio silvera
Oct
19
¿Cómo podríamos resolver la estructura del Universo?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Lo que no sabemos ~
Clasificado en Lo que no sabemos ~
 Comments (0)
Comments (0)


“Imaginaos este instante en que los murmullos se arrastran discretamente y las espesas tinieblas llenan el gran navío del Universo.”
Esas palabras de Chakesperare en Enrique V (acto IV, esc. 1), nos podría valer ahora a nosotros estrapolarlas a este tiempo y haciendo un ejercicio de imaginación, convertir esas tiniebles en la “materia oscura imaginaria”, esa clase de materia que postulan los cosmólogos, que no podemos ver, que no emite radiación, que no sabemos de qué está hecha y, en realidad, tampoco sabemos donde está (sólo lo suponemos) pero, nos soluciona, de un plumazo, todos los problemas de la estructura del Universo. Esa clase de materia “invisible e indetectable” que sí emite, sin embargo, la fuerza gravitatoria y podría explicar el ritmo a grandes escalas que hemos podido observar en el comportamiento de nuestro universo y que antes de la llegada de la “materia oscura”, no sabíamos, a qué era debido… “¡ahora sí lo sabemos!”. Bueno, al menos, eso dicen algunos pero, lo tienen que demostrar.

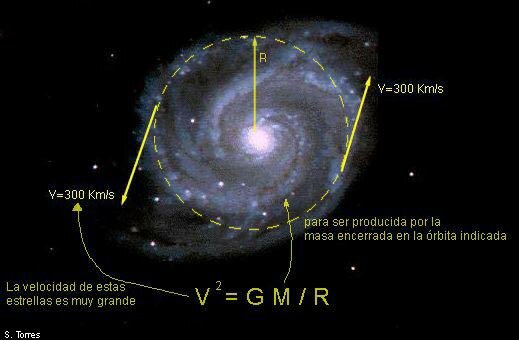
Sabemos, por ejemplo que, en el centro de la Galaxia, en Sagitario A, reside un gran mostruo que tiene tres millones de masas solares y, en la imagen de arriba podemos ver a un grupo de estrellas que lo orbitan en un perído de 15 años. Hemos hablado aquí de ese lugar, del Centro galáctico y, también de otras regiones que tienen inmensos Agujeros Negros que, al ser singularidades, hacen que el tiempo allí se distorsione y que el espacio adquiera una curvatura infinita. Sin embargo, la “materia oscura” no está compuesta por esos objetos exóticos y, según los cosmólogos, es otra cosa diferente, algo que no sabemos lo que es, algo que no podemos ver, algo que no tenemos ni idea de cómo se pudo formar ni de cuanto tiempo lleva aquí y de qué clase de partículas estará formada. La “materia oscura” es, en realidad, un auténtico misterio. Todos hablamos de ella pero…, ¡nadie sabe lo que es!

Hablar de la materia oscura es mí como hacerlo de esos personajes y animales míticos que sólo están en la mente del autor que nos narra una historia en la que, pueden estar presentes los Unicornios y también los más extraños personajes y animales que sólo existen en las peores pasadillas de mundos inimaginalbes.
Con la Materia Oscura nos pasa como cuando un enfermo terminar recibe la noticia de que ha aparecido un medicamento milagroso que podría curar su mal. Allí ponen todas sus esperanzas. parecer extraño que los cosmólogos pongan todas sus esperanzas en comprender el Universo centrándolo en una materia tan misteriosa como esa, pero eso es lo que está sucediendo en nuestros días.
Y no es que se trate simplemente de agarrarse a un “clavo ardiendo”: aprovecharnos de la ignorancia de la naturaleza de la materia oscura adjudicarle todas las propiedades que se requieran para resolver los problemas más inmediatos. ¿Qué falta hace conocer las propiedades de clase de materia para que nos resuelva, por ejemplo, el problema de la formación de las galaxias? Según la expansión de Hubble, las galaxias no tendrían que haberse formado, toda vez que la materia estaba “corriendo” y no hubiera tenido tiempo para formarlas. Sin embargo, algo tenía que estar allí presente que la !agarró” y la retuvo para que las galaxias se pudieran formar. ¿Sería la “materia oscura”?
Cuando nos encontramos con un problema desconocido del que ignoramos los motivos que lo producen, rápidamente construimos un modelo hipotético que lo resuelve y, nuestra ignorancia, queda a salvo y fuera de la vista de los demás.Según las leyes de la mecánica de Newton, la velocidad de una estrella a lo largo de su órbita depende de la masa de la galaxia contenida dentro de la órbita de la estrella. Sin embargo, la masa visible es mucho menor que lo esperado. ¿Donde está la masa que falta?
De la misma manera, las galaxias en el Universo se agrupan en cúmulos y supercúmulos de galaxias que para mantenerse unidos necesitan una inmensa cantidad de materia que genere la fuerza de gravedad necesaria para conseguirlo. Sin embargo, esa masa requerida no se observa ¿Donde está? ¿Cómo se comportan las galaxias como si estiuviera allí pero no se deja ver?
¿Cómo podríamos detectar la presencia de la Materia Oscura? ¿Cual será la naturaleza de la Materia Oscura? ¿Será posible que los objetos que constituyen la materia oscura del universo (si es que finalmente existe esa materia), esten formados por partículas que no hemos llegado a conocer por no emitir radiación y ser diferentes a los Quarks a los leptones que conforman los átomos de materia bariónica? A mí particularmente lo que más me llama la atención es que no teniendo ninguna de las propiedades que tiene la materia radiante, sí en cambio pueda emitir la fuerza gravitatoria que es, en definitiva, la que conviene en este caso explicar lo inesplicable.

Lo cierto es que andamos perdidos. Hay cosas en el vasto universo que no podemos explicar. La idea básica del papel de la materia oscura es fácil de entender. Como todos hemos llegado a saber, partimos de una dificultad primera que no hemos sabido resolver, nadie ha podido imaginar cómo evolucionó el universo, ya que tiene que ver con el hecho de que, si el cosmos entero está hecho de materia normal, la formación de galaxias no pudo haber empezado hasta muy avanzado el “juego”, después de que el universo se ha enfriado hasta el punto de que pueden existir átomos y la radiación se pueda desaparejar. entonces, la expansión de Hubble habría diseminado tanto la materia que la gravedad por sí sola no sería suficientemente fuerte reunir cúmulos antes de que todo se escapara de su alcance.

¿Y si la materia oscura no importa? Para todo aquellos escépticos, un matemático italiano ha conseguido lo nunca antes visto. El hombre ha llegado a través de una serie de fórmulas complejas y con extraordinaria similitud, trazar las curvas de la rotación de las galaxias espirales sin necesidad de materia oscura. Dicho de otra , a través de sus cálculos, el matemático ha representado la fuerza que mantiene unidas a las galaxias sin la necesidad de materia oscura. El ha sido expuesto en contra y frente al razonamiento deductivo de toda la comunidad científica.
Hasta ahora todos los experimentos científicos tenían a la materia oscura como esencial del entendimiento de las galaxias, para explicar aquello que no vemos. Si contamos la cantidad de masa en las galaxias espirales como la nuestra y luego tomamos el modelo de su rotación, obtenemos una imagen muy diferente a la que empíricamente se observa. La cantidad de masa en el centro de las galaxias espirales es enorme pero las estrellas exteriores se mueven alrededor de los discos galácticos con tanta rapidez que deberían volar hacia el espacio interestelar.

Lo cierto es que, no todos están de acuerdo con la existencia de la materia oscura y creen que los fenómenos que observamos se deben a otros parámetros que nos son desconocidos, e, incluso, podría tratarsde de alguna propiedad desconocida de la Fuerza de la Gravedad, o, ¿por qué no? podrían ser fluctuaciones del vacío que rasgan el espaciotiempo y dejan entrar, en nuestro universo, esa fuerza misteriosa que incide directamente en el comportamiento de nuestras galaxias y estrellas…lo cierto es que, no sabemos, realmente lo que pueda ser el motor conductor de esa anomalía observada y, sin embargo, ahí estamos con “la materia oscura por aquí” “la matería oscura por allá” y, la representamos de mil maneras distintas para poder convencer, a los excepticos .

El colmo de los colmos está en noticias como esta:
“3 marzo 2012. Los astrónomos que usan datos del Telescopio Hubble de la NASA han observado lo que parece ser un grupo de materia oscura que es parte de restos de un naufragio entre los cúmulos masivos de galaxias. El resultado podría desafiar las teorías actuales sobre la materia oscura que predicen que las galaxias deberían estar ancladas a la sustancia invisible, incluso durante el choque de una colisión.” (¿ … ?).

Abell 520. Imaged January 2012.
Credit: NASA
Abell 520 es una fusión gigante de cúmulos de galaxias situadas a 2,4 mil millones de años luz de distancia. La materia oscura no es visible, aunque su presencia y la distribución se encuentra indirectamente a través de sus efectos. La materia oscura puede actuar como una lupa, curvar la luz y causar la distorsión de las galaxias y cúmulos detrás de ella. Los astrónomos pueden usar este efecto, llamado lente gravitacional, inferir la presencia de materia oscura en los cúmulos de galaxias masivas”.
¿”…han observado lo que parece ser un grupo de materia oscura que es de restos de un naufragio entre los cúmulos masivos de galaxias”? ¿Qué tonteria es esa?

Imágenes estas tratan de explicar lo que no tiene explicación y, “explican” a su conveniente manera lo que ahí se está viendo y que, no es, necesariamente, lo que la explicación que se nos da quiere dar a entender. Me recuerda a los astrónomos de la antigüedad, cuando miraban al cielo y explicaban los fenómenos observados que estaban relacionados con el futuro de su rey, o, si eran los sacerdotes del templo los que lo explicaban, aquellos fenómenos estaban siempre relacionados con su religión y creencias. Ahora, guardando las distancias, son los mismos astrónomos y sacerdotes los que nos hablan de la materia oscura.
Un grupo de astrónomos que utilizó telescopios de ESO anunció en abril una sorprendente falta de “materia oscura” en la galaxia dentro de la vecindad del Sistema Solar. Pero, me pregunto yo, si no sabemos es la materia oscura, ¿de qué manera podemos detectar su falta o su presencia? Las contradicciones saltan a la vista cuando escuchamos lo que dicen diferentes grupos de astrónomos y cosmólogos que, estando a ciegas (como todos) en esa realidad que ignoran, echan mano de la materia oscura con desesperación.


Por otra , el galimatias que se está formando en torno a la materia oscura es descomunal. ¿Cuántos estudios se han realizado con resultados dispares? Unos dicen que la materia oscura “se observa alrededor de las Galaxias” y otros, por el contrario, vienen a decirnos que la falta de materia oscura en las galaxias es desconcertante. ¿En qué quedamos?
Así las cosas, tenemos que convenir en una realidad que nadie puede negar: La materia oscura (al menos de momento) es algo intangible, algo que ¡se ha pensado que pueda existir! a partir de las anomalías observadas en el comportamiento de las galaxias y que nadie sabe explicar a qué puede ser debido y, en esas estábamos cuando alguien, mencionó la “materia oscura” y, todos se lanzaron en tropel sobre ella…, ¡era la salvación!
De todos es bien conocido mi excepticismo hacia la dichosa “materia oscura” que, no niego que pueda existir pero, lo que siempre me ha chocado es que todos hablan de “ella” como si estuviera ahí, a la vista. La han convertido en algo familiar y cercano cuando…, ¡está tan lejos…! Incluso el Gravitón, del que todos hablan como una partícula hipotética, un Bosón mediador en la fuerza gravitatoria, tiene más sentido que la materia oscura. Todas las fuerzas tienen partículas mediadoras como los Gluones la fuerza nuclear fuerte, las W+, W– y Zº la fuerza débil, el fotón para el electromagnetismo y, el Gravitón para la fuerza de Gravedad que siendo la más débil de todas, no deja ver el cuanto de energía intercambiado en una interacción gravitacional.
¿La materia oscura? Sí, es la prueba palpable de nuestra ignorancia, de lo que decimos que sabemos pero que, en realidaddad desconocemos.
emilio silvera
Oct
19
¿Quién nos observa?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La vida ~
Clasificado en La vida ~
 Comments (0)
Comments (0)


En galaxias lejanas de cientos de miles de millones de estrellas y en otras de menor volumen pero no por ello menos interesantes, existen extraños mundos que, aunque diferentes al nuestro, también viven y se nutren de la radiación y la luz estelar que les llega. Unos tienen soles azules y otros blancos, también los hay amarillos como el nuestro y muchos de ellos son rojos. Cada una de esas estrellas, configuran el color de sus respectivos mundos y los hace de color mortecino, de un azulado brillante o incluso, en ocasiones, de un color que influye en la atmósfera del planeta hasta hacerlo parecer de sangre. También los hay, como el nuestro, son luminosos y están alumbrados por estrellas blanco-azuladas que le dan un tono de exquisita presencia.

No todos los planetas que alberguen alguna clase de vida, ni en nuestra Galaxia ni en otras lejanas, tienen que ser como la Tierra. Existen planetas en los que se nos encogería el corazón por su aspectos terrorífico y de inabitable naturaleza, mientras que otros, nos parecerían una fantasía sacada de esos cuentos de hadas que de ñinos podíamos leer, tal es su belleza natural. En la Tierra tenemos muchas de lugares que hacen honor a ese pensamiento.

De la misma manera que existen estrellas de mil tipos diferentes, así ocurre con los mundos que podemos encontrar repartidos por el universo orbitando estrellas que los configuran de mil diferentes maneras. Si nos fijamos en nuestro planeta que ha hecho posible nuestra presencia aquí, en el que junto a miles de otras especies hemos evolucionado, veremos que se han dado unas específicas para que todo eso sea posible.
Hemos podido llegar a un estado de evolución “aceptable” y alcanzado un nivel tecnológico que va más allá de lo que, hace sólo 200 años nos pudiéramos haber imaginado. Desde comienzo de la década de 1960, los programas de TV han emitido desde la Tierra hacia el espacio a un nivel de medio millón de watios. En la actualidad, la energía total emitida por las emisoras de televisión de todo el mundo es muy superior a los mil millones de watios. Durante los últimos quince años, esa cobertura expansiva de las emisoras de televisión, emitiendo desde la Tierra a la velocidad de la luz, ha podido llegar hasta centenares de estrellas y de mundos.

Enormes radares situados por todo el mundo lanzando ondas han podido ser la evidencia inequívoca de que aquí, en la Tierra, existen seres inteligentes que tratan de captar señales venidas del espacio exterior, de vigilar los posibles peligros que nos puedan llegar de mñás allá de los confines del solar, o, de captar esas señales que denoten la presencia de otros seres inteligentes que, situados en otros mundos lejanos, nos quieren decir alguna cosa o transmitir algún mensaje. Nosotros ya lo hemos intentado y continuamos haciendolo.
¿Cómo serán ellos?
Lo cierto es que hemos llegado a comprender que la vida en la Tierra, toda sin excepción está basada en el Carbono y, como también sabemos que las leyes del Universo son las mismas en todas , es lógico pensar que lo que pasó aquí habrá podido pasar allí, en cualquier planeta lejano situado en nuestra Galaxia o en cualquiera de la multitud de galaxias que conforman nuestro universo en el que cientos de miles de millones de mundos, no pueden estar vacíos y carentes de vida.

Todas esas señales y las que emitimos con nuestro quehacer diario, hacen que nuestro planeta brille hasta parecer un ascua encendida en la oscuridad . Las frecuencias de televisión y las bandas de FM de las emisoras de nos delatan ante posibles inteligencias en otros mundos. Radioastrónomos situados en otros sistemas solares notarán, al enfocar sus antenas en nuestra dirección, una emisión de energía y advertirán que, en esta estrella amararilla, existe una sociedad científicamente avanzada.

El gráfico de AbstruseGoose (después del salto) nos muestra lo que las civilizaciones extraterrestres estarían viendo en este momento si pudieran monitorear trasmisiones de televisión de la Tierra, de esas trasmisiones del pasado que ingresaron al y se propagan a la velocidad constante de c (la velocidad de la luz en el vacío).
Claro que nuestras señales televisivas le dicen a los extraterrestres mucho más que todo eso. A partir de sutiles cambios en las frecuencia de las señales provocados por la rotación de la Tierra, podrían deducir la distancia que hay entre la Tierra y el Sol, la probable temperaturta de la superficie de nuestro planeta y, a partir de aquí, que de vida puede haber en la Tierra. ¡Sabrían de nosotros mucho más que nosotros sabemos de ellos! Bueno, en realidad, de ellos no sabemos nada.

Si los astrónomos extraterrestres de otros sistemas solares han estado haciendo un seguimiento de nuestros progresos, tienen ya los datos de que nuestra especie, nuestra forma de vida, ha atravesado ya un importante nivel tecnológico, el umbral de las comunicaciones de radio. Los científicos extraterrestres pueden deducir a partir de su propia experiencia que esa conquista puede verse pronto continuada por un dominio de los viajes por el espacio que es la siguiente escala perseguida. Primero de un planeta a otro cercano. En nuestro caso, digamos a Marte, y, a continuación, y no mucho después. Comenzarán los viajes que nos llevarán a los confines del Sistema Solar en busca de otras fronteras. Sin que nos demos cuenta, ya hemos enviado el mensaje de nuestra presencia que es el precursor de nuestra entrada en la Comunidad Galáctica.

Si realmente existen esos seres que imaginamos en otros mundos y, si como es lógico pensar, al igual que nosotros han podido evolucionar hasta alcanzar aceptables niveles del saber sobre la Naturaleza y los secretos del Universo, también habrán podido alcanzar una avanzada tecnología que, más o menos como la nuestra, les posibilite para enviar señales y hacer viajes espaciales que (no me extrañaría nada) estuvieran ya camino hacia nosotros.
Millones de mundos que, como el nuestro, brillaran en la noche delatando la presencia de Sociedades avanzadas que, situadas en grandes ciudades dejan transcurrir sus vidas mientras, también como nosotros, no dejan de investigar y de hacerse preguntas que, tampoco ellos, saben contestar. El saber del mundo, de los mundos, está repartido por todo el Universo que es, en definitiva, el que tiene todas esas respuestas que buscamos.

Muchas veces me hago esta pregunta: ¿De qué estrella vendrá esa primera señal de inteligencia que esperamos? Las civilizaciones que la envíe ¿a qué distancia estará, cómo será su mundo, cuánto tiempo ha tardado en llegar a nosotros, y, cuando la podamos descifrar, y contestemos, cuánto tardarán en tener la respuesta? Incluso es posible -seguramente lo normal-, que esas señales hayan sido enviadas ya por ambas partes y que, ni ellos ni nosotros, debido a las distancias que nos separan, la hemos podido recibir. ¡Qué frustración, pensar que eso es así y no poder hacer nada por remediarlo!
Ya hablamos el otro día de las estrellas cercanas, las que estaban situadas dentro de un radio de unos doce años-luz y de las posibilidades que podían existir de que, en alguna de ellas (de sus planetas), pudiera existir alguna clase de vida. La presencia de vida inteligente en el inmenso universo, debe ser una cosa cotidiana, nada excepcional. Sin embargo, tal como están dispuestas las cosas, lo que no parece tan cotidiano es, el hecho de que, entre civilizaciones inteligentes nos podamos encontrar, las inconmensurables distancias que nos pueden separar son… ¡casi inaccesibles! y, el tiempo necesario para recorrerlas, vería pasar ante él a muchas generaciones de individuos antes de que, entre ellos, pudiera darse ese tantas veces imaginado.

Es poco probable que los que, ilusionados, lanzaron la señal hacia otros mundos. El mensaje que les hermanaría gracias a la inteligencia, pudiera ver realizados sus sueños de recibir una respuesta. El Proyecto OZMA y SETI son un buen ejemplo de ello. Y, por otra parte, no todas las estrellas están en disposición de poder dar a sus planetas lo que estos necesitan para albergar la vida. Pensemos que una estrella si es muy joven, digamos de unos cientos de millones de años, radiará en el ultravioleta con tal virulencia que, vida en sus inmediaciones sería imposible. Si por el contraria es una estrella vieja que, al final de su vida está a punto de explotar como supernova… tampoco parece que su entorno sea el adecuado.
Las estrellas y los mundos que puedan ser idóneas para que la vida esté presente, tendrán que tener esas mínimos exigidas para que, el agua esté presente, para que una atmósfera aceptablemente importante configure el planeta, que éste tenga una serie de parámetros de magnetismo, tectónica, oceános y otros que lo haga un planeta vivo, que la luz de la estrella lo caliente sin achicharrarlo… Si todo eso y algunas cosas más están presentes… La vida también lo estará.
Pero lo cierto es que, aunque la lógica nos dice que están ahí… ¡Seguimos sin recibir señales de que la vida está ahí fuera! El principal problema de que así sea, está en las distancias que nos separan y, simplemente tenemos que pensar que cualquier estrella orbitada por planetas está a muchos años-luz de nosotros y, las que puedan tener alguna posible forma de vida inteligente, no sabemos uán lejos podrán estar situadas y, para llegar a nosotros, esas señales, necesitan recorrer el espacio que nos separa a la máxima velocidad que el universo permite, es decir, la velocidad de la luz de 299.792,458 km/s. Un viaje algo lento para que llegue a nosotros en un tiempo prudencial.
Seguramente, para cuando ese se pueda producir, las civilizaciones que se encuentren, tendrán otros medios más avanzados que el de los viajes clásicos de las naves viajeras tal como las conocemos y, serán otras naves y otros caminos los que serán recorridos para viajar entre las estrellas. El Hiperespacio y los agujeros de gusano son dos buenas opciones pero… ¡habrá tántas!
emilio silvera
















 Totales: 77.774.948
Totales: 77.774.948 Conectados: 1
Conectados: 1