Sobre el Modelo Estándard de la Física

Existen límites a los que aún no han podido llegar nuestras teorías, y, el Límite de Planck es el que marca las fronteras de las teorías actuales que, nunca han podido llegar tan lejos como lo que nos dice simple ecuación:

Un día de 1.900, se publicó un artículo de ocho páginas que sentaron las bases de la Mecánica Cuántica. Su autor, Max Planck, cambió conceptos clásicos traernos una nueva visión del universo infinitesimal (10 con exponente -35 m.) a una distancia conocida como límite de Planck , mucho más allá de donde los Quarks están confinados en tripletes formando protones y neutrones y la fuerza nuclear fuerte tiene su dominio y se deja sentir a través de los bosones portadores, los Gluones.

Los agujeros de gusano del inter-universo que asocian un universo con otro diferente y son denominados agujeros de gusano de Schwarzschild. Esto nos permite especular si tales agujeros de gusano podrían usarse para viajar de un universo a otro paralelo. Otra aplicación de un agujero de gusano podría ser el viaje en el tiempo. En ese caso sería un atajo para desplazarse de un punto espaciotemporal a otro diferente. En la teoría de cuerdas un agujero de gusano es visualizado como la conexión dos D-branas, donde las bocas están asociadas a las branas y conectadas por un tubo de flujo. Se cree que los agujeros de gusano son una de la espuma cuántica o espaciotemporal.

El vacío estable y absoluto de Newton, con trayectorias continuas y determinadas, ha dejado paso al vacío cuántico asociado a unas extrañas trayectorias (*) discontinuas y fracturadas, llamadas por ello trayectorias fractales (no son propiamente trayectorias). La existencia del cuanto de acción o constante de Planck (se llama acción al producto de una energía por un tiempo), base de la física cuántica, es la causa de ese cambio fundamental, y de otros muchos, con profundas consecuencias. Mediante la geometría fractal, este marco nos ofrece nuevas e interesantes perspectivas.

Planck, nos habló del “cuanto” de acción h, y nos dijo que la energía se transmite en paquetes de manera discontinua. Aquello, asombró al mundo y el mismo Planck fue consciente de que, sus creencias sobre la Física, a partir de ese momento, serían otras.

Inspirado en el de Planck, Albert Einstein desarrollo un sobre el “Efecto Fotoeléctrico ” – que le valió el Nobel de Física de 1.921 – y, contribuyó de manera activa al desarrollo de la Mecánica Cuántica que, más tarde, combatió.

La noción del entrelazamiento cuántico es una idea nada nueva que se remonta a principio del siglo XX, a 1900, cuando el físico alemán Max Planck, considerado el padre de la teoría cuántica, propuso que no podemos hablar de una cantidad infinita de energía, sino que se transmite en pequeñas cantidades o paquetes llamados cuantos. En 1905, Albert Einstein, basándose en los experimentos de otro gran físico, Philipp Lenard, sobre el efecto fotoeléctrico, propuso que las ondas de luz se pueden propagar como ondas y como partículas al mismo tiempo. De hecho, propuso al fotón como la partícula portadora de la luz.

Llegaron nuevos Físicos como Werner Heisenberg, Schrödinger, Dirac, Feynman y otros que, desarrollaron lo que hoy conocemos como Mecánica Cuántica. Heisenberg con su Principio de Incertidumbre nos demostró que no podíamos saberlo todo al mismo tiempo. Si queremos conocer la situación de un electrón y para ello utilizamos un microscopio electrónico, el mismo hecho de su utilización transformará el medio observado, ya que, los fotones enviados por el microscopio cambiarán la dirección de dicho electrón. De esta manera, podemos saber dónde está, pero no sabremos a donde se dirige.

Schrödinger, con su función de onda, nos dio una buena herramienta buscar la partícula mediante un sistema de alta probabilidad de su situación.

La Mecánica cuántica describe el instantáneo de un sistema (estado cuántico) con una función de onda que codifica la distribución de probabilidad de todas las propiedades medibles, u observables. Algunos observables posibles sobre un sistema dado son la energía, posición, momento y momento angular. La mecánica cuántica no asigna valores definidos a los observables, sino que hace predicciones sobre sus distribuciones de probabilidad. Las propiedades ondulatorias de la materia son explicadas por la interferencia de las funciones de onda. Estas funciones de onda pueden variar con el transcurso del tiempo. Esta evolución es determinista si sobre el sistema no se realiza ninguna medida aunque esta evolución es estocástica y se produce mediante colapso de la función de onda cuando se realiza una medida sobre el sistema. Por ejemplo, una partícula moviéndose sin interferencia en el espacio vacío puede ser descrita mediante una función de onda que es un paquete de ondas centrado alrededor de alguna posición media. Según pasa el tiempo, el centro del paquete puede trasladarse, cambiar, de modo que la partícula parece estar localizada más precisamente en otro lugar. La evolución temporal determinista de las funciones de onda es descrita por la Ecuación de Schrödinger.

La Mecánica Cuántica ha alcanzado unas cotas increíbles de consistencia y experimentalmente, es una de las teorías más acreditadas. Sin embargo, mi parecer es que siendo una herramienta muy útil para los Físicos, no es la definitiva, en un futuro próximo tendremos muchas sorpresas de la mano del LHC que en este mismo año nos dará alguna alegría importante para el mundo de la Física.

El otro gran pilar en el que se apoya la Física, se llama Relatividad Especial. Todos sabéis lo que fue para la Física el año 1.905. Esa primera de la teoría relativista de Einstein, nos legó conocimientos muy importantes, tales como que un objeto viajando a velocidades cercanas a la de la luz aumenta su masa o que el hipotético viajero de una nave espacial que viaje a ésas velocidades relativistas, habrá conseguido ralentizar su tiempo. El tiempo pasa más lento cuando la velocidad es grande. Y, el otro logro importante que fue resumido en la ecuación más famosa de la historia de la Física, fue el hecho de que la masa y la energía son dos aspectos de la misma cosa. E=mc2 ¡cuánta belleza y profundidad expresado en tan poco espacio!

Albert Einstein realizó una verdadera hazaña intelectual y nos legó su teoría General de la Relatividad, una teoría construida la pura geometría, excediéndose en elegancia y efectiva en su espacio de aplicación. La relación entre el cuerpo y la curvatura del espacio-tiempo, es equivalente (Gµv). Significa, la manifestación visible o invisible de la energía [m=e/c2], y en este caso, manifestada en la forma masiva del cuerpo, curva el espació-tiempo.

La Humanidad ha conseguido logros increíbles en el campo de la Física, siempre acompañada de las matemáticas, han llegado a dejar al descubierto cuestiones misteriosas y muy bien escondidas en lo más profundo de la materia y de las fuerzas fundamentales que interaccionan con ella.

nos podemos plantear preguntas que nadie sabe contestar e incluso algunas que no sabemos ni plantear, nos faltan conocimientos para hacer tales preguntas. Sin embargo, en el futuro, las respuestas llegaran.

¿Cómo podría haber preguntado Pitágoras por el significado de m=E/c2 (E=mc2), si Einstein nació más de 2.000 años más tarde?

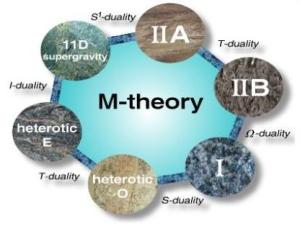
Dualidades teoría de cuerdas y teoría M.

Los análisis bibliométricos del ISI Web of Science parecen indicar que, con 4 artículos los 10 más candentes en física en 2009, la teoría de cuerdas está viviendo su tercera revolución gracias a la teoría de M2-branas de Bagger-Lambert. La segunda revolución, la de la dualidad, resaltó la importancia de la teoría M, pero sólo logró que entendiéramos muy bien las D-branas. La tercera revolución parece que tiene por objeto entender bien las M-branas, de las que prácticamente no se sabía nada antes de la teoría de Bagger-Lambert. Curiosa manera tienen los físicos de cuerdas de celebrar las bodas de plata de su primera revolución. Fuente: Simon Mitton, “Is This the Third Revolution for String Theory?,” en “HAT´S HOT IN…PHYSICS, March/Aprin 2.000,” del Thomson/Reuters ISI Science Watch. Los Hot Papers son los artículos que más rápidamente están siendo citados en el ISI Web of Science. Entre los 10 hot papers de Física en 2009, los 4 sobre teoría de cuerdas están en los puestos #4, #6, #9, y #10, y todos describen propiedades de las M2-branas. Hacía 10 años ( la segunda revolución de la teoría de cuerdas) que no ocurría algo así. ¿Estamos viviendo la tercera revolución de la teoría de cuerdas?

De la misma manera estamos hoy haciendo preguntas o formulando teorías que no pueden ser contestadas o comprobadas. La energía de Planck (10¹⁹ GeV) nos vendría muy bien para poder comprobar la teoría M que ha unificado todas las teorías existentes sobre la teoría de cuerdas. Sin embargo, nuestra civilización actual no tiene la posibilidad de alcanzar dicha energía y habrá que esperar mucho tiempo para que eso sea posible.

No podemos dejar por ello de de trabajar en ese campo de las cuerdas, es prometedor e ilusionante, allí, en las más altas dimensiones, parece que es posible hermanar a la Mecánica Cuántica y a la Relatividad General. Esta teoría nos promete por fin una teoría cuántica de la gravedad.

Esquema de la gravedad cuántica de bucles, una de las líneas de trabajo actualmente en la gravedad cuántica. Existen muchas otras y ello, viene a denotar nuestra ignorancia del tema que, en realidad, no dominamos y no dejamos de teorizar lanzando conjeturas e hipótesis que aún no se han visto cumplidas y, lo más cerca que estamos de esa teoría que consigue el casamiento de la Relatividad General con la Mecánica cuántica, está en la Teoría de cuerdas que, como sabéis, tampoco es verificable.

La verdad es que, hay muy pocos lugares en el universo donde la relatividad general sea importante. Para la vida cotidiana, para enviar sondas por el sistema solar, y para cualquier otra situación en la que es probable que nos hallemos, no necesitamos preocuparnos por la relatividad general. teoría es importante en el ámbito del Universo cuando se habla de grandes masas como estrellas y galaxias, o, planetas…cuerpos con mas de cierta importancia. Para las partículas individuales subatómicas, la fuerzas es despreciable. Sin embargo, en presencia de planetas como Júpiter, el espaciotiempo se curva.

Puede parecer ciencia ficción hablar y exponer hechos y conceptos que no pueden ser demostrados, sin embargo, Einstein esperó largos años con su teoría de la Relatividad General bien asentada en su cabeza, sin poder exponerla al mundo por no tener las matemáticas necesarias para ello, y, cuando su amigo Marcel Grossman, al que había pedido ayuda, le envió algunos documentos los que se encontraba la famosa Conferencia de Riemann, Einstein quedó paralizado ante el Tensor Métrico de Riemann, allí tenía la herramienta que estaba buscando y que le permitía formular de manera precisa los espacios curvados de la relatividad general.

Las grandes masas determinan la geometría del Universo forman espacios curvos que se comportan como calles y laberintos por los que discurren los objetos de materia que deambulan por el espaciotiempo tetradimensional de nuestro universo que, si tiene dimensiones extra, las tiene bien escondidas.

Algún día, alguien surgirá y nos traerá las matemáticas necesarias para que, la teoría M se pueda exponer de manera clara y completa. ¿Serán las funciones modulares de Ramanujan las que nos sacará del atolladero? Todos sabéis que las matemáticas topológicas de la Teoría M, son extremadamente difíciles, pocos tienen acceso a ellas, y, de momento, parece que nadie está en posesión de los conocimientos matemáticos que se precisan.

Tendremos que esperar un poco. Sin embargo, la Ciencia futura está a la vuelta de la esquina:

La nanotecnología es un campo de las ciencias aplicadas dedicado a la manipulacion de material a la escala menor de un micrometro es decir al nivel de atomos y moeculas (nanometria) lo mas habitual es que tal manipulacion se produsca uno o 1000 nanometros para hacer una idea de como son los nanobotts un nanobot mide 50 nm sus capas son de 5 molecula.

                               Pronto veremos que la nanotecnología nos llevará a un mundo futuro que ahora, ni podemos imaginar

¿Qúe no podremos contruir con las nuevas técnicas de nanotecnología? Inundaremos los planetas lejanos de minúsculos robots que no serán detectados y nos podrán inviar información fidedigna de todo lo que queramos? Por ahí podría ir el futuro, menos coste en los lanzamientos bases lunares o marcianas y, en pequeñas naves podrían ir cientos de robots que se espacirían por todo el pequeño o gran mundo a explorar.

nuestra curiosidad es inagotable, nos empuja a preguntar, trabajar, estudiar, investigar y profundizar en todas estas cuestiones que atrae a todos aquellos que, como yo, enamorados de la Física, saben que, algún día lejano en el futuro, nuestra Civilización alcanzará el nivel requerido para poder abrir esas puertas que tenemos cerradas y de las que no tenemos las llaves para poder abrirlas. Encima de estas puertas, los letreros dicen: Teoría M, Materia Oscura, Densidad Crítica, Universos paralelos, Viajes en el Tiempo, Singularidades, etc.

Me gustaría estar presente cuando pasados algunos siglos, nuestra especie tenga como fuente de energía inagotable la que generan los Agujeros Negros. Esa energía nos dará la posibilidad de viajar a las estrellas y de llegar al fondo de la teoría M.

Cuerdas vibrantes de cuyas resonancias surgen nuevas partículas.

No debemos olvidar que, todo lo grande está hecho de cosas pequeñas. Así es. Al menos hasta donde sabemos, los planetas, las estrellas y Galaxias y demás objetos estelares (nosotros también), están hechos de infinitesimales objetos: Quarks y Leptones. Todo lo que podemos ver en el Universo está hecho de materia bariónica, existe otra clase de materia que aún no sabemos lo que es, dónde está o se genera y de qué está hecha (esa que nuestra ignorancia denomina Materia Oscura)..

         La materia primordial del Universo fue denominada por los griegos clásicos como Ylem

¡Nuestra imaginación! algo que solo ser comparada con la grandiosidad del Universo que… es casi tan grande como ella.

La Mecánica Cuántica.

La Relatividad Especial y la Relatividad General.

El Modelo Estándar.

Las fuerzas Fundamentales.

Las Constantes Universales.

Las familias de partículas: Quarks (u, d, s, c, t, b), Hadrónes (bariones y mesones), los Leptones (electrón, muón, tau y sus respectivos neutrinos).

La Teoría M y la de Supersimetría, Supergravedead, la de cuerdas, la cuerda heterótica.

En su día la teoría de Kaluza-Klein (la primera de más altas dimensiones)

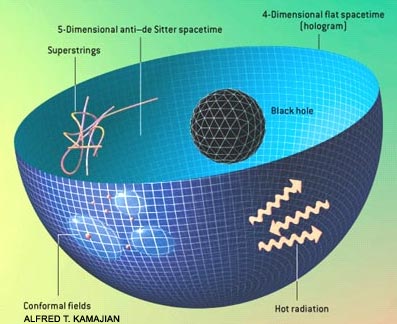
                Hablamos de Universos holográficos

Y, de esta manera podríamos exponiendo ejemplos enormes de la imaginación que poseemos y que es el don que la humanidad tiene para descubrir los misterios del Universo. Einstein llamaba a esto ejercicios mentales. Está bien que nuestras mentes no tengan límites a la hora de imaginar. Creo que, a excepción de las imposibilidades y barreras impuestas por nuestro físico, todo lo demás, con el tiempo podrá ser posible. Hasta tal punto es así que, hasta podremos (ya lo hemos hecho) hacer que nuestras vidas sean más duraderas.

Alguien dijo que Genio es aquel que es capaz de plasmar en realidad sus pensamientos. Pues, amigos, en la Física han sido muchos los genios que han aportado su imaginación.

La pregunta que hay que responder aquí es lo que se entiende por Física. Por mi parte, Física es todo lo que aquí he dejado escrito y muchísimo más. Creo firmemente que la Física es el arma más poderosa con la que la Humanidad para resolver todos los problemas que tiene planteados a plazo fijo en el futuro lejano.

                          Hasta la vida es Física y Química

¿Habéis pensado alguna vez que el Sol tiene una cantidad de combustible nuclear – hidrógeno – limitado? El día que se acabe, dentro de 4.000 millones de años ¿dónde iremos? La pregunta parece tonta, sin embargo, no lo es. No debemos descansar en el avance del saber científico de la Física y las matemáticas (además de en los otros campos), ya que, en ese no parar estará la solución a todos nuestros problemas presentes y futuros, y, la llave que abrirá la puerta principal, se llama Física (siempre acompañada por la llave maestra de las matemáticas).

Y, mientras tanto, continuará el proceso de humanización que aún está por terminar…¡Nos queda tanto!

emilio silvera

Algunos  creen que que Einstein sacó a la luz su relatividad especial, las leyes de Newton habían quedado olvidadas en un cuarto oscuro y, nada más lejos de la realidad. La física newtoniana siguen utilizándose ampliamente en la vida cotidiana, en la mayoría de los campos de la ciencia y en la mayor parte de la tecnología. No atención a la dilatación del tiempo cuando hacemos un viaje en avión, y los ingenieros no se preocupan  por la contracción de la longitud cuando diseña la nave. La dilatación y la contracción son demasiado pequeñas para que sean tomadas en consideración.

Por supuesto, podríamos utilizar, si quisoéramos, las leyes de Einstein  en lugar de las leyes de Newton en la vida de día. Las dos dan casi exactamente las mismas predicciones para todos los efectos físicos, puesto que la vida diaria implica velocidades relativas que son muy pequeñas comparadas con la velocidad de la luz.

Las predicciones de Einstein y Newton comienzan a diferir fuertemente sólo cuando las velocidades relativasd se aproximan a la velcoidad de la luz, Entonces, y sólo entonces debemos abandonar las predicciones de Newton y atenernos estrictamente a las de Eonstein. Este es un ejemplo de una pauta muy general. Es una pauta que se ha repetido una y otra vez a lo largo de la historia de la física del siglo XX: un conjunto de leyes (en este caso las leyes newtonianas) es ampliamente aceptado al principio, porque concuerda muy bien con el experimento.

Pero los experimentos vez se hacen más prcisos y este conjunto de leyes resultan funcionar bien sólo en un dominio limitado, su dominio de validez (para las leyes de Newton) el dominio de velocidades pequeñas comparadas con la velocidad de la luz en el vacío. Entonces los físicos se esfuerzan, experimental y teóricamente, para comprender qué está pasando en el límite de dicho dominio de validez, finalmente formulan un conjunto de leyes que es muy acertado dentro, cerca y más allá del límite (en el caso de Newton, la relatividad especial de Einstein, que sí es válida a velocidades próximas a las de la luz tanto a más bajas velocidades.

Hoy día, el mundo moderno de la física se funda notablemente en dos teorías principales, la realtividad general y la mecánica cuántica, aunque ambas teorías parecen contradecirse mutuamente. Los postulados que definen la teoría de la realtividad de Einstein y la teoría del quántum estan incuestionablemente apoyados por rigurosa y repetida evidencia empiríca. Sin embargo, ambas se resisten a ser incorporadas dentro de un mismo modelo coherente.

Nuevas maneras de sondear la Naturaleza y desvelar sus secretos están en marcha y, más adelante en el futuro, saldrán a la luz nuevas formas y nuefvas teorías que, entonces, sí que se podrán comprobar de manera experimental. Pero sigamos con la relatividad ede Einstein que, en su primera fase, la relatividad especial comienza a fracasar cuando se hace presente la Gravedad dde una manera importante, entonces, tiene que ser reemplazada por un conjunto de leyes que llamamos relatividad general; ésta fracasa en presencia de una singularidad interna de un agujero negro y, entonces, debe ser reemplazada por otro conjunto de leyes que conocemos como Gravedad Cuántica y que aún, no hemos podido dominar.

Einstein  nos decía que el espacio se curva en presencia de grandes masas

Lo cierto que es que, se ha dado una carqacterística sorprendente en cada transición de un viejo conjunto de leyes a otro : en casa caso, los físicos (si demostraban ser suficientemente inteligentes) no necesitaban ninguna guía experimental que les dijera dónde empezaría a fallar el viejo conjunto, es decir, que les indicara el límite de su dominio de validez. Ya hemos podido ver eso para la física newtoniana: las leyes de la electrodinámica de Maxwell no encajaban bien con el espacio absoluto de la física newtoniana. En reposo en el espacio absoluto (en aquel sistema del éter), las leyes de Maxwell eran simples y bellas -por ejemplo, las lineas de campo magnético no tienen extremo. En los sistmas en movimiento se vuelven complicadas y feas- las lineas de campo magnético tienen a vedces extremos. Sin embargo, las complicaciones tienen una influencia despreciable sobre el resultado de los experimentos cuando los sistmas se mueven., con relación al espacio absoluto, a velocidades pequeñas comparadasd con la de la luz; entonces casi nuinguna linea de campo tiene extremos. Sólo a velocidades que se aproximan a la de la luz era previsible que las feas complicaciones tuvierqan una influencia suficientemente grande como para ser medidas con facilidad: montenes de extremos. De este modo,  eera razonable sospechar, incluso en ausencia del experimento de Michelson-Morley, que el dominio de validez de la física newtoniana podría ser el de las velocidades pequeñas comparadas con la de la Luz, y que las leyes newtonianas podrían venirse abajo a velocidades cercanas a la de la luz.

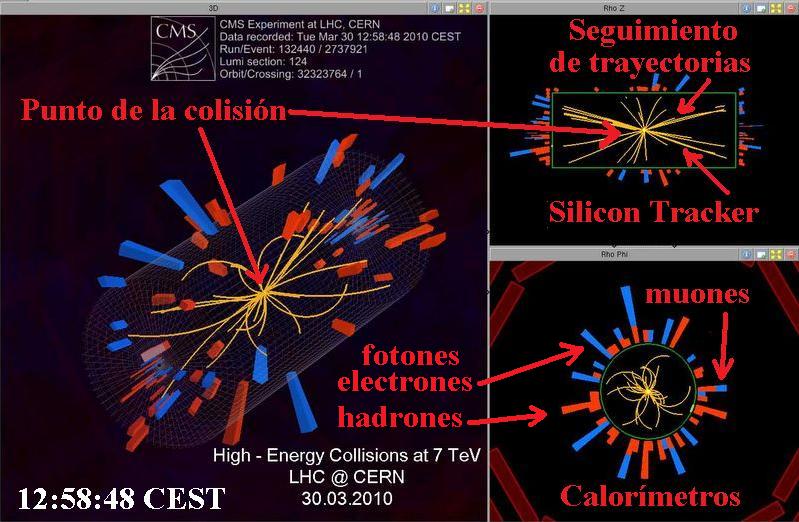
El LHC es un esfuerzo internacional, donde participan alrededor de siete mil físicos de 80 países. Consta de un túnel en de anillo, con dimensiones interiores parecidas a las del metro subterráneo de la Ciudad de México, y una circunferencia de 27 kilómetros. Está ubicado entre las fronteras de Francia y Suiza, cerca de la ciudad de Ginebra, a profundidades que van entre los 60 y los 120 metros debido a que una parte se encuentra bajo las montañas del Jura.

Claro que, hablando de lo quen nos ocupa, al contemplar la secuencia anterior de conjuntos de leyes (física newtoniana, relativisdata especial, relativista general, gravedad cuántica), y una secuencia similar de leyes que gobiernan la estructura de la materia y las partículas elementales, la mayoría de los físicos tienen a creer que estas secuencias están convergiendo un conjunto de leyes últimas que verdaderamente gobiernan el Universo, leyes que obligan al Universo a mostrarse como es y comportarse como nosotros vemos que lo hace, que obligan a la lluvia a condensarse en las cristaleras de las ventanas, obliga al Sol a quemar combistible nuclear convertir lo elemental y sencillo en más complejo que, más tasrde tendrá su función determinada, obliga a los agujeros negros a producir ondas gravitatorias cuando colisionan ellos, a que las estrellas masivas, al final de sus vidas explotan como supernovas para formar hermosas Nebulosas y conformar nuevos objetos masivos como púlsares, estrellas de neutrones y agujeros negros… Y, por eso…

¡La Gravedad! Siempre está presente e incide en los comportamientos de la materia

Todo esto ha podido ser comprendido con el paso del tiempo y a medida que se sumaban los descubrimientos y los pensamientos de unos y otros, y, por ejemplo, Einstein también concluyó que si un cuerpo pierde una energía L, su masa disminuye en L/c2. Einstein generalizó conclusión al importante postulado de que la masa de un cuerpo es una medida de su contenido en energía, de acuerdo con la ecuación m=E/c2 ( o la más popular E=mc2).

Otras de las conclusiones de la teoría de Einstein en su modelo especial, está en el hecho de que quien viaje a velocidades cercanas a c (la velocidad de la luz en el vacío), el tiempo transcurrirá más lento. Dicha afirmación también ha sido experimentalmente comprobada.

Todos estos conceptos, por nuevos y revolucionarios, no fueron aceptados por las buenas y en un primer , algunos físicos no estaban preparados para comprender cambios tan radicales que barrían de un plumazo, conceptos largamente arraigados.

      Todo lo grande está hecho de cosas pequeñas

Claro que, podríamos objetar que, cada conjunto de leyes en la secuencia “tiene un aspecto” muy diferente del conjunto precedente. (Por ejemplo, el tiempo absoluto de la física newtoniana tiene un aspecto muy diferente de los muchos flujos de tiempos diferentes de la relatividad especial.) ¿Por qué,  entonces, deberíamos esperar una convergencia? La respuesta es que hay que distinguir claramente entre las predicciones hechas a partir de un conjunto de leyes y las imágenes mentales que las leyes transmiten (lo que las leyes “aparentan”). Yo espero la convergencia en términos  de predicciones, pero esto es todo lo que finalmente . Las Imágenes mentales (un tiempo absoluto en la Física newtoniana frente a los muchos flujos de tiempo en la física relativista) no son importantes para la naturaleza última de la realidad.

Se podría objetar que cada conjunto de leyes en la secuencia, tiene su propio su aspecto y que, no tienen porque converger. El mismo conjunto de leyes de Newton tiene un aspecto muy diferente de los muchos flujos de tiempos diferentes de la relatividad especial. En los aspectos de las leyes no existe ningún de convergencia y, desde luego, las caracteristicas de cada conjunto de leyes, aunque sean diferentes,  no son importantes esas diferencias para el resulta último final de la realidad última a la que la Naturaleza quiere llegar.

Un agujero negro es lo definitivo en distorsión espaciotemporal, según las ecuaciones de Einstein: está hecho única y exclusivamente a partir de dicha distorsión. Su enorme distorsión está causada por una inmensa cantidad de energía compactada: energía que reside no en la materia, sino en la propia distorsión. La distorsión genera más distorsión sin la ayuda de la materia. Esta es la esencia del agujero negro.relatividad/”>

En cuanto a la distorsión del espacio y el tiempo, tenekos que Hermann Mynkowski unificaba el espacio y el Teimpo y Einstein lo distorsionaba.

“Las ideas de espacio u tiempo que deseo exponer ante ustedes han brotado del suelo de la física experimental, y en ello reside su fuerza. Son radicales. En lo sucesio, el espacio por sí mismo, y el tiempo por sí mismo, están condenados a desvanecerse en meras sombras, y sólo un de unión de ambos conservará una realidad independiente: ¡El Espaciotiempo!”

Con esas palabras proféticas Minkiwski reveló al mundo, en septiembre de 1908, un descuberimiento sobre la naturaleza del espacio y el tiempo. Einstein había demostrado que el espacio u el tiempo eran “relativos”. La longitud de un objeto y el flujo del tiempo eran diferentes cuando se miran diferentes sistemas de referencia.

Minkouski comprendió, de manera perfecta, la profundidad y el verdadero mendaje que la teoría de Eisntein llevaba consigo y, habiéndola entendido a la pefección, le expuso al mundo el nacimiento del espaciotiempo: Ambos, Tiempo y Espacio conformados como un todo.

Hay una historia (adaptada de Tauylor y Wheeler (1992) que ilusta la ideqa subyacente al descubrimiento de Minkowski pero, la dejaré para otra ocasión. El tema de las leyes de Newton, las dos versiones relativistas y la no hallada gravedad cuántica, nos daría para glunos abultados tomos que, no pueden ser escritos aquí

emilio silvera