Sep
22
Buscando la Gravedad-Cuántica
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
Entre los teóricos, el casamiento de la relatividad general y la teoría cuántica es el problema central de la física moderna. A los esfuerzos teóricos que se realizan con ese propósito se les llama “supergravedad”, “súpersimetría”, “supercuerdas” “teoría M” o, en último caso, “teoría de todo o gran teoría unificada”.

Ahí tenemos unas matemáticas exóticas que ponen de punta hasta los pelos de las cejas de algunos de los mejores matemáticos del mundo (¿y Perelman? ¿Por qué nos se ha implicado?). Hablan de 10, 11 y 26 dimensiones, siempre, todas ellas espaciales menos una que es la temporal. Vivimos en cuatro: tres de espacio (este-oeste, norte-sur y arriba-abajo) y una temporal. No podemos, ni sabemos o no es posible instruir, en nuestro cerebro (también tridimensional), ver más dimensiones. Pero llegaron Kaluza y Klein y compactaron, en la longitud de Planck las dimensiones que no podíamos ver. ¡Problema solucionado!
¿Quién puede ir a la longitud de Planck para verlas?

Ni vemos la longitud de Planck ni las dimensiones extra
La puerta de las dimensiones más altas quedó abierta y, a los teóricos, se les regaló una herramienta maravillosa. En el Hiperespacio, todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí si es posible encontrar esa soñada teoría de la Gravedad cuántica.
Así que, los teóricos, se han embarcado a la búsqueda de un objetivo audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos, una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.
¿Dónde radica el problema?

Nuestro universo es tridimensional y no podemos ver otro más allá… ¡si existe!
El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el nuevo acelerador de partículas LHC que con sus 14 TeV no llegaría ni siquiera a vislumbrar esas cuerdas vibrantes de las que tanto se habla.
La verdad es que, la teoría que ahora tenemos, el Modelo Estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías.

Con sus 20 parámetros aleatorios (parece que uno de ellos ha sido hallado -el bosón de Higgs-), el Modelo estándar de la f´çisica de partículas que incluye sólo tres de las interacicones fundamentales -las fuerzas nucleares débil y fuerte y el electromagnetismo-, ha dado un buen resultado y a permitido a los físicos trabajar ampliamente en el conocimiento del mundo, de la Naturaleza, del Universo. Sin embargo, deja muchas preguntas sin contestar y, lo cierto es que, se necesitan nuevas maneras, nuevas formas, nuevas teorías que nos lleven más allá.
¡Necesitamos algo más avanzado!
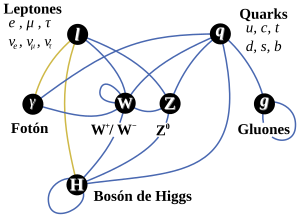
Se ha dicho que la función de la partícula de Higgs es la de dar masa a las partículas que conocemos y están incluidas en el Modelo estándar, se nos ha dicho que ha sido encontrada pero, nada se ha dicho de cómo ésta partícula transmite la masa a las demás. Faltan algunas explicaciones.
El secreto de todo radica en conseguir la simplicidad: el átomo resulto ser complejo lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones, resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún, los quarks que estaban instalados en nubes de otras partículas llamadas gluones y, ahora, queremos continuar profundizando, sospechamos, que después de los quarks puede haber algo más.
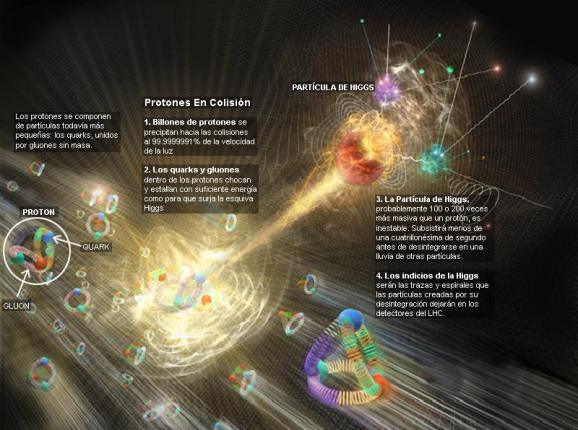
¿Acaso las partículas circulan por el campo de Higgs y se ven frenadas por éste que les adosa la masa?
Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes. Es decir, que si miramos a las estrellas en una noche clara estamos mirando el campo de Higgs. Las partículas influidas por este campo, toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado, del campo gravitatorio o del electromagnético. Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquiriría energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra.

Como E=mc2, ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del Sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein. La masa, m, tiene en realidad dos partes. Una es la masa en reposo, m0, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c) o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.
Pero la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas.
Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs.

La influencia de Higgs en las masas de los quarks y de los leptones, nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.
Hasta ahora no tenemos ni idea de que reglas controlan los incrementos de masa generados por el Higgs (de ahí la expectación creada cuando se estrenó el nuevo acelerador de partículas LHC). Pero el problema es irritante: ¿por qué sólo esas masas –Las masas de los W+, W–, y Zº, y el up, el down, el encanto, el extraño, el top y el bottom, así como los leptones – que no forman ningún patrón obvio? Y, desde luego, aunque hace algún tiempo que nos dijeron que la tal partícula de Higgs había sido encontrada, no nos han explicado muchas cosas más que faltan en esa fiesta para que la podamos celebrar.

No dejamos de experimentar para saber ccómo es nuestro mundo, la Naturaleza, el Universo que nos acoge
Las masas van de la del electrón 0’0005 GeV, a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnéticas y débiles. En la unidad hay cuatro partículas mensajeras sin masa –los W+, W–, Zº y fotón que llevan la fuerza electrodébil. Además está el campo de Higgs, y, rápidamente, los W y Z chupan la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos) y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen los teóricos. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa. Claro que nadie ha explicado cómo lo hace.
Las masas de los W y el Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil. Y las relajadas sonrisas de los físicos teóricos nos recuerdan que Gerard ^t Hooft y Veltman dejaron sentado que la teoría entera esta libre de infinitos.

En esta última dirección ha publicado numerosos libros y artículos, donde aborda la asignatura pendiente de la unificación de la mecánica cuántica y la teoría del campo gravitatorio. El camino que ha seguido Penrose es encontrar una base común a ambas.
Para ello ha introducido dos modelos: los “spin networks” y los “twistors”, el primero discreto, con una métrica intrínseca, no relativista, previo al concepto de espacio, el segundo continuo, con una métrica extrínseca, relativista e inmerso en un espacio-tiempo dado.
Claro que son varias las corrientes que quieren abrirse camino hacia otras físicas nuevas.

Cuando no sabemos de qué estamos hablando, lo representamos de cualquier manera y, no siempre acertamos
La teoría de supercuerdas tiene tantas sorpresas fantásticas que cualquiera que investigue en el tema reconoce que está llena de magia. Es algo que funciona con tanta belleza… Cuando cosas que no encajan juntas e incluso se repelen, si se acerca la una a la otra alguien es capaz de formular un camino mediante el cual, no sólo no se rechazan, sino que encajan a la perfección dentro de ese sistema, como ocurre ahora con la teoría M que acoge con naturalidad la teoría de la relatividad general y la teoría mecánico-cuántica; ahí, cuando eso se produce, está presente la belleza.
Lo que hace que la teoría de supercuerdas sea tan interesante es que el marco estándar mediante el cual conocemos la mayor parte de la física es la teoría cuántica y resulta que ella hace imposible la gravedad. La relatividad general de Einstein, que es el modelo de la gravedad, no funciona con la teoría cuántica. Sin embargo, las supercuerdas modifican la teoría cuántica estándar de tal manera que la gravedad no sólo se convierte en posible, sino que forma parte natural del sistema; es inevitable para que éste sea completo.
¿Por qué es tan importante encajar la gravedad y la teoría cuántica? Porque no podemos admitir una teoría que explique las fuerzas de la naturaleza y deje fuera a una de esas fuerzas. Así ocurre con el Modelo Estándar que deja aparte y no incluye a la fuerza gravitatoria que está ahí, en la Naturaleza.
La teoría de supercuerdas se perfila como la teoría que tiene implicaciones si tratamos con las cosas muy pequeñas, en el microcosmos; toda la teoría de partículas elementales cambia con las supercuerdas que penetra mucho más; llega mucho más allá de lo que ahora es posible.

La topología es, el estudio de aquellas propiedades de los cuerpos geométricos que permanecen inalteradas por transformaciones continuas. La topología es probablemente la más joven de las ramas clásicas de las matemáticas. En contraste con el álgebra, la geometría y la teoría de los números, cuyas genealogías datan de tiempos antiguos, la topología aparece en el siglo diecisiete, con el nombre de analysis situs, ésto es, análisis de la posición.
De manera informal, la topología se ocupa de aquellas propiedades de las figuras que permanecen invariantes, cuando dichas figuras son plegadas, dilatadas, contraídas o deformadas, de modo que no aparezcan nuevos puntos, o se hagan coincidir puntos diferentes. La transformación permitida presupone, en otras palabras, que hay una correspondencia biunívoca entre los puntos de la figura original y los de la transformada, y que la deformación hace corresponder puntos próximos a puntos próximos. Esta última propiedad se llama continuidad, y lo que se requiere es que la transformación y su inversa sean ambas continuas: así, trabajarnos con homeomorfismos.

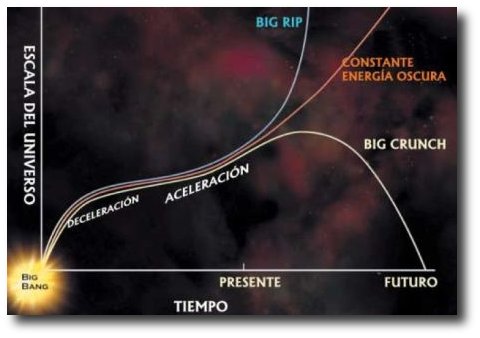
En cuanto a nuestra comprensión del universo a gran escala (galaxias, el Big Bang…), creo que afectará a nuestra idea presente, al esquema que hoy rige y, como la nueva teoría, el horizonte se ampliará enormemente; el cosmos se presentará ante nosotros como un todo, con un comienzo muy bien definido y un final muy bien determinado.
Para cuando eso llegue, sabremos lo que es, como se genera y dónde están situados los orígenes de esa “fuerza”, “materia”, o, “energía” que ahora no sabemos ver para explicar el movimiento de las galaxias o la expansión del espacio mismo.
emilio silvera
Sep
21
De la vida y la muerte de las partículas y…otros
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
Por aquel tiempo pudimos leer en la prensa de todo el mundo: ESTOCOLMO, Suecia.- El premio Nobel de Física (2.008) fue atribuido hoy al norteamericano Yoichiro Nambu y a los japoneses Makoto Kobayashi y Toshihide Maskawa por sus trabajos separados sobre la física de las partículas que mejoraron la comprensión de la materia, Demos un repaso hoy aquí a esos componentes de la materia, y, profundicemos en sus propiedades., en sus “vidas”.

Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida media, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.

También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.
Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, ksi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales manera de desintegración, veríamos como difieren las unas de las otras.
| Quarks | Antiquarks | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Nombre | Símbolo[1] | Generación | Carga eléctrica (e) |
Masa en reposo (MeV/c²) |
Nombre | Símbolo | Generación | Carga eléctrica (e) |
Masa en reposo (MeV/c²) |
| Arriba | 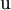 |
Primera | 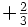 |
— | Antiarriba |  |
Primera | 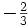 |
— |
| Abajo |  |
Primera | 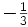 |
— | Antiabajo | 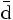 |
Primera |  |
— |
| Encanto |  |
Segunda | 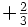 |
— | Antiencanto | 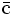 |
Segunda | 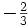 |
— |
| Extraño | 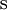 |
Segunda | 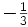 |
— | Antiextraño | 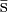 |
Segunda |  |
— |
| Cima | 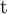 |
Tercera | 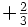 |
— | Anticima | 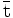 |
Tercera | 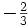 |
— |
| Fondo | 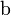 |
Tercera | 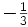 |
— | Antifondo | 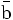 |
Tercera |  |
— |
- Las iniciales de los símbolos los toma del inglés: u: up, arriba; d: down, abajo; c: charmed, encantado; s: strange, extraño; t: top, alto, superior, cima; b: bottom bajo, fondo.
Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.

Todas las partículas elementales vistas hasta ahora en esta serie, incluido el neutrino. Claro que, aquí no está todavía el Bosón de Higgs que será confirmado en breve…al parecer. Esas son las últimas noticias, el Bosón de Higgs está “casi” localizado y sólo está a la espera de confirmar el hallazgo no una, sino miles de veces.
 |
| The CMS detector.Image © CERN |
 |
| The ATLAS detector. Image © CERN |
Por fin, los físicos empiezan a recoger los frutos de una búsqueda que dura ya casi cincuenta años. Dos de los principales detectores del LHC, el gran acelerador europeo de partículas (el Atlas y el muones“>CMS) han encontrado señales que podrían delatar la presencia del esquivo Higgs“>bosón de Higgs, la última particula subatómica que queda por descubrir para completar el Modelo Estandar de la Física y la que encierra, además, el secreto de por qué las demás partículas tienen masa.
Pero sigamos. ¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

Una colisión entre un prtón y un antiprotón registrada mediante una cámara de chispas del experimento UA5 del CERN.
Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.
| Leptones cargados | Neutrinos | |||||||
|---|---|---|---|---|---|---|---|---|
| Nombre | Símbolo | Carga | Masa en reposo | Nombre | Símbolo | Carga | Masa en reposo | |
| 1ª generación | Electrón | 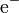 |
−1 | 0,511 |  |
0 | < 3·10−6 | |
| Positrón | 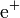 |
+1 | Neutrino electrónico |
 |
0 | |||
| 2ª generación | Muón | 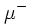 |
−1 | 105,658 | Neutrino muónico | 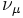 |
0 | < 0,19 |
| Antimuón |  |
+1 | Antineutrino muónico | 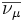 |
0 | |||
| 3ª generación | Tauón |  |
−1 | 1776,99 | Neutrino tauónico |  |
0 | < 18,2 |
| Antitauón |  |
+1 | Antineutrino tauónico | 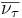 |
0 | |||
En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su carta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas, Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.

Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.
Bariones
| Partícula | Símbolo[1] | Quarks[2] | Spin | Masa en reposo (MeV/c²) |
S | C | B | Vida media (s) |
Desintegraciones más importantes |
|---|---|---|---|---|---|---|---|---|---|
| Protón | 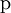 |
 |
 |
938,27 | 0 | 0 | 0 | Estable [3] | — |
| Neutrón |  |
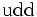 |
 |
939,56 | 0 | 0 | 0 | 885,7 [4] |  |
| Delta doble positiva | 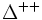 |
 |
 |
≈1.232 | 0 | 0 | 0 | 6·10-24 | 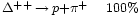 |
| Delta positiva |  |
 |
 |
≈1.232 | 0 | 0 | 0 | 6·10-24 | 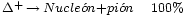 |
| Delta neutra | 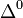 |
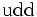 |
 |
≈1.232 | 0 | 0 | 0 | 6·10-24 |  |
| Delta negativa |  |
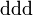 |
 |
≈1.232 | 0 | 0 | 0 | 6·10-24 |  |
| Lambda neutra |  |
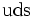 |
 |
1.115,68 | −1 | 0 | 0 | 2,63·10-10 |  |
| Sigma positiva | 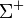 |
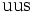 |
 |
1.189,37 | −1 | 0 | 0 | 8,01·10-11 |  |
| Sigma neutra |  |
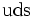 |
 |
1.192,64 | −1 | 0 | 0 | 7,4·10-20 |  |
| Sigma negativa | 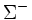 |
 |
 |
1.197,45 | −1 | 0 | 0 | 1,48·10-10 | 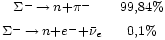 |
| Xi neutra | 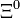 |
 |
 |
1.314,83 | −2 | 0 | 0 | 2,90·10-10 | 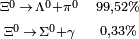 |
| Xi negativa | 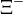 |
 |
 |
1.321,31 | −2 | 0 | 0 | 1,64·10-10 | 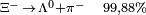 |
| Omega |  |
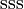 |
 |
1.672,45 | −3 | 0 | 0 | 8,21·10-11 | 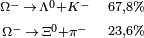 |
| Omega encantada |  |
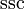 |
 |
2.697,5 | −2 | +1 | 0 | 6,90·10-14 |  |
| Xi positiva encantada | 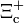 |
 |
 |
2.468 | −1 | +1 | 0 | 4,42·10-13 |  |
| Xi neutra encantada | 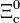 |
 |
 |
2.471 | −1 | +1 | 0 | 1,12·10-13 |  |
| Lambda encantada | 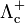 |
 |
 |
2.284,9 | 0 | +1 | 0 | 2,00·10-13 |  |
| Xi doble encantada | 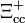 |
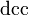 |
 |
3.519 | 0 | +2 | 0 | <3,30·10-14 | — |
| Lambda inferior |  |
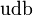 |
 |
5.624 | 0 | 0 | −1 | 1,23·10-12 |  |
- [1] El símbolo de los antibariones es el mismo pero con una barra superpuesta.
- [2] Los antibariones están formados por los respectivos antiquarks.
- [3] Debe ser superior a 1030 años.
- [4] Vida media de los neutrones libres. En los núcleos atómicos son estables.
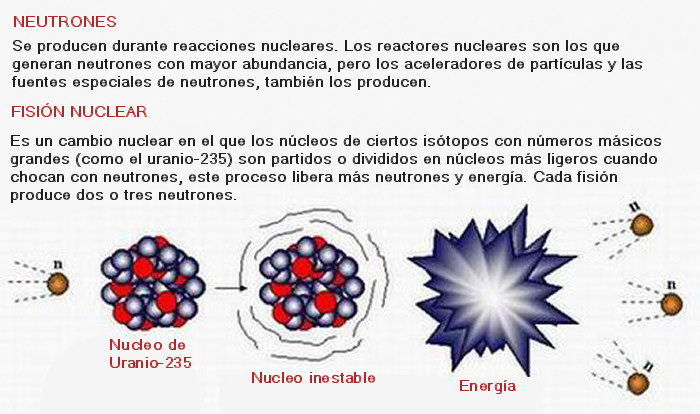
- Se ha conseguido observar por primera vez la desintegración radiactiva del neutrón. Dentro de los núcleos de los átomos hay neutrones y protones. En condiciones normales y mientras que están ahí los neutrones son estables. Sin embargo los neutrones libres son inestables, tienen una vida media de unos 10 minutos, y se desintegran produciendo un protón un electrón y un antineutrino. Pero los físicos nucleares teóricos predijeron que una de cada mil veces los neutrones decaerían en todas esas partículas y además en un fotón.
Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.
Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.
Bosones
| Nombre | Símbolo | Carga eléctrica (e) |
Carga de color | Spin | Masa en reposo (GeV/c²) |
Existencia | Vida media | Desintegraciones más importantes |
|---|---|---|---|---|---|---|---|---|
| Fotón |  |
Neutra | Neutra | 1 | Nula | Confirmada | Estable | — |
| Bosón W | 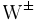 |
± 1 | Neutra | 1 | 80,425 | Confirmada | 3·10-25 |  [1] [1] |
| Bosón Z |  |
Neutra | Neutra | 1 | 91,187 | Confirmada | 3·10-25 | — |
| Gluón |  |
Neutra | Color + Anticolor | 1 | Nula | Confirmada | Estable | — |
| Gravitón |  |
Neutra | Neutra | 2 | Nula | Hipotética | Estable | — |
| Higgs“>Bosón de Higgs |  |
Neutra | Neutra | 0 | > 114 | Hipotética | Inestable |  |
Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”
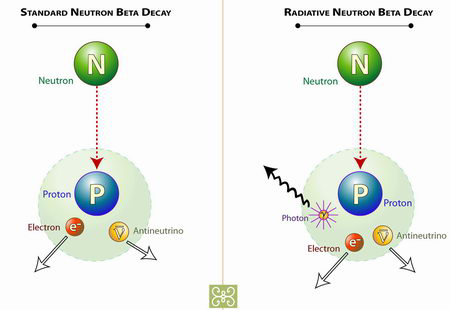
Típicamente el neutrón decae en un protón, un antineutrino y un electrón. Muy raramente lo hace radiativamente emitiendo además un fotón. Diagrama: Zina Deretsky, National Science Foundation. Fue difícil observar los fotones porque el haz está contaminado con fotones que fondo que producen mucho “ruido” en las medidas, por lo que era como buscar una aguja en un pajar. El decaimiento radiativo del neutrón es importante porque conecta directamente con el modelo estándar de partículas.
Si la vida de una partícula es tan corta como 10ˉ²³ segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.
Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.
Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).

En el Universo existen muchas clases de resonancias…inesperadas
Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.
Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:
∆⁺⁺→р + π⁺; ∆⁰→р + πˉ; o п+π⁰
En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.

El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (materia), es aún limitado. Los cuadros que aparecen arriba, están referidos a las partículas más usuales como los Quarks y los Leptones (verdaderos componentes de la materia) que a su vez, son: Los Quarks los que forman a los Hadrones y los Leptones los que completan el núcleo atómico de la materia para conformar los átomos. He dejado a los mesones y a las supuestas partículas supersimétricas centrándome en las que me parecen principales en la conformación de la materia.
emilio silvera
Sep
17
El “universo” de lo muy pequeño. ¡Resulta fasciante!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)

¿Os acordais? ¿Cuántos niños no habrán soñado con escenas como estas?
Cuando hablo de lo muy pequeño, puedo llegar a entender muy bien lo que es, lo que son, “licencias literarias” el papel de nada se queja y el lápiz puede escribir lo que quiera y piense el que lo sostiene, según le dicte su imaginación. Claro que, cuando comparamos ese mundo de ilusiones e imaginación con el mundo real, todo el edificio se viene abajo. ¡Lástima!
Todos los niños pequños juegan con pequeños muñecos que son soldados, guerreros o seres de otras galaxias con poderes mágicos y, ellos, en su inocente mundo sin maldad, los dirigen con sus manitas gordezuelas al desarrollo de luchas y aventuras sin fin. Jonathan Swift, nos deleitó con aquellas aventuras de Gulliver, un aventurero que llegó a las tierras de Lilliput: Allí, todo era muy pequeño, la naturaleza, las plantas, los habitantes del lugar y sus casas y palacios, embarcaciones y todos los animales.
Gulliver era allí un gigante de proporciones inmensas: Incluso llegó a extinguir un fuego con una simple chorrada (es decir, hizo pipí) y acabó de inmediato con el (para ellos) enorme fuego.

Su tamaño podía, sin dificultad alguna, decidir el resultado de una guerra entre aquellos pequeñísimos seres que, ante un gigante como él, no tenían defensa alguna y, sus armas, resultaban ridículas para poder causarle algún daño. Dormido lo tuvieron que coger para poder atarlo.
Durante otro viaje, las fuerzas ignotas del destino llevaron a Gulliver a un pais llamado Brobdingnag, donde la gente y todos los seres animados e inanimados eran mucho más grandes que él. Allí era un enano, mimado por una niña pequeña llamada Glumdalclitch. Al final, Gulliver es recogido en una jaula por un águila que lo deja caer en el mar de donde lo rescataron unos marineros a los que, al contarles esas historias, pusieron incrédulas caras de asombro.

Claro que, cuando nos trasladamos al mundo real, las cosas no suelen ser de esa manera. Poco importa lo fascinantes que las historias de este tipo nos puedan resultar. Las cosas no funcionan de esa manera. Todos sabemos, por ejemplo que la llama de una vela pequeña y la de una vela grande, son aproximadamente del mismo tamaño. ¿De qué tamaño serían las llamas de las velas de Lilliput? Y, desde luego, si pensamos un poco, más cuestiones nos surgen: ¿Cómo serían las gotas de lluvia en Lilliput y en Brobdingnag?, ¿eran las leyes físicas para el agua diferentes allí que en nuestro propio mundo? Y, finalmente, los físicos se preguntarían: ¿De qué tamaño eran los átomos en esos lugares?, ¿qué clase de reacciones químicas podrían tener lugar con los átomos del cuerpo de Gulliver?
Claro que, con esas preguntas esas historias fallan. La verdadera razón por la que los mundos de Los Viajes de Gulliver no pueden existir es que las leyes de la Naturaleza no permanecen exactamente iguales cuando se cambian las escalas. A veces, esto es evidente en las películas de desastres, donde quizá se ha construído una maqueta a escala para simular una gran ola o un rascacielos en llamas.

El ojo experto puede, sin problemas, distinguir entre la maqueta y la realidad. Los mejores resultados se obtienen cuando el factor de escala para el tiempo se elige igual a la raíz cuadrada de la escala espacial. Así, si el rascacielos de turno se construye a escala 1:9, hay que rodar la película a un 1/3 de su velocidad real. Pero incluso así, como antes señalo, el ojo entrenado distingue la diferencia entre lo que sucede en la película y lo que se observaría en el mundo real.

En resumen, las leyes que gobiernan el mundo físico tienen dos características importantes: muchas leyes de la Naturaleza permanecen inalterables, no se alteran cuando cambia la escala, pero hay otros fenómenos, tales como una vela encendida o las gotas de agua, que no cambian del mismo modo. La implicación final es que el mundo de los objetos muy pequeños será completamente diferente del mundo ordinario.
Justamente en el mundo de los seres vivos la escala crea importantes diferencias. En muchos aspectos, la anatomía de un ratón se podría considerar (más o menos y, guardando las distancias) como una copia de la de un elefante, pero mientras que un ratón puede trepar por una pared de piedra prácticamente vertical sin mucha dificultad (incluso se puede caer desde una altura varias veces mayor que su tamaño sin hacerse gran daño), un elefante sería incapaz de realizar tal hazaña. Así llegamos a comprender que la Gravedad, se deja sentir en menor grado a medida que los objetos disminuyen de tamaño.

Cuando llegamos a los seres unicelulares, se ve que para ellos no hay distinción entre arriba y abajo. Para ellos, la tensión superficial del agua es mucho más importante que la fuerza de gravedad. Basta observar que la tensión superficial es la fuerza que da forma a una gota de agua y comparar el tamaño de esa gota con los seres unicelulares, muchísimo menores, para que sea evidente que la tensión superficial es muy importante a esta escala.

La tensión superficial es una consecuencia de que todas las moléculas y los átomos se atraen unos a otros con una fuerza que nosotros llamamos fuerza de Van der Vaalls. esta fuerza tiene un alcance muy corto. para ser más precisos, diremos que la intensidad de esta fuerza a una distancia r es aproximadamente proporcional a 1/r7. Esto significa que si se reduce la distancia entre dos átomos a la mitad, la fuerza de Van der Vaalls con la que se atraen uno a otro se hace 2 x 2 x 2 x 2 x 2 x 2 x 2 = 128 veces más intensa. Cuando los átomos y las moléculas se acercan mucho unos a otros quedan unidos muy fuertemente a través de esta fuerza.
Ahora tendríamos que hablar algo de la mecánica cuántica y, en ese ámbito, las reglas de la mecánica cuántica funcionan tan bien que resultaría realmente difícil refutarlas.
Acordaos de los trucos ingeniosos descubiertos por Werner Hesinberg, Paul Dirac, o, Schrödinger que vinieron a mejorar y completar las reglas generales. Sin embargo, algunos de aquellos pioneros (Einstein y el mismo Schrödinger), sin embargo, presentaron serias objeciones a dicha interpretación de la naturaleza de lo muy pequeño.

Podríamos formular una simple pregunta que pondría en un brete a más de uno: ¿Dónde está realmente el electrón, en el punto x o en el punto y? En pocas palabras, ¿dónde está en realidad? Si prestamos atención a Bohr, no tiene ningún sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores serían las únicas realidades a las que deberíamos prestar atención y de las que podemos hablar.
Muchas veces me sorprende oír a muchos “científicos” que hablan con una seguridad de lo que dicen como si, de una verdad inamovible se tratara. Ellos (en realidad) creen que saben y, no llegan a darse cuenta de que están hablando de un Modelo que ha sido construído matemáticamente hablando, para poder explicar eso que, nosotros, los humanos, creemos que es la realidad del mundo. Sin embargo, más de una vez hemos tenido que cambiar esos modelos y rectificar esa “realidad” por otra que, resultó ser “más real”.
¡Sabemos tan poco
emilio silvera
Sep
17
Siempre queriendo saber ¡De tantas cosas!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

Einstein nos dijo el límite con el que podríamos recibir información en el universo, la velocidad de c. Que la velocidad de la luz era una constante sobrehumana fundamental de la Naturaleza. También sabía el maestro que en el proceso de nuevas teorías, la búsqueda de la teoría final que incluyera a otras fuerzas de la naturaleza distintas de la gravedad, daría lugar a teorías nuevas y cada vez mejores que irían sustituyendo a las antiguas teorías. De hecho, él mismo la buscó durante los 30 últimos años de su vida pero, desgraciadamente, sin éxito. Ahora se ha llegado a la teoría de supercuerdas que sólo funciona en 10 y 26 dimensiones y es la teoría más prometedora para ser la candidata a esa teoría final de la que hablan los físicos.

¿Cuerdas? Me parece que estoy confundiendo el principal objetivo de este trabajo y, me quiero situar en el tiempo futuro que va, desde los quarks de Gell-Mann hasta las cuerdas de Veneziano y John Schwarz y más tarde Witten. Esto de la Física, a veces te juega malas pasadas y sus complejos caminos te llevan a confundir conceptos y momentos que, en realidad, y de manera individualizada, todos han tenido su propio tiempo y lugar. Esta teoría tan avanzada es que, ni podemos verificarla en nuestro tiempo, pertenece al futuro y la dejaremos por el momento para volver a los números puros de la Naturaleza.
El físico espera que las constantes de la naturaleza respondan en términos de números puros que pueda ser calculado con tanta precisión como uno quiera. En ese sentido se lo expresó Einstein a su amiga Ilse Rosenthal-Schneider, interesada en la ciencia y muy amiga de Planck y Einstein en la juventud.
Lo que Einstein explicó a su amiga por cartas es que existen algunas constantes aparentes que son debidas a nuestro hábito de medir las cosas en unidades particulares. La constante de Boltzmann es de este tipo. Es sólo un factor de conversión entre unidades de energía y temperatura, parecido a los factores de conversión entre las escalas de temperatura Fahrenheit y Centígrada. Las verdaderas constantes tienen que ser números puros y no cantidades con “dimensiones”, como una velocidad, una masa o una longitud. Las cantidades con dimensiones siempre cambian sus valores numéricos si cambiamos las unidades en las que se expresan.
| Mp = | (hc/G)½ = | 5’56 × 10-5 gramos |
| Lp = | (Gh/c3) ½ = | 4’13 × 10-33 centímetros |
| Tp = | (Gh/c5) ½ = | 1’38 × 10-43 segundos |
| Temp.p = | K-1 (hc5/G) ½ = | 3’5 × 1032 ºKelvin |
Estas formulaciones con la masa, la longitud, el tiempo y la temperatura de Planck incorporan la G (constante de gravitación), la h (la constante de Planck) y la c, la velocidad de la luz. La de la temperatura incorpora además, la K de los grados Kelvin. Estos números infinitesimales definen el mundo cuántico y marcan el límite de nuestras actuales teorías. Nunca hemos logrado ir más allá. De hecho, cuando los científicos y los grandes matemáticos han querido ir más allá del Tiempo de Planck, para conocer qué pasó en esos primeros momentos del Big Bang… Nunca se logró, aparecen resultados sin sentido si pretendemos ir más allá de 10-43 segundos.

La interpretación de las unidades naturales de Stoney y Planck no era en absoluto obvia para los físicos. Aparte de ocasionarles algunos quebraderos de cabeza al tener que pensar en tan reducidas unidades, y sólo a finales de la década de 1.960 el estudio renovado de la cosmología llevó a una plena comprensión de estos patrones extraños. Uno de los curiosos problemas de la Física es que tiene dos teorías hermosamente efectivas (la mecánica cuántica y la relatividad general) pero gobiernan diferentes dominios de la Naturaleza.
La mecánica cuántica domina en el micromundo de los átomos y de las partículas “elementales”. Nos enseña que en la Naturaleza cualquier masa, por sólida o puntual que pueda parecer, tiene un aspecto ondulatorio. Esta onda no es como una onda de agua. Se parece más a una ola delictiva o una ola de histeria: es una onda de información. Nos indica la probabilidad de detectar una partícula. La longitud de onda de una partícula, la longitud cuántica, se hace menor cuanto mayor es la masa de esa partícula.

Por el contrario, la relatividad general era siempre necesaria cuando se trataba con situaciones donde algo viaja a la velocidad de la luz, o está muy cerca o donde la gravedad es muy intensa. Se utiliza para describir la expansión del universo o el comportamiento en situaciones extremas, como la formación de agujeros negros. Sin embargo, la gravedad es muy débil comparada con las fuerzas que unen átomos y moléculas y demasiado débil para tener cualquier efecto sobre la estructura del átomo o de partículas subatómicas, se trata con masas tan insignificantes que la incidencia gravitatoria es despreciable. Todo lo contrario que ocurre en presencia de masas considerables como planetas, estrellas y galaxias, donde la presencia de la gravitación curva el espacio y distorsiona el tiempo.
Como resultado de estas propiedades antagónicas, la teoría cuántica y la teoría relativista gobiernan reinos diferentes, muy dispares, en el universo de lo muy pequeño o en el universo de lo muy grande. Nadie ha encontrado la manera de unir, sin fisuras, estas dos teorías en una sola y nueva de Gravedad-Cuántica.

¿Cuáles son los límites de la teoría cuántica y de la teoría de la relatividad general de Einstein? Afortunadamente, hay una respuesta simple y las unidades de Planck nos dicen cuales son. En las unidades de Planck, una vez más, vemos un contraste entre la pequeña, pero no escandalosamente reducida unidad natural de la masa y las unidades naturales fantásticamente extremas del tiempo, longitud y temperatura. Estas cantidades tenían una significación sobrehumana para Planck. Entraban en La Base de la realidad física:
“Estas cantidades conservarán su significado natural mientras la Ley de Gravitación y la de Propagación de la luz en el vacío y los dos principios de la termodinámica sigan siendo válidos; por lo tanto, siempre deben encontrarse iguales cuando sean medidas por las inteligencias más diversas con los métodos más diversos.”
¿Quién sabe cómo serán?
En sus palabras finales alude a la idea de observadores en otro lugar del universo que definen y entienden estas cantidades de la misma manera que nosotros. Lo cierto es que, estas unidades, al tener su origen en la Naturaleza y no ser invenciones de los seres humanos, de la misma manera que nosotros y, posiblemente por distintos caminos, seres de otros mundos también las hallarán y serán idénticas a las nuestras. De entrada había algo muy sorprendente en las unidades de Planck, como lo había también en las de Stoney. Entrelazaban la gravedad con las constantes que gobiernan la electricidad y el magnetismo. Planck nos decía:
“La creciente distancia entre la imagen del mundo físico y el mundo de los sentidos no significa otra cosa que una aproximación progresiva al mundo real.”

Supongamos que tomamos toda la masa del universo visible y determinamos su longitud de onda cuántica. Podemos preguntarnos en qué momento esta longitud de onda cuántica del universo visible superará su tamaño. La respuesta es: cuando el universo sea más pequeño en tamaño que la longitud de Planck, es decir, 10-33 de centímetros, más joven que el tiempo de Planck, 10-43 segundos y supere la temperatura de Planck de 1032 grados. Las unidades de Planck marcan la frontera de aplicación de nuestras teorías actuales. Para comprender en que se parece el mundo a una escala menor que la longitud de Planck tenemos que comprender plenamente cómo se entrelaza la incertidumbre cuántica con la gravedad. Para entender lo que podría haber sucedido cerca del suceso que estamos tentados a llamar el principio del universo, o el comienzo del tiempo, tenemos que penetrar la barrera de Planck. Las constantes de la naturaleza marcan las fronteras de nuestro conocimiento existente y nos dejan al descubierto los límites de nuestras teorías.

Los límites últimos que podemos esperar para el almacenamiento y los ritmos de procesamiento de la información están impuestos por las constantes de la Naturaleza. En 1.981, el físico israelí, Jacob Bekenstein, hizo una predicción inusual que estaba inspirada en su estudio de los agujeros negros. Calculó que hay una cantidad máxima de información que puede almacenarse dentro de cualquier volumen. Esto no debería sorprendernos. Lo que debería hacerlo es que el valor máximo está precisamente determinado por el área de la superficie que rodea al volumen, y no por el propio volumen. El número máximo de bits de información que puede almacenarse en un volumen viene dado precisamente por el cómputo de su área superficial en unidades de Planck. Supongamos que la región es esférica. Entonces su área superficial es precisamente proporcional al cuadrado de su radio, mientras que el área de Planck es proporcional a la longitud de Planck al cuadrado, 10-66 cm2. Esto es muchísimo mayor que cualquier capacidad de almacenamiento de información producida hasta ahora. Asimismo, hay un límite último sobre el ritmo de procesamiento de información que viene impuesto por las constantes de la Naturaleza.
No debemos descartar la posibilidad de que seamos capaces de utilizar las unidades de Planck-Stoney para clasificar todo el abanico de estructuras que vemos en el universo, desde el mundo de las partículas elementales hasta las más grandes estructuras astronómicas. Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias. Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y mprotón.

|
α = 2πe2 / hc ≈ 1/137 |
|
αG = (Gmp2)2 / hc ≈ 10-38 |
La identificación de constantes adimensionales de la Naturaleza como a (alfa) y aG, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro. Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala. La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.

Siempre estamos tratando de desvelar los secretos de la Naturaleza. La naturaleza cuántica nos llevará a otros mundos, sin salir de este.
El cuásar 3C191 fue localizado con un desplazamiento al rojo de 1,95 y por eso su luz salió cuando el universo tenía sólo una quinta parte de su edad actual, hace casi once mil millones de años, llevando información codificada sobre el valor de la constante de estructura fina en ese momento. Con la precisdión de las medidas alcanzables entonces, se encontró que la constante de estructura fina era la misma entonces que ahora dentro de un margen de unos pocos por ciento:
α (z = 1,95/α(z = 0) = 0,97 ± 0,05

Algunas imágenes que nos muestran a distintos cuáres de los muchos que pueblan el Universo. El cuásar es una fuente inmensa de energía electromagnética, que incluye radiofrecuencias y luz visible. Los cuásares visibles muestran un desplazamiento al rojo muy alto. El consenso científico dice que esto es un efecto de la expansión métrica del universo entre los cuásares y la Tierra. Combinando esto con la Ley de Hubble se sabe que los cuásares están muy distantes. Para ser observables a esas distancias, la energía de emisión de los quasares hace empequeñecer a casi todos los fenómenos astrofísicos conocidos en el universo, exceptuando comparativamente a eventos de duración breve como supernpovas y brotes de rayos gamma. Los cuásares pueden fácilmente liberar energía a niveles iguales que la combinación de cientos de galaxias medianas. La luz producida sería equivalente a la de cientos de miles de soles.
Poco después , en 1967, Bahcall y Schmidt observaron un par de líneas de emisión de oxígeno que aparecen en el espectro de cinco galaxias que emiten radioondas, localizadas con un desplazamiento hacia el rojo promedio de 0,2 (emitiendo así su luz hace unos dos mil millones de años: Aproximadamente la época en que el reactor de Oklo estaba activo en la Tierra y obtuvieron un resultado consistente con ausencia de cambio en la constante de estructura fina que era aún diez veces más fuerte:
α (z = 0,2)/α(z = 0) = 1,001 ± 0,002
Estas observaciones excluían rápidamente la propuesto por Gamow de que la constante de estructura fina estaba aumentando linealmente con la edad del universo. Si hubiese sido así, la razón α(z = 0,2)/α(z = 0) debería haberse encontrado con un valor próximo a 0,8.

La Constante de la Estructura Fina
Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck). Si se duplica el valor de todas las masas no se puede llegar a saber, por qué todos los números puros definidos por las razones de cualquier par de masas son invariables.
Cuando surgen comentarios de números puros y adimensionales, de manera automática aparece en mi mente el número 137. Ese número encierra más de lo que estamos preparados para comprender; me hace pensar y mi imaginación se desboca en múltiples ideas y teorías. Einstein era un campeón en esta clase de ejercicios mentales que él llamaba “libre invención de la mente”. El gran físico creía que no podríamos llegar a las verdades de la naturaleza sólo por la observación y la experimentación. Necesitamos crear conceptos, teorías y postulados de nuestra propia imaginación que posteriormente deben ser explorados para averiguar si existe algo de verdad en ellos.

Sí, algunas cosas nos quedan muy lejos pero, sobre todo recordad:
“Todos los físicos del mundo, deberían tener un letrero en el lugar más visible de sus casas, para que al mirarlo, les recordara lo que no saben. En el cartel sólo pondría esto: 137. Ciento treinta y siete es el inverso de algo que lleva el nombre de constante de estructura fina”.
α = 2πe2 /hc = 1/137
Este número guarda relación con la posibilidad de que un electrón emita un fotón o lo absorba. La constante de estructura fina responde también al nombre de “alfa” y sale de dividir el cuadrado de la carga del electrón, por el producto de la velocidad de la luz y la constante de Planck. Todo esto no significan otra cosa sino que ese solo numero, 137, encierra los misterios del electromagnetismo (el electrón, e–), la relatividad (la velocidad de la luz, c), y la teoría cuántica (la constante de Planck, h).
Nuestro destino es el de seguir preguntando. Nunca lo podremos saber todo sobre todo y, por cada respuesta que podamos lograr, aparecerán mil preguntas nuevas que plantear. El Universo es inmenso y en él se esconde todo lo que existe y, entre los muchos secretos que guarda, está el más grande de todos: ¡El surgir de las consciencias! Desde que la inteligencia y la consciencia de Ser aparecieron en el Universo, desde siempre estuvo acompañada por la curiosidad y la necesidad de saber. El conocimiento es nuestro destino y, seguramente también, nuestra salvación.

Una cosa es cierta: Todos los seres vivos que puedan estar presentes en los mundos de todas las galaxias que pueblan nuestro Universo, todos sin excepción, están aquí gracias a que las constantes universales de la Naturaleza son las que son y hacen posible mundos como el nuestro que, contienen todos los ingredientes necesarios para albergar la vida. Si la carga del electrón, la masa del protón, o, la velocidad de la luz variara tan sólo en una diexmilésima… ¡Nuestro Universo sería distinto y, la vida, no estaría presente!
emilio silvera
Sep
15
La Ilusión de simplificar la Naturaleza
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
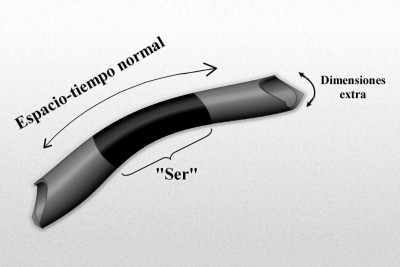
El gráfico representa un modelo de manguera de un espacio-tiempo de dimensiones más altas de tipo Kaluza-Kleim donde la longitud, o mejor, la dimensión a lo largo de la longitud de la manguera representa el 4-espacio-tiempo normal, y la dimensión alrededor de la manguera representa la dimensión extra “pequeñas” (quizá escala de Planck). Imaginemos un “ser” que habite en este mundo, que rebasa estas dimensiones extra “pequeñas”, y por ello no es realmente consciente de ellas.

Nuestras Mentes están conformadas de forma tridimensional, nuestro mundo es de tres dimensiones espaciales, la cuarta, el Tiempo, no incide en la posible alteración evolucitva que podríamos acoger para experimentar el poder vislumbrar más altas dimensiones pero, ¿podrán alterarse las percepciones? En lo que a lo material se refiere, nuestros cerebros sólo perciben las tres dimensiones de las que ellos mismos está hechos. Sin embargo, el cerebro es tan complejo que puede generar algo que llamamos Mente y, a partir de ahí… ¡Cualquier cosa sería posible!
Nunca nos ha resultado fácil encontrar esas otras dimensiones extra
Nuestras mentes hacen posible ver las cosas de diferentes maneras, incluso aquellas que no podemos ver.
Para ver cómo dimensiones más altas simplifican las leyes de la Naturaleza, recordemos que un objeto tiene longitud, anchura y altura. Puesto que tenemos libertad para girar un objeto 90º, podemos transformar su longitud en anchura y su anchura en altura. Mediante una simple rotación, podemos intercambiar cualquiera de las tres dimensiones espaciales.
Ahora bien, si el tiempo es la cuarta dimensión, entonces es posible hacer “rotaciones” que convierten el espacio en tiempo y el tiempo en espacio. Estas rotaciones tetradimensionales son precisamente las distorsiones del espacio y del tiempo exigidas por la relatividad especial. En otras palabras, espacio y tiempo se mezclan de una forma esencial, gobernada por la relatividad. El significado del tiempo como la cuarta dimensión es que pueden hacerse relaciones entre el tiempo y el espacio de una forma matemáticamente precisa. A partir de entonces, deben ser tratados como dos aspectos de la misma magnitud: el espacio-tiempo. Así han quedado unificadas las leyes de la Naturaleza al pasar de tres a cuatro dimensiones.

Con esta imagen apareció la leyenda: “Varapalo para la teoría de cuerdas: Existe una teoría cuántica de la gravedad en 4D (cuatro dimensiones) finita, la supergravedad N = 8.
En esta otra imágen gráfica se preguntaba: ” Qué pasaría si el espaciotiempo tuviera ndomensiones espaciales y m dimensiones temporales.
En topología diferencial se descubrió que el espacio cuatridimensional euclídeo admite estructuras diferenciables exóticas que no son equivalentes a la convencional; se sabe que existen las exóticas pero su descripción explícita en coordenadas es muy complicada, salvo bajo ciertas restricciones. Hay un número infinito no numerable de estructuras diferenciables en R4, pero sólo existe una en Rn, para n≠4. Esta propiedad de un universo con cuatro dimensiones lo distingue de un universo con cualquier otro número de dimensiones posibles.
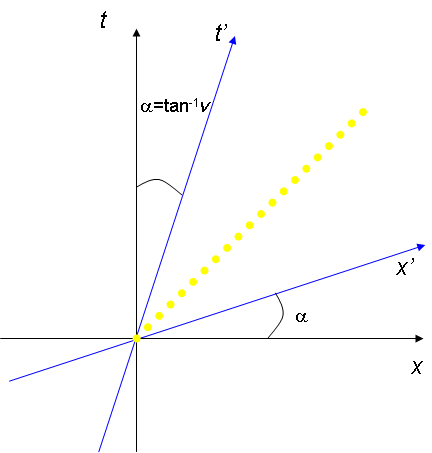
El espacio tiempo de Minkowski apareció en escena tras leer éste, la relatividad espacial de Einstein
La discusión de la unificación de las leyes de la Naturaleza fue más bien abstracta, y lo habría seguido siendo si Einstein no hubiese dado el siguiente paso decisivo. Él comprendió que si el espacio y el tiempo pueden unificarse en una sola entidad, llamada espaciotiempo, entonces quizá la materia y la energía pueden unirse también en una relación dialéctica. Si las reglas pueden contraerse y los relojes pueden frenarse, razonó, entonces cualquier cosa que midamos con regla y relojes también debe cambiar.
Sin embargo, casi todo en el laboratorio de un físico se mide con regla y relojes. Esto significa que los físicos tendrán que recalibrar todas las magnitudes del laboratorio que una vez dieron por hecho que eran constantes.

Hay que evitsr por todos los medios el choque frontal del vehículo con cualquier cosa
En concreto, la energía es una cantidad que depende de cómo midamos las distancias y los intervalos de tiempo. Un automóvil de prueba que choca a gran velocidad contra una pared de ladrillos tiene obviamente energía. No obstante, si el veloz automóvil se aproxima a la velocidad de la luz, sus propiedades se distorsionan. Se contrae como un acordeón y los relojes en su interior se frenan.
Lo que es más importante, Einstein descubrió que la masa del automóvil también aumenta cuando reacelera. Pero ¿de dónde procede este exceso de masa? Y él concluyó que procedía de la energía.
Esto tuvo consecuencias perturbadoras. Dos de los grandes descubrimientos de la física del siglo XIX fueron la conversación de la masa y la conservación de la energía; es decir, la masa total y la energía total de un sistema cerrado, tomadas por separado, no cambian. Por ejemplo, si el coche veloz choca contra el muro de ladrillos, la energía del automóvil no desaparece, sino que se convierte en energía sonora del choque, energía cinética de los fragmentos de ladrillo que vuelan por los aires, energía calorífica, y así sucesivamente. La energía total (y la masa total) antes y después del choque es la misma.

Emergía calorífica
Sin embargo, Einstein decía ahora que la energía del automóvil podía convertirse en masa (un nuevo principio de conservación que decía que la suma total de la masa y la energía debe siempre permanecer constante. La materia no desaparece repentinamente, ni la energía brota de la nada. En este sentido, la materia desaparece sólo para liberar enormes cantidades de energía o viceversa.
Cuando Einstein tenía 26 años, calculó exactamente cómo debía cambiar la energía si el principio de la relatividad era correcto, y descubrió la relación E=mc2. Puesto que la velocidad de la luz al cuadrado (C2) es un número astronómicamente grande, una pequeña cantidad de materia puede liberar una enorme cantidad de energía. Dentro de las partículas más pequeñas de materia hay un almacén de energía, más de un millón de veces la energía liberada en una explosión química. La materia, en cierto sentido, puede verse como un depósito casi inagotable de energía; es decir, la materia es en realidad, energía condensada.
Einstein supo ver que las dimensiones más altas tienen un propósito: unificar los principios de la Naturaleza. Al añadir dimensiones más altas podía unir conceptos físicos que, en un mundo tridimensional, no tienen relación, tales como la materia y la energía o el espacio y el tiempo que, gracias a la cuarta dimensión de la relatividad especial, quedaron unificados.

Y, a todo esto, no podemos dejar de asombrarnos de nuestra presencia aquí, de todo lo que hemos sido capaces de entender en la configuración del mundo, y, como decía Eintein: “lo incomprensible del Universo es, que lo podamos comprender”.
Desde entonces, estos conceptos, los tenemos que clasificar, no por separado, sino siempre juntos como dos aspectos de un mismo ente materia-energía por una parte y espacio-tiempo por la otra. El impacto directo del trabajo de Einstein sobre la cuarta dimensión fue, por supuesto, la bomba de hidrógeno, que se ha mostrado la más poderosa creación de la ciencia del siglo XX. Claro que, en contra del criterio de Einstein que era un pacifista y nunca quiso participar en proyectos de ésta índole.

¿Dónde estará la puerta de la Quinta Dimensión? ¿Existirán en realidad las dimensiones más altas?
Einstein completó su teoría de la relatividad con una segunda etapa que, en parte, estaba inspirada por lo que se conoce como principio de Mach, la guía que utilizó Einstein para crear esta parte final y completar su teoría de relatividad general.
Einstein enunció que, la presencia de materia-energía determina la curvatura del espacio-tiempo a su alrededor. Esta es la esencia del principio físico que Riemann no logró descubrir: la curvatura del espacio está directamente relacionada con la cantidad de energía y materia contenida en dicho espacio.

La masa del planeta, de la estrella o de la galaxia curva el espacio-tiempo a su alrededor y configura la geometría local de esa región que está bajo el dominio de la Gravedad. ?Os iagináis la curvatura “infinta” alrededor de un Agujero Negro?
Albert Einstein realizó una verdadera hazaña intelectual y nos legó su teoría General de la Relatividad, una teoría construida desde la pura geometría, excediéndose en elegancia y efectiva en su espacio de aplicación. La relación entre el cuerpo y la curvatura del espacio-tiempo, es equivalente (Gµv). Significa, la manifestación visible o invisible de la energía [m=e/c2], y en este caso, manifestada en la forma masiva del cuerpo, curva el espació-tiempo.
Esto, a su vez, puede resumirse en la famosa ecuación de Einstein, que esencialmente afirma:
Materia-energía determina la curvatura del espacio-tiempoyse denota

Esta ecuación engañosamente corta es uno de los mayores triunfos de la mente humana (me he referido a ella en otras muchas ocasiones). De ella emergen los principios que hay tras los movimientos de las estrellas y las galaxias, los agujeros negros, el big bang, y seguramente el propio destino del Universo.
Es curiosa la similitud que se da entre la teoría del electromagnetismo y la relatividad general, mientras que Faraday experimentó y sabía los resultados, no sabía expresarlos mediante las matemáticas y, apareció Maxwell que, finalmente formuló la teoría.
Einstein, al igual que Faraday, había descubierto los principios físicos correctos, pero carecía de un formulismo matemático riguroso suficientemente potente para expresarlo (claro que Faraday no era matemático y Einstein si lo era). Carecía de una versión de los campos de Faraday para la Gravedad. Irónicamente, Riemann tenía el aparato matemático, pero no el principio físico guía, al contrario que Einstein. Así que, finalmente, fue Einstein el que pudo formular la teoría con las matemáticas de Riemann.
 El Tensor métrico de Riemann que salvó a Einstein cuando estaba atrancado y no sabía cómo expresar, la ecuación de su Relatividad General que, al fín pudo escribir y decir al mundo cómo sería la Cosmología moderna. En esos “garabatos de arriba, Einstein `lasmóp una ecuación engañosamente corta y es uno de los mayores triunfos de la mente humana.
El Tensor métrico de Riemann que salvó a Einstein cuando estaba atrancado y no sabía cómo expresar, la ecuación de su Relatividad General que, al fín pudo escribir y decir al mundo cómo sería la Cosmología moderna. En esos “garabatos de arriba, Einstein `lasmóp una ecuación engañosamente corta y es uno de los mayores triunfos de la mente humana.
“¡Qué extraño sería que la teoría final se descubriera durante nuestra vida! El descubrimiento de las leyes finales de la Naturaleza marcará una discontinuidad en la Historia del intelecto humano, la más abrupta que haya ocurrido desde el comienzo de la ciencia moderna del siglo XVII. ¿Podemos imaginar ahora como sería?”
STEVEN WEINBERG

¿Son tántas las clases de belleza en el Universo?
¿Es la belleza un principio Físico? Bueno, podríamos decir que también, pudiera ser un principio del Sentimiento de la Mente Humana, aunque, en Física, por ejmplo, el concepto de belleza tenga otras connotaciones.
La teoría de supercuerdas nos da una formulación convincente de la teoría del Universo, sin embargo, el problema fundamental radica en que una comprobación de dicha teoría, está más allá de nuestras posibilidades actuales. De hecho, la misma teoría predice que la unificación de todas las fuerzas ocurre a la energía de Planck, o 1019 miles de millones de electronvoltios, que como sabéis, es alrededor de mil billones de veces mayor que las energías actualmente disponibles en nuestros aceleradores de partículas, se denota por la ecuación:

Como la masa de Planck es del orden de 10-8 kg (equivalente a una energía de 1019 GeV), y, por ejemplo, la masa el protón es del orden de 10-27 kg y las mayores energías alcanzables en los aceleradores de partículas actuales son de un orden muy inferior, los efectos de la gravitación cuántica no aparecen en los laboratorios de física de partícula (ni el LHC ni en el Fermilab). Sin embargo, en el universo primitivo las partículas tenían energías del orden de la masa de Planck, de acuerdo con la teoría el big bang, y es, por tanto, necesaria una teoría cuántica de la gravedad para estudiar las condiciones en la época conocida como Tiempo de Planck.
David Gross
Ya he comentado otras veces que el físico David Gross (el de más edad de los miembros conocidos como el “cuarteto de cuerdos” y autores de la teoría llamada la cuerda heterótica) dijo en una ocasión: “El coste de generar esta fantástica energía, necesitaría el dinero de las tesorerías de todos los países del mundo juntos, y quizá, no llegara. Es verdaderamente astronómico.”
Siendo así, de momento estamos condenados a no poder verificar experimentalmente este motor (parado) que haría marchar el vehículo de la Física. La teoría decadimensional está paralizada en dos sentidos: el económico y el técnico – matemático. El primero por falta de dinero que nos pudiera construir aceleradores tan potentes como para descubrir la partícula de Higgs, los quarks e incluso las cuerdas vibrantes, esos previsibles y minúsculos objetos primordiales que conforman la materia. En segundo lugar, las formulaciones matemáticas complejas que, según parece, aún no se han inventado. Parece que hoy, ni siquiera Witten o Perelman, conocen el secreto de los números mágicos que nos puedan llevar hasta el final del camino iniciado con Einstein y Kaluza-klein.

Estaría bueno que, al final se descubriera que alfa (α) tuviera un papel importante en la compleja teoría de cuerdas, ¿Por qué no? En realidad alfa, la constante de estructura fina, nos habla del magnetismo, de la constante de Planck y de la relatividad especial, es decir, la velocidad de la luz y, todo eso, según parece, emergen en las ecuaciones topológicas de la moderna teoría de cuerdas. ¡Ya veremos!
Sí, es cierto, que la teoría tiene muchos detractores y algunos han llegado a denominarla Física de Circo pero, particularmente opino que la teoría de cuerdas nos dará muchas alegrías y que en ella están las respuestas a muchas preguntas que no sabemos contestar. Simplemente se trata (como nos dice E. Eitten) de una teoría adelantada a su tiempo.
Dentro del mundo de la Física, los hay de todas las opiniones: en contra y a favor. Es famosa la postura detractora del Nóbel Sheldoy Glasgow de Harvard, no quiere ni oír hablar de la teoría de supercuerdas a la que califica de física de Teatro.
Otros muchos, la mayoría, como Murray Gell-Marn, Steven Weinberg (ambos Premios Nóbel) o el mismo. E. Witten (Medalla Field), opinan lo contrario y ven en esta teoría de dimensiones más altas el futuro de la Física.
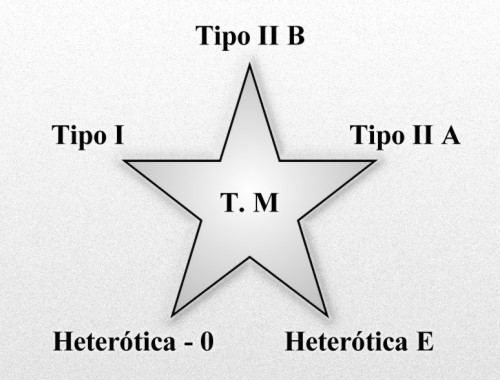
Todas las versiones de las diversas Teorías de cuerdas han sido unificadas en una, la Teoría M de E. Witte, y, esperemos que no se quede ahí estancada y que, aparezca algún genio matemático como Ramanujan o Riemman y nos saque del agujero en el que actualmente estamos metidos y del que no podemos salir, no existen ideas que la hagan avanzar ni matemáticas complejas que la puedan hacer andar.

La recreación del mundo no parece cosa fácil, y, en estas teorías queremos recrear mucho más
Ya sabemos que en física toda teoría debe ser verificada, una y otra vez, en uno y en otro lugar, experimentalmente, obteniendo siempre el mismo resultado, es la única manera de que sea aceptada por la comunidad científica, mientras tanto, la teoría no es fiable y queda a la espera de ser comprobada, verificada sin ningún lugar para la duda.
Pero, ¿Se puede recrear la creación?
La teoría de supercuerdas trata de eso. Quiere explicarnos todos los misterios del Universo a partir de ese primer momento, ¡la creación!
emilio silvera
















 Totales: 83.777.300
Totales: 83.777.300 Conectados: 45
Conectados: 45






















