Mar
21
¡La Física! ¿Estará perdiendo el Norte?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

Curiosity descubre un antiguo Lago en Marte

¿Queremos imitar el salto cuántico viajar más rápido?
A finales del siglo XIX y principios del XX algunos podían creer que los secretos de la Naturaleza estaban todos descubiertos gracias a los hallazgos que en el pasado hicieran Newton y otros y más recientemente Maxwell, Planck, Einstein y otros muchos que, con sus trabajos nos desvelaron cómo funcionaba la gravedad, qué era en realidad la electricidad y el magnetismo y también, nos llevaron el fascinante mundo de lo muy pequeño con el cuanto de acción, h, de Planck que nos trajo poco más tarde, la mecánica cuántica.
La mecánica, la óptica, la electricidad… todo estaba descubierto y explicado. Los científicos de la época pansaban que sus futuros colegas sólo se dedicarían a realizar medidas para obtener las constantes con mayor precisión vez. Después de todo aquello, se siguió avanzando y continuamos haciéndonos preguntas creyendo que nos llevarían a las respuestas últimas.
Si, por ejemplo, las supercuerdas nos conducen a las respuestas últimas, entonces, ¿en qué dirección debemos nuestra investigación?, ¿es que nos hemos introducido tanto en el mundo de lo desconocido y lo ininteligible que estamos a punto de ahogarnos en un mar de lo absurdo?, ¿estamos enterrados bajo tántas preguntas de los imposibles que deberíamos considerarnos perdidos?, ¿tiene algún sentido especular acerca de la “Teoria de Todo” en un mundo extraño de las unidades de Planck?

Bueno, si queremos ser sinceros…, podemos discrepar de algunas de las cuestiones que hoy se están debatiendo y ser críticos con otras. Sin embargo, no podremos negar los avances que realmente se están logrando en el mundo de las nuevas tecnologías que, gracias a la Física, ya están en el futuro y, en nuestras vidas cotidianas lo estamos viendo continuamente.
Por otra , nada despierta más nuestra curiosidad que lo ininteligible y, precisamente por eso, tiene tanto éxito y llama la atención teorías como la de las supercuerdas. Miremos, por ejemplo, lo que es tan curioso en el mundo de la longitud de Planck es que no podemos encontrar absolutamente ningún modelo que nos pueda dar una descripción razonablemente autoconsistente de partículas que interaccionan entre sí con fuerzas gravitatorias tan intensas y que, al mismo tiempo, obedezcan a las leyes de la mecánica cuántica. Por tanto, incluso si hubiéramos sido capaces de realizar experimentos con choques de partículas con energías planckianas, no hubiéramos sabido como comparar los resultados con una teoría. Aquí hay para los físicos: hacer una teoría. No nos importa demasiado como describa esa teoría la interacción gravitatoria, pero tenemos suficientes requisitos en la lista como para que encontrar esa candidata a ser la teoría sea una labor extremadamente difícil. La Teoría de Supercuerdas parecía estar a punto de conseguirlo, pero falló en los últimos momentos. Dicen que necesitamos la energía de Planck para poder verificarla y, si es así, nos queda espera para rato.

Mientras buscamos esas teorías que están más allá de nuestras posibilidades reales de hoy, la Ciencia no se para y sigue avanzando en otros muchos campos que, como antes decía, nos están llevando a pasos agigantados un futuro que ya está con nosotros y, lo está haciendo con tal rapidez que ni nos hemos percatado de ello.
En cuanto a esa soñada Teoria de Todo, en primer lugar debe ser matemáticamente exacta y tiene que permitirnos calcular con extrema precisión el comportamiento de las partículas bajo todas las circunstancias imaginables. Por ahí circulan una y mil “teorías” que exponen las ideas más variopintas que imaginarnos podamos pero, desgraciadamente, son inútiles para los físicos porque sus descripciones no reúnen el rigor ni la prcisión que deben estar presentes en toda buena teoría. Por otra , los físicos prefieren que la teoría trate la fuerza gravitatoria de tal manera que esté de acuerdo con la obtenida en la formulación de la teoría de la relatividad general de Einstein. Sabemos que la fuerza gravitatoria cuerpos pesados como las estrellas y los planetas obedece a esta teoría con gran exactitud (como ha sido confirmado espectacularmente en las observaciones de los púlsares, estrellas compactas que rotan a gran velocidad. Nuestra teoría candidata debería explicar estas observaciones).
No digamos de los intrincados caminos que la Física ha sobrevolado cuando se ha querido meter en la posibilidad de viajes en el Tiempo y, los físicos se encontraron con una y mil paradojas extrañas. Además, como nos ocurre con la Teoría de cuerdas, al meternos en un sendero desconocido y de intrincados peligros…nunca hemos podido llegar al final después de largos y costosos recorridos. ¿Servirá para algo los muchos esfuerzos realizados?
Por otra somos conscientes y conocedores de que las leyes de la mecánica cuántica son inexorables y, por tanto, queremos que nuestra teoría sea formulada en términos de la mecánica cuántica. Tanto la mecánica cuántica como la teoría de la relatividad tienen la propiedad de que, tan pronto como uno admita la más pequeña desviación de esos principios, ambas darían lugar a una teoría totalmente diferente, que de ninguna manera se parecería al mundo que conocemos (o pensamos conocer). “Un poco relativista” o “un poco mecanicuántico” tan poco sentido como “un poco embarazado”. Podríamos imaginar, por otra parte, que la mecánica cuántica o la relatividad general, o ambas, serían marcos demasiado restrictivos nuestra avanzada teoría, de manera que habría que extender sus principios, llegar más lejos.


La cuerda es cuántica y gravitatoria, de sus entrañas surge, por arte de magia, la partícula mensajera de la fuerza de gravedad: el gravitón. Funde de natural las dos teorías físicas más poderosas de que disponemos, la mecánica cuántica y la relatividad general, y se convierte en supercuerda -con mayores grados de libertad- es capaz de describir bosones y fermiones, partículas de fuerza y de materia. La simple vibración de una cuerda infinitesimal podría unificar todas la fuerzas y partículas fundamentales.
Parece que todo está hecho de cuerdas, incluso el espacio y el tiempo podrían emerger de las relaciones, más o menas complejas, cuerdas vibrantes. La materia-materia, que tocamos y nos parece tan sólida y compacta, ya sabíamos que está casi vacía, pero no imaginábamos que era tan sutil como una cuerda de energía vibrando. Los átomos, las galaxias, los agujeros negros, todo son marañas de cuerdas y supercuerdas vibrando en diez u once dimensiones espaciotemporales.
Está claro que no trato de explicar aquí una teoría que no comprendo y, el tratar el tema se debe a la curiosidad de tratar de indicar el camino, o, los caminos, por los que se podría llegar más lejos, al , algo más allá. De una cosa si que estoy seguro: ¡Las cuatro fuerzas fundamentales del Universo, un día fueron una sola fuerza!

En el universo existen numerosas estrellas cuyas masas son considerablemente mayores que las del Sol, debido a lo cual, la fuerza gravitotoria en su superficie es considerablemente más intensa que sobre la Tierra o sobre el Sol. La enorme cantidad de materia de una de esas estrellas causa una presión inimaginablemente alta en su interior, pero como las tenperaturasd en el interior de las estrellas es también altísima, se produce una presión contraria que evita que la estrella se colapse. La estrella, sin embargo, pierde calor continuamente. Al proncipio de su vida, en las estrellas se producen todo de reacciones nucleares que mantienen su temperatura alta y que incluso la pueden elevar, pero antes o después el combustible nuclear se acaba. Cuanto más pesada sea la estrella, mayor es la prsión y la temperatura, y más rápidamente se consume su combustible. La contrapresión disminuye progresivamente y la estrella se va colapsando bajo la presión, según dismunye el tamaño de la estrella, la fuerza gravitatoria aumenta hasta que finalmente se produce una implosión -un colapso repentino y completo- que no puede ser evitado por más tiempo: ¡ha nacido un agujero negro!

Según todos los indicios, cuando la estrella es muy masiva, la Improsión finaliza convirtiendo toda la inmensa masa de la estrella en un A. N., pero antes, explota como supernova y llena el espacio de los materiales coplejos que han sido fabricados en sus nucleares, siembra el espacio con una Nebulosa de la que, años más tarde, nacerán nuevas estrellas y nuevos mundos…Y, ¿quién sabe? ¡Si nuevas formas de Vida!
A menudo implosión libera tanto calor que las capas exteriores de la estrella explotan por la presión de la radiación, y la implosión queda interrumpida produciéndose una esfera extremadamente compacta de “material nuclear” que conocemos como una estrella de neutrones. Algunas veces, estas estrellas de neutrones rotan con una tremenda velocidad (más de 500 revoluciones/segundo), y, debido a irregularidades en la superficie, emiten una señal de radio que pulsa con esa velocidad.
Si todos estos sucesos pudieran ser observados una distancia segura, las señales emitidas por el material durante la implosión pronto serían demasiado débiles para ser detectadas y, en el caso de un afgujero negro, el objeto se vuelve de ese color y desaparece de nuestra vista convertido en una “bola de gravedad pura”, se pueden calcular sus propiedades con precisión matemática. Sólo se necesitan tres parámetros para caracterizar completamente al agujero negro: su masa, su movimiento angular (cantidad de movimiento de rotación) y su carga eléctrica.
También se calcular como se comportan los chorros de partículas cuando se aventuiran cerca del agujero negro. Hawking ya nos habló de ello y explicó con suficiente claridad, lo que pasaba era que, en contra de lo que pudiéramos pensar, el agujero emite un débil flujo de partículas en ciertas circunstancias. ¿Esas partículas son reales! Agujero Negro está emitiendo un flujo constante de partículas de todas las especies concebibles.

El Telescopio Espacial Hubble y Chandra han captado la imagen de un impresionante anillo de Agujeros negros. La fotografía corresponde al conjunto Arp 147, en el que aparecen 2 galaxias interactuando entre sí y que se ubican a una distancia de 430 millones de años luz de la Tierra. La NASA combinó datos del Chandra con imágenes del Hubble. Mientras los tonos rojos, azules y verdes fueron resultado del trabajo del Hubble; los de color magenta, del Chandra. La captura muestra un anillo formado por estrellas masivas que evolucionaron rápidamente y explotaron en supernovas, como consecuencia de una colisión galáctica. Es así como dejaron densas estrellas de neutrones y posiblemente, también agujeros negros.
En el Universo ocurren sucesos que no podemos ni imaginar, tales son las fuerzas y energías que ahí están presentes y que dan lugar a maravillas que desembocan en transiciones de fase que convierten unas cosas en otras muy distintas haciendo que la diversidad exista, que la belleza permanezca, que la monotonía no sea el camino.

Es cierto que nunca hemos podido estar tan cerca de un agujero negro como poder comprobar, in situ, la radiación Hawking que, para su formulación, sólo utilizó leyes bien establecidas de la naturaleza y que, por tanto, el resultado debería ser incuestionable, pero no es del todo cierto por dos razones:
La primera razón es que nunca ( he dicho) hemos sido capaces de observar un agujero negro de cerca y mucho de un tamaño tan pequeño que su radiación Hawking pueda ser detectada. Ni siquiera sabemos si tales miniagujeros negros existen en nuestro universo, o si sólo forman una minoría extremadamente escasa entre los objetos del cielo. Aunque pensemos conocer la teoría, no nos habría hecho ningún daño haber podido comprobar sus predicciones de una o de otra. ¿Sucede todo exactamente como pensamos actualmente que debería suceder?
Otros, como Gerald ´t Hooft, consiguieron construir otro de teorías alternativas y le dieron resultados distintos a los de Hawking, en la que el Agujero Negro podia radiar con una intensidad considerablemente mayor que la que la teoría de Stephen predecía.

Hay un aspecto relacionado con la radiación Hawking mucho más importante. El agujero negro disminuye su tamaño al emitir partículas, y la intensidad de su radiación crece rápidamente según se reduce su tamaño. Justo de llegar a los estadios finales, el tamaño del agujero negro se hará comparable a la longitud de Planck y toda la masa llegará a ser sólo un poco mayor que la masa de Planck, Las energías de las partículas emitidas corresponderan a la masa de Planck.
¡Solamente una teoría completa de la Gravedad Cuántica podrá predecir y describir exactamente lo que sucede al agujero negro en ese ! es la importancia de los Agujeros Negros la teoría de partículas elementales en la Longitud de Planck. Los agujeros negros serían un laboratorio ideal para experimentos imaginarios. Todos alcanzan, por sí mismos, el régimen de energía de los números de Planck, y una buena teoría debe ser capaz de decirnos como calcular en ese caso. casi una década, Gerad ´t Hoofft ha resaltando esa objeción en la teoría de supercuerdas: no nos dice nada de los agujeros negros y mucho de cómo un agujero negro comenzar su vida como un agujero negro de tamaño “astronómico” y acabar su vida explosivamente.
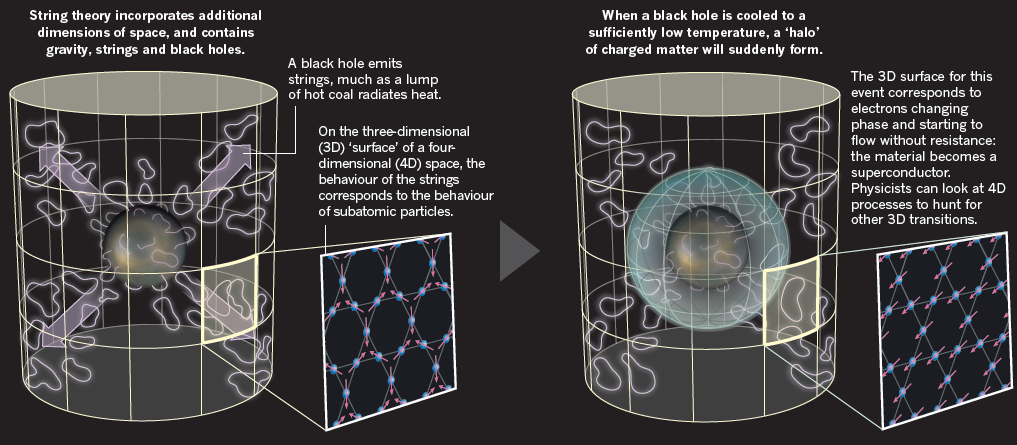
Lo cierto es que, andamos un poco perdidos y no pocos físicos (no sabemos si de manera interesada), insisten una y otra vez, en cuestiones que parecen no llevar a ninguna parte y que, según las imposibilidades que nos presentan esos caminos, no sería conveniente elegir otros derroteros para indagar nuevas físicas mientras tanto, avanzan las tecnologías, se adquieren más potentes y nuevas formas de energías que nos puedan permitir llegar a sondear las cuerdas y poder vislumbrar si, es cierto, que pueda existir alguna “materia oscura”, o, si existen bosones dadores de masa, o…¡tántas cosas más que, la lista, sería interminable! de las cosas que no sabemos.
emilio silvera
Mar
17
La relatividad especial
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Relativista ~
Clasificado en Física Relativista ~
 Comments (3)
Comments (3)
En cualquier parte que podamos buscar información nos dirán:
“Henri Poincqaré, matemático francés, sugirió a finales del siglo XIX que el principio de relatividad establecido desde Galileo (la invariancia galileana) se mantiene para todas las leyes de la naturaleza. Joseph Larmor y Hendrik Lorentz descubrieron que las ecuaciones de Maxwell, la piedra angular del electromagnetismo, eran invariantes solo por una variación en el tiempo y una cierta unidad longitudinal, lo que produjo mucha confusión en los físicos, que en aquel tiempo estaban tratando de argumentar las bases de la teoría del éter, la hipotética substancia sutil que llenaba el vacío y en la que se transmitía la luz. El problema es que este éter era incompatible con el principio de relatividad.”
En su publicación de 1905 en electrodinámica, Henri Poincaré y Albert Einstein explicaron que, con las transformaciones hechas por Lorentz, este principio se mantenía perfectamente invariable. La contribución de Einstein fue el elevar a este axioma a principio y proponer las transformaciones de Lorentz como primer principio. Además descartó la noción de tiempo absoluto y requirió que la velocidad de la luz en el vacío sea la misma para todos los observadores, sin importar si éstos se movían o no. Esto era fundamental para las ecuaciones de Maxwell, ya que éstas necesitan de una invarianza general de la velocidad de la luz en el vacío.

Como en otras ocasiones, aquí dejamos una muestra de la velocidad de la luz cuando viaja desde la Tierra a la Luna. Podemos ver como la linea amarilla (la luz) recorre el camino que las separan y el Tiempo que tarda en recorrerlo.
La aparición de la Teoría de la relatividad fue tan poco convencional como su autor. El ya famoso artículo que escribió en 1905 (con el apoyo de los trabajos de los arriba mencionados) y que enunciaba por primera vez la teoría, era algo rústico y sencillo y no mencionaba o contenía cita científico-literaria alguna, tampoco mencionaba ayuda de ninguna persona a excepción de su amigo Besso, que dicho sea de paso no era científico (él, por aquel entonces, no conocía a científico alguno). La primera conferencia de Einstein explicando la Teoría, en Zurich, no fue dada en ninguna universidad sino en el salón del Sindicato de Carpinteros, duró más de una hora, y luego repentinamente se interrumpió para preguntar la hora, explicando que no tenía reloj. Sin embargo, a pesar de los modestos comienzos, allí comenzó a reformarse los conceptos del espacio y del tiempo.

Lo cierto es que, con su teoría de la relatividad, Einstein finalmente resolvió la paradoja que se había presentado a los dieciseis años, por la que las ecuciaones de Maxwell pierden su validez si uno atrapa un haz de luz a la velocidad de la luz. Lo hizo mediante la conclusión de que no se puede acelerar la velocidad de la luz, de que la velocidad de la luz es la misma para todos los observadores, cualquiera que sea su movimiento relativo. Si un astronáuta que vuela hacia la estrella más cercana a una velocidad del cincuenta por ciento de la de la luz, , midiera la velocidad de la luz a bordo de la nave, el resultado sería exactamente igual que el que daría la medición de otro colega suyo situado en la Tierra.

Podrían ocurrir fenómenos que ni podemos imaginar pero, quedándonos en lo que más llama la atención al público en general, podríamos conseguir que el tiempo … ¡Se ralentizara y pasara más despacio para el viajero relativista! Si miráis el diagrama del Minkouski os hablará de los fenómenos que se pueden producir al viajar a la velocidad de la luz, cuando el Tiempo se ralentiza.
Diferentes sistemas de referencia para el mismo fenómeno. Claro que, en la teoría están presentes factores y trabajos que no se mencionan y, la fórmula.
siguiente:  es el llamado factor de Lorentz donde
es el llamado factor de Lorentz donde  es la velocidad de la luz en el vacío. Contrario a nuestro conocimiento actual, en aquel momento esto era una completa revolución, debido a que se planteaba una ecuación para transformar al tiempo, cosa que para la época era imposible. En la mecánica clásica, el tiempo era un invariante. Y para que las mismas leyes se puedan aplicar en cualquier sistema de referencia se obtiene otro tipo de invariante a grandes velocidades (ahora llamadas relativistas), la velocidad de la luz. Los sucesos que se realicen en el sistema en movimiento S’ serán más largos que los del S. La relación entre ambos es esa
es la velocidad de la luz en el vacío. Contrario a nuestro conocimiento actual, en aquel momento esto era una completa revolución, debido a que se planteaba una ecuación para transformar al tiempo, cosa que para la época era imposible. En la mecánica clásica, el tiempo era un invariante. Y para que las mismas leyes se puedan aplicar en cualquier sistema de referencia se obtiene otro tipo de invariante a grandes velocidades (ahora llamadas relativistas), la velocidad de la luz. Los sucesos que se realicen en el sistema en movimiento S’ serán más largos que los del S. La relación entre ambos es esa  . Este fenómeno se lo conoce como dilatación del tiempo. Si se dice que el tiempo varía a velocidades relativistas, la longitud también lo hace.
. Este fenómeno se lo conoce como dilatación del tiempo. Si se dice que el tiempo varía a velocidades relativistas, la longitud también lo hace.
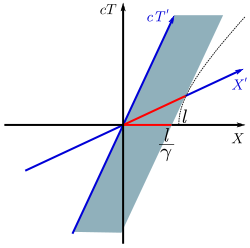
En el gráfico se escenifica la contracción de Lorentz
Para cuantificar aquella extraña situación, Einstein se vio obligado a emplear la contracción de Lorentz (En aquel momento no conocía a Lorentz al que más tarde consideraría “el hombre más grande y más noble de nuestro tiempo… una obrta de arte viviente.)” En manos de Einstein, las ecuciones de Lorentz esopecifican que, cuando aumenta la velocidad a la que se desplaza un observador, sus dimensiones, y la de la nave espacial y todo aparato de medición que haya a bordo, se contrae a lo largo de su movimiento en la cantidad requerida para hacer que la medición de la velocidad de la luz sea siempre la misma.
Esta era la razón de que Michelson y Morley no hallasen ningún rastrodel “arrastre del éter”. En verdad, el éter es superfluo, al igual que el espacio y el tiempo absolutos de Newton, pues no hay ninguna necesidad de un marco de referencia inmóvil. “Al concepto de reposo absoluto no le corresponde ninguna propiedad de los fenómenos, ni en la mecánica ni en la electromecánica.” Lo importante son los sucesos observables, y no puede observarse ningún suceso hasta que la luz (o las ondas de radio o cualquier otra forma de radiación electromagnética) que lleve noticias de él no llegue al observador. Einstein reemplazó el espacio de Newton por una red de haces de luz; la de ellos era una red absoluta dentro de la cual el espacio mismo se vuelve flexible.

Los observadores en movimiento experimentan también una lentificación del paso del tiempo. Un astronáuta que viaje al 90 por 100 de la velocidad de la luz sólo envejecerá a la mitad de rápido que su colega de la Tierra. Ya conocéis la paradoja de los gemelos en la que se explica tal fenómeno.

También en aquel primer artículo Einstein nos habló sobre la igualdad entre la masa y la energía. Él demostró que la masa de un cuerpo aumenta cuando absorbe energía. Se sigue de ello que su masa disminuye cuando irradia energía. Esto es verdadero no sólo para una nave espacial que se desplaza hacia las estrellas, sino también para un objeto en reposo. Una máquina fotográfica pierde algo (muy poco) de masa cuando el flash se dispara, y la gente cuya fotografía se saca se vuelve también, un poco más masiva al absorber sus cuerpos aquella radiación perdida por la máquina. Masa y energía son intercambiables.
m = E/c2
donde m es la masa del objeto, E su energía y c la velocidad de la luz. Al formular esta ecuación particularmente sencilla, que unifica los conceptos de energía y materia, y relaciona ambos con la velocidad de la luz, Einstein inicialmente estaba interesado en la masa. En cambio, si despejamos la energía, adquiere una forma más familiar y presagiosa:
en la Isla de los Museos (Berlín). Festejando el Año mundial de la Física en 2005, en el centenario de la publicación de la ecuación más famosa del mundo. Contemplada desde esta perspectiva, la teoría dice que la materia es energía congelada. Esto, por supuesto, es la clave de la fuerza nuclear y, en manos de los astrofísicos, la ecuación sería usada para descubrir los procesos termonucleares en el corazón de las estrellas.
Pero pese a todos sus variados logros, la relatividad especial no decía nada de la gravitación y, su autor, la veía incompleta. Aquella teoría sin la presencia de la otra gran fuerza más conocida del universo se veíoa desvalída: Había que vincularla con la masa inercial. La resistencia al cambio que ofrecen los objetos en estado de movimiento, su “peso” por decirlo así. La gravitación actúa sobre los objetos según su masa gravitacional, esto es, su “peso”. Todos sabem,os lo que es la masa inercial y de ella, tendremos que hablar cuando acometamos la p´çagina sobre la relatividad general. Dejemos aquí el apunte de que, la masa inercial y la gravitación de cualquier objeto son iguales. También se podría decir que, es la masa de los cuerpos que pueblan el universo, la que moldea y modela la geometría del del Cosmos, del espacio-tiempo.

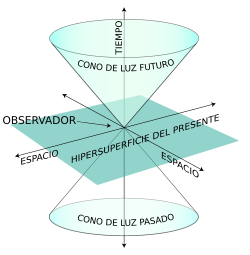
Terminemos con la misma imagen del comienzo. Causalidad e imposibilidad de movimientos más rápidos que la luz. Previo a esta teoría, el concepto de causalidad estaba determinado: para una causa existe un efecto. Anteriormente, gracias a los postulados de Laplace, se creía que para todo acontecimiento se debía obtener un resultado que podía predecirse. La revolución en este concepto es que se “crea” un cono de luz de posibilidades (Véase gráfico adjunto).
Se observa este cono de luz y ahora un acontecimiento en el cono de luz del pasado no necesariamente nos conduce a un solo efecto en el cono de luz futuro. Desligando así la causa y el efecto. El observador que se sitúa en el vértice del cono ya no puede indicar qué causa del cono del pasado provocará el efecto en el cono del futuro.
Asumiendo el principio de causalidad obtenemos que ninguna partícula de masa positiva puede viajar más rápido que la luz. A pesar que este concepto no es tan claro para la relatividad general. Pero no solo el principio de causalidad imposibilita el movimiento más rápido que el de la luz. Ya hablaremos de ello.
emilio silvera
Mar
5
El Micro Mundo de los Átomos
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (2)
Comments (2)


Sí, existe otro mundo que no vemos pero…, ¡está en éste!
La mecánica cuántica domina en el micromundo de los átomos y de las partículas “elementales”. Nos enseña que en la naturaleza cualquier masa, por sólida o puntual que pueda parecer, tiene un aspecto ondulatorio. Esta onda no es como una onda de agua. Es una onda de información. Nos indica la probabilidad de detectar una partícula. La longitud de onda de una partícula, la longitud cuántica, se hace menor cuanto mayor es la masa de esa partícula.
Por el contrario, la relatividad general era siempre necesaria cuando se trataba con situaciones donde algo viaja a la velocidad de la luz, o está muy cerca o donde la gravedad es muy intensa. Se utiliza para describir la expansión del universo o el comportamiento en situaciones extremas, como la formación de agujeros negros. Sin embargo, la gravedad es muy débil comparada con las fuerzas que unen átomos y moléculas y demasiado débil para tener cualquier efecto sobre la estructura del átomo o de partículas subatómicas, se trata con masas tan insignificantes que la incidencia gravitatoria es despreciable. Todo lo contrario que ocurre en presencia de masas considerables como planetas, estrellas y galaxias, donde la presencia de la gravitación curva el espacio y distorsiona el tiempo.

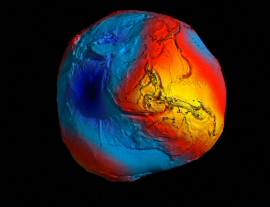
La Gravedad hace que la Tierra se vea como un mapa. Es una vista altamente exagerada, pero ilustra a las claras cómo la atracción gravitatoria que se manifiesta desde la masa de roca bajo nuestros pies no es la misma en todo lugar. La gravedad es más fuerte en áreas amarillas y más débil en las azules. (Imagen tomada por el satélite Goce)
Como resultado de estas propiedades antagónicas, la teoría cuántica y la teoría relativista gobiernan reinos diferentes, muy dispares, en el universo de lo muy pequeño o en el universo de lo muy grande. Nadie ha encontrado la manera de unir, sin fisuras, estas dos teorías en una sola y nueva de Gravedad-Cuántica.
¿Cuáles son los límites de la teoría cuántica y de la teoría de la relatividad general de Einstein? Afortunadamente, hay una respuesta simple y las unidades de Planck nos dicen cuales son.

Supongamos que tomamos toda la masa del universo visible y determinamos su longitud de onda cuántica. Podemos preguntarnos en qué momento esta longitud de onda cuántica del universo visible superará su tamaño. La respuesta es: cuando el universo sea más pequeño en tamaño que la longitud de Planck, es decir, 10-33 centímetros, más joven que el Tiempo de Planck, 10-43 segundos y supere la temperatura de Planck de 1032 grados. Las unidades de Planck marcan la frontera de aplicación de nuestras teorías actuales. Para comprender en que se parece el mundo a una escala menor que la longitud de Planck tenemos que comprender plenamente cómo se entrelaza la incertidumbre cuántica con la gravedad. Para entender lo que podría haber sucedido cerca del suceso que estamos tentados a llamar el principio del universo, o el comienzo del tiempo, tenemos que penetrar la barrera de Planck. Las constantes de la naturaleza marcan las fronteras de nuestro conocimiento existente y nos dejan al descubierto los límites de nuestras teorías.
En los intentos más recientes de crear una teoría nueva para describir la naturaleza cuántica de la gravedad ha emergido un nuevo significado para las unidades naturales de Planck. Parece que el concepto al que llamamos “información” tiene un profundo significado en el universo. Estamos habituados a vivir en lo que llamamos “la edad de la información”. La información puede ser empaquetada en formas electrónicas, enviadas rápidamente y recibidas con más facilidad que nunca antes.

Los tiempos cambian y la manera de informar también, lejos nos queda ya aquellos toscos aparatos impresores del pasado, ahora, en espacios muy reducidos, tenemos guardada más información que antes había en una colección de libros.
Nuestra evolución en el proceso rápido y barato de la información se suele mostrar en una forma que nos permite comprobar la predicción de Gordon Moore, el fundador de Intel, llamada ley de Moore, en la que, en 1.965, advirtió que el área de un transistor se dividía por dos aproximadamente cada 12 meses. En 1.975 revisó su tiempo de reducción a la mitad hasta situarlo en 24 meses. Esta es “la ley de Moore” cada 24 meses se obtiene una circuiteria de ordenador aproximadamente el doble, que corre a velocidad doble, por el mismo precio, ya que, el coste integrado del circuito viene a ser el mismo, constante.

Los límites últimos que podemos esperar para el almacenamiento y los ritmos de procesamiento de la información están impuestos por las constantes de la naturaleza. En 1.981, el físico israelí, Jacob Bekenstein, hizo una predicción inusual que estaba inspirada en su estudio de los agujeros negros. Calculó que hay una cantidad máxima de información que puede almacenarse dentro de cualquier volumen. Esto no debería sorprendernos. Lo que debería hacerlo es que el valor máximo está precisamente determinado por el área de la superficie que rodea al volumen, y no por el propio volumen. El número máximo de bits de información que puede almacenarse en un volumen viene dado precisamente por el cómputo de su área superficial en unidades de Planck. Supongamos que la región es esférica. Entonces su área superficial es precisamente proporcional al cuadrado de su radio, mientras que el área de Planck es proporcional a la longitud de Planck al cuadrado, 10-66 cm2. Esto es muchísimo mayor que cualquier capacidad de almacenamiento de información producida hasta ahora. Asimismo, hay un límite último sobre el ritmo de procesamiento de información que viene impuesto por las constantes de la naturaleza.

La información llega a todos los rincones del Mundo
No debemos descartar la posibilidad de que seamos capaces de utilizar las unidades de Planck-Stoney para clasificar todo el abanico de estructuras que vemos en el universo, desde el mundo de las partículas elementales hasta las más grandes estructuras astronómicas. Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias.
Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y mprotón.
α = 2πe2 / hc ≈ 1/137
αG = (Gmp2)2 / hc ≈ 10-38
La identificación de constantes adimensionales de la naturaleza como a (alfa) y aG, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro.

Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala. La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.
Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck). Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.
Cuando surgen comentarios de números puros y adimensionales, de manera automática aparece en mi mente el número 137. Ese número encierra más de lo que estamos preparados para comprender; me hace pensar y mi imaginación se desboca en múltiples ideas y teorías. Einstein era un campeón en esta clase de ejercicios mentales que él llamaba “libre invención de la mente”. El gran físico creía que no podríamos llegar a las verdades de la naturaleza sólo por la observación y la experimentación. Necesitamos crear conceptos, teorías y postulados de nuestra propia imaginación que posteriormente deben ser explorados para averiguar si existe algo de verdad en ellos. Con los adelantos actuales, estudiando la luz lejana de cuásares muy antiguos, se estudia si la constante de estructura fina (α) ha variado con el paso del tiempo.
El Universo es muy grande, inmensamente grande y, probablemente, todo lo que nuestras mentes puedan imaginar podrá exisitr en alguna parte de esas regiones perdidas en las profundidades cósmicas, en los confines del Espacio- Tiempo, en lugares ignotos de extraña belleza en los que otros mundos y otras criaturas tendrán, su propio habitat que, siendo diferente al nuestro, también, sus criaturas, estarán buscando el significado de las leyes del Universo.
emilio silvera
Mar
3
¡Supersimetría!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (10)
Comments (10)

En cualquier sitio que miremos nos dirán que la supersimetría en la física de partículas es: La supersimetría es una simetría hipotética propuesta que relacionaría las propiedades de los bosones y los fermiones. Aunque todavía no se ha verificado experimentalmente que la supersimetría sea una simetría de la naturaleza, es parte fundamental de muchos modelos teóricos, incluyendo la teoría de supercuerdas. La supersimetría también es conocida por el acrónimo inglés SUSY.
La Supersimetría tiene unas matemáticas muy bellas y por esa razón los artículos sobre el tema están llenos de ellas. Como ha sucedido antes, por ejemplo, cuando se propuso la teo´ria de Yang – Mills, tenemos un esquema matemático brillante que aún no sabemos como encajar en el conjunto de las leyes naturales. No tiene ningún sentido, todavía, pero esperamos que lo tenga en un tiempo futuro.

Hay otro escenario mucho más atractivo para nuestra imaginación. Hemos podido ver que los átomos están formados por pequeños constituyentes, los fotones, neutrones y electrones. Luego descubrimos que esos constituyentes, a su vez, tienen una subestructura: están formados de quarks y gluones. ¿Por qué, como probablemente hayas pensado tú antes, el proceso no continúa así? Quizñá esos Quarks y Gluones, e igualmente los electrones y todas las demás partículas aún llamadas “elementales” en el Modelo Estándar, estén también construidas de unos granos de materia aún menores y, finalmente, toda esa materia, si seguimos profundizando, nos daría la sorpresa de que toda ella es pura luz, es decir, la esencia de la materia.
Yo he tenido esa idea muy frecuentemente, nadie me quita de la cabeza que la materia, en lo más profundo de su “ser”, es la luz congelada en trozos de materia que, cuando llegan los sucesos, las transiciones de fase, se deja ver y sale a la “luz” del mundo para que la podamos contemplar.

Simetría es nuestra presencia aquí como observadores, la concha de un caracol, una galaxia, una flor
Todos sabemos de las grandes estructuras (inertes o vivas) que, en su inmensidad, transportan dentro de ellas o en la misma superficie, otras estructuras más pequeñas que, no por ello, dejan de ser también complejas. Grandes pulgas transportan pequeñas pulgas en su piel y, al igual que nosotros, llevan en ellas mismas a otros animáculos más pequeños, o, infinitesimales que, también, como nosotros, animales más grandes, tienen una misión encomendada sin la cual, seguramente nosotros, ni podríamos ser. Así que, tenemos que prestar mucha atención a lo que creemos “ínfimo” y que, en la mayoría de las veces, resulta ser más importante de lo que podemos llegar a imaginar.
Si miramos a los Quarks de un protón, por ejemplo, la mecánica cuántica (esa teoría maravillosa que controla todo el micromundo con increíble precisión), exige que el producto de la masa por la velocidad, el llamado “momento”, debe ser inversamente proporcional al tamaño de la “caja” en la cual ponemos nuestro sistema. El protón puede ser considerado como una de tales cajas y es tan pequeño que los quarks en su interior tendrían que moverse con una velocidad cercana a la de la luz. Debido a esto, la masa efectiva de los quarks máss pequeños, u y d, es aproximadamente de 300 MeV, que es mucho mayor que el valor que vemos en las Tablas de Partículas; eso también expñlica porque la masa del Protón es de 900 MeV, mucho mayor que la suma de las masas en reposo de los quarks /y Gluones).

El interior de un Quarks… ¿qué habrá allí?
Sí, dentro de los protones y neutrones, seguramente pueda haber mucho más de lo que ahora podemos vislumbrar. Nuestros aceleradores de partículas han podido llegar hasta ciertos límites que nos hablan de Quarks y ahora se buscan partículas supersimétricas o bosones traficantes de masa (como diría Ton Wood), y, nosotros, no sabemos si esos objetos existen o si podremos llegar a encontrarlos pero, por intentarlo… No dudamos en gastar ingentes cantidades y en utilizar cuantos recursos humanos sean precisos. El conocimiento de la Naturaleza es esencial para que, el futuro de la Física, sea la salvación de la Humanidad o, en su caso, de la raza que vendrá detrás de nosotros.
Algunas Teorías, como todos conocemos, han intentado unificar teorías de color con las de supersimetría. Quizá los nuevos Aceleradores de Hadrones (LHC) y otros similares que estarán acabamos poco después de estas primeras décadas del siglo XXI, nos puedan dar alguna pista y desvelar algunos de los nuevos fenómenos asociados a los nuevos esquemas que se dibujan en las nuevas teorías.
Los astrofísicos están muy interesados en estas ideas que predicen una gran cantidad de nuevas partículas superpesadas y, también varios tipos de partículas que interaccionan ultradébilmente. Estas podrían ser las “famosas” WIMPs que pueblan los huecos entre galaxias para cumplir los sueños de los que, al no saber explicar algunas cuestiones, acudieron a la “materia oscura” que, como sabeis, les proporcionó el marco perfecto para ocultar su inmensa ignorancia. “¡La masa perdida!” ¿Qué masa es esa? Y, sin embargo, los Astrofísicos, incansables, se aferran a ella y la siguen buscando…¡Ilusos!

¡El Universo! ¡Son tántas cosas! Desde nosotros los observadores, hasta la más ínfina partícula de materia
Yo, en mi inmensa ignorancia, no puedo explicar lo que ahí pueda existir. Sin embargo, sospecho que, deberíamos ahondar algo más en esa fuerza que llamamos Gravedad y que, me da la sensación de que nos esconde secretos que aún no hemos sabido desvelar. Y, por otra parte, tengo la sospecha de que la Luz, es más de lo que podemos suponer.


Feb
26
¿Qués es la luz? hace 340 años que supimos de su velocidad
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

En estos lugares se vivía a base de antorchas y velas para alumbrar los lóbregos pasillos
Está claro que, los estudiosos de la época antigua y medieval estaban por completo a oscuras acerca de la naturaleza de la luz. Especulaban sobre que consistía en partículas emitidas por objetos relucientes o tal vez por el mismo ojo. Establecieron el hecho de que la luz viajaba en línea recta, que se reflejaba en un espejo con un ángulo igual a aquel con el que el rayo choca con el espejo, y que un rayo de luz se inclina (se refracta) cuando pasa del aire al cristal, al agua o a cualquier otra sustancia transparente.

Cuando la luz entra en un cristal, o en alguna sustancia transparente, de una forma oblicua (es decir, en un ángulo respecto de la vertical), siempre se refracta en una dirección que forma un ángulo menor respecto de la vertical. La exacta relación entre el ángulo original y el ángulo reflejado fue elaborada por primera vez en 1.621 por el físico neerlandés Willerbrord Snell. No publicó sus hallazgos y el filósofo francés René Descartes descubrió la ley, independientemente, en 1.637.
Los primeros experimentos importantes acerca de la naturaleza de la luz fueron llevados a cabo por Isaac Newton en 1.666, al permitir que un rayo de luz entrase en una habitación oscura a través de una grieta e las persianas, cayendo oblicuamente sobre una cara de un prisma de cristal triangular. El rayo se refracta cuando entra en el cristal y se refracta aún más en la misma dirección cuando sale por una segunda cara del prisma. (Las dos refracciones en la misma dirección se originan por que los dos lados del prisma de se encuentran en ángulo en vez de en forma paralela, como sería el caso en una lámina ordinaria de cristal.)

Newron y sus experimentos con la luz
Cuando Newton empezó su lucha por establecer un método inductivo correcto en física, estaba trabajando en el campo de la óptica, no en cinemática o en astronomía. En sus primeros años, mucho antes de que los Principia le dieran la fama, llevó a cabo un estudio de la luz y los colores, un estudio que ha sido descrito como “la más excelsa investigación experimental del siglo XVII
Newton atrapó el rayo emergente sobre una pantalla blanca para ver el efecto de la refracción reforzada. Descubrió que, en vez de formar una mancha de luz blanca, el rayo se extendía en una gama de colores: rojo, anaranjado, amarillo, verde, azul, y violeta, en este orden.
Newton dedujo de ello que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores. La amplia banda de sus componentes se denominó spectrum (palabra latina que significa “espectro”, “fantasma”).

Newton llegó a la conclusión de que la luz se componía de diminutas partículas (“corpúsculos”), que viajaban a enormes velocidades.

Le surgieron y se planteó algunas inquietudes cuestiones. ¿Por qué se refractaban las partículas de luz verde más que los de luz amarilla? ¿Cómo se explicaba que dos rayos de luz se cruzaran sin perturbase mutuamente, es decir, sin que se produjeran colisiones entre partículas?
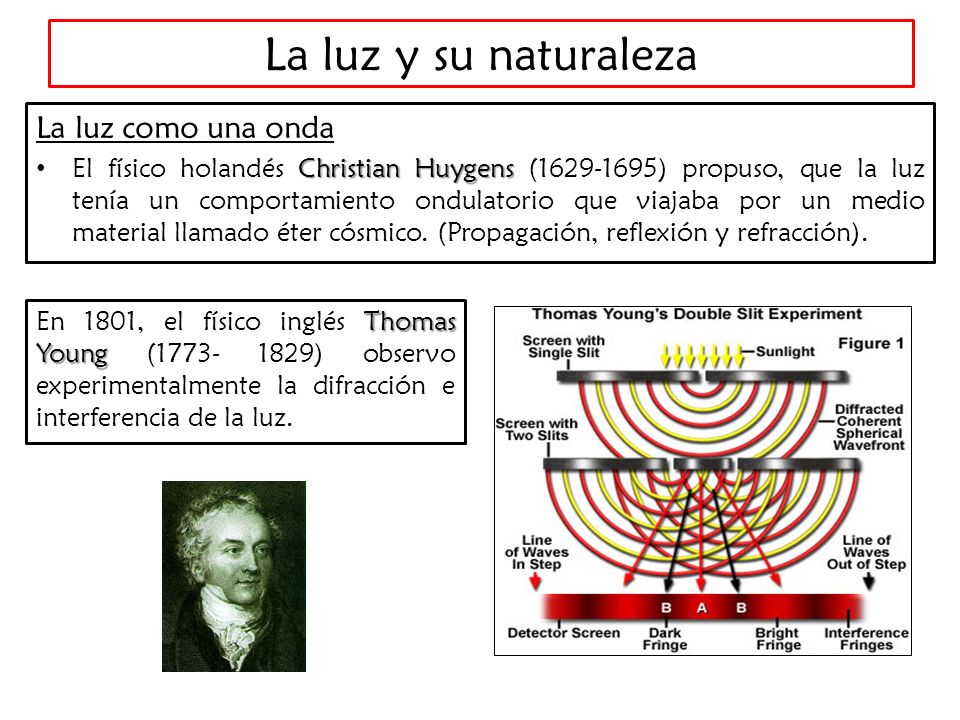
En 1.678, el físico neerlandés Christian Huyghens (un científico polifacético que había construido el primer reloj de péndulo y realizado importantes trabajos astronómicos) propuso una teoría opuesta: la de que la luz se componía de minúsculas ondas. Y si sus componentes fueran ondas, no sería difícil explicar los diversos difracciones de los diferentes tipos de luz a través de un medio refractante, siempre y cuando se aceptara que la luz se movía más despacio en ese medio refractante que en el aire. La cantidad de refracción variaría con la longitud de las ondas: cuanto más corta fuese tal longitud, tanto mayor sería la refracción. Ello significaba que la luz violeta (la más sensible a este fenómeno) debía de tener una longitud de onda mas corta que la luz azul, ésta, más corta que la verde, y así sucesivamente.

Lo que permitía al ojo distinguir los colores eran esas diferencias entre longitudes de onda. Y, como es natural, si la luz estaba integrada por ondas, dos rayos podrían cruzarse sin dificultad alguna. (Las ondas sonoras y las del agua se cruzan continuamente sin perder sus respectivas identidades.)
Pero la teoría de Huyqhens sobre las ondas tampoco fue muy satisfactoria. No explicaba por qué se movían en línea recta los rayos luminosos; ni por qué proyectaban sombras recortadas; ni aclaraba por qué las ondas luminosas no podían rodear los obstáculos, del mismo modo que pueden hacerlo las ondas sonoras y de agua. Por añadidura, se objetaba que si la luz consistía en ondas, ¿cómo podía viajar por el vacío, ya que cruzaba el espacio desde el Sol y las Estrellas? ¿cuál era esa mecánica ondulatoria?

Aproximadamente durante un siglo, contendieron entre sí estas teorías. La teoría corpuscular, de Newton, fue, con mucho, la más popular, en parte, porque la respaldó el famoso nombre de su autor. Pero hacia 1.801, un físico y médico ingles, de nombre Thomas Young, llevó a cabo un experimento que arrastró la opinión pública al campo opuesto. Proyectó un fino rayo luminoso sobre una pantalla, haciéndolo pasar antes por dos orificios casi juntos. Si la luz estuviera compuesta por partículas, cuando los dos rayos emergieran de ambos orificios, formarían presuntamente en la pantalla una región más luminosa donde se superpusieran, y regiones menos brillantes, donde no se diera tal superposición. Pero no fue esto lo que descubrió Young. La pantalla mostró una serie de bandas luminosas, separadas entre sí por bandas oscuras. Pareció incluso que, en esos intervalos de sombra, la luz de ambos rayos contribuía a intensificar la oscuridad.

Sería fácil explicarlo mediante la teoría ondulatoria. La banda luminosa representaba el refuerzo presado por las ondas de un rayo a las ondas del otro. Dicho de otra manera: Entraba “en fase” dos trenes de ondas, es decir, ambos nodos, al unirse, se fortalecían el uno al otro. Por otra parte, las bandas oscuras representaban puntos en que las ondas estaban “desfasadas” porque el vientre de una neutralizaba el nodo de la otra. En vez de aunar sus fuerzas, las ondas se interferían mutuamente, reduciendo la energía luminosa neta a las proximidades del punto cero.
Considerando la anchura de las bandas y la distancia entre los dos edificios por los que surgen ambos rayos, se pudo calcular la longitud de las ondas luminosas, por ejemplo, de la luz roja a la violeta o los colores intermedios. Las longitudes de onda resultaron ser muy pequeñas. Así, la de la luz roja era de unos 0’000075 cm. (Hoy se expresan las longitudes de las ondas luminosas mediante una unidad muy práctica ideada por Angströn. Esta unidad, denominada, en honor a su autor Ángstrom (Á), es la cienmillonésima parte de un centímetro. Así, pues, la longitud de onda de la luz roja equivale más o menos a 7.500 Á, y la de la luz violeta, a 3.900 Å, mientras que las de colores visibles en el espectro oscilan entre ambas cifras.)

La cortedad de estas ondas es muy importante. La razón de que las ondas luminosas se desplacen en línea recta y proyecten sombras recortadas se debe a que todas son incomparablemente más pequeñas que cualquier objeto; pueden contornear un obstáculo sólo si éste no es mucho mayor que la longitud de onda. Hasta las bacterias, por ejemplo, tienen un volumen muy superior de una onda luminosa y, por tanto, la luz puede definir claramente sus contornos bajo el microscopio. Sólo los objetos cuyas dimensiones se asemejan a la longitud de la onda luminosa (por ejemplo, los virus y otras partículas submicroscópicas) son lo suficientemente pequeños como para que puedan ser contorneados por las ondas luminosas.

Un físico francés, Augustin-Jean Fresnel, fue quien demostró por vez primera, en 1.818, que si un objeto es lo suficientemente pequeño, la onda luminosa lo contorneará sin dificultad. En tal caso, la luz determina el llamado fenómeno de “difracción”. Por ejemplo, las finísimas líneas paralelas de una “reja de disfracción” actúan como una serie de minúsculos obtáculos, que se refuerzan entre si. Puesto que la magnitud de la difracción va asociada a la longitud de onda, se produce el espectro. A la inversa, se puede calcular la longitud de onda midiendo la difracción de cualquier color o porción del espectro, así como la separación de las marcas sobre el cristal.

A través de los rayos espectrales se supo de qué estaban hechas las estrellas y los obbjetos celestes
Fraunhofer exploró dicha reja de difracción con objeto de averiguar sus finalidades prácticas, progreso que suele olvidarse, pues queda eclipsado por su descubrimiento más famoso: los rayos espectrales. El físico americano Henry Augustus Rowlane ideó la reja cóncava y desarrolló técnicas para regularlas de acuerdo con 20.000 líneas por pulgada. Ello hizo posible la sustitución del prisma por el espectroscopio.
Ante tales hallazgos experimentales, más el desarrollo metódico y matemático del movimiento ondulatorio, debido a Fresnel, pareció que la teoría ondulatoria de la luz había arraigado definitivamente, desplazando y relegando para siempre a la teoría corpuscular.

La luz tiene una naturaleza dual: se comporta como onda y partícula. Entre las propiedades de la onda luminosa se incluyen la refracción de la onda cuando …
No sólo se aceptó las existencias de ondas luminosas, sino que también se midió su longitud con una precisión cada vez mayor. Hacia 1.827, el físico francés Jacques Babinet sugirió que se empleara la longitud de onda luminosa (una cantidad física inalterable) como unidad para medir tales longitudes, en vez de las muy diversas unidades ideadas y empleadas por el hombre. Sin embargo, tal sugerencia no se llevó a la práctica hasta 1.880 cuando el físico germano-americano Albert Abraham Michelson inventó un instrumento, denominado “interferómetro”, que podía medir las longitudes de ondas luminosas con una exactitud sin precedentes. En 1.893, Michelson midió la onda de la raya roja en el espectro del cadmio y determinó que su longitud era de 1/1.553.164 m.

Pero la incertidumbre reapareció al descubrirse que los elementos estaban compuestos por isótopos diferentes, cada uno de los cuáles aportaba una raya cuya longitud de onda difería ligeramente de las restantes. En la década de 1.930 se midieron las rayas del criptón 86. Como quiera que este isótopo fuera gaseoso, se podía abordar con bajas temperaturas, para frenar el movimiento atómico y reducir el consecutivo engrosamiento de la raya.
En 1.960, el Comité Internacional de Pesos y Medidas adoptó la raya del criptón 86 como unidad fundamental de longitud. Entonces se restableció la longitud de metro como 1.650.763’73 veces la longitud de onda de dicha raya espectral. Ello aumento mil veces la precisión de las medidas de longitud. Hasta entonces se había medido el antiguo metro patrón con un margen de error equivalente a una millonésima, mientras que en lo sucesivo se pudo medir la longitud de onda con un margen de error equivalente a una milmillonésima.
Ahora, después de todo esto, sabemos algo más sobre la luz.
Pero ¿qué pasa con su velocidad?
¡Veámoslo!

Está claro que, la luz se desplaza a enormes velocidades. Si pulsamos el interruptor de apagado de la lámpara de nuestro salón, todo queda a oscuras de manera instantánea.
La velocidad del sonido es más lenta, por ejemplo, si vemos a un leñador que está cortando leña en un lugar alejado de nosotros, sólo oiremos los golpes momentos después de que caiga el hacha. Así, pues, el sonido tarda cierto tiempo en llegar a nuestros oídos. En realidad es fácil medir la velocidad de su desplazamiento: unos 1.206 km/h en el aire y a nivel del mar.

Galileo fue el primero en intentar medir la velocidad de la luz. Se colocó en lo alto de una colina, mientras que su ayudante, se situaba en otro lugar alto de la colina vecina; luego sacó una linterna encendida: tan pronto como su ayudante vió la luz, hizo una señal con otra linterna. Galileo repitió el experimento a distancias cada vez mayores, suponiendo que el tiempo requerido por su ayudante para responder mantendría una uniformidad constante, por lo cual, el intervalo entre la señal de su propia linterna y la de su ayudante representaría el tiempo empleado por la luz para recorrer cada distancia. Aunque la idea era lógica, la luz viajaba demasiado aprisa como para que Galileo pudiera percibir las sutiles diferencias con un método tan rudimentario.


Observaciones de Röemer
En 1.676, el astrónomo danés Olau Roemer logró cronometrar la velocidad de la luz a escala de distancias astronómicas. Estudiando los eclipses de Júpiter en sus cuatro grandes satélites, Roemer observó que el intervalo entre eclipses consecutivos era más largo cuando la Tierra se alejaba de Júpiter, y más corto cuado se movía en su órbita hacía dicho astro. Al parecer, la diferencia entre las duraciones del eclipse reflejaba la diferencia de distancias entre la Tierra y Júpiter. Y trataba, pues, de medir la distancia partiendo del tiempo empleado por la luz para trasladarse desde Júpiter hasta la Tierra. Calculando aproximadamente el tamaño de la órbita terrestre y observando la máxima discrepancia en las duraciones del eclipse que, según Roemer, representaba el tiempo que necesitaba la luz para atravesar el eje de al órbita terrestre, dicho astrónomo computó la velocidad de la luz. Su resultado, de 225.000 km/s., parece excelente si se considera que fue el primer intento, y resultó bastante asombroso como para provocar la incredulidad de sus coetáneos.

![[foto de la noticia] [foto de la noticia]](http://estaticos01.elmundo.es/elmundo/imagenes/2009/03/31/1238489169_extras_ladillos_3_2.jpg)
Sin embargo, medio siglo después se confirmaron los cálculos de Roemer en un campo totalmente distinto. Allá por 1.728, el astrónomo británico James Bradley descubrió que las estrellas parecían cambiar de posición con los movimientos terrestres; y no por el paralaje, sino porque la traslación terrestre alrededor del Sol era una fracción mensurable (aunque pequeña) de la velocidad de la luz. La analogía empleada usualmente es la de un hombre que camina con el paraguas abierto bajo un temporal. Aun cuando las gotas caigan verticalmente, el hombre debe inclinar hacia delante el paraguas, porque ha de abrirse paso entre las gotas.
Cuanto más acelere su paso, tanto más deberá inclinar el paraguas. De manera semejante la Tierra avanza entre los ligeros rayos que caen desde las estrellas, y el astrónomo debe inclinar un poco su telescopio y hacerlo en varias direcciones, de acuerdo con los cambios de la trayectoria terrestre (no olvidemos que nuestro planeta Tierra, es como una enorme nave espacial que nos lleva en un viaje eterno, alrededor del Sol, a la velocidad de 30 km/s. + -) Mediante ese desvío aparente de los astros (“aberración de la luz”), Bradley pudo evaluar la velocidad de la luz y calcularla con gran precisión.
Sus cálculos fueron de 285.000 km/s, bastante más exacto que los de Roemer, pero aún un 5’5% más bajos.
Poco a poco, con medios tecnológicos más sofisticados y más conocimientos matemáticos, los científicos fueron obteniendo medidas más exactas aún, conforme se fue perfeccionando la idea original de Galileo y sus sucesores.

En 1.849, el físico francés Armand-Hippolyte-Louis Fizeau ideó un artificio mediante el cual se proyectaba la luz sobre un espejo situado a 8 km de distancia, que devolvía el reflejo al observador. El tiempo empleado por la luz en su viaje de ida y vuelta no rebasó apenas la 1/20.000 de segundo, por Fizeau logró medirlo colocando una rueda dentada giratoria en la trayectoria del rayo luminoso. Cuando dicha rueda giraba a cierta velocidad, regulada, la luz pasaba entre los dientes y se proyectaba contra el siguiente, al ser devuelta por el espejo; así, Fizeau, colocado tras la rueda, no pudo verla. Entonces se dio más velocidad a la rueda, y el reflejo pasó por la siguiente muesca entre los dientes, sin intercepción alguna. De esa forma, regulando y midiendo la velocidad de la rueda giratoria, Fizeau pudo calcular el tiempo transcurrido y, por consiguiente, la velocidad a que se movía el rayo de luz.
Experimento de Focault



Cuando el espejo gira a una velocidad suficientemente elevada para que el tiempo de que tarda en dar una vuelta sea comparable al tiempo que tarda la luz en ir y volver en su recorrido, la señal luminosa se observa a una distancia fácilmente medible del orificio por el que sale el rayo luminoso.
En estas circunstancias es fácil determinar el ángulo que se ha desviado el rayo. Como se conoce la velocidad de rotación, se determina el tiempo que ha tardado el espejo en girar la mitad de ese ángulo. En este tiempo la luz ha recorrido y de esa cifra se obtiene el valor de la velocidad.
La velocidad del espejo fue de 400 revoluciones por segundo y la distancia entre el espejo giratorio y el espejo fijo era de 5 metros.

Un año más tarde, Jean Foucault (quien realizaría poco después su experimento con los péndulos) precisó más estas medidas empleando un espejo giratorio en ve de una rueda dentada. Entonces se midió el tiempo transcurrido desviando ligeramente el ángulo de reflexión mediante el veloz espejo giratorio. Foucault obtuvo un valor de la velocidad de la luz de 300.883 km/s. También, el físico francés utilizó su método para determinar la velocidad de la luz a través de varios líquidos. Averiguó que era notablemente inferior a la alcanzada en el aire. Esto concordaba también con la teoría ondulatoria de Huyghens.

Experimento Michelson-Morley Reposo con el éter luminífero Interferómetro de Michelson y Morley en reposo respecto al éter luminífero.
Michelson fue más preciso aún en sus medidas. Este autor, durante cuarenta años largos, a partir de 1.879, fue aplicando el sistema Fizeau-Foucault cada vez con mayor refinamiento, para medir la velocidad de la luz. Cuando se creyó lo suficientemente informado, proyectó la luz a través de vacío, en vez de hacerlo a través del aire, pues este frena ligeramente su velocidad, y, empleó para ello tuberías de acero cuya longitud era superior a 1’5 km. Según sus medidas, la velocidad de la luz en el vacío era de 299.730 km(seg. (sólo un 0’006% más bajo). Demostraría también que todas las longitudes de ondas luminosas viajan a la misma velocidad en el vacío.
En 1.972, un equipo de investigadores bajo la dirección de Kenneth M. Eveson efectuó unas mediciones aún más exactas y vio que la velocidad de la luz era de 299.727’74 km/seg. Una vez se conoció la velocidad de la luz con semejante precisión, se hizo posible usar la luz, o por lo menos formas de ella, para medir distancias.
Aunque para algunos resulte alto tedioso el tema anterior, no he podido resistirme a la tentación de exponerlo, así podrá saber algo más sobre la luz y, habrán conocido a personajes que hicieron posible el que ahora nosotros, la conozcamos mejor.
Las ondas de luz están presentes en el Espacio Interestelar
Podría continuar, hasta el final de este trabajo, hablando de la luz y sus distintas formas o aplicaciones: ondas de luz a través del espacio, de cómo se transmite la luz en el “vacío”, nos llega a través del espacio desde Galaxias situadas a miles de millones de años luz; las líneas de fuerzas electromagnéticas de Faraday y Maxwell de campos eléctricos y magnéticos cambiantes (todo ello explicado en un simple conjunto de cuatro ecuaciones, que describían casi todos los fenómenos referentes a esta materia electromagnética), o de los enigmas aún por descubrir (aunque predichos).
Ahora, en Física, se dice que la luz es una forma de radiación electromagnética a la que el ojo humano es sensible y sobre la cual depende nuestra consciencia visual del universo y sus contenidos.
Sí, el ojo humano puede ver todo objeto en el que incida la luz
Patrón de referencia
En el año 1983, el Bureau Internacional de Poids et Mesures resolvió modificar la definición del metro como unidad de longitud del Sistema Internacional, estableciendo su definición a partir de la velocidad de la luz

El metro como patrón en barras de platino e Iridio
En consecuencia, el mínimo reajuste arbitrario efectuado en la definición del metro, permite que la velocidad de la luz, lógicamente, tenga un valor exacto de 299 792 458 m/s cuando se expresa en metros/segundo. Esta modificación aprovecha de forma práctica una de las bases de la teoría de la relatividad de Einstein: la inmutabilidad de la velocidad de la luz en el vacío, sea cual sea el sistema de referencia utilizado para medirla, convirtiendo esta propiedad en uno de los patrones de los que se deducen otras unidades.
Aparte de todo lo que antes hemos explicado, no sería justo finalizar el trabajo sin exponer aquí que, en 1905, Albert Einstein, inspirado en el cuanto de Planck, realizó un importante avance en el conocimiento de lo que es la luz. Demostró que el Efecto fotoeléstrico sólo podía ser explicado con la hipótesis de que la luz consiste en un chorro de fotones de energía electromagnética discretos.
El conflicto entre la teoría ondulatoria y corpuscular de la luz fue resuelto con la evolución de la teoría cuántica y la mecánica ondulatoria que ha dejado claro que, los electrones y las otras partículas elementales tienen propiedades duales de partículas y onda.
sería mucho más largo, pero creo que está bien con lo dicho.
emilio silvera
















 Totales: 83.646.672
Totales: 83.646.672 Conectados: 53
Conectados: 53























