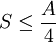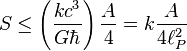Jun
27
¿La Física? ¡Una maravilla! Nos dice cómo funciona la Naturaleza
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

Ylia Prigogine haciendo lo que sólo unos privilegiados pueden hacer: desvelando los principios del mundo. Enn la pizarra, la entropía. La irreversibilidad del tiempo trae el orden al caos, decía. De alguna manera pretendía explicar que nada permanece y todo cambia bajo los efectos del inexorable paso del Tiempo.

“En el mundo de los seres vivos, la escala o tamaño crea importantes diferencias. En muchos aspectos, la anatomía de un ratón es una copia de la de un elefante, pero mientras que un ratón trepar por una pared prácticamente vertical sin mucha dificultad (y se puede caer desde una altura varias veces mayor que su propio tamaño sin hacerse daño), un elefante no sería capaz de realizar tal hazaña. Con bastante generalidad se puede afirmar que los efectos de la gravedad son menos importantes cuanto menores sean los objetos que consideremos (sean vivos o inanimados).


Cuando llegamos a los seres unicelulares, se ve que ellos no hay distinción entre arriba y abajo. Para ellos, la tensión superficial del agua es mucho más importante que la fuerza de la gravedad a esa escala. Tranquilamente se pueden mover y desplazar por encima de una superficie acuática. Los pluricelulares no pueden hacer tal cosa.

La tensión superficial es una consecuencia de que todas las moléculas y los átomos se atraen unos a otros con una fuerza que nosotros llamamos de Van der Waals. fuerza tiene un alcance muy corto; para ser precisos, diremos que la intensidad de esta fuerza a una distancia r es aproximadamente 1/r7. Esto significa que si se reduce la distancia dos átomos a la mitad de la fuerza de Van der Waals con la que se atraen uno a otro se hace 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128 veces más intensa. Cuando los átomos y las moléculas se acercan mucho unos a otros quedan unidos muy fuertemente a través de esta fuerza. El conocimiento de esta fuerza se debe a Johannes Diderik Van der Waals (1837 – 1923) con su tesis sobre la continuidad del líquido y gaseoso que le haría famoso, ya que en esa época (1873), la existencia de las moléculas y los átomos no estaba completamente aceptado.
La tensión superficial del agua, es el efecto físico (energía de atracción entre las moléculas) que “endurece” la capa superficial del agua en reposo y permite a algunos insectos, como el mosquito y otros desplazarse por la superficie del agua sin hundirse.

El famoso físico inglés James Clerk Maxwell, que formuló la teoría del electromagnetismo de Faraday, quedó muy impresionado por este de Van der Waals.
Los tamaños de los seres uniceculares, animales y vegetales, se miden en micrómetros o “micras”, donde 1 micra es 1/1.000 de milímetro, aproximadamente el tamaño de los detalles más pequeños que se pueden observar con un microscopio ordinario. El mundo de los microbios es fascinante, pero no es el objeto de este trabajo, y continuaremos el viaje emprendido las partículas elementales que forman núcleos, átomos, células y materia, así como las fuerzas que intervienen en las interacciones fundamentales del universo y que afecta a todo lo que existe.

Hemos hablado del electrón que rodea el núcleo, de su carga eléctrica negativa que complementa la positiva de los protones y hace estable al átomo; una masa de solamente 1/1.836 de la del núcleo más ligero (el del hidrógeno). La importancia del electrón es vital en el universo.
Pero busquemos los “cuantos”. La física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menor intensidad, por los objetos más fríos (radiación de cuerpo negro).

Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si utilizamos las leyes de la termodinámica para calcular la intensidad de una radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano y, luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para menores. Esta longitud de onda característica es inversamente proporcional a la temperatura absoluta de objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273º bajo cero). Cuando a 1.000º C un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.
Radiación de Cuerpo Negro
Un cuerpo negro es un objeto teórico o ideal que absorbe toda la luz y toda la energía radiante que incide sobre él. Nada de la radiación incidente se refleja o pasa a través del cuerpo negro. A pesar de su , el cuerpo negro emite luz y constituye un modelo ideal físico para el estudio de la emisión de radiación electromagnética. El nombre Cuerpo negro fue introducido por Gustav Kirchhoff en 1862.

La luz emitida por un cuerpo negro se denomina radiación de cuerpo negro. Todo cuerpo emite energía en de ondas electromagnéticas, siendo esta radiación, que se emite incluso en el vacío, tanto más intensa cuando más elevada es la temperatura del emisor. La energía radiante emitida por un cuerpo a temperatura ambiente es escasa y corresponde a longitudes de onda superiores a las de la luz visible (es decir, de menor frecuencia). Al elevar la temperatura no sólo aumenta la energía emitida sino que lo hace a longitudes de onda más cortas; a esto se debe el cambio de color de un cuerpo cuando se calienta. Los cuerpos no emiten con igual intensidad a todas las frecuencias o longitudes de onda, sino que siguen la ley de Planck.
Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda, y por tanto, proporcional a la frecuencia de radiación emitida. La fórmula es E = hν, donde E es la energía del paquete, ν es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo nueva condición, el resultado coincidió perfectamente con las observaciones.
Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: él sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck. El príncipe francés Louis-Victor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene energía, sino que cualquier cosa con energía se debe comportar una “onda” que se extiende en una cierta región del espacio, y que la frecuencia ν de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilantes de campos de fuerza, esto lo veremos más adelante.
El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de de Broglie. Poco después, en 1926, Edwin Schrödinger descubrió cómo escribir la teoría ondulatoria de de Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de ondas cuánticas”.
Está bien comprobado que la mecánica cuántica funciona de maravilla…, pero, sin embargo, surge una pregunta muy formal: ¿qué significan realmente estas ecuaciones?, ¿qué es lo que están describiendo? Isaac Newton, allá en 1867 formuló cómo debían moverse los planetas alrededor del Sol, estaba claro todo el mundo qué significaban sus ecuaciones: que los planetas estaban siempre en una posición bien definida des espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades en el tiempo.
Pero los electrones todo es diferente. Su comportamiento parece estar envuelto en misterio. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?
Niels Bohr consiguió responder a esta pregunta de tal que con su explicación se pudo seguir trabajando, y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la interpretación de Copenhague de la mecánica cuántica.

Si la mecánica cuántica tiene cosas extrañas y el espín es una de ellas. Y si uno piensa que la intuición le ayudará a comprender todo esto, pues no lo hará, o es poco probable que lo haga. Las partículas tienen un espín fundamental. Al igual que la carga eléctrica o la masa, el espín ayuda a definir que de partícula es cada una.
Las leyes de la mecánica cuántica han sido establecidas con mucha precisión; permite cómo calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas de manera simultánea. Por ejemplo, podemos determinar la velocidad de una partícula con mucha precisión, pero entonces no sabremos exactamente dónde se encuentra; o a la inversa, podemos determinar la posición con precisión, pero entonces su velocidad queda mal definida. Si una partícula tiene espín (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.

La posición y el momento de una partícula nunca lo podremos saber con precisión ilimitada.
No es fácil explicar de forma sencilla de dónde viene esta incertidumbre, pero existen ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar. Para afinar un instrumento se debe escuchar una nota durante un cierto intervalo de tiempo y compararla, por ejemplo, con un diapasón que debe vibrar también durante un tiempo. Notas muy breves no tienen bien definido el tono.
Para que las reglas de la mecánica cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuando más grande y más pesado es un objeto, más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica. Me gustaría referirme a exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por holismo, y que podría definir como “el todo es más que la suma de sus partes”. Si la física nos ha enseñado algo es justo lo contrario. Un objeto compuesto de un gran de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (partículas); basta que sepamos sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes. Por ejemplo, la constante de Planck, h, que es igual a 6’626075… × 10-34 Julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.

La mecánica cuántica es muy extraña a nuestro “sentido común”, sabemos que se desenvuelve en ese “universo” de lo muy pequeño, alejado de nuestra vida cotidiana en el macrocosmos tetradimensional que, no siempre coincide con lo que, en aquel otro ininitesimal acontece.
Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisemberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros como Erwin Schrödinger siempre presentaron serias objeciones a interpretación. Quizá funcione bien, pero ¿dónde está exactamente el electrón?, ¿en el punto x o en el punto y? En pocas palabras, ¿dónde está en realidad?, y ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.
Es cierto que, existe otro universo dentro de nuestro del que, aún, nos queda mucho por aprender.

La mecánica cuántica puede ser definida o resumida así: en principio, con las leyes de la naturaleza que conocemos se puede predecir el resultado de cualquier experimento, en el sentido que la predicción consiste en dos factores: el primer factor es un cálculo definido con exactitud del efecto de las fuerzas y estructuras, tan riguroso como las leyes de Isaac Newton para el movimiento de los planetas en el Sistema Solar; el segundo factor es una arbitrariedad estadística e incontrolable definida matemáticamente de estricta. Las partículas seguirán una distribución de probabilidades dadas, primero de una forma y luego de otra. Las probabilidades se pueden calcular utilizando la ecuación de Schrödinger de función de onda (Ψ) que, con muchas probabilidades nos indicará el lugar probable donde se encuentra una partícula en un dado.
Muchos estiman que esta teoría de las probabilidades desaparecerá cuando se consiga la teoría que explique, de forma completa, todas las fuerzas; la buscada teoría del todo, lo que implica que nuestra descripción actual incluye variables y fuerzas que (aún) no conocemos o no entendemos. Esta interpretación se conoce como hipótesis de las variables ocultas.”

También Gerard ‘t Hooft es el autor de lo que han dado en llamar l principio holográfico es una conjetura especulativa acerca de las teorías de la Gravedad Cuántica propuesta en 1993 por este autor, y mejorada y promovida por Leonard Susskin en 1995. Postula que toda la información contenida en cierto volumen de un espacio concreto se puede conocer a partir de la información codificable sobre la frontera de dicha región. Una importante consecuencia es que la cantidad máxima de información que puede contener una determinada región de espacio rodeada por una superficie diferenciable está limitada por el área total de dicha superficie.
Por ejemplo, se pueden modelar todos los eventos que ocurran en un cuarto o una habitación creando una teoría en la que sólo tome en cuenta lo que suceda en sus paredes. En el principio holográfico también se afirma que por cada cuatro Unidades de Planck existe al menos un grado de libertad (o una unidad constante de Bolttzmann k de máxima entropía). Esto se conoce como frontera de Bekenstein:
donde S es la entropía y A es la unidad de mensura considerada. En unidades convencionales la fórmula anterior se escribe:
donde:
 , es la constante de Boltzmann.
, es la constante de Boltzmann.
 , es la vecolcidad de la luz.
, es la vecolcidad de la luz.
 , es la constante gravitacional universal.
, es la constante gravitacional universal.
 , es la constante de Planck racionalizada.
, es la constante de Planck racionalizada. , es la longitud de Planck.
, es la longitud de Planck.
Claro que esta… ¡Es otra Historia!
emilio silvera
Jun
22
Los núcleos, la masa, la energía…¡La Luz!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)
Hay veces en las que nos cuentan cosas y hechos de los que nunca hemos tenido noticias y, resultan del máximo interés. Nuestra curiosidad nos llama a desentrañar los misterios y secretos que, tanto a nuestro alrededor, como en las regiones más lejanas del Universo, puedan haber ocurrido, puedan estar sucediendo ahora, o, en el futuro pudieran tener lugar, ya que, de alguna manera, todas ellas tienen que ver con nosotros que, de alguna manera, somos parte de la Naturaleza, del Universo y, lo que sucedió, lo que sucede y lo que sucederá… ¡Nos importa!
El saber ocupa un lugar en nuestras mentes

Algunos hablan de una nueva Humanidad, una nueva Conciencia
No podemos saber si la Humanidad como tal, estará aquí mucho tiempo más y, si con el tiempo y los cambios que se avecinan, nosotros los humanos, mutaremos hacia seres más completos y de mayor poder de adaptación al medio. Y, desde luego, nuestros descendientes, llegara un dia lejano en el futuro en el cual, habrán dejado la Tierra antes de que se convierta en Gigante Roja y calcine el Planeta y, habrán colonizado otros mundos. Para eso faltan mucho miles de millones de años. En la actualidad, solo estamos dando los inseguros primeros pasos por los alrededores de nuestro hogar, plantearnos ir mucho mas allá, es impensable. No tenemos ni la capacidad tecnológica ni la inteligencia necesaria para desarrollar los medios que se necesitan para poder desplazarnos a otros mundos lejanos que, posiblemente, estando situados en zona habitable como la misma Tierra, nos podrían dar el cobijo necesario para su colonización y hacer de ellos nuestros futuros hogares.
El futuro: Siempre será incierto
Pero, hablemos de Física

La partícula emitida por un núcleo radiactivo, por lo general lleva una considerable cantidad de energía. Y, ¿de dónde procede esa energía? Es el resultado de la conversión en energía de una pequeña parte del núcleo (E = mc2); en otras palabras, el núcleo siempre pierde un poco de masa en el acto de expeler la partícula.
Los físicos se vieron durante mucho tiempo turbados por el hecho de que, a menudo, la partícula beta emitida en una desintegración del núcleo no alberga energía suficiente para compensar la masa perdida por el núcleo. En realidad, los electrones no eran igualmente deficitarios. Emergían con un amplio espectro de energías, y el máximo (corregido por muy pocos electrones) era casi correcto, pero todos los demás no llegaban a alcanzarlo en mayor o menos grado. Las partículas alfa emitidas por un nucleido particular poseían iguales energías en cantidades inesperadas. En ese caso, ¿qué era erróneo en la emisión de partículas beta?, ¿qué había sucedido con la energía perdida?
En 1.922, Lise Maitner se hizo por primera vez esta pregunta, y hacia 1.936 Niels Bohr estaba dispuesto a abandonar el gran principio de conservación de la energía, al menos en lo concerniente a partículas subatómicas. En 1.931 Wolfgang Pauli sugirió una solución para el enigma de la energía desaparecida. Tal solución era muy simple: junto con la partícula beta del núcleo se desprendía otra, que se llevaba la energía desaparecida. Esa misteriosa segunda partícula tenía propiedades bastante extrañas; no poseía carga ni masa. Lo único que llevaba mientras se movía a la velocidad de la luz era cierta cantidad de energía. A decir verdad, aquello parecía un cuerpo ficticio creado exclusivamente para equilibrar el contraste de energías.

Habitualmente aceptamos que la física es la ciencia que estudia la estructura y propiedades de la materia y la energía, las formas de existencia de las mismas en el espacio y el tiempo, así como las leyes de rigen sus interacciones. En este definición no hay limitaciones precisas entre la naturaleza viviente e inanimada, y aunque ello no implica la reducción de todas las ciencias a la física, se deduce que las bases teóricas finales de cualquier dominio de las ciencias naturales tienen una naturaleza física.
Pero, sigamos…
Sin embargo, tan pronto como se propuso la posibilidad de su existencia, los físicos creyeron en ella ciegamente. Y esta certeza se incrementó al descubrirse el neutrón y al saberse que se desintegraba en un protón y liberaba un electrón que, como en la decadencia beta, portaba insuficientes cantidades de energía. Enrico Fermi dio a esta partícula putativa el nombre de neutrino, palabra italiana que significa “pequeño neutro”.
El neutrón dio a los físicos otra prueba palpable de la existencia del neutrino. Como ya he comentado en otra página de este trabajo, casi todas las partículas describen un movimiento rotatorio. Esta rotación se expresa, más o menos, en múltiplos de una mitad, según la dirección del giro. Ahora bien, el protón, el neutrón y el electrón tienen rotación de una mitad. Por tanto, si el neutrón con rotación de una mitad origina un protón y un electrón, cada uno con rotación de una mitad, ¿qué sucede con la ley sobre conservación del momento angular? Aquí hay algún error. El protón y el electrón totalizan una mitad con sus rotaciones (si ambas rotaciones siguen la misma dirección) o cero (si sus rotaciones son opuestas); pero sus rotaciones no pueden sumar jamás una mitad. Sin embargo, por otra parte, el neutrino viene a solventar la cuestión. Supongamos que la rotación del neutrón sea +½, y admitamos también que la rotación del protón sea +½ y la del electrón -½, para dar un resultado neto de cero. Demos ahora al neutrino una rotación de +½ y la balanza quedará desequilibrada.
+½ (n) = +½ (p) – ½ (e) + ½ (neutrino)
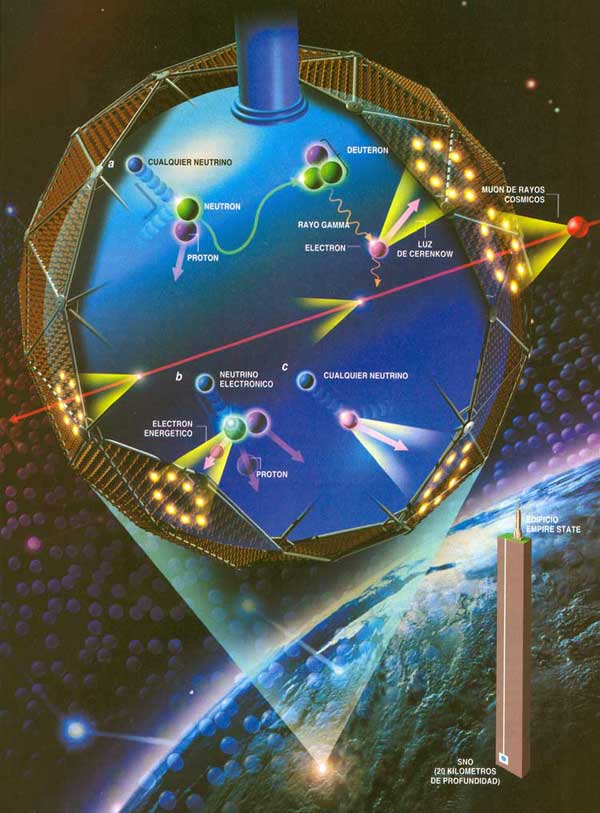
Detectando Neutrinos
En otras palabras, la existencia de neutrinos y antineutrinos debería salvar no una, sino tres, importantes leyes de conservación: la conservación de la energía, la de conservación del espín y la de conservación de partícula/antipartícula.
Pero aún queda algo por desequilibrar. Una sola partícula (el neutrón) ha formado dos partículas (el protón y el electrón), y si incluimos el neutrino, tres partículas. Parece más razonable suponer que el neutrón se convierte en dos partículas y una antipartícula. En otras palabras: lo que realmente necesitamos equilibrar no es un neutrino, sino un antineutrino.
El propio neutrino surgiría de la conversión de un protón en un neutrón. Así pues, los productos serían un neutrón (partícula), un positrón (antipartícula) y un neutrino (partícula). Esto también equilibra la balanza.

Impresionante vista de la Vía Láctea desde el Manua Kea. La Galaxia, el Universo…Todo es energía.
Es importante conservar esas leyes puesto que parece estar presentes en toda clase de relaciones nucleares que no impliques electrones o positrones, y sería muy útil si también se hallasen presentes en reacciones que incluyesen esas partículas. Las más importantes conversiones protón-neutrón son las relacionadas con las reacciones nucleares que se desarrollan en el Sol y en los astros. Por consiguiente, las estrellas emiten radiaciones rápidas de neutrinos, y se calcula que tal vez pierdan a causa de esto el 6 u 8% de su energía. Pero eso sería meternos en otra historia y, por mi parte, con la anterior explicación sólo trataba de dar una muestra del ingenio del hombre que, como habréis visto, no es poco.
Desde que puedo recordar, he sido un amante de la física. Me asombran cuestiones como la luz, su naturaleza de un conglomerado de colores, ondas y partículas, su velocidad que nos marca el límite del máximo que podemos correr en nuestro universo, y en fin, muchos otros misterios que encierra esa cosa tan cotidiana que nos rodea y lo inunda todo haciendo posible que podamos ver por donde vamos, que las plantas vivan y emitan oxígeno o que nos calentemos. Realmente, sin luz, nuestra vida no sería posible. Entonces, ¿qué es realmente la luz?

Muchos (casi todos) opinan que es algo inmaterial. Los objetos materiales grandes o muy pequeños como las galaxias o los electrones, son materia. La luz, sin embargo, se cree que es inmaterial; dos rayos de luz se cruzan sin afectarse el uno al otro. Sin embargo, yo creo que la luz es simplemente una forma de energía lumínica, una más de las diversas formas en las que puede presentarse la materia. Nosotros mismos, en última instancia, somos luz.
Está claro que los estudiosos de la época antigua y medieval estaban por completo a oscuras acerca de la naturaleza de la luz. Especulaban sobre que consistía en partículas emitidas por objetos relucientes o tal vez por el mismo ojo. Establecieron el hecho de que la luz viajaba en línea recta, que se reflejaba en un espejo con un ángulo igual a aquel con el que el rayo choca con el espejo, y que un rayo de luz se inclina (se refracta) cuando pasa del aire al cristal, al agua o a cualquier otra sustancia transparente.
Cuando la luz entra en un cristal o en alguna sustancia transparente, de una forma oblicua (es decir, en un ángulo respecto de la vertical), siempre se refracta en una dirección que forma un ángulo menor respecto de la vertical. La exacta relación entre el ángulo original y el ángulo reflejado fue elaborada por primera vez en 1.621 por el físico neerlandés Willerbrord Snell. No publicó sus hallazgos y el filósofo francés René Descartes descubrió la ley, independientemente, en 1.637.

¿Nos suplirán un día? Seguro que en el futuro, serán otros los que hagan experimentos con la luz y busquen su verdadera naturaleza.
Los primeros experimentos importantes acerca de la naturaleza de la luz fueron llevados a cabo por Isaac Newton en 1.666, al permitir que un rayo de luz entrase en una habitación oscura a través de una grieta de las persianas, cayendo oblicuamente sobre una cara de un prisma de cristal triangular. El rayo se refracta cuando entra en el cristal y se refracta aún más en la misma dirección cuando sale por una segunda cara del prisma (las dos refracciones en la misma dirección se originan porque los lados del prisma se encuentran en ángulo en vez de en forma paralela, como sería el caso de una lámina ordinaria de cristal).

Newton dedujo que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores. La amplia banda de sus componentes se denominó spectrum (palabra latina que significa “espectro” fantasma).
Newton atrapó el rayo emergente sobre una pantalla blanca para ver el efecto de la refracción reforzada. Descubrió que, en vez de formar una mancha de luz blanca, el rayo se extendía en una gama de colores: rojo, anaranjado, amarillo verde, azul y violeta, en este orden. Newton dedujo de ello que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores. La amplia banda de sus componentes se denominó spectrum (palabra latina que significa espectro o fantasma). Newton llegó a la conclusión de que la luz se componía de diminutas partículas (“corpúsculos”), que viajaban a enormes velocidades. Le surgieron y se planteó algunas inquietantes cuestiones: ¿por qué se refractaban las partículas de luz verde más que las de luz amarilla? ¿Cómo se explicaba que dos rayos de luz se cruzaran sin perturbarse mutuamente, es decir, sin que se produjeran colisiones entre partículas?
En 1.678, el físico neerlandés Christian Huyghens (un científico polifacético que había construido el primer reloj de péndulo y realizado importantes trabajos astronómicos) propuso una teoría opuesta: la de que la luz se componía de minúsculas ondas. Y si sus componentes fueran ondas, no sería difícil explicar las diversas difracciones de los diferentes tipos de luz a través de un medio refractante, siempre y cuando se aceptara que la luz se movía más despacio en ese medio refractante que en el aire. La cantidad de refracción variaría con la longitud de las ondas: cuanto más corta fuese tal longitud, tanto mayor sería la refracción. Ello significaba que la luz violeta (la más sensible a este fenómeno) debía de tener una longitud de onda más corta que la luz azul; ésta, más corta que la verde, y así sucesivamente.

Lo que permitía al ojo distinguir los colores eran esas diferencias entre longitudes de onda. Y como es natural, si la luz estaba integrada por ondas, dos rayos podrían cruzarse sin dificultad alguna (las ondas sonoras y las del agua se cruzan continuamente sin perder sus respectivas identidades).
Pero la teoría de Huyghens sobre las ondas tampoco fue muy satisfactoria. No explicaba por qué se movían en línea recta los rayos luminosos, ni por qué proyectaban sombras recortadas, ni aclaraba por qué las ondas luminosas no podían rodear los obstáculos, del mismo modo que pueden hacerlo las ondas sonoras y de agua. Por añadidura, se objetaba que si la luz consistía en ondas, ¿cómo podía viajar por el vacío, ya que cruzaba el espacio desde el Sol y las estrellas? ¿Cuál era esa mecánica ondulatoria?

Con el éxito de Newton de su ley de la Gravitación Universal, no es extraño que afirmara de forma tajante que la luz es corpuscular. Newton se opuso violentamente a la naturaleza ondulatoria de la luz, ya que no veía cómo se podía explicar con ella la propagación rectilínea de la misma. Por otro lado estaba Christian Huygens, 13 años mayor que Newton que defendía la naturaleza ondulatoria con algunas ventajas.

Ambas teorías explicaban perfectamente la reflexión y refracción de la luz. Pero diferían en una cosa. La teoría corpuscular afirmaba que las partículas de luz se acelerarían al pasar por un material de mayor densidad óptica y las ondas a menor. Esto no era comprobable por aquella época. Debido a la influencia de Newton y a la poca habilidad de Huygens para desarrollarla matemáticamente, la teoría ondulatoria quedó descartada durante un siglo.
Aproximadamente durante un siglo, contendieron entre sí estas teorías. La teoría corpuscular de Newton fue, con mucho, la más popular, en parte porque la respaldó el famoso nombre de su autor. Pero hacia 1.801, un físico y médico inglés, de nombre Thomas Young, llevó a cabo un experimento que arrastró la opinión pública al campo opuesto. Proyectó un fino rayo luminoso sobre una pantalla, haciéndolo pasar antes por dos orificios casi juntos; si la luz estuviera compuesta por partículas, cuando los dos rayos emergieran de ambos orificios, formarían presuntamente en la pantalla una región más luminosa donde se superpusieran, y regiones menos brillantes, donde no se diera tal superposición. La pantalla mostró una serie de bandas luminosas, separadas entre sí por bandas oscuras; pareció incluso que en esos intervalos de sombra, la luz de ambos rayos contribuía a intensificar la oscuridad.
Sería fácil explicarlo mediante la teoría ondulatoria; la banda luminosa representaba el refuerzo prestado por las ondas de un rayo a las ondas del otro, dicho de otra manera, entraban “en fase” dos trenes de ondas, es decir, ambos nodos, al unirse, se fortalecían el uno al otro. Por otra parte, las bandas oscuras representaban puntos en los que las ondas estaban “desfasadas” porque el vientre de una neutralizaba el nodo de la otra. En vez de aunar sus fuerzas, las ondas se interferían mutuamente, reduciendo la energía luminosa neta a las proximidades del punto cero.

Considerando la anchura de las bandas y la distancia entre los dos orificios por lo que surgen ambos rayos, se pudo calcular la longitud de las ondas luminosas, por ejemplo, de la luz roja a la violeta o de los colores intermedios. Las longitudes de onda resultaron ser muy pequeñas. Así, la de la luz roja era de unos 0’000075 cm. Hoy se expresan las longitudes de las ondas luminosas mediante una unidad muy práctica ideada por Ángstrom; esta unidad, denominada igualmente Ángstrom (Å) en honor a su autor, es la cienmillonésima parte de un centímetro. Así pues, la longitud de onda de la luz roja equivale más o menos a 7.500 Å, y la de la luz violeta a 3.900 Å, mientras que las de colores visibles en el espectro oscilan entre ambas cifras.
La cortedad de estas ondas es muy importante. La razón de que las ondas luminosas se desplacen en línea recta y proyecten sombras recortadas se debe a que todas son incomparablemente más pequeñas que cualquier objeto; pueden contornear un obstáculo sólo si este no es mucho mayor que la longitud de onda. Hasta las bacterias, por ejemplo, tienen un volumen muy superior al de una onda luminosa, y por tanto, la luz puede definir claramente sus contornos bajo el microscopio. Sólo los objetos cuyas dimensiones se asemejan a la longitud de onda luminosa (por ejemplo, los virus y otras partículas subatómicas) son lo suficientemente pequeños como para que puedan ser contorneados por las ondas luminosas.
Un físico francés, Agustin-Jean Fresnel, fue quien demostró por vez primera en 1.818 que si un objeto es lo suficientemente pequeño, la onda luminosa lo contorneará sin dificultad. En tal caso, la luz determina el llamado fenómeno de “difracción”. Por ejemplo, las finísimas líneas paralelas de una “reja de difracción” actúan como una serie de minúsculos obstáculos, que se refuerzan entre sí. Puesto que la magnitud de la difracción va asociada a la longitud de onda, se produce el espectro. A la inversa, se puede calcular la longitud de onda midiendo la difracción de cualquier color o porción del espectro, así como la separación de las marcas sobre el cristal.

La mano del Universo juguetea con unos puntos luminosos que quieren llegar a ser cegadores…Son nuestras Mentes, productos de la evolución del Universo que, a partir de la materia inerte, ha podido alcanzar el estadio bio-químico de la consciencia y, al ser conscientes, hemos podido descubrir que existen “números misteriosos” dentro de los cuales subyacen mensajes que tenemos que desvelar.
Fraunhofer exploró dicha reja de difracción con objeto de averiguar sus finalidades prácticas, progreso que suele olvidarse, pues queda eclipsado por su descubrimiento más famoso, los rayos espectrales. El físico americano Henry Augustus Rowland ideó la reja cóncava y desarrolló técnicas para regularlas de acuerdo con 20.000 líneas por pulgada. Ello hizo posible la sustitución del prisma por el espectroscópio.
Ante tales hallazgos experimentales, más el desarrollo metódico y matemático del movimiento ondulatorio, debido a Fresnel, pareció que la teoría ondulatoria de la luz había arraigado definitivamente, desplazando y relegando para siempre a la teoría corpuscular.
No sólo se aceptó la existencia de ondas luminosas, sino que también se midió su longitud con una precisión cada vez mayor. Hacia 1.827, el físico francés Jacques Babinet sugirió que se empleara la longitud de onda luminosa (una cantidad física inalcanzable) como unidad para medir tales longitudes, en vez de las muy diversas unidades ideadas y empleadas por el hombre. Sin embargo, tal sugerencia no se llevó a la práctica hasta 1.880 cuando el físico germano-americano Albert Abraham Michelson inventó un instrumento denominado “interferómetro”, que podía medir las longitudes de ondas luminosas con una exactitud sin precedentes. En 1.893, Michelson midió la onda de la raya roja en el espectro del cadmio y determinó que su longitud era de 1/1.553.164 m.

Tubo de descarga lleno de kriptón puro
Pero la incertidumbre reapareció al descubrirse que los elementos estaban compuestos por isótopos diferentes, cada uno de los cuales aportaba una raya cuya longitud de inda difería ligeramente de las restantes. En la década de 1.930 se midieron las rayas del criptón 86. Como quiera que este isótopo fuera gaseoso, se podía abordar con bajas temperaturas, para frenar el movimiento atómico y reducir el consecutivo engrosamiento de la raya.
En 1.960, el Comité Internacional de Pesos y Medidas adoptó la raya del criptón 86 como unidad fundamental de la longitud. Entonces se reestableció la longitud del metro como 1.650.763’73 veces la longitud de onda de dicha raya espectral. Ello aumentó mil veces la precisión de las medidas de longitud. Hasta entonces se había medido el antiguo metro patrón con un margen de error equivalente a una millonésima, mientras que en lo sucesivo se pudo medir la longitud de onda con un margen de error equivalente a una milmillonésima.
emilio silvera
Jun
21
La desintegración de un Neutrón
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (3)
Comments (3)
La desintegración Beta del neutrón está mediada por un Bosón W-,que transforma uno de sus quarks, y se desintegra en el par electrón-antineutrino. Ahora leamos el reportaje de la Revista “Investigación y Ciencia”, referido a la física de partículas y a unas mediciones efectuadas que no son coincidentes.
“Dos técnicas de precisión arrojan valores distintos para el tiempo que tardan los neutrones en desintegrarse. ¿Se trata de un error experimental, o hay un misterio más profundo?

En síntesis
Los neutrones libres no son estables: pasados unos 15 minutos, un neutrón se desintegra en un protón, un electrón y un antineutrino. Conocer con exactitud su vida media es clave para abordar varias cuestiones en física y cosmología.
Existen dos métodos para determinar con precisión la vida media de esta partícula. El primero cuenta los neutrones que quedan en un recipiente después de cierto tiempo; el segundo cuenta los protones generados en su desintegración.
Hace años que una y otra técnica arrojan valores considerablemente dispares. Se cree que la discrepancia obedece a errores sistemáticos en alguno de los experimentos; sin embargo, hasta ahora nadie ha logrado dar con ellos.
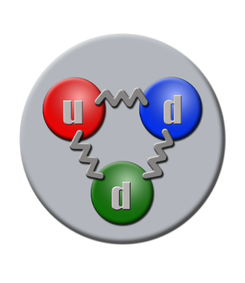
Un neutrón está formado por dos quarks dowm (abajo) y un quark up (arriba), tiene una vida media de 14,761 minutos, es una partícula de la familia de los hadrones en su vertiente bariónica, interacción: con la Gravedad, la nuclear débil y la nuclear fuerte, su símbolo es n, su antipartícula es el antineutrón, la teorízo Rutherford y la descubrio James Chadwick, su masa es de 1,674 927 29(28)×10−27 K., la carga eléctrica es cero, espín ½. Se conoce cuando forma parte del átomo por nucleón.
Por suerte para la vida en la Tierra, la mayor parte de la materia no es radiactiva. Aunque no solemos darle demasiada importancia, este hecho no deja de resultar sorprendente, ya que el neutrón (uno de los constituyentes, junto con el protón, de los núcleos atómicos) es propenso a desintegrarse. En el interior de un núcleo típico el neutrón puede vivir durante largo tiempo, pero, aislado, se desintegra en otras partículas en unos 15 minutos. Decimos «unos 15 minutos» para ocultar nuestra ignorancia al respecto, ya que, hasta ahora, no hemos sido capaces de medir con exactitud la vida media de esta partícula.
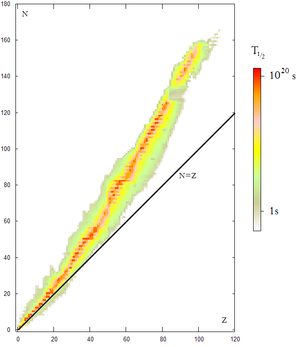
Diagrama de Segrè. El color indica el periodo de semidesintegración de los isótopos radiactivos conocidos, también llamado semivida. Observe que un ligero exceso de neutrones favorece la estabilidad en átomos pesados.
Resolver este «rompecabezas de la vida media del neutrón» no solo supone una cuestión de orgullo para nuestro gremio, el de los físicos experimentales, sino que resulta también vital para comprender mejor las leyes físicas. La desintegración del neutrón constituye uno de los procesos más sencillos en los que interviene la interacción débil, una de las cuatro fuerzas fundamentales de la naturaleza. Para entenderla por completo, hemos de saber cuánto tarda un neutrón aislado en desintegrarse. Por otro lado, la vida media del neutrón condicionó cómo se formaron los elementos químicos más ligeros después de la gran explosión que dio origen a nuestro universo. A los cosmólogos les gustaría poder calcular las abundancias esperadas de los distintos elementos y contrastarlas con los datos obtenidos por los astrofísicos. Un acuerdo apuntalaría nuestras teorías cosmológicas, mientras que una discrepancia indicaría la existencia de fenómenos físicos aún por descubrir. Pero, para poder llevar a cabo dicha comparación, hemos de conocer con exactitud cuánto vive un neutrón antes de desintegrarse.
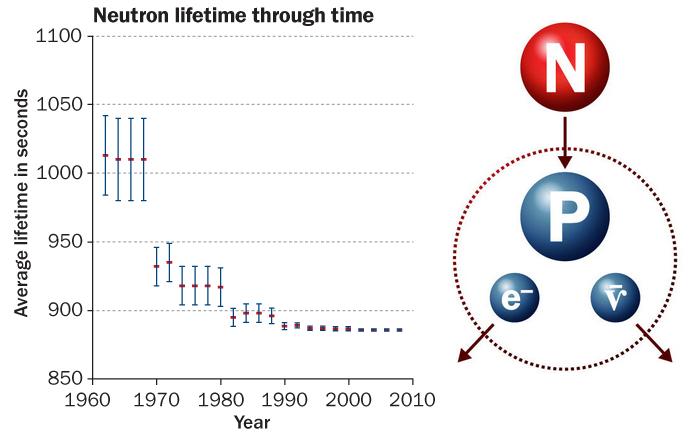
Hace más de diez años, dos grupos experimentales, uno en Francia y otro en EE.UU., intentaron medir con precisión la vida media del neutrón. Uno de nosotros (Geltenbort) pertenecía al primer equipo, mientras que el otro (Greene) trabajaba en el segundo. Con sorpresa y cierta inquietud, comprobamos que nuestros resultados diferían de manera considerable. Algunos teóricos sugirieron que la discrepancia podría deberse a fenómenos físicos exóticos, como que parte de los neutrones se hubiesen desintegrado en partículas nunca antes observadas. Nosotros, sin embargo, achacamos la diferencia a una razón mucho más mundana: uno de los grupos —o ambos— tenía que haber cometido algún error o sobre-estimado la precisión de sus resultados.
Hace poco, el equipo estadounidense completó un largo y concienzudo proyecto para estudiar la principal fuente de error que afectaba a sus mediciones. Lejos de zanjar la cuestión, sus esfuerzos solo confirmaron los resultados previos. Al mismo tiempo, otros investigadores verificaron los resultados del grupo de Geltenbort. Esta discrepancia nos ha dejado más perplejos de lo que ya estábamos, pero no hemos abandonado. Por el momento, ambos equipos y otros físicos experimentales seguimos buscando una respuesta.
CRONOMETRAR NEUTRONES
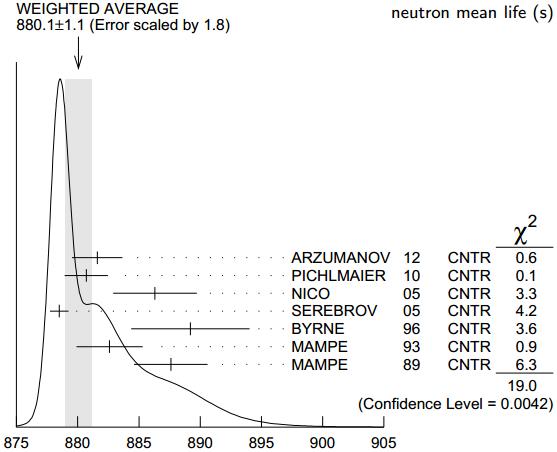
El neutrón y el protón forman los núcleos de los átomos; el protón es estable (su vida media es superior a 10³² años, según PDG 2012), pero el neutrón es inestable (vía la interacción electrodébil se desintegra en un protón) y aislado su vida media es de solo 880,1 ± 1,1 segundos (14 minutos y 40,1 segundos)
En teoría, determinar la vida media del neutrón es sencillo. Entendemos bien la física del proceso y disponemos de las herramientas adecuadas para estudiarlo. Sabemos que, siempre que una partícula pueda desintegrarse en otras de menor masa, acabará haciéndolo si en el proceso se conservan ciertas propiedades, como la carga eléctrica o el espín. En la llamada desintegración beta, un neutrón se transforma en un protón, un electrón y un antineutrino. Las masas de estas tres partículas suman algo menos que la masa del neutrón, pero la carga y el espín totales permanecen idénticos. Entre las cantidades conservadas se incluye la suma de masa y energía, por lo que las tres partículas finales incorporan esa pequeña diferencia de masa en forma de energía cinética.”
Nota: El artículo me ha sido enviado por Don José Gómez, un contertulio y visitante de ésta página que, con buen criterio, apunta que en cuanto a esas diferencias, las pruebas deben ser repetidas en distintos lugares y, si es posible, por distintos científicos también, ya que, en física de partícula, los resultados de un experimento, debe coincidir sin fisuras.
Jun
14
La Sinfonía de los Agujeros Negros binarios, ¿La oiremos alguna vez?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Relativista ~
Clasificado en Física Relativista ~
 Comments (0)
Comments (0)
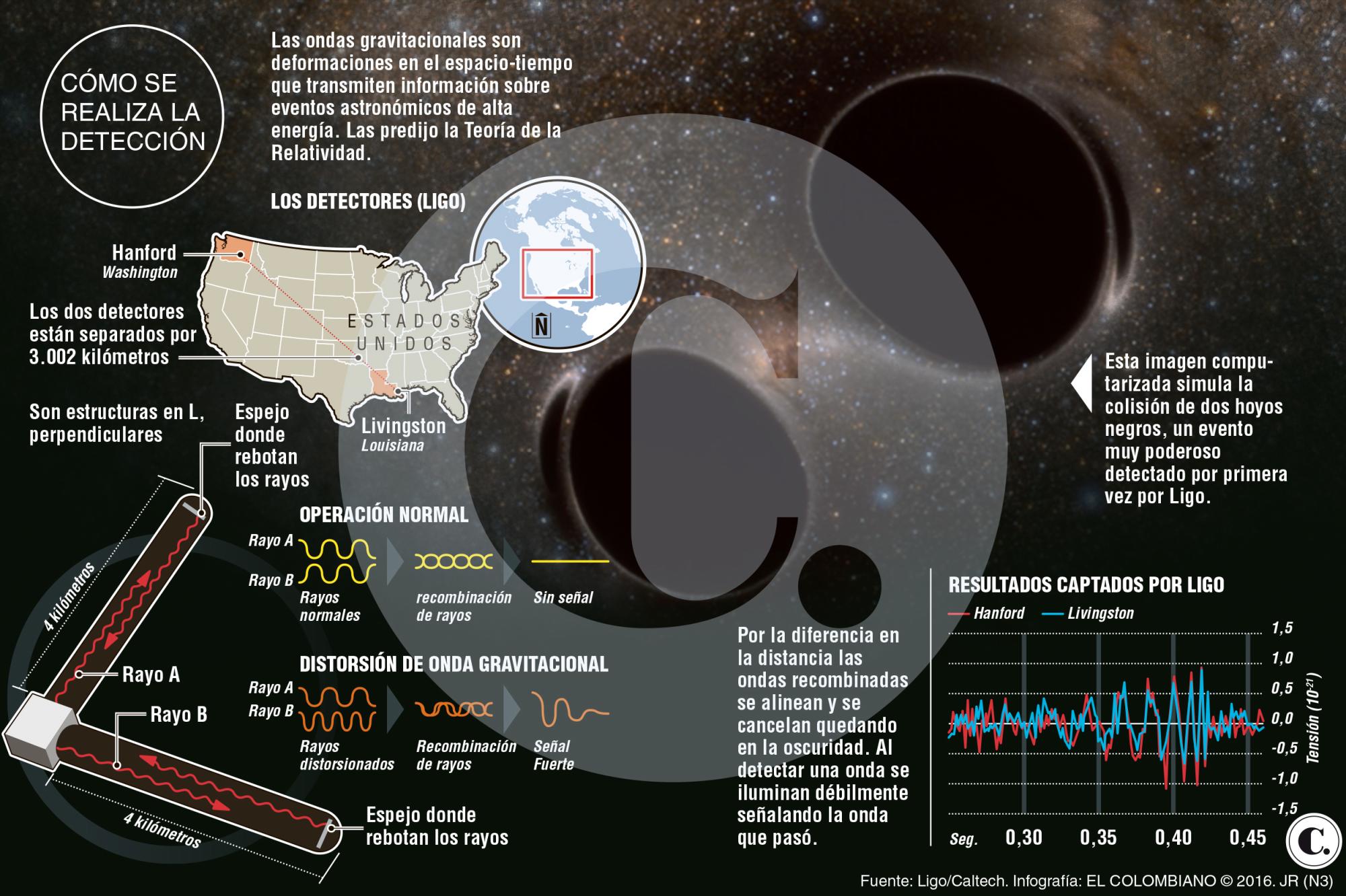
Me parece al caso traer aquí este trabajo que puse hace algún tiempo ya, toda vez que el hallazgo de las Ondas gravitatorias lo ha renovado y su contenido puede resultar interesante al filo de aquellas noticias. Decía por aquel entonces:

Kip Stephen Thorne
Lo que nos cuentan Kip S. Thorne y otros especialistas en Agujeros negros nos posibilitan para entender algo mejor los mecanismos de estos extraños objetos que aún esconden misterios que no hemos sabido resolver (leer comentario de Kike en el anterior trabajo). Está claro que muchas de las cosas que sobre agujeros negros podemos leer, son en realidad, especulaciones de cosas que se deducen por señales observadas pero que, de ninguna manera, se pueden tomar como irrefutables verdades, más bien, las tomaremos como probables o muy probables de acuerdo a los resultados obtenidos de muchos experimentos y, ¿por qué no? de muchas horas de prácticas teóricas y pizarras llenas de ecuaciones que tratan de llegar al fondo de un saber que, desde luego, nos daría la clave de muchas cuestiones que en nuestro Universo son aún desconocidas.

En el corazón de una galaxia lejana, a más de 1.000 millones de años-luz de la Tierra y hace 1.000 millones de años, se acumuló un denso aglomerado de gas y cientos de millones de estrellas. El aglomerado se contrajo gradualmente, a medida que algunas estrellas escapaban y los 100 millones de estrellas restantes se hundían más hacia el centro. Al cabo de 100 millones de años, el aglomerado se había contraído hasta un tamaño de varios años-luz, y pequeñas estrellas empezaron, ocasionalmente, a colisionar y fusionarse, formando estrellas mayores. Las estrellas mayores consumieron su combustible y luego implosionaron para formar agujeros negros; y, en ocasiones, cuando dos de estos agujeros pasaban uno cerca del otro, quedaban ligados formando pares en los que cada agujero giraba en órbita alrededor del otro.

Cuando se forma un par de agujeros negros binarios semejantes, cada agujero crea un pozo profundo (intensa curvatura espacio-temporal) en la superficie insertada y, a medida que los agujeros giran uno en torno al otro, los pozos en órbita producen ondulaciones de curvatura que se propagan hacia afuera a la velocidad de la luz. Las ondulaciones forman una espiral en el tejido del espacio-tiempo en torno al sistema binario, muy semejante a la estructura espiral del agua que procede de un aspersor de cesped que gira rápidamente. Los fragmentos de curvatura forman un conjunto de crestas y valles en espiral en el tejido espacio-temporal.

Puesto que la curvatura-espaciotemporal es lo mismo que la gravedad, estas ondulaciones de curvatura son realmente ondas de gravedad, u ondas gravitatorias. La Teoría de la Relatividad General de Einstein predice, de forma inequívoca, que tales ondas gravitatorias deben producirse siempre que dos agujeros negros orbiten uno en torno al otro.
Cuando parten hacia el espacio exterior, las ondas gravitatorias producen una reacción sobre los agujeros de la misma forma que una bala hace retroceder el fusil que la dispara. El retroceso producido por las ondas aproxima más los agujeros y les hace moverse a velocidades mayores; es decir, hacen que se muevan en una espiral que se cierra lentamente y hace que se vayan acercando el uno hacia el otro. Al cerrarse la espiral se genera poco a poco energía gravitatoria, una mitad de la cual va a las ondas y la otra mitad va a incrementar las velocidades orbitales de los agujeros.

El movimiento en espiral de los agujeros es lento al principio; luego, a medida que los agujeros se acercan, se mueven con mayor velocidad, radian sus ondulaciones de curvatura con más intensidad, y pierden energía y se cierran en espiral con más rapidez. Finalmente, cuando cada agujero se está moviendo a una velocidad cercana a la de la luz, sus horizontes se tocan y se fusionan. Donde una vez hubo dos agujeros, ahora sólo hay uno.
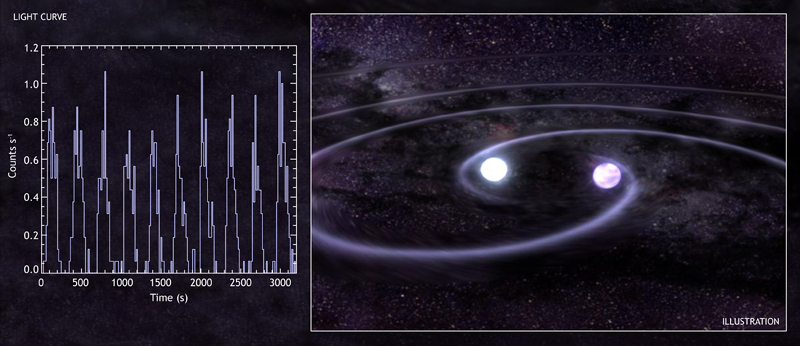
El horizonte del agujero giratorio queda perfectamente liso y con su sección ecuatorial circular, con la forma descrita precisamente por la solución de Kerr a la ecuación de campo de Einstein. Cuando se examina el agujero negro liso final, no hay ningún modo de descubrir su historia pasada. No es posible distinguir si fue creado por la colisión de dos agujeros más pequeños, o por la implosión directa de una estrella súpermasiva construida por materia, o por la implosión directa de una estrella constituida por antimateria. El agujero negro no tiene “pelo” a partir del cual se pueda descifrar su historia.

También dos estrellas de neutrones pueden producir ondas
Sin embargo, la historia no se ha perdido por completo: ha quedado un registro codificado en las ondulaciones de la curvatura espacio-temporal que emitieron los agujeros coalescentes. Dichas ondulaciones de curvatura son muy parecidas a las ondas sonoras de una sinfonía. De la misma forma que la sinfonía está codificada en las modulaciones de las ondas sonaras (mayor amplitud aquí, menor allí), también la historia de la coalescencia está codificada en modulaciones de las ondulaciones de curvatura. Y de la misma forma que las ondas sonoras llevan su sinfonía codificada desde la orquesta que la produce hasta la audiencia, también las ondulaciones de curvatura llevan su historia codificada desde los agujeros fusionados hasta los rincones más lejanos del Universo lejano.

Las ondulaciones de curvatura viajan hacia afuera por el tejido del espacio-tiempo a través del conglomerado de estrellas y gas del que nacieron los agujeros. El aglomerado no absorbe las ondulaciones ni las distorsiona en absoluto; la historia codificada de las ondulaciones permanece perfectamente invariable, se expanden hacia el exterior de la galaxia madre del aglomerado y el espacio intergaláctico, atraviesan el cúmulo de galaxias del que forma parte la galaxia progenitora, luego siguen atravesando un cúmulo de galaxias tras otro hasta llegar a nuestro propio cúmulo, dentro del cual está nuestra Vía Láctea con nuestro Sistema Solar, atraviesan la Tierra, y continúan hacia otras galaxias distantes.
Claro que, en toda esta historia hay un fallo, nosotros, los humanos, aún no somos lo suficientemente hábiles para haber podido construir aparatos capaces de detectar y oir las sinfonías mencionadas con entusiamos por el Sr. Thorne y, que según el cree, son mensajes que nos traen esas ondas de gravedad de los agujeros negros binarios. Es como si no pudiéramos oir esa hermosa sinfonía que nos mostraría un nuevo Universo por nosotros desconocido. Ahora sabemos que por medio de potentes telescopios podemos conocer lo que es el Universo, podemos observar galaxias lejanas y estudiar cúmulos de galaxias o de estrellas y captar las imágenes de bonitas Nebulosas, todo eso es posible gracias a que al captar la luz que emitieron esos objetos cosmológicos hace decenas, cientos, miles o millones de años como señal electromagnética que viajando a la velociodad de c, hace posible que podamos ver lo observado como era entonces, en aquel pasado más o menos lejano. De la misma manera, se cree que, las ondas gravitatorias emitidas por estos objetos misteriosos, se podrán llegar a captar con tal claridad que nos permitirá saber de otra faseta (ahora) desconocida del Universo, y, sobre todo, podremos entender el pasado de esos densos objetos que, de momento, nos resultan exóticos y también extraños.
emilio silvera
Jun
12
Creemos cosas que…, ¿serán ciertas?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
La verdadera Historia de la Teoría del Cáos

Diagrama de la trayectoria del sistema de Lorenz para los valores r = 28, σ = 10, b = 8/3.
Teoría del cáos es la denominación popular de la rama de las matemáticas, la física y otras disciplinas científicas que trata ciertos tipos de sistemas dinámicos muy sensibles a las variaciones en las condiciones iniciales. Pequeñas variaciones en dichas condiciones iniciales pueden implicar grandes diferencias en el comportamiento futuro, imposibilitando la predicción a largo plazo. Esto sucede aunque estos sistemas son en rigor determinísticos, es decir; su comportamiento puede ser completamente determinado conociendo sus condiciones iniciales.
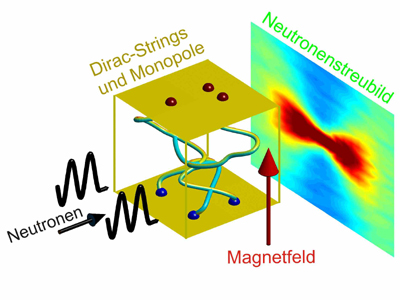
Montaje experimental. Foto: HZB, D.J.P. Morris y A. Tennant. Monopolos magneticos .
Hubo un tiempo, el el Universo muy temprano, en el que la temperatura estaba encima de algunos cientos de veces la masa del protón, cuando la simetría aún no se había roto, y la fuerza débil y electromagnética no sólo eran la misma matemáticamente, sino realmente la misma. Un físico que hibiera podido estar allí presente, en aquellos primeros momento, no habría podido observar ninguna diferencia real entre las fuerzas producidas por el intercambio de estas cuatro partículas: las W, la Z y el Fotón.

Muchas son las sorpresas que nos podríamso encontrar en el universo primitivo, hasta la presencia de agua ha sido detectada mediante la técnica de lentes gravitacionales en la galaxia denominada MG J0414+0534 que está situada en un tiempo en el que el Universo sólo tenía dos mil quinientos millones de años de edad. El equipo investigador pudo detectar el vapor de agua presente en los chorros de emisión de un agujero negro supermasivo. Este tipo de objeto es bastante raro en el universo actual. El agua fue observada en forma de mases, una emisión de radiación de microondas provocada por las moléculas (en este caso de agua) al ser amplificadas por una onda o un campo magnético.
Siguiendo con el trabajo, dejemos la noticia de más arriba (sólo insertada por su curiosidad y rareza), y, sigamos con lo que hemos contado repetidas veces aquí de las fuerzas y la simetría antes de que, el universo se expandiera y enfriara para que, de una sóla, surgieran las cuatro fuerzas que ahora conocemos: Gravedad que campa sola y no quiere juntarse con las otras fuerzas del Modelo Estándar, el electromagnetismo y las nucleares débil y fuerte.
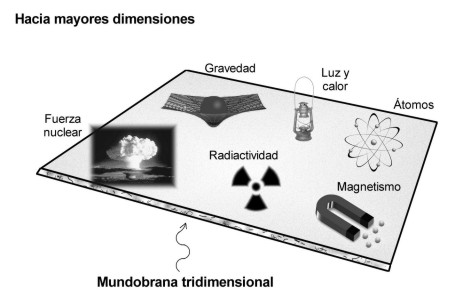
Las fuerzas de la naturaleza que gobiernan la electricidad, el magnetismo, la radiactividad y las reacciones nucleares están confinadas a un “mundobrana” tridimensional, mientras que la gravedad actúa en todas las dimensiones y es consecuentemente más débil. Seguramente ese será el motivo por el cual, encontrar al Bosón mediador de la fuerza, el Gravitón, resulta tan difícil.
De manera similar, aunque menos clara, las teorías de supersimetrías conjeturaban que las cuatro fuerzas tal vez estaban ligadas por una simitría que se manifestaba en los niveles de energía aún mayores que caracterizaban al universo ya antes del big bang. La intodución de un eje histórico en la cosmolo´gia y la física de particulas (como decía ayer en uno de los trabajos), beneficio a ambos campos. Los físicos proporcionaron a los cosmólogos una amplia gama de herramientas útiles para saber cómo se desarrolló el universo primitivo. Evidentemente, el Big Bang no fue una muralla de fuego de la que se burló Hoyle, sino un ámbito de suscesos de altas energías que muy posiblemente pueden ser comprensibles en términos de teoría de campo relativista y cuántica.

La cosmología, por su parte, dio un tinte de realidad histórica a las teorías unificadas. Aunque ningún acelerador concebible podrían alcanzar las titánicaqs energías supuestas por las grandes teorías unificadas y de la supersimetría, esas exóticas ideas aún pueden ser puestas a prueba, investigando las partículas constituyentes del universo actual y tratar de ver si son compatibles con el tipo de historia primitiva que implican las teorías.
Gell-Mann, el premio Nobel de física, al respeto de todo esto decía: “Las partículas elementales aparentemente proporcionan las claves de algunos de los misterios fundamentales de la Cosmología temprana… y resulta que la Cosmología brinda una especia de terreno de prueba para alguna de las ideas de la física de partículas elementales.” Hemos podido llegar a descubrir grandes secretos de la naturaleza mediante los pensamientos que, surgidos de la mente desconocida y misteriosa de algunos seres humanos, han podido ser intuidos mediante ráfagas luminosas que nunca sabremos de dónde pudieron surgir )Lorentz, Planck, Einstein, Heisenmberg, Dirac, Eddigton, Feymann, Wheeler… Y, una larga lista de privilegiados que pudieron ver, lo que otros no podían.

Moléculas, átomos y conexiones para formar pensamientos
Hemos llegado a poder discernir la relación directa que vincula el tamaño, la energía de unión y la edad de las estructuras fundamentales de la Naturaleza. Una molécula es mayor y más fácil de desmembrar que un átomo; lo mismo podemos decir de un átomo respecto al núcleo atómico, y de un núcleo con respecto a los quarks que contiene. La cosmología sugiere que esta relación resulta del curso de la historia cósmica, que los quarks se unieron primero en las energías extremadamente altas del big bang original y que a medida que el Universo se expandió, los protones y neutrones compuestos de quarks se unieron para formar núcleos de átomos, los cuales, cargados positivamente, atrajeron a los electrones cargados con electricidad negativa estableciéndose así como átomos completos, que al unirse formaron moléculas.

Si es así (que lo es), cuanto más íntimamente examinemos la Naturaleza, tanto más lejos hacia atrás vamos en el tiempo. Alguna vez he puesto el ejemplo de mirar algo que no es familiar, el dorso de la mano, por ejemplo, e imaginemos que podemos observarlo con cualquier aumento deseado.
Con un aumento relativamente pequeño, podemos ver las células de la piel, cada una con un aspecto tan grande y complejo como una ciudad, y con sus límites delineados por la pared celular. Si elevamos el aumento, veremos dentro de la célula una maraña de ribosomas serpenteando y mitocondrias ondulantes, lisosomas esféricos y centríolos, cuyos alrededores están llenos de complejos órganos dedicados a las funciones respiratorias, sanitarias y de producción de energía que mantienen a la célula.
Ya ahí tenemos pruebas de historia. Aunque esta célula particular solo tiene unos pocos años de antigüedad, su arquitectura se remonta a más de mil millones de años, a la época en que aparecieron en la Tierra las células eucariota o eucarióticas como la que hemos examinado.
Abajo vemos el dorso de la mano algo aumentado
Para determinar dónde obtuvo la célula el esquema que le indicó como formarse, pasemos al núcleo y contemplemos los delgados contornos de las macromoléculas de ADN segregadas dentro de sus genes. Cada una contiene una rica información genética acumulada en el curso de unos cuatro mil millones de años de evolución.

Almacenado en un alfabeto de nucleótidos de cuatro “letras”- hecho de moléculas de azúcar y fosfatos, y llenos de signos de puntuación, reiteraciones para precaver contra el error, y cosas superfluas acumuladas en los callejones sin salida de la historia evolutiva-, su mensaje dice exactamente cómo hacer un ser humano, desde la piel y los huesos hasta las células cerebrales.
Si elevamos más el aumento veremos que la molécula de ADN está compuesta de muchos átomos, con sus capas electrónicas externas entrelazadas y festoneadas en una milagrosa variedad de formas, desde relojes de arena hasta espirales ascendentes como largos muelles y elipses grandes como escudos y fibras delgadas como puros. Algunos de esos electrones son recién llegados, recientemente arrancados a átomos vecinos; otros se incorporaron junto a sus núcleos atómicos hace más de cinco mil millones de años, en la nebulosa de la cual se formó la Tierra.
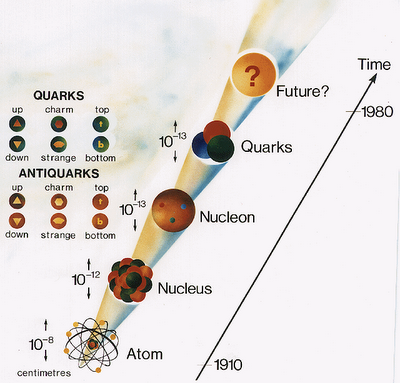
Una molécula es mayor y más fácil de desmembrar que un átomo; lo mismo podemos decir de un átomo respecto al núcleo atómico, y de un núcleo con respecto a los quarks que contiene. Sion embargo, nos queda la duda de: ¿qué podrá haber más allá de los Quarks?
¿Qué no podremos hacer cuando conozcamos la naturaleza real del átomo y de la luz? El fotón, ese cuánto de luz que parece tan insignificante, nos tiene que dar muchas satisfacciones y, en él, están escondidos secretos que, cuando sean revelados, cambiará el mundo. Esa imagen de arriba que está inmersa en nosotros en en todo el Universo, es la sencilles de la complejidad. A partir de ella, se forma todo: la muy pequeño y lo muy grande.
Si elevamos el aumento cien mil veces, el núcleo de un átomo de carbono se hinchará hasta llenar el campo de visión. Tales núcleos y átomos se formaron dentro de una estrella que estalló mucho antes de que naciera el Sol. Si podemos aumentar aún más, veremos los tríos de quarks que constituyen protones y neutrones. Los quarks han estado unidos desde que el Universo sólo tenía unos pocos segundos de edad.
Al llegar a escalas cada vez menores, también hemos entrado en ámbitos de energías de unión cada vez mayores. Un átomo puede ser desposeído de su electrón aplicando sólo unos miles de electrón-voltios de energía. Sin embargo, para dispersar los nucleones que forman el núcleo atómico se requieren varios millones de electrón-voltios, y para liberar los quark que constituyen cada nucleón.

Uno de los misterios de la naturaza, están dentro de los protomes y netrones que, confromados por Quarks, resulta que, si estos fueran liberados, tendrían independientemente, más energía que el protón que conformaban. ¿cómo es posible eso?
Introduciendo el eje de la historia, esta relación da testimonio del pasado de las partículas: las estructuras más pequeñas, más fundamentales están ligadas por niveles de energía mayores porque las estructuras mismas fueron forjadas en el calor del big bang. Esto implica que los aceleradores de partículas, como los telescopios, funcionen como máquinas del tiempo. Un telescopio penetra en el pasado en virtud del tiempo que tarda la luz en desplazarse entre las estrellas; un acelerador recrea, aunque sea fugazmente, las condiciones que prevalecían en el Universo primitivo. El acelerador de 200 Kev diseñado en los años veinte por Cockroft y Walton reproducía algunos de los sucesos que ocurrieron alrededor de un día después del comienzo del big bang. Los aceleradores construidos en los años cuarenta y cincuenta llegaron hasta la marca de un segundo. El Tevatrón del Fermilab llevó el límite a menos de una milmillonésima de segundo después del comienzo del Tiempo. El nuevo LHC proporcionara un atisbo del medio cósmico cuando el Universo tenía menos de una billonésima de segundo de edad.
Esta es una edad bastante temprana: una diez billonésima de segundo es menos que un pestañeo con los párpados en toda la historia humana registrada. A pesar de ello, extrañamente, la investigación de la evolución del Universo recién nacido indica que ocurrieron muchas cosas aún antes, durante la primera ínfima fracción de un segundo.
Todos los teóricos han tratado de elaborar una explicación coherente de los primeros momentos de la historia cósmica. Por supuesto, sus ideas fueron esquemáticas e incompletas, muchas de sus conjeturas, sin duda, se juzgaran deformadas o sencillamente erróneas, pero constituyeron una crónica mucho más esclarecedora del Universo primitivo que la que teníamos antes.
A los cien millones de años desde el comienzo del tiempo, aún no se habían formado las estrellas, si acaso, algunas más precoces. Aparte de sus escasas y humeantes almenaras, el Universo era una sopa oscura de gas hidrógeno y helio, arremolinándose aquí y allá para formar protogalaxias.

He aquí la primera imagen jamás obtenida de antimateria, específicamente un “anti-átomo” de anti-hidrógeno. Este experimento se realizó en el Aparato ALPHA de CERN, en donde los anti-átomos fueron retenidos por un récord de 170 milisegundos (se atraparon el 0.005% de los anti-átomos generados).
A la edad de mil millones de años, el Universo tiene un aspecto muy diferente. El núcleo de la joven Vía Láctea arde brillantemente, arrojando las sobras de cumulonimbos galácticos a través del oscuro disco; en su centro brilla un quasar blanco-azulado. El disco, aún en proceso de formación, es confuso y está lleno de polvo y gas; divide en dos partes un halo esférico que será oscuro en nuestros días, pero a la sazón corona la galaxia con un brillante conjunto de estrellas calientes de primera generación.
Para determinar dónde obtuvo la célula es esquema que le indicó como formarse, pasemos al núcleo y contemplemos los delgados contornos de las macromoléculas de ADN segregadas dentro de sus genes. Cada una contiene una rica información genética acumulada en el curso de unos cuatro mil millones de años de evolución.
Claro que, nuestra historia está relacionada con todo lo que antes de llegar la vida al Universo pudo pasar. ¡Aquella primera célula! Se replicó en la sopa primordial llamada Protoplasma vivo y, sigguió evolucionando hasta conformar seres de diversos tipos y, algunos, llegaron a adquirir la conciencia.
Macromolécula
Almacenado en un alfabeto de nucleótidos de cuatro “letras”- hecho de moléculas de azúcar y fosfatos, y llenos de signos de puntuación, reiteraciones para precaver contra el error, y cosas superfluas acumuladas en los callejones sin salida de la historia evolutiva-, su mensaje dice exactamente cómo hacer un ser humano, desde la piel y los huesos hasta las células cerebrales.
célula cerebral
Si elevamos más el aumento veremos que la molécula de ADN está compuesta de muchos átomos, con sus capas electrónicas externas entrelazadas y festoneadas en una milagrosa variedad de formas de una rareza y de una incleible y extraña belleza que sólo la Naturaleza es capaz de conformar.
Molécula de ADN
Si elevamos el aumento cien mil veces, el núcleo de un átomo de carbono se hinchará hasta llenar el campo de visión. Tales núcleos átomos se formaron dentro de una estrella que estalló mucho antes de que naciera el Sol. Si podemos aumentar aún más, veremos los tríos de quarks que se constituyen en protones y neutrones.

Átomo de Carbono
Los quarks han estado unidos desde que el Universo sólo tenía unos pocos segundos de edad. Una vez que fueron eliminados los antiquarks, se unieron en tripletes para formar protones y neutrones que, al formar un núcleo cargado positivamente, atrayeron a los electrones que dieron lugar a formar los átomos que más tarde, conformaron la materia que podemos ver en nuestro unioverso.
Al llegar a escalas cada vez menores, también hemos entrado en ámbitos de energías de unión cada vez mayores. Un átomo puede ser desposeído de su electrón aplicando sólo unos miles de electrón-voltios de energía. Sin embargo, para dispersar los nucleaones que forman el núcleo atómico se requieren varios millones de electrón-voltios, y para liberar los quarks que constituyen cada nucleón se necesitaría cientos de veces más energía aún.

Los Quarks dentro del núcleo están sometidos a la Interacción fuerte, es decir, la más potente de las cuatro fuerzas fundamentales del Universo, la que mantiene a los Quarks confinados dentro del núcleo atómico por medio de los Gluones.
Introduciendo el eje de la historia, esta relación da testimonio del pasado de las partículas: las estructuras más pequeñas, más fundamentales están ligadas por niveles de energía mayores porque las estructuras mismas fueron forjadas en el calor del Big Bang.

Haces de protones que chocan cuando viajan a velocidad relativista en el LHC
Esto implica que los aceleradores de partículas, como los telescopios, funcionen como máquinas del tiempo. Un telescopio penetra en el pasado en virtud del tiempo que tarda la luz en desplazarse entre las estrellas; un acelerador recrea, aunque sea fugazmente, las condiciones que prevalecían en el Universo primitivo.
El acelerador de 200 kev diseñado en los años veinte por Cockroft y Walton reproducía algunos de los sucesos que ocurrieron alrededor de un día después del comienzo del big bang.

Aquel acelerador nada tenía que ver con el LHC de ahora, casi un siglo los separa
Los aceleradores construidos en los años cuarenta y cincuenta llegaron hasta la marca de un segundo. El Tevatrón del Fermilab llevó el límite a menos de una milmillonésima de segundo después del comienzo del Tiempo. El nuevo supercolisionador superconductor proporcionara un atisbo del medio cósmico cuando el Universo tenía menos de una billonésima de segundo de edad.
El Tevatrón del Fermilab ya estaba en el camino de la modernidad en los avances de la Física
Esta es una edad bastante temprana: una diez billonésima de segundo es menos que un pestañeo con los párpados en toda la historia humana registrada. A pesar de ello, extrañamente, la investigación de la evolución del Universo recién nacido indica que ocurrieron muchas cosas aún antes, durante la primera ínfima fracción de un segundo.
Todos los teóricos han tratado de elaborar una explicación coherente de los primeros momentos de la historia cósmica. Por supuesto, sus ideas fueron esquemáticas e incompletas, muchas de sus conjeturas, sin duda, se juzgaran deformadas o sencillamente erróneas, pero constituyeron una crónica mucho más aclaradora del Universo primitivo que la que teníamos antes.
Recreación del Universo primitivo
Bueno amigos, el trabajo era algo más extenso y entrábamos a explicar otros aspectos y parámetros implicados en todo este complejo laberinto que abarca desde lo muy grande hasta la muy pequeño, esos dos mundos que, no por ser tan dispares, resultan ser antagónicos, porque el uno sin el otro no podría exisitir. Otro día, seguiremos abundando en el tema apasionante que aquí tratamos.
emilio silvera
















 Totales: 83.633.264
Totales: 83.633.264 Conectados: 40
Conectados: 40