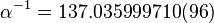Jul
20
¡La Luz! ¡La Mecánica Cuántica! Nuestro Universo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)

Cuando en nuestro Uni9verso quedaron libres los fotones… ¡Se hizo la Luz!
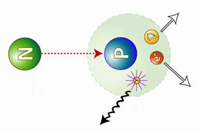
En alguna parte he podido leer que para comprender la realidad en sus niveles más elementales, basta con conocer el comportamiento de dos infinitesimales objetos: el electrón y el fotón. Todo el argumento de la QED [electrodinámica cuántica] gira en torno a un proceso fundamental: la emisión de un único fotón por un único electrón.
Cuando el movimiento de un electrón es alterado súbitamente, puede responder desprendiendo un fotón. La emisión de un fotón es el suceso básico de la mecánica cuántica:


Un equipo de científicos lograron filmar por primera vez un electrón en movimiento gracias a una tecnología reciente que genera pulsos cortos e intensos de luz láser.
Toda la luz visible que vemos, así como las ondas de radio, la radiación infrarroja y los rayos X, está compuesta de fotonesque han sido emitidos por electrones, ya sea en el Sol, el filamento de una bombilla, una antena de radio o un aparato de rayos.
Los electrones no son las únicas partículas que pueden emitir fotones. Cualquier partícula eléctricamente cargada puede hacerlo, incluido el protón. Esto significa que los fotones pueden saltar entre dos protones o incluso entre un protón y un electrón. Este hecho es de enorme importancia para toda la ciencia y la vida en general. El intercambio continuo de fotonesentre el núcleo y los electrones atómicos proporciona la fuerza que mantiene unido al átomo. Sin estos fotones saltarines, el átomo se desharía y toda la materia dejaría de existir.
 |
Se ha conseguido observar por primera vez la desintegración radiativa del neutrón.
Dentro de los núcleos de los átomos hay neutrones y protones. En condiciones normales y mientras que están ahí los neutrones son estables. Sin embargo los neutrones libres son inestables, tienen una vida media de unos 10 minutos, y se desintegran produciendo un protón un electrón y un antineutrino. Pero los físicos nucleares teóricos predijeron que una de cada mil veces los neutrones decaerían en todas esas partículas y además en un fotón.
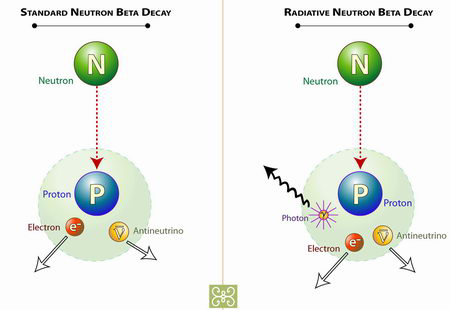 Típicamente el neutrón decae en un protón, un antineutrino y un electrón. Muy raramente lo hace radiativamente emitiendo además un fotón. Diagrama: Zina Deretsky, National Science Foundation.
Típicamente el neutrón decae en un protón, un antineutrino y un electrón. Muy raramente lo hace radiativamente emitiendo además un fotón. Diagrama: Zina Deretsky, National Science Foundation.
Mientras que un electrón pertenece al grupo de partículas llamadas fermiones, los fotones pertenecen a la familia de los bosones. Intentemos comprender esta película que es la intermediaria de todas las formas de radiación electromagnética.
…protagonizada por bosones…
Los fermiones hacen posible la materia “al estilo tradicional”, mientras que los bosones son elementos muy raros desde la forma de pensar a que estamos acostumbrados el común de los mortales. Para no complicarnos, la tabla periódica de elementos existe porque los fermiones no pueden “ser iguales”: no pueden solaparse uno sobre otro y se repelen si los obligamos. Es lo que damos por hecho cuando hablamos de materia, que cada pedazo de ésta ocupa su lugar y tiene sus propias cualidades.
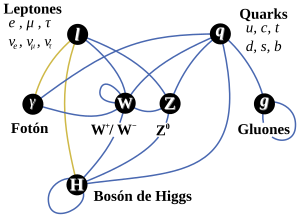
Toda la materia que conocemos, la que forma las estrellas y los mundos y las galaxias, esa que llamamos luminosa o bariónica, la que emite radiación, está hecha de Leptones y Quarks, partículas que son Fermiones, y, esas otras partículas intermediarias de las cuatro fuerzas fundamentales, son las que pertenecen a la familia de los Bosones, tales como el Fotón, las W+, W- y Zº, los Gluones y el Gravitón.

Los bosones carecen de este sentido de la individualidad que tienen los Fermiones, digamos que poseen “alma grupal” y, en su estado más puro, todos forman una misma “súperpartícula”.
Para entenderlo mejor, conviene recordar que las partículas no son bolitas como nos siguen enseñando en la escuela, sino que más allá de esta imagen existen como ondas o, al menos, sus funciones se equiparan al comportamiento de una onda.
En la década de 1920, Albert Einstein y el hindú Satyendra Nath Bose pronosticaron un quinto estado de la materia: el condensado de Bose-Einstein (BEC), el cual fue conseguido en laboratorio en 1995, algo que le valió el premio Nobel de 2001 a los científicos que lo lograron.
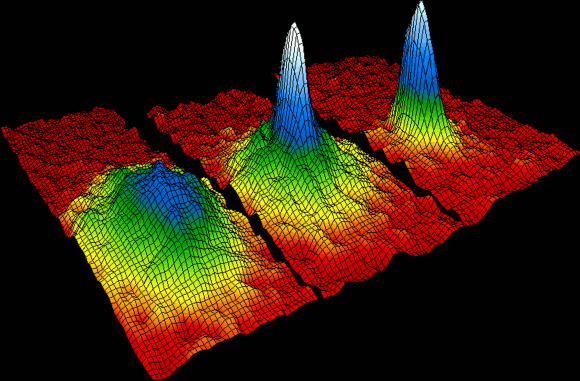
Un condensado de Bose-Einstein es un estado de la materia que se da en ciertos materiales a muy baja temperatura. En este estado de la materia, todos los átomos que lo constituyen se encuentran en el nivel de mínima energía, denominado estado fundamental. Descubierto en 1924 para los fotones por el indio Bose y por Einstein, no fue obtenido en laboratorio hasta 1995 por Cornell y Wieman al enfriar átomos a pocos nanokelvin por encima del cero absoluto. El condensado de Bose-Einstein fue la “molécula del año” según la revista Science en 1995 ya que se trata de un sistema cuántico macroscópico similar a una molécula pero con millones de átomos. Un átomo en un gas se mueve a una velocidad de unos unos 1000 km/h (unos 300 m/s) pero un condensado de Bose-Einstein se mueve a sólo 1 cm/s. Un condensado de Bose-Einstein es respecto a la materia ordinaria, como la luz de un láser es respecto a la de una bombilla. Gracias a ello se puede fabricar un láser de átomos, que en lugar de producir un haz de luz como un láser óptico, produce un haz (coherente) de átomos. En 1997 Ketterle fabricó el primer láser de átomos que producía un haz de átomos de sodio.

Cuando ciertas formas de materia [bosones] se enfrían hasta casi el cero absoluto, sus átomos se ponen en el estado de energía más baja, de modo que todos sus átomos vibran al unísono y se hacen coherentes. Las funciones de onda de todos los átomos se solapan, de manera que, en cierto sentido, un BEC [condensado de Bose-Einstein] es como un “superátomo” gigante en donde todos los átomos individuales vibran al unísono.
Al enfriar los átomos, su velocidad disminuye hasta que las longitudes de onda de cada uno de ellos se vuelven casi planas, superponiéndose unas a otras para formar una única onda que los describe a todos.

Así que un BEC se forma cuando los átomos en un gas sufren la transición de comportarse como “bolas de billar” al estilo de la física clásica, a comportarse como una onda gigante de materia al estilo de mecánica cuántica:
Si creamos dos BECs y los colocamos juntos, no se mezclan como gases ordinarios ni rebotan como lo harían dos sólidos. Donde los dos BECs se superponen, ellos “interfieren” como las ondas: delgadas capas paralelas de materia son separadas por capas delgadas de espacio vacío. El patrón se forma porque las dos ondas se suman donde sus crestas coinciden, y se cancelan donde una cresta se encuentra con un valle — a lo cual llamamos interferencia “constructiva” y “destructiva” respectivamente. El efecto es similar al de dos ondas que se superponen cuando dos piedras son lanzadas a un lago.
…ambientada en el vacío…
Y ahora, retrocedamos un poco más en este asunto del misterio que nos ocupa. Gracias a la tecnología láser, la física ha podido comprobar el extremo poder de la luz. Los láseres pueden hacer que las partículas virtuales se vuelvan reales. Pero, primero, aclaremos conceptos…
Las “Partículas virtuales”son partículas fundamentales que están constantemente surgiendo aparentemente de la nada y permanecen en el espacio-tiempo la friolera de una milésima de trillonésima de segundo –una cantidad que se forma poniendo una veintena de ceros a la derecha de la coma—. A pesar de denominarse “virtuales”, sus efectos son muy reales: la constante agitación de este burbujeo cuántico de partículas hace que el vacío tenga energía. Y esto es algo que afecta a la realidad, pues en ésta las fuerzas de atracción y repulsión dependen de la masa, y la masa no es sino energía expresada en unidades diferentes: E=mc².
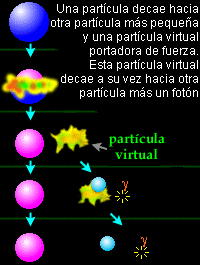
Partículas virtuales que surgen de la NADA. Claro que, surgieron,¡es porque había! La Nada no existe.!
En el uso corriente la palabra vacío significa espacio vacío, espacio del que se ha extraído todo el aire, vapor de agua u otro material. Eso es también lo que significa para un físico experimental que trabaja con tubos de vacío y bombas de vacío. Pero para un físico teórico, el término vacío tiene muchas más connotaciones. Significa una especie de fondo en el que tiene lugar el resto de la física. El vacío representa un potencial para todas las cosas que pueden suceder en ese fondo. Significa una lista de todas las partículas elementales tanto como de las constantes de la Naturaleza que se pondrían de manifiesto mediante experimentos en dicho vacío. En resumen, significa un ambiente en el que las leyes de la física toman una forma particular. Un vacío diferente significa leyes de la física diferentes; cada punto en el paisaje representa un conjunto de leyes que son, con toda probabilidad, muy diferentes de las nuestras pero que son, en cualquier caso, posibilidades consistentes. El modelo estándar es meramente un punto en el paisaje de posibilidades.

La energía del vacío es, por tanto, la suma total de las energías de todas las partículas posibles. Es la llamada “energía oscura” que hace que el universo se expanda, haciendo frente a la atracción de la gravedad, y que proporciona alrededor del 80% de la materia-energía al universo –un 26% es “materia oscura”, y sólo un 4% es la materia conocida hasta el momento—.
Pero, ¿cómo una partícula virtual se convierte en real? Es decir, ¿cómo queda “atrapada” en el espacio-tiempo de forma más estable?

¡Los fotones de Yang-Mills adquieren su masa y el principio gauge se sigue cumpliendo! Al principio esta visión no mereció la atención que merecía. Por una parte, la gente pensó que el modelo era feo. El principio gauge estaba ahí, pero ya no era el tema central. El “Campo de Higgs” había sido puesto ahí “a propósito” y la “partícula de Higgs”, en sí misma, no era una “partícula gauge”
La Teoría de la Sipersimetría establece que, por cada partícula de materia, nace una gemela de antimateria. La antimateria es igual que la materia, pero con carga opuesta. Por ejemplo, el electrón tiene carga negativa, y su partícula de antimateria, el positrón, positiva. Materia y antimateria se aniquilan mutuamente pero, por algún motivo aún no aclarado, la simetría se rompió en algún momento, surgiendo más materia que antimateria, de ahí que nuestro universo, materia, pueda existir.
Pero hay algo más en todo esto. Y para ello, la luz es la clave.

Controlar los estados cuánticos macroscópicos de osciladores micromecánicos no es fácil; hacerlo con luz (fotones) requiere el acoplamiento coherente entre …
Una de los modelos teóricos elaborados para superar la visión de la gravedad de Einstein indica que los fotones de los rayos gamma de alta energía viajarían algo más despacio que los de baja energía, lo que viola el axioma del sabio alemán acerca de que toda radiación electromagnética, desde las ondas radio hasta los rayos gamma, viajan en el vacío a la misma velocidad (la de la luz). Sin embargo, no ha sido verificado mediante experimento, con lo cual, Einstein sigue teniendo razón.
… protagonizada por la “luz” como la propia …
Ya en los años 30, los físicos predijeron que un campo eléctrico muy fuerte, que no es sino un espacio alterado por la actividad de un montón de fotones coordinados, podría impulsar a las partículas virtuales con carga opuesta en diferentes direcciones, impidiendo que la materia y la antimateria se aniquilen.

Según el efecto de creación de pares, un fotón con energía suficiente, lo que equivale a tener el doble de la energía que posee un electrón en reposo, da lugar a una pareja de electrón y positrón.
Aunque esto ya se consiguió en los años 90 a pequeña escala, gracias al desarrollo de la tecnología láser los científicos creen que estarán cerca de conseguir crear materia “en serie” mediante este proceso en unos pocos años.

Sabemos desde 1932, que un fotón gama con suficiente energía, puede formar un par de antipartículas, al interactuar con un átomo masivo, como el plomo. Pero el problema no termina, sino que, el electrón formado por un rayo gama, no interactúa con este tipo de fotón (gama), sino uno de luz visible,
Por otra parte, una vez que existen las partículas, los fotones interactúan sin cesar con ellas, siendo absorbidos y emitidos por las mismas de manera ininterrumpida.
Y de ello nace el movimiento gracias al cual todo existe en el espacio-tiempo. Sin movimiento, nuestra realidad desaparecería.
La carencia de masa de un fotón está ligada a su movimiento. Para que un cuerpo alcance la velocidad de la luz, su masa ha de ser cero. Y, como Einstein explicó en su día, la luz se mueve siempre a la velocidad de la luz. Si pretendemos que un fotónse pare, en lugar de ralentizarse observaremos que desaparece. Y, como se ha dicho al principio, si estos “fotones saltarines” desaparecieran, toda la materia dejaría de existir.
Su esencia es el movimiento y su misión, según parece, hacer girar la rueda de la existencia.
Ello es así debido al impacto de los fotones sobre las partículas elementales. La energía transmitida por un fotón es inversamente proporcional a su longitud de onda. Cuanto menos longitud de onda, más energía. Así, un fotón de luz visible tiene la energía suficiente para hacer reaccionar a un bastón de la retina. Si nos movemos en el espectro electromagnético, los fotones con longitud de onda ultravioleta pueden expulsar a los electrones de los átomos. Más allá, los rayos gamma pueden romper protones y neutrones…
Y ahora, vayamos al meollo de la cuestión e indaguemos en la cita con que se iniciaba este artículo: ¿qué hace que los electrones absorban y emitan fotones? Esto, en otros términos, vendría a ser lo mismo que preguntarnos: ¿por qué existe nuestro universo?
…con un misterio: el 137…
¿Qué determina el momento exacto en que un electrón emite un fotón? La física cuántica dice que nada lo hace, pues la Naturaleza es caprichosa en sus niveles más elementales. Aunque no es caótica en extremo, sólo probabilística.
A diferencia de la física newtoniana, la mecánica cuántica nunca predice el futuro en función del pasado. En su lugar, ofrece reglas muy precisas para computar la probabilidad de varios resultados alternativos de un experimento.
Y la probabilidad de que un electrón emita o absorba un fotón es la constante de estructura fina. El valor de esa constante es 1/137.

En otras palabras, sólo un afortunado electrón de cada 137 emite un fotón. Este es el significado de alfa: es la probabilidad de que un electrón, cuando se mueve a lo largo de su trayectoria, emita caprichosamente un fotón.
El inverso de la constante de estructura fina es 137. Desde su descubrimiento, éste número ha traído de cabeza a los grandes científicos.
No puedo recordar si fue Richard Feynman o León Lederman, quien sugirió que todos los físicos pusiesen un cartel en sus despachos o en sus casas que les recordara cuánto es lo que no sabemos. En el cartel no pondría nada más que esto: 137. Ciento treinta y siete es el inverso de algo que lleva el nombre de constante de estructura fina. Este número guarda relación con la probabilidad de que un electrón emita o absorba un fotón. La constante de estructura fina responde también al nombre de alfa, y sale de dividir el cuadrado de la carga del electrón por el producto de la velocidad de la luz y la constante de Planck. Tanta palabra no significa otra cosa sino que ese solo número, 137, encierra los meollos del electromagnetismo (el electrón), la relatividad (la velocidad de la luz) y la teoría cuántica (la constante de Planck). Menos perturbador sería que la relación entre todos estos importantes conceptos hubiera resultado ser un uno o un tres o quizás un múltiplo de pi. Pero ¿137?
![]()
… es un número que determina la fuerza de una interacción) y equivale a 1/137,03599911.
“Lo más notable de este notable número es su adimensionalidad. La velocidad de la luz es de unos 300.000 kilómetros por segundo. Abraham Lincoln medía 1,98 metros. La mayoría de los números vienen con dimensiones. Pero resulta que cuando uno combina las magnitudes que componen alfa, ¡se borran todas las unidades! El 137 está solo: se exhibe desnudo a donde va. Esto quiere decir que a los científicos de Marte, o a los del decimocuarto planeta de la estrella Sirio, aunque usen Dios sabe qué unidades para la carga y la velocidad y qué versión de la constante de Planck, también les saldrá 137. Es un número puro.”
(Leon Ledderman, La partícula divina)

Uno de los padres de la mecánica cuántica, Wolfgang Pauli, se obsesionó tanto con este número que dijo que, de poder hacerle una pregunta a Dios, sería esta: “¿Por qué 137?”
Gracias a su gran amistad con Carl G. Jung, Pauli conoció el mundo “alternativo” de los estudios sobre la psique y accedió a la tradición esotérica que ha acompañado al hombre desde el principio de los tiempos. Es así como supo que 137 se aproxima al valor correspondiente al ángulo áureo. Esto es, la versión circular del número áureo o φ (phi).

Sin fotones… ¡El Universo sería inestable, sería otro universo diferente!
En realidad, el ángulo de oro es, más o menos, 137,5º, y está presente en todo proceso natural donde se dé una combinación de espirales. Así, por ejemplo, las hojas de una planta surgen a lo largo del tallo cada 137,5º, pues así se logra la mayor eficiencia de espacio y de captación de la luz solar, ya que únicamente con éste ángulo es posible evitar que ninguna hoja obstaculice a las demás en la toma de luz sin que existan espacios muertos o vacíos.
Esta semejanza entre los valores de la constante de estructura fina y el ángulo áureo llevó a la doctora Raji Heyrovska a buscar el ángulo áureo en el universo atómico (véase versión en español de su estudio).
Que esto sea así no debería extrañarnos, pues si el número áureo es una constante en toda la Naturaleza, su versión angular es la apropiada para estar presente en el universo cuántico, donde, recordemos, los elementos básicos de la realidad se reducen a funciones de onda.
…y un final místico.
Los fotones no tienen masa ni carga eléctrica. Sin embargo, pueden “extraer” del vacío partículas con masa y carga, tanto negativa como positiva.
Más allá de la matería y la energía, del tiempo y del espacio, el concepto de función de onda nos introduce en una realidad abstracta de donde surge todo.Y si, como hemos dicho, a menor longitud de onda mayor energía, también es posible afirmar que, en eso que David Bohm llamaba “orden implicado”, cuanto menor es la longitud de una onda cuántica, mayor es la presencia de masa en el espacio-tiempo.
Para la física, las matemáticas se han mostrado como la realidad que subyace a la materia. Todo se puede reducir a números, entidades que forman y organizan el espacio-tiempo. En este nivel de realidad, ni la materia ni la energía existen como tales, sino que demuestran ser el resultado de la interacción de entidades abstractas.

En esta pasión por los números, no podemos evitar recordar la versión cabalística de la filosofía perenne. Para la Kabbalah, lo divino responde a la “Nada”, ya que lo trascendente no puede ser aprehendido desde nuestra posición en el mundo finito.
En el momento de la Creación, la luz infinita se habría divido, quedando encerrada en conductos que, al romperse, producen la materia y, en definitiva, la fractura de la unidad primordial de la luz.
Esta materia o qelippot, en el sentido de “conchas” o caparazones que “encierran” la luz y rompen la harmonía unitaria de la luz, es el origen del mundo, de su finitud y causa del mal en la realidad no-divina. El mundo creado es así una fractura de la harmonía de la luz que crea la diferenciación y la tensión entre unas cosas y otras: este es el origen del mal, de la falta de harmonía que debe recuperarse en el curso de la historia.

¡Qué a estas alturas de la vida, existan personas, que estén inmersos en estas patrañas! No lo entenderé munca
La Kabbalah enseña, según esto, el camino para desarrollar la Vasija interior donde recibir la Luz, la cual, según va llenando dicha vasija, nos acerca a la unidad del Espíritu. Es así que la Luz, al tiempo que “absorbida” por el alma, puede ser “proyectada” en el mundo mediante los actos del hombre trascendido.
Que la luz ha sido usada por todos los movimientos espirituales para referirse a lo divino es algo que a nadie se le escapa. La imagen que la Kabbalah ofrece aquí no es muy diferente de la que podríamos encontrar en textos rosacruces o en escritos orientales, entre otros.
Sin embargo, si esta vez he preferido usar el hermetismo hebreo es, como he mencionado, por su pasión hacia los números. Y es que el valor numérico para el término hebreo de “kabbalah” (cuya traducción es “recepción”) es…
como muchos ya sabrán…
Efectivamente…
137.

Ciencia y tradición hermética unidas por un número que, en ambas, define la interacción entre luz y materia.
Cosas…
Luz que, también en ambos casos, procede de la Nada.
Decía Jung que el espacio y el tiempo son conceptos hipostasiados, fenómenos que hemos decidido convertir en reales. La física teórica y la consolidación de la mecánica cuántica han dejado claro, a lo largo de las últimas décadas, que toda esta realidad por la que combatimos, matamos, morimos, odiamos, repudiamos, humillamos, codiciamos, envidiamos o ansiamos consiste, simplemente, en Nada.
Nada…

Una ilusión de la psique por la que renunciamos a indagar en el misterio de la Vida y nuestra experiencia momentánea en el espacio-tiempo se convierte en un vagar ausentes, asumiendo que todo es un sinsentido.
A veces, en momentos de bajón, me pregunto si no será por eso por lo que, casi cien años después, nos siguen diciendo que la física cuántica es muy complicada para que lleguemos a entenderla…
Lo más triste, sin embargo, es que lo aceptamos…
Todo esto lo he leido o aprendido de gente que son más sabias que yo, ideas que tienen sus fuentes en trabajos realizados con la misión y el propósito de desvelar los secretos de la Naturaleza para saber, como es el Universo.
Lo conseguiremos alguna ve?
emilio silvera
Jul
19
¡El Límite de las Teorías!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
Presentado en la XIX Edición del

Siempre andamos a vueltas con las teorías, y, tenemos que ser conscientes que las teorías tienen unos límites que están bien determinados. Veamos:
¿Cuáles son los límites de la teoría cuántica y de la teoría de la relatividad general de Einstein? Afortunadamente, hay una respuesta simple y las unidades de Planck nos dicen cuales son.

Y precisamente esta constante es el segundo motivo por el que no encuentras los muebles en una posición diferente cada vez que entras en el salón.
Supongamos que tomamos toda la masa del universo visible y determinamos su longitud de onda cuántica. Podemos preguntarnos en qué momento esta longitud de onda cuántica del universo visible superará su tamaño. La respuesta es: cuando el universo sea más pequeño en tamaño que la longitud de Planck, es decir, 10-33 centímetros, más joven que el tiempo de Planck 10ˉ⁴³ segundos y supere la temperatura de Planck de 1032 grados. Las unidades de Planck marcan la frontera de aplicación de nuestras teorías actuales. Para comprender en que se parece el mundo a una escala menor que la longitud de Planck tenemos que comprender plenamente cómo se entrelaza la incertidumbre cuántica con la gravedad. Para entender lo que podría haber sucedido cerca del suceso que estamos tentados a llamar el principio del universo, o el comienzo del tiempo, tenemos que penetrar la barrera de Planck. Las constantes de la naturaleza marcan las fronteras de nuestro conocimiento existente y nos dejan al descubierto los límites de nuestras teorías.
La Gravedad Cuántica, el eslabón perdido para comprender la evolución del Universo. Los físicos teóricos la han encontrado, ellos saben que dicha teoría subyace en la Teoría de Supercuerdas que, desgraciadamente, es inverificable… ¡Por el momento! Se cree que llegar hasta las cuerdas requeriría disponer de la energía de Planck (1019 GeV).

En los intentos más recientes de crear una teoría nueva para describir la naturaleza cuántica de la gravedad ha emergido un nuevo significado para las unidades naturales de Planck. Parece que el concepto al que llamamos “información” tiene un profundo significado en el universo. Estamos habituados a vivir en lo que llamamos “la edad de la información”.

La información puede ser empaquetada en formas electrónicas, enviadas rápidamente y recibidas con más facilidad que nunca antes. Nuestra evolución en el proceso rápido y barato de la información se suele mostrar en una forma que nos permite comprobar la predicción de Gordon Moore, el fundador de Intel, llamada ley de Moore, en la que, en 1.965, advirtió que el área de un transistor se dividía por dos aproximadamente cada 12 meses. En 1975 revisó su tiempo de reducción a la mitad hasta situarlo en 24 meses. Esta es “la ley de Moore” cada 24 meses se obtiene una circuiteria de ordenador aproximadamente el doble, que corre a velocidad doble, por el mismo precio, ya que, el coste integrado del circuito viene a ser el mismo, constante.

Representación gráfica de la obtención experimental de la constante de Planck
Los límites últimos que podemos esperar para el almacenamiento y los ritmos de procesamiento de la información están impuestos por las constantes de la naturaleza. En 1981, el físico israelí, Jacob Bekenstein, hizo una predicción inusual que estaba inspirada en su estudio de los agujeros negros. Calculó que hay una cantidad máxima de información que puede almacenarse dentro de cualquier volumen. Esto no debería sorprendernos. Lo que debería hacerlo es que el valor máximo está precisamente determinado por el área de la superficie que rodea al volumen, y no por el propio volumen. El número máximo de bits de información que puede almacenarse en un volumen viene dado precisamente por el cómputo de su área superficial en unidades de Planck. Supongamos que la región es esférica. Entonces su área superficial es precisamente proporcional al cuadrado de su radio, mientras que el área de Planck es proporcional a la longitud de Planck al cuadrado, 10-66 cm2. Esto es muchísimo mayor que cualquier capacidad de almacenamiento de información producida hasta ahora. Asimismo, hay un límite último sobre el ritmo de procesamiento de información que viene impuesto por las constantes de la naturaleza.

No debemos descartar la posibilidad de que seamos capaces de utilizar las unidades de Planck-Stoney para clasificar todo el abanico de estructuras que vemos en el universo, desde el mundo de las partículas elementales hasta las más grandes estructuras astronómicas. Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias. Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y mprotón.

En nuestro Universo todo es energía y el resultado de dos fuerzas contrapuestas que, al ser iguales en potencia, equilibran el todo y hace posible la estabilidad que podemos contemplar en las estrellas y en los átomos.
| α = 2πe2 / hc ≈ 1/137 |
| αG = (Gmp2)2 / hc ≈ 10-38 |
La identificación de constantes adimensionales de la naturaleza como a (alfa) y aG, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro. Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala. La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.

Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck). Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.

Nunca nadie ha explicado el valor numérico de ninguna de las constantes de la naturaleza. ¿Recordáis el 137? Ese número puro, adimensional, que guarda los …
Cuando surgen comentarios de números puros y adimensionales, de manera automática aparece en mi mente el número 137. Ese número encierra más de lo que estamos preparados para comprender; me hace pensar y mi imaginación se desboca en múltiples ideas y teorías. Einstein era un campeón en esta clase de ejercicios mentales que él llamaba “libre invención de la mente”. El gran físico creía que no podríamos llegar a las verdades de la naturaleza sólo por la observación y la experimentación. Necesitamos crear conceptos, teorías y postulados de nuestra propia imaginación que posteriormente deben ser explorados para averiguar si existe algo de verdad en ellos.
Para poner un ejemplo de nuestra ignorancia poco tendríamos que buscar, tenemos a mano miles de millones.

Hablamos de portales cuánticos, fluctuaciones de vacío… Cuerdas y de Taquiones pero…
Un gran Físico nos decía:
“Todos los físicos del mundo, deberían tener un letrero en el lugar más visible de sus casas, para que al mirarlo, les recordara lo que no saben. En el cartel sólo pondría esto: 137. Ciento treinta y siete es el inverso de algo que lleva el nombre de constante de estructura fina”.
Este número guarda relación con la posibilidad de que un electrón emita un fotón o lo absorba. La constante de estructura fina responde también al nombre de “alfa” y sale de dividir el cuadrado de la carga del electrón, por el producto de la velocidad de la luz y la constante de Planck. Tanta palabrería y numerología no significan otra cosa sino que ese solo numero, 137, encierra los misterios del electromagnetismo (el electrón, e–), la relatividad (la velocidad de la luz, c), y la teoría cuántica (la constante de Planck, h).
¡Sabemos aun tan poco!
emilio silvera
Jul
14
Partículas, anti-partículas, fuerzas…
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
Bajo la “definición basada en quarks y leptones”, las partículas elementales y compuestas formadas de quarks (en púrpura) y leptones (en verde) serían la “materia”; mientras los bosones “izquierda” (en rojo) no serían materia. Sin embargo, la energía de interacción inherente a partículas compuestas (por ejemplo, gluones, que implica a los neutrones y los protones) contribuye a la masa de la materia ordinaria.

Esquema de una aniquilación electrón-positrón.
Ya hemos descrito en trabajos anteriores las dos familias de partículas elementales: Quarks y Leptones. Pero hasta ahí, no se limita la sociedad del “universo” infinitesimal. Existen además las anti-familias. A quarks y electrones se asocian, por ejemplo, anti-quarks y anti-electrones. A cada partícula, una anti-partícula.
Uno de los primeros éxitos de la teoría relativista del campo cuántico fue la predicción de las anti-partículas: nuevos cuantos que eran la imagen especular de las partículas ordinarias. Las anti-partículas tienen la misma masa y el mismo spin que sus compañeras las partículas ordinarias, pero cargas inversas. La anti-partícula del electrón es el positrón, y tiene, por tanto, carga eléctrica opuesta a la del electrón. Si electrones y positrones se colocan juntos, se aniquilan, liberando la energía inmensa de su masa según la equivalencia masa-energía einsteniana.

¿Cómo predijeron los físicos la existencia de anti-partículas? Bueno, por la «interpretación estadística» implicaba que la intensidad de un campo determinaba la probabilidad de hallar sus partículas correspondientes. Así pues, podemos imaginar un campo en un punto del espacio describiendo la creación o aniquilación de sus partículas cuánticas con una probabilidad concreta. Si esta descripción matemática de la creación y aniquilación de partículas cuánticas se inserta en el marco de la teoría relativista del campo cuántico, no podemos contar con la posibilidad de crear una partícula cuántica sin tener también la de crear un nuevo género de partícula: su anti-partícula. La existencia de anti-materia es imprescindible para una descripción matemáticamente coherente del proceso de creación y aniquilación según la teoría de la relatividad y la teoría cuántica.

La misteriosa sustancia conocida como “materia oscura” puede ser en realidad una ilusión, creada por la interacción gravitacional entre partículas de corta vida de materia y anti-materia. Un mar hirviente de partículas en el espacio puede crear la gravedad repulsiva.
Puede ser posible que las cargas gravitacionales en el vacío cuántico podrían proporcionar una alternativa a la “materia oscura”. La idea se basa en la hipótesis de que las partículas y anti-partículas tienen cargas gravitacionales de signo opuesto. Como consecuencia, los pares de partícula-anti-partícula virtuales en el vacío cuántico y sus dipolos de forma gravitacional (una carga gravitacional positivos y negativos) pueden interactuar con la materia bariónica para producir fenómenos que se suele atribuir a la materia oscura. Fue el físico del CERN, Dragan Slavkov Hajdukovic, quien propuso la idea, y demostró matemáticamente que estos dipolos gravitacionales podrían explicar las curvas de rotación de las galaxias observadas sin la materia oscura en su estudio inicial. Sin embargo, señaló que quedaba mucho por hacer.
Pero sigamos con la cuántica…

El pionero en comprender que era necesario que existiesen anti-partículas fue el físico teórico Paul Dirac, que hizo varías aportaciones importantes a la nueva teoría cuántica. Fue él quien formuló la ecuación relativista que lleva hoy su nombre, y a la que obedece el campo electrónico; constituye un descubrimiento comparable al de las ecuaciones del campo electromagnético de Maxwell. Cuando resolvió su ecuación, Dirac se encontró con que además de describir el electrón tenía soluciones adicionales que describían otra partícula con una carga eléctrica opuesta a la del electrón. ¿Qué significaría aquello? En la época en que Dirac hizo esta observación, no se conocían más partículas con esta propiedad que el protón. Dirac, que no deseaba que las partículas conocidas proliferasen, decidió que las soluciones adicionales de su ecuación describían el protón.
Pero, tras un análisis más meticuloso, se hizo evidente que las partículas que describían las soluciones adicionales tenían que tener exactamente la misma masa que el electrón. Quedaba así descartado el protón, cuya masa es por lo menos, 1.800 veces mayor que la del electrón. Por tanto, las soluciones adicionales tenían que corresponder a una partícula completamente nueva de la misma masa que el electrón, pero de carga opuesta: ¡El anti-electrón! Esto quedó confirmado a nivel experimental en 1932 cuando Carl Anderson, físico del Instituto de Tecnología de Calífornia, detectó realmente el anti-electrón, que hoy se llama positrón.

Antes de empezar, debemos recordar que el Premio Nobel de Física de 1936 se repartió a partes iguales entre Victor Franz Hess y Carl David Anderson. Merece la pena leer la Nobel Lecture de Carl D. Anderson, “The production and properties of positrons,” December 12, 1936, quien nos explica que en esta imagen un “electrón” de 63 MeV atraviesa un placa de plomo de 6 mm y emerge con una energía de 23 MeV, pero lo hace con la curvatura “equivocada” como si fuera una partícula de carga positiva, como si fuera un protón pero con la masa de un electrón. La Nobel Lecture muestra muchas otras fotografías de positrones y electrones. Anderson afirma: “The present electron theory of Dirac provides a means of describing many of the phenomena governing the production and annihilation of positrons.”
Por otro lado, el Premio Nobel de Física de 1933 se repartió a partes iguales entre Erwin Schrödinger y Paul Adrien Maurice Dirac. También vale la pena leer la Nobel Lecture de Paul A. M. Dirac, “Theory of electrons and positrons,” December 12, 1933, aunque no cuente la historia de su descubrimiento, afirma que su ecuación predice el “antielectrón” de soslayo: ”There is one other feature of these equations which I should now like to discuss, a feature which led to the prediction of the positron.” (fuente: Francis (th)E mule Science’s News).


La aparición de las antipartículas cambió definitivamente el modo de pensar de los físicos respecto a la materia. Hasta entonces, se consideraba la materia permanente e inmutable. Podían alterarse las moléculas, podían desintegrarse los átomos en procesos radiactivos, pero los cuántos fundamentales se consideraban invariables. Sin embargo, tras el descubrimiento de la antimateria realizado por Paul Dirac hubo que abandonar tal criterio. Heisenberg lo expresaba así:
“Creo que el hecho de que Dirac haya descubierto partículas y antipartículas, ha cambiado toda nuestra visión de la física atómica… creo que, hasta entonces, todos los físicos habían concebido las partículas elementales siguiendo los criterios de la filosofía de Demócrito, es decir, considerando esas partículas elementales como unidades inalterables que se hallan en la naturaleza como algo dado y son siempre lo mismo, jamás cambian, jamás pueden transmutarse en otra cosa. No son sistemas dinámicos, simplemente existen en sí mismas. Tras el descubrimiento de Dirac, todo parecía distinto, porque uno podía preguntar: ¿por qué un protón no podría ser a veces un protón más un par electrón-positrón, etc.?… En consecuencia, el problema de la división de la materia había adquirido una dimensión distinta.”
Dado que la anti-materia tiene la misma masa que la materia, es decir son de la misma magnitud y signo (la definición de masa es positiva siempre), el efecto gravitacional de la anti-materia no debe ser distinto de la materia, es decir, siempre sera un efecto atractivo. Pero, ¿acaso no importa la equivalencia establecida de anti-partícula viajando al futuro = partícula viajando al pasado?

Existe un “universo” que se nos escapa de la comprensión
La respuesta es sí. Dicha equivalencia proviene de algo llamado simetría CPT (Charge-Parity-Time), y nos dice que la equivalencia entre las partículas y anti-partículas no solo corresponde a realizar una transformación sobre la carga, sino también sobre la paridad y el tiempo. La carga no afecta la gravedad, pero la paridad y el tiempo si la afectan. En otras palabras, al modificarse el tiempo (poner el tiempo al reves) y el espacio (la paridad es “girar” el espacio), estamos alterando el espacio-tiempo, y como la teoría general de la relatividad lo afirma, es la geometría de este el que determina la gravedad.
El carácter mutable de la materia se convirtió en piedra angular de la nueva física de partículas. El hecho de que partículas y anti-partículas puedan crearse juntas a partir del vacío si se aporta energía suficiente, no sólo es importante para entender cómo se crean las partículas en aceleradores de alta energía, sino también para entender los procesos cuánticos que se produjeron en el Big Bang.
Como ya lo hemos expresado, el conocimiento que se obtuvo sobre la existencia de antifamilias de partículas o familias de anti-partículas es una consecuencia de la aplicación de la teoría relativista del campo cuántico, para cada partícula existe una partícula que tiene la misma masa pero cuya carga eléctrica (y otras llamadas cargas internas) son de signo opuesto. Estas son las anti-partículas. Así, al conocido electrón, con carga negativa, le corresponde un «electrón positivo» como anti-partícula, llamado positrón, descubierto en 1932. El anti-protón, descubierto en 1956, tiene la misma masa que el protón, pero carga eléctrica negativa de igual valor. El fotón, que no tiene masa ni carga eléctrica, puede ser considerada su propia anti-partícula.
Un agujero negro es un objeto que tiene tres propiedades: masa, espin y carga eléctrica. La forma del material en un agujero negro no se conoce, en parte porque está oculta para el universo externo, y en parte porque, en teoría, el material continuaría colapsando hasta tener radio cero, punto conocido como Singularidad, de densidad infinita.
Un agujero negro tiene tres propiedades: masa, espín y carga eléctrica. La forma del material de un agujero negro no se conoce, en parte porque está oculta para el universo externo, y en parte porque, en teoría, el material continuaría colapsando hasta tener radio cero, punto conocido como singularidad, de densidad infinita.

La luz (fotones), no son una onda distinta que un electrón o protón, etc.

1°- “No se dispersan”, no son más pequeñas, como las ondas del agua (olitas) cuando tiramos una piedrita, a medida que se alejan de su centro; sino que en el caso de la luz son menos partículas, pero son siempre el mismo tipo de onda (determinada frecuencia), igual tamaño.
2°- Las ondas con más energía son más grandes, los fotones al igual que las partículas son más pequeñas, contra toda lógica (contracción de Lorentz).
3°- No necesitan de un medio material para desplazarse. Viajan en el vacío. El medio que usan para viajar, es el mismísimo espacio.
4°- Su cualidad de onda no es diferente de las partículas. Lo podemos ver en la creación de pares y la cualidad de onda de las partículas, etc. En ningún momento la partícula, es una cosa compacta (ni una pelotita), siempre es una onda, que no se expande. En la comparación con la ola, sería como un “montón” o un “pozo” de agua, con una dirección, lo que conocemos como ecuación de Schrödinger. En ningún momento la partícula, es una pelotita; la ola sobre el agua, no es un cuerpo que se mueve sobre el agua, no es un montón de agua que viene (aunque parece), sino una deformación del agua. Así la partícula, no es un montón de algo, sino una deformación del espacio.

La curvatura está relacionadas con la probabilidad de presencia, no es una bolita que está en uno de esos puntos, sino que es una onda en esa posición. El fotón es una onda que no necesita de un medio material para propagarse, se propaga por el espacio vacío. Así como una onda de sonido es una contracción-expansión del medio en que se propaga, el fotón es una contracción-expansión del espacio (del mismísimo espacio), razón por la cual entendemos que el espacio se curva, se contrae y expande. La rigidez del medio, da la velocidad de la deformación (velocidad de la onda), en el caso de la rigidez del espacio da una velocidad “c”.Esta onda por causa de la contracción del tiempo (velocidad “c”), no se expande, sino que se mantiene como en su origen (para el observador ), como si fuese una “burbuja”, expandida o contraída, en cada parte, positiva-negativa
Cada partícula está caracterizada por un cierto número de parámetros que tienen valores bien definidos: su masa, carga eléctrica, spin o rotación interna y otros números, conocidos como cuánticos. Estos parámetros son tales que, en una reacción, su suma se mantiene y sirve para predecir el resultado. Se dice que hay conservación de los números cuánticos de las partículas. Así, son importantes el número bariónico, los diversos números leptónicos y ciertos números definidos para los quarks, como la extrañeza, color, etc. Estos últimos y sus antipartículas tienen cargas eléctricas (± 1/3 o ± 2/3) y números bariónicos (±1/3) fraccionarios. No todos los números asociados a cada partícula han sido medidos con suficiente precisión y no todas las partículas han sido detectadas en forma aislada, por lo menos de su ligamento, como el caso deloquarksy de los gluones.

Los gluones son una especie de «partículas mensajeras» que mantienen unidos a los quarks. Su nombre proviene del término inglés “glue”, que significa pegamento, en español quizás podría ser gomón. Ahora, en cuanto a los quarks, ya hicimos referencia de ellos anteriormente. Pero recordemos aquí, que fueron descubiertos en 1964 por Murray Gell-Mann, como los componentes más reducidos de la materia. Hasta entonces se pensaba que los átomos consistían simplemente en electrones rodeando un núcleo formado por protones y electrones.
En estado natural, quarks y gluones no tienen libertad. Pero si se eleva la temperatura a niveles 100.000 veces superiores, como se ha hecho en aceleradores de partículas, a la del centro del Sol, se produce el fenómeno del deconfinamiento y por un brevísimo tiempo quedan libres. En ese preciso momento aparece lo que se suele llamar plasma, «una sopa de quarks y gluones» que equivale al estado en que se podría haber encontrado la naturaleza apenas una milésima de segundo luego del Big Bang.
Recientemente se ha descubierto un nuevo estado de la materia, esta vez a niveles muy altos de energía, que los científicos han denominado Plasma Gluón-Quark. La transición ocurre a temperaturas alrededor de cien mil millones de grados y consiste en que se rompen las fuertes ligaduras que mantienen unidos los quarks dentro de los núcleos atómicos. Los protones y neutrones están formados, cada uno, por 3 quarks que se mantienen unidos gracias a los gluones (El gluón es la partícula portadora de interacción nuclear fuerte, fuerza que mantiene unida los núcleos atómicos). A temperaturas superiores se vence la fuerza nuclear fuerte y los protones y neutrones se dividen, formando esta sopa denominada plasma Gluón-Quark.

Pero por ahora aquí, nos vamos a quedar con los quarks al natural. Normalmente, los quarks no se encuentra en un estado separados, sino que en grupos de dos o tres. Asimismo, la duración de las vidas medias de las partículas, antes de decaer en otras, es muy variable (ver tablas).
Por otra parte, las partículas presentan una o más de las siguientes interacciones o fuerzas fundamentales entre ellas. Por un lado se tiene la gravitación y el electromagnetismo, conocidas de la vida cotidiana. Hay otras dos fuerzas, menos familiares, que son de tipo nuclear y se conocen como interacciones fuertes y débiles.
La gravitación afecta a todas las partículas, es una interacción universal. Todo cuerpo que tiene masa o energía está sometido a esta fuerza. Aunque es la más débil de las interacciones, como las masas son siempre positivas y su alcance es infinito, su efecto es acumulativo. Por ello, la gravitación es la fuerza más importante en cosmología.

Los campos magnéticos están presentes por todo el Universo
La fuerza electromagnética se manifiesta entre partículas con cargas eléctricas. A diferencia de las demás, puede ser de atracción (entre cargas de signos opuestos) o de repulsión (cargas iguales). Esta fuerza es responsable de la cohesión del átomo y las moléculas. Mantiene los objetos cotidianos como entidades con forma propia. Un vaso, una piedra, un auto, el cuerpo humano. Es mucho más fuerte que la gravitación y aunque es de alcance infinito, las cargas de distinto signo se compensan y sus efectos no operan a grandes distancias. Dependiendo de las circunstancias en que actúen, estas interacciones pueden manifestarse como fuerzas eléctricas o magnéticas solamente, o como una mezcla de ambos tipos.
La Fuerza Nuclear Débil: otra fuerza nuclear, considerada mucho más débil que la Fuerza Nuclear Fuerte. El fenómeno de decaimiento aleatorio de la población de las partículas subatómicas (la radioactividad) era difícil de explicar hasta que el concepto de esta fuerza nuclear adicional fue introducido.
La interacción nuclear débil es causa de la radioactividad natural y la desintegración del neutrón. Tiene un rol capital en las reacciones de fusión del hidrógeno y otros elementos en el centro de las estrellas y del Sol. La intensidad es débil comparada con las fuerzas eléctricas y las interacciones fuertes. Su alcance es muy pequeño, sólo del orden de 10-15 cm.
La interacción fuerte es responsable de la cohesión de los núcleos atómicos. Tiene la intensidad más elevada de todas ellas, pero es también de corto alcance: del orden de 10-13 cm. Es posible caracterizar las intensidades de las interacciones por un número de acoplamiento a, sin dimensión, lo que permite compararlas directamente:
Fuerte as = 15
Electromagnéticas a = 7,3 x 10-3
Débil aw 3,1 x 10-12
Gravitacional aG = 5,9 x 10-39
Por otro lado, la mecánica cuántica considera que la interacción de dos partículas se realiza por el intercambio de otras llamadas «virtuales». Tienen ese nombre porque no son observables: existen por un tiempo brevísimo, tanto más corto cuanto mayor sea su masa, siempre que no se viole el principio de incertidumbre de Heisenberg de la teoría cuántica (que en este contexto dice que el producto de la incertidumbre de la energía por el tiempo de vida debe ser igual o mayor que una constante muy pequeña). Desaparecen antes de que haya tiempo para que su interacción con otras partículas delate su existencia.
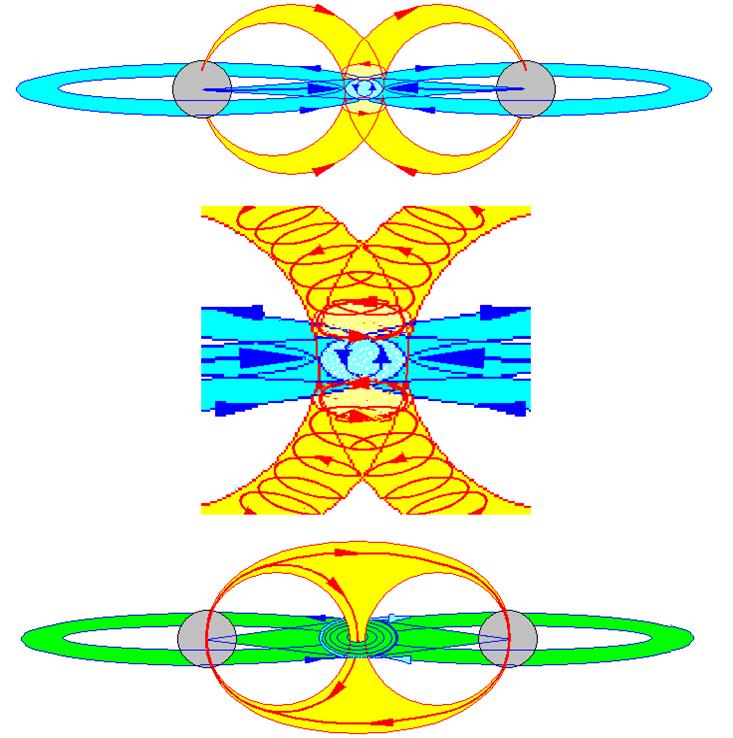
El fotón virtual común se desplaza hacia la partícula menos energética.
Dos partículas interactúan al emitir una de ellas una partícula virtual que es absorbida por la otra. Su emisión y absorción cambia el estado de movimiento de las originales: están en interacción. Mientras menos masa tiene la partícula virtual, más lejos llega, mayor es el rango de la interacción. El alcance de la interacción es inversamente proporcional a la masa de la partícula portadora o intermedia. Por ejemplo, la partícula portadora de la fuerza electromagnética es el fotón, de masa nula y, por lo tanto, alcance infinito. La interacción gravitacional también tiene alcance infinito y debe corresponder a una partícula de masa nula: se le denomina gravitón. Naturalmente tiene que ser neutro. (Aún no ha sido vistos ni en pelea de perros).
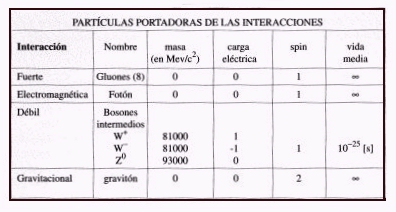
Como ya hicimos mención de ello, a las fuerzas nucleares se les asocian también partículas portadoras. Para la interacción débil estas partículas se llaman bosones intermedios, expresados como W+, W- y Zº (neutro). El W- es antipartícula del W+. Los W tienen masas elevadas comparadas con las otras partículas elementales. Lo de bosones les viene porque tienen spin entero, como el fotón y el gravitón, que también los son, pero que tienen masas nulas. Las fuerzas fuertes son mediadas por unas partículas conocidas como gluones, de los cuales habría ocho. Sin embargo, ellos no tienen masa, pero tienen algunas de las propiedades de los quarks, que les permiten interactuar entre ellos mismos. Hasta ahora no se han observado gluones propiamente tal, ya que lo que mencionamos en párrafos anteriores corresponde a un estado de la materia a la que llamamos plasma. Claro está, que es posible que un tiempo más se puedan detectar gluones libres cuando se logre aumentar, aún más, la temperatura, como está previsto hacerlo en el acelerador bautizado como “Relativistic Heavy Ion Collider”, empotrado en Estados Unidos de Norteamérica.
TABLA DE LAS PRINCIPALES PROPIEDADES DE LAS PARTÍCULAS PORTADORAS DE LAS INTERACCIONES FUNDAMENTALES
Una partícula y su anti-partícula no pueden coexistir si están suficientemente cerca como para interactuar. Si ello ocurre, ellas se destruyen mutuamente: hay aniquilación de las partículas. El resultado es radiación electromagnética de alta energía, formada por fotones gamma. Así, si un electrón está cercano a un positrón se aniquilan en rayos gamma. Igual con un par protón-anti-protón muy próximos.
La reacción inversa también se presenta. Se llama «materialización o creación de partículas» de un par partícula-antipartícula a partir de fotones, pero se requieren condiciones físicas rigurosas. Es necesario que se creen pares partícula-antipartícula y que los fotones tengan una energía mayor que las masas en reposo de la partículas creadas. Por esta razón, se requieren fotones de muy alta energía, de acuerdo a la relación de Einstein E=mc2 . Para dar nacimiento a electrones/positrones es necesario un campo de radiación de temperaturas mayores a 7×109 °K. Para hacer lo mismo con pares protón/anti-protón es necesario que ellas sean superiores a 2×1012 °K. Temperaturas de este tipo se producen en los primeros instantes del universo.

Se detectan grandes emisiones de rayos gamma en explosiones supernovas y otros objetos energéticos
Los rayos gamma están presentes en explosiones de supernovas, colisión de estrellas de neutrones… Todos los sucesos de altas energías los hace presente para que nuestros ingenios los detecten y podamos conocer lo que la materia esconde en lo más profundo de sus “entrañas”. Aún no hemos podido conocer en profundidad la materia ni sabemos, tampoco, lo que realmente es la luz.
emilio silvera
Jul
11
¿La Conservación de la Energía? No siempre es así
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
En un universo en expansión, la energía no se conserva
La matemática Emmy Noether demostró, a principios del siglo XX, que la conservación de la energía solo se cumple si las leyes de la Física que empleamos son independientes del tiempo

Fräulein Noether fue el genio matemático más creativo e importante desde que comenzó la educación superior de las mujeres. WIKIPEDIA
Invierno de 1915, Göttingen (Alemania), la Primera Gran Guerra asola Europa, arrasando ciudades, cortando centenarias rutas de suministros y generando un odio inconcebible hasta el momento. Entre todo el caos y destrucción imperante, alguien permanece ajeno a la situación que le rodea. Su mente divaga en torno a las extrañas ecuaciones garabateadas sobre un sinfín de papeles dispersos. Emmy Noether, sentada ante su escritorio de roble, se frota los ojos, atónita ante su reciente descubrimiento. Los últimos meses los ha dedicado de manera incansable a desarrollar el simple y elegante resultado que tiene ante sí.

La respuesta ante luz incidente polarizada de los dos estados superconductores es diferente si se viola la simetría de inversión temporal.
Ella acaba de demostrar que, si existe una simetría en las leyes físicas que gobiernan un determinado sistema, hay una cantidad que se conserva. No se trata de una conclusión irrelevante, y ella es consciente de ello. Físicos, químicos e ingenieros hacen uso diariamente de cantidades conservadas para realizar cualquiera de sus cálculos. Por ejemplo, para determinar si un proyectil alcanzará a un enemigo situado a una cierta distancia, solo es necesario calcular la energía liberada por la pólvora en combustión. Esta energía se transferirá al proyectil y, usando las ecuaciones de Newton, es posible calcular exactamente si la bala alcanzará el objetivo. Noether acababa de demostrar por tanto que, para saber si se conservará la energía de un sistema (como el sistema pólvora-bala), tan solo es necesario atender a la simetría de las ecuaciones que describen dicho sistema. En concreto, la conservación de la energía solo necesita de la simetría temporal de las ecuaciones, es decir, que éstas se cumplan tanto ahora como dentro de 1.000 años u otros tantos años atrás.
La uniformidad del tiempo
Noether demostró que, para saber si se conservará la energía de un sistema, tan solo es necesario atender a la simetría de las ecuaciones que describen dicho sistema.

Prácticamente en ese mismo momento, solo tres años mayor que ella, un treintañero llamado Albert Einstein repasaba asombrado las ecuaciones maestras de su teoría de la Relatividad General. Sorprende comprobar cómo en los momentos más oscuros de la humanidad afloran las mentes más brillantes. Cimentaba así una nueva forma de mirar al Universo, insólita hasta entonces, ya que el espacio y el tiempo se entrelazaban de manera inseparable con la materia, poniendo punto final a las inconsistencias que habían comenzado a aparecer en la física desarrollada durante el último siglo. Consecuencia de su abstracta teoría son fenómenos tan sorprendentes como el de la expansión del Universo (obtenida gracias a Lemaître, Friedmann, Robertson y Walker), que predice que el propio espacio se estira como un globo hinchándose, provocando que las galaxias se alejen unas de otras, algo que se observaría con precisión en 1922.

Muchos años después, los científicos serían capaces de fusionar ambas teorías, proponiendo un resultado que muchos de nosotros aún tratamos de comprender y de explorar. Si el Universo se expande, las ecuaciones que lo controlan pierden su simetría temporal, ya que las distancias entre objetos aumentan en el tiempo y nos veríamos obligados a reescalarlas. De una manera directa, podemos concluir que la energía en el universo NO se conserva. Debemos por tanto despedirnos de esa frase que tantas veces nos repitieron desde niños: “La energía ni se crea ni se destruye, solo se transforma”. Demos la bienvenida a una nueva versión de la misma: “La energía se crea y se destruye y, a veces, se conserva”.

Sorprende comprobar cómo en los momentos más oscuros de la humanidad afloran las mentes más brillantes
No obstante, esta última afirmación la tenemos que repetir con cautela, ya que lo técnicamente correcto es decir que la energía de la materia del Universo no se conserva. Esto es debido a que en el Universo no hay únicamente materia, sino materia y espacio-tiempo. Las ecuaciones de Einstein contienen otras simetrías que conllevan conservaciones de cantidades que se parecen a la energía, pero contienen términos extra. Estos términos pueden asociarse a la energía propia del espacio-tiempo, pero dista de proporcionar una interpretación clara, ya que conduce a preguntas que no somos capaces de contestar aún, tales como: ¿cómo medimos esta energía? ¿de qué tipo es? ¿podemos usarla para, por ejemplo, viajes espaciales?

Mayo, 1935. Estados Unidos. Albores de la Segunda Guerra Mundial, Emmy Noether muere tras ser expulsada en 1933 de su puesto de trabajo en la Universidad de Göttingen y obligada a abandonar el país por un nazismo que no veía con buenos ojos su ascendencia judía. Albert Einstein, temiendo que la muerte de la mejor matemática del siglo XX pasara inadvertida para el mundo, escribe las siguientes palabras en el New York Times:
La energía se crea y se destruye y, a veces, se conserva”
“[…] En el transcurso de los últimos días, la distinguida matemática Emmy Noether, anteriormente de la Universidad de Göttingen y durante los dos últimos años vinculada a la Universidad de Bryn Mawr, ha fallecido a los 53 años. A juicio de los matemáticos vivos más competentes, Fräulein Noether fue el genio matemático más creativo e importante desde que comenzó la educación superior de las mujeres. En el campo del álgebra […] descubrió métodos de enorme relevancia para el desarrollo de actuales generaciones de matemáticos más jóvenes. La Matemática pura es, a su modo, la poesía de las ideas lógicas. Uno busca las ideas más generales con las que formar de una manera simple, lógica y unificada, el círculo más grande posible de las relaciones formales. En este esfuerzo hacia la belleza lógica, se descubren fórmulas espirituales necesarias para una penetración más profunda en las leyes de la Naturaleza.[…]”
Fuente: El Pais.
Marcos Pellejero Ibáñez es estudiante de doctorado en el Instituto de Astrofísica de Canarias (IAC). Se licenció en la Universidad de Zaragoza y ha estudiado posteriormente en el Imperial College de Londres teorías alternativas al modelo estándar cosmológico. El tema de su tesis es la estructura de las más grandes escalas cósmicas.
Rafael Tapia Rojo es investigador postdoctoral en la Universidad de Columbia, NYC. Se licenció y doctoró en la Universidad de Zaragoza, estudiando métodos de energía libre para comprender modelos de biomoléculas. Actualmente trabaja en el estudio de las propiedades mecánicas de proteínas con técnicas de molécula individual y paisajes de energía libre.
Jul
7
La Física y el Tiempo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (3)
Comments (3)

Para el topólogo, un nudo es una curva continua, cerrada y sin puntos dobles. Esta curva está situada en un espacio de tres dimensiones y se admite que pueda ser deformada, estirada, comprimida, aunque está “prohibido” hacerle cortes. Cuando se puede, a través de diversas manipulaciones, se pasa de un nudo a otro y se dice que son equivalentes. Claro que, algunos se abstraen en cuestiones con otras, al parecer, no relacionadas.
Un viejo amigo bromeaba diciendo que el Andante en do menor de la Sinfonía Concertante de Mozart conseguía devolverle a su intimidad anímica de partida, y que por eso, en su opinión, plasmaba de forma inefable el tiempo cíclico, o mejor aún, una CTC (“curva de género de tiempo cerrada”). Y transcurridos los doce minutos que dura ese movimiento, volvíamos a escucharlo una vez más. Mientras, discutíamos sin cesar sobre el tiempo, esa abstracción de la Mente que nadie ha sabido explicar.

No es bueno perder la perspectiva
Hay un tiempo para cada cosa. Un tiempo para soñar, inconmensurable, un tiempo para vivir, siempre corto, un tiempo para filosofar, misterioso,…, y un tiempo para la ciencia, sujeto a número.
Me gustaría empezar definiendo el tiempo, pero no sé. Sesudos pensadores, como Platón y Aristóteles, lo ensayaron con brillantez. El tiempo es una imagen móvil de la eternidad. Esta imagen es eterna, pero se mueve según número, dirá Platón en el TIMEO. El tiempo es el número de movimiento según el antes y el después…El tiempo no es movimiento, sino movimiento en tanto en cuanto admite enumeración. El tiempo es una especie de número. El tiempo es obviamente aquello que se cuenta, no aquello con lo cual contamos, escribirá Aristóteles en su FÍSICA.

Alguna vez, en simbiosis con la Naturaleza, podemos sentir como se ha parado el tiempo
Son definiciones muy sugestivas, aunque teñidas de circularidad: movimiento en el tiempo, tiempo a través del movimiento. Agustín de Hipona vio esto claramente. Célebre es asimismo su declaración: Si nemo a me quaerat, scio; si quaerenti explicari velim, nescio (CONFESIONES). En uno de los análisis más penetrantes del tema, sugirió Agustín la Mente como fuente de tiempo: En ti es, mente mía, donde mido los tiempos.
Time is what happens when nothing else happens, afirma Feynman; para a continuación advertir que toda definición del tiempo es necesariamente circular, y que lo importante no es decir qué es el tiempo, sino decir cómo se mide lo que llamamos tiempo. En su enciclopédico tratado sobre la gravitación, Misner, Thorne y Wheeler nos recuerdan de forma sencilla y profunda lo que toda medida del tiempo físico debe cumplir: Time is defined so that motion looks simple.

El tiempo es un concepto inventado por el hombre para ordenar, primero, sus sensaciones y actos, y luego, los fenómenos. Decían los escolásticos: Tempus est ens rationis cum fundamento in re. La primera unidad natural debió ser el día, por la ciclidad conspicua de las salidas del Sol. Los grandes avances científicos y tecnológicos a lo largo de los siglos han estado vinculados a los adelantos en la precisión con que se ha ido midiendo el tiempo. Hoy disponemos de relojes que aseguran un segundo en 20 millones de años, y el paso de la femtoquímica a la attofísica empieza a ser una realidad.

No pocas veces nos podemos ver perdidos en la vorágina de lo que llamamos tiempo, algo tan enorme que, en realidad, no sabemos lo que es. No lo hemos llegado a comprender, y, por si fuera poco, tampoco sabemos, si en realidad existe.
El tiempo antes de Einstein.
La física nació en torno al tiempo. Las regularidades en los ciclos astrales permitieron al acierto en las predicciones apoyadas en esta periodicidad, y con ello despertó sin duda la confianza del hombre en la racionalidad, inclinándole a escoger el cosmos frente al cáos.
Breve historia de la medida del tiempo
La longitud de las sombras fue uno de los primeros métodos usados para fijar las horas. En el Museo Egipcio de Berlín hay un fragmento de piedra que posiblemente sea de un reloj de sol de alrededor de 1500 a.C. Los babilonios desarrollaron los relojes de sol, y se dice que el astrónomo Anaximandro de Mileto los introdujo en Grecia en el siglo VI a.C.
En el siglo II a C, Eratóstenes, de la biblioteca de Alejandría, concibió y llevó a cabo la primera medida de las dimensiones de la Tierra de la que se tiene noticia. En el Año Internacional de la Astronomía, una de las actividades que se llevaron a cabo fue, precisamente averiguar el radio terrestre por el mismo método.
Aparte de relojes de sol, en la antigüedad se usaron también relojes de arena, de agua, cirios y lámparas de aceite graduadas.

En la segunda mitad del siglo XIII aparecen los primeros relojes mecánicos. Su precisión era muy baja (10-20%). En el XIV se mejoran, con el invento del escape de rueda catalina, y ya se alcanzan precisiones de 20 a 30 minutos por día (1-2%). Por allá al año 1345 se empieza a dividir las horas en minutos y segundos.
El tiempo físico asoma en el siglo XIV, en el Merton College Oxford y luego en la Universidad de París, con Oresme. Se representa en una línea horizontal, mientras en vertical se disponen las cualidades variables. Son los primeros gráficos de función (en este caso, función del tiempo). La cinemática celeste brinda un buen reloj a través de la segunda ley de Kepler, midiendo tiempos mediante áreas. La ley armónica de Kepler permitirá medirlos a través de longitudes. Galileo desarrolló la cinemática terrestre, y sugirió el reloj de péndulo. A Huygens debemos la técnica de medida del tiempo que ha llegado a nuestros días, y que suministró relojes más precisos y transportables mediante volantes oscilatorios acoplados a resortes de calidad.

Diseño del reloj de péndulo de Huygens, 1656 (imagen de dominio público).
La importancia, no sólo científica sino económica, de disponer de relojes precisos y estables, queda reflejada en el premio ofrecido por el gobierno inglés de la reina Ana en 1714, que dispuso that a reward be settled by Parliament upon such person o persons as shall discover a more certain and practicable method of ascertainig longitude that any yet in practice. La recompensa era de 20, 000 libras para el que presentara un cronómetro capaz de determinar la longitud con error menor de 30´ de arco al término de un viaje a las Indias occidentales, equivalente a mantener el tiempo con error menor de 2 minutos tras seis semanas de viaje. Se la llevó casi medio siglo después el relojero británico John Harrison (1693-1776), con un reloj, conocido como H4, que incorporaba correcciones por variación en la temperatura, y que en un primer viaje de 81 días desde Porstmouth a Puerto Real (Jamaica) en 1761-62 se retrasó 5 s, esto es, de precisión 10⁻⁶ (10; 44).
Después se pasó a los de diapasón, de aquí a los de cuarzo, y hoy los atómicos ofrecen precisiones desde 10⁻¹² – 10⁻¹⁵ (Cs) hasta 10⁻¹⁶ (máser de H).
Una red de relojes atómicos de cesio, sincronizados mediante ondas de radio, velan actualmente por la exactitud de la hora sobre el planeta. Como señala Davies (10), ya no nos sirve como cronómetro el giro de la Tierra alrededor de su eje. Aunque durante siglos ha sido este viejo trompo un magnífico reloj de referencia, la falta de uniformidad de su giro (las mareas, por ejemplo, lo frenan incesantemente y alargan con ello el día en un par de milésimas de segundo por siglo, perceptible para los finos cronómetros actuales), y otras desviaciones estacionales, cuantitativamente similares a estos retrasos seculares, pero irregulares y de signo variable, son circunstancias que en conjunto obligan a añadir al tiempo civil un segundo intercalar cada uno o dos años (el último lo fue el 1 de enero de 1999, a las 0 horas) con el fin de remediar la asincronía entre los tiempos atómicos y los días astronómicos. El día no tiene 86 400 s justos (donde el segundo se define como la duración de 9 192 631 770 períodos de una determinada vibración de los átomos de Cs. Hoy la tecnología alcanza precisiones fabulosas: relojes que en treinta millones de años se desviarían a lo sumo en un diminuto segundo, como el NIST-F1 (Boulder, Colorado).
Por norma general y para mayor exactitud del sistema, dentro del campo visual de cualquier receptor GPS siempre hay por lo menos 8 satélites presentes. Cada uno de esos satélites mide 5 m de largo y pesa 860 kg . La energía eléctrica que requieren para su funcionamiento la adquieren a partir de dos paneles compuestos de celdas solares adosadas a sus costados. Están equipados con un transmisor de señales codificadas de alta frecuencia, un sistema de computación y un reloj atómico de cesio, tan exacto que solamente se atrasa un segundo cada 30 mil años.

La posición que ocupan los satélites en sus respectivas órbitas facilita que el receptor GPS reciba, de forma constante y simultánea, las señales de por lo menos 6 u 8 de ellos, independientemente del sitio donde nos encontremos situado. Mientras más señales capte el receptor GPS, más precisión tendrá para determinar las coordenadas donde se encuentra situado.
Incluso hay relojes de pulsera comerciales (receptores de señales de radio) con precisión de un segundo por millón de años garantizada por un reloj atómico en una lejana estación. La naturaleza de altísima precisión: la estabilidad del púlsar binario b1855+09 puede ser de unas partes en 10¹⁵ o incluso mejor.
El tiempo en Newton:
En los PRINCIPIA, Newton empieza con una renuncia a definir el tiempo: El tiempo, el espacio, el lugar y el movimiento son de todos bien conocidos. Y no los defino. Pero digo que el vulgo no concibe esas cantidades más que por su relación a cosas sensibles. Para evitar ciertos prejuicios que de aquí se originan, es conveniente distinguirlas en absolutas y relativas, verdaderas y aparentes, matemáticas y vulgares.
A continuación, sin embargo, Newton se arrepiente de su primer impulso y aclara: El tiempo absoluto, verdadero y matemático, de suyo y por su propia naturaleza fluye uniformemente sin relación a nada externo y se llama también duración: el tiempo relativo, aparente y vulgar es cualquier medida sensible y externa (exacta o no uniforme) de la duración por medio del movimiento y se usa vulgarmente en lugar del tiempo verdadero: tal como la hora, el día, el mes, el año.

Sabemos del fluir del tiempo por el cambio que se produce en nuestro Universo, en el Mundo, en Nuestras Vidas. Con el paso del Tiempo las cosas cambian y nada permanece. Por eso sabemos que está ahí
¿Qué significa que el tiempo fluye? ¿Qué el tiempo “se mueve en el tiempo”? De nuevo la pescadilla mordiéndose la cola. El absolutismo del tiempo newtoniano recibió encendidas críticas. Leibniz opuso su idea de espacio y tiempos puramente relativos, el primero como un orden de coexistencia, el segundo como un orden de sucesiones de las cosas; ambos, espacio y tiempo, son phœnomena bene fundata. Los argumentos dinámicos con que Newton arropa su tesis de la naturaleza absoluta de la rotación y con ello la de un espacio absoluto, apoyo posterior para el tiempo absoluto, también hallan fuertes objeciones. Para Berkeley esas razones de Newton lo único que muestran es la importancia del giro respecto de las masas lejanas del Universo y no respecto de un espacio absoluto, que él no acepta. Ernst Mach, en la segunda mitad del XIX, insistirá decididamente en este punto de vista, y desde su positivismo acosará los absolutos newtonianos. De “medieval”, “no científico”, “metafísico”, tilda Mach a Newton: No tenemos derecho a hablar de un tiempo “absoluto”: de un tiempo independiente de todo cambio. Tal tiempo absoluto no puede medirse por comparación con ningún movimiento; por tanto no tiene valor práctico ni científico, y nadie tiene derecho a decir que sabe algo de él. Es una concepción metafísica vana.

El tiempo en Einstein:
El tiempo newtoniano, absoluto, el nos es familiar, tuvo que dejar paso al tiempo einsteniano, mutable y relativo, con tantos “ahora” por suceso cuantos estados de movimiento mutuo imaginemos.
El tercero de los trabajo enviados por Albert Einstein (AE) en su Annus Mirabilis de 1905 a Annalen der Physik lleva por título “Zur Elektrodynamik Bewegter Körper” (“Sobre la electrodinámica de los cuerpos en movimiento”). Junto con el quinto, titulado “Ist der Trägheit eines Körpers von seinem Energieinhalt abhängig?” (“¿Depende la inercia de un cuerpo de su contenido de energía?”), constituyen lo que hoy se llama TEORÍA ESPECIAL DE LA RELATIVIDAD.

Velocidad de la luz desde la Tierra a la Luna, situada a más de 380.000 km.
Da Albert Einstein un par de razones para justificar su tercer trabajo:
- La insatisfacción que le produce la asimetría en la descripción maxwelliana de los fenómenos electromagnéticos: la acción entre un conductor y un imán depende solo del movimiento relativo entre ambos, pero la teoría de Maxwell distingue entre el caso de conductor en reposo y el caso de imán en reposo: a) En el primer caso el campo magnético móvil engendra un campo eléctrico, con una energía determinada, que a su vez produce corrientes en el conductor en reposo. b) En el segundo caso, no se produce ningún campo electrónico, sino una fuerza electromotriz en el conductor, sin energía asociada, que engendra una corriente como en el caso anterior.
- La incapacidad de la óptica y del electromagnetismo (EM) para detectar el movimiento respecto del lichtmedium, es decir, de un inercial privilegiado. Esto le sugiere que la óptica y el EM tienen las mismas ecuaciones en todos los inerciales (sistemas en los que las leyes de la mecánica de Newton son las mismas). Y AE eleva esto a un principio, que llama “Prinzip der Relativität”, y le añade un compañero, aparentemente incompatible con él: “La velocidad de la luz en vacío es siempre la misma, con independencia del estado de movimiento del cuerpo emisor”

¿Será ese de arriba el rayo de luz de Einstein, o, por el contrario, será un asteroide que se nos viene encima?
Siendo todavía muy joven, en 1895-1896, ya le preocupaba el EM y la luz, como recordaba en 1955: “Si persiguiéramos a la velocidad de la luz un rayo de luz, veríamos una onda independiente del tiempo. ¡Tal cosa, sin embargo, no existe! Este fue el primer experimento mental, infantil, en relación con la teoría especial de la relatividad”.
Este tercer trabajo de Einstein en 1905 no contiene ninguna referencia a otros trabajos, ni suyos ni de otros (como Lorentz o Poincaré).
Consciente de que su postulado de la constancia de la velocidad de la luz choca frontalmente con la ley galileana de adición de velocidades, Albert Einstein revisa los cimientos de la Física, empezando por definir físicamente y con sumo cuidado el concepto de Gleichzeitigkeit o simultaneidad entre sucesos. Considera un sistema inercial, para el que supone válida la geometría euclidiana para calcular distancias entre objetos estacionarios a través de sus coordenadas respecto de sus ejes cartesianos. Si A, B son dos observadores estacionarios, provistos de relojes iguales, y A (B) manda una señal luminosa a B (A), quien la devuelve sin tardanza a A (B), diremos que el reloj de A está sincronizado con el reloj de B si
t(B) – t(A) = t’(A) – t(B),
donde t(A) es el tiempo marcado por el reloj de A cuando envía la señal a B, t(B) lo que marca el reloj de B al llegarle la señal de A y reemitirla, y t’(A) la lectura del reloj de A al recibir la devolución de B.

No parece el mejor método para medir la velocidad de la luz, el empleado por Galileo. Claro que, en aquellos tiempos…¿Qué se podía hacer?
Supone Albert Einstein que esta definición no lleva a contradicciones, que es en principio posible entre cualquier par de observadores estacionarios en el inercial, y que la relación de sincronización anterior es de equivalencia: Si A está sincronizada con B, también B lo está con A, y si además B lo está con C, también A y C lo están. A esto le siguen ecuaciones que quiero obviar para no dar complejidad al trabajo.
No existe “el” presente
Pasa Albert Einstein a enunciar con precisión el principio de relatividad y el postulado de la constancia de la velocidad de la luz en el vacío:
- Las leyes que rigen los cambios de los sistemas físicos son las mismas en todos los inerciales.
- Todo rayo de luz se mueve en cualquier inercial con una misma velocidad, c, independientemente del movimiento de su fuente.
Como consecuencia, demuestra que el concepto de sincronía, y por ende de simultaneidad, es relativo, no absoluto. La noción de “presente”, “ahora” o cualquier instante determinado depende del referencial inercial.

Algunos incluso hablaron de energía taquiónica
¿Más rápido que la luz?
¿Existen partículas que se muevan con velocidad superior a la de la luz? Sí; por ejemplo, cualquier partícula que lleve en agua, a temperatura entre 0 y 50 ºC, una velocidad ν > c / n, n = 1.3, irá más deprisa en ese medio que los fotones del espectro visible. Lo mismo ocurre con la mayoría de los rayos cósmicos que llegan a la atmósfera; son superlumínicos en relación con la velocidad de la luz en el aire. Precisamente en esta posibilidad de rebasar la velocidad de la luz en un medio reside el efecto Cherenkov.

Lo que no se conocen son taquiones, o partículas que se muevan más deprisa que la luz en el vacío. Si existieran, podrían utilizarse para mandar información al pasado. Violando el orden causa-efecto. Por ello se “decreta” su inexistencia.
En fin, que la velocidad de la luz en el vacío, al menos que sepamos, es infranqueable. Es un límite impuesto por la Naturaleza al que habrá que vencer, no superándolo (que no se puede), sino mediante una artimaña física inteligente que logre burlar dicho límite.
Aparte de algún que otro añadido, el artículo (parcialmente expuesto aquí -se obviaron partes complejas), es del Físico de la Universidad Complutense D. Alberto Galindo Tixaire. Fue publicado en el Volumen 19, número 1 de la Revista Española de Física en 2005 Año Mundial de la Física

En realidad, un Homenaje a Einstein por haber pasado más de un siglo desde aquel acontecimiento memorable de la Relatividad Especial en el año 1.905 y estar a punto de cumplirse otro siglo desde su relatividad general de 1915. Dos acontecimientos que marcaron el camino de la Física y la Cosmología. Hace ahora un par de años que se cumplieron los 100 años desde que Einstein diera al mundo la segunda parte de su Teoría.
emilio silvera
















 Totales: 83.628.970
Totales: 83.628.970 Conectados: 61
Conectados: 61