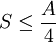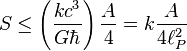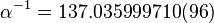Oct
16
¿La Física? ¡Una maravilla! Nos dice cómo funciona la Naturaleza
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (11)
Comments (11)
Ylia Prigogine ¡Qué personaje!
El Universo y la Vida… ¡Nuestra imaginación!

En su Libro Partículas, Gerard ´t Hofft, Premio Nobel de Física, nos cuenta:
“En el mundo de los seres vivos, la escala o tamaño crea importantes diferencias. En muchos aspectos, la anatomía de un ratón es una copia de la de un elefante, pero mientras que un ratón trepar por una pared prácticamente vertical sin mucha dificultad (y se puede caer desde una altura varias veces mayor que su propio tamaño sin hacerse daño), un elefante no sería capaz de realizar tal hazaña. Con bastante generalidad se puede afirmar que los efectos de la gravedad son menos importantes cuanto menores sean los objetos que consideremos (sean vivos o inanimados).”


Cuando llegamos a los seres unicelulares, se ve que ellos no hay distinción entre arriba y abajo. Para ellos, la tensión superficial del agua es mucho más importante que la fuerza de la gravedad a esa escala. Tranquilamente se pueden mover y desplazar por encima de una superficie acuática. Los pluricelulares no pueden hacer tal cosa.
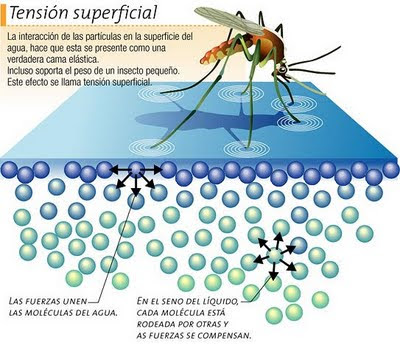
La tensión superficial es una consecuencia de que todas las moléculas y los átomos se atraen unos a otros con una fuerza que nosotros llamamos de Van der Waals. fuerza tiene un alcance muy corto; para ser precisos, diremos que la intensidad de esta fuerza a una distancia r es aproximadamente 1/r7. Esto significa que si se reduce la distancia dos átomos a la mitad de la fuerza de Van der Waals con la que se atraen uno a otro se hace 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128 veces más intensa. Cuando los átomos y las moléculas se acercan mucho unos a otros quedan unidos muy fuertemente a través de esta fuerza. El conocimiento de esta fuerza se debe a Johannes Diderik Van der Waals (1837 – 1923) con su tesis sobre la continuidad del líquido y gaseoso que le haría famoso, ya que en esa época (1873), la existencia de las moléculas y los átomos no estaba completamente aceptado.
La tensión superficial del agua, es el efecto físico (energía de atracción entre las moléculas) que “endurece” la capa superficial del agua en reposo y permite a algunos insectos, como el mosquito y otros desplazarse por la superficie del agua sin hundirse.

El famoso físico inglés James Clerk Maxwell, que formuló la teoría del electromagnetismo de Faraday, quedó muy impresionado por este de Van der Waals.
Los tamaños de los seres uniceculares, animales y vegetales, se miden en micrómetros o “micras”, donde 1 micra es 1/1.000 de milímetro, aproximadamente el tamaño de los detalles más pequeños que se pueden observar con un microscopio ordinario. El mundo de los microbios es fascinante, pero no es el objeto de este trabajo, y continuaremos el viaje emprendido las partículas elementales que forman núcleos, átomos, células y materia, así como las fuerzas que intervienen en las interacciones fundamentales del universo y que afecta a todo lo que existe.

Hemos hablado del electrón que rodea el núcleo, de su carga eléctrica negativa que complementa la positiva de los protones y hace estable al átomo; una masa de solamente 1/1.836 de la del núcleo más ligero (el del hidrógeno). La importancia del electrón es vital en el universo.
Pero busquemos los “cuantos”. La física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menor intensidad, por los objetos más fríos (radiación de cuerpo negro).

Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si utilizamos las leyes de la termodinámica para calcular la intensidad de una radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano y, luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para menores. Esta longitud de onda característica es inversamente proporcional a la temperatura absoluta de objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273º bajo cero). Cuando a 1.000º C un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.
Radiación de Cuerpo Negro
Un cuerpo negro es un objeto teórico o ideal que absorbe toda la luz y toda la energía radiante que incide sobre él. Nada de la radiación incidente se refleja o pasa a través del cuerpo negro. A pesar de su , el cuerpo negro emite luz y constituye un modelo ideal físico para el estudio de la emisión de radiación electromagnética. El nombre Cuerpo negro fue introducido por Gustav Kirchhoff en 1862.

La luz emitida por un cuerpo negro se denomina radiación de cuerpo negro. Todo cuerpo emite energía en de ondas electromagnéticas, siendo esta radiación, que se emite incluso en el vacío, tanto más intensa cuando más elevada es la temperatura del emisor. La energía radiante emitida por un cuerpo a temperatura ambiente es escasa y corresponde a longitudes de onda superiores a las de la luz visible (es decir, de menor frecuencia). Al elevar la temperatura no sólo aumenta la energía emitida sino que lo hace a longitudes de onda más cortas; a esto se debe el cambio de color de un cuerpo cuando se calienta. Los cuerpos no emiten con igual intensidad a todas las frecuencias o longitudes de onda, sino que siguen la ley de Planck.

La “constante de Planck”, desempeña un papel central en la teoría de la mecánica cuántica y recibe su nombre de su descubridor, Max Planck, uno de los padres de dicha teoría. Expresada como  , es la constante física que frecuentemente se define como el cuanto elemental de acción.
, es la constante física que frecuentemente se define como el cuanto elemental de acción.
Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda, y por tanto, proporcional a la frecuencia de radiación emitida. La fórmula es E = h?, donde E es la energía del paquete, ? es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo nueva condición, el resultado coincidió perfectamente con las observaciones.
Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: él sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck. El príncipe francés Louis-Victor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene energía, sino que cualquier cosa con energía se debe comportar una “onda” que se extiende en una cierta región del espacio, y que la frecuencia ? de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilantes de campos de fuerza, esto lo veremos más adelante.

El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de de Broglie. Poco después, en 1926, Edwin Schrödinger descubrió cómo escribir la teoría ondulatoria de de Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de ondas cuánticas”.
Está bien comprobado que la mecánica cuántica funciona de maravilla…, pero, sin embargo, surge una pregunta muy formal: ¿qué significan realmente estas ecuaciones?, ¿qué es lo que están describiendo? Isaac Newton, allá en 1867 formuló cómo debían moverse los planetas alrededor del Sol, estaba claro todo el mundo qué significaban sus ecuaciones: que los planetas estaban siempre en una posición bien definida des espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades en el tiempo.
Pero los electrones todo es diferente. Su comportamiento parece estar envuelto en misterio. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?
Niels Bohr consiguió responder a esta pregunta de tal que con su explicación se pudo seguir trabajando, y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la interpretación de Copenhague de la mecánica cuántica.

Si la mecánica cuántica tiene cosas extrañas y el espín es una de ellas. Y si uno piensa que la intuición le ayudará a comprender todo esto, pues no lo hará, o es poco probable que lo haga. Las partículas tienen un espín fundamental. Al igual que la carga eléctrica o la masa, el espín ayuda a definir que de partícula es cada una.

Las leyes de la mecánica cuántica han sido establecidas con mucha precisión; permite cómo calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas de manera simultánea. Por ejemplo, podemos determinar la velocidad de una partícula con mucha precisión, pero entonces no sabremos exactamente dónde se encuentra; o a la inversa, podemos determinar la posición con precisión, pero entonces su velocidad queda mal definida. Si una partícula tiene espín (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.

La posición y el momento de una partícula nunca lo podremos saber con precisión ilimitada.
No es fácil explicar de forma sencilla de dónde viene esta incertidumbre, pero existen ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar. Para afinar un instrumento se debe escuchar una nota durante un cierto intervalo de tiempo y compararla, por ejemplo, con un diapasón que debe vibrar también durante un tiempo. Notas muy breves no tienen bien definido el tono.
Para que las reglas de la mecánica cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuando más grande y más pesado es un objeto, más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica. Me gustaría referirme a exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”.

El protón está conformado por 2 quarks up y 1 quark dowm
Esto no es exactamente lo mismo que entienden algunos filósofos por holismo, y que podría definir como “el todo es más que la suma de sus partes”. Si la física nos ha enseñado algo es justo lo contrario. Un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (partículas); basta que sepamos sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes. Por ejemplo, la constante de Planck, h, que es igual a 6’626075… × 10-34 Julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.

La mecánica cuántica es muy extraña a nuestro “sentido común”, sabemos que se desenvuelve en ese “universo” de lo muy pequeño, alejado de nuestra vida cotidiana en el macrocosmos tetradimensional que, no siempre coincide con lo que, en aquel otro infinitesimal acontece.
Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisemberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros como Erwin Schrödinger siempre presentaron serias objeciones a interpretación. Quizá funcione bien, pero ¿dónde está exactamente el electrón?, ¿en el punto x o en el punto y? En pocas palabras, ¿dónde está en realidad?, y ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.
Es cierto que, existe otro universo dentro de nuestro del que, aún, nos queda mucho por aprender.

La mecánica cuántica puede ser definida o resumida así: en principio, con las leyes de la naturaleza que conocemos se puede predecir el resultado de cualquier experimento, en el sentido que la predicción consiste en dos factores: el primer factor es un cálculo definido con exactitud del efecto de las fuerzas y estructuras, tan riguroso como las leyes de Isaac Newton para el movimiento de los planetas en el Sistema Solar; el segundo factor es una arbitrariedad estadística e incontrolable definida matemáticamente de estricta. Las partículas seguirán una distribución de probabilidades dadas, primero de una forma y luego de otra. Las probabilidades se pueden calcular utilizando la ecuación de Schrödinger de función de onda (?) que, con muchas probabilidades nos indicará el lugar probable donde se encuentra una partícula en un dado.
Muchos estiman que esta teoría de las probabilidades desaparecerá cuando se consiga la teoría que explique, de forma completa, todas las fuerzas; la buscada teoría del todo, lo que implica que nuestra descripción actual incluye variables y fuerzas que (aún) no conocemos o no entendemos. Esta interpretación se conoce como hipótesis de las variables ocultas.”

También Gerard ‘t Hooft es el autor de lo que han dado en llamar l principio holográfico es una conjetura especulativa acerca de las teorías de la Gravedad Cuántica propuesta en 1993 por este autor, y mejorada y promovida por Leonard Susskin en 1995. Postula que toda la información contenida en cierto volumen de un espacio concreto se puede conocer a partir de la información codificable sobre la frontera de dicha región. Una importante consecuencia es que la cantidad máxima de información que puede contener una determinada región de espacio rodeada por una superficie diferenciable está limitada por el área total de dicha superficie.
Por ejemplo, se pueden modelar todos los eventos que ocurran en un cuarto o una habitación creando una teoría en la que sólo tome en cuenta lo que suceda en sus paredes. En el principio holográfico también se afirma que por cada cuatro Unidades de Planck existe al menos un grado de libertad (o una unidad constante de Bolttzmann k de máxima entropía). Esto se conoce como frontera de Bekenstein:
donde S es la entropía y A es la unidad de mensura considerada. En unidades convencionales la fórmula anterior se escribe:
donde:
 , es la constante de Boltzmann.
, es la constante de Boltzmann.
 , es la vecolcidad de la luz.
, es la vecolcidad de la luz.
 , es la constante gravitacional universal.
, es la constante gravitacional universal.
 , es la constante de Planck racionalizada.
, es la constante de Planck racionalizada. , es la longitud de Planck.
, es la longitud de Planck.
Claro que esta… ¡Es otra Historia!
emilio silvera
Oct
14
¿Sin la luz? ¡Sería otro Universo!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

Nuestro Universo es de Luz, todo lo que podemos observar es posible gracias a la luz que incide en los objetos y se refleja en nuestras retinas, así podemos contemplar los planetas y las estrellas del cielo y cualquier cosa hecha de materia, es decir, materia radiante, conformada por átomos se deja ver por nosotros. Decía Leonard Susskind que, para comprender la realidad en sus niveles más elementales, basta con conocer el comportamiento de dos elementos: el electrón y el fotón.
Todo el argumento de la electrodinámica cuántica (QED) gira en torno a un proceso fundamental: la emisión de un único fotón por un único electrón.

Cuando el movimiento de un electrón es alterado súbitamente, puede responder desprendiendo un fotón. La emisión de un fotón es el suceso básico de la mecánica cuántica:
Toda la luz visible que vemos, así como las ondas de radio, la radiación infrarroja y los rayos X, está compuesta de fotones que han sido emitidos por electrones, ya sea en el Sol, el filamento de una bombilla, una antena de radio o un aparato de rayos.


Los electrones no son las únicas partículas que pueden emitir fotones. Cualquier partícula eléctricamente cargada puede hacerlo, incluido el protón. Esto significa que los fotones pueden saltar entre dos protones o incluso entre un protón y un electrón. Este hecho es de enorme importancia para toda la ciencia y la vida en general. El intercambio continuo de fotones entre el núcleo y los electrones atómicos proporciona la fuerza que mantiene unido al átomo. Sin estos fotones saltarines, el átomo se desharía y toda la materia dejaría de existir.

Mientras que un electrón pertenece al grupo de partículas llamadas fermiones, los fotones pertenecen a la familia de los bosones. Intentemos comprender esta película que es la existencia…
…protagonizada por bosones…
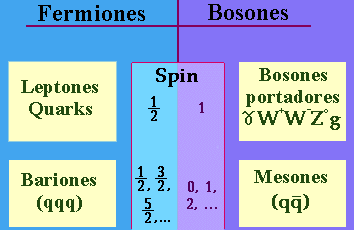
Los fermiones hacen posible la materia “al estilo tradicional”, mientras que los bosones son elementos muy raros desde la forma de pensar a que estamos acostumbrados el común de los mortales. Para no complicarnos, la tabla periódica de elementos existe porque los fermiones no pueden “ser iguales”: no pueden solaparse uno sobre otro y se repelen si los obligamos. Es lo que damos por hecho cuando hablamos de materia, que cada pedazo de ésta ocupa su lugar y tiene sus propias cualidades.
En cambio, los bosones carecen de este sentido de la individualidad, digamos que poseen “alma grupal” y, en su estado más puro, todos forman una misma “superpartícula”.
Para entenderlo mejor, conviene recordar que las partículas no son bolitas como nos siguen enseñando en la escuela, sino que más allá de esta imagen existen como ondas o, al menos, sus funciones se equiparan al comportamiento de una onda.


El caos cuántico en condensados de Bose-Einstein con acoplamiento espín-órbita
En la década de 1920, Albert Einstein y el hindú Satyendra Nath Bose pronosticaron un quinto estado de la materia: el condensado de Bose-Einstein (BEC), el cual fue conseguido en laboratorio en 1995, algo que le valió el premio Nobel de 2001 a los científicos que lo lograron.

Imagínese una taza de té caliente, las partículas que contiene circulan por toda la taza. Sin embargo cuando se enfría y queda en reposo, las partículas tienden a ir en reposo hacia el fondo. Análogamente, las partículas a temperatura ambiente se encuentran a muchos niveles diferentes de energía. Sin embargo, a muy bajas temperaturas, una gran proporción de éstas alcanza a la vez el nivel más bajo de energía, el estado fundamental. (Fuente: wikipedia)
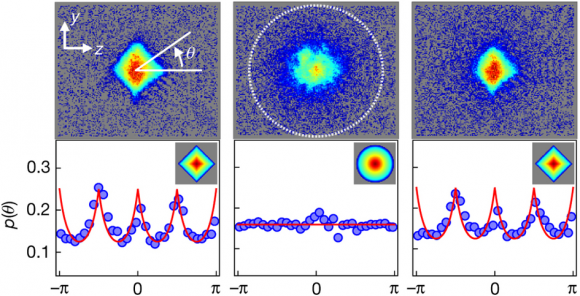
“A priori, un condensado de Bose–Einstein (BEC) es el fluido cuántico menos turbulento que uno puede imaginar. Sin embargo se puede forzar una cascada de Kolmogorov–Obukhov en un condensado formado por unos cien mil átomos de rubidio en una trampa óptica cilíndrica de unos 30 micrómetros de longitud que están enfriados a unos 50 nanokelvin (milmillonésimas de grado sobre el cero absoluto). El método usa un campo magnético oscilatorio que inyecta energía en los modos de momento más bajo del condensado.”
Cuando ciertas formas de materia [bosones] se enfrían hasta casi el cero absoluto, sus átomos se ponen en el estado de energía más baja, de modo que todos sus átomos vibran al unísono y se hacen coherentes. Las funciones de onda de todos los átomos se solapan, de manera que, en cierto sentido, un BEC [condensado de Bose-Einstein] es como un “superátomo” gigante en donde todos los átomos individuales vibran al unísono.
Al enfriar los átomos, su velocidad disminuye hasta que las longitudes de onda de cada uno de ellos se vuelven casi planas, superponiéndose unas a otras para formar una única onda que los describe a todos.
Así que un BEC se forma cuando los átomos en un gas sufren la transición de comportarse como “bolas de billar” al estilo de la física clásica, a comportarse como una onda gigante de materia al estilo de mecánica cuántica:

Un grupo de físicos experimentales afirman haber creado fluido con “masa negativa”

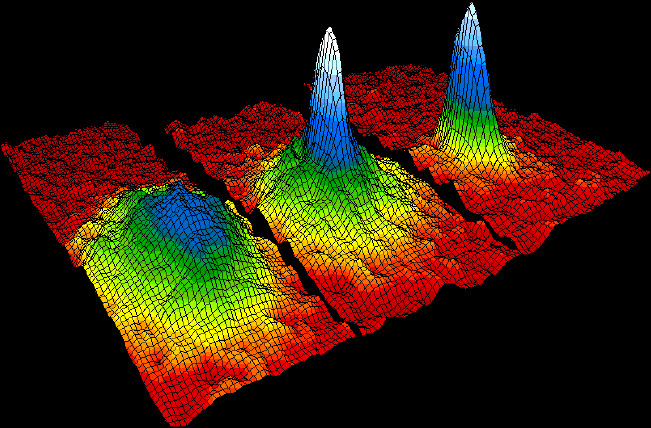
En el primero (el de la izquierda) se encuentra un sistema con átomos en diferentes estados vibratorios, es decir, con diferentes energías. Por eso tienen distintas ondas asociadas a diferentes velocidades. La cubeta de abajo representa el sistema, las franjas horizontales representan los diferentes estados energéticos y los puntos son los átomos situados en estos distintos estados.
El segundo sistema (el de la derecha) representa un conjunto de átomos que han sido enfriados hasta llegar a formar un condensado de Bose-Einstein. Todos los átomos tienen la energía más baja del sistema.
Dado que para alcanzar el estado de CBE es necesario enfriar muchísimo los átomos, su velocidad disminuye hasta que su longitud de onda se hace tan larga que su onda es casi plana. En este punto, las ondas de todos los átomos enfriados se superponen, formando una única onda y alcanzando el estado de condensado de Bose-Einstein.
Por eso se dice que los átomos se encuentran en el mismo lugar, porque todos son descritos por una única onda.

Y la siguiente simulación computarizada nos dá una mejor perspectiva sobre la formación de los vórtices en un condensado Bose-Einstein conformado por 200 mil átomos de rubidio contenidos dentro de una trampa magnética
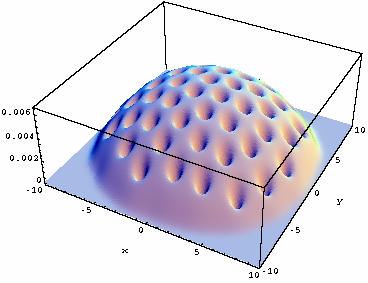
Un BEC es un grupo de unos cuantos millones de átomos que se unen para formar una sola onda de materia de aproximadamente un milímetro de diámetro. Si creamos dos BECs y los colocamos juntos, no se mezclan como gases ordinarios ni rebotan como lo harían dos sólidos. Donde los dos BECs se superponen, ellos “interfieren” como las ondas: delgadas capas paralelas de materia son separadas por capas delgadas de espacio vacío. El patrón se forma porque las dos ondas se suman donde sus crestas coinciden, y se cancelan donde una cresta se encuentra con un valle — a lo cual llamamos interferencia “constructiva” y “destructiva” respectivamente. El efecto es similar al de dos ondas que se superponen cuando dos piedras son lanzadas a un lago.
(Fuente: ciencia NASA)
…ambientada en: el vacío…
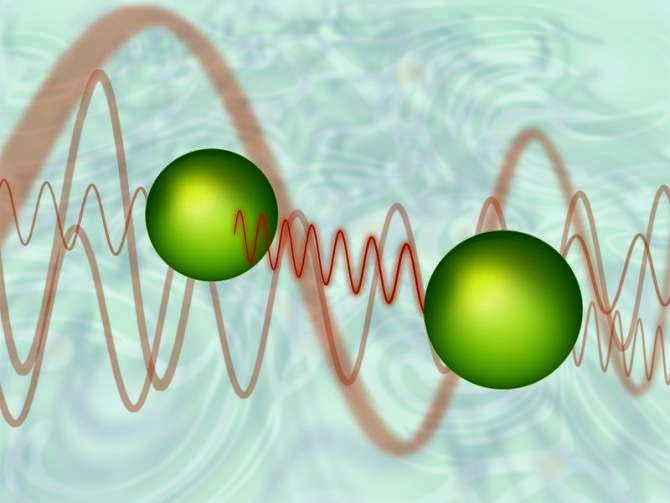
El hecho de que se puedan intercambiar partículas virtuales modifica el vacío alrededor de los átomos, y esto lleva a una fuerza. De las llamadas fluctuaciones de vacío pueden surgir, partículas virtuales y quién sabe que cosas más… Hasta un nuevo Universo.
Y ahora, retrocedamos un poco más en este asunto del misterio que nos ocupa. Gracias a la tecnología láser, la física ha podido comprobar el extremo poder de la luz. Los láseres pueden hacer que las partículas virtuales se vuelvan reales. Pero, primero, aclaremos conceptos…
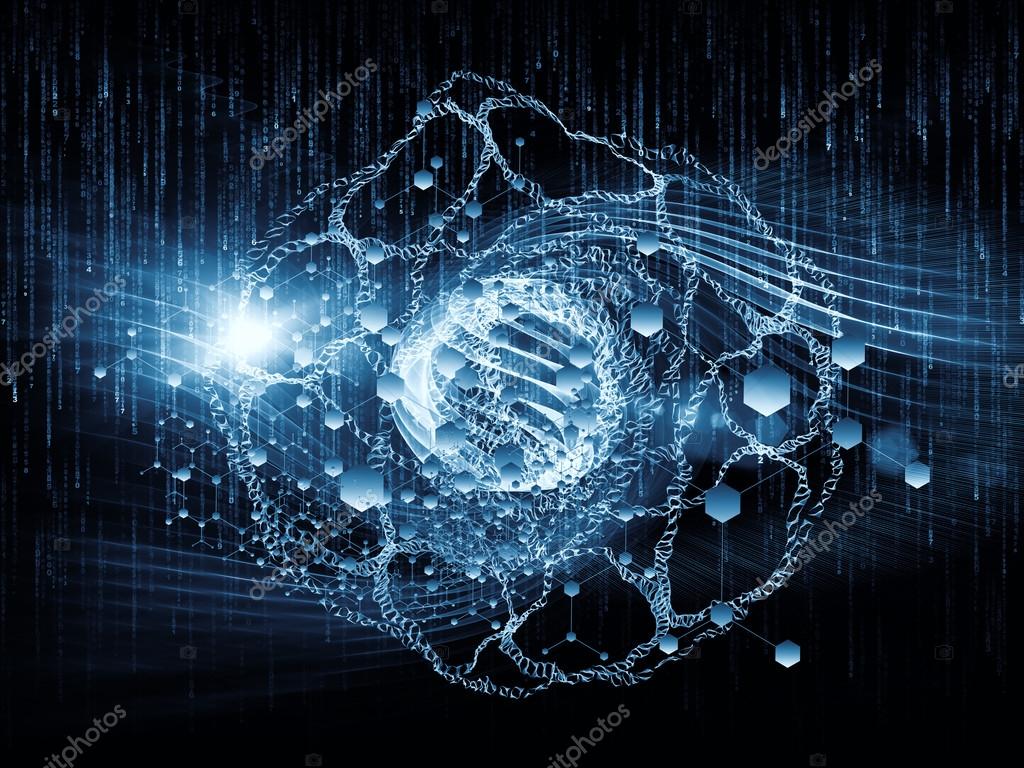
Las “partículas virtuales” son partículas fundamentales que están constantemente surgiendo aparentemente de la nada y permanecen en el espacio-tiempo la friolera de una milésima de trillonésima de segundo –una cantidad que se forma poniendo una veintena de ceros a la derecha de la coma—. A pesar de denominarse “virtuales”, sus efectos son muy reales: la constante agitación de este burbujeo cuántico de partículas hace que el vacío tenga energía. Y esto es algo que afecta a la realidad, pues en ésta las fuerzas de atracción y repulsión dependen de la masa, y la masa no es sino energía expresada en unidades diferentes: E=mc².

En el uso corriente la palabra vacío significa espacio vacío, espacio del que se ha extraído todo el aire, vapor de agua u otro material. Eso es también lo que significa para un físico experimental que trabaja con tubos de vacío y bombas de vacío. Pero para un físico teórico, el término vacío tiene muchas más connotaciones. Significa una especie de fondo en el que tiene lugar el resto de la física. El vacío representa un potencial para todas las cosas que pueden suceder en ese fondo. Significa una lista de todas las partículas elementales tanto como de las constantes de la Naturaleza que se pondrían de manifiesto mediante experimentos en dicho vacío. En resumen, significa un ambiente en el que las leyes de la física toman una forma particular. […] Un vacío diferente significa leyes de la física diferentes; cada punto en el paisaje representa un conjunto de leyes que son, con toda probabilidad, muy diferentes de las nuestras pero que son, en cualquier caso, posibilidades consistentes. El modelo estándar es meramente un punto en el paisaje de posibilidades.

… la energía del vacío es tomada como la base para la constante cosmológica. A nivel experimental, la energía del punto cero genera el efecto Casimir, … Se dice que:
La energía del vacío es, por tanto, la suma total de las energías de todas las partículas posibles. Es la (hipotética) llamada “energía oscura” que hace que el universo se expanda, haciendo frente a la atracción de la gravedad, y que proporciona alrededor del 80% de la materia-energía al universo –un 26% es “materia oscura”, y sólo un 4% es la materia conocida hasta el momento—.
Pero, ¿cómo una partícula virtual se convierte en real? Es decir, ¿cómo queda “atrapada” en el espacio-tiempo de forma más estable?

La teoría de cuerdas, también llamada de supercuerdas, pues la supersimetría es necesaria para incluir los quarks y otros fermiones, es una teoría …
La teoría de la supersimetría establece que, por cada partícula de materia, nace una gemela de antimateria. La antimateria es igual que la materia, pero con carga opuesta. Por ejemplo, el electrón tiene carga negativa, y su partícula de antimateria, el positrón, positiva. Materia y antimateria se aniquilan mutuamente pero, por algún motivo aún no aclarado, la simetría se rompió en algún momento, surgiendo más materia que antimateria, de ahí que nuestro universo, materia, pueda existir.
Pero hay algo más en todo esto. Y para ello, la luz es la clave.
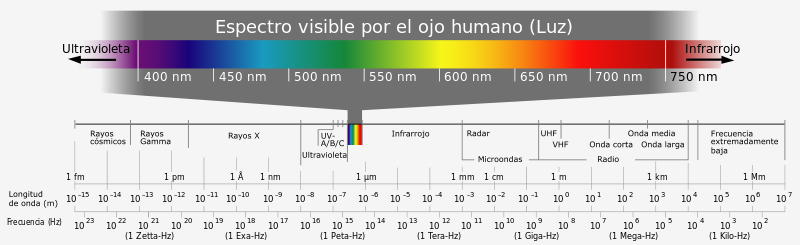
Si nos movemos en el espectro electromagnético, los fotones con longitud de onda ultravioleta pueden expulsar a los electrones de los átomos. Pero veámos.

…starring “light” as itself…
Ya en los años 30, los físicos predijeron que un campo eléctrico muy fuerte, que no es sino un espacio alterado por la actividad de un montón de fotones coordinados, podría impulsar a las partículas virtuales con carga opuesta en diferentes direcciones, impidiendo que la materia y la antimateria se aniquilen.

Según el efecto de creación de pares, un fotón con energía suficiente, lo que equivale a tener el doble de la energía que posee un electrón en reposo, da lugar a una pareja de electrón y positrón. Aunque esto ya se consiguió en los años 90 a pequeña escala, gracias al desarrollo de la tecnología láser los científicos creen que estarán cerca de conseguir crear materia “en serie” mediante este proceso en unos pocos años. Por otra parte, una vez que existen las partículas, los fotones interactuan sin cesar con ellas, siendo absorbidos y emitidos por las mismas de manera ininterrumpida.Y de ello nace el movimiento gracias al cual todo existe en el espacio-tiempo. Sin movimiento, nuestra realidad desaparecería.

Así, si el fotón tiene suficiente energía, el par será electrón-positrón, caso contrario será un par virtual (absorción), si la energía del fotón fuere mayor, la diferencia estará dada por la velocidad opuesta de las antipartículas (masa de las antipartículas), correspondiente a la energía “sobrante” de acuerdo a E=mc2. Si la energía del fotón fuere suficiente, como para llegar al umbral mínimo, se creará un protón-antiprotón, y si fuere mayor, se manifestará en velocidad opuesta (masa de las antipartículas). La energía del fotón (cantidad de movimiento, efecto Compton) será la energía correspondiente al total de las dos antipartículas (masa, E=mc2)

La carencia de masa de un fotón está ligada a su movimiento. Para que un cuerpo alcance la velocidad de la luz, su masa ha de ser cero. Y, como Einstein explicó en su día, la luz se mueve siempre a la velocidad de la luz. Si pretendemos que un fotón se pare, en lugar de ralentizarse observaremos que desaparece. Y, como se ha dicho al principio, si estos “fotones saltarines” desaparecieran, toda la materia dejaría de existir.

Su esencia es el movimiento y su misión, según parece, hacer girar la rueda de la existencia. Sin la existencia de los fotones estaríamos hablando de otro Universo.
Ello es así debido al impacto de los fotones sobre las partículas elementales. La energía transmitida por un fotón es inversamente proporcional a su longitud de onda. Cuanto menos longitud de onda, más energía. Así, un fotón de luz visible tiene la energía suficiente para hacer reaccionar a un bastón de la retina. Si nos movemos en el espectro electromagnético, los fotones con longitud de onda ultravioleta pueden expulsar a los electrones de los átomos. Más allá, los rayos gamma pueden romper protones y neutrones…

Cuando la tensión llega a un punto insostenible la corteza de neutrones revienta en un temblor estelar, dejando escapar rayos gamma y rayos X. En una potencia descomunal capaz de destruir otras particulas cuando interaccionan.
Y ahora, vayamos al meollo de la cuestión e indaguemos en la cita con que se iniciaba este artículo: ¿qué hace que los electrones absorban y emitan fotones? Esto, en otros términos, vendría a ser lo mismo que preguntarnos: ¿por qué existe nuestro Universo?
…con un misterio: el 137…
“Por ejemplo, Richard Feynman, uno de los físicos más importantes del siglo 20, escribió lo siguiente sobre el número 137: “Ha sido un misterio desde su descubrimiento hace más de cincuenta años, y todo físico teórico competente coloca este número en su pared y se preocupa por éste. Es uno de los malditos misterios más grandes: un número mágico que nos llega sin el entendimiento del hombre.”

¿Qué determina el momento exacto en que un electrón emite un fotón? La física cuántica dice que nada lo hace, pues la Naturaleza es caprichosa en sus niveles más elementales. Aunque no es caótica en extremo, sólo probabilística.
A diferencia de la física newtoniana, la mecánica cuántica nunca predice el futuro en función del pasado. En su lugar, ofrece reglas muy precisas para computar la probabilidad de varios resultados alternativos de un experimento.

La constante de estructura fina fue introducida en la física en 1916 por Arnol Sommerfeld, como una medida relativista de las desviaciones en las lineas espectrales atómicas de las predicciones hechas por el modelo de Bohr.
Históricamente, la primera interpretación física de la constante de estructura fina,  , fue el cociente de la velocidad del electrón en la primera órbita circular del átomo de Bohr relativista con la velocidad de la luz en el vacío. De igual forma, era el cociente entre el momento angular mínimo permitido por la relatividad para una órbita cerrada bajo fuerza electromagnética y el momento angular mínimo permitido por la mecánica cuántica. Aparece de forma natural en el análisis de Sommerfeld y determina el tamaño de la separación o estructura fina de las lineas espectrales del hidrógeno.
, fue el cociente de la velocidad del electrón en la primera órbita circular del átomo de Bohr relativista con la velocidad de la luz en el vacío. De igual forma, era el cociente entre el momento angular mínimo permitido por la relatividad para una órbita cerrada bajo fuerza electromagnética y el momento angular mínimo permitido por la mecánica cuántica. Aparece de forma natural en el análisis de Sommerfeld y determina el tamaño de la separación o estructura fina de las lineas espectrales del hidrógeno.
La QED predice una relación entre el momento magnético sin dimensiones del electrón (o el g-factor de Lande,  ) y la constante de estructura fina
) y la constante de estructura fina  . Una nueva medida de
. Una nueva medida de  usando un ciclotrón cuántico de un electrón, junto con un cálculo QED que involucra 891diagrama de Feynman, determina el valor actual más preciso de
usando un ciclotrón cuántico de un electrón, junto con un cálculo QED que involucra 891diagrama de Feynman, determina el valor actual más preciso de  :
:
esto es, una medida con una precisión de 0.70 partes por mil millones. Las incertidumbres son 10 veces más pequeñas que aquellas de los métodos rivales más próximos. Las comparaciones de los valores medidos y los calculados de  suponen un test muy fuerte de QED, y ponen un límite para cualquier estructura interna del electrón posible.
suponen un test muy fuerte de QED, y ponen un límite para cualquier estructura interna del electrón posible.
En 2010, el científico John Webb publicó un estudio en el que revelaba datos que afirmaban que la constante no era igual en todo el universo y que se observaban cambios graduales en torno a un eje concreto de éste.
Algunos científicos sostienen que las constantes de la naturaleza no sean en realidad constantes, y la constante de estructura fina no escapa a estas afirmaciones.
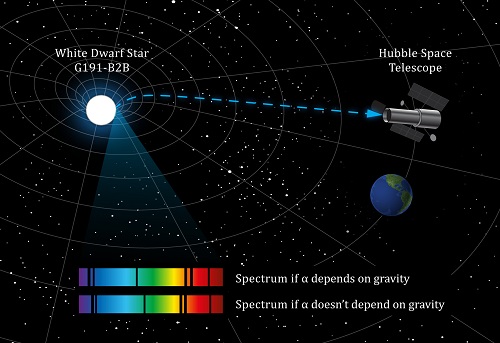
Físicos de la University of New Wales (UNSW) tienen una teoría cuando menos controvertida, y es la de que la constante de estructura fina, α (alpha), en realidad no es constante. Y estudian los alrededores de una enana blanca lejana, con una gravedad más de 30.000 veces mayor que la de la tierra, para comprobar su hipótesis.
Recientemente, la detección de los mapas de enlace-dimensional de la constante de estructura fina
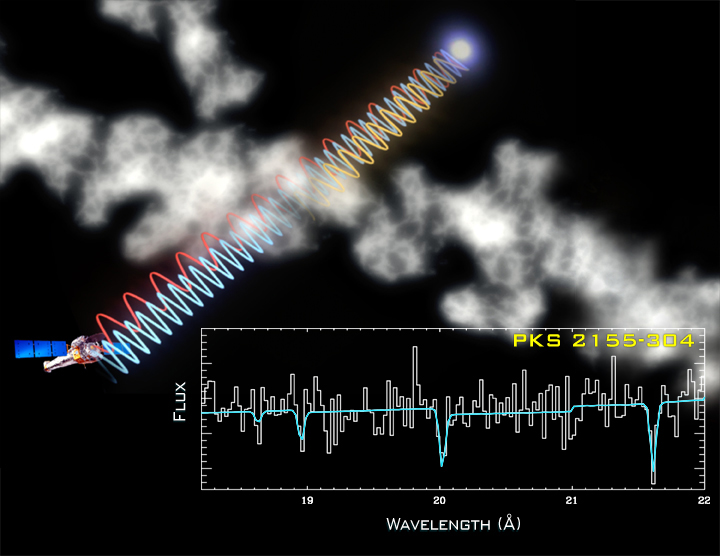
Y la probabilidad de que un electrón emita o absorba un fotón es la constante de estructura fina. El valor de esa constante es 1/137.
En otras palabras, sólo un afortunado electrón de cada 137 emite un fotón. Este es el significado de alfa: es la probabilidad de que un electrón, cuando se mueve a lo largo de su trayectoria, emita caprichosamente un fotón.
El inverso de la constante de estructura fina es 137. Desde su descubrimiento, éste número ha traído de cabeza a los grandes científicos.
LA MAGIA DEL 137
El 137 es el mayor misterio y el número más importante en toda la ciencia. Sin duda.

¿Qué mensaje nos transmite ese número puro y adimensional?
No recuerdo si fue Richard Feynman o León Lederman, el que sugirió que todos los físicos pusiesen un cartel en sus despachos o en sus casas que les recordara cuánto es lo que no sabemos. En el cartel no pondría nada más que esto: 137. Ciento treinta y siete es el inverso de algo que lleva el nombre de constante de estructura fina. Este número guarda relación con la probabilidad de que un electrón emita o absorba un fotón. La constante de estructura fina responde también al nombre de alfa, y sale de dividir el cuadrado de la carga del electrón por el producto de la velocidad de la luz y la constante de Planck. Tanta palabra no significa otra cosa sino que ese solo número, 137, encierra los meollos del electromagnetismo (el electrón), la relatividad (la velocidad de la luz) y la teoría cuántica (la constante de Planck). Menos perturbador sería que la relación entre todos estos importantes conceptos hubiera resultado ser un uno o un tres o quizás un múltiplo de pi. Pero ¿137?

“Lo más notable de este notable número es su adimensionalidad. La velocidad de la luz es de unos 300.000 kilómetros por segundo. Abraham Lincoln medía 1,98 metros. La mayoría de los números vienen con dimensiones. Pero resulta que cuando uno combina las magnitudes que componen alfa, ¡se borran todas las unidades! El 137 está solo: se exhibe desnudo a donde va. Esto quiere decir que a los científicos de Marte, o a los del decimocuarto planeta de la estrella Sirio, aunque usen Dios sabe qué unidades para la carga y la velocidad y qué versión de la constante de Planck, también les saldrá 137. Es un número puro.”
(Leon Ledderman, La partícula divina)
Uno de los padres de la mecánica cuántica, Wolfgang Pauli, se obsesionó tanto con este número que dijo que, de poder hacerle una pregunta a Dios, sería esta: “¿Por qué 137?”
Gracias a su gran amistad con Carl G. Jung, Pauli conoció el mundo “alternativo” de los estudios sobre la psique y accedió a la tradición esotérica que ha acompañado al hombre desde el principio de los tiempos. Es así como supo que 137 se aproxima al valor correspondiente al ángulo áureo. Esto es, la versión circular del número áureo o φ (phi).

En realidad, el ángulo de oro es, más o menos, 137, 5º, y está presente en todo proceso natural donde se dé una combinación de espirales. Así, por ejemplo, las hojas de una planta surgen a lo largo del tallo cada 137,5º, pues así se logra la mayor eficiencia de espacio y de captación de la luz solar, ya que únicamente con éste ángulo es posible evitar que ninguna hoja obstaculice a las demás en la toma de luz sin que existan espacios muertos o vacíos.
Esta semejanza entre los valores de la constante de estructura fina y el ángulo áureo llevó a la doctora Raji Heyrovska a buscar el ángulo áureo en el universo atómico (véase versión en español de su estudio).
Que esto sea así no debería extrañarnos, pues si el número áureo es una constante en toda la Naturaleza, su versión angular es la apropiada para estar presente en el universo cuántico, donde, recordemos, los elementos básicos de la realidad se reducen a funciones de onda.
…y un final místico.
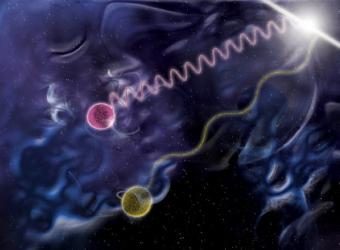
Los fotones no tienen masa ni carga eléctrica. Sin embargo, pueden “extraer” del vacío partículas con masa y carga, tanto negativa como positiva.
Más allá de la matería y la energía, del tiempo y del espacio, el concepto de función de onda nos introduce en una realidad abstracta de donde surge todo. Y si, como hemos dicho, a menor longitud de onda mayor energía, también es posible afirmar que, en eso que David Bohm llamaba “orden implicado”, cuanto menor es la longitud de una onda cuántica, mayor es la presencia de masa en el espacio-tiempo.
Para la física, las matemáticas se han mostrado como la realidad que subyace a la materia. Todo se puede reducir a números, entidades que forman y organizan el espacio-tiempo. En este nivel de realidad, ni la materia ni la energía existen como tales, sino que demuestran ser el resultado de la interacción de entidades abstractas.
Fuentes diversas y algunos pasajes propios
Oct
4
Hay que recorrer un largo camino para saber
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)

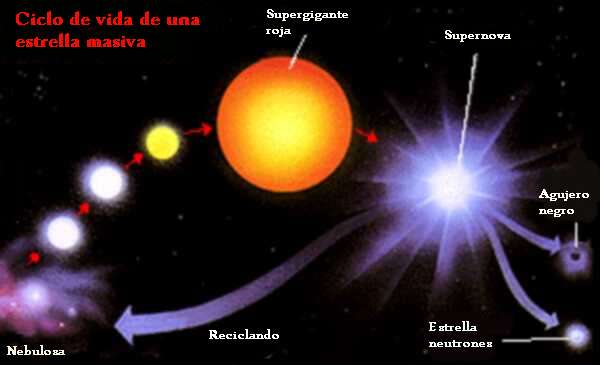
“La masa con la que nace una estrella determina su historia y, sobre todo, la duración de su vida. Llamamos estrellas masivas a todas aquellas estrellas aisladas que explotan como supernovas al final de su existencia debido al colapso gravitatorio. Para que exploten como supernovas deben tener un mínimo de alrededor de ocho masas solares. Estrellas con menos masa pueden explotar, pero no por sí mismas (deben darse otras condiciones). Y hay parámetros secundarios que pueden introducir cambios, pero la masa es determinante.”
“En cuanto al máximo, el límite está en lo que la naturaleza sea capaz de producir. Hasta hace poco se creía que este límite estaba en torno a monstruos de 150 masas solares, aunque recientes trabajos lo elevan hasta 300. No obstante, no es un dato seguro ya que, cuanto más masiva es una estrella, menos vive, con lo cual estrellas más grandes serían difíciles de observar.”

Verdaderamente si pudiéramos contemplar de cerca, el comportamiento de una estrella cuando llega el final de su vida, veríamos como es, especialmente intrigante las transiciones de fase de una estrella en implosión observada desde un sistema de referencia externo estático, es decir, vista por observadores exteriores a la estrella que permanecen siempre en la misma circunferencia fija en lugar de moverse hacia adentro con la materia de la estrella en implosión. La estrella, vista desde un sistema externo estático, empieza su implosión en la forma en que uno esperaría.

Al igual que una pesada piedra arrojada desde las alturas, la superficie de la estrella cae hacia abajo (se contrae hacia adentro), lentamente al principio y luego cada vez más rápidamente. Si las leyes de gravedad de Newton hubieran sido correctas, esta aceleración de la implosión continuaría inexorablemente hasta que la estrella, libre de cualquier presión interna, fuera aplastada en un punto de alta velocidad. Pero no era así según las fórmulas relativistas que aplicaron Oppenheimer y Snyder. En lugar de ello, a medida que la estrella se acerca a su circunferencia crítica su contracción se frena hasta hacerse a paso lento. Cuanto más pequeña se hace la estrella, más lentamente implosiona, hasta que se congela exactamente en la circunferencia crítica y, dependiendo de su masa, explosiona como supernova para formar una inmensa nebulosa o, se tranforma en nebulosa planetaria, más pequeña.

La gran erupción de Eta Carinae en la década de 1840 creó la nebulosa del Homúnculo, mostrada aquí en una imagen tomada por el Hubble. Con una longitud ahora de un año-luz, la nube en expansión contiene suficiente material para hacer por lo menos 10 copias de nuestro Sol. Los astrónomos aún no pueden explicar qué causó esta explosión. Crédito: NASA, ESA, y el Hubble SM4 ERO Team
Ahí podemos observar a una estrella muy joven, de dos o tres millones de años que, en un futuro lejano será una gran Supernova. Los procesos que podríamos observar al final de la vida de una estrella gigante… ¡Son fascinantes! Ese punto azulado que vemos envuelto en una masa de gas y polvo, no es otra cosa que la estrella Eta Carinae, una variable luminosa azul hipermasiva. Su masa puede osciular entre las 100 y 150 masas solares y, como el límite para la masa de una estrella está estipulado en 120 masas solares, ésta de arriba, para no ser destruída por su propia radiación, eyecta material al espacio interestelar para descongestionarse.

En la escena que antes explicabamos, por mucho tiempo que nos quedemos esperando y comtemplando el suceso, si uno está en reposo fuera de la estrella (es decir, en reposo en el sistema de referencia externo estático), uno nunca podrá ver que la estrella implosiona a través de la circunferencia crítica. Ese fue el mensaje inequívoco que Oppenheimer y Snyder nos enviaron. Para poder ver eso, habría que estar dentro de la estrella, instalado en la materia que está sufriendo la contracción y, no sabemos porque eso es así.


¿Se debe esta congelación de la implosión a alguna fuerza inesperada de la relatividad general en el interior de la estrella? No, en absoluto, advirtieron Oppenheimer y Snyder. Más bien se debe a la dilatación gravitatoria del tiempo (el frenado del flujo del tiempo) cerca de la circunferencia crítica. Tal como lo ven los observadores estáticos, el tiempo en la superficie de la estrella en implosión debe fluir cada vez más lentamente cuando la estrella se aproxima a la circunferencia crítica; y, consiguientemente, cualquier cosa que ocurre sobre o en el interior de la estrella, incluyendo su implosión, debe aparecer como si el movimiento se frenara poco a poco hasta congelarse.
Por extraño que esto pueda parecer, aún había otra predicción más extrañas de las fórmulas de Oppenheimer y Snyder: si bien es cierto que vista por observadores externos estáticos la implosión se congela en la circunferencia crítica, no se congela en absoluto vista por los observadores que se mueven hacia adentro con la superficie de la estrella. Si la estrella tiene una masa de algunas masas solares y empieza con un tamaño aproximado al del Sol, entonces vista desde su propia superficie implosiona hacia la circunferencia crítica en aproximadamente una hora, y luego sigue implosionando más allá de la criticalidad hacia circunferencias más pequeñas.
Allá por el año 1939, cuando Oppenheimer y Snyder descubrieron estas cosas, los físicos ya se habían acostumbrados al hecho de que el tiempo es relativo; el flujo del tiempo es diferente medido en diferentes sistemas de referencia que se mueven de diferentes formas a través del Universo. Claro que, nunca antes había encontrado nadie una diferencia tan extrema entre sistemas de referencia. Que la implosión se congele para siempre medida en el sistema externo estático, pero continúe avanzando rápidamente superando al punto de congelación medida en el sistema desde la superficie de la estrella era extraordinariamente difícil de comprender. Nadie que estudiara las matemáticas de Oppenheimer y Snyder se sentía cómodo con semejante distorsión extrema del tiempo. Pero ahí estaba, en sus fórmulas. Algunos podían agitar sus brazos con explicaciones heurísticas, pero ninguna explicación parecía muy satisfactoria. No sería completamente entendido hasta finales de los cincuenta.
Fue Wheeler el que discrepó del trabajo de Oppenheimer y Snyder, alegando, con toda la razón que, cuando ellos habían realizado su trabajo, habría sido imposible calcular los detalles de la implosión con una presión realista (presión térmica, presión de degeneración y presión producida por la fuerza nuclear), y con reacciones nucleares, ondas de choque, calor, radiación y expulsión de masa. Sin embargo, los trabajos desde las armas nucleares de los veinte años posteriores proporcionaron justamente las herramientas necesarias.

Presión, reacciones nucleares, ondas de choque, calor radiación y expulsión de masa eran todas ellas características fundamentales de una bomba de hidrógeno; sin ellas, una bomba no explosionaría. A finales de los años cincuenta, Stirling Colgate quedó fascinado por el problema de la implosión estelar. Con el apoyo de Edward Teller, y en colaboración con Richard White y posteriormente Michael May, Colgate se propuso simular semejante implosión en un ordenador. Sin embargo, cometieron un error, mantuvieron algunas de las simplificaciones de Oppenheimer al insistir desde el principio en que la estrella fuera esférica y sin rotación, y, aunque tuvieron en cuenta todos los argumentos que preocupaban a Wheeler, aquello no quedó perfeccionado hasta después de varios años de esfuerzo y, a comienzo de los años sesenta ya estaban funcionando correctamente.

Un día a principio de los años sesenta, John Wheeler entró corriendo en la clase de relatividad de la Universidad de Princeton. Llegaba un poco tarde, pero sonreía con placer. Acababa de regresar de una visita a Livermore donde había visto los resultados de las simulaciones recientes de Colgate y su equipo. Con excitación en su voz dibujó en la pizarra un diagrama tras otro explicando lo que sus amigos de Livermore habían aprendido.

Cuando la estrella en implosión tenía una masa pequeña, desencadenaba una implosión de supernova y formaba una estrella de neutrones precisamente en la forma que Fritz Wicky había especulado treinta años antes. Sin embargo, si la estrella original era más masiva lo que allí se producía (aparte de la explosión supernova) era un agujero negro notablemente similar al altamente simplificado modelo que veinticinco años calcularon Oppenheimer y Snyder. Vista desde fuera, la implosión se frenaba y se quedaba congelada en la circunferencia crítica, pero vista por alguien en la superficie de la estrella, la implosión no se congelaba en absoluto. La superficie de la estrella se contraía a través de la circunferencia crítica y seguía hacia adentro sin vacilación.

Lo cierto fue que allí, por primera vez, se consiguió simular por ordenador la implosión que debía producir agujeros negros. Está claro que la historia de todo esto es mucho más larga y contiene muchos más detalles que me he saltado para no hacer largo el trabajo que, en realidad, sólo persigue explicar a ustedes de la manera más simple posible, el trabajo que cuesta obtener los conocimientos que no llegan (casi nunca) a través de ideas luminosas, sino que, son el resultado del trabajo de muchos.
Hoy, sabemos mucho más de cómo finaliza sus días una estrella y, dependiendo de su masa, podemos decir de manera precisa que clase de Nebulosa formará, que clase de explosión (si la hay) se producirá, y, finalmente, si el resultado de todo ello será una estrella enana blanca que encuentra su estabilidad final por medio del Principio de exclusión de Pauli (en mecánica cuántica)que se aplica a los fermiones pero no a los Bosones (son fermiones los quarks, electrones, protones y neutrones), en virtud del cual dos partículas idénticas en un sistema, como los electrones en un átomo o quarks en un hadrón (protón o neutrón, por ejemplo), no pueden poseer un conjunto idéntico de números cuánticos.

La estrella azul cerca del centro de esta imagen es Zeta Ophiuchi. Cuando se ve en luz visible aparece como una estrella roja relativamente débil rodeada de otras estrellas tenues y sin polvo. Sin embargo, en esta imagen infrarroja tomada con campo amplio por el Explorador Infrared Survey de la NASA, o WISE, un punto de vista completamente diferente emerge. Zeta Ophiuchi es en realidad una muy masiva y caliente estrella azul, brillante que traza su camino a través de una gran nube de polvo y gas interestelar.

Una estrella masiva alejándose de su antiguo compañero se manifiesta haciendo un imponente surco a través de polvo espacial, como si se tratase de la proa de un barco. La estrella, llamada Zeta Ophiuchi, es enorme, con una masa de cerca de 20 veces la de nuestro Sol. En esta imagen, en los que se ha traducido la luz infrarroja a colores visibles que vemos con nuestros ojos, la estrella aparece como el punto azul en el interior del arco de choque. Zeta Ophiuchi orbitó una vez alrededor de una estrella aún más grande. Pero cuando la estrella explotó en una supernova, Zeta Ophiuchi se disparó como una bala. Viaja a la friolera velocidad de 24 kilómetros por segundo arrastrando con ella un conglomerado de polvo que distorsiona la región por la que pasa.
Mientras la estrella se mueve través del espacio, sus poderosos vientos empujan el gas y el polvo a lo largo de su camino en lo que se llama un arco de choque. El material en el arco de choque está tan comprimido que brilla con luz infrarroja que WISE puede captar. El efecto es similar a lo que ocurre cuando un barco cobra velocidad a través del agua, impulsando una ola delante de él. Esta onda de choque queda completamente oculta a la luz visible. Las imágenes infrarrojas como esta son importantes para arrojar nueva luz sobre lo que ocurre en situaciones similares.

Pero, siguiendo con el tema de las implosiones de las estrellas, ¿cuál es la razón por la que la materia no se colapsa, totalmente, sobre sí misma? El mismo principio que impide que las estrellas de neutrones y las estrellas enanas blancas implosionen totalmente y que, llegado un momento, en las primeras se degeneran los neutrones y en las segundas los electrones, y, de esa manera, se frena la compresión que producía la gravedad y quedan estabilizadas gracias a un principio natural que hace que la materia normal sea en su mayor parte espacio vacio también permite la existencia de los seres vivos. El nombre técnico es: El Principio de Exclusión de Pauli y dice que dos fermiones (un tipo de partículas fundamentales) idénticos y con la misma orientación no pueden ocupar simultáneamente el mismo lugar en el espacio. Por el contrario, los bosones (otro tipo de partículas, el fotón, por ejemplo) no se comportan así, tal y como se ha demostrado recientemente por medio de la creación en el laboratorio de los condensados de Bose-Einstein.
¿Cuál es la diferencia?
Los bosones son sociables; les gusta estar juntos. Como regla general, cualquier átomo con un número par de electrones+protones+neutrones es un bosón. Así, por ejemplo, los átomos del sodio ordinario son bosones, y pueden unirse para formar condensados Bose-Einstein.
Izquierda: Los bosones son sociables; los fermiones son antisociales.
Los fermiones, por otro lado, son antisociales. No pueden juntarse en el mismo estado cuántico (por el Principio de Exclusión de Pauli de la mecánica cuántica). Cualquier átomo con un número impar de electrones+protones+neutrones, como el potasio-40, es un fermión.
Pero, estábamos diciendo: “…no pueden poseer un conjunto idéntico de números cuánticos.” A partir de ese principio, sabemos que, cuando una estrella como nuestro Sol deja de fusionar Hidrógeno en Helio que hace que la estrella deje de expandirse y quede a merced de la Gravedad, ésta implosionará bajo el peso de su propia masa, es decir, se contraerá sobre sí misma por la fuerza gravitatoria pero, llegará un momento en el cual, los electrones, debido a ese principio de exclusión de Pauli que les impide estar juntos, se degeneran y se moverán de manera aleatoria con velocidades relativista hasta el punto de ser capaces de frenar la fuerza provocada por la gravedad, y, de esa manera, quedará estabilizada finalmente una estrella enana blanca.

Si hablamos de una estrella supermasiva, su produce la implosión arrojando las capas externas al espacio interestelar mientras que el grueso de la estrella se comprime más y más sin que nada la pueda frenar, aquí no sirve el Principipo de exclusión de Pauli para los fermiones y, es tal la fuerza gravitatoria que se desencadena como consecuencia de que la estrella supergigante no puede seguir fusionando y queda a merce4d de una sola fiuerza: La Gravedad, que ésta, la comprime hasta lo inimaginable para convertir toda aquella ingente masa en una singularidad, es decir, un punto de densidad y energía “infinitas” que ni la luz puede escapar de allí, y, el tiempo se ralentiza y el espacio se curva a su alrededor.

Si la estrella original es más masiva, la degeneración de los electrones no será suficiente para frenar la fuerza gravitatoria y, los electrones se fusionaran con los protones para convertirse en neutrones que, bajo el mismo principio de exclusión sufrirán la degeneración que frenará la fuerza de gravedad quedando entonces una estrella de neutrones. Por último, si la estrella es, aún más masiva, ni la degeneración de los neutrones será suficiente para frenar la inmensa fuerza gravitatoria generada por la masa de la estrella que, continuará la implosión contrayéndose cada vez más hasta desaparecer de nuestra vista convertida en un agujero negro.
¿Qué forma adoptará, qué transición de fase se produce en la materia dentro de una Singularidad?
¡Resulta todo tan complejo!
emilio silvera
Oct
4
¡La Naturaleza! Además de Bella, es… ¡Asombrosa!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

No pocas veces nos encontramos con hechos que aunque han tenido la participación de los humanos, parecen tener su origen en otro ámbito más alto de éste nuestro, en otro lugar donde el entendimiento sería superior y las mentes tuvieran la potestad de ver secretos de la Naturaleza profundamente escondidos. En física tenemos multitud de ejemplos de esto que digo: Me vienen a la mente las ecuaciones conocidas como de Yang-Mills que indicaban que los gluones, las partículas gauge que transportan la fuerza más poderosa de las cuatro conocidas para mantener unidos los Quarks dentro del núcleo, debían carecer de masa, como los fotones y los gravitones.
¿Por qué, entonces la fuerza nuclear fuerte se hace sentir sólo a corta distancia, cuando la luz y la gravitación tienen un alcanza infinito?

La respuesta la tenemos en la Cromodinámica cuántica, la teoría de la fuerza intensa, es que ésta aumenta su poder cuando los Quarks que aprisiona tratan de separarse, en vez de debilitarse como el electromagnetismo y la gravitación con la distancia, la fuerza nuclear fuerte aumenta. Ahí surgió el origen de confinamiento de los Quarks” que, obligados por una “nube” de Gluones, el Bosón mediador de esta fuerza.

También aclaró la Cromodinámica cuántica el funcionamiento de la fuerza débil: el fenómeno antes misterioso de la desintegración radiactiva Beta que pudo ser interpreta ahora como la conversión de un Quark down en un Quark up, convirtiéndose el neutrón, formado por dos Quarks down y un Quark up, en un protón que consiste en dos Quarks up y un Quark down.
La simetría como se pudo ver más tarde, iba a desempeñar un papel destacado en el ulterior desarrollo de la teoría cuántica de campo, y hasta señaló el camino hacia una teoría unificada de la “supersimetría”, capaz de unir todas las partículas y campos bajo el manto de un sólo conjunto de ecuaciones. Yang escribió:
“La Naturaleza parece aprovechar la representación matemática simple de las leyes de simetría. La elegancia intrínseca y la bella perfección del razonamiento matemático involucrado, así como la complejidad y profundidad de sus consecuencias físicas, son una gran fuente de estímulo para los físicos. Uno aprende a alentar la esperanza de que la Naturaleza posee un orden que podemos aspirar a comprender.”



La Simetría de la Naturaleza nos rodea por todas partes y, a nuestro alrededor, mirémos donde podamos mirar, allí está presente y, sin embargo, de ninguna manera son manifiestas todas las simitrías de la Naturaleza. Vivímos en un mundo imperfecto, en el que muchas de las simetrías que aparecen en las ecuciones están rotas.
De todos es bien conocido que, el mismo Yang, en colobaración con Tsung Dao Lee, identificó una discreta simetría en la fuerza débil, llamada violación de la paridad. En 1956, ambos predijeron sobre bases teóricas, que el espín de las partículas provenientes de la desintegración Beta mostrarían una ligera preferencia por una dirección sobre la otra. Experimentos realizados, así lo confirmaron y les valió el Premio Nobel a Lee y Yang (aunque no a Wu por razones desconocidas). Aquello sirvió para atraer la atención sobre el hecho de que la Naturaleza, sea simétrica en algunos aspectos y asimétrica en otros.

Las conocidas como moléculas quirales pueden existir en dos formas, siendo una la imagen especular no superponible de una sobre la otra, incluso aunque ambas tienen la misma composición química … Si bien los experimentos de laboratorio tienden a producir cantidades iguales de las versiones dextrógiras y levógiras, muchas de las moléculas quirales encontradas en organismos vivos proceden de una de las variedades … Por ejemplo, los aminoácidos que forman las proteínas solo aparecen en la forma levógira, mientras que los azúcares del ADN sólo en la dextrógira … ( la dextrosa o glucosa, es un azúcar que desvía el plano de polarización a la derecha) …
Los científicos han debatido desde hace mucho sobre esta asimetría en los seres vivos … Algunos han defendido que un número igual de ambas versiones de la molécula quiral estaba presente en el inicio de la vida, y que sólo durante la evolución biológica tuvo lugar el desequilibrio … Esa visión se ha ido haciendo cada vez menos popular, no obstante, al darnos cuenta de que el proceso fundamentalmente importante del plegamiento de proteínas parece requerir un desequilibrio quiral, aunque el que la naturaleza haya seleccionado la quiralidad derecha o izquierda para cada molécula durante la evolución implicaría procesos extremadamente complejos …


Los cuernos de una cabra paquistaní, la imagen de un ciclón visto desde el espacio, una galaxia o una concha, la chica que arriba nos mira. Son formas que se nos viene a la vista, aspectos de la realidad que llaman poderosamente nuestra atención y nos lleva a preguntar: ¿Por qué se forman y repiten esas figuras una y otra vez, y, en cada caso, una es la “copia exacta” de todas las demás de su género? ¿Es posible que el hombre, al contemplar tales maravillas comenzara a hacer preguntas y diera lugar al nacimiento de la Ciencia? Las matemáticas comenzaron por el asombro que despertaban las formas geométricas y de la misma manera, nacieron los primeros problemas de la física clásica centrada en las órbitas de los astros y las trayectorias de proyectiles.
La geología estudia la forma de las piedras y volcanes y la biología se ocupa de las formas de los seres vivos y de como ésta ha ido cambiando a lo largo del tiempo. Pero, ¿cómo explicar los mecanismos que crean el aspecto exterior de la realidad que podemos percibir? ¿Y por qué existen las mismas estructuras tanto en los organismos vivos como en el mundo inanimado?

Observamos la Naturaleza y podemos contemplar formas armoniosas y elegantes, entendiendo que son cuerpos bellos y simétricos en todas sus versiones. Por ejemplo, amí siempre me llamó la atención la simetría por traslación que se puede encontrar en la disposición de las hojas.
Si nos fijamos y analizamos como se van desarrollando hacia la estremidad de su rama, aparecen con la misma forma inicial. Un asimetría que está presente en los arganismos que cuentan con una estructura en la que se repiten segmentos iguales, con los mismos aparatos y los mismos órganos, como el trilobites, fósil del Paleozóico (lombriz y sanguijuela), y algunas plantas.

En cambio la simetría por rotación se encuentra en los pétalos de una flor o en los tentáculos de una medusa: aunque sus cuerpos roten, permanecen iguales. No debemos olvidar la simetría bilateral que hace que los lados derecho e izquierdo sean iguales y se presenta en casi todos los animales, incluido nosotros. Pero es uniendo estos aspectos cuando se obtienen figuras realmente armoniosas. Si se trata de desplazamiento y rotación en un mismo plano hablamos de una espiral, mientras que en el espacio sería una hélice, aunque ambas se encuentran por todas partes en la naturaleza.
Las simetrías se generan mediante las fuerzas que actúan sobre los cuerpos, descritas por leyes rigurosas e inequívocas, como una fórmula matemática y dependen de la existencia de fuerzas distintas que actúan en diversas direcciones. Si éstas permanecen en equilibrio, no hay preferencia alguna hacia arriba o abajo, a la derecha o a la izquierda, y los cuerpos tenderán a ser perfectamente esféricos, como suele ocurrir en el caso de virus y bacterias. Además, cuando el aspecto no es el de una esfera perfecta, la Naturaleza hará todo lo posible para acercarse a esta forma.

En todo esto, y, para que así ocurra, tiene que estar presente la Gravedad. Veamos:
Parémonos un momento en la gravitación y generalicemos el concepto de simetría, ampliándolo a las fórmulas matemáticas. Veamos la fórmula de Newton, pero expresándola con palabras, de esta manera: la fuerza de atracción entre dos cuerpos es proporcional al producto de dos términos: el primero es la masa de un cuerpo dividido por su distancia al otro. El segundo término es la masa del otro cuerpo dividido por su distancia al primero.
Con símbolos matemáticos escribiríamos:
F![]() (M/d) × (m/d)
(M/d) × (m/d)
Es la misma fórmula de siempre, pero la hemos puesto así para visualizar que la gravitación se puede expresar con una fórmula bastante simétrica: los dos términos de la derecha de la ecuación son “casi” simétricos ¿no es verdad?
Este concepto más general de simetría es muy profundo, porque nos lleva a pensar que la Naturaleza y las leyes físicas que la describen también obedecen a las leyes de la simetría, igual que la materia, en sus manifestaciones externas, las obedece en muchos casos.”
¿Sería posible que la simetría material tuviera un paralelismo en la abstracción intelectual que son las leyes físicas? Desde luego hace falta un esfuerzo mental considerable para pasar de lo material a lo intelectual, pero cuando se profundiza en ellla, la conexión aparece.
En la naturaleza existen muchas cosas que nos pueden llevar a pensar en lo complejo que puede llegar a resultar entender cosas que, a primera vista, parecían sencillas. Me explico:

Fijémonos, por ejemplo, en una Flor de Girasol y en las matemáticas que sus semillas conllevan. Forman una serie de números en la que cada cifra es la suma de las dos precedentes (por ejemplo 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…) se denomina, en términos matemáticos, sucesión de Fibonacci, una ley que se cumple incluso en el mundo vegetal, como hemos podido comprobar en las semillas del girasol, dispuestas en espiral y que respetan ésta fórmula.
En el mundo inorgánico las leyes de la cristalización del agua congelada, determinadas por las fuerzas que actúan entre las moléculas, hacen que los cristales adopten formas que son infinitas y varían con respecto a un tema común: la estrella de seis puntas. Sin embargo, los planetas son esféricos porque han nacido en la nube primordial que rodeaba al Sol, atrayendo materia indeferentemente de todas partes.
Por otro lado, cuando la fuerza de la Gravedad actúa en una dirección y permite distinguir lo alto de lo bajo, los cuerpos asumen formas que gozan de simetría por rotación, en torno a un eje vertical, como las flores, los árboles, las medusas. Si este organismo presente ojos y boca sobre la parte anterior del cuerpo para alcanzar la comida antes que sus competidores (que es lo que sucede con los animales superiores) tenderá a mantener una correrspondencia bilateral, lo que hace relativamente intercambiables derecha e izquierda.
Los seres humanos (su exterior) somos buenos ejemplos de esto. Tenemos una casi igualdad entre las dos partes de nuestro cuerpo que se obtendrían dividiéndolo por una línea que pasa por el centro de la nariz y por el centro del ombligo. La figura de arriba muestra el famoso estudio sobre la simetría del cuerpo humano.

¿Cómo podemos llegar a la simetría presente en las manchas del leopardo? Pues, tiene su explicación científica, tanto en este animal como en otros felinos, ocurre ésta particularidad de ser poseedores de una piel exterior que los singulariza de otros por su perfecta simetría y belleza de las formas en su conjunto.
Claro que, en la Naturaleza, nada ocurre porque sí, todo tiene su por qué, y, todo lo que en ella podemos contemplar posee una funcionalidad que está directamente relacionada con su mecánica, con el medio en el que habita, con lo que el Universo espera que haga en su medio y, para ello, dota a cada figura con aquellos “trajes” que mejor les permita realizar aquello para lo que están destinados.

Simetría en las galaxias espirales
Vamos a generalizar un paso más el concepto de simetría, planteándonos ahora si es posible que una ley física se cumpla en cualquier lugar. ¿En cualquier lugar… de dónde?, ¿de nuestra ciudad?, ¿de nuestro planeta? No: del universo. Una ley que fuera válida en cualquier lugar del universo sería una ley simétrica respecto al espacio. Se cumpliría dondequiera que se hiciese un experimento para comprobarla.
Fíjense que nuestra idea de simetría se va haciendo más compleja y más profunda. Ahora no nos detenemos en ver si la forma material de un objeto es simétrica, ni de si la escritura de una fórmula matemática es simétrica. Ahora nos preguntamos si una ley física es válida en todo el Universo.
La otra simetría interesante para una ley física es la que se refiere al tiempo. Cierta ley física se cumple ahora; ¿antes también?, ¿se cumplirá pasado algún tiempo? Una ley que fuera cierta en cualquier instante de la historia del universo sería una ley simétrica respecto al tiempo.
Lo que ahora nos preguntamos es: ¿son simétricas o no las leyes de la física?

Simetría radial de la Gravedad
Hasta donde alcanzan nuestras medidas, las leyes físicas (y, por tanto, la interacción gravitatoria) sí son simétricas respecto al espacio y respecto al tiempo. En cualquier lugar y momento temporal del universo, la Naturaleza se comporta igual que aquí y ahora en lo que se refiere a estas leyes.
Esta simetría es un arma muy poderosa para investigar hacia el pasado y hacia el futuro, ya que nos permite suponer (y, en la medida en que confiemos en la seguridad de la simetría,conocer) condiciones locales donde jamás podremos llegar por la distancia espacial y temporal que nos separa de muchas partes del universo. Así, por ejemplo, gracias a esta simetría, podemos calcular que el Sol lleva 5.000 millones de años produciendo energía y que le quedan, probablemente, otros 5.000 millones hasta que consuma toda su masa. Esto lo podemos aventurar suponiendo que en ese enorme tramo de 5.000 + 5.000 = 10.000 millones de años las leyes físicas que determinan los procesos mediante los cuales el Sol consume su propia masa como combustible (las reacciones nucleares que le permiten producir energía), fueron, son y serán las mismas aquí en el Brazo de orión donde nos encontramos como en los arrabales de la Galaxia Andrómeda donde luce una estrella como nuestro Sol que, también envía luz y calor a sus planetas circundantes, y, por muy lejos que podamos mirar, siempre veremos lo mismo.

Por tanto, en cierto modo, la simetría se vuelve tan importante o más que la propia ley física.
La regularidad de las formas de la Naturaleza se refleja incluso en la cultura humana, que desde siempre intenta inspirarse en el mundo natural para conformar su propio mundo. Existen hélices en las escaleras de palacios, castillos y minaretes y en las decoraciones de esculturas y columnas. Las espirales abundan en los vasos, en los bajorrelieves, en los cuadros, en las esculturas en los collares egipcios, griegos, celtas, precoolombinos e hindúes e, incluso, en los tatuajes con los que los maoríes neozelandeses se decoran el rostro.

La búsqueda de la perfección geométrica y de las propiedades matemáticas pueden ser también una guía importante en el estudio científico del mundo. Paul Dirac, una de los padres de la moderna mecánica cuántica, solía decir que “si una teoría es bella desde el punto de vista matemático, muy probablemente es también verdadera”.

A todo esto, no debemos olvidar que todo, sin excepción, en nuestro Universo, está sometido a la Entropía que nos trae el paso inexorable de eso que llamamos “Tiempo”, y que, convierte perfectas simetrias de joven belleza, en deteriorados objetos o entidades que, nos viene a recordar que nada es perpetuo, que todo pasa y se transforma.

Dos son uno. Las dos mitades que, al unirse completan el todo del Ser
Un dolor que llevo dentro de mí es el no poder contemplar la verdadera belleza que, estando presente en los seres vivos inteligentes, en la mayoría de los casos, se nos queda oculta a nuestra percepción, toda vez que, esa clase de belleza que no podemos ver pero sí percibir, sólo la podemos captar con el trato y la convivencia y, verdaderamente, tengo que admitir que, algunas bellezas que he tenido la suerte de poder “ver” con los ojos del espíritu, llegan a ser segadoras, deslumbrantes, su explendor es muy superior al de la estrella más brillante del cielo, y, seguramente (estoy seguro) como a muchos de ustedes les pasa, tengo la suerte de tenerla junto a mí desde hace muchos años. y, si pienso en ello en profundidad y detenimiento, no tengo más tremedio que concluir que es ese brillo y esplendor el que me da la fuerza para seguir cada dia en la dura lucha que nos ha tocado participar.
¡Sí que es importante la Belleza! Dirac tenía toda la razón.
emilio silvera
Oct
3
Entropía, Gravedad. Materia… ¡Vida!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (7)
Comments (7)
La verdadera Historia de la Teoría del Caos

Diagrama de la trayectoria del sistema de Lorenz para los valores r = 28, σ = 10, b = 8/3.
Teoría del cáos es la denominación popular de la rama de las matemáticas, la física y otras disciplinas científicas que trata ciertos tipos de sistemas dinámicos muy sensibles a las variaciones en las condiciones iniciales. Pequeñas variaciones en dichas condiciones iniciales pueden implicar grandes diferencias en el comportamiento futuro, imposibilitando la predicción a largo plazo. Esto sucede aunque estos sistemas son en rigor determinísticos, es decir; su comportamiento puede ser completamente determinado conociendo sus condiciones iniciales.
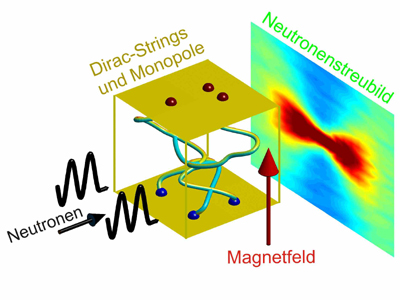
Montaje experimental. Foto: HZB, D.J.P. Morris y A. Tennant. Monopolos magneticos .
Hubo un tiempo, el el Universo muy temprano, en el que la temperatura estaba encima de algunos cientos de veces la masa del protón, cuando la simetría aún no se había roto, y la fuerza débil y electromagnética no sólo eran la misma matemáticamente, sino realmente la misma. Un físico que hibiera podido estar allí presente, en aquellos primeros momento, no habría podido observar ninguna diferencia real entre las fuerzas producidas por el intercambio de estas cuatro partículas: las W, la Z y el Fotón.

Muchas son las sorpresas que nos podríamso encontrar en el universo primitivo, hasta la presencia de agua ha sido detectada mediante la técnica de lentes gravitacionales en la galaxia denominada MG J0414+0534 que está situada en un tiempo en el que el Universo sólo tenía dos mil quinientos millones de años de edad. El equipo investigador pudo detectar el vapor de agua presente en los chorros de emisión de un agujero negro supermasivo. Este tipo de objeto es bastante raro en el universo actual. El agua fue observada en forma de mases, una emisión de radiación de microondas provocada por las moléculas (en este caso de agua) al ser amplificadas por una onda o un campo magnético.

Los astrónomos han encontrado el más distante indicio de agua en el Universo hasta la fecha. El vapor de agua se cree está contenido en un máser, un chorro sale de un agujero negro supermasivo en el centro de una galaxia, denominada MG J0414 0534. La radiación del agua máser fue emitida cuando el Universo tenía sólo alrededor de 2,5 mil millones de años, una quinta parte de su actual edad. “La radiación que se ha detectado ha tardado 11.1 mil millones de años para llegar a la Tierra, dijo el Dr. John McKean del Instituto de Radio Astronomía (ASTRON) en los Paises Bajos. “Sin embargo, debido a que el Universo se ha expandido como un globo inflado en todo ese tiempo, extiendiendose hacia afuera la distancia entre los puntos ha aumentado y la galaxia en la que el agua se ha detectado esta a aproximadamente 19,8 mil millones de años luz de nosotros actualmente.”
Siguiendo con el trabajo, dejemos la noticia de más arriba (sólo insertada por su curiosidad y rareza), y, sigamos con lo que hemos contado repetidas veces aquí de las fuerzas y la simetría antes de que, el universo se expandiera y enfriara para que, de una sóla, surgieran las cuatro fuerzas que ahora conocemos: Gravedad que campa sola y no quiere juntarse con las otras fuerzas del Modelo Estándar, el electromagnetismo y las nucleares débil y fuerte.
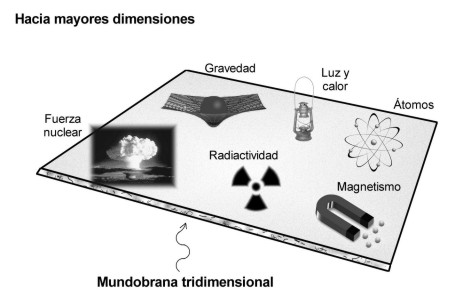
Las fuerzas de la naturaleza que gobiernan la electricidad, el magnetismo, la radiactividad y las reacciones nucleares están confinadas a un “mundobrana” tridimensional, mientras que la gravedad actúa en todas las dimensiones y es consecuentemente más débil. Seguramente ese será el motivo por el cual, encontrar al Bosón mediador de la fuerza, el Gravitón, resulta tan difícil.
De manera similar, aunque menos clara, las teorías de supersimetrías conjeturaban que las cuatro fuerzas tal vez estaban ligadas por una simitría que se manifestaba en los niveles de energía aún mayores que caracterizaban al universo ya antes del big bang. La intodución de un eje histórico en la cosmolo´gia y la física de particulas (como decía ayer en uno de los trabajos), beneficio a ambos campos. Los físicos proporcionaron a los cosmólogos una amplia gama de herramientas útiles para saber cómo se desarrolló el universo primitivo. Evidentemente, el Big Bang no fue una muralla de fuego de la que se burló Hoyle, sino un ámbito de suscesos de altas energías que muy posiblemente pueden ser comprensibles en términos de teoría de campo relativista y cuántica.

La cosmología, por su parte, dio un tinte de realidad histórica a las teorías unificadas. Aunque ningún acelerador concebible podrían alcanzar las titánicas energías supuestas por las grandes teorías unificadas y de la supersimetría, esas exóticas ideas aún pueden ser puestas a prueba, investigando su las partículas constituyentes del universo actual son compatibles con el tipo de historia primitiva que implican las teorías.
Gell-Mann, el premio Nobel de física, al respeto de todo esto decía: “Las partículas elementales aparentemente proporcionan las claves de algunos de los misterios fundamentales de la Cosmología temprana… y resulta que la Cosmología brinda una especia de terreno de prueba para alguna de las ideas de la física de partículas elementales.” Hemos podido llegar a descubrir grandes secretos de la naturaleza mediante los pensamientos que, surgidos de la mente desconocida y misteriosa de algunos seres humanos, han podido ser intuidos mediante ráfagas luminosas que nunca sabremos de dónde pudieron surgir )Lorentz, Planck, Einstein, Heisenmberg, Dirac, Eddigton, Feymann, Wheeler… Y, una larga lista de privilegiados que pudieron ver, lo que otros no podían.

Moléculas, átomos y conexiones para formar pensamientos
Hemos llegado a poder discernir la relación directa que vincula el tamaño, la energía de unión y la edad de las estructuras fundamentales de la Naturaleza. Una molécula es mayor y más fácil de desmembrar que un átomo; lo mismo podemos decir de un átomo respecto al núcleo atómico, y de un núcleo con respecto a los quarks que contiene. La cosmología sugiere que esta relación resulta del curso de la historia cósmica, que los quarks se unieron primero en las energías extremadamente altas del big bang original y que a medida que el Universo se expandió, los protones y neutrones compuestos de quarks se unieron para formar núcleos de átomos, los cuales, cargados positivamente, atrajeron a los electrones cargados con electricidad negativa estableciéndose así como átomos completos, que al unirse formaron moléculas.

Si es así (que lo es), cuanto más íntimamente examinemos la Naturaleza, tanto más lejos hacia atrás vamos en el tiempo. Alguna vez he puesto el ejemplo de mirar algo que no es familiar, el dorso de la mano, por ejemplo, e imaginemos que podemos observarlo con cualquier aumento deseado.
Con un aumento relativamente pequeño, podemos ver las células de la piel, cada una con un aspecto tan grande y complejo como una ciudad, y con sus límites delineados por la pared celular. Si elevamos el aumento, veremos dentro de la célula una maraña de ribosomas serpenteando y mitocondrias ondulantes, lisosomas esféricos y centríolos, cuyos alrededores están llenos de complejos órganos dedicados a las funciones respiratorias, sanitarias y de producción de energía que mantienen a la célula.
Ya ahí tenemos pruebas de historia. Aunque esta célula particular solo tiene unos pocos años de antigüedad, su arquitectura se remonta a más de mil millones de años, a la época en que aparecieron en la Tierra las células eucariota o eucarióticas como la que hemos examinado.
Abajo vemos el dorso de la mano algo aumentado

Para determinar dónde obtuvo la célula el esquema que le indicó como formarse, pasemos al núcleo y contemplemos los delgados contornos de las macromoléculas de ADN segregadas dentro de sus genes. Cada una contiene una rica información genética acumulada en el curso de unos cuatro mil millones de años de evolución.

Almacenado en un alfabeto de nucleótidos de cuatro “letras”- hecho de moléculas de azúcar y fosfatos, y llenos de signos de puntuación, reiteraciones para precaver contra el error, y cosas superfluas acumuladas en los callejones sin salida de la historia evolutiva-, su mensaje dice exactamente cómo hacer un ser humano, desde la piel y los huesos hasta las células cerebrales.
Si elevamos más el aumento veremos que la molécula de ADN está compuesta de muchos átomos, con sus capas electrónicas externas entrelazadas y festoneadas en una milagrosa variedad de formas, desde relojes de arena hasta espirales ascendentes como largos muelles y elipses grandes como escudos y fibras delgadas como puros. Algunos de esos electrones son recién llegados, recientemente arrancados a átomos vecinos; otros se incorporaron junto a sus núcleos atómicos hace más de cinco mil millones de años, en la nebulosa de la cual se formó la Tierra.
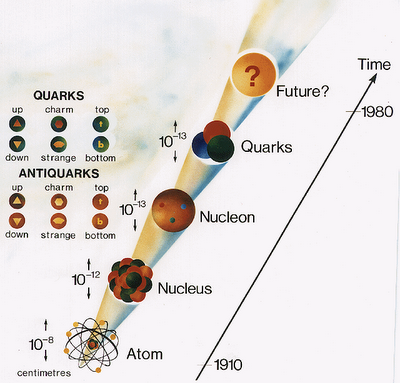
Una molécula es mayor y más fácil de desmembrar que un átomo; lo mismo podemos decir de un átomo respecto al núcleo atómico, y de un núcleo con respecto a los quarks que contiene. Sion embargo, nos queda la duda de: ¿qué podrá haber más allá de los Quarks?
¿Qué no podremos hacer cuando conozcamos la naturaleza real del átomo y de la luz? El fotón, ese cuánto de luz que parece tan insignificante, nos tiene que dar muchas satisfacciones y, en él, están escondidos secretos que, cuando sean revelados, cambiará el mundo. Esa imagen de arriba que está inmersa en nosotros en en todo el Universo, es la sencillez de la complejidad. A partir de ella, se forma todo: la muy pequeño y lo muy grande.

Si elevamos el aumento cien mil veces, el núcleo de un átomo de carbono se hinchará hasta llenar el campo de visión. Tales núcleos y átomos se formaron dentro de una estrella que estalló mucho antes de que naciera el Sol. Si podemos aumentar aún más, veremos los tríos de quarks que constituyen protonesy neutrones. Los quarks han estado unidos desde que el Universo sólo tenía unos pocos segundos de edad.
Al llegar a escalas cada vez menores, también hemos entrado en ámbitos de energías de unión cada vez mayores. Un átomo puede ser desposeído de su electrón aplicando sólo unos miles de electrón-voltios de energía. Sin embargo, para dispersar los nucleones que forman el núcleo atómico se requieren varios millones de electrón-voltios, y para liberar los quark que constituyen cada nucleón.

Uno de los misterios de la naturaleza, están dentro de los protoes y neutrones que, conformados por Quarks, resulta que, si estos fueran liberados, tendrían independientemente, más energía que el protónque conformaban. ?cómo es posible eso?
Introduciendo el eje de la historia, esta relación da testimonio del pasado de las partículas: las estructuras más pequeñas, más fundamentales están ligadas por niveles de energía mayores porque las estructuras mismas fueron forjadas en el calor del big bang. Esto implica que los aceleradores de partículas, como los telescopios, funcionen como máquinas del tiempo. Un telescopio penetra en el pasado en virtud del tiempo que tarda la luz en desplazarse entre las estrellas; un acelerador recrea, aunque sea fugazmente, las condiciones que prevalecían en el Universo primitivo. El acelerador de 200 Kev diseñado en los años veinte por Cockroft y Walton reproducía algunos de los sucesos que ocurrieron alrededor de un día después del comienzo del big bang. Los aceleradores construidos en los años cuarenta y cincuenta llegaron hasta la marca de un segundo. El Tevatrón del Fermilab llevó el límite a menos de una milmillonésima de segundo después del comienzo del Tiempo. El nuevo LHC proporcionara un atisbo del medio cósmico cuando el Universo tenía menos de una billonésima de segundo de edad.
Esta es una edad bastante temprana: una diez billonésima de segundo es menos que un pestañeo con los párpados en toda la historia humana registrada. A pesar de ello, extrañamente, la investigación de la evolución del Universo recién nacido indica que ocurrieron muchas cosas aún antes, durante la primera ínfima fracción de un segundo.
Todos los teóricos han tratado de elaborar una explicación coherente de los primeros momentos de la historia cósmica. Por supuesto, sus ideas fueron esquemáticas e incompletas, muchas de sus conjeturas, sin duda, se juzgaran deformadas o sencillamente erróneas, pero constituyeron una crónica mucho más esclarecedora del Universo primitivo que la que teníamos antes.
A los cien millones de años desde el comienzo del tiempo, aún no se habían formado las estrellas, si acaso, algunas más precoces. Aparte de sus escasas y humeantes almenaras, el Universo era una sopa oscura de gas hidrógeno y helio, arremolinándose aquí y allá para formar protogalaxias.

He aquí la primera imagen jamás obtenida de antimateria, específicamente un “anti-átomo” de anti-hidrógeno. Este experimento se realizó en el Aparato ALPHA de CERN, en donde los anti-átomos fueron retenidos por un récord de 170 milisegundos (se atraparon el 0.005% de los anti-átomos generados).
A la edad de mil millones de años, el Universo tiene un aspecto muy diferente. El núcleo de la joven Vía Láctea arde brillantemente, arrojando las sobras de cumulonimbos galácticos a través del oscuro disco; en su centro brilla un quasar blanco-azulado. El disco, aún en proceso de formación, es confuso y está lleno de polvo y gas; divide en dos partes un halo esférico que será oscuro en nuestros días, pero a la sazón corona la galaxia con un brillante conjunto de estrellas calientes de primera generación.

Para determinar dónde obtuvo la célula el esquema que le indicó como formarse, pasemos al núcleo y contemplemos los delgados contornos de las macromoléculas de ADN segregadas dentro de sus genes. Cada una contiene una rica información genética acumulada en el curso de unos cuatro mil millones de años de evolución.

Claro que, nuestra historia está relacionada con todo lo que antes de llegar la vida al Universo pudo pasar. ¡Aquella primera célula! Se replicó en la sopa primordial llamada Protoplasma vivo y, siguió evolucionando hasta conformar seres de diversos tipos y, algunos, llegaron a adquirir la conciencia.
Macromolécula
Almacenado en un alfabeto de nucleótidos de cuatro “letras”- hecho de moléculas de azúcar y fosfatos, y llenos de signos de puntuación, reiteraciones para precaver contra el error, y cosas superfluas acumuladas en los callejones sin salida de la historia evolutiva-, su mensaje dice exactamente cómo hacer un ser humano, desde la piel y los huesos hasta las células cerebrales.
célula cerebral
Si elevamos más el aumento veremos que la molécula de ADN está compuesta de muchos átomos, con sus capas electrónicas externas entrelazadas y festoneadas en una milagrosa variedad de formas de una rareza y de una incleible y extraña belleza que sólo la Naturaleza es capaz de conformar.
Molécula de ADN
Si elevamos el aumento cien mil veces, el núcleo de un átomo de carbono se hinchará hasta llenar el campo de visión. Tales núcleos átomos se formaron dentro de una estrella que estalló mucho antes de que naciera el Sol. Si podemos aumentar aún más, veremos los tríos de quarks que se constituyen en protones y neutrones.

Átomo de Carbono
Los quarks han estado unidos desde que el Universo sólo tenía unos pocos segundos de edad. Una vez que fueron eliminados los antiquarks, se unieron en tripletes para formar protones y neutrones que, al formar un núcleo cargado positivamente, atrayeron a los electrones que dieron lugar a formar los átomos que más tarde, conformaron la materia que podemos ver en nuestro universo.
Al llegar a escalas cada vez menores, también hemos entrado en ámbitos de energías de unión cada vez mayores. Un átomo puede ser desposeído de su electrón aplicando sólo unos miles de electrón-voltios de energía. Sin embargo, para dispersar los nucleones que forman el núcleo atómico se requieren varios millones de electrón-voltios, y para liberar los quarks que constituyen cada nucleón se necesitaría cientos de veces más energía aún.
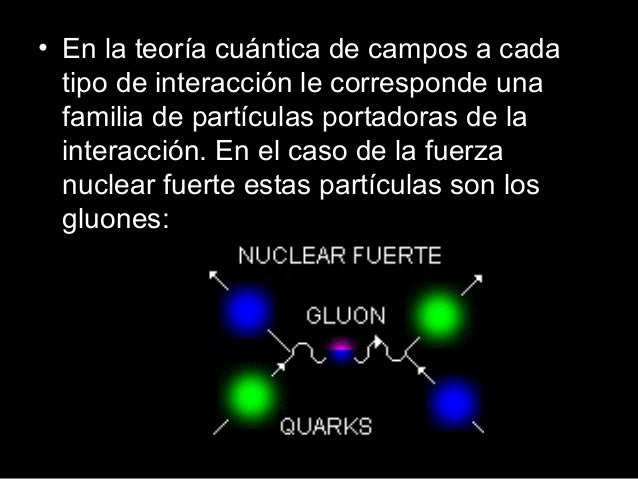
Los Quarks dentro del núcleo están sometidos a la Interacción fuerte, es decir, la más potente de las cuatro fuerzas fundamentales del Universo, la que mantiene a los Quarks confinados dentro del núcleo atómico por medio de los Gluones.
Introduciendo el eje de la historia, esta relación da testimonio del pasado de las partículas: las estructuras más pequeñas, más fundamentales están ligadas por niveles de energía mayores porque las estructuras mismas fueron forjadas en el calor del big bang.

Haces de protones que chocan cuando viajan a velocidad relativista en el LHC
Esto implica que los aceleradores de partículas, como los telescopios, funcionen como máquinas del tiempo. Un telescopio penetra en el pasado en virtud del tiempo que tarda la luz en desplazarse entre las estrellas; un acelerador recrea, aunque sea fugazmente, las condiciones que prevalecían en el Universo primitivo.
El acelerador de 200 kev diseñado en los años veinte por Cockroft y Walton reproducía algunos de los sucesos que ocurrieron alrededor de un día después del comienzo del big bang.

Aquel acelerador nada tenía que ver con el LHC de ahora, casi un siglo los separa
Los aceleradores construidos en los años cuarenta y cincuenta llegaron hasta la marca de un segundo. El Tevatrón del Fermilab llevó el límite a menos de una milmillonésima de segundo después del comienzo del Tiempo. El nuevo supercolisionador superconductor proporcionara un atisbo del medio cósmico cuando el Universo tenía menos de una billonésima de segundo de edad.
El Tevatrón del Fermilab ya estaba en el camino de la modernidad en los avances de la Física
Esta es una edad bastante temprana: una diez billonésima de segundo es menos que un pestañeo con los párpados en toda la historia humana registrada. A pesar de ello, extrañamente, la investigación de la evolución del Universo recién nacido indica que ocurrieron muchas cosas aún antes, durante la primera ínfima fracción de un segundo.
Todos los teóricos han tratado de elaborar una explicación coherente de los primeros momentos de la historia cósmica. Por supuesto, sus ideas fueron esquemáticas e incompletas, muchas de sus conjeturas, sin duda, se juzgaran deformadas o sencillamente erróneas, pero constituyeron una crónica mucho más aclaradora del Universo primitivo que la que teníamos antes.
Recreación del Universo primitivo
Bueno amigos, el trabajo era algo más extenso y entrábamos a explicar otros aspectos y parámetros implicados en todo este complejo laberinto que abarca desde lo muy grande hasta la muy pequeño, esos dos mundos que, no por ser tan dispares, resultan ser antagónicos, porque el uno sin el otro no podría existir. Otro día, seguiremos abundando en el tema apasionante que aquí tratamos.
emilio silvera
















 Totales: 83.490.798
Totales: 83.490.798 Conectados: 60
Conectados: 60