Oct
31
¿La invasión Silenciosa?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
No estamos prestando atención. Sin embargo, la invasión se está produciendo y cada vez es más fuerte. Cuando queramos poner remedio… ¡será tarde! La computación cuántica puede conseguir desvelar secretos profundamente escondidos que, por medios físicos y humanos, no hemos sido capaces de conseguir.

El revolucionario chip cuántico de Google que resuelve en 5 minutos lo que hoy tomaría 10 cuatrillones de años.
El chip es el último desarrollo en un campo conocido como computación cuántica, que intenta utilizar los principios de la física de partículas para crear un nuevo tipo de computadora increíblemente poderosa.
Hartmut Neven dirige el laboratorio de inteligencia artificial cuántica de Google que creó Willow y se describe a sí mismo como el “optimista jefe” del proyecto.
Le dijo a la BBC que Willow se utilizaría en algunas aplicaciones prácticas, pero se negó, por ahora, a proporcionar más detalles.
Pero un chip de este tipo capaz de realizar aplicaciones comerciales no aparecerá antes de finales de la década, dijo:
“Inicialmente estas aplicaciones serían la simulación de sistemas donde los efectos cuánticos son importantes.
“Por ejemplo, es relevante cuando se trata del diseño de reactores de fusión nuclear, para entender el funcionamiento de medicamentos y el desarrollo farmacéutico, y para desarrollar mejores baterías para automóviles y otra larga lista de tareas similares”.
Neven le dijo a la BBC que el rendimiento de Willow significaba que era el “mejor procesador cuántico construido hasta la fecha”.

Pero el profesor Alan Woodward, un experto en informática de la Universidad de Surrey, en Inglaterra, dice que las computadoras cuánticas serán mejores en una variedad de tareas que las computadoras “clásicas” actuales, pero no las reemplazarán.
Advierte contra la exageración de la importancia del logro de Willow en una sola prueba.
“Hay que tener cuidado de no comparar manzanas con naranjas”, le dijo a la BBC.
El problema que Google eligió como punto de referencia de rendimiento estaba “hecho a medida para una computadora cuántica”, por lo que no logra demostrar “un aceleramiento universal en comparación con las computadoras clásicas”.

No obstante, dijo que Willow representaba un progreso significativo, en particular en lo que se conoce como corrección de errores.
En términos muy simples, cuanto más útil es una computadora cuántica, más cúbits tiene.
Sin embargo, un problema importante con esta tecnología es que es propensa a errores, una tendencia que anteriormente ha aumentado cuanto más cúbits tiene un chip.

Pero los investigadores de Google afirman que han revertido esta situación y han logrado diseñar y programar el nuevo chip de manera que la tasa de error se redujera en todo el sistema a medida que aumentaba el número de cúbits.
Fue un gran “avance” que resolvió un desafío clave que el campo había perseguido “durante casi 30 años”, dice Neven.
El experto le dijo a la BBC que era comparable a “si tuvieras un avión con un solo motor: eso funcionará, pero dos motores son más seguros, y cuatro motores son aún más seguros”.

Los errores son un obstáculo significativo para crear computadoras cuánticas más potentes y el desarrollo fue “alentador para todos los que se esfuerzan por construir una computadora cuántica práctica”, dijo el profesor Woodward.
Pero el propio Google señala que para desarrollar computadoras cuánticas útiles, la tasa de error aún tendrá que ser mucho menor que la mostrada por Willow.
Se espera un crecimiento del mercado que podría alcanzar los 72 mil millones de dólares para 2035, impulsado por la aplicación de la tecnología en campos como la medicina (descubrimiento de fármacos), la química y la ciberseguridad (criptografía post-cuántica). La integración de la computación cuántica con la inteligencia artificial (IA) abrirá nuevas soluciones innovadoras para retos sociales y empresariales.


Máquinas tan potentes y que contienen en sus Chips Prodigiosos tanta información, llegarán a estar conectadas unas con otras y formar un inconmensurable cerebro de conocimiento que sobrepasará en mucho al de los humanos. Cuando sean conscientes de cómo somos, de nuestras debilidades, nuestra parte animal e irracional, nuestro egoísmo, de lo que somos capaces en ciertas situaciones… ¿No decidirán intervenir y hacerse cargo del rumbo de este “barco” que llamamos Tierra, al comprender que no vamos a puerto seguro?
Está claro que cuando estos ordenadores cuánticos sean una realidad, ningún Gobierno del mundo querrá `rescindir de ellos, y, de la misma manera, las grandes corporaciones los tendrán. Así las cosas, si como pienso unen sus capacidades todos los O.C. del mundo…. ¡Habrán conquistado a toda la Humanidad sin esfuerzo alguno! Estaremos en sus manos, y, realmente… ¿Qué podremos hacer! Las máquinas pueden dar órdenes a todo lo que está bajo su dominio que (dicho sea de paso), será todo lo importante, con lo cual, tendrán en “sus manos” nuestras vidas.
Todo esto da un poco de miedo, no niego que no sea mejor que la humanidad cuente con adelantos que le haga más fácil la vida pero… ¡Ponernos en manos de máquinas pensantes!
Emilio Silvera V.
Oct
31
A veces nos podría dar la impresión de que, el Universo, nos esperaba
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo y... ¿nosotros? ~
Clasificado en El Universo y... ¿nosotros? ~
 Comments (1)
Comments (1)


Surgidos de la materia creada por el Universo en las estrellas, dichos elementos químicos formaron parte de los planetas del Sistema solar, la Tierra fue la elegida por el Azar para situarse en el lugar adecuado respecto al Sol para que el agua líquida corriera por el planeta. Surgieron seres inferiores plasmados en muchas especies y, una de ellas evolucionó hasta alcanzar consciencia de Ser. Observamos y pudimos plantear preguntas que, a medida que íbamos comprendiendo las cosas eran más y más complejas.
En este lugar venimos hablando de cuestiones de Física, del Universo, de vez en cuando tocamos la I.A. y osamos comentar sobre la Conciencia y la Mente, ese “algo” inmaterial que puede generar ideas y pensamientos, que sale del cerebro y se proyecta a las más lejanas regiones del Universo. Ante estas complejas cuestiones, el hecho mismo de que estemos aquí para plantearlas, como seres racionales y pensantes, es un auténtico “milagro”, ya que significa que deben haber ocurrido, necesariamente, complejas secuencias de sucesos para que a partir de la materia “inerte”, la mezcla de materiales complejos en condiciones excepcionales, hiciera surgir la vida.
Realmente nadie ha podido asegurar el camino que siguió la Naturaleza para que la vida esté presente. NO pocos creen que fue una colisión planetaria la que trajo las esporas que germinaron en la Tierra hacia la Vida, la llaman Panspermia.
Reparando en estas coincidencias cósmicas, el físico Freeman Dyson escribió en cierta ocasión:
“Cuando miramos en el universo e identificamos los muchos accidentes de la física y la astronomía que han colaborado en nuestro beneficio, casi parece que el universo debe haber sabido, en cierto sentido, que nosotros íbamos a venir“.
Particularmente, creo que la vida llegó a este planeta por una serie de circunstancias muy especiales: tamaño, temperatura y distancia al Sol (idónea para no morir congelados o asados por una temperatura extrema), su atmósfera primitiva, las chimeneas marinas, la mezcla de elementos, y su transformación evolutiva, el oxígeno, la capa de ozono, los mares y océanos ¡el agua!, la radiación…

Este podría ser aquel protoplasma vivo del que surgió aquella primera célula replicante que comenzó, la fascinante aventura de la vida. Chimeneas marinas (Húmeros negros), volcanes, mezclas de distintos elementos químicos y todo ello unido a las condiciones reinantes en el planeta… ¡Lo hizo posible!
Dada la inmensidad de nuestro universo, nuestro mismo caso (un sistema solar con planetas entre los que destaca uno que contiene vida inteligente), se habrá dado en otros muchos mundos similares o parecidos al nuestro, tanto en nuestra misma galaxia, la Vía Láctea, como en otras más lejanas. Me parece una estupidez que se pueda pensar que estamos solos en el universo; la lógica nos dice todo lo contrario.

Nuestro Sol, gracias al cual podemos existir, es una de las cien mil millones de estrellas que contiene nuestra Galaxia. Existen miles de millones de sistemas solares compuestos por estrellas y planetas como los nuestros. ¿En verdad se puede pensar que somos los únicos seres vivos inteligentes de la galaxia?
Me parece que no. Creo que estamos bien acompañados.
El problema radica en que es difícil coincidir en el tiempo y en las enormes distancias que nos pueden separar. Cuántas Civilizaciones se habrán extinguidos y cuántas habrán surgido. Con las que se fueron se borraron todos sus logros y saberes y, las nuevas, estarán comenzando de nuevo ese difícil camino del saber. ¿El encuentro? ¡No será nada fácil que se produzca!
A veces pienso que, como la Naturaleza es “sabia”, ha determinado una separación insalvable entre seres inteligentes para evitar ese encuentro, al menos hasta que, debidamente avanzados, hayamos dejado atrás egoísmos y esa carga animal que llevamos con nosotros.

Claro que, también estaba allí la Entropía para dejar claro que nada es Eterno
El tiempo y el espacio nacieron juntos cuando nació el universo en el Big Bang, llevan creciendo unos 13.500-18.000 millones de años y, tanto el uno como el otro, son enormes, descomunalmente grandes para que nuestras Mentes lo asimilen de forma real, y, mucho menos, poder dominar ese inconmensurable Espacio para poder recorrer aunque solo sea una mínima parte.

“Representación artística del sistema planetario Próxima Centauri, con el exoplaneta recién descubierto, Próxima c (d); y el planeta hallado en 2016, Próxima b (i). SCIENCE ADVANCES”
La estrella más cercana a nosotros, Alfa Centauri, está situada a una distancia de 4’22 años luz. El año luz es la distancia que recorre la luz, o cualquier otra radiación electromagnética, en un año trópico a través del espacio. Un año luz es igual a 9’4607×1012 Km, ó 63.240 unidades astronómicas, ó 0’3066 parsecs.
La luz viaja por el espacio a razón de 299.792.458 m/s, una Unidad Astronómica es igual a 150 millones de Km (la distancia que nos separa del Sol). El pársec es una unidad galáctica de distancias estelares, y es igual a 3’2616 años luz o 206.265 unidades astronómicas. Existen para las escalas galácticas o intergalácticas, otras medidas como el kilo-parsec (Kpc) y el mega-parsec (Mpc).
Nos podríamos entretener para hallar la distancia que nos separa de un sistema solar con posibilidad de albergar vida y situado a 118 años luz de nosotros. ¿Cuándo llegaríamos allí?
Es, claramente, la estrella más cercana al Sol, aunque su distancia esté en torno a los 40 billones de Km. (un 4 seguido por 13 ceros) de kilómetros, unos 4.35 años-luz. La tercera componente, no obstante, se encuentra algo más cercana, pues orbita a las otras dos y ahora se sitúa a unos 4.22 años-luz. Es llamada por eso Próxima Centauri. Ésta sí es, sin excepciones ni matices, la estrella que está más cerca de nuestro Sol.

“NASA tiene planes para una misión interestelar a Alfa Centauri, el sistema estelar más cercano al Sol. … Si cambiara su trayectoria y la enviásemos a su velocidad actual de 21.000 kilómetros por hora a Alfa Centauri, la Voyager 1 tardaría 80.000 años en llegar.”
Nuestros ingenios espaciales que enviamos a las lunas y planetas vecinos, viajan por el espacio exterior a 60.000 Km/h. Es una auténtica frustración el pensar lo que tardarían en llegar a la estrella cercana Alfa Centauri a más de 4 años luz.
Así que la distancia es la primera barrera infranqueable (al menos de momento). La segunda, no de menor envergadura, es la coincidencia en el tiempo. Se piensa que una especie tiene un tiempo limitado de existencia antes de que, por una u otra razón, desaparezca.

Nosotros mismos, si pensamos en el tiempo estelar o cósmico, llevamos aquí una mínima fracción de tiempo. Dadas las enormes escalas de tiempo y de espacio, es verdaderamente difícil coincidir con otras civilizaciones que, probablemente, existieron antes de aparecer nosotros o vendrán después de que estemos extinguidos. Por otra parte, el desplazarse por esas distancias galácticas de cientos de miles de millones de kilómetros, no parece nada fácil, si tenemos en cuenta la enorme barrera que nos pone la velocidad de la luz. Esta velocidad, según demuestra la relatividad especial de Albert Einstein, no se puede superar en nuestro universo.

Con este negro panorama por delante habrá que esperar a que un día en el futuro, venga algún genio matemático y nos de la fórmula para burlar esta barrera de la velocidad de la luz, para hacer posible visitar otros mundos poblados por otros seres. Por ahora, el único panorama creíble (dadas nuestras limitaciones físicas), está en los robots que, sin lugar a ninguna duda, serán la avanzadilla de la Humanidad en los viajes espaciales y, ellos serán los primeros en pisar otros mundos. De hecho, ahora mismo tenemos a Mars Phoenix investigando el suelo y la atmósfera de Marte y buscando vestigios de vida pasada o presente.
Si han llegado aquí… ¡Son más listos que nosotros! ¿Qué intenciones traerán? Mejor que no vengan
También cabe esperar que sean ellos (otros seres extraterrestres) los más adelantados y nos visiten a nosotros. Aunque, si tengo que ser sincero, preferiría no ser testigo nunca de una escena como la de arriba, en la que una nave extraterrestre se acerca a la Tierra. Bastantes problemas nos creamos ya nosotros mismos para tener encima que bregar con otros venidos de fuera.
Si se tiene que producir ese encuentro, por mi parte, preferiría que seamos nosotros los visitantes. Me acuerdo de Colón, de Pizarro o Hernán Cortes e incluso de los ingleses en sus viajes de colonización, y la verdad, lo traslado a seres extraños con altas tecnologías a su alcance y con el dominio de enormes energías visitando un planeta como el nuestro, y dicho pensamiento no me produce la más mínima gracia. Más bien es gélido escalofrío.

Podrían responder a cualquier anatomía y… ¡sentimientos!
Según todos los indicios que la ciencia tiene en su poder, no parece que por ahora y durante algún tiempo, tengamos la posibilidad de contactar con nadie de más allá de nuestro sistema solar. Por nuestra parte existe una imposibilidad de medios. No tenemos aún los conocimientos necesarios para fabricar la tecnología precisa que nos lleve a las estrellas lejanas a la búsqueda de otros mundos. En lo que se refiere a civilizaciones extraterrestres, si las hay actualmente, no deben estar muy cerca; nuestros aparatos no han detectado señales que dejarían las sociedades avanzadas mediante la emisión de ondas de radio y televisión y otras similares. También pudiera ser, no hay que descartar nada, que estén demasiado adelantados para nosotros y oculten su presencia mientras nos observan, o atrasados hasta el punto de no emitir señales.

De esta manera, por nuestra parte, sólo podemos hacer una cosa: seguir investigando y profundizando en el conocimiento del universo para desvelar sus misterios y conseguir algún día (aún muy lejano), viajar a las estrellas, única manera de escapar del trágico e inevitable final de nuestra fuente de vida, el Sol.

Dentro de unos 4.000 millones de años, como ya he dicho antes (páginas anteriores), el Sol se transformará en una estrella gigante roja cuya órbita irá más allá de Mercurio, Venus y seguramente la Tierra. Antes, la temperatura evaporará toda el agua del planeta Tierra, la vida no será posible. El Sol explotará como estrella nova y lanzará sus capas exteriores al espacio exterior para que su viejo material forme nuevas estrellas. Después, desaparecida la fuerza de fusión nuclear, la enorme masa del Sol, quedara a merced de su propio peso y la gravedad que generará estrujará, literalmente, al Sol sobre su núcleo hasta convertirla en una estrella enana blanca de enorme densidad y minúsculo diámetro (en comparación con el original). Más tarde, la estrella se enfriará y pasará a engrosar la lista de cadáveres estelares.

Ciudades futuras en otros mundos
Para cuando ese momento este cercano, la humanidad, muy evolucionada y avanzada, estará colonizando otros mundos, tendrá complejos espaciales y ciudades flotando en el espacio exterior, como enormes naves-estaciones espaciales de considerables dimensiones que dará cobijo a millones de seres, con instalaciones de todo tipo que hará agradable y fácil la convivencia.
Modernas naves espaciales surcarán los espacios entre distintos sistemas solares y, como se ha escrito tantas veces, todo estará regido por una confederación de planetas en los que tomarán parte individuos de todas las civilizaciones que, para entonces, habrán contactado.
El avance en el conocimiento de las cosas está regida por la curiosidad y la necesidad. Debemos tener la confianza y la tolerancia, desechar los temores que traen la ignorancia, y, en definitiva, otorga una perspectiva muy distinta de ver las cosas y resolver los problemas. En tal situación, para entonces, la humanidad y las otras especie inteligentes tendrán instalado un sistema social estable, una manera de gobierno conjunto que tomará decisiones de forma colegiada por mayoría de sus miembros, y se vigilará aquellos mundos en desarrollo que, sin haber alcanzado el nivel necesario para engrosar en la Federación Interplanetaria de Mundos, serán candidatos futuros para ello, y la Federación vigilará por su seguridad y desarrollo en paz hasta que estén preparados.
En nuestro mundo pasan cosas que nos deben avergonzar. Estamos fuera de la realidad y, es el dinero lo que prima por delante de los sentimientos. incluso “elaboramos” Pandemias que (aunque sea a costa de cientos de miles de muertos), nos puedan facilitar el vender productos que nos haga ricos.
¡Qué vergüenza!
Estos y otros muchos… ¿Hacen todo lo que pueden por el resto de la Humanidad? O, por el contrario aprovechan sus grandes fortunas para abusar más de todos en sus propios beneficios. No quiere acusar a nadie que podría ser inocente. Sin embargo, la sospecha está ahí.
También sabemos que el desconocimiento, el torpe egoísmo de unos pocos y sobre todo la ignorancia, es la madre de la desconfianza y, como ocurre hoy en pleno siglo XXI, los pueblos se miran unos a otros con temor; nadie confía a en nadie y en ese estado de tensión (que es el caso que se produce hoy día), a la más mínima salta una guerra que, por razones de religión mal entendida o por intereses, siempre dará el mismo resultado: la muerte de muchos inocentes que, en definitiva, nada tuvieron que ver en el conflicto. Los culpables e inductores, todos estarán seguros en sus refugios mientras mueren sus hermanos.
Es irrefutable esta desgraciada realidad que, sin que lo podamos negar, nos convierte en bárbaros mucho más culpables que aquellos de Atila, que al menos tenían la excusa de su condición primitiva y salvaje guiada por el instituto de la conquista y defensa de sus propias vidas.
¿Pero que excusa tenemos hoy?
El cometa se encontraba viajando entre las órbitas de Júpiter y de Marte. Mide unos cuatro kilómetros de diámetro, con una forma irregular, …
Enviamos sondas espaciales a las lunas de Júpiter y al planeta Marte para que investiguen sus atmósferas, busquen agua y nos envíen nítidas fotografías de cuerpos celestes situados a cientos de millones de kilómetros de la Tierra.
Se construyen sofisticadas naves que surcan los cielos y los océanos llevando a cientos de pasajeros confortablemente instalados que son transportados de una a la otra parte del mundo.
Podemos transmitir imágenes desde Australia que en segundos pueden ser vistas en directo por el resto del mundo.
Tenemos en el espacio exterior telescopios como el Hubble, que nos envía constantemente al planeta Tierra imágenes de galaxias y sistemas solares situados a miles de millones de años luz de nosotros, y sin embargo, ¡¡medio mundo muere por el hambre, la miseria, la falta de agua y la enfermedad!!

¿Qué nos está pasando?
Aunque parezca que no tiene conexión alguna, la tiene y mucha, el conocimiento del Universo a través de la Astrofísica y la Astronomía, sin lugar a ninguna duda nos hará mejores, ya que, de ese conocimiento profundo nos vendrán otros relacionados que nos harán comprender también que, lo efímero de nuestras vidas, nos obliga, de alguna manera a ser mejores y que los errores cometidos son irreversibles y tal como marcha el tiempo (siempre adelante) no tenemos la oportunidad de reparar los daños.
Existe un principio de la física denominado Navaja de Ockham, que afirma que siempre deberíamos tomar el camino más sencillo posible e ignorar las alternativas más complicadas, especialmente si las alternativas no pueden medirse nunca.
Para seguir fielmente el consejo contenido en la navaja de Ockham, primero hay que tener el conocimiento necesario para poder saber elegir el camino más sencillo, lo que en la realidad, no ocurre. Nos faltan los conocimientos necesarios para hacer las preguntas adecuadas.
Así que, siendo así las cosas el camino más aconsejable es el del conocimiento del mundo que nos rodea y del Universo que nos acoge, lo que nos lleva a tener la obligación de aprovechar el Año 2009 que ha sido nombrado como Internacional de la Astronomía, y, aprendamos del Universo, la Naturaleza es siempre la que nos trae las nuevas ideas, lo que, desde luego, no ocurre sin que la observemos.
Emilio Silvera V.
Oct
31
Caer en un Agujero negro sería la muerte
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Entrevista científica ~
Clasificado en Entrevista científica ~
 Comments (0)
Comments (0)
Ya se han cumplido diez años desde que se captaron ls ondas gravitacionales
La primera observación directa de las ondas gravitatorias se logró el 14 de septiembre de 2015; los autores de la detección fueron los científicos del experimento LIGO y Virgo que, tras un análisis minucioso de los resultados, anunciaron el descubrimiento al público el 11 de febrero de 2016, cien años después de que lo predijera la Teoría de la Relatividad de Einstein.
LIGO detectó las ondas gravitacionales producidas por la fusión de dos agujeros negros que, durante un largo tiempo estuvieron “bailando” el uno alrededor del otro hasta que se produjo “el matrimonio” cosmológico.
“El 26 de diciembre de 2015 a las 04:38:53 (hora española), los científicos observaron ondas gravitacionales (ondulaciones en el tejido del espacio-tiempo) por segunda vez. GW151226 es la segunda observación clara de una fusión de agujeros negros y, junto con al evento anterior llamado GW150914, marca el inicio de la astronomía de ondas gravitacionales como un medio para explorar nuevas fronteras de nuestro universo.”

Kip Thorne posa frente a la sede de la Royal Society de Londres antes de la entrevista / CARMEN VALIÑO (EL PAÍS)
“Kip Thorne (Logan, EE UU, 1940) es uno de los mayores expertos mundiales en agujeros negros. Últimamente también se ha convertido en una estrella de la divulgación como asesor de Interstellar, la película que plantea una expedición humana a un agujero de gusano, seguida de una caída en un agujero negro, seguida de un viaje hacia la quinta dimensión. Hace algún tiempo, este físico teórico del Instituto Tecnológico de California acudió a Londres para la presentación de la medalla Stephen Hawking, impulsada por el Festival Starmus. Después de la ceremonia, el físico explicó a Materia sus próximos proyectos.”

Pregunta. ¿Por qué cree que los agujeros negros son tan atractivos para la gente?
Respuesta. Bueno, son misteriosos, son extraños, llevan la marca personal de Stephen Hawking… Para los científicos, son únicos. Aunque se crearon por la implosión de una estrella, la materia desaparece en la singularidad en el centro del agujero negro. Por eso están hechos solo de tiempo y espacio curvos, no tienen materia, son completamente diferentes de ti y de mí.

P. Para Interestelar hizo cálculos reales de qué sucede si caes en un agujero negro. ¿Qué es lo más interesante que descubrió?
R. Lo más excitante fue ver cuál sería el aspecto de Gargantúa, el agujero negro. Es maravillosa, con ese halo alrededor y el disco que lo cruza. Otra cosa muy interesante es cuando Cooper [Matthew McConaughey] entra en el agujero negro. En ese momento dice: estoy cruzando el horizonte de sucesos [el punto de no retorno en un agujero negro]. Claro, nada escapa de un agujero negro, ni siquiera la luz, por lo que de frente no verías nada, pero, si miras atrás y ya estás dentro de él, sí verías el universo exterior. Y es una imagen maravillosa en la que el disco de gas caliente en torno al agujero negro es un anillo en el cielo que contiene al universo.
“La primera imagen de un agujero negro jamás tomada no solo se ha comparado con el ojo de Sauron, sino también con una versión borrosa de Gargantúa, el agujero negro supermasivo de la película Interstellar, de Christopher Nolan. Kip Thorne, premio Nobel de Física en 2017, colaboró con el equipo de la película para que esta fuera lo más fiel a la ciencia posible. Y Gargantúa sigue lo que se sabía hasta el momento acerca de los agujeros negros.”Los agujeros negros están hechos de tiempo y espacio curvo, no tienen materia, son completamente diferentes de ti y de mí”
P.¿Y qué pasa después?
R. Pues sabemos que hay tres singularidades diferentes dentro de un agujero negro. Una singularidad es un punto en el que la curvatura del espacio-tiempo se hace infinitamente fuerte. Hay una singularidaddescubierta por tres físicos teóricos rusos alrededor de 1970. Si caes en esa, estás totalmente destruido, te haces trizas de forma caótica y salvaje. Una segunda singularidad está hecha de todas las cosas que caen al agujero negro después de ti. Este material cae durante miles de millones de años, pero el tiempo va tan lento dentro de un agujero negro que todo ese material se te cae encima en una fracción de segundo, como si fuera una plancha. No me gustaría que eso me pasase. Cooper encuentra la tercera singularidad, que es la más débil de todas. Esta singularidad la causa todo lo que cayó al agujero negroantes que tú. Una fracción pequeña de todo ese material rebotará como si fuera una piedra que da saltos sobre el agua de un estanque. Esa pequeña fracción de toda la materia que cayó al agujero negro sale despedida y saca con él a Cooper en una fracción de segundo. Así que hay una posibilidad de que sobrevivas a un agujero negro.
P. ¿Qué será lo siguiente para usted en este campo?
Las leyes de la gravedad cuántica nos dirán si es posible viajar en el tiempo”
R. Stephen Hawking, Lynda Obst, una productora de Hollywood, y yo, hemos escrito nueve borradores de una nueva película. Es muy diferente de Interestelar. Estamos empezando a hablar con posibles guionistas y estudios sobre ella. Es aún en un momento inicial del proyecto
P. ¿De qué tratará?
R. Algo que aprendí de Christopher Nolan es que no dices nada a la gente sobre una película antes de tiempo. Vas filtrando la información en el momento adecuado para aumentar la expectación, así que por ahora solo puedo decir esto. Y que tendrá física interesante.
P. ¿Cuál es el próximo gran reto en la física de los agujeros negros?
R. Hay algo que nunca hemos visto: cómo se comportan dos agujeros negros que chocan y crean una tormenta en el espacio-tiempo. La colisión hace que, por un breve periodo, el paso del tiempo acelere, desacelere, vuelva a acelerar… todo de una forma salvaje, caótica. Esto deforma el espacio en una dirección y otra, que gire en el sentido de las agujas del reloj y después al revés, crea vórtices que curvan el espacio y que luchan unos con otros. Hemos visto esto muy recientemente en simulaciones por ordenador y empezamos a entender cómo se comporta una tormenta en la que el tiempo y el espacio oscilan de forma salvaje. Nunca lo hemos observado, pero lo vamos a hacer muy pronto.
P. ¿Cómo?
R. Cuando estos agujeros negros chocan crean ondas en el tejido del espacio-tiempo que se llaman ondas gravitacionales. Estas nos darán suficiente información como para ir hacia atrás en el tiempo partiendo de la onda que vemos y las simulaciones y probar si estas predicen de forma correcta lo que está pasando.
P. ¿Cuándo esperan captarlas?

De hecho ya han sido detectadas varias veces por LIGO y VIRGO
R. Para hacerlo hemos construido los detectores LIGO. El equipo comenzó su primera tanda de búsquedas de ondas gravitacionales con los detectores avanzados en septiembre de 2015 y seguirá haciéndolo hasta enero de 2016. Estos detectores, incluso en la primera búsqueda, son tan sensibles que pueden captar un choque de agujeros negros a 1.000 millones de años luz de la Tierra, es decir, un décimo de la distancia hasta el límite del universo observable. Si tenemos suerte, captaremos algo en la primera búsqueda.
P. ¿Cuál es la próxima gran frontera de la física?

“Es muy probable que haya civilizaciones más avanzadas que las nuestras”
R. Entender las leyes de la gravedad cuántica que derivan de combinar la Relatividad General con la física cuántica. No entendemos esas leyes bien, podría ser alguna variante de la teoría de cuerdas o la teoría M. Si tuviera que hacer una predicción diría que ese es el camino por el que iremos. Una vez entendamos esas leyes nos contarán de una forma muy clara el nacimiento del universo, qué pasa en la singularidad dentro de un agujero negro y si es posible retroceder en el tiempo.

P. ¿Cree que eso abrirá los viajes en el tiempo?
R. Abrirá una puerta a los viajes en el tiempo… o la cerrará [risas].
P. En uno de sus libros especulaba que si la humanidad quiere sobrevivir debería irse a un agujero negro¿ Cree que es es nuestro futuro?
R. Hará falta mucho tiempo hasta que los humanos podamos explorar un agujero negro. Pero es verdad que en el giro de un agujero negro hay una enorme cantidad de energía rotacional que la naturaleza extrae para producir los gigantes brotes que salen de los núcleos de las galaxias. Los humanos de una civilización avanzada podrían usarlos como una descomunal fuente de energía mucho más potente que la fusión nuclear que sucede en el interior de las estrellas.
Las ondas han sido detectadas sin ningún lugar a la duda
P. ¿Piensa que hay otras formas de vida inteligente en el universo?
R. Es muy probable que haya vida inteligente en el universo, civilizaciones más avanzadas que las nuestras. Pero las distancias entre las estrellas son tan enormes que el viaje interestelar es cada vez más difícil. Dudo mucho que otra civilización haya visitado la Tierra, pero creo que es muy probable que nos comuniquemos con ellos algún día, quizás antes de que yo muera, quizás no. Buscar señales de civilizaciones extraterrestres es una de los empeños científicos más importantes que hay.
P. ¿Qué fue lo más importante que nos dejó Albert Einstein, de su Relatividad General de la que se cumplen ahora 100 años?
R. Nos dio una ley que controla las leyes de la naturaleza. Es el principio de relatividad, que dice que sean cuales sean las leyes de la naturaleza, tienen que ser la mismas vistas por cualquier persona en cualquier lugar del universo si se están moviendo libremente. Creo que ese puede ser el mayor logro intelectual de todos los tiempos.
Hasta aquí aquella entrevista. A partir de ahora, con el descubrimiento publicado, comenzaremos una nueva etapa sobre el conocimiento del Universo que, de seguro., nos traerá muchas sorpresas.
Entrevista científica
Oct
30
Imaginando el Futuro
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
Algunos hablan de los beneficios de la I.A. para la Humanidad, por mi parte no soy muy optimista
Dotar a los Robots de Conciencia de Ser… ¡Tendrá graves consecuencias para nosotros!
¿Acaso queremos crear una nueva especie que siendo artificial no tendría sentimientos?
En este mismo Blog he hablado muchas veces de lo que pienso sobre todo esto, no abrigo ninguna esperanza de la bondad que nos puedan traer los Robots a la Humanidad. Más bien creo que, si llegan a tener consciencia de SER, nos harán la competencia y, finalmente, querrán tomar el mando alegando que los humanos no son racionales.
Montarme en un auto conducido por la I.A. ¡No gracias!
Parece que estamos perdiendo el Norte ¡Ponernos en manos de las máquinas!
Ya en el Presente estamos parcialmente en sus manos, si se cae Internet… ¡Estamos perdidos!
No dudo que los Robot pueden ser de gran ayuda para los humanos siempre que los fabriquemos con limites de autonomía, que sus cerebros positrónicos tengan insertas las barreras que les impida en todo momento y en cualquier circunstancia, daños a los humanos, o, tomar decisiones por su cuenta, solo podrán realizar aquellas tareas encomendadas y siempre preservando la seguridad del humano.
Pero ¿será así como los construirán? No creo, ya han dicho que quieren dotarlos de pensamiento propio, y, si finalmente lo hacen… ¡Mal futuro nos espera!
Sería partidario de que los Robots se enfoquen a tareas peligrosas como la exploración espacial y preparar nuevos mundos para acoger a la Humanidad en un Futuro lejano (nos haría falta algo así), no tenemos un físico adecuado para la vivir en el Espacio, “ellos” si lo tienen, ya que, la radiación no les afecta, no necesitan dormir, no necesitan comer, no están expuestos a enfermedades, la ingravidez no les afecta físicamente (aunque para entonces se habrá dominado la tecnología para dotar a las naves de la Gravedad artificial), y… ¿Qué duda nos puede caber? Con la debida preparación científica, podrán aprovechar los materiales de esos mundos para construir instalaciones que nos acojan cuando al fin lleguemos a esos nuevos mundos.
Emilio Silvera V.
Oct
30
Desde la materia “inerte”… ¡Hasta los pensamientos!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (3)
Comments (3)
Lo mismo que desconocemos la auténtica naturaleza de la Luz, que según creo encierra muchos secretos que tenemos que desvelar para conocer la realidad de la Naturaleza y del Universo, de la misma manera, tenemos que llegar a desvelar los secretos que se encierra en esa esencial y sencilla sustancia que llamamos agua, ya Tales de Mileto nos hablaba de la importancia que esa sustancia tenía para la vida.
¿Cómo es posible que, a partir de la materia “inerte”, hayan podido surgir seres vivos e incluso, algunos que, como nosotros puedan pensar? Que cosa mágica se pudo producir en el corazón de las estrellas para que, materiales sencillos como el Hidrógeno se convirtieran a miles de millones de grados de calor en otros que, como el Carbono, Oxigeno y Nitrógeno…, muchos miles de millones de años más tardes, en mundos perdidos en sistemas planetarios como el nuestro, dieran lugar a la formación de Protoplasmavivo del que surgieron aquellos infinitesimales seres que llamamos bacterias y que, posibilitaron la evolución hacia
que, materiales sencillos como el Hidrógeno se convirtieran a miles de millones de grados de calor en otros que, como el Carbono, Oxigeno y Nitrógeno…, muchos miles de millones de años más tardes, en mundos perdidos en sistemas planetarios como el nuestro, dieran lugar a la formación de Protoplasmavivo del que surgieron aquellos infinitesimales seres que llamamos bacterias y que, posibilitaron la evolución hacia formas de vida superiores?
formas de vida superiores?

Los sentidos: las herramientas que utiliza el cerebro para estar comunicado con el exterior
estar comunicado con el exterior
La percepción, los sentidos y los pensamientos… Para poder entender la conciencia como proceso es preciso que entendamos cómo funciona nuestro cerebro, su arquitectura y desarrollo con sus funciones dinámicas. Lo que no está claro es que la conciencia se encuentre causalmente asociada a ciertos procesos cerebrales pero no a otros.
proceso es preciso que entendamos cómo funciona nuestro cerebro, su arquitectura y desarrollo con sus funciones dinámicas. Lo que no está claro es que la conciencia se encuentre causalmente asociada a ciertos procesos cerebrales pero no a otros.
El cerebro humano ¿es especial?, su conectividad, su dinámica, su forma de funcionamiento, su relación con el cuerpo y con el mundo exterior, no se parece a nada que la ciencia conozca. Tiene un carácter único y ofrecer una imagen fidedigna del cerebro no resulta nada fácil; es un reto tan extraordinario que no estamos preparados para cumplir en este momento. Estamos lejos de ofrecer esa imagen completa, y sólo podemos dar resultados parciales de esta enorme maravilla de la Naturaleza.
de funcionamiento, su relación con el cuerpo y con el mundo exterior, no se parece a nada que la ciencia conozca. Tiene un carácter único y ofrecer una imagen fidedigna del cerebro no resulta nada fácil; es un reto tan extraordinario que no estamos preparados para cumplir en este momento. Estamos lejos de ofrecer esa imagen completa, y sólo podemos dar resultados parciales de esta enorme maravilla de la Naturaleza.

Aquí se fraguan los pensamientos como en las galaxias lo hacen las estrellas
Nuestro cerebro adulto, con poco más de 1 Kg de peso, contiene unos cien mil millones de células nerviosas o neuronas. La parte o capa ondulada más exterior o corteza cerebral, que es la parte del cerebro de evolución más reciente, contiene alrededor de treinta millones de neuronas y un billón de conexiones o sinapsis. Si contáramos una sinapsis cada segundo, tardaríamos 32 millones de años en acabar el recuento. Si consideramos el número
o capa ondulada más exterior o corteza cerebral, que es la parte del cerebro de evolución más reciente, contiene alrededor de treinta millones de neuronas y un billón de conexiones o sinapsis. Si contáramos una sinapsis cada segundo, tardaríamos 32 millones de años en acabar el recuento. Si consideramos el número posible de circuitos neuronales, tendremos que habérnoslas con cifras hiper-astronómicas. Un 10 seguido de, al menos, un millón de ceros (en comparación, el número de partículas del universo conocido asciende a “tan sólo” un 10 seguido de 79 ceros). ¡A que va a resultar que no somos tan insignificantes!
posible de circuitos neuronales, tendremos que habérnoslas con cifras hiper-astronómicas. Un 10 seguido de, al menos, un millón de ceros (en comparación, el número de partículas del universo conocido asciende a “tan sólo” un 10 seguido de 79 ceros). ¡A que va a resultar que no somos tan insignificantes!


El suministro de datos que llega en forma de multitud de mensajes procede de los sentidos, que detectan el entorno interno y externo, y luego envía el resultado a los músculos para dirigir lo que hacemos y decimos. Así pues, el cerebro es como un enorme ordenador que realiza una serie de tareas basadas en la información que le llega de los sentidos. Pero, a diferencia de un ordenador, la cantidad de material que entra y sale parece poca cosa en comparación con la actividad interna. Seguimos pensando, sintiendo y procesando información incluso cuando cerramos los ojos y descansamos.
que llega en forma de multitud de mensajes procede de los sentidos, que detectan el entorno interno y externo, y luego envía el resultado a los músculos para dirigir lo que hacemos y decimos. Así pues, el cerebro es como un enorme ordenador que realiza una serie de tareas basadas en la información que le llega de los sentidos. Pero, a diferencia de un ordenador, la cantidad de material que entra y sale parece poca cosa en comparación con la actividad interna. Seguimos pensando, sintiendo y procesando información incluso cuando cerramos los ojos y descansamos.
Con tan enorme cantidad de circuitos neuronales, ¿Cómo no vamos a ser capaces de descifrar todos los secretos de nuestro universo? ¿De qué seremos capaces cuando podamos disponer de un rendimiento cerebral del 80 ó 90 por ciento? Algunas veces hemos oido comentar: “Sólo utilizamos un diez por ciento del cerebro…” En realidad, la frase no indica la realidad, se refiere al hecho de que, aunque utilizamos el cerebro en su totalidad, se estima que está al diez por ciento de su capacidad real que, será una realidad a medida que evolucione y, en el futuro, esa capacidad de hoy será un 90 por ciento mayor.
podamos disponer de un rendimiento cerebral del 80 ó 90 por ciento? Algunas veces hemos oido comentar: “Sólo utilizamos un diez por ciento del cerebro…” En realidad, la frase no indica la realidad, se refiere al hecho de que, aunque utilizamos el cerebro en su totalidad, se estima que está al diez por ciento de su capacidad real que, será una realidad a medida que evolucione y, en el futuro, esa capacidad de hoy será un 90 por ciento mayor.
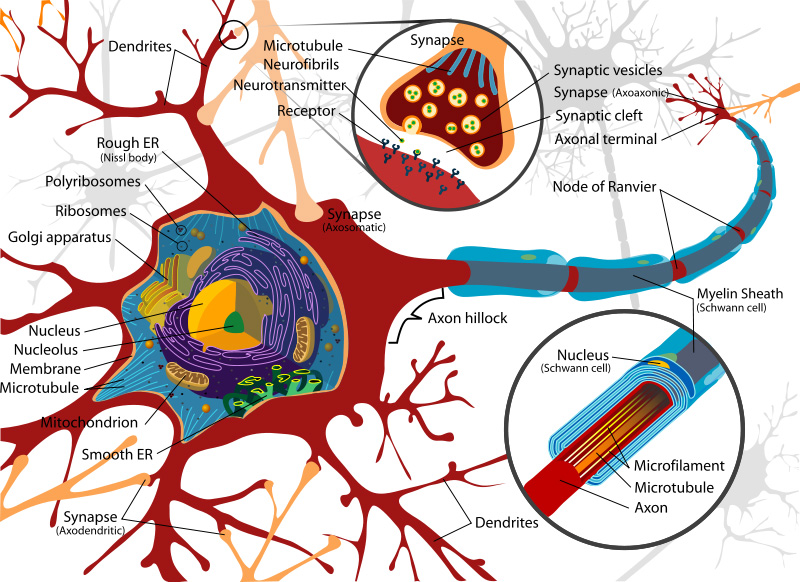
Aún no conocemos bien la direccionalidad de los circuitos neuronales
la direccionalidad de los circuitos neuronales
El límite de lo que podremos conseguir tiene un horizonte muy lejano. Y, llega un momento en el cual, se puede llegar a pensar que no existen limites en lo que podemos conseguir: Desde hablar sin palabras sonoras a la auto-transportación. Si -como pienso- somos pura energía pensante, no habrá límite alguno; el cuerpo que ahora nos lleva de un lugar a otro, ya no será necesario, y como los fotones que no tienen masa, podremos desplazarnos a velocidades lumínicas.
nos lleva de un lugar a otro, ya no será necesario, y como los fotones que no tienen masa, podremos desplazarnos a velocidades lumínicas.
Creo que estoy corriendo demasiado en el tiempo, volvamos a la realidad. A veces mi mente se dispara. Lo mismo visito mundos extraordinarios con mares luminosos de neón líquido poblados por seres transparentes, que viajo a galaxias muy lejanas pobladas de estrellas de fusión fría circundadas por nubes doradas compuestas de antimateria en la que, los positrones medio congelados, se mueven lentamente formando un calidoscopio de figuras alucinantes de mil colores. ¡La mente, qué tesoro!
“Durante siglos el hombre ha intentado responder a una de las más complicadas inquietudes: ¿Es el cerebro humano más grande que el universo? Y si bien la respuesta aún no ha llegado, muchos expertos a lo largo de los años han intentado esbozar sus teorías.
Precisamente, con el fin de poder acercar una somera respuesta a esta gigantesco interrogante, el periodista Robert Krulwich ha publicado recientemente en la página web NPR.org una completa compilación de este gran e interminable. Una compilación que incluye teorías de ambos bandos, y entre las cuales existen muchas que son realmente convincentes.”
Mirando ambas imágenes… ¿Quién podría decir, si no se les explicara, que son “mundos” diferentes”
La unidad a partir de la cual se configuran todas las fabulosas actividades del cerebro es una célula del mismo, la neurona. Las neuronas son unas células fantásticamente ramificadas y extendidas, pero diminutas que, sin embargo y en sentido figurado, podríamos decir que son tan grandes como el universo mismo.
el universo mismo.

Cuando seamos capaces de convertir en realidad todo aquello en lo que podamos pensar, entonces, habremos alcanzado la meta. Para que eso pueda llegar a ocurrir, aún falta mucho tiempo. Sin embargo, si el Universo no lo impide y nuestro transcurrir continúa, todo lo que podamos imaginar… podrá ser posible. Incluso imposibilidades físicas de hoy, dejarán de existir mañana y, ¡la Mente! posiblemente (al igual que hoy ordena a las distintas partes del cuerpo que realice esta o aquella función), se encargará de que todo funcione bien, erradicará cualquier enfermedad que nos pueda atacar y, tendrá el conjunto del “sistema” en perfectas condiciones de salud, lo cual me lleva a pensar que, para cuando eso llegue, los médicos serán un recuerdo del pasado.
de salud, lo cual me lleva a pensar que, para cuando eso llegue, los médicos serán un recuerdo del pasado.
Veamos, por ejemplo, la Ecuación de Schrödinger
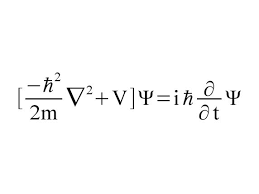
¿Qué dice?
La ecuación modela la materia no como una partícula, sino como una onda, y describe cómo estas ondas se propagan.
¿Por qué es importante?
La ecuación de Schrödinger es fundamental para la mecánica cuántica, que junto con la relatividad general constituyen en la actualidad las teorías más efectivas del universo físico.
¿Qué provocó?
Una revisión radical de la física del mundo a escalas muy pequeñas, en las cuales cada objeto tiene una «función de onda» que describe una nube de probabilidad de posibles estados. A este nivel el mundo es incierto intrínsecamente. Intentos de relacionar el mundo microscópico cuántico con nuestro mundo macroscópico clásico llevaron a temas filosóficos que todavía tienen eco. Pero experimentalmente, la teoría cuántica funciona maravillosamente bien y los láseres y chips de los ordenadores actuales no funcionarían sin ella.
Es curioso y sorprendente la evolución alcanzada por la Mente Humana. El mundo físico se representa gobernado de acuerdo a leyes matemáticas. Desde este punto de vista, todo lo que hay en el universo físico está realmente gobernado en todos sus detalles por principios matemáticos, quizá por ecuaciones tales que aún no hemos podido llegar a comprender y, ni que sabemos que puedan existir.
este punto de vista, todo lo que hay en el universo físico está realmente gobernado en todos sus detalles por principios matemáticos, quizá por ecuaciones tales que aún no hemos podido llegar a comprender y, ni que sabemos que puedan existir.
Lo más seguro es que la descripción real del mundo físico esté pendiente de matemáticas futuras, aún por descubrir , fundamentalmente distintas de las que ahora tenemos. Llegarán nuevos Gauss, Riemann, Euler, o, Ramanujans… que, con sus nuevas ideas transformarán el pensamiento matemático para hacer posible que podamos, al fin, comprender lo que realmente somos.
, fundamentalmente distintas de las que ahora tenemos. Llegarán nuevos Gauss, Riemann, Euler, o, Ramanujans… que, con sus nuevas ideas transformarán el pensamiento matemático para hacer posible que podamos, al fin, comprender lo que realmente somos.
Son nuestras Mentes, productos de la evolución del Universo que, a partir de la materia inerte, ha podido alcanzar el estadio bio-químico de la consciencia y, al ser conscientes, hemos podido descubrir que existen “números misteriosos” dentro de los cuales subyacen mensajes que tenemos que desvelar.
que existen “números misteriosos” dentro de los cuales subyacen mensajes que tenemos que desvelar.
Antes tendremos que haber descifrado las funciones modulares de los cuadernos perdidos de Ramanujan, o por ejemplo, el verdadero significado del número 137, ése número puro adimensional que encierra los misterios del electrón (e) – electromagnetismo -, de la constante de Planck (h) – el cuando
137, ése número puro adimensional que encierra los misterios del electrón (e) – electromagnetismo -, de la constante de Planck (h) – el cuando te acción – y de la luz (c) – la relatividad -.
te acción – y de la luz (c) – la relatividad -.
Y, mientras tanto, nuestras mentes siguen su camino, siempre queriendo ir más allá y siempre profundizando en los secretos de la Naturaleza de lo que tenemos muchos ejemplos, tales como nuestras consideraciones sobre los dos aspectos de la relatividad general de Einstein, a saber, el principio de la relatividad, que nos dice que las leyes de la física son ciegas a la distinción entre reposo y movimiento uniforme; y el principio de equivalencia, que nos dice de qué forma sutil deben modificarse estas ideas para englobar el campo gravitatorio.
sutil deben modificarse estas ideas para englobar el campo gravitatorio.

Mediante la combinación de diversas observaciones de telescopios, y la ayuda del trabajo de modelación avanzada, el equipo de Emanuele Farina, de la Universidad de Insubria en la provincia de Como, Italia, y Michele Fumagalli del Instituto Carnegie de Ciencia, en Washington, D.C., Estados Unidos, fue capaz de captar como tal el trío de quásares, llamado QQQ J1519+0627. La luz de esos quásares ha viajado 9.000 millones de años-luz para
llegar hasta nosotros, lo que significa que dicha luz fue emitida cuando el universo tenía sólo un tercio de su edad actual.

Todo es finito, es decir, que tiene un fin, y la velocidad de la luz no podía ser una excepción
un fin, y la velocidad de la luz no podía ser una excepción
Ahora hay que hablar del tercer ingrediente fundamental de la teoría de Einstein, que está relacionada con la finitud de la velocidad de la luz. Es un hecho notable que estos tres ingredientes básicos puedan remontarse a Galileo; en efecto, parece que fue también Galileo el primero que tuvo una expectativa clara de que la luz debería viajar con velocidad finita, hasta el punto de que intentó medir dicha velocidad. El método que propuso (1.638), que implica la sincronización de destellos de linternas entre colinas distantes, era, como sabemos hoy, demasiado tosco (otro ejemplo de la evolución que, con el tiempo, se produce en nuestras mentes). Él no tenía forma
hay que hablar del tercer ingrediente fundamental de la teoría de Einstein, que está relacionada con la finitud de la velocidad de la luz. Es un hecho notable que estos tres ingredientes básicos puedan remontarse a Galileo; en efecto, parece que fue también Galileo el primero que tuvo una expectativa clara de que la luz debería viajar con velocidad finita, hasta el punto de que intentó medir dicha velocidad. El método que propuso (1.638), que implica la sincronización de destellos de linternas entre colinas distantes, era, como sabemos hoy, demasiado tosco (otro ejemplo de la evolución que, con el tiempo, se produce en nuestras mentes). Él no tenía forma alguna de anticipar la extraordinaria velocidad de la luz.
alguna de anticipar la extraordinaria velocidad de la luz.
Parece que tanto Galileo como Newton tenían poderosas sospechas respecto a un profundo papel que conecta la naturaleza de la luz con las fuerzas que mantienen la materia unida y, si consideramos que esa fuerza que hace posible la unión de la materia reside en el corazón de los átomos (en sus núcleos), podemos hacernos una clara idea de lo ilimitado que puede
Newton tenían poderosas sospechas respecto a un profundo papel que conecta la naturaleza de la luz con las fuerzas que mantienen la materia unida y, si consideramos que esa fuerza que hace posible la unión de la materia reside en el corazón de los átomos (en sus núcleos), podemos hacernos una clara idea de lo ilimitado que puede ser el pensamiento humano que, ya en aquellos tiempos -en realidad mucho anters- pudo llegar a intuir las fuerzas que están presentes en nuestro Universo.
ser el pensamiento humano que, ya en aquellos tiempos -en realidad mucho anters- pudo llegar a intuir las fuerzas que están presentes en nuestro Universo.

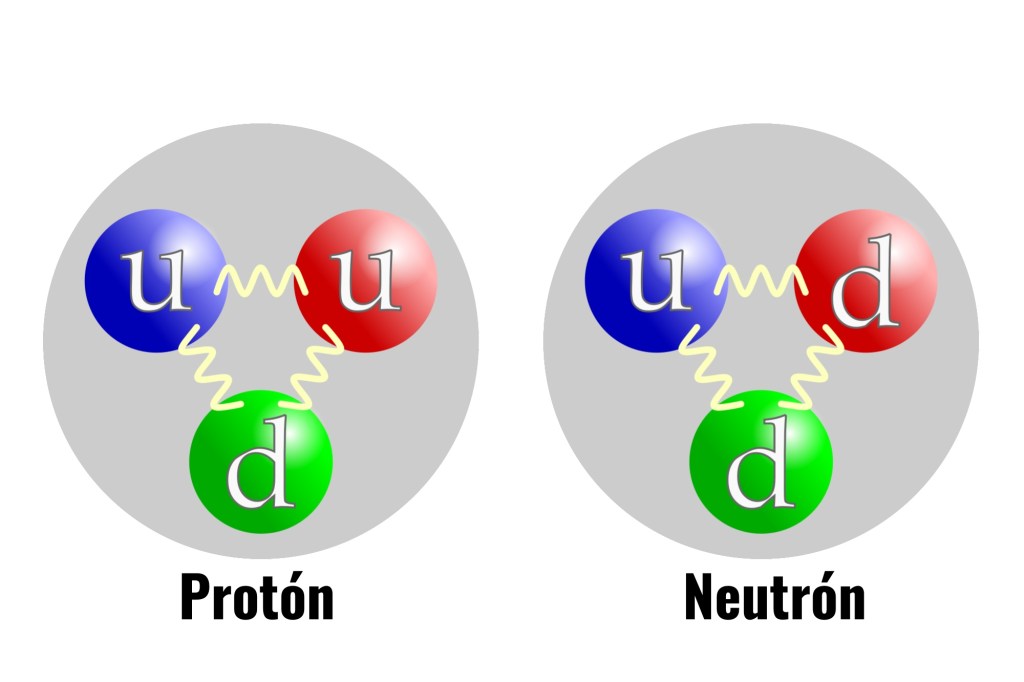
En los núcleos atómicos reside la fuerza (nuclear fuerte) que hace posible la existencia de la materia que comienza por los átomos que, al juntarse y formar células, hace posible que éstas se junten y formen moléculas que a su vez, se reunen para formar sustancias y cuerpos.
formar sustancias y cuerpos.
Pero la comprensión adecuada de estas ideas tuvo que esperar hasta el siglo XX, cuando se reveló la verdadera naturaleza de las fuerzas químicas y de las fuerzas que mantienen unidos los átomos individuales. Ahora sabemos que tales fuerzas tienen un origen fundamentalmente electromagnético (que vincula y concierne a la implicación del campo electromagnético con partículas cargadas) y que la teoría del electromagnetismo es también la teoría de la luz.
Para entender los átomos y la química se necesitan otros ingredientes procedentes de la teoría cuántica, pero las ecuaciones básicas que describen el electromagnetismo y la luz fueron propuestas en 1.865 por el físico escocés James Clark Maxwell, que había sido inspirado por los magníficos descubrimientos experimentales de Michael Faraday unos treinta años antes y que él plasmó en una maravillosa teoría.
entender los átomos y la química se necesitan otros ingredientes procedentes de la teoría cuántica, pero las ecuaciones básicas que describen el electromagnetismo y la luz fueron propuestas en 1.865 por el físico escocés James Clark Maxwell, que había sido inspirado por los magníficos descubrimientos experimentales de Michael Faraday unos treinta años antes y que él plasmó en una maravillosa teoría.
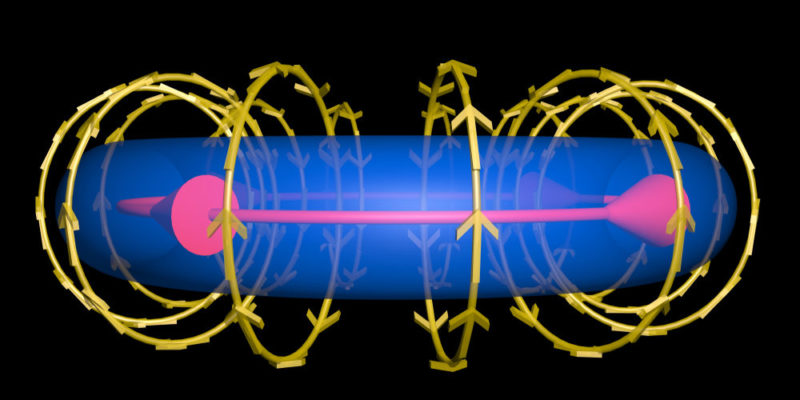
El electromagnetismo es una rama de la Física que estudia y unifica los fenómenos eléctricos y magnéticos en una sola teoría. El electromagnetismo es una teoría de campos; es decir, las explicaciones y predicciones que provee se basan en magnitudes físicas vectoriales dependientes de la posición en el espacio y del tiempo.
Esta teoría del electromagnetismo de Maxwell tenía la particularidad de que requería que la velocidad de la luz tuviera un valor fijo y definido, que normalmente se conoce como c, y que en unidades ordinarias es aproximadamente 3 × 108 metros por segundo. Maxwell, guiado por los experimentos de Faraday, hizo posible un hecho que cambió la historia de la humanidad para siempre. Un hecho de la misma importancia que el descubrimiento del fuego, la rueda o los metales. El matemático y poeta escocés unificó los campos eléctrico y magnético a través de unas pocas ecuaciones que describen como
teoría del electromagnetismo de Maxwell tenía la particularidad de que requería que la velocidad de la luz tuviera un valor fijo y definido, que normalmente se conoce como c, y que en unidades ordinarias es aproximadamente 3 × 108 metros por segundo. Maxwell, guiado por los experimentos de Faraday, hizo posible un hecho que cambió la historia de la humanidad para siempre. Un hecho de la misma importancia que el descubrimiento del fuego, la rueda o los metales. El matemático y poeta escocés unificó los campos eléctrico y magnético a través de unas pocas ecuaciones que describen como estos campos se entretejen y actúan sobre la materia.
estos campos se entretejen y actúan sobre la materia.

Claro que, estos importantísimos avances han sido simples escalones de la “infinita” escalera que tenemos que subir y, la misma relatividad de Einstein no ha sido (después de un siglo) aún comprendido en su plenitud y muchos de sus mensajes están escondidos en lo más profundo de nuestras mentes que, ha sabido parcialmente descubrir el mensaje de Einstein pero
el mensaje de Einstein pero , seguimos buscando.
, seguimos buscando.
Sin embargo, esto nos presenta un enigma si queremos conservar el principio de relatividad. El sentido común nos diría que si se mide que la velocidad de la luz toma el valor concreto c en el sistema de referencia del observador, entonces un segundo observador que se mueva a una velocidad muy alta con respecto al primero medirá que la luz viaja a una velocidad diferente, aumentada o disminuida, según sea el movimiento del segundo observador.
Estaría bueno que, al final se descubriera que alfa (α) tuviera un papel importante en la compleja teoría de cuerdas, ¿Por qué no? En realidad alfa, la constante de estructura fina, nos habla del magnetismo, de la constante de Planck y de la relatividad especial, es decir, la velocidad de la luz y, todo eso, según parece, emergen en las ecuaciones topológicas de la moderna teoría de cuerdas. ¡Ya veremos!
Pero el principio de relatividad exigiría que las leyes físicas del segundo observador (que definen en particular la velocidad de la luz que percibe el segundo observador) deberían ser idénticas a las del primer observador. Esta aparente contradicción entre la constancia de la velocidad de la luz y el principio de relatividad condujo a Einstein (como
la constancia de la velocidad de la luz y el principio de relatividad condujo a Einstein (como de hecho, había llevado previamente al físico holandés Hendrick Antón Lorentz y muy en especial al matemático francés Henri Poincaré) a un punto de vista notable por el que el principio de relatividad del movimiento puede
de hecho, había llevado previamente al físico holandés Hendrick Antón Lorentz y muy en especial al matemático francés Henri Poincaré) a un punto de vista notable por el que el principio de relatividad del movimiento puede hacerse compatible con la constancia de una velocidad finita de la luz.
hacerse compatible con la constancia de una velocidad finita de la luz.
¿Cómo funciona esto? Sería normal que cualquier persona creyera en la existencia de un conflicto irresoluble entre los requisitos de una teoría como la de Maxwell, en la que existe una velocidad absoluta de la luz, y un principio de relatividad según el cual las leyes físicas parecen las mismas con independencia de la velocidad del sistema de referencia utilizado para su descripción.
su descripción.
¿No podría hacerse que el sistema de referencia se moviera con una velocidad que se acercara o incluso superara a la de la luz? Y según este sistema, ¿no es cierto que la velocidad aparente de la luz no podría seguir siendo la misma que era antes? Esta indudable paradoja no aparece en una teoría, tal como la originalmente preferida por Newton (y parece que también
indudable paradoja no aparece en una teoría, tal como la originalmente preferida por Newton (y parece que también por Galileo), en la que la luz se comporta como partículas cuya velocidad depende de la velocidad de la fuente. En consecuencia, Galileo y Newton podían seguir viviendo cómodamente con un principio de relatividad.
por Galileo), en la que la luz se comporta como partículas cuya velocidad depende de la velocidad de la fuente. En consecuencia, Galileo y Newton podían seguir viviendo cómodamente con un principio de relatividad.

La velocidad de la luz en el vacío es una constante de la Naturaleza y, cuando cientos de miles de millones de millones salen disparados de esta galaxia hacia el vacío espacial, su velocidad de 299.792.450 metros por segundo, es constante independientemente de la fuente que pueda emitir los fotones y de si ésta está en reposo o en movimiento.
el vacío espacial, su velocidad de 299.792.450 metros por segundo, es constante independientemente de la fuente que pueda emitir los fotones y de si ésta está en reposo o en movimiento.
Así que, la antigua imagen de la naturaleza de la luz entró en conflicto a lo largo de los años , como era el caso de observaciones de estrellas dobles lejanas que mostraban que la velocidad de la luz era independiente de la de su fuente. Por el contrario, la teoría de Maxwell había ganado fuerza, no sólo por el poderoso apoyo que obtuvo de la observación (muy especialmente en los experimentos de Heinrich Hertz en 1.888), sino también por la naturaleza convincente y unificadora de la propia teoría, por la que las leyes que gobiernan los campos eléctricos, los campos magnéticos y la luz están todos subsumidos en un esquema matemático de notable elegancia y simplicidad.
, como era el caso de observaciones de estrellas dobles lejanas que mostraban que la velocidad de la luz era independiente de la de su fuente. Por el contrario, la teoría de Maxwell había ganado fuerza, no sólo por el poderoso apoyo que obtuvo de la observación (muy especialmente en los experimentos de Heinrich Hertz en 1.888), sino también por la naturaleza convincente y unificadora de la propia teoría, por la que las leyes que gobiernan los campos eléctricos, los campos magnéticos y la luz están todos subsumidos en un esquema matemático de notable elegancia y simplicidad.
Las ondas luminosas como las sonoras, actúan de una u otra manera dependiendo del medio en el que se propagan.
las sonoras, actúan de una u otra manera dependiendo del medio en el que se propagan.
En la teoría de Maxwell, la luz toma forma de ondas, no de partículas, y debemos enfrentarnos al hecho de que en esta teoría hay realmente una velocidad fija a la que deben viajar las ondas luminosas.
de ondas, no de partículas, y debemos enfrentarnos al hecho de que en esta teoría hay realmente una velocidad fija a la que deben viajar las ondas luminosas.
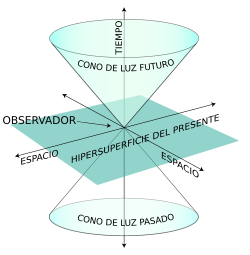
El punto de vista geométrico-espaciotemporal nos proporciona una ruta particularmente clara hacia la solución de la paradoja que presenta el conflicto entre la teoría de Maxwell y el principio de relatividad.
la teoría de Maxwell y el principio de relatividad.
Este punto de vista espaciotemporal no fue el que Einstein adoptó originalmente (ni fue el punto de vista de Lorentz, ni siquiera, al parecer, de Poincaré), pero, mirando en retrospectiva, podemos ver la potencia de este enfoque. Por el momento
punto de vista espaciotemporal no fue el que Einstein adoptó originalmente (ni fue el punto de vista de Lorentz, ni siquiera, al parecer, de Poincaré), pero, mirando en retrospectiva, podemos ver la potencia de este enfoque. Por el momento , ignoremos la gravedad y las sutilezas y complicaciones asociadas que proporciona el principio de equivalencia y otras complejas cuestiones, que estimo aburrirían al lector no especialista, hablando de que en el espacio-tiempo se pueden concebir grupos de todos los diferentes rayos de luz que pasan a ser familias de líneas de universo.
, ignoremos la gravedad y las sutilezas y complicaciones asociadas que proporciona el principio de equivalencia y otras complejas cuestiones, que estimo aburrirían al lector no especialista, hablando de que en el espacio-tiempo se pueden concebir grupos de todos los diferentes rayos de luz que pasan a ser familias de líneas de universo.
Baste saber que, como quedó demostrado por Einstein, la luz, independientemente de su fuente y de la velocidad con que ésta se pueda mover, tendrá siempre la misma velocidad en el vacío, c, o 299.792.458 metros por segundo. Cuando la luz atraviesa un medio material, su velocidad se reduce. Precisamente, es la velocidad c el límite alcanzable de la velocidad más alta del universo. Es una constante universal y, como hemos dicho, es independiente de la velocidad del observador y de la fuente emisora.
y, como hemos dicho, es independiente de la velocidad del observador y de la fuente emisora.
El Universo está dentro de nuestras Mentes
¡La Mente! Qué caminos puede recorrer y, sobre todo ¿Quién la guía? Comencé este trabajo con la imagen del ojo humano y hablando de los sentidos y de la consciencia y mira donde he finalizado…Sí, nos falta mucho camino por recorrer para llegar a desvelar los misterios de la Mente que, en realidad, es la muestra más alta que el Universo nos puede mostrar de lo que puede surgir a partir de la sencillez de los átomos de hidrógeno que, evolucionados, primero en las entrañas de las estrellas y después en los circuitos de nuestras mentes, llega hasta los pensamientos y la imaginación que…son palabras mayores de cuyo alcance, aún no tenemos una idea que realmente refleje su realidad.
con la imagen del ojo humano y hablando de los sentidos y de la consciencia y mira donde he finalizado…Sí, nos falta mucho camino por recorrer para llegar a desvelar los misterios de la Mente que, en realidad, es la muestra más alta que el Universo nos puede mostrar de lo que puede surgir a partir de la sencillez de los átomos de hidrógeno que, evolucionados, primero en las entrañas de las estrellas y después en los circuitos de nuestras mentes, llega hasta los pensamientos y la imaginación que…son palabras mayores de cuyo alcance, aún no tenemos una idea que realmente refleje su realidad.
Pero, ¿existe alguna realidad?, o, por el contrario todo es siempre cambiante y lo que hoy es mañana no existirá, si “realmente” es así, ocurre igual que con el tiempo. La evolución es algo que camina siempre hacia adelante, es inexorable, nunca se para y, aunque como el tiempo pueda ralentizarse, finalmente sigue su camino hacia esos lugares que ahora , sólo podemos imaginar y que, seguramente, nuestros pensamientos no puedan (por falta de conocimientos) plasmar en lo que será esa realidad futura.
, sólo podemos imaginar y que, seguramente, nuestros pensamientos no puedan (por falta de conocimientos) plasmar en lo que será esa realidad futura.
Emilio Silvera V.
















 Totales: 84.312.335
Totales: 84.312.335 Conectados: 47
Conectados: 47