May
17
Sobre las simetrías
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Simetrías ~
Clasificado en Simetrías ~
 Comments (0)
Comments (0)
La simetría esférica del planeta Marte
La simetría es una propiedad universal tanto en la vida corriente, desde un punto de vista matemático como desde el quehacer de la Física Teórica. En realidad, lo que observamos en la vida corriente es siempre lo repetitivo, lo simétrico, lo que se puede relacionar entre sí por tener algo común.
En un sentido dinámico, la simetría podemos entenderla como lo que se repite, lo reiterativo, lo que tiende a ser igual. Es decir, los objetos que, por mantener la misma geometría, son representativos de otros objetos. En el Caos matemático encontramos esta concepción de la simetría en el mundo los fractales. Sin embargo, la simetría es mucho más.
Distintos ángulos de simetría
Cuando miro en mi diccionario de Física la palabra Simetría, lo que me dice que es: “Conjunto de invariancias de un sistema. Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado, la simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y las rotaciones en las moléculas y las translaciones en las redes cristalinas. Las simetrías pueden ser discretas (es decir, cuando hay un número finito de transformaciones de simetría), como el conjunto de rotaciones de una molécula octaédrica, o continuas (es decir, cuando no hay número finito), como el conjunto de rotaciones de un átomo o núcleo. Existen simetrías más generales y abstractas, como la invariancia CTP y las simetrías asociadas a las teorías gauge.”
La simetría gauge es reveladora de interacciones fundamentales
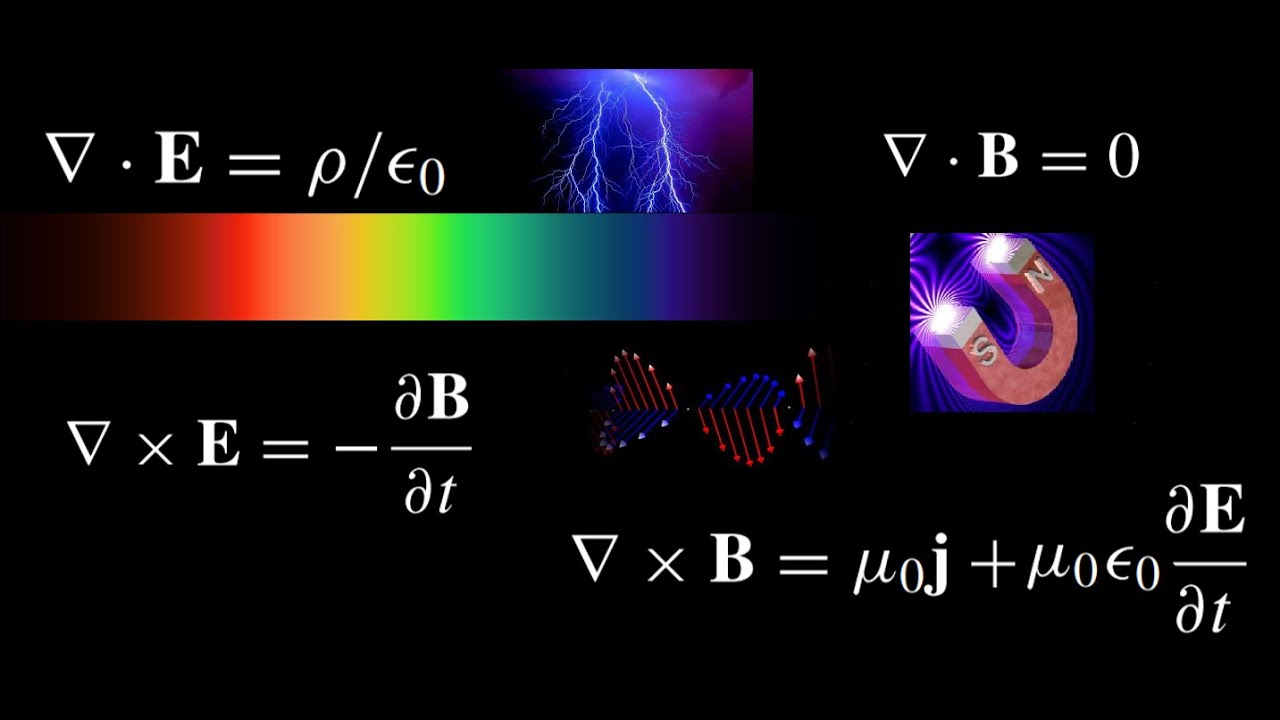
Las ecuaciones de Maxwell, que describen la electrodinámica clásica, tienen cierta simetría “de gauge” que se manifiesta al escribirlas en términos de los potenciales eléctrico y magnético. En la segunda, destacamos que se puede deducir las eM requiriendo invariancia gauge. Así, descubrir la interacción a partir de la simetría constituye un cambio de paradigma que ha permitido deducir correctamente las leyes físicas para las interacciones débiles y fuertes que – junto a la electrodinámica cuántica- conforman el llamado Modelo Estándar de partículas elementales (ME). Hay argumentos convincentes para pensar que la teoría que generalice el ME a energías mayores también será de gauge, no así para la que unifique el ME con la Gravedad.
La invariancia CPT, que postula que la física es la misma bajo ciertas transformaciones (conjugación de carga, paridad y tiempo), y las simetrías asociadas a las teorías gauge, que permiten describir interacciones fundamentales como el electromagnetismo, son conceptos fundamentales en la Física moderna.
La invariancia CPT postula que las leyes físicas permanecen iguales bajo la combinación de tres transformaciones: conjugación de carga (C), paridad (P) y inversión temporal (T).


El experimento BABAR ha medido las ocho tasas de desintegración relevantes para determinar el parámetro ω: las resultantes de combinar en el estado final los dos posibles sabores para el leptón ℓ±, los dos posibles estados hadrónicos con CP definido, J/ψ KS y J/ψ KL, y las dos posibles ordenaciones temporales.
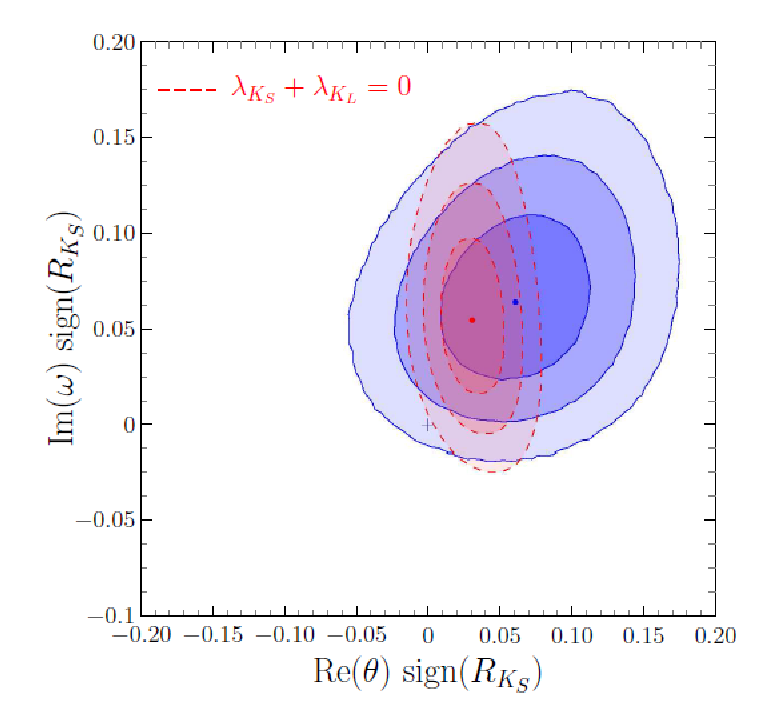
El análisis ha encontrado un valor de Im(ω) que difiere de cero en unas 2σ. Además, este efecto es independiente de la posible violación de CPT debida a la parte real del parámetro θ, para la que el análisis también arroja un valor no nulo, de nuevo con unas 2σ de significación estadística. De hecho, si se repite el análisis asumiendo ω = 0 y considerando las asimetrías en T, CP y CPT por separado, el valor de θ obtenido no difiere del que se deduce en el caso anterior [3].

El Universo está lleno de simetrías por todas partes
También podemos hablar de simetría rota y de super-simetrías. Durante los últimos tiempos, los Físicos han elevado los principios de simetría al más alto nivel en la escala de lo que podemos entender por una explicación. Cuando encontramos una Ley propuesta de la Naturaleza, una pregunta se nos viene a la mente: ¿por qué esta ley? ¿Por qué la relatividad especial y la general? ¿Por qué el electromagnetismo de Maxwell? ¿Por qué las teorías de Yang-Mills de las fuerzas nucleares fuerte y débil? Claro que, una respuesta de importancia es que, las teorías hacen predicciones que han sido repetidamente conformadas con precisos experimentos, con diversidad de científicos y lugares y que, siempre, en todos los casos, dieron el mismo resultado. Esto, por supuesto, es la base de la confianza esencial que los físicos tienen en esas teorías.

Las observaciones nos llevan al convencimiento de que en todos los lugares del Universo rigen las mismas leyes, pasan las mismas cosas, y, están presentes todos los objetos y elementos que lo conforman
Claro que, se deja fuera algo esencial: Los físicos creen también que están en el camino correcto porque, de algún modo que no pueden explicar, tienen la convicción de que son correctas, y las ideas de simetría son esenciales para esa intuición. Se presiente que es correcto que ningún lugar del Universo es especial comparado con cualquier otro lugar del Universo, así que los físicos tienen la confianza de que la simetría de traslación debería estar entre las simetrías de las leyes de la Naturaleza. Se presiente que es correcto que ningún movimiento a velocidad constante es especial comparado con cualquier otro. De modo que los físicos tienen confianza en que la relatividad especial, al abrazar plenamente la simetría entre todos los observadores con velocidad constante, es una parte esencial de las leyes de la Naturaleza.
Así que las simetrías de la Naturaleza no son meras consecuencias de las leyes de la Naturaleza. Desde nuestra perspectiva moderna, las simetrías son la base de la que manan las leyes y, siendo así (que lo es), cuando un físico observa una simetría, agudiza su atención, ya que, allí, en aquel lugar, podría encontrarse alguna ley de la Naturaleza que siguiendo aquella presencia, se podría descubrir.
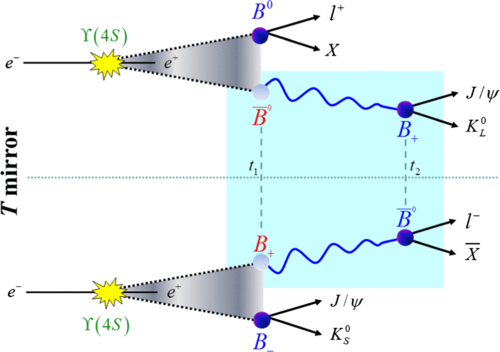
Esquema que explica el experimento para comprobar la ruptura de la simetría temporal a nivel cuántico. Imagen: J. Bernabéu y F. Martínez-Vidal
Un estudio español sobre la ruptura de la simetría en el tiempo, portada de la revista con mayor impacto en Física.
“Investigadores del Instituto de Física Corpuscular (IFIC, Valencia) encontraron evidencias en 2012 de la ruptura de la simetría temporal en las leyes de la Física. El hallazgo fue realizado con la ayuda del experimento BaBar en la Universidad de Standford (EE UU) y fue considerado uno de los hitos científicos de aquel año tras el descubrimiento del bosón de Higgs. Ahora la revista con mayor índice de impacto en el campo de la Física, Reviews of Modern Physics, ha elegido este trabajo para su portada.”
Más allá de su papel en dar forma a las leyes que gobiernan las fuerzas de la Naturaleza, las ideas de simetría son vitales para el propio concepto del tiempo.

Representación del proceso de transformación de un tipo de mesón B en otro con el paso del tiempo, mostrando como un B rojo se convierte en uno azul. / Greg Stewart, SLAC.
Nadie ha sabido encontrar todavía definición fundamental y definitiva del tiempo. Sin embargo, es indudable que el papel del tiempo en la constitución del cosmos es llevar una especie de registro de los sucesos y acontecimientos que en el universo ocurren: Nace una estrella, se forma una nueva galaxia, explota una supernova, muere una estrella masiva y surge un agujero negro…

Sí, todos fuimos jóvenes y el paso del tiempo nos transformó en más viejos pero, no por ello más sabios. Eso sí, con algo más de experiencia y más prudentes a la hora de decidir sobre las cosas importantes que siempre, aunque de joven no le prestemos atención, trae consecuencias.
Reconocemos el transcurrir del tiempo al mirar y ver que, las cosas, no son iguales hoy que lo fueron ayer. Con el transcurrir del tiempo todo cambia y nada permanece. ¿Será el tiempo otra simetría? Debe serlo, ya que, ningún cambio le afecta y, su transcurrir queda inalterado por mucho camino que pudiera haber recorrido y, eso, lo hace diferente de todo lo demás: Todo cambia excepto el tiempo.
Así, tenemos que llegar a la conclusión de que, el concepto de simetría es, para los Físicos, indispensable como punto de referencia en el descubrimiento de las teorías que más tarde, llegan a convertirse en leyes de la Naturaleza al comprobarse que, son inalterables: Otra vez la Simetría. El desarrollo de la moderna teoría cosmológica, por ejemplo, tiene mucho que ver con la simetría. El significado del Tiempo, su aplicabilidad al universo en su conjunto, la forma global del espacio, e incluso el marco subyacente de la relatividad especial, todo descansa sobre fundamentos de simetría.
Durante el último siglo un concepto muy importante en Física, sobre todo en Mecánica Cuántica, ha sido y es el de simetría. Uno de los resultados más bonitos de la Física dice que allá donde hay una simetría hay una cantidad conservada. Es lo que se llama teorema de Noether. De este modo, las leyes de la Física pueden ser iguales bajo una u otra simetría y para cada uno de esos casos se conservará algo. Así por ejemplo, la simetría de traslación temporal corresponde a una cantidad conservada: la energía. También ocurre que las leyes de la física son las mismas bajo unas transformaciones de rotación en el espacio tridimensional y eso significa que se conserva el momento angular.
Emmy Noether, la matemática que Einstein calificó como un genio matemático
El teorema de Noether revela que las leyes más poderosas y trascendentales de la física son, de hecho, meros reflejos de una profunda simplicidad oculta bajo la piel de la realidad . Como lo indica el título del excelente libro de Lee Phillips, Noether descubrió su teorema cuando era, en efecto, la «tutora de Einstein».
En física clásica, el teorema de Noether establece que existe una corriente conservada para cada invariancia de la acción clásica bajo una transformación continua, interna o de simetría espaciotemporal de los campos . Este teorema también permite un método iterativo para construir acciones invariantes, denominado método de Noether.
Este es el teorema de Noether, que establece que la conservación de la energía se cumple en un sistema aislado si las leyes de la física no cambian con el tiempo [1,13]. Este resultado se obtiene bajo un lagrangiano estándar que se aplica en condiciones de convexidad (cuando se cumple el teorema del hiperplano separador y se considera lineal).
Albert Einstein: La señorita Noether fue el genio matemático creativo más importante que haya existido desde que comenzó la educación superior para las mujeres”
Entre algunas de sus aportaciones destacan sobre todo dos: el desarrollo del teorema de conservación conocido como Teorema de Noether, así como el trabajo en álgebra abstracta. Concretamente, el primero le sirvió para poner fin a uno de los grandes problemas que presentaba la Teoría de la Relatividad de Einstein.
« Mis métodos son, en realidad, métodos de trabajo y de pensamiento; por eso se han infiltrado en todas partes de forma anónima. »
Emmy Noether, 1931.
Pero continuemos.
Allí donde veamos presente la simetría, debemos prestar atención, ya que, podría ser el indicio de que algo importante se podría derivar de esa simetría presente que, en física, como hemos comentado, es un principio de gran importancia.

Artificial o natural, por todas partes nos asedia la simetría que quiere alcanzar la perfección y la belleza. Desde las galaxias a la vida, nos muestran la simetría.
















 Totales: 82.268.492
Totales: 82.268.492 Conectados: 55
Conectados: 55