« El Universo y la Mente »

Descarga gratuita
Emilio Silvera Vázquez

« Imagen del Día »

« Colaboraciones »

La cuántica fácil
Fandila Soria Martínez
Física global
Germán Vidal
Inteligencia extrema
Germán Vidal
Cosmología no convencional
Ramón Marqués
Modelo Cosmológico 2017
Germán Vidal
Monopolos Gravitacionales
Germán Vidal
Física del Todo
Germán Vidal
Física del Todo. Capítulo 33
Germán Vidal
Inocentes como ellos
Fandila Soria Martínez
J E N A R O
Fandila Soria Martínez
La caverna
Fandila Soria Martínez
Los inciertos frutos
Fandila Soria Martínez
Tres cuentos y uno más
Fandila Soria Martínez
Un artístico triángulo
Fandila Soria Martínez
~~Una cuántica razonable~~ Temporalmente en revisión
Fandila Soria Martínez
Agujeros Negros, origen y dinámica relativista
Germán Vidal
Fase de ruptura ambiental
Germán Vidal
Procedimiento FRP
Germán Vidal
Folleto oficial de FRPV
Germán Vidal
Alerta de calentamiento global
Germán Vidal
Teoría de la planificación universal
Dante Pracilio

« Escrito recientemente »

Últimos comentarios

« Categorías »

30 Millones de visitas! (1)
a (1)
a otros mundos (18)
a pesar de todo (4)
Acelerador en Huelva (1)
Aceleradores de partículas futuros (3)
Agujeros de gusano (1)
Agujeros negros (69)
AIA-IYA2009 (206)
- ¿Quiénes somos? ¿De donde venimos? (5)
Albert Einstein (3)
Alcanzar otra dimensión (2)
Algo de Cine (2)
Algo de lo que pasó desde el Big Bang (8)
Alquimia (10)
Alquimia estelar (31)
Ancestros (1)
Andrómeda (2)
Anécdotas de personajes de la Ciencia (6)
Antimateria (8)
Aquella cancioncilla (1)
Aquellos filósofos de la naturaleza (3)
Aquellos genios (3)
Artículo de Prensa (9)
Así etán las cosas (9)
Asteroides (4)
Astrofísica (54)
Astronomía y Astrofísica (571)
Avances hacia el futuro (6)
Bacterias nosivas (1)
Belleza sí (5)
Big Bang (1)
Biologia (96)
Bioquímica (31)
Breve historia del Universo (1)
Burlar la Velocidad de la Luz (1)
Cambios inesperados (1)
Canción de desamor (2)
Caos y Complejidad (11)
Carnaval de Física (4)
Carnaval de Matematicas (15)
Catástrofes Naturales (83)
Causalidad… Ese Principio (3)
Celebraciones (5)
Cerebro y Mente (13)
Ciencia futura (49)
Ciencia y Pseudociencia (1)
Ciencia y religión (3)
Ciencia y Vida (16)
Ciencias de la Tierra (13)
Civilizaciones antiguas (10)
Colaboración (6)
Colaboraciones (2)
Comentario a la imagen del día (4)
Computación cuantica (1)
conciencia (28)
Conferencia (2)
Conjeturas (5)
Conocer el Universo (3)
Conocer la Naturaleza (3)
Conociendo el Sistema Solar (5)
Constantes universales (20)
Contaminación radiactiva (1)
Cosas curiosas (46)
Cosas que no deben pasar (2)
Cosas que pasan (5)
Cosmología (43)
Cosmología de los Antiguos pueblos (4)
Cosmología de vacío (1)
Curiosidades (31)
De estrella a púlsar (2)
De lo pequeño a lo grande (4)
Debates (20)
Dehumanizados (1)
del pasado al presente (1)
Densidad Crítica (8)
Descubriendo secretos del Universo (10)
Descubrir y aprender (39)
desde la materia inerte hasta los pensamientos (5)
Desde la materia inerte ¡Hasta los pensamientos! (4)
Deseos que nunca serán cumplidos (1)
Dignidad (1)
Divagando (63)
Diversidad (8)
Divulgando la ciencia (5)
Divulgar la Ciencia (1)
Ecos del Big Bang (5)
El "universo de las galaxias" (2)
El "universo" de la Consciencia (5)
El "universo" de los Fractales (1)
El agua de Marte (1)
El agua… ¡esa maravilla! (3)
El Agua: Un tesoro para la vida (1)
El Amor (4)
El Arte (5)
El Carbono (1)
El Centro Galáctico (1)
El cerebro (33)
El CERN (2)
El cielño en febrero/2015 (1)
El comentario del visitante (2)
El Cuerpo Humano (3)
El Destino… Esa variable (1)
EL DETERIORO DEL PLANETA tIOERRA (1)
El divagar de la Mente (13)
El Espacio Exterior y nosotros (11)
El fin del Universo (2)
El Final del ciclo solar (3)
el futuro (41)
El Futuro incierto (75)
El futuro tecnológico (14)
El hombre en el Universo (31)
El Invento del Alma (2)
El libre pensamiento (4)
El maldito dinero (1)
El Medio Ambiente (1)
El mejor amigo: Un libro (2)
El Metano Marciano (2)
El misterio de las Galaxias que se destruyen (1)
El misterioso número Pi (2)
El Modelo Estánfar (5)
el Mundo y nosotros (23)
El núclo atómico (6)
El origen (23)
El Origen de las cosas (21)
El origen de los elementos (5)
El pasado (6)
El pasado nunca volvera (1)
El placer de descubrir (3)
El Planeta Tierra (1)
El Plasma: cuarto estado de la materia (3)
el presente y el futuro incierto. (3)
El primer contacto (6)
El saber del mundo (27)
El saber ocupa lugar y tiempo (2)
El saber: ¡Ese viaje interminable! (44)
El Ser consciente (2)
El Sistema Saturno (1)
El Sistema Solar (9)
El Tiempo inexorable (9)
El Tiempo pasa…¿O somos nosotros? (14)
El Tiempo siempre presente (4)
El Universo (80)
El Universo asombroso (394)
El Universo cambiante (37)
El Universo de Ayar y el Universo de Hoy (10)
El Universo de la Conciencia (18)
El Universo dinámico (157)
El Universo Hiperdimensional (15)
El Universo misterioso (206)
El Universo y la Entropía (22)
El Universo y la Mente (73)
El Universo y la Química de la Vida (89)
El Universo y la Vida (324)
El Universo y los pensamientos (67)
El Universo y… ¿nosotros? (217)
El Universo: Todo Energía (21)
elementos (1)
En nuestro Universo: La Eternidad no existe (1)
Encuentros Espaciales (1)
Encuesta (1)
Energía = Materia (9)
Energia de fusión (2)
Energías de la Tierra (8)
Enigmas del Corazón (2)
enigmas por resolver (5)
Entrevista (4)
Entrevista científica (10)
Entropía (5)
Es bueno recordar lo que pasó (4)
Esa Ilusión llamada ¡Tiempo! (1)
ese misterio (5)
Especulando (5)
Este mundo injusto (2)
Estrellas (22)
Estrellas de neutrones y Púlsares (2)
Estrellas fugaces (1)
Estrellas masivas (4)
Estructuras fundamentales (6)
Eternidad? (1)
Eva mitocondrial (1)
evadirnos (1)
Evadirnos del mundo por un momento (1)
Eventos (2)
Evolución (15)
Experimentos espaciales (1)
Exploración de los mundos (2)
exploración del espacio (4)
explorando lo "nano" (1)
Extinciones (4)
Extinciones de origen desconocido (1)
Extraño sueño (1)
Fallida Misión a Marte (1)
Felicidad para todos (1)
Felicitar a un amigo (1)
Fenómenos naturales (1)
Ficción (1)
Filosofía (7)
Fin de la Misión Cassini (1)
Física (1.650)
- Física Cuántica (517)
- Física Relativista (68)
- La Mujer en la Ciencia (2)
Física de vacío (9)
Física en las estrellas (2)
Física Solar (1)
Física y cosmología (6)
Física-química (16)
Física… ¡Y mucho más! (20)
Formación de elementos (2)
Fuerzas de la Naturaleza (3)
Fusión de galaxias (1)
Futuro (17)
Gaia (12)
Gases nobles (1)
General (3.717)
Genética (1)
Gracias al visitante (1)
Grandes extinciones (1)
Hacia el futuro (21)
Hacienda somos todos (2)
Hay que sentir (1)
Hiperespacio (2)
Historia para mirar (6)
Humanidad (16)
I. A. (15)
Imaginación (19)
Imaginando (2)
Implosión de una estrella (1)
Injusticia sin fin (3)
Inocentada (1)
Interacciones fundamentales (2)
Internet (1)
Investigación y Ciencia (3)
La Astronomía y la Humanidad (4)
La Belleza (1)
La Belleza y la Ciencia (5)
La Ciencia (6)
La Ciencia debe avanzar (2)
La Ciencia en el pasado (2)
La Ciencia Fiscción (1)
La Complejidad (9)
La complejidad de la Vida (12)
La Conquista del Espacio (4)
La contaminaciñon del planeta (1)
La Entropía lo destruye todo (6)
la Entropía siempre presente (2)
La estructura del Espacio (1)
La física en la vida cotidiana (2)
La Física y el Universo (1)
La Física y la Salud (2)
La formación de las galaxias (2)
La fotosíntesis (1)
La fragilidad HUmana (1)
La Geotectónica (1)
La ignorancia nos acompaña siempre (30)
La Imagen del día (1)
La Implosión de las estrellas (1)
La importancia del tiempo (1)
La inmortalidad no existe (1)
La justa medida (5)
La libertad de pensar (2)
La luna Europa (1)
La Luz esconde muchos secretos (13)
La magia de la Tierra (6)
La mágica Naturaleza (4)
La maldad Humana (1)
La materia tiene memoria (5)
la mente (3)
La Mente – Filosofía (135)
La muerte de las estrellas (1)
La muerte del Sol (1)
La mujer y la Ciencia (1)
La música son sentimientos (6)
La músuca. (2)
La NASA (1)
La NASA experimenta (1)
La naturaleza de la Luz (1)
La Naturaleza ¡Es sabia! (7)
La Naturaleza…El Universo (39)
La Oración (2)
La realidad cambiante (7)
La realidad humana ¿es realidad? (16)
la realidad presente (2)
La Teoría de Cuerdas (6)
La Tierra se recicla (2)
La Tierra y su energía (20)
La Tierra: Pasado y futuro (1)
La Unión hace la fuerza (1)
La vecindad galáctica (3)
La Vía Láctea (1)
La vida (20)
La Vida de las Partículas (1)
La Vida en la Tierra (4)
La Vida en otros mundos (4)
La vida sigue (3)
Las bacterias y nosotros (1)
Las constantes de la Naturaleza (9)
las constantes y la Vida (2)
Las constantes y las inesperadas (2)
Las distancias en el Espacio (6)
Las ecuaciones (3)
las estrellas y la Vida (20)
Las galaxias generan entropía negativa (3)
Las huellas del pasado (8)
Las nuevas tecnologías (1)
Las prodigiosas ideas (2)
Las religiones (1)
Libre Albedrío (1)
Lo que creemos que sabemos (7)
lo que es (4)
Lo que no sabemos (24)
lo que será (1)
Los 100 descubrimientos más grandes (1)
Los cráteres de la Tierra (1)
Los Elementos (3)
Los estados de la materia (3)
Los Ingleses en Huelva (1)
Los misterios del Universo (8)
Los Pensamientos (28)
Los pilares del Sol en la Tierra (1)
Los primeros pasos (2)
Los recuerdos (2)
Los secretos del Universo (5)
Los sentimientos (4)
Los terremotos (1)
Lunas misteriosas (5)
malos tiempos (1)
Maravillosa Teoría (3)
Marte (81)
Matemáticas (6)
Materia extraña (11)
Materiales increibles (5)
Materias diversas (4)
Mecánica cuántica (8)
Memorias del pasado (1)
Meteoritos (3)
Meteoritos asesinos (3)
Mi hija María (2)
Mi Huelva (1)
Mi Tierra (4)
Mirar el futuro con los pies en el suelo (1)
Misterios de Júpiter (1)
Misterios de la Mente (3)
Misterios del Universo (8)
Misterios sin resolver (13)
Moléculas precursoras de la vida (5)
Mujer y hombre: 2 caras de la misma moneda (1)
Mujeres científicas (1)
Multiverso (16)
Mundo Futuro (6)
Nada muere y todo cambia (2)
nada permanece (6)
Nada puede surgir de la Nada (1)
Nanotecnología (8)
Naturaleza (19)
Naturaleza misteriosa (36)
Naturaleza-Imaginación (3)
Nebulosas (23)
Nebulosas y estrellas (11)
Newton (2)
Niburu El Planeta X (1)
no lo comprendo! (1)
No solo de pan vive el hombre (6)
No todo es Ciencia (1)
nosotros (1)
Nostalgia (1)
Noticia comentada (20)
Noticias (154)
Noticias NASA (2)
Nuestra Salud (1)
Nuestro entorno (5)
Nuestro entorno…Nuestro futuro (6)
nuestro entrañable hermano (1)
Nuestro increíble planeta (1)
Nuestro origen (1)
Nuestro recorrido histórico (1)
Nuevas posibilidades (3)
Nuevas revoluciones científicas (2)
Nuevos materiales (4)
Nuevos mundos (8)
números adimensionales (1)
Nunca dejaremos de hacer preguntas (3)
Omega Negro (1)
Ondas gravitacionales (19)
Origen de las matemáticas (1)
Orion (2)
Otras clases de vida (3)
otras formas de vida (4)
Otras teorias (1)
Otros mundos (25)
Panspermia (1)
Paradojas de la relatividad (2)
Pasado que sigue siendo presente (1)
Pensamientos (8)
Pequeño reportaje (2)
pero Eternidad… (1)
Personajes de la Historia (11)
Personajes ilustres (5)
Planetas imposibles para la vida (2)
Preguntas que no sabemos contestar (1)
presente y futuro de la Ciencia (2)
Pueblos de Huelva (1)
Púlsares y galaxias (6)
Querencias (2)
Queriendo saber (12)
Química (33)
Química estelar y Vida (2)
Radiación Cósmica (2)
realidad mañana (1)
Recordando el pasado (9)
Recordar la vijeo y querer lo nuevo (1)
Refinando teorías (1)
Relación del Sol con la Tierra (3)
Relatiovidad Especial (3)
Rememorando el pasado (8)
Reportajes de prensa (10)
Resumen del año (2)
Rotura de la simetrísa CP (1)
RSEF (1)
Rumores del Saber (250)
Rumores del saber del mundo (34)
sabremos (3)
Saturno (1)
Se puede traspasar la Memoria? (1)
Secretos del Universo (1)
Seguimos elucubrando (1)
Siempre hacienda pregutas (1)
siempre misteriosa (2)
Simetrías (22)
Singularidad (2)
Son tantas las cosas que no sabemos (2)
Sueños de hoy (1)
Sueños de la Humanidad (4)
Superconductores y el campo de Higgs (2)
Supergravedad (2)
Supernova (1)
Sustancias (1)
También los planetas evolucionan (1)
Tecnología futura (2)
Tenemos que saber (6)
Teoría de cuerdas y dimensiones extra (4)
Teoría de Supercuerdas (8)
Teorías ¿Imposibles? (2)
Teorísa del Todo (1)
Titán (4)
todo es número (1)
Transiciones de fase (3)
Transiciónes de fase en las estrellas (1)
Un desahogo (2)
Un Genio Matemático (1)
Un Mundo justo (1)
Un mundo mejor (2)
Un recorrido desde el comienzo del tiempo (2)
Un Universo con dimensiones extra (1)
Una pequeña entrevista (1)
Unificar la Naturaleza (1)
universo (1)
Universo de fantasías (1)
Universo estacionario y elementos (1)
Universo primitivo (1)
Universos paralelos (18)
Vía Láctea (1)
Viajar al Espacio (13)
Viajar al pasado (15)
vida (1)
Vida en otros mundos (24)
WIMPs (1)
¡Asombroso! (2)
¡Cosas del Universo! (3)
¡El futuro es imparable! (1)
¡El maldito dinero! (1)
¡El Tiempo! ¿Qué será? (1)
¡El Tiempo! ¿Qués es el Tiempo? (8)
¡Energías! (1)
¡Humanidad! (8)
¡Imaginación! (7)
¡Indignados! (1)
¡La amistad! (1)
¡La Ciencia! esa maravilla (1)
¡La Curiosidad! (1)
¡La Gravedad! Esa fuerza misteriosa (1)
¡La Humanidad! (2)
¡La Materia Oscura! (2)
¡La Mente! Ese prodigio (5)
¡La Mujer! ¿Cuando reconoceremos su valía? (1)
¡La música nos hace mejores! (1)
¡La vida! El misterio persiste (6)
¡Las estrellas! (3)
¡Las matemáticas! (1)
¡Los pensamientos! (3)
¡Los pensamientos! ¿quién los sujeta? (1)
¡Maldita desigualdad! (1)
¡Males del mundo! (2)
¡Maravillas del Universo! (1)
¡Naturaleza! (1)
¡Necesitamos saber! (6)
¡No estamos sólos! (3)
¡NO! (1)
¡Noticias! (9)
¡Partículas! (1)
¡Pueblos y lugares! (1)
¡Qué cosas! (2)
¡Qué mundo este nuestro! (1)
¡Tenemos que saber! (12)
¡Tiempo! (3)
¡Viajar en el Tiempo! ¿Podremos? (5)
¡vIAJES EN EL tIEMPO! (1)
¡¡La Ciencia!! (2)
¿Alma inmortal? (1)
¿Biofísica? (1)
¿Cómo se formaron las galaxias? (1)
¿Cuánta materia hay en el Universo? (1)
¿Cuánta materia vemos? (1)
¿De dónde venimos? (1)
¿De donde venimos? ¿Quiénes somos? (1)
¿Dónde estamos dentro de la Galaxia? (1)
¿El primer contacto? ¡Tndrá que esperar! (1)
¿El Universo? ¡Tenemos que conocerlo mejor! (2)
¿Estrellas de Quarks? (1)
¿Extraterrestres? (1)
¿Hacia dónde nos lleva la ignorancia? (1)
¿Igualdad? ¿Dónde? (1)
¿La materia Oscura! (2)
¿Libre albedrío? (1)
¿Materia oscura? (1)
¿Materia Oscura? ¿Dónde? (1)
¿Mensajes del futuro? (1)
¿Multiverso? (2)
¿Mutación? (1)
¿Observadores del Universo! (2)
¿Ondas gravitacionales? (1)
¿otra clase de materia? (1)
¿Otros Universos? (2)
¿Panspermia? (1)
¿Qué es el Tiempo? (1)
¿Qué es en realidad la Luz? (1)
¿Qué es la belleza? No es lo mismo para todos (1)
¿qué sorpresa nos dará? (1)
¿Quiénes somos? (1)
¿Recordar u olvidar? Qué será mejor (1)

« Archivo »

marzo 2024

L M X J V S D

1 2 3

4 5 6 7 8 9 10

11 12 13 14 15 16 17

18 19 20 21 22 23 24

25 26 27 28 29 30 31

« Feb Abr »

marzo 2024
L	M	X	J	V	S	D
	1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30	31

« Enlaces internos »

« Enlaces »

Asociación Huelva Nueva York
Carnaval de Física
Ciencia Kanija
El Tamiz
Escritores
Gravedad Cero
HIRISE
NovaCiencia
Off-Topic Observatorio
Real Sociedad Española de Física
¡Maldito Capital! - Se describe lo que es la realidad del mundo

« Administración »

« Buscar »

« Suscripciones web »

Geolocalizador

« Visitas »

Totales: 80.120.507
Conectados: 54

Archivo de marzo de 2024

« Entradas anteriores

Mar

31

La Ciencia es bella

Autor por Emilio Silvera ~ Archivo Clasificado en El Universo misterioso, Noticias ~ Comentarios Comments (0)

Suscribirse por correo a los comentarios

EN PORTADA UN REPORTAJE DE EL PAÍS

Ritmo y simetría son conceptos comunes a ciencia y arte. El Nobel Frank Wilczek es el último en traspasar en su nueva obra la frontera entre ambas

Resultado de imagen de On Growth and Form (en español en Akal, 2011) del escocés D’Arcy Thomson

Fotografías de la serie de los años veinte ‘Formas artísticas de la naturaleza’, de Karl Blossfeldt.

¿Es el mundo una obra de arte? Tal es la cuestión que el autor se propone indagar desde el título y el prólogo de este ensayo. La idea tiene su dificultad porque en principio induce a pensar en el gran artista y en sus intenciones a la hora de crear el mundo. Sin embargo, el autor no se lanza directamente en esta dirección, sino a todo un conjunto de cuestiones que se descuelgan de la pregunta inicial. Por un lado, se trata de comparar el mundo de las ideas en las que se mueve la mente del artista cuando crea y el mundo de los cuerpos físicos de la realidad en la que está inmerso. Por otro lado, se trata de enfrentar la belleza que vive el artista cuando hace arte con la belleza que vive el científico cuando hace ciencia. Aplicamos el concepto de belleza tanto a un atardecer, que es un paisaje en condiciones efímeras, como al sonido de una música, como a un pedazo de conocimiento concebido por una mente humana. En la propuesta de Wilczek destaca un concepto sobre todos los demás: la simetría. Simetría exhiben los cristales, las plantas y los animales, simetría hay también en sus maneras de cambiar, hay simetría en las obras de arte y, sobre todo, hay simetría también en las teorías científicas. La creación científica y la creación artística ofrecen una buena pista para empezar.

Fotografías de la serie de los años veinte 'Formas artísticas de la naturaleza', de Karl Blossfeldt.

Se equivocan los que aseguran que ciencia y arte son la misma cosa y se equivocan los que dicen que arte y ciencia nada tienen que ver. Sin embargo, enfrentar estas dos grandes formas de conocimiento interesa tanto por lo que comparten como por lo que difieren. La intersección no puede ser más fértil. La grandeza de la ciencia está en que un científico puede llegar a comprender sin necesidad de intuir y la grandeza del artista en que puede llegar a intuir sin necesidad de comprender. Un físico comprende el comportamiento cuántico de una partícula porque lo anticipa usando la ecuación de Schrödinger, pero no lo intuye porque sus sentidos no han experimentado nunca nada similar. No hay intuición cuántica porque no hay observadores cuánticos. En cambio, un artista puede distorsionar la realidad y fabricarse una metáfora para intuir algo que no tiene por qué comprender y que ni siquiera tiene por qué existir en la naturaleza. Oscar Reutersvärd, por ejemplo, fue un artista gráfico que inventó objetos en tres dimensiones que se pueden dibujar, pero que desafían la intuición porque no se pueden construir. Es la idea de los objetos imposibles que cautivó al gran físico y matemático Roger Penrose y al que tanto debe el celebérrimo Maurits Cornelius Escher, el artista que finalmente ha quedado en la historia como padre de la idea.

Trazos, notas, teoremas

Resultado de imagen de On Growth and Form (en español en Akal, 2011) del escocés D’Arcy Thomson

Se enganchó tanto a esta cuestión que se pasó toda la vida reescribiendo el mismo libro. Se trata de On Growth and Form (en español en Akal, 2011) del escocés D’Arcy Thomson (1860-1948). Apareció por primera vez en 1917 con 793 páginas, pero la última edición de 1942 alcanza las 1116 páginas. Aún se puede conseguir en casi todos los idiomas y aún es tema de discusión tanto por sus aciertos como por sus errores. Sus críticos le reprochan que no acabara de comprender el mecanismo de la selección natural, aunque todo el mundo reconoce su tremenda influencia en otros autores. Yo me cuento entre los seducidos y mi réplica fue el ensayo La rebelión de las formas (Tusquets, 2004). Una obra maestra que conmovió a artistas y científicos es Gödel, Escher, Bach (Tusquets, 1987) de Douglas Hofstadter, profesor de ciencias cognitivas e hijo de un premio Nobel de física, donde se relacionan las obras del matemático autor del teorema más bello de la historia, del artista que ilustró el mundo de los objetos imposibles y del compositor barroco que revolucionó la música. Un ensayo más moderno es Truth and Beauty: Science and the Quest of Order (Oxford University Press, 2011) de David Orrell.

Resultado de imagen de El mundo como obra de arte, del premio Nobel de Física Frank Wilczek

El mundo como obra de arte, del premio Nobel de Física Frank Wilczek, se sumerge en estas fértiles tierras fronterizas. ¿Qué es la belleza? ¿Qué es la belleza natural de los objetos reales y qué es la belleza cultural del conocimiento humano? ¿En qué punto se dan la mano ambas concepciones? El número áureo es una proporción conocida desde la antigüedad como un canon de belleza que se deduce por un razonamiento puramente mental. Basta imponer la armonía y el equilibrio que resulta más agradable y natural a nuestros sentidos. Por ello no es raro encontrarlo en todo tipo de estructuras de diseño humano, desde la arquitectura a los muebles, pasando por un simple encendedor. Pero ¿cómo demonios se explica que ese mismo número aparezca también en las formas y estructuras vivas? ¿Será como decía Oscar Wilde que la naturaleza copia al arte? La cuestión es de una profundidad sin fondo y no se limita a los objetos naturales o culturales. La belleza no está solo en los resultados visibles de las teorías científicas y matemáticas. La belleza está también en el origen, en las hipótesis de trabajo y en la concepción del mundo que han estimulado el pensamiento de los grandes creadores científicos.

Resultado de imagen de La belleza de los objetos naturales

Wilczek revisa las formas más bellas del pensamiento científico y de los objetos naturales para llegar a varias conclusiones no siempre explícitas en su texto. Aún antes de acordar una definición de belleza, digamos que la belleza es un concepto frecuente en el arte, propio del arte, pero que no es necesario para hacer arte. Y aún antes de acordar una definición de lo que es comprensible, digamos que la inteligibilidad es un concepto omnipresente y propio de la ciencia, pero que no es suficiente para hacer ciencia. Sin embargo, en todos los casos elegidos por Wilczek se filtra una relación esencial entre lo que es bello y lo que es comprensible. La forma más simple de belleza es la iteración en el espacio y en el tiempo, esto es, la armonía y el ritmo. Y la forma más inmediata de lograr esta belleza es la simetría. Se diría que la belleza es una especie de no cambio dentro del cambio. ¿Qué es una ley de la naturaleza? Pues algo muy parecido: es el cambio que menos cambia. Todos los movimientos de los planetas son diferentes, pero todos obedecen a las mismas ecuaciones de las mismas leyes. Los físicos buscan siempre principios de conservación (conservación de la masa, de la carga, de la energía, de la cantidad de movimiento, del momento angular…) porque con ellos se pueden anticipar los cambios que experimenta un sistema. Wilczek no puede disimular su emoción en el capítulo que dedica a Emmy Noether, la gran matemática que tanto admiró Einstein, cuyos teoremas establecen la relación entre los principios de conservación por un lado y las propiedades de simetría del espacio y del tiempo por otro. A Einstein se le debieron saltar las lágrimas con los trabajos de Noether (lo sé porque a mí me ocurrió lo mismo cuando los vi por primera vez en la pizarra de la facultad). Después de todo, tanto la teoría especial como la teoría general de la relatividad se levantan sobre el mismo pilar: el mundo puede ser complejo, misterioso, extraño…, ¡pero no feo! Es un principio estético como también queda claro en el capítulo que este ensayo dedica a la relatividad, sin duda la más grande y más bella teoría jamás concebida por una sola mente.

Fotografías de la serie de los años veinte 'Formas artísticas de la naturaleza', de Karl Blossfeldt.

El caso de la física cuántica, que el libro también se entretiene en saborear a través de los trabajos seminales de Einstein y Bohr, tiene un valor añadido: invita a comprender los fundamentos de la física cuántica a través de intuiciones musicales. No alcanza quizá raíces tan profundas en la fusión de los conceptos de belleza e inteligibilidad, pero sí ofrece un camino que es bastante más que una metáfora. Comprender es buscar lo que hay de común entre cosas aparentemente diferentes. Los objetos fractales, por ejemplo, ofrecen un lenguaje común para dar cuenta de la autosimilitud y la irregularidad, de nuevo el no cambio dentro del cambio, lo que afecta tanto a los hexágonos de un panal de abejas, de la estructura de un material sintético como el grafeno o a la estructura de un copo de nieve.

El propósito de Michelson y Morley era medir la velocidad relativa a la que se mueve la Tierra con respecto al éter. Cada año, la Tierra recorre una distancia enorme en su órbita alrededor del Sol, a una velocidad de 30 km/s (más de 100.000 km/h). Se creía que la dirección del “viento del éter” con respecto a la posición de nuestra estrella variaría al medirse desde la Tierra, y así podría ser detectado. Por esta razón, y para evitar los efectos que podría provocar el Sol en el “viento” al moverse por el espacio, el experimento debería llevarse a cabo en varios momentos del año.

El libro recorre las ideas más bellas y trascendentes de la física con Galileo, Newton, Maxwell o Einstein, pero no esquiva las ideas bellas que han resultado ser falsas. La concepción geométrica de los átomos de Platón, el sistema solar de Kepler, el éter que buscaban Michelson y Morley, etcétera. Queda claro: aunque la belleza predispone a comprender, hay que reconocer que la belleza no es una garantía de verdad. Sin embargo, Wilczek consigue seducir al lector tácita y subliminalmente en favor de una respuesta a la pregunta inicial del libro: ¿es el mundo una obra de arte? Y ésta no es otra que un sonoro y apasionado ¡sí!

La teoría especial y la general de la relatividad se levantan sobre el mismo pilar: el mundo puede ser complejo, pero no feo

Wilczek es un físico teórico de amplísima cultura dentro y fuera de la física. Recibió el Premio Nobel de Física en 2004 por un tema aparentemente tan contradictorio como la libertad asintótica en la teoría de las interacciones fuertes, esto es, cuando dos quarks se acercan mucho entre ellos su fuerza de interacción se debilita tanto que se convierten en partículas libres. El libro equivale a un paseo a través de la historia de la física de la mano de alguien que comprende la realidad desde una concepción estética global del mundo…, como todos los grandes científicos.

Emilio Silvera

[?]

Mar

29

¿La Física? ¡Una maravilla! Nos dice cómo funciona la Naturaleza

Autor por Emilio Silvera ~ Archivo Clasificado en Física ~ Comentarios Comments (5)

Ylia Prigogine ¡Qué personaje!

El Universo y la Vida… ¡Nuestra imaginación!

En su Libro Partículas, Gerard ´t Hofft, Premio Nobel de Física, nos cuenta:

“En el mundo de los seres vivos, la escala o tamaño crea importantes diferencias. En muchos aspectos, la anatomía de un ratón es una copia de la de un elefante, pero mientras que un ratón trepar por una pared prácticamente vertical sin mucha dificultad (y se puede caer desde una altura varias veces mayor que su propio tamaño sin hacerse daño), un elefante no sería capaz de realizar tal hazaña. Con bastante generalidad se puede afirmar que los efectos de la gravedad son menos importantes cuanto menores sean los objetos que consideremos (sean vivos o inanimados).”

Cuando llegamos a los seres unicelulares, se ve que ellos no hay distinción entre arriba y abajo. Para ellos, la tensión superficial del agua es mucho más importante que la fuerza de la gravedad a esa escala. Tranquilamente se pueden mover y desplazar por encima de una superficie acuática. Los pluricelulares no pueden hacer tal cosa.

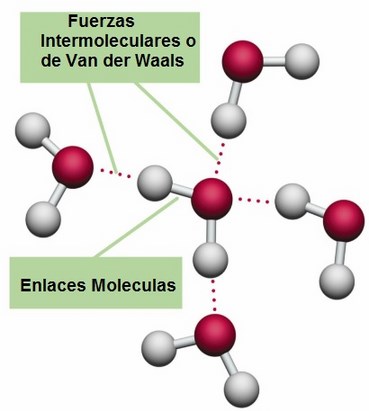
La tensión superficial es una consecuencia de que todas las moléculas y los átomos se atraen unos a otros con una fuerza que nosotros llamamos de Van der Waals. fuerza tiene un alcance muy corto; para ser precisos, diremos que la intensidad de esta fuerza a una distancia r es aproximadamente 1/r⁷. Esto significa que si se reduce la distancia dos átomos a la mitad de la fuerza de Van der Waals con la que se atraen uno a otro se hace 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128 veces más intensa. Cuando los átomos y las moléculas se acercan mucho unos a otros quedan unidos muy fuertemente a través de esta fuerza. El conocimiento de esta fuerza se debe a Johannes Diderik Van der Waals (1837 – 1923) con su tesis sobre la continuidad del líquido y gaseoso que le haría famoso, ya que en esa época (1873), la existencia de las moléculas y los átomos no estaba completamente aceptado.

La tensión superficial del agua, es el efecto físico (energía de atracción entre las moléculas) que “endurece” la capa superficial del agua en reposo y permite a algunos insectos, como el mosquito y otros desplazarse por la superficie del agua sin hundirse.

El famoso físico inglés James Clerk Maxwell, que formuló la teoría del electromagnetismo de Faraday, quedó muy impresionado por este de Van der Waals.

Los tamaños de los seres uniceculares, animales y vegetales, se miden en micrómetros o “micras”, donde 1 micra es 1/1.000 de milímetro, aproximadamente el tamaño de los detalles más pequeños que se pueden observar con un microscopio ordinario. El mundo de los microbios es fascinante, pero no es el objeto de este trabajo, y continuaremos el viaje emprendido las partículas elementales que forman núcleos, átomos, células y materia, así como las fuerzas que intervienen en las interacciones fundamentales del universo y que afecta a todo lo que existe.

Hemos hablado del electrón que rodea el núcleo, de su carga eléctrica negativa que complementa la positiva de los protones y hace estable al átomo; una masa de solamente 1/1.836 de la del núcleo más ligero (el del hidrógeno). La importancia del electrón es vital en el universo.

Pero busquemos los “cuantos”. La física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menor intensidad, por los objetos más fríos (radiación de cuerpo negro).

Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si utilizamos las leyes de la termodinámica para calcular la intensidad de una radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano y, luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para menores. Esta longitud de onda característica es inversamente proporcional a la temperatura absoluta de objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273º bajo cero). Cuando a 1.000º C un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.

Radiación de Cuerpo Negro

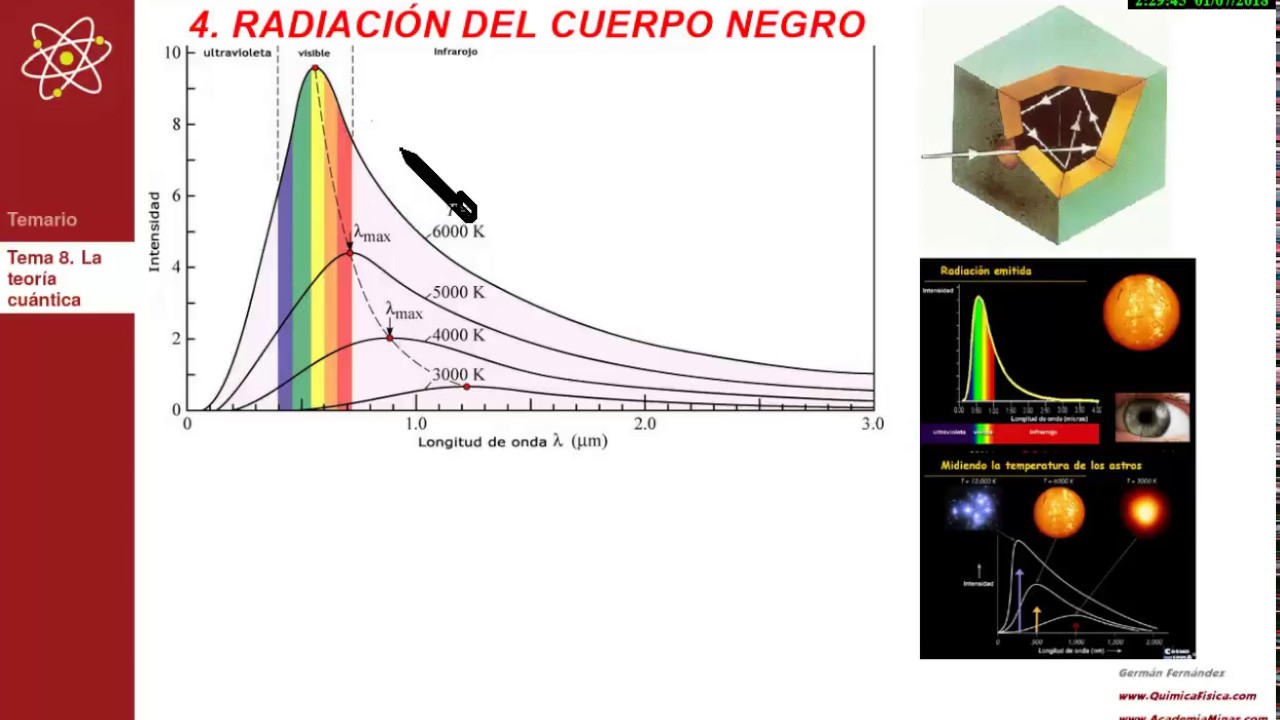
Un cuerpo negro es un objeto teórico o ideal que absorbe toda la luz y toda la energía radiante que incide sobre él. Nada de la radiación incidente se refleja o pasa a través del cuerpo negro. A pesar de su , el cuerpo negro emite luz y constituye un modelo ideal físico para el estudio de la emisión de radiación electromagnética. El nombre Cuerpo negro fue introducido por Gustav Kirchhoff en 1862.

La luz emitida por un cuerpo negro se denomina radiación de cuerpo negro. Todo cuerpo emite energía en de ondas electromagnéticas, siendo esta radiación, que se emite incluso en el vacío, tanto más intensa cuando más elevada es la temperatura del emisor. La energía radiante emitida por un cuerpo a temperatura ambiente es escasa y corresponde a longitudes de onda superiores a las de la luz visible (es decir, de menor frecuencia). Al elevar la temperatura no sólo aumenta la energía emitida sino que lo hace a longitudes de onda más cortas; a esto se debe el cambio de color de un cuerpo cuando se calienta. Los cuerpos no emiten con igual intensidad a todas las frecuencias o longitudes de onda, sino que siguen la ley de Planck.

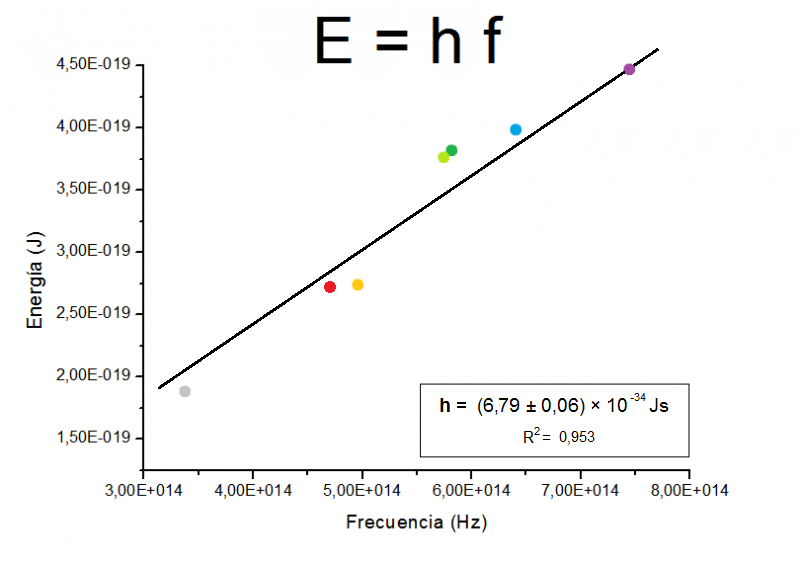
Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda, y por tanto, proporcional a la frecuencia de radiación emitida. La fórmula es E = hν, donde E es la energía del paquete, ν es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo nueva condición, el resultado coincidió perfectamente con las observaciones.

Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: él sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck. El príncipe francés Louis-Victor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene energía, sino que cualquier cosa con energía se debe comportar una “onda” que se extiende en una cierta región del espacio, y que la frecuencia ν de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilantes de campos de fuerza, esto lo veremos más adelante.

El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de de Broglie. Poco después, en 1926, Edwin Schrödinger descubrió cómo escribir la teoría ondulatoria de de Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de ondas cuánticas”.

Está bien comprobado que la mecánica cuántica funciona de maravilla…, pero, sin embargo, surge una pregunta muy formal: ¿qué significan realmente estas ecuaciones?, ¿qué es lo que están describiendo? Isaac Newton, allá en 1867 formuló cómo debían moverse los planetas alrededor del Sol, estaba claro todo el mundo qué significaban sus ecuaciones: que los planetas estaban siempre en una posición bien definida des espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades en el tiempo.

Pero los electrones todo es diferente. Su comportamiento parece estar envuelto en misterio. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?

Niels Bohr consiguió responder a esta pregunta de tal que con su explicación se pudo seguir trabajando, y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la interpretación de Copenhague de la mecánica cuántica.

Si la mecánica cuántica tiene cosas extrañas y el espín es una de ellas. Y si uno piensa que la intuición le ayudará a comprender todo esto, pues no lo hará, o es poco probable que lo haga. Las partículas tienen un espín fundamental. Al igual que la carga eléctrica o la masa, el espín ayuda a definir que de partícula es cada una.

Las leyes de la mecánica cuántica han sido establecidas con mucha precisión; permite cómo calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas de manera simultánea. Por ejemplo, podemos determinar la velocidad de una partícula con mucha precisión, pero entonces no sabremos exactamente dónde se encuentra; o a la inversa, podemos determinar la posición con precisión, pero entonces su velocidad queda mal definida. Si una partícula tiene espín (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.

La posición y el momento de una partícula nunca lo podremos saber con precisión ilimitada.

No es fácil explicar de forma sencilla de dónde viene esta incertidumbre, pero existen ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar. Para afinar un instrumento se debe escuchar una nota durante un cierto intervalo de tiempo y compararla, por ejemplo, con un diapasón que debe vibrar también durante un tiempo. Notas muy breves no tienen bien definido el tono.

Para que las reglas de la mecánica cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuando más grande y más pesado es un objeto, más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica. Me gustaría referirme a exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por holismo, y que podría definir como “el todo es más que la suma de sus partes”. Si la física nos ha enseñado algo es justo lo contrario. Un objeto compuesto de un gran de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (partículas); basta que sepamos sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes. Por ejemplo, la constante de Planck, h, que es igual a 6’626075… × 10^-34 Julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.

La mecánica cuántica es muy extraña a nuestro “sentido común”, sabemos que se desenvuelve en ese “universo” de lo muy pequeño, alejado de nuestra vida cotidiana en el macrocosmos tetradimensional que, no siempre coincide con lo que, en aquel otro infinitesimal acontece.

Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisenberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros como Erwin Schrödinger siempre presentaron serias objeciones a interpretación. Quizá funcione bien, pero ¿dónde está exactamente el electrón?, ¿en el punto x o en el punto y? En pocas palabras, ¿dónde está en realidad?, y ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.

Es cierto que, existe otro universo dentro de nuestro del que, aún, nos queda mucho por aprender.

La mecánica cuántica puede ser definida o resumida así: en principio, con las leyes de la naturaleza que conocemos se puede predecir el resultado de cualquier experimento, en el sentido que la predicción consiste en dos factores: el primer factor es un cálculo definido con exactitud del efecto de las fuerzas y estructuras, tan riguroso como las leyes de Isaac Newton para el movimiento de los planetas en el Sistema Solar; el segundo factor es una arbitrariedad estadística e incontrolable definida matemáticamente de estricta. Las partículas seguirán una distribución de probabilidades dadas, primero de una forma y luego de otra. Las probabilidades se pueden calcular utilizando la ecuación de Schrödinger de función de onda (Ψ) que, con muchas probabilidades nos indicará el lugar probable donde se encuentra una partícula en un dado.

Muchos estiman que esta teoría de las probabilidades desaparecerá cuando se consiga la teoría que explique, de forma completa, todas las fuerzas; la buscada teoría del todo, lo que implica que nuestra descripción actual incluye variables y fuerzas que (aún) no conocemos o no entendemos. Esta interpretación se conoce como hipótesis de las variables ocultas.”

¿Podría ser el Universo un Holograma?

También Gerard ‘t Hooft es el autor de lo que han dado en llamar l principio holográfico es una conjetura especulativa acerca de las teorías de la Gravedad Cuántica propuesta en 1993 por este autor, y mejorada y promovida por Leonard Susskin en 1995. Postula que toda la información contenida en cierto volumen de un espacio concreto se puede conocer a partir de la información codificable sobre la frontera de dicha región. Una importante consecuencia es que la cantidad máxima de información que puede contener una determinada región de espacio rodeada por una superficie diferenciable está limitada por el área total de dicha superficie.

Por ejemplo, se pueden modelar todos los eventos que ocurran en un cuarto o una habitación creando una teoría en la que sólo tome en cuenta lo que suceda en sus paredes. En el principio holográfico también se afirma que por cada cuatro Unidades de Planck existe al menos un grado de libertad (o una unidad constante de Bolttzmann k de máxima entropía). Esto se conoce como frontera de Bekenstein:

$S\le\frac{A}{4}$

donde S es la entropía y A es la unidad de mensura considerada. En unidades convencionales la fórmula anterior se escribe:

$S\le \left( \frac{kc^3}{G\hbar} \right) \frac{A}{4} = k \frac{A}{4\ell_P^2}$

donde:

$k\,$ , es la constante de Boltzmann.
$c\,$ , es la vecolcidad de la luz.
$G\,$ , es la constante gravitacional universal.
$\hbar\,$ , es la constante de Planck racionalizada.
$\ell_P\,$ , es la longitud de Planck.

Claro que esta… ¡Es otra Historia!

Emilio Silvera

[?]

Mar

28

Siempre buscando la realidad de las cosas

Autor por Emilio Silvera ~ Archivo Clasificado en La justa medida ~ Comentarios Comments (3)

¡Si dejamos de soñar y dejamos de imaginar…!

¿Os acordais de la Mars Climater Orbiter? Allá por el mes de Septiembre de 1998, la NASA preparaba a bombo y platillo la gran noticia que sacudiría el “mundo” de Prensa con una gran noticia. En breve (dijeron), saldría para el planeta Marte la nueva misión comocida como la Mars Climater Orbiter, diseñada para estudiar la atmósfera superior de Marte y, estaba acondicionada para poder enviarnos datos importantes sobre el clima y la atmósfera marciana. En lugar de ello, simplemente se estrelló contra la superficie del planeta.

La distancia entre la nave espacial y la superficie del planeta Marte era de 96,6 kilómetros inferior de lo que pensaban los controladores de la misión, y 125 millones de dolares desaparecieron en el rojo polvo de la superficie Marte. La pérdida ya era suficientemente desastrosa, pero aún, hubo que morder más el polvo cuando se descubrió la causa: Lockheed-Martin, la empresa que controlaba el funcionamiento diario de la nave espacial, estaba enviando datos al control de la misión en unidades imperiales -millas, pies y libras de fuerza- mientras que el equipo de investigación de la NASA estaba suponiendo, como el resto del mundo científico internacional, que recibián las instrucciones en unidades métricas. La diferencia entre millas y kilómetros fue lo suficiente para desviar la nave unas 60 millas el curso previsto y llevarla a una órbita suicida hacia la suprficie marciana, en la que quedó chafada e inservible dando al traste, no ya con el dinero (que también) sino con un montón de ilusionados componentes del equipo que esperaban grandes acontecimientos del Proyecto.

La lección que podemos obtener de esta catástrofe está muy clara: ¡Las Unidades de medida son importantes!

Resultado de imagen de Medidas de peso

El peso es una unidad de medida. Medir es comparar. La unidad de medida de la masa o peso es el gramo y se escribe g. Sus múltiplos son: decagramo(dag), hectogramo(hg), kilogramo(kg) y submúltiplos decigramo(dg), centigramo(cg) y miligramo(mg).

Rústica unidades de medida de líquidos

Nuestros predecesores nos han legado incontables unidades de medida de uso cotidiano que tendemos a utilizar en situaciones diferentes por razones de conveniencia. Compramos huevos por docenas, pujamos en la subasta en guineas, medimos las carreras de caballos en estadios, las profundidades oceánicas en brazas, el trigo en fanegas, el petróleo en barriles, la vida en años y el peso de las piedras preciosas en quilates. Las explicaciones de todos los patrones de medida existentes en el pasado y en el presente llenan cientos de volúmenes.

Todo era plenamente satisfactorio mientras el comercio era local y sencillo. Pero cuando se inició el comercio internacional en tiempos antiguos, se empezaron a encontrar otras formas e contar. Las cantidades se median de forma diferente de un pais a otro y se necesitaban factores de conversión, igual que hoy cambiamos la moneda cuando viajamos al extranjero a un pais no comunitario. Esto cobró mayor importancia una vez que se inició la colaboración internacional de proyectos técnicos. La Ingenieria de precisión requiere una intercomparación de patrones exacta. Está muy bien decir a tus colaboradores en el otro lado del mundo que tienen que fabricar un componente de un avión que sea exactamente de un metro de longitud, pero ¿cómo sabes que su metro es el mismo que el tuyo?

No todas las medidas se regían por los mismos patrones

En origen, los patrones de medidas eran completamente locales y antropométricos. Las longitudes se derivaban de la longitud del brazo del rey o de la palma de la mano. Las distancias reflejaban el recorrido de un día de viaje. El Tiempo seguía las variaciones astronómicas de la Tierra y la Luna. Los pesos eran cantidades convenientes que podían llevarse en la mano o a la espalda.

Muchas de esas medidas fueron sabiamente escogidas y aún siguen con nostros hoy a pesar de la ubicuidad oficial del sistema decimal. Ninguna es sacrosanta. Cada una está diseñada por conveniencia en circunstancias concretas.Muchas medidas de distancia se derivan antropomórficamente de las dimensiones de la anatomía humana:

El “pie” es la unidad más obvia dentro de esta categoría. Otras ya no resultan tan familiares. La “yarda” era la longitud de una cinta tendida desde la punta de la nariz de un hombre a la punta del dedo más lejano de su brazo cuando se extendía horizontalmente hacia un lado. El “codo” era la distancia del codo de un hombre a la punta del dedo más lejano de su mano estirada, y varía entre los 44 y los 64 cm (unas 17 y 25 pulgadas) en las diferentes culturas antiguas que lo utilizaban.

La unidad náutica de longitud, la “braza” era la mayor unidad de distancia definida a partir de la anatomía humana, y se definía como la máxima distancia entre las puntas de los dedos de un hombre con los brazos abiertos en cruz.

El movimiento de Mercaderes y Comerciantes por la región mediterránea en tiempos antiguos habría puesto de manifiesto las diferentes medidas de una misma distancia anatómica. Esto habría hecho difícil mantener cualquier conjunto único de unidades. Pero la tradición y los hábitos nacionales era una poderosa fuerza que se resistía a la adopción de patrones extranjeros.

El problema más evidente de tales unidades es la existencia de hombres y mujeres de diferentes tamaños. ¿A quién se mide como patrón? El rey o la reina son los candidatos obvios. Claro que, había que recalibrar cada vez que, el titular del trono cambiaba por diversos motivos.

La depuración de patrones de medidas comenzó de forma decisiva en Francia en la época de la Revolución Francesa, a finales del siglo XVIII. La introducción de nuevos pesos y medidas conlleva una cierta comvulsión en la Sociedad y raramente es recibida con entusiamo por el pueblo. Así, dos años más tarde, se introdujo el “metro” como patrón de longitud, definido como la diezmillonésima parte de un cuadrante de meridiano terrestre. Aunque esta es una forma plausible de identificar un patrón de longitud, es evidente que no resulta práctica a efectos de comparación cotidiana. Consecuentemente, en 1795 las unidades fueron referidas directamente a objetos hechos de forma especial.

Siempre hemos tratado de medirlo todo, hasta las distancias que nos separan de las estrellas.

Sí, siempre hemos tenido que medirlo todo. Al principio, como unidad de masa se tomó el gramo, definido como la masa de un centímetro cúbico de agua a cero grados centígrados. Más tarde fue sustituido por el kilogramo (mil gramos), definido como la masa de mil centímetos cúbicos de agua… Finalmente, en 1799 se construyó una barra de metro prototipo junto con una masa kilogramo patrón, que fueron depositadas en los Archivos de la nueva República Francesa. Incluso hoy, la masa kilogramo de referencia se conoce como el “Kilogramme des Archives”.

Contar la historia aquí de todas las vicisitudes por las que han pasado los patrones de pesos y medidas en todos los paises, sería demasiado largo y hasta tedioso. Sabemos que en Francia, en 1870, cuando se creo y reunió por primera vez en Paris la Comisión Internacional del Metro, con el fin de coordinar los patrones y supervisar la construcción de nuevas masas y longitudes patrón. El Kilogramo era la masa de un cilindro especial, de 39 milímetros de altura y de diámetro, hecho de una aleación de platino e iridio, protegido bajo tres campanas de cristal y guardado en una cámara de la Oficina Internacional de Patrones en Sèvres, cerca de Paris. Su definición es simple:

El kilogrtamo es la unidad de masa: es igual a la masa del prototipo internacional del kilogramo.

Esta tendencia hacia la estándarización vio el establecimiento de unidades científicas de medidas. Como resultado medimos habitualmente las longitudes, masas y tiempos en múltiplos de metro, kilográmo y segundos. Cada unidad da una cantidad familiar fácil de imaginar: un metro de tela, un kilogramo de patatas. esta conveniencia de tamaño testimonia inmediatamente su pedigrí antropocéntrico. Pero sus ventajas también se hacen patentes cuando empezamos a utilizar dichas unidades para describir cantidades que corresponden a una escala superior o inferior a la humana:

Los átomos son diez millones de veces más pequeños que un metro. El Sol tiene una masa de más de 10³⁰ kilogramos. Y, de esa manera, los humanos hemos ido avanzando en la creación, ideando patrones para todo y, no digamos en la medida de las distancias astronómicas en las que, el año-luz, la Unidad Astronómica, el Parsec, el Kiloparsec o el Megaparsec nos permiten medir las distancias de galaxias muy lejanas.

Lo que decimos siempre: Nuestra curiosidad nunca dejará de querer saber el por qué de las cosas y, siempre tratará de racionalizarlo todo para hacernos fácil nuestras interacciones con el mundo que nos rodea. Y, aunque algunas cosas al principio nos puedan parecer mágicas e ilusorias, finalmente, si nuestras mentes la pensaron… ¡Pueden llegar a convertirse en realidad!

Emilio Silvera

[?]

Mar

26

Telescopio espacial James Webb

Autor por Emilio Silvera ~ Archivo Clasificado en General ~ Comentarios Comments (1)

[?]

Mar

25

La “Vida” y la “Muerte” de las Partículas

Autor por Emilio Silvera ~ Archivo Clasificado en General ~ Comentarios Comments (0)

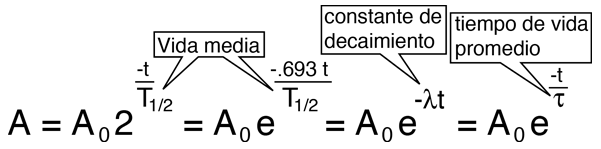
“La vida media es el promedio de vida de un núcleo o de una partícula subatómica libre antes de desintegrarse. Se representa con la letra griega $\tau$ (Tau). La desintegración de partículas es un proceso probabilístico (en concreto sigue la ley de Poisson) por lo que esto no significa que un determinado núcleo vaya a tardar exactamente ese tiempo en desintegrarse. La vida media no debe confundirse con el periodo de semidesintegración, semiperiodo, vida mitad o semivida: son conceptos relacionados, pero diferentes. En particular el periodo de semidesintegración se aplica solamente a sustancias radiactivas y no a partículas libres como se dice.”

Haces de partículas lanzadas a velocidades relativistas chocan con el haz contrario y surgen partículas nuevas.

la velocidad de la luz (c)

La mayoría de las partículas subatómicas que son producidas en los aceleradores de partículas, tiene una existencia muy breve, pero aun así ha producido asombro que una, como el quark top – cima en español-, puede vivir tan efímero espacio de tiempo. Los experimentos realizados han permitido a los físicos determinar el tiempo de vida del quark top que es apenas de 3 x 10^-25 segundos. Una fracción de tiempo asombrosamente pequeña.

Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida medio, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.

También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.

Archivo:Interacciones del modelo estándar de la física de particulas.png - Wikipedia, la enciclopedia libre

Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, ksi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales manera de desintegración, veríamos como difieren las unas de las otras.

Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.

Mean Lifetime for Particle Decay

¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

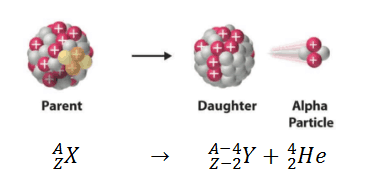
EL FÍSICO LOCO: Desintegración alfa, beta y gamma Qué es la desintegración alfa? - Radiactividad alfa - Definición

Desintegración Alfa

9.a (izquierda) Desintegración beta negativa (β --) de un núcleo y el... | Download Scientific Diagram

Desintegración Beta

Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.

Early Earth | The Planetary Society Early Earth's Atmosphere was Similar to Present-Day One | Geology, Paleoclimatology | Sci-News.com

Aunque el tiempo sea distinto, como le pasa a las partículas le pasa a todo lo demás. Toda nace y muere

En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su corta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas,

Un descanso el en trabajo.

Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.

Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.

centripetal centrifugal positive negative The examples that I just used are examples of spirals that we are able to see galaxies hurricanes subatomic particles shells but everything arround us each person each arom each planet or star all have electromagnetic fields arround them that we arent able to see in an ordinary

Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.

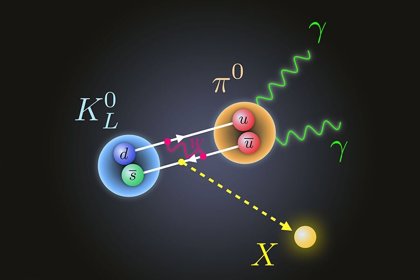
Proponen nueva física tras la rara desintegración de una partícula

Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.

Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”

Partículas, antipartículas, fuerzas… : Blog de Emilio Silvera V. MATERIAL PARA PPT - 100ciator

Si la vida de una partícula es tan corta como 10ˉ²³ segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.

No confundir con resonancia magnética

Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.

Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).

Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.

Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:

“La resonancia ϒ(1S), observada por la colaboración E288, dirigida por Leon Lederman, en Fermilab en 1977. La resonancia se sitúa a 9.5 GeV, lo que se corresponde con la masa del mesón ϒ(1S).”

∆⁺⁺→р + π⁺; ∆⁰→р + πˉ; o п+π⁰

En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.

El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (materia), es aún limitado.

emilio silvera

[?]

« Entradas anteriores