Abr
4
Simetría, una guía para descubrir
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Simetrías ~
Clasificado en Simetrías ~
 Comments (0)
Comments (0)

La simetría esférica del planeta Marte
La simetría es una propiedad universal tanto en la vida corriente, desde un punto de vista matemático como desde el quehacer de la Física Teórica. En realidad, lo que observamos en la vida corriente es siempre lo repetitivo, lo simétrico, lo que se puede relacionar entre sí por tener algo común.
En un sentido dinámico, la simetría podemos entenderla como lo que se repite, lo reiterativo, lo que tiende a ser igual. Es decir, los objetos que, por mantener la misma geometría, son representativos de otros objetos. En el Caos matemático encontramos esta concepción de la simetría en el mundo los fractales. Sin embargo, la simetría es mucho más.
Cuando miro en mi diccionario de Física la palabra Simetría, lo que me dice es: “Conjunto de invariancias de un sistema. Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado, la simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y las rotaciones en las moléculas y las translaciones en las redes cristalinas. Las simetrías pueden ser discretas (es decir, cuando hay un número finito de transformaciones de simetría), como el conjunto de rotaciones de una molécula octaédrica, o continuas (es decir, cuando no hay número finito), como el conjunto de rotaciones de un átomo o núcleo. Existen simetrías más generales y abstractas, como la invariancia CTP y las simetrías asociadas a las teorías gauge.”

El Universo está lleno de simetrías por todas partes
También podemos hablar de simetría rota y de supersimetrías. Durante los últimos tiempos, los Físicos han elevado los principios de simetría al más alto nivel en la escala de lo que podemos entender por una explicación. Cuando encontramos una Ley propuesta de la Naturaleza, una pregunta se nos viene a la mente: ¿por qué esta ley? ¿Por qué la realatividad especial y la general? ¿Por qué el electromagnetismo de Maxwell? ¿Por qué las teorías de Yang-Mills de las fuerzas nucleares fuerte y débil? Claro que, una respuesta de importancia es que, las teorías hacen predicciones que han sido repetidamente conformadas con precisos experimentos, con diversidad de científicos y lugares y que, siempre, en todos los casos, dieron el mismo resultado. Esto, por supuesto, es la base de la confianza esencial que los físicos tienen en esas teorías.
Claro que, se deja fuera algo esencial: Los físicos creen también que están en el camino correcto porque, de algún modo que no pueden explicar, tienen la convicción de que son correctas, y las ideas de simetría son esenciales para esa intuición. Se presiente que es correcto que ningún lugar del Universo es especial comparado con cualquier otro lugar del Universo, así que los físicos tienen la confianza de que la simetría de traslación debería estar entre las simetrías de las leyes de la Naturaleza. Se presiente que es correcto que ningún movimiento a velocidad constante es especial comparado con cualquier otro. De modo que los físicos tienen confianza en que la relatividad especial, al abrazar plenamente la simetría entre todos los observadores con velocidad constante, es una parte esencial de las leyes de la Naturaleza.

Los hongos atómicos también guardan cierta simetría
Así que las simetrías de la Naturaleza no son meras consecuencias de las leyes de la Naturaleza. Desde nuestra perspectiva moderna, las simetrías son la base de la que manan las leyes y, siendo así (que lo es), cuando un físico observa una simetría, agudiza su atención, ya que, allí, en aquel lugar, podría encontrarse alguna ley de la Naturaleza que siguiendo aquella presencia, se podría descubrir.
Más allá de su papel en dar forma a las leyes que gobiernan las fuerzas de la Naturaleza, las ideas de simetría son vitales para el propio concepto del tiempo. Nadie ha sabido encontrar todavía definición fundamental y definitiva del tiempo. Sin embargo, es indudable que el papel del tiempo en la constitución del cosmos es llevar una especie de registro de los sucesos y acontecimientos que en el universo ocureren: Nace una estrella, se forma una nueva galaxia, explota una supernova, muere una estrella masiva y surge un agujero negro…

Sí, todos fuímos jóvenes y el paso del tiempo nos transformó en más viejos pero, no por ello más sabios. Eso sí, con algo más de experiencia y más prudentes a la hora de decidir sobre las cosas importantes que siempre, aunque de joven no le prestemos atención, trae consecuencias.
Reconocemos el transcurrir del tiempo al mirar y ver que, las cosas, no son iguales hoy que lo fueron ayer. Con el transcurrir del tiempo todo cambia y nada permanece. ¿Será el tiempo otra simetría? Debe serlo, ya que, ningún cambio le afecta y, su transcrrir queda inalterado por mucho camino que pudiera haber recorrido y, eso, lo hace diferente de todo lo demás: Todo cambia excepto el tiempo.
Así, tenemos que llegar a la conclusión de que, el concepto de simetría es, para los Físicos, indispensable como punto de referencia en el descubrimiento de las teorías que más tarde, llegan a convertirse en leyes de la Naturaleza al comprobarse que, son inalterables: Otra vez la Simetría. El desarrollo de la moderna teoría cosmológica, por ejemplo, tiene mucho que ver con la simetría. El signioficado del Tiempo, su aplicabilidad al universo en su conjunto, la forma global del espacio, e incluso el marco subyacente de la relatividad especial, todo descansa sobre fundamentos de simetría.
Durante el último siglo un concepto muy importante en Física, sobre todo en Mecánica Cuántica, ha sido y es el de simetría. Uno de los resultados más bonitos de la Física dice que allá donde hay una simetría hay una cantidad conservada. Es lo que se llama teorema de Noether. De este modo, las leyes de la Física pueden ser iguales bajo una u otra simetría y para cada uno de esos casos se conservará algo. Así por ejemplo, la simetría de traslación temporal corresponde a una cantidad conservada: la energía. También ocurre que las leyes de la física son las mismas bajo unas transformaciones de rotación en el espacio tridimensional y eso significa que se conserva el momento angular.
Allí donde veámos presente la simetría, debemos prestar atención, ya que, podría ser el indicio de que algo importante se podría derivar de esa simetría presente que, en física, como hemos comentado, es un principio de gran importancia.

Abr
3
La búsqueda interminable
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Divagando ~
Clasificado en Divagando ~
 Comments (1)
Comments (1)

Hay frases que están vacías y formamos oraciones que no podemos cumplir
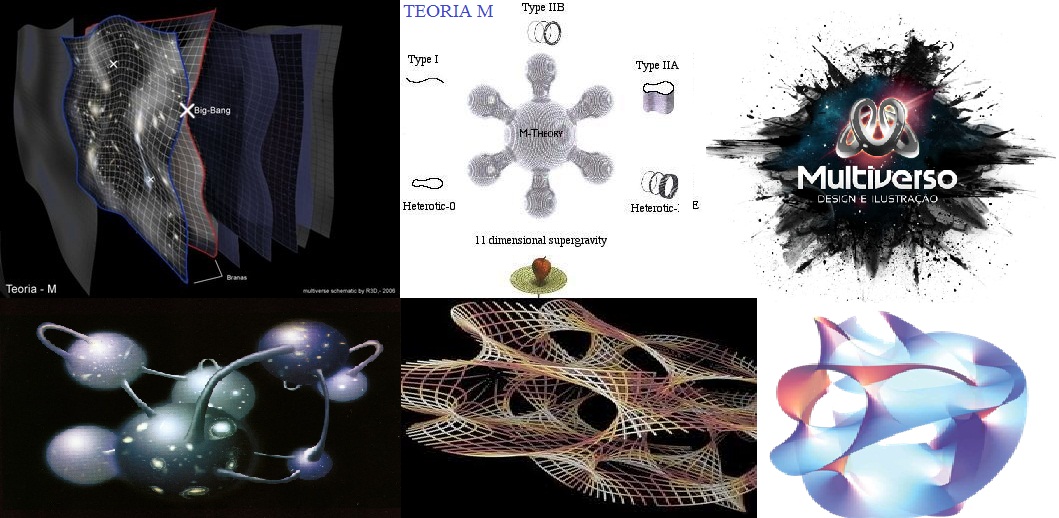
Los tiempos cambian, y, con los cambios llegan las nuevas doctrinas o creencias, o, ¿por qué no? nuevas teorías. Desde hace algún tiempo venimos dando vueltas y vueltas, en el campo de la Física, a esas avanzadas teorías que no podemos demostrar, toda vez que, al contrario del Modelo Estándar, no son (por ahora) verificables sus predicciones. Me estoy refiriendo, como habeis podido suponer a la Teoría de supercuerdas, La cuerdad Heterótica, la Supergravedad y Supersimetría, y, finalmente, la última versión que viene a ser un compendio de todas las demás, la Teoría M.
Como nos dice Brian Greene en uno de los capítulos del libro El tejido del cosmos, que él titula: “Especulaciones sobre el espacio y el tiempo en la teoría M”, hoy, tres décadas después de la articulación de la teoría de cuerdas,la mayoría de los que trabajan en ella, creen que aún no tenemos una respuesta general para la pregunta fundamental: ¿qué es la teoría de cuerdas? A pesar de que sabemos bastante de la teoría, sus características más elementales son familiares y, a estas alturas, casi cercanas. Tampoco debemos despreciar los éxitos que ha cosechado y, desde luego, es bien sabido todo lo que nos promete y también ¿cómo no? los desafíos que suponen lograr todas esas promesas que en ella están encerradas.
La relatividad especial tiene la constancia de la Velocidad de la luz, la relatividad general tiene el principio de Equivalencia, la mecánica cuántica tiene, el principio de Incertidumbre y, sin embargo, los teóricos de cuerdas aún siguen buscando algo de lo que carece la teoría de cuerdas que, precisamente es: el tipo de principio nuclear que se encontraron en aquellas otras teorías y le dan razón de ser y la sólida base que toda teo´ria necesita para ser.
Esa nueva teorías quiere explicarlo todo. Nada puede estar fuera de ella: El Universo que es, todo lo que existe, ahí estará
Un universo de Supercuerdas. El sueño de Einstein comienza a tomar realidad, a través de un nuevo paradigma de la ciencia que viene a romper con la toda la visión del mundo y del universo que teníamos hasta ahora, más allá de lo imaginable. Si la Teoría de cuerdas, finalmente resultase ser cierta, ese descubrimiento llevaría al mundo y a la conciencia humana hasta una nueva dimensión de su propia conciencia.

Una de las primeras controversias sobre la teoría de supercuerdas que salta al tapete en las discusiones entre físicos teóricos es aquella en las que se subrayan diferencias como el caso del modelo estándar (que explica la interacción de fuerzas y partículas) y sobre el cual la física ha sido capaz de extraer predicciones contrastables en laboratorios, a diferencia en el marco de las supercuerdas que ello no ha sido posible, ya que no se han logrado hacer predicciones verificables con experimentos. Es decir, que todos los esfuerzos que se han gastado en su elaboración pueden acabar siendo un excelente ejercicio de especulación matemática. Claro que, de tener éxito, no sería esta la primera vez que un descubrimiento puramente teórico en la ciencia de la física acaba dando en el clavo y profundizando espectacularmente en el conocimiento de la naturaleza.
Según la Teoría de Supercuerdas, todo el universo manifestado, todo lo que percibimos como materia, desde las partículas subatómicas, hasta las galaxias, estaría soportado por una gran Matriz Subyacente, o Supercuerdas, que actuaría como una “gran sinfonía musical” detrás de todo lo que contemplamos como materia.
Ciertamente, si en realidad existen, están tan lejos de nostros que, el viaje para “verlas” es demasiado costoso…, al menos de momento.
Hemos tratado, sin conseguirlo, de llegar hasta ellas, hasta las cuerdas vibrantes que residen en lo más profundo, más allá de los propios Quarks, y, hemos podido constatar que, nuestros ingenios y aceleradores, no son suficientes, no disponen la energía requerida para llegar hasta las cuerdas que serían la matriz del mundo. Allí, en su región de once dimensiones, todo es comprensión y armonía, todo cabe e incluso, la díscola Gravedad se junta apasiblemente con la Mecánica cuántica. Por eso algunos la llaman la Teoría del Todo, allí podemos encontrar todas las respuestas.
La supercuerda una poderosa estructura que no podemos localizar. Dicen que para poder hacerlo necesitamos de la energía de Planck, es decir, 1019 GeV, y, tal fuente de energía no existe aquí en nuestro mundo. Bueno, al menos no podemos disponer de ella, nuestras tecnologías no llegan a tener esa capacidad.

De la misma manera que no podemos sostener una galaxia en la mano, su inmensidad nos lo impide. Tampoco tenemos la capacidad de poder sujetar una “cuerda”, su infinitesimal tamaño, tampoco nos lo permite. Y, lo curioso del caso es que, de exisitr las cuerdas, esas enormes galaxias que podemos captar en el espacio interestelar, todas ellas, sin excepción, estarían hechas de cuerdas vibrantes que, al parecer, son los objetos que estarían más allá de los Quarks.
Uno de los problemas ligados a la teoría de supercuerdas y que más resalta es el que tiene que ver con la propia pequeñez de las cuerdas. Mientras más pequeño es algo, más difícil es de ver. Y estas supercuerdas son tan superpequeñas que no se observan esperanzas para hacer experimentos que nos puedan acercar a sus dimensiones. Sin experimentos no se pueden hacer comprobaciones de sus predicciones ni saber si son correctas o no. Exagerado, puede ser. Pero cada día se hace más insostenible su consideración sosteniéndola, tan sólo, con los fundamentos de un muy bien elaborado pensamiento experimental con el soporte de bellas ecuaciones matemáticas, o con algunas verificaciones experimentales que, para este caso, vienen a ser como indirectas, llámese Helio-3 y su superfluidez, etc…

Branas, universos paralelos…¡cuerdas!
En esta teoría, hay problemas que se encuentran dentro de los enunciados de sus propios conceptos. Para desarrollar su formulación es necesario apelar a lo menos a diez dimensiones (en algunos casos, se han llegado hasta un número de veintiséis): espacio (3), tiempo (1) y a ellas se le agregan seis más como mínimo, que parecen estar enroscadas e invisibles para nosotros. Por qué aparecieron estas dimensiones adicionales a las cuatro que nos son familiares y por qué se atrofiaron en algún momento. Si en verdad existen, no lo sabemos. También, la teoría tiene decenas de miles de alternativas aparentemente posibles que no sabemos si son reales, si corresponden a miles de posibles universos distintos, o si sólo hay una realmente posible. En algunas de sus versiones se predice la existencia de 496 fuerzones, partículas como el fotón, que transmiten la fuerza entre 16 diferentes tipos de carga como la carga eléctrica. Afirmaciones como éstas, no comprobables por la imposibilidad de hacer experimentos, son las que plagan a la teoría de una multiplicidad de cuerdas. Ahora, las explicaciones más frecuentes que se dan para lo anterior, es de que los problemas surgen porque esta teoría se adelantó a su tiempo y no existe aún la estructura matemática consistente para formularla adecuadamente.

Incluso el salto cuántico es más fácil de verificar
Las conclusiones a las que periódicamente llegan los adeptos a la TSC, se centran en el entusiasmo de proclamar que ésta otorga la única forma, hasta ahora, de poder contar en un futuro con una Teoría Cuántica consistente con la Gravedad. Como prácticamente todas las teorías de cuerdas, la TSC’s comienza con el concepto de dimensiones adicionales de Kaluza-Klein y comporta una enorme complejidad muy difícil de comprender para los que no están directamente involucrados en sus modelos. Con ella se aspira a resolver el más enigmático problema matemático que comporta la Física teórica en los finales del siglo veinte: la incompatibilidad matemática de los pilares fundamentales de la Mecánica Cuántica con la Teoría de la Relatividad General.

En cosmología, las partículas exóticas no sólo hay que proponerlas, es necesario también comprobar su existencia en experimentos de laboratorio y/o en observaciones.
La carencia de esa estructura matemática ha sido uno de los inconvenientes más serios que enfrentaba, y todavía lo es, la TSC y ello radica en las dificultades que presenta para hacer cálculos detallados. Sin embargo, en los últimos años, en alguna medida, especialmente después de la reunión de físicos teóricos cuerdistas realizada en la ciudad de Madrid, España, en el año 1995, ello se ha venido soslayando, ya que a través de el desarrollo de un conjunto de nuevas herramientas se ha logrado superar, en parte, las limitaciones matemáticas de la teoría.
Esas herramientas son las dualidades que vienen a ser como una especie, si se puede llamar así, de diccionario unificador que permite a los físicos «traducir» sus cálculos realizados en marcos teóricos asequibles a los modelos conocidos a marcos en que lo convencional no funciona. Es como si sabiendo calcular la electricidad y no el magnetismo; al descubrir que ambas fuerzas son dos caras de la misma moneda, se traducen las cantidades de una a otra, haciendo abordable el problema.
Sabemos de átomos y de Galaxias pero, ¿que es una cuerda?
Hasta ahora, ninguna propuesta de la teoría de supercuerdas ha podido ser contrastada con experiencias experimentales y, mucho menos, observacionales. Sus logros sólo han podido ser chequeados en los correspondientes archivos computacionales y las pizarras de las oficinas de los matemáticos. Ellos han demostrado una serie de conjeturas matemáticas que surgen de manera natural de la TSC. Ahora, ello también a implicado que se haya venido generando una coincidencia o relación entre distintas estructuras matemáticas, de las que ni se sospechaba su existencia y han servido de motor e inspiración para algunos matemáticos.
La interpretación de los cálculos que se realizan describe un objeto tan diminuto, como las supercuerdas, que querer imaginarlas es como querer encontrar un grano de arroz perdido en algún lugar del Universo; es imposible. Su calculada pequeñez las hace inimaginable para la gran mayoría de los mortales humanos. Por hacernos una idea: la Tierra es 10-20 más pequeña que el universo y el núcleo atómico es 10-20 veces más pequeño que la Tierra. Pues bien, una supercuerda es 10-20 veces más pequeña que el núcleo atómico.
Es indudable que se trata de una teorización matemática que expuesta al común de la gente se hace casi «indigerible» o poco realista. A los especialistas en física teórica les pasa lo mismo. La física que hoy se maneja se hace cada vez más distante de la generalidad de los seres humanos, ya que no es tan sencilla como la de antaño; no sólo por que la descripción matemática de los fenómenos naturales se haya vuelto más complicada, sino porque resulta cada vez más difícil de imaginar. Esto se debe a que cada vez nos alejamos más y más de los objetos de nuestra experiencia cotidiana. Adentrándonos en el “universo” de la física cuántica, llegamos a ser conscientes de que, nuestro mundo, es una realidad propia de nuestras mentes, ya que, el “mundo real” la Naturaleza, es otra cosa bien distinta y, precisamente por eso, nos cuesta tanto comprender.

Ese “universo” de lo infinitamente pequeño, vibrante y luminoso, ¿dónde estará?
Con la teoría de supercuerdas se ha llegado a un punto de abstracción que cuando nos zambullimos en su estudio y cálculos se llega a un momento en que la cabeza parece estallar, no por asombro, sino que por las incertidumbres que llega a concitar. Se parte con esperanzas y en el camino afloran –no voy a decir frustraciones– sino que una multiplicidad de inquietudes, ya que se va generando la sensación de que los resultados de los esfuerzos que se están realizando, nunca podrán ser comprobados.
Es cierto que en los procesos de hacer ciencia no se ha establecido como requisito que las teorías que se elaboran deban ser comprobadas en un pari-paso, de ello los científicos, por formación, están muy consciente. Pero la mera especulación intelectual, limitada para ser experimentada, en el tiempo tampoco es muy útil, ya que dejaría de ser considerada inserta dentro de los rangos de las exigencias consuetudinarias de lo que llamamos hacer ciencia.
Es aceptable considerar que aún la teoría de supercuerdas no ha alcanzado un desarrollo suficiente en el cual sus pronósticos puedan ser contrastados con experimentaciones en los actuales aceleradores de partículas. Pienso que aún se encuentra lejos de arrimarse a una maduración matemática que permita precisar cuales son sus predicciones. Los cálculos son bellos, pero sumamente difíciles.


Y, a todo esto, las ecuaciones de Eisntein de la Relatividad General, subyacen en lo más profundo de la Teoría de Cuerdas, ya que, cuando se están desarrollando sus ecuaciones, allí aparecen, sin que nadie las llame, las ecuaciones de campo de la relatividad general que, es un subproducto de aquella otra teoría más avanzada. Tal secuencia, nos lleva a pensar que, la Teoría de supercuerdas es cierta, ya que, en caso contrario, ¿Por qué estaría allí Einstein?
También en la TSC, se encuentran involucradas las fuerzas fuertes de una manera tal que, antes de comenzar, comúnmente ya se encuentra limitadas las actuales capacidades humanas para calcular. Hay importantes pasos a realizar para poder aprender como llegar a inferir cálculos predictibles y poder ser testeados experimentalmente. Está claro que esta teoría se adelantó a su tiempo.
Es posible que para algunos sea inadmisible que se encuentre en el tapete de las discusiones de física teórica una teoría que todavía no precisa sus predicciones con una contractación experimental. Sin embargo, por las trayectorias que ya han experimentado las teorías de cuerdas, no reúnen aún los méritos como para ser consideradas científicas, o meros ejercicios de matemática abstracta. Por ahora, se puede señalar que parece ser que los físicos cuerdistas han ido más allá de los umbrales matemáticos aconsejables, con saltos de pasos que algún día deberán dar.

En el mundo de la física existen detractores de las supercuerdas de la talla y del genio como la de Richard Feymman, quien acerca del trabajo de los teóricos de las supercuerdas, afirmaba en una entrevista poco antes de morir, en 1988, «No me gusta que no calculen nada, no me gusta que no comprueben sus ideas, no me gusta que, para cada cosa que está en desacuerdo con un experimento, cocinen una explicación, un arreglo para decir bueno, todavía podría ser verdad.»
La teoría de supercuerdas es relativamente joven aún y durante su existencia ha mostrado una alta propensión a ser enfermiza. Surgen problemas, y se la deja de lado; se solucionan los problemas y una avalancha de trabajos resucitan la esperanza. En sus cerca de treinta años de vida, este vaivén ha ocurrido más de una vez.
Todo tiene su tiempo, y, Feymman, era ya un físico de bastante edad y de que ello a lo mejor era la causa de su resistencia a las ideas nuevas como algunos de sus maestros se resistían ante los profundos cambios conceptuales registrados en la física cuando él era joven. Las supercuerdas, dicen sus defensores, integrarían la física actual como la teoría de la relatividad de Einstein integró la gravitación de Newton explicando que sólo era un caso (el de nuestra escala del universo) de leyes más profundas y generales.
Nuevas geometrías, como en aquel tiempo en que llegó el llamado corte de Riemann, mediante el cual, se podia acceder a dos regiones distantes del espacio, nos han traído estas nuevas teorías que cambian el concepto actual que, del Universo tenemos. El tensor métrico de Riemann permitió a Einstein formular su famosa teoría de la gravedad. Siempre ha sido así, las nuevas ideas nos trajeron las nuevas realidades de la Naturaleza y, si es así (que lo es), ¿por qué la teoría de cuerdas sería diferente?
Los matemáticos encuentran interesante esta teoría porque las dimensiones extra pueden tener geometrías muy complicadas y hay toda una rama matemática dedicada a explicar sus propiedades.
Los físicos-matemáticos piensan que, por ahora, es más lógico estudiar y observar el desarrollo de estas ideas teóricas cuerdistas como una consecuencia estética y grata en la consecución de una simple y definitiva teoría unificadora que reúna todos los requisitos necesarios para que pueda ser contrastada con pruebas experimentales.
Hemos sido capaces de inventar aparatos para medir las ondas gravitatorias provenientes de los agujeros negros, y, como no podemos parar en el querer descubrir y saber lo que el Universo es, queremos seguir avanzando y tratamos de conseguir una teoría de la Gravedad Cuántica que, según todos los indicios va implícita en esta teoría de supercuerdas de más dimensiones.
No sé si se ha llegado a un límite en que la abstracción matemática sea un medio coadyuvante o una pesadilla para los físicos. Se quiere simplificar las cosas y, al final, se hacen más incomprensibles y complejas. Ya convertimos la gravedad, la fuerza electromagnética y las fuerzas nuclear fuerte y débil en campos. La gravedad, que no sabemos qué cosa es, pero que hace caer una piedra, ha pasado a ser algo mucho más abstracto que lo propuesto por Newton: un campo, una modificación de la estructura del espacio que nos rodea. Como nos movemos dentro de ese espacio, su estructura nos influye y nos hace actuar de cierta manera. Por eso caen la piedras, porque seguimos la forma del espacio, su geometría que viene dada por la materia que contiene.
Ya para el común de los humano ese, el más simple nivel de abstracción, les parece que se trata de algo que nunca podrán llegar a comprender. Pero ese sentimiento empeora cuando se pasa al siguiente nivel. Se trata de aquel que es considerado como los grandes almacenes de la física teórica, el objeto de estudio son los grupos de simetría mediante los cuales se relacionan esos campos y las partículas.
Grupos de simetría que relacionan campos y partículas donde las fuerzas están presentes.
El no va más del nivel de abstracción, se encuentra el mundo donde se creee que vive el constituyente fundamental de la materia: las supercuerdas. Estos objetos definen a través de su comportamiento esos estados que provocan la aparición de los grupo de simetría que a su vez relacionan la fuerza con la materia, y que al mismo tiempo explican la interacción de las partículas subatómicas y el comportamiento de los átomos.

Y, a todo esto, la Topología tiene mucho que decir en el mundo de la cuerda, toda vez que, en esta rama de las matemáticas pueden estar las respuestas a tan extraño objeto vibrante que nos dicen que podría ser lo más pequeño y al mismo tiempo lo más esencial que en el universo existe para su conformación
Al final, se trata de explicar todo y, a su vez, complicar todo. Por ello, decir que una supercuerda es un diminuto objeto vibrante que cohabita en un espacio con más dimensiones de simetría peculiar que el conocido tetradimensional es, prácticamente, no decir nada.
Hasta principios del año 2001, la premisa que se habían colocado los físicos de contar ya con una muy simple y gran teoría unificadora de las cuatro fuerzas, no se ha cumplido. Es posible que dentro del primer cuarto del siglo el intento culmine con un final feliz. Pero también es probable que no encontremos esa anhelada teoría, sino sólo una multiplicidad de teorías, cada vez más bellas y mejores.
Por ahora, lo cierto del caso es que, a pesar de algunas luces y pequeños éxitos, lo único firme y coherente es que el mundo se puede armar a partir de sesenta objetos puntuales cuyo origen desconocemos. Si se alcanzara algún día el objetivo de obtener todas las partículas y sus propiedades a partir de principios de simetría o de alguna cuerda única, por ejemplo, habríamos encontrado un nuevo nivel donde se concentra lo más elemental. Ya no serían los átomos, ni tampoco las partículas puntuales mismas, sino las simetrías o la cuerda. ¿Habríamos terminado? Es más que probable que no, pues nos preguntaríamos entonces de dónde salen esas simetrías o esa cuerda, y con alta probabilidad su estudio en detalle nos mostraría que en realidad hay más complejidad que la que aparecía a simple vista. La historia (¡la sabia historia!) muestra que este es un cuento sin final, y pareciera que cada vez que simplificamos las cosas, nuevos niveles de complejidad aparecen como fantasmas que están siempre acechándonos a la vuelta de cada esquina.

Parece que siempre estaremos entrando por una puerta misteriosa que nos lleva a un lugar oscuro en el que nunca sabemos lo que podemos encontrar. Es la Incertidumbre de la mecánica cuántica que, no se limita a estar allí, en ese mini-universo de lo pequeño. La Incertidumbre está presente en todo el Universo, y, nosotros, curiosos y deseosos de saber, no dudamos de adentrarnos en esos lugares desconocidos en busca de esas respuestas anheladas.
Así, podemos leer en cualquier diccionario que si preguntamos por la supercuerda, comienza diciéndonos: “La teoría de supercuerdas es un esquema teórico para explicar todas las partículas y fuerzas fundamentales de la naturaleza en una sola teoría, que modela las partículas y campos físicos como vibraciones de delgadas cuerdas supersimétricas, las cuales se mueven en un espacio-tiempo de más de 4 dimensiones.”
Y, a todo esto, de vez en cuando podemos encontrarnos con noticias llamativas como esta:
“Científicos norteamericanos detectan la existencia de dimensiones adicionales. Las colisiones de neutrinos de alta energía con otras partículas corroboran uno de los postulados de la Teoría de Supercuerdas.
Científicos norteamericanos han detectado por primera vez indicios de la existencia de otras dimensiones más allá de las tres conocidas. Utilizando datos del telescopio Amanda, enterrado en el Polo Sur, han podido observar una decena de colisiones de neutrinos de alta energía con otras partículas elementales, obteniendo así la evidencia de las dimensiones adicionales sugerida por la Teoría de Supercuerdas. El descubrimiento no es concluyente y encontrará nuevas oportunidades cuando se inicie en 2009 el funcionamiento de otro telescopio 30 veces más potente, el Ice Cube, en el que participan diversas universidades europeas.”
¡Vivir para ver! Claro que, nosotros, que vivímos en un mundo de tres dimensiones espaciales y una temporal, lo único que podemos hacer es tener paciencia y espewrar a que, esas lumbreras de la física, nos lleven de la mano hacia ese mundo mágico de las cuerdas que, según parece, nos mostrará un universo diferente, más completo y más real que el que ahora podemos observar.
emilio silvera
Abr
3
“SABER QUE SE PUEDE, CREER QUE SE PUEDA”
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Colaboración ~
Clasificado en Colaboración ~
 Comments (1)
Comments (1)

Hoy día podemos considerar que existen dos posturas enfrentadas acerca del funcionamiento del Universo. Por un lado están los que piensan que el Universo es cómo es debido al azar y, en el bando opuesto, están los que consideran que existe un patrón oculto, una especie de imperativo cósmico que subyace encriptado en las leyes que rigen la naturaleza, la materia, los ciclos de los planetas o la vida en general.
Ambas posturas presentan sólidos argumentos a su favor, argumentos que aunque puedan ser criticados no por ello están exentos de razón. Los que dan crédito a la posibilidad del azar básicamente sustentan su opinión en el comportamiento que observamos en las partículas a nivel fundamental. En este nivel, que es el nivel al que se encuentran las partículas más pequeñas que podemos detectar, ciertamente todo parece regirse en base a la probabilidad. Los que opinan, por el contrario, que existe una especie de “orden implicado” básicamente basan sus creencias en la irrazonable efectividad que presentan las matemáticas para describir la realidad.

La analogía del relojero es un argumento teleológico que sostiene que el diseño implica un diseñador. Ha tenido un papel prominente en la teología natural y el “argumento del diseño”, donde se ha usado para argüir a favor de la existencia de Dios y el diseño inteligente del universo.(la imagen y el pequeño texto de abajo no pertenecen al trabajo original, y, sólo se añade para hacer más dinámica la lectura).
Ciertamente parece complicado conciliar ambas posturas. Si es cierto que existe una especie de “diseño inteligente” ¿Cómo podría éste basarse en el azar o la probabilidad? Pero si, por el contrario, todo se debiera al azar ¿Cómo explicamos que nuestras leyes universales se basen en criterios que involucran una lógica racional?
La única posibilidad de unificar ambos criterios sería aceptar que existe una manera de organizar el azar de forma racional, una especie de “principio cosmo-caótico” al que hizo referencia Celeb Scharf. Si esto fuera cierto simplemente implicaría que la lógica que subyace en el comportamiento de todo cuanto acontece en el Universo sería la más simple que cabría imaginar, dado que exigiría únicamente la combinación de dos elementos: uno y su opuesto, que es la única condición que permite o acepta el criterio del azar. En otras palabras, si pudiéramos unificar ambas posturas en una teoría global o unificada implicaría que lo imposible es la única posibilidad. Pues bien, de esta posibilidad es de la que vamos a hablar, de qué manera se puede “materializar” el azar.

Esta proporción ha fascinado desde hace siglos al ser humano, que lo ha considerado un indicador de la perfección y la estética.
Para ello utilizaré un patrón “oculto” que hace ya tiempo descubrimos en la naturaleza, tratando de seguir su rastro para ver dónde nos lleva. Se trata de la “Proporción Áurea”, a veces denominada “Divina Proporción”.
La proporción áurea es perfecta cómo ejemplo para explicar todos estos aspectos tan contradictorios de la naturaleza y de paso entender la esencia de una teoría unificada. Esta relación puede describirse tanto de forma física como de forma matemática, es compatible con el criterio del azar y además representa un patrón organizado de comportamiento en sí misma. Es un patrón que además es independiente de la forma que tengamos de referirnos a él: es una proporción intemporal que ha existido siempre y siempre existirá. Si una civilización situada en el extremo opuesto del Universo la descubriera seguramente utilizaría una simbología completamente distinta de la nuestra, pero lo que nunca podría hacer es alterar su esencia. Se trata, por tanto, de un patrón tan universal cómo podría serlo la relación entre el diámetro y el arco de una circunferencia.

De acuerdo con el conocido físico y divulgador Paul Davies (la existencia de patrones intemporales de comportamiento) “(…) implica que las leyes del Universo han diseñado su propia comprensión y que la mente y el conocimiento no son más que subproductos derivados de su evolución”. Si esto fuera cierto implicaría necesariamente que las leyes universales que conocemos no sólo gobiernan nuestra existencia, sino que también gobiernan nuestros pensamientos (Se trata del conocido “Pienso, luego existo”). Este autor acaba su frase diciendo: “Esta es una asombrosa visión de la naturaleza, magnífica y estimulante en su majestuosa visión de conjunto. Espero que sea correcta. Sería maravilloso si fuera correcta. Pero si lo es, representaría un cambio en la cosmovisión científica tan profundo como el iniciado por Copérnico y Darwin juntos”.
Suele utilizarse el ejemplo de la reproducción de los conejos para explicar la proporción áurea, dado que fue el ejemplo que utilizó su descubridor, Fibonacci, para exponerla. Aunque serviría igual si utilizamos patos, seres humanos o partículas. Este pensador equiparó las virtudes matemáticas de la divina proporción con “Dios”, entre otros motivos porque en cualquier unidad de medida dada siempre habrá una proporción áurea implicada

Comencemos. Tomemos una pareja macho-hembra de conejos. Estos se encuentran, se gustan y sin más preámbulos llevan a cabo la fecundación. Al mes exacto del feliz encuentro dan a luz a una nueva pareja de conejos macho-hembra. Al final del primer mes, por tanto, tenemos dos parejas: una pareja adulta y una pareja de conejos bebe. Los conejos bebe han de esperar un mes para alcanzar la fertilidad y poder fecundar. La pareja adulta no se espera y el mismo día del feliz alumbramiento, haciendo honor a su fama, la hembra vuelve a quedarse preñada. Al final del segundo mes, por consiguiente, tenemos tres parejas: la pareja inicial, la pareja de bebes convertidos en adultos fértiles y la nueva pareja que acaba de nacer.
Si seguimos esta progresión al final del tercer mes tendremos 5 parejas, dos parejas adultas, una pareja que acaba de alcanzar la edad fértil, y dos parejas de bebes conejo que acaban de nacer. Al final del cuarto mes tendremos 8 parejas y así sucesivamente….
La relación que existe entre el número de parejas de un mes dado en comparación con el número de parejas del mes precedente es la que va componiendo progresivamente el valor que conocemos como proporción áurea o sucesión de Fibonacci (2/1, 3/2, 5/3, 8/5, 13/8, 21/13, etc….) Cada vez que una pareja alcanza la edad adulta una nueva secuencia comienza y se “entrelaza” con la anterior generación en el tiempo.

Bueno… pues ¡Manos a la obra!….
Vamos a empezar a “descomponerla”…
Comencemos eliminando los conejos de la sucesión. Aunque sean prácticos en el ejemplo no son necesarios; Cualquier pareja de elementos con la capacidad de auto-duplicarse a sí misma nos serviría.
Sigamos eliminando conceptos innecesarios. Eliminemos el factor-tiempo. En el ejemplo hemos utilizado la magnitud “mes” como periodo de fertilidad o duplicación. Pero la sucesión no cambiaría su aspecto si en lugar de un mes fuera un día, un simple segundo o incluso si la duplicación fuera casi instantánea.
Ahora podemos observar más claramente la simplicidad de su comportamiento: “Pasado un cierto tiempo (sea el que sea) tiene lugar la aparición de un nuevo elemento” ¡Ya está!, No hay más… ese es todo su “secreto”.

Parece sencillo ¿No es cierto? Pues bien, en la comprensión o el descubrimiento de este sencillo funcionamiento se asienta lo que conocemos como “mecánica cuántica”, basada en que cada cierto tiempo un electrón emite (de forma “espontánea”) un fotón. En terminología algo más técnica diríamos que las oscilaciones electromagnéticas se suceden de forma cuantificada (unitaria) y la energía implicada está directamente relacionada con la frecuencia.
¿Cada cuánto tiempo sucede esto? Lo cierto es que es difícil responder a esta pregunta porque no tenemos manera de cuantificar este suceso. Sabemos que ocurre de forma “casi” instantánea (si lo observamos a escala humana) pero no hay forma ni manera de establecer un criterio objetivo basado en el tiempo.
La única manera paralela que tenemos de hacerlo no es utilizando un criterio basado en el tiempo, sino utilizando un criterio basado en la frecuencia o la probabilidad. Si tenemos 137 electrones uno de ellos emitirá espontáneamente un fotón; Dicho de otra manera, la probabilidad de que se emita un fotón en un instante dado de tiempo es 1/137. A este cociente lo llamamos “Constante de estructura fina” y se trata de la constante más representativa de toda la física conocida. Aunque no lo parezca a primera vista este cociente es el resultado de mezclar tres constantes fundamentales de la naturaleza: la velocidad de la luz, la constante de Planck y la carga del electrón. Lo más sorprendente de esta constante es que no viene definida por ninguna unidad física de medida, es un simple número… ¡Sin más!
Sí, parece que todo es una aventura en el Universo
A veces se denomina “Constante de acoplamiento universal” y nos proporciona una referencia de lo milimétricamente diseñado que está el Universo, pues si su valor cambiara ligeramente no existiría el Universo cómo lo conocemos. Dada su independencia respecto del tiempo, su esencia continua inalterada: cada cierto tiempo algo pasa dentro del electrón y el resultado es que se emite (o absorbe) un fotón. Esta constante (como vemos) conserva la misma esencia en que se basa la divina proporción.
A esta actividad (no sabemos si frenética o no) que tiene lugar en los núcleos atómicos a veces se le denomina “Energía del vacío” (la energía que surge de la nada, la “Chispa de la Creación”) y básicamente implica que toda partícula en el Universo tiene literalmente una especie de” vida interior”, una vida que se expande en base a este movimiento de duplicación y que es el germen primigenio de lo que denominamos “Expansión del Universo”. Como sabemos gracias a Edwin Hubble el Universo se está expandiendo, lo que implica que las galaxias se alejan unas con respecto de las otras desde el principio de los tiempos. A veces decimos que la expansión del Universo no tiene sentido físico, dado que no sabemos lo que implica que tanto el espacio como el tiempo se estén creando en este mismo momento.
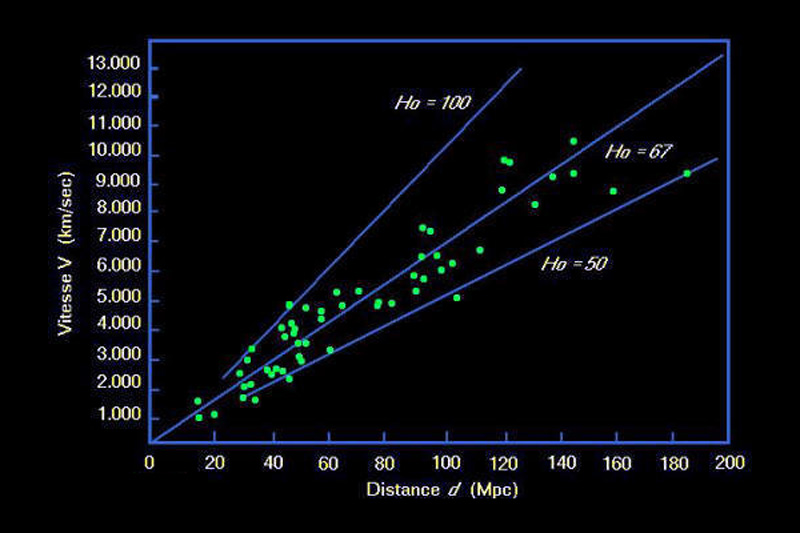
La imagen original era más atractiva pero, la página no la aceptó
Pero lo más sorprendente no es que este movimiento duplicativo o expansivo no tenga sentido físico, lo más sorprendente es que tan sólo podamos definirlo en base a relaciones numéricas. Pero incluso en este sentido este comportamiento guarda una extraña y misteriosa correlación con la “divina proporción” pues este patrón se basa también única y exclusivamente en relaciones numéricas.
Heisenberg, quien formuló la ley fundamental de la mecánica cuántica (que básicamente establece que un estado cuántico es indeterminado) solía decir que los átomos no son cosas, sino que son “tendencias” ¿Podemos aplicar también esta idea a nuestra mágica proporción? Pues resulta que sí, que también podemos hacerlo.
Aunque parezca paradójico la divina proporción es un teorema matemático (en el sentido de que sigue una regla de comportamiento) y no lo es al mismo tiempo. Un teorema podemos definirlo como una regla estática de equilibrio; Sin embargo dicha proporción es una regla dinámica, un valor que se va aproximando a él mismo a medida que vamos añadiendo más y más decimales a su valor. La divina proporción representa una tendencia, siendo ésta además una tendencia indeterminada, dado que se trata de una sucesión que nunca se acaba. De forma matemática la proporción áurea es una imposibilidad pero, sin embargo… ¡Ahí está!
Max Planck
Max Planck decía que: “La materia se origina y existe sólo en virtud de una fuerza que hace vibrar las partículas del átomo” refiriéndose a éste como el más diminuto de los sistemas solares. Poco tiempo después de sus descubrimientos los físicos comprendieron que las matemáticas que describen las frecuencias del sonido emitido por un tambor podían usarse también para calcular los niveles energéticos de vibración de los electrones en un átomo. El problema era descifrar la forma del tambor matemático que determinaba esos niveles energéticos del núcleo. La sorpresa fue descubrir que una función matemática creada por Riemann para tratar de cartografiar la distribución de los números primos coincidía a la perfección con las distribuciones que ellos buscaban. Resultaba que los “átomos de los números” y los “átomos de la materia” se encontraban sometidos a la misma distribución o a la misma estructura.
Cuando decimos que un patrón (matemático o no) es intemporal o independiente del tiempo también solemos referirnos a este hecho diciendo que la información que transmite tan sólo existe en un tiempo imaginario, una especie de plano temporal que opera en una dimensión no-material. El mejor ejemplo para describir esto lo encontramos en el teorema más famoso de la humanidad: el “Teorema de Pitágoras”. Dicho teorema, al margen de las aplicaciones prácticas que todos conocemos, establece una especie de verdad inmutable y universal: “Siempre que tengamos dos elementos absolutamente opuestos entre ellos, dichos elementos estarán relacionados”.
En el caso de la divina proporción esto no sólo es cierto, sino que dicha relación por si sola ya define la misma relación en que se basa el Teorema de Pitágoras. Y es que la divina proporción es el único valor matemático cuyo valor y su valor opuesto resultan ser el mismo valor; Algo aparentemente imposible, pero cierto.
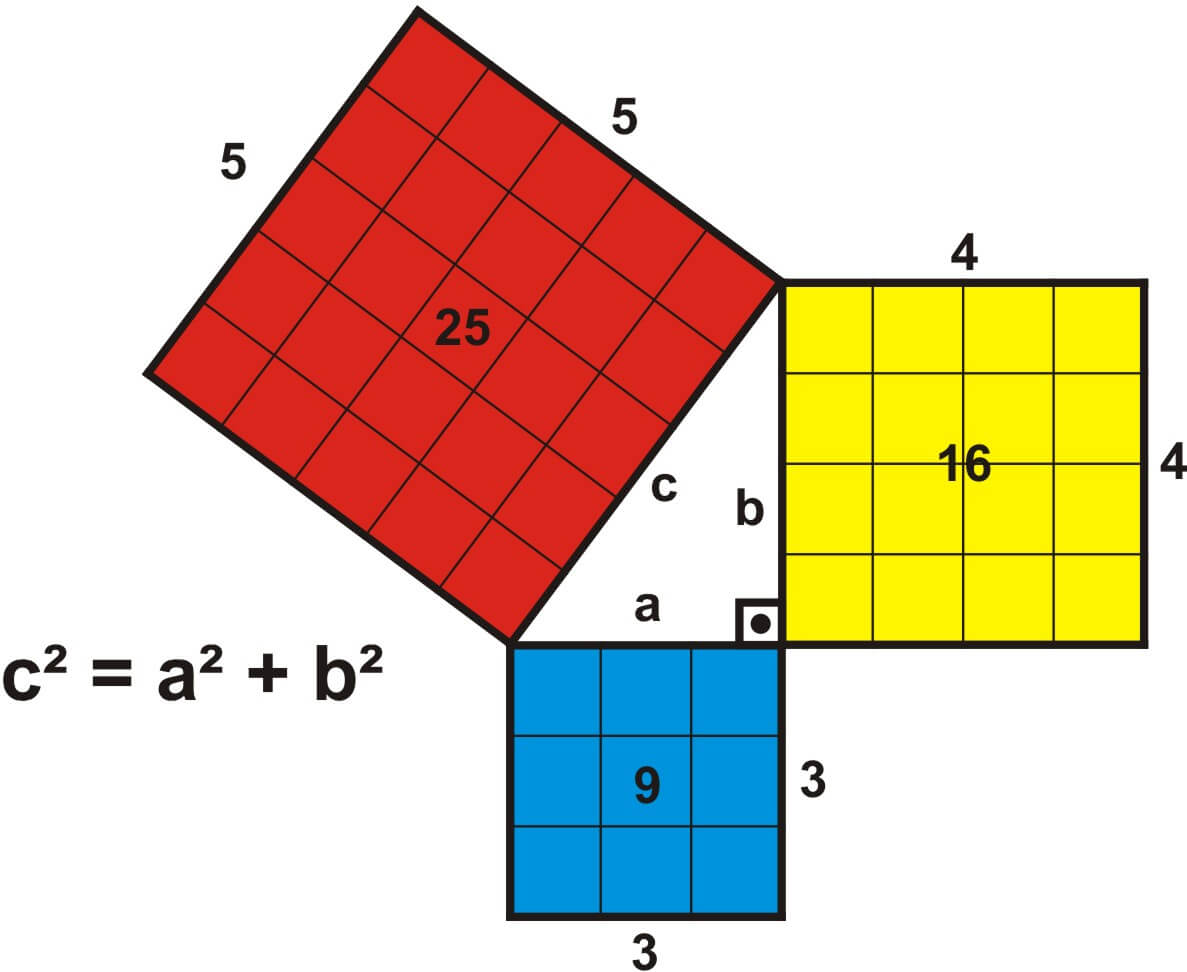
El Teorema de Pitágoras es muy especial. No sólo por ser el único criterio capaz de unificar toda la geometría conocida, sino porque constituye la única regla de Entrelazamiento Dimensional entre dos elementos conocida en matemáticas. Es lo que se conoce como “Conjetura de Fermat” que (básicamente) establece que en el Universo matemático tan sólo es posible relacionar dos elementos opuestos entre ellos cuando los elevamos al cuadrado. Esta propiedad tan sorprendente es la base de lo que conocemos como “Ley de la Gravedad”, que dictamina que dos elementos tan opuestos entre ellos como son las masas y las distancias que las separan coinciden en una dimensión diferente: la dimensión de los cuadrados de sus elementos.
De hecho, la relación de los cuadrados está presente en todos lados donde hemos podido encontrar un patrón de comportamiento. La ondulatoriedad en mecánica cuántica se basa en el cuadrado absoluto de la función de onda, la fuerza electromagnética se debilita en proporción inversa al cuadrado de la distancia entre dos fuerzas eléctricas; Incluso los planetas dan vueltas alrededor del Sol en tiempos cuyos cuadrados son iguales a los cubos de sus distancias.

Pero… ¿Qué sentido físico tiene la elevación al cuadrado? Lo cierto es que tampoco lo sabemos porque queda literalmente en una dimensión diferente. Nuestra capacidad de captar el mundo a través de los sentidos es lineal, de la misma forma que lo es nuestra forma de pensar. No podemos pensar en dos cosas al mismo tiempo y por este motivo la única operación lógica que puede hacer nuestro cerebro es “triangular”.
Las coincidencias son sorprendentes. La proporción áurea es el único valor que incorpora automáticamente una dimensión matemáticamente posible, pero físicamente inexistente. Se trata de un valor doblemente irracional, no tan sólo por incorporar el infinito en su formulación, sino por incorporar también el plano imaginario, que es precisamente el plano que da sentido a la descripción probabilística del mundo a nivel cuántico o fundamental.
Como indican los controvertidos físicos y gemelos Bodganov: “Los grandes teóricos de los números están convencidos: en el corazón de estas series interminables, en esos miles de millones de cifras que giran en el infinito hay un secreto. Una clave que, abriendo las puertas del infinito, nos hace regresar al cero. Y por tanto a la creación del Universo”.
No podría estar más de acuerdo. Es más, creo que es cierto y que existe una demostración maravillosa al respecto. A fin de cuentas, si es cierto que el Universo se basa en la probabilidad, tan sólo es cuestión de tiempo que lo imposible se haga realidad.
Ricard Jiménez
Abr
2
La libertad es una ficción cerebral
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La realidad humana ¿es realidad? ~
Clasificado en La realidad humana ¿es realidad? ~
 Comments (0)
Comments (0)

Todo, en nuestro Universo, está determinado por unas fuerzas y unas constantes de cuyos números depende todo lo que aquí sucede, sin excluir el comportamiento y evolución de nuestras mentes que, al igual que el propio universo, no deja de expandirse y crecer para que, algún día, muy lejos en el fiuturo, se pueda fundir con la matería expresada en su más alto grado: ¡La Luz! Todo en el Universo es energía y, nosotros, también.
Todo en nuestro Universo se comporta como determinan dos fuerzas contrapuestas, en el átomo están presentes la carga electrica positiva del núcleo que está equilibrada por la negativa de los electrones que lo orbitan. Las estrellas de la secuencia principal, llevan a cabo la fusión nuclear que hace que la estrella se expanda, y, sólo puede ser retenida por esa otra fuerza, la de Gravedad que, hace que la masa de la estrella tienda a contraerse sobre sí misma, bajo el peso de su propia masa, así queda equilibrada. Miles de ejemplos más se podrían poner.
Nada en nuestro Universo está disfrutando de una verdadera libertad y todo está supeditado a algo. Tampoco nosotros, aunque tengamos esa sensación, somos libre de hacer lo que nos venga en ganas y, estamos limitados como todas las demás cosas.

Estamos determinados, como el resto del Universo, por las leyes naturales
La libertad es una ficción cerebral, según confirman las últimas investigaciones sobre neurociencias. Estas investigaciones han determinado que la actividad cerebral previa a un movimiento, realizado por el sujeto en un tiempo por él elegido, es muy anterior ( 10 segundos) a la impresión subjetiva del propio sujeto de que va a realizar ese movimiento. Y aunque la falta de libertad es algo contraintuitivo, los experimentos indican que estamos determinados por las leyes de la Naturaleza. Por eso en Alemania algunos especialistas están reclamando la revisión del código penal para adecuarlo a los resultados de la neurociencia. Y aunque sigamos encarcelando a los que violen las leyes, ¿cambiará la imagen que tenemos tanto de esos criminales como de nosotros mismos?

No siempre podemos dominar los impulsos de la mente
No pocas veces, nuestras mentes se ven abocadas a tener que retener, ese primer impulso, esa iniciativa de libertad, o, de libre albedrío. La complejidad en la que estamos inmersos nos prohibe, en la mayor parte de las ocasiones, poder desarrollar y poner en práctica ese “ de libertad” que ¿nos fue dado? pero que, en realidad, podría ser una ficción de la mente. Decidir lo que se dice decidir…, como todo en el universo, es algo limitado.

Claro que pretender que la llama de una vela ilumine nuestra ignorancia…, no será posible y necesitaremos algo más. La evolución de nuestra especie (llevamos cientos de miles de años evolucionando), es lenta y alcanzar el estadio de “visión” perfecta del mundo, nos queda un largo camino por recorrer.

… cerrar los ojos ante la inmensa ignorancia que tenemos que soportar en relación a muchos secretos del Universo a los que no podemos dar explicación…
Sabemos (casi) de que está hecha la materia que podemos ver y detectar, suponemos y sospechamos que otra materia (más abundante) pulula por todo el Universo sin que podamos encontrarla, sospechamos de otras dimensiones, de otros universos y, luego, de otra Física. Sí, es verdad, todas son sospechas y, las sospechas en Física…tienen que ser demostradas, ya que, en caso contrario, se quedan en nada, en pensamientos vacíos.
Sospecho que, nuestros conocimientos de la mente…son muy limitados y que, todo esto, nos viene grande. Mientras sigamos preguntándo: ¿Quiénes somos? ¿De dónde venimos? ¿ dónde vamos? ¿Estamos sólos en el Universo? Estamos dejando al descubierto nuestra gran ignorancia pero, el simple hecho de preguntar y de querer saber…nos pone en el camino correcto.
emilio silvera
Abr
2
Alguien dijo hace mucho tiempo: “Todo es número”
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en todo es número ~
Clasificado en todo es número ~
 Comments (5)
Comments (5)

¿Conocieron los antiguos constructores los secretos del Universo?
¿Conocían los antiguos egipcios hace miles de años la que hoy día se conoce como la fórmula más bella del Universo? Si esto fuera cierto representaría que los antiguos constructores debieron entender el Universo de forma geométrica, como (de hecho) apuntan todas las evidencias. Y es que la fórmula de Euler es pura geometría, y, como tal, representa el lenguaje más perfecto en que puede expresarse el Universo: el lenguaje numérico.
Déjame explicarte la ecuación de Euler en términos coloquiales para que entiendas como convergen todos los conceptos, como podemos conciliar el antiguo conocimiento con nuestra forma, radicalmente opuesta, de pensar. Para ello utilizaré un razonamiento previo que considero irrefutable, ya que se basa en la más pura lógica. Y después haremos arqueología matemática.

Una conjetura no es más que una afirmación que aún no hemos podido refutar, que no sabemos si es o no cierta. En su versión opuesta una conjetura también es una afirmación, para la que tampoco nunca hemos podido demostrar que no sea cierta. De hecho todas las evidencias en las más importantes conjeturas matemáticas, después de millones o billones de intentos o experimentos, nos hacen pensar que éstas son ciertas, pero que aún no hemos encontrado la manera de demostrarlo inequívocamente.
Todas las conjeturas que tenemos hoy día, al menos en el campo que denominamos “Teoría de Números” indican que los números siguen en su composición algún tipo de patrón organizado, que…, de alguna manera, parecen comunicarse entre ellos. La más famosa de todas, la Conjetura de Riemann establece, por ejemplo, que los números primos siguen un criterio de densidad en su comportamiento. Si esto fuera cierto denotaría que los números tendrían de forma subyacente un criterio inteligente que dictaminaría su distribución. Si todas ellas fueran correctas implicaría que los números, de forma independiente, tienen un criterio subyacente que es totalmente independiente de la manera en que nos refiramos a él. En otras palabras, dicho patrón sería incluso independiente de las matemáticas, una especie de código fuente que es intemporal o, en otras palabras, que siempre ha sido y será.

Aunque suene antiguo decirlo, si todas esas conjeturas fueran ciertas, querría decir como pensaron los antiguos que los números son el Universo, pues siempre y en todo momento siguen un patrón organizado de comportamiento que es independiente incluso del espacio y del tiempo. Un patrón intemporal que siempre ha sido y será, y que siempre se cumplirá incluso en los extremos de nuestro Universo.
Por lo tanto si los números son intemporales e independientes de las matemáticas, podemos incluso prescindir de ellas y admirar la belleza conceptual (y visual) de la más pura identidad. Esta es la idea subyacente en este razonamiento.

La ecuación de Euler se considera (con permiso de Pitágoras) como la ecuación más bella de las matemáticas, sin ninguna duda. Keith Devlin se refirió a ella en los siguientes términos: “ Como un soneto de Shakespeare que capta la esencia del amor o un cuadro que saca a relucir la belleza de la forma, que es mucho más profundo que solo la piel, la ecuación de Euler llega a lo más profundo de la existencia”.
La ecuación de Euler “vive” en muchos mundos, es “algo” que trasciende al lenguaje matemático. Vamos a tratar de entender la ecuación de Euler desde su perspectiva más trascendente, desde una perspectiva más humana, para llegar a comprobar finalmente que la ecuación de Euler es capaz de conectar incluso nuestras conciencias, dando sentido a la existencia de un patrón espacio-temporal que nos dirá claramente que nunca podremos determinar lo que es o no real. Y es que este patrón es incluso capaz de determinar nuestra forma de pensar. Realmente se trata de una especie de “código fuente” universal.
Lo primero que hay que decir al respecto es que la ecuación de Euler no es una ecuación normal. En contra de las creencias no se trata de una fórmula ni de un teorema matemático. Todas estas ideas hacen referencia a la existencia de un criterio humano y racional, es decir algo que es consecuencia de nuestra forma de pensar. La ecuación de Euler va más allá, porque es independiente de todos nuestros criterios. Dicha ecuación es una identidad numérica que podemos calificar de universal e intemporal. Tan sólo necesitamos números (aunque sean irracionales) para describirla, no utiliza ninguna variable, ninguna x arbitraría, tan sólo utiliza números universales.

En cualquier unidad siempre podremos inscribir, por ejemplo, la divina proporción, pues este valor es totalmente independiente de cualquier unidad de medida, el gran hándicap de la física. Toda distancia unitaria puede ser siempre dividida entre la media y la extrema razón. La divina proporción hace referencia a un tipo de equilibrio matemático, pero que también podemos observar en el mundo real, en la propia naturaleza. A esta relación hicieron referencia los antiguos egipcios con el símbolo de la balanza, o… inscribiendo sus medidas en las pirámides de Egipto. Bajo este punto de vista unificado también podemos comparar a esta ecuación, incluso, con nuestra propia evolución. Es decir… ¿Conoció otra civilización anterior este patrón? Esta es la idea subyacente, establecer que la identidad de Euler se puede entender de muchas formas diferentes, porque es independiente incluso del lenguaje.
Las matemáticas reflejan conceptos, ideas mentales, ideas abstractas que tienen lugar en un espacio mental e imaginario. En este contexto el simbolismo es necesario, para mecanizar de forma más eficiente el lenguaje que empleamos. La geometría también puede ser vista como un lenguaje conceptual e imaginario. La geometría es la parte más sensitiva, la más directa de todas las ramas matemáticas y, como tal, constituye un efectivo lenguaje visual.
Los símbolos matemáticos, como sabemos, son creaciones humanas, sin embargo en algunos casos incluso su simbolismo es independiente de las matemáticas, constituyen un lenguaje por sí mismo. Se trata del lenguaje áureo, un lenguaje propio que tienen estos valores sagrados e irracionales que aparecen en la identidad de Euler.
Keith Devlin nos decía que la ecuación de Euler es como un soneto de Shakespeare. Y debe de ser correcto, sobre todo si hacemos referencia al más famoso de todos ellos: “Ser o no ser, esa es la cuestión”. A lo que añadiríamos que, en efecto, esto es correcto, sólo que incompleto, porque ser o no ser también puede ser la solución. De esta forma podríamos compatibilizar la causa con el efecto o, en otros términos, comprobar cómo el “Todo” siempre está contenido en la parte. En términos totalmente opuestos, sería algo así como admitir que los últimos serán los primeros.
Ser o no ser expresa la existencia de dos formas diferentes de entender la realidad, en esencia expresa la dualidad, la necesaria presencia de dos conceptos opuestos entre ellos. Es como si nos dijera que la existencia del mundo físico y real que podemos observar necesitara de la existencia de un mundo opuesto, un mundo material que podemos simbolizar matemáticamente y, por lo tanto, que es meramente conceptual. En otras palabras, que las ideas matemáticas pueblan el mundo del alma, como decía Platón.
La ecuación de Euler puede ser vista desde diferentes simbolismos, por lo que también es independiente incluso del simbolismo propiamente matemático. Así pues, libera tu mente, observa la Identidad de Euler de forma diferente. No la veas de forma lineal, como si de un simple teorema se tratará, vamos a ver cómo la ecuación de Euler es una ecuación multi-dimensional, la llave que abre la puerta a dimensiones diferentes, el patrón que impone un orden al ritmo de lo infinito y lo irracional. Una eterna verdad que nos dice claramente que todo está conectado como si fuera una unidad, nos dice cómo se conecta el mundo irracional y arbitrario con nuestra idea de un mundo determinado.

La esencia del problema de conectar dimensiones diferentes la Ecuación de Euler lo resuelve de una forma elegante e impecable y, a su vez, imposible de modificar, pues tan sólo se basa en la probabilidad. La ecuación de Euler nos dice que hay que apelar siempre a la regla universal: la dualidad que los opuestos representan. Piensa, por ejemplo, que un cuadro, como al que hacía referencia Devlin y la realidad sólo son dos concepciones diferentes de una misma existencia, que el cuadro no es más que el reflejo en el mundo inmaterial de las ideas, una especie de holograma, un reflejo de lo que vemos en el mundo “real”.
Los únicos valores en el infinito matemático que cumplen siempre la regla de la dualidad son los valores áureos o sagrados. Son los únicos que tienen la capacidad de moverse entre dos planos diferentes de la realidad: el plano real y el plano irracional o imaginario. Podemos decir nuevamente que sus formas siempre han sido y serán. Pongamos un ejemplo para cada uno de ellos para entenderlo mejor.
La divina proporción es el único valor matemático, cuyo valor (precisamente) coincide con el valor que representa su inversa. Realmente toda una incoherencia. Las matemáticas ocultan esta coincidencia, no le dan relevancia y relegan a una de las soluciones al plano de lo inexistente. Tan sólo la divina proporción, por tanto, es capaz de situarse a medio camino, realmente de forma equilibrada, entre el plano de lo que es real matemáticamente hablando y el plano opuesto, o el plano del (aparentemente) inexistente mundo imaginario. La divina proporción representa con exquisita perfección el concepto subyacente al número i, o número imaginario, la posibilidad de ser capaz de situarse en dos planos diferentes de la realidad.
Con pi pasa exactamente lo mismo. Pi es el único valor en el infinito matemático que puede dar lugar a la esfera tridimensional, una construcción matemática que situamos en una cuarta dimensión imaginaria.
















 Totales: 75.877.469
Totales: 75.877.469 Conectados: 62
Conectados: 62