Este trabajo lo presenté  en el Carnaval de la Física en homenaje a Riemann.

Georg Friedrich Bernhard Riemann fue un matemático alemán que realizó contribuciones muy importantes al análisis y la geometría diferencial, algunas de las cuales allanaron el camino para el desarrollo más avanzado de la relatividad general. Hay personajes que parecen estar destinados al olvido a pesar, de sus muchas contribuciones alñsaber del mundo.

Recordemos aquí un extraño caso que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: la teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann que dio su célebre conferencia en la facultad de la Universidad de Göttingen en Alemania. Aquello fue como abrir de golpe todas las ventanas cerradas durante 2.000 años de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.

Su ensayo, de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del universo y su evolución mediante su asombrosa teoría de la relatividad general. Ciento treinta años después de su conferencia, los físicos utilizarían la geometría decadimensional para intentar unir todas las leyes del universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.

Contradictoriamente, Riemann era la persona menos indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria que arruinó su vida en la miseria abyecta y la tuberculosis.

Riemann nació en 1.826 en Hannover, Alemania, segundo de los seis hijos de un pobre pastor luterano que trabajó y se esforzó como humilde predicador para alimentar a su numerosa familia que, mal alimentada, tendrían una delicada salud que les llevaría a una temprana muerte. La madre de Riemann también murió antes de que sus hijos hubieran crecido.

A edad muy temprana, Riemann mostraba ya los rasgos que le hicieron famoso: increíble capacidad de cálculo que era el contrapunto a su gran timidez y temor a expresarse en público. Terriblemente apocado era objeto de bromas de otros niños, lo que le hizo recogerse aún más en un mundo matemático intensamente privado que le salvaba del mundo hostil exterior.

Para complacer a su padre, Riemann se propuso hacerse estudiante de teología, obtener un puesto remunerado como pastor y ayudar a su familia.  En la escuela secundaria estudió la Biblia con intensidad, pero sus pensamientos volvían siempre a las matemáticas. Aprendía tan rápidamente que siempre estaba por delante de los conocimientos de sus instructores, que encontraron imposible mantenerse a su altura. Finalmente, el director de la escuela dio a Riemann un pesado libro para mantenerle ocupado. El libro era la Teoría de números de Adrien-Marie Legendre, una voluminosa obra maestra de 859 páginas, el tratado más avanzado del mundo sobre el difícil tema de la teoría de números. Riemann devoró el libro en seis días.

Portada de la décimo primera edición de los “Eléments de Geométrie” de A. M. Legendre (1794)

Cuando el director le preguntó:

“¿hasta dónde has leído?”, el joven Riemann respondió: “este es un libro maravilloso. Ya me lo sé todo”.

Sin creerse realmente la afirmación de su pupilo, el director le planteó varios meses después cuestiones complejas sobre el contenido del libro, que Riemann respondió correctamente.

Con mil sacrificios, el padre de Riemann consiguió reunir los fondos necesarios para que a los 19 años pudiera acudir a la Universidad de Göttingen, donde encontró a Carl Friedrich Gauss, el aclamado por todos “Príncipe de las Matemáticas”, uno de los mayores matemáticos de todos los tiempos. Incluso hoy, si hacemos una selección por expertos para distinguir a los matemáticos más grandes de la Historia, aparecerá indudablemente Euclides, Arquímedes, Newton y Gauss.

La ciencia la construyen las personas, pero también es interesante prestar atención a los lugares en los que se desarrolla. Gotinga, en Alemania, albergó uno de los centros más importantes para las matemáticas, del que formaron parte Gauss, Riemann, Klein, Hilbert, Minkowski, Heisenberg, Born, Jordan, Wigner, Teller, Von Neuman y muchos otros grandes nombres de la historia de la ciencia. Lamentablemente, la guerra, el odio y la barbarie redujeron el lugar a un viejo recuerdo. Fernando Jiménez Alburquerque, investigador postdoctoral de la Technische Universität München (Alemania), dedica la siguiente entrada a éste santuario del saber.

Los estudios de Riemann no fueron un camino de rosas precisamente.  Alemania sacudida por disturbios, manifestaciones y levantamientos, fue reclutado en el cuerpo de estudiantes para proteger al rey en el palacio real de Berlín y sus estudios quedaron interrumpidos.

En aquel ambiente, el problema que captó el interés de Riemann fue el colapso que, según el pensaba, suponía la geometría euclidiana, que mantiene que el espacio es tridimensional y “plano” (en el espacio plano, la distancia más corta entre dos puntos es la línea recta; lo que descarta la posibilidad de que el espacio pueda estar curvado, como en una esfera).

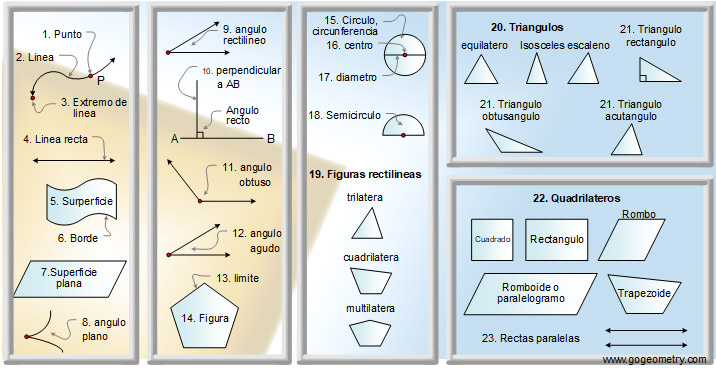
Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna parte veía Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita. Riemann, ante aquella realidad, se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos, descubrió él, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.

Euclides nos habló de la obviedad de que un punto no tiene dimensión.  Una línea tiene una dimensión: longitud. Un plano tiene dos dimensiones: longitud y anchura. Un sólido tiene tres dimensiones: longitud, anchura y altura. Y allí se detiene. Nada tiene cuatro dimensiones, incluso Aristóteles afirmó que la cuarta dimensión era imposible. En Sobre el cielo, escribió: “La línea tiene magnitud en una dirección, el plano en dos direcciones, y el sólido en tres direcciones, y más allá de éstas no hay otra magnitud porque los tres son todas”. Además, en el año 150 d. C. el astrónomo Ptolomeo de Alejandría fue más allá de Aristóteles y ofreció, en su libro sobre la distancia, la primera “demostración” ingeniosa de que la cuarta dimensión es imposible.

En realidad, lo único que Ptolomeo demostraba era que era imposible visualizar la cuarta dimensión con nuestros cerebros tridimensionales (de hecho, hoy sabemos que muchos objetos matemáticos no pueden ser visualizados, aunque puede demostrarse que en realidad, existen). Ptolomeo puede pasar a la Historia como el hombre que se opuso a dos grandes ideas en la ciencia: el sistema solar heliocéntrico y la cuarta dimensión.

La ruptura decisiva con la geometría euclidiana llegó cuando Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.

Riemann desarrolló su teoría de dimensiones más altas.

Finalmente, cuando hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, esta fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante dos milenios.

Riemann creó su tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a² + b² = c².  El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).

¿Que habría podido hacer Einstein sin el Tnsor métrico de Riemann?

El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de supergravedad, supersimetría y, finalmente, las supercuerdas.

Una corredora que se llama imaginación deambula por nuestras mentes y, en el momento menos esperado… ¡Surge la Luz! Así podemos decir que ocurrió en el caso de Riemann que, para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio cuenta de que allí estaba la clave para resolver su problema.  Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la relatividad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc². La reinterpretación física de la famosa conferencia de Riemann se denomina ahora relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.

No sería justo reconocer aquí que Riemann, tiene mucho que ver en ese gran logro de Einstein (Relatividad General), y de toda la física en lo que a la geometría de espacios curvos se refiere…

emilio silvera

 « ¡La Vida! ¿En cuántos planetas estará instalada?

trabajo fue presentado en el Carnaval de la Física en homenaje a Riemann.

Recordemos aquí un extraño caso que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: la teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann que dio su célebre conferencia en la facultad de la Universidad de Göttingen en Alemania. Aquello fue como abrir de golpe todas las ventanas cerradas 2.000 años de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.

Su ensayo, de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del universo y su evolución mediante su asombrosa teoría de la relatividad general. Ciento treinta años después de su conferencia, los físicos utilizarían la geometría decadimensional para intentar unir todas las leyes del universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.

Contradictoriamente, Riemann era la persona indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria que arruinó su vida en la miseria abyecta y la tuberculosis.

Riemann nació en 1.826 en Hannover, Alemania, segundo de los seis hijos de un pobre pastor luterano que trabajó y se esforzó como humilde predicador para alimentar a su numerosa familia que, mal alimentada, tendrían una delicada salud que les llevaría a una temprana muerte. La madre de Riemann también murió de que sus hijos hubieran crecido.

A edad muy temprana, Riemann mostraba ya los rasgos que le hicieron famoso: increíble capacidad de cálculo que era el contrapunto a su gran timidez y temor a expresarse en público. Terriblemente apocado era objeto de bromas de otros niños, lo que le hizo recogerse aún más en un mundo matemático intensamente privado que le salvaba del mundo hostil exterior.

Para complacer a su padre, Riemann se propuso hacerse estudiante de teología, obtener un puesto remunerado pastor y ayudar a su familia.  En la escuela secundaria estudió la Biblia con intensidad, pero sus pensamientos volvían siempre a las matemáticas. Aprendía tan rápidamente que siempre estaba por delante de los conocimientos de sus instructores, que encontraron imposible mantenerse a su altura. Finalmente, el director de la escuela dio a Riemann un pesado libro para mantenerle ocupado. El libro era la Teoría de números de Adrien-Marie Legendre, una voluminosa obra maestra de 859 páginas, el tratado más avanzado del mundo sobre el difícil tema de la teoría de números. Riemann devoró el libro en seis días.

Cuando el director le preguntó: “¿ dónde has leído?”, el joven Riemann respondió: “ es un libro maravilloso. Ya me lo sé todo”.

Sin creerse realmente la afirmación de su pupilo, el director le planteó varios meses después cuestiones complejas sobre el contenido del libro, que Riemann respondió correctamente.

Con mil sacrificios, el padre de Riemann consiguió reunir los fondos necesarios que a los 19 años pudiera acudir a la Universidad de Göttingen, donde encontró a Carl Friedrich Gauss, el aclamado por todos “Príncipe de las Matemáticas”, uno de los mayores matemáticos de todos los tiempos. Incluso hoy, si hacemos una selección por expertos para distinguir a los matemáticos más grandes de la Historia, aparecerá indudablemente Euclides, Arquímedes, Newton y Gauss.

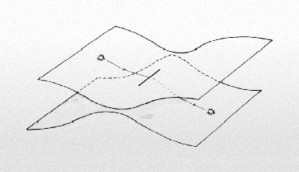
Gráfico: Un corte de Riemann, con dos hojas conectadas a lo largo de una línea.  Si caminamos alrededor del corte, permanecemos dentro del mismo espacio.  Pero si atravesamos el corte, pasamos de una hoja a la continua.  es una superficie múltiplemente conexa

Los estudios de Riemann no fueron un camino de rosas precisamente.  Alemania sacudida por disturbios, manifestaciones y levantamientos, fue reclutado en el cuerpo de estudiantes para proteger al rey en el palacio real de Berlín y sus estudios quedaron interrumpidos.

En aquel ambiente, el problema que captó el interés de Riemann fue el colapso que, según el pensaba, suponía la geometría euclidiana, que mantiene que el espacio es tridimensional y “plano” (en el espacio plano, la distancia más corta dos puntos es la línea recta; lo que descarta la posibilidad de que el espacio pueda estar curvado, como en una esfera).

Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna veía Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita. Riemann, ante aquella realidad, se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos, descubrió él, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.

Euclides nos habló de la obviedad de que un punto no tiene dimensión.  Una línea tiene una dimensión: longitud. Un plano tiene dos dimensiones: longitud y anchura. Un sólido tiene tres dimensiones: longitud, anchura y altura. Y allí se detiene. Nada tiene cuatro dimensiones, incluso Aristóteles afirmó que la cuarta dimensión era imposible. En Sobre el cielo, escribió: “La línea tiene magnitud en una dirección, el plano en dos direcciones, y el sólido en tres direcciones, y más allá de éstas no hay otra magnitud porque los tres son todas”. Además, en el año 150 d. C. el astrónomo Ptolomeo de Alejandría fue más allá de Aristóteles y ofreció, en su libro sobre la distancia, la primera “demostración” ingeniosa de que la cuarta dimensión es imposible.

En realidad, lo único que Ptolomeo demostraba era que era imposible visualizar la cuarta dimensión con nuestros cerebros tridimensionales (de hecho, hoy sabemos que muchos objetos matemáticos no pueden ser visualizados, aunque demostrarse que en realidad, existen). Ptolomeo puede pasar a la Historia como el hombre que se opuso a dos grandes ideas en la ciencia: el sistema solar heliocéntrico y la cuarta dimensión.

La ruptura decisiva con la geometría euclidiana llegó Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.

Riemann desarrolló su teoría de dimensiones más altas.

Finalmente, cuando hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante dos milenios.

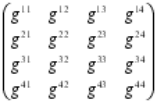
El tensor de Riemann contiene toda la información necesaria poder describir un espacio curvo en N-dimensiones. Se necesita dieciséis números para describir el tensor métrico en un espacio tetradimensional. Estos números pueden disponerse en una matriz cuadrada (seis de dichos números son realmente redundantes; de modo que el tensor métrico diez números independientes).

Riemann creó su tensor métrico que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a² + b² = c².  El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).

El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de supergravedad, supersimetría y, finalmente, las supercuerdas.

Para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio de que allí estaba la clave para resolver su problema.  Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la relatividad general. fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc². La reinterpretación física de la famosa conferencia de Riemann se denomina relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.

No sería justo reconocer aquí que Riemann, tiene mucho que ver en ese gran logro de Einstein (Relatividad General), y de toda la física en lo que a la geometría de espacios curvos se refiere..

emilio silvera